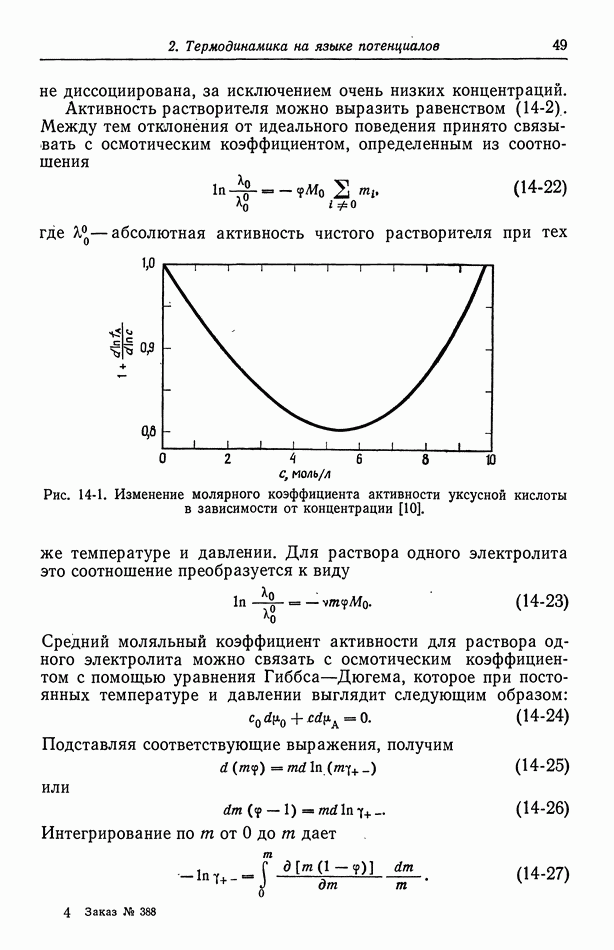
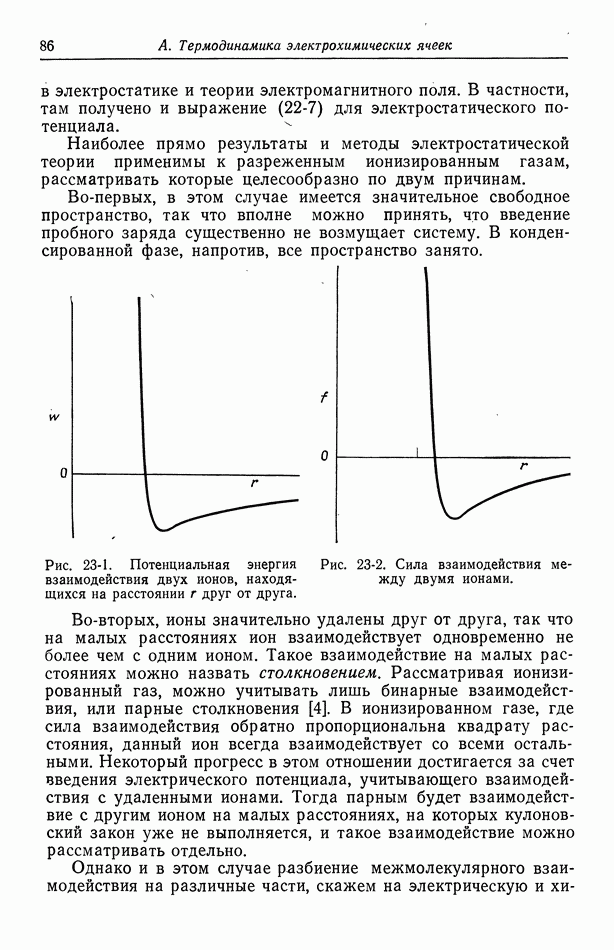
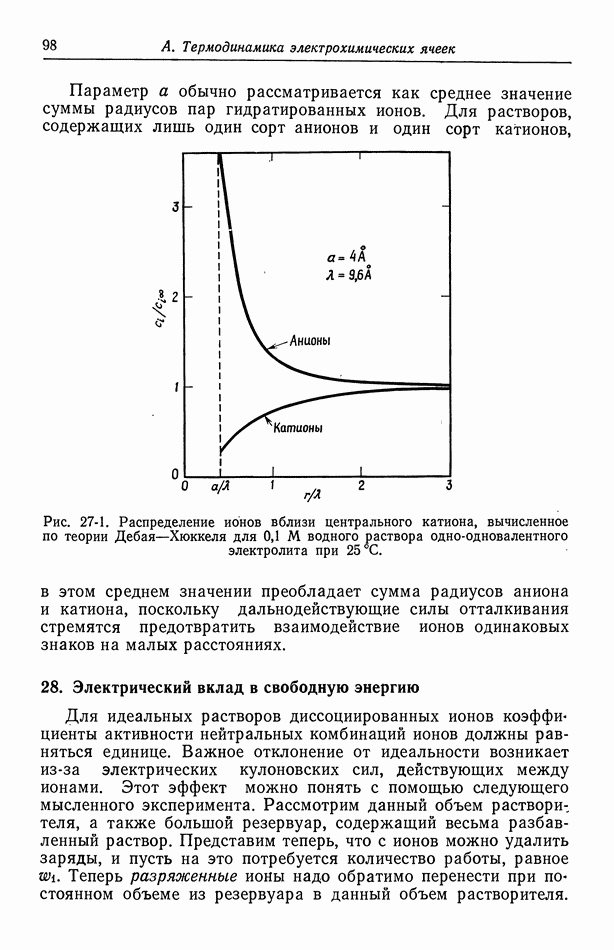
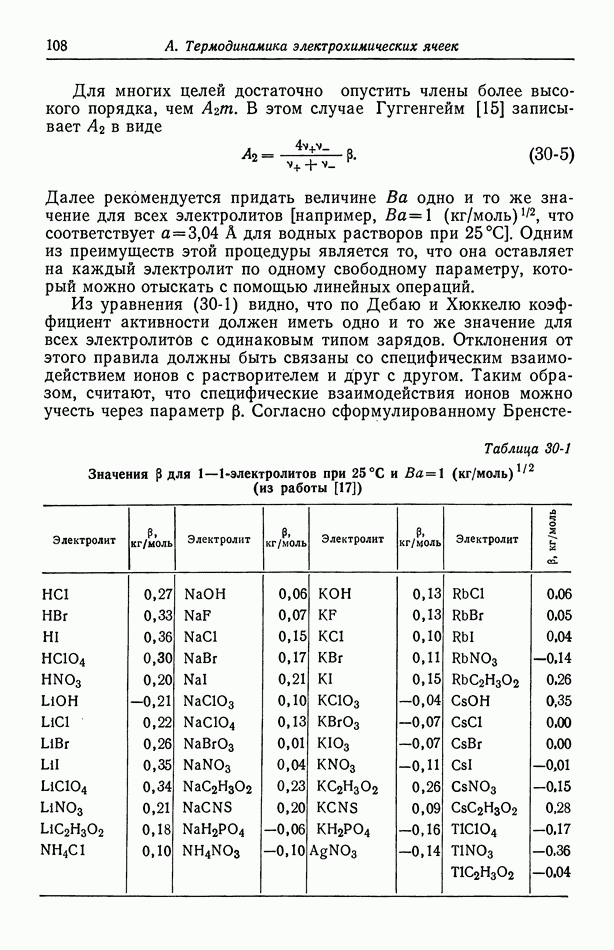
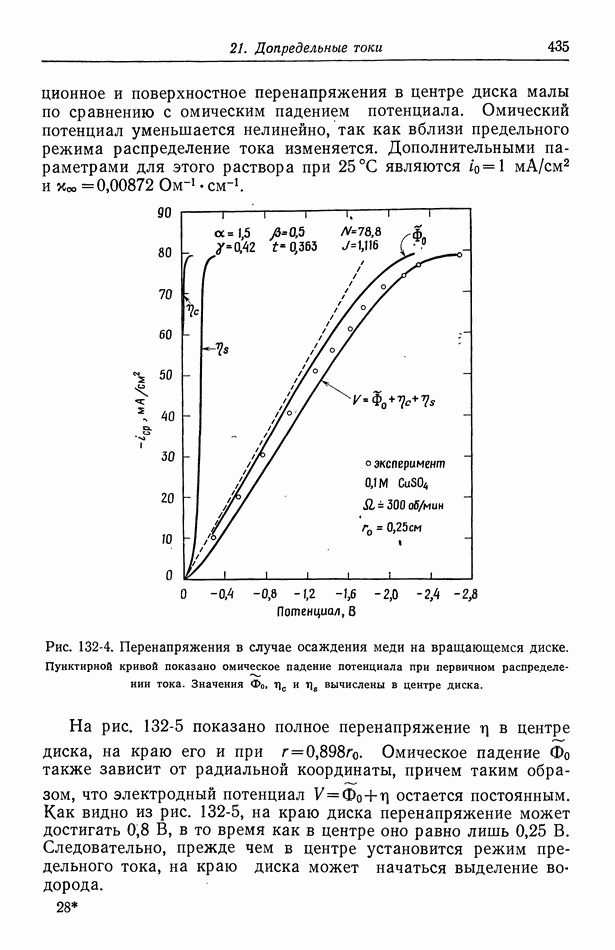
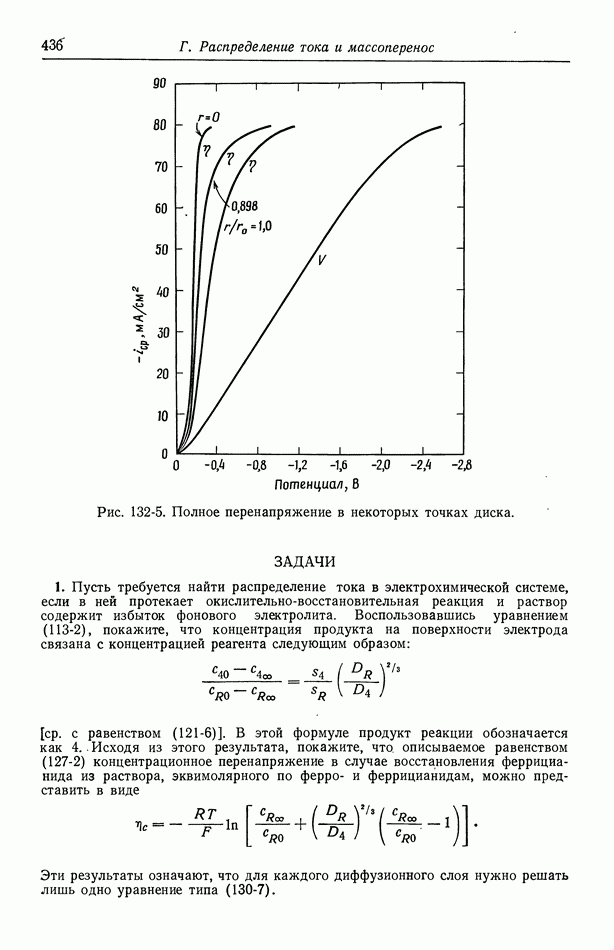
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
В настоящем разделе будут рассматриваться ячейки с двумя электролитами в растворе. Предполагается, что один из электролитов имеет почти однородную концентрацию, в то время как концентрация другого изменяется от точки к точке. Ячейка такого типа обсуждалась в разд. 15:

В этой ячейке переходная область означает область переменной концентрации  . Хлорид лития имеет почти однородную концентрацию, хотя она может слегка изменяться вблизи твердого хлорида таллия.
. Хлорид лития имеет почти однородную концентрацию, хотя она может слегка изменяться вблизи твердого хлорида таллия.
Потенциал этой ячейки выражается в виде

Так же как и в разд. 17, в это уравнение входит разность электрохимических потенциалов ионного компонента, взятых в двух точках раствора. Однако в данном случае эта разность рассматривается как небольшой дополнительный член в выражении, которое в прочих ситуациях связывает потенциал ячейки с термодинамическими величинами, тогда как в разд. 17 такие разности давали существенный вклад в потенциал ячейки. Эти дополнительные члены оценены в работе [4], результатами которой мы здесь пользуемся.
Равенство (15-15), которое мы еще раз воспроизведем,

позволяет найти величину этой разности. Таким образом,

В противоположность ситуации, имевшей место в разд. 17, этот
интеграл нельзя точно вычислить, не располагая детальной информацией о концентрационных профилях в области контакта, поскольку числа переноса и химические потенциалы зависят от концентраций  Между тем мы хотим лишь найти величину члена, которым обычно пренебрегают, для чего воспользуемся приближениями, обычными для разбавленных растворов, и будем считать подвижности ионов равными друг другу. Для чисел переноса эти приближения дают
Между тем мы хотим лишь найти величину члена, которым обычно пренебрегают, для чего воспользуемся приближениями, обычными для разбавленных растворов, и будем считать подвижности ионов равными друг другу. Для чисел переноса эти приближения дают

Из уравнения (14-10) можно найти изменения химического потенциала хлорида таллия:

Аналогичное выражение можно записать для хлорида лития. Подставляя эти равенства в уравнение (18-3), получаем

Для разбавленных растворов коэффициенты активности можно выразить формулой Дебая-Хюккеля (разд. 28)

где а — постоянная Дебая-Хюккеля, равная  для воды и 2,57 для диметилсульфоксида [4] при
для воды и 2,57 для диметилсульфоксида [4] при  В приближении Дебая-Хюккеля для электролитов с одинаковым типом зарядов коэффициенты активности одни и те же и зависят лишь от ионной силы
В приближении Дебая-Хюккеля для электролитов с одинаковым типом зарядов коэффициенты активности одни и те же и зависят лишь от ионной силы  равной здесь
равной здесь 
Теперь уравнение (18-7) приобретает вид

а интегрирование позволяет переписать уравнение (18-4) в виде

где  моляльность хлорида лития в фазе
моляльность хлорида лития в фазе 
Для определения коэффициентов активности и стандартных потенциалов при использовании ячеек такого типа измерения проводят при низких концентрациях  и результаты экстраполируют к бесконечному разбавлению этого электролита, тем самым устанавливая стандартное состояние, определяемое условием (14-5). Ясно, что измерения при низких концентрациях
и результаты экстраполируют к бесконечному разбавлению этого электролита, тем самым устанавливая стандартное состояние, определяемое условием (14-5). Ясно, что измерения при низких концентрациях  чрезвычайно важны с точки зрения термодинамики. Многие
чрезвычайно важны с точки зрения термодинамики. Многие
ошибки при этих измерениях обусловлены рассматриваемыми здесь жидкостными контактами. Изменение концентрации от раствора  можно приближенно выразить следующим образом:
можно приближенно выразить следующим образом:

где  произведение растворимости хлорида таллия. Чтобы точность измеряемого потенциала ячейки была не менее
произведение растворимости хлорида таллия. Чтобы точность измеряемого потенциала ячейки была не менее  при
при  произведение растворимости слаборастворимой соли должно быть меньше примерно
произведение растворимости слаборастворимой соли должно быть меньше примерно 
Другой ячейкой этого типа, содержащей водный раствор, является

где растворы  различаются в основном тем, что раствор
различаются в основном тем, что раствор  насыщен хлоридом серебра. Потенциал ячейки определяется выражением
насыщен хлоридом серебра. Потенциал ячейки определяется выражением

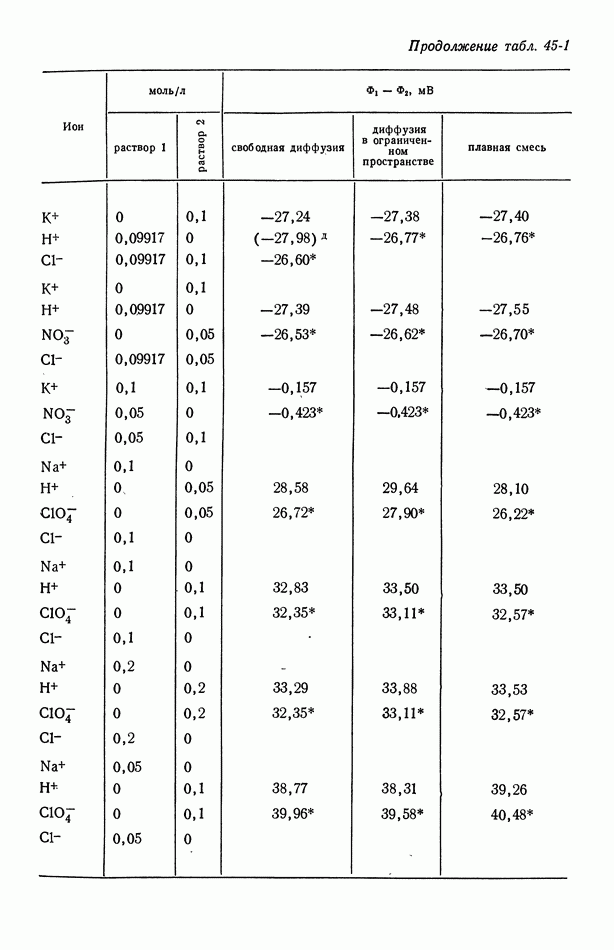
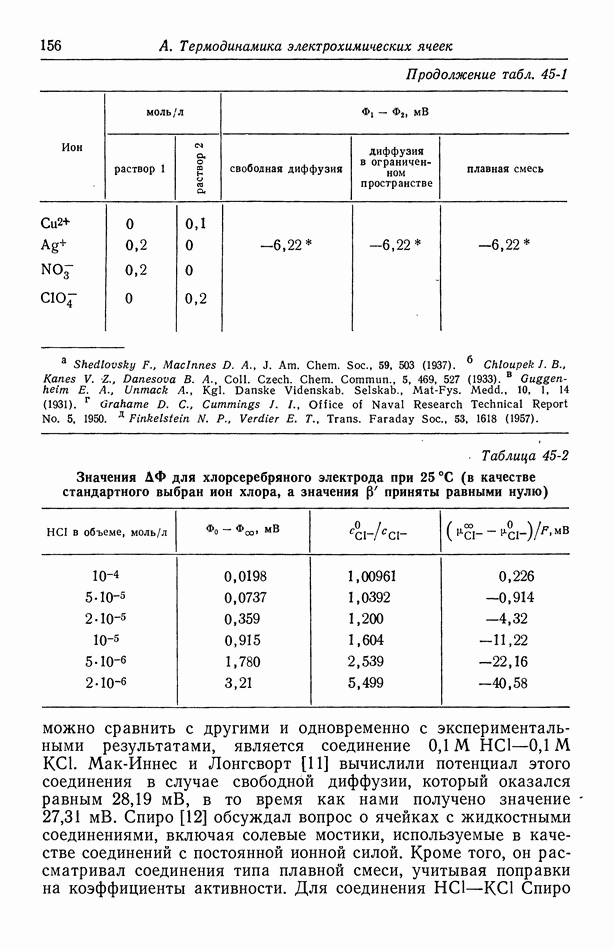
В табл. 18-1 представлены значения  для
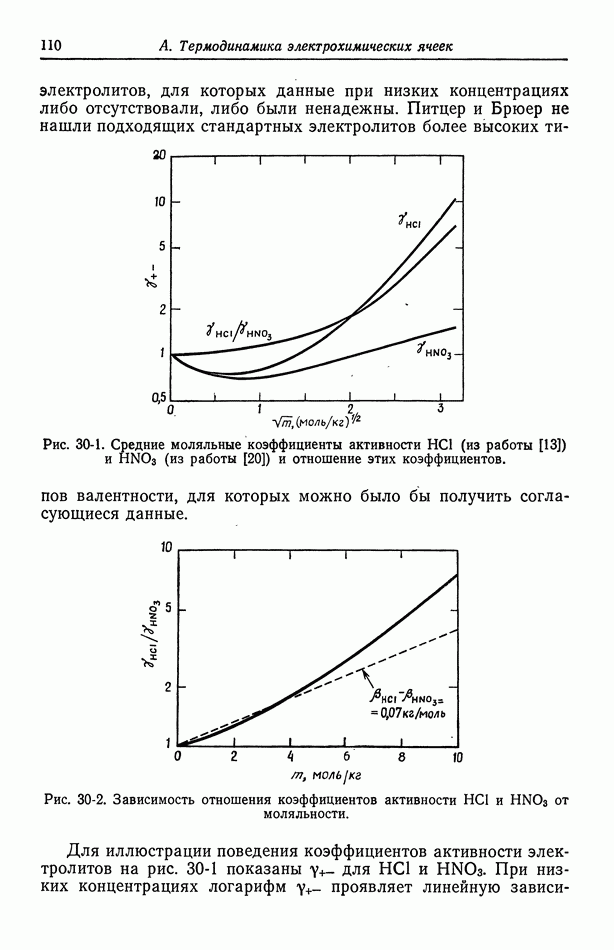
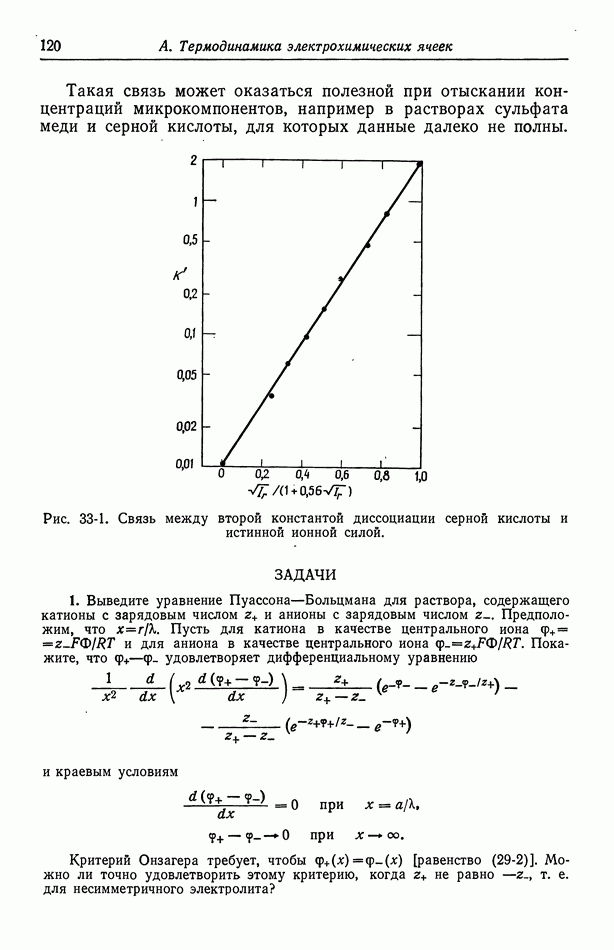
для  рассчитанные методом [5], который будет изложен в следующей главе. Для сравнения приведены значения, полученные из уравнений (18-10) и (18-11). При практически используемых концентрациях в неводных системах, исследованных в работе [4], эффект гораздо больше, поскольку он становится заметным при объемных концентрациях порядка корня квадратного из произведения растворимости.
рассчитанные методом [5], который будет изложен в следующей главе. Для сравнения приведены значения, полученные из уравнений (18-10) и (18-11). При практически используемых концентрациях в неводных системах, исследованных в работе [4], эффект гораздо больше, поскольку он становится заметным при объемных концентрациях порядка корня квадратного из произведения растворимости.
Влияние слаборастворимой соли на потенциал ячейки, рассмотренное выше, при анализе ячеек (17-21) и (17-23) не учитывалось.
Согласно названию данного раздела, логически мы могли бы отнести сюда и ячейки, содержащие инертный электролит почти однородной концентрации, где реагирующий на электродах компонент присутствует в гораздо меньших концентрациях. Примером является ячейка

Таблица 18-1 (см. скан)
Влияние растворимости хлорида серебра при убывающих значениях объемной концентрации 
в которой концентрация  практически однородна. В переходной области переменными являются концентрации как
практически однородна. В переходной области переменными являются концентрации как  так и
так и  Потенциал ячейки можно выразить в виде
Потенциал ячейки можно выразить в виде

в предположении, что  не участвует в установлении межфазного равновесия на электродах и лишь изменяет химические потенциалы других электролитов в растворах.
не участвует в установлении межфазного равновесия на электродах и лишь изменяет химические потенциалы других электролитов в растворах.
В тех же приближениях, что использовались выше, можно написать

Таким образом, изменения потенциала ячейки в основном обусловлены изменениями концентраций ионов серебра и натрия. Если ионная сила достаточно однородна, то последним членом, связанным с поправками к коэффициенту активности, можно пренебречь. Заметим, что отношение  определено однозначно в соответствии с соображениями разд. 14.
определено однозначно в соответствии с соображениями разд. 14.
Если коэффициентами активности пренебречь, то равенство (18-16) превращается в одну из форм так называемого уравнения Нернста, связывающего потенциалы ячеек с логарифмами ионных концентраций. Часто его записывают через молярные концентрации, как, например, сделано в соотношении (10-1). Уравнение Нернста можно использовать в том случае, когда имеется избыток инертного электролита почти однородной концентрации, а реагирующие компоненты присутствуют в гораздо меньших концентрациях. Оценкой возникающих при этом ошибок мы займемся в гл. 6.
Потенциалы ячеек часто зависят от транспортных свойств растворов электролитов, а также от их термодинамических свойств. Кроме того, они зависят от детальной формы концентрационных профилей в области контакта. При определенных условиях, рассмотренных в данном разделе, потенциал ячейки можно приближенно выразить через одни лишь термодинамические характеристики. Являются ли эти приближения достаточно точными, зависит от конкретных целей расчета.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
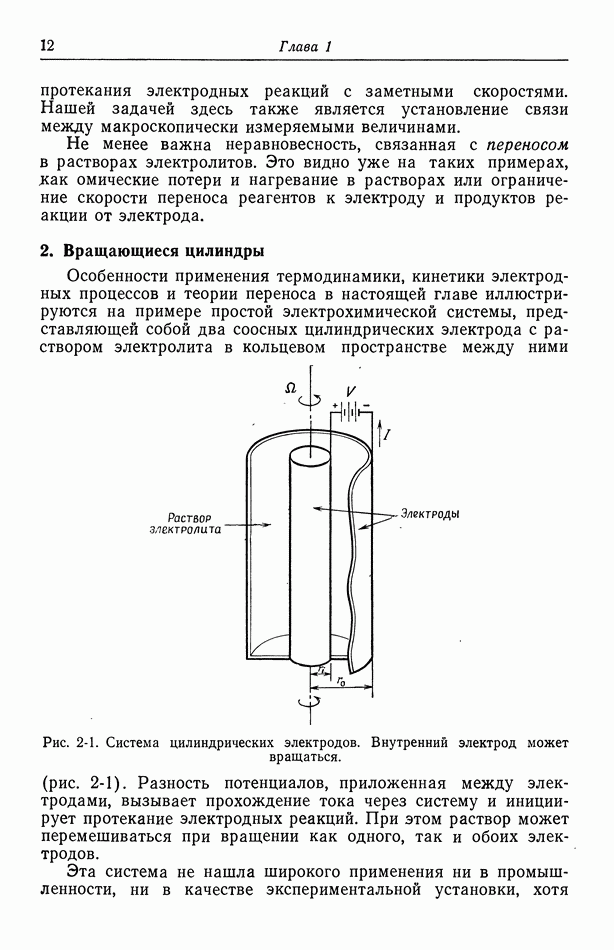
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
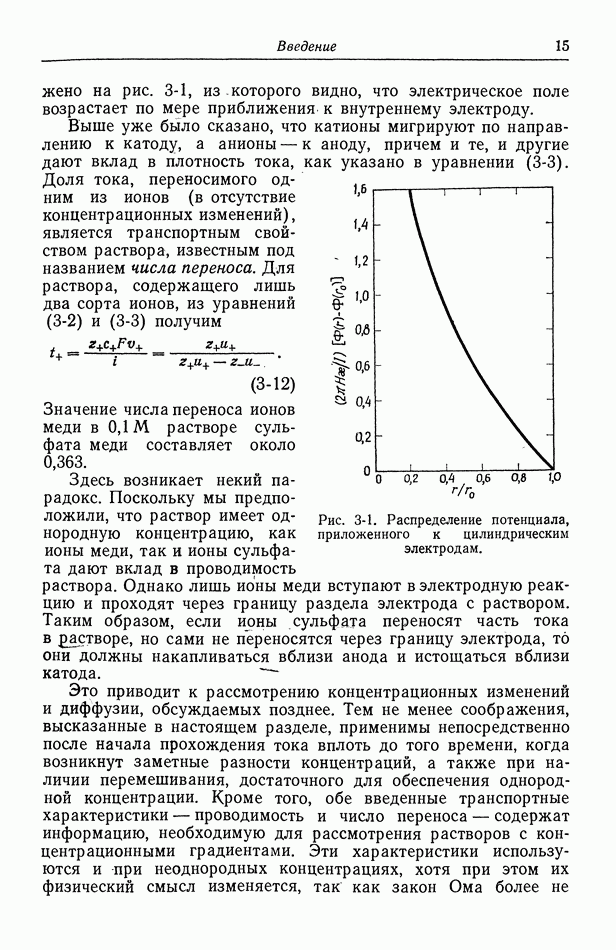
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
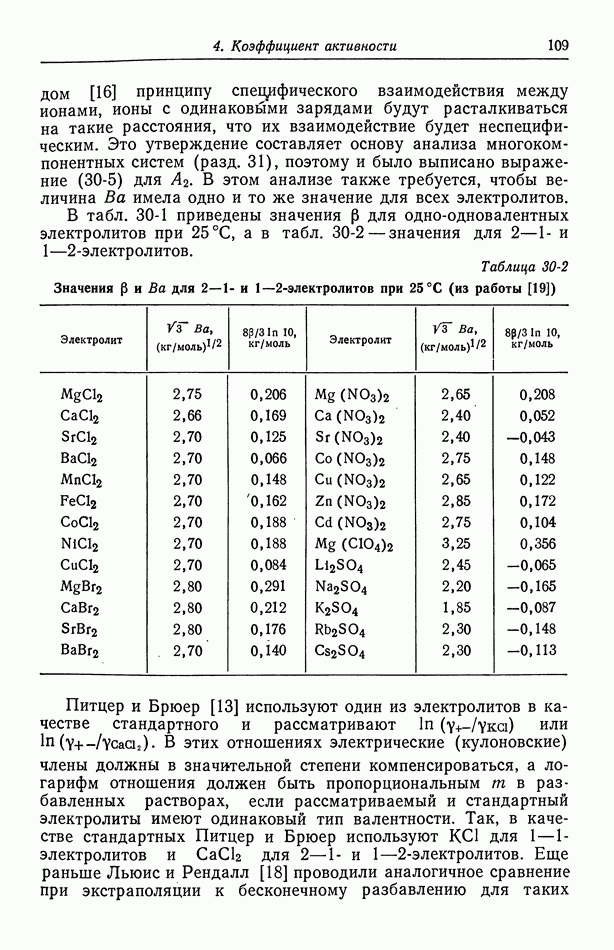
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
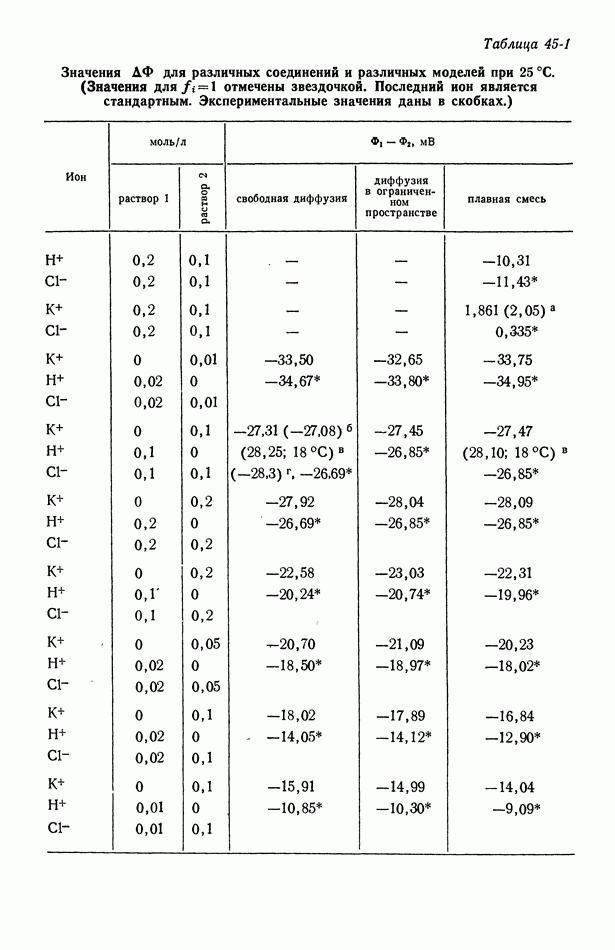
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
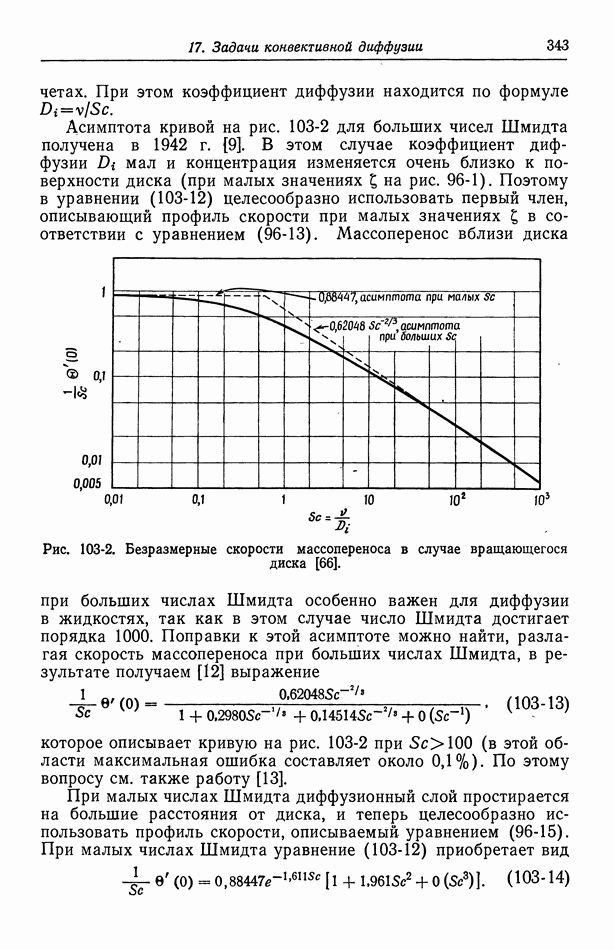
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
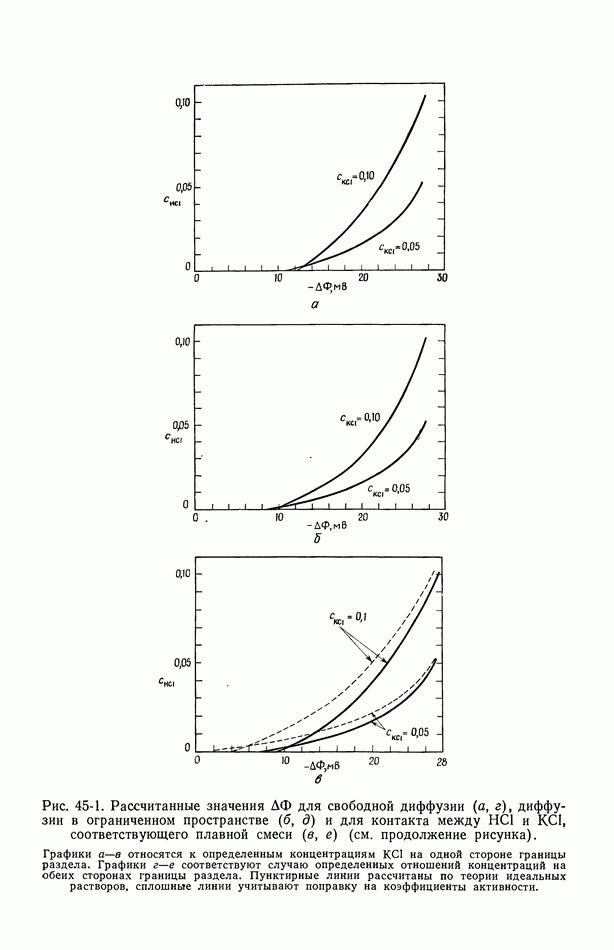
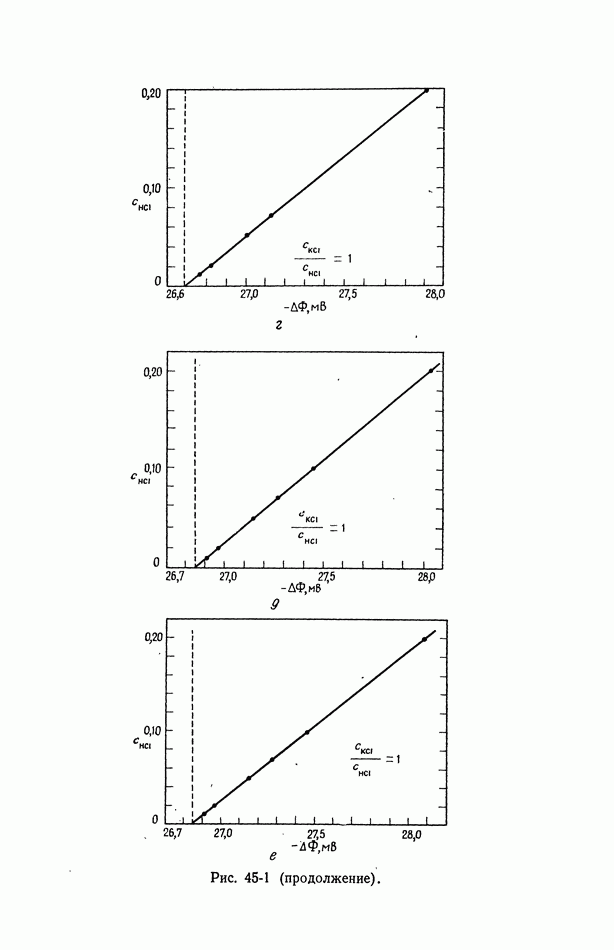
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
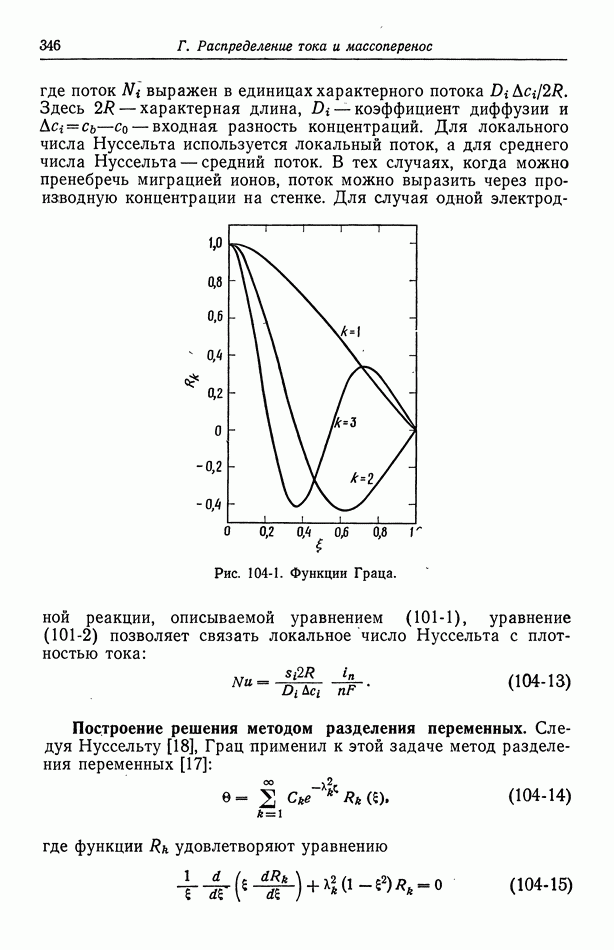
- 48. Мембранные потенциалы
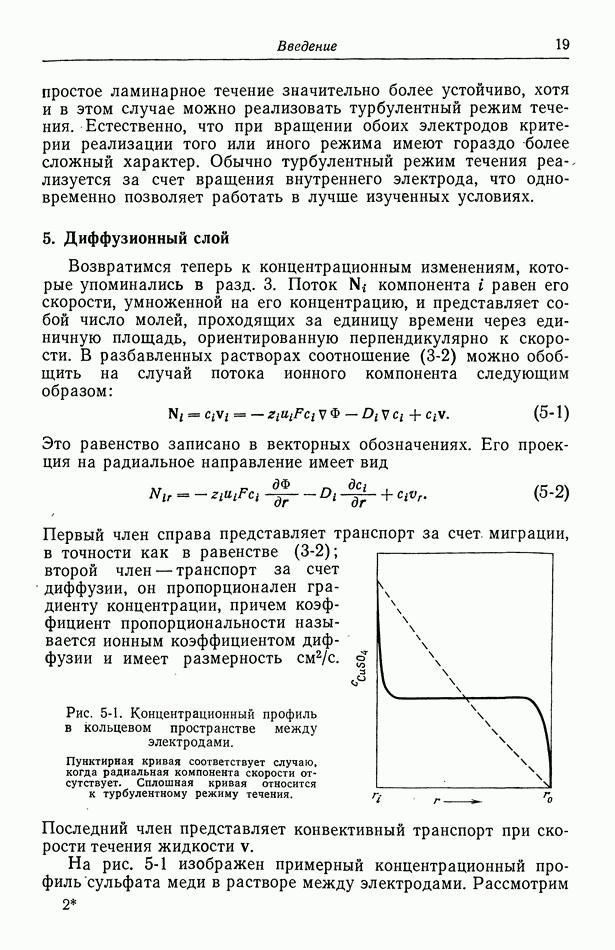
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
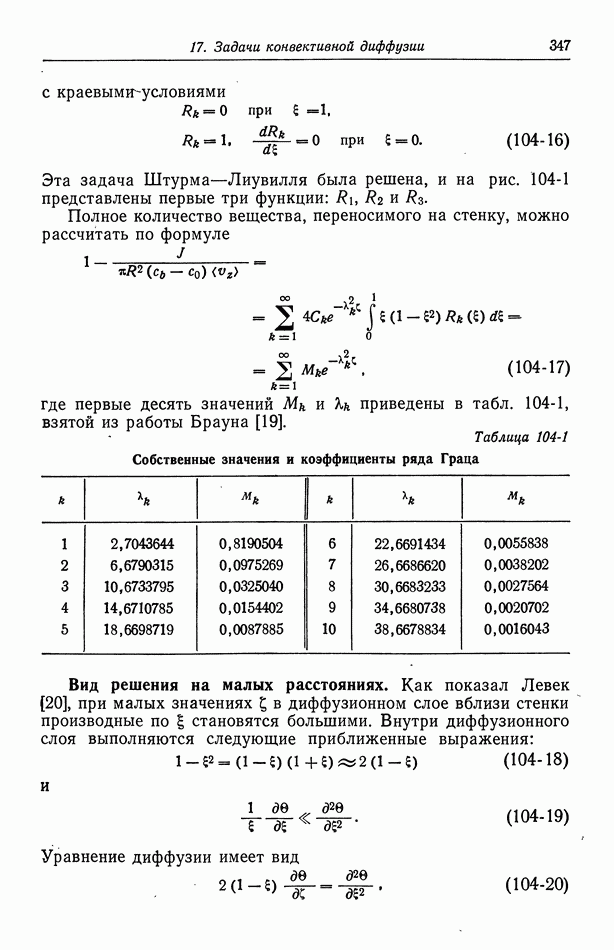
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
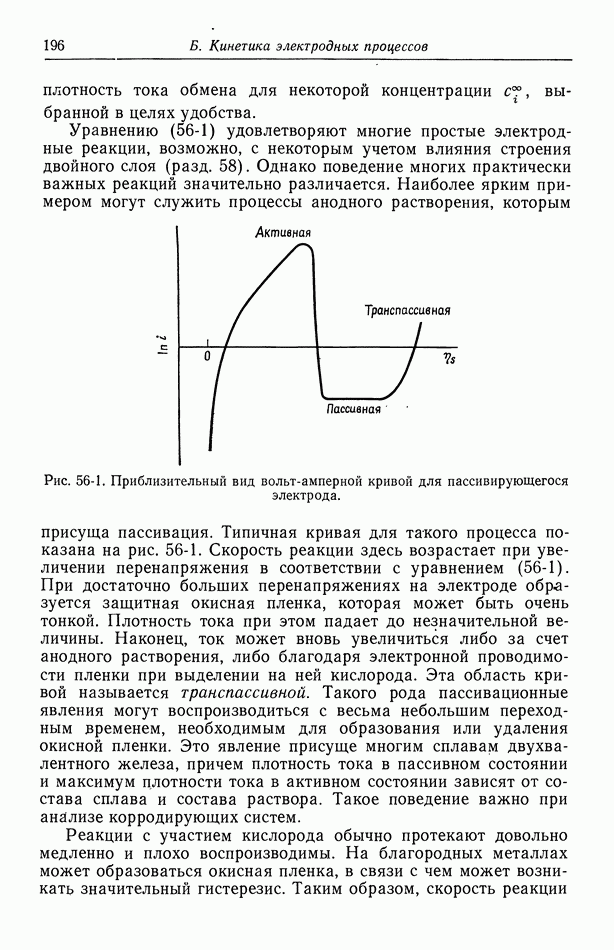
- 56. Зависимость плотности тока от поверхностного перенапряжения
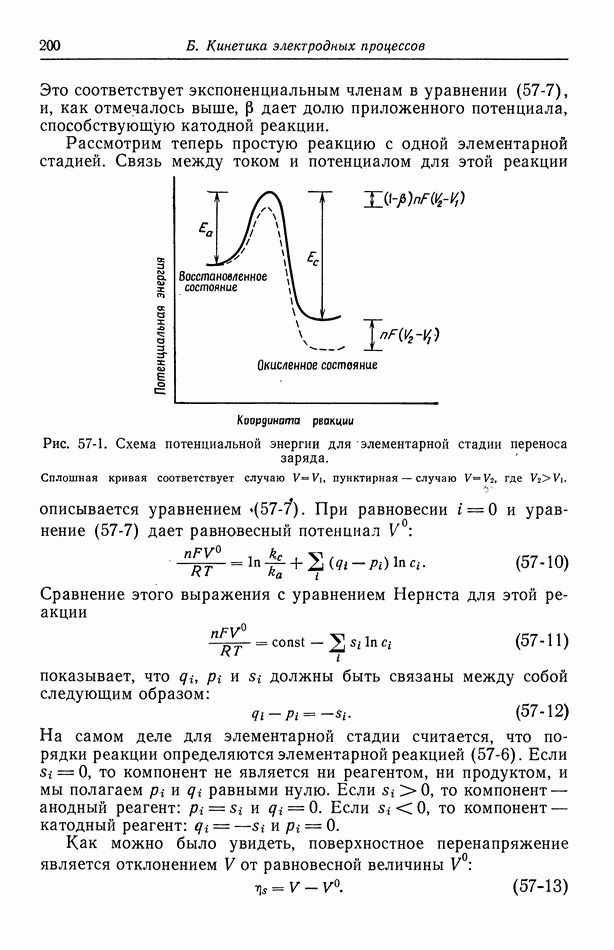
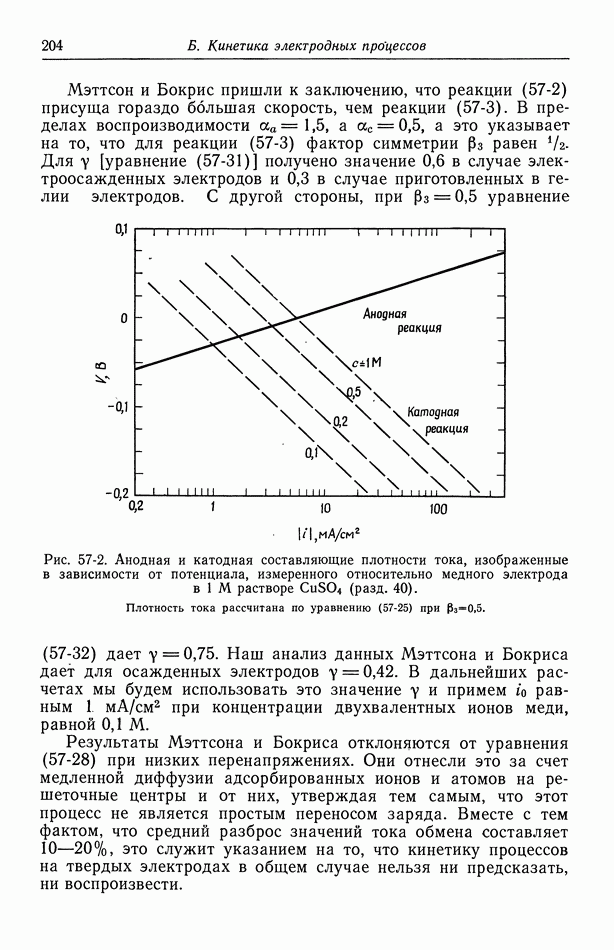
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
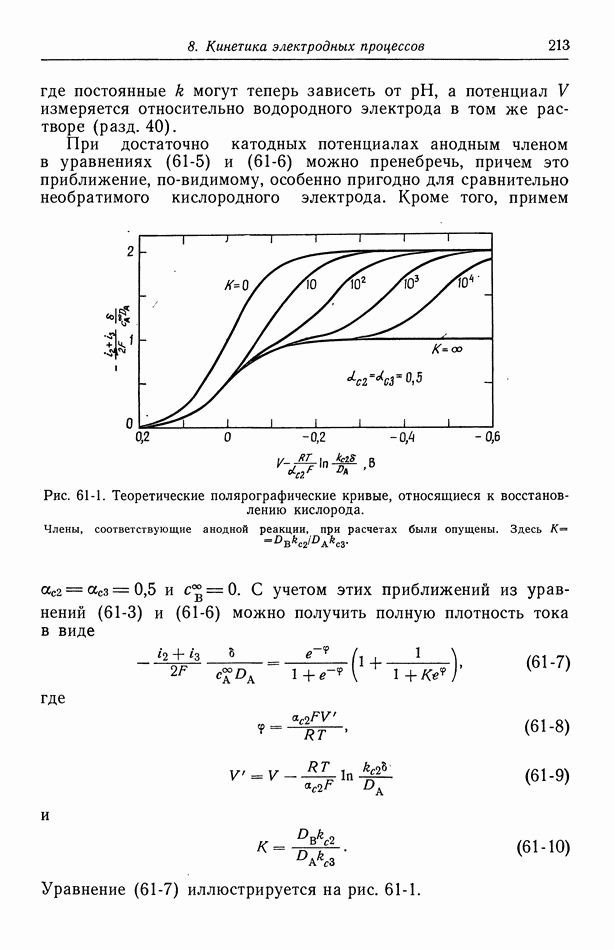
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
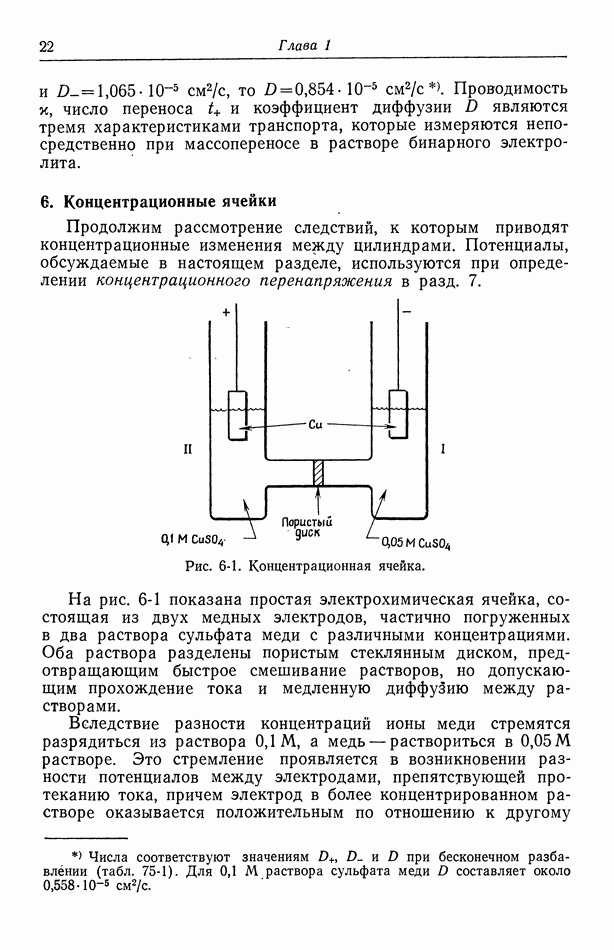
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
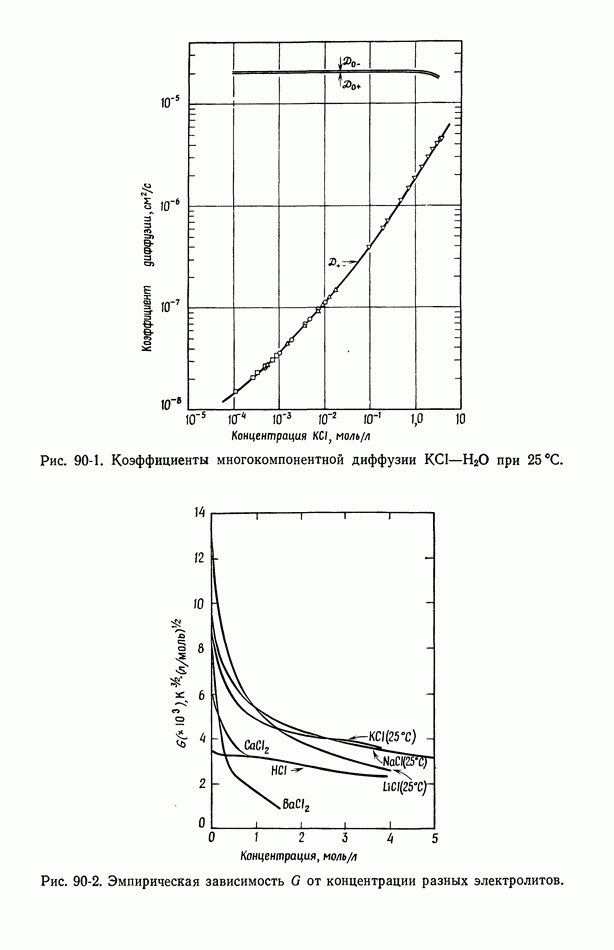
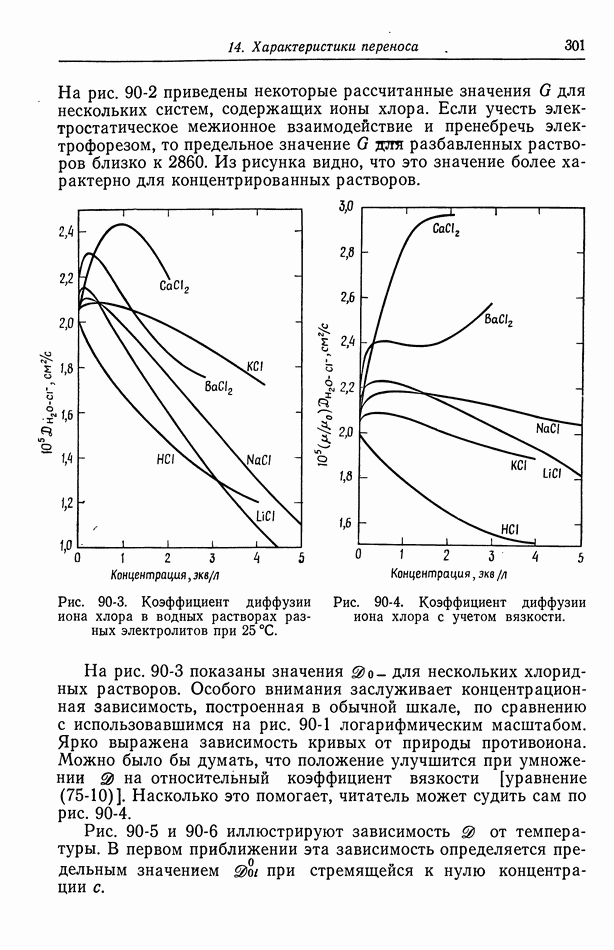
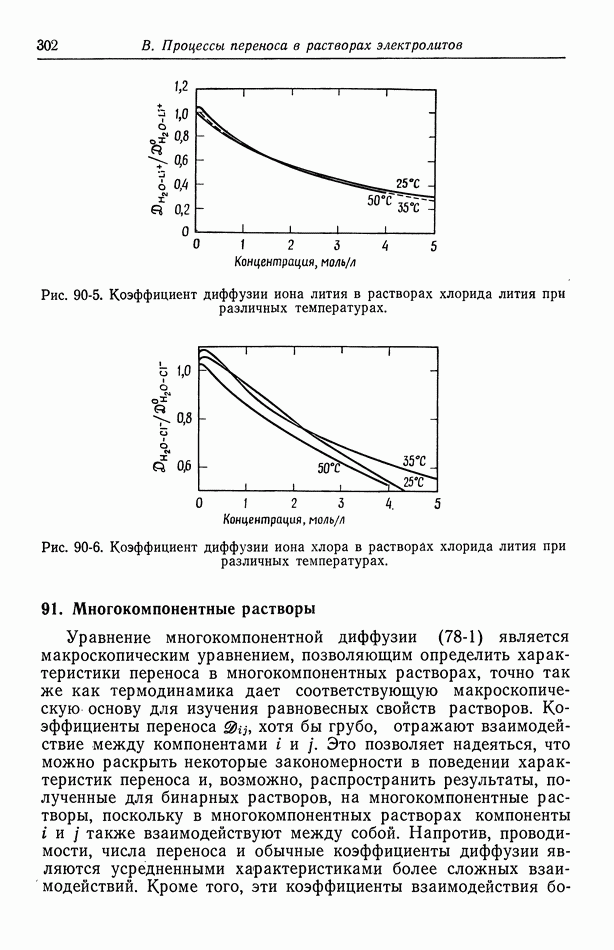
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
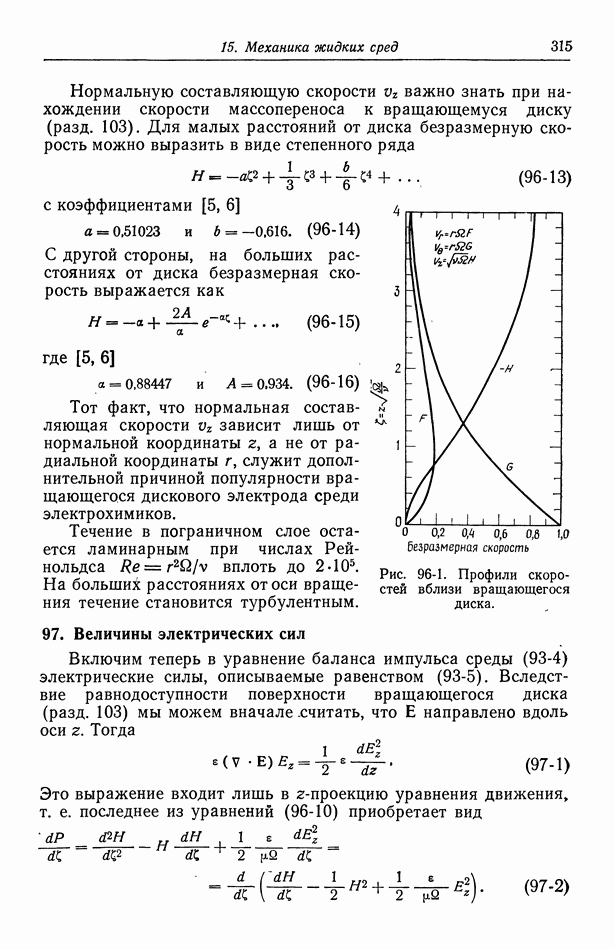
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
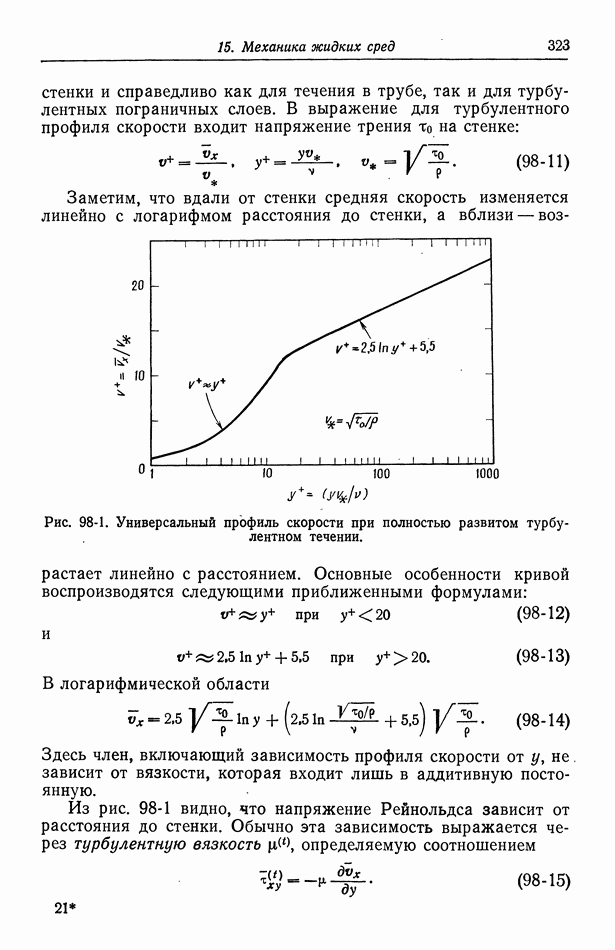
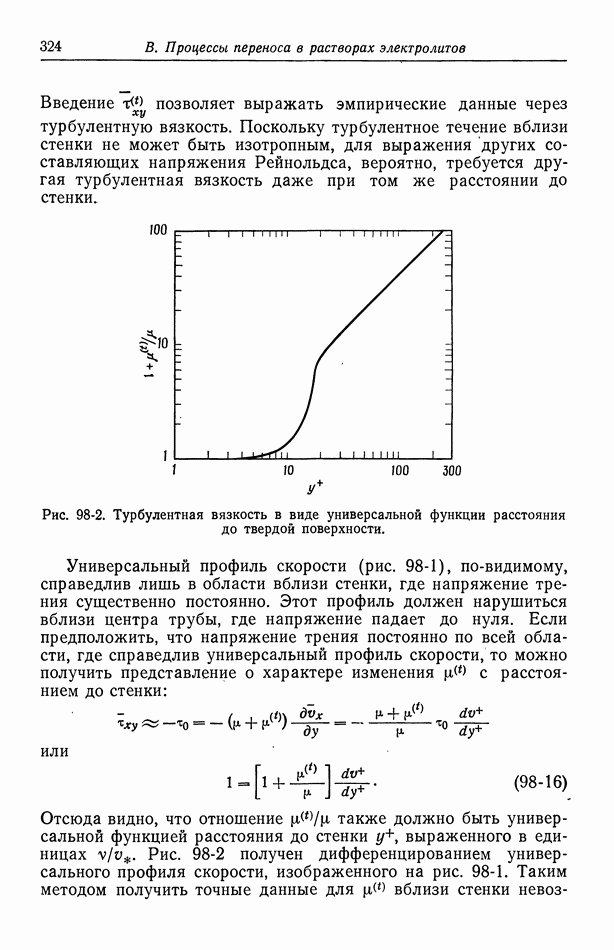
- 98. Турбулентное течение
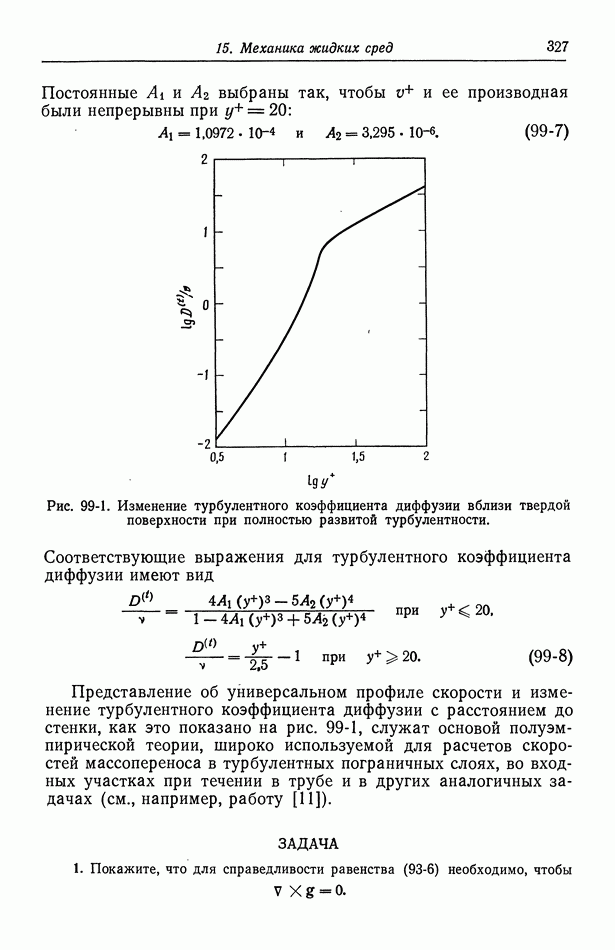
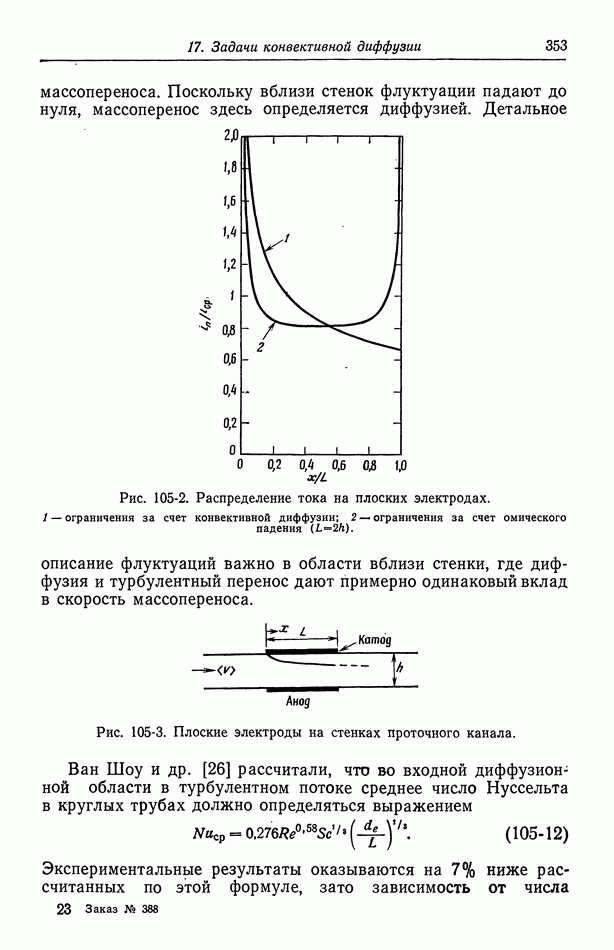
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
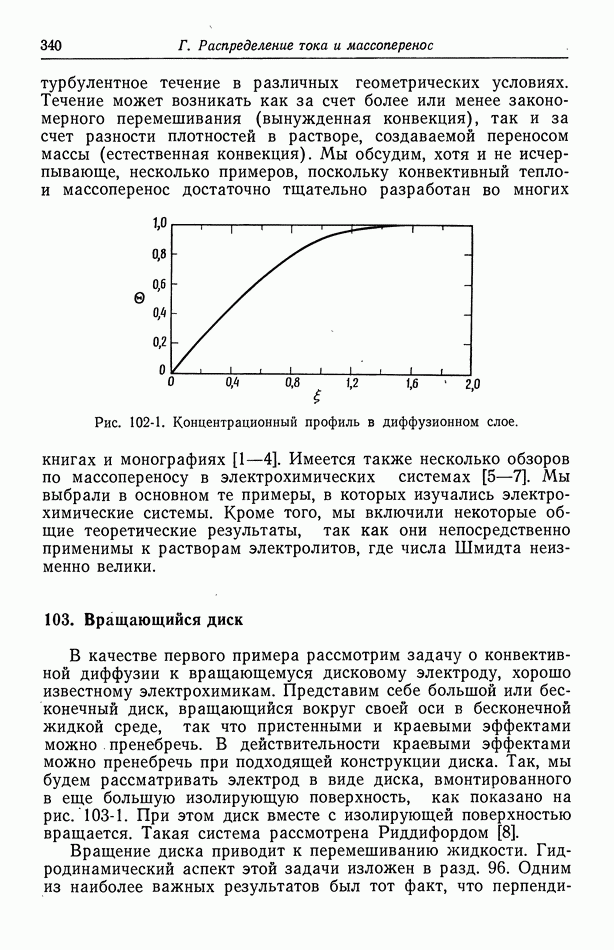
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
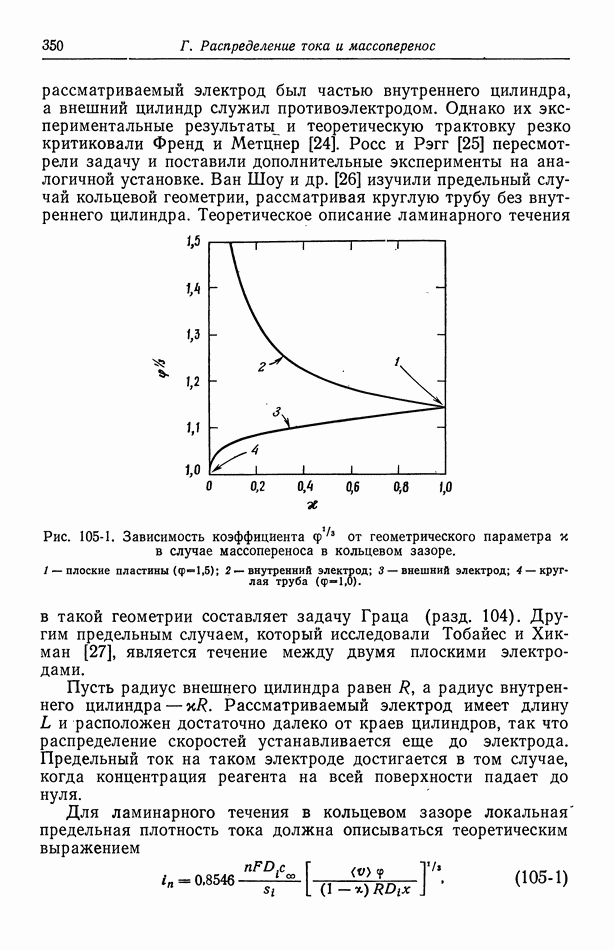
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
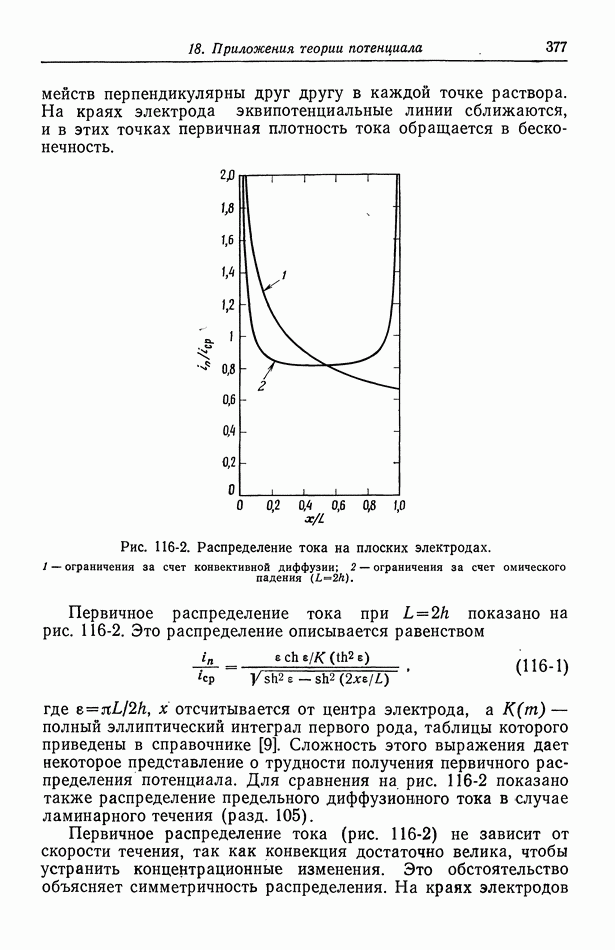
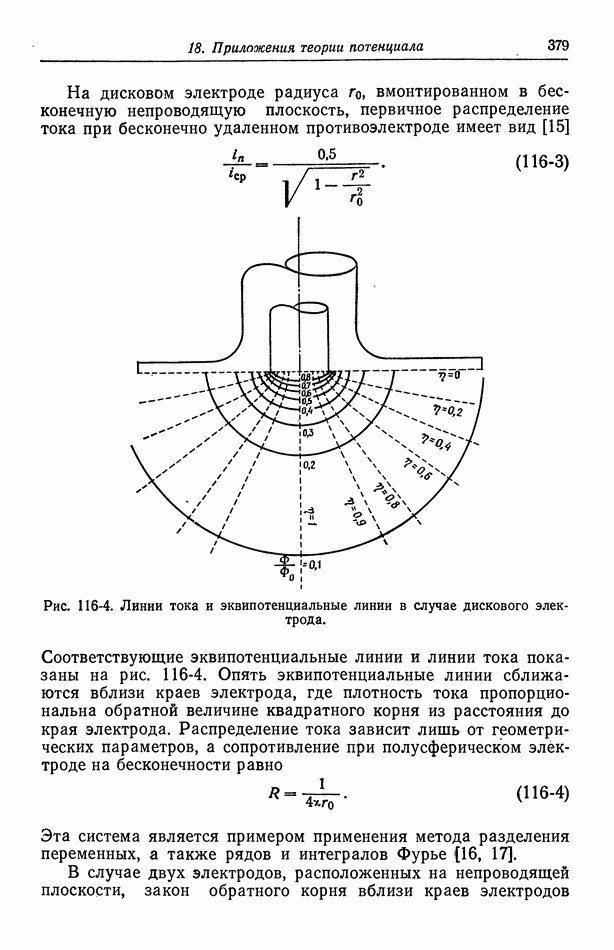
- 116. Первичное распределение тока
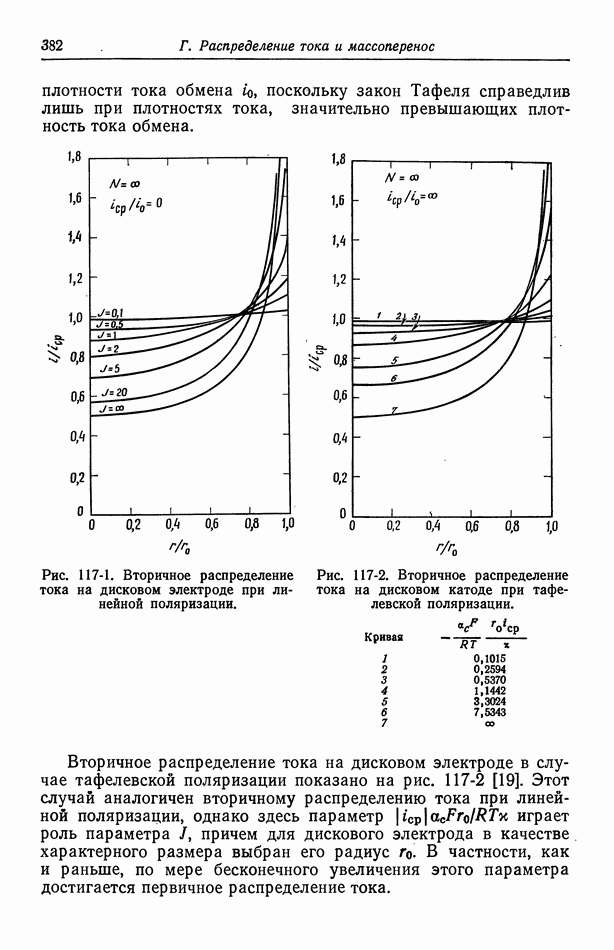
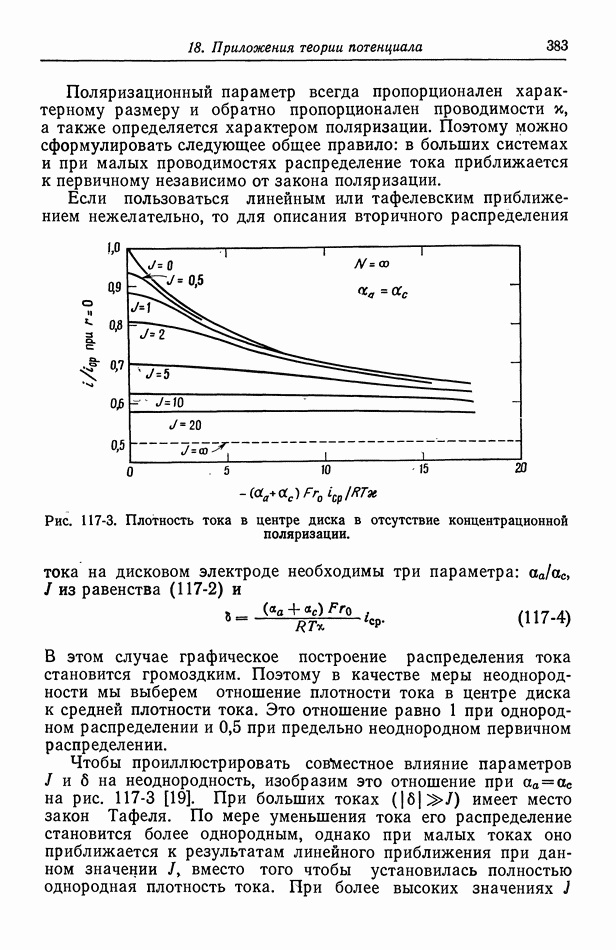
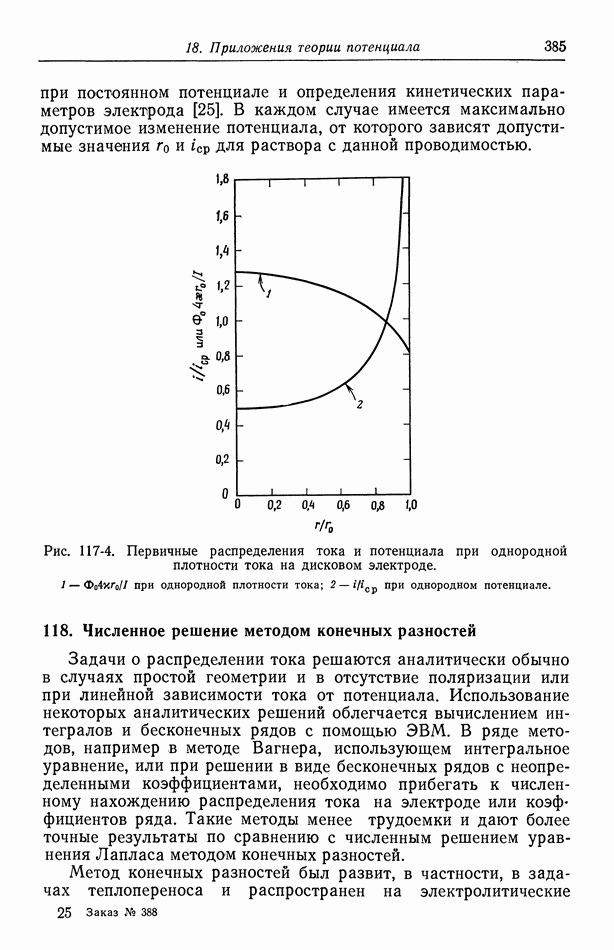
- 117. Вторичное распределение тока
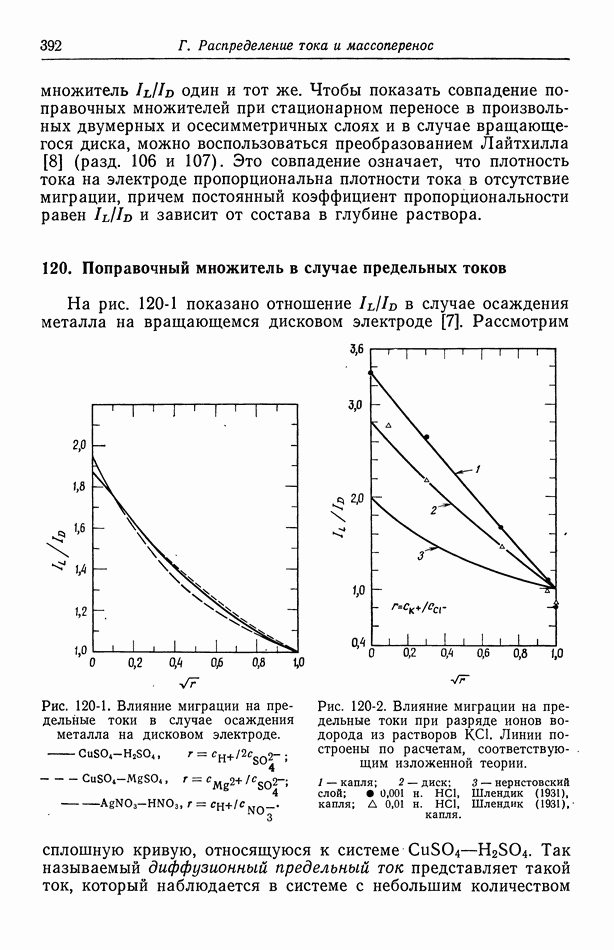
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
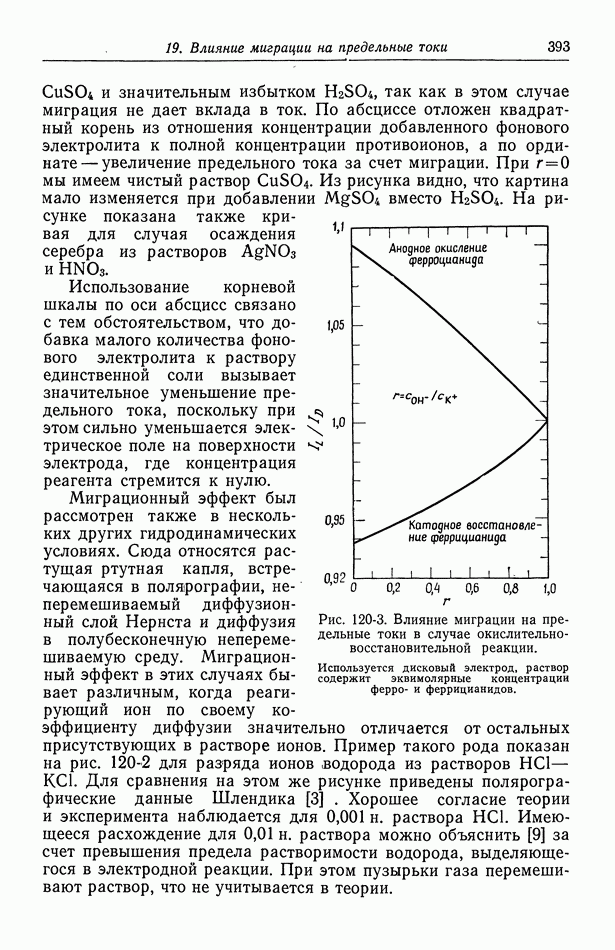
- 120. Поправочный множитель в случае предельных токов
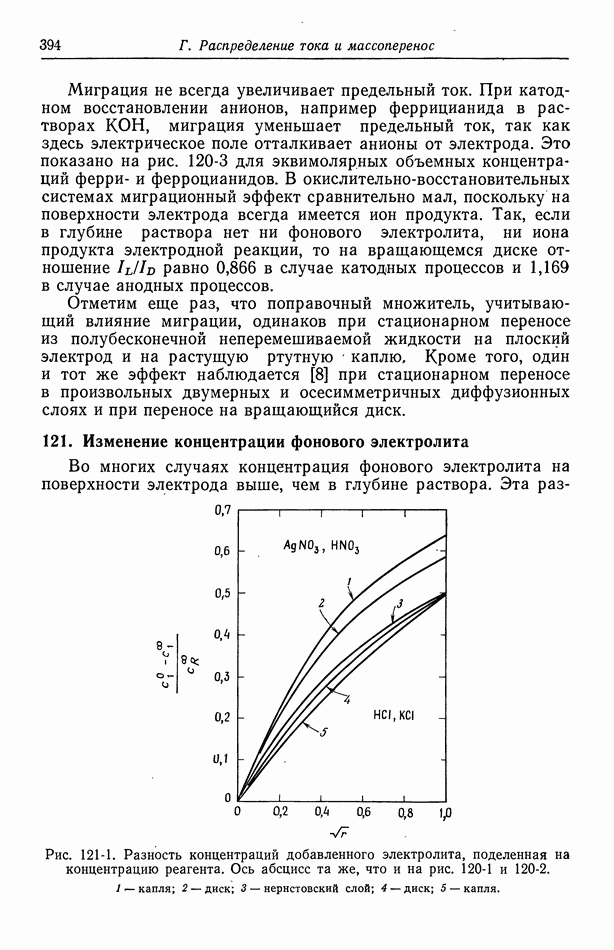
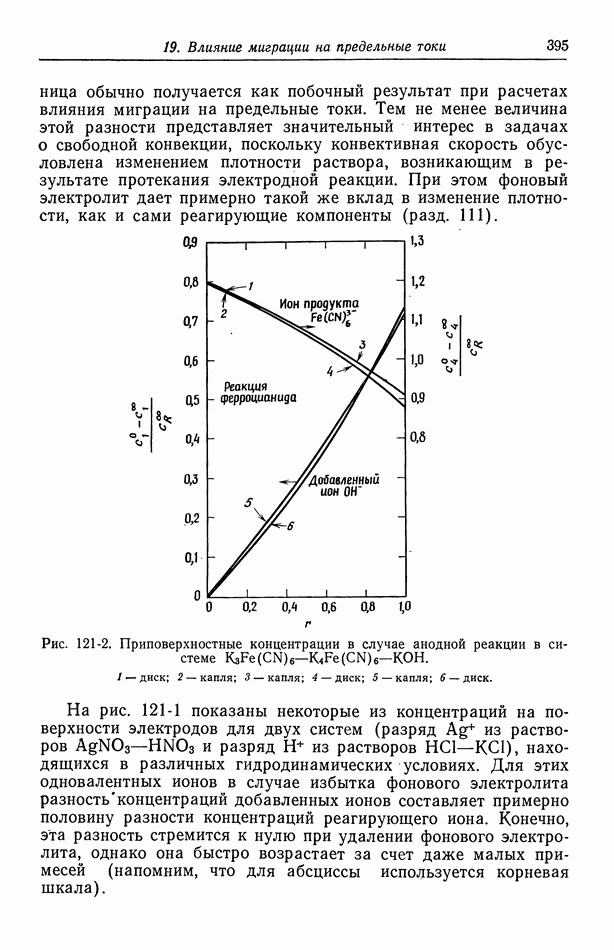
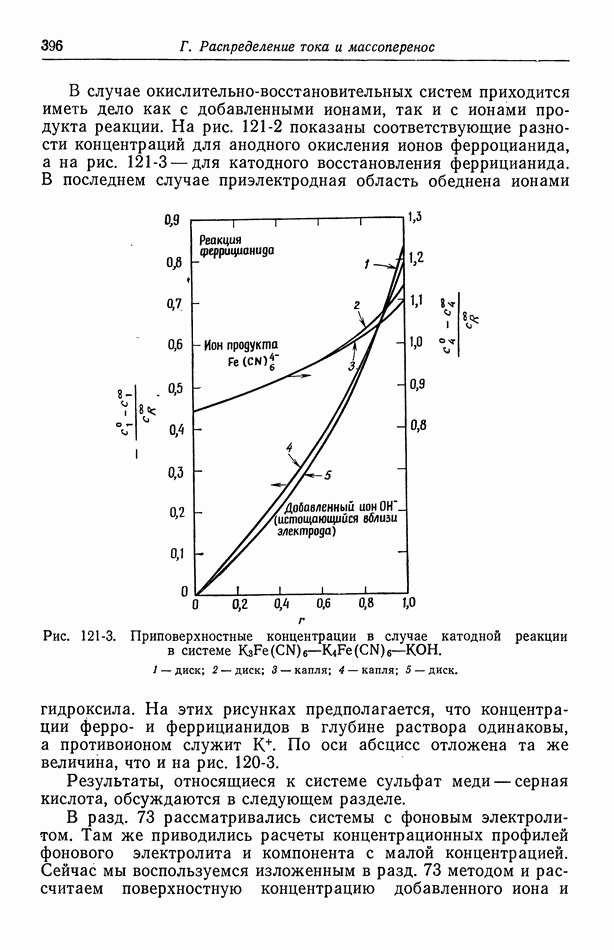
- 121. Изменение концентрации фонового электролита
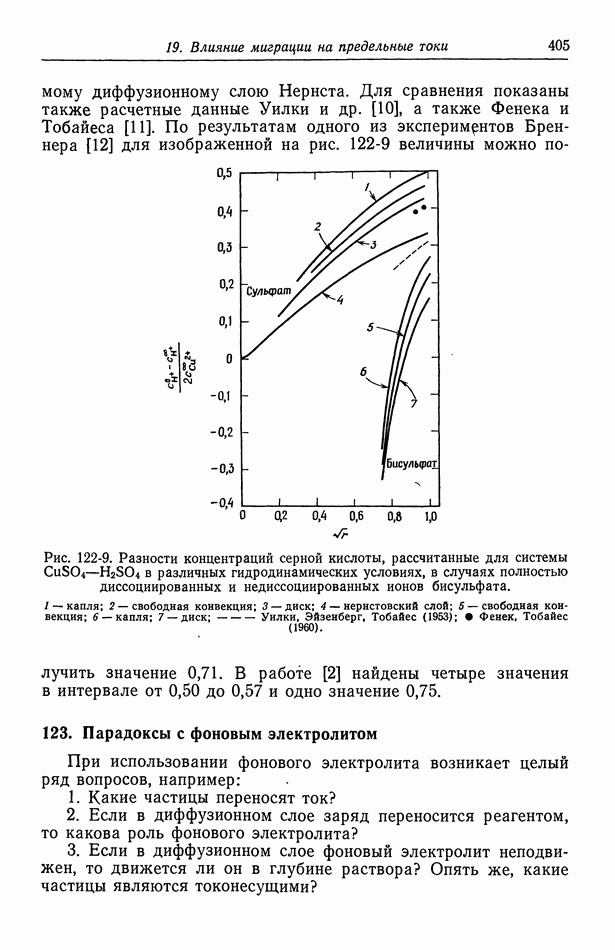
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
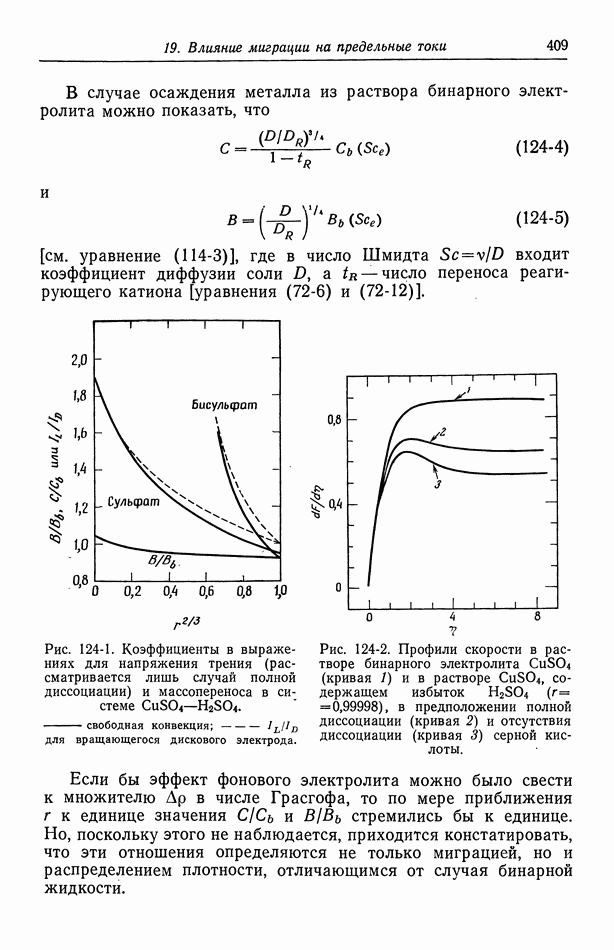
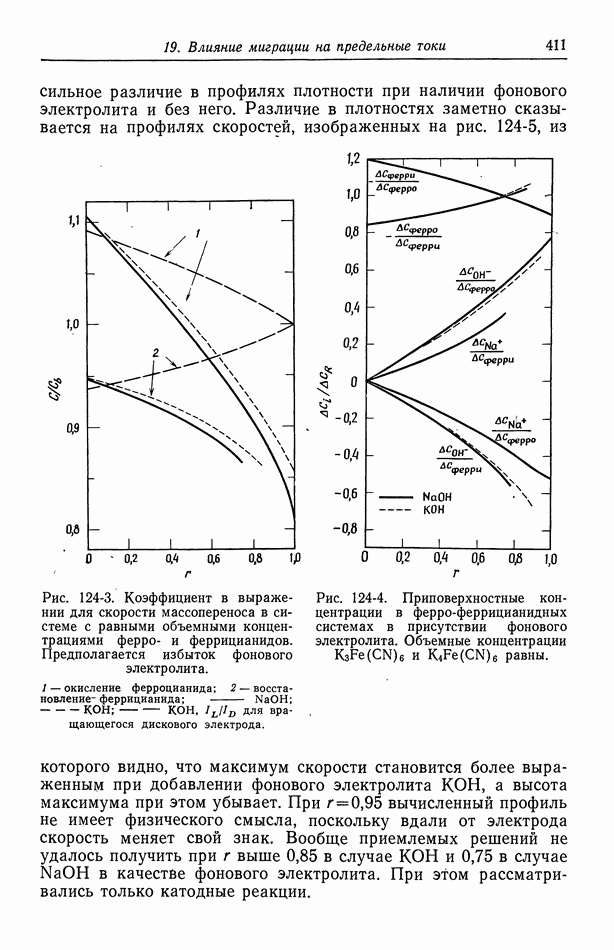
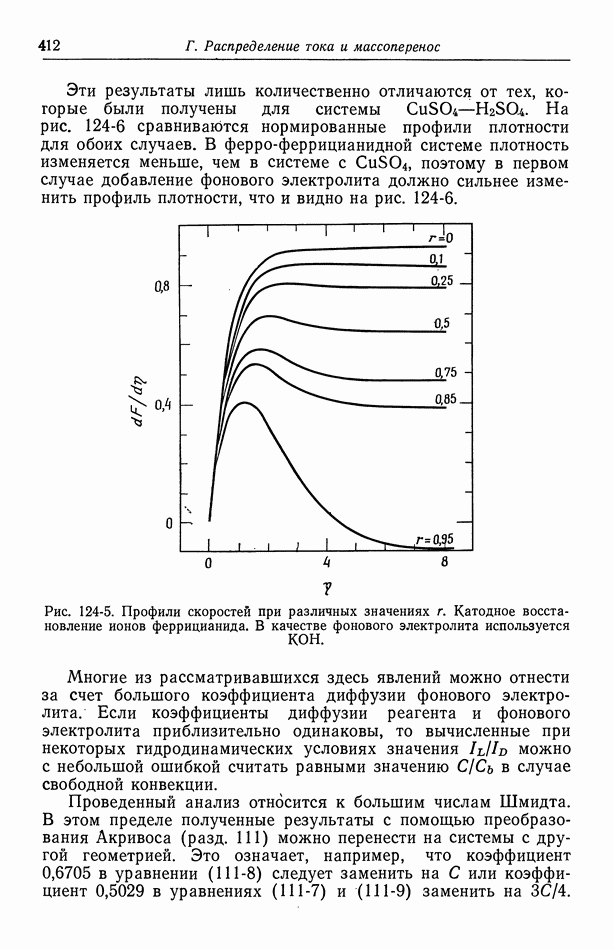
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ