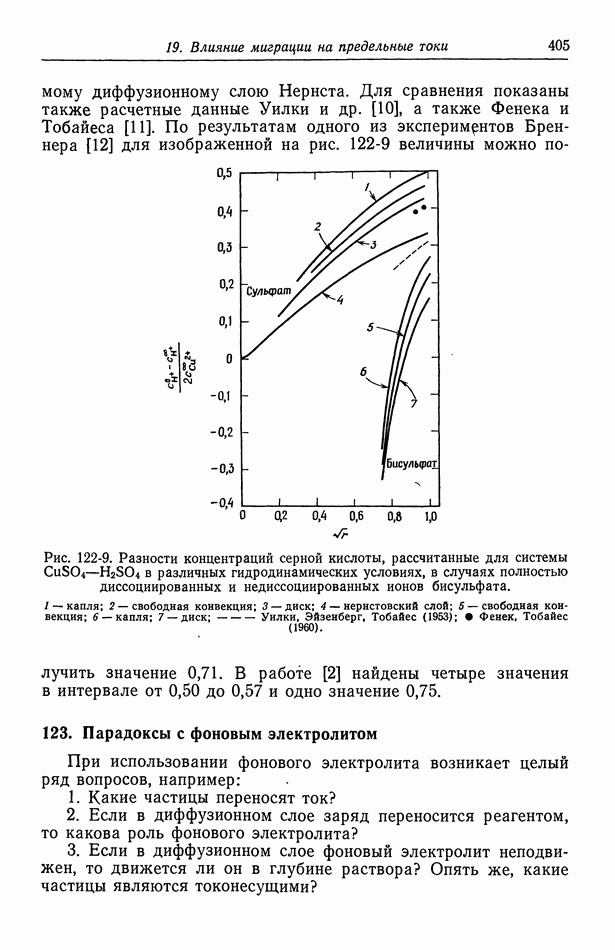
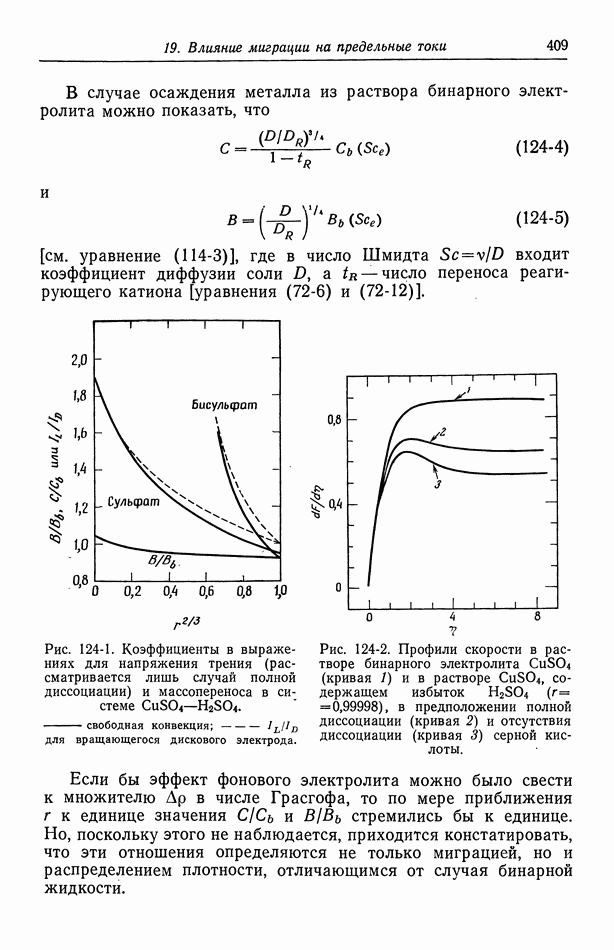
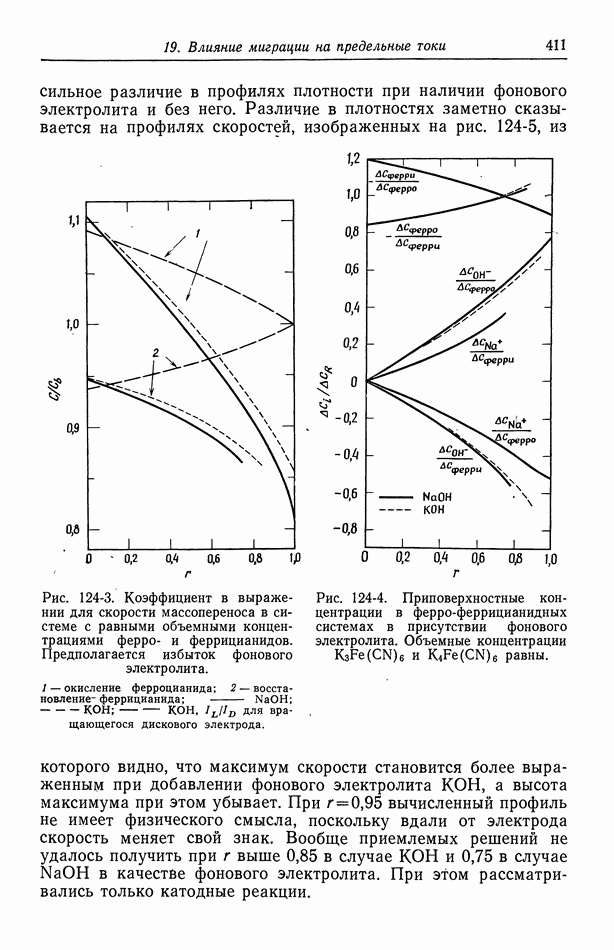
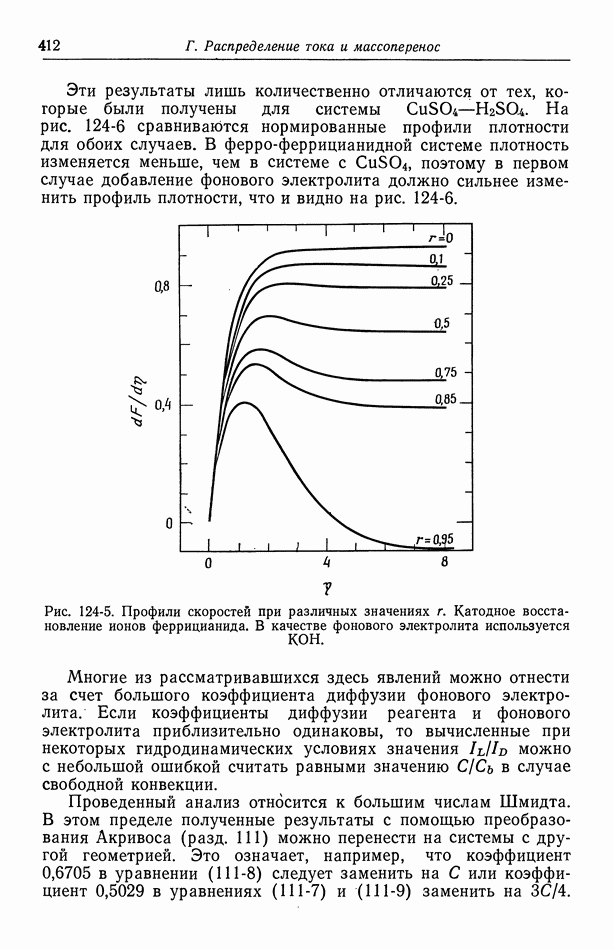
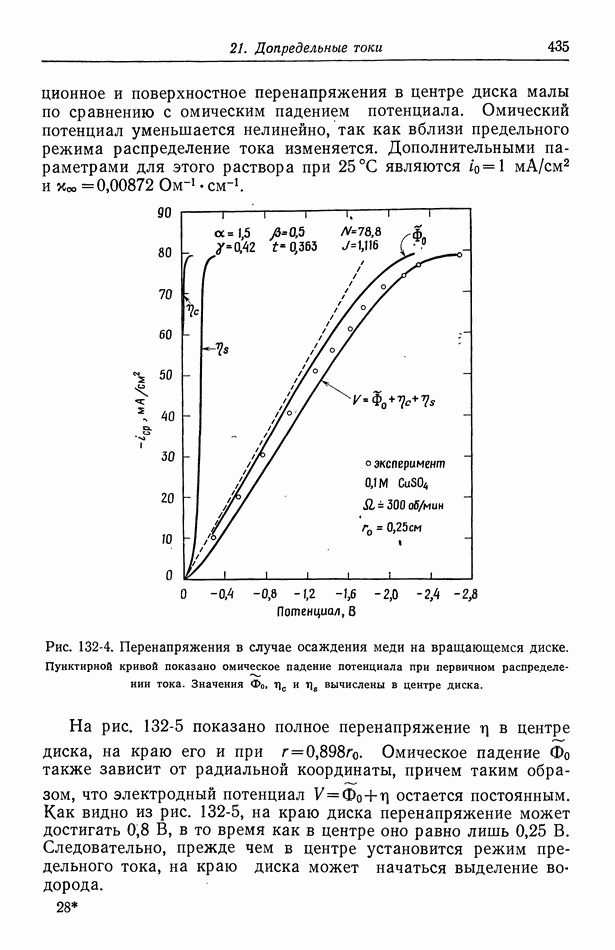
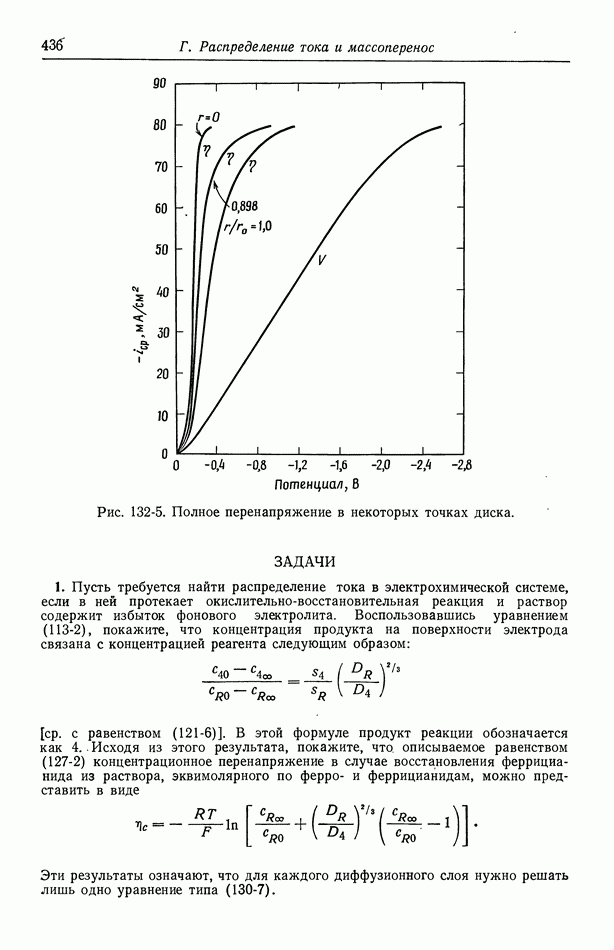
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
63. Электроосмос и потенциал течения
Рассмотрим капилляр радиуса  в диэлектрическом веществе. Капилляр заполнен раствором электролита, и имеется однородное электрическое поле в направлении оси
в диэлектрическом веществе. Капилляр заполнен раствором электролита, и имеется однородное электрическое поле в направлении оси  капилляра. Однако радиальная компонента поля не равна нулю. Вместо этого условия выполняется уравнение Пуассона в форме
капилляра. Однако радиальная компонента поля не равна нулю. Вместо этого условия выполняется уравнение Пуассона в форме

Член  равен нулю, поскольку проекция поля
равен нулю, поскольку проекция поля  на ось
на ось  постоянна. Уравнение баланса импульса
постоянна. Уравнение баланса импульса  можно записать в виде
можно записать в виде

где электрическая сила  компенсирует вязкую силу.
компенсирует вязкую силу.
Подставляя уравнение (63-2) в уравнение (63-1) и интегрируя его дважды по  при условиях
при условиях  при
при  и
и  конечны при
конечны при  получаем
получаем

Следовательно, объемную скорость течения  можно выразить как
можно выразить как

Обратимся теперь к электрическому току. Поток вещества запишем в виде [уравнение (69-1)]

При данном значении  концентрации не изменяются в направлении
концентрации не изменяются в направлении  Следовательно, в уравнении (63-5) диффузионного члена нет. Плотность тока в растворе равна
Следовательно, в уравнении (63-5) диффузионного члена нет. Плотность тока в растворе равна

где

есть проводимость [уравнение (70-3)] и

есть плотность электрического заряда. Полный ток  можно представить в виде
можно представить в виде

Подставим сюда  из уравнения (63-3) и
из уравнения (63-3) и  из уравнения (63-1):
из уравнения (63-1):

Заметим, что коэффициент при  в уравнении (63-4) равен коэффициенту при
в уравнении (63-4) равен коэффициенту при  в уравнении (63-10). Это является примером соотношения взаимности Онзагера.
в уравнении (63-10). Это является примером соотношения взаимности Онзагера.
Чтобы получить обозримое выражение для распределения потенциала внутри капилляра, воспользуемся приближением Дебая-Хюккеля (27-7):

где  — концентрация компонента
— концентрация компонента  на оси капилляра.
на оси капилляра.
Теперь уравнение (63-1) приобретает вид или

или

где

а

есть дебаевская длина.
Решением уравнения (63-13) служит

где  модифицированная функция Бесселя первого рода нулевого порядка. Коэффициент при
модифицированная функция Бесселя первого рода нулевого порядка. Коэффициент при  вычисляется из условия
вычисляется из условия  при
при  Другое решение однородной формы уравнения (63-13), равное
Другое решение однородной формы уравнения (63-13), равное  следует отбросить ввиду его неограниченности при
следует отбросить ввиду его неограниченности при 
Приближенное выражение для плотности заряда имеет вид

Заметим, что плотность заряда на оси капилляра не равна нулю. Теперь нам хотелось бы связать постоянную  с поверхностной плотностью заряда на единицу площади стенки капилляра:
с поверхностной плотностью заряда на единицу площади стенки капилляра:

или

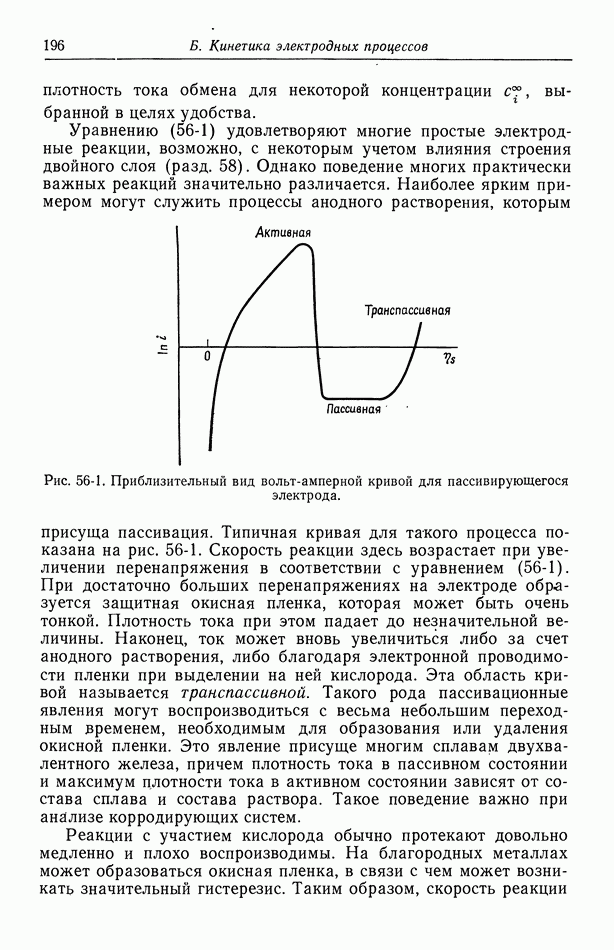
откуда

где  модифицированная функция Бесселя первого рода первого порядка. Кроме того, имеем
модифицированная функция Бесселя первого рода первого порядка. Кроме того, имеем

и

Можно вычислить интегралы в уравнениях (63-4) и (63-10):


и

где

и

есть проводимость на оси капилляра.
Теперь уравнение (63-10) преобразуется к виду

а уравнение (63-4) к виду

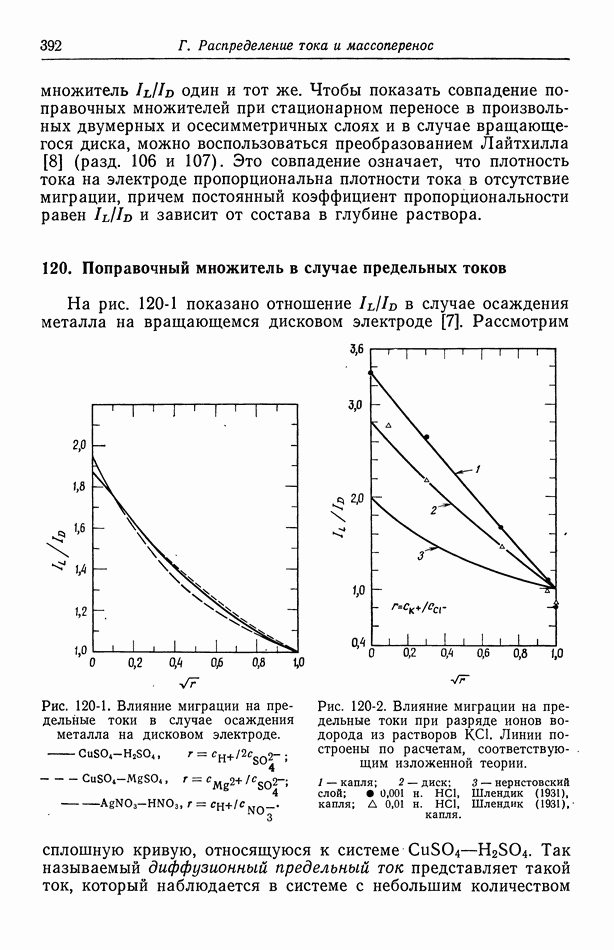
На рис. 63-1 показан профиль скорости в капилляре в отсутствие перепада давления, т. е. при  Его можно получить из уравнения (63-3):
Его можно получить из уравнения (63-3):

Направленное вдоль оси капилляра электрическое поле может вызывать течение внутри капилляра даже в отсутствие перепада давления, и это явление называется электроосмосом.
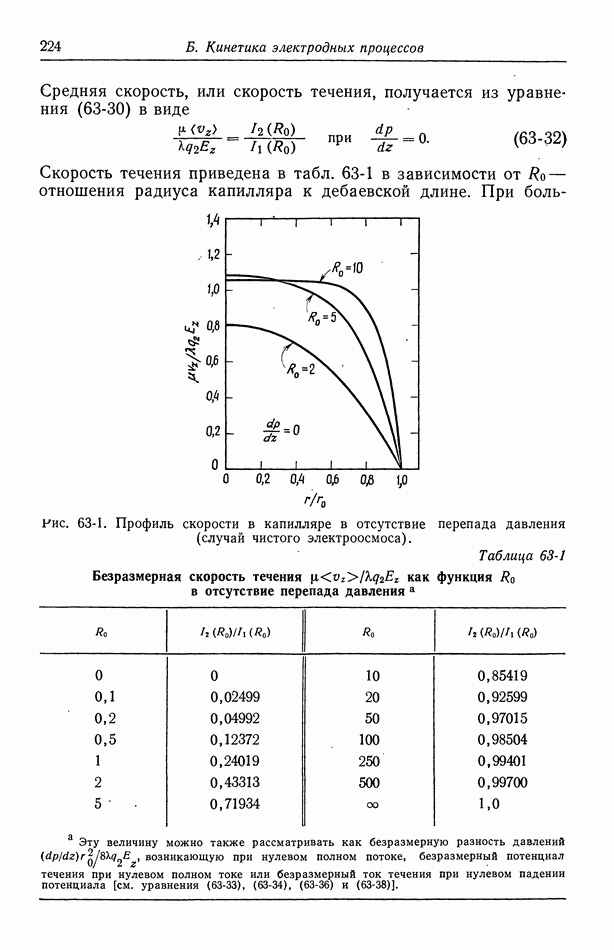
Средняя скорость, или скорость течения, получается из уравнения (63-30) в виде

Скорость течения приведена в табл. 63-1 в зависимости от  отношения радиуса капилляра к дебаевской длине. При
отношения радиуса капилляра к дебаевской длине. При

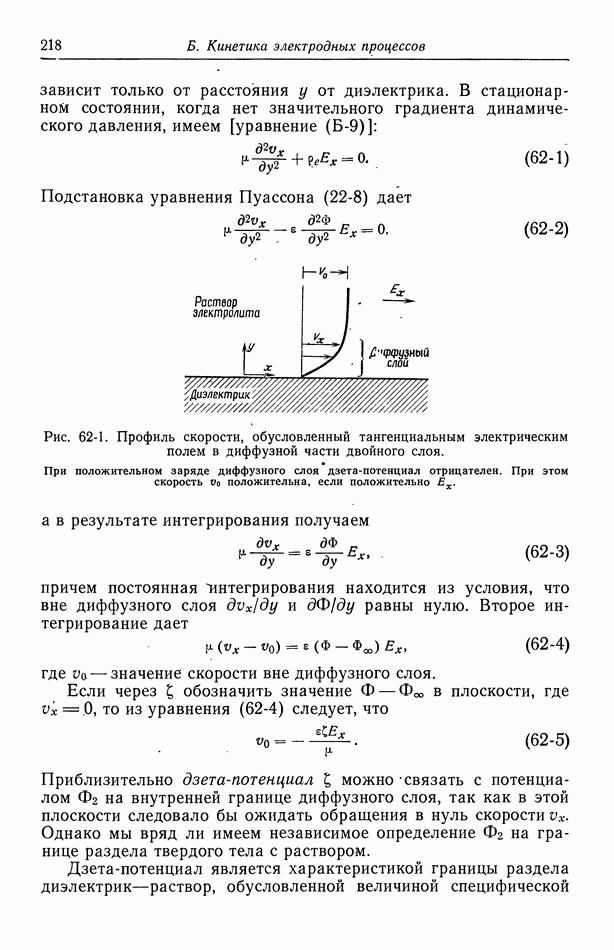
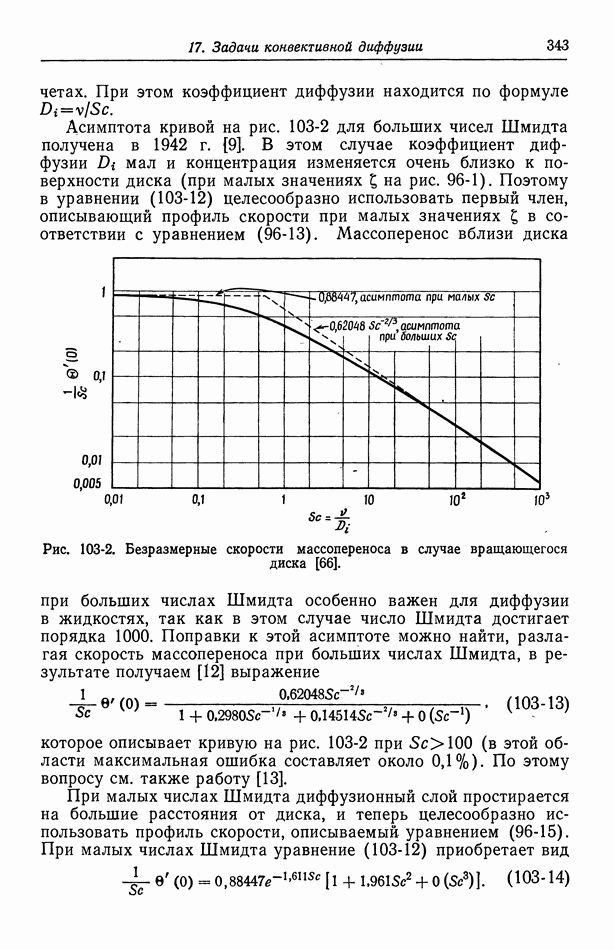
Рис. 63-1. Профиль скорости в капилляре в отсутствие перепада давления (случай чистого электроосмоса).
Таблица 63-1 (см. скан) Безразмерная скорость течения  как функция
как функция  в отсутствие перепада давления а
в отсутствие перепада давления а
больших значениях  диффузный слой сравнительно тонок, и изменение скорости происходит около стенки. Это изменение скорости приблизительно равно
диффузный слой сравнительно тонок, и изменение скорости происходит около стенки. Это изменение скорости приблизительно равно  и по существу совпадает с выражением (62-7).
и по существу совпадает с выражением (62-7).
Второй член в правой части уравнения (63-31) соответствует обычному профилю скорости, вызванному градиентом давления  В эксперименте может встретиться условие отсутствия полного потока
В эксперименте может встретиться условие отсутствия полного потока  вместо отсутствия перепада давления. В этом случае направленное вдоль оси капилляра электрическое поле создает перепад давления, который в соответствии с уравнением (63-30) равен
вместо отсутствия перепада давления. В этом случае направленное вдоль оси капилляра электрическое поле создает перепад давления, который в соответствии с уравнением (63-30) равен


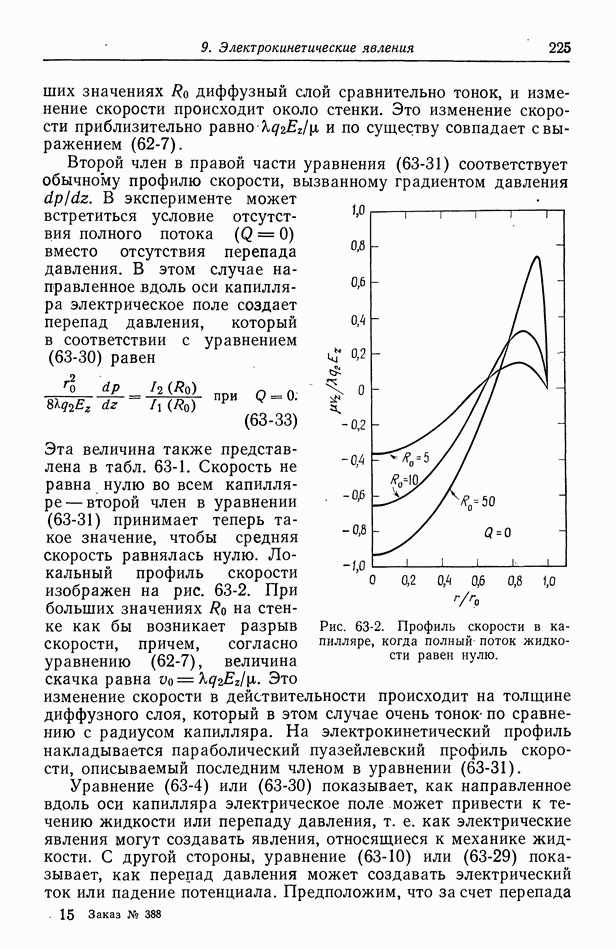
Рис. 63-2. Профиль скорости в капилляре, когда полный поток жидкости равен нулю.
Эта величина также представлена в табл. 63-1. Скорость не равна нулю во всем капилляре — второй член в уравнении (63-31) принимает теперь такое значение, чтобы средняя скорость равнялась нулю. Локальный профиль скорости изображен на рис. 63-2. При больших значениях  на стенке как бы возникает разрыв скорости, причем, согласно уравнению (62-7), величина скачка равна
на стенке как бы возникает разрыв скорости, причем, согласно уравнению (62-7), величина скачка равна  Это изменение скорости в действительности происходит на толщине диффузного слоя, который в этом случае очень тонок - по сравнению с радиусом капилляра. На электрокинетический профиль накладывается параболический пуазейлевский профиль скорости, описываемый последним членом в уравнении (63-31).
Это изменение скорости в действительности происходит на толщине диффузного слоя, который в этом случае очень тонок - по сравнению с радиусом капилляра. На электрокинетический профиль накладывается параболический пуазейлевский профиль скорости, описываемый последним членом в уравнении (63-31).
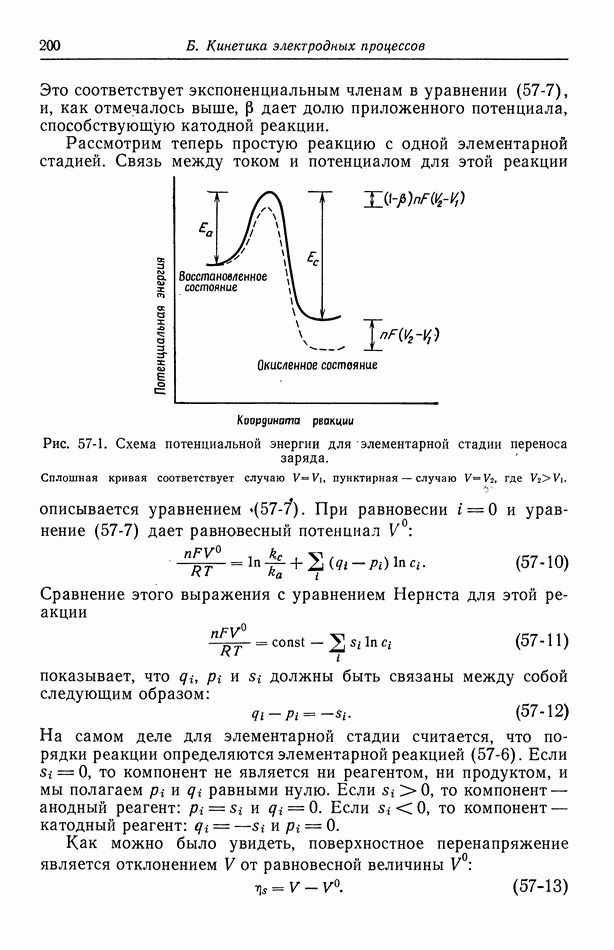
Уравнение (63-4) или (63-30) показывает, как направленное вдоль оси капилляра электрическое поле может привести к течению жидкости или перепаду давления, т. е. как электрические явления могут создавать явления, относящиеся к механике жидкости. С другой стороны, уравнение (63-10) или (63-29) показывает, как перепад давления может создавать электрический ток или падение потенциала. Предположим, что за счет перепада
давления через капилляр течет раствор электролита, а электрические условия таковы, что полный ток равен нулю. Тогда течение жидкости порождает так называемый потенциал течения, который получается из уравнения (63-29) в виде

где

Может оказаться, что лучше связать потенциал течения со скоростью течения, чем с перепадом давления. Тогда, исключая  из уравнений (63-29) и (63-30), получаем
из уравнений (63-29) и (63-30), получаем

где

Если электрические условия таковы, что разность потенциалов равна нулю, например за счет замыкания накоротко больших обратимых электродов на концах капилляра, то возникающий ток течения можно выразить в соответствии с уравнениями (63-29) и (63-30) в виде

Все изложенное выше дает пример единообразного подхода к описанию явлений электроосмоса и Потенциала течения. В первом случае электрические эффекты приводят к течению жидкости, во втором — течение жидкости порождает электрические эффекты. В действительности оба случая связаны уравнениями (63-29) и (63-30), в которых имеются две движущие силы  и две величины типа потока
и две величины типа потока  Однако в этих уравнениях электрические эффекты и явления, связанные с течением жидкости, не разделяются.
Однако в этих уравнениях электрические эффекты и явления, связанные с течением жидкости, не разделяются.
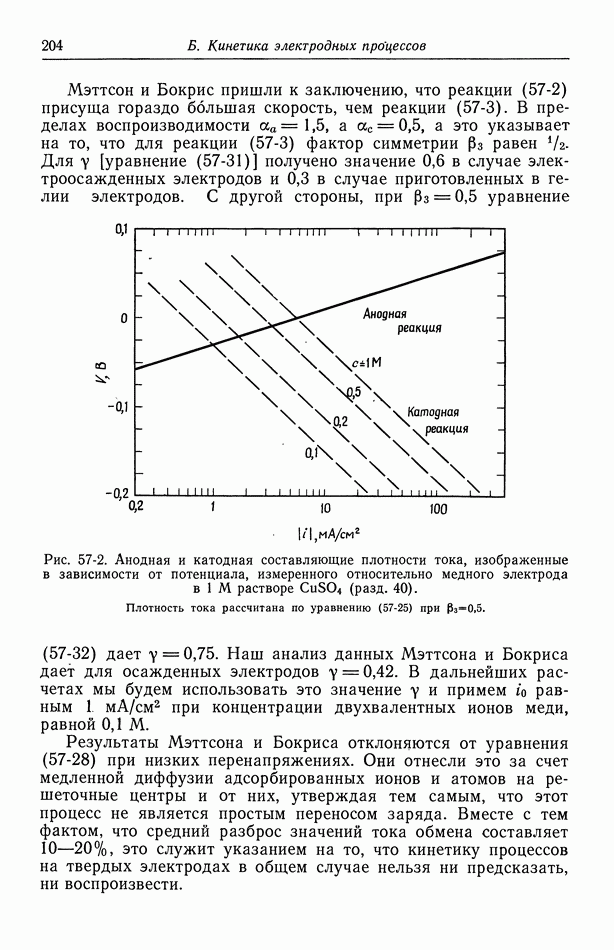
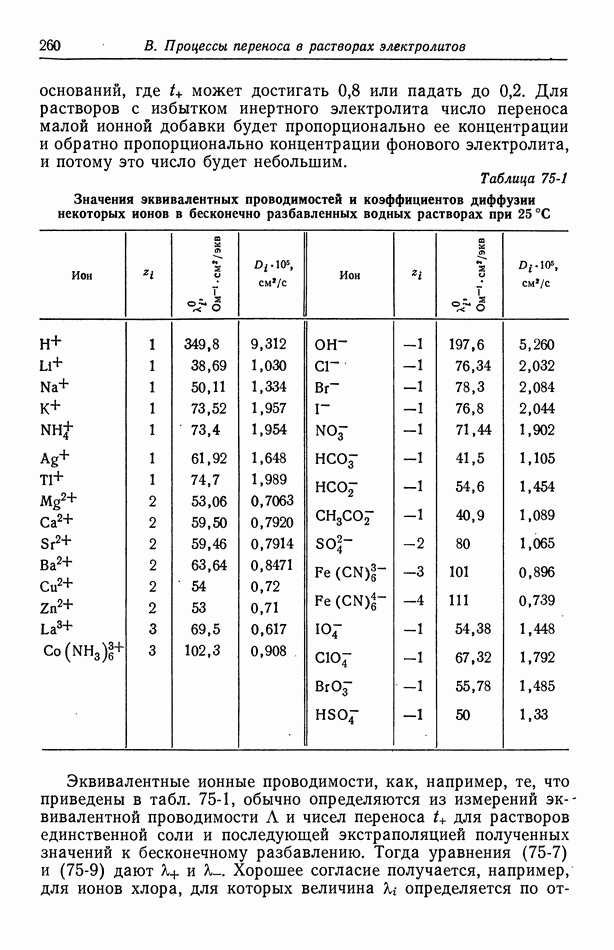
Рассмотрим пример чистой воды в капилляре радиуса  см. Предположим, что единственными ионами являются
см. Предположим, что единственными ионами являются  и
и  с концентрациями
с концентрациями  при 25 °С. Тогда дебаевская длина X равна
при 25 °С. Тогда дебаевская длина X равна  составляет приблизительно 20. Примем
составляет приблизительно 20. Примем  что
что
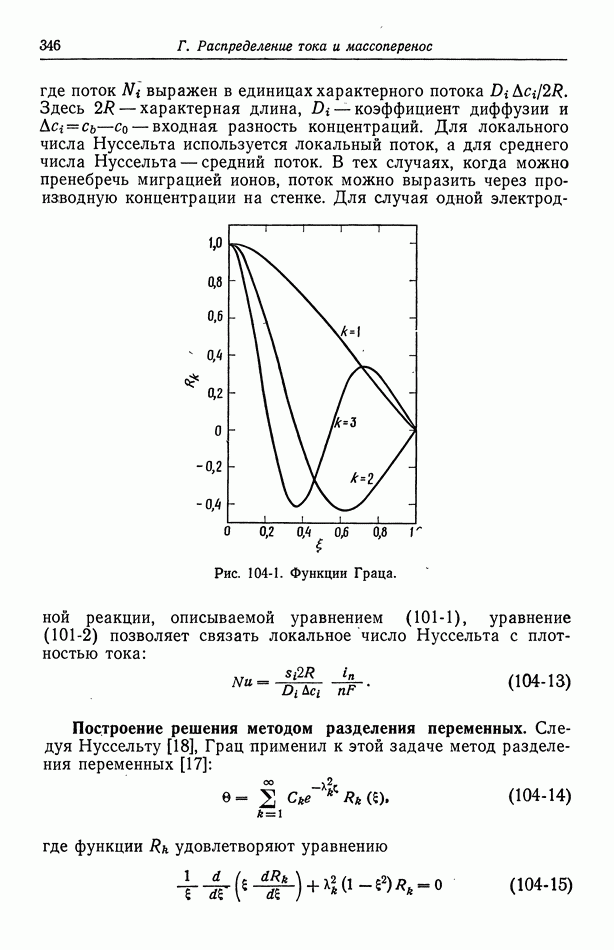
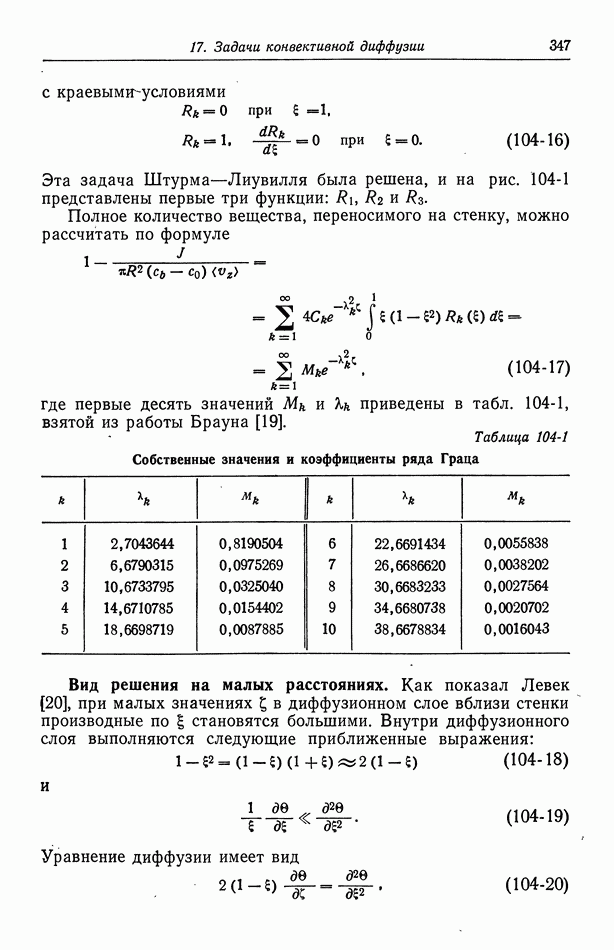
соответствует дзета-потенциалу около  Используя эти значения, находим
Используя эти значения, находим

Если в этих условиях приложить к капилляру напряжение 100 В при отсутствии суммарного потока жидкости, то должна возникнуть разность давлений, которую дает водяной столб высотой 7,3 см.
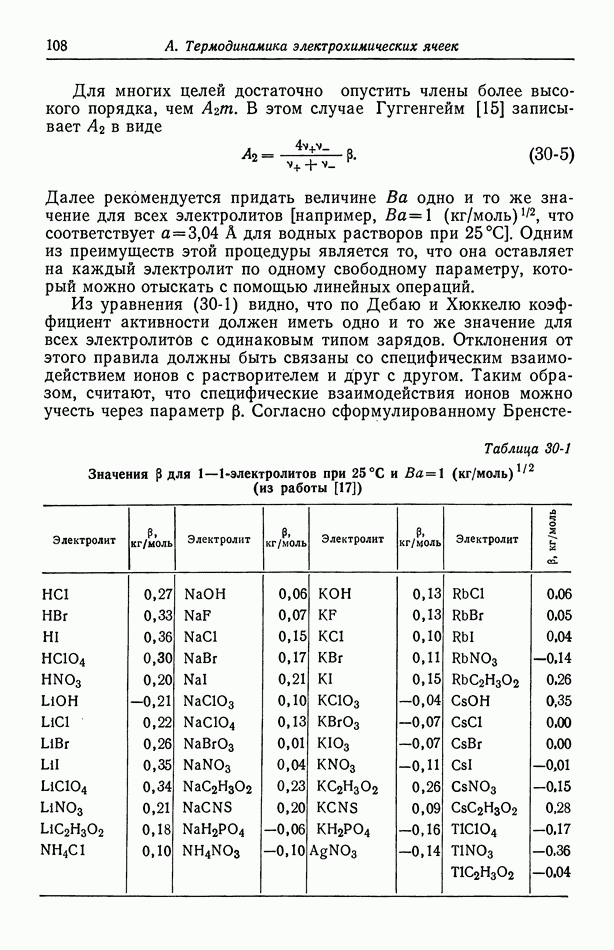
Очень часто диффузный слой бывает весьма тонким по сравнению с другими характерными длинами, определяемыми геометрией системы. Учитывая это обстоятельство, было бы желательно развить приближенный метод анализа. При больших значениях  диффузный слой ограничен областью вблизи стенки, где цилиндрическая геометрия несущественна. Вне этой области раствор электрически нейтрален. Сначала рассмотрим течение жидкости, а затем — электрический ток.
диффузный слой ограничен областью вблизи стенки, где цилиндрическая геометрия несущественна. Вне этой области раствор электрически нейтрален. Сначала рассмотрим течение жидкости, а затем — электрический ток.
При больших значениях  уравнение (63-31) сводится к
уравнение (63-31) сводится к

где

Равенство (63-39) справедливо вне диффузного слоя и соответствует решению уравнения (63-2) при нулевой плотности заряда и граничном условии  при
при  Это значение
Это значение  следует из расчета, основанного на приближении тонкого диффузного слоя (разд. 62).
следует из расчета, основанного на приближении тонкого диффузного слоя (разд. 62).
Таким образом, задача о движении жидкости решается так, как если бы раствор был электрически нейтральным, но со скоростью скольжения на твердой стенке, связанной с тангенциальной составляющей электрического поля уравнением (63-40), (62-7) или (62-5). На рис. 63-1 и 63-2 показано приближение к такой ситуации по мере возрастания 
Уравнение (63-39) дает скорость течения в виде

что получается также из уравнения (63-30) при бесконечном  Выражения для тока в этом случае также достаточно просты.
Выражения для тока в этом случае также достаточно просты.
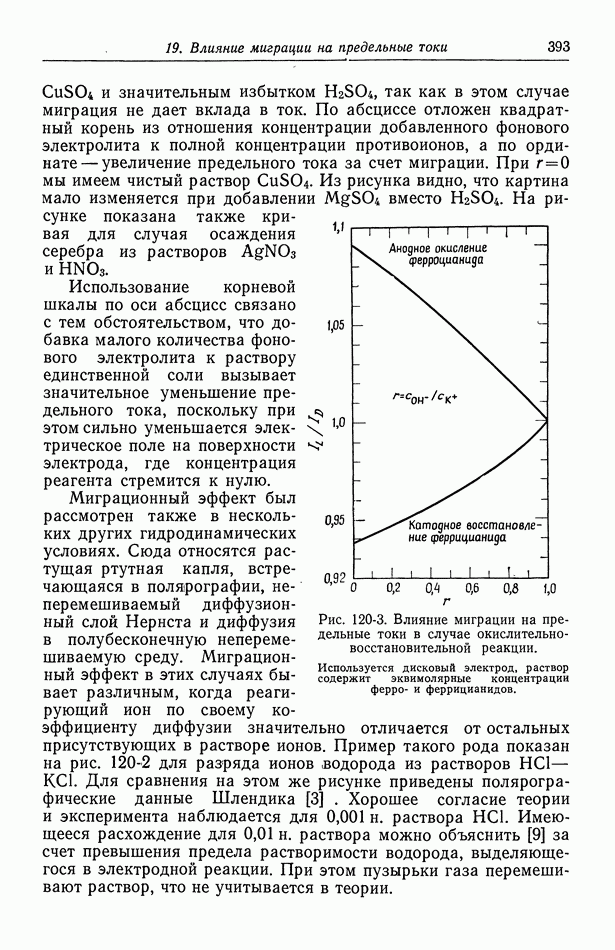
По мере приближения  к бесконечности
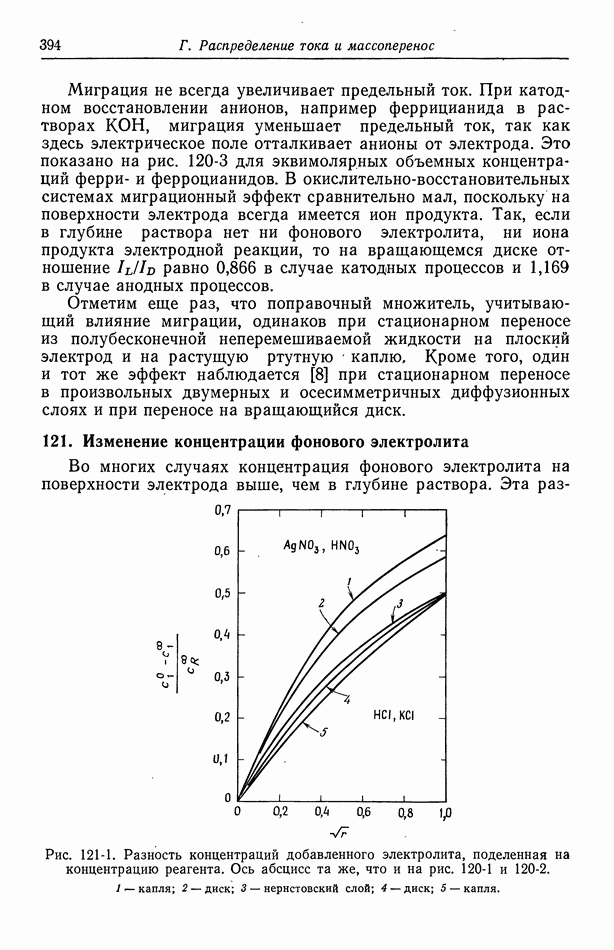
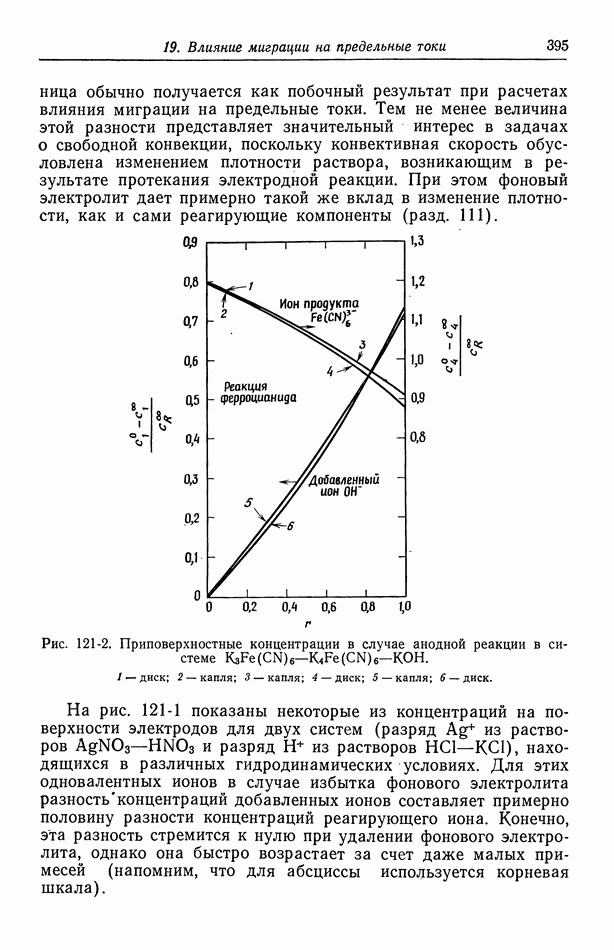
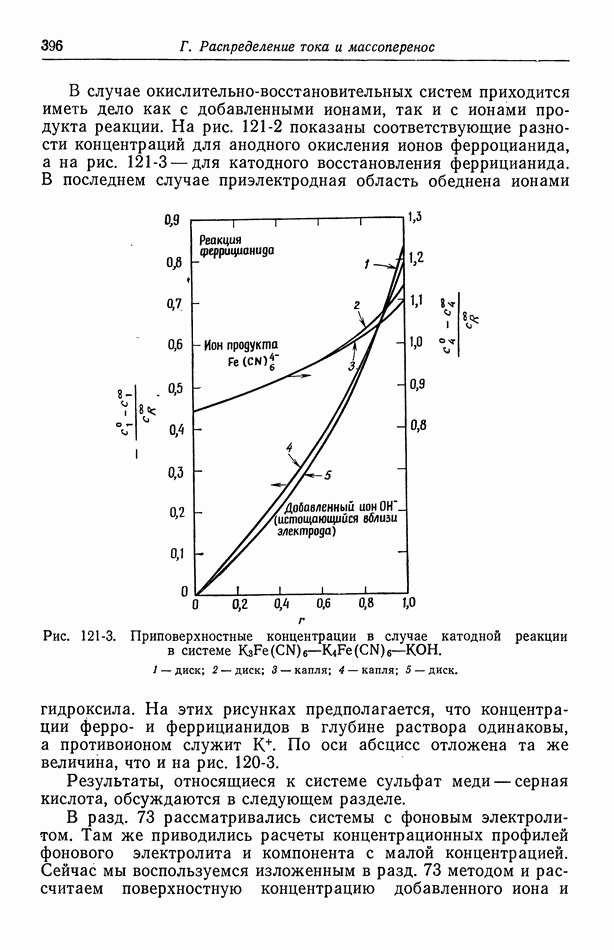
к бесконечности  и приближаются к
и приближаются к  и уравнение (63-29) приобретает вид
и уравнение (63-29) приобретает вид

Из этого выражения можно вывести правильные асимптотические соотношения для потенциала и тока течения в соответствии с уравнениями (63-34), (63-36) и (63-38). Вне диффузного слоя раствор считается электрически нейтральным и обладает проводимостью  Эта область дает очевидный вклад
Эта область дает очевидный вклад  в уравнение (63-42). Тогда последний член должен быть обусловлен диффузным слоем.
в уравнение (63-42). Тогда последний член должен быть обусловлен диффузным слоем.
Для установления вклада диффузного слоя определим поверхностную плотность тока  отнесенную к диффузному слою, так чтобы полный ток выражался как
отнесенную к диффузному слою, так чтобы полный ток выражался как

где для получения вклада в полный ток поверхностная плотность тока умножается на длину окружности. Подставляя равенство (63-43) в уравнение (63-29), находим в пределе больших 

где

есть поверхностная проводимость и  производная скорости вне диффузного слоя
производная скорости вне диффузного слоя  (здесь у — расстояние от поверхности). В данном случае
(здесь у — расстояние от поверхности). В данном случае

[ср. с уравнением (63-39)].
Члены в уравнениях (63-44) и (63-45) можно интерпретировать физически. Первый член в правой части уравнения (63-45) можно было бы назвать избыточной поверхностной проводимостью, вызванной тем, что значения ионных концентраций внутри диффузного слоя отличаются от объемных. Эта величина может быть положительной или отрицательной и равна нулю для симметричного электролита с равными подвижностями катионов и анионов. В приближении Дебая-Хюккеля (вновь для симметричного электролита) значение  внутри диффузного слоя постоянно. Поэтому замена менее подвижных ионов более подвижными противоионами увеличила бы локальную проводимость. Если отказаться от этого приближения, то
внутри диффузного слоя постоянно. Поэтому замена менее подвижных ионов более подвижными противоионами увеличила бы локальную проводимость. Если отказаться от этого приближения, то
следовало бы ожидать, что ионная сила в диффузном слое увеличивается, и это привело бы к более положительным значениям избыточной поверхностной проводимости.
Последний член в уравнении (63-45) можно было бы назвать конвективной поверхностной проводимостью, обусловленной движением жидкости в диффузном слое, которое вызвано электрическим полем. Поскольку индуцированная скорость и плотность заряда пропорциональны получается, что конвективная поверхностная проводимость пропорциональна квадрату и всегда положительна.
Напряжение трения в жидкости вблизи поверхности вызывает движение жидкости в диффузном слое и приводит к дополнительному конвективному вкладу в поверхностную плотность тока. Этот член записан через  —величину, связанную с локальными условиями на поверхности. В некоторых случаях с этим последним членом в уравнении (63-44) может быть связана эрозионная коррозия, так как напряжение трения может изменяться по поверхности
—величину, связанную с локальными условиями на поверхности. В некоторых случаях с этим последним членом в уравнении (63-44) может быть связана эрозионная коррозия, так как напряжение трения может изменяться по поверхности  . В результате происходит изменение поверхностной плотности тока, и если объем раствора из-за малой проводимости не может обеспечить этот ток, то он может вызвать коррозию металла.
. В результате происходит изменение поверхностной плотности тока, и если объем раствора из-за малой проводимости не может обеспечить этот ток, то он может вызвать коррозию металла.
Если бы двигалась еще и сама твердая поверхность, то в уравнение (63-44) пришлось бы включать дополнительный конвективный член при условии, что в поверхностную плотность тока входит лишь ток на подвижной стороне двойного слоя. Это вызвано тем, что в целом граница раздела остается электрически нейтральной.
Уравнения (6343) и (63-44) приводят к выражению для полного тока

Сравнение с уравнением (63-42) показывает, что при больших значениях  поверхностной проводимостью можно пренебречь.
поверхностной проводимостью можно пренебречь.
Уравнение (63-44) и уравнение (63-40) или (62-5) являются векторными уравнениями, относящимися к поверхностной плотности тока, скорости скольжения на поверхности, тангенциальному электрическому полю и напряжению трения. Они применимы и в системах с другой геометрией, если диффузный слой может считаться тонким по сравнению с другими характерными длинами. В таких случаях диффузный слой по существу является плоским, и эти уравнения можно уточнить, учитывая то обстоятельство, что задачу о плоском диффузном слое можно решить, не прибегая к приближению Дебая-Хюккеля.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
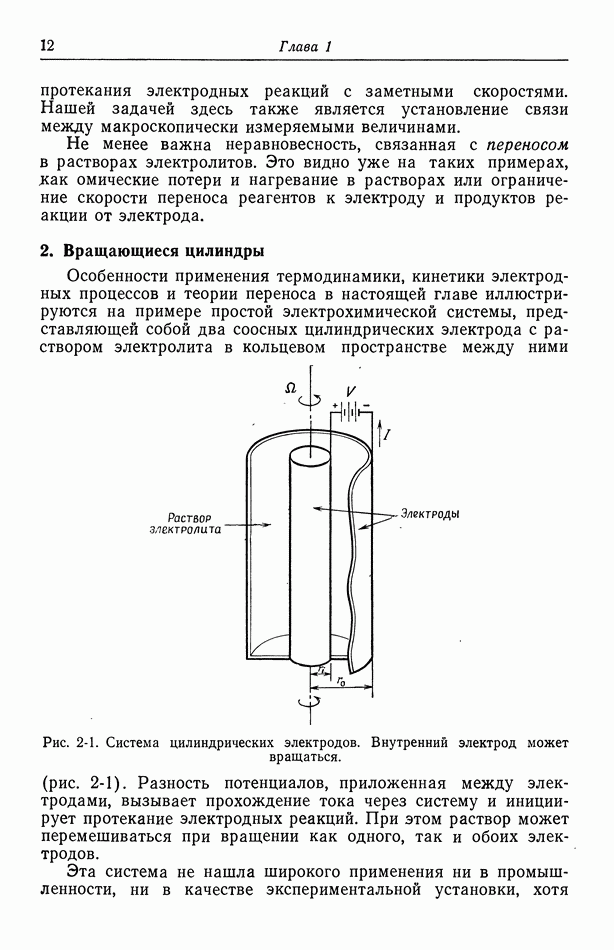
- 2. Вращающиеся цилиндры
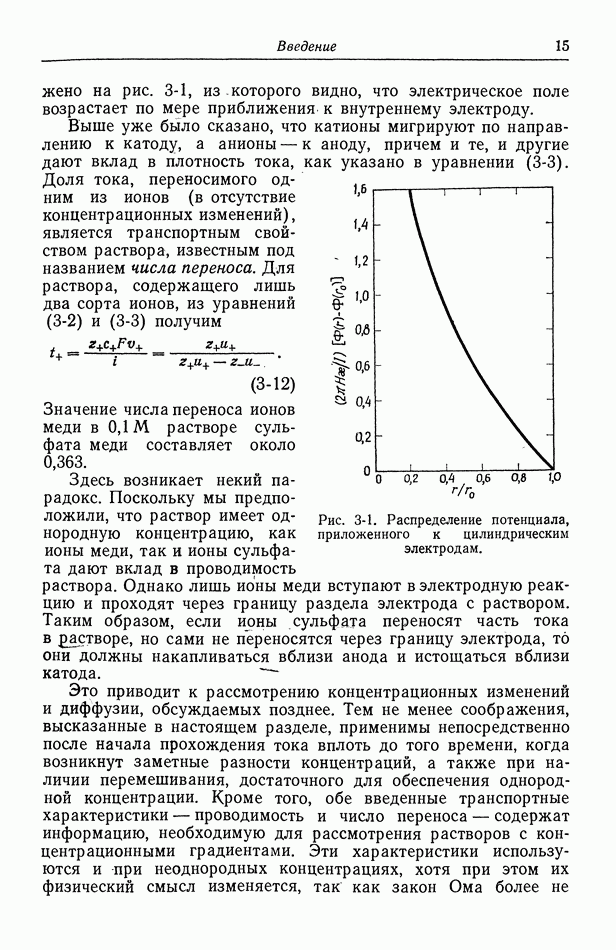
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
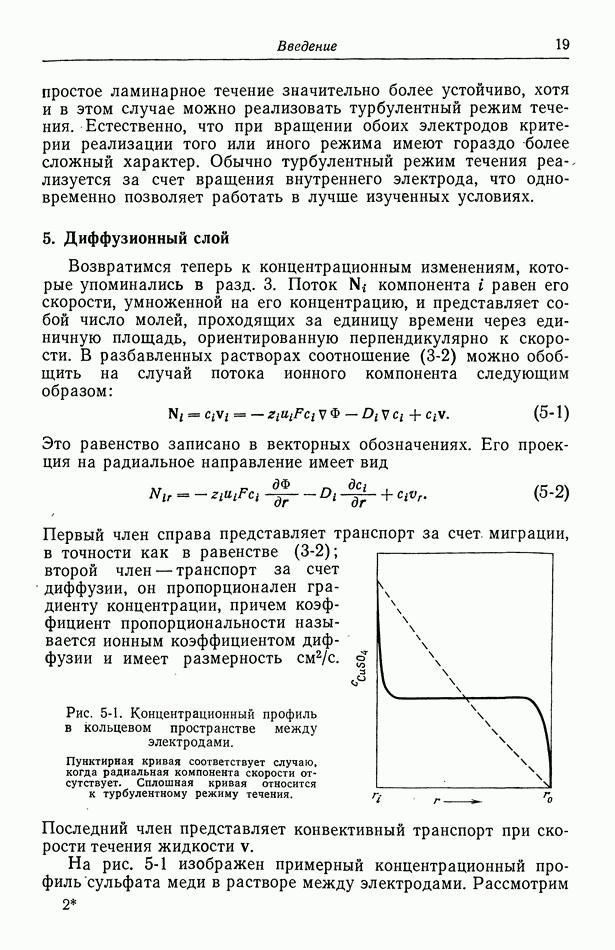
- 5. Диффузионный слой
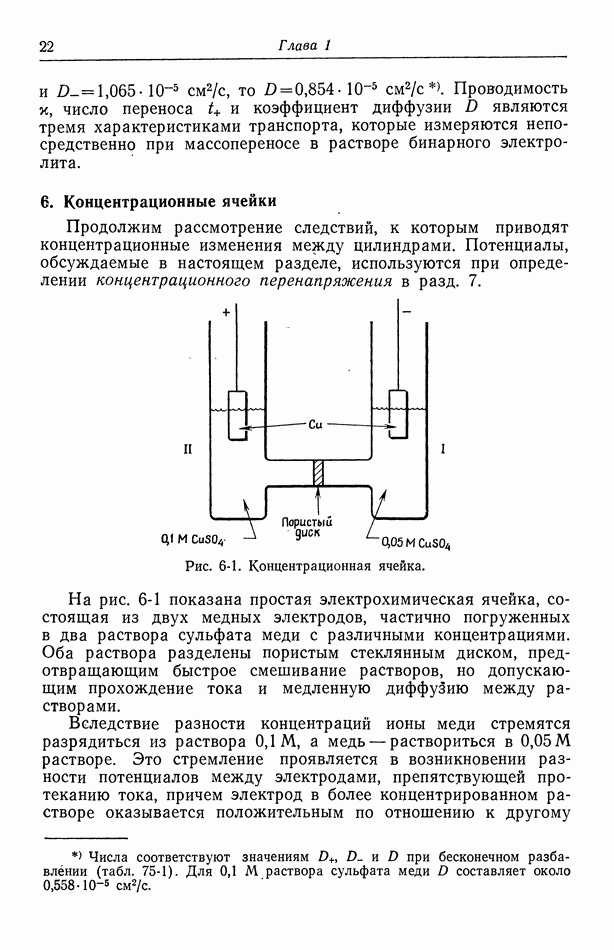
- 6. Концентрационные ячейки
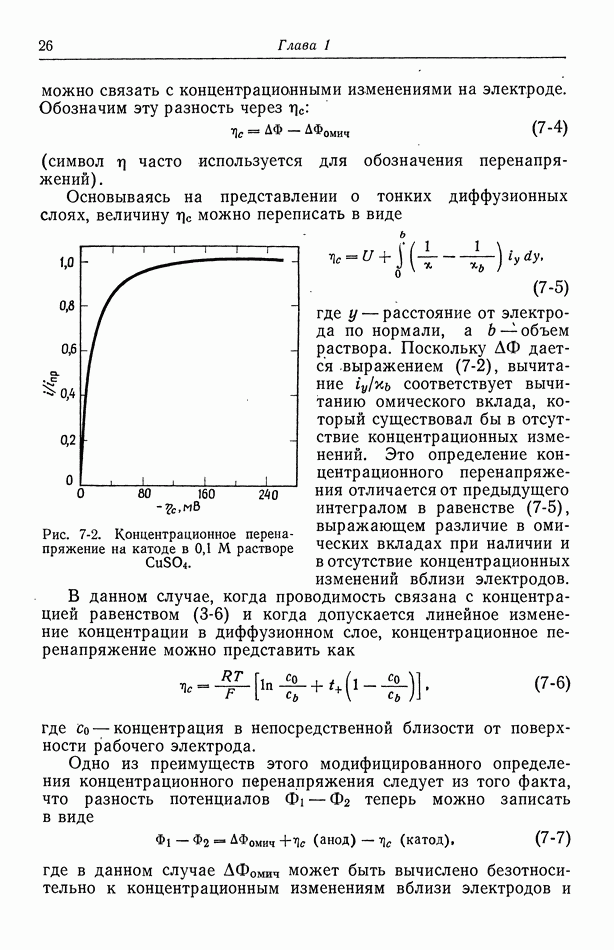
- 7. Концентрационное перенапряжение
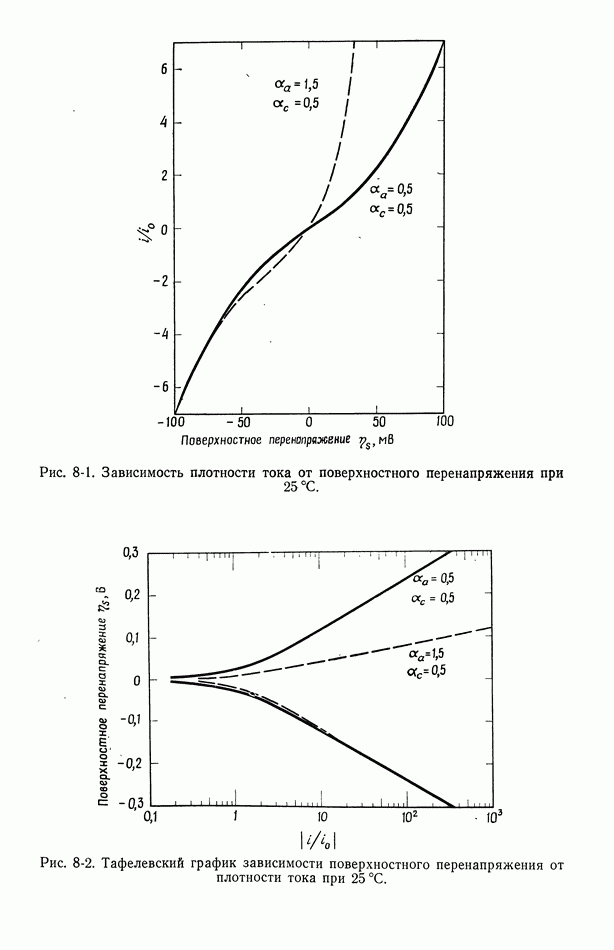
- 8. Поверхностное перенапряжение
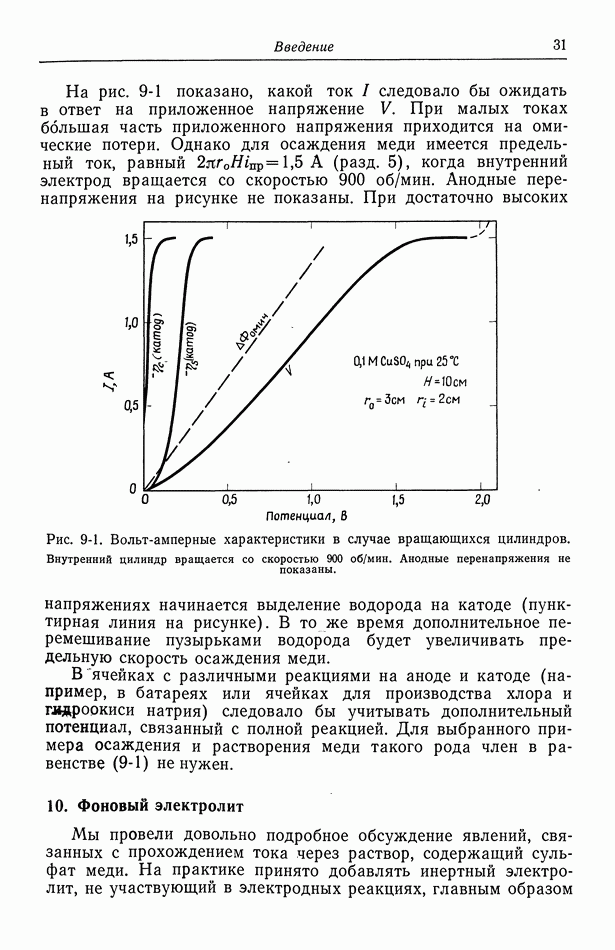
- 9. Потенциал ячейки
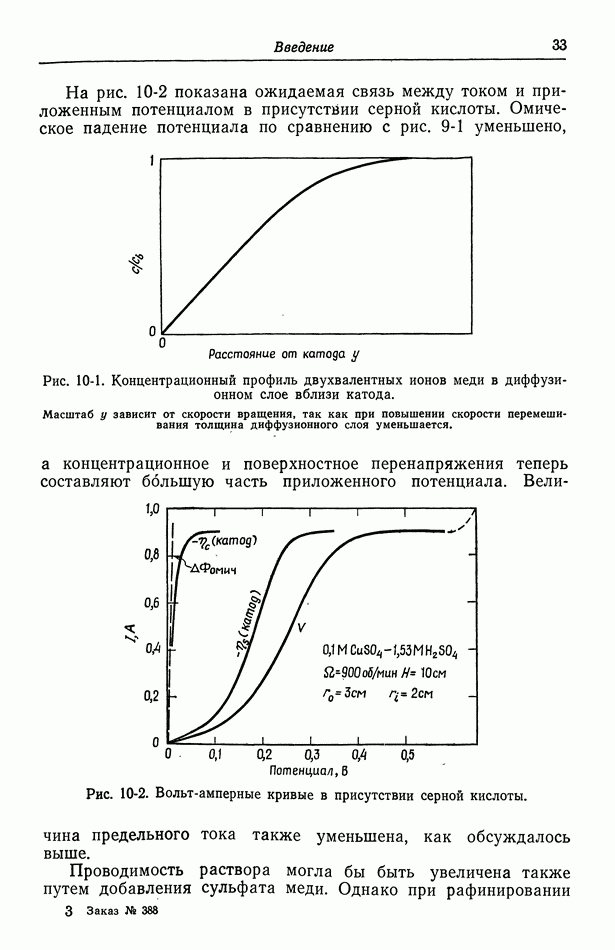
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
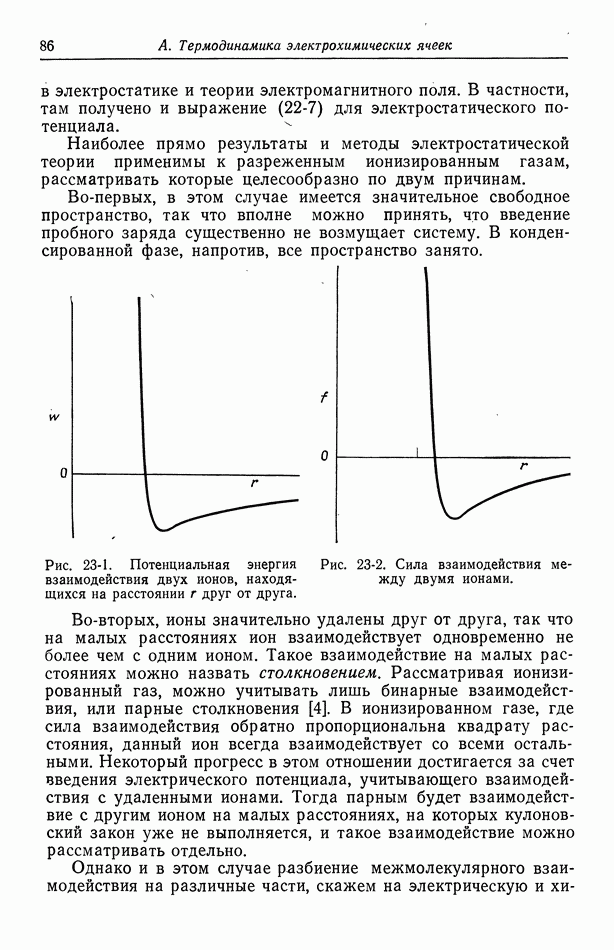
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
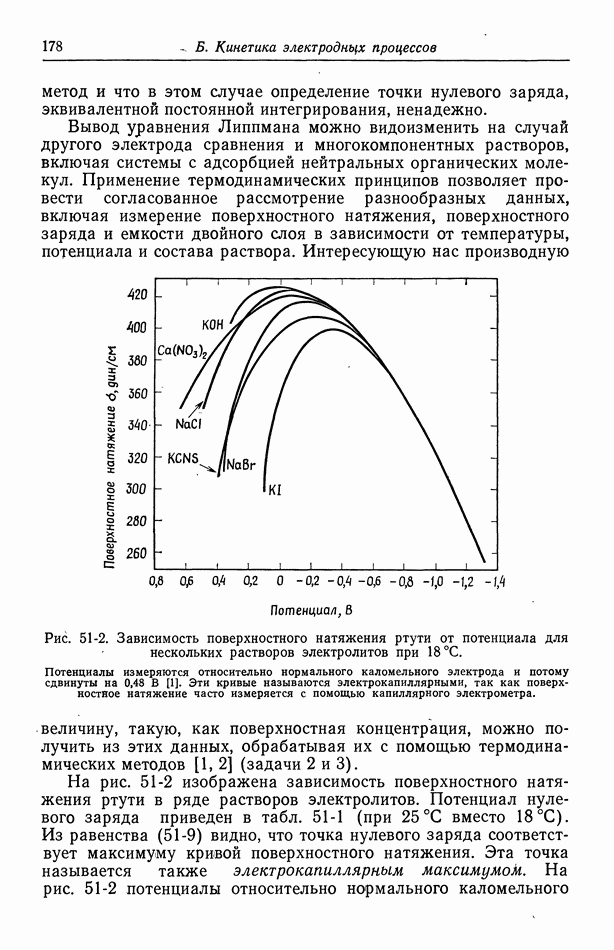
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
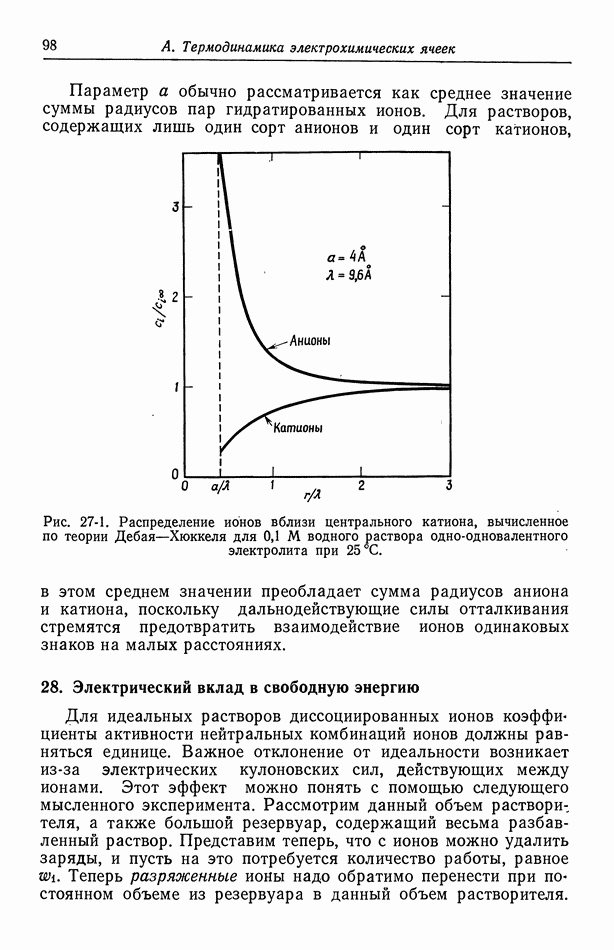
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
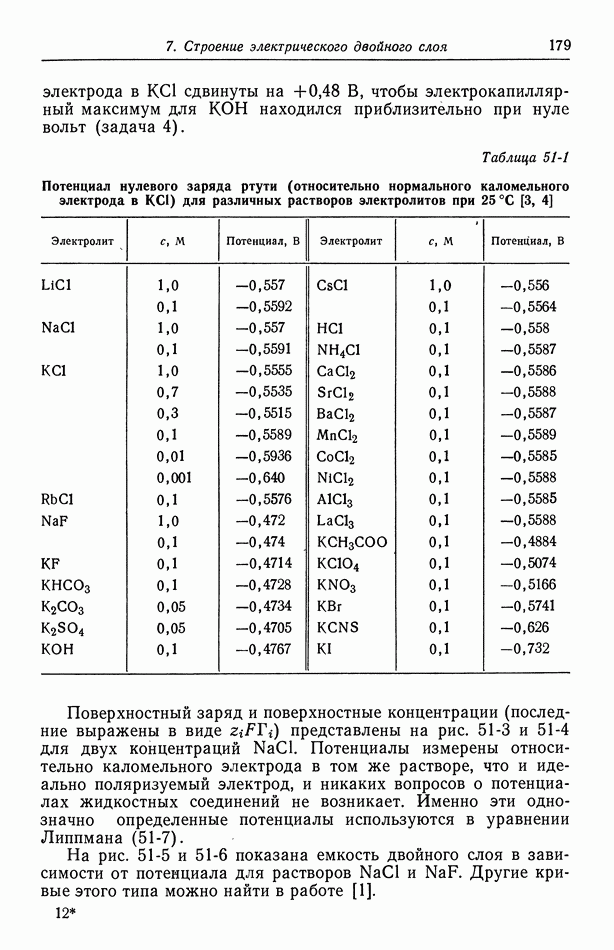
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
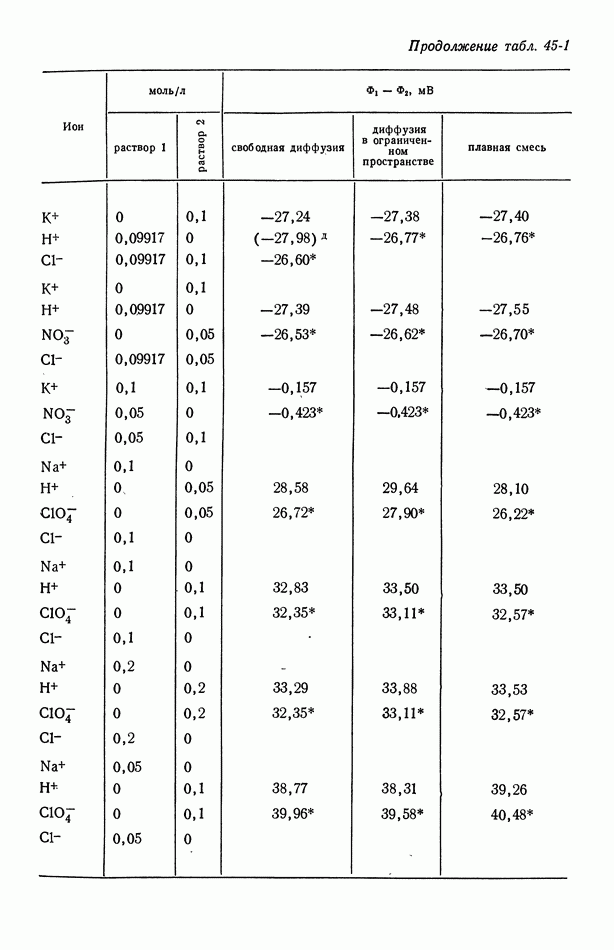
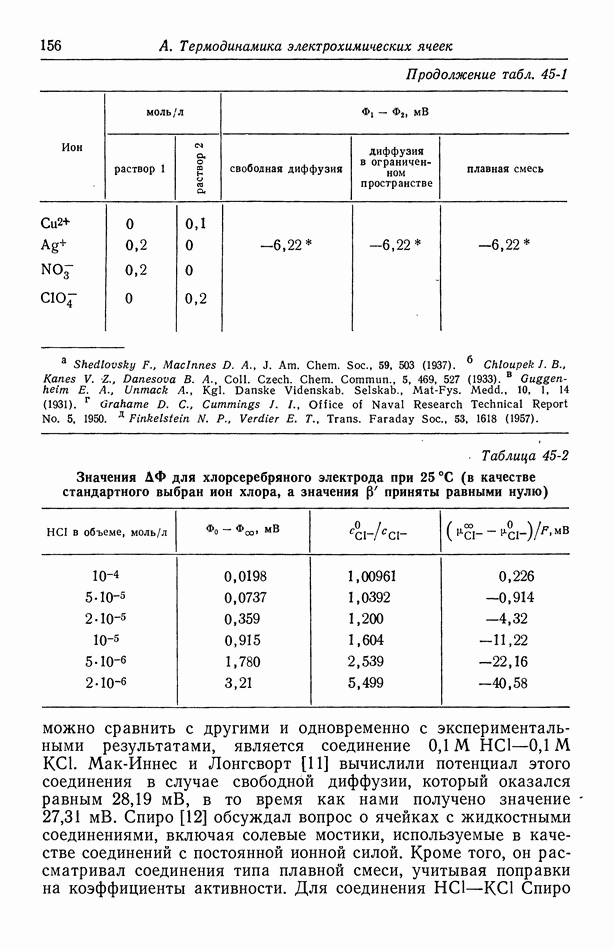
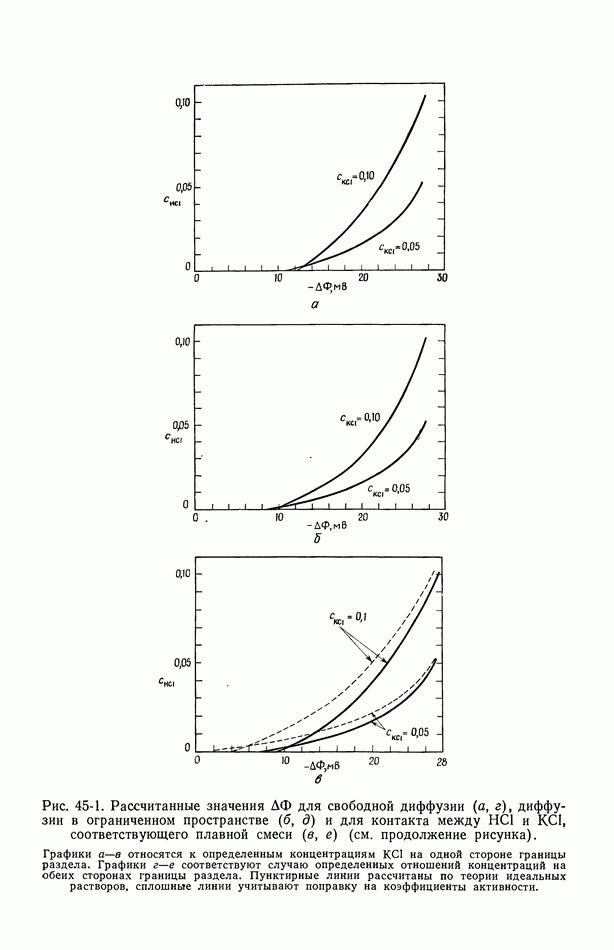
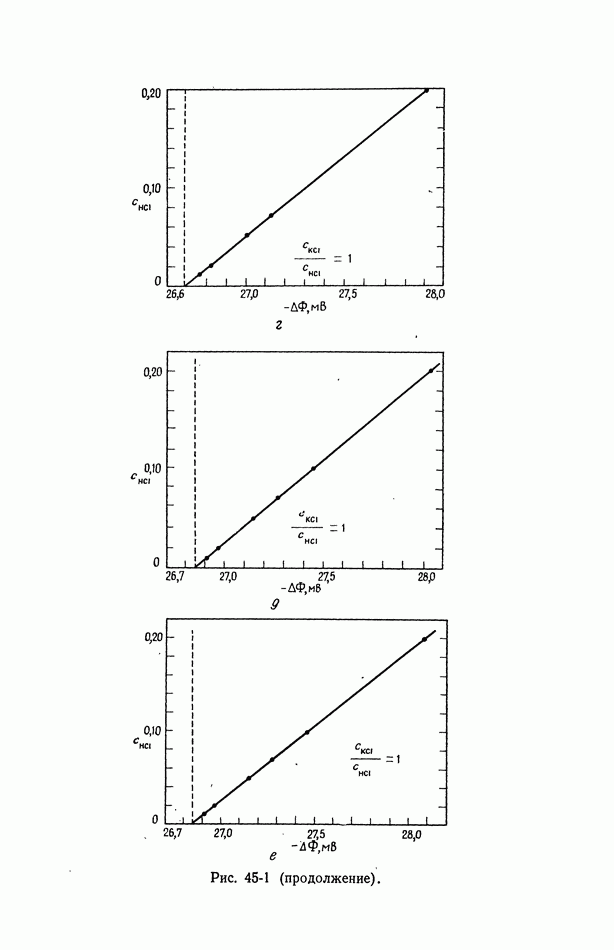
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
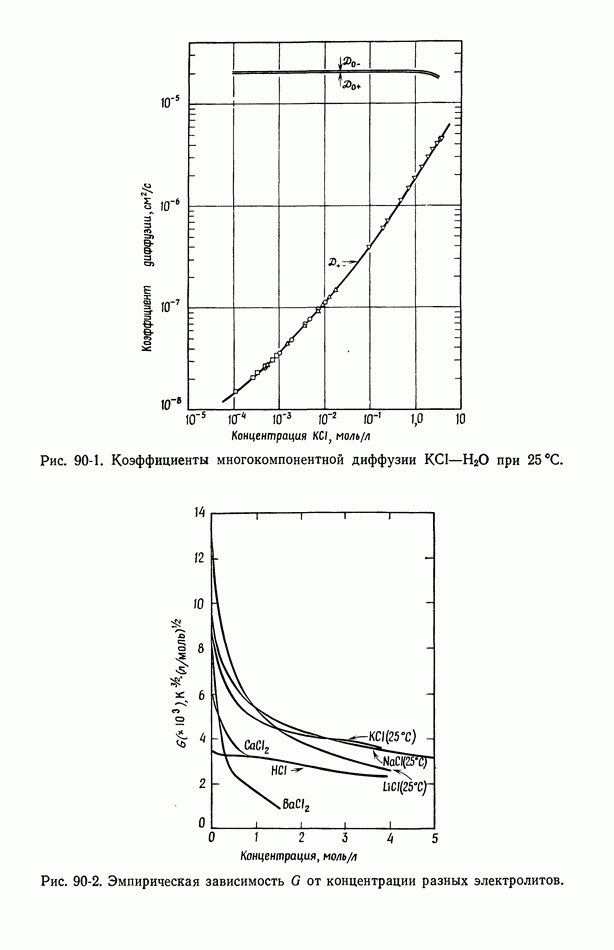
- 90. Растворы, содержащие одну соль
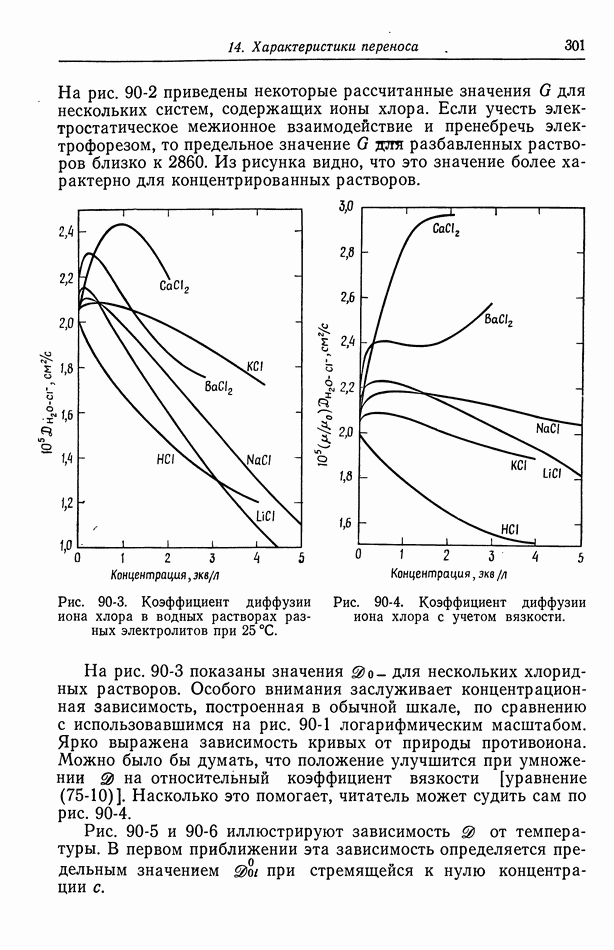
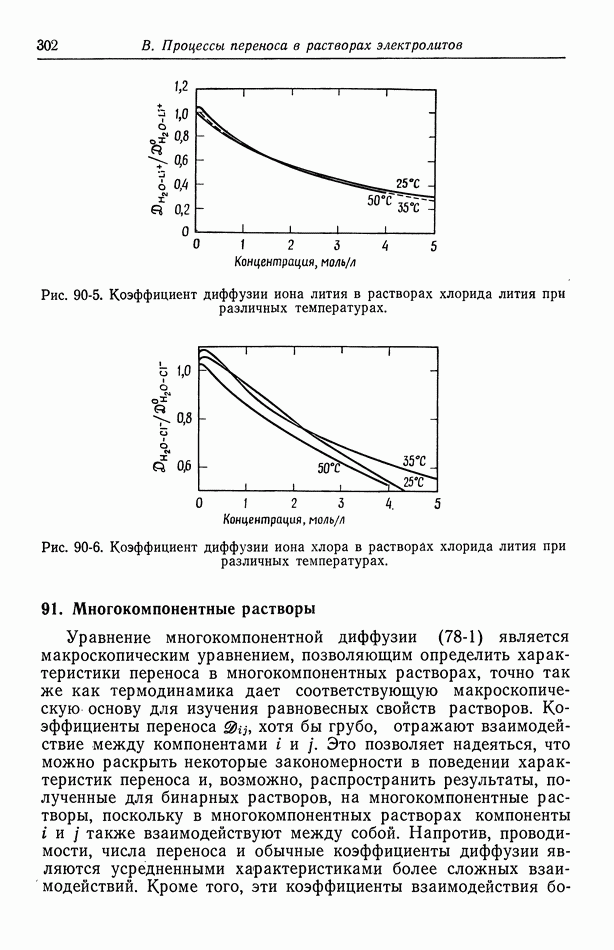
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
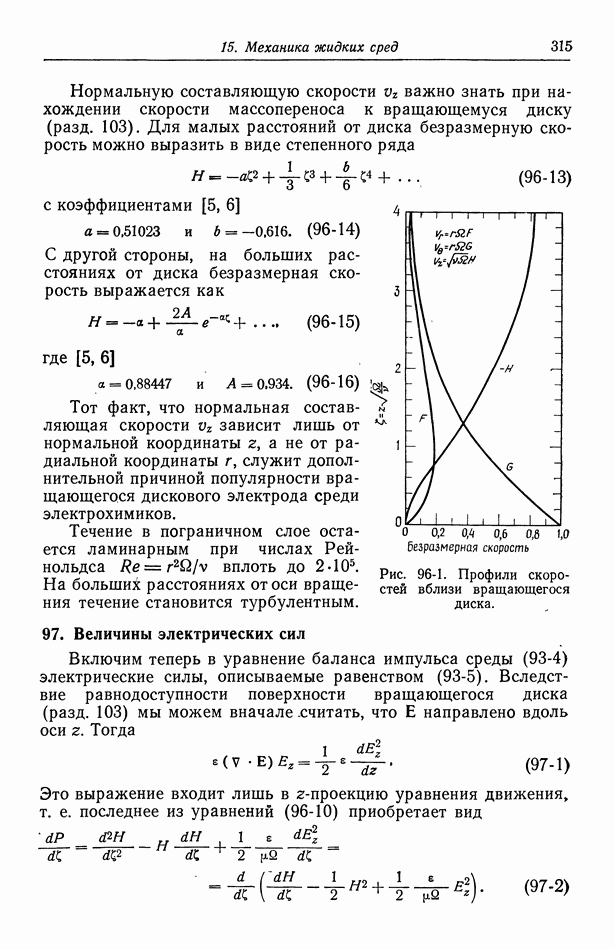
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
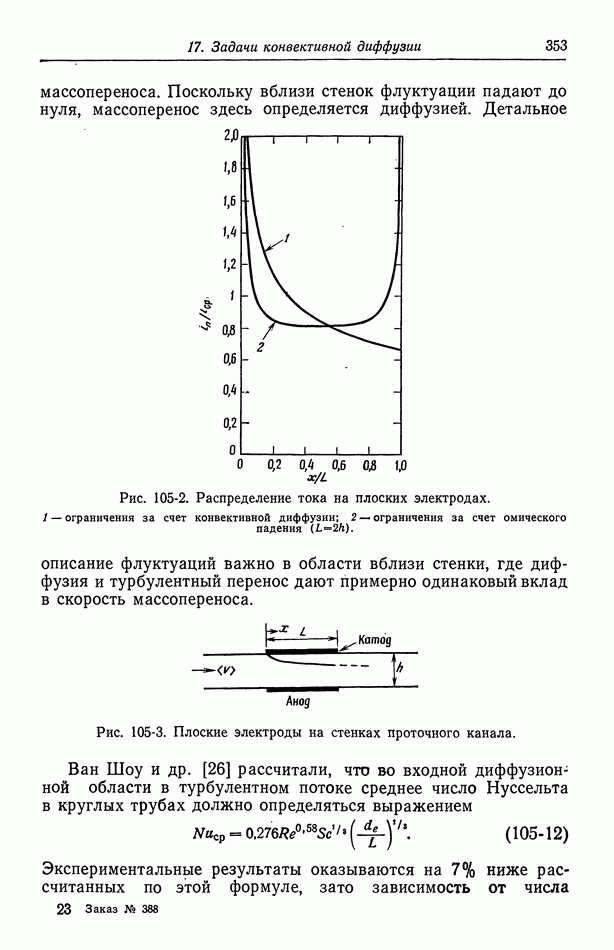
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
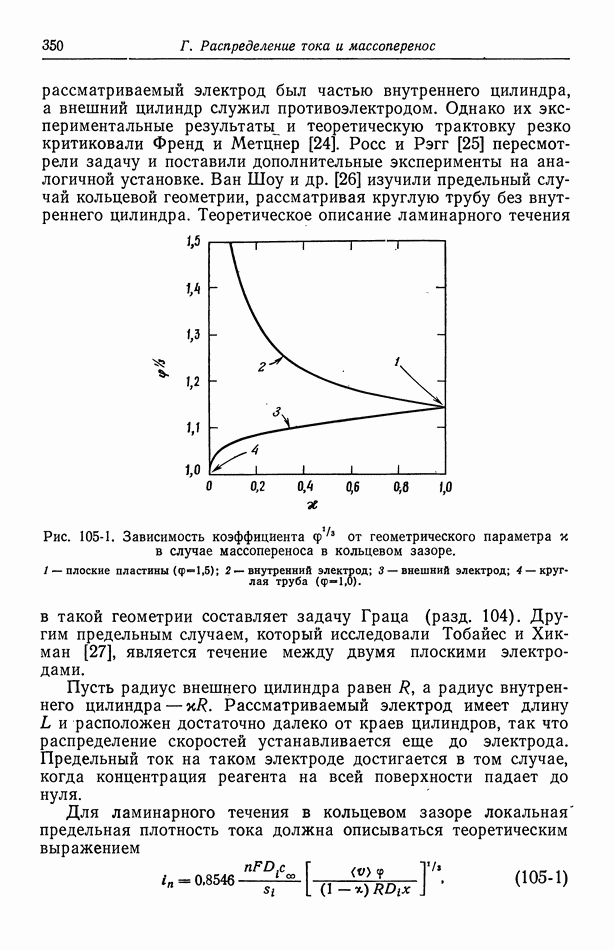
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
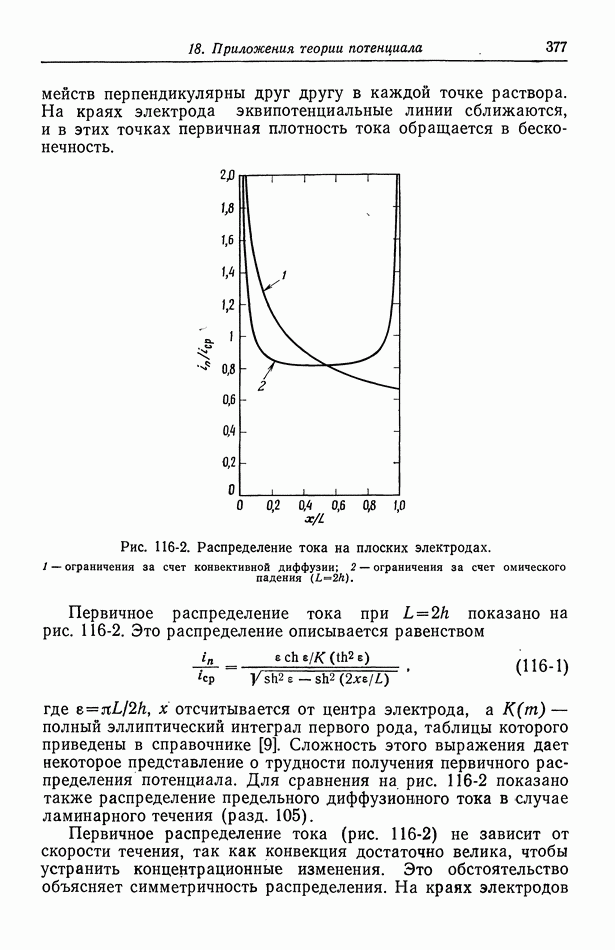
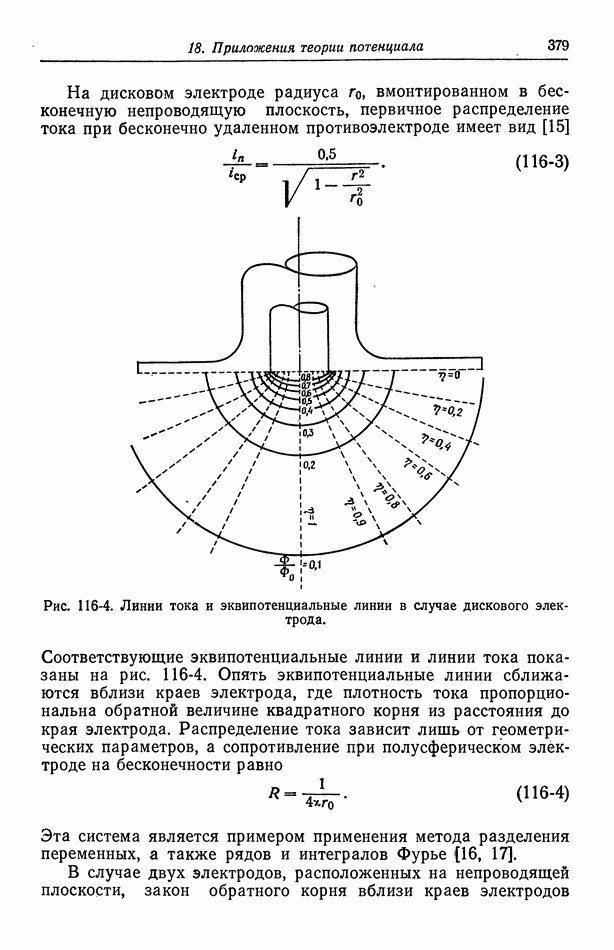
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ