| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
116. Первичное распределение тока
Так называемые первичные распределения тока и потенциала имеют место в том случае, когда можно полностью пренебречь поверхностным перенапряжением. Тогда раствор вблизи электрода можно считать эквипотенциальной поверхностью.

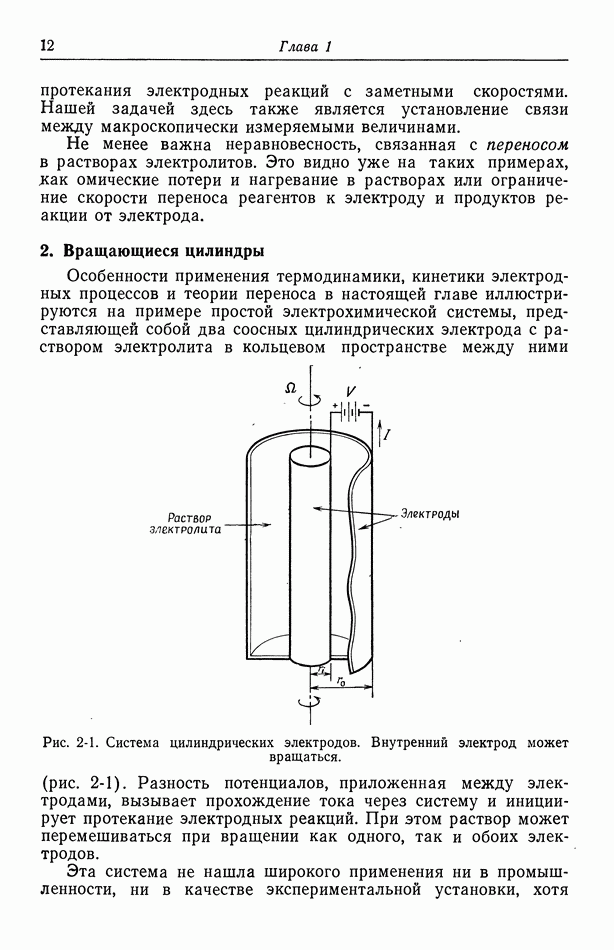
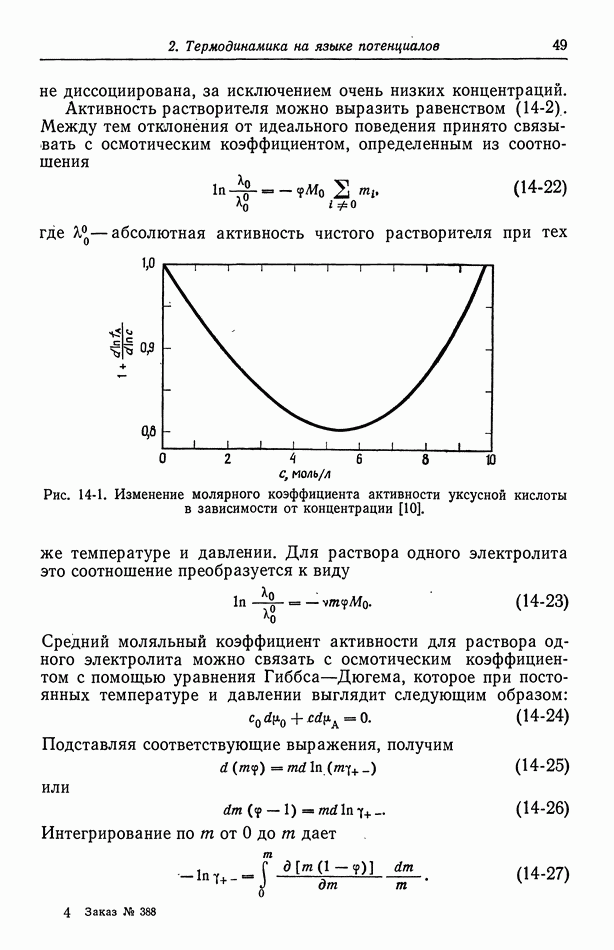
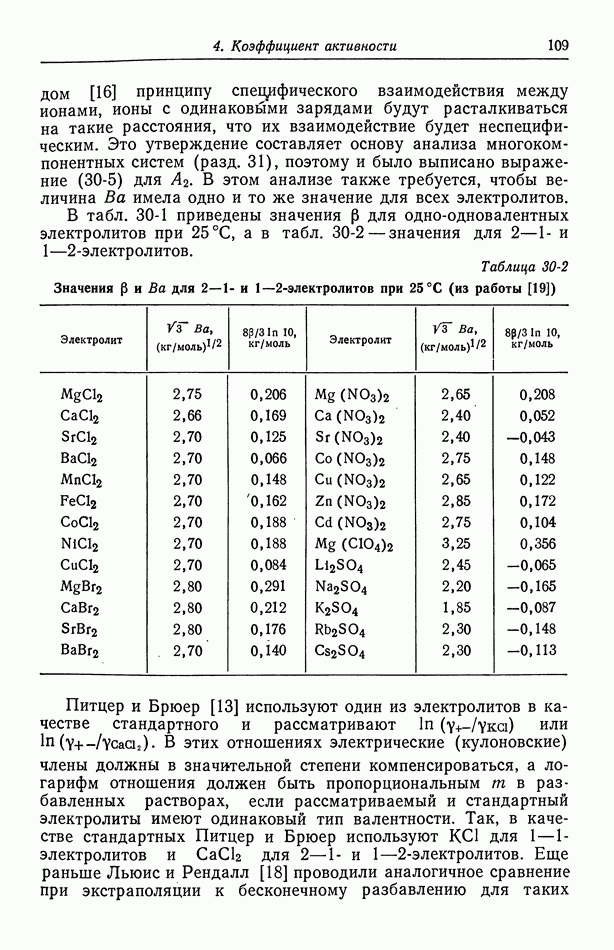
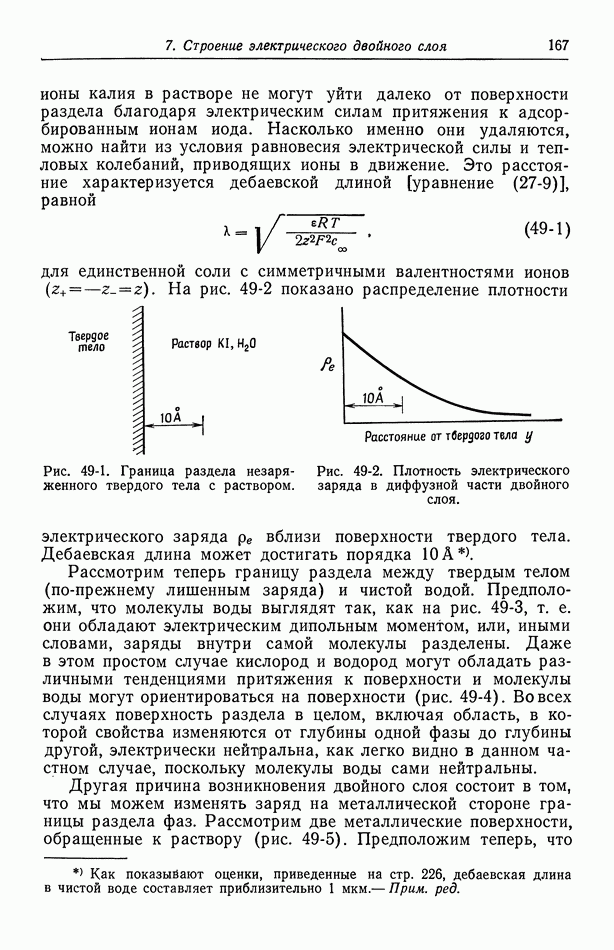
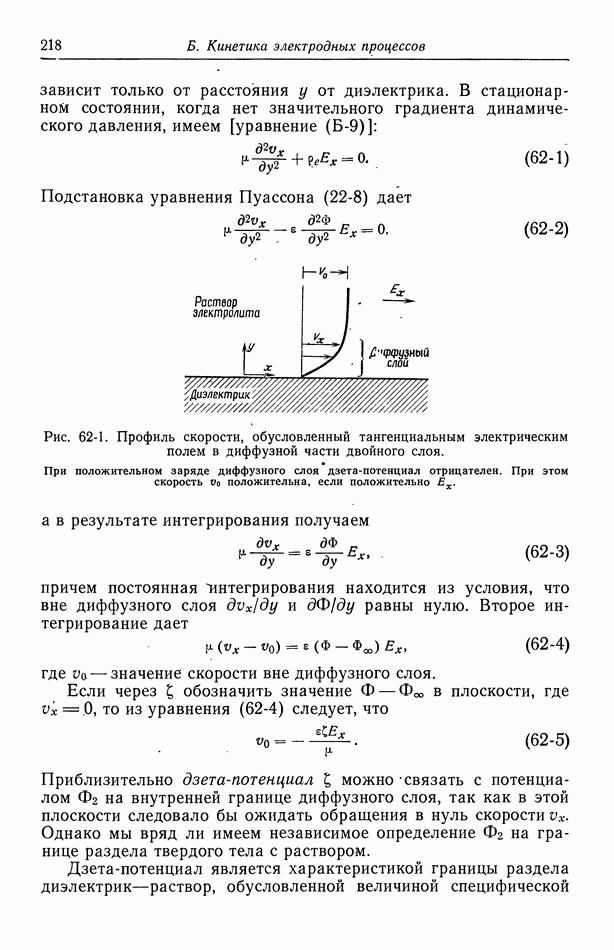
Рис. 116-1. Два плоских электрода, расположенные напротив друг друга на непроводящих стенках проточного канала.
При этом решение уравнения Лапласа — не совсем тривиальная задача даже в случаях сравнительно простой геометрии.
Мултон [7] дал классическое решение задачи о первичном распределении тока в системе из двух электродов, расположенных произвольно на сторонах прямого угла. Его работа служит примером решения уравнения Лапласа с помощью конформного отображения [8], в данном случае использующего преобразование Шварца-Кристоффеля.
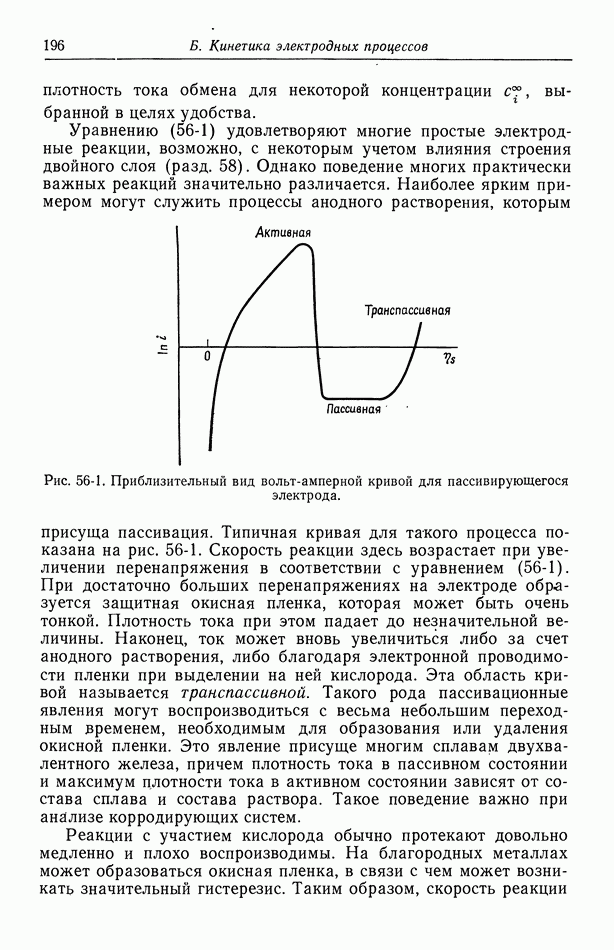
Рассмотрим частный случай двух электродов, расположенных напротив друг друга на стенках проточного канала (рис. 105-3). Распределение потенциала при  показано на рис. 116-1, где линии тока изображены сплошными кривыми, а эквипотенциальные поверхности — пунктирными. Кривые этих двух
показано на рис. 116-1, где линии тока изображены сплошными кривыми, а эквипотенциальные поверхности — пунктирными. Кривые этих двух
семейств перпендикулярны друг другу в каждой точке раствора. На краях электрода эквипотенциальные линии сближаются, и в этих точках первичная плотность тока обращается в бесконечность.

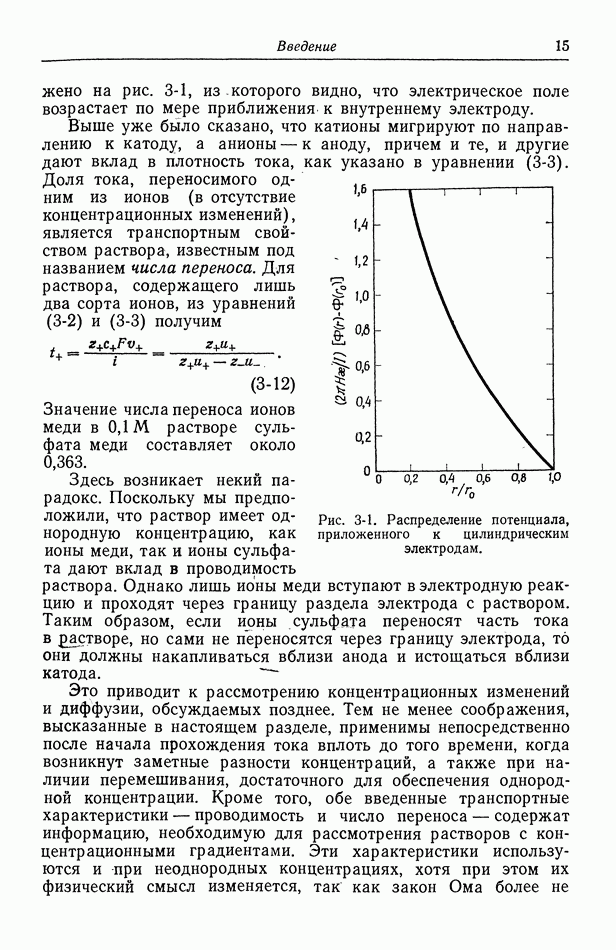
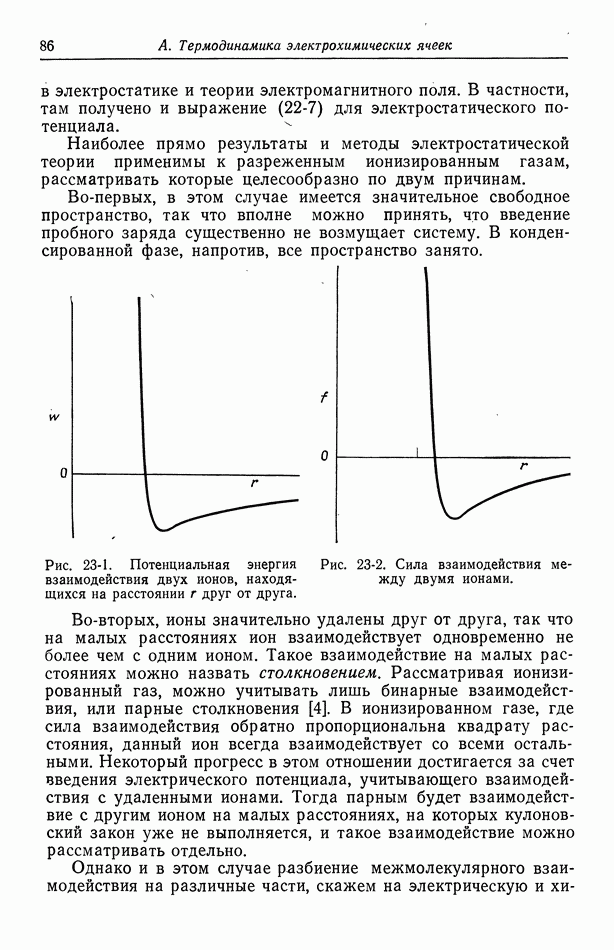
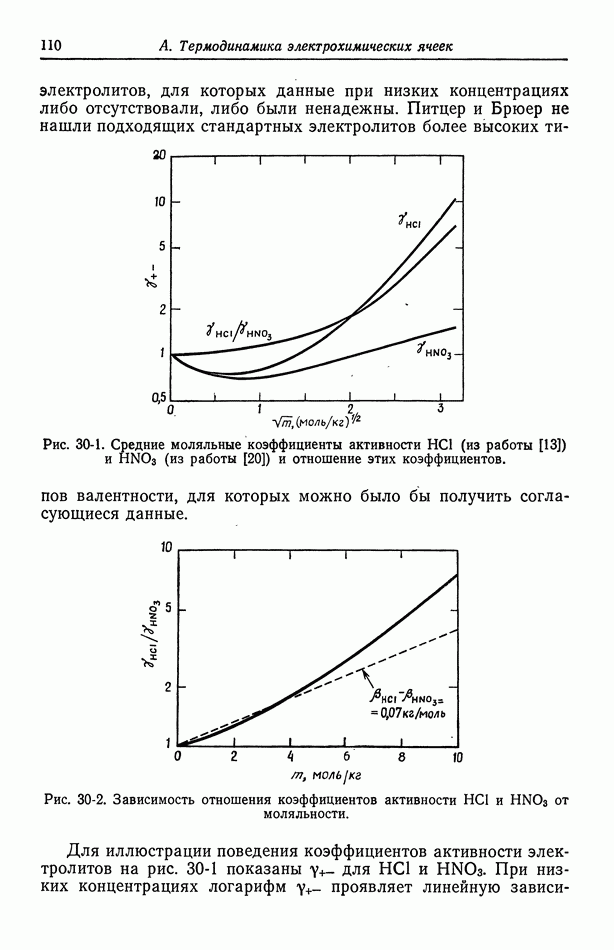
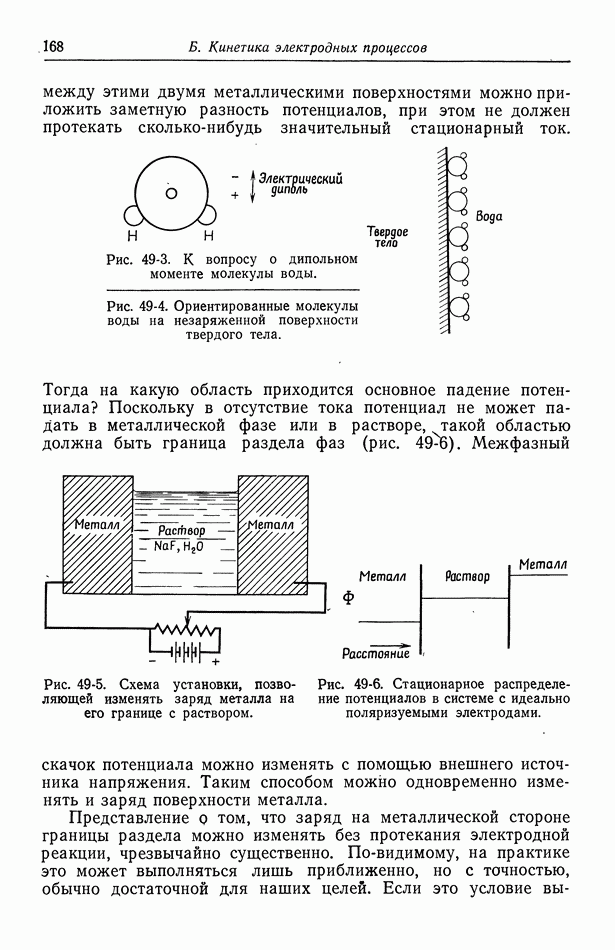
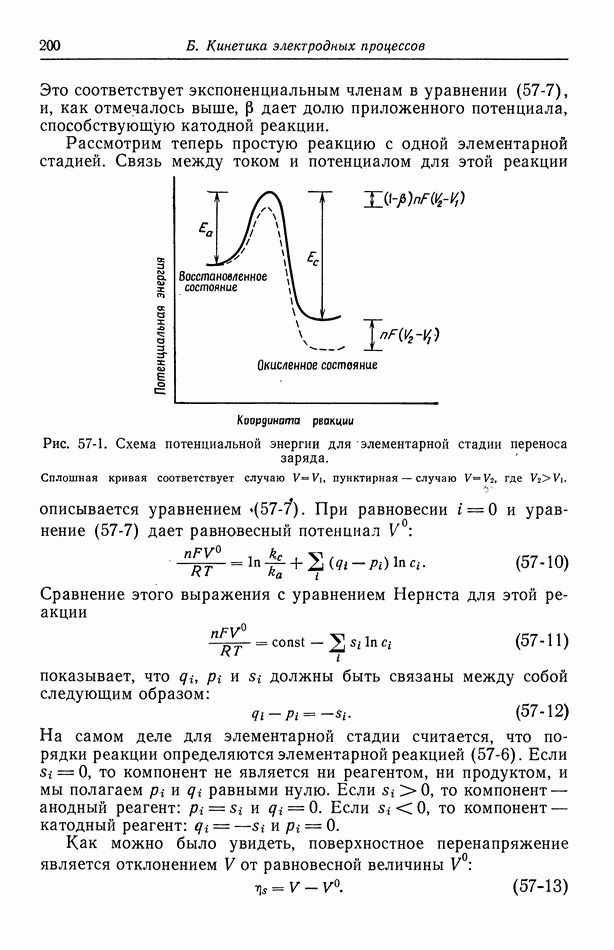
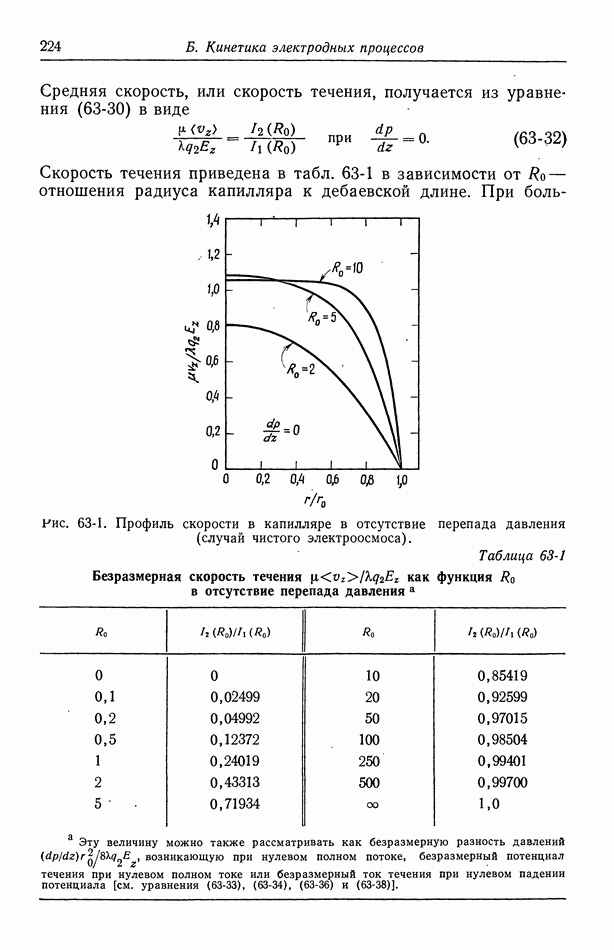
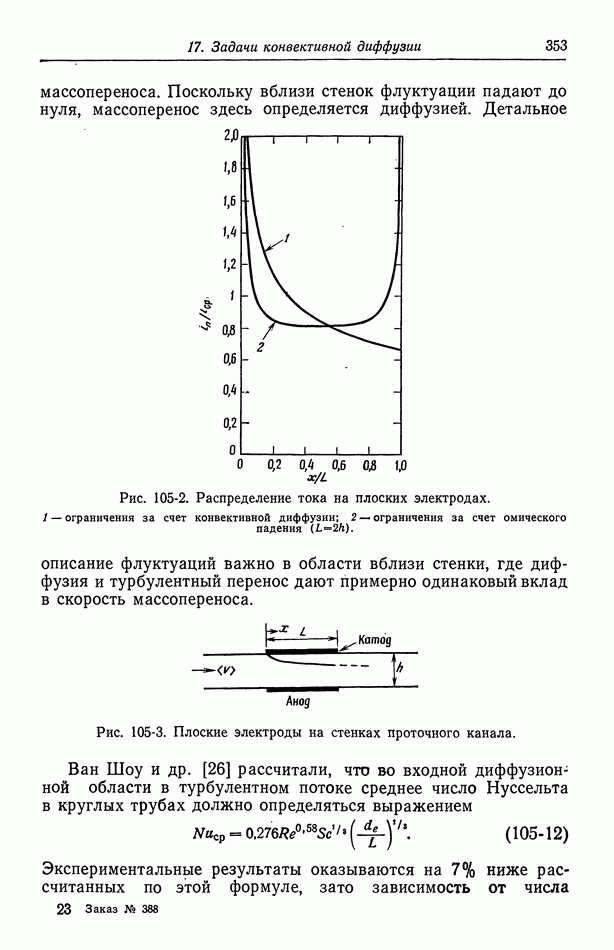
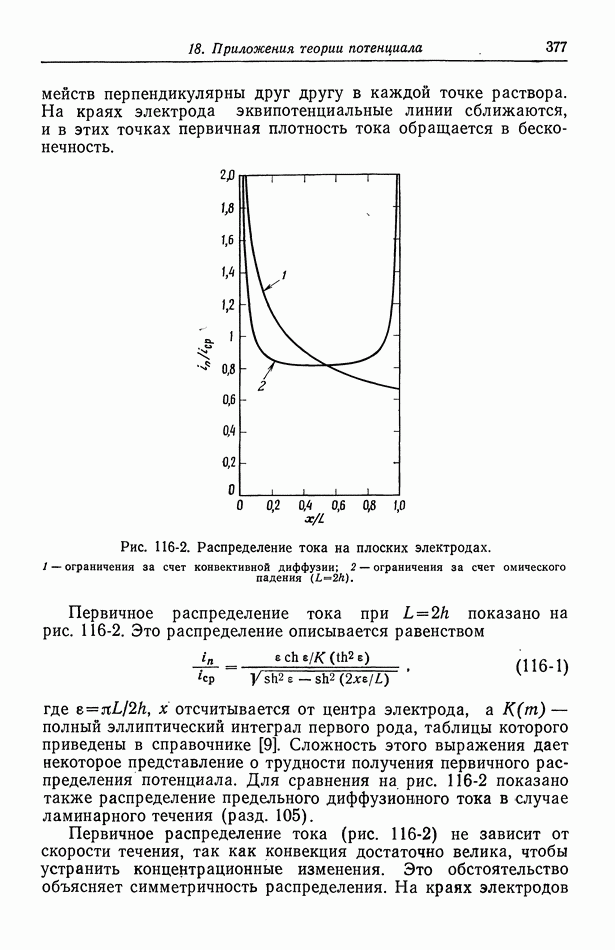
Рис. 116-2. Распределение тока на плоских электродах. 1 — ограничения за счет конвективной диффузии; 2 — ограничения за счет омического падения 
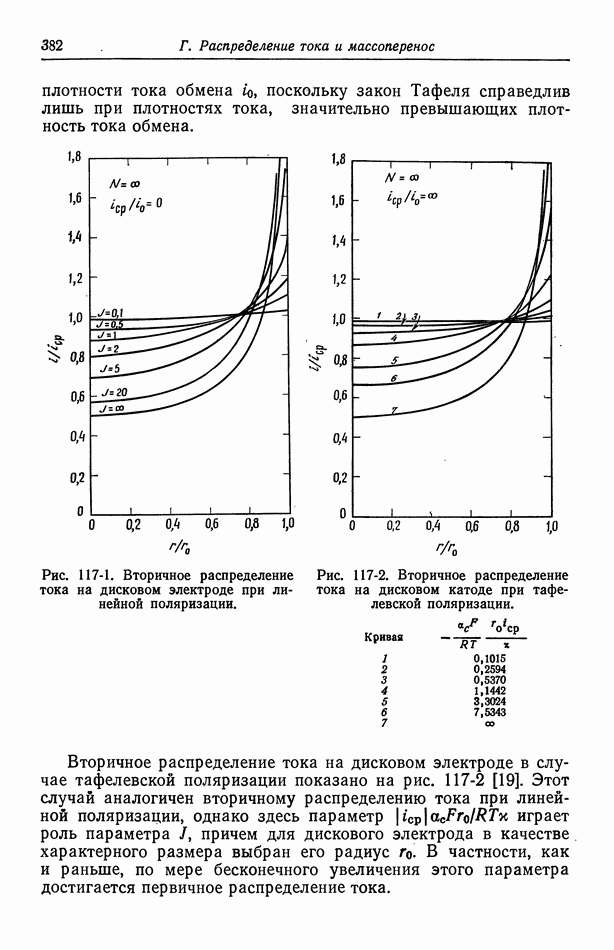
Первичное распределение тока при  показано на рис. 116-2. Это распределение описывается равенством
показано на рис. 116-2. Это распределение описывается равенством

где  отсчитывается от центра электрода, а
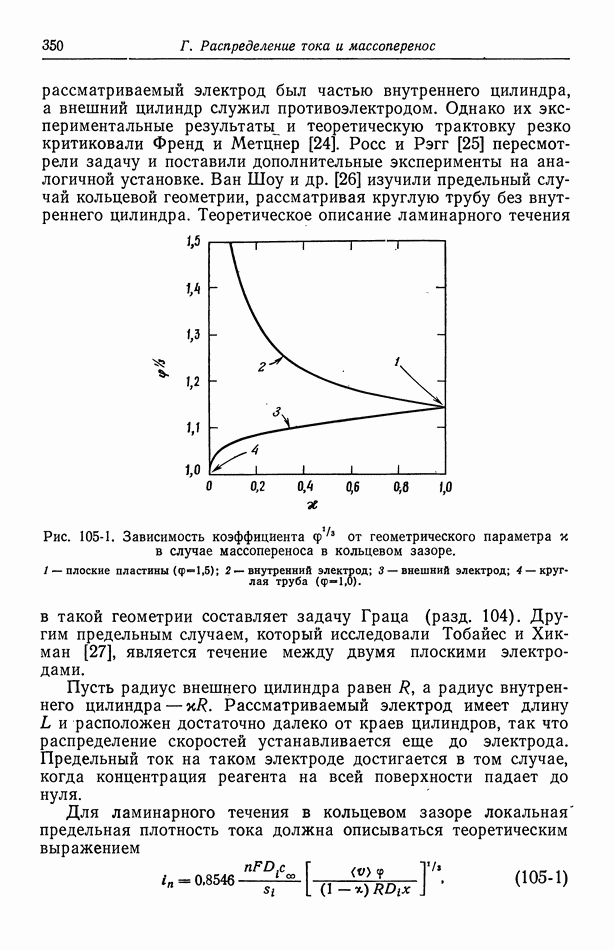
отсчитывается от центра электрода, а  полный эллиптический интеграл первого рода, таблицы которого приведены в справочнике [9]. Сложность этого выражения дает некоторое представление о трудности получения первичного распределения потенциала. Для сравнения на рис. 116-2 показано также распределение предельного диффузионного тока в случае ламинарного течения (разд. 105).
полный эллиптический интеграл первого рода, таблицы которого приведены в справочнике [9]. Сложность этого выражения дает некоторое представление о трудности получения первичного распределения потенциала. Для сравнения на рис. 116-2 показано также распределение предельного диффузионного тока в случае ламинарного течения (разд. 105).
Первичное распределение тока (рис. 116-2) не зависит от скорости течения, так как конвекция достаточно велика, чтобы устранить концентрационные изменения. Это обстоятельство объясняет симметричность распределения. На краях электродов
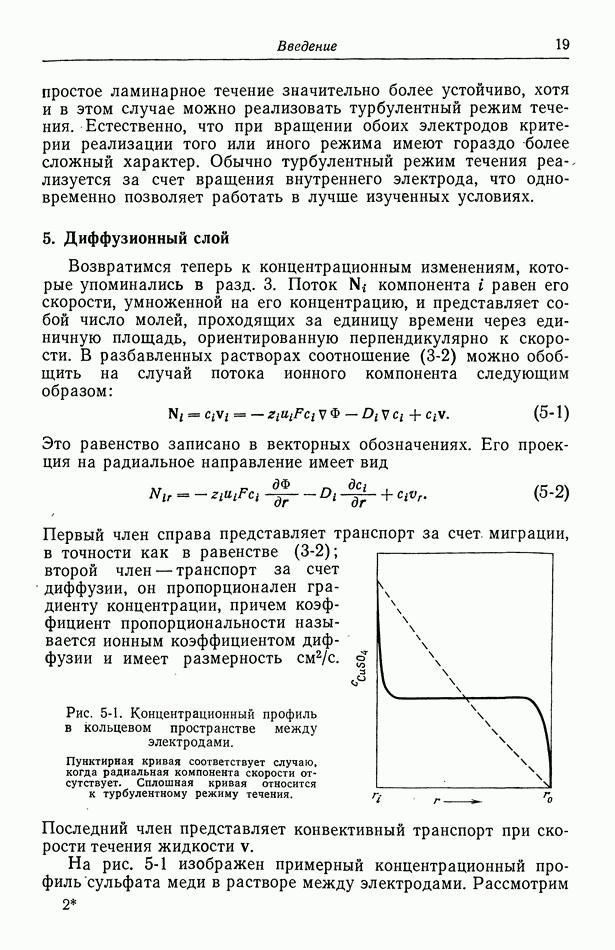
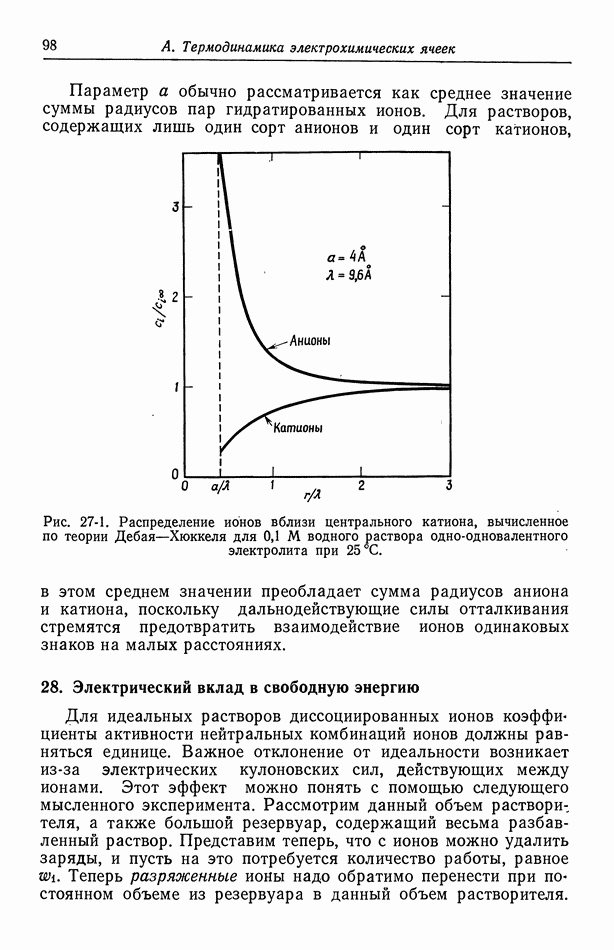
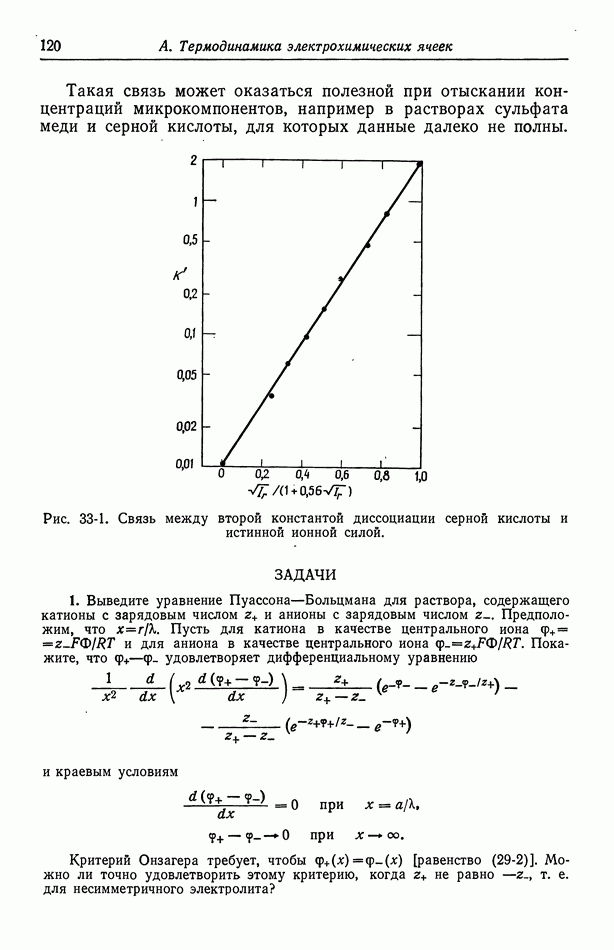
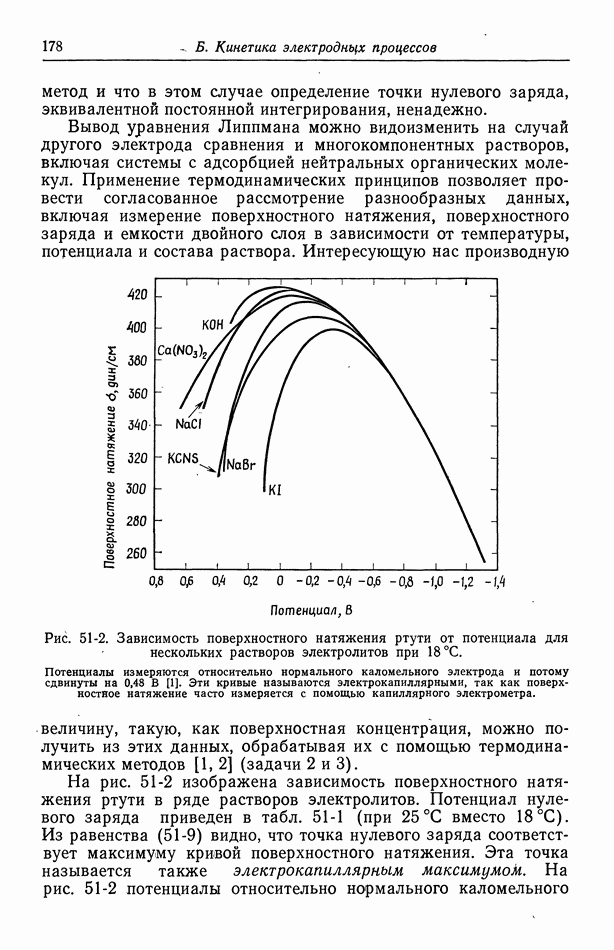
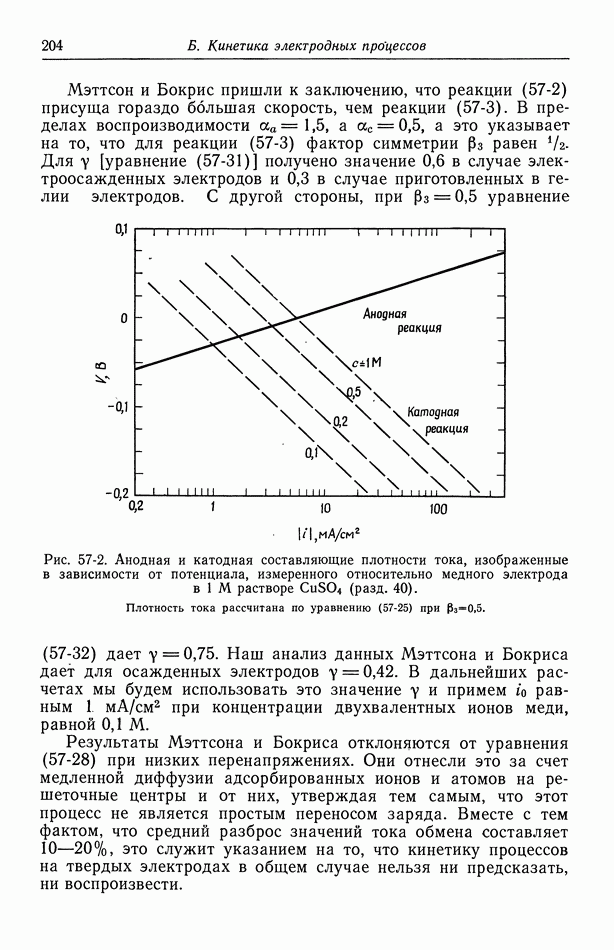
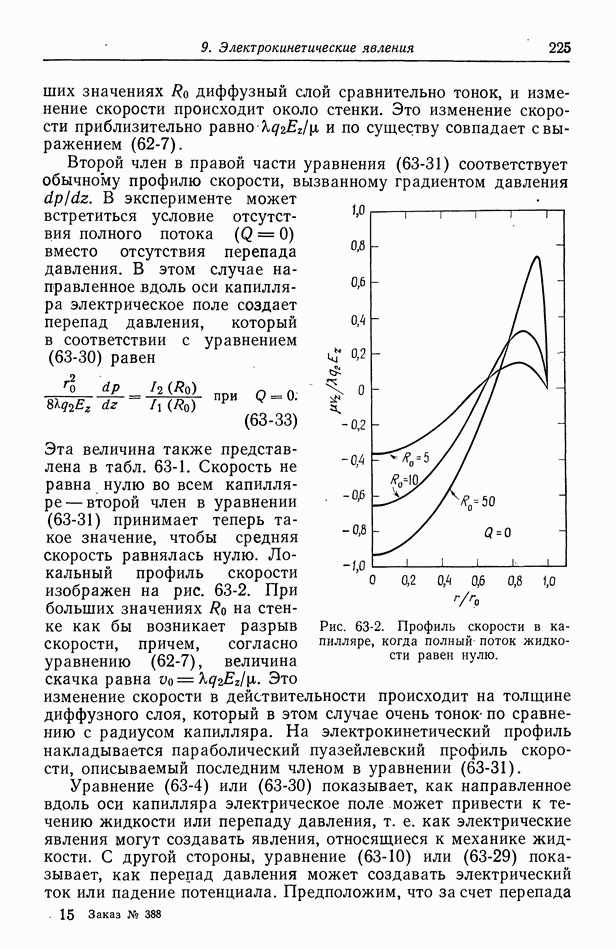
плотность тока бесконечна, поскольку ток может проходить через раствор за пределами электродной области (рис. 116-1). Это — общее свойство первичных распределений тока. В точке соприкосновения электрода с изолятором плотность тока либо бесконечна, либо равна нулю, если только поверхности электрода и изолятора не пересекаются под прямым углом (рис. 116-3). Если электрод и изолятор расположены в одной и той же плоскости, то на малых расстояниях от края электрода плотность тока обратно пропорциональна квадратному корню из расстояния. Такой тип зависимости дает равенство  задающее плотность тока. В общем случае первичное распределение тока показывает, что на менее доступных частях электрода плотность тока понижена.
задающее плотность тока. В общем случае первичное распределение тока показывает, что на менее доступных частях электрода плотность тока понижена.

Рис. 116-3. Особенности первичного распределения тока вблизи края электрода.
Первичное распределение тока определяется лишь геометрическими факторами. Так, в параметр  входят только безразмерные комбинации геометрических характеристик ячейки, а от проводимости раствора
входят только безразмерные комбинации геометрических характеристик ячейки, а от проводимости раствора  не зависит. Сопротивление этой ячейки равно
не зависит. Сопротивление этой ячейки равно

где  ширина электродов.
ширина электродов.
В работе Каспера [10] приведено первичное распределение тока для точечного и плоского электродов, для линейных электродов, параллельных плоским электродам и плоским изоляторам, а также для цилиндрических электродов в различных конфигурациях. Для таких систем удобно применять метод изображений. Хайн и др. [11] описали первичное распределение тока в системе двух плоских электродов бесконечной длины и конечной ширины, помещенных между двумя бесконечными непроводящими плоскостями, перпендикулярными к электродам, но не соприкасающимися с ними. Вагнер [12] вычислил распределение тока в случае двумерной щели на плоском электроде. Эти задачи также являются примерами применения преобразования Шварца-Кристоффеля. Коджима [13] составил подборку формул для сопротивлений между двумя электродами различных конфигураций. Имеются аналогичные подборки для сопротивления теплопереносу в твердых телах [14] и для емкости двух электродов.
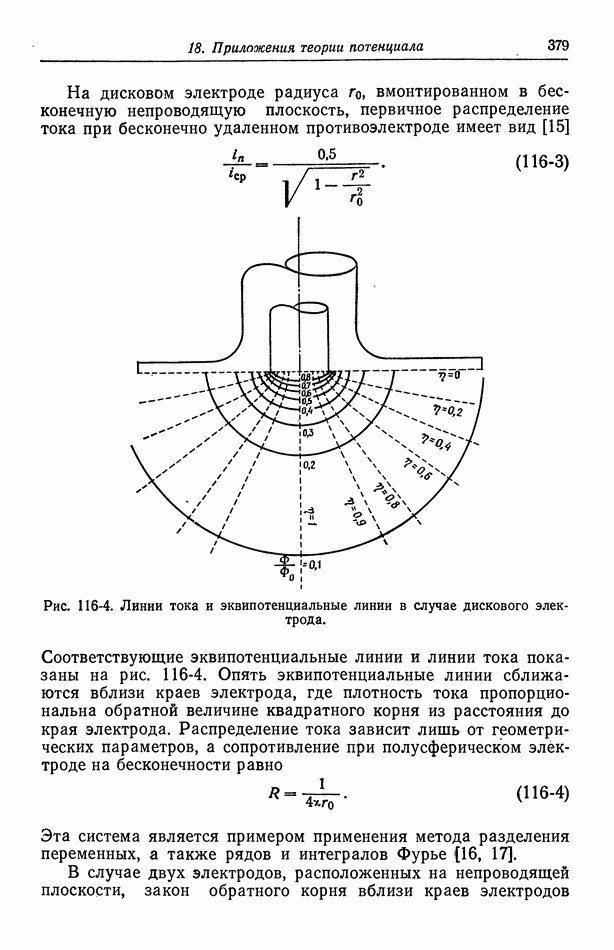
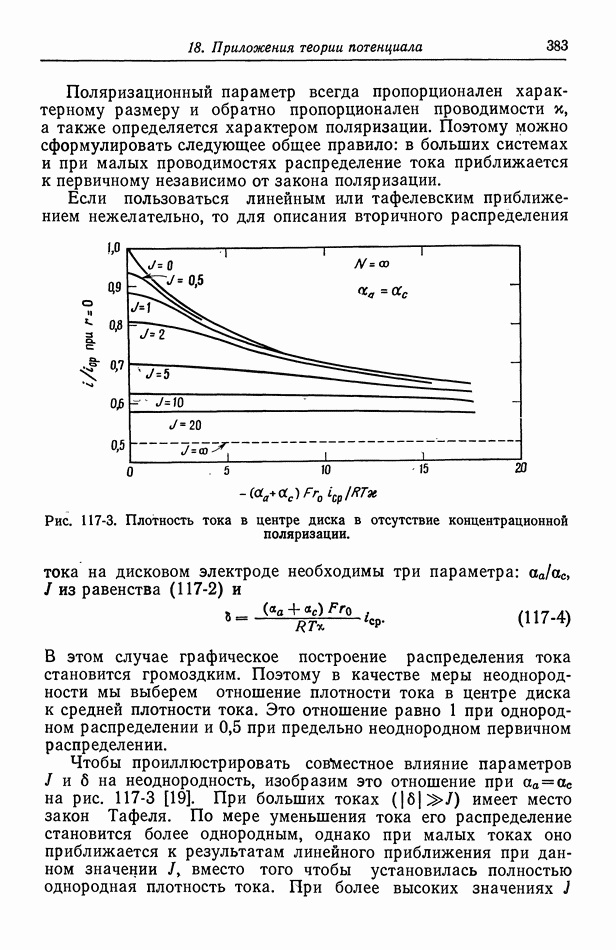
На дисковом электроде радиуса  вмонтированном в бесконечную непроводящую плоскость, первичное распределение тока при бесконечно удаленном противоэлектроде имеет вид [15]
вмонтированном в бесконечную непроводящую плоскость, первичное распределение тока при бесконечно удаленном противоэлектроде имеет вид [15]


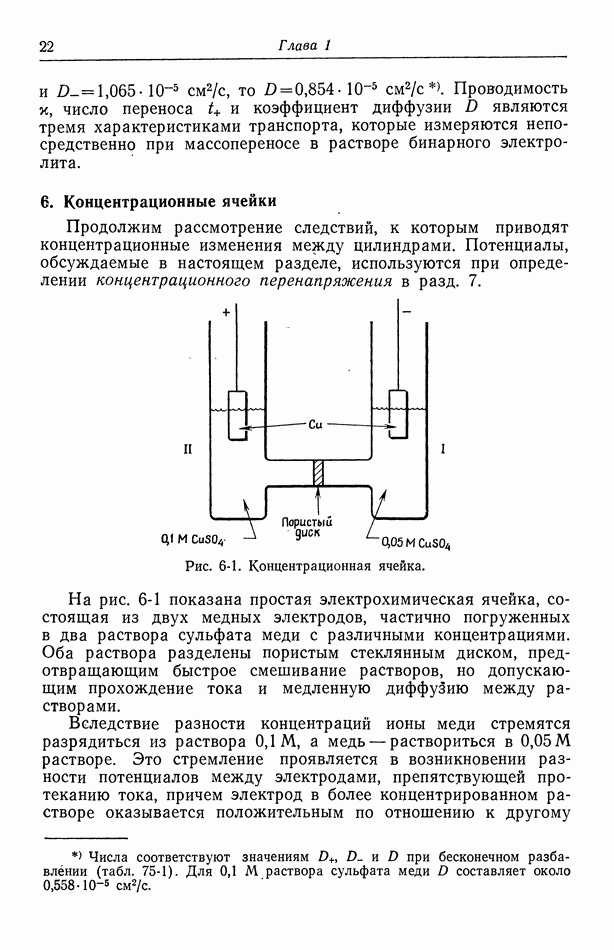
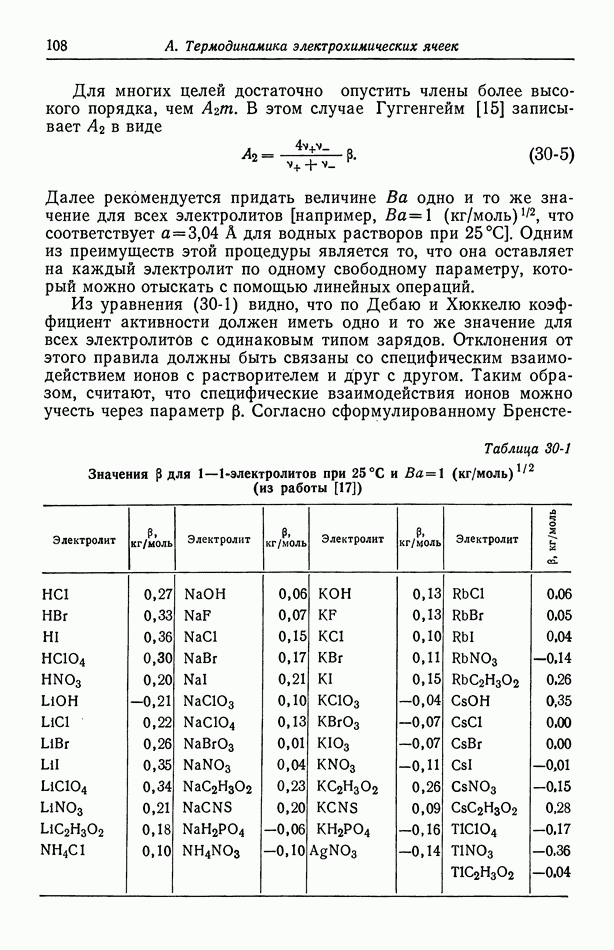
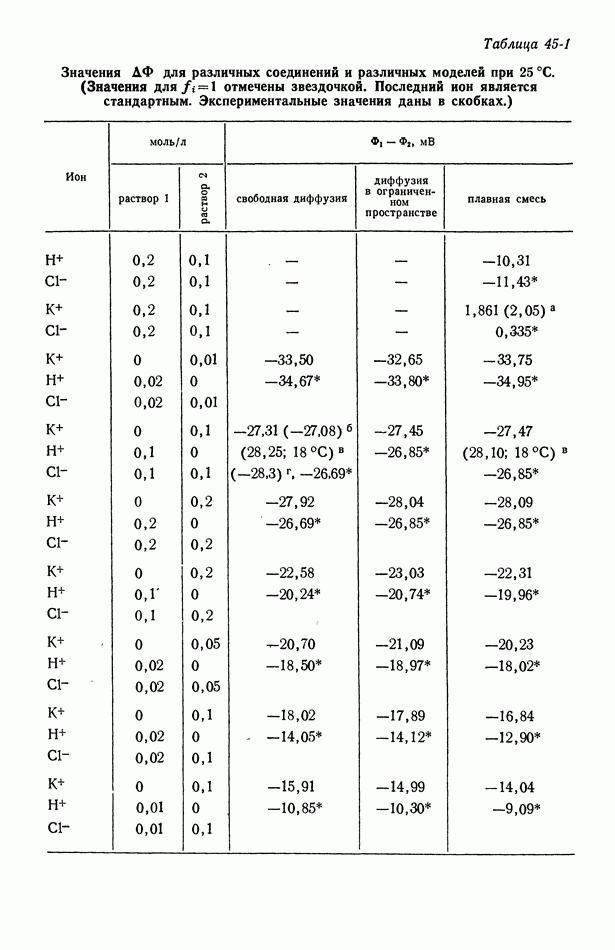
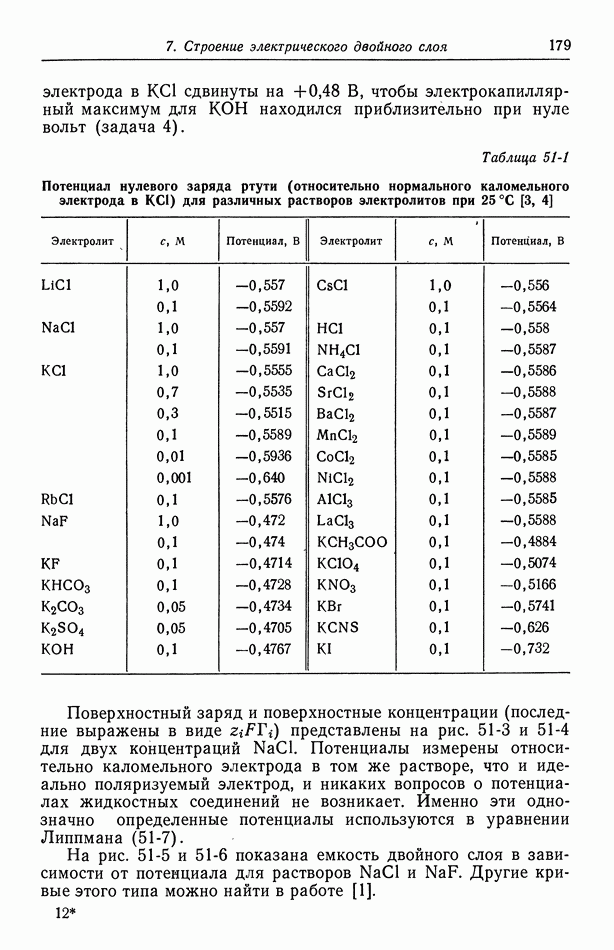
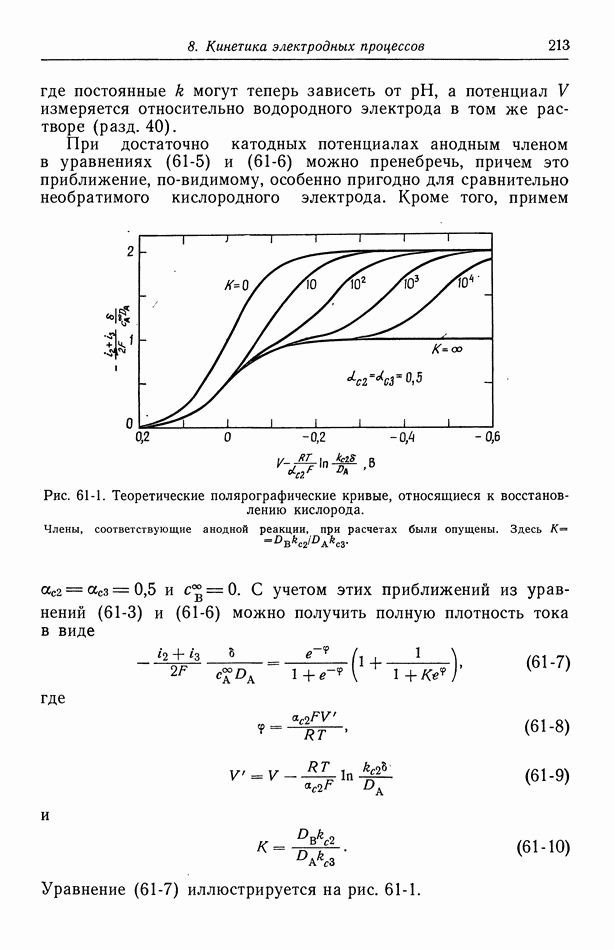
Рис. 116-4. Линии тока и эквипотенциальные линии в случае дискового электрода.
Соответствующие эквипотенциальные линии и линии тока показаны на рис. 116-4. Опять эквипотенциальные линии сближаются вблизи краев электрода, где плотность тока пропорциональна обратной величине квадратного корня из расстояния до края электрода. Распределение тока зависит лишь от геометрических параметров, а сопротивление при полусферическом электроде на бесконечности равно

Эта система является примером применения метода разделения переменных, а также рядов и интегралов Фурье (16, 17].
В случае двух электродов, расположенных на непроводящей плоскости, закон обратного корня вблизи краев электродов
по-прежнему справедлив. Однако по мере уменьшения расстояния между электродами коэффициент пропорциональности при обратном корне обращается в бесконечность таким образом, что при исчезновении промежутка между электродами полный ток становится бесконечным. Следовательно, решать задачу о первичном распределении тока в случае контакта двух электродов, находящихся при различных потенциалах, физически бессмысленно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
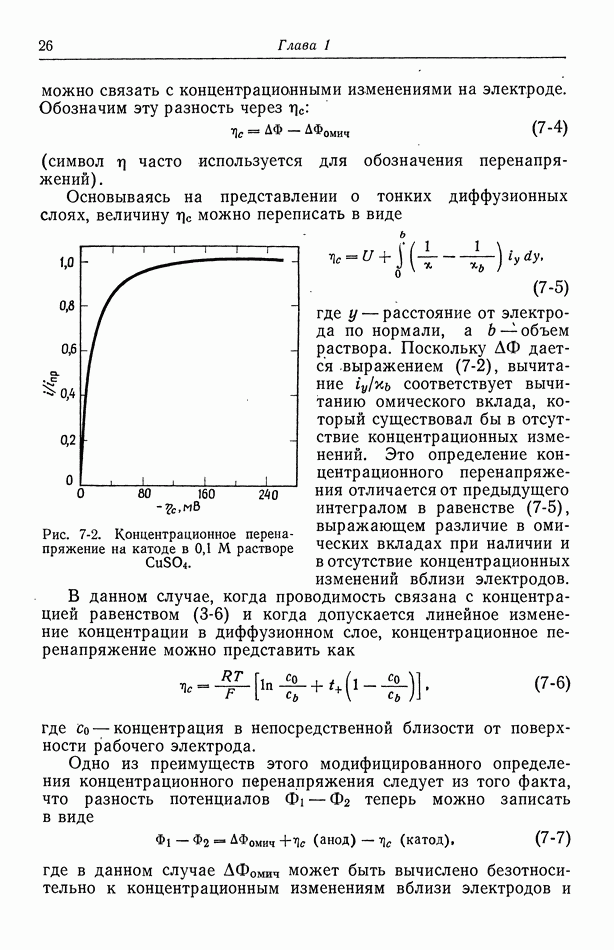
- 7. Концентрационное перенапряжение
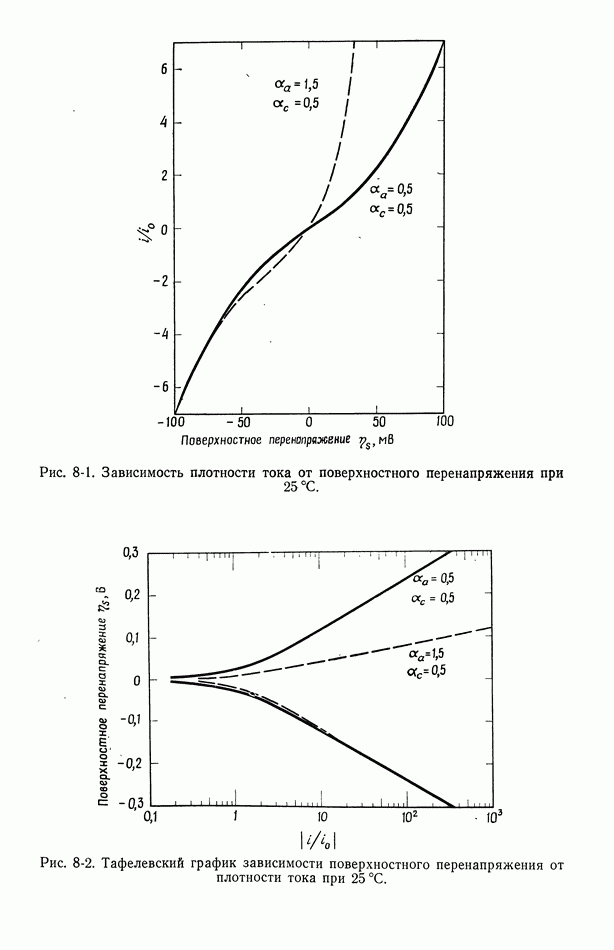
- 8. Поверхностное перенапряжение
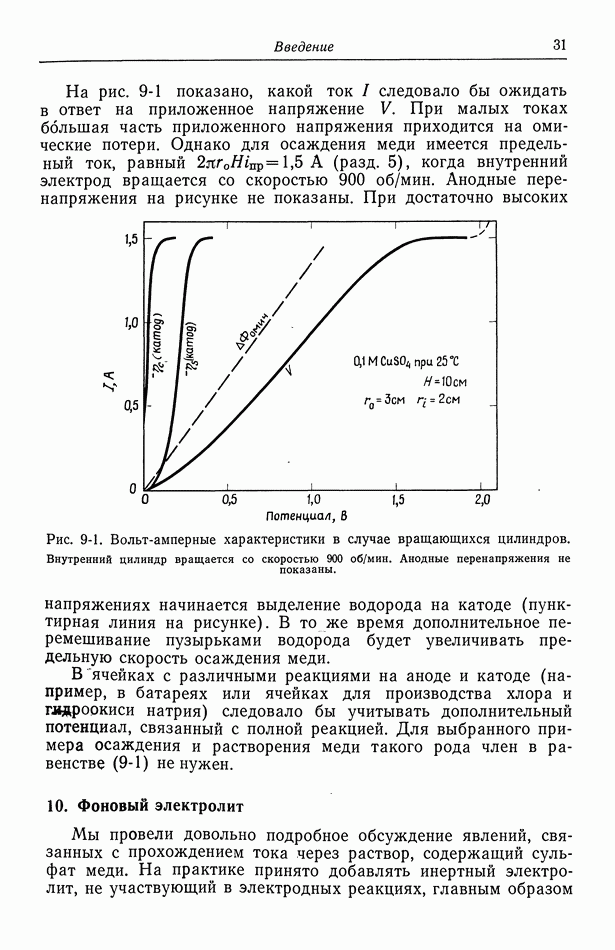
- 9. Потенциал ячейки
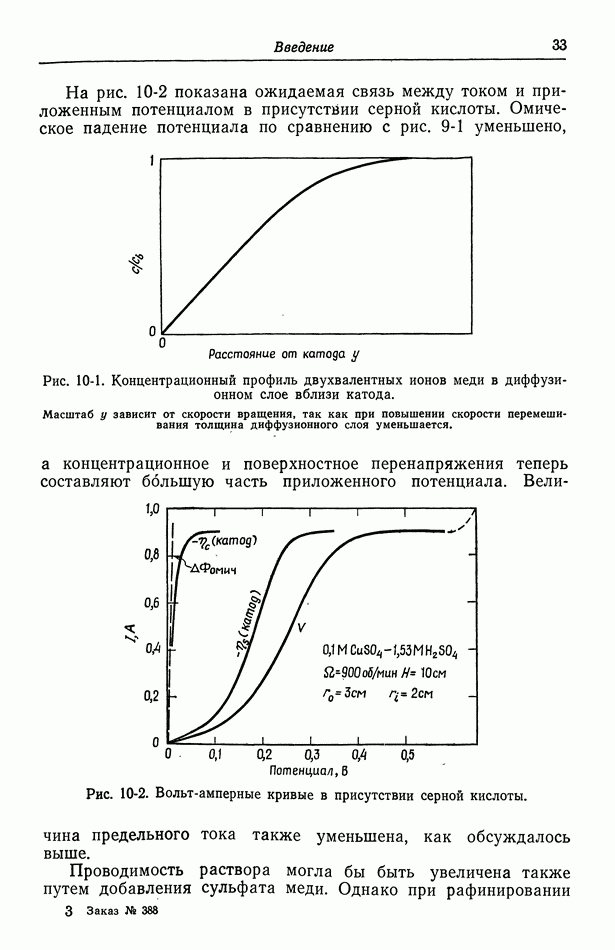
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
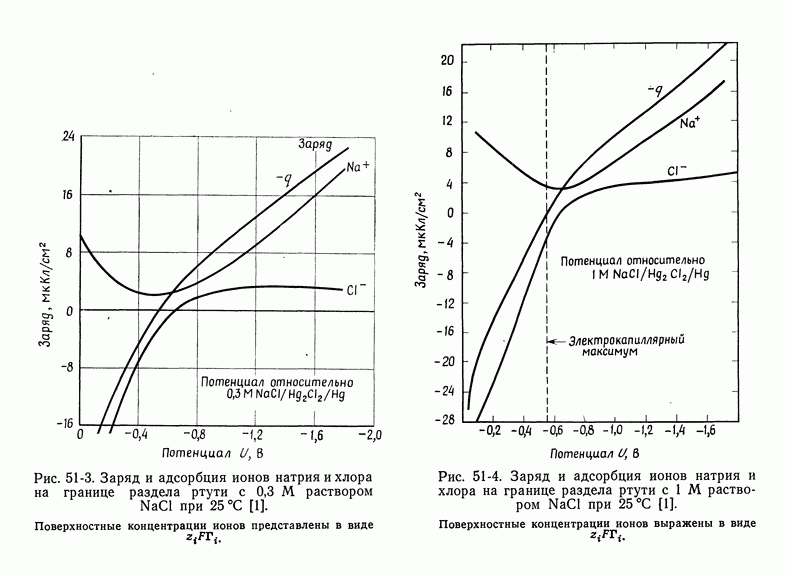
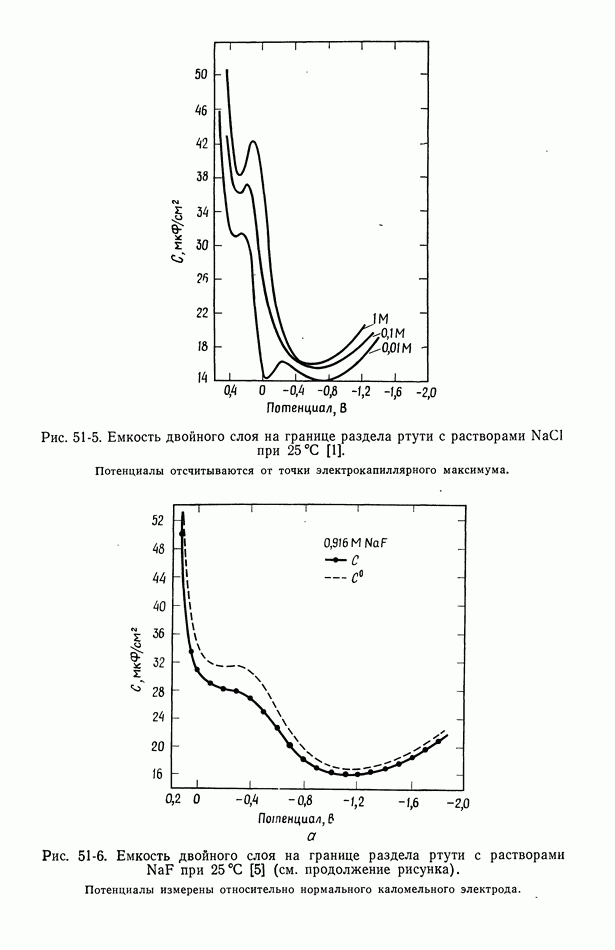
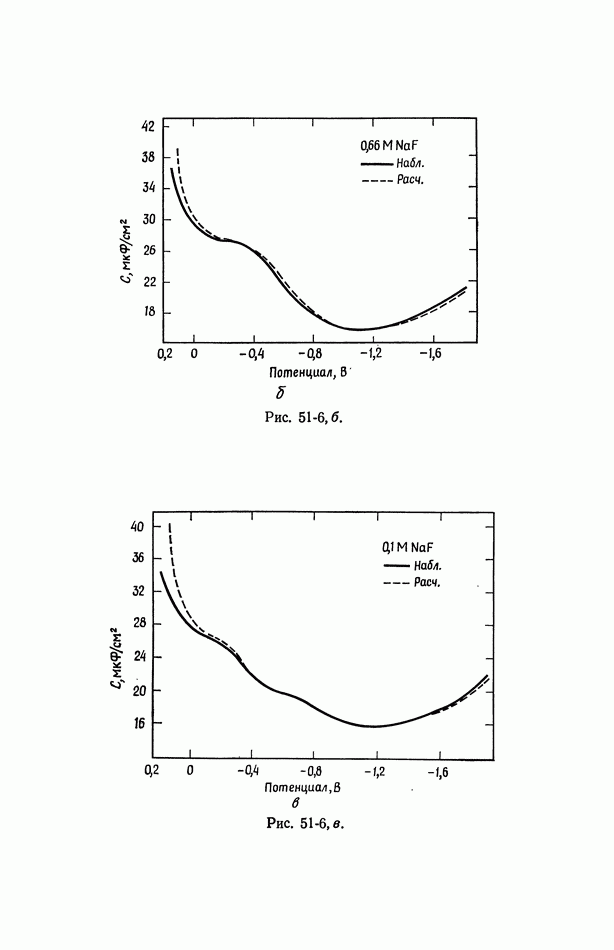
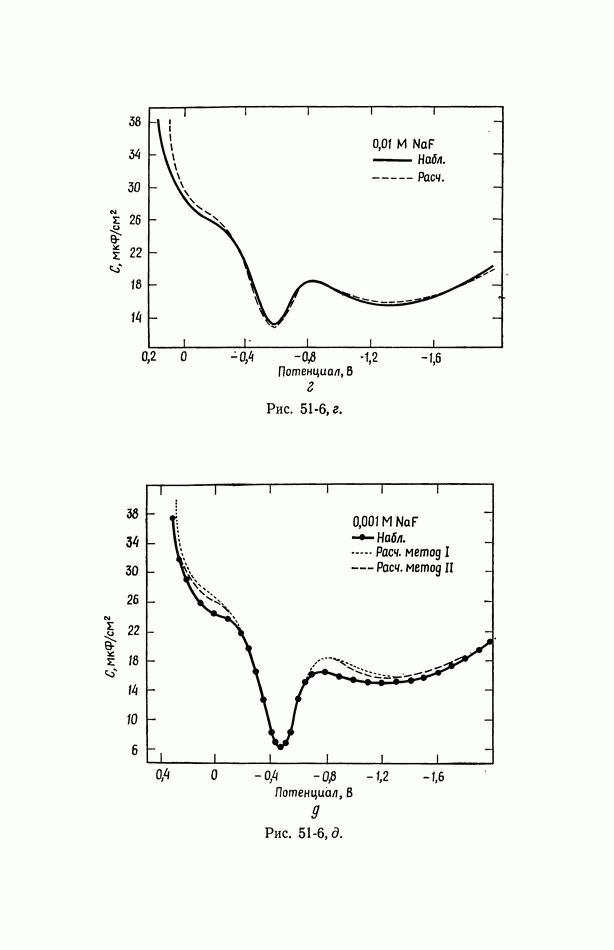
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
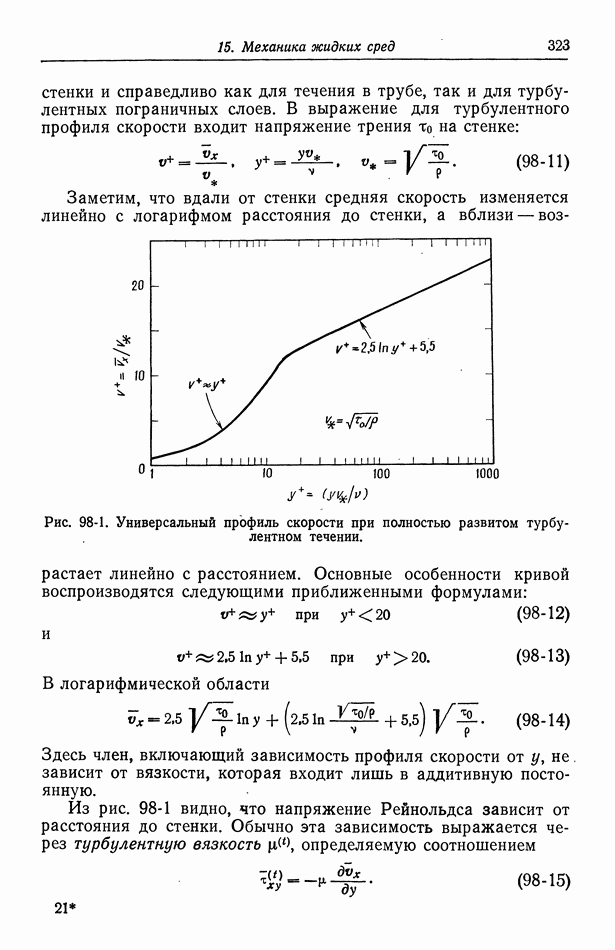
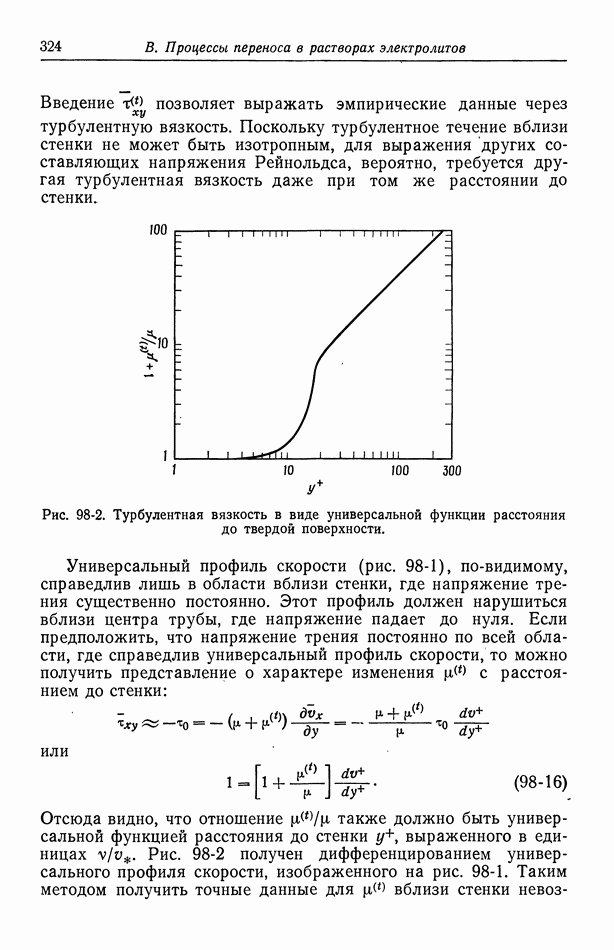
- 98. Турбулентное течение
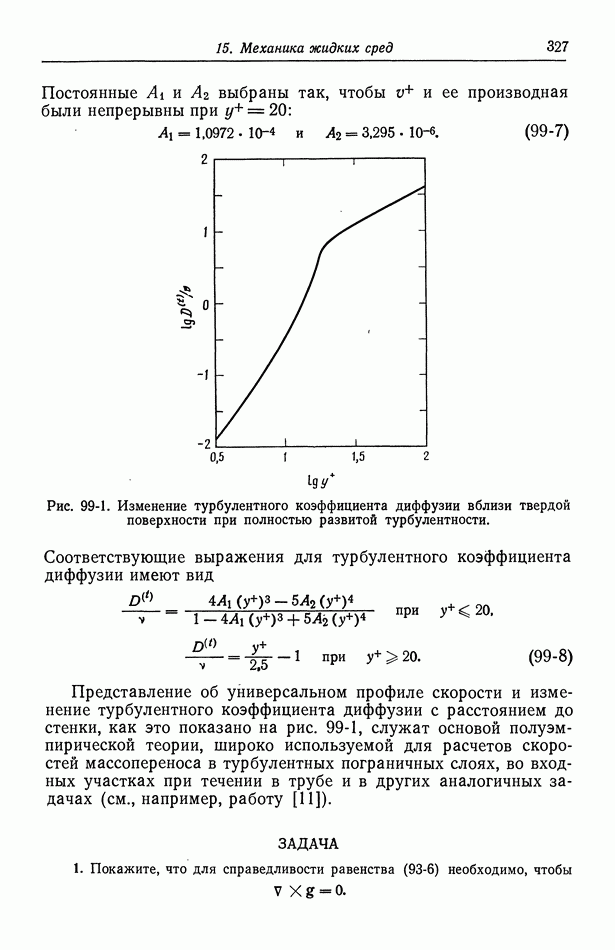
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
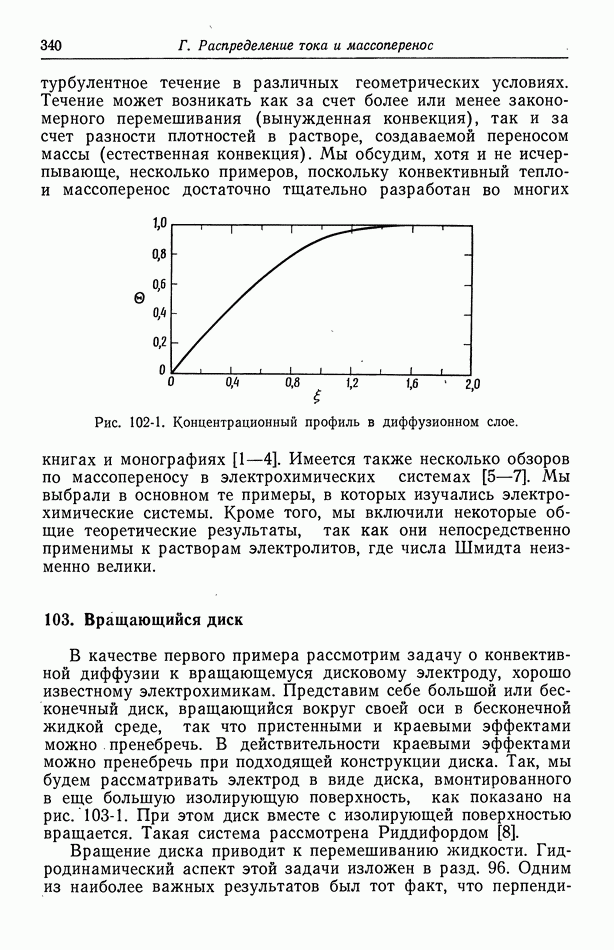
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
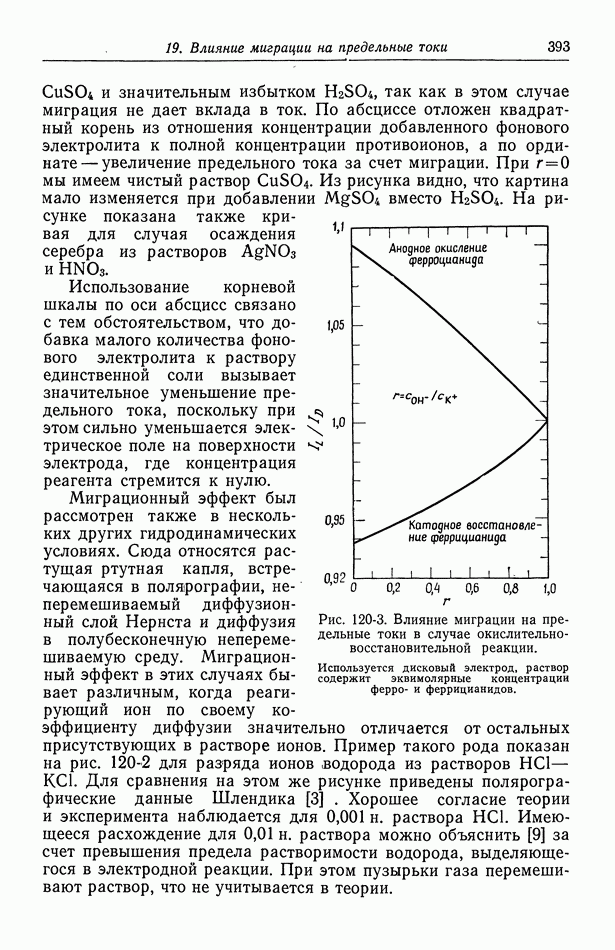
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 120. Поправочный множитель в случае предельных токов
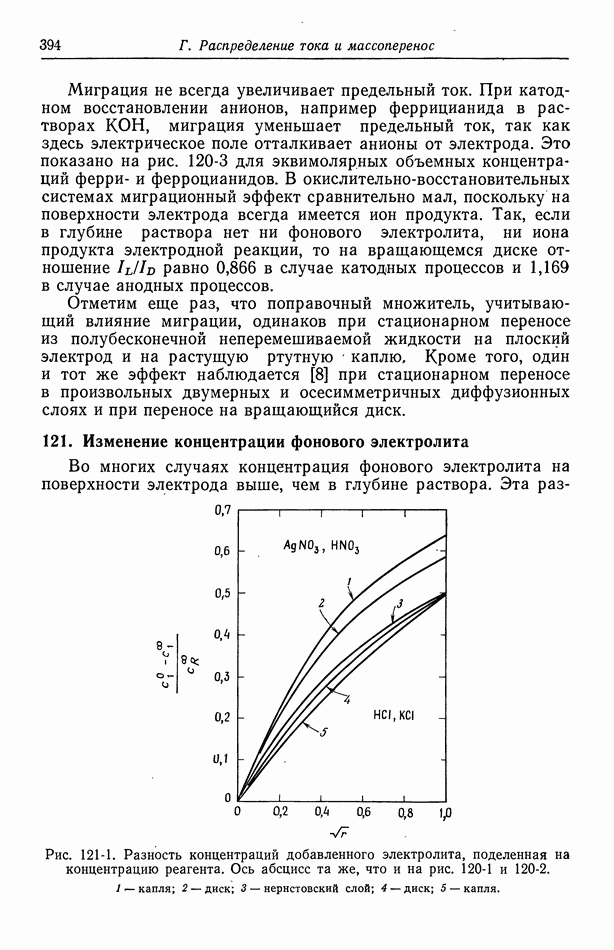
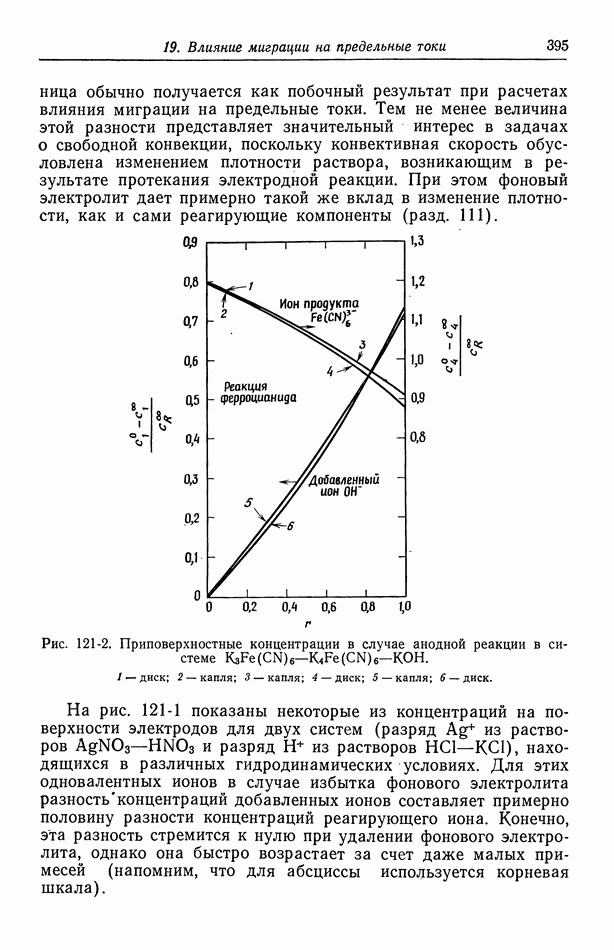
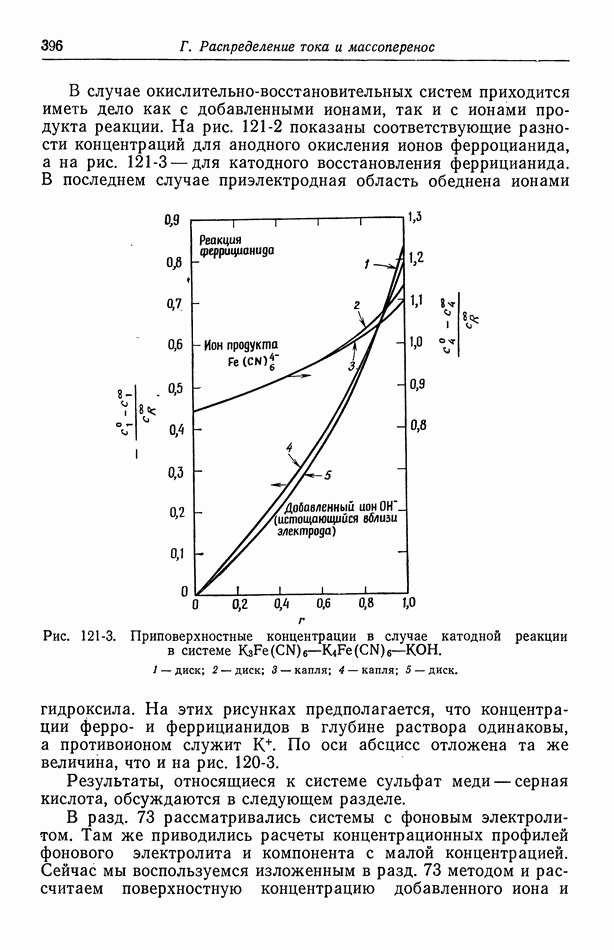
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ