| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
110. Растущие ртутные капли
При количественном анализе растворов электролитов весьма важно знать предельный диффузионный ток на капельный ртутный электрод. Пусть ртуть вытекает из капилляра с постоянной скоростью, образуя каплю на кончике капилляра. Радиус капли увеличивается во времени в. соответствии с формулой

Толщина диффузионного слоя на капле пропорциональна  Илькович [41, 42], а также Мак-Гилаври и Райдил [43] рассматривали эту задачу в предположении, что диффузионный слой тонок по сравнению с радиусом капли.
Илькович [41, 42], а также Мак-Гилаври и Райдил [43] рассматривали эту задачу в предположении, что диффузионный слой тонок по сравнению с радиусом капли.
В случае радиального роста капли без тангенциального движения поверхности предельная плотность тока равна

Без поправочного члена это равенство впервые было получено Ильковичем. Поправочный член, учитывающий конечную толщину диффузионного слоя, впервые правильно вычислен Коутецким [44]. В литературе встречается по меньшей мере три разных значения поправочного коэффициента. Мы несколько развили [45] расчет Коутецкого и выразили коэффициент через гамма-функции:

Полный ток на каплю, усредненный по времени жизни капли  приобретает вид
приобретает вид

где  объемная скорость течения ртути
объемная скорость течения ртути 
То обстоятельство, что в отсутствие тангенциального движения поверхности конвективное течение хорошо известно, определяет широкое использование капельных ртутных электродов для нахождения коэффициентов диффузии.
111. Свободная конвекция
Под свободной конвекцией подразумевается гидродинамическое течение, вызванное изменениями плотности раствора. В рассматриваемом здесь случае плотность изменяется вследствие
концентрационных изменений вблизи электрода. Широко изучалась свободная конвекция вблизи вертикального плоского электрода. В случае осаждения металла плотность раствора вблизи электрода ниже, чем в растворе. Поэтому вблизи электрода жидкость течет вверх. Это течение обеспечивает конвективный перенос реагента к электродному диффузионному слою. Обзор экспериментальных работ по этому вопросу сделал Ибл [46]. Там же приводится выражение для предельной плотности тока на электрод длиной 

или

где

есть число Грасгофа. Эти результаты справедливы в области изменения произведения  от 104 до 1012.
от 104 до 1012.
Задача о свободной конвекции в бинарном растворе вблизи вертикальной пластины рассматривалась теоретически. Табл. 111-1 иллюстрирует зависимость коэффициента в уравнении (111-2) от числа Шмидта. Поскольку в растворах электролитов число Шмидта по порядку величины близко к 1000, согласие с уравнением (111-2) хорошее.
Таблица 111-1 (см. скан) Коэффициент С, выражающий скорость массопереноса при свободной конвекции вблизи вертикальной пластины. Бинарный раствор имеет однородную разность плотностей между вертикальной поверхностью и глубиной раствора [48—50]
Свободная конвекция в растворах с избытком фонового электролита осложняется тем обстоятельством, что концентрация
фонового электролита в диффузионном слое также изменяется, давая вклад в изменение плотности. Это привело к использованию приближенных методов, позволяющих оценить поверхностную разность концентраций, входящую в число Грасгофа. Одним из широко распространенных методов оказался метод Уилки и др. [47]. Этот вопрос будет рассмотрен, в разд. 124.
Для естественной турбулентной конвекции вблизи вертикальной пластины Фуад и Ибл [51] вывели соотношение

справедливое в интервале 
Шютц [52] экспериментально исследовал массоперенос на сферу и на горизонтальные цилиндры в случае свободной конвекции и получил среднее число Нуссельта для сфер

в области  и для цилиндров
и для цилиндров

при  При составлении этих безразмерных комбинаций было принято
При составлении этих безразмерных комбинаций было принято  где
где  диаметр сферы или цилиндра. Методом секционного электрода Шютц измерил локальные числа Нуссельта.
диаметр сферы или цилиндра. Методом секционного электрода Шютц измерил локальные числа Нуссельта.
Акривос [53] получил асимптотическое решение при  уравнений пограничного слоя при ламинарной свободной конвекции для произвольных двумерных и осесимметричных поверхностей. Эти результаты представляют некоторый интерес, так как число Шмидта для растворов электролитов велико. Вычисленная предельная плотность тока имеет вид
уравнений пограничного слоя при ламинарной свободной конвекции для произвольных двумерных и осесимметричных поверхностей. Эти результаты представляют некоторый интерес, так как число Шмидта для растворов электролитов велико. Вычисленная предельная плотность тока имеет вид

а средняя по области  предельная плотность тока равна
предельная плотность тока равна

где  угол между нормалью к поверхности и вертикальной линией. Для вертикального электрода
угол между нормалью к поверхности и вертикальной линией. Для вертикального электрода  При этом можно непосредственно сравнить коэффициент 0,6705 в уравнении (111-8) с экспериментальным коэффициентом в уравнении (111-1) или с теоретическим значением 0,670327 в табл. 111-1.
При этом можно непосредственно сравнить коэффициент 0,6705 в уравнении (111-8) с экспериментальным коэффициентом в уравнении (111-1) или с теоретическим значением 0,670327 в табл. 111-1.
Для поверхности, обладающей осью симметрии, обозначая вновь через  расстояние от оси до поверхности, предельную плотность тока можно записать в виде
расстояние от оси до поверхности, предельную плотность тока можно записать в виде

Для осесимметричного распределения скоростей необходимо совпадение оси симметрии поверхности и направления силы тяжести.
Вычисленные по формулам Акривоса коэффициенты перед  в выражениях для средних чисел Нуссельта равны 0,58 для сферы и 0,50 для горизонтальных цилиндров. Эти числа можно сопоставить с экспериментальными коэффициентами в уравнениях (111-5) и (111-6).
в выражениях для средних чисел Нуссельта равны 0,58 для сферы и 0,50 для горизонтальных цилиндров. Эти числа можно сопоставить с экспериментальными коэффициентами в уравнениях (111-5) и (111-6).
Свободная конвекция вблизи горизонтальной пластины существенно отличается от обсуждавшегося выше случая, поскольку здесь нет возможности образования ламинарного пограничного слоя и продвижения свежего раствора мимо пластины. На горизонтальном электроде с малым градиентом плотности раствор вначале остается стратифицированным. При более высоких разностях плотности возникает течение ячеистого типа, а для еще больших разностей плотности течение турбулентно. Эту картину можно сравнить с описанием характера течения между двумя вращающимися цилиндрами (разд. 4). В области турбулентности Фенек и Тобайес [54] предложили для электрода, размеры которого не меньше 2 см, формулу

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
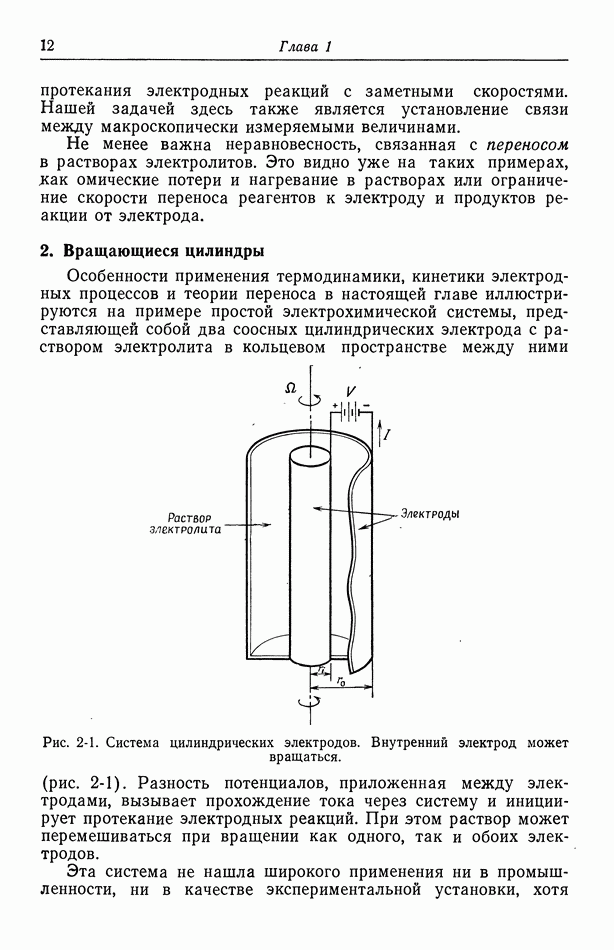
- 2. Вращающиеся цилиндры
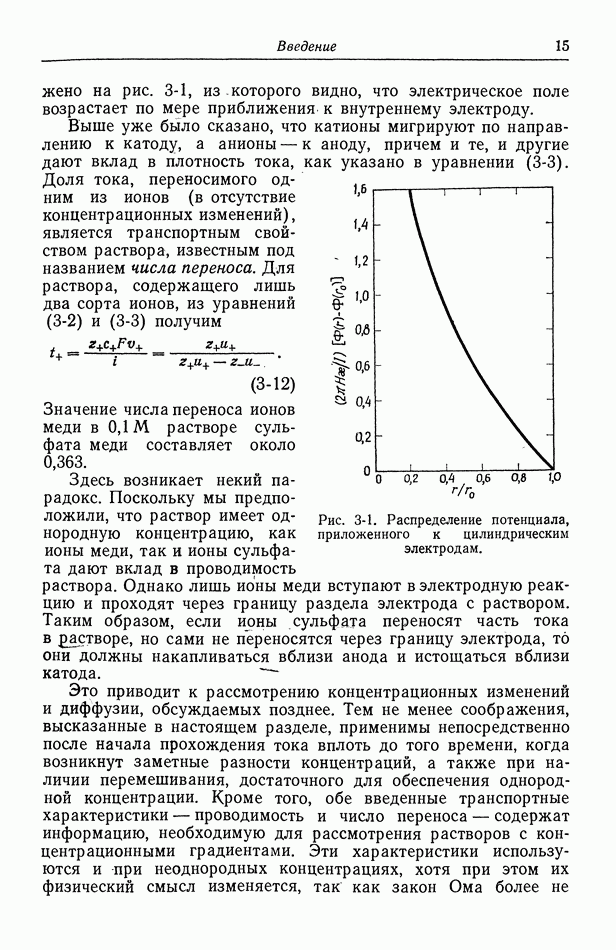
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
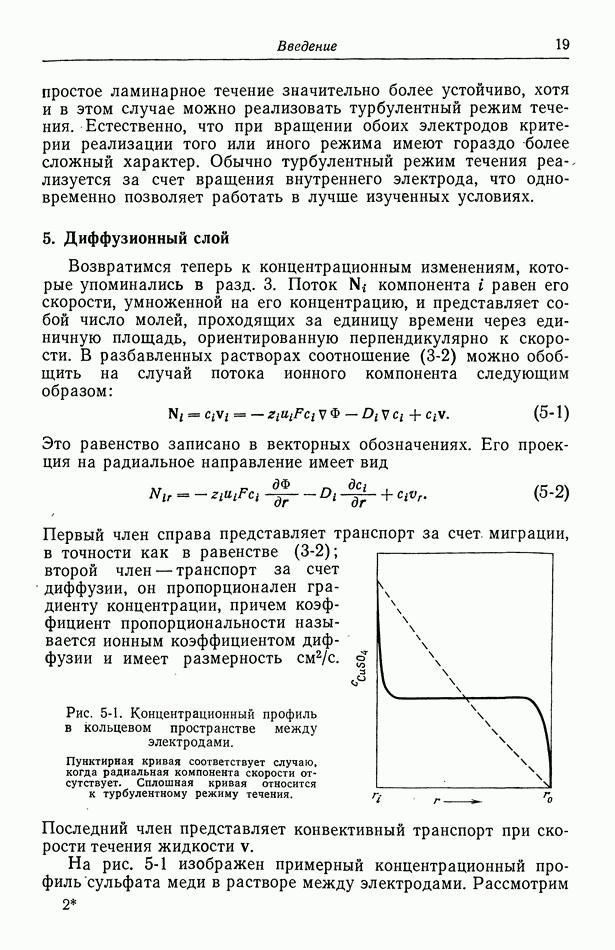
- 5. Диффузионный слой
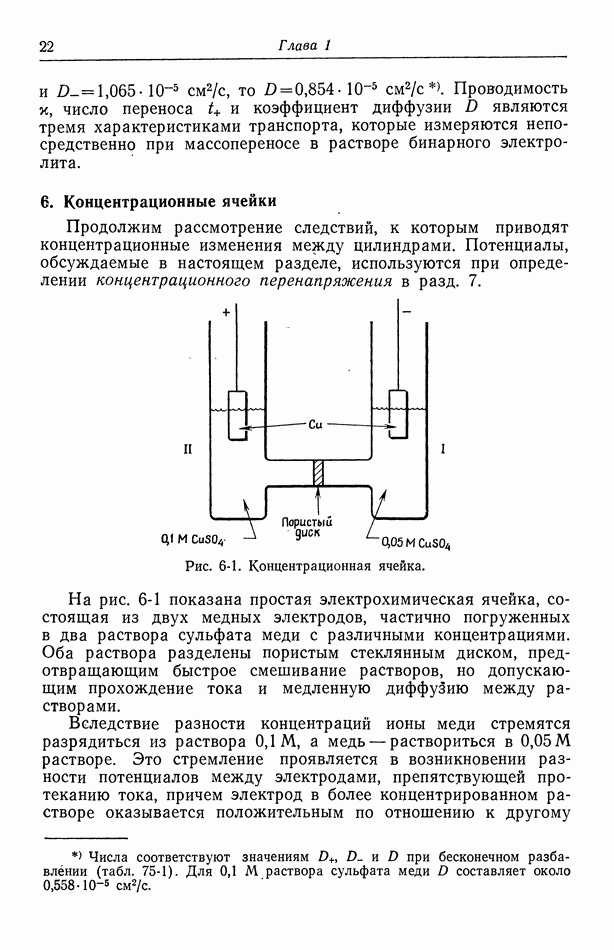
- 6. Концентрационные ячейки
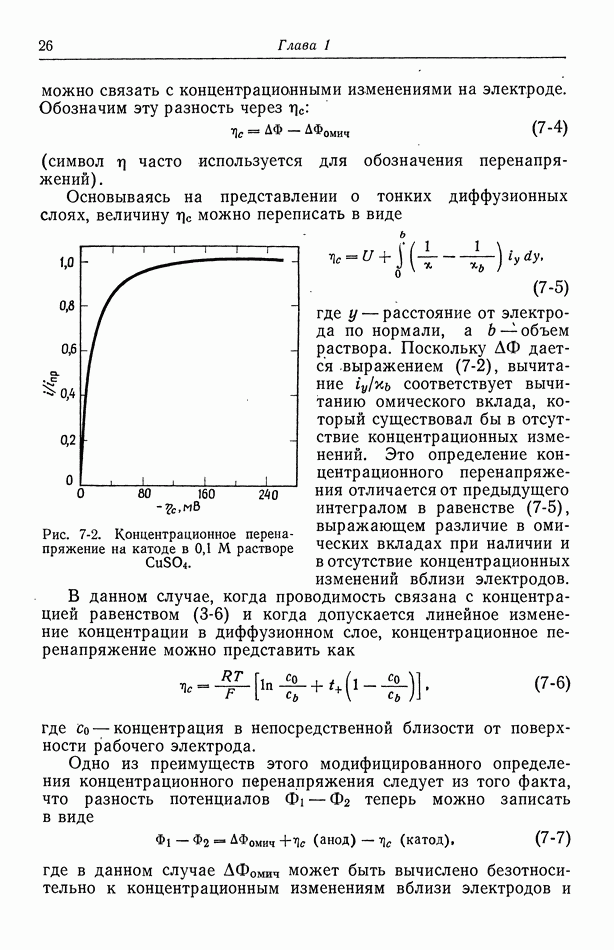
- 7. Концентрационное перенапряжение
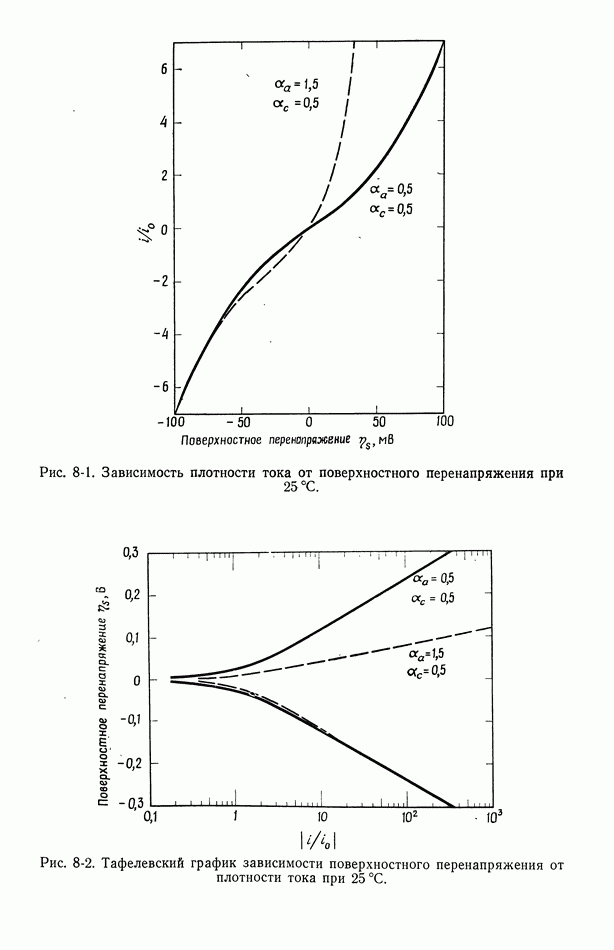
- 8. Поверхностное перенапряжение
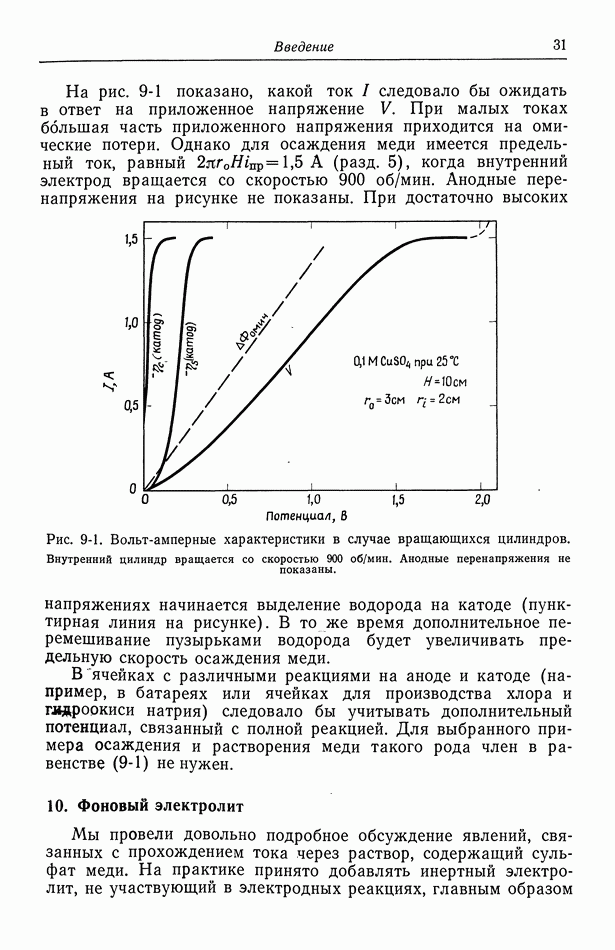
- 9. Потенциал ячейки
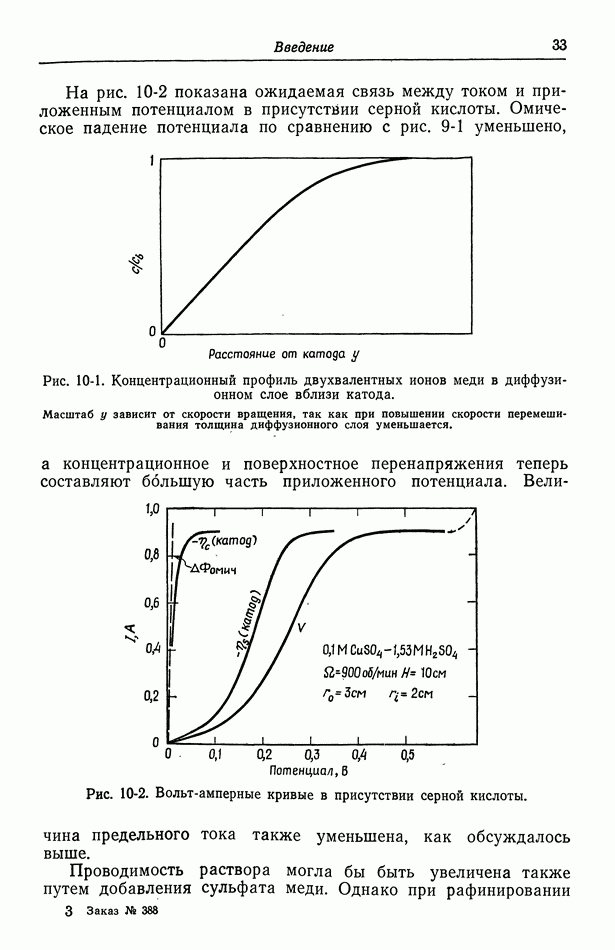
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
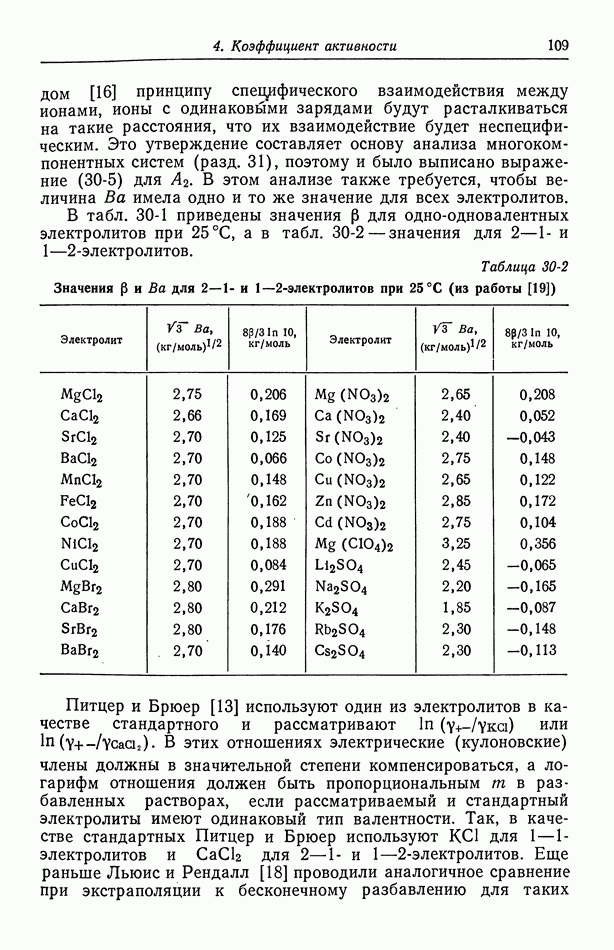
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
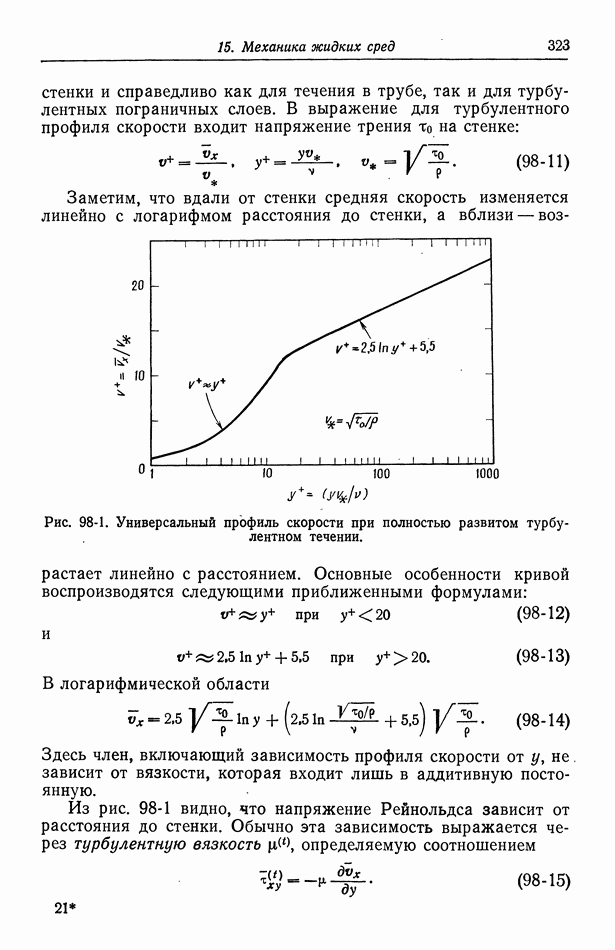
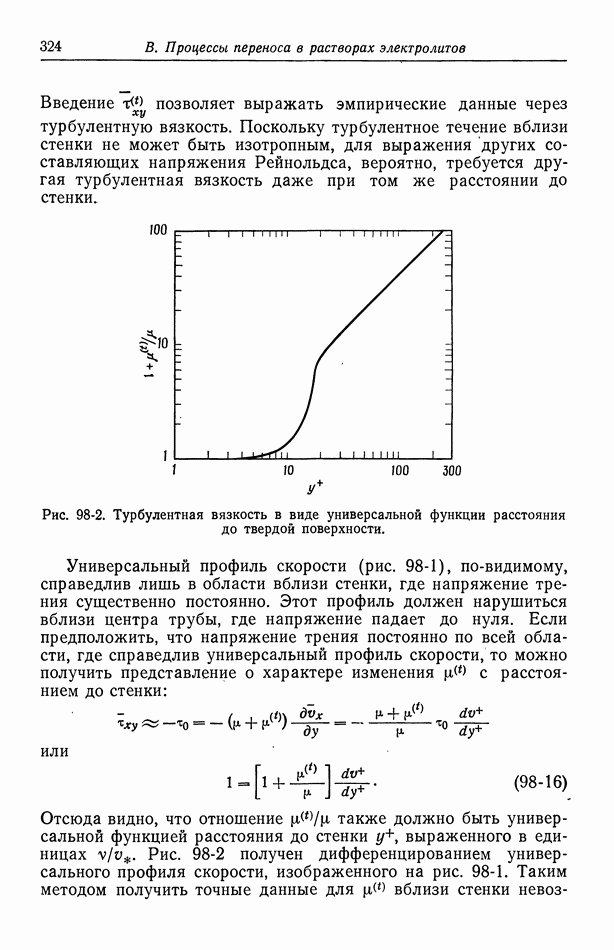
- 98. Турбулентное течение
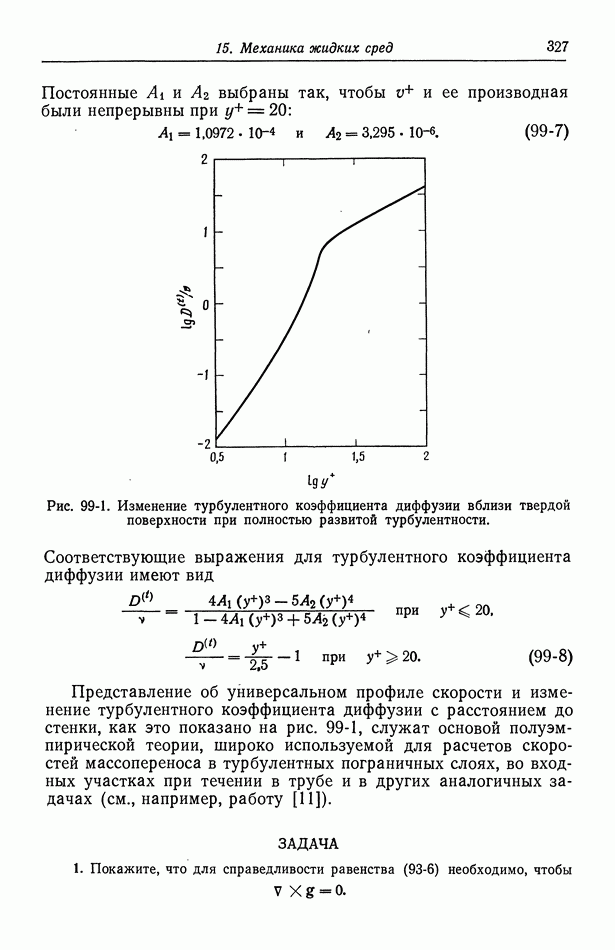
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
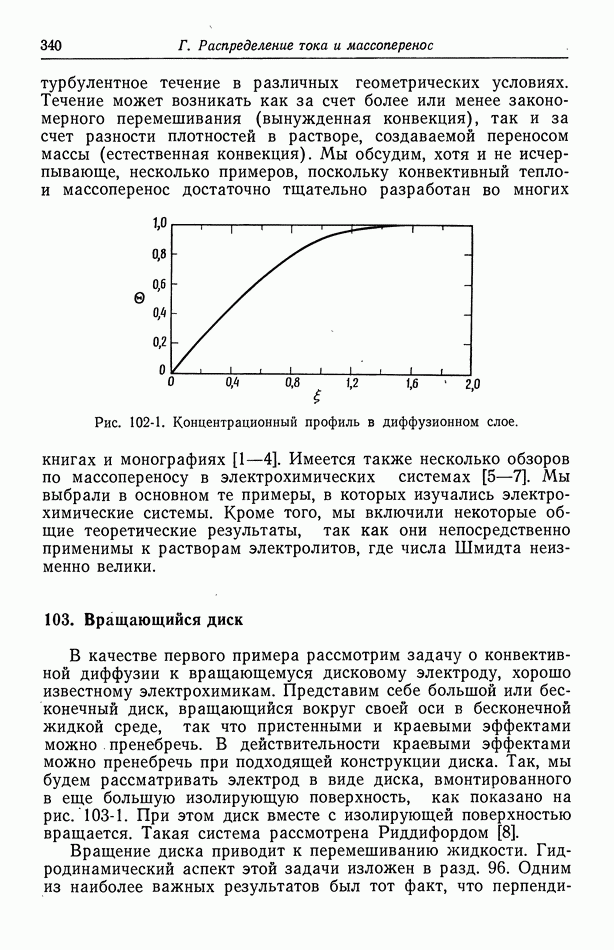
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
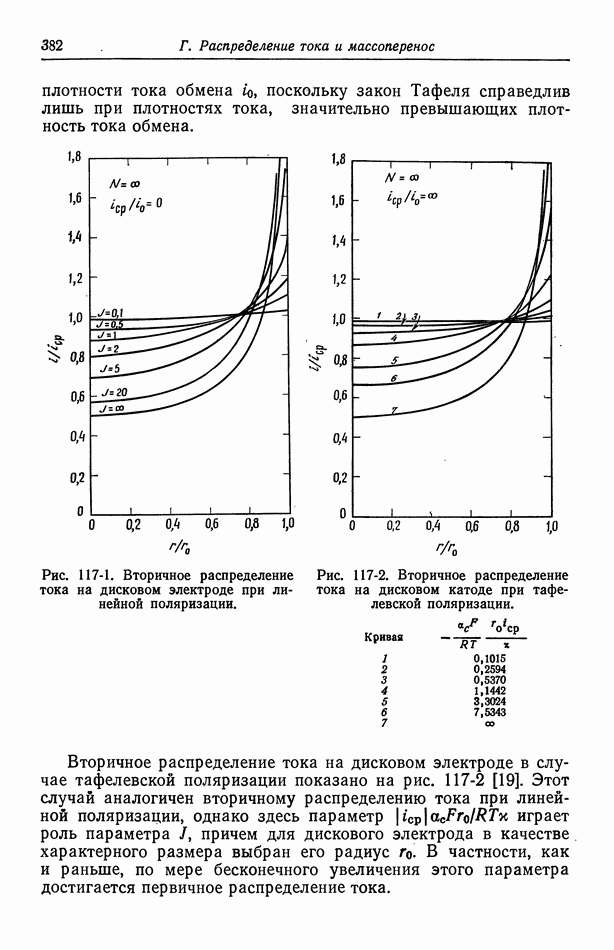
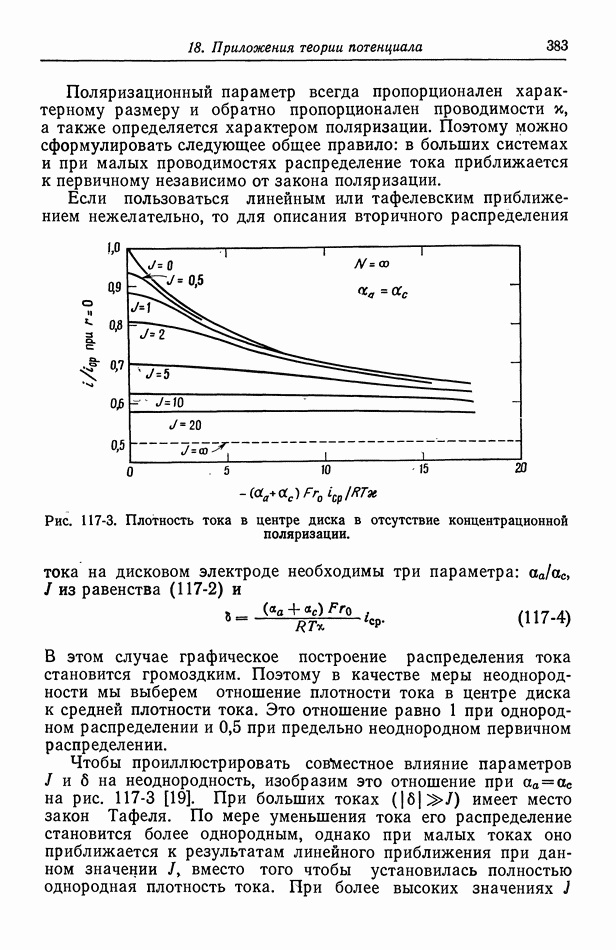
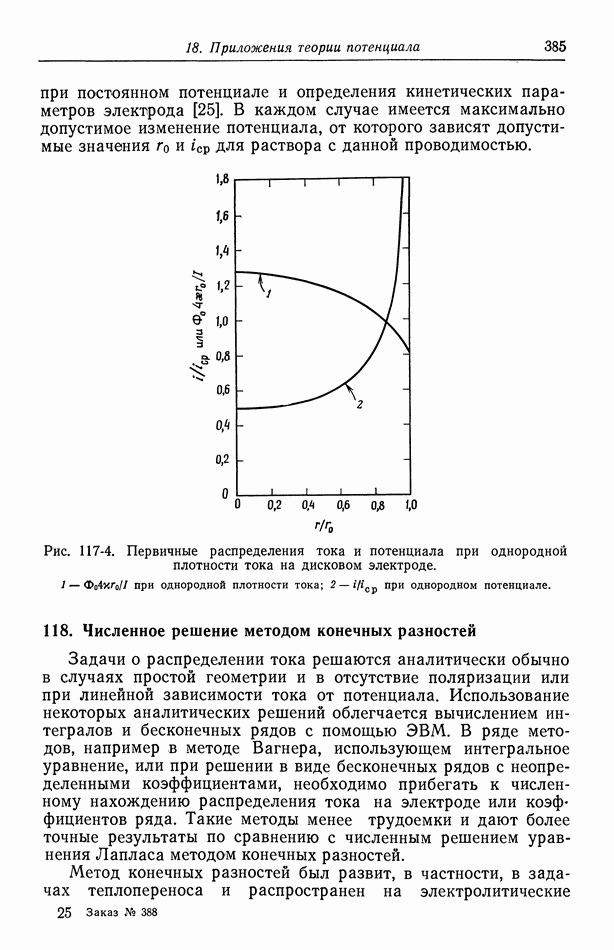
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
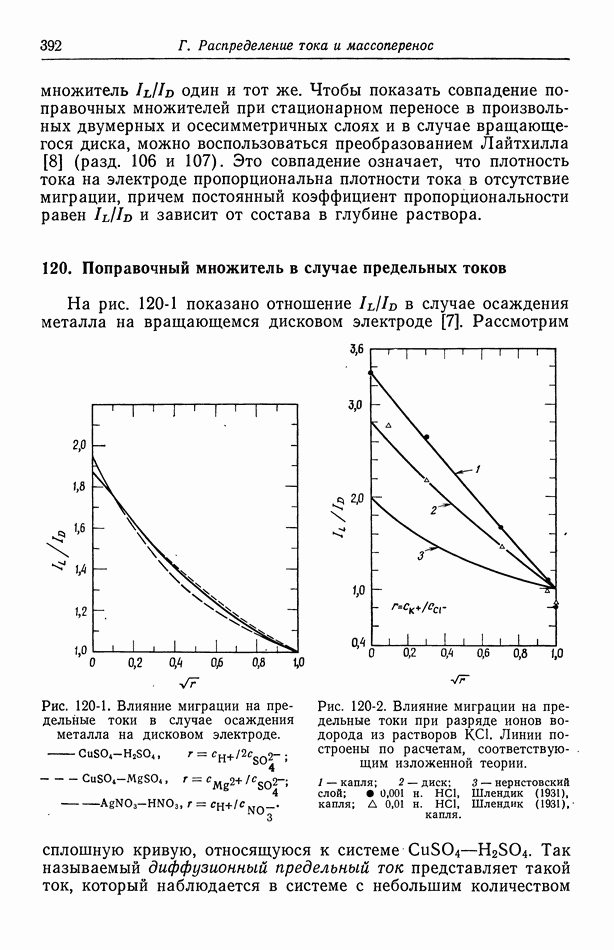
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ