| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
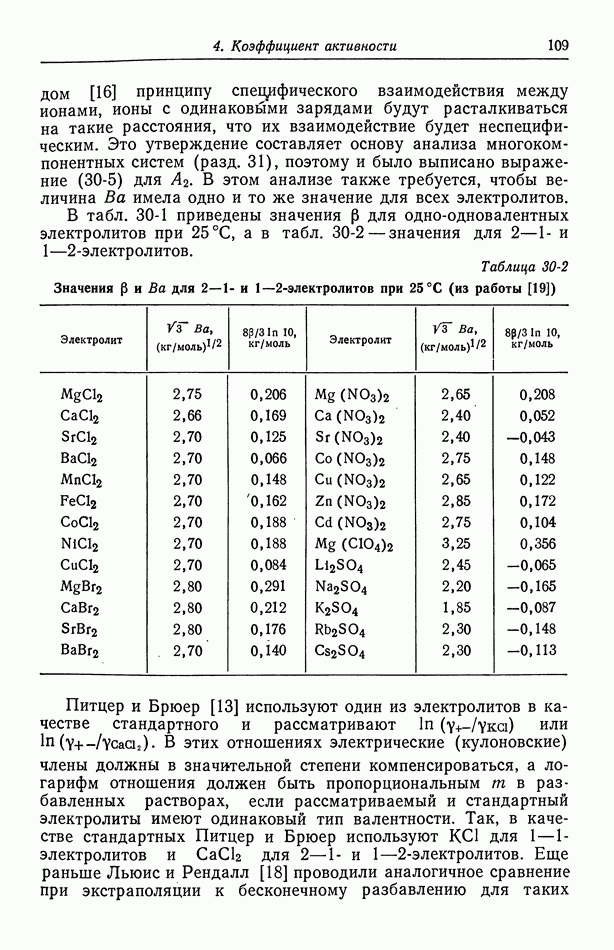
90. Растворы, содержащие одну соль
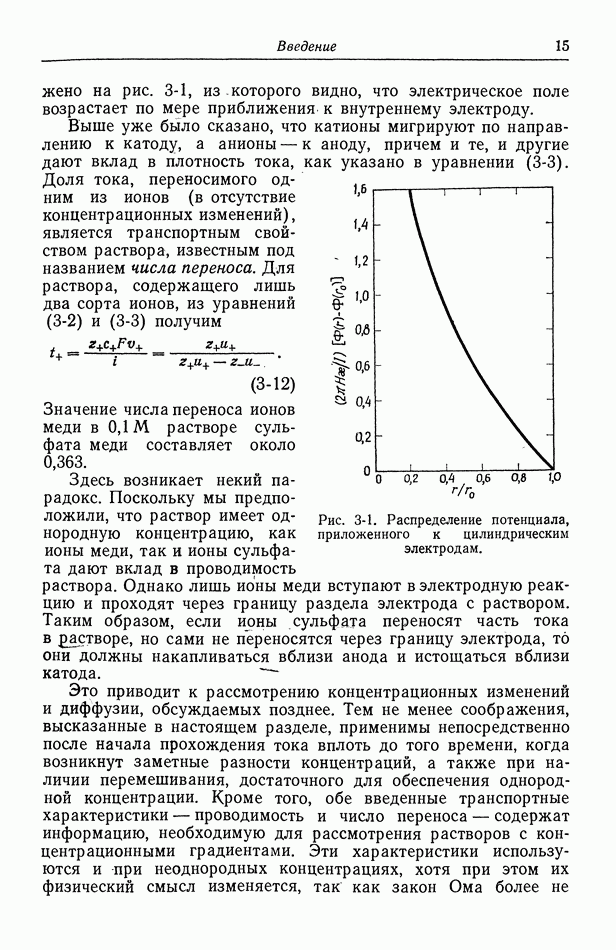
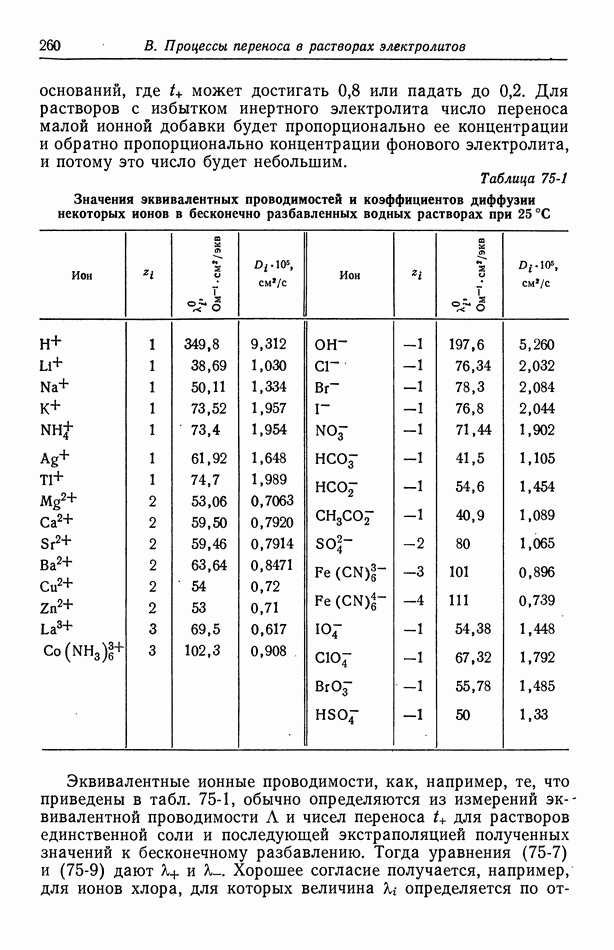
В разд. 79 и 81 указывалось, что растворам единственной соли свойственны три характеристики переноса: проводимость к, коэффициент диффузии  и число переноса
и число переноса  Эти величины можно измерять как функции концентрации и температуры [1]. Проводимость обычно находится из измерения на переменном токе сопротивления раствора, помещенного между двумя электродами. В методе Гитторфа, сводящемся к измерению чисел переноса, определяют изменения концентрации вблизи анода и катода при прохождении тока. В методе движущейся границы, обычно считающемся более точным, чем метод Гитторфа, измеряют скорость перемещения границы между двумя растворами, например
Эти величины можно измерять как функции концентрации и температуры [1]. Проводимость обычно находится из измерения на переменном токе сопротивления раствора, помещенного между двумя электродами. В методе Гитторфа, сводящемся к измерению чисел переноса, определяют изменения концентрации вблизи анода и катода при прохождении тока. В методе движущейся границы, обычно считающемся более точным, чем метод Гитторфа, измеряют скорость перемещения границы между двумя растворами, например  при пропускании тока через границу [2]. Коэффициенты диффузии можно измерять путем прослеживания концентрационных изменений поперек пористой стеклянной диафрагмы. Точные результаты можно также получить с помощью оптических измерений концентрационных изменений в области контакта двух растворов с различными концентрациями. Эти измерения можно выполнять либо на малых временах, и тогда начальная граница будет резкой, либо на очень больших временах [3], когда диффузия происходит в ограниченном пространстве протяженностью около 7 см.
при пропускании тока через границу [2]. Коэффициенты диффузии можно измерять путем прослеживания концентрационных изменений поперек пористой стеклянной диафрагмы. Точные результаты можно также получить с помощью оптических измерений концентрационных изменений в области контакта двух растворов с различными концентрациями. Эти измерения можно выполнять либо на малых временах, и тогда начальная граница будет резкой, либо на очень больших временах [3], когда диффузия происходит в ограниченном пространстве протяженностью около 7 см.
В течение ряда лет множество данных было получено по характеристикам переноса в растворах единственной соли. Хорошим источником данных по проводимости может служить справочник [4]. Каймаков и Варшавская [5] собрали литературу по числам переноса. Робинсон и Стоке [1] привели обзор данных
по коэффициентам диффузии и коэффициентам активности, а Чэпмен и Ньюмен [6] собрали данные для целого ряда систем.
Проводимость, коэффициент диффузии и число переноса представляют собой три совершенно различные характеристики переноса. Имеются основания полагать, что более единообразное описание можно получить, работая с эквивалентными коэффициентами переноса и  определенными уравнением (78-1). Эти коэффициенты можно найти по измеренным значениям
определенными уравнением (78-1). Эти коэффициенты можно найти по измеренным значениям  решая уравнения (79-5), (79-6) и (81-4):
решая уравнения (79-5), (79-6) и (81-4):

Ясно, что вначале нужно найти 2 по известному значению  в соответствии с уравнением (79-7):
в соответствии с уравнением (79-7):

Это уравнение требует, чтобы был известен также коэффициент активности (задача 2-1).
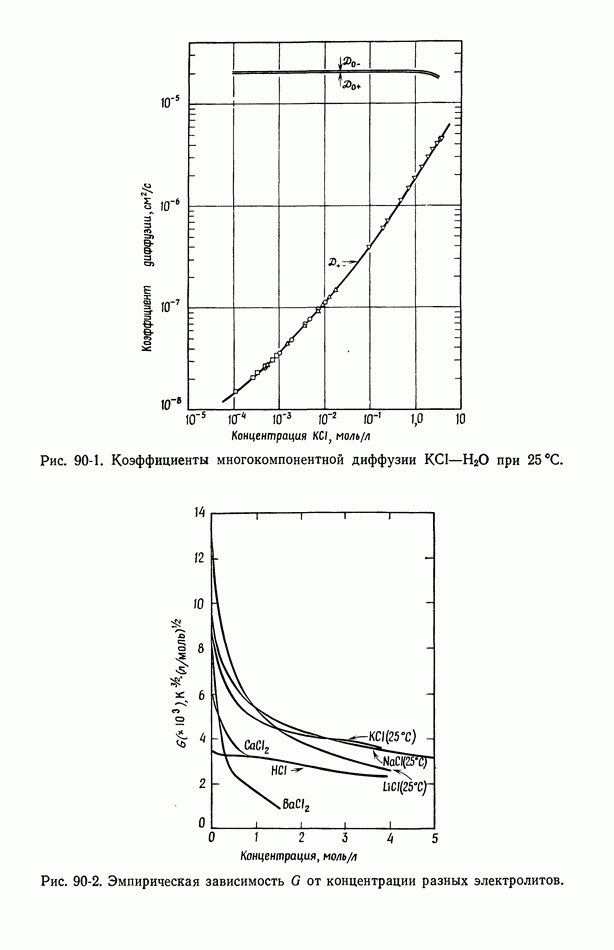
Имеется свыше тридцати бинарных систем [3], информация о которых позволяет рассчитать значения На рис. 90-1 показаны коэффициенты многокомпонентной диффузии  в воде при
в воде при  Можно отметить, что коэффициенты взаимодействия ионов с растворителем практически постоянны, в то время как коэффициенты ион-ионного взаимодействия проявляют зависимость, близкую к корню квадратному из концентрации, что характерно для теории Дебая-Хюккеля-Онзагера, описывающей взаимодействие ионов в разбавленных растворах.
Можно отметить, что коэффициенты взаимодействия ионов с растворителем практически постоянны, в то время как коэффициенты ион-ионного взаимодействия проявляют зависимость, близкую к корню квадратному из концентрации, что характерно для теории Дебая-Хюккеля-Онзагера, описывающей взаимодействие ионов в разбавленных растворах.
Исходя из этого, определим функцию 

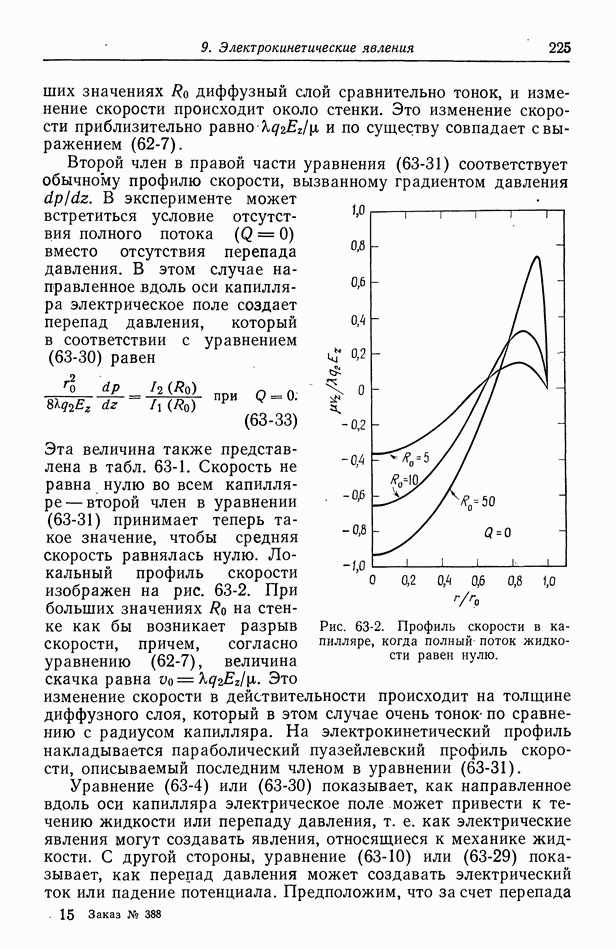
где

и  — эквивалентные ионные проводимости при бесконечном разбавлении. По существу значение
— эквивалентные ионные проводимости при бесконечном разбавлении. По существу значение  равно
равно  а остальные множители основаны на теории разбавленных растворов.
а остальные множители основаны на теории разбавленных растворов.

(кликните для просмотра скана)
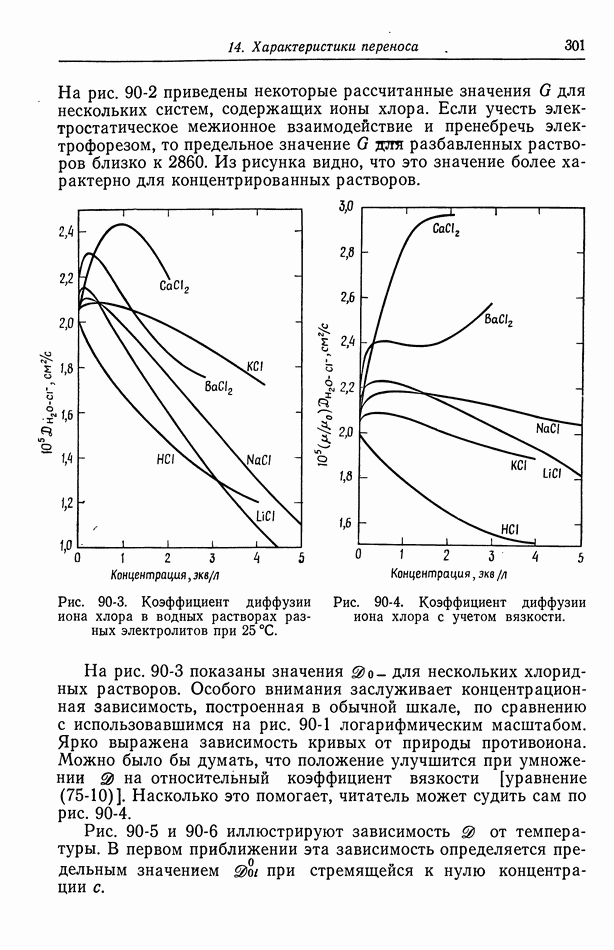
На рис. 90-2 приведены некоторые рассчитанные значения  для нескольких систем, содержащих ионы хлора. Если учесть электростатическое межионное взаимодействие и пренебречь электрофорезом, то предельное значение
для нескольких систем, содержащих ионы хлора. Если учесть электростатическое межионное взаимодействие и пренебречь электрофорезом, то предельное значение  для разбавленных растворов близко к 2860. Из рисунка видно, что это значение более характерно для концентрированных растворов.
для разбавленных растворов близко к 2860. Из рисунка видно, что это значение более характерно для концентрированных растворов.

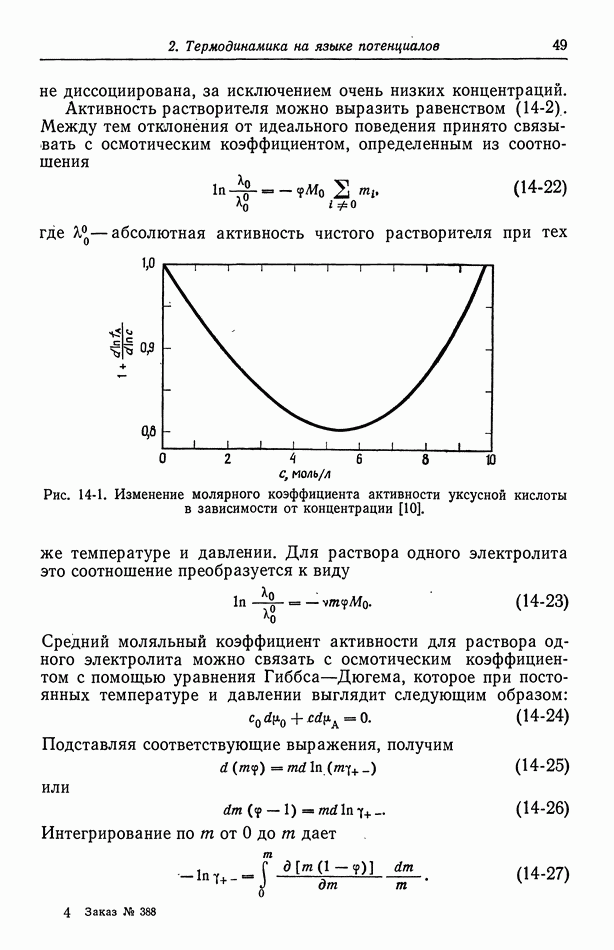
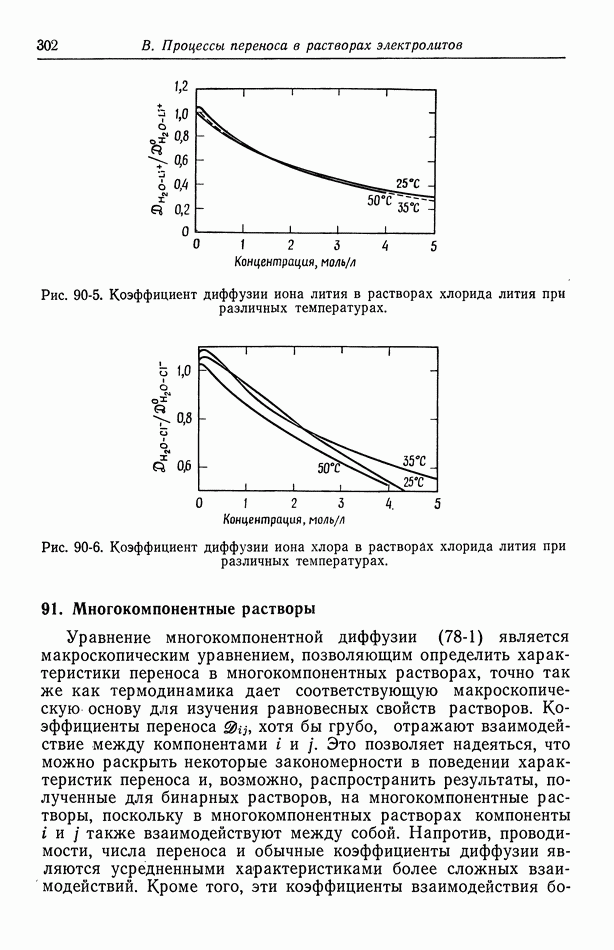
Рис. 90-3. Коэффициент диффузии иона хлора в водных растворах разных электролитов при 25 °С.

Рис. 90-4. Коэффициент диффузии иона хлора с учетом вязкости.
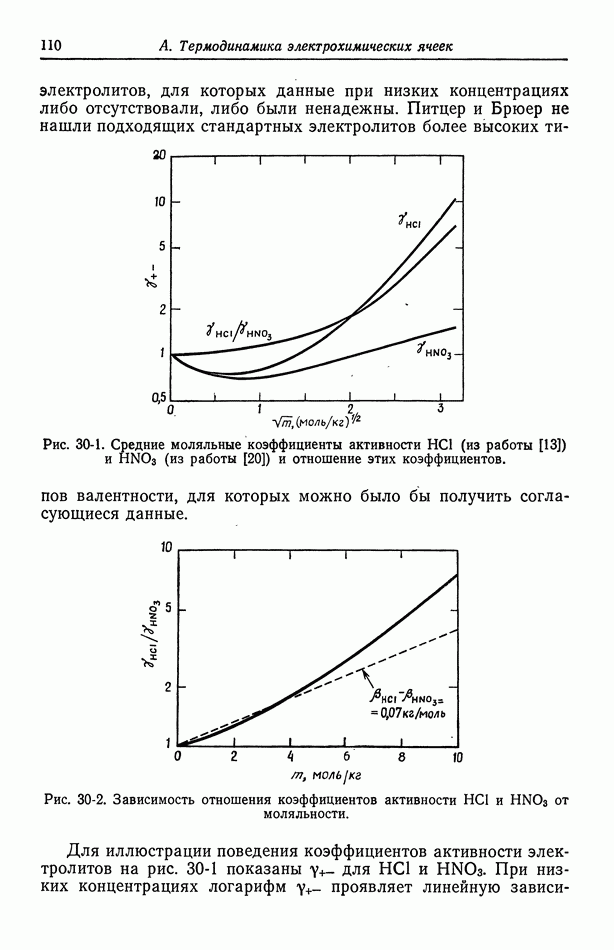
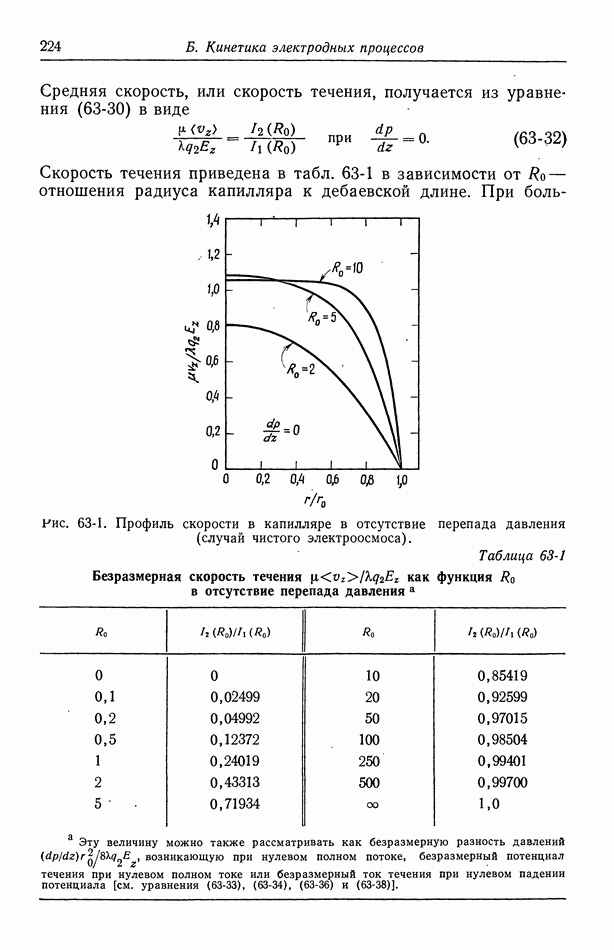
На рис. 90-3 показаны значения для нескольких хлоридных растворов. Особого внимания заслуживает концентрационная зависимость, построенная в обычной шкале, по сравнению с использовавшимся на рис. 90-1 логарифмическим масштабом. Ярко выражена зависимость кривых от природы противоиона. Можно было бы думать, что положение улучшится при умножении  на относительный коэффициент вязкости [уравнение (75-10)]. Насколько это помогает, читатель может судить сам по рис. 90-4.
на относительный коэффициент вязкости [уравнение (75-10)]. Насколько это помогает, читатель может судить сам по рис. 90-4.
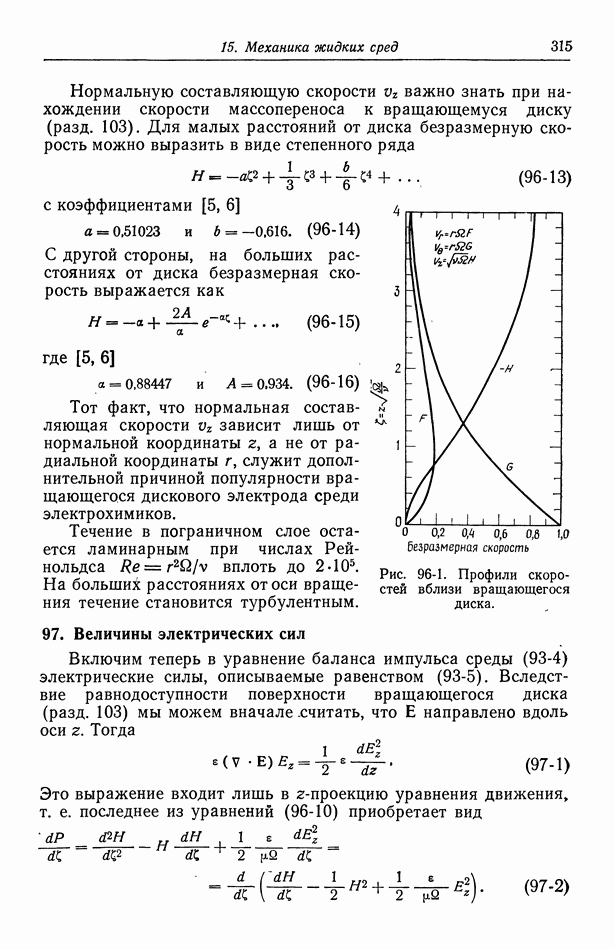
Рис. 90-5 и 90-6 иллюстрируют зависимость  от температуры. В первом приближении эта зависимость определяется предельным значением
от температуры. В первом приближении эта зависимость определяется предельным значением  при стремящейся к нулю концентрации с.
при стремящейся к нулю концентрации с.

Рис. 90-5. Коэффициент диффузии иона лития в растворах хлорида лития при различных температурах.

Рис. 90-6. Коэффициент диффузии иона хлора в растворах хлорида лития при различных температурах.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
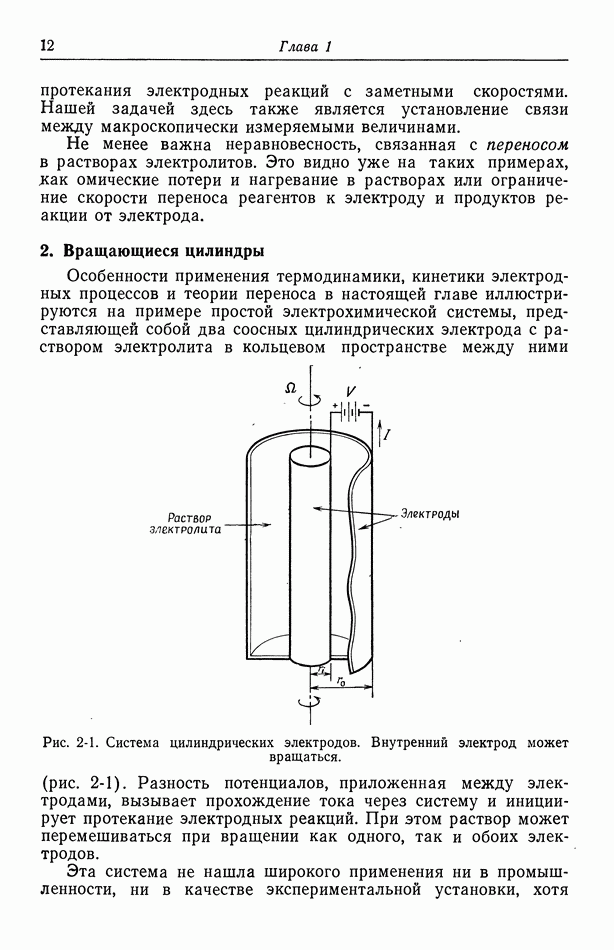
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
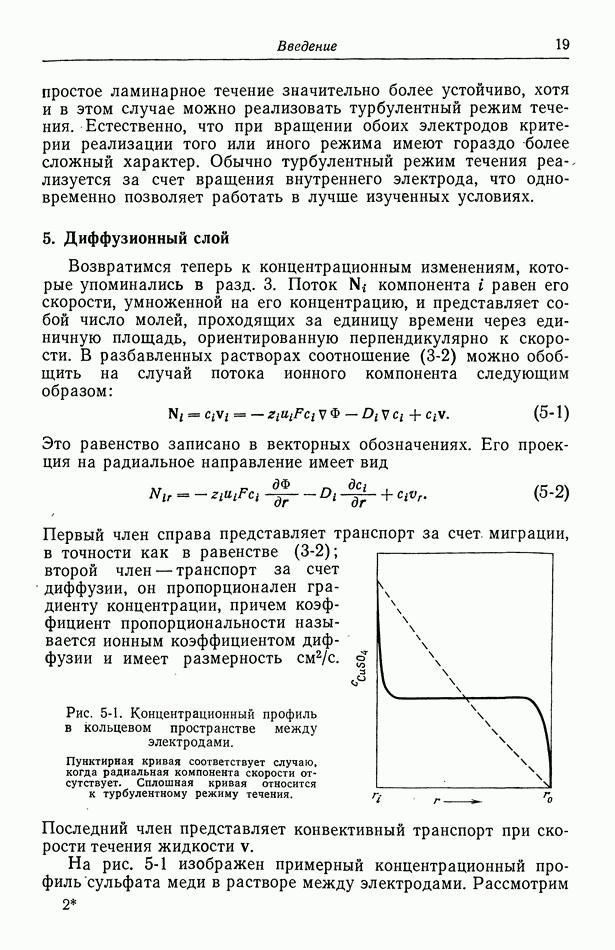
- 5. Диффузионный слой
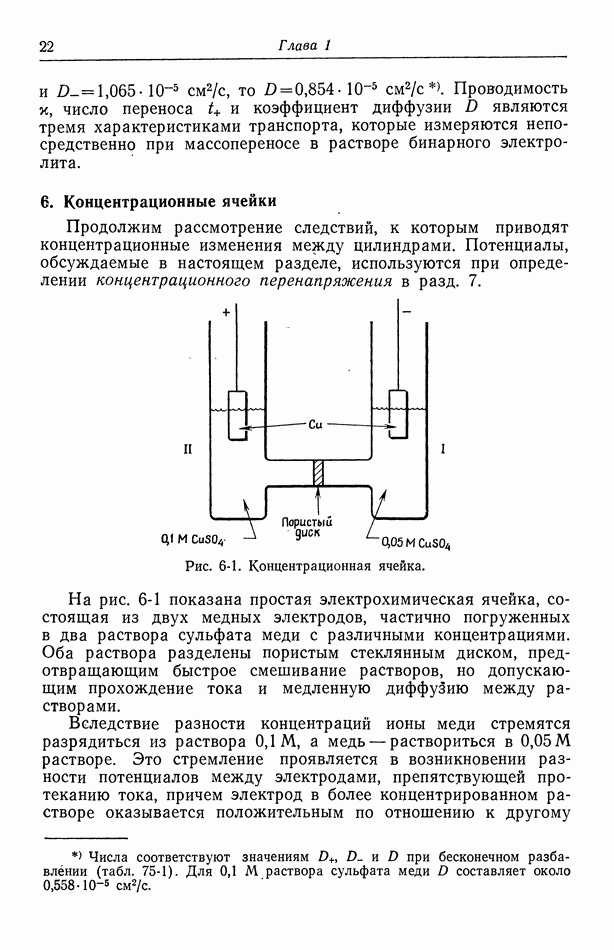
- 6. Концентрационные ячейки
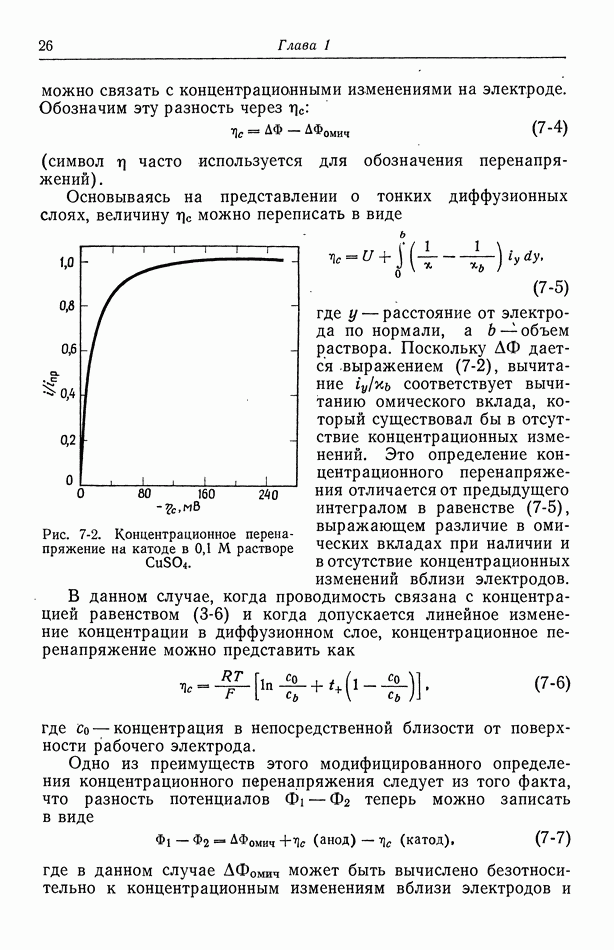
- 7. Концентрационное перенапряжение
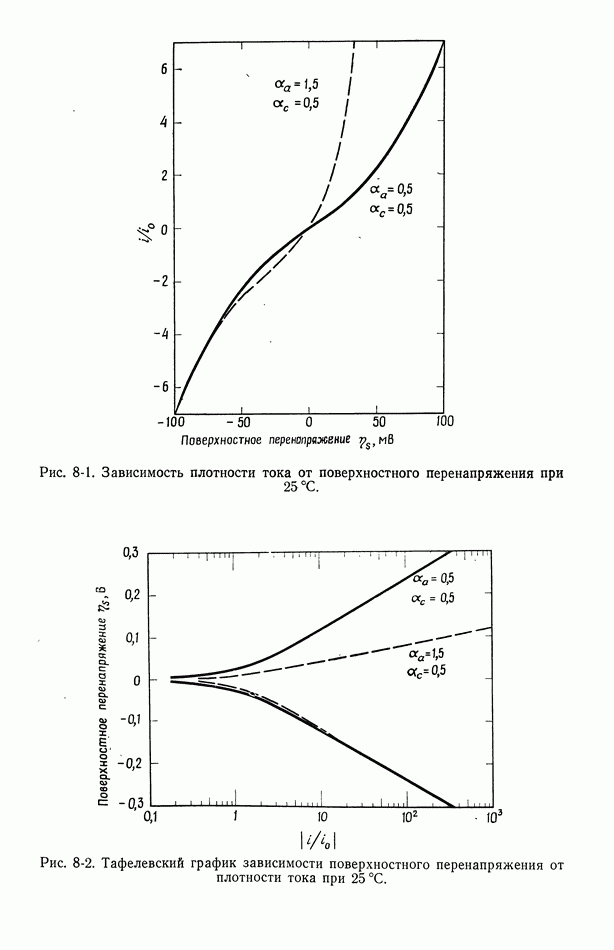
- 8. Поверхностное перенапряжение
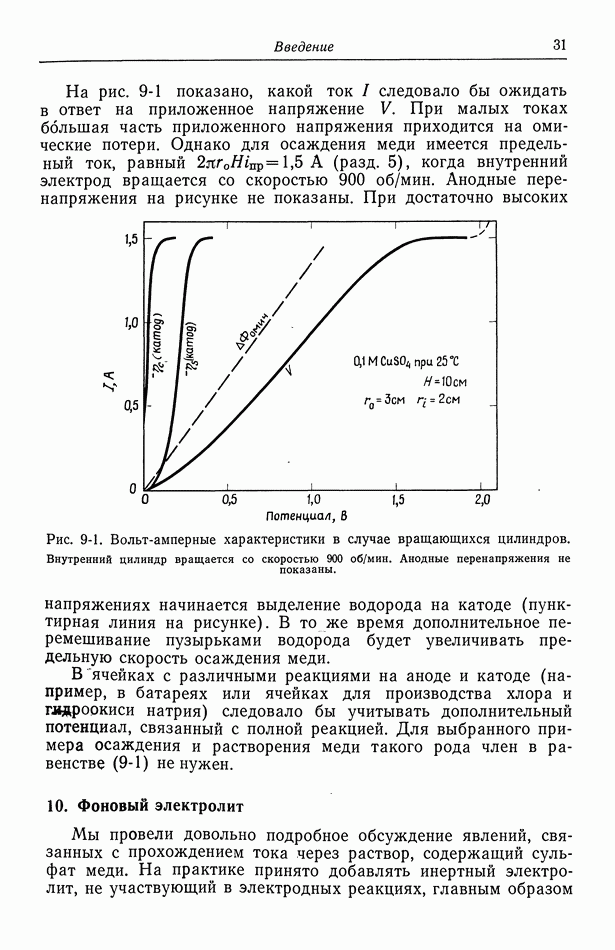
- 9. Потенциал ячейки
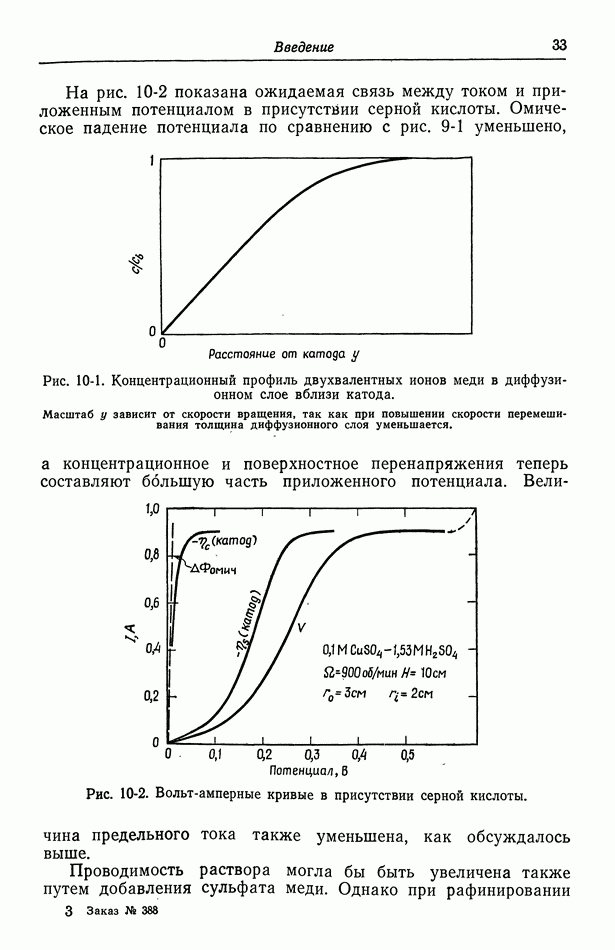
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
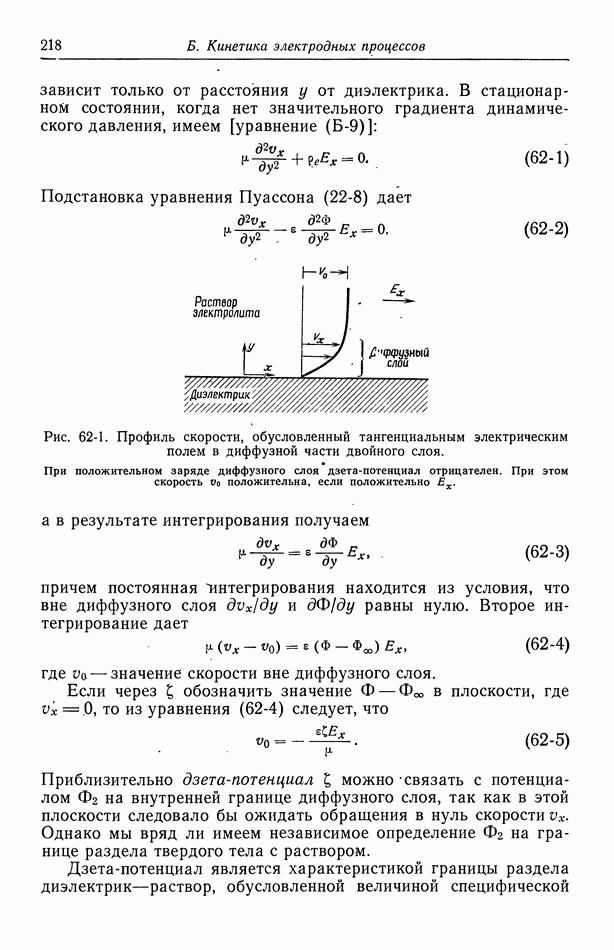
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
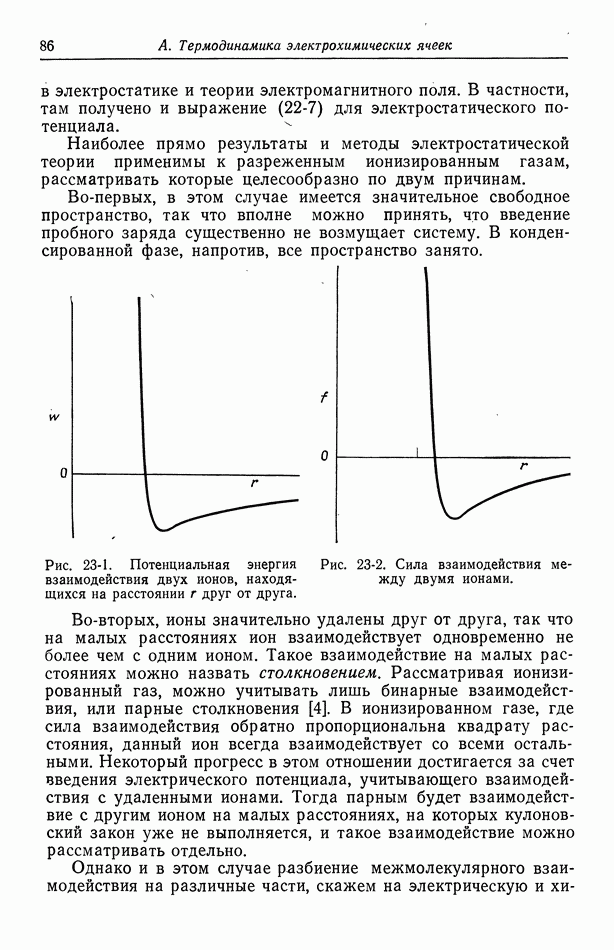
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
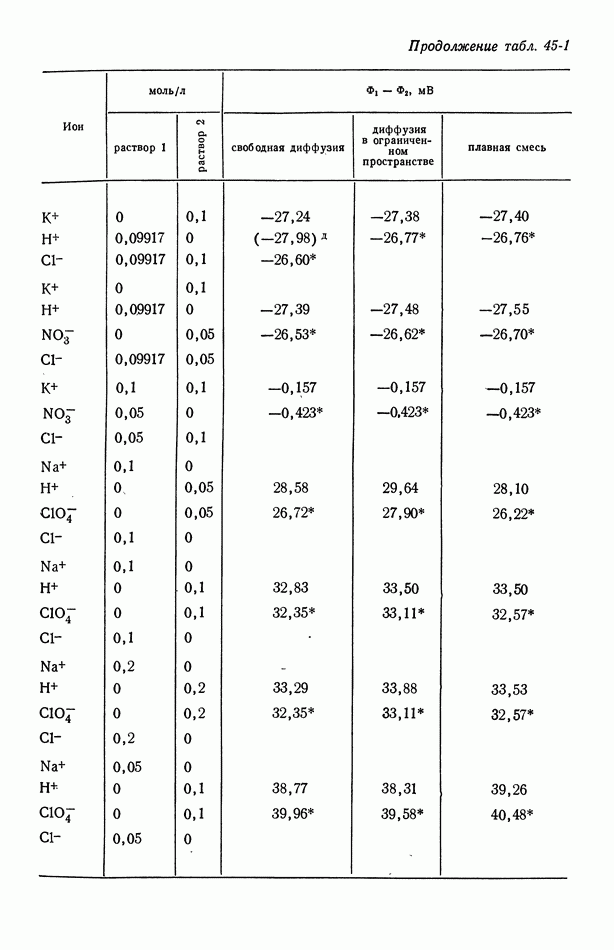
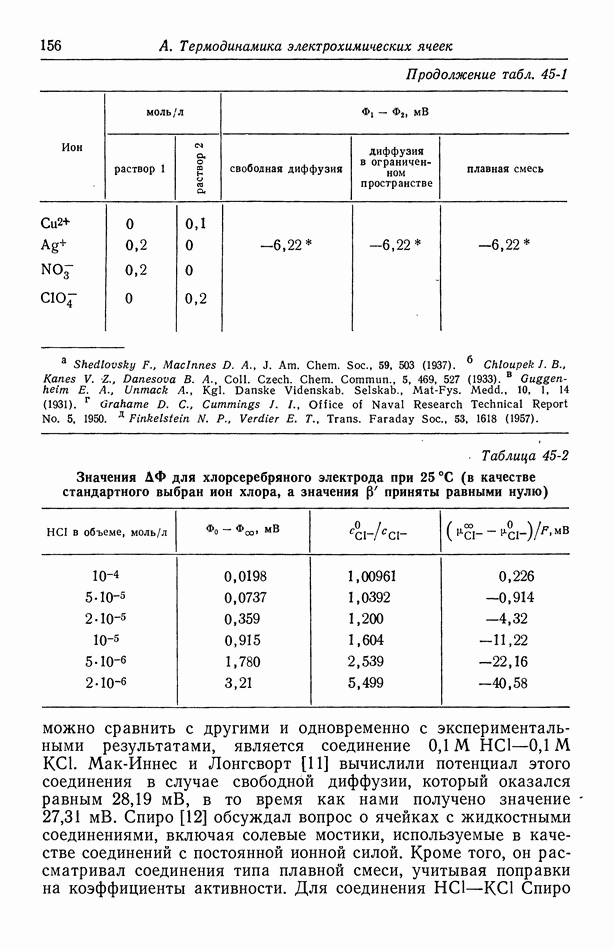
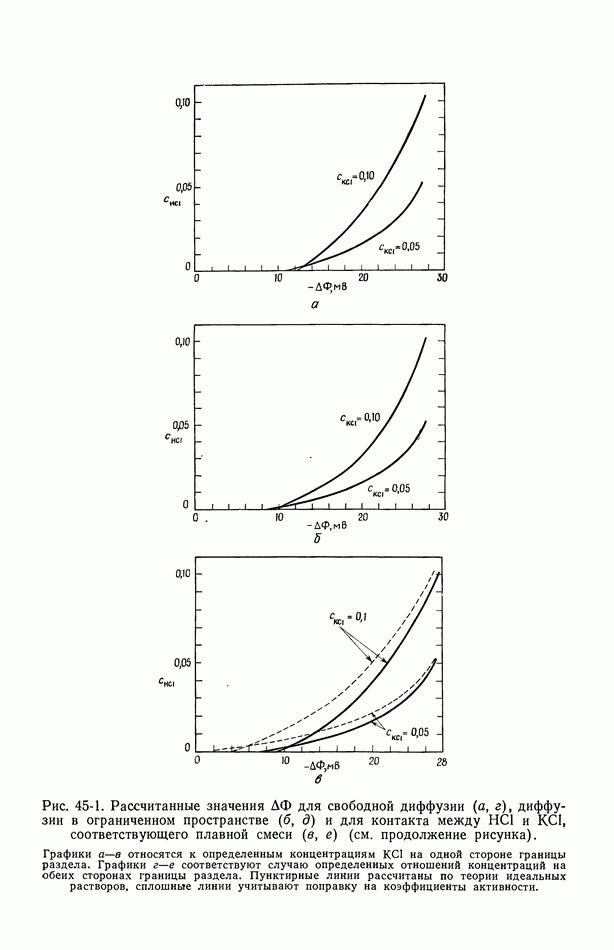
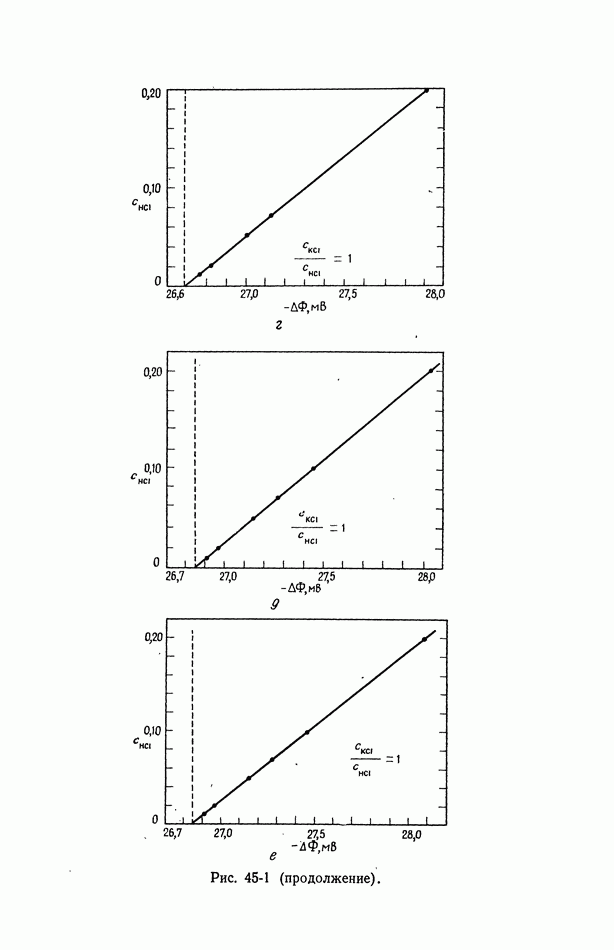
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
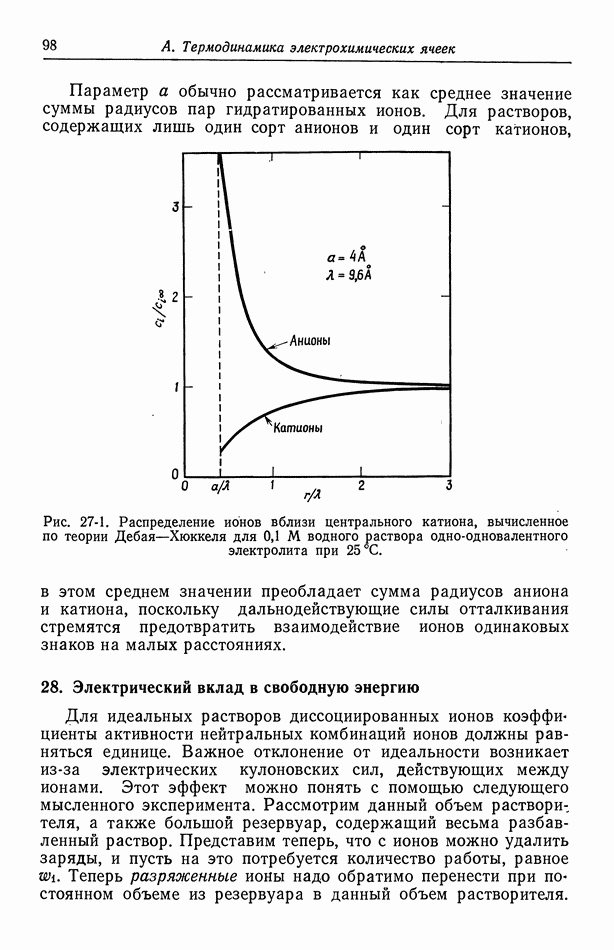
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
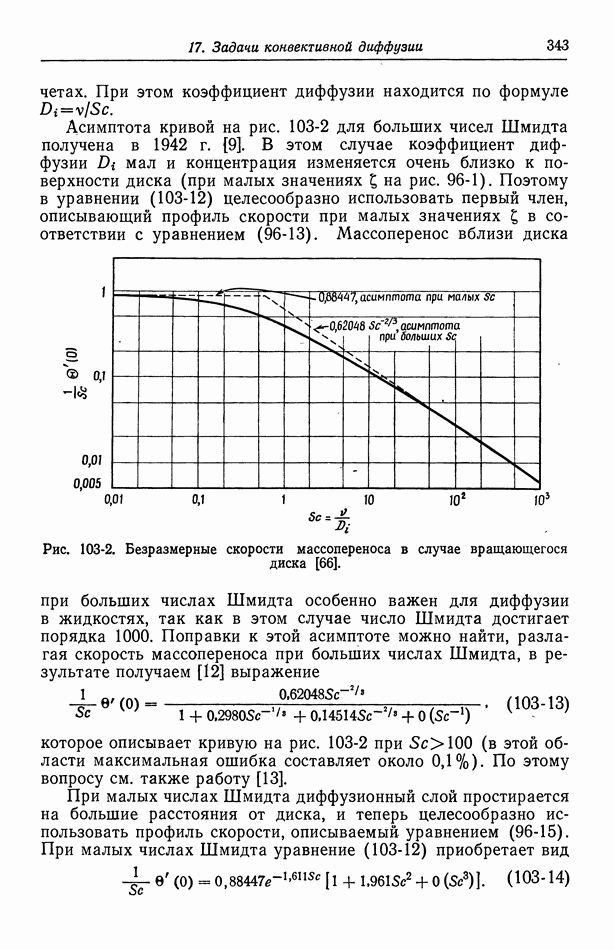
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
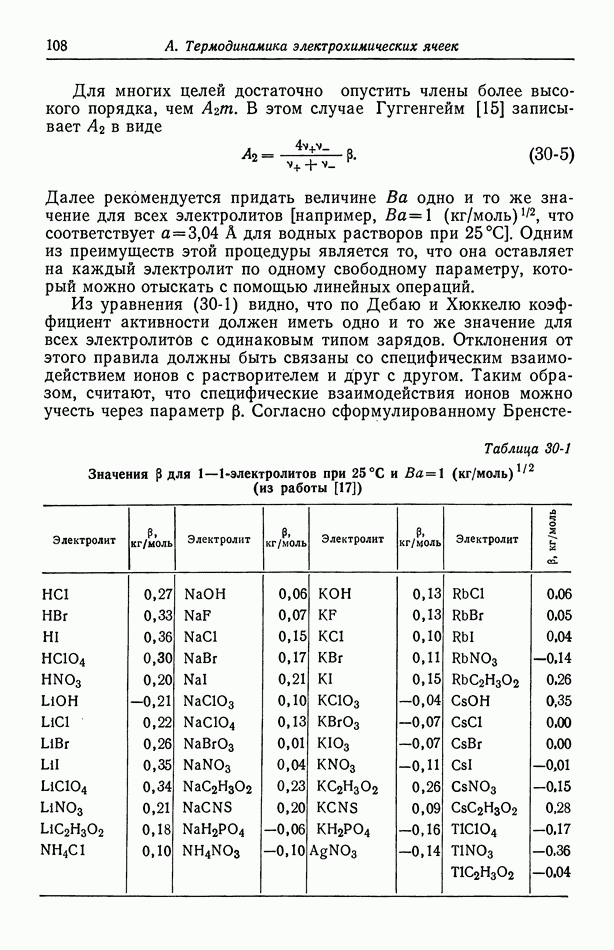
- 55. Гетерогенные электродные реакции
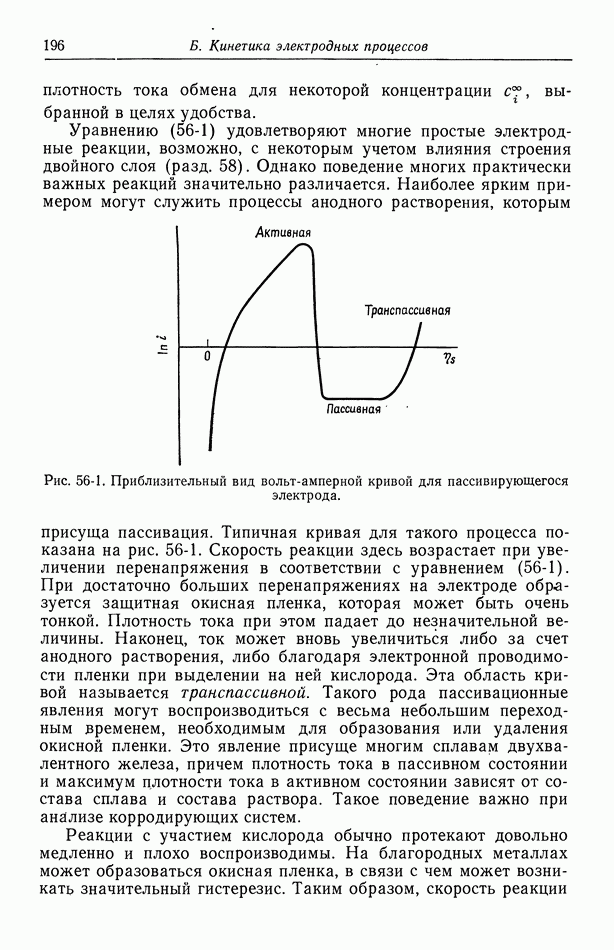
- 56. Зависимость плотности тока от поверхностного перенапряжения
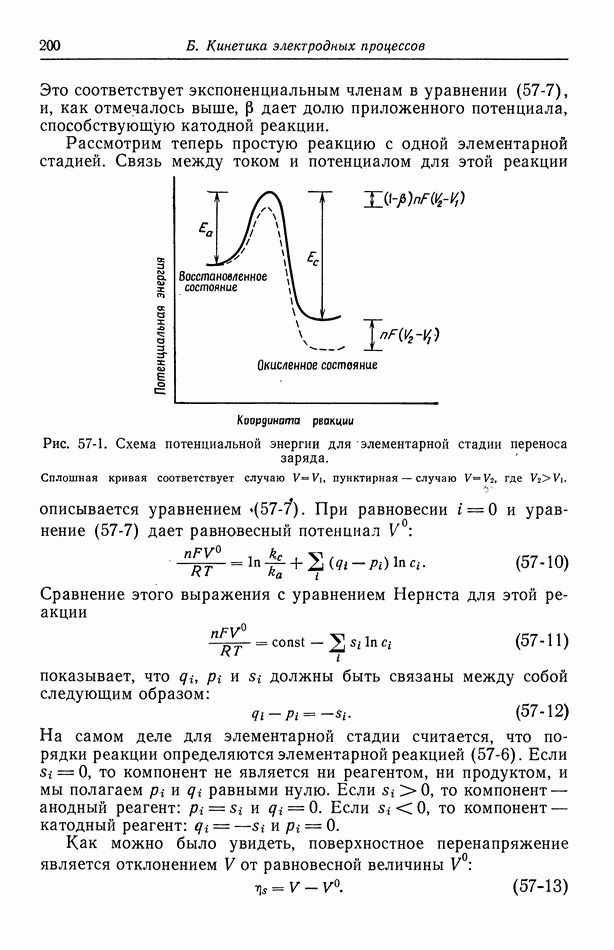
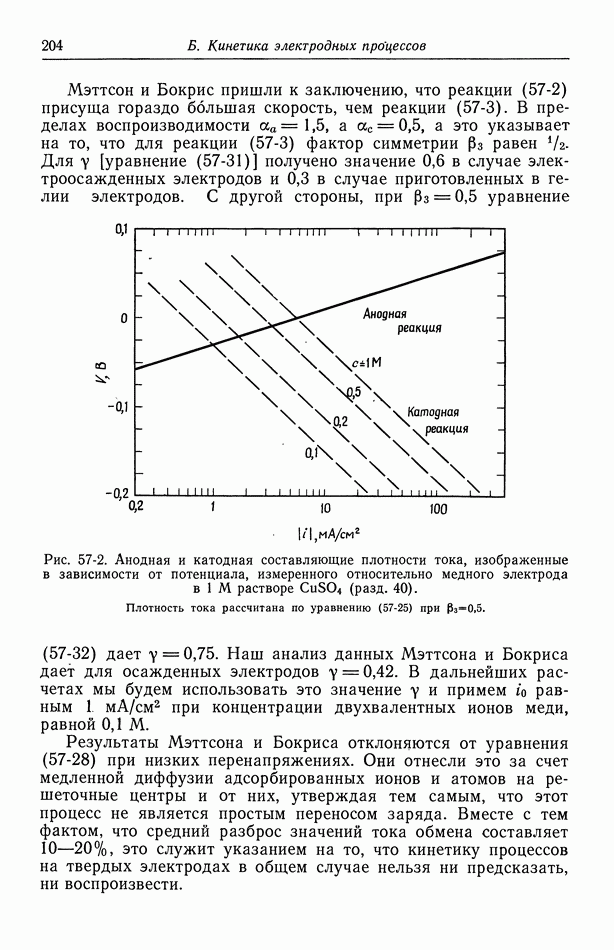
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
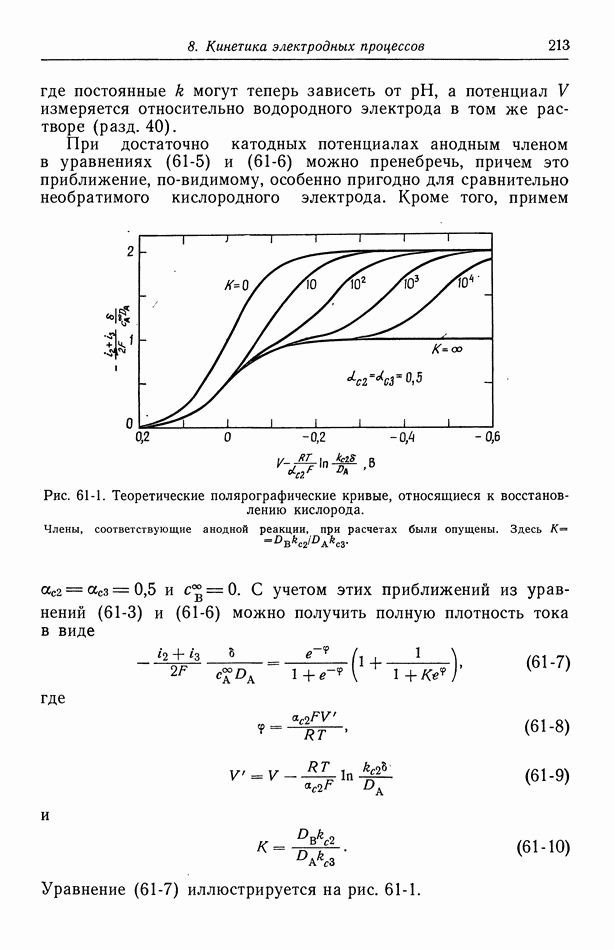
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
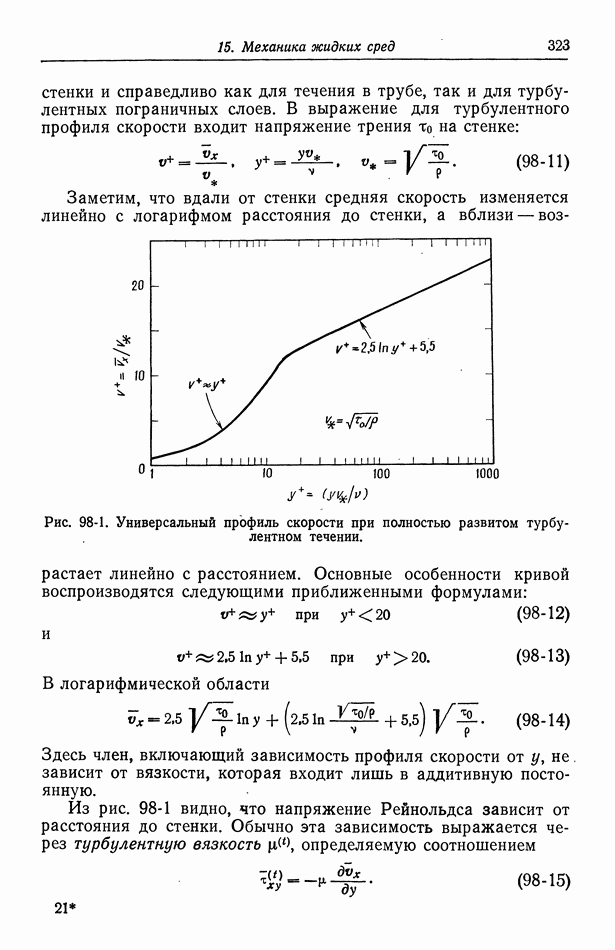
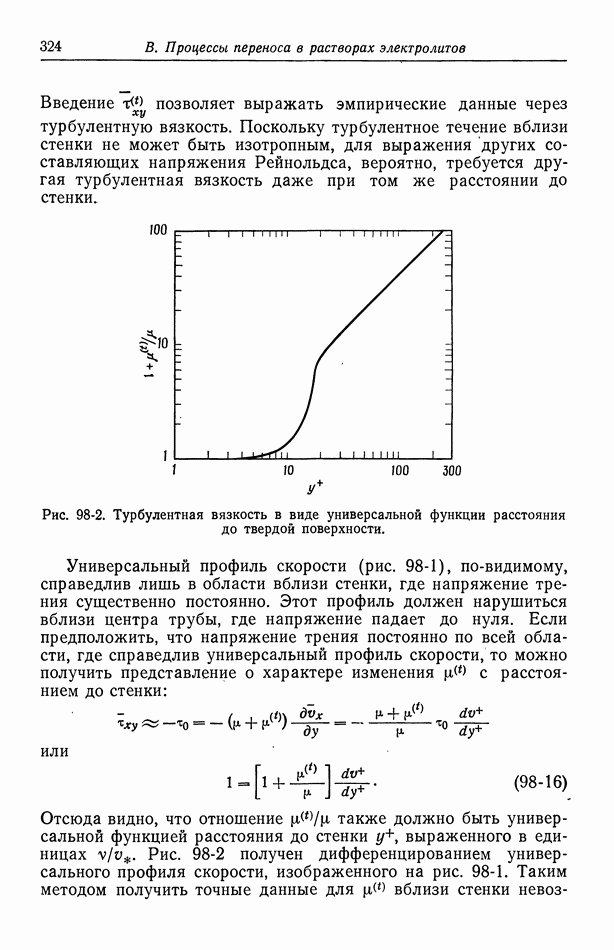
- 98. Турбулентное течение
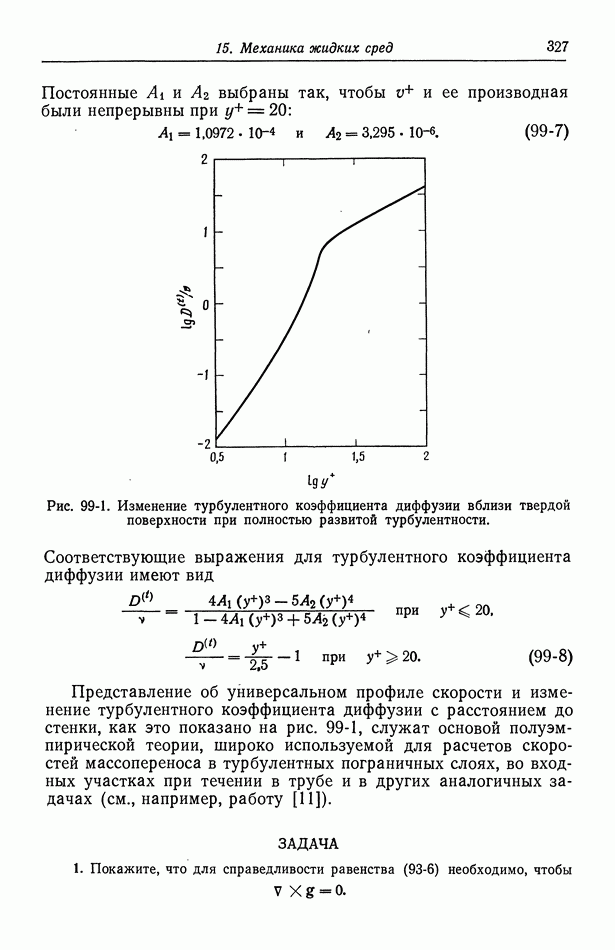
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
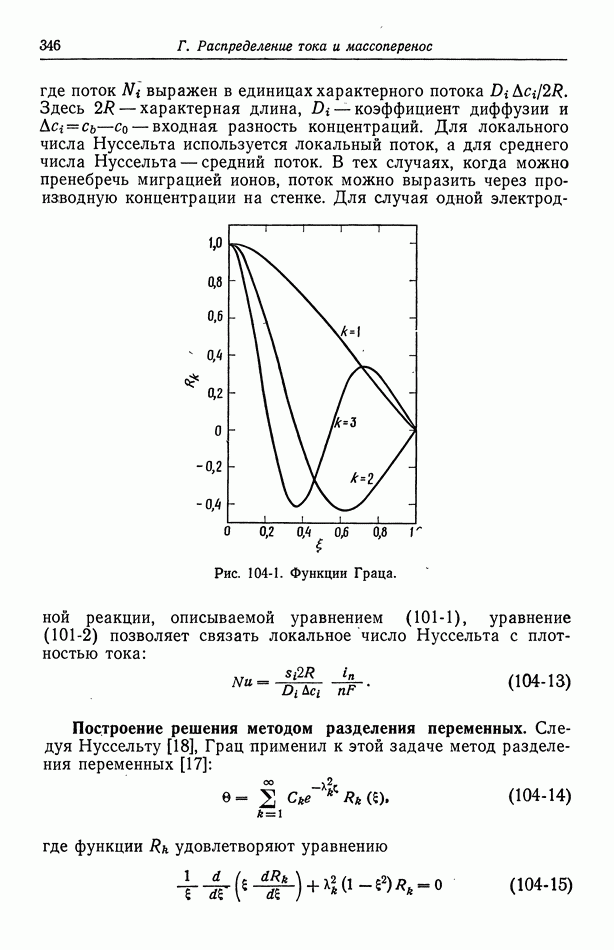
- 101. Кинетика электродных процессов
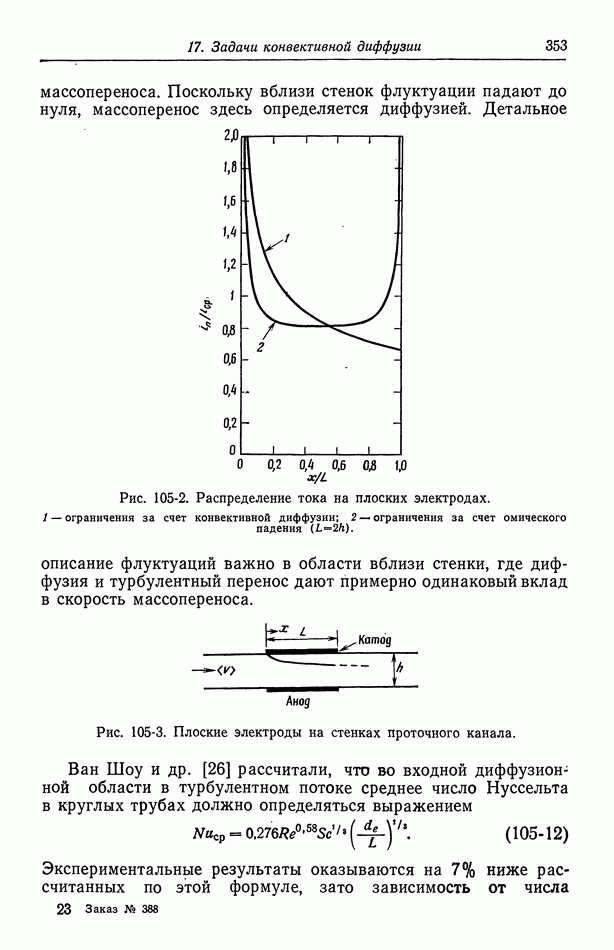
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
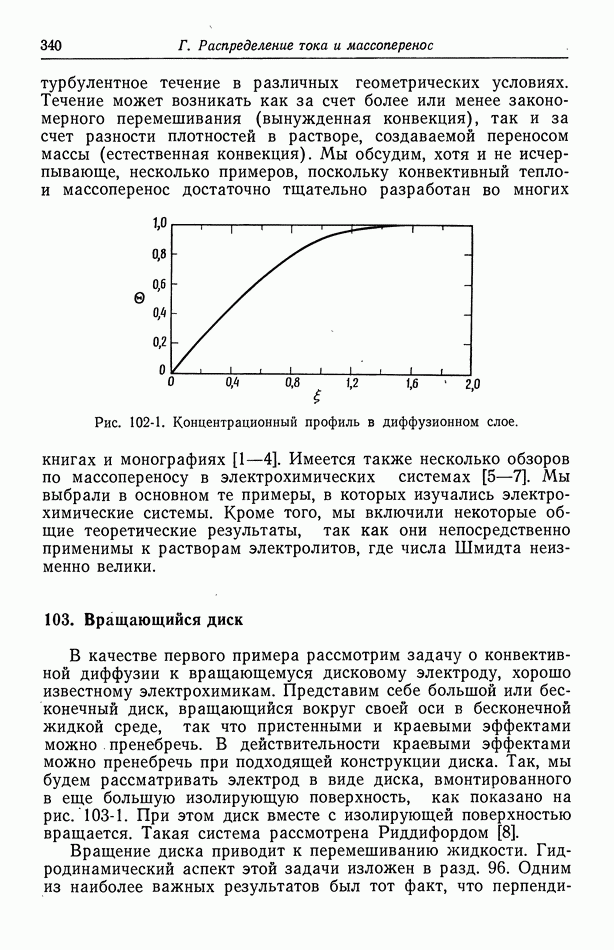
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
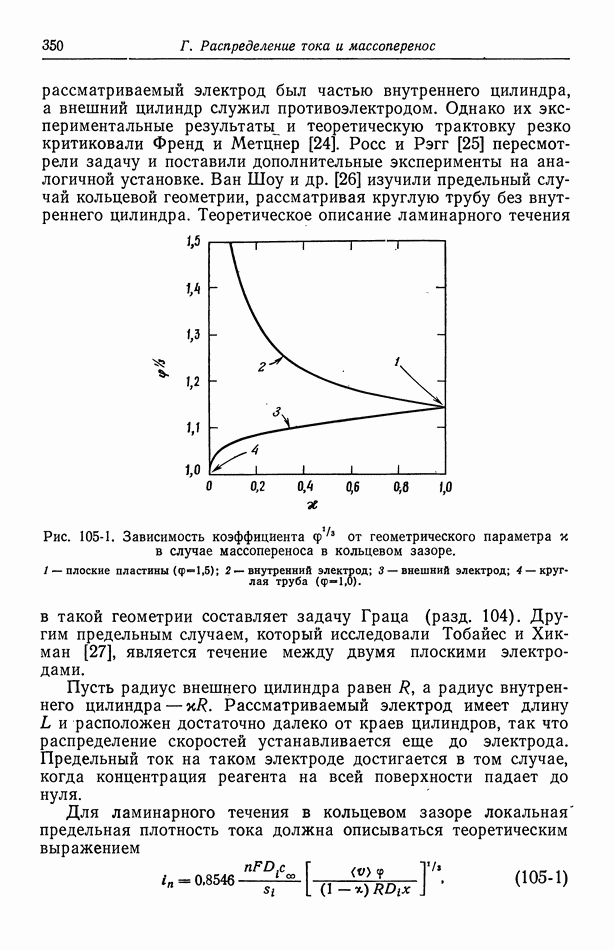
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
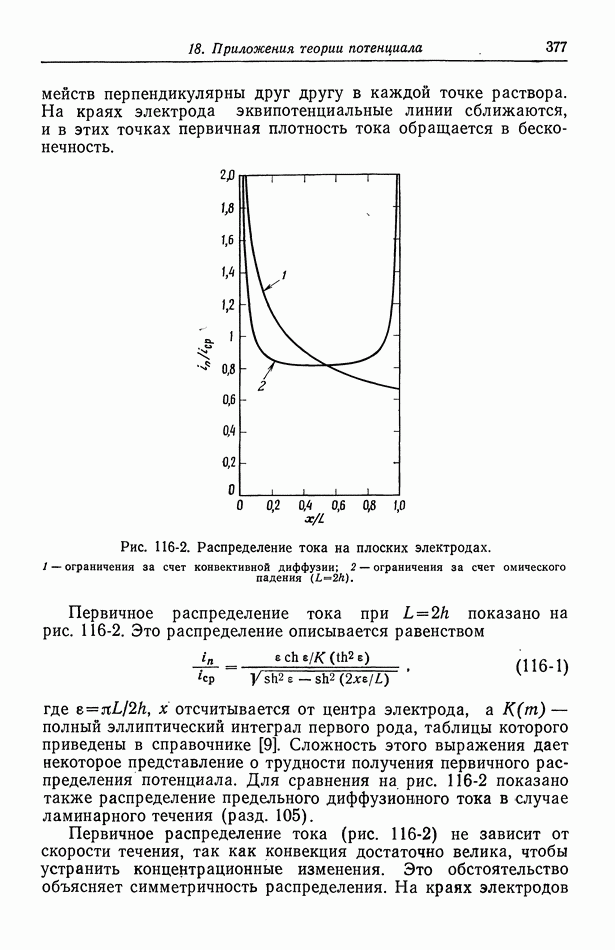
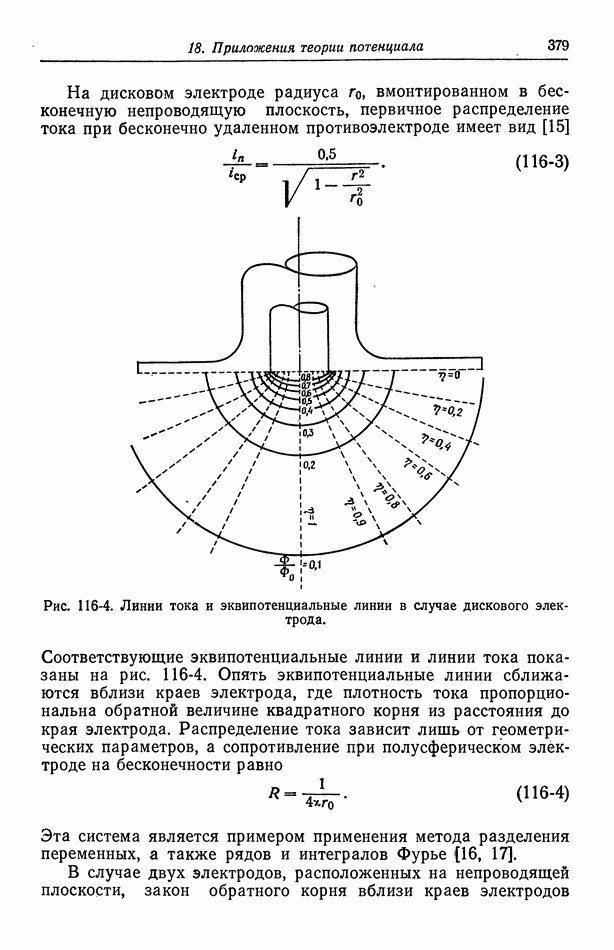
- 116. Первичное распределение тока
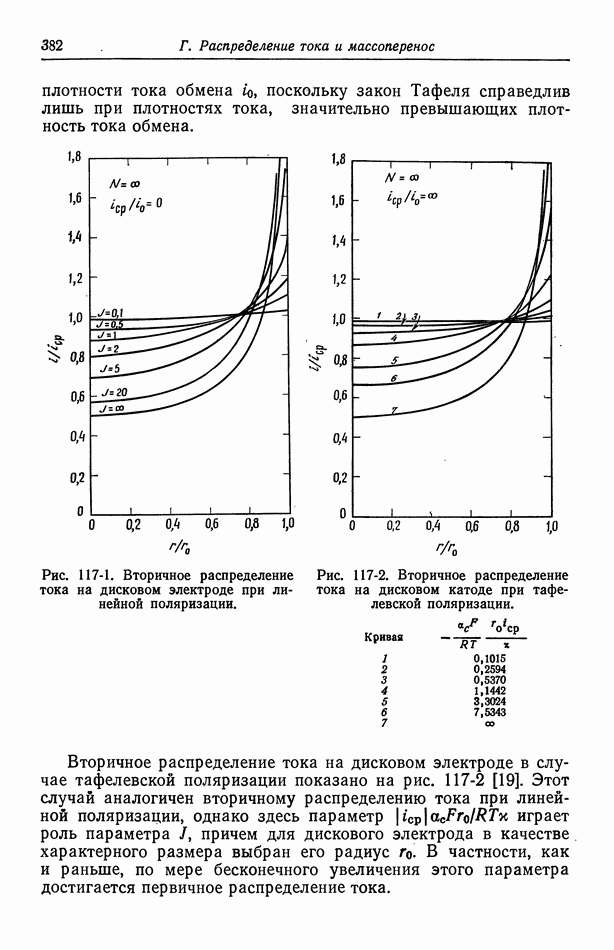
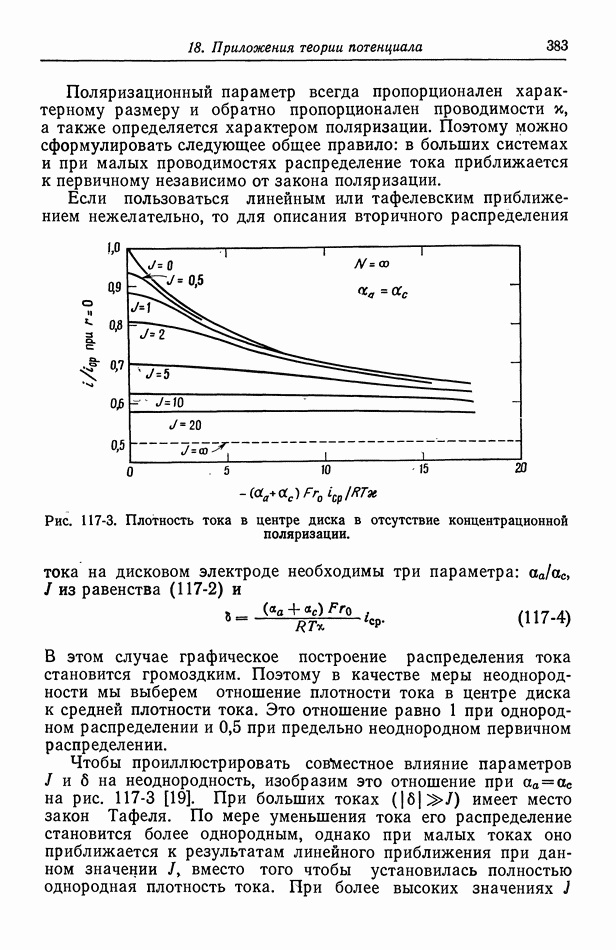
- 117. Вторичное распределение тока
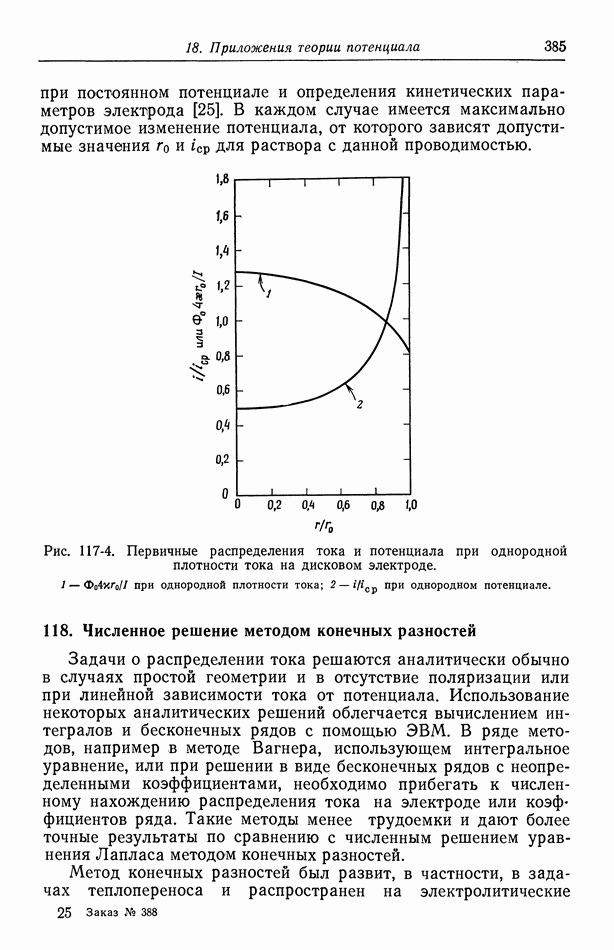
- 118. Численное решение методом конечных разностей
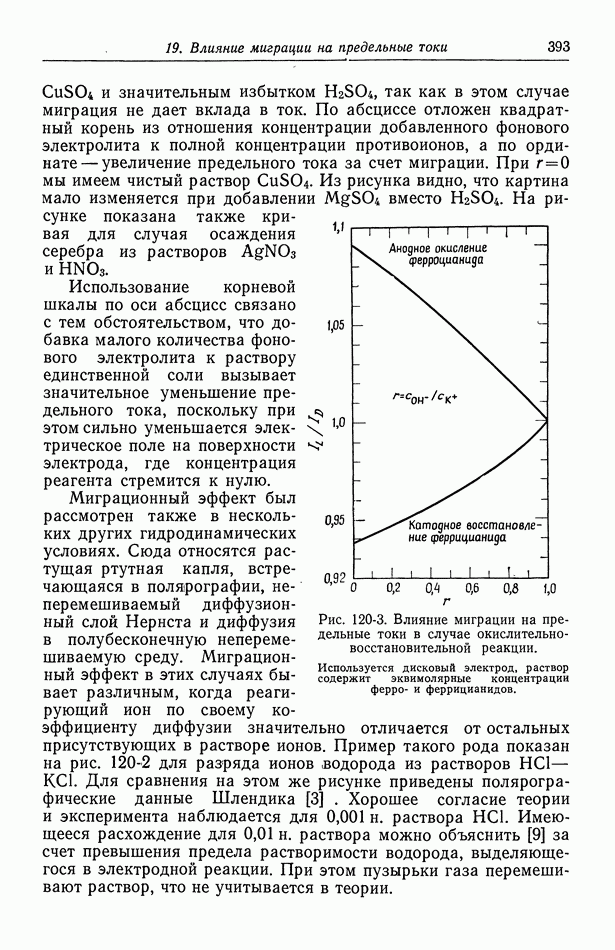
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
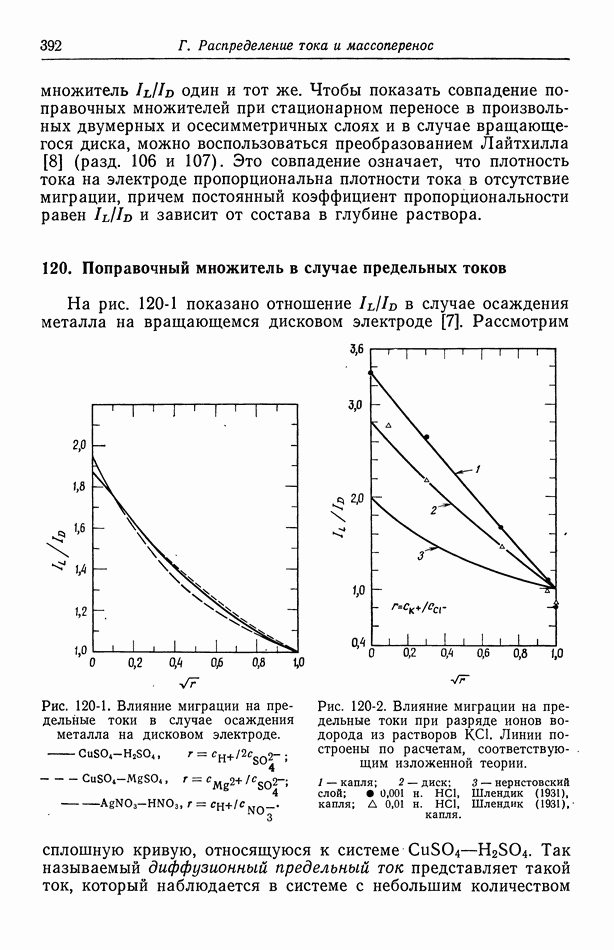
- 120. Поправочный множитель в случае предельных токов
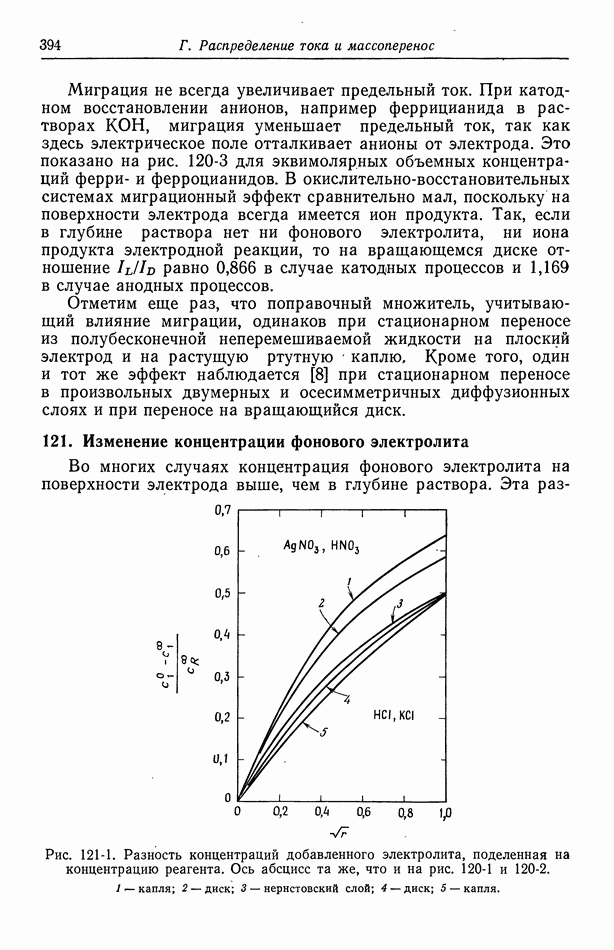
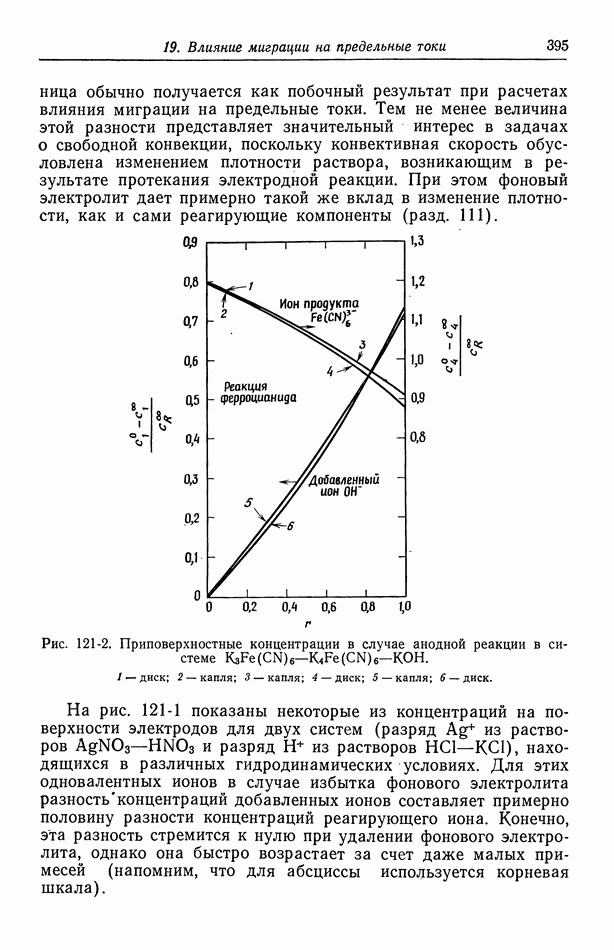
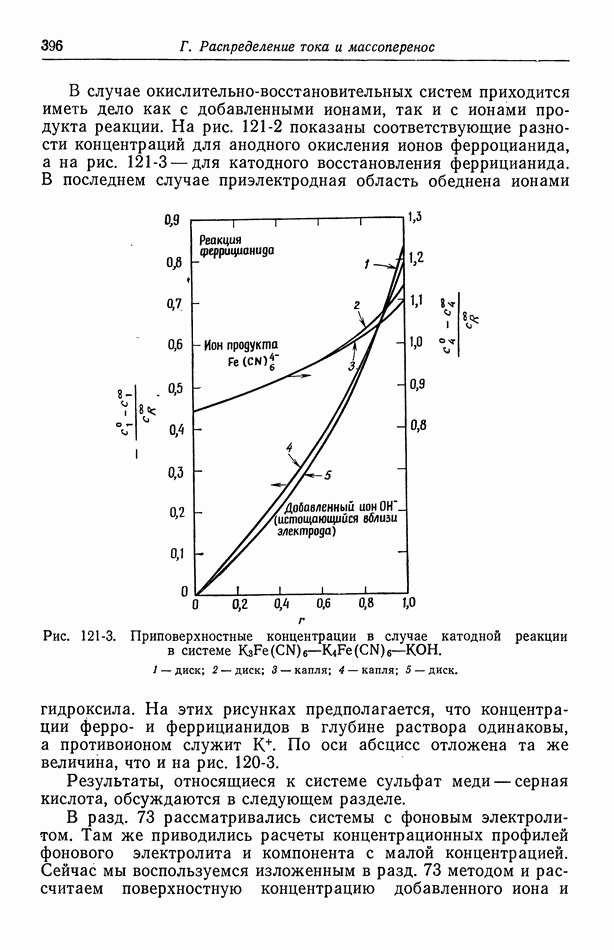
- 121. Изменение концентрации фонового электролита
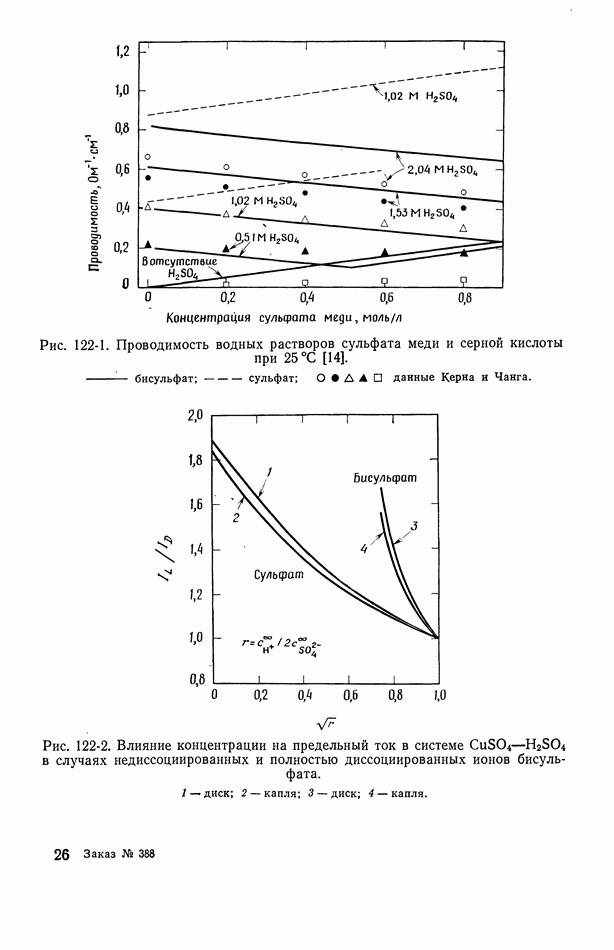
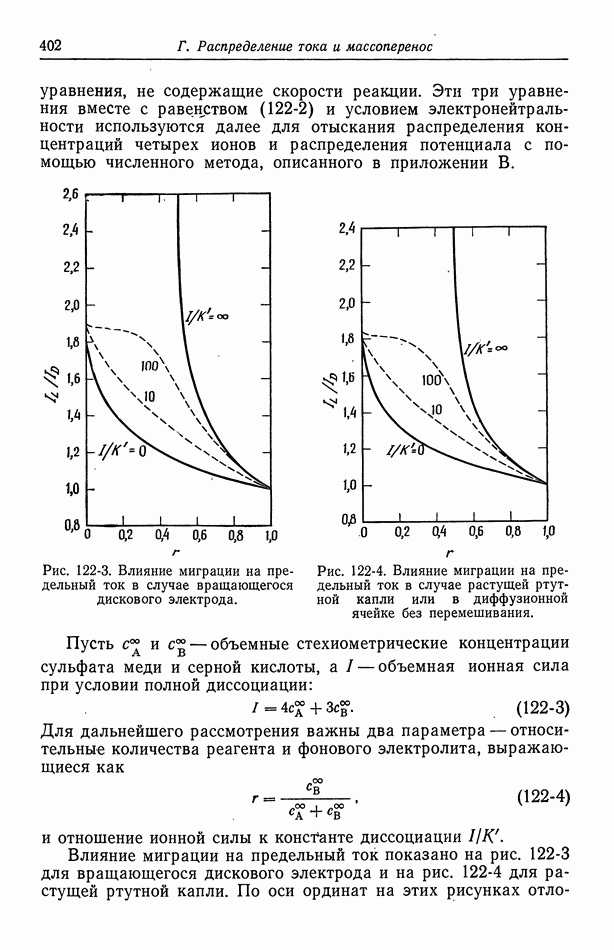
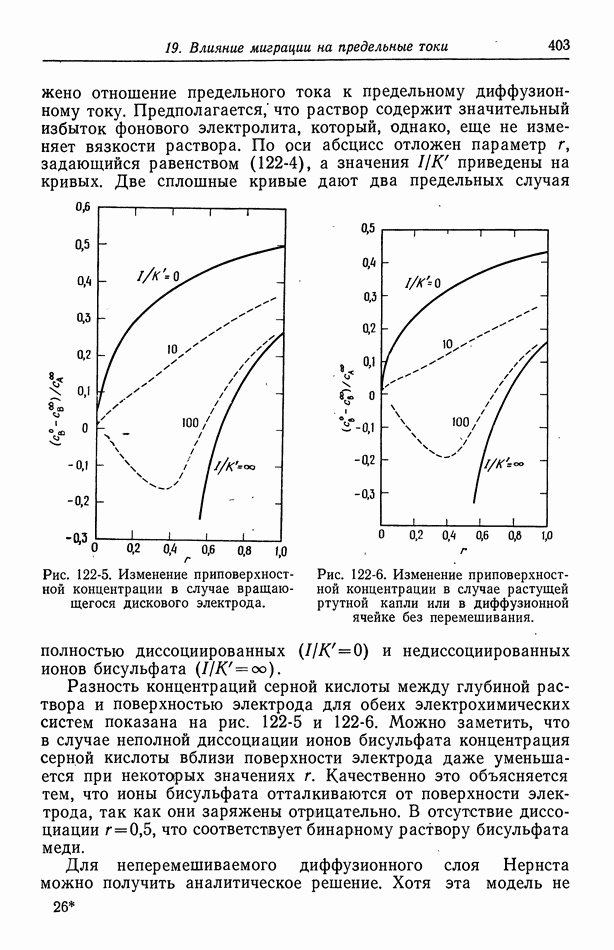
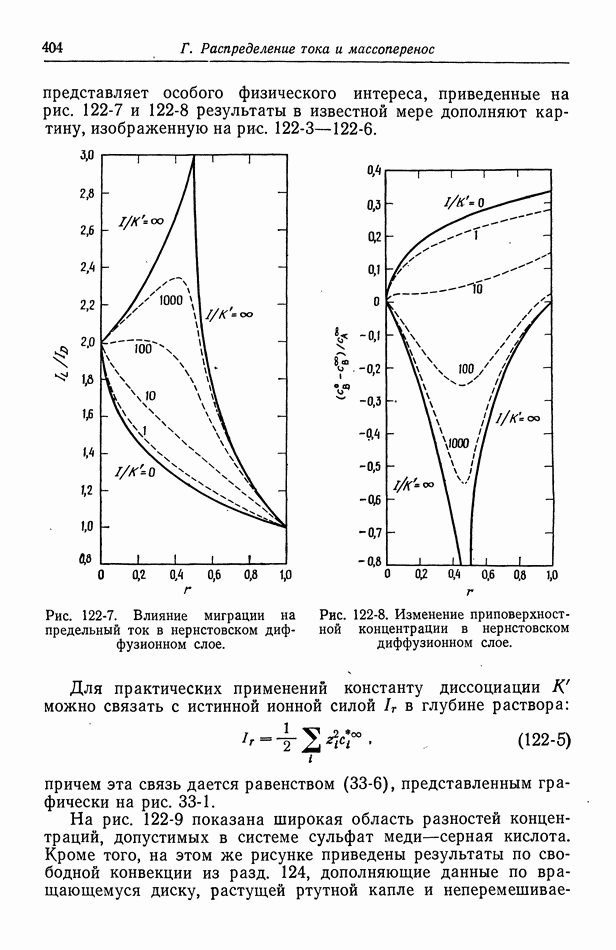
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
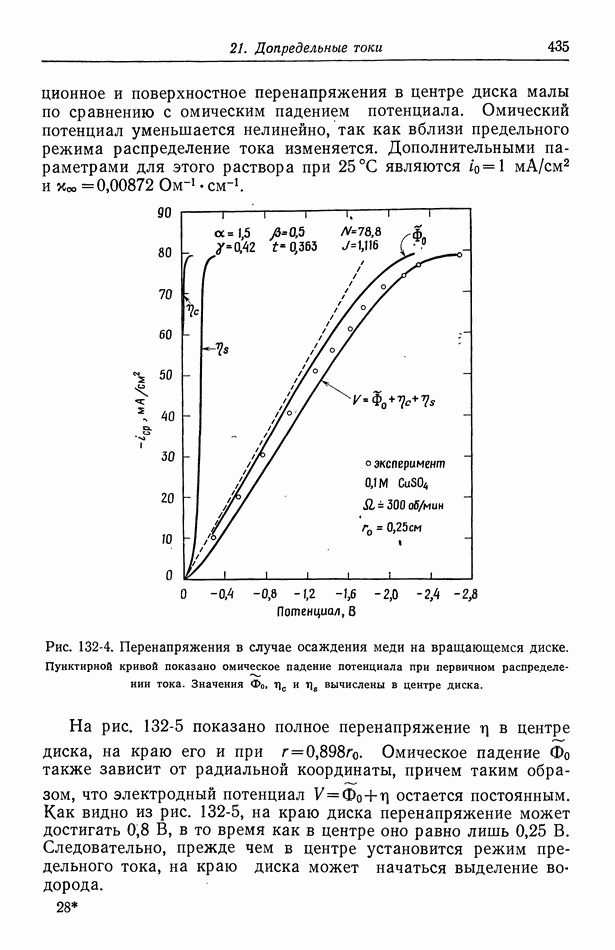
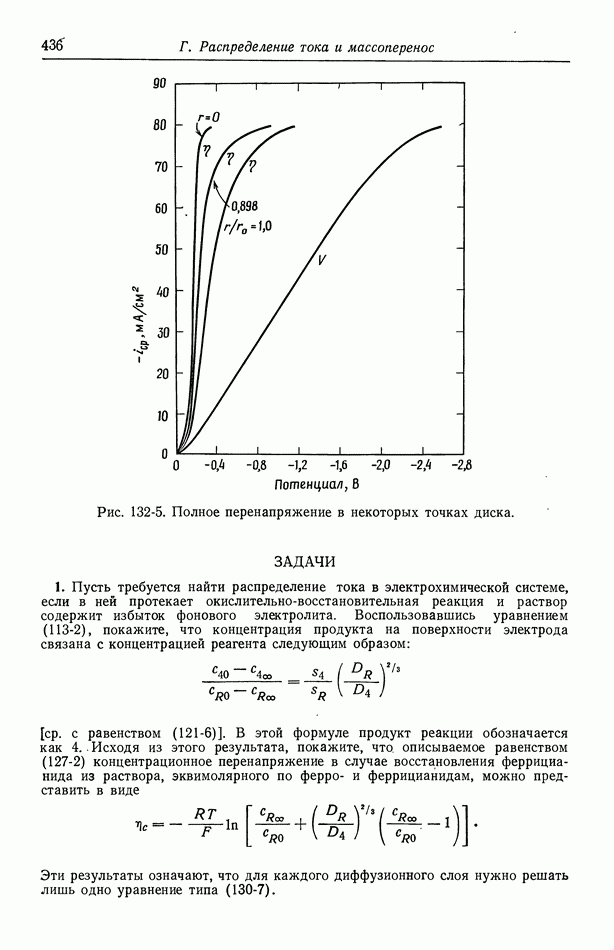
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ