| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
131. Граничные условия и метод решения
Некоторые граничные условия уже обсуждались в связи с диффузионными слоями и объемом среды. Потенциал  в глубине раствора должен удовлетворять условию (129-3), связывающему производную потенциала с плотностью внешнего тока. Этот потенциал позволяет также получить полное перенапряжение, если воспользоваться равенством (129-4). Чтобы решить задачу в диффузионной области, потоки и плотность тока необходимо связать с помощью уравнения (130-5). Это уже делалось при выводе уравнения (130-7).
в глубине раствора должен удовлетворять условию (129-3), связывающему производную потенциала с плотностью внешнего тока. Этот потенциал позволяет также получить полное перенапряжение, если воспользоваться равенством (129-4). Чтобы решить задачу в диффузионной области, потоки и плотность тока необходимо связать с помощью уравнения (130-5). Это уже делалось при выводе уравнения (130-7).
Плотность тока в диффузионном слое должна сшиваться с объемными плотностями тока. Уравнение для плотности тока имеет вид

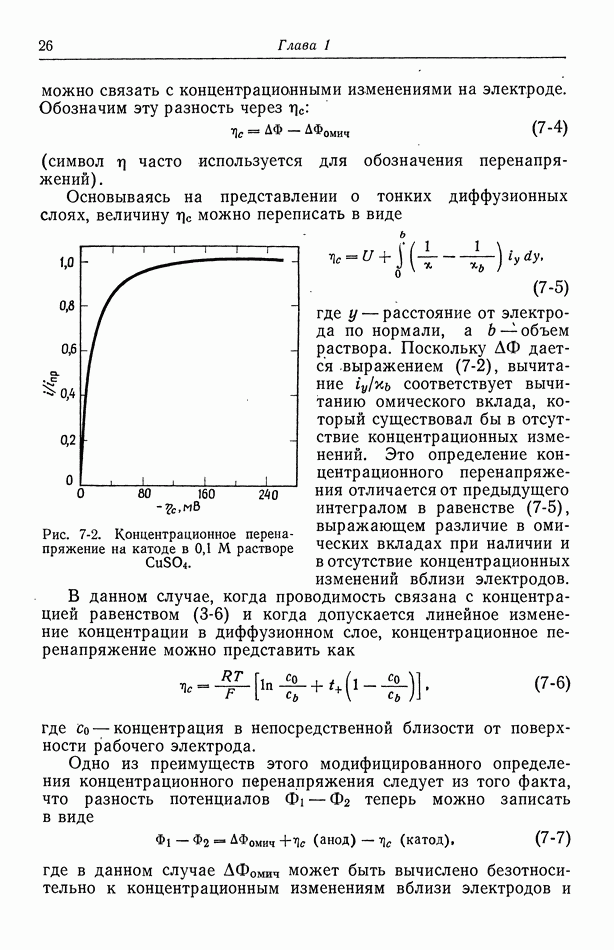
Для двумерного диффузионного слоя это равенство можно переписать в виде

или

Ввиду малой толщины диффузионного слоя значение  внутри этого слоя можно приближенно считать постоянным. Поэтому в граничном условии (120-3), которому должно удовлетворять решение уравнения Лапласа, можно использовать значение
внутри этого слоя можно приближенно считать постоянным. Поэтому в граничном условии (120-3), которому должно удовлетворять решение уравнения Лапласа, можно использовать значение  на твердой поверхности.
на твердой поверхности.
Нам осталось установить вид выражений для концентрационного перенапряжения  и поверхностного перенапряжения
и поверхностного перенапряжения  Первое из них можно рассчитать по уравнению (125-7). Однако более удобны уравнения (126-8) и (127-2), поскольку в них фигурируют лишь концентрации на поверхности электрода, но
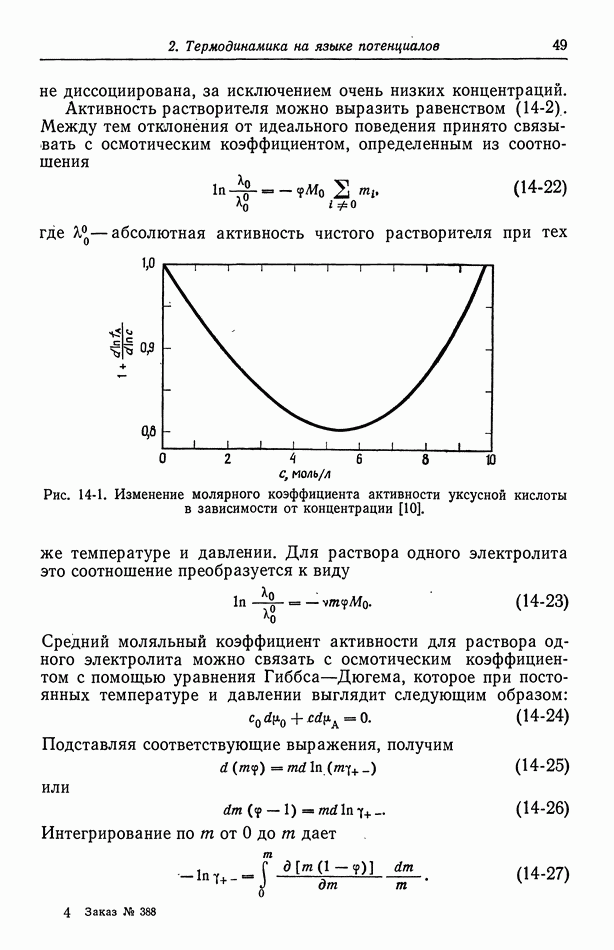
Первое из них можно рассчитать по уравнению (125-7). Однако более удобны уравнения (126-8) и (127-2), поскольку в них фигурируют лишь концентрации на поверхности электрода, но
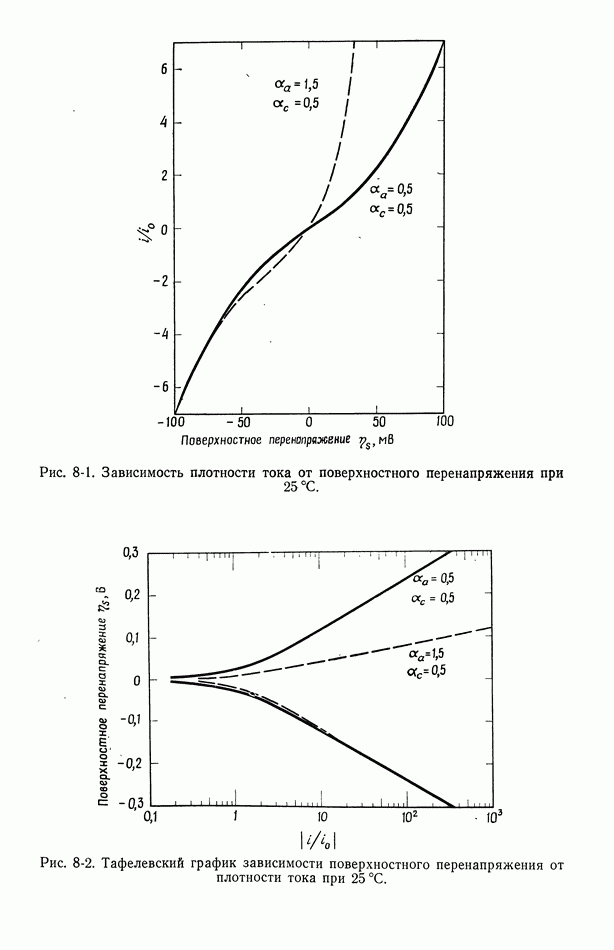
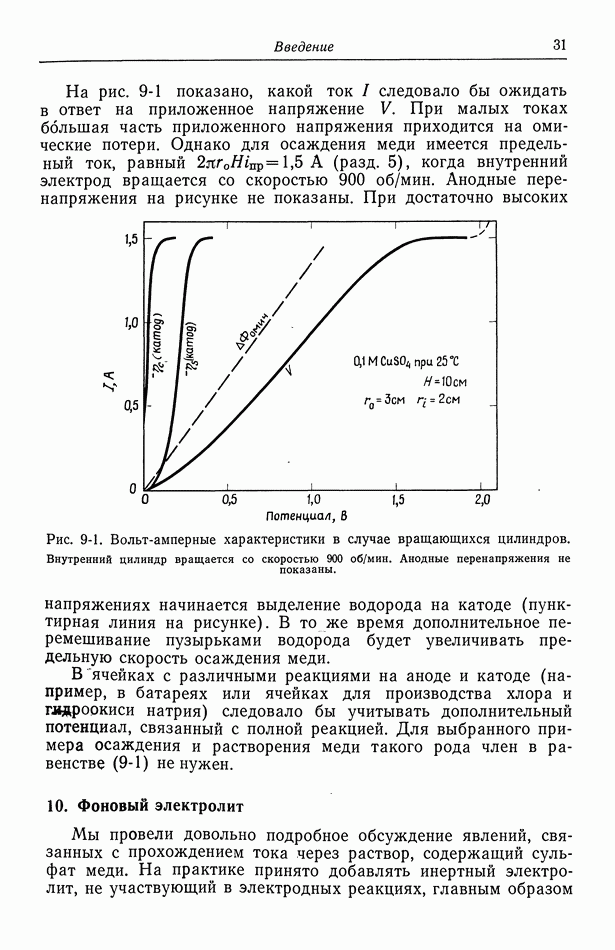
не концентрационные профили в диффузионном слое. Таким образом, предпочтение следует отдать этим уравнениям, если использовано уравнение (130-7). Для многих электродов равенство (101-4) связывает поверхностное перенапряжение с плотностью тока:

где плотность тока обмена зависит от состава раствора вблизи электрода.
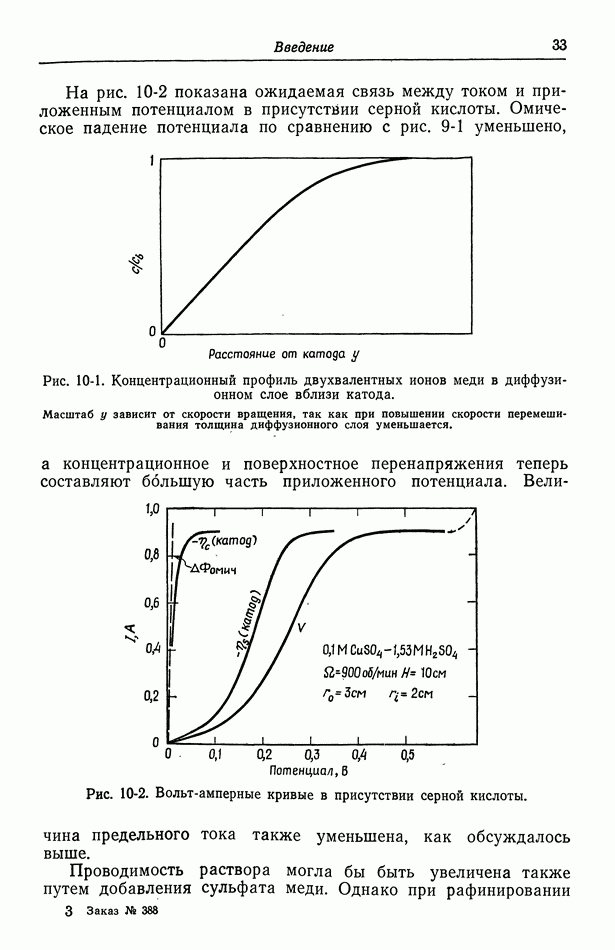
Ситуация сейчас может выглядеть достаточно запутанной, особенно в отношении диффузионного слоя, так как мы привели несколько альтернативных уравнений. Предположим, что имеется только один реагент и что уравнение (130-7) описывает диффузионный слой, а уравнение (126-8) или (127-2) - концентрационное перенапряжение. Тогда основными неизвестными величинами являются плотность тока и концентрация на поверхности электрода. Эти величины должны согласоваться с величиной полного перенапряжения  которое получается после вычитания омического падения потенциала из электродного потенциала.
которое получается после вычитания омического падения потенциала из электродного потенциала.
Представим себе, что распределение  на электроде известно. Тогда величину
на электроде известно. Тогда величину  в уравнении (131-4) можно заменить на
в уравнении (131-4) можно заменить на  где
где  связано с поверхностной концентрацией равенством (126-8) или (127-2). Подстановка уравнения (131-4) в уравнение (130-7) дает интегральное уравнение для поверхностной концентрации. Это уравнение довольно просто решается численными методами, поскольку нелинейное уравнение для
связано с поверхностной концентрацией равенством (126-8) или (127-2). Подстановка уравнения (131-4) в уравнение (130-7) дает интегральное уравнение для поверхностной концентрации. Это уравнение довольно просто решается численными методами, поскольку нелинейное уравнение для  необходимо решать лишь однажды при каждом значении
необходимо решать лишь однажды при каждом значении 
Для решения задачи можно предложить следующую процедуру:
1. Примем некоторое распределение  на поверхностях электродов.
на поверхностях электродов.
2. Из уравнения Лапласа и граничного условия (129-3) вычислим распределение потенциала в объеме среды. Решение будет содержать произвольную аддитивную постоянную.
3. Вычислим распределение полного перенапряжения  на электроде.
на электроде.
4. Для этого электрода решим интегральное уравнение относительно поверхностной концентрации, которое выводится в соответствии со сказанным выше из уравнений (130-7), (131-4), (126-8) и (129-5). Кроме поверхностной концентрации, эти расчеты позволяют также найти распределение тока  и разложить полное перенапряжение
и разложить полное перенапряжение  на составляющие
на составляющие 
5. При расчете полного перенапряжения в пункте 3 мы сталкиваемся с некоторой неопределенностью, связанной с аддитивной постоянной. Эта неопределенность устраняется конкретизацией электродного потенциала и выбором аддитивной постоянной в пункте 2. При этом в случае одного электрода в расчетах можно избежать метода проб и ошибок, если поведение электрода не искажено введением в систему противоэлектрода. Для этого следует определить электродный потенциал с помощью правильно расположенного электрода сравнения или по плотности тока, или по полному перенапряжению в начале диффузионного слоя. Теперь, как только найден ток на электрод, необходимо подобрать постоянную в пункте 3 из условия установления заданного тока. Таким образом, операции 3 и 4 повторяются до тех пор, пока не будет достигнут нужный ток. В системе с двумя непосредственно влияющими друг на друга электродами также нужно определить полный ток (так чтобы он был одинаковым для обоих электродов), и опять приходится прибегать к итерациям по пунктам 3 и 4.
6. В случае двух электродов действия, указанные в пунктах 3—5, следует выполнить для второго электрода.
7. Выполнение действий в пунктах 3—6 позволяет найти новое распределение тока на электродах, которое теперь может отличаться от использованного в пункте 2. При новом распределении плотности тока операции 2—6 должны повторяться до тех пор, пока полученное в пунктах 3—6 распределение не будет достаточно хорошо согласоваться с найденным в пункте 2. Сходимость этой процедуры достигается обычно в том случае, если новое распределение тока выбирается как некоторая средняя величина между предшествовавшим распределением, использованным в пункте 2, и полученным в пунктах 3—6.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
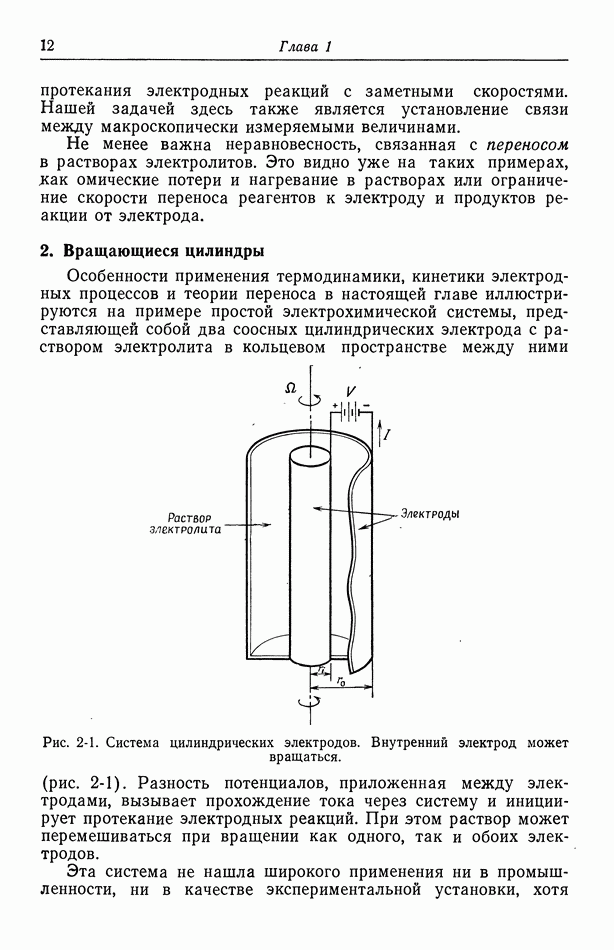
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
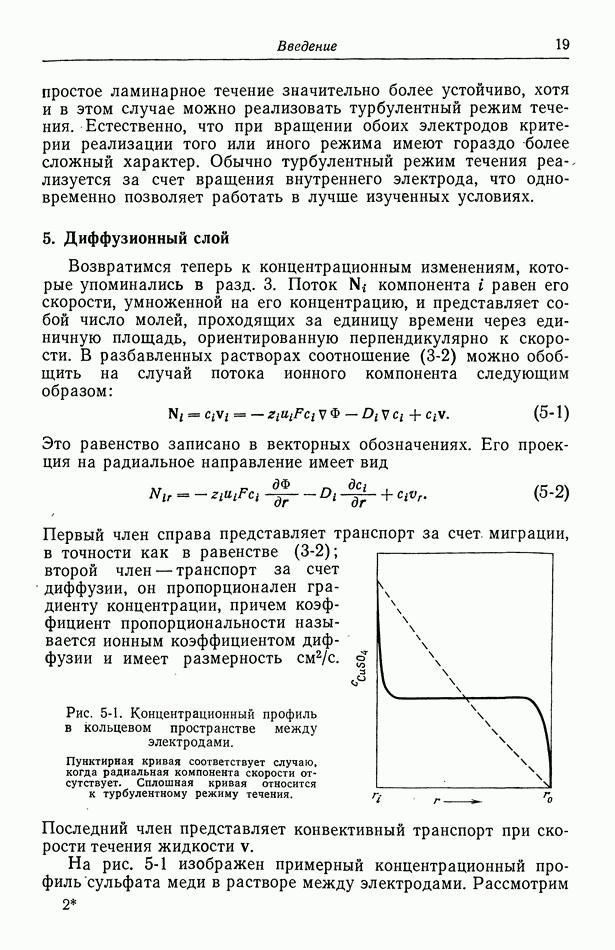
- 5. Диффузионный слой
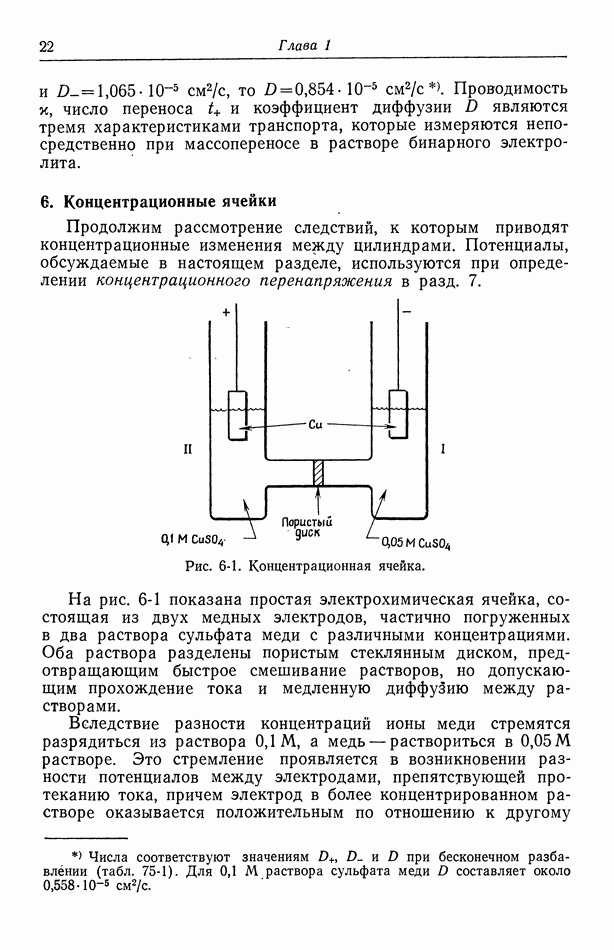
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
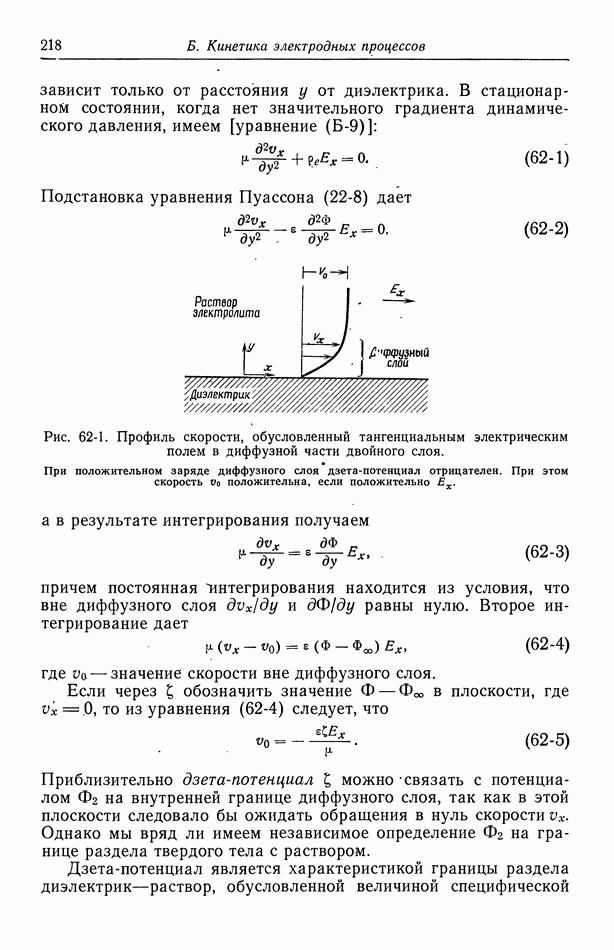
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
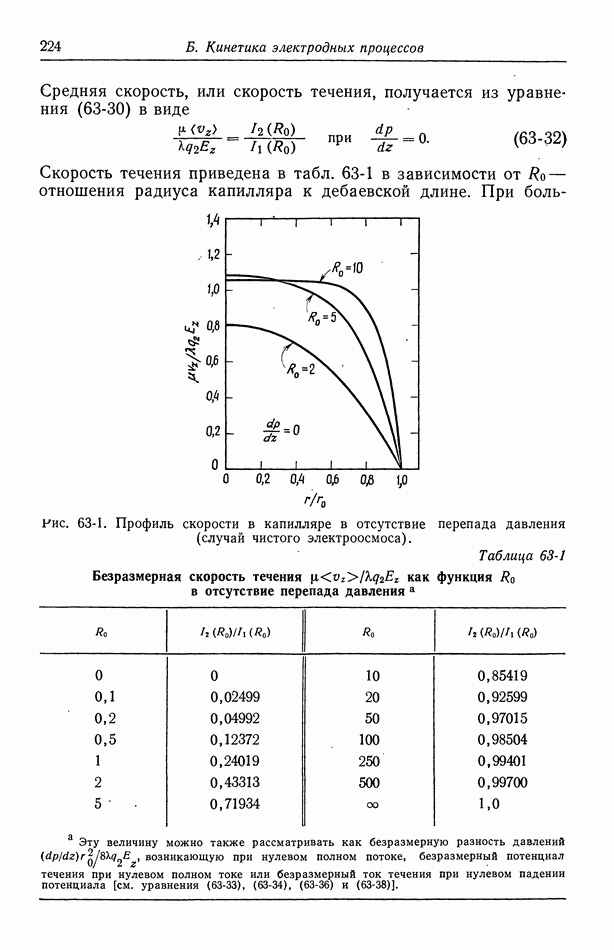
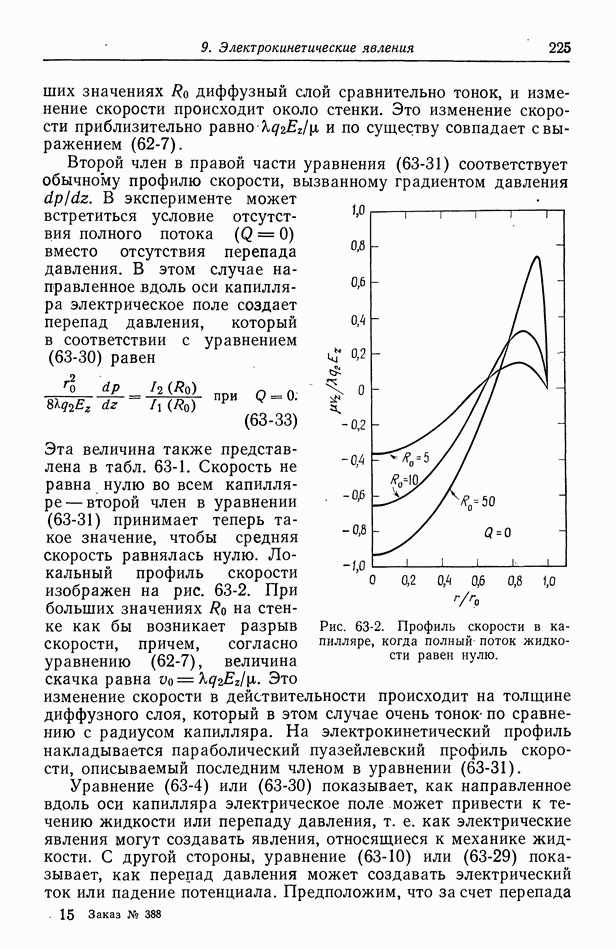
- 22. Электростатический потенциал
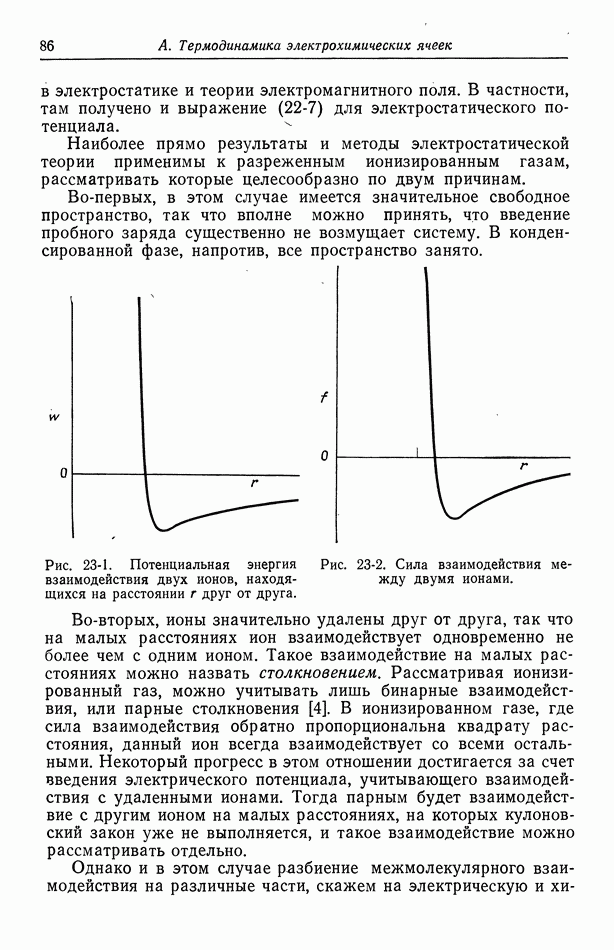
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
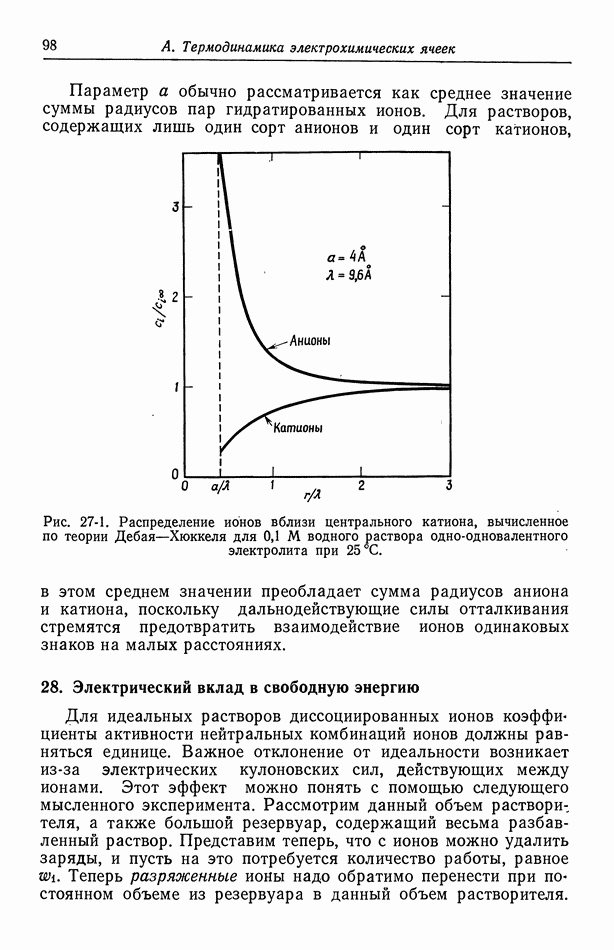
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
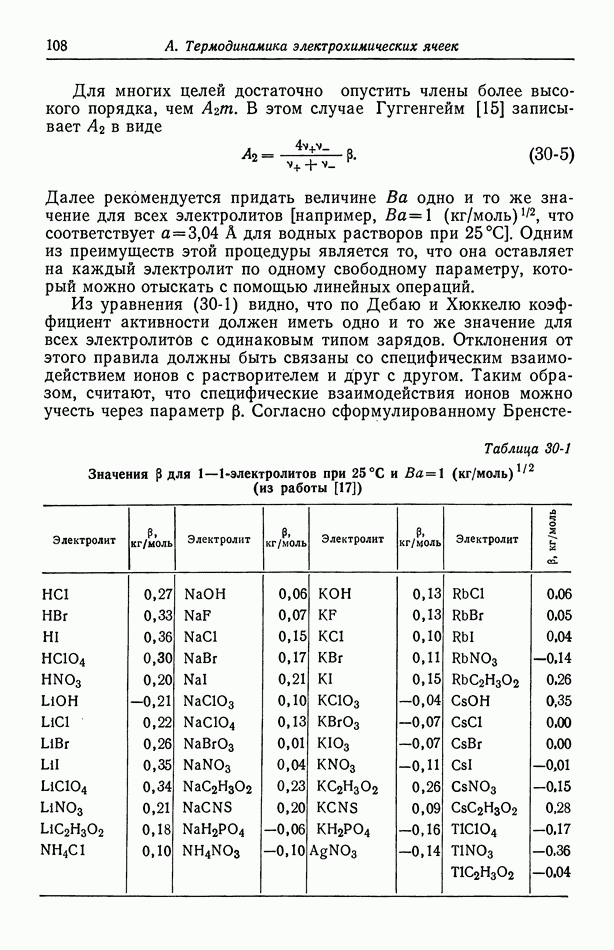
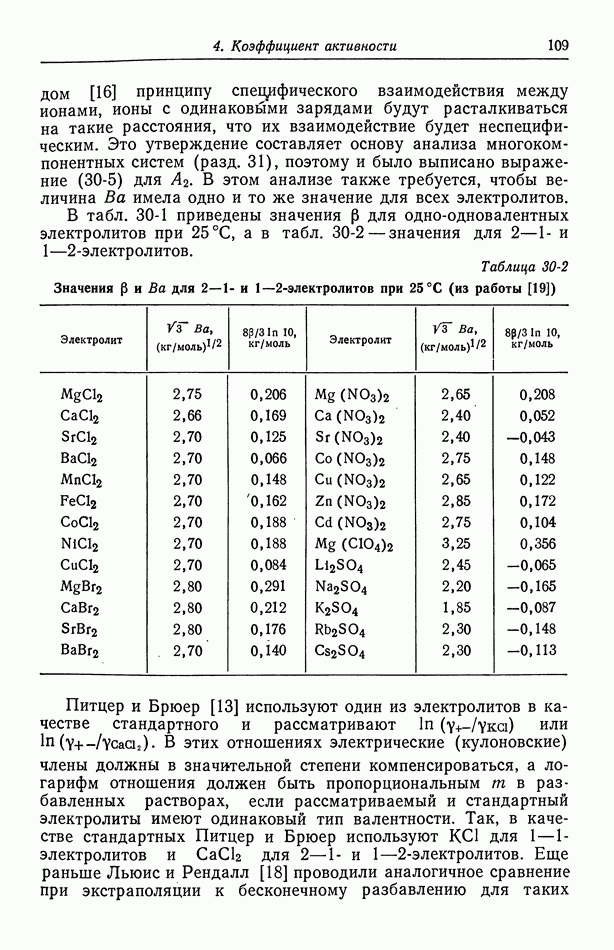
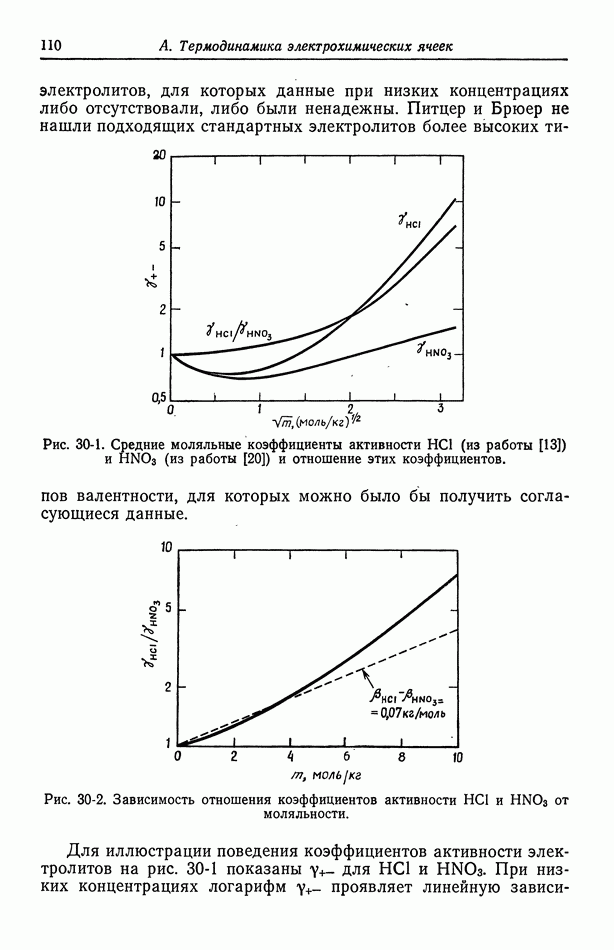
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
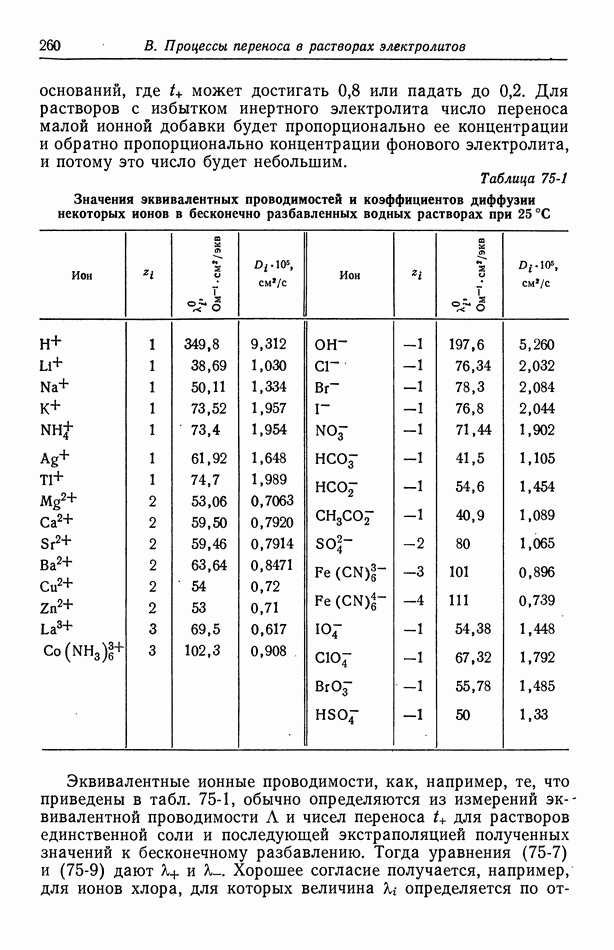
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
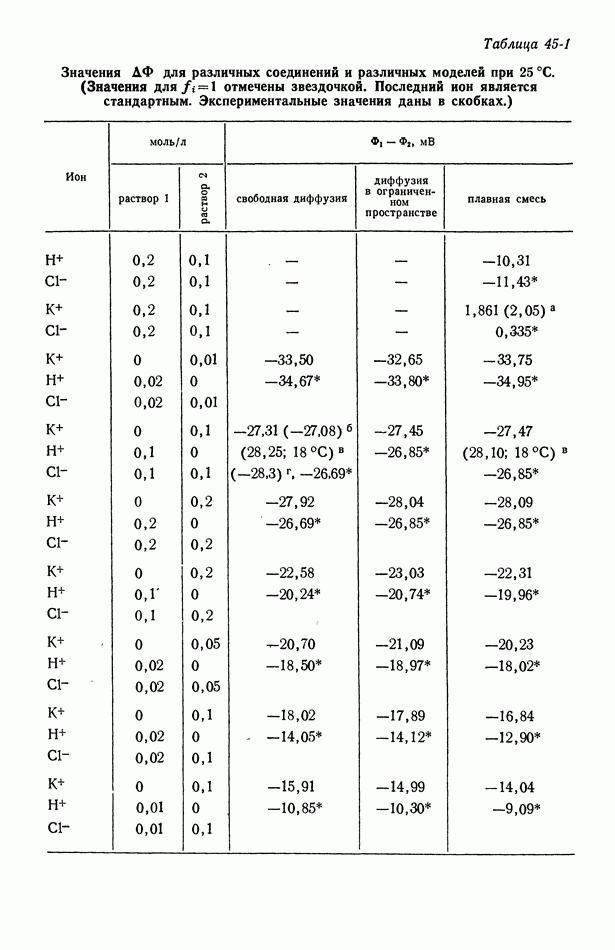
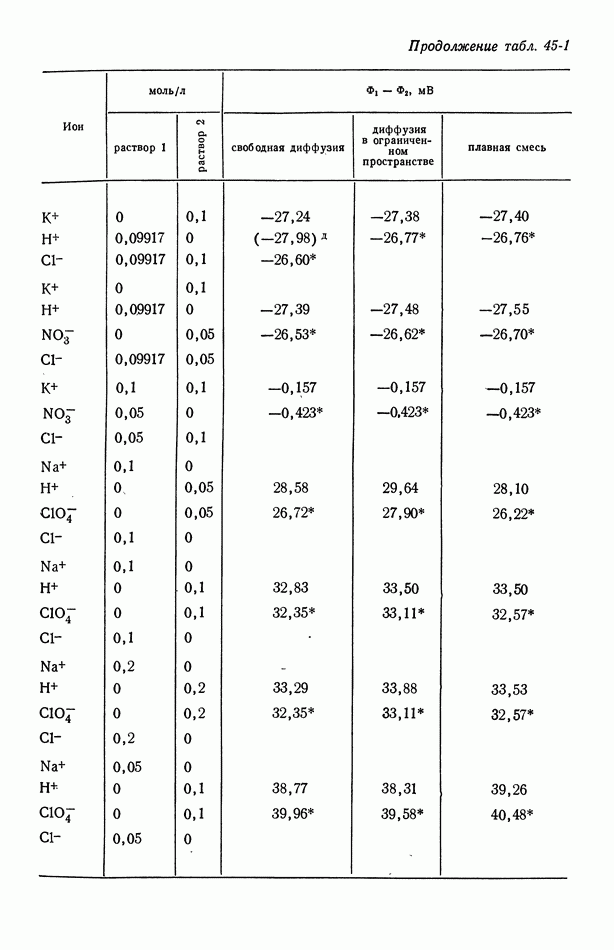
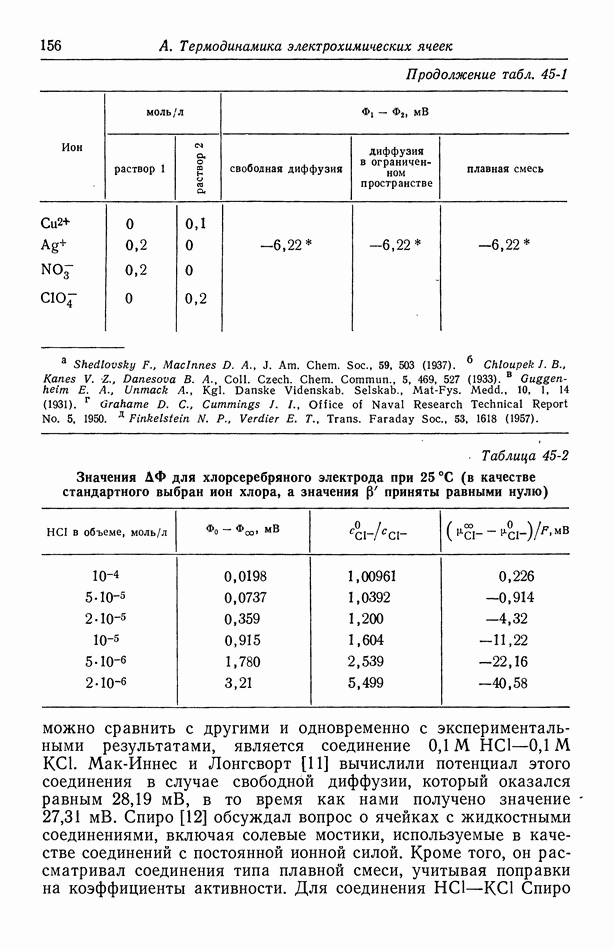
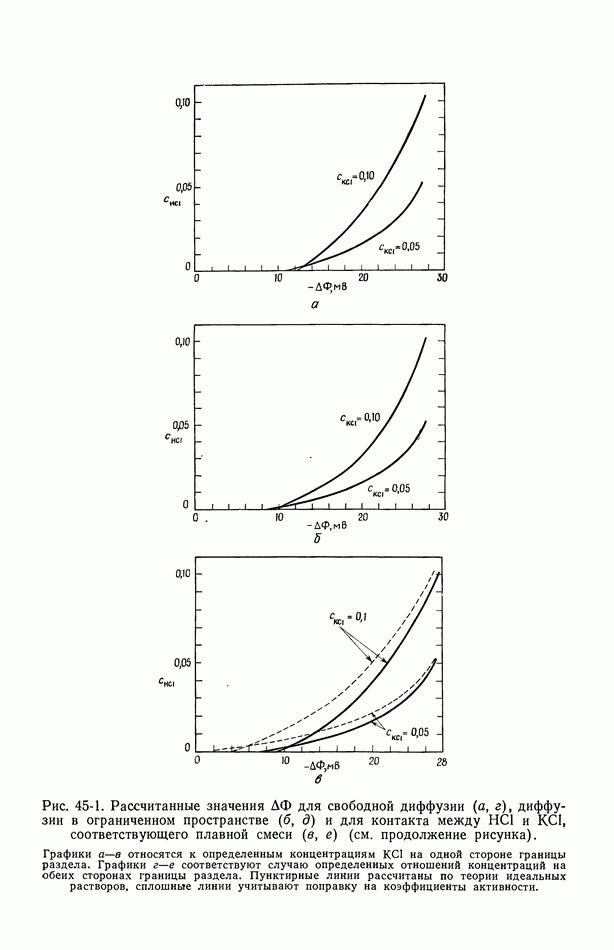
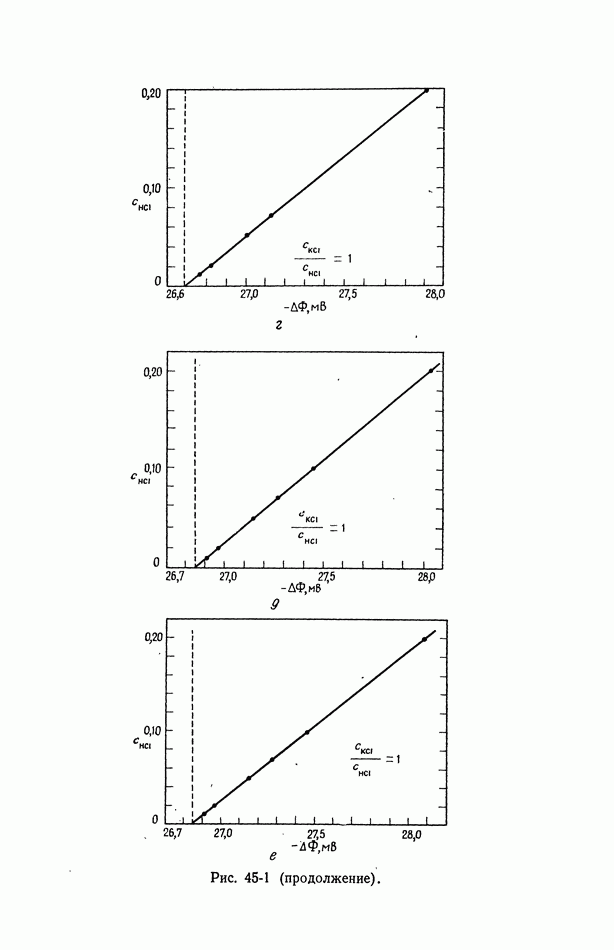
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
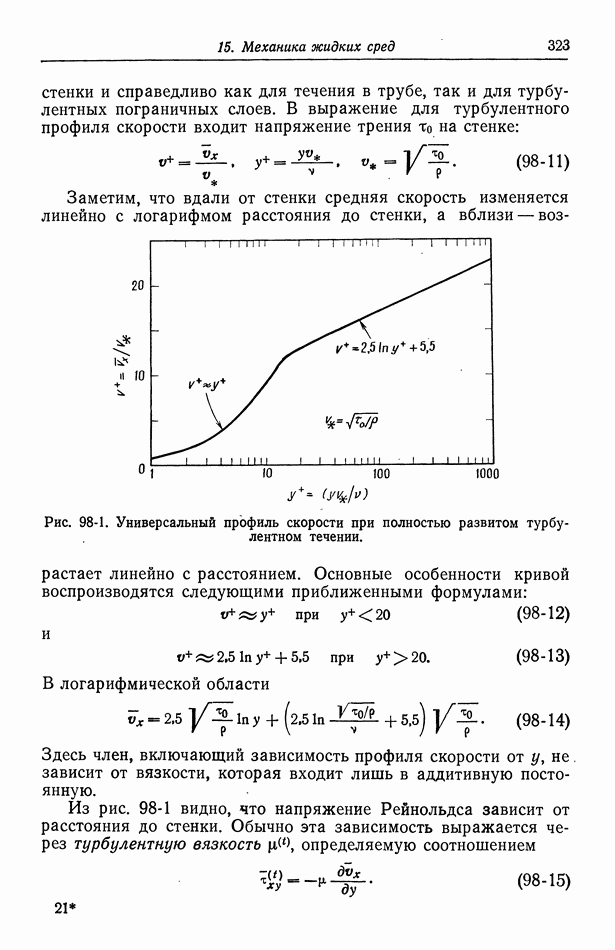
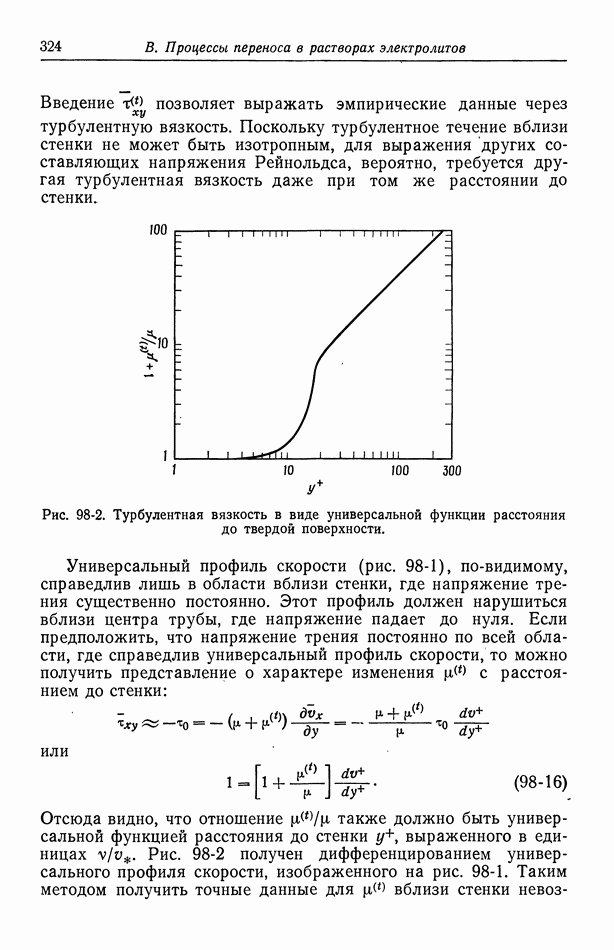
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
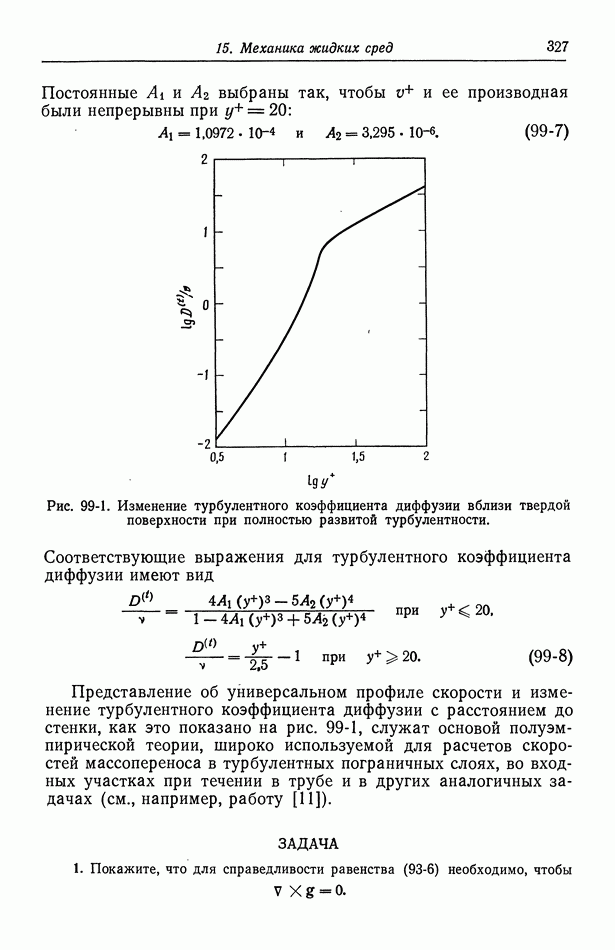
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
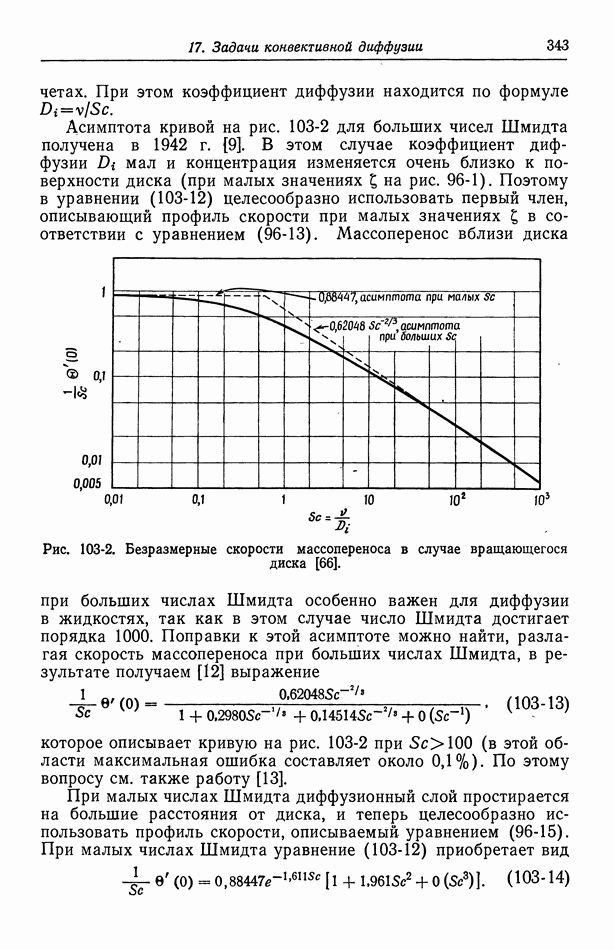
- 57. Модели в кинетике электродных процессов
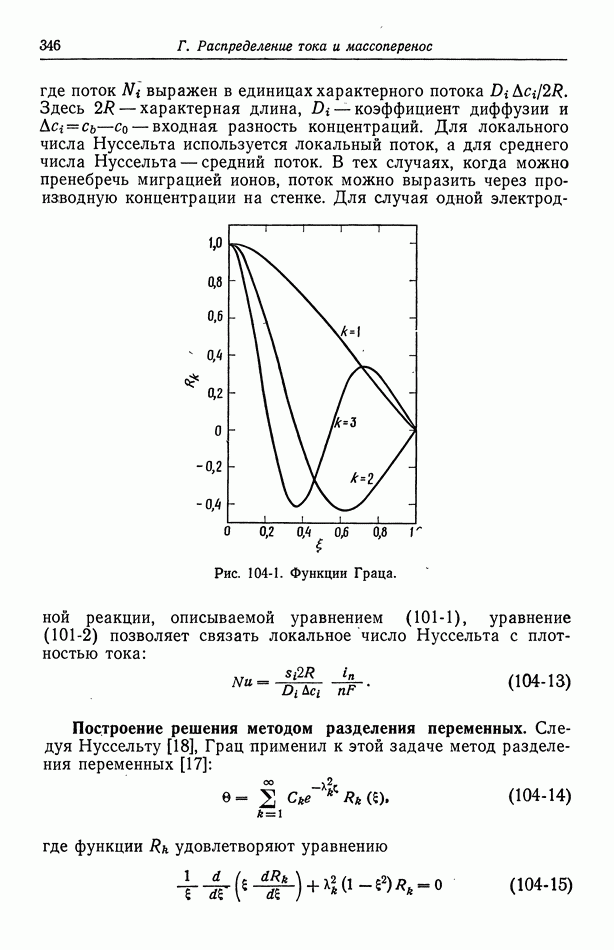
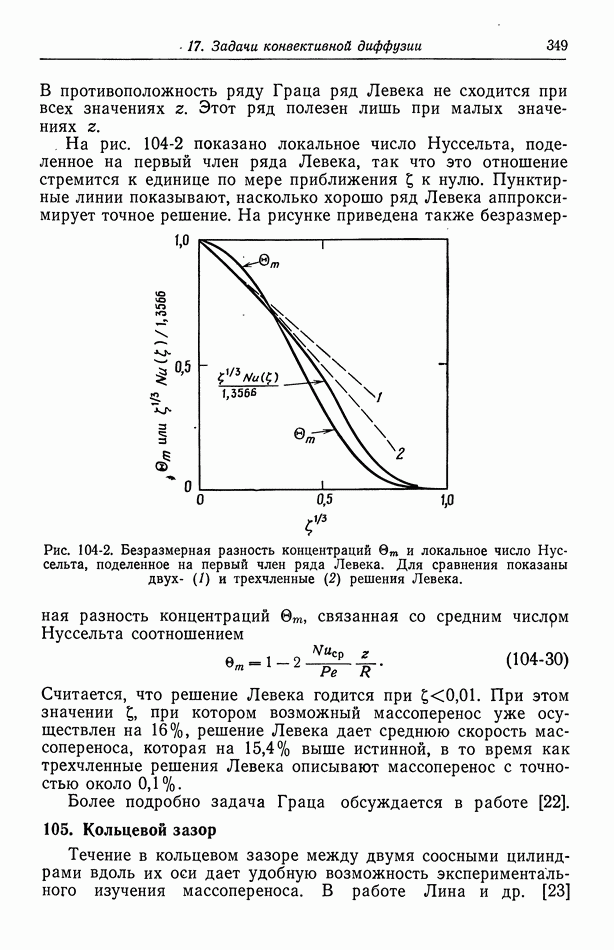
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
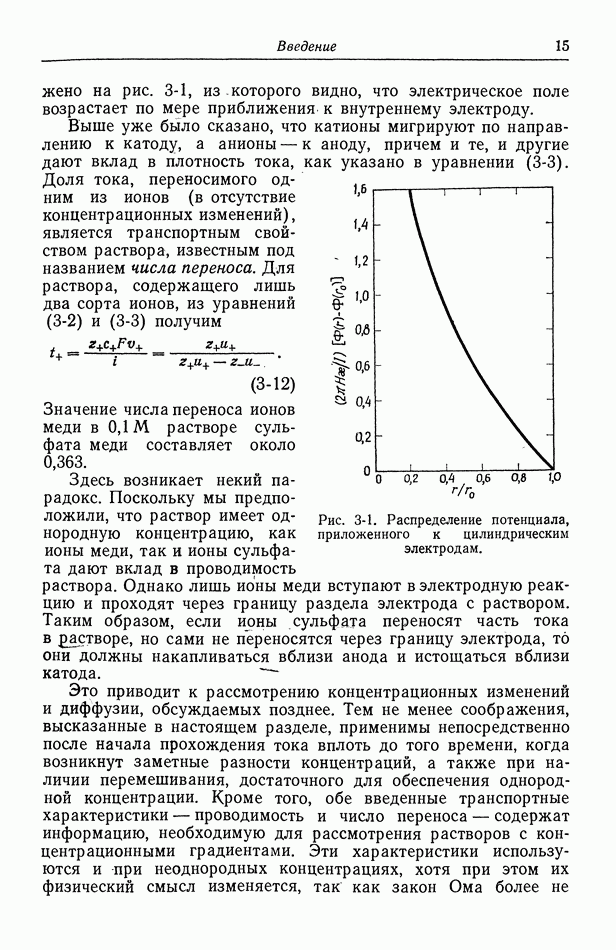
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
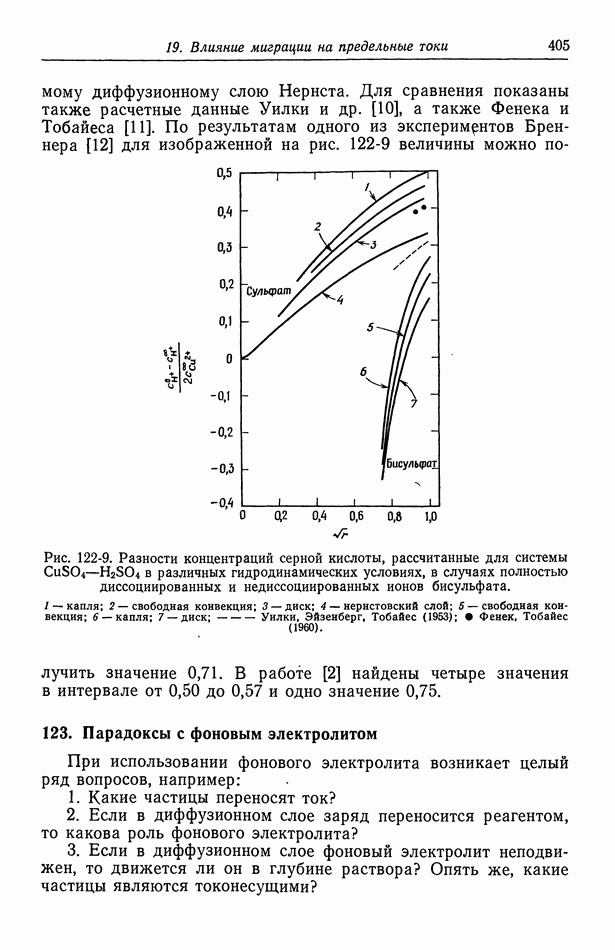
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
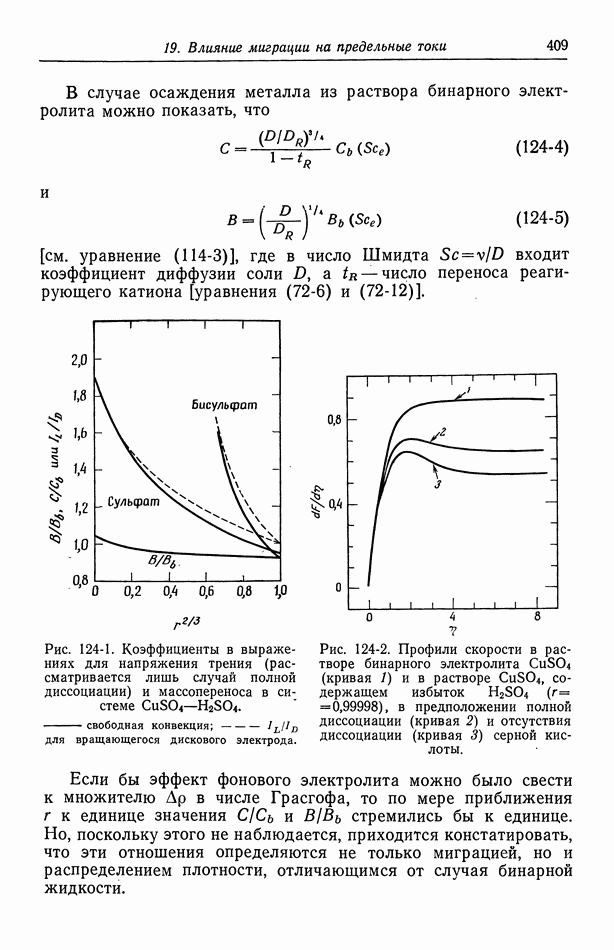
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
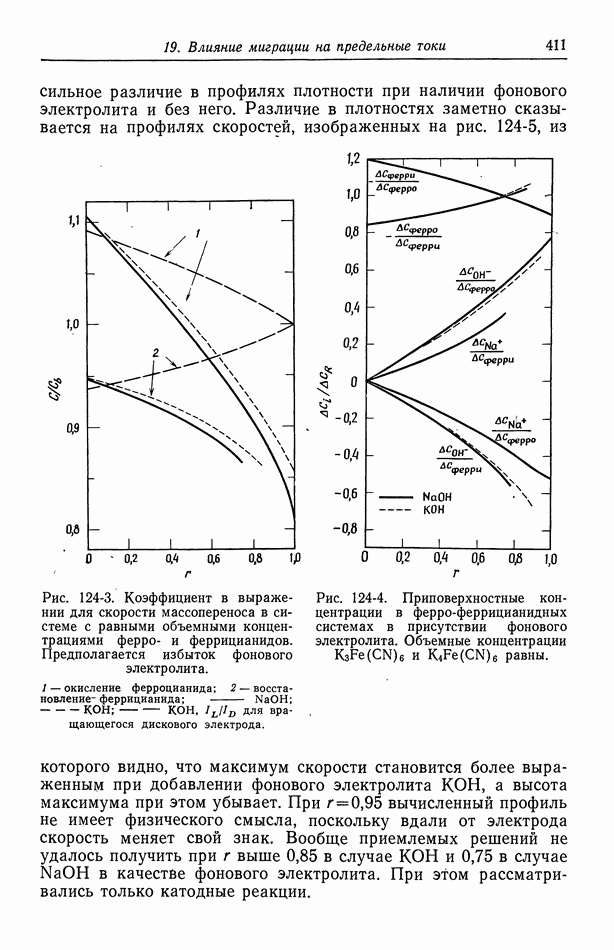
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
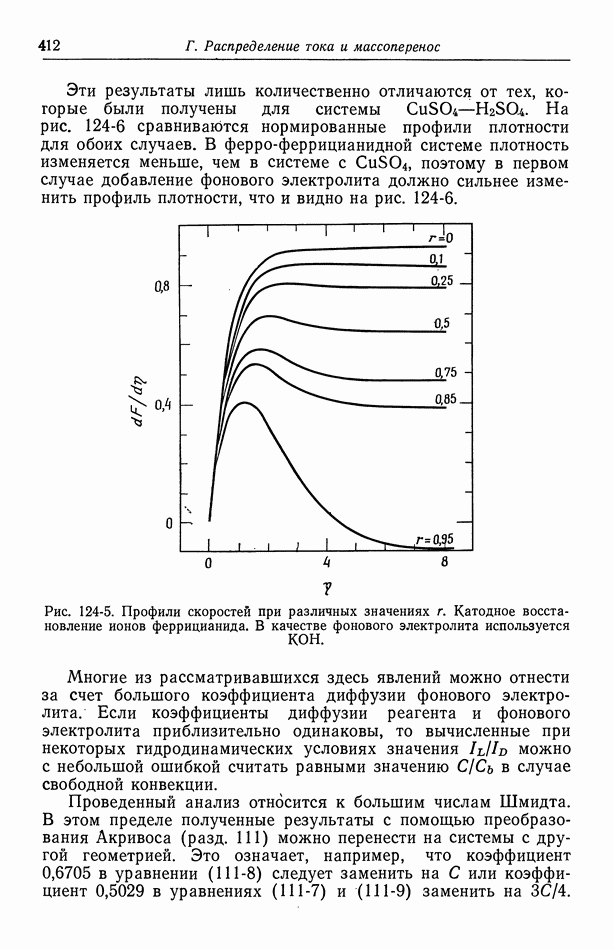
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
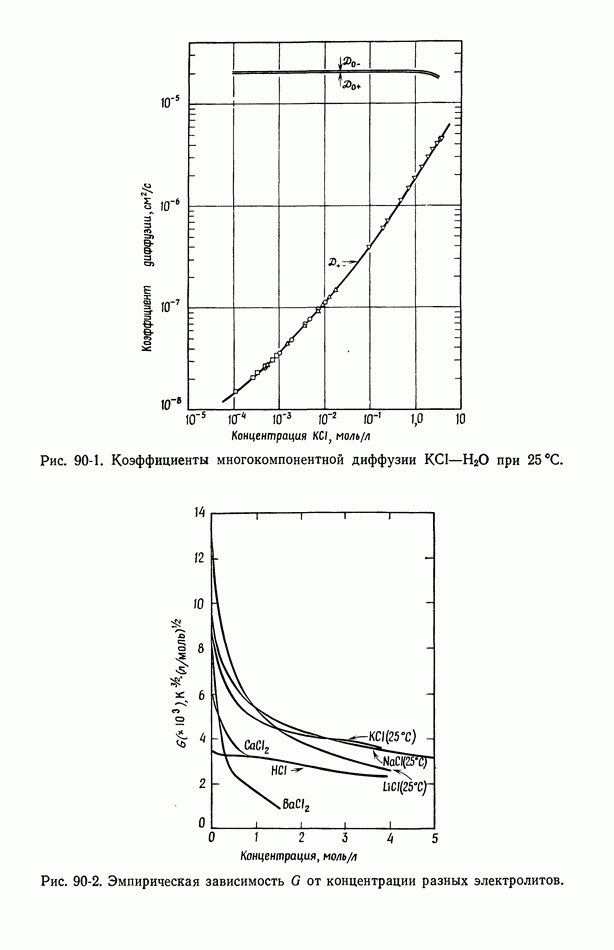
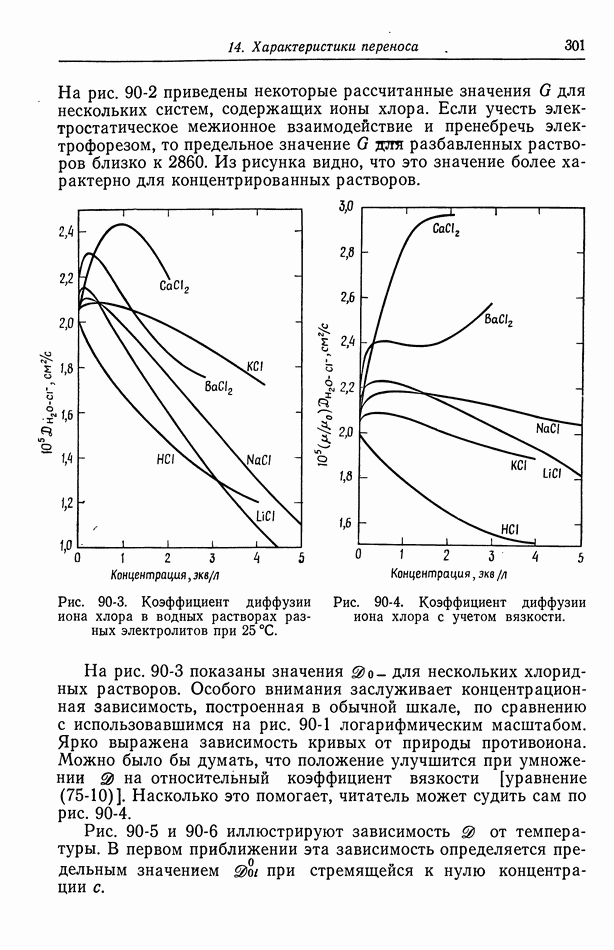
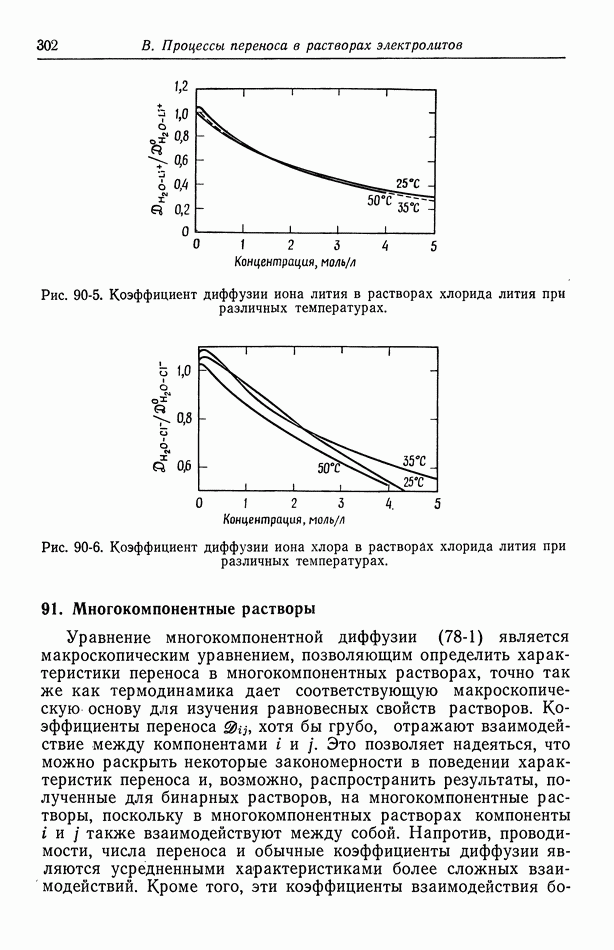
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
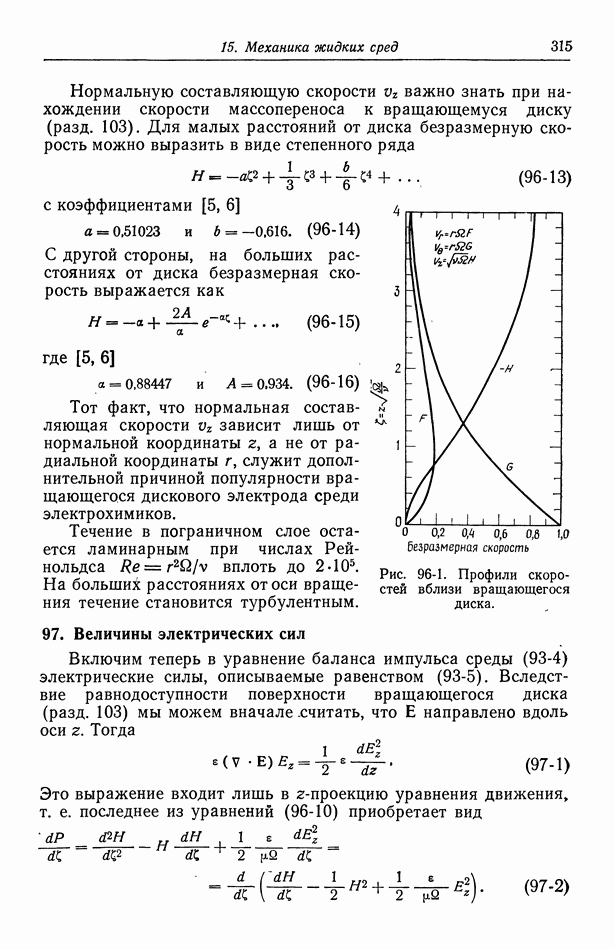
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
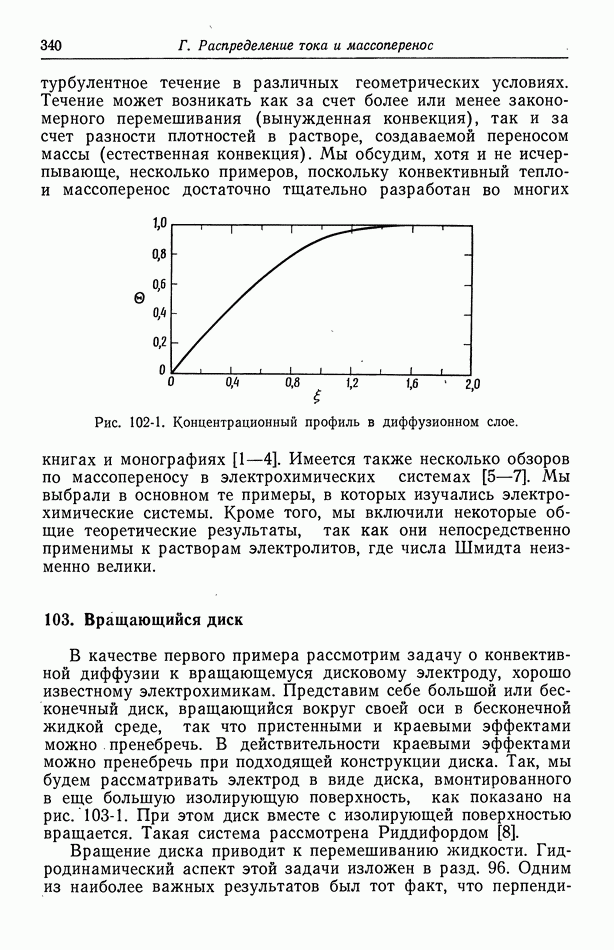
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
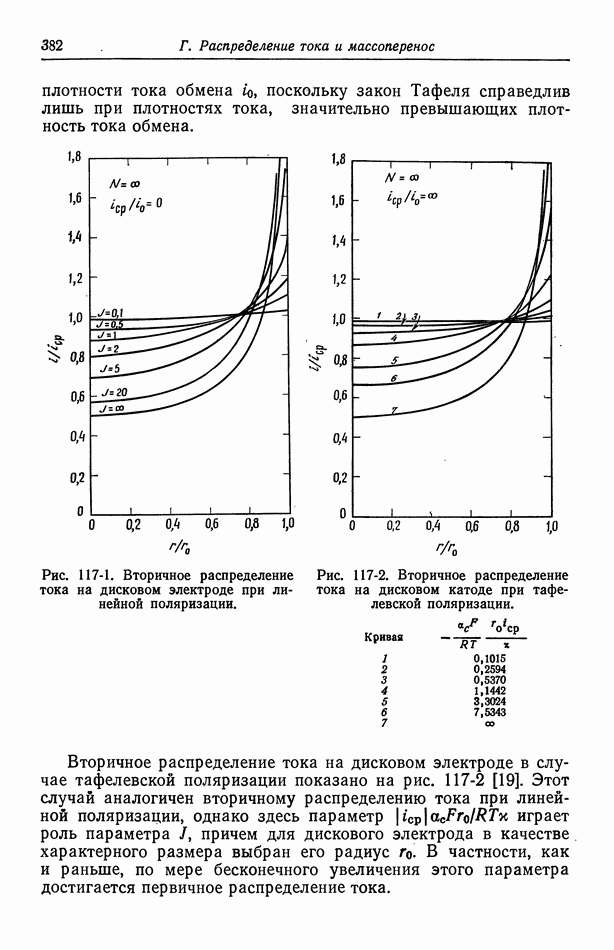
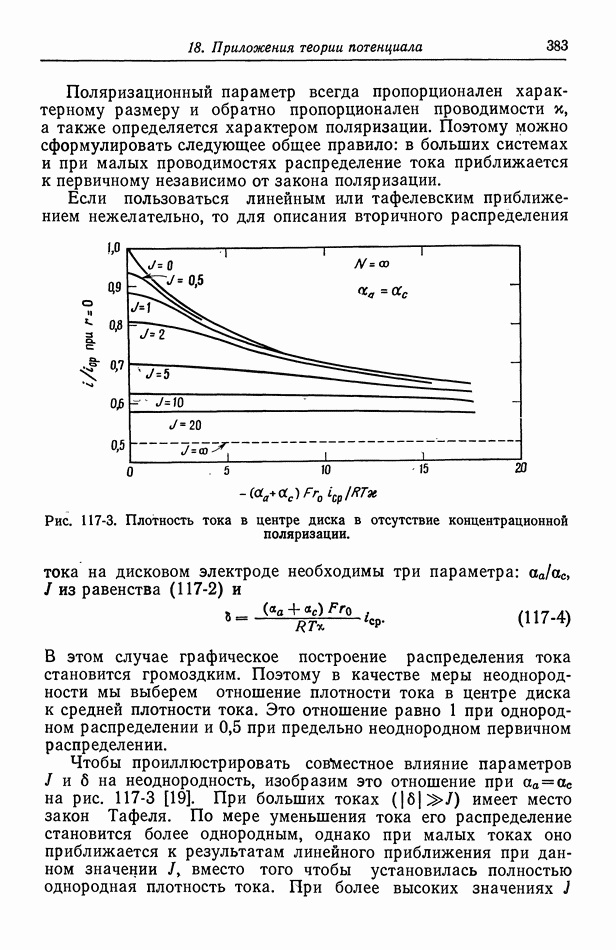
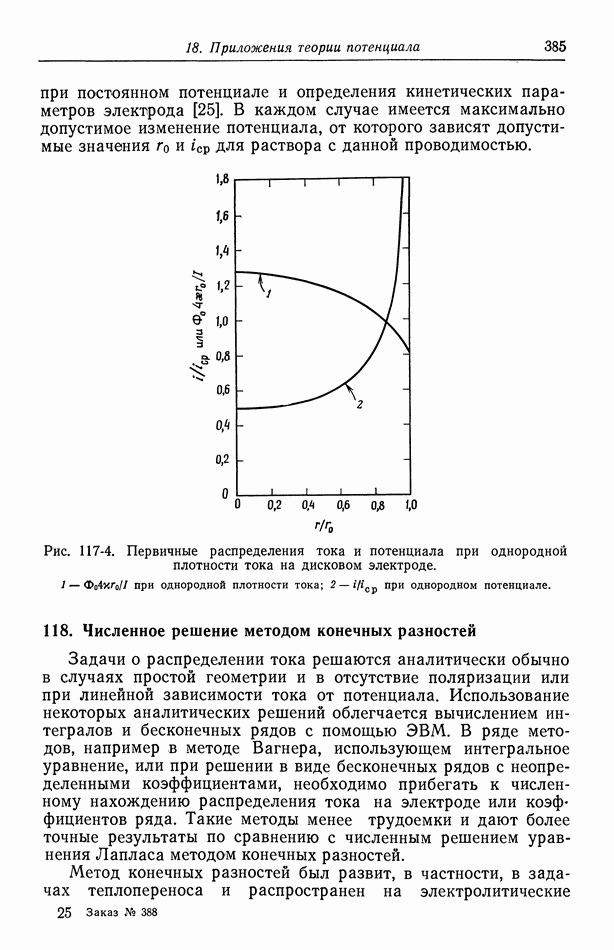
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
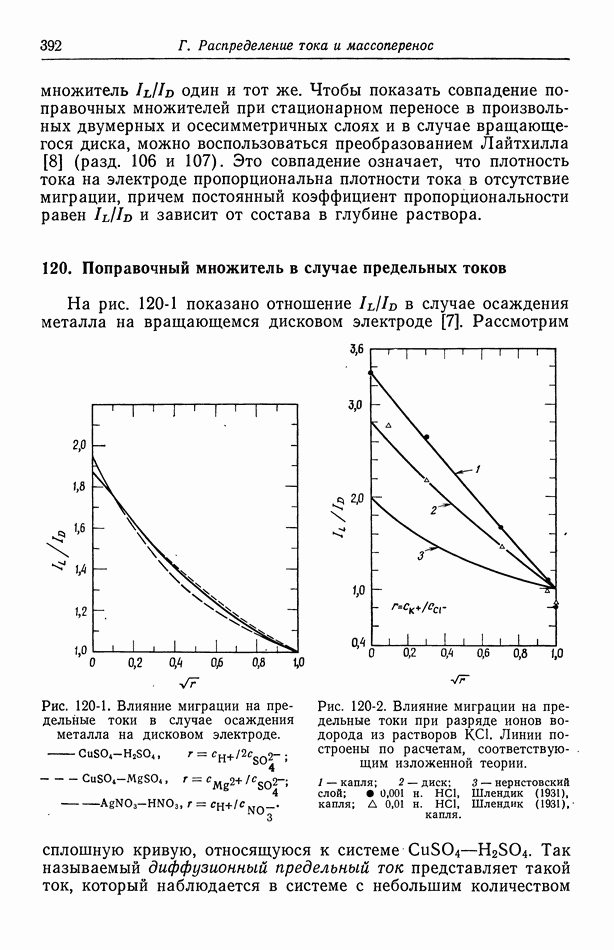
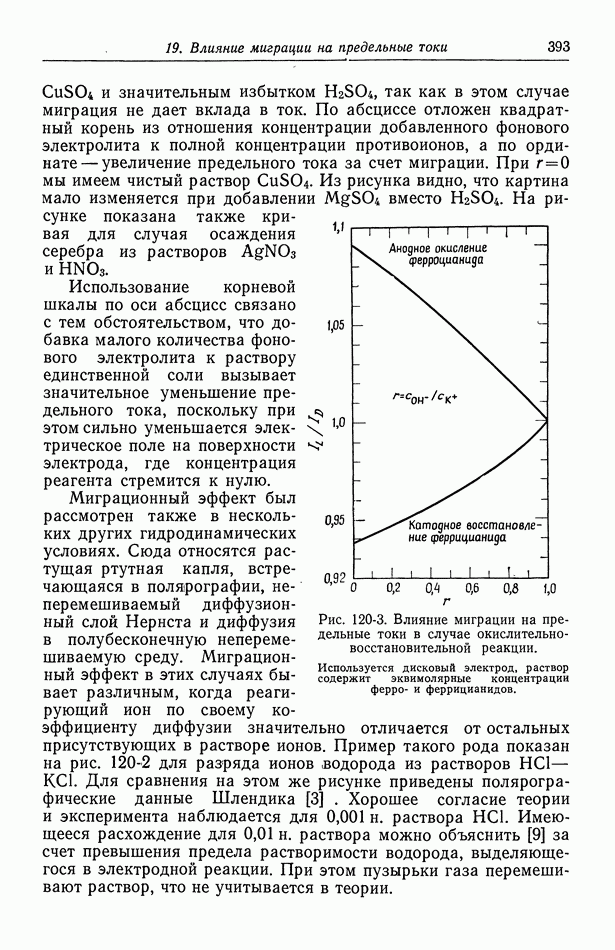
- 120. Поправочный множитель в случае предельных токов
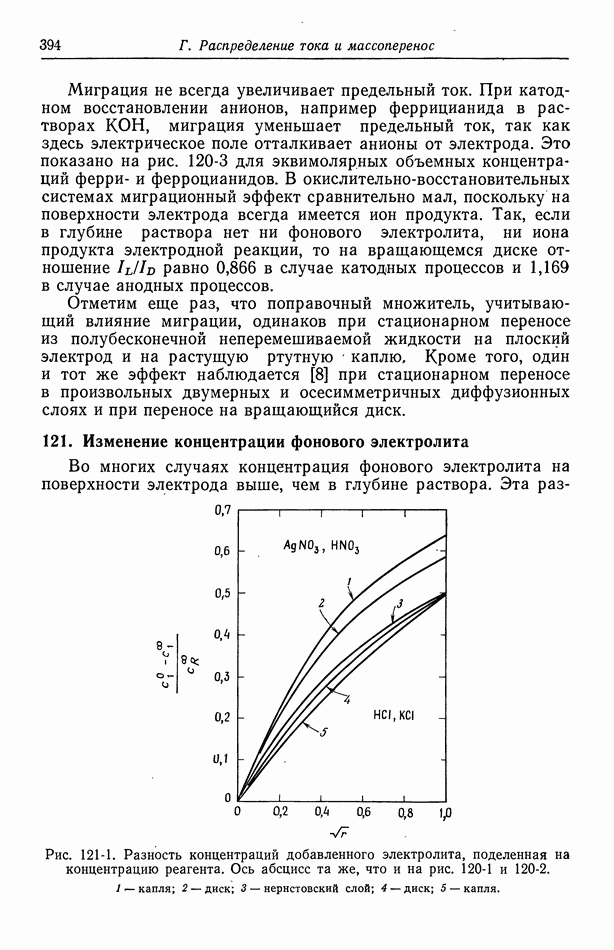
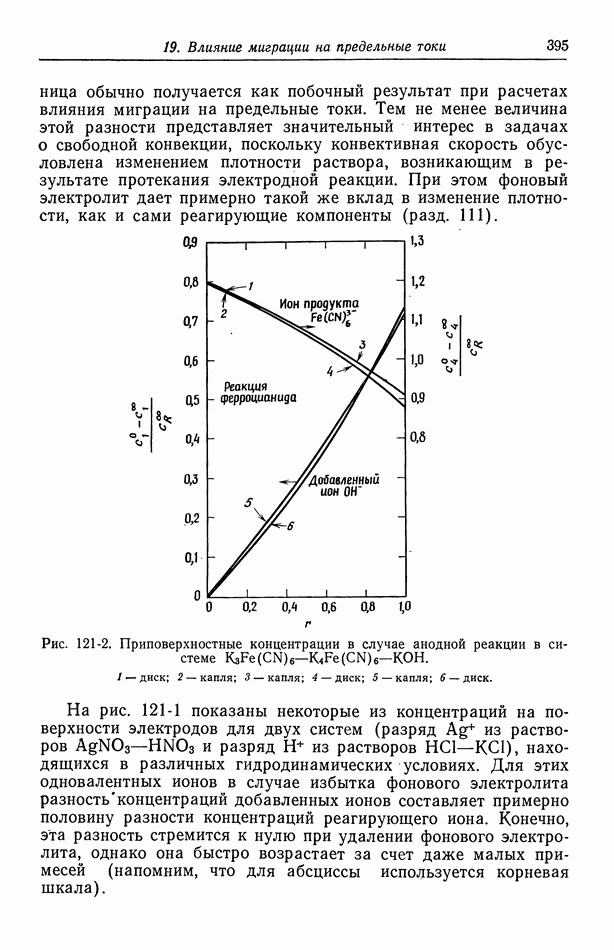
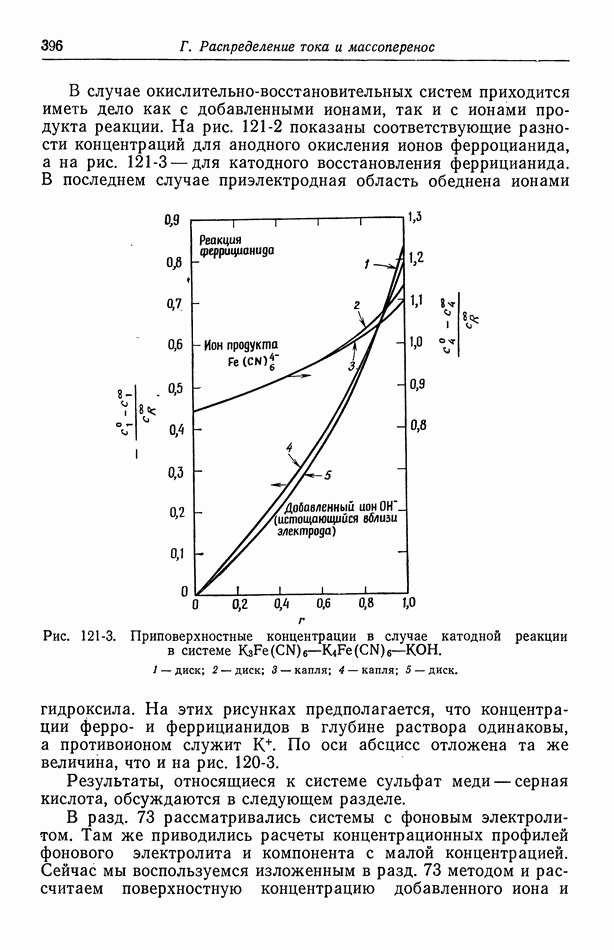
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ