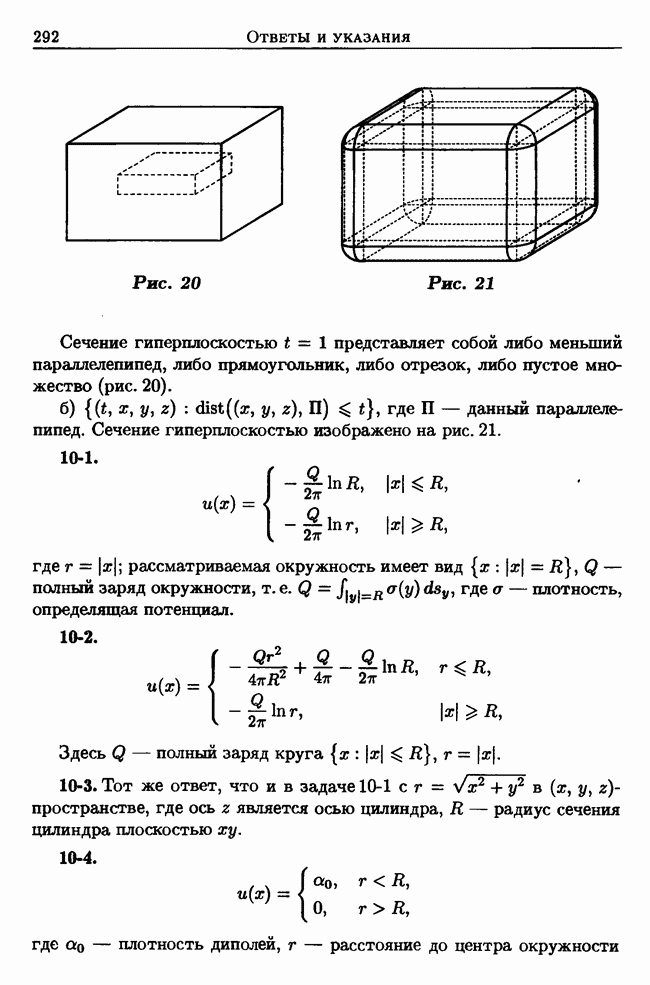
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Пространства обобщённых функции
Описанная выше процедура перехода от пространства Е к дуальному пространству Е дает возможность определить пространства  как пространства, дуальные к
как пространства, дуальные к  Мы не вводили никакой топологии в
Мы не вводили никакой топологии в  (естественная топология в
(естественная топология в  ) вводится нетривиально), но нам это не понадобится: мы определим сразу пространство
) вводится нетривиально), но нам это не понадобится: мы определим сразу пространство  как пространство таких линейных функционалов
как пространство таких линейных функционалов  на
на  что ограничение непрерывно на
что ограничение непрерывно на  для любого компакта
для любого компакта  .
.
Определение 4.3. а) Элементы пространства  называются обобщёнными функциями в
называются обобщёнными функциями в  .
.
б) Элементы пространства  называются обобщёнными функциями с компактным носителем в
называются обобщёнными функциями с компактным носителем в 
в) Элементы пространства  называются обобщёнными функциями умеренного роста на
называются обобщёнными функциями умеренного роста на 
Пример 4.1. «Обычные» или «регулярные» обобщённые функции в 
Пусть  — пространство функций на
— пространство функций на  , абсолютно интегрируемых по мере Лебега на любом компакте
, абсолютно интегрируемых по мере Лебега на любом компакте  . Сопоставим каждой функции
. Сопоставим каждой функции  функционал на
функционал на  (мы будем обозначать его той же буквой
(мы будем обозначать его той же буквой  ), полагая
), полагая

где  Очевидно, что при этом мы получаем обобщённую функцию в
Очевидно, что при этом мы получаем обобщённую функцию в  (она называется в этом случае «обычной» или «регулярной»). Важный факт состоит в том, что если две функции
(она называется в этом случае «обычной» или «регулярной»). Важный факт состоит в том, что если две функции  определяют одну и ту же обобщённую функцию, то они совпадают почти везде. Это следствие следующей известной леммы.
определяют одну и ту же обобщённую функцию, то они совпадают почти везде. Это следствие следующей известной леммы.
Лемма 4.4. Пусть  для любой функции
для любой функции  . Тогда
. Тогда  для почти всех х.
для почти всех х.
Доказательство этой леммы требует использования в той или иной форме факта существования достаточно большого числа функций в  . Пока ещё мы не знаем, существуют ли такие нетривиальные функции. Построим некоторый запас функций, принадлежащих
. Пока ещё мы не знаем, существуют ли такие нетривиальные функции. Построим некоторый запас функций, принадлежащих  .
.
Прежде всего, пусть  где
где  — функция Хевисайда, т. е.
— функция Хевисайда, т. е.  при
при  при
при  . Ясно, что
. Ясно, что  Поэтому если теперь рассмотреть в
Поэтому если теперь рассмотреть в  функцию
функцию  то мы получим функцию
то мы получим функцию  при
при  при
при  Удобно нормировать функцию
Удобно нормировать функцию  рассмотрев вместо неё функцию
рассмотрев вместо неё функцию  где
где  . Теперь положим
. Теперь положим  Тогда
Тогда  при
при  при
при  .
.
Введём теперь важную операцию усреднения: по функции  построим свёртку
построим свёртку

определённую при  Из теоремы Лебега ясно, что последний интеграл в (4.10) можно дифференцировать, причем
Из теоремы Лебега ясно, что последний интеграл в (4.10) можно дифференцировать, причем

так что  Отметим также следующие свойства операции усреднения:
Отметим также следующие свойства операции усреднения:
а) Если  вне компакта
вне компакта  то
то  вне
вне  -окрестности компакта К.
-окрестности компакта К.
В частности, в этом случае  при достаточно малом
при достаточно малом 
В частности, если  — характеристическая функция то
— характеристическая функция то  при
при  ;
;
в) Если  то
то  при
при  равномерно на любом компакте
равномерно на любом компакте  .
.
В самом деле,

откуда

так что утверждение следует из равномерной непрерывности  на
на  -окрестности компакта К.
-окрестности компакта К.
г) Если  где
где  , то
, то  при
при  по норме
по норме  для любого компакта
для любого компакта  .
.
Поскольку значения  при
при  зависят лишь от значений
зависят лишь от значений  на
на  -окрестности компакта К, можно считать, что
-окрестности компакта К, можно считать, что  при
при  где
где  — некоторый компакт в
— некоторый компакт в  . Будем через
. Будем через  обозначать норму
обозначать норму  т.е.
т.е.

Имеем:

В силу п. в) утверждение п. г) верно при  Но если
Но если  вне компакта
вне компакта  то мы можем приблизить
то мы можем приблизить  по норме
по норме  ступенчатыми и затем непрерывными функциями, равными 0 вне компакта
ступенчатыми и затем непрерывными функциями, равными 0 вне компакта  Пусть
Пусть  — такая непрерывная функция на
— такая непрерывная функция на  равная
равная  вне
вне  что
что  Тогда получим:
Тогда получим:

откуда ввиду произвольности числа  вытекает, что
вытекает, что

что и требовалось.
Докажем теперь утверждение леммы 4.4. Пусть  для любой функций
для любой функций  Но отсюда следует, что
Но отсюда следует, что  при всех
при всех  Поэтому утверждение леммы вытекает из п. г).
Поэтому утверждение леммы вытекает из п. г).
Лемма 4.4 позволяет отождествить функции  с обобщёнными функциями, определяемыми ими по формуле (4.9). Заметим, что запись
с обобщёнными функциями, определяемыми ими по формуле (4.9). Заметим, что запись

часто употребляется и для обобщённых функций  (в этом случае левая часть (4.12) является определением правой; в случае, когда правая часть имеет смысл, это определение непротиворечиво).
(в этом случае левая часть (4.12) является определением правой; в случае, когда правая часть имеет смысл, это определение непротиворечиво).
Пример 4.2. «Регулярные» обобщённые функции в  . Если
. Если  , т.е.
, т.е.  вне некоторого компакта
вне некоторого компакта  , то мы можем построить по стандартной формуле (4.12) функционал на
, то мы можем построить по стандартной формуле (4.12) функционал на  являющийся обобщённой функцией с компактным носителем. Мы будем отождествлять
являющийся обобщённой функцией с компактным носителем. Мы будем отождествлять  и соответствующий элемент
и соответствующий элемент  . Если
. Если  и
и

при некотором  то формула (4.12) задаёт функционал на
то формула (4.12) задаёт функционал на  являющийся обобщённой функцией умеренного роста. В частности, (4.13) выполнено, если
являющийся обобщённой функцией умеренного роста. В частности, (4.13) выполнено, если  измерима и
измерима и

Пример 4.3.  -функция Дирака.
-функция Дирака.
Это функционал, определяемый формулой

Если  то
то  При любом
При любом  ясно, что
ясно, что  Вместо (4.15) в соответствии с вышеупомянутым соглашением часто пишут
Вместо (4.15) в соответствии с вышеупомянутым соглашением часто пишут

хотя ясно, что  не является регулярной обобщённой функцией, поскольку из леммы 4.4 вытекало бы в этом случае, что она равна
не является регулярной обобщённой функцией, поскольку из леммы 4.4 вытекало бы в этом случае, что она равна  почти везде вне точки
почти везде вне точки 
Пример 4.4. Пусть L — линейный дифференциальный оператор в  — гладкая компактная поверхность в
— гладкая компактная поверхность в  — элемент площади поверхности Г. Тогда формула
— элемент площади поверхности Г. Тогда формула

определяет нерегулярную обобщённую функцию с компактным носителем в  . В качестве Г можно брать компактное подмногообразие (возможно, с краем) любой коразмерности в
. В качестве Г можно брать компактное подмногообразие (возможно, с краем) любой коразмерности в  . В этом случае в качестве
. В этом случае в качестве  можно брать любую плотность на Г (или дифференциальную форму максимальной размерности, если фиксирована ориентация Г). В частности, если Г — точка, то мы получим
можно брать любую плотность на Г (или дифференциальную форму максимальной размерности, если фиксирована ориентация Г). В частности, если Г — точка, то мы получим  -функцию, определённую выше.
-функцию, определённую выше.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
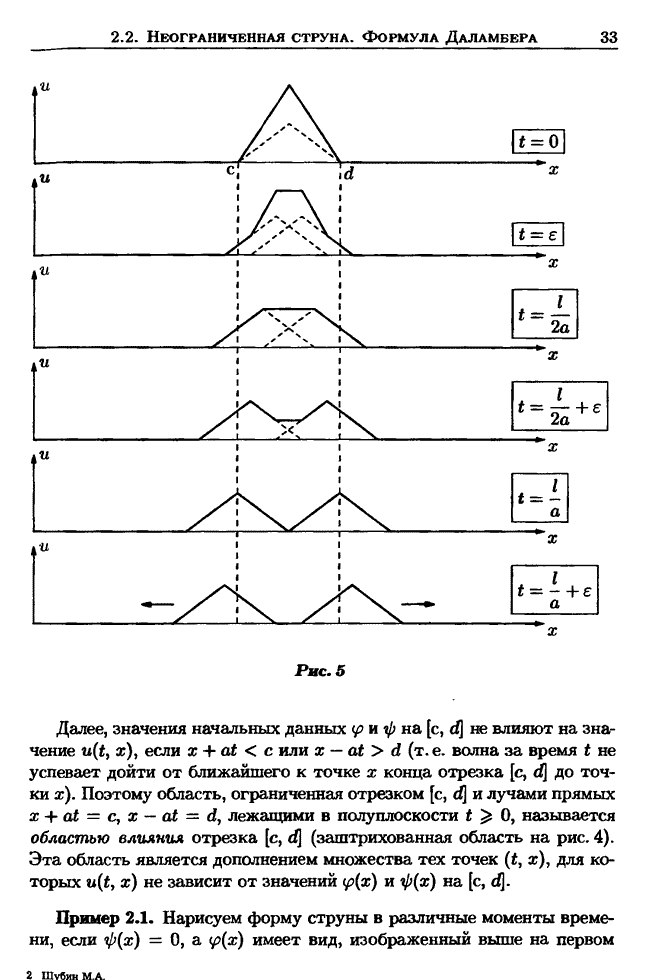
- § 2. Одномерное волновое уравнение
- 2.1. Уравнение колебании струны
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
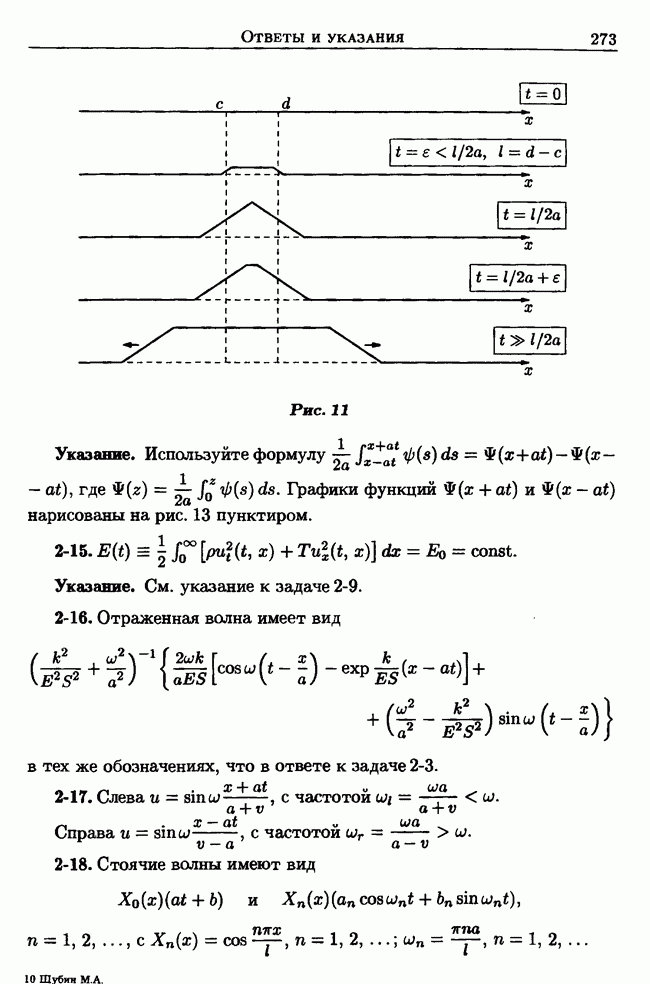
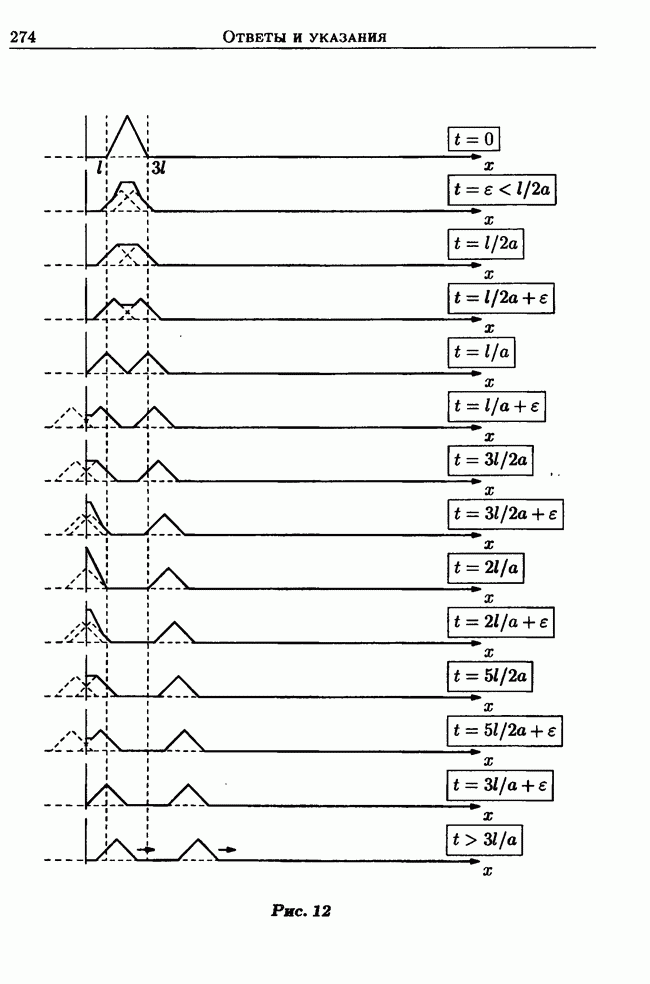
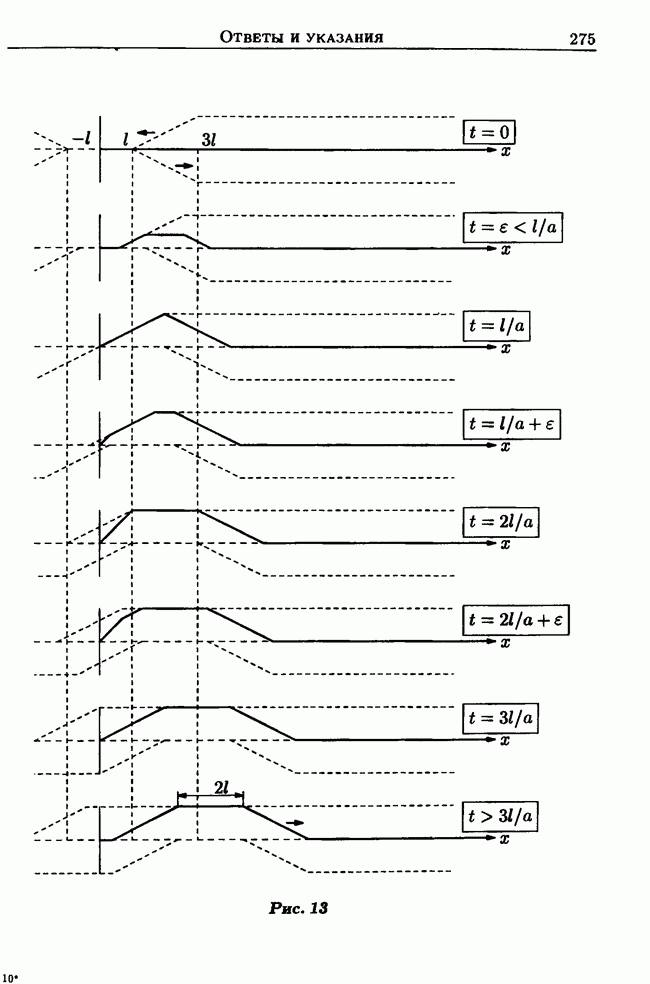
- 2.3. Полуограниченная струна. Отражение волн от конца струны
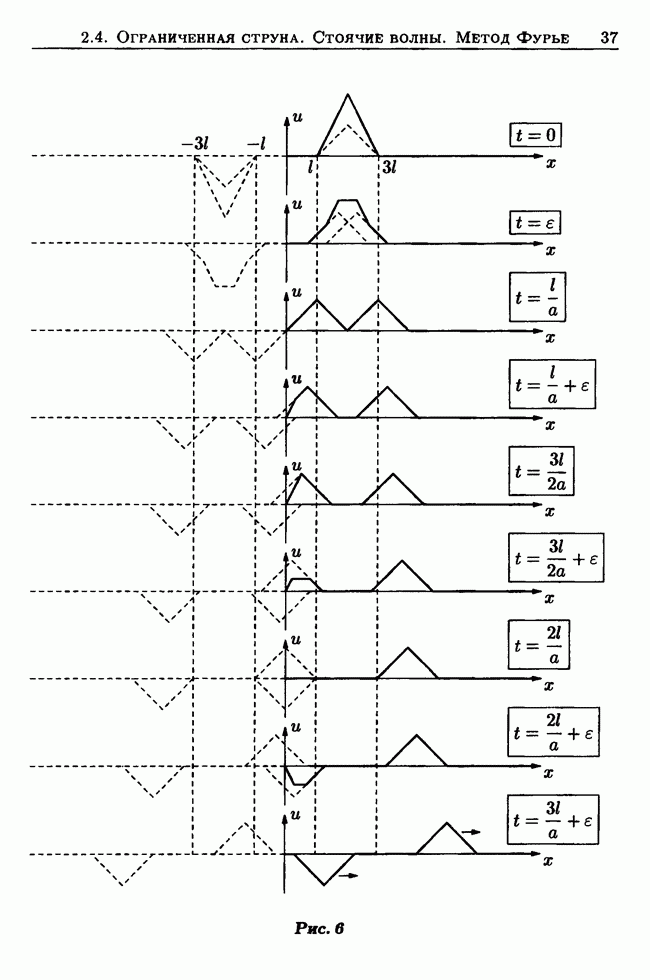
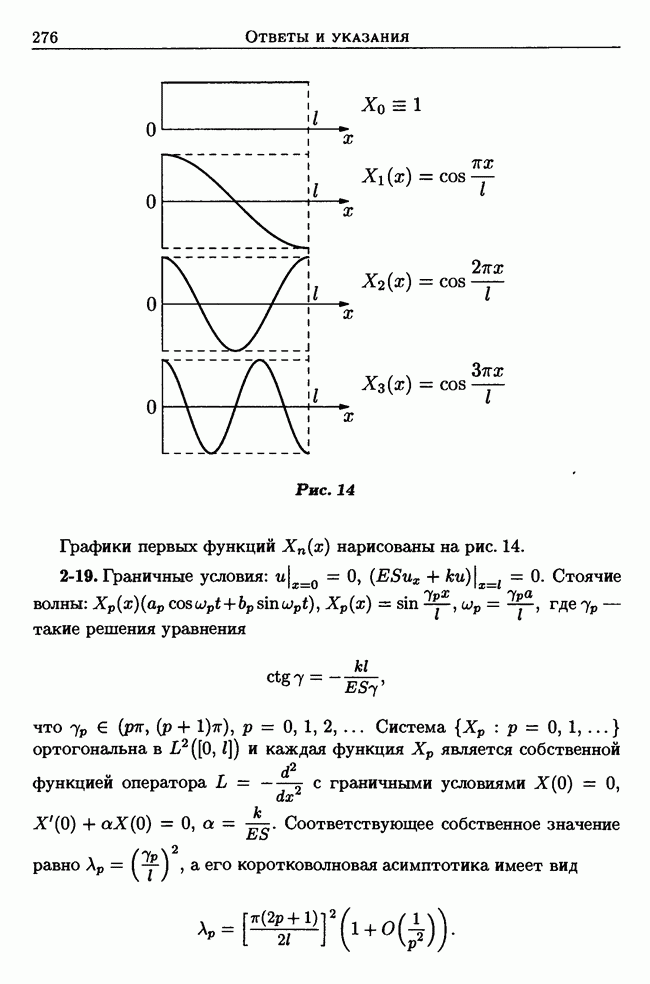
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы