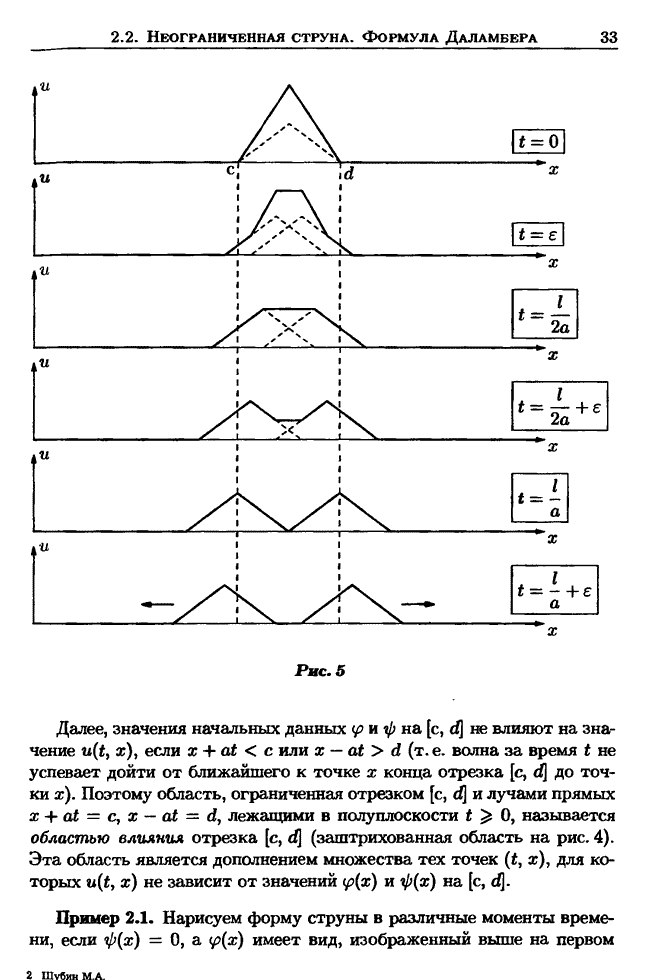
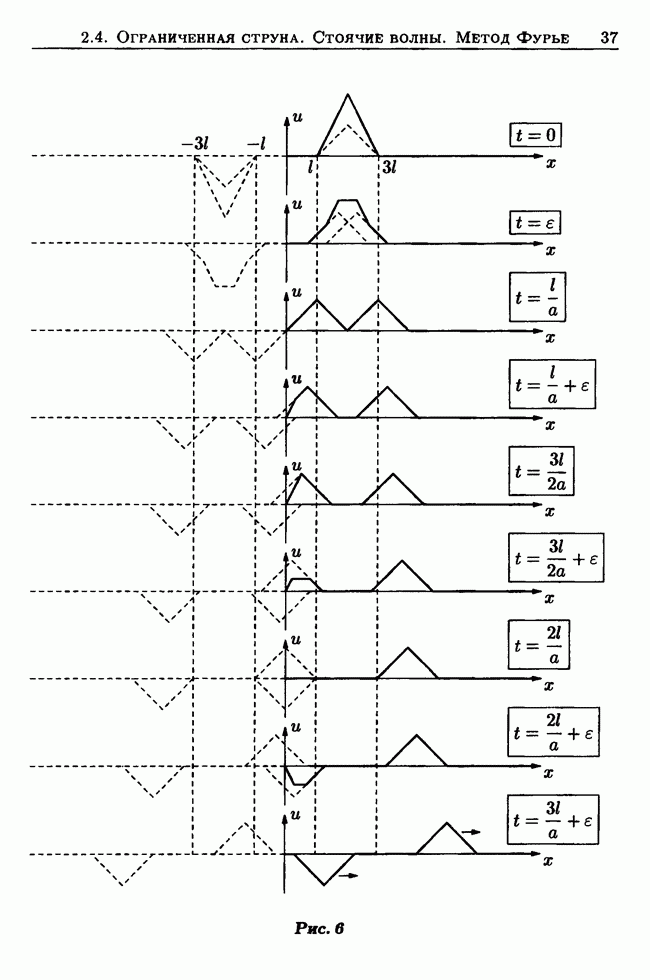
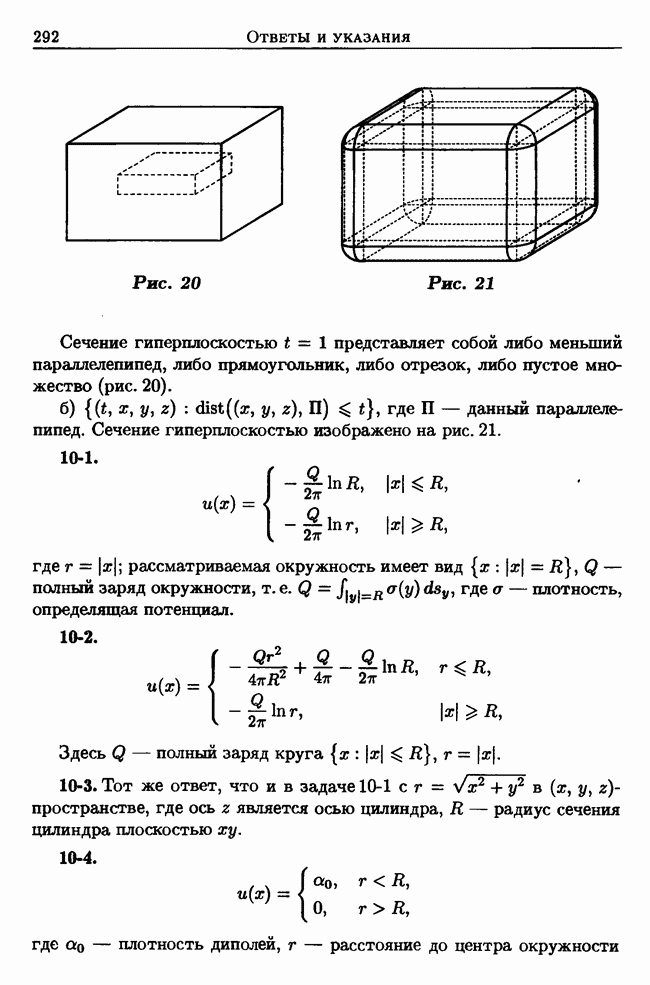
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.4. Задача Дирихле (обобщённое решение)
Мы рассмотрим две обобщённых постановки краевой задачи Дирихле для оператора Лапласа. В обоих случаях существование и единственность решения после проведённой подготовительной работы легко вытекает из общих теорем функционального анализа.
Первая постановка имеет в качестве классического аналога следующую задачу (задачу с нулевыми граничными условиями для уравнения Пуассона):

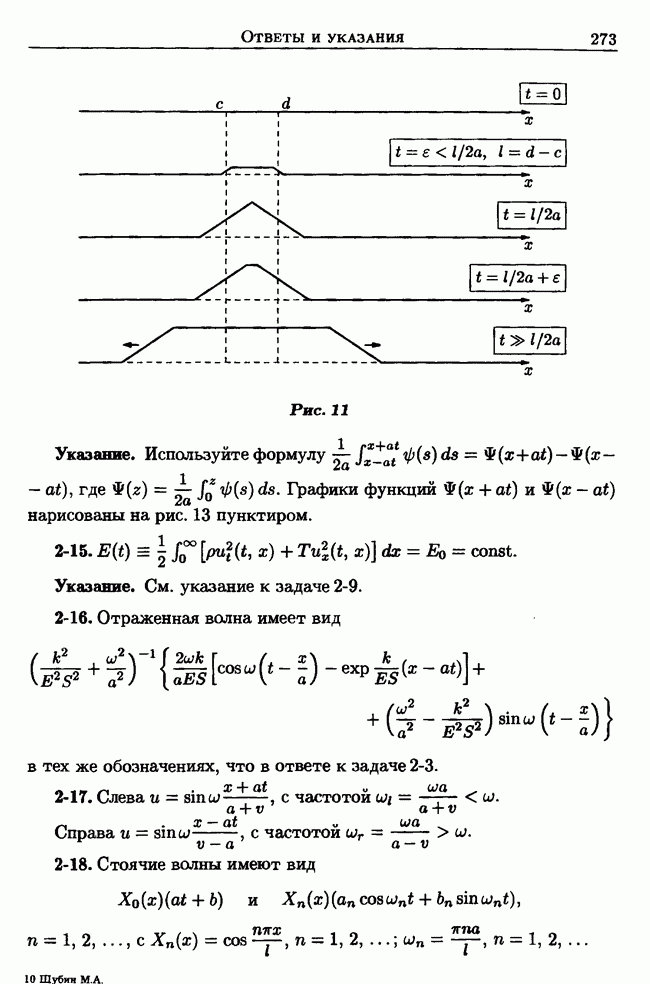
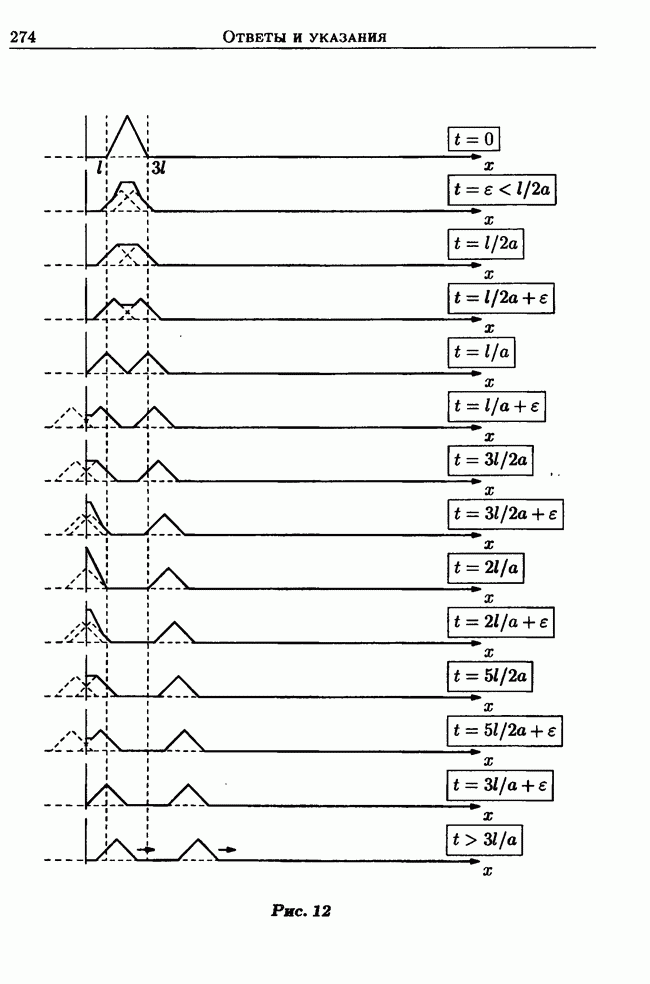
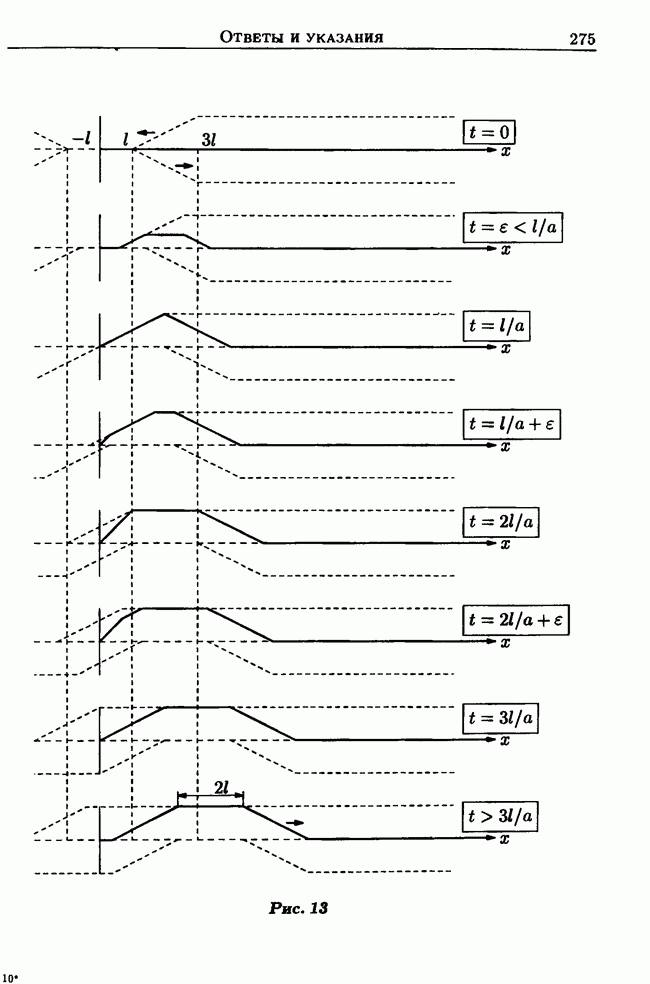
Вместо граничного условия  напишем:
напишем:

Теперь попробуем записать уравнение  . Пусть вначале
. Пусть вначале  . Тогда если
. Тогда если  то выполняя интегрирование по частям, получим:
то выполняя интегрирование по частям, получим:

Если  , то это означает, что
, то это означает, что

где  — скалярное произведение в
— скалярное произведение в  . Заметим теперь, что если обе части (7.17) рассматривать как функционалы от v, то эти функционалы линейны и непрерывны по норме
. Заметим теперь, что если обе части (7.17) рассматривать как функционалы от v, то эти функционалы линейны и непрерывны по норме  пространства
пространства  Поэтому (7.17) верно, когда v принадлежит замыканию
Поэтому (7.17) верно, когда v принадлежит замыканию  , т. е. когда
, т. е. когда  .
.
Обратно, пусть область  ограничена и имеет гладкую границу, и
ограничена и имеет гладкую границу, и  и (7.17) выполнено при любой функции
и (7.17) выполнено при любой функции  . Докажем, что тогда и является решением задачи (7.15).
. Докажем, что тогда и является решением задачи (7.15).
Вначале заметим, что из условия и  вытекает, что
вытекает, что  . Это вытекает
. Это вытекает  того, что отображение и продолжается до непрерывного отображения
того, что отображение и продолжается до непрерывного отображения  которое переводит в 0 все функции из
которое переводит в 0 все функции из  и, тем самым, все функции
и, тем самым, все функции  . Отметим, что здесь мы фактически используем лишь тот факт, что если и
. Отметим, что здесь мы фактически используем лишь тот факт, что если и  . Этот факт легко получить непосредственно, минуя теорему 7.5 и её распространение на случай многообразий. Укажем схему соответствующего рассуждения, не входя в подробности. Применяя разбиение единицы и выпрямляя локально границу с помощью диффеоморфизма, мы можем затем, рассуждая как в доказательстве неравенства Фридрихса, получить, что
. Этот факт легко получить непосредственно, минуя теорему 7.5 и её распространение на случай многообразий. Укажем схему соответствующего рассуждения, не входя в подробности. Применяя разбиение единицы и выпрямляя локально границу с помощью диффеоморфизма, мы можем затем, рассуждая как в доказательстве неравенства Фридрихса, получить, что

для функции  , сосредоточенной в малой окрестности фиксированной точки границы. Поэтому если
, сосредоточенной в малой окрестности фиксированной точки границы. Поэтому если  , то и нельзя приблизить функциями из
, то и нельзя приблизить функциями из  по норме пространства
по норме пространства  . Итак, если и
. Итак, если и  .
.
На самом деле, если и  , то и обратно из условия
, то и обратно из условия  вытекает, что
вытекает, что  Этот факт может быть доказан следующим образом. Строя усреднение характеристической функции множества
Этот факт может быть доказан следующим образом. Строя усреднение характеристической функции множества  , где
, где

мы получим такую функцию  что
что  при
при  и
и

(постоянная  не зависит от
не зависит от  ). Если теперь
). Если теперь  , то
, то  . Из условия
. Из условия  вытекает, что если
вытекает, что если  , то
, то  , где С здесь и ниже зависит от u, но не зависит от е.
, где С здесь и ниже зависит от u, но не зависит от е.
Это позволяет оценить выражение

где  — норма в
— норма в  — интеграл Дирихле. Поскольку имеет меру Лебега, не превосходящую
— интеграл Дирихле. Поскольку имеет меру Лебега, не превосходящую  , то
, то

(здесь u и  гасят друг друга). Итак и по норме
гасят друг друга). Итак и по норме  можно приблизить функциями из
можно приблизить функциями из  носитель которых — компакт в
носитель которых — компакт в  . Их, в свою очередь, легко приблизить функциями из
. Их, в свою очередь, легко приблизить функциями из  по норме
по норме  с помощью операции усреднения.
с помощью операции усреднения.
Итак, условие  на функциях и
на функциях и  для ограниченной области
для ограниченной области  с гладкой границей равносильно включению и
с гладкой границей равносильно включению и  . Это оправдывает замену граничного условия в (7.15) включением (7.16).
. Это оправдывает замену граничного условия в (7.15) включением (7.16).
Далее, выполнение тождества (7.17) для и  при любой функции
при любой функции  равносильно тому, что
равносильно тому, что  (где
(где  применяется в обобщенном смысле). В самом деле, если выполнено (7.17), то выбрав
применяется в обобщенном смысле). В самом деле, если выполнено (7.17), то выбрав  мы получим, перебрасывая производные с u на
мы получим, перебрасывая производные с u на  , что
, что  , что и означает, что
, что и означает, что  Обратно, если
Обратно, если  , то тождество (7.17) верно при
, то тождество (7.17) верно при  , а значит по непрерывности при любом
, а значит по непрерывности при любом  .
.
Всё это оправдывает следующую обобщённую постановку задачи (7.15):
Пусть  — произвольная ограниченная область в
— произвольная ограниченная область в  надо найти такую функцию
надо найти такую функцию  , что тождество (7.17) выполнено для любой функции
, что тождество (7.17) выполнено для любой функции  (или, что то же самое, для любой функции
(или, что то же самое, для любой функции  ).
).
Функцию и будем называть в зтом случае обобщённым решением задачи (7.15). Выше мы видели, что если  ограничена и имеет гладкую границу,
ограничена и имеет гладкую границу,  , то и является обобщённым решением задачи (7.15) тогда и только тогда, когда оно является решением этой задачи в классическом смысле.
, то и является обобщённым решением задачи (7.15) тогда и только тогда, когда оно является решением этой задачи в классическом смысле.
Теорема 7.9. Обобщённое решение задачи (7.15) существует и единственно.
Доказательство. Перепишем (7.17) в виде

и рассмотрим правую часть как функционал от v при  Это линейный непрерывный функционал. Его линейность очевидна, а непрерывность вытекает из неравенства Коши-Буняковского:
Это линейный непрерывный функционал. Его линейность очевидна, а непрерывность вытекает из неравенства Коши-Буняковского:

где  — норма в
— норма в  .
.
По теореме Рисса мы можем (и притом единственным образом) записать этот функционал в виде  , где u — некоторый фиксированный элемент пространства
, где u — некоторый фиксированный элемент пространства  . Это доказывает однозначную разрешимость задачи (7.15) (в обобщённой постановке).
. Это доказывает однозначную разрешимость задачи (7.15) (в обобщённой постановке).
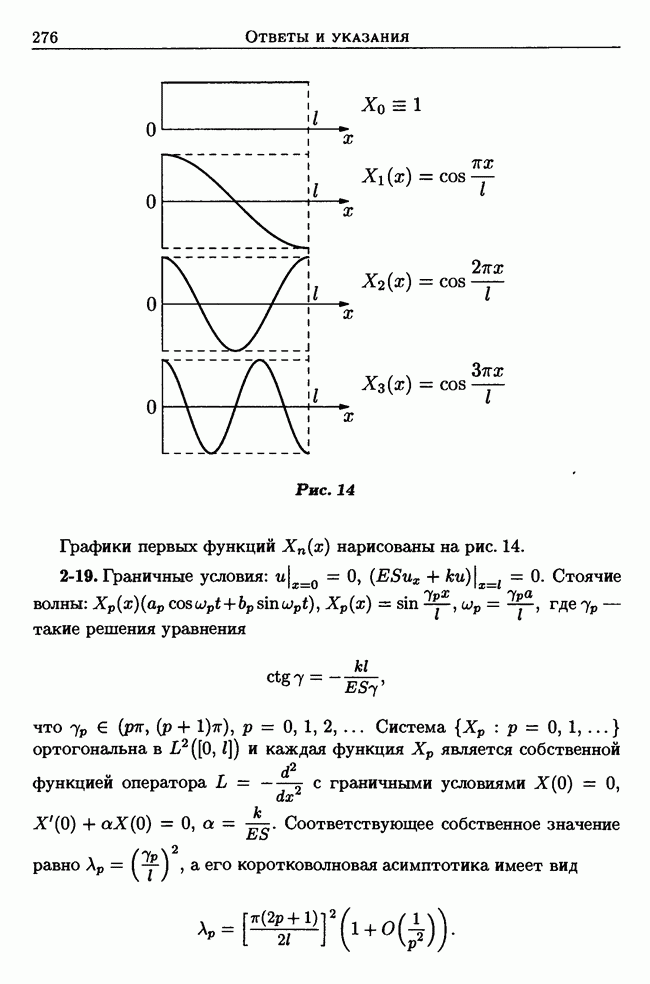
Обобщённая постановка задачи Дирихле оставляет открытыми два важных вопроса: 1) точное описание класса всех решений и при  существование более гладкого решения при большей гладкости
существование более гладкого решения при большей гладкости  . Заметим, что локальные вопросы о гладкости легко решаются тем замечанием, что если
. Заметим, что локальные вопросы о гладкости легко решаются тем замечанием, что если  — фундаментальное решение оператора Лапласа в
— фундаментальное решение оператора Лапласа в  , то свёртка
, то свёртка

(определённая при почти всех  ) является решением уравнения
) является решением уравнения  и, значит,
и, значит,  т. е. и — но — аналитическая функция в
т. е. и — но — аналитическая функция в  . Поэтому гладкость и локально совпадает с гладкостью
. Поэтому гладкость и локально совпадает с гладкостью  и может быть легко описана (например, если
и может быть легко описана (например, если  ), то и
), то и  как это уже было доказано ранее). Сложнее решается вопрос о гладкости вблизи границы. Более того, для случая негладкой границы он не выяснен до конца и по сей день. Однако в случае, когда граница
как это уже было доказано ранее). Сложнее решается вопрос о гладкости вблизи границы. Более того, для случая негладкой границы он не выяснен до конца и по сей день. Однако в случае, когда граница  гладкая (класса
гладкая (класса  ), имеются точные (хотя и не очень просто доказываемые) теоремы, описывающую гладкость и через гладкость
), имеются точные (хотя и не очень просто доказываемые) теоремы, описывающую гладкость и через гладкость  . Мы приведём две такие теоремы без доказательства.
. Мы приведём две такие теоремы без доказательства.
Итак, пусть ограниченная область  имеет границу класса
имеет границу класса  .
.
Если  то
то  Обратно, очевидно, что если
Обратно, очевидно, что если  , то
, то  . Таким образом, оператор
. Таким образом, оператор  осуществляет изоморфизм:
осуществляет изоморфизм:

В частности, в этом случае все обобщённые решения (при  ) пробегают пространство
) пробегают пространство  .
.
Другой вариант точного описания гладкости имеется в шкале функций, удовлетворяющих условию Гёльдера. Будем писать, что  где
где  если
если  (говорят тогда, что
(говорят тогда, что  удовлетворяет условию Гёльдера с показателем 7). Класс функций
удовлетворяет условию Гёльдера с показателем 7). Класс функций  , где
, где  , состоит из таких функций
, состоит из таких функций  что
что  при
при  . Если и — решение задачи (7.15) в ограниченной области
. Если и — решение задачи (7.15) в ограниченной области  с гладкой границей и
с гладкой границей и  где
где  то
то  .
.
Отметим, что такого сорта теорема неверна в обычных классах  даже локально, а именно, из условия
даже локально, а именно, из условия  не следует даже, что
не следует даже, что  .
.
Перейдём к рассмотрению обобщённой постановки обычной задачи Дирихле

Прежде всего возникает вопрос об интерпретации граничного условия. Мы сделаем это так: будем считать, что дана такая функция v, что  Будем считать, что
Будем считать, что  а граничное условие для и интерпретируем так:
а граничное условие для и интерпретируем так:  . Отсюда следует, что
. Отсюда следует, что  Введение функции v избавляет нас от необходимости описывать гладкость
Введение функции v избавляет нас от необходимости описывать гладкость  и, тем самым, от использования пространств Соболева с нецелым индексом на
и, тем самым, от использования пространств Соболева с нецелым индексом на  . Кроме того, удаётся рассмотреть случай области с негладкой границей.
. Кроме того, удаётся рассмотреть случай области с негладкой границей.
Итак, сформулируем обобщённую постановку задачи Дирихле (7.19):
Пусть дана ограниченная область  ; найти такую функцию
; найти такую функцию  что
что  .
.
На первый взгляд кажется, что эта задача сводится к предыдущей, если искать  и обозначить
и обозначить  Однако ниоткуда не следует, что
Однако ниоткуда не следует, что  , а более общий случай мы не рассматривали.
, а более общий случай мы не рассматривали.
Поэтому рассмотрим эту задачу независимо от первой, тем более, что решается она столь же просто.
Из вышеизложенного ясно также, что если  и u — обобщённое решение задачи (7.19), то и является обычным классическим решением этой задачи.
и u — обобщённое решение задачи (7.19), то и является обычным классическим решением этой задачи.
Теорема 7.10. Обобщённое решение и задачи Дирихле существует и единственно для любой ограниченной области  и для любой функции
и для любой функции  . Это решение имеет строго минимальный интеграл Дирихле
. Это решение имеет строго минимальный интеграл Дирихле  среди всех функций и
среди всех функций и  для которых
для которых  . Обратно, если и является стационарной точкой интеграла Дирихле в классе всех функций и
. Обратно, если и является стационарной точкой интеграла Дирихле в классе всех функций и  для которых
для которых  , то на самом деле интеграл Дирихле имеет строгий минимум на функции и, причём и является обобщённым решением задачи Дирихле.
, то на самом деле интеграл Дирихле имеет строгий минимум на функции и, причём и является обобщённым решением задачи Дирихле.
Доказательство. Пусть  . Условие
. Условие  можно записать в виде:
можно записать в виде:

или, что то же самое, в виде

Поскольку скалярное произведение  является по w непрерывным функционалом на
является по w непрерывным функционалом на  по непрерывности имеем
по непрерывности имеем

Это условие равносильно уравнению  Итак, мы должны найти такую функцию и
Итак, мы должны найти такую функцию и  что и ортогональна подпространству
что и ортогональна подпространству  относительно скалярного произведения
относительно скалярного произведения  причём
причём  . Но это означает, что и является перпендикуляром, опущенным из v на подпространство
. Но это означает, что и является перпендикуляром, опущенным из v на подпространство  Как известно, в гильбертовом пространстве такой перпендикуляр единствен, причём он является наименьшим по длине вектором и
Как известно, в гильбертовом пространстве такой перпендикуляр единствен, причём он является наименьшим по длине вектором и  удовлетворяющим условию
удовлетворяющим условию  Условие стационарности и, как известно, приводит к условию ортогональности.
Условие стационарности и, как известно, приводит к условию ортогональности.
Однако имеется небольшая неприятность: «скалярное произведение»  определяет структуру гильбертова пространства на
определяет структуру гильбертова пространства на  но не на
но не на  . Поэтому следует слегка уточнить приведённые рассуждения.
. Поэтому следует слегка уточнить приведённые рассуждения.
Рассмотрим  так что
так что  . Из условия (7.20) вытекает, что
. Из условия (7.20) вытекает, что

Но отсюда очевиден способ доказательства существования решения. А именно, рассмотрим  как линейный непрерывный функционал от w на
как линейный непрерывный функционал от w на  и представим его (по теореме Рисса это возможно и притом единственным образом) в виде
и представим его (по теореме Рисса это возможно и притом единственным образом) в виде  , где z — фиксированный элемент
, где z — фиксированный элемент  . Остаётся положить
. Остаётся положить  По построению z выполнено условие (7.21), откуда следует (7.20). Условие
По построению z выполнено условие (7.21), откуда следует (7.20). Условие  очевидно.
очевидно.
Единственность решения очевидна из того, что если  — два решения, то
— два решения, то  удовлетворяет условию (7.20), откуда
удовлетворяет условию (7.20), откуда  .
.
Покажем теперь минимальность интеграла Дирихле на решении и в классе всех  для которых
для которых  . Положим
. Положим  , так что
, так что  . Ясно, что
. Ясно, что  и из (7.20) находим
и из (7.20) находим

причём равенство достигается лишь при  , т. е. при
, т. е. при  или, что то же самое, при
или, что то же самое, при  .
.
Проверим, наконец, что если интеграл Дирихле стационарен на функции  в классе всех
в классе всех  , для которых
, для которых  то
то  — обобщённое решение задачи Дирихле (и, значит, интеграл Дирихле достигает строгого минимума на u). Стационарность интеграла Дирихле на и означает, что
— обобщённое решение задачи Дирихле (и, значит, интеграл Дирихле достигает строгого минимума на u). Стационарность интеграла Дирихле на и означает, что

Но

Стационарность даёт:  для любого
для любого  . Но мы можем заменить z на
. Но мы можем заменить z на  откуда
откуда  при любом
при любом  что даёт условие (7.20). Теорема 7.10 доказана.
что даёт условие (7.20). Теорема 7.10 доказана.
В заключение укажем без доказательства правильное описание гладкости решений по информации о функции  в граничной задаче (7.19) для области
в граничной задаче (7.19) для области  с гладкой границей.
с гладкой границей.
Мы уже говорили, что если  , то
, то  . Оказывается, что верно и обратное: если
. Оказывается, что верно и обратное: если  , где
, где  , то существует и единственно решение
, то существует и единственно решение  задачи (7.19) (см., например, Лионе и Мадженес [34]).
задачи (7.19) (см., например, Лионе и Мадженес [34]).
Аналогично, если  где
где  , то существует (и единственно) решение
, то существует (и единственно) решение  .
.
Объединяя описанные свойства гладкости решений задач (7.15) и (7.19), легко получить, что отображение

продолжается до изоморфизма

а также до изоморфизма

Аналогичные теоремы могут быть доказаны и для общих эллиптических уравнений с общими граничными условиями, удовлетворящими алгебраическому условию, называемому условием эллиптичности (или коэрцитивности, накрывания, Шапиро-Лопатинского). Изложение общей теории эллиптических граничных задач можно найти, например, у Лионса, Мадженеса [34] или Хёрмандера [55-2].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
- § 2. Одномерное волновое уравнение
- 2.1. Уравнение колебании струны
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
- 2.3. Полуограниченная струна. Отражение волн от конца струны
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы