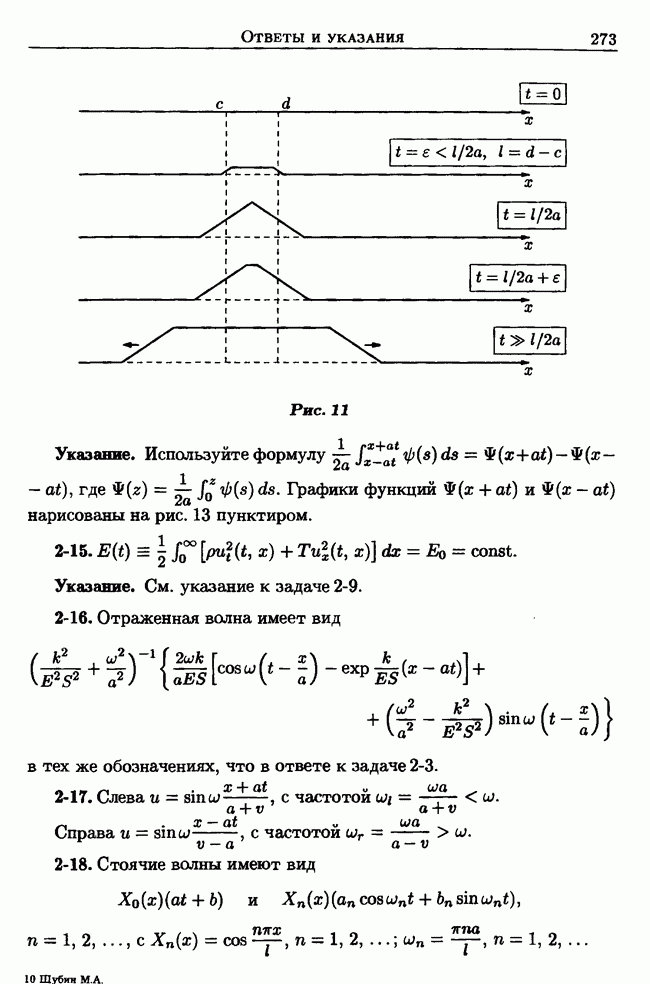
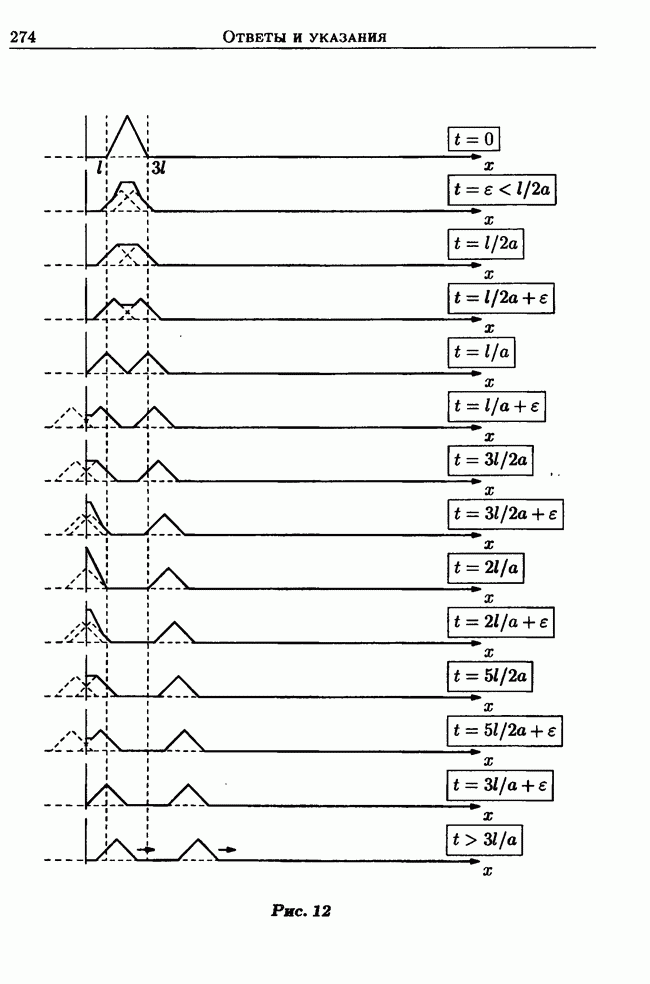
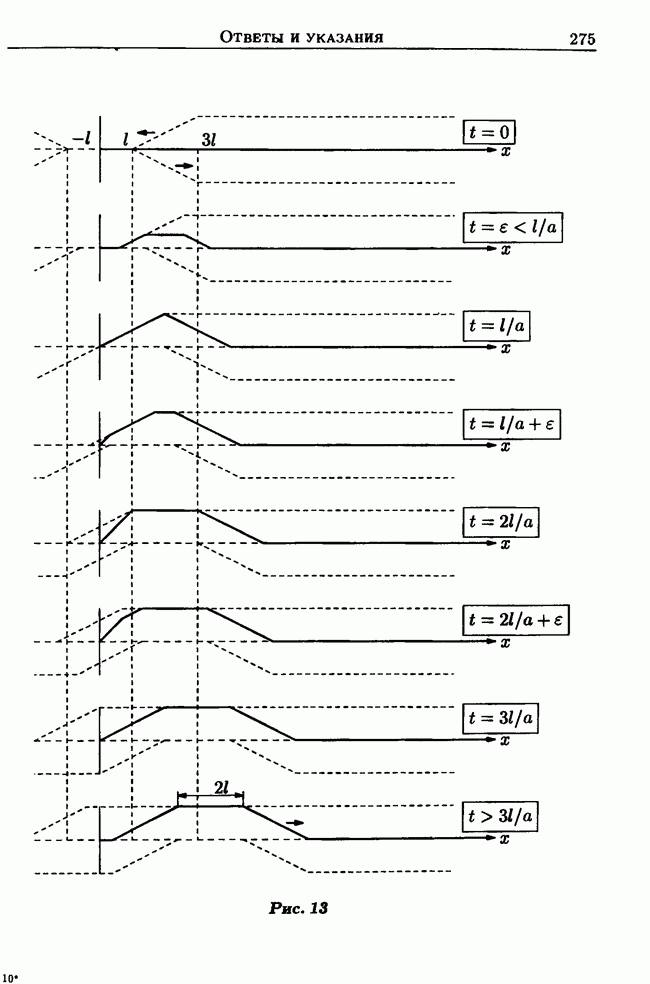
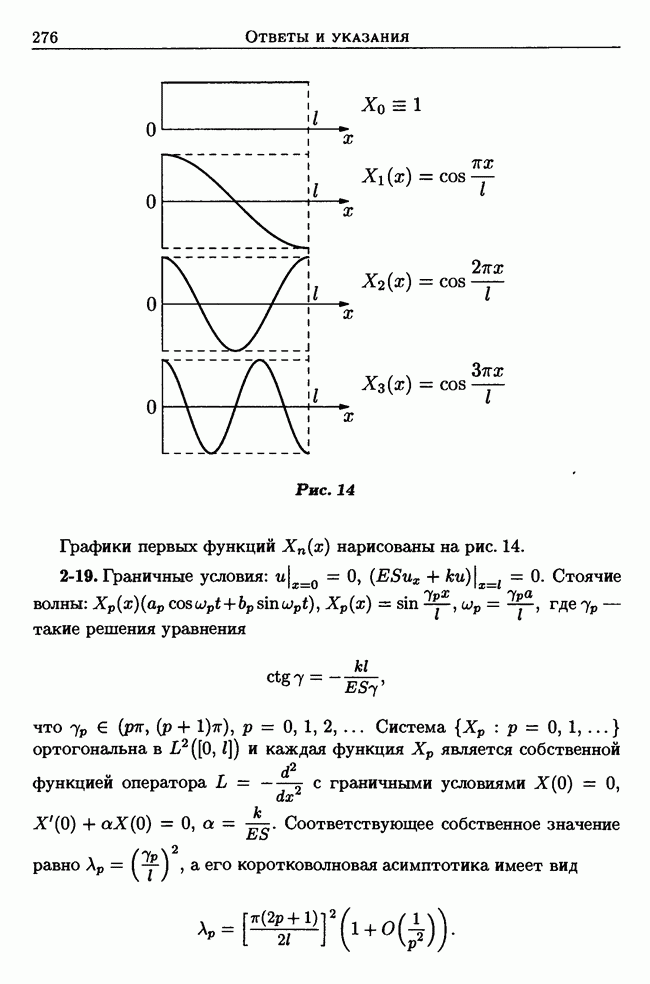
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
Мы исследуем сейчас задачу Коши (6.2). Будем вначале считать, что  при каждом
при каждом  причем
причем  является непрерывной функцией от t при
является непрерывной функцией от t при  со значениями в
со значениями в  и, более того, бесконечно дифференцируемой функцией от t при
и, более того, бесконечно дифференцируемой функцией от t при  значениями в
значениями в  . Как мы увидим ниже, решение
. Как мы увидим ниже, решение  с описанными свойствами существует (и в очень широком классе решений единственно). Пока же заметим, что мы можем сделать преобразование Фурье по х, а поскольку оператор преобразования Фурье осуществляет топологический изоморфизм
с описанными свойствами существует (и в очень широком классе решений единственно). Пока же заметим, что мы можем сделать преобразование Фурье по х, а поскольку оператор преобразования Фурье осуществляет топологический изоморфизм  , то его можно менять местами с производной
, то его можно менять местами с производной  . Итак, пусть
. Итак, пусть

(здесь и в дальнейшем при отсутствии указания области интегрирования подразумевается интеграл по  ).
).
Стандартное интегрирование по частям даёт:

Таким образом, уравнение (6.1) равносильно уравнению

Начальное же условие, очевидно, приобретает вид

где  .
.
Уравнение (6.10) представляет собой обыкновенное дифференциальное уравнение по t с параметром Оно легко решается, и мы получим с учётом начального условия (6.11):

Взглянув на эту формулу, мы видим, что  действительно является непрерывной при
действительно является непрерывной при  и бесконечно дифференцируемой при
и бесконечно дифференцируемой при  функцией от t со значениями в
функцией от t со значениями в  . Поэтому совершая обратное преобразование Фурье, мы получим решение задачи Коши
. Поэтому совершая обратное преобразование Фурье, мы получим решение задачи Коши  удовлетворяющее описанным выше условиям. Напишем более явную формулу. Имеем:
удовлетворяющее описанным выше условиям. Напишем более явную формулу. Имеем:

Меняя порядок интегрирования (это возможно по теореме Фубини), мы получаем:

где

(по существу мы повторили выкладку, доказывающую, что преобразование Фурье переводит умножение в свёртку). Вычислим явно  взяв интеграл в (6.14). Для этого нужно выделить полный квадрат в показателе экспоненты:
взяв интеграл в (6.14). Для этого нужно выделить полный квадрат в показателе экспоненты:

Делая замену переменных  , т. е. сдвигая контур интегрирования по каждому
, т. е. сдвигая контур интегрирования по каждому  , мы получим:
, мы получим:

(мы сделали ещё замену переменных  ). Используя формулу
). Используя формулу

получим окончательно:

Решение задачи Коши записывается в виде

называемом интегралом Пуассона. Проанализируем эту формулу.
Заметим прежде всего, что она имеет смысл для значительно более широкого класса начальных функций  , чем класс
, чем класс  , с которого мы начинали. Ясно, например, что если
, с которого мы начинали. Ясно, например, что если  непрерывна и
непрерывна и

то интеграл в (6.16) сходится при  т.е. при
т.е. при  При этом сам интеграл и интегралы, полученные из него взятием любых производных по t и
При этом сам интеграл и интегралы, полученные из него взятием любых производных по t и  сходятся равномерно для
сходятся равномерно для  , где
, где  . Поэтому можно дифференцировать сколько угодно раз под знаком интеграла. Полученная функция
. Поэтому можно дифференцировать сколько угодно раз под знаком интеграла. Полученная функция  будет при указанных значениях t решением уравнения теплопроводности (6.1). В самом деле, достаточно показать, что функция
будет при указанных значениях t решением уравнения теплопроводности (6.1). В самом деле, достаточно показать, что функция  является решением уравнения (6.1) при
является решением уравнения (6.1) при  . Это можно проверить непосредственно, а можно вместо непосредственной проверки заметить, что мы уже знаем, что
. Это можно проверить непосредственно, а можно вместо непосредственной проверки заметить, что мы уже знаем, что

для любой функции  откуда следует, что
откуда следует, что

Легко проверяется также, что в этом случае выполнено начальное условие  в смысле, что при каждом
в смысле, что при каждом 

Мы сделаем это даже двумя способами.
1-й способ. Заметим, что  где
где  так что
так что  при
при  . Мы имеем дело с классическим
. Мы имеем дело с классическим  -образным семейством положительных функций (в частности,
-образным семейством положительных функций (в частности,  )
)  при
при  Теперь проверка (6.18) проводится по стандартной схеме доказательства
Теперь проверка (6.18) проводится по стандартной схеме доказательства  -образности (см. § 4, пример 4.5). Соответствующие подробности, которые мы опускаем, читателю полезно восстановить в качестве упражнения.
-образности (см. § 4, пример 4.5). Соответствующие подробности, которые мы опускаем, читателю полезно восстановить в качестве упражнения.
2-й способ. Пусть мы хотим проверить соотношение (6.18) при  . Разложим функцию
. Разложим функцию  в сумму
в сумму

где  непрерывна, совпадает с
непрерывна, совпадает с  при
при  и равна 0 при
и равна 0 при  . Соответственно,
. Соответственно,  непрерывна, равна 0 при
непрерывна, равна 0 при  и удовлетворяет оценке (6.17).
и удовлетворяет оценке (6.17).
Интеграл Пуассона (6.16) для  распадается в сумму таких интегралов для
распадается в сумму таких интегралов для  и для
и для  (мы обозначим их
(мы обозначим их  )
)  . Соотношение (6.18) достаточно проверить отдельно для
. Соотношение (6.18) достаточно проверить отдельно для  и для
и для  .
.
Займёмся вначале функцией  Имеем:
Имеем:

Ясно, что подынтегральная функция стремится к 0 при  (поскольку
(поскольку  при
при  ), причём она имеет при
), причём она имеет при  интегрируемую мажоранту (вида
интегрируемую мажоранту (вида  ), не зависящую от
), не зависящую от  . По теореме Лебега
. По теореме Лебега  .
.
Остаётся рассмотреть случай финитной начальной функции. Здесь рассуждения из примера 4.5, § 4 проходят без всяких изменений. Однако есть и другой способ, основанный на аппроксимации гладкими функциями и последующем предельном переходе. Здесь полезно вначале заметить, что имеет место
Лемма 6.3 (принцип максимума). Пусть функция  задаётся интегралом Пуассона (6.16). Тогда
задаётся интегралом Пуассона (6.16). Тогда

При этом если одно из неравенств здесь обращается в равенство при каких-нибудь  то
то  .
.
Доказательство. Имеем:

Аналогично доказывается второе неравенство в (6.19). Поскольку  при всех
при всех  то равенство возможно лишь если
то равенство возможно лишь если  почти всюду, а тогда
почти всюду, а тогда  , что и требовалось.
, что и требовалось.
Закончим доказательство соотношения (6.18). Пусть  — финитная непрерывная функция,
— финитная непрерывная функция,  — такая последовательность функций из
— такая последовательность функций из  что
что  при к
при к  (последовательность
(последовательность  можно построить, например, с помощью операции усреднения — см. § 4, п. 4.2.
можно построить, например, с помощью операции усреднения — см. § 4, п. 4.2.
Пусть

Поскольку  то
то  в топологии
в топологии  (и, в частности, равномерно на
(и, в частности, равномерно на  ). Но по лемме 6.3
). Но по лемме 6.3

откуда ясно, что  . В самом деле, если дано
. В самом деле, если дано  , то
, то  мы можем выбрать такое к, что
мы можем выбрать такое к, что  затем такое
затем такое  что
что  при
при  . Отсюда ясно, что
. Отсюда ясно, что

что и требовалось.
Отметим ещё, что интеграл Пуассона часто имеет смысл и для обобщённых функций  . Например, если
. Например, если  , то он имеет следующий естественный смысл:
, то он имеет следующий естественный смысл:

поскольку  при любых
при любых  . Здесь также легко проверяется, что
. Здесь также легко проверяется, что  — решение уравнения (6.1). Соотношение
— решение уравнения (6.1). Соотношение  верно теперь в смысле слабой сходимости в
верно теперь в смысле слабой сходимости в  . В самом деле, легко проверить, что если
. В самом деле, легко проверить, что если  то
то

где  — интеграл Пуассона, соответствующий начальной функции
— интеграл Пуассона, соответствующий начальной функции  (проверка перестановочности интеграла по а: и операции применения функционала
(проверка перестановочности интеграла по а: и операции применения функционала  обеспечивается тем, что интеграл сходится в топологии
обеспечивается тем, что интеграл сходится в топологии  — см. точно такое же рассуждение в доказательстве предложения 5.2).
— см. точно такое же рассуждение в доказательстве предложения 5.2).
Поскольку  при
при  в топологии
в топологии  , то
, то

а это и означает, что  .
.
Выше мы уже отмечали, что  . Это соотношение часто записывается более коротко в виде
. Это соотношение часто записывается более коротко в виде

и является частным случаем только что доказанного утверждения.
Наконец, пусть оценка (6.17) выполнена для любого  (с постоянной
(с постоянной  , зависящей от b). Тогда интеграл Пуассона и, следовательно, решение задачи Коши определены при любом
, зависящей от b). Тогда интеграл Пуассона и, следовательно, решение задачи Коши определены при любом  . Так будет, например, если
. Так будет, например, если  при некотором
при некотором  и, в частности, если функция
и, в частности, если функция  ограничена.
ограничена.
Если  при каком-нибудь
при каком-нибудь  , то интеграл Пуассона сходится в силу неравенства Гёльдера. В этом случае
, то интеграл Пуассона сходится в силу неравенства Гёльдера. В этом случае  по норме
по норме  (доказательство аналогично рассуждениям, доказывающим сходимость усреднений по
(доказательство аналогично рассуждениям, доказывающим сходимость усреднений по  — см. п. 4.2).
— см. п. 4.2).
Легко проверить, что если  удовлетворяет оценке (6.17), то для функции
удовлетворяет оценке (6.17), то для функции  задаваемой интегралом Пуассона, верна аналогичная оценка
задаваемой интегралом Пуассона, верна аналогичная оценка

где постоянные  зависят от
зависят от  и В. Оказывается, что решение, удовлетворяющее такой оценке, единственно — мы докажем это ниже. В то же время оказывается, что оценка
и В. Оказывается, что решение, удовлетворяющее такой оценке, единственно — мы докажем это ниже. В то же время оказывается, что оценка

ни при каком  не обеспечивает единственность.
не обеспечивает единственность.
Единственность решения обеспечивает естественность применения интеграла Пуассона для нахождения разумного решения (как правило, быстро растущие решения не имеют физического смысла). Например, имеется единственность решения в классе ограниченных функций.
Благодаря принципу максимума (лемма 6.3) задача Коши корректна в классе ограниченных функций (если  равномерно мало меняется, то равномерно мало меняется и
равномерно мало меняется, то равномерно мало меняется и  ).
).
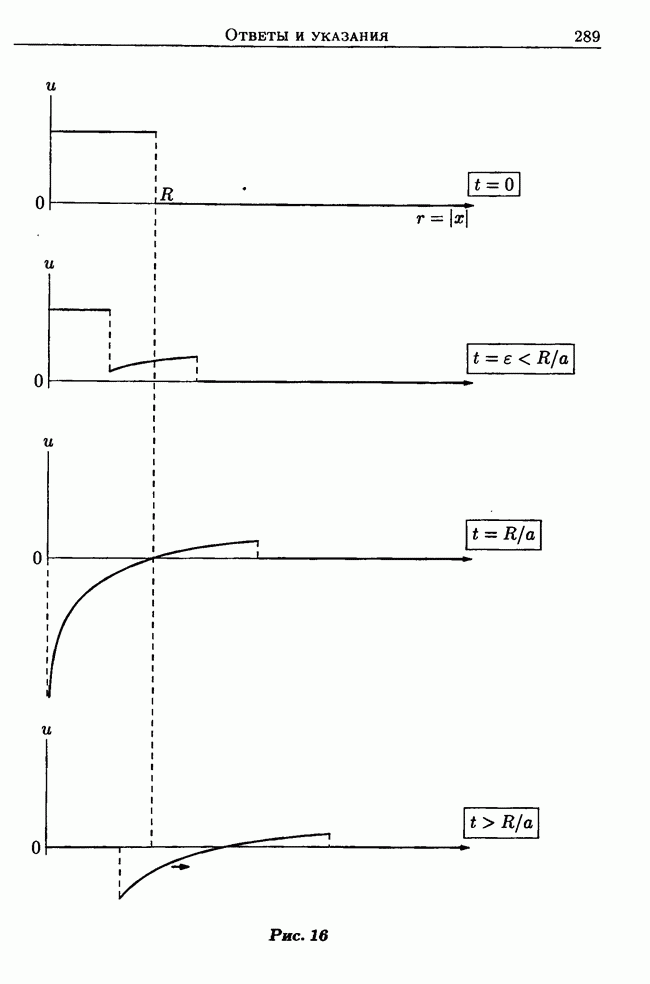
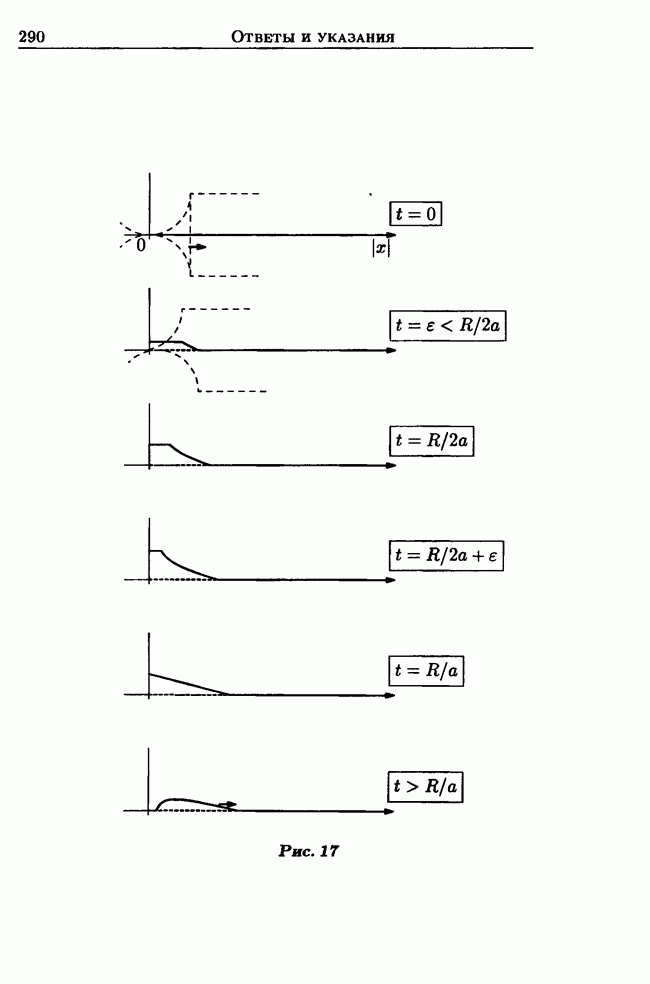
В заключение заметим, что тот факт, что  при всех
при всех  означает, что имеется «бесконечная скорость распространения тепла» (ведь начальное возмущение сосредоточено в нуле!). Однако функция
означает, что имеется «бесконечная скорость распространения тепла» (ведь начальное возмущение сосредоточено в нуле!). Однако функция  быстро убывает при
быстро убывает при  что практически равносильно конечной скорости распространения тепла.
что практически равносильно конечной скорости распространения тепла.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
- § 2. Одномерное волновое уравнение
- 2.1. Уравнение колебании струны
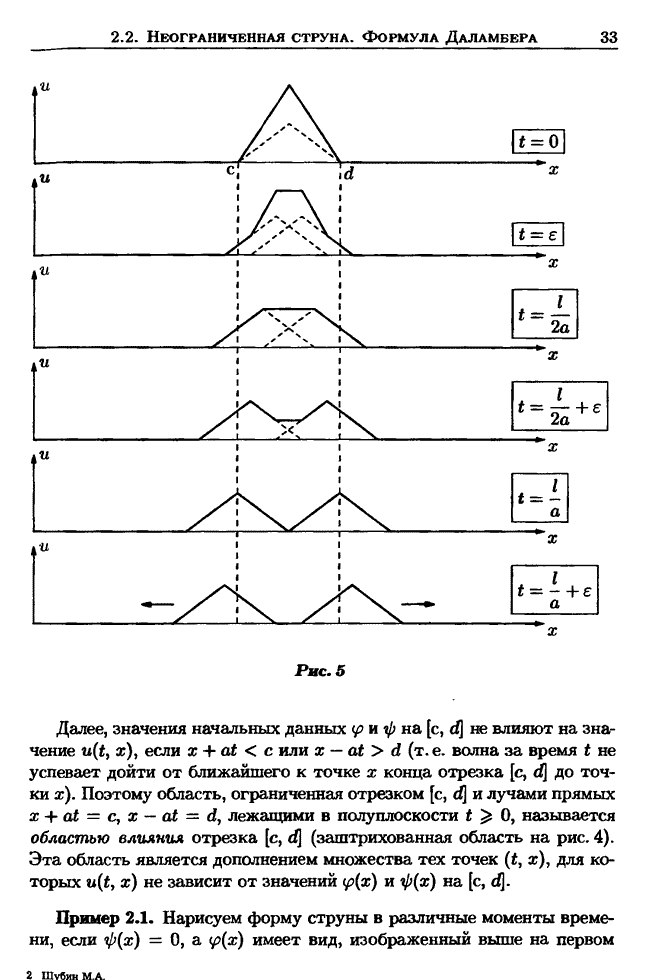
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
- 2.3. Полуограниченная струна. Отражение волн от конца струны
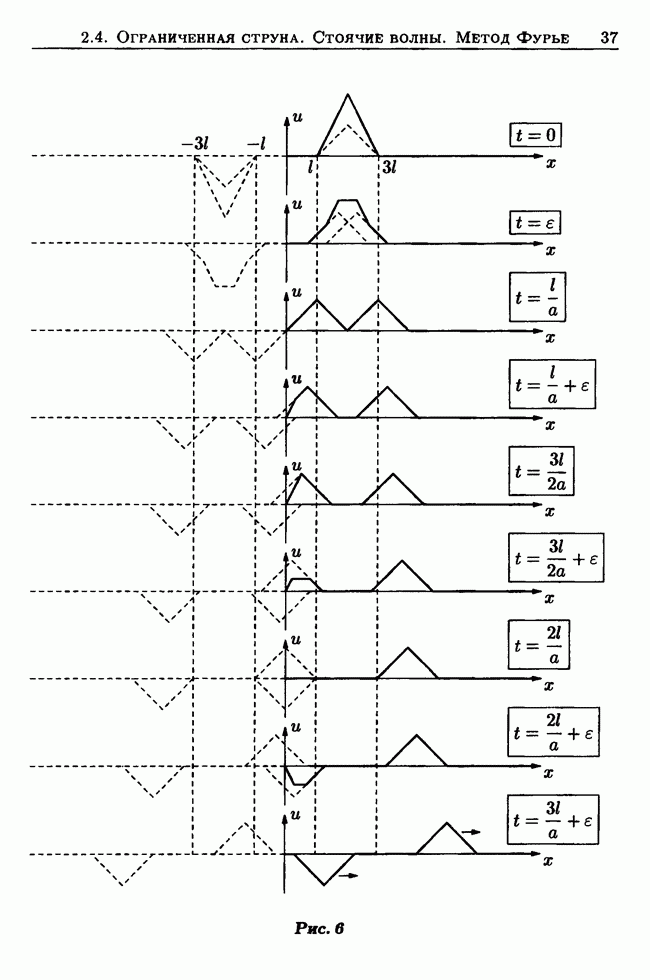
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы