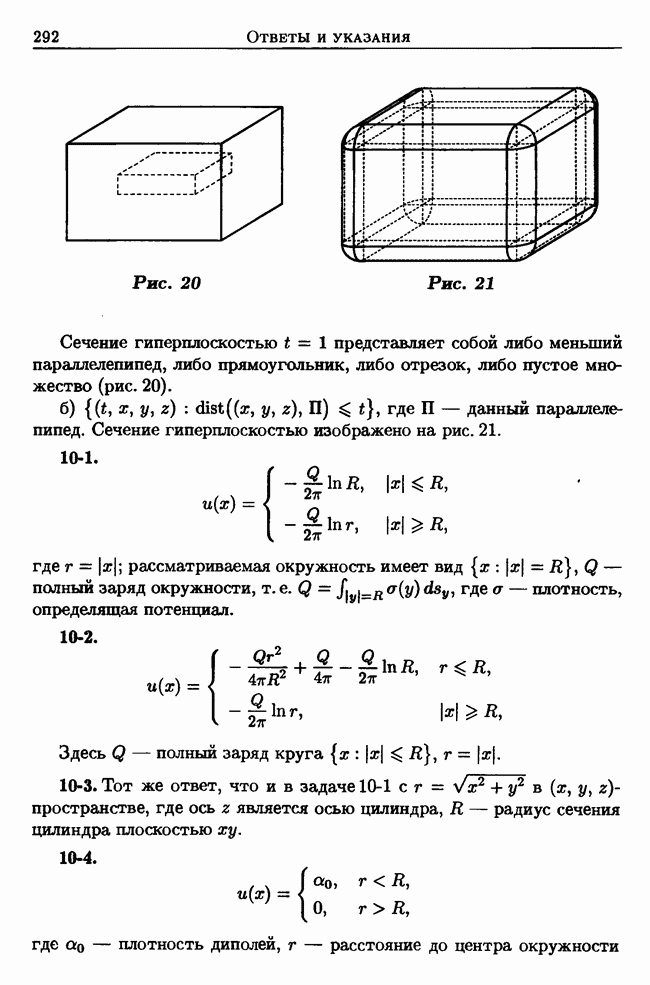
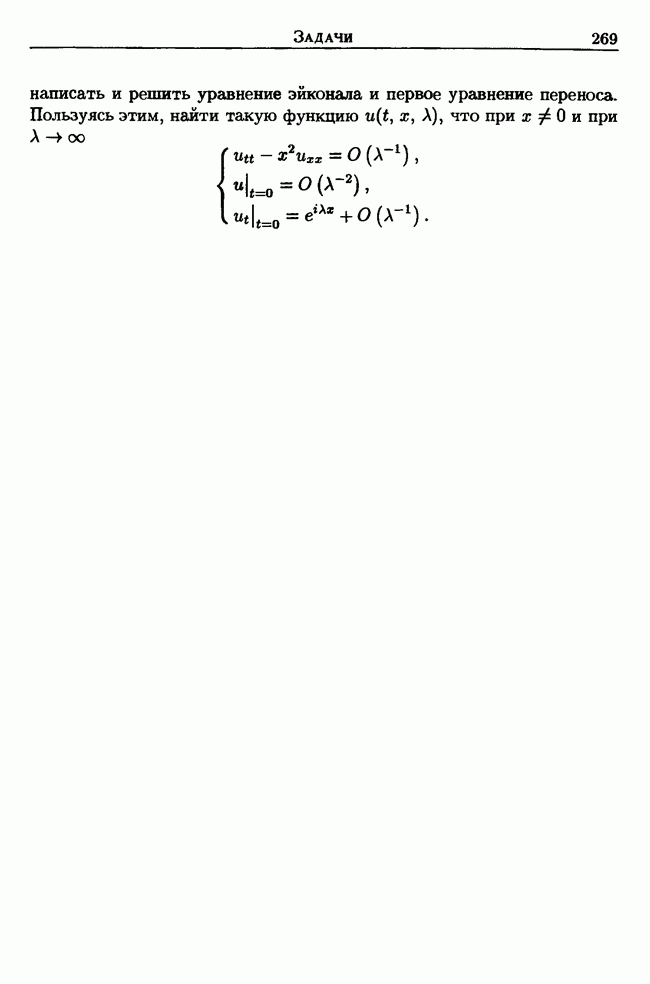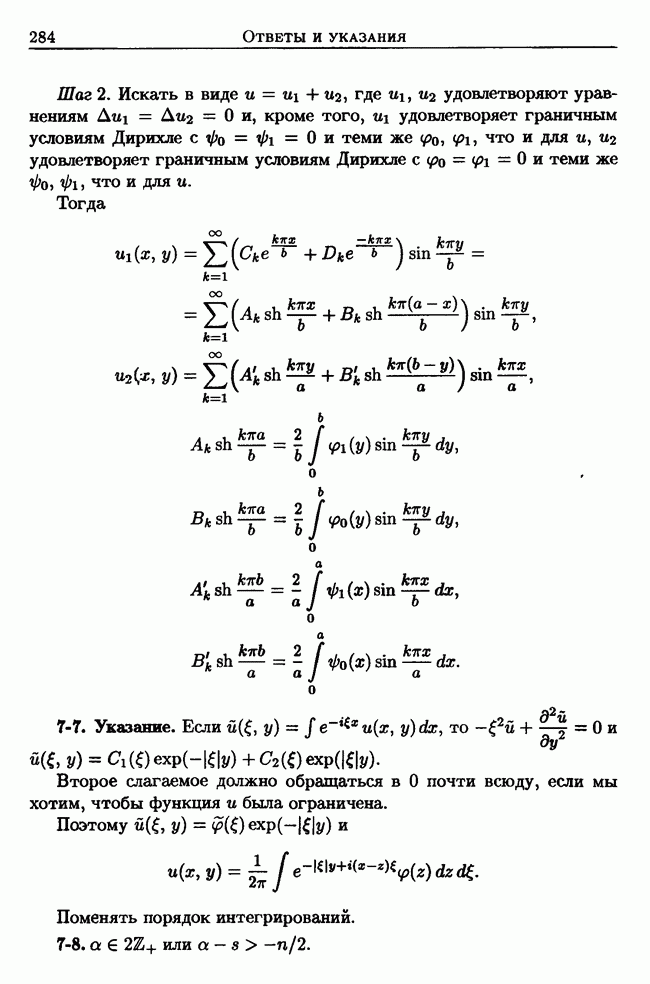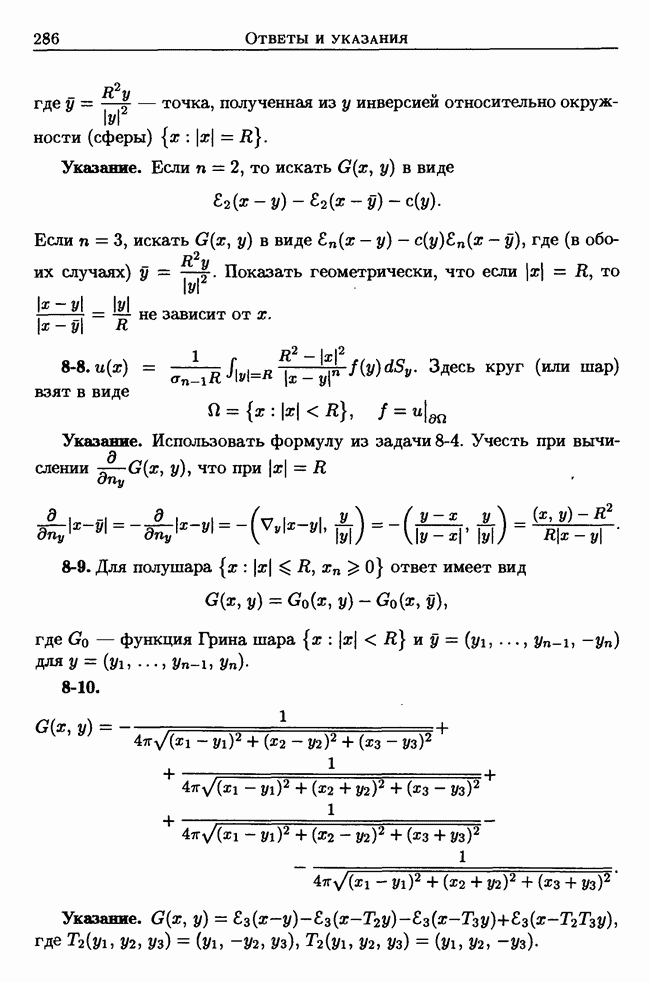| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
Операции дифференцирования и умножения на гладкую функцию являются частными случаями следующей общей конструкции. Пусть  — две области в
— две области в  задан какой-то оператор
задан какой-то оператор  и существует такой оператор
и существует такой оператор  , что
, что

если  . Оператор
. Оператор  называется транспонированным к оператору L. Предположим, что для любого компакта
называется транспонированным к оператору L. Предположим, что для любого компакта  найдётся такой компакт
найдётся такой компакт  , что
, что  и отображение
и отображение  непрерывно. Тогда формула (4.70) позволяет продолжить оператор L до оператора
непрерывно. Тогда формула (4.70) позволяет продолжить оператор L до оператора  .
.
Если  и оператор
и оператор  продолжается до непрерывного оператора
продолжается до непрерывного оператора  то ясно, что оператор L задаёт отображение
то ясно, что оператор L задаёт отображение 
Отметим, что оператор L, построенный с помощью этой конструкции, всегда слабо непрерывен. Это очевидно из формулы (4.70), поскольку  — это полунорма общего вида для
— это полунорма общего вида для  — некоторая полунорма для
— некоторая полунорма для  .
.
Примеры транспонированных операторов: а) если  , то
, то  ; б) если
; б) если  (оператор умножения на функцию
(оператор умножения на функцию  )
)  , то
, то  . В частности, операторы
. В частности, операторы  непрерывны на
непрерывны на  в слабой топологии. Оператор
в слабой топологии. Оператор  , кроме того, непрерывен на
, кроме того, непрерывен на  .
.
Приведём новые примеры. Пусть дан диффеоморфизм  . Он обычным образом определяет отображение
. Он обычным образом определяет отображение  , а именно
, а именно  . Ясно, что той же формулой можно определить отображение
. Ясно, что той же формулой можно определить отображение  . Кроме того,
. Кроме того,  переводит
переводит  . Мы хотим продолжить
. Мы хотим продолжить  до линейного непрерывного оператора
до линейного непрерывного оператора

Для этого найдём транспонированный оператор. Пусть  . Тогда
. Тогда

где  — отображение, обратное к
— отображение, обратное к  якобиан.
якобиан.
Теперь ясно, что транспонированный оператор имеет вид:

Поскольку  ясно, что
ясно, что  отображает
отображает  в
в  причём он задаёт непрерывное отображение
причём он задаёт непрерывное отображение  . Поэтому по общей схеме определено непрерывное отображение
. Поэтому по общей схеме определено непрерывное отображение  . Если
. Если  и отображение
и отображение  является аффинным преобразованием (или хотя бы совпадает с аффинным преобразованием вне некоторого компакта), то
является аффинным преобразованием (или хотя бы совпадает с аффинным преобразованием вне некоторого компакта), то  непрерывно отображает
непрерывно отображает  (в этом случае
(в этом случае  ), так что задано непрерьшное отображение
), так что задано непрерьшное отображение  .
.
Примеры, а) Оператор сдвига  , где
, где  продолжается до линейного непрерывного оператора из
продолжается до линейного непрерывного оператора из  и из
и из  . В частности, ранее употреблявшееся обозначение
. В частности, ранее употреблявшееся обозначение  согласуется с определением сдвига на
согласуется с определением сдвига на 
б) Оператор гомотетии  где
где  определён на
определён на  и отображает
и отображает  Вычислим, например,
Вычислим, например,  . Имеем:
. Имеем:

Итак,

Определение 4.11. Обобщенная функция  называется однородной порядка
называется однородной порядка  , если
, если

На самом деле легко проверить, что требование  можно заменить включением
можно заменить включением  (из (4.75) тогда автоматически вытекает, что
(из (4.75) тогда автоматически вытекает, что  .
.
Примеры.
1. Если  и при любом
и при любом  почти всюду по
почти всюду по  выполнено (4.75), то
выполнено (4.75), то  однородна порядка
однородна порядка  как обобщённая функция.
как обобщённая функция.
2.  -функция
-функция  однородна порядка
однородна порядка  .
.
Легко проверяется, что  .
.
Поэтому, если  однородна порядка
однородна порядка  , то однородна порядка
, то однородна порядка  . Например,
. Например,  однородна порядка
однородна порядка  .
.
Соображения однородности позволяют без вычислений понять, как устроено фундаментальное решение оператора Лапласа и его степеней. А именно, обобщённая функция  при
при  имеет порядок однородности
имеет порядок однородности  и при
и при  удовлетворяет уравнению
удовлетворяет уравнению  . Поэтому
. Поэтому  сосредоточена в нуле и имеет порядок однородности
сосредоточена в нуле и имеет порядок однородности  . Но поскольку порядок однородности
. Но поскольку порядок однородности  равен
равен  , то ясно, что
, то ясно, что  . При
. При  имеем
имеем  при
при  и производные
и производные  однородны порядка —1. Поэтому
однородны порядка —1. Поэтому  сосредоточена в нуле и имеет порядок однородности —2, так что
сосредоточена в нуле и имеет порядок однородности —2, так что  .
.
Неясно заранее, почему не может оказаться, что  Мы увидим в дальнейшем, однако, что если и
Мы увидим в дальнейшем, однако, что если и  и
и  (и даже более того: и вещественно-аналитична в
(и даже более того: и вещественно-аналитична в  ). Поскольку
). Поскольку  имеет особенность в нуле, то
имеет особенность в нуле, то  , откуда
, откуда  где
где  . Аналогично при
. Аналогично при  имеем
имеем  .
.
Отметим, наконец, что оператор поворота определён в  и это позволяет придать точный смысл рассуждениям об усреднении, на основании которых мы выше сделали вывод о существовании сферически симметричного фундаментального решения для оператора
и это позволяет придать точный смысл рассуждениям об усреднении, на основании которых мы выше сделали вывод о существовании сферически симметричного фундаментального решения для оператора  .
.
Пример 4.15. Фундаментальные решения для степеней оператора Лапласа.
Из соображений сферической симметрии и однородности ясно, что для нахождения фундаментального решения оператора  в
в  естественно рассмотреть функцию
естественно рассмотреть функцию  . Тогда мы получим, что
. Тогда мы получим, что  .
.
Может ли быть  ? Оказывается, что если
? Оказывается, что если  (т.е.
(т.е.  не является чётным неотрицательным числом), или, что то же самое,
не является чётным неотрицательным числом), или, что то же самое,  , то мы получим, что
, то мы получим, что  и, значит,
и, значит,  , где
, где  . В самом деле, при
. В самом деле, при  имеем при любом
имеем при любом 

Поэтому

и при последовательном применении  к
к  мы будем получать множитель вида
мы будем получать множитель вида  затем
затем  —
—  и т. д., откуда следует, что
и т. д., откуда следует, что  при
при  .
.
Поэтому при  фундаментальное решение
фундаментальное решение  оператора
оператора  имеет вид
имеет вид

Далее, пусть  так что
так что  — многочлен от
— многочлен от  Тогда нужно рассмотреть функцию
Тогда нужно рассмотреть функцию  . Тогда получим
. Тогда получим

(постоянная  зависит от
зависит от  ), где
), где  . Рассмотрим для определённости случай
. Рассмотрим для определённости случай  . Заметим, что
. Заметим, что

а  , так что
, так что

поскольку  — многочлен от
— многочлен от  степени
степени  . Здесь
. Здесь  , потому что
, потому что  а уравнение
а уравнение  не имеет решений с особенностями (если бы оказалось, что
не имеет решений с особенностями (если бы оказалось, что  , то при некотором к мы получили бы, что
, то при некотором к мы получили бы, что  имеет особенность в точке 0 и удовлетворяет уравнению
имеет особенность в точке 0 и удовлетворяет уравнению  ).
).
Впрочем, постоянную  можно легко вычислить непосредственно. Таким образом, при
можно легко вычислить непосредственно. Таким образом, при  имеем:
имеем:

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
- § 2. Одномерное волновое уравнение
- 2.1. Уравнение колебании струны
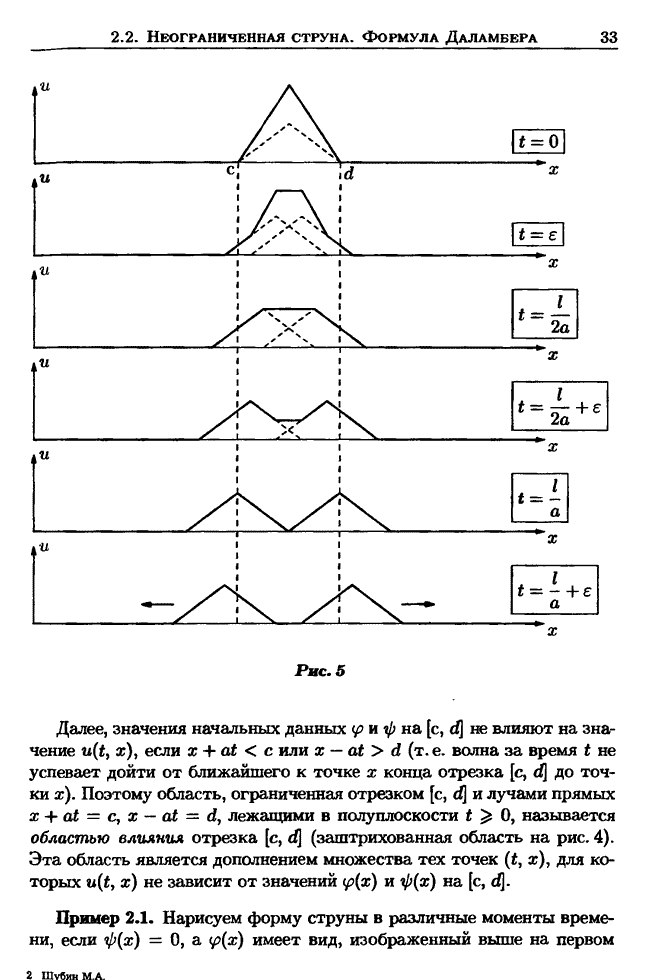
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
- 2.3. Полуограниченная струна. Отражение волн от конца струны
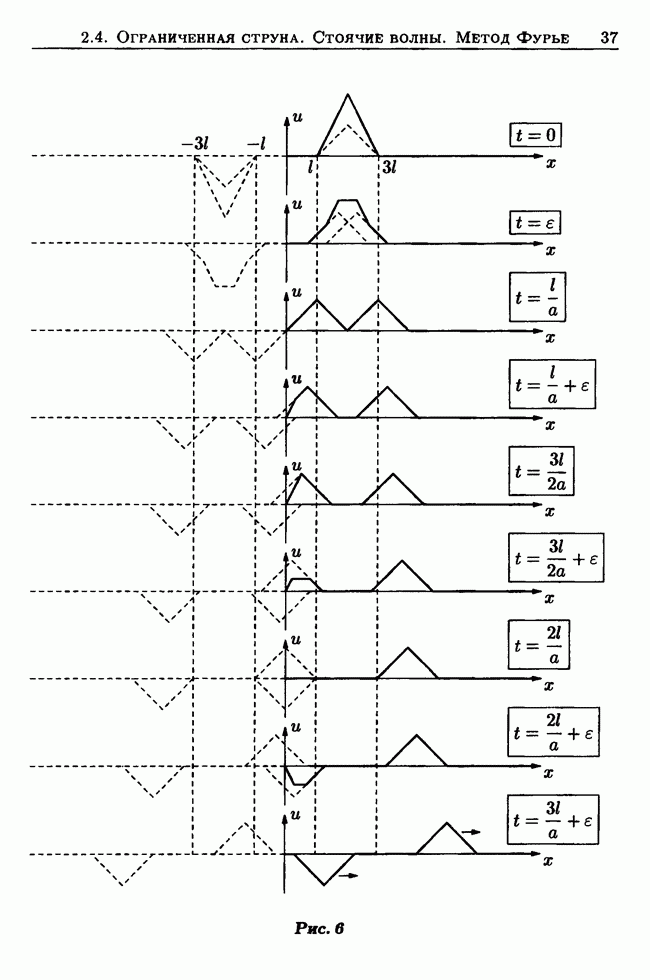
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы