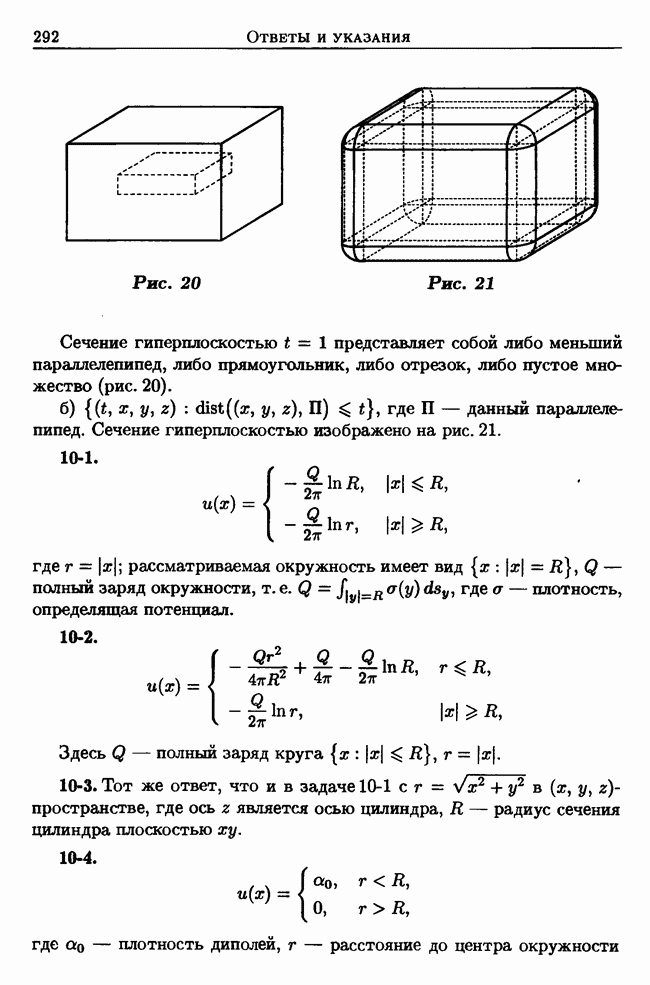
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
Теорема 6.4. Фундаментальным решением оператора  является локально интегрируемая функция
является локально интегрируемая функция

где  — функция Хевисайда
— функция Хевисайда  при
при  при
при  .
.
Доказательство. Приведём вначале эвристическое обоснование того, что  — фундаментальное решение. Мы видели, что
— фундаментальное решение. Мы видели, что  — непрерывная функция от t со значениями в
— непрерывная функция от t со значениями в  при
при  . Функция
. Функция  не является непрерывной функцией от t со значениями в
не является непрерывной функцией от t со значениями в  , а имеет при
, а имеет при  скачок, равный
скачок, равный  . Поэтому после применения оператора мы получим
. Поэтому после применения оператора мы получим  , где
, где  в аналогичном смысле непрерывна по t. Но тогда
в аналогичном смысле непрерывна по t. Но тогда

поскольку непрерывное по t слагаемое должно исчезнуть ввиду того, что —  при
при  Это важное рассуждение позволяет писать фундаментальное решение во всех случаях, когда мы умеем писать решение задачи Коши в виде интеграла типа интеграла Пуассона. Однако возиться с его обоснованием мы не будем, поскольку проще непосредственно проверить, что
Это важное рассуждение позволяет писать фундаментальное решение во всех случаях, когда мы умеем писать решение задачи Коши в виде интеграла типа интеграла Пуассона. Однако возиться с его обоснованием мы не будем, поскольку проще непосредственно проверить, что  — фундаментальное решение.
— фундаментальное решение.
Начнём с проверки локальной интегрируемости  Легко видеть, что
Легко видеть, что  так что нужно лишь проверить локальную интегрируемость в окрестности начала координат. Поскольку
так что нужно лишь проверить локальную интегрируемость в окрестности начала координат. Поскольку

для любого  , то
, то

Пусть  так что
так что  . Из (6.23) мы видим, что функция
. Из (6.23) мы видим, что функция  мажорируется интегрируемой в окрестности точки
мажорируется интегрируемой в окрестности точки  функцией, так что она сама локально интегрируема. Пусть теперь
функцией, так что она сама локально интегрируема. Пусть теперь  . Имеем:
. Имеем:

Перебросим в интеграле производную — и лапласиан  обратно на
обратно на  . Поскольку
. Поскольку  при
при  , то в результате получится лишь граничный интеграл по плоскости
, то в результате получится лишь граничный интеграл по плоскости  возникающий от переброски интегрированием по частям:
возникающий от переброски интегрированием по частям:

Последний интеграл представляет собой  , где
, где  — интеграл Пуассона с начальной функцией
— интеграл Пуассона с начальной функцией  Рассмотрим ещё интеграл Пуассона u(t, х) с начальной функцией
Рассмотрим ещё интеграл Пуассона u(t, х) с начальной функцией  По принципу максимума
По принципу максимума

Отсюда ясно, что

Но, как мы уже видели,

Отсюда  , что даёт тождество
, что даёт тождество

означающее в силу (6.24) справедливость утверждения теоремы.
Следствие 6.5. Если  где
где  — область в
— область в  то
то 
Таким образом, оператор теплопроводности представляет собой пример гипоэллиптического, но не эллиптического оператора. Отметим, что уравнение теплопроводности имеет бесконечно дифференцируемые, но неаналитические решения (например,  ) в окрестности точки
) в окрестности точки  , где
, где  .
.
Знание фундаментального решения позволяет решать неоднородное уравнение. Например, решение u(t, х) задачи

имеет вид

при надлежащих предположениях относительно  , которые мы не будем точно формулировать. Интересен первый интеграл в (6.26). Его внутренний интеграл
, которые мы не будем точно формулировать. Интересен первый интеграл в (6.26). Его внутренний интеграл

представляет собой решение задачи Коши

Представление решения задачи Коши (6.25) с нулевой начальной функцией  в виде
в виде 

где  — решение задачи Коши (6.27) (уже для однородного
— решение задачи Коши (6.27) (уже для однородного  ), называется формулой Дюамеля. Аналогичное представление возможно для любых эволюционных уравнений. В частности, точно такое же представление годится для операторов вида
), называется формулой Дюамеля. Аналогичное представление возможно для любых эволюционных уравнений. В частности, точно такое же представление годится для операторов вида  где
где  — линейный дифференциальный оператор по
— линейный дифференциальный оператор по  с переменными коэффициентами; разумеется
с переменными коэффициентами; разумеется  в (6.27) надо в этом случае заменить на
в (6.27) надо в этом случае заменить на  . Формальная проверка очень проста: при применении оператора
. Формальная проверка очень проста: при применении оператора  к обеим частям (6.28), мы получим справа
к обеим частям (6.28), мы получим справа 

что и требовалось.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
- § 2. Одномерное волновое уравнение
- 2.1. Уравнение колебании струны
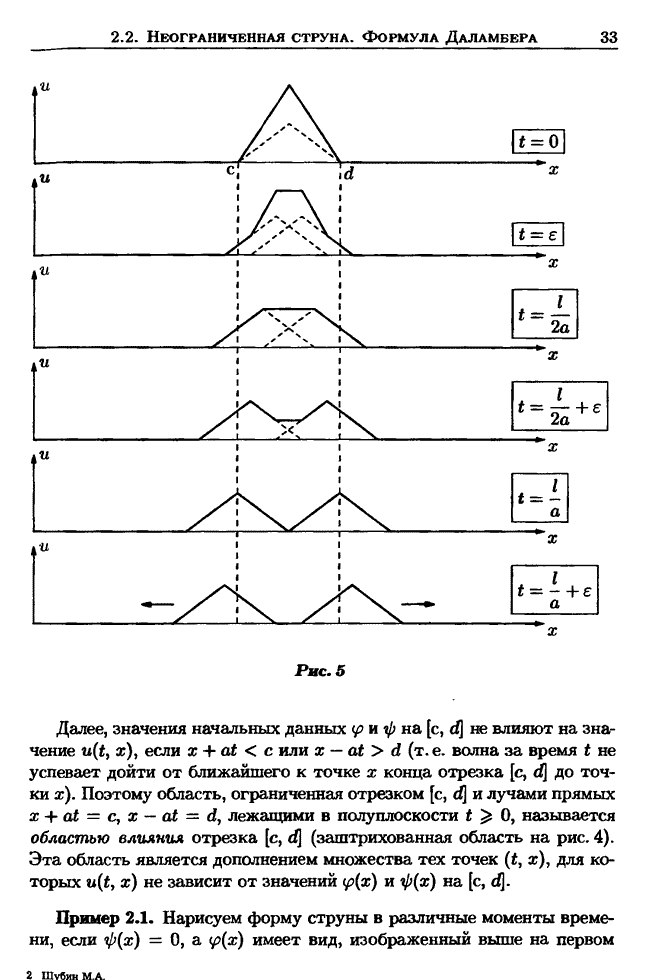
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
- 2.3. Полуограниченная струна. Отражение волн от конца струны
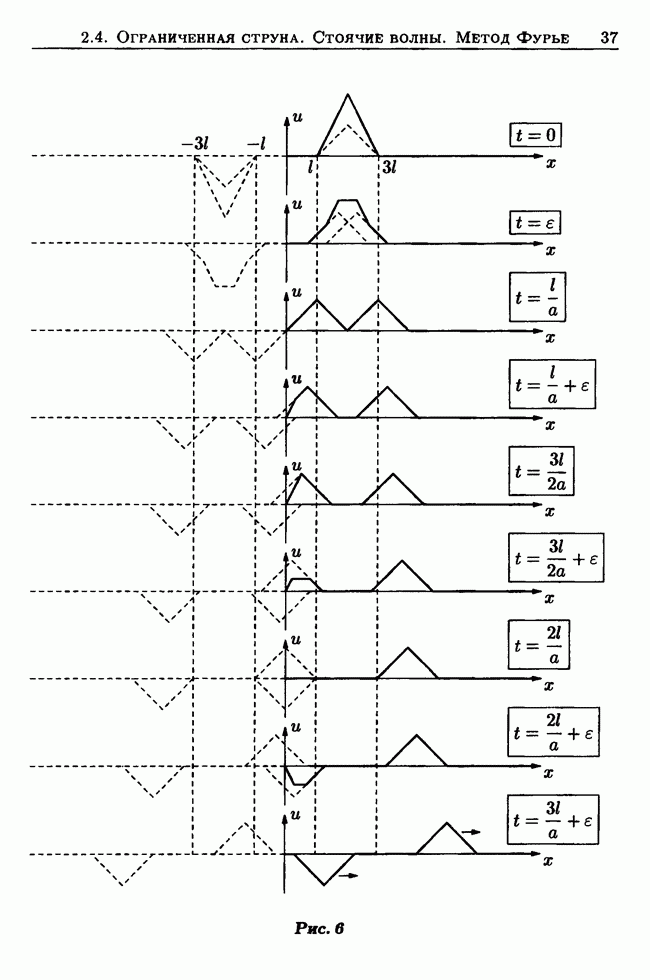
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы