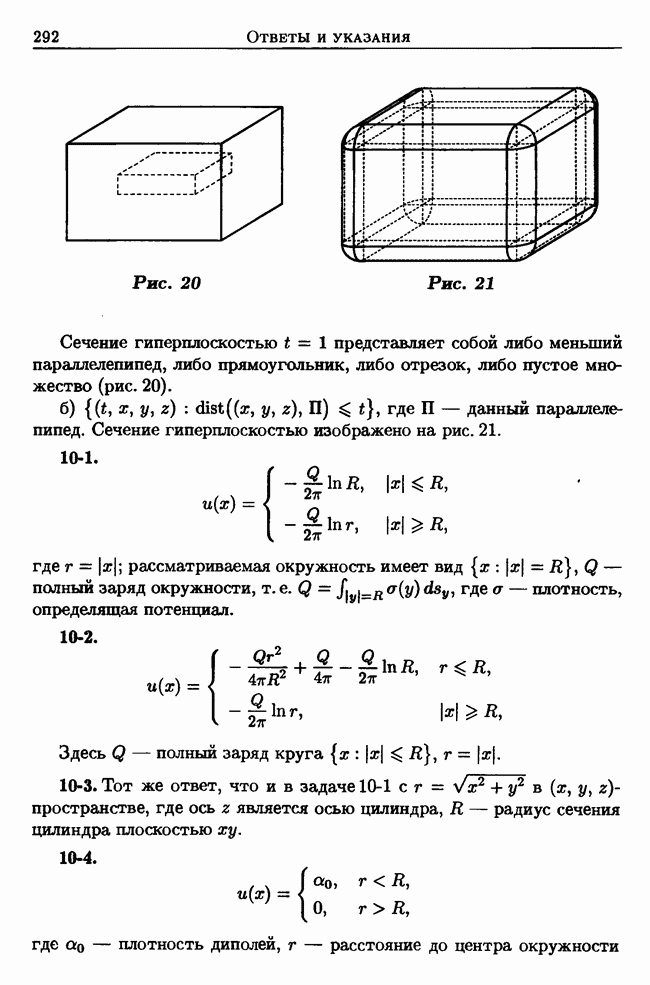
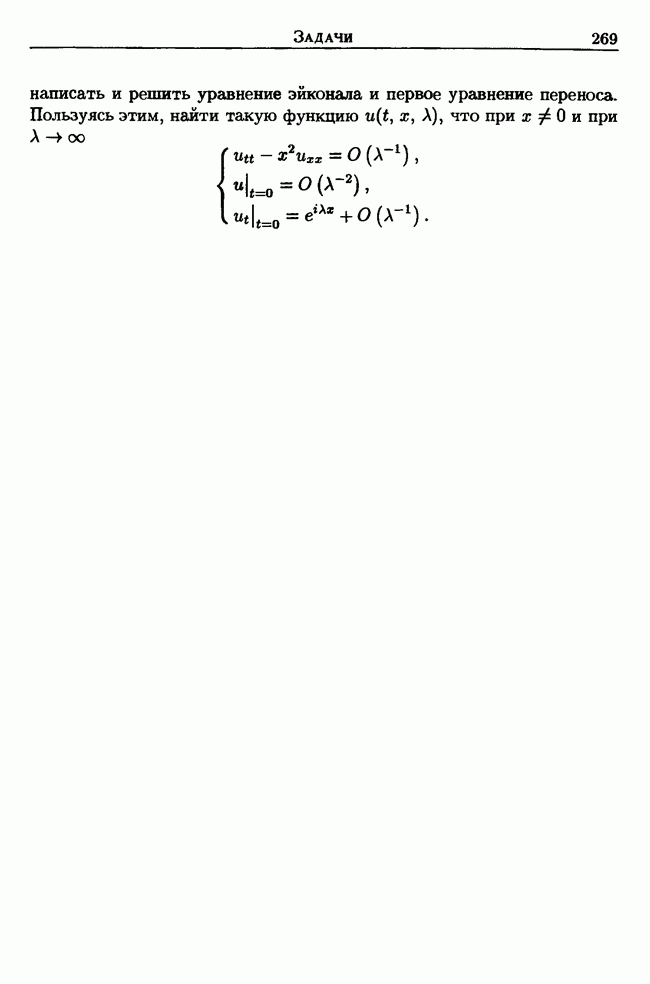| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. Топология и сходимость в пространствах обобщённых функций
Пусть  — одно из пространств основных функций
— одно из пространств основных функций  или
или  — соответствующее пространство линейных непрерывных функционалов на
— соответствующее пространство линейных непрерывных функционалов на  (обобщённых функций). Мы будем рассматривать пространство
(обобщённых функций). Мы будем рассматривать пространство  с так называемой слабой топологией, т. е. топологией, определяемой полунормами
с так называемой слабой топологией, т. е. топологией, определяемой полунормами

В частности, сходимость  в этой топологии означает, что
в этой топологии означает, что

для любого  . Мы будем использовать в этом случае и обычное обозначение
. Мы будем использовать в этом случае и обычное обозначение  .
.

Пример  последовательность. Рассмотрим построенные выше функции
последовательность. Рассмотрим построенные выше функции  . Напомним, что они обладают свойствами:
. Напомним, что они обладают свойствами:

Докажем, что отсюда вытекает соотношение

в  . В самом деле, это означает, что
. В самом деле, это означает, что

для любой функции  . Учитывая свойство б), мы можем переписать (4.20) в виде соотношения
. Учитывая свойство б), мы можем переписать (4.20) в виде соотношения  , очевидным образом верного ввиду оценки
, очевидным образом верного ввиду оценки

Отметим, что (4.19) верно не только в  , но и в
, но и в  и даже в
и даже в  если
если  .
.
Последовательности «обычных» функций, сходящиеся к  -функции, называют
-функции, называют  -образными. Можно значительно ослабить свойства
-образными. Можно значительно ослабить свойства  сохранив
сохранив  -образность последовательности. Так, в теории рядов Фурье доказывается
-образность последовательности. Так, в теории рядов Фурье доказывается  -образность (например, в
-образность (например, в  ) последовательности ядер Дирихле:
) последовательности ядер Дирихле:

определяемых тем условием, что  есть сумма к первых членов ряда Фурье функции
есть сумма к первых членов ряда Фурье функции  при
при  . Аналогичным образом,
. Аналогичным образом,  -образную последовательность в
-образную последовательность в  образуют ядра Фейера
образуют ядра Фейера

определяемые из того условия, что  есть среднее арифметическое к первых частичных сумм ряда Фурье. В дальнейшем мы встретим и ряд других важных примеров
есть среднее арифметическое к первых частичных сумм ряда Фурье. В дальнейшем мы встретим и ряд других важных примеров  -образных последовательностей. Отметим, что по сути дела всегда и в более сложных ситуациях
-образных последовательностей. Отметим, что по сути дела всегда и в более сложных ситуациях  -образность доказывается тем же самым приёмом, что и для
-образность доказывается тем же самым приёмом, что и для  .
.
Пример 4.6. Обобщенные функции  .
.
«Обычные» функции  переменного
переменного  при
при  определяют обобщённые функции умеренного роста (элементы
определяют обобщённые функции умеренного роста (элементы  ). Оказывается, что в
). Оказывается, что в  существуют пределы
существуют пределы

(левые части здесь по определению равны пределам, написанным в правых частях).
Проверим, например, существование предела в  .
.
Нужно доказать, что если  то предел
то предел

существует и представляет собой линейный непрерывный функционал от  .
.
Это проще всего сделать, проведя интегрирование по частям. А именно, имеем

где ветвь  выбирается произвольно (но непрерывно при всех
выбирается произвольно (но непрерывно при всех  . Интегрирование по частям даёт теперь
. Интегрирование по частям даёт теперь

Поскольку  , то ясно, что по теореме Лебега правая часть (4.25) имеет при
, то ясно, что по теореме Лебега правая часть (4.25) имеет при  предел, равный
предел, равный

Поскольку  растет на бесконечности не быстрее
растет на бесконечности не быстрее  при любом
при любом  , то ясно, что в правой части (4.26) стоит конечная величина, задающая непрерывный функционал от
, то ясно, что в правой части (4.26) стоит конечная величина, задающая непрерывный функционал от  . Этот функционал и обозначается
. Этот функционал и обозначается
Изучим подробнее первое слагаемое в (4.26). Имеем

поскольку  . В частности мы доказали, что последний предел в (4.27) существует и задаёт функционал из
. В частности мы доказали, что последний предел в (4.27) существует и задаёт функционал из  . Этот функционал обозначается v. р. - (буквы v. р. — начальные буквы французских слов «valeur principale», что означает «главное значение»).
. Этот функционал обозначается v. р. - (буквы v. р. — начальные буквы французских слов «valeur principale», что означает «главное значение»).
Таким образом, по определению

Кроме того, теперь мы можем переписать (4.26) в виде

Аналогично получается, что

Формулы (4.29) и (4.30) называются формулами Сохоцкого. Из них вытекает, в частности, что

Существование пределов в (4.24) и в (4.28) можно также доказать, разложив  в сумму функции, равной
в сумму функции, равной  в окрестности точки 0 и функции, равной 0 в точке 0. Для каждого из слагаемых существование пределов легко проверяется. Таким образом можно получить и формулы Сохоцкого.
в окрестности точки 0 и функции, равной 0 в точке 0. Для каждого из слагаемых существование пределов легко проверяется. Таким образом можно получить и формулы Сохоцкого.
Обобщенные функции и v. р. — представляют собой различные «регуляризации» неинтегрируемой функции  , т. е. позволяют придать смысл расходящемуся интегралу
, т. е. позволяют придать смысл расходящемуся интегралу  . Мы видим, что это делается неоднозначно, так что неинтегрируемой функции — можно поставить в соответствие много обобщённых функций. Процедура регуляризации важна, если мы хотим использовать - как обобщённую функцию (например, если мы хотим её дифференцировать). Такая или подобная процедура применимы и ко многим другим неинтегрируемым функциям.
. Мы видим, что это делается неоднозначно, так что неинтегрируемой функции — можно поставить в соответствие много обобщённых функций. Процедура регуляризации важна, если мы хотим использовать - как обобщённую функцию (например, если мы хотим её дифференцировать). Такая или подобная процедура применимы и ко многим другим неинтегрируемым функциям.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
- § 2. Одномерное волновое уравнение
- 2.1. Уравнение колебании струны
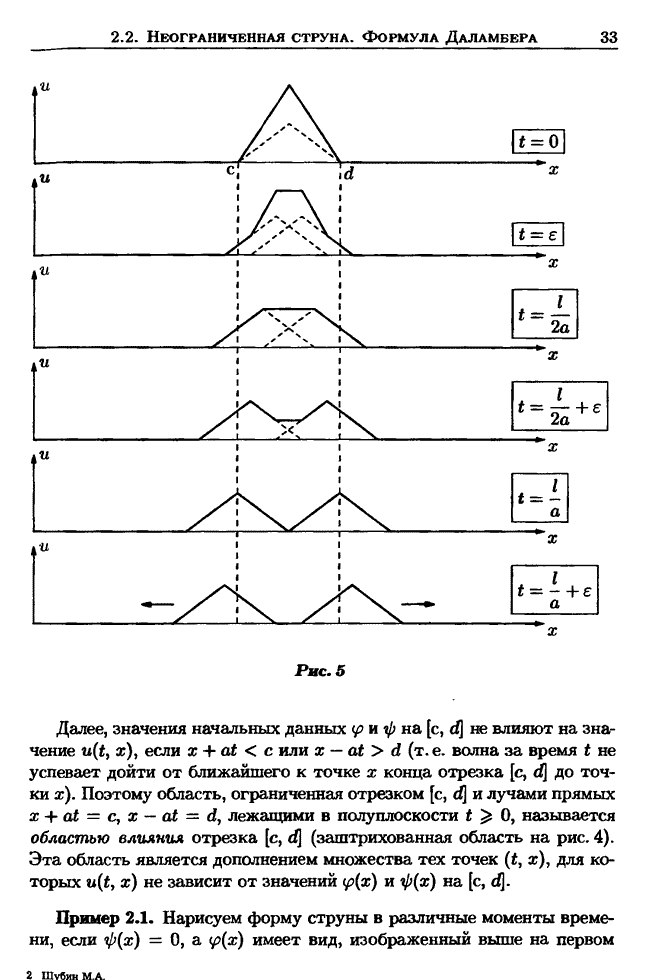
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
- 2.3. Полуограниченная струна. Отражение волн от конца струны
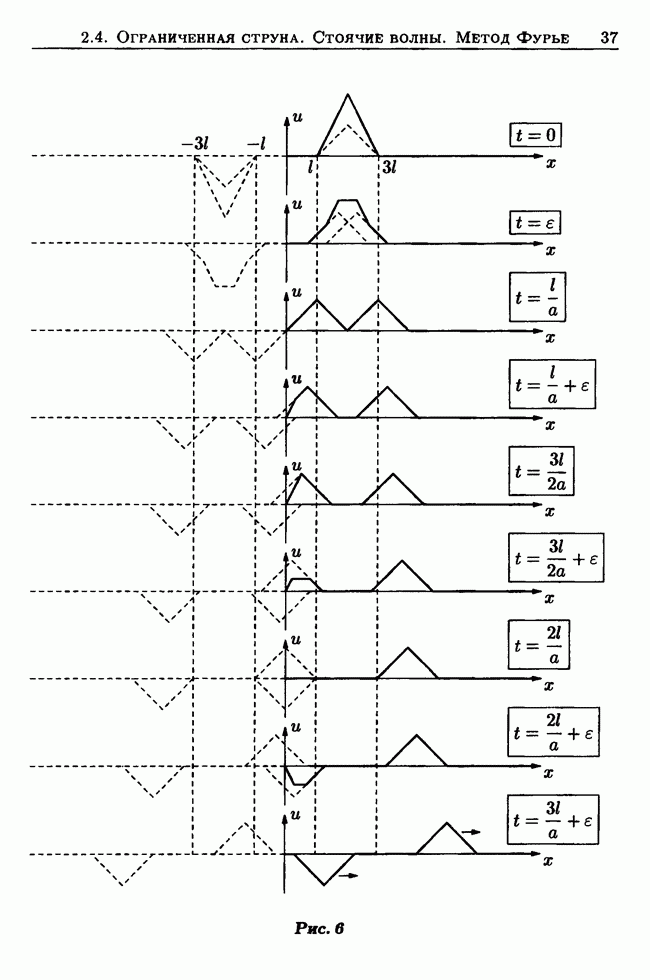
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
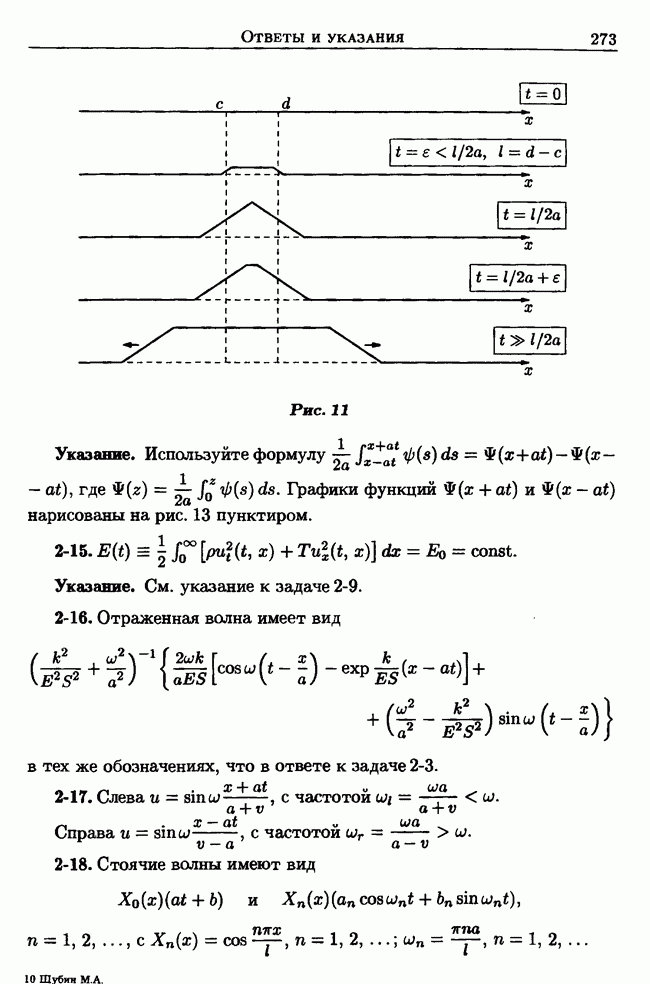
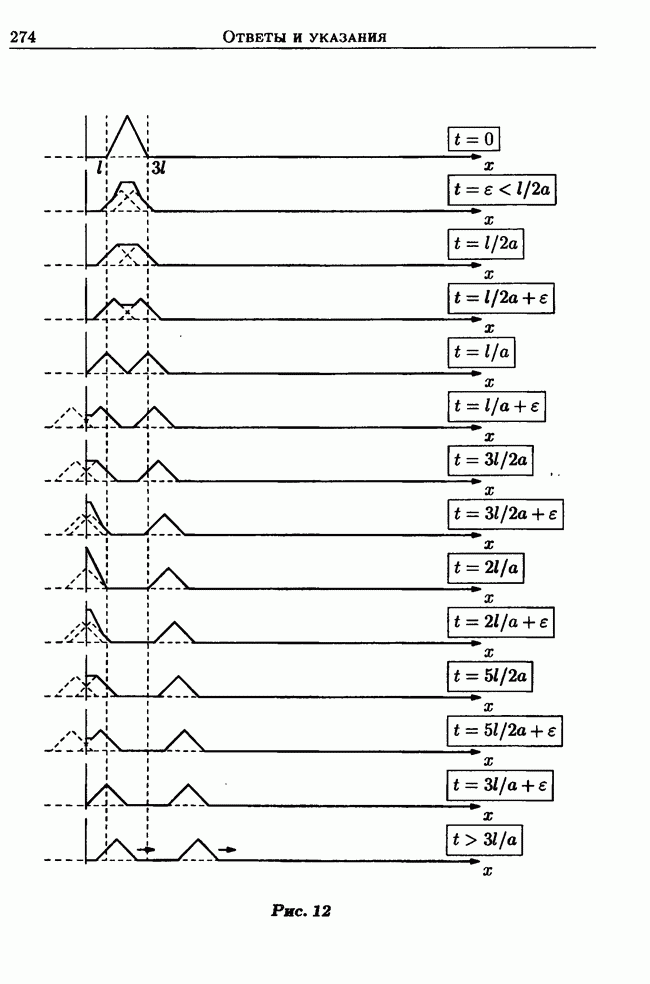
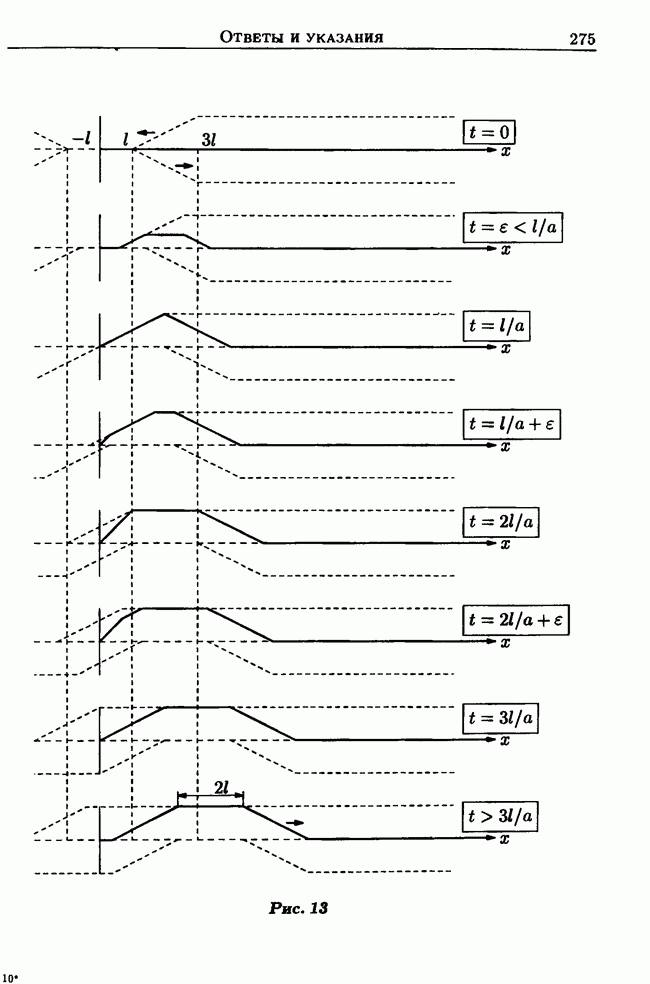
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
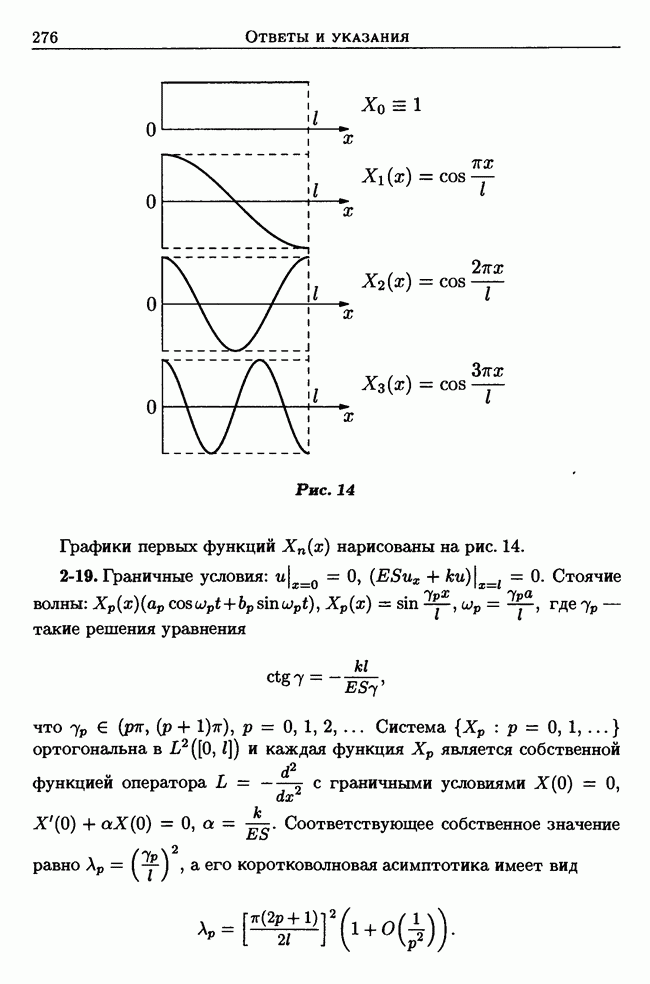
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы