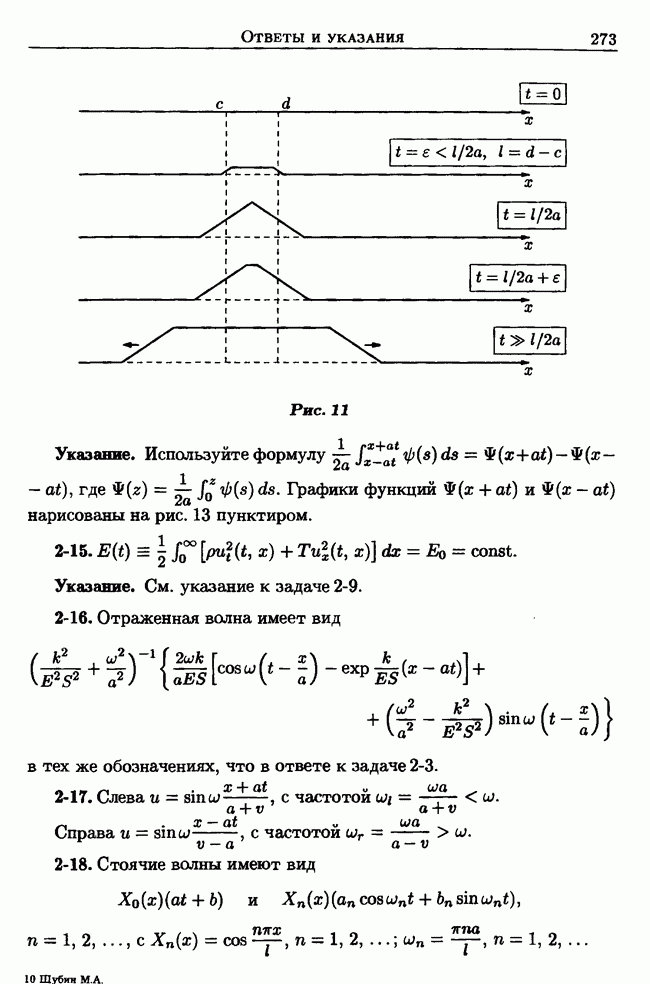
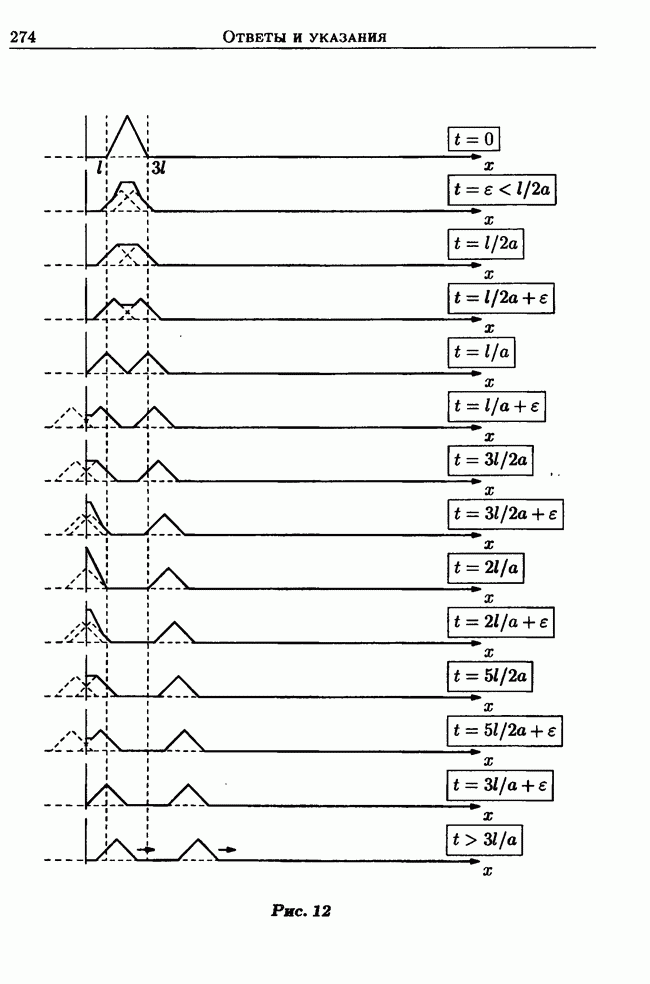
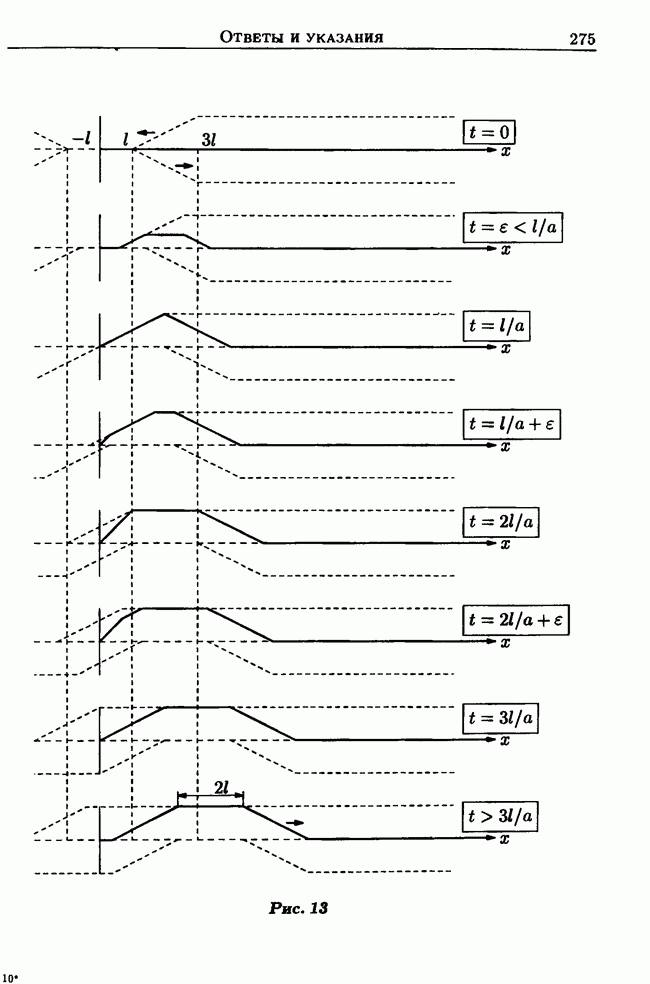
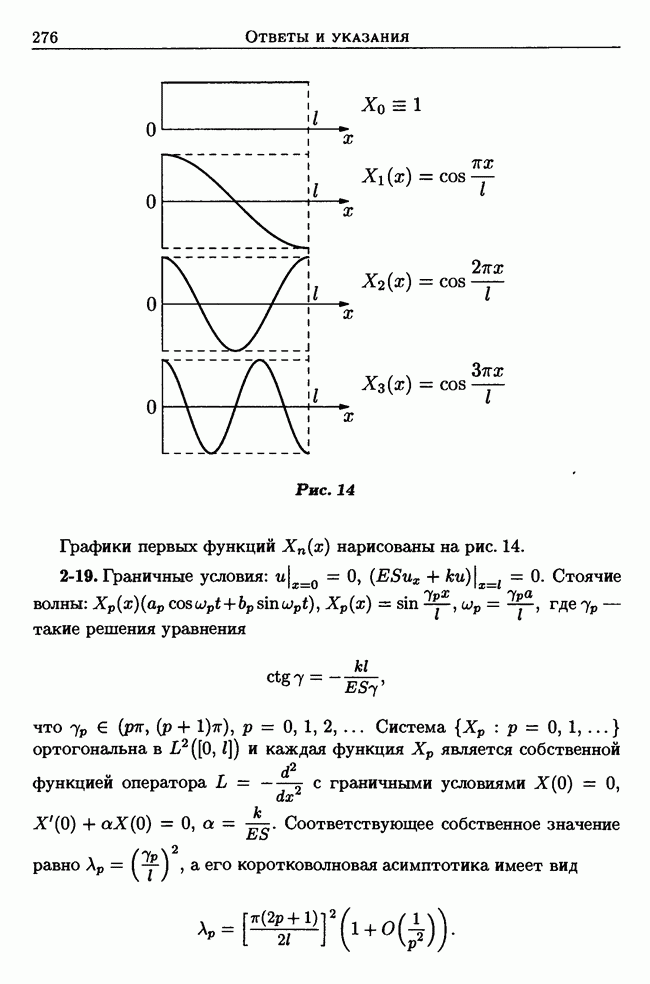
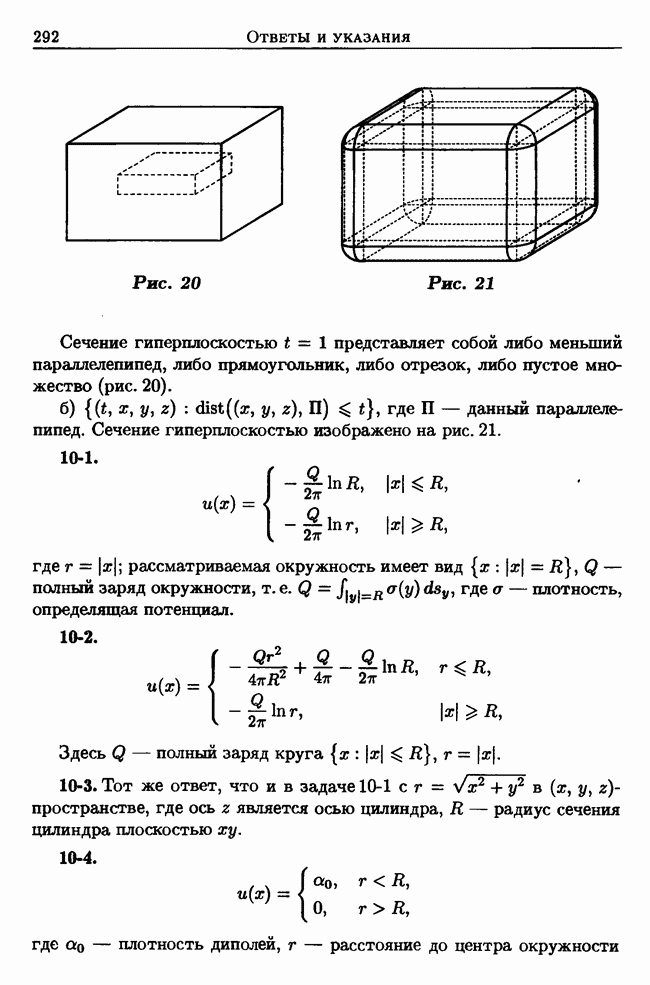
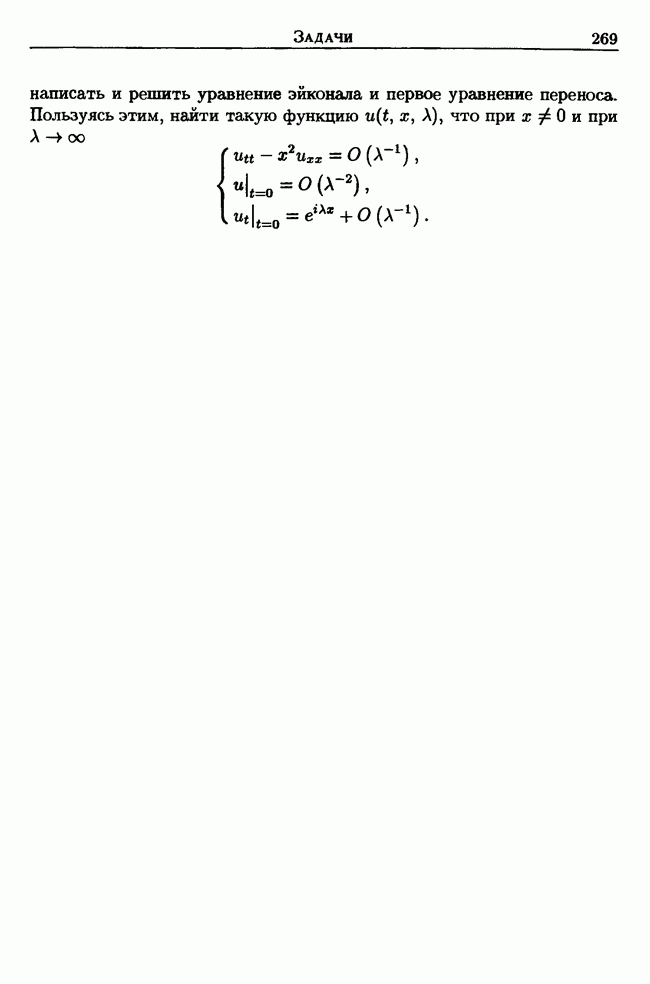| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Пространства Соболева. Обобщённое решение задачи Дирихле
7.1. Пространства
Пусть  — открытое подмножество в
— открытое подмножество в  .
.
Определение 7.1. Пространство Соболева  состоит из таких и
состоит из таких и  что
что  при
при  (а — мультииндекс), где производная понимается в смысле обобщённых Функций.
(а — мультииндекс), где производная понимается в смысле обобщённых Функций.
Введём в  скалярное произведение
скалярное произведение

где скобки  означают скалярное произведение в
означают скалярное произведение в  Введём также соответствующую норму
Введём также соответствующую норму

Ясно, что  при
при  . Далее,
. Далее,  . В частности, каждое пространство
. В частности, каждое пространство  вложено в
вложено в 
Предложение 7.2. Скаллрное произведение  определяет в
определяет в  структуру сепарабельного гильбертова пространства.
структуру сепарабельного гильбертова пространства.
Доказательство. Не очевидны лишь полнота и сепарабельность. Проверим полноту. Пусть последовательность фундаментальна  . Это означает в силу определения нормы
. Это означает в силу определения нормы  , что все последовательности (при
, что все последовательности (при  ) фундаментальны в
) фундаментальны в  . Но тогда в силу полноты пространства
. Но тогда в силу полноты пространства  они сходятся, т.е.
они сходятся, т.е.  по норме
по норме  . В частности,
. В частности,  . Но тогда
. Но тогда  , а поскольку, с другой стороны,
, а поскольку, с другой стороны,  , то
, то  Таким образом,
Таким образом,  при
при  . Но это и означает, что
. Но это и означает, что 
Проверим сепарабельность. Отображение и задаёт
изометричное вложение  в прямую сумму нескольких экземпляров пространства
в прямую сумму нескольких экземпляров пространства  . Теперь сепарабельность
. Теперь сепарабельность  вытекает из сепарабельности
вытекает из сепарабельности  .
.
Рассмотрим подробнее случай  . Пространство
. Пространство  можно описать в терминах преобразования Фурье (понимаемого в обобщённом смысле — в
можно описать в терминах преобразования Фурье (понимаемого в обобщённом смысле — в  ).
).
Напомним, что по теореме Планшереля преобразование Фурье

задает изометрию  на
на  , где пространство
, где пространство  строится по мере
строится по мере  . Поясним смысл этого утверждения и то, как оно выглядит с точки зрения теории обобщённых функций. Из курса анализа известно, что равенство Парсеваля
. Поясним смысл этого утверждения и то, как оно выглядит с точки зрения теории обобщённых функций. Из курса анализа известно, что равенство Парсеваля

выполнено при и  . Поскольку оператор F задаёт изоморфизм
. Поскольку оператор F задаёт изоморфизм  на
на  плотно в
плотно в  , то оператор F продолжается до изометрии
, то оператор F продолжается до изометрии  Поскольку из сходимости в
Поскольку из сходимости в  вытекает сходимость (слабая) в
вытекает сходимость (слабая) в  , то отображение
, то отображение  непрерывно в ограничениях слабых топологий
непрерывно в ограничениях слабых топологий  Поэтому оно на самом деле является ограничением обобщённого преобразования Фурье
Поэтому оно на самом деле является ограничением обобщённого преобразования Фурье

Заметим теперь, что преобразование Фурье переводит  Поэтому условие и
Поэтому условие и  — равносильно тому, что
— равносильно тому, что  при
при  Но вместо этого можно написать, что
Но вместо этого можно написать, что  Поскольку имеют место очевидные оценки
Поскольку имеют место очевидные оценки

где  не зависит от то условие
не зависит от то условие  равносильно тому, что
равносильно тому, что  , а норма (7.2) при
, а норма (7.2) при  эквивалентна норме
эквивалентна норме

которую мы будем обозначать так же, как и норму (7.3) (опасность путаницы не возникнет). Таким образом, доказано
Предложение 7.3. Пространство  состоит из тех и только тех и
состоит из тех и только тех и  , для которых
, для которых

а норма в нём может быть задана формулой (7.4).
Это предложение может служить основой для определения пространств  при любом действительном s. А именно, при любом
при любом действительном s. А именно, при любом  мы можем составить пространство тех и
мы можем составить пространство тех и  что
что  введя на нём норму (7.4). Мы снова получим сепарабельное гильбертово пространство, которое и обозначается
введя на нём норму (7.4). Мы снова получим сепарабельное гильбертово пространство, которое и обозначается 
В дальнейшем нам понадобится банахово пространство  (здесь к
(здесь к  ), состоящее из функций и
), состоящее из функций и  производные которых
производные которых  к, ограничены при всех
к, ограничены при всех  Норма в
Норма в  задается формулой
задается формулой

Теорема 7.4 (теорема вложения С. Л. Соболева). При  к имеет место вложение
к имеет место вложение

причём оператор вложения непрерывен.
Поясним формулировку теоремы. На первый взгляд кажется, что она бессмысленна, поскольку функцию и  можно как угодно изменять на любом множестве меры нуль, не меняя соответствующей обобщённой функции (и элемента пространства
можно как угодно изменять на любом множестве меры нуль, не меняя соответствующей обобщённой функции (и элемента пространства  ). Изменяя же функцию и во всех точках с рациональными координатами, мы можем добиться того, что она будет всюду разрывной.
). Изменяя же функцию и во всех точках с рациональными координатами, мы можем добиться того, что она будет всюду разрывной.
Поэтому включение (7.6) следовало бы более точно формулировать так: если  , то существует и единственна функция
, то существует и единственна функция  совпадающая с исходной функцией
совпадающая с исходной функцией  почти всюду (для краткости вместо
почти всюду (для краткости вместо  мы снова будем писать u). Заметим, что единственность непрерывного представителя очевидна, так как в любой окрестности точки
мы снова будем писать u). Заметим, что единственность непрерывного представителя очевидна, так как в любой окрестности точки  найдутся точки любого множества полной меры, так что изменение непрерывной функции на множестве меры нуль приводит к функции, которая разрывна во всяком случае во всех точках, где произошло изменение.
найдутся точки любого множества полной меры, так что изменение непрерывной функции на множестве меры нуль приводит к функции, которая разрывна во всяком случае во всех точках, где произошло изменение.
Доказательство теоремы 7.4. Докажем вначале, что имеет место оценка

где постоянная С не зависит от u. Удобнее всего действовать с помощью преобразования Фурье. Имеем:

откуда

и, следовательно,

Деля и умножая подынтегральное выражение на  и используя неравенство Коши-Буняковского, мы получаем:
и используя неравенство Коши-Буняковского, мы получаем:

Интеграл в первом из двух сомножителей сходится в силу того, что  , следовательно, подынтегральная функция при
, следовательно, подынтегральная функция при  убывает быстрее, чем при достаточно малом
убывает быстрее, чем при достаточно малом  Второй же сомножитель равен
Второй же сомножитель равен  . В итоге при
. В итоге при  получаем неравенство (7.7).
получаем неравенство (7.7).
Заметим теперь, что  плотно в
плотно в  при любом
при любом  . В самом деле, введём оператор
. В самом деле, введём оператор  умножающий преобразование Фурье
умножающий преобразование Фурье  на
на  .
.
Этот оператор изоморфно и изометрично отображает  на
на  переводя
переводя  изоморфно на
изоморфно на  . Поэтому плотность
. Поэтому плотность  вытекает из плотности
вытекает из плотности  .
.
Пусть теперь  . Но из неравенства (7.7) следует, что последовательность
. Но из неравенства (7.7) следует, что последовательность  фундаментальна по норме
фундаментальна по норме  Следовательно,
Следовательно,  . Но тогда v и
. Но тогда v и  совпадают как обобщённые функции, и, следовательно, почти всюду. Неравенство (7.7) по непрерывности верно при всех и
совпадают как обобщённые функции, и, следовательно, почти всюду. Неравенство (7.7) по непрерывности верно при всех и  что доказывает непрерывность вложения (7.6).
что доказывает непрерывность вложения (7.6).
В частности, теорема 7.4 показывает, что для функций и  при
при  имеет смысл говорить об их значениях в точке.
имеет смысл говорить об их значениях в точке.
Интересен также вопрос о том, когда имеет смысл ограничение на подмногообразие произвольной размерности. Однако нам он в общем виде не понадобится и мы обсудим лишь наиболее важный случай многообразия коразмерности 1. Для простоты обсудим просто случай гиперплоскости  Точку
Точку  будем записывать в виде
будем записывать в виде  , где
, где  .
.
Теорема 7.5 (теорема С. Л. Соболева о следах). Оператор ограничения и  при
при  продолжается (с
продолжается (с  ) до линейного непрерывного отображения
) до линейного непрерывного отображения

Доказательство. Запишем оператор ограничения через преобразование Фурье (для и  ):
):

Отсюда видно, что если через F обозначить преобразование Фурье по  , то мы получим:
, то мы получим:

Положим для краткости  , так что
, так что

Требуемое утверждение записывается в виде оценки

где  означает норму в пространстве
означает норму в пространстве  , а С не зависит от u. Докажем эту оценку. Имеем:
, а С не зависит от u. Докажем эту оценку. Имеем:

Из (7.8) находим при любом  :
:

Оценим первый сомножитель. Имеем:

(мы воспользовались здесь тем, что  благодаря чему последний интеграл сходится). Таким образом, (7.11) записывается в виде
благодаря чему последний интеграл сходится). Таким образом, (7.11) записывается в виде

Используя это неравенство для оценки  мы получаем требуемую оценку (7.9).
мы получаем требуемую оценку (7.9).
Замечание. На самом деле оператор ограничения и  является эпиморфизмом
является эпиморфизмом  на
на  (см., например, Хёрмандер [55-2, гл. II]), так что утверждение теоремы является точным (индекс
(см., например, Хёрмандер [55-2, гл. II]), так что утверждение теоремы является точным (индекс  не может быть увеличен).
не может быть увеличен).
Теорема 7.5 означает, что если  , то корректно определён след
, то корректно определён след  функции и на гиперплоскости
функции и на гиперплоскости  и он является элементом
и он является элементом  .
.
Получать его нужно так: представить и в виде предела  по норме
по норме  функций
функций  . Тогда следы
. Тогда следы  при
при  имеют предел по норме
имеют предел по норме  в пространстве
в пространстве  причем этот предел не зависит от выбора аппроксимирующей последовательности.
причем этот предел не зависит от выбора аппроксимирующей последовательности.
При желании ограничиться целыми значениями s можно воспользоваться тем, что  . Таким образом, след
. Таким образом, след  функции и
функции и  принадлежит
принадлежит  .
.
Можно определить пространства  , где М — гладкое компактное многообразие (без края). А именно будем писать, что и
, где М — гладкое компактное многообразие (без края). А именно будем писать, что и  если для любого координатного диффеоморфизма
если для любого координатного диффеоморфизма  (здесь U — область в
(здесь U — область в  — область в
— область в  ) и для любой функции
) и для любой функции  имеет место включение
имеет место включение  Здесь и о
Здесь и о  — это обобщённая функция и, перенесённая на О с помощью диффеоморфизма
— это обобщённая функция и, перенесённая на О с помощью диффеоморфизма  . Она умножается на
. Она умножается на  чтобы получилась обобщённая функция, носитель которой лежит в
чтобы получилась обобщённая функция, носитель которой лежит в  . Тем самым,
. Тем самым,  в частности
в частности  так что имеет смысл говорить о включении
так что имеет смысл говорить о включении  Локализация позволяет, например, доказать следующий аналог теоремы 7.5: если
Локализация позволяет, например, доказать следующий аналог теоремы 7.5: если  — ограниченная область с гладкой границей
— ограниченная область с гладкой границей  , то при
, то при  оператор ограничения и продолжается
оператор ограничения и продолжается  до линейного непрерывного оператора
до линейного непрерывного оператора 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
- § 2. Одномерное волновое уравнение
- 2.1. Уравнение колебании струны
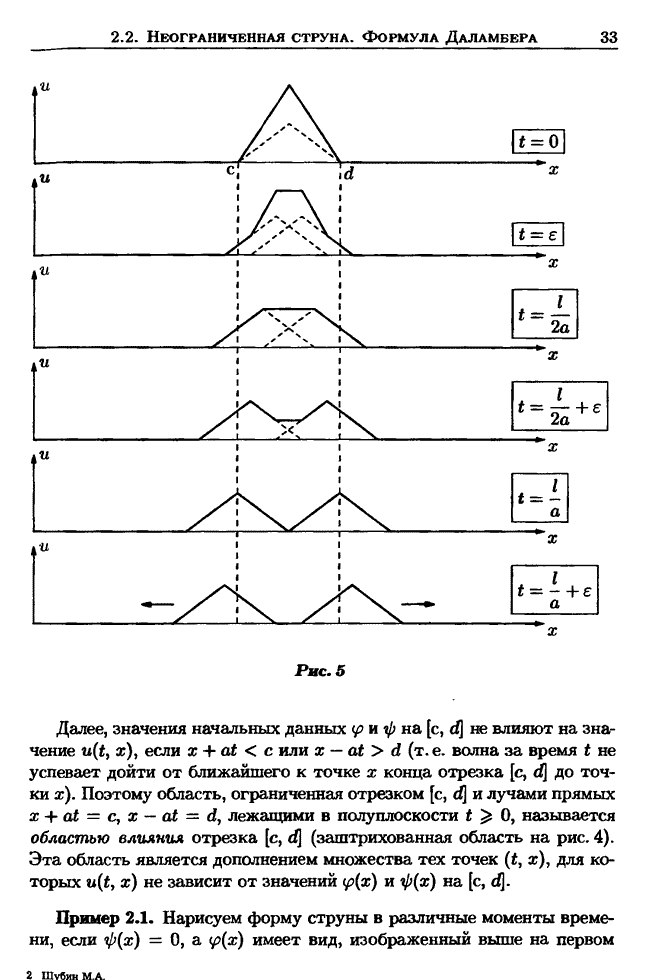
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
- 2.3. Полуограниченная струна. Отражение волн от конца струны
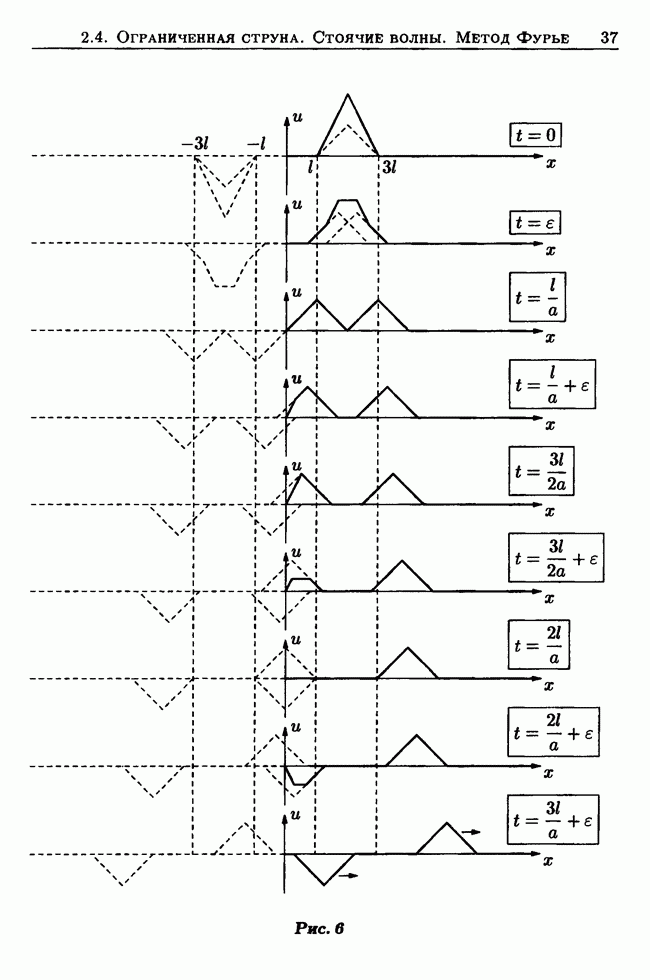
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы