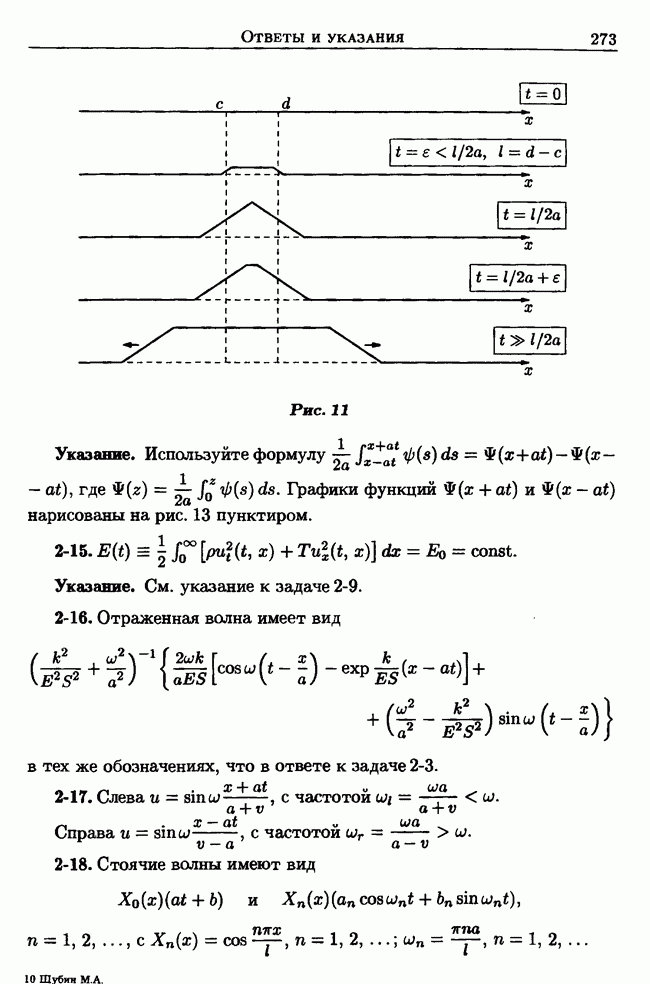
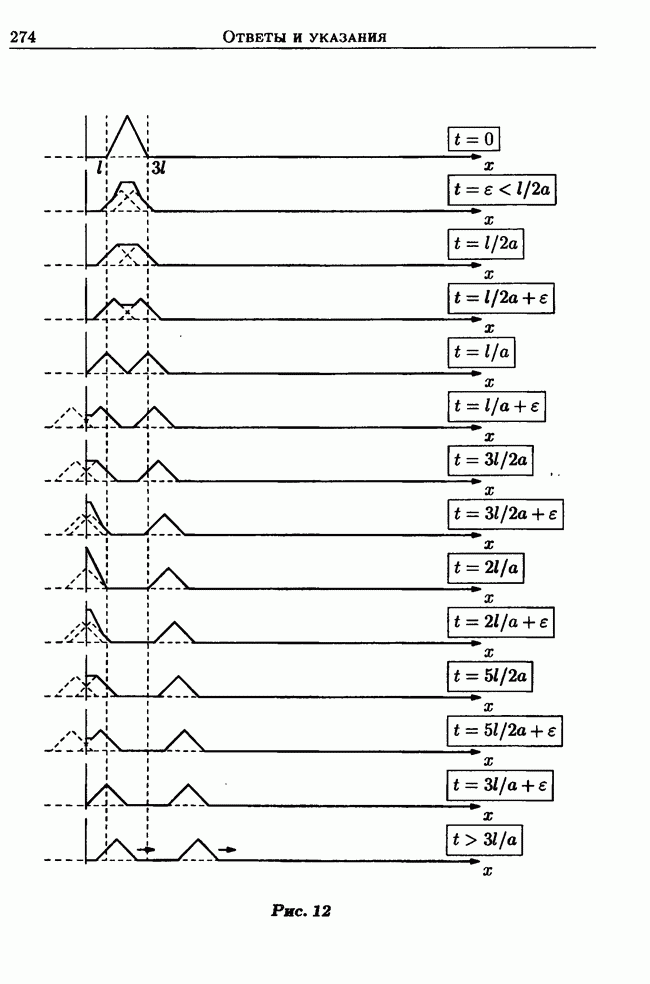
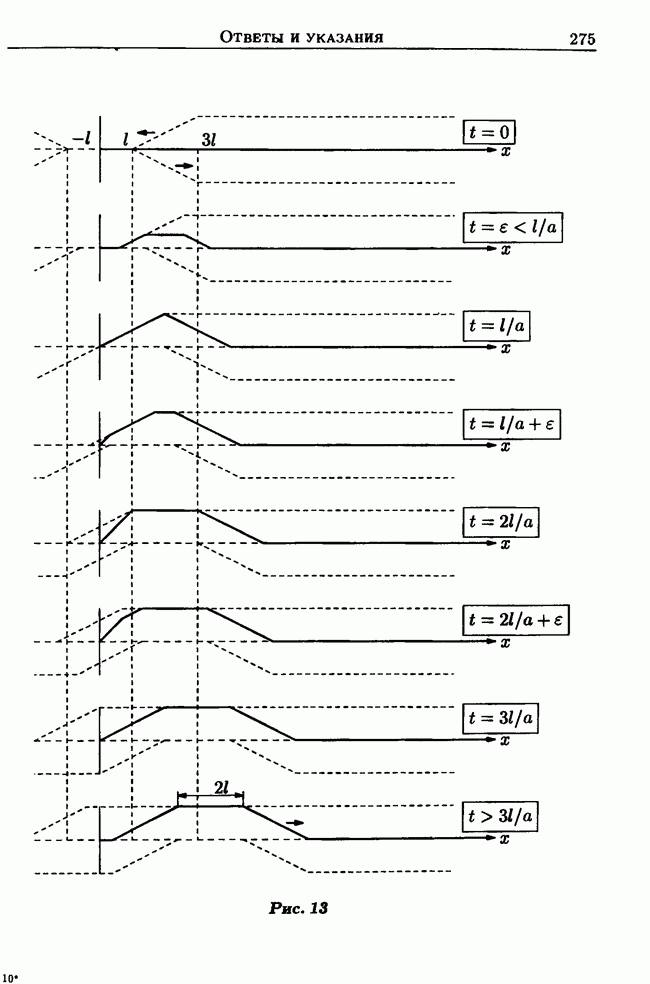
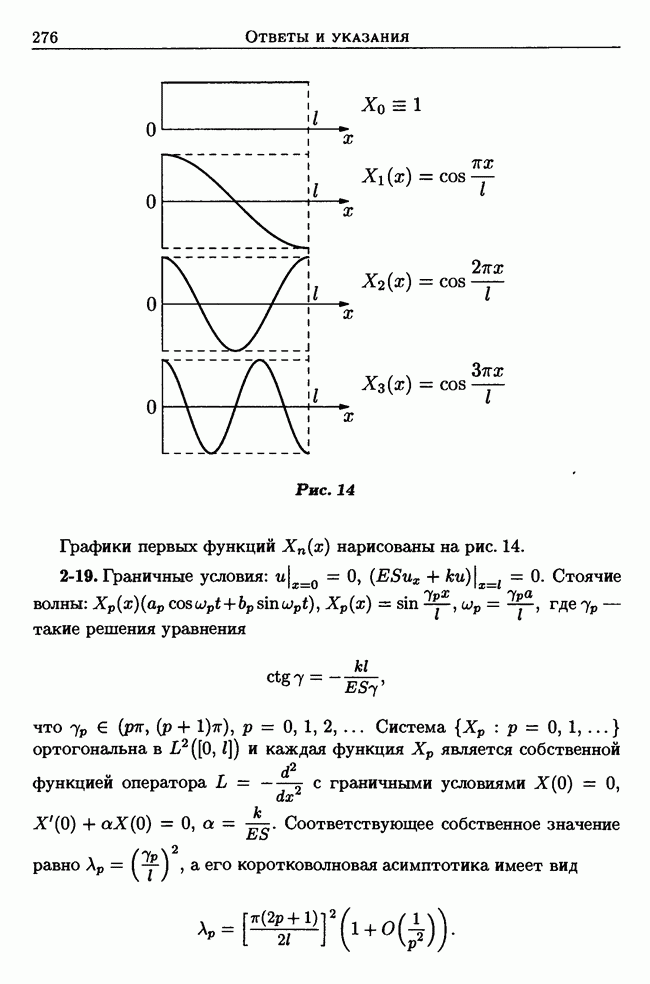
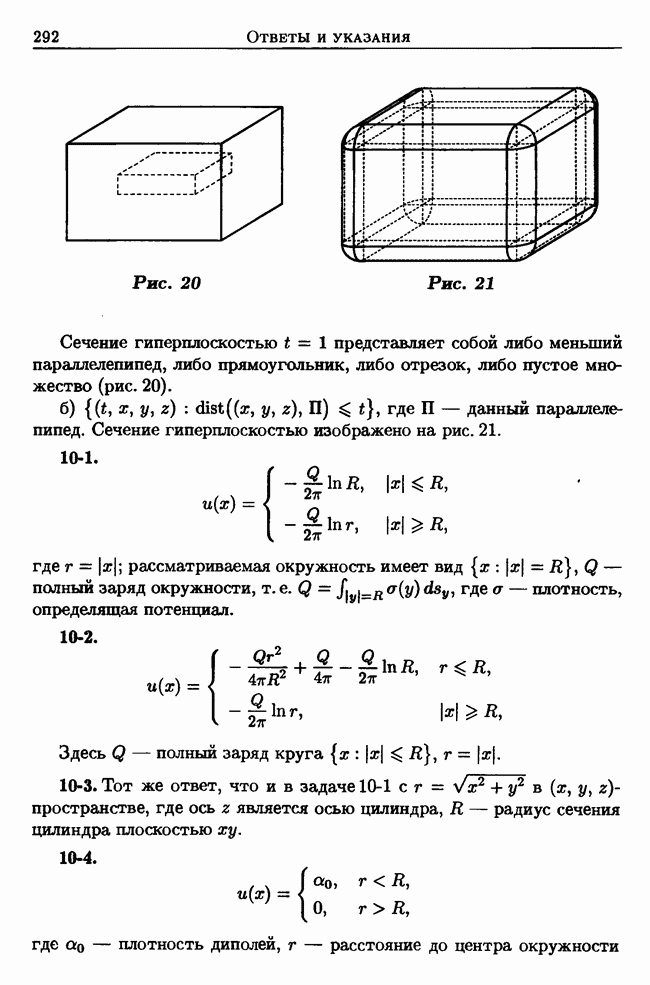
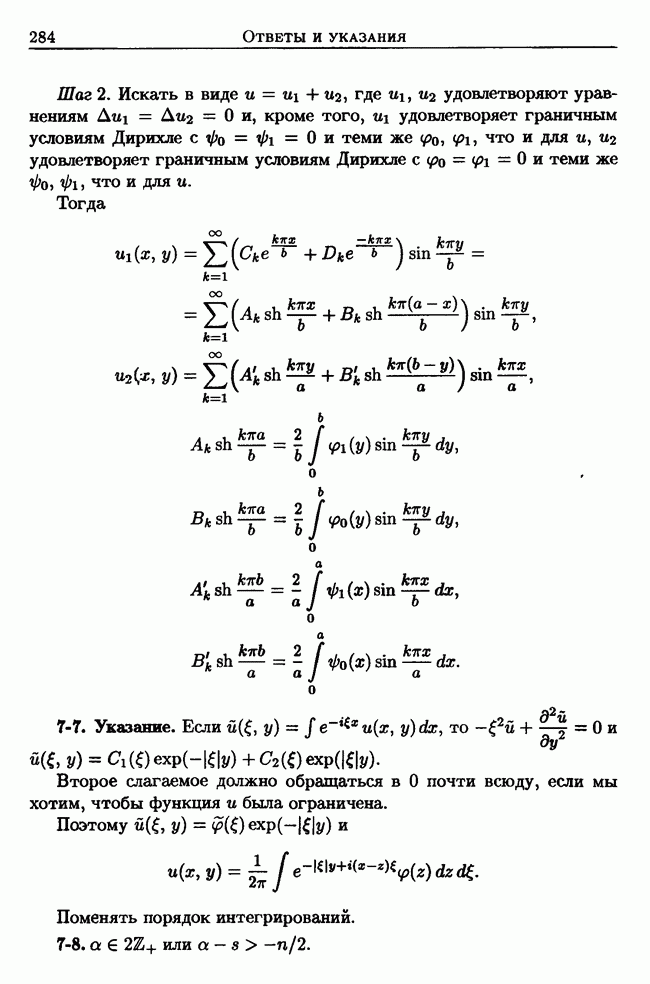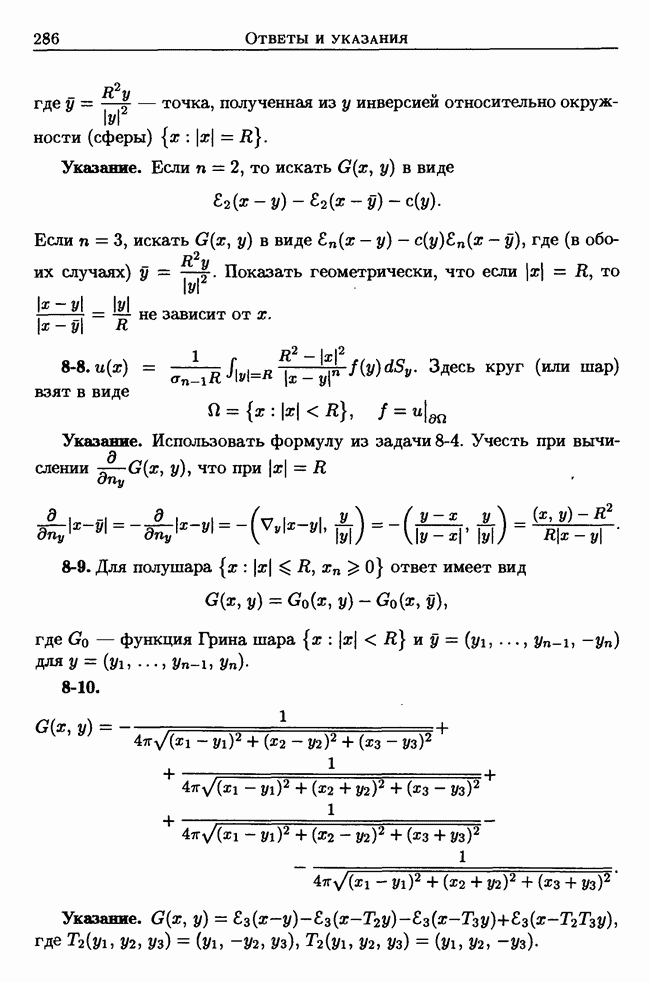| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.9. Теорема Лиувилля
Теорема 5.19. Пусть оператор  имеет символ
имеет символ  обращающийся в 0 (при
обращающийся в 0 (при  ) лишь в точке
) лишь в точке  . Тогда если и
. Тогда если и  , то
, то  — многочлен по переменному
— многочлен по переменному  . В частности, если
. В частности, если  , где
, где  — ограниченная измеримая функция на
— ограниченная измеримая функция на  то
то  .
.
Замечание, а) Условие  выполнено, например, если
выполнено, например, если  при каких-нибудь С и N.
при каких-нибудь С и N.
б) Если  при некотором
при некотором  , то уравнение
, то уравнение  имеет ограниченное решение не являющееся постоянным. Поэтому условие
имеет ограниченное решение не являющееся постоянным. Поэтому условие  при
при  необходимо для справедливости теоремы.
необходимо для справедливости теоремы.
в) Если  при всех
при всех  , то из условия
, то из условия  при
при  вытекает, как будет видно из доказательства теоремы, что
вытекает, как будет видно из доказательства теоремы, что  .
.
Доказательство теоремы 5.19. Применяя преобразование Фурье, получаем:

Поскольку  при
при  , то ясно, что
, то ясно, что  сосредоточена в точке 0.
сосредоточена в точке 0.
Подробнее: если  то
то  , а отсюда следует, что
, а отсюда следует, что

Итак,  . Поэтому
. Поэтому

Но отсюда

что и требовалось.
Пример. Если  — гармоническая функция всюду на
— гармоническая функция всюду на  , то
, то  (это утверждение часто называют теоремой Лиувилля для гармонических функций). Если и
(это утверждение часто называют теоремой Лиувилля для гармонических функций). Если и  гармонична на
гармонична на  и
и  то
то  — многочлен. Те же утверждения верны для решений уравнения
— многочлен. Те же утверждения верны для решений уравнения  .
.
Для гармонических функций можно доказать более точное утверждение: если и гармонична и ограничена с одной стороны, т.е. и  то
то  (см., например, Петровский [43]). Это утверждение неверно уже для уравнения
(см., например, Петровский [43]). Это утверждение неверно уже для уравнения  которому удовлетворяет неотрицательный многочлен и
которому удовлетворяет неотрицательный многочлен и  .
.
Приведем один пример применения теоремы Лиувилля. Пусть при n 3 нам дана функция  определенная и гармоническая во внешности некоторого шара, т. е. при
определенная и гармоническая во внешности некоторого шара, т. е. при  причём
причём  при
при  . Мы хотим описать поведение
. Мы хотим описать поведение  при
при  более детально. Для этого можно поступить, например, следующим образом. Выберем функцию
более детально. Для этого можно поступить, например, следующим образом. Выберем функцию  так, что
так, что  при
при  при
при  . Теперь рассмотрим функцию
. Теперь рассмотрим функцию  равную
равную  при
при  и 0 при
и 0 при  . Ясно, что
. Ясно, что  . Проверим, что
. Проверим, что

где  — стандартное фундаментальное решение оператора Лапласа.
— стандартное фундаментальное решение оператора Лапласа.
Ясно, что  при
при  , а по предположению то же самое верно для
, а по предположению то же самое верно для  значит, для
значит, для  поскольку
поскольку  при
при  . Кроме того,
. Кроме того,

так что  всюду на
всюду на  . Но по теореме Лиувилля отсюда получается, что
. Но по теореме Лиувилля отсюда получается, что  , что и требовалось. Формула (5.57) может быть записана в виде
, что и требовалось. Формула (5.57) может быть записана в виде

Из явного вида  вытекает теперь, например, что
вытекает теперь, например, что

Приведённое рассуждение применимо и в более общих ситуациях. Для гармонических функций же более детальную информацию о поведении  при
при  можно получить с помощью так называемого преобразования Кельвина. Это преобразование переводит функцию
можно получить с помощью так называемого преобразования Кельвина. Это преобразование переводит функцию  в функцию
в функцию  и сохраняет гармоничность функции (при
и сохраняет гармоничность функции (при  это замена переменной, индуцированная инверсией). Если
это замена переменной, индуцированная инверсией). Если  определена при больших
определена при больших  то
то  определена в проколотой окрестности точки 0, т.е.
определена в проколотой окрестности точки 0, т.е.  , где
, где  — окрестность точки
— окрестность точки  при
при  то мы видим, что
то мы видим, что  при
при  , а тогда по теореме об устранимой особенности
, а тогда по теореме об устранимой особенности  гармонична всюду в
гармонична всюду в  .
.
Заметим, что преобразование Кельвина обратно самому себе (или, как говорят, является инволюцией), т.е. наоборот можно выразить u через v той же формулой  . Разлагая
. Разлагая  в ряд Тейлора при
в ряд Тейлора при  мы видим, что
мы видим, что  в окрестности бесконечности имеет сходящееся разложение в ряд вида
в окрестности бесконечности имеет сходящееся разложение в ряд вида

В частности, ясно, что при 

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- § 1. Линейные дифференциальные операторы
- 1.2. Полный и главный символы
- 1.3. Замена переменной
- 1.4. Приведение к каноническому виду операторов 2-го порядка с постоянными коэффициентами
- 1.5. Характеристики. Эллиптичность и гиперболичность
- 1.6. Характеристики и приведение к каноническому виду операторов и уравнении 2-го порядка при n = 2
- 1.7. Общее решение однородного гиперболического уравнения с постоянными коэффициентами при n = 2
- § 2. Одномерное волновое уравнение
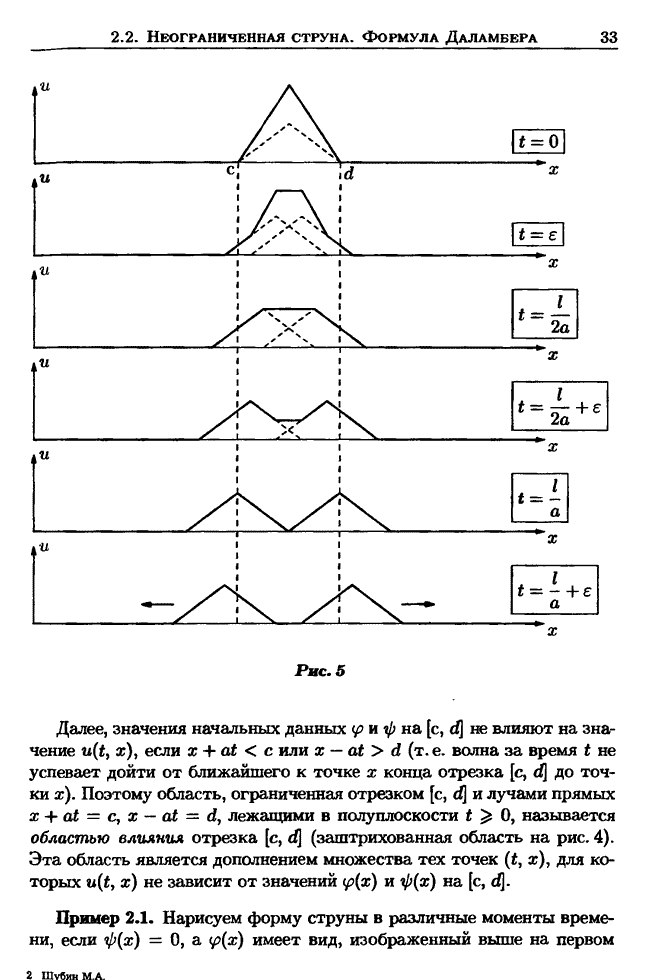
- 2.1. Уравнение колебании струны
- 2.2. Неограниченная струна. Задача Каши. Формула Даламбера
- 2.3. Полуограниченная струна. Отражение волн от конца струны
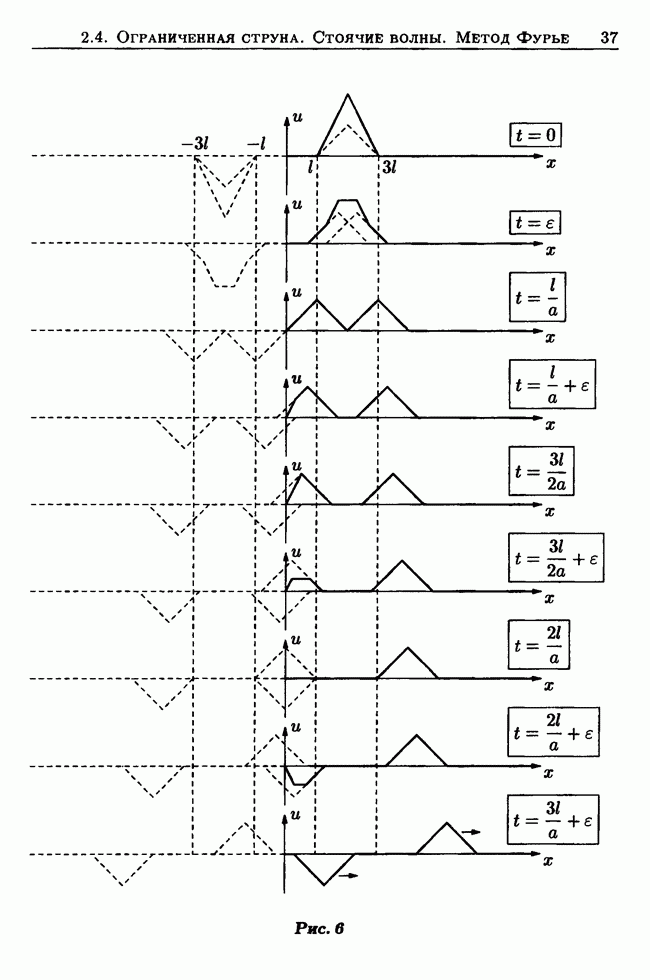
- 2.4. Ограниченная струна. Стоячие волны. Метод Фурье (метод разделения переменных)
- Задачи
- § 3. Задача Штурма-Лиувилля
- 3.2. Простейшие свойства собственных значении и собственных функций
- 3.3. Коротковолновая асимптотика
- 3.4. Функция Грина и полнота системы собственных функций
- Задачи
- § 4. Обобщённые функции
- 4.1. Мотивировка определения. Пространства основных функций
- 4.2. Пространства обобщённых функции
- 4.3. Топология и сходимость в пространствах обобщённых функций
- 4.4. Носитель обобщённой функции
- 4.5. Дифференцирование обобщённых функции и их умножение на гладкую функцию
- 4.6. Общее понятие транспонированного оператора. Замена переменных. Однородные обобщённые функции
- Задачи
- § 5. Свёртка и преобразование Фурье
- 5.1. Свёртка и прямое произведение обычных функций
- 5.2. Прямое произведение обобщённых функций
- 5.3. Свёртка обобщённых функций
- 5.4. Дальнейшие свойства свертки. Носитель и носитель сингулярности свёртки
- 5.5. Связь между свойствами гладкости фундаментального решения и решений однородного уравнения
- 5.6. Решения с изолированными особенностями. Теорема об устранимой особенности для гармонических функций
- 5.7. Преобразование Фурье обобщённых функций умеренного роста
- 5.8. Схема применения преобразования Фурье для нахождения фундаментальных решении
- 5.9. Теорема Лиувилля
- Задачи
- § 6. Уравнение теплопроводности
- 6.1. Физический смысл уравнения теплопроводности
- 6.2. Простейшие краевые задачи для уравнения теплопроводности и уравнения Лапласа
- 6.3. Пример обоснования гармоничности предельной функции
- 6.4. Решение задачи Коши для уравнения теплопроводности. Интеграл Пуассона
- 6.5. Фундаментальное решение для оператора теплопроводности. Формула Дюамеля
- 6.6. Оценка производных решения гипоэллиптического уравнения
- 6.7. Принцип Хольмгрена. Единственность решения задачи Коши для уравнения теплопроводности
- 6.8. Схема решения первой и второй краевых задач методом Фурье
- Задачи
- § 7. Пространства Соболева. Обобщённое решение задачи Дирихле
- 7.2. Пространства
- 7.3. Интеграл Дирихле. Неравенство Фридрихса
- 7.4. Задача Дирихле (обобщённое решение)
- Задачи
- § 8. Собственные значения и собственные функции оператора Лапласа
- 8.1. Симметрические и самосопряженные операторы в гильбертовом пространстве
- 8.2. Расширение по Фридрихсу
- 8.3. Дискретность спектра оператора Лапласа в ограниченной области
- 8.4. Фундаментальное решение оператора Гельмгольца и аналитичность собственных функции оператора Лапласа во внутренних точках области. Уравнение Бесселя
- 8.5. Вариационные принципы. Поведение собственных значений при изменении области. Оценки собственных значений
- Задачи
- § 9. Волновое уравнение
- 9.1. Физические задачи, приводящие к волновому уравнению
- 9.2. Плоские, сферические и цилиндрические волны
- 9.3. Волновое уравнение как гамильтонова система
- 9.4. Сферическая волна от мгновение» вспышки и решение задачи Коши для трехмерного волнового уравнения
- 9.5. Фундаментальное решение трёхмерного волнового оператора и решение неоднородного волнового уравнения
- 9.6. Двумерное волновое уравнение (метод спуска)
- Задачи
- § 10. Свойства потенциалов и их вычисление
- 10.2. Функции, гладкие вплоть до Г с каждой стороны, и их производные
- 10.3. Скачки потенциалов
- 10.4. Вычисление потенциалов
- Задачи
- § 11. Волновые фронты и коротковолновое приближение для гиперболических уравнений
- 11.1. Характеристики, как поверхности разрывов
- 11.2. Уравнение Гамильтона — Якоби. Волновые франты, бихарактеристики и лучи
- 11.3. Характеристики гиперболического уравнения
- 11.4. Быстро осциллирующие решения. Уравнение эйконала и уравнения переноса
- 11.5. Задача Коши с быстро осциллирующими начальными данными
- Задачи
- Ответы и указания
- Список литературы