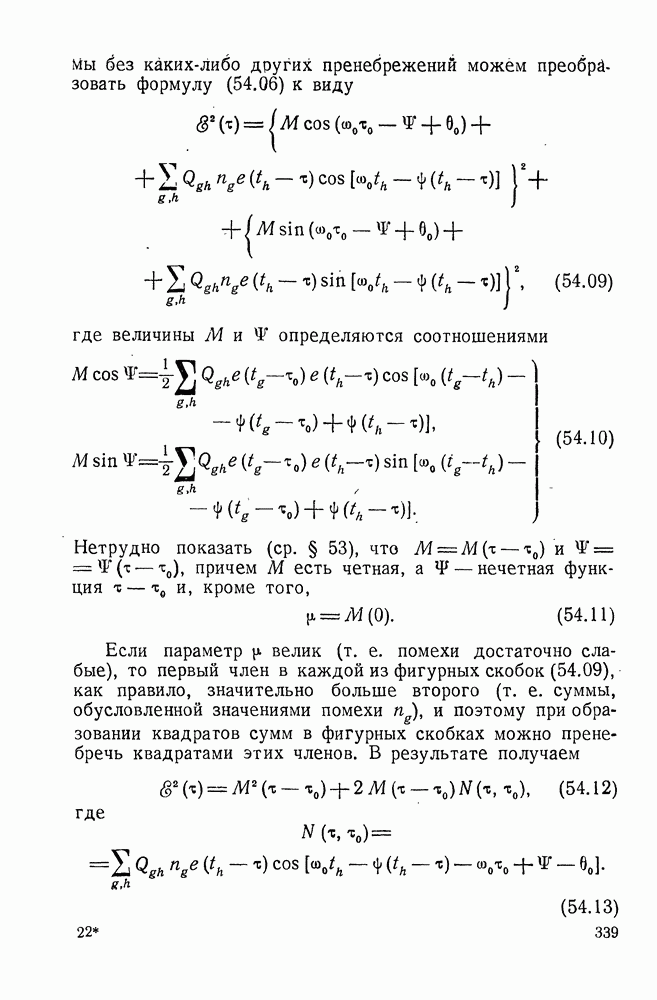| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9. ОПРЕДЕЛЕНИЕ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ОПТИМАЛЬНОГО ФИЛЬТРА II ТИПА
В § 8 мы свели уравнение (8.03) для оптимального фильтра II типа к двум соотношениям (8.17) и (8.18). В дальнейшем мы будем считать, что функции  являются аналитическими в пределах полосы
являются аналитическими в пределах полосы

охватывающей вещественную ось, причем функция  в этой полосе нигде не обращается в нуль. В частности предполагается, что при всех вещественных со
в этой полосе нигде не обращается в нуль. В частности предполагается, что при всех вещественных со

В дальнейшем (см. § 11) мы от этих ограничений попытаемся избавиться, однако в данном параграфе мы будем на них опираться.
Применим теперь лемму I к соотношениям (8.17) и (8.18). Будем считать, что  удовлетворяют лемме I также и в отношении поведения на бесконечности, иначе выписанные интегралы не имели бы смысла. По лемме I можно написать
удовлетворяют лемме I также и в отношении поведения на бесконечности, иначе выписанные интегралы не имели бы смысла. По лемме I можно написать

Есл 1 взять в лемме I полосу, расположенную ниже вещественной оси  то для нее формула (8.17) дает
то для нее формула (8.17) дает

и, следовательно,

Аналогичным образом для полосы, лежащей выше вещественной оси  из соотношения (8.18) получаем
из соотношения (8.18) получаем

и

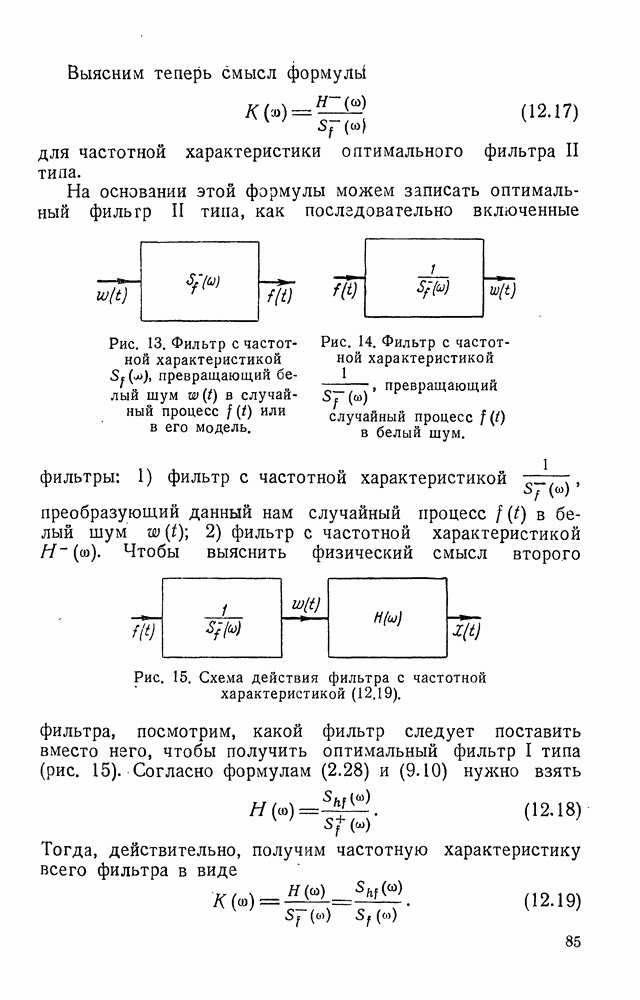
Это значит, что для оптимального фильтра функция  должна быть аналитической функцией во всей верхней полуплоскости,
должна быть аналитической функцией во всей верхней полуплоскости,  аналитической во всей нижней полуплоскости. Мы показали необходимость этого, опираясь на соотношения (8.17) и (8.18). Достаточность этих условий для соотношений (8.17) и (8.18) легко доказывается с помошью теоремы Коши, а для соотношений (8.11) и (8.13) на основании леммы Жордана, если функции
аналитической во всей нижней полуплоскости. Мы показали необходимость этого, опираясь на соотношения (8.17) и (8.18). Достаточность этих условий для соотношений (8.17) и (8.18) легко доказывается с помошью теоремы Коши, а для соотношений (8.11) и (8.13) на основании леммы Жордана, если функции  убывают равномерно на бесконечности в тех полуплоскостях, где они являются аналитическими Действительно, в силу аналитичности функции
убывают равномерно на бесконечности в тех полуплоскостях, где они являются аналитическими Действительно, в силу аналитичности функции  в верхней полуплоскости мы можем преобразовать интеграл по прямолиней ному контуру в левой части формулы (8.13) в интеграл по бесконечной полуокружности С (рис. 8)
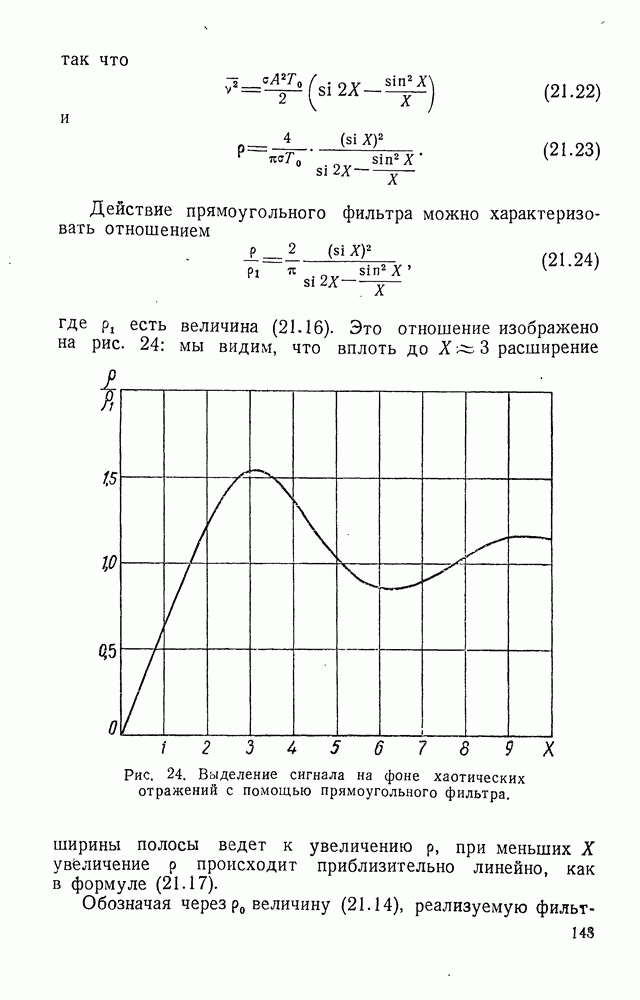
в верхней полуплоскости мы можем преобразовать интеграл по прямолиней ному контуру в левой части формулы (8.13) в интеграл по бесконечной полуокружности С (рис. 8)

Он равен нулю при  если функция
если функция  убывает на бесконечности. Это соотношение удовлетворяется и при
убывает на бесконечности. Это соотношение удовлетворяется и при  если
если  убывает быстрее, чем —
убывает быстрее, чем —  тогда интеграл по полуокружности исчезает и при
тогда интеграл по полуокружности исчезает и при  Если функция
Если функция  на бесконечности исчезает равномерно, то к ней тоже можно применить лемму Жордана и написать
на бесконечности исчезает равномерно, то к ней тоже можно применить лемму Жордана и написать

при  где
где  полуокружность в нижней полуплоскости.
полуокружность в нижней полуплоскости.
Таким образом, мы приходим к следующим требованиям:
А. Функция  должна быть аналитической в нижней полуплоскости
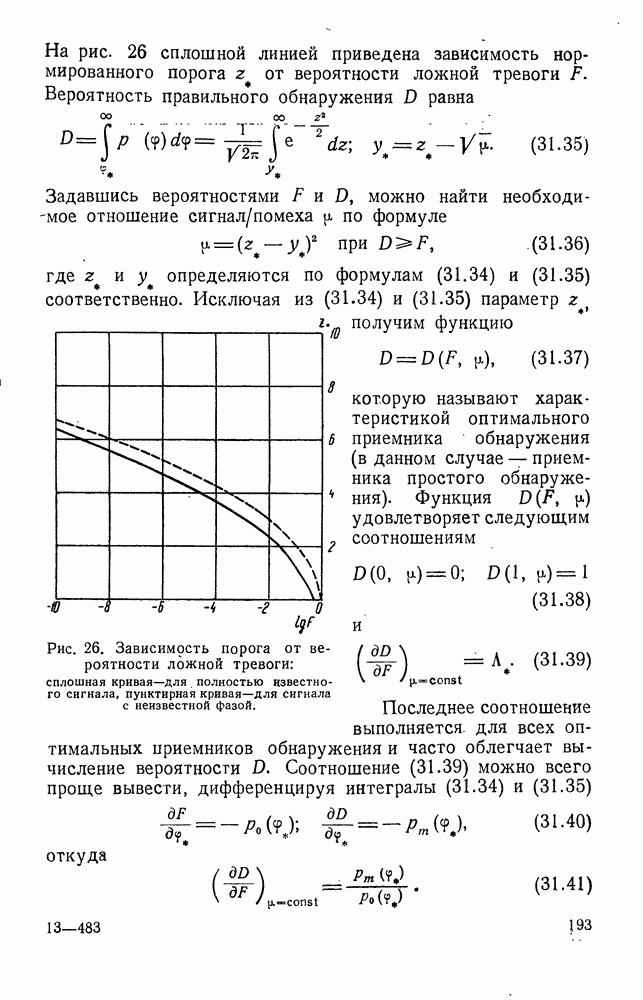
должна быть аналитической в нижней полуплоскости  и исчезать при
и исчезать при  равномерно (в этой полуплоскости). В соответствии с формулой (8.09) частотная характеристика
равномерно (в этой полуплоскости). В соответствии с формулой (8.09) частотная характеристика  должна представлять собой
должна представлять собой
аналитическую функцию в нижней полуплоскости и расти в ней не быстрее некоторого полинома 
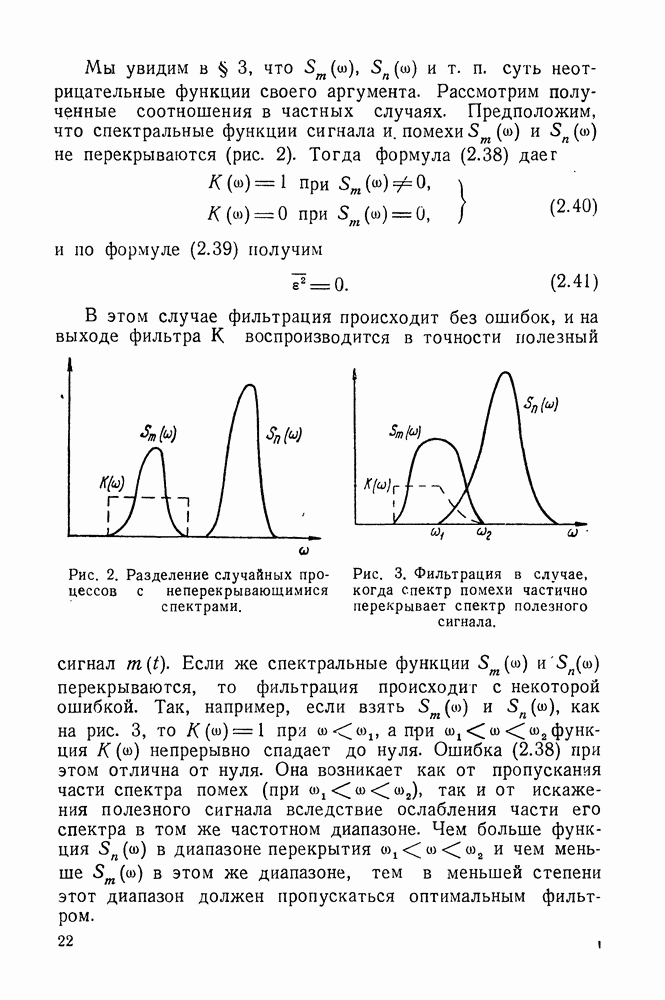
В. Функция  должна быть аналитической фунцией в верхней полуплоскости
должна быть аналитической фунцией в верхней полуплоскости  и должна в ней убывать при
и должна в ней убывать при  быстрее, чем
быстрее, чем 
Из требований  можно получить решение задачи, которое выражается через вспомогательные функции
можно получить решение задачи, которое выражается через вспомогательные функции  произведение которых равно данной функции
произведение которых равно данной функции  т. е.
т. е.

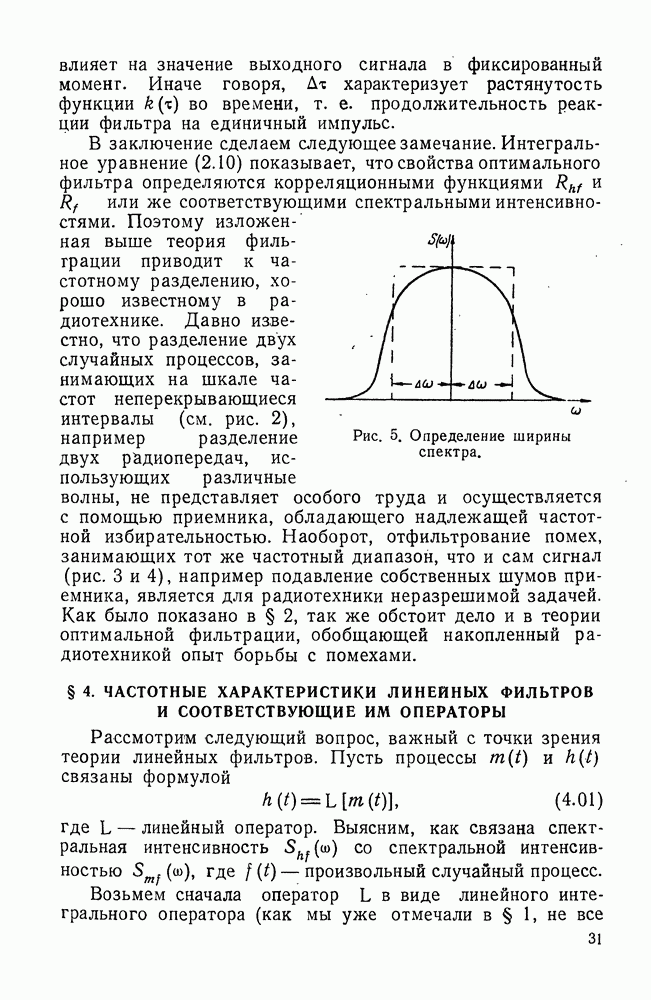
где  подобно функции
подобно функции  являются аналитическими в полосе (9.01) и не имеют в ней нулей, кроме того функция
являются аналитическими в полосе (9.01) и не имеют в ней нулей, кроме того функция  является аналитической и не обращается в нуль во всей верхней полуплоскости (при
является аналитической и не обращается в нуль во всей верхней полуплоскости (при  а функция
а функция  обладает теми же свойствами в нижней полуплоскости (при
обладает теми же свойствами в нижней полуплоскости (при 
Разумеется, это разбиение на множители неоднозначно, и формулу (9.10) нужно чем-то дополнить, чтобы точно определить  и
и  Известно [см. формулу (3.02)], что
Известно [см. формулу (3.02)], что  есть четная функция
есть четная функция  Поэтому
Поэтому

Отсюда естественно принять, что

Будем считать, что на бесконечности в нашей полосе функция  убывает, как где
убывает, как где  и с — положительная постоянная. Это значит, что
и с — положительная постоянная. Это значит, что

Чтобы фактически найти  введем функцию
введем функцию

где  — произвольное число, большее
— произвольное число, большее  Будем считать, что при вещественных значениях со функция
Будем считать, что при вещественных значениях со функция  тоже вещественна, для чего возьмем главную ветвь логарифма. Кроме того,
тоже вещественна, для чего возьмем главную ветвь логарифма. Кроме того,  аналитическая функция в пределах полосы. Поэтому лемма I применима к
аналитическая функция в пределах полосы. Поэтому лемма I применима к  ибо
ибо  при
при 
Используя формулу (9.10) и тождество

Получим

Первый логарифм формулы (9.16) является функцией, аналитической в верхней полуплоскости, второй логарифм является функцией, аналитической в нижней полуплоскости. Иначе говоря, в силу формулы (8.23) можно положить

откуда функции  и
и  получаются в виде
получаются в виде

причем сами функции  определяются формулами (8.26).
определяются формулами (8.26).
Недостаток этих формул в том, что в них входит произвольное число  и что они выведены при условии (9.13). В дальнейшем мы постараемся избавиться от этих ограничений.
и что они выведены при условии (9.13). В дальнейшем мы постараемся избавиться от этих ограничений.
Функции  и определенные формулами (9.18), обладают свойствами, сформулированными выше. Таким образом, лемма I позволила разбить функцию
и определенные формулами (9.18), обладают свойствами, сформулированными выше. Таким образом, лемма I позволила разбить функцию  по формуле (9.10). В дальнейшем мы всюду будем под
по формуле (9.10). В дальнейшем мы всюду будем под  понимать выражения (9.18). На бесконечности (в тех
понимать выражения (9.18). На бесконечности (в тех
полуплоскостях, где они являются аналитическими) они удовлетворяют предельным соотношениям

Выписанные выше формулы на первый взгляд довольно сложны. Однако в приложениях часто можно взять  в виде рациональной функции, т. е. отношения двух полиномов
в виде рациональной функции, т. е. отношения двух полиномов  формулу (4.33)]
формулу (4.33)]

Это — полиномы степени а и  от
от  поскольку они должны быть четными функциями
поскольку они должны быть четными функциями  Будем считать, что
Будем считать, что

и

Тогда функцию  можно представить в виде произведения
можно представить в виде произведения

и функции  равны
равны

Здесь мы через  обозначили корни знаменателя и числителя, находящихся в верхней полуплоскости
обозначили корни знаменателя и числителя, находящихся в верхней полуплоскости  а через
а через  и
и  корни в нижней полуплоскости. Действительно, выражения (9.24) удовлетворяют соотношениям (9.10), (9.12) и (9.19) и поэтому совпадают с выражениями (9.18).
корни в нижней полуплоскости. Действительно, выражения (9.24) удовлетворяют соотношениям (9.10), (9.12) и (9.19) и поэтому совпадают с выражениями (9.18).
В силу формулы (9.10) мы имеем

откуда получаем соотношение

в котором  — известные функции,
— известные функции,  и
и  -неизвестные. Значит, левая часть соотношения (9.26) — известная функция, которую мы обозначим через
-неизвестные. Значит, левая часть соотношения (9.26) — известная функция, которую мы обозначим через  а правая — неизвестная, причем первое слагаемое по условию А есть функция, аналитическая в нижней полуплоскости, а второе слагаемое по условию В — функция, аналитическая в верхней полуплоскости. Из свойств функций
а правая — неизвестная, причем первое слагаемое по условию А есть функция, аналитическая в нижней полуплоскости, а второе слагаемое по условию В — функция, аналитическая в верхней полуплоскости. Из свойств функций  и
и  вытекает, что
вытекает, что  удовлетворяет условиям леммы 1, кроме, быть может, условия о поведении на бесконечности. Если последнее условие также выполняется, то функцию
удовлетворяет условиям леммы 1, кроме, быть может, условия о поведении на бесконечности. Если последнее условие также выполняется, то функцию  можно представить согласно лемме I в виде
можно представить согласно лемме I в виде

где  есть функция, аналитическая в верхней полуплоскости,
есть функция, аналитическая в верхней полуплоскости,  нижней. Если отождествить слагаемые в правых частях формул (9.26) и (9.27), являющиеся аналитическими функциями в тех же полуплоскостях, то мы получим
нижней. Если отождествить слагаемые в правых частях формул (9.26) и (9.27), являющиеся аналитическими функциями в тех же полуплоскостях, то мы получим

так что

причем

Если мы определим функции  с помощью формул (9.29), то, очевидно, они будут аналитическими в тех полуплоскостях, где это требуется по условиям А и В. В отношении поведения на бесконечности условие В выполняется, поскольку функции
с помощью формул (9.29), то, очевидно, они будут аналитическими в тех полуплоскостях, где это требуется по условиям А и В. В отношении поведения на бесконечности условие В выполняется, поскольку функции  обе убывают на бесконечности в верхней полуплоскости, а условие А будет выполнено, если
обе убывают на бесконечности в верхней полуплоскости, а условие А будет выполнено, если  и
и  рациональные функции.
рациональные функции.
Рассмотрим теперь случай, когда  рациональные функции, но функция Я И не убывает на
рациональные функции, но функция Я И не убывает на
бесконечности. Тогда ее можно представить в виде суммы двух функций — полинома  и функции
и функции  уже удовлетворяющей всем условиям леммы I
уже удовлетворяющей всем условиям леммы I

Мы образуем  по лемме 1, полагаем
по лемме 1, полагаем

и опять определяем функции  с помощью
с помощью  мул (9.29). Проверим теперь условие В в отношении поведения на бесконечности. Пусть функции
мул (9.29). Проверим теперь условие В в отношении поведения на бесконечности. Пусть функции  на бесконечности удовлетворяют соотношениям (9.13) и (9.19). Считая, что
на бесконечности удовлетворяют соотношениям (9.13) и (9.19). Считая, что  убывает, как (где 1), мы будем иметь
убывает, как (где 1), мы будем иметь

и

так что функция  действительно удовлетворяет условию В. Условие
действительно удовлетворяет условию В. Условие  в отношении поведения на бесконечности автоматически выполняется, поскольку спектральные интенсивности суть рациональные функции.
в отношении поведения на бесконечности автоматически выполняется, поскольку спектральные интенсивности суть рациональные функции.
В предыдущем изложении мы не учли одного существенного обстоятельства, без которого задача будет неоднозначной и решение (9.29) — лишь одним из возможных. Действительно, наряду с разбиением функции  выбранным выше, можно взять другое разбиение
выбранным выше, можно взять другое разбиение

в котором функции  являются аналитическими в тех же полуплоскостях, что и
являются аналитическими в тех же полуплоскостях, что и  но ведут себя на бесконечности иначе. Сравнивая последнее выражение со взятым выше разбиением (6.27), мы будем иметь
но ведут себя на бесконечности иначе. Сравнивая последнее выражение со взятым выше разбиением (6.27), мы будем иметь

где левая часть — аналитическая функция в верхней полуплоскости, правая часть — в нижней. Поэтому обе части равенства (9.36) являются аналитической функцией во всей плоскости комплексного неременного со.
Воспользуемся теперь теоремой Лиувилля, которую можно сформулировать так: если функция — аналитическая во всей плоскости комплексного переменного  то она или неограниченно возрастает при
то она или неограниченно возрастает при  или сводится к постоянной. Поэтому функция
или сводится к постоянной. Поэтому функция  уже не будет убывать на бесконечности, а будет расти или стремиться к постоянному пределу.
уже не будет убывать на бесконечности, а будет расти или стремиться к постоянному пределу.
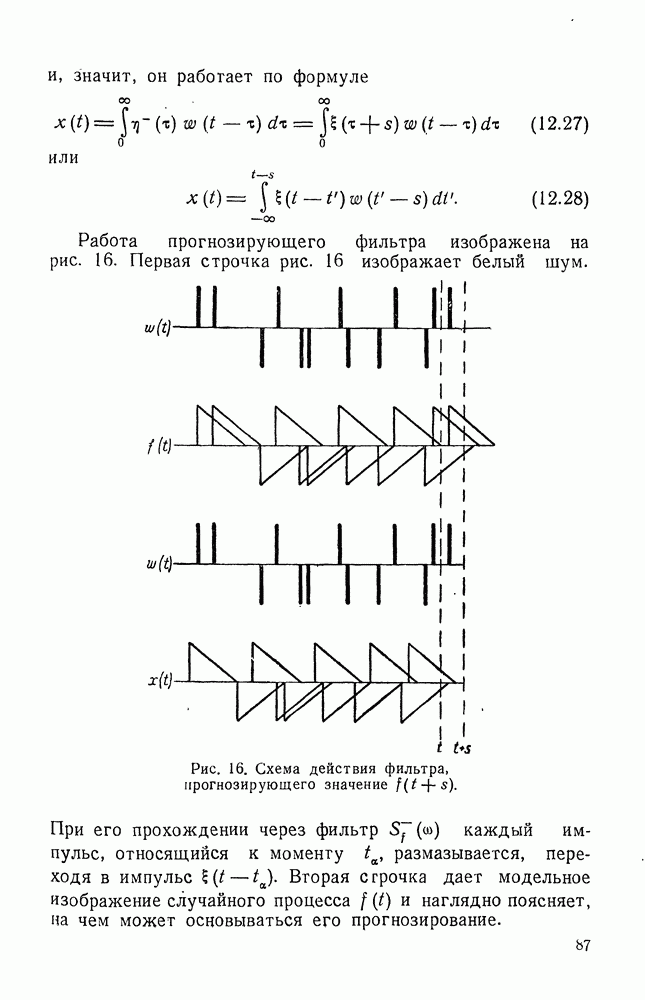
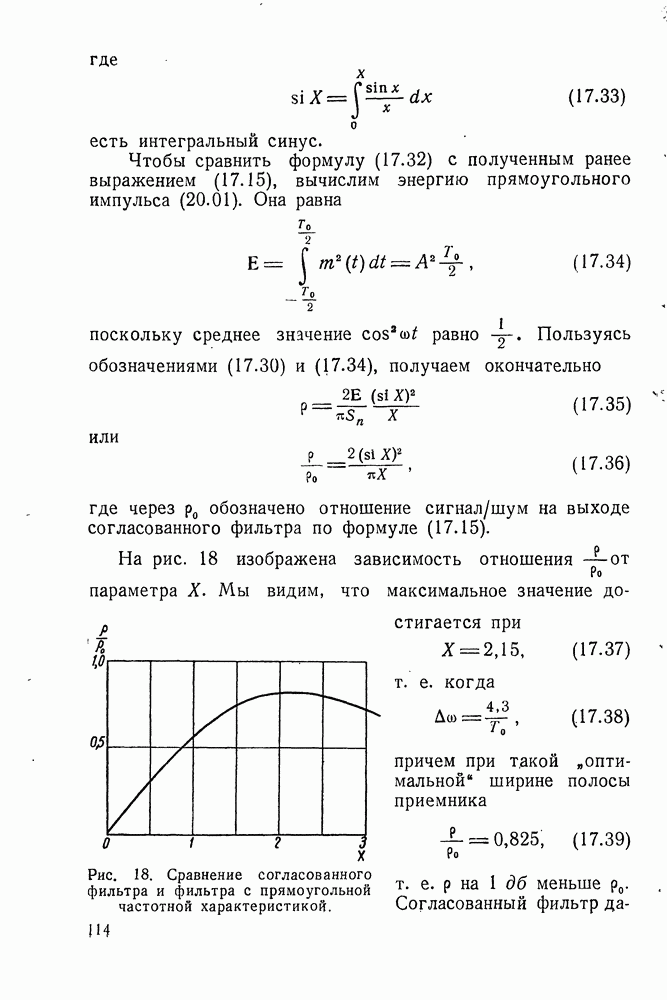
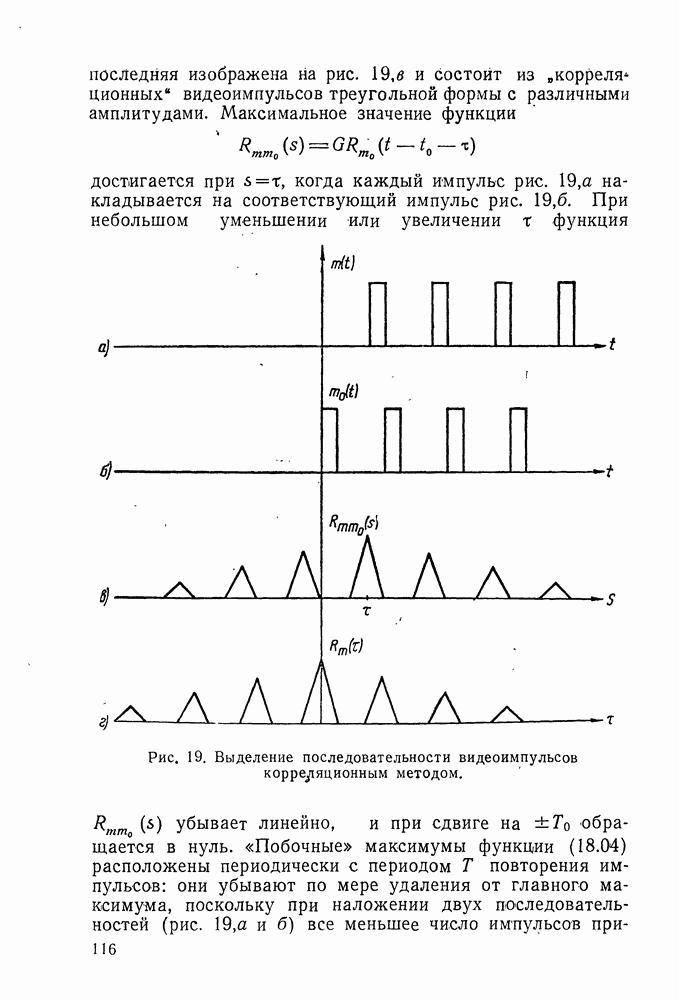
Вычислим интенсивность процесса на выходе оптимального фильтра

входящую в выражение (5.26) для средней квадратичной ошибки. При вещественных значениях со мы имеем тождество

которое будет обосновано ниже (см. § 11). Поэтому формулы (9.29) и (9.37) дают

так что для получения конечного значения  (без чего найденное решение никакого смысла не имеет), функция
(без чего найденное решение никакого смысла не имеет), функция  должна убывать при
должна убывать при  быстрее, чем
быстрее, чем 
Функции  определяемые формулами (9.30) и (9.32), этому условию удовлетворяют, в то время как любая другая функция о которой мы говорили выше, будет давать
определяемые формулами (9.30) и (9.32), этому условию удовлетворяют, в то время как любая другая функция о которой мы говорили выше, будет давать  Условие
Условие

как раз и обеспечивает однозначность нашей задачи, по крайней мере в рамках данного метода ее решения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. СТАТИСТИЧЕСКАЯ ТЕОРИЯ ОПТИМАЛЬНЫХ ЛИНЕЙНЫХ ФИЛЬТРОВ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФИЛЬТРАЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 2. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ОПТИМАЛЬНОГО ЛИНЕЙНОГО ФИЛЬТРА
- § 3. КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ И СПЕКТРАЛЬНЫЕ ИНТЕНСИВНОСТИ
- § 4. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ФИЛЬТРОВ И СООТВЕТСТВУЮЩИЕ ИМ ОПЕРАТОРЫ
- § 5. ОБОБЩЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ОПТИМАЛЬНОГО ФИЛЬТРА
- § 6. ФИЛЬТРАЦИЯ КВАЗИМОНОХРОМАТИЧЕСКИХ СИГНАЛОВ С ПОМОЩЬЮ ФИЛЬТРА I ТИПА
- § 7. ОБ ОСНОВНЫХ ПОЛОЖЕНИЯХ СТАТИСТИЧЕСКОЙ ТЕОРИИ ФИЛЬТРАЦИИ
- ГЛАВА II. ФИЛЬТРАЦИЯ И ПРОГНОЗИРОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 8. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ОПТИМАЛЬНОГО ЛИНЕЙНОГО ФИЛЬТРА II ТИПА
- § 9. ОПРЕДЕЛЕНИЕ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ОПТИМАЛЬНОГО ФИЛЬТРА II ТИПА
- § 10. ИССЛЕДОВАНИЕ ФУНКЦИЙ …
- § 11. ПОСТРОЕНИЕ ОПТИМАЛЬНОГО ФИЛЬТРА II ТИПА
- § 12. ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ТЕОРИИ ФИЛЬТРАЦИИ И ПРОГНОЗИРОВАНИЯ
- § 13. ПРОГНОЗИРОВАНИЕ СИНГУЛЯРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 14. ОБЩИЕ СООБРАЖЕНИЯ О ФИЛЬТРАЦИИ
- § 15. ВЫДЕЛЕНИЕ КВАЗИМОНОХРОМАТИЧЕСКИХ СИГНАЛОВ ФИЛЬТРАМИ II ТИПА
- ГЛАВА III. ВЫДЕЛЕНИЕ СИГНАЛОВ ИЗВЕСТНОЙ ФОРМЫ НА ФОНЕ СЛУЧАЙНЫХ ПОМЕХ
- § 17. СОГЛАСОВАННЫЙ ФИЛЬТР ИЛИ КОРРЕЛЯТОР
- § 18. КОРРЕЛЯТОР В ВИДЕОКАНАЛЕ РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- § 19. ТЕОРЕМА КОТЕЛЬНИКОВА И СОПРЯЖЕННАЯ ТЕОРЕМА
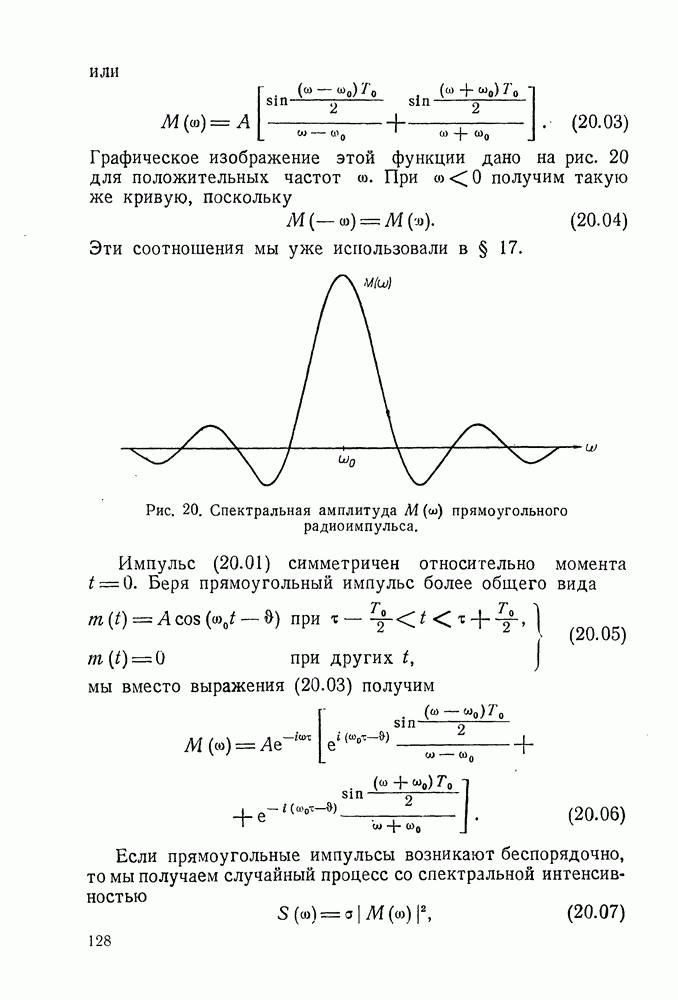
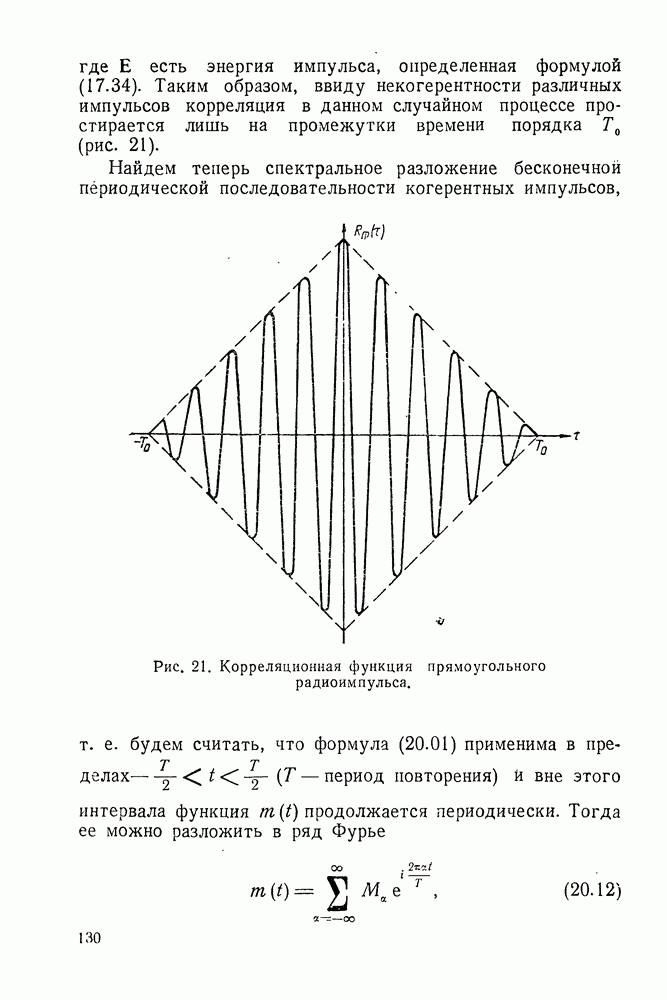
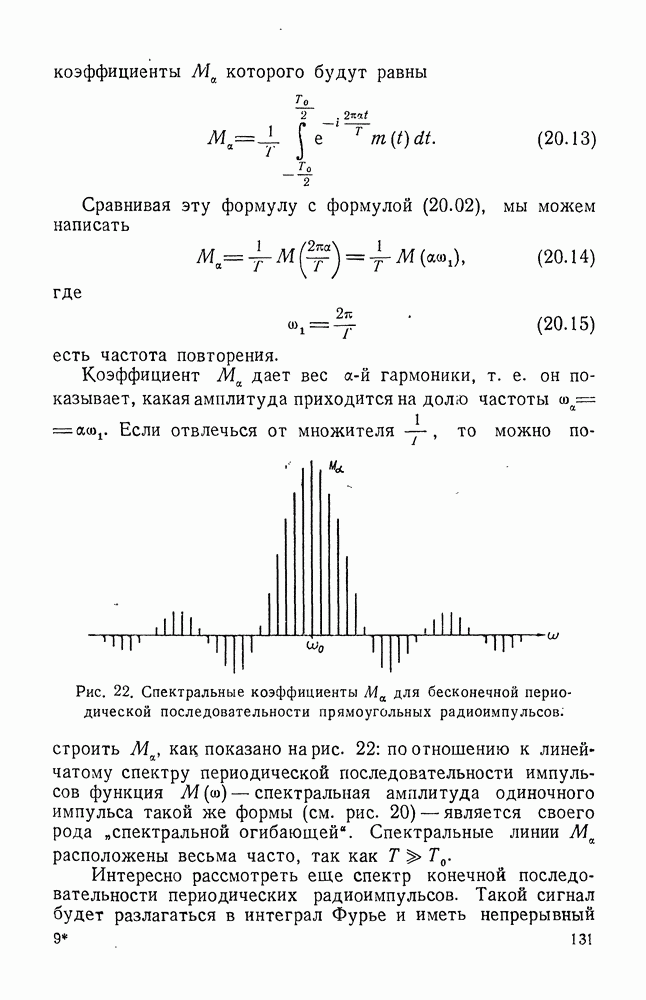
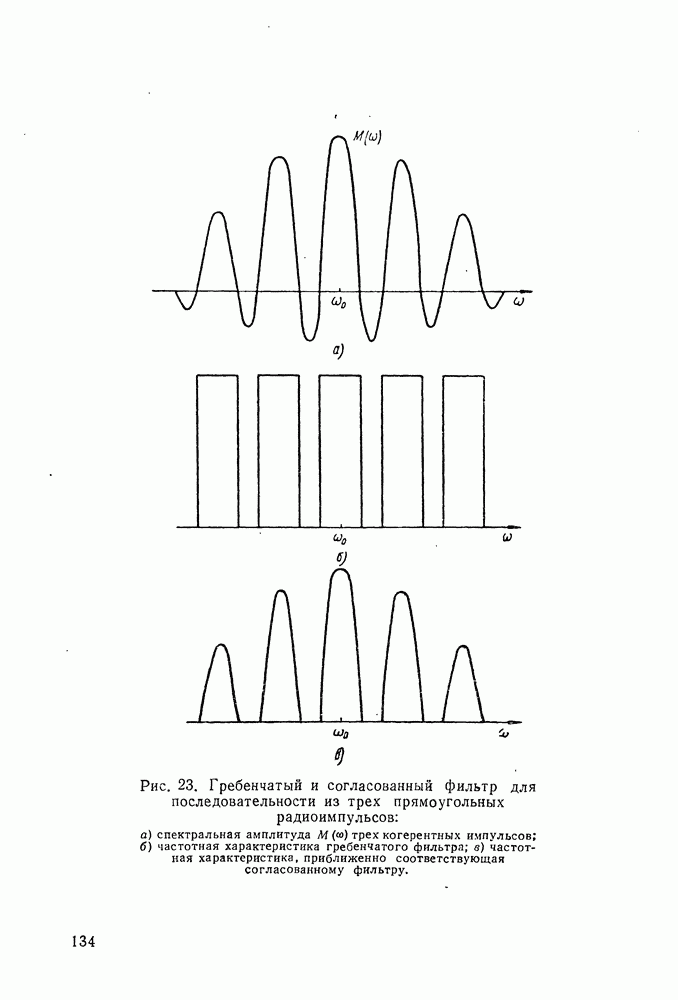
- § 20. ГРЕБЕНЧАТЫЙ ФИЛЬТР И СОГЛАСОВАННЫЙ ФИЛЬТР (КОРРЕЛЯТОР) ДЛЯ ПОСЛЕДОВАТЕЛЬНОСТИ РАДИОИМПУЛЬСОВ
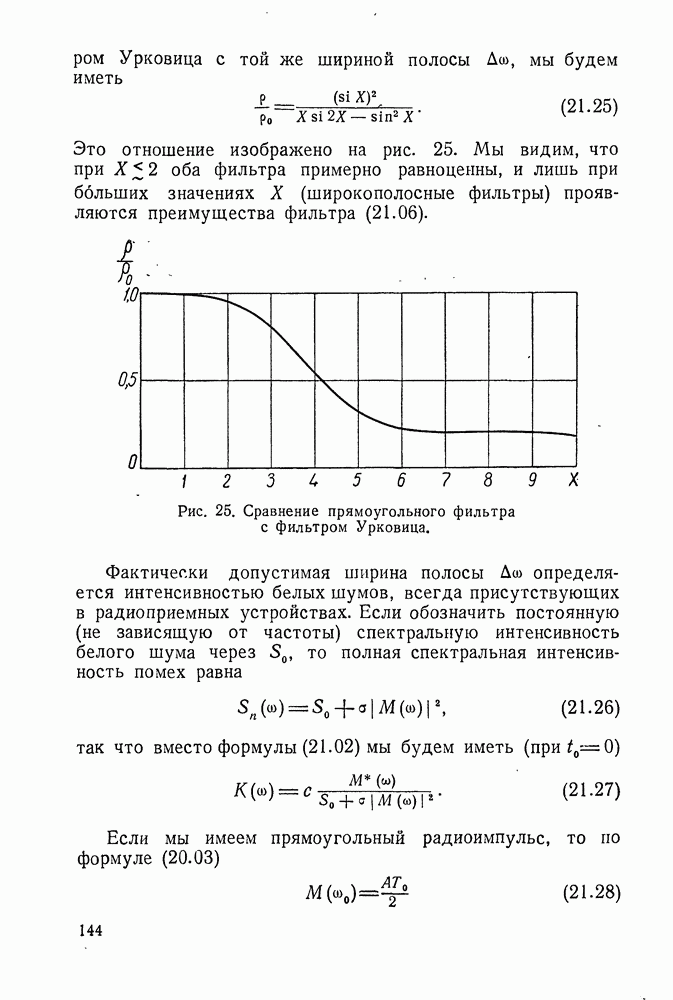
- § 21. ФИЛЬТР УРКОВИЦА
- § 22. О ФИЛЬТРАХ, ВЫДЕЛЯЮЩИХ СИГНАЛЫ ИЗВЕСТНОЙ ФОРМЫ
- ГЛАВА IV. СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 23. ФИЛЬТРАЦИЯ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- § 24. ТЕОРЕМА ХИНЧИНА ДЛЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ. НЕКОТОРЫЕ ВОПРОСЫ ФИЛЬТРАЦИИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- § 25. ФИЛЬТР ДЛЯ ВЫДЕЛЕНИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ИЗВЕСТНОЙ ФОРМЫ
- § 26. ФИЛЬТРАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ПРОЦЕССОВ I
- § 27. ФИЛЬТРАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ПРОЦЕССОВ. II
- ЧАСТЬ ВТОРАЯ. СТАТИСТИЧЕСКАЯ ТЕОРИЯ ОПТИМАЛЬНЫХ ПРИЕМНИКОВ
- § 28. ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ПРИЕМА
- § 29. АПОСТЕРИОРНЫЕ ВЕРОЯТНОСТИ И КОЭФФИЦИЕНТЫ ПРАВДОПОДОБИЯ
- § 30. АПРИОРНЫЕ ВЕРОЯТНОСТИ. РЕШАЮЩИЕ СХЕМЫ
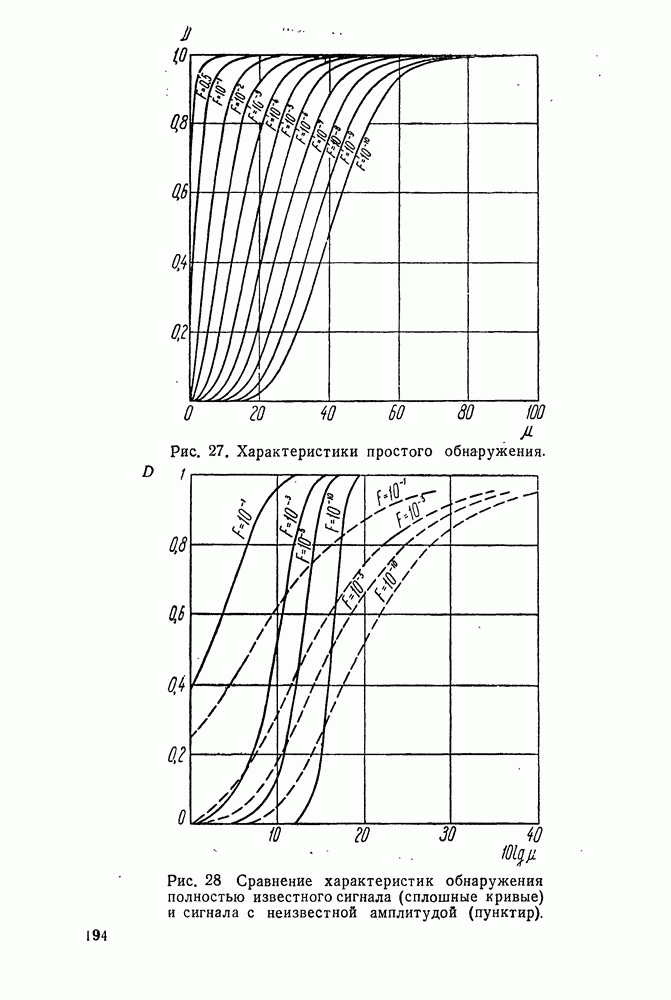
- § 31. ПРОСТОЕ ОБНАРУЖЕНИЕ СИГНАЛА НА ФОНЕ КОРРЕЛИРОВАННЫХ НОРМАЛЬНЫХ ПОМЕХ
- § 32. СЛОЖНОЕ ОБНАРУЖЕНИЕ СИГНАЛА С НЕИЗВЕСТНОЙ АМПЛИТУДОЙ
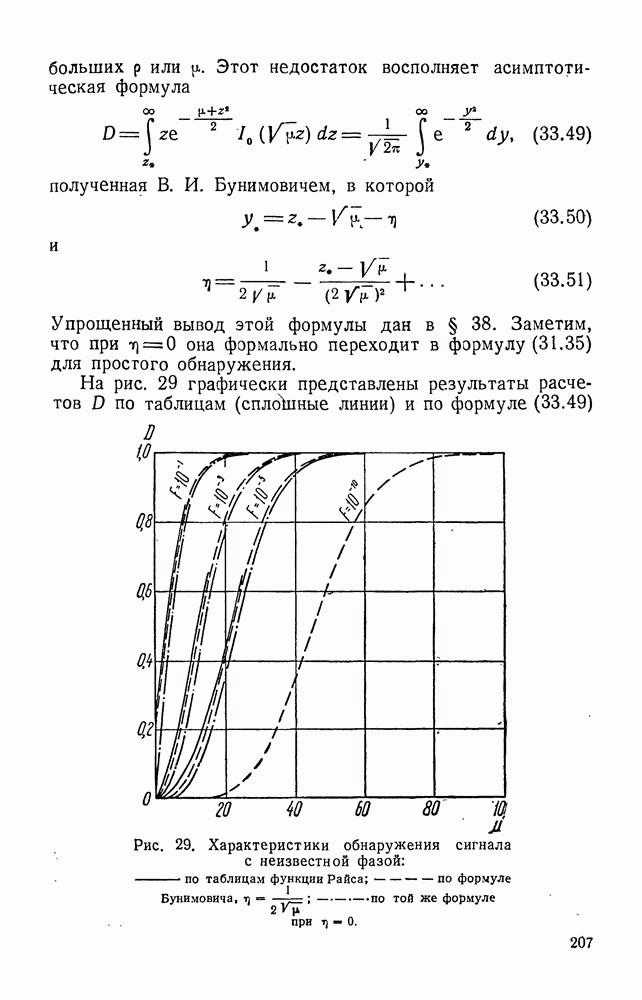
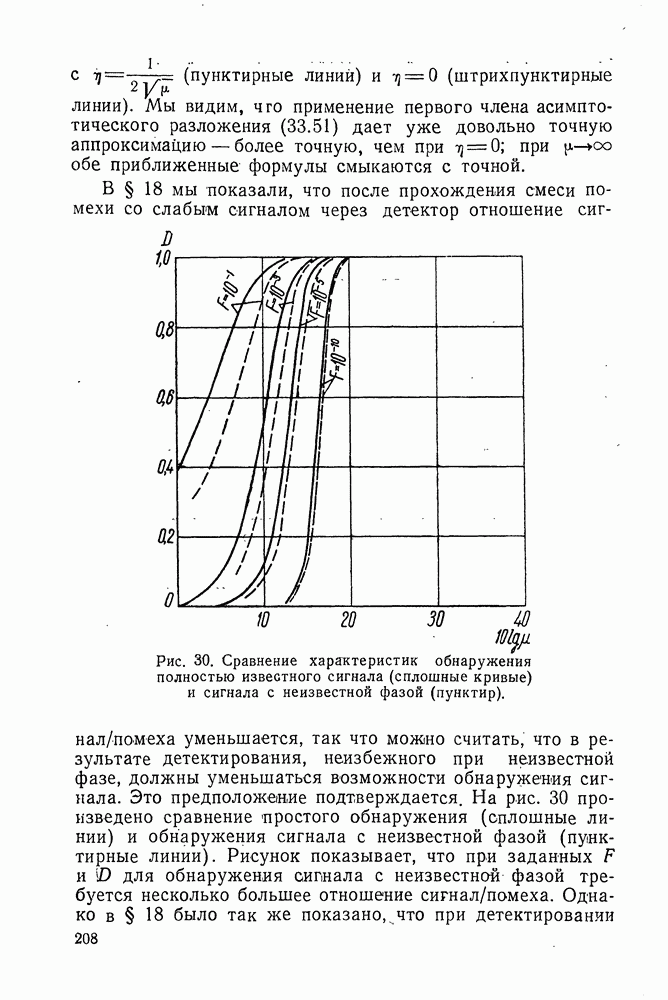
- § 33. ОБНАРУЖЕНИЕ СИГНАЛА С НЕИЗВЕСТНОЙ ФАЗОЙ
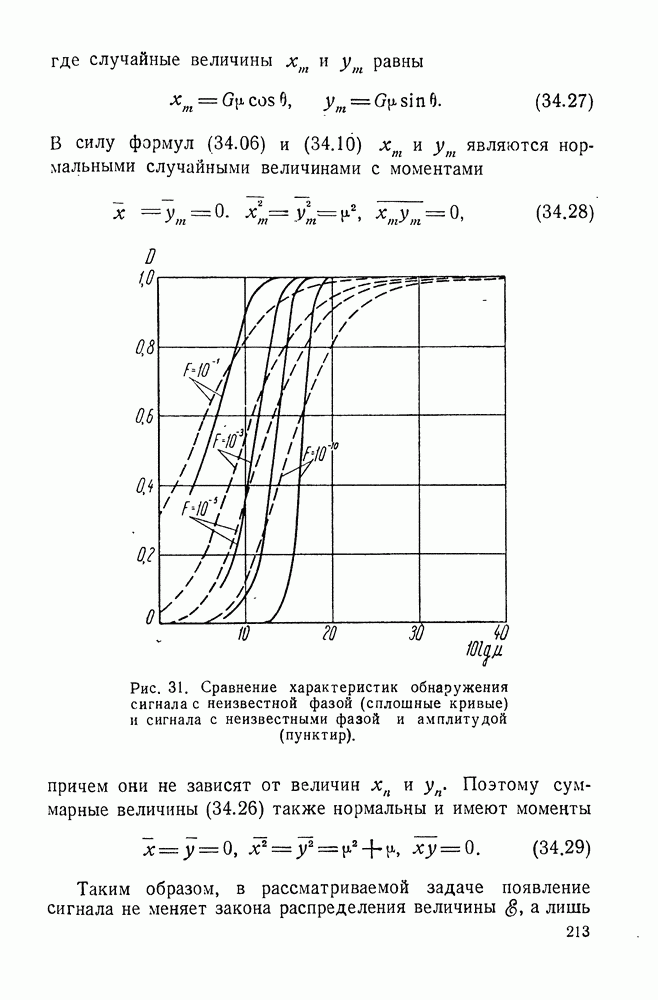
- § 34. ОБНАРУЖЕНИЕ СИГНАЛА С НЕИЗВЕСТНЫМИ ФАЗОЙ И АМПЛИТУДОЙ
- § 35. ОБНАРУЖЕНИЕ СЛУЧАЙНОГО ПРОЦЕССА (ПОЛЕЗНОГО СИГНАЛА) НА ФОНЕ ДРУГОГО СЛУЧАЙНОГО ПРОЦЕССА (ПОМЕХИ) ПРИ ЗАДАННЫХ КОРРЕЛЯЦИОННЫХ СВОЙСТВАХ ОБОИХ ПРОЦЕССОВ
- ГЛАВА VI. ОБНАРУЖЕНИЕ ПАЧКИ СИГНАЛОВ
- § 36. КОГЕРЕНТНАЯ И НЕКОГЕРЕНТНАЯ ПАЧКИ СИГНАЛОВ. О КОРРЕЛИРОВАННЫХ ПОМЕХАХ В РАДИОЛОКАЦИИ
- § 37. ОБНАРУЖЕНИЕ НЕКОГЕРЕНТНОЙ ПАЧКИ СИГНАЛОВ НА ФОНЕ НОРМАЛЬНЫХ ПОМЕХ
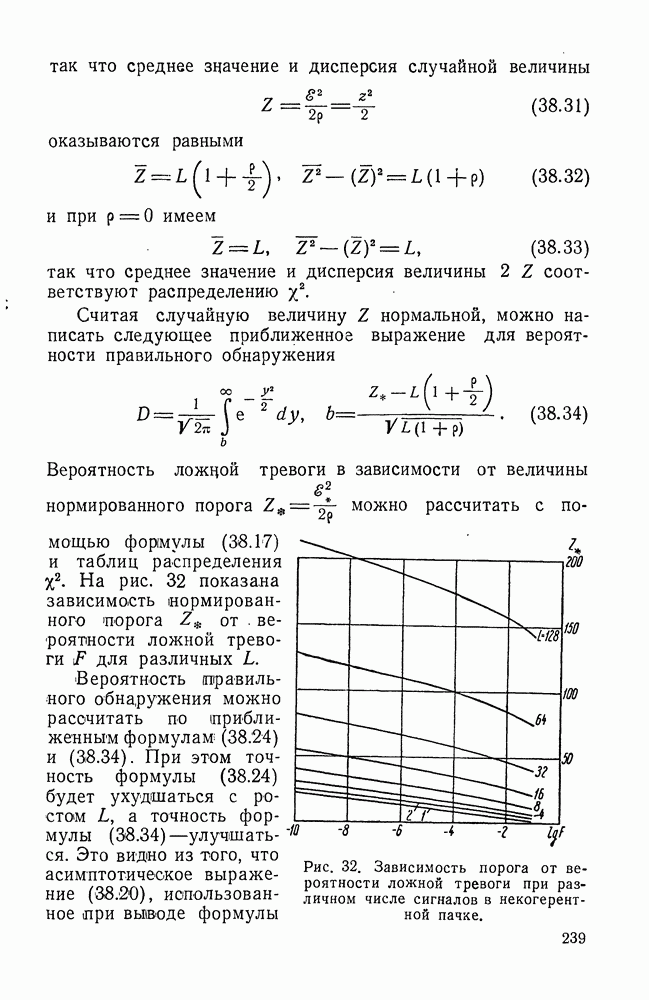
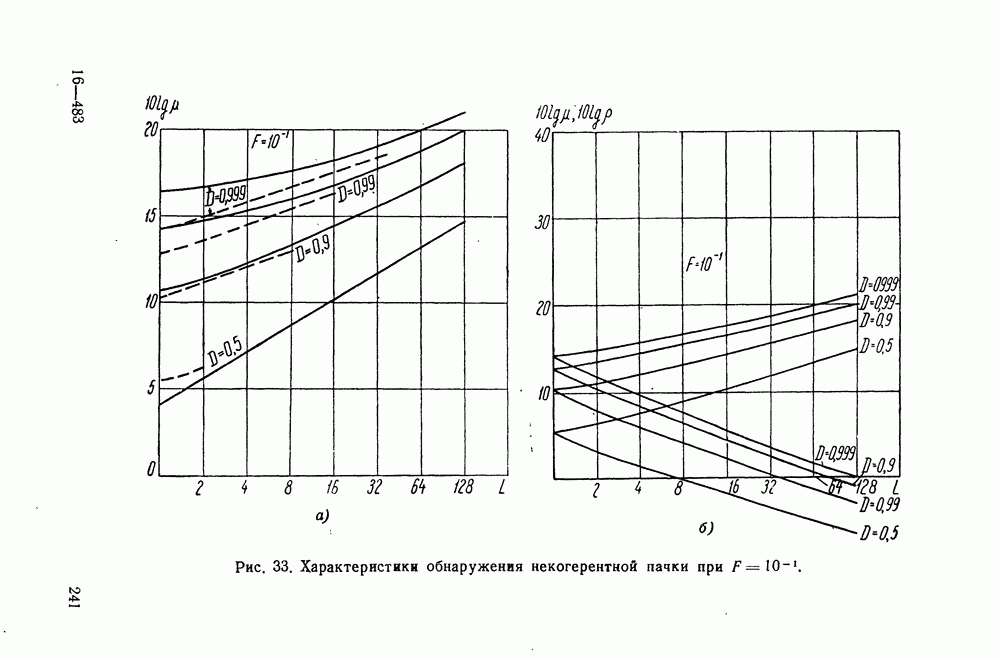
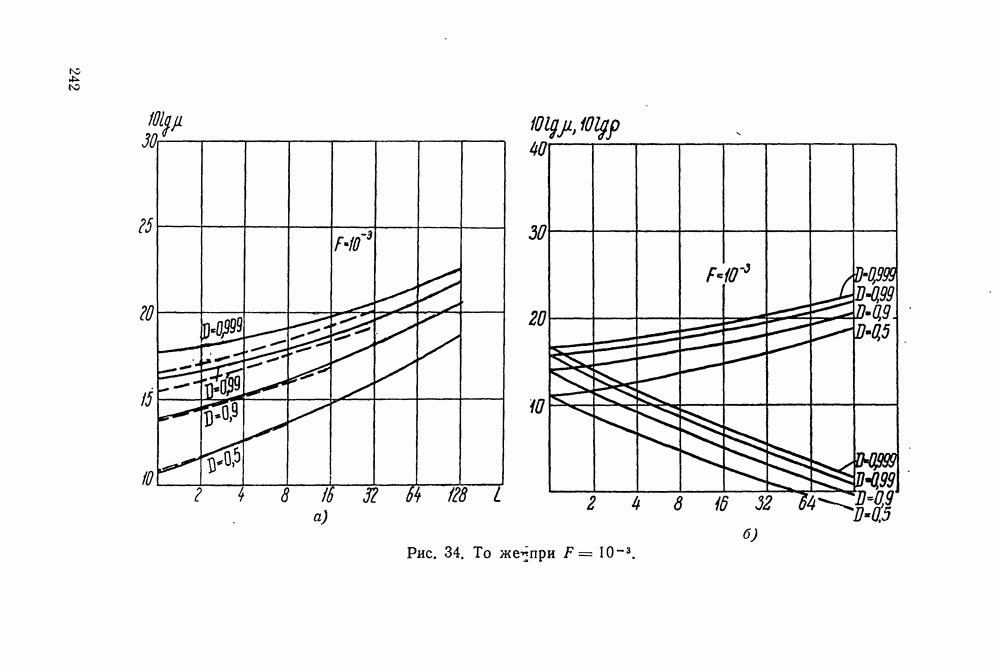
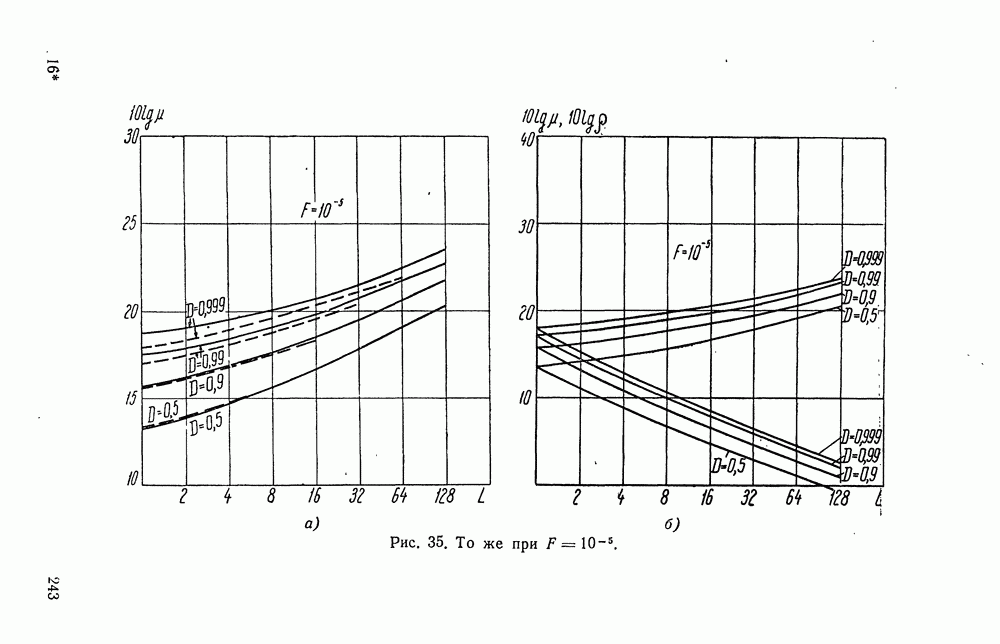
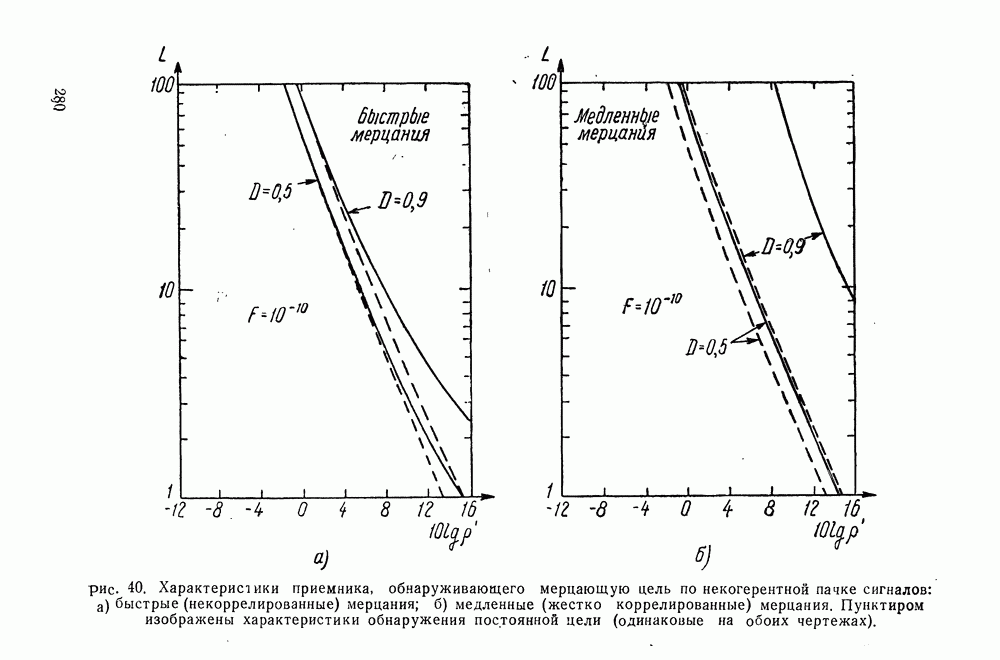
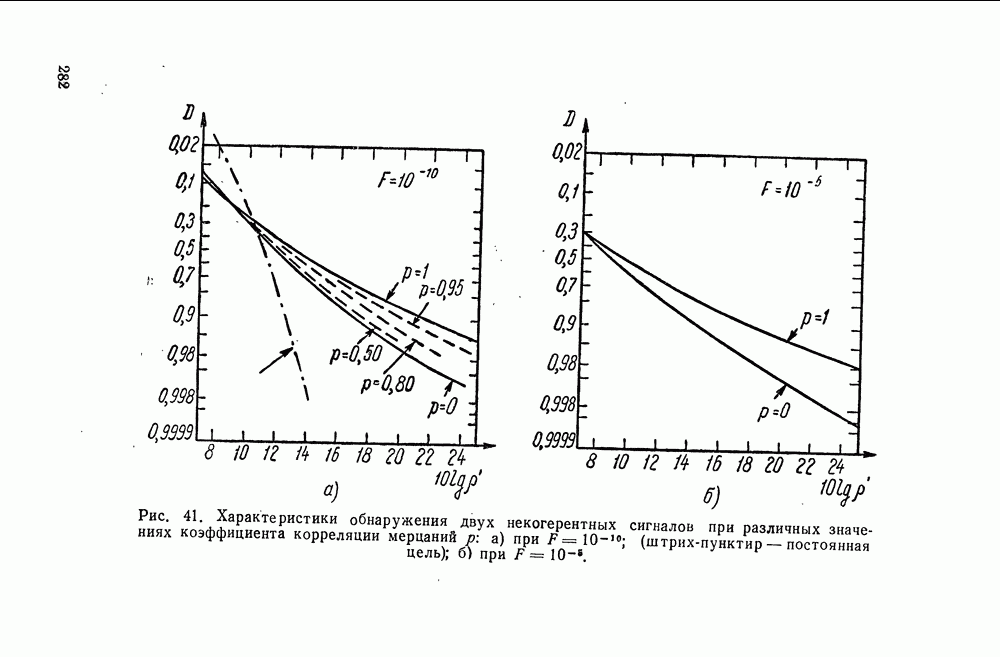
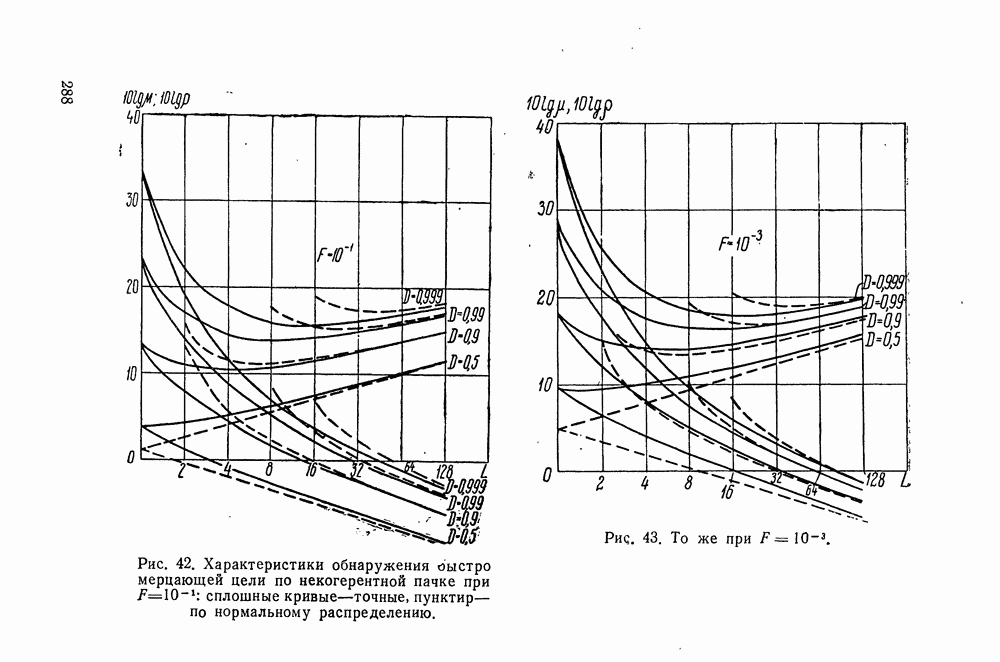
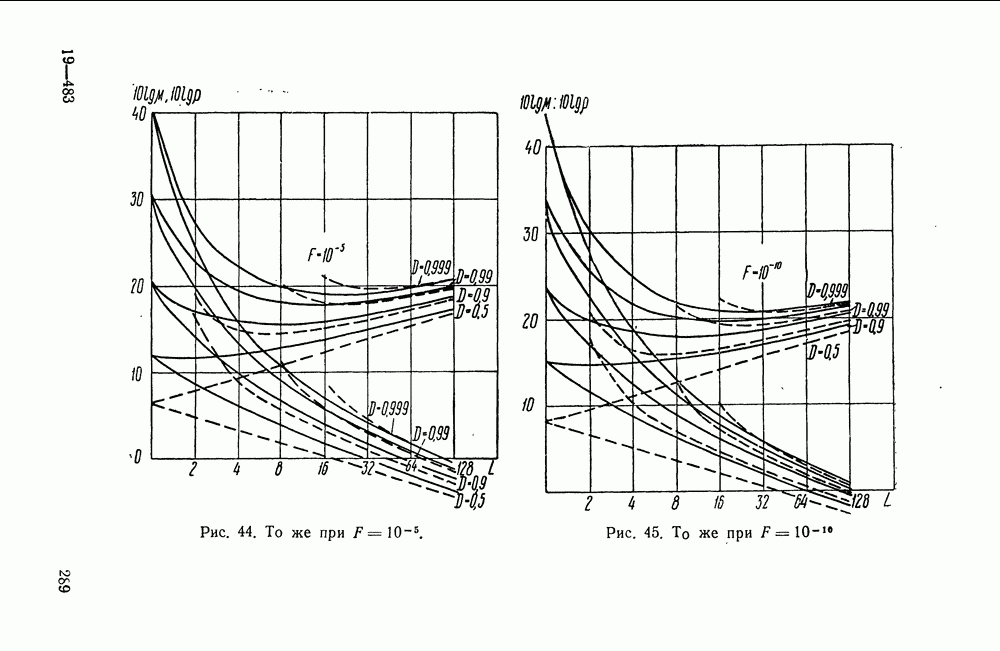
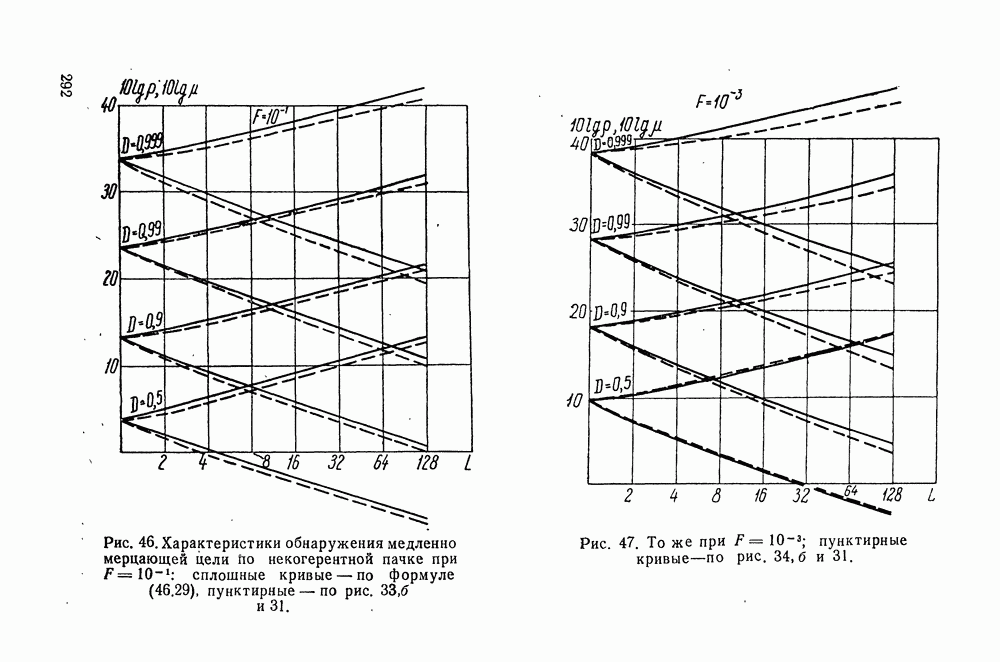
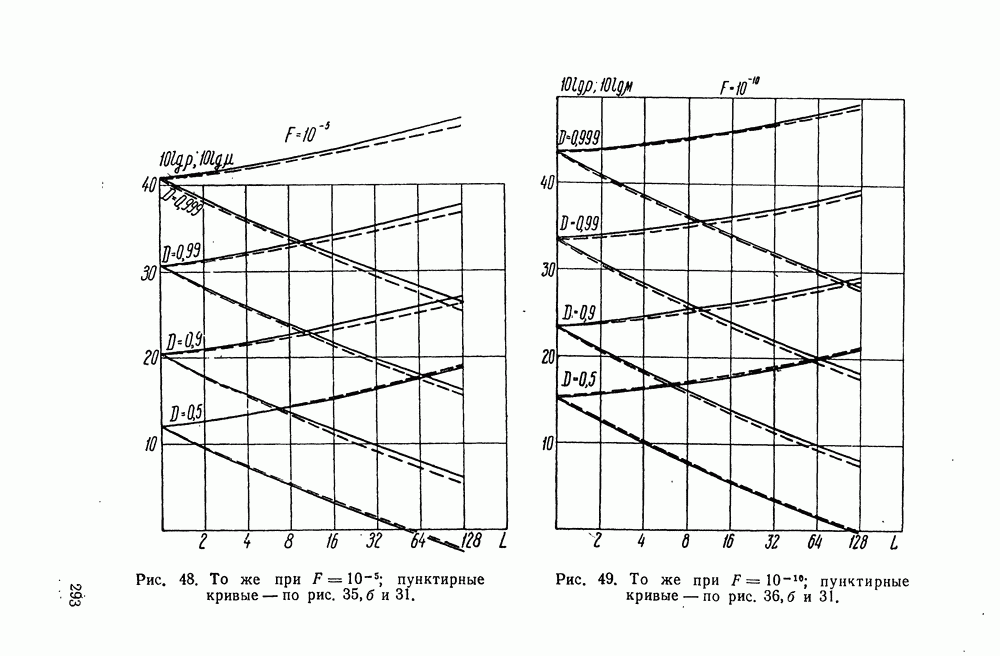
- § 38. ХАРАКТЕРИСТИКИ ПРИЕМНИКА, ОБНАРУЖИВАЮЩЕГО НЕКОГЕРЕНТНУЮ ПАЧКУ
- § 39. ОБНАРУЖЕНИЕ КОГЕРЕНТНОЙ ПАЧКИ НА ФОНЕ НОРМАЛЬНЫХ КОРРЕЛИРОВАННЫХ ПОМЕХ
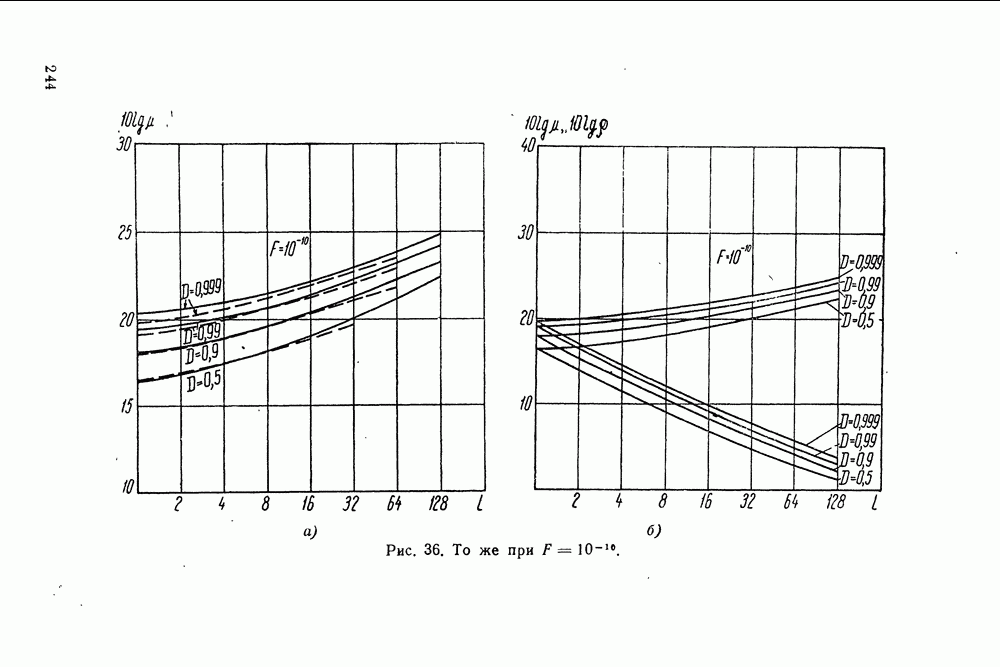
- § 40. ОПТИМАЛЬНОЕ ОБНАРУЖЕНИЕ КОГЕРЕНТНОЙ ПАЧКИ ПРИ РАЗЛИЧНЫХ СКОРОСТЯХ ЦЕЛИ
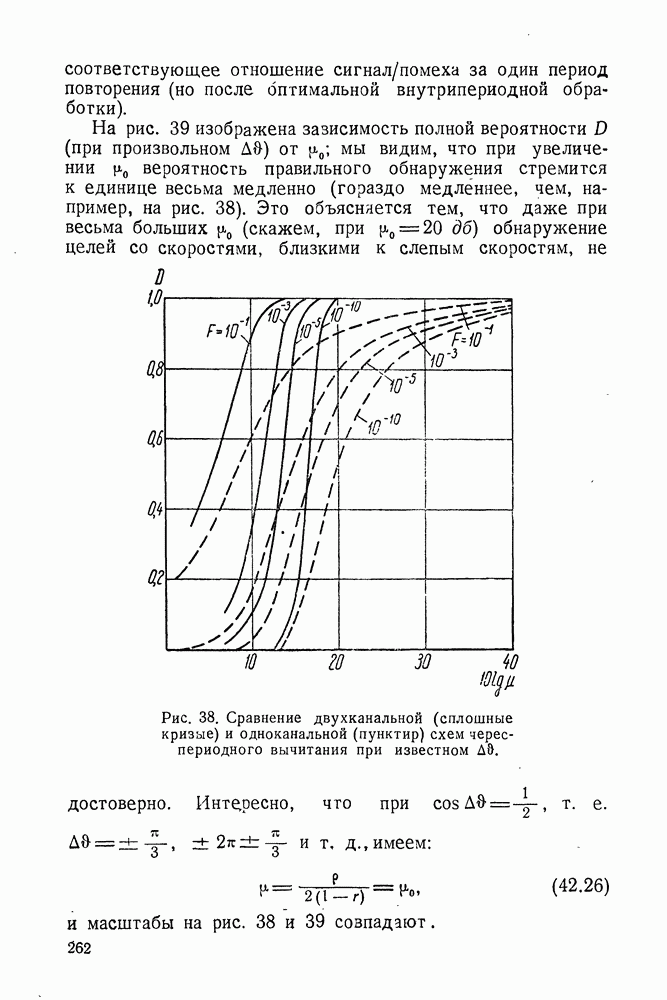
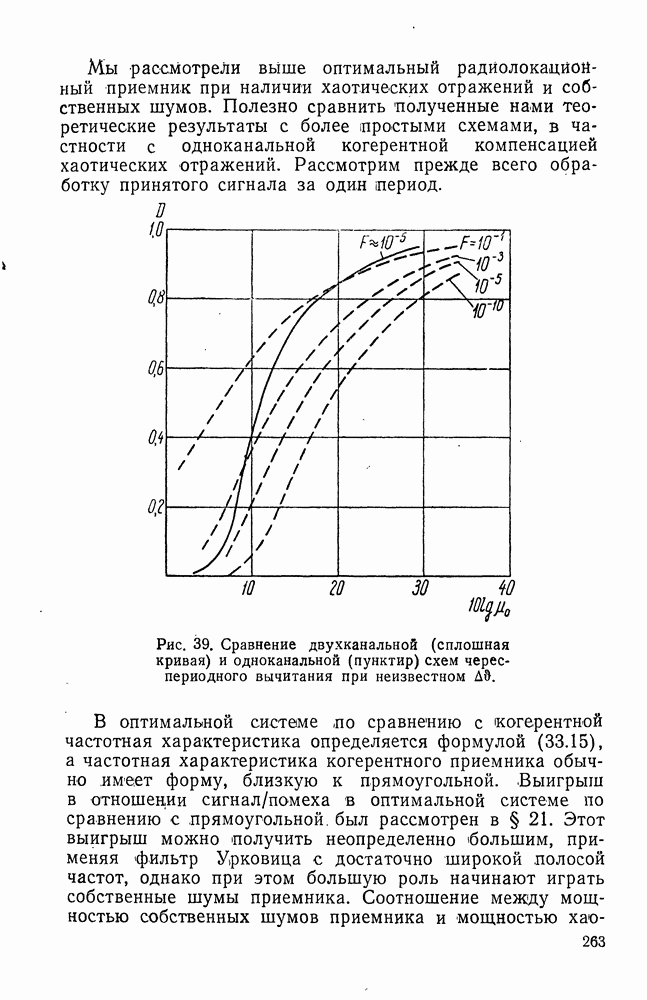
- § 41. ОБНАРУЖЕНИЕ КОГЕРЕНТНОЙ ПАЧКИ СИГНАЛОВ ЗА ДВА ПЕРИОДА ПОВТОРЕНИЯ ПРИ ИЗВЕСТНОМ И НЕИЗВЕСТНОМ СМЕЩЕНИИ ЧАСТОТЫ
- § 42. ВЕРОЯТНОСТИ F И D ПРИ ЧЕРЕСПЕРИОДНОМ ВЫЧИТАНИИ
- ГЛАВА VII. РАДИОЛОКАЦИОННОЕ ОБНАРУЖЕНИЕ «МЕРЦАЮЩЕЙ ЦЕЛИ»
- § 44. КОЭФФИЦИЕНТ ПРАВДОПОДОБИЯ ДЛЯ НЕКОГЕРЕНТНОЙ ПАЧКИ
- § 45. ХАРАКТЕРИСТИКИ ПРИЕМНИКА, ПРОИЗВОДЯЩЕГО КВАДРАТИЧНОЕ СУММИРОВАНИЕ
- § 46. РАЗЛИЧНЫЕ АППРОКСИМАЦИИ В ЗАДАЧАХ ОБ ОБНАРУЖЕНИИ НЕКОГЕРЕНТНОЙ ПАЧКИ
- § 47. КОЭФФИЦИЕНТ ПРАВДОПОДОБИЯ ДЛЯ КОГЕРЕНТНОЙ ПАЧКИ
- § 48. ОПТИМАЛЬНЫЙ ПРИЕМНИК В ЧАСТНЫХ СЛУЧАЯХ
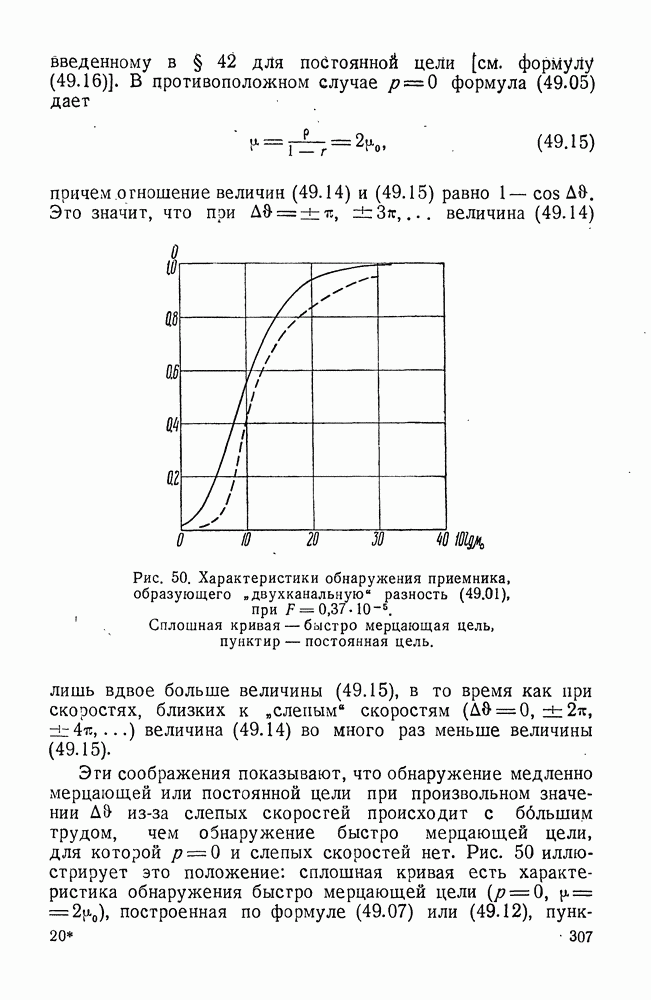
- § 49. ХАРАКТЕРИСТИКИ ПРИЕМНИКА, ОБРАЗУЮЩЕГО ЧЕРЕСПЕРИОДНУЮ РАЗНОСТЬ
- ГЛАВА VIII. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ПОЛЕЗНОГО СИГНАЛА ПРИ НАЛИЧИИ ПОМЕХ
- § 50. ИЗМЕРЕНИЕ ПАРАМЕТРА ПО МАКСИМУМУ АПОСТЕРИОРНОЙ ВЕРОЯТНОСТИ
- § 51. ВЫДЕЛЕНИЕ СЛУЧАЙНОГО СИГНАЛА НА ФОНЕ СЛУЧАЙНЫХ ПОМЕХ
- § 52. ИЗМЕРЕНИЕ ПАРАМЕТРА СИГНАЛА ПРИ СЛАБЫХ И СИЛЬНЫХ ПОМЕХАХ
- § 53. ПРОСТОЕ ИЗМЕРЕНИЕ ВРЕМЕНИ ПРИХОДА СИГНАЛА ПРИ СЛАБЫХ ПОМЕХАХ
- § 54. СЛОЖНОЕ ИЗМЕРЕНИЕ ВРЕМЕНИ ПРИХОДА СИГНАЛА ПРИ СЛАБЫХ ПОМЕХАХ
- § 55. ИЗМЕРЕНИЕ МОМЕНТА ПРИХОДА СИГНАЛА ПРИ ПРОИЗВОЛЬНЫХ ПОМЕХАХ
- § 56. ЗАДАЧА О РАЗЛИЧЕНИИ M ОРТОГОНАЛЬНЫХ СИГНАЛОВ
- § 57. ОБНАРУЖЕНИЕ СИГНАЛА С ДИСКРЕТНЫМ ПАРАМЕТРОМ И ИЗМЕРЕНИЕ ЭТОГО ПАРАМЕТРА
- ЧАСТЬ ТРЕТЬЯ. ВСПОМОГАТЕЛЬНЫЕ ВОПРОСЫ
- ГЛАВА IX. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И СЛУЧАЙНЫЕ ПРОЦЕССЫ НОРМАЛЬНОГО ТИПА
- § 59. МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ГАУССА
- § 60. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ДЛЯ ОГИБАЮЩИХ
- § 61. ТЕПЛОВЫЕ И ДРОБОВЫЕ ШУМЫ КАК ПРИМЕРЫ НОРМАЛЬНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- ГЛАВА Х. ТЕОРИЯ ФЛЮКТУАЦИОННОЙ МОДУЛЯЦИИ
- § 63. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И СПЕКТР МОДУЛИРОВАННЫХ КОЛЕБАНИЙ
- § 64. МОДУЛЯЦИЯ С ПОМОЩЬЮ МОНОХРОМАТИЧЕСКИХ КОЛЕБАНИЙ (КВАЗИСИНУСОИДАЛЬНАЯ МОДУЛЯЦИЯ)
- § 65. ПРЕДЕЛЬНЫЕ СЛУЧАИ СПЕКТРАЛЬНЫХ РАСПРЕДЕЛЕНИЙ
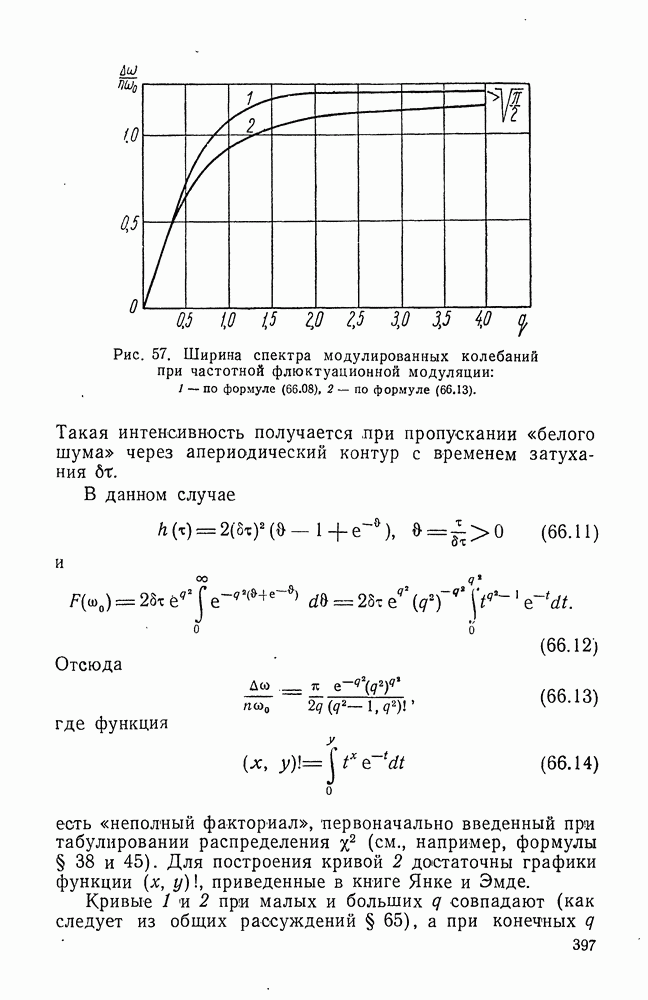
- § 66. ЗАВИСИМОСТЬ ШИРИНЫ СПЕКТРА МОДУЛИРОВАННЫХ КОЛЕБАНИЙ ОТ ШИРИНЫ СПЕКТРА МОДУЛИРУЮЩИХ КОЛЕБАНИЙ
- ГЛАВА XI. ХАОТИЧЕСКИЕ ОТРАЖЕНИЯ
- § 67. ПОМЕХИ, ОБУСЛОВЛЕННЫЕ ХАОТИЧЕСКИМИ ОТРАЖЕНИЯМИ
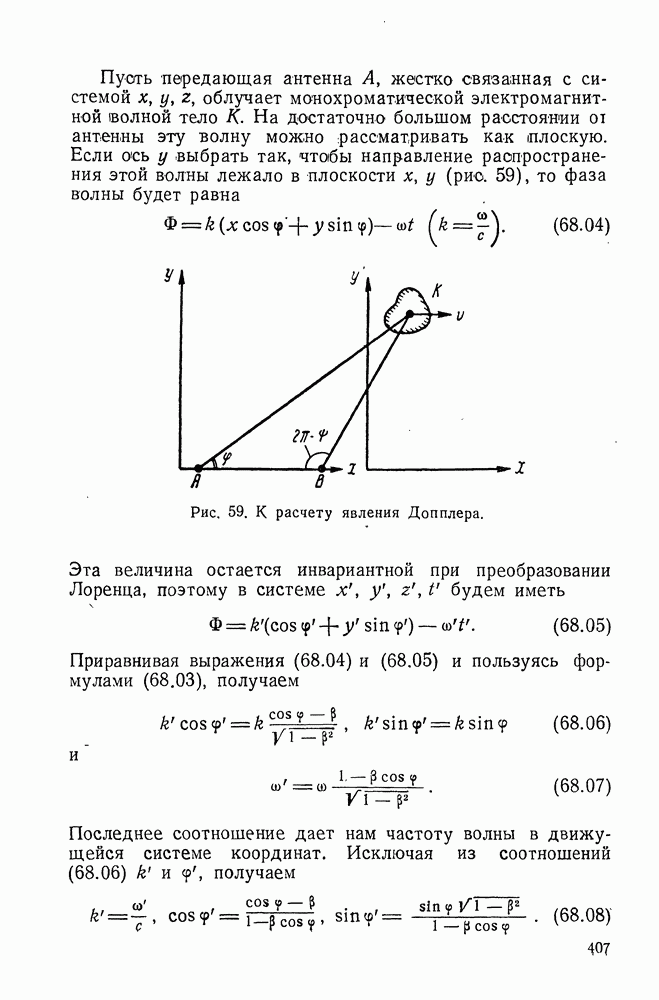
- § 68. ЯВЛЕНИЕ ДОППЛЕРА
- § 69. ФУНКЦИЯ КОРРЕЛЯЦИИ ПОМЕХИ, ОБУСЛОВЛЕННОЙ ХАОТИЧЕСКИМИ ОТРАЖЕНИЯМИ
- § 70. РАССЕЯНИЕ РАДИОВОЛН НА БЛУЖДАЮЩИХ ЧАСТИЦАХ
- § 71. ПРИМЕНЕНИЕ ТЕОРИИ ФЛЮКТУАЦИОННОИ МОДУЛЯЦИИ К ХАОТИЧЕСКИМ ОТРАЖЕНИЯМ
- ПРИЛОЖЕНИЕ I. ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ И ОПТИМАЛЬНЫЕ ПРИЕМНИКИ
- ПРИЛОЖЕНИЕ II. ОБ ОТНОШЕНИИ СИГНАЛ/ПОМЕХА ПРИ НЕОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ОБРАБОТКЕ ВХОДНЫХ ДАННЫХ
- ПРИЛОЖЕНИЕ III. О ПАРАДОКСАХ В ТЕОРИИ ОБНАРУЖЕНИЯ
- ПРИЛОЖЕНИЕ IV. ПРЕОБРАЗОВАНИЕ НЕМОНОХРОМАТИЧЕСКИХ СИГНАЛОВ ВСЛЕДСТВИЕ ЯВЛЕНИЯ ДОППЛЕРА
- ПРИЛОЖЕНИЕ V. О «СВЕТЯЩИХСЯ ТОЧКАХ»
- ЛИТЕРАТУРА