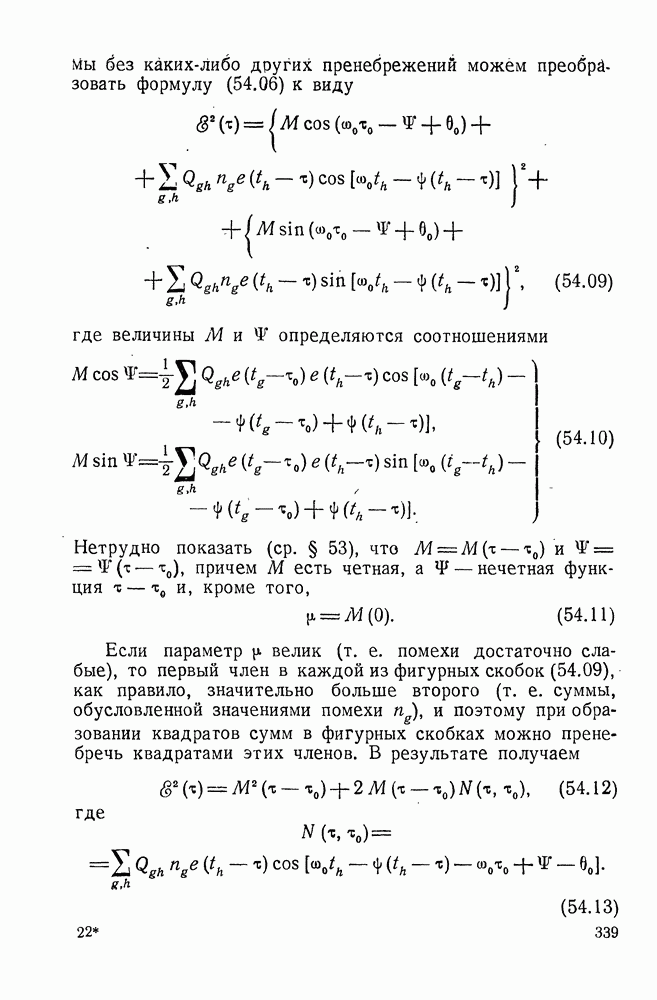| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА II. ФИЛЬТРАЦИЯ И ПРОГНОЗИРОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
§ 8. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ОПТИМАЛЬНОГО ЛИНЕЙНОГО ФИЛЬТРА II ТИПА
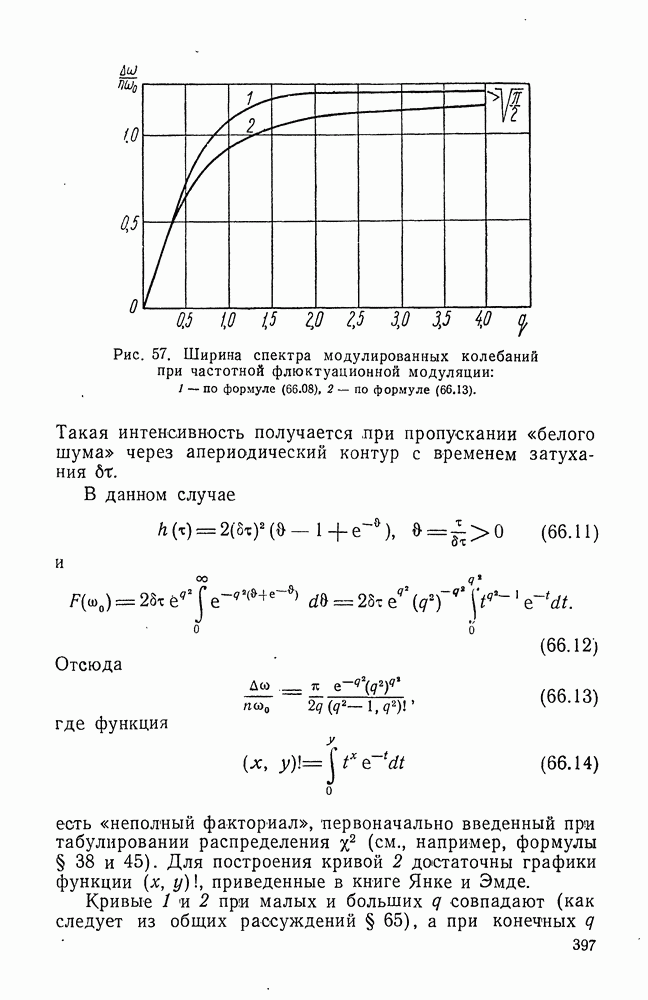
Для фильтров II типа функция  удовлетворяет добавочному условию
удовлетворяет добавочному условию

аналогичному условию (1.14), и формула (4.39) принимает вид

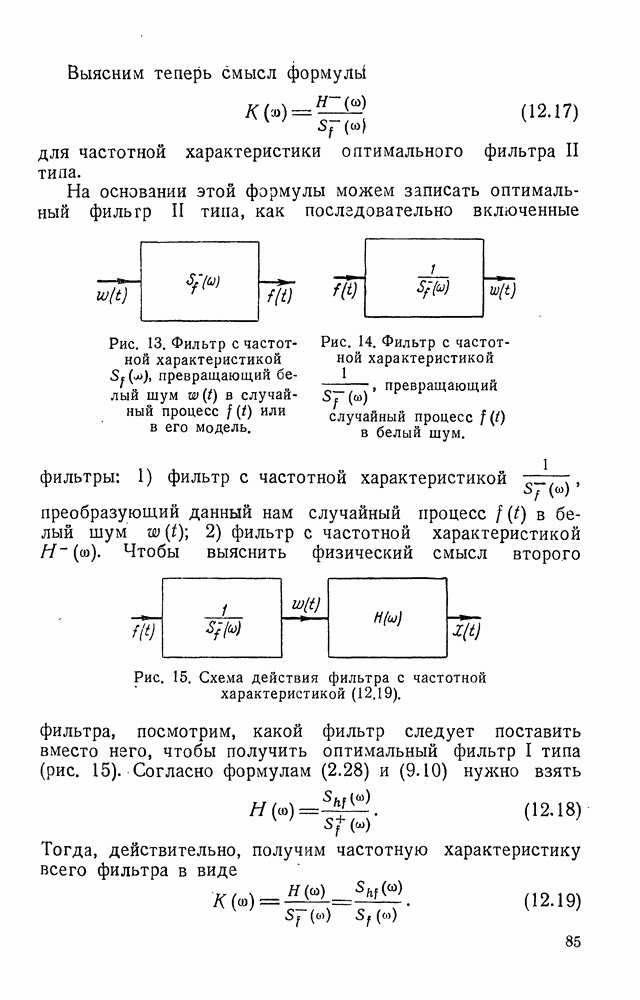
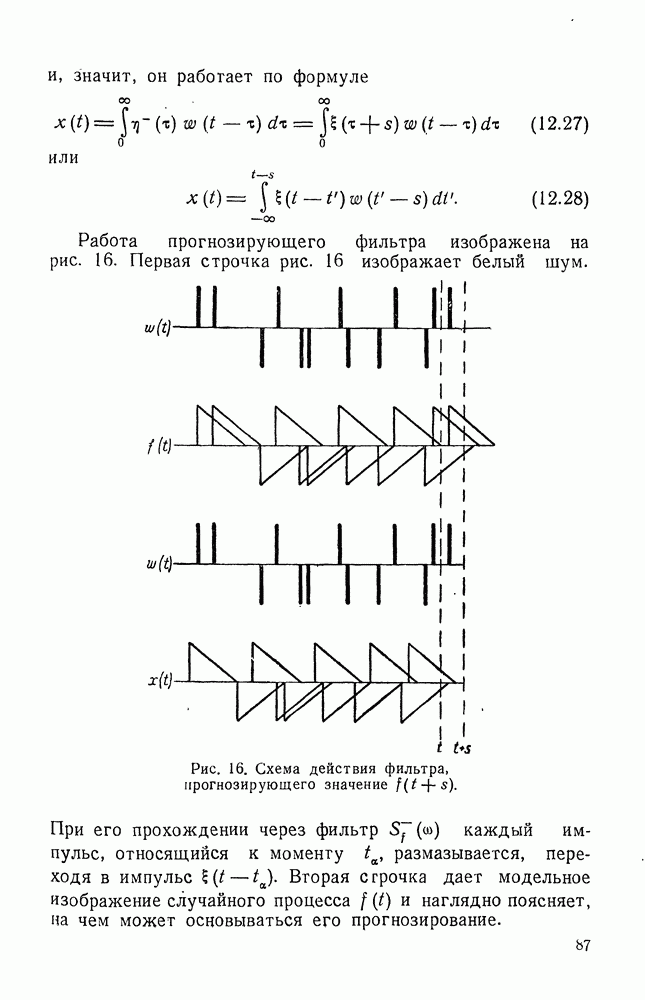
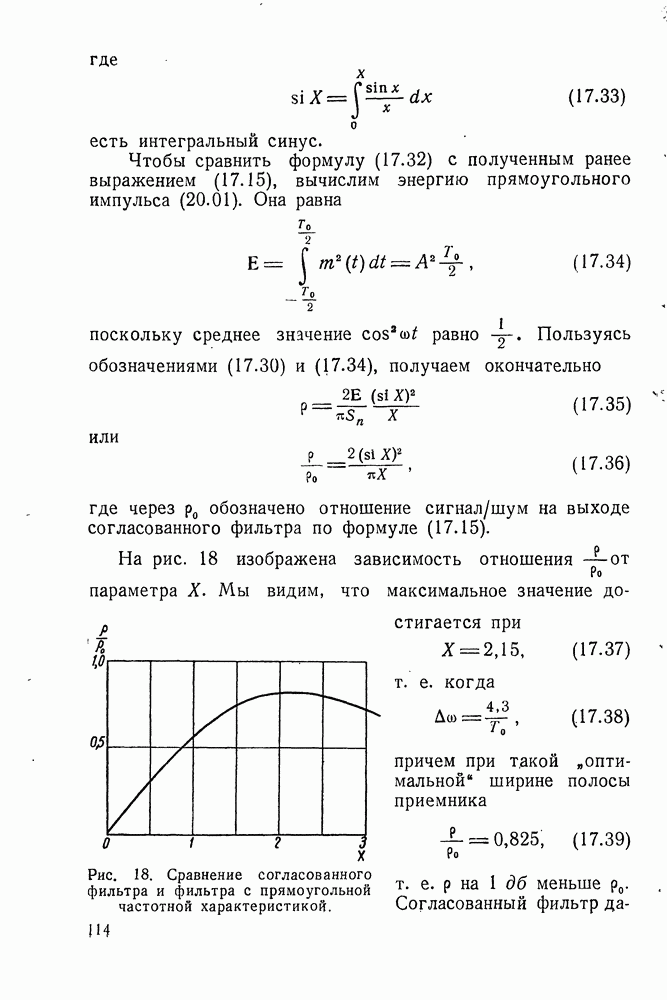
Таким образом, фильтр II типа использует входной процесс за полубесконечный промежуток времени. Фильтр I типа использует информацию за промежуток времени, бесконечный в обе стороны, поэтому он более эффективен, чем фильтр II типа, и, в частности, его средняя квадратичная ошибка меньше.
При  коэффициенты
коэффициенты  и функция
и функция  оптимального фильтра II типа должны удовлетворять тому же уравнению (5.08)
оптимального фильтра II типа должны удовлетворять тому же уравнению (5.08)

что и в случае фильтров I типа, однако, при  это уравнение не должно выполняться, поскольку
это уравнение не должно выполняться, поскольку

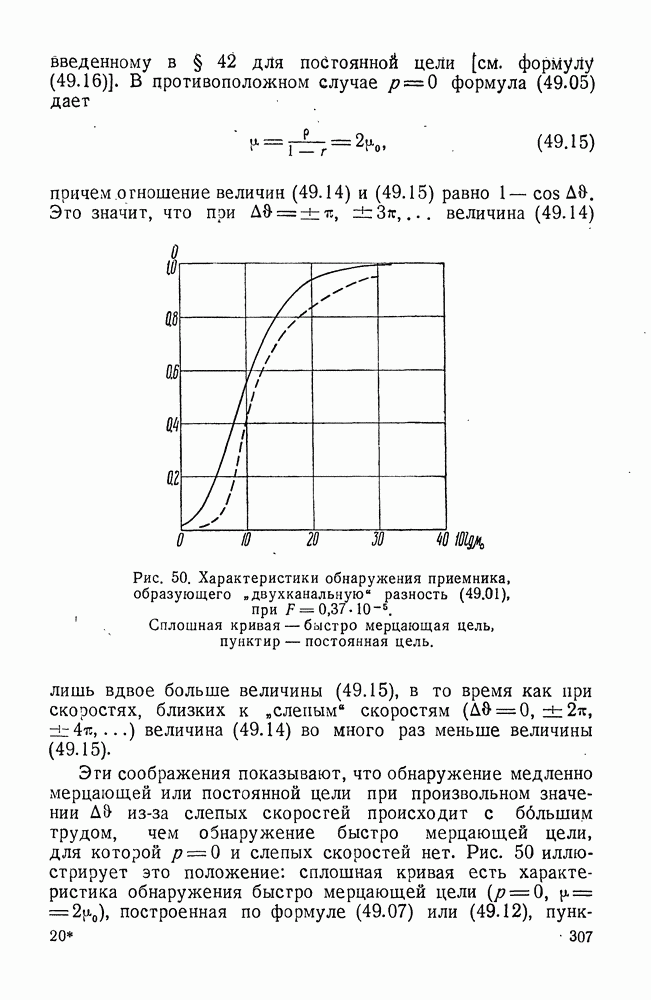
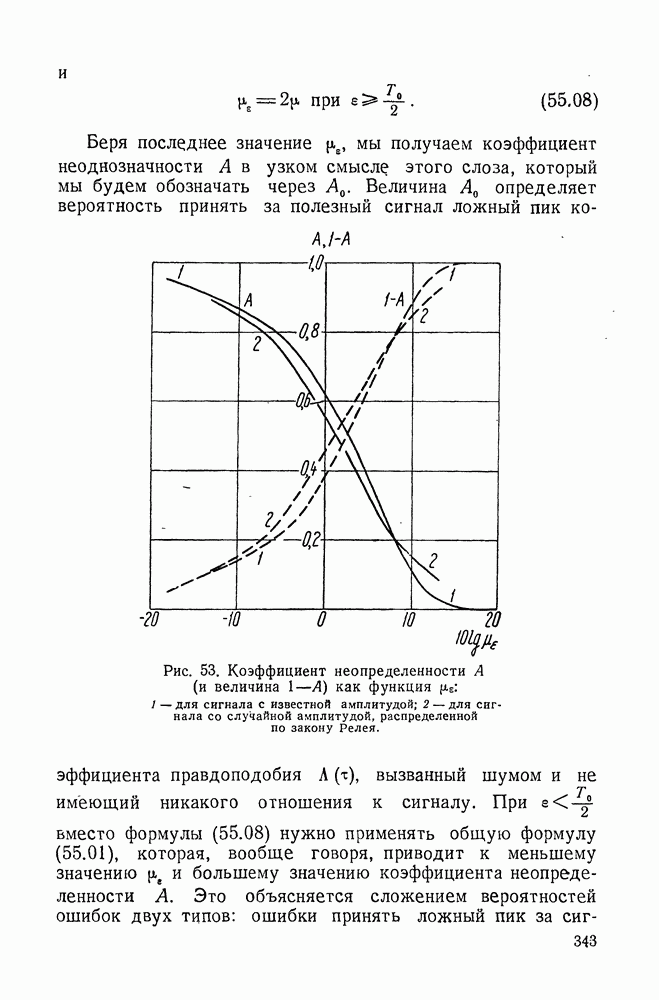
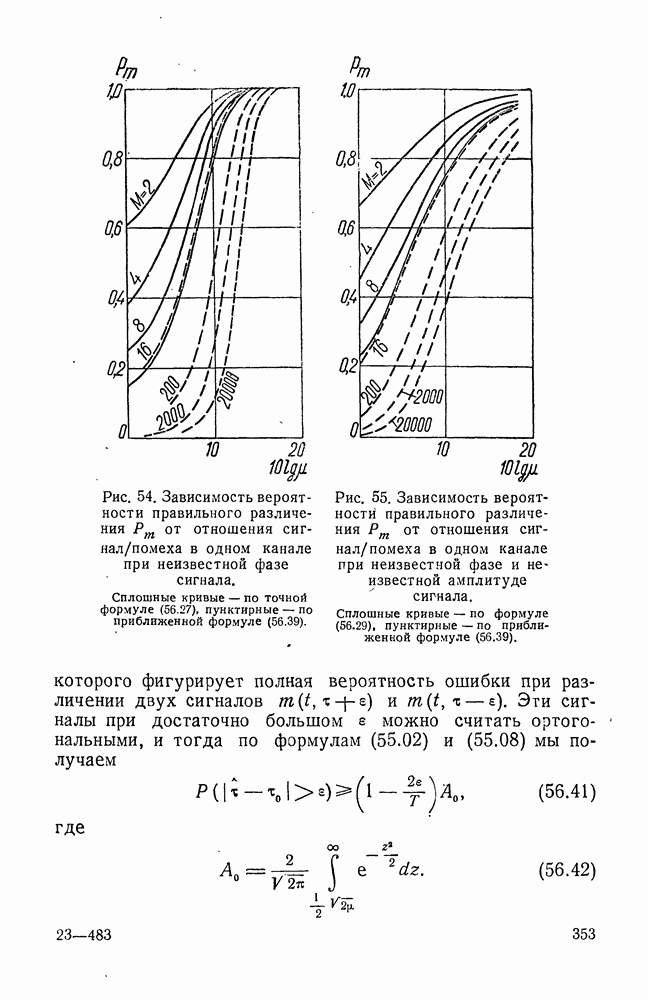
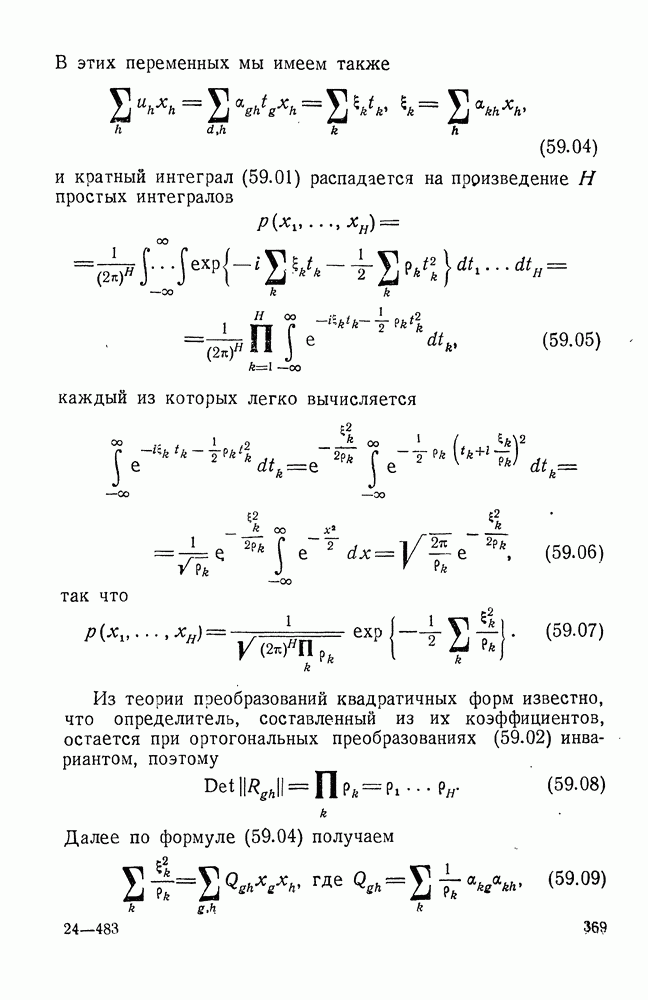
Вместо этого должно выполняться условие (8.01), благодаря чему задача становится гораздо сложнее.
Применим к уравнению (8.03) преобразование Фурье. Для этого воспользуемся формулами

и

Воспользовавшись также соотношением

мы преобразуем уравнение (8.03) к виду 00

где

есть неизвестная нам частотная характеристика (коэффициент передачи) искомого фильтра, причем слагаемое  исчезает при
исчезает при  и допускает преобразование Фурье,
и допускает преобразование Фурье,  известные спектральные функции.
известные спектральные функции.
Если бы функция К И была нам известна, то мы могли бы представить ее в виде (8.09) и по функции  вычислить [ср. формулу (4.40)] функцию
вычислить [ср. формулу (4.40)] функцию

которая должна удовлетворять условию (8.01). Поэтому наряду с уравнением (8.08) должно выполняться еще уравнение

Вся трудность состоит в том, что функция  должна удовлетворять двум соотношениям (8.08) и (8.11). Мы будем искать неизвестную функцию
должна удовлетворять двум соотношениям (8.08) и (8.11). Мы будем искать неизвестную функцию  предполагал сначала, что функции
предполагал сначала, что функции  даны нам не в виде эмпирических кривых, а в виде формул, допускающих аналитическое продолжение в область комплексных частот,
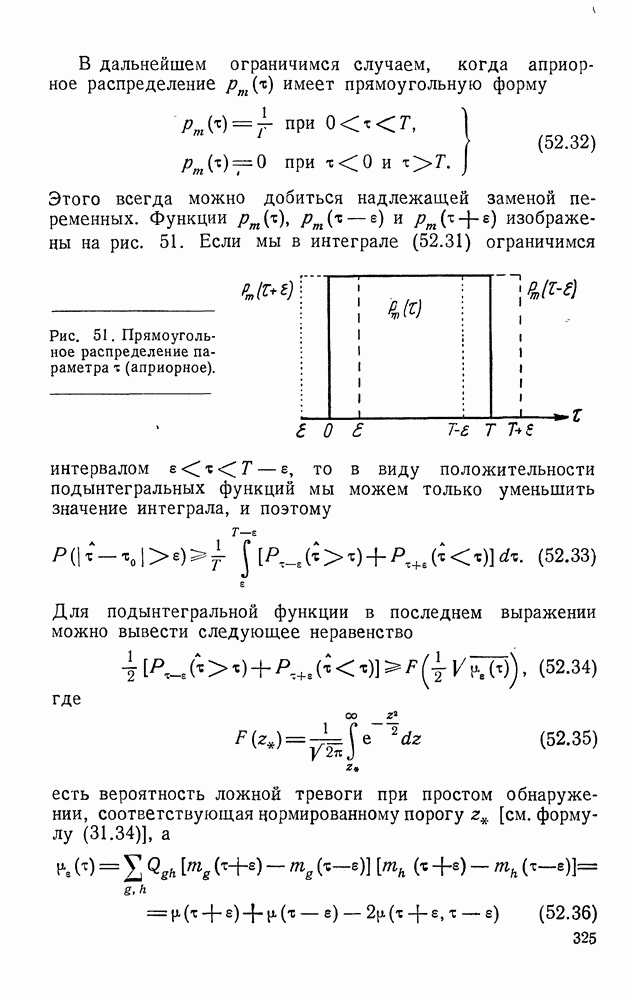
даны нам не в виде эмпирических кривых, а в виде формул, допускающих аналитическое продолжение в область комплексных частот,  будем считать,
будем считать,  функциями комплексного переменного, аналитическими в некоторой окрестности вещественной оси на плоскости комплексного переменного
функциями комплексного переменного, аналитическими в некоторой окрестности вещественной оси на плоскости комплексного переменного  .
.
Вводя обозначение

мы можем переписать уравнение (8.08) в виде

Для дальнейшего преобразуем его следующим образом. Умножим обе части на  и проинтегрируем от 0 до
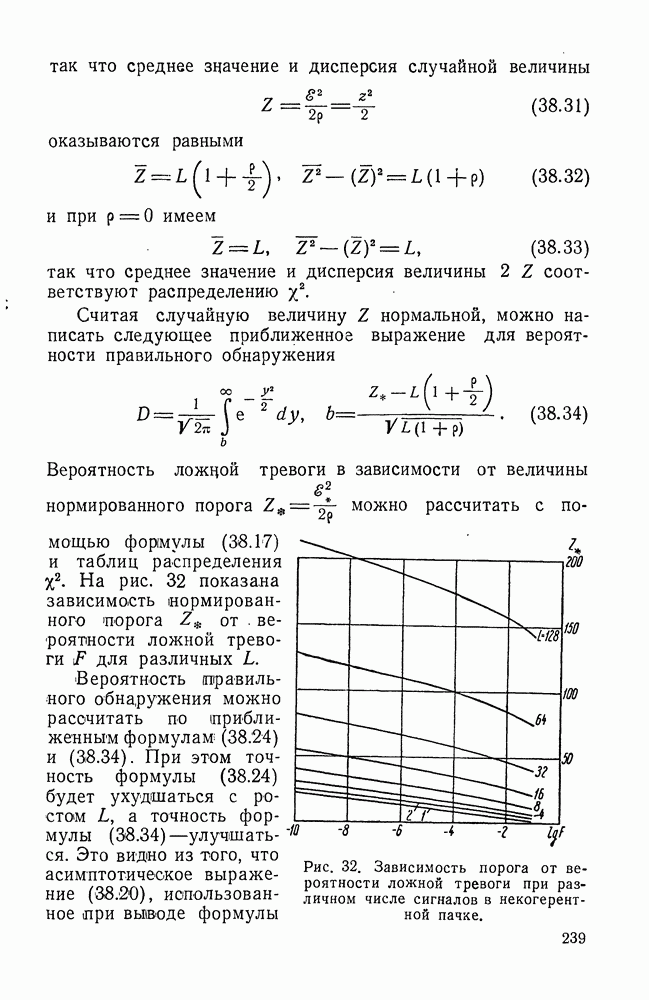
и проинтегрируем от 0 до 

Если  есть комплексное число, лежащее в нижней полуплоскости (ниже вещественной оси), так что
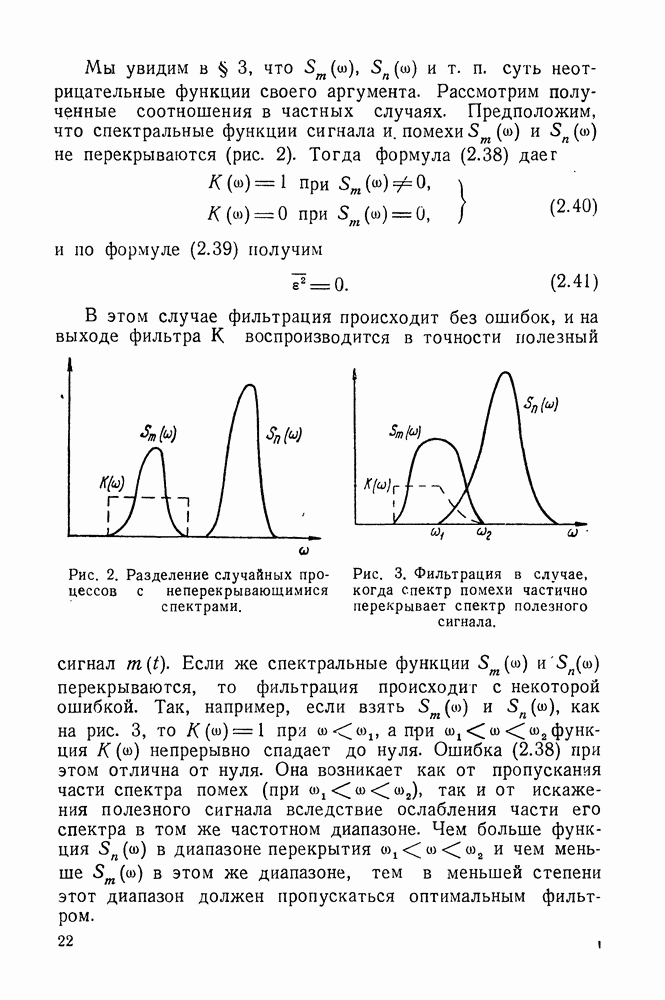
есть комплексное число, лежащее в нижней полуплоскости (ниже вещественной оси), так что  то в интеграле (8.14) можно изменить порядок интегрирования
то в интеграле (8.14) можно изменить порядок интегрирования

поскольку внутрений интеграл

сходится.
Окончательно уравнение (8.08) можно переписать в виде

Поступая так же с соотношением (8.11), т. е. умножая на  и интегрируя от
и интегрируя от  до 0, мы преобразуем его к виду
до 0, мы преобразуем его к виду

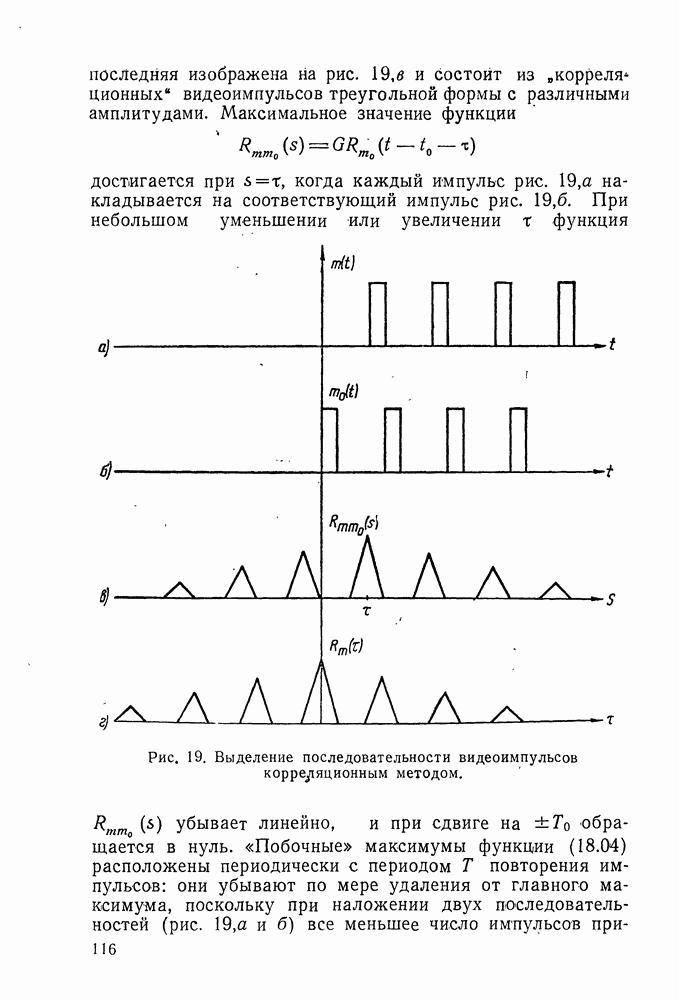
Интегралы, стоящие в левых частях формул (8.17) и (8.18), называются в теории функций комплексного переменного интегралами типа Коши. В следующем параграфе мы увидим, что теория функций комплексного переменного позволяет найти неизвестные нам функции  из соотношений (8.17) и (8.18). Предварительно мы рассмотрим некоторые положения теории функций комплексного переменного, которые нам понадобятся в дальнейшем.
из соотношений (8.17) и (8.18). Предварительно мы рассмотрим некоторые положения теории функций комплексного переменного, которые нам понадобятся в дальнейшем.
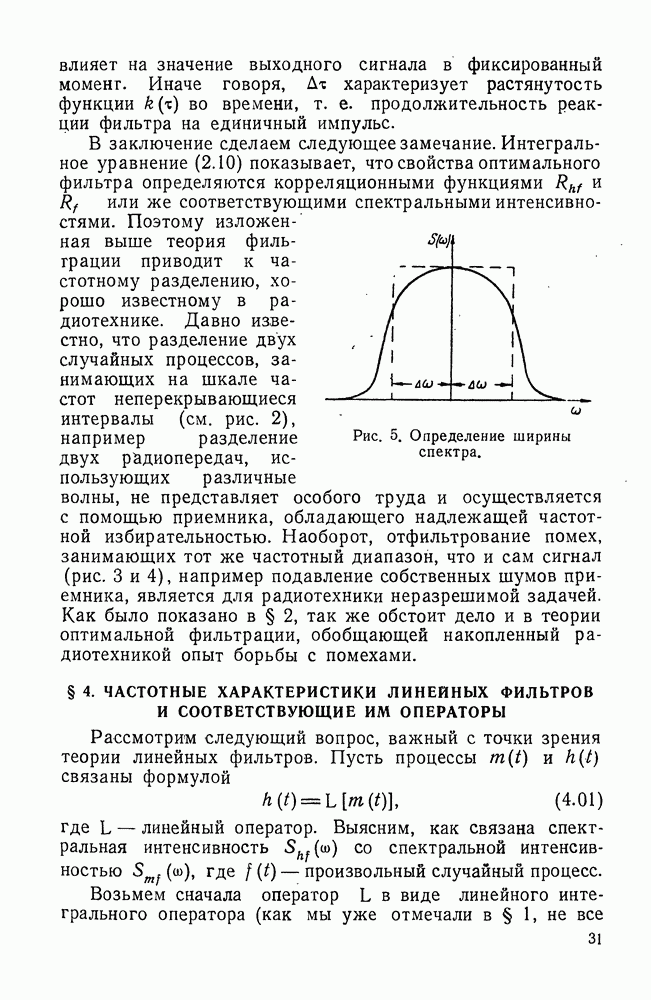
Теорема Коши. По теореме Коши, если функция  является аналитической в некоторой односвязной области, то ее значение в любой точке
является аналитической в некоторой односвязной области, то ее значение в любой точке  этой области выражается через значения этой функции на замкнутом контуре С, окружающем эту точку (см. рис. 7), следующей формулой
этой области выражается через значения этой функции на замкнутом контуре С, окружающем эту точку (см. рис. 7), следующей формулой

где  — переменная интегрирования, а интеграл берется в положительном направлении (против часовой стрелки).
— переменная интегрирования, а интеграл берется в положительном направлении (против часовой стрелки).
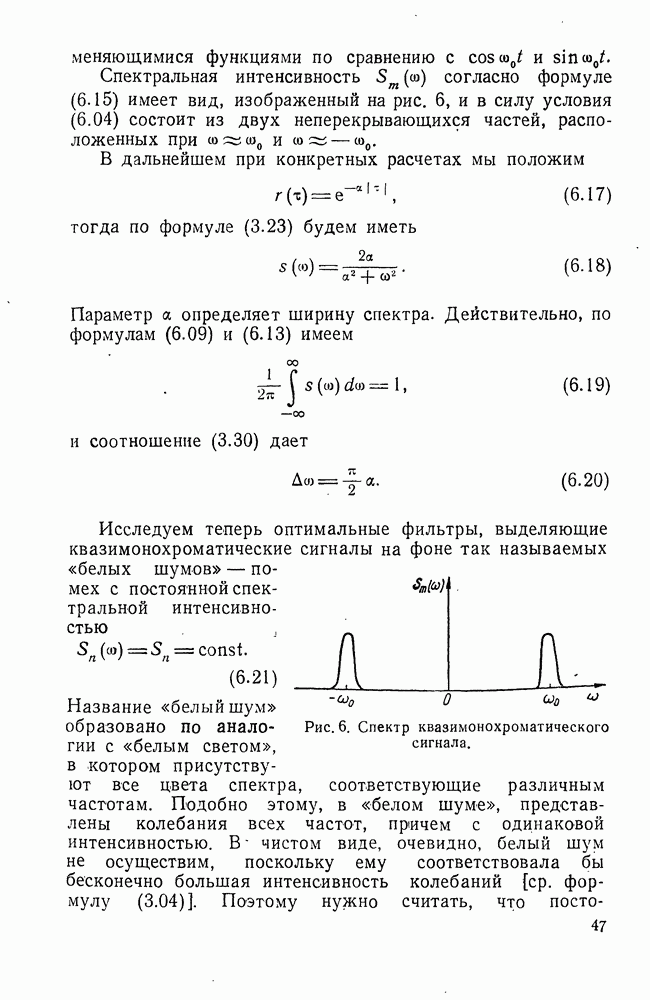
Лемма Жордана. Эту лемму можно сформулировать так. Если функция  в верхней полуплоскости и на вещественной оси (т. е. при
в верхней полуплоскости и на вещественной оси (т. е. при  ) удовлетворяет условию
) удовлетворяет условию

 есть некоторое положительное число, то при
есть некоторое положительное число, то при  имеем
имеем

где  полуокружность с центром в начале координат и радиусом
полуокружность с центром в начале координат и радиусом  находящаяся в верхней полуплоскости (рис. 8).
находящаяся в верхней полуплоскости (рис. 8).

Рис. 7. Контур С на комплексной плоскости (к теореме Коши).

Рис. 8. Контур  на комплексной плоскости (к лемме Жордана).
на комплексной плоскости (к лемме Жордана).
Если  то соотношение (8.21) справедливо, если в нижней полуплоскости и на вещественной оси (т. е. при
то соотношение (8.21) справедливо, если в нижней полуплоскости и на вещественной оси (т. е. при  выполняются те же условия, тогда полуокружность
выполняются те же условия, тогда полуокружность  лежит в нижней полуплоскости.
лежит в нижней полуплоскости.
Нам понадобится также следующая лемма.
Лемма  Пусть функция
Пусть функция  является аналитической в полосе
является аналитической в полосе

и на концах этой полосы (при  ) убывает достаточно быстро, по крайней мере, быстрее, чем
) убывает достаточно быстро, по крайней мере, быстрее, чем  где
где  в приложениях мы будем брать
в приложениях мы будем брать  так что полоса (8.22) содержит вещественную ось. Тогда, какова бы ни была функция
так что полоса (8.22) содержит вещественную ось. Тогда, какова бы ни была функция  вне полосы, она может быть разложена на сумму
вне полосы, она может быть разложена на сумму

где  функция, аналитическая во всей верхней полуплоскости, включая полосу (8.22), т. е. при
функция, аналитическая во всей верхней полуплоскости, включая полосу (8.22), т. е. при
 функция, аналитическая по всей нижней полуплоскости, включая полосу (8.22), т. е. при
функция, аналитическая по всей нижней полуплоскости, включая полосу (8.22), т. е. при 
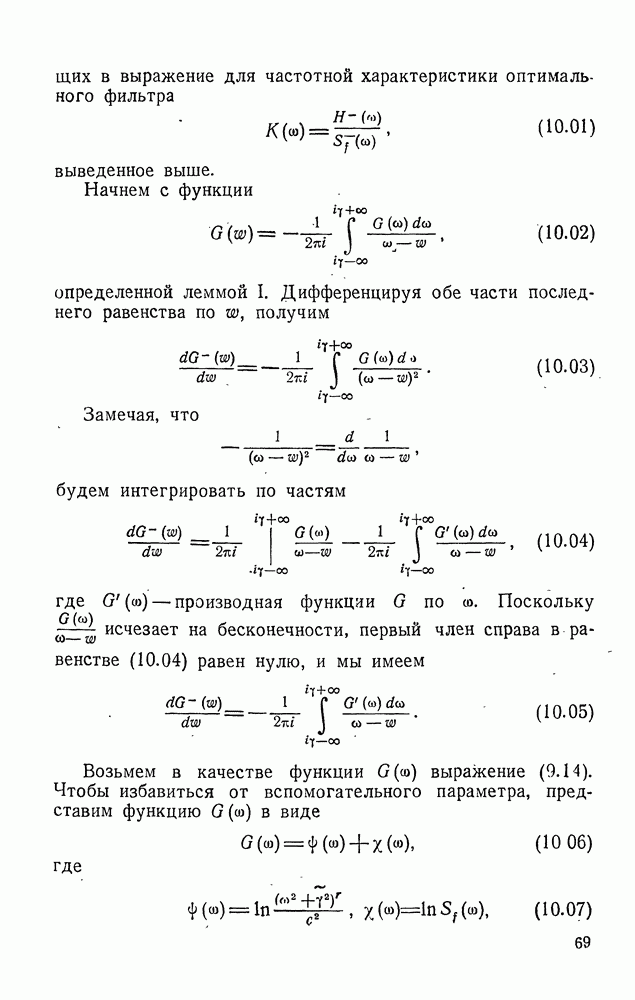
Доказательство леммы вытекает из теоремы Коши (8.19) для функции  Действительно, возьмем в качестве контура интегрирования прямоугольник (рис. 9) и будем концы этого контура продолжать до бесконечности, причем направление обхода контура будем брать против часовой стрелки. Тогда благодаря убыванию
Действительно, возьмем в качестве контура интегрирования прямоугольник (рис. 9) и будем концы этого контура продолжать до бесконечности, причем направление обхода контура будем брать против часовой стрелки. Тогда благодаря убыванию  при
при  интеграл по каждой горизонтали сходится быстрее, чем интеграл
интеграл по каждой горизонтали сходится быстрее, чем интеграл

т. е. стремится к определенному пределу. По той же причине интегралы по вертикальным отрезкам стремятся к нулю.

Рис. 9. Прямоугольный контур (к лемме I).
Поэтому функцию  в полосе (8.22) можно представить так
в полосе (8.22) можно представить так

где первый интеграл берется по нижнему краю полосы, а второй — по верхнему краю. Обозначим

Первый интеграл представляет собой аналитическую функцию выше пути интегрирования. Ниже пути интегрирования  тоже аналитическая функция, но уже другая, поскольку при переходе через путь интегрирования функция терпит скачок. Второй интеграл представляет собой функцию, аналитическую ниже пути интегрирования, т. е.
тоже аналитическая функция, но уже другая, поскольку при переходе через путь интегрирования функция терпит скачок. Второй интеграл представляет собой функцию, аналитическую ниже пути интегрирования, т. е.  можно продолжить аналитически во всю нижнюю полуплоскость.
можно продолжить аналитически во всю нижнюю полуплоскость.
Дадим оценку поведения функций  на бесконечности; она имеет различный вид для случаев
на бесконечности; она имеет различный вид для случаев  Если
Если  то при
то при 

где интеграл

в силу условия  сходится.
сходится.
Если число  заключено между 0 и 1 (или
заключено между 0 и 1 (или  ), то мы получаем расходящийся интеграл
), то мы получаем расходящийся интеграл  . В этом случае можно показать, что функция
. В этом случае можно показать, что функция  убывает медленнее, чем Действительно, разобьем интеграл для функции
убывает медленнее, чем Действительно, разобьем интеграл для функции  на три интеграла по промежуткам, изображенным на рис. 10. Интеграл по промежутку 2 есть интеграл в конечных пределах, и для него справедлива оценка
на три интеграла по промежуткам, изображенным на рис. 10. Интеграл по промежутку 2 есть интеграл в конечных пределах, и для него справедлива оценка  Что касается интегралов но участкам 1 и 3, то при достаточно большом
Что касается интегралов но участкам 1 и 3, то при достаточно большом  их можно оценить, если положить на них
их можно оценить, если положить на них  где С — константа. Тогда, например, интеграл по промежутку 3 равен
где С — константа. Тогда, например, интеграл по промежутку 3 равен

где  Интеграл в правой части равенства (8.29) при
Интеграл в правой части равенства (8.29) при  либо конечен (если
либо конечен (если  ), либо возрастает, как
), либо возрастает, как  (если
(если  ), поскольку
), поскольку

Аналогичную оценку будем иметь и для интеграла по левому промежутку 1. Следовательно,  убывает, как
убывает, как  или
или  т. е. медленнее, чем
т. е. медленнее, чем  Такие же свойства имеет и функция
Такие же свойства имеет и функция 

Рис. 10. Разбиение интервала интегрирования на три части (к лемме I).
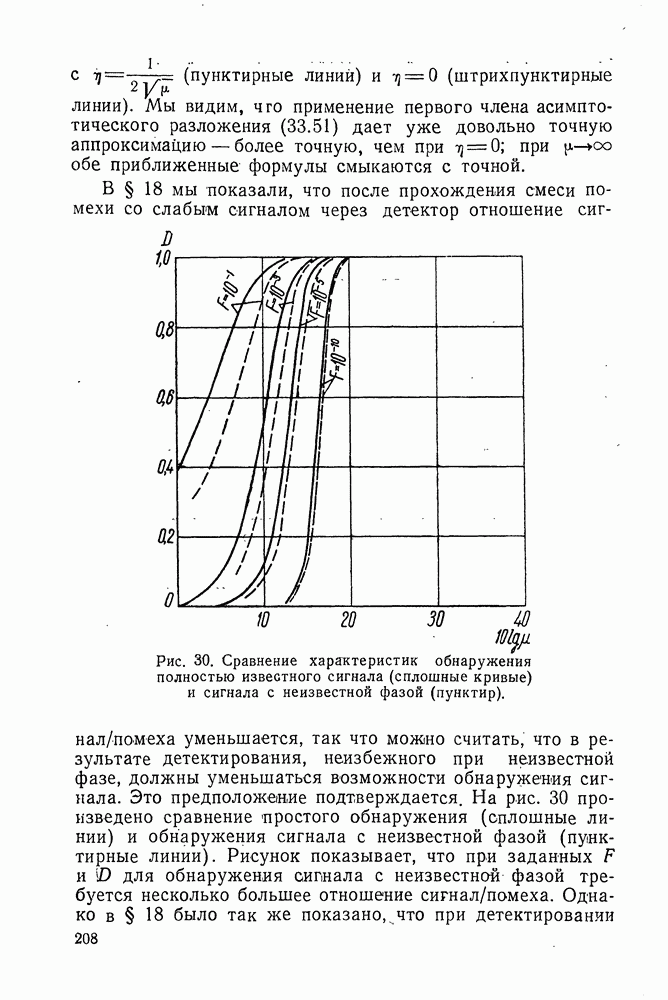
Теория интегральных уравнений, к которым сводится исследование оптимальных фильтров II типа, дана Винером и Хопфом и с более общей точки зрения — В. А. Фоком. В нашем изложении методики решения уравнения (8.03) мы, в основном, следуем работе Фока.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. СТАТИСТИЧЕСКАЯ ТЕОРИЯ ОПТИМАЛЬНЫХ ЛИНЕЙНЫХ ФИЛЬТРОВ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФИЛЬТРАЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 2. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ОПТИМАЛЬНОГО ЛИНЕЙНОГО ФИЛЬТРА
- § 3. КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ И СПЕКТРАЛЬНЫЕ ИНТЕНСИВНОСТИ
- § 4. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ФИЛЬТРОВ И СООТВЕТСТВУЮЩИЕ ИМ ОПЕРАТОРЫ
- § 5. ОБОБЩЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ОПТИМАЛЬНОГО ФИЛЬТРА
- § 6. ФИЛЬТРАЦИЯ КВАЗИМОНОХРОМАТИЧЕСКИХ СИГНАЛОВ С ПОМОЩЬЮ ФИЛЬТРА I ТИПА
- § 7. ОБ ОСНОВНЫХ ПОЛОЖЕНИЯХ СТАТИСТИЧЕСКОЙ ТЕОРИИ ФИЛЬТРАЦИИ
- ГЛАВА II. ФИЛЬТРАЦИЯ И ПРОГНОЗИРОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 8. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ОПТИМАЛЬНОГО ЛИНЕЙНОГО ФИЛЬТРА II ТИПА
- § 9. ОПРЕДЕЛЕНИЕ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ОПТИМАЛЬНОГО ФИЛЬТРА II ТИПА
- § 10. ИССЛЕДОВАНИЕ ФУНКЦИЙ …
- § 11. ПОСТРОЕНИЕ ОПТИМАЛЬНОГО ФИЛЬТРА II ТИПА
- § 12. ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ТЕОРИИ ФИЛЬТРАЦИИ И ПРОГНОЗИРОВАНИЯ
- § 13. ПРОГНОЗИРОВАНИЕ СИНГУЛЯРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 14. ОБЩИЕ СООБРАЖЕНИЯ О ФИЛЬТРАЦИИ
- § 15. ВЫДЕЛЕНИЕ КВАЗИМОНОХРОМАТИЧЕСКИХ СИГНАЛОВ ФИЛЬТРАМИ II ТИПА
- ГЛАВА III. ВЫДЕЛЕНИЕ СИГНАЛОВ ИЗВЕСТНОЙ ФОРМЫ НА ФОНЕ СЛУЧАЙНЫХ ПОМЕХ
- § 17. СОГЛАСОВАННЫЙ ФИЛЬТР ИЛИ КОРРЕЛЯТОР
- § 18. КОРРЕЛЯТОР В ВИДЕОКАНАЛЕ РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- § 19. ТЕОРЕМА КОТЕЛЬНИКОВА И СОПРЯЖЕННАЯ ТЕОРЕМА
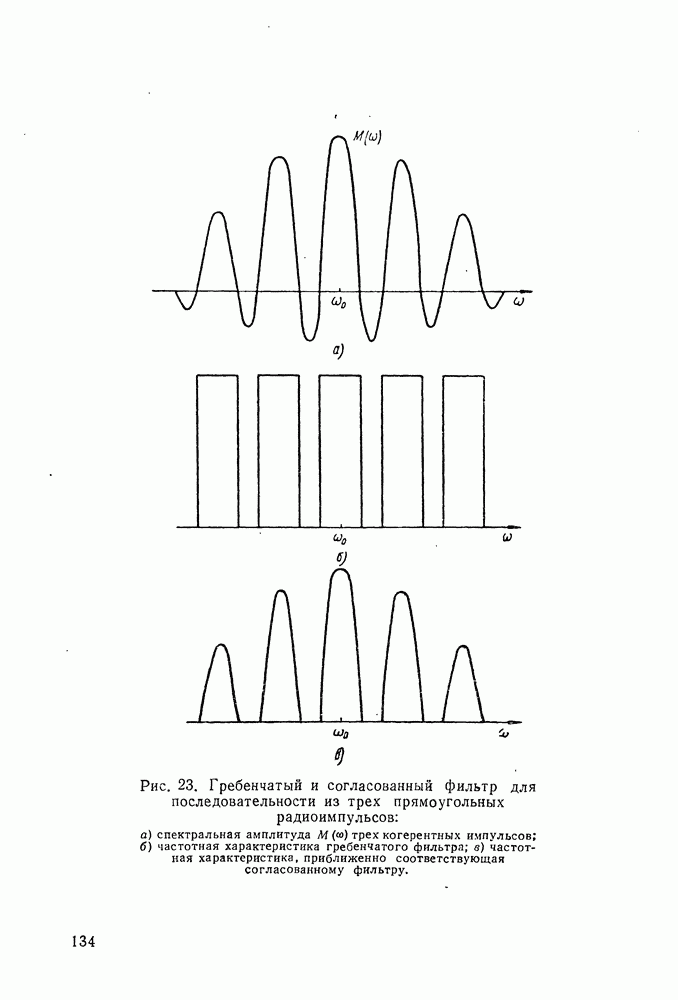
- § 20. ГРЕБЕНЧАТЫЙ ФИЛЬТР И СОГЛАСОВАННЫЙ ФИЛЬТР (КОРРЕЛЯТОР) ДЛЯ ПОСЛЕДОВАТЕЛЬНОСТИ РАДИОИМПУЛЬСОВ
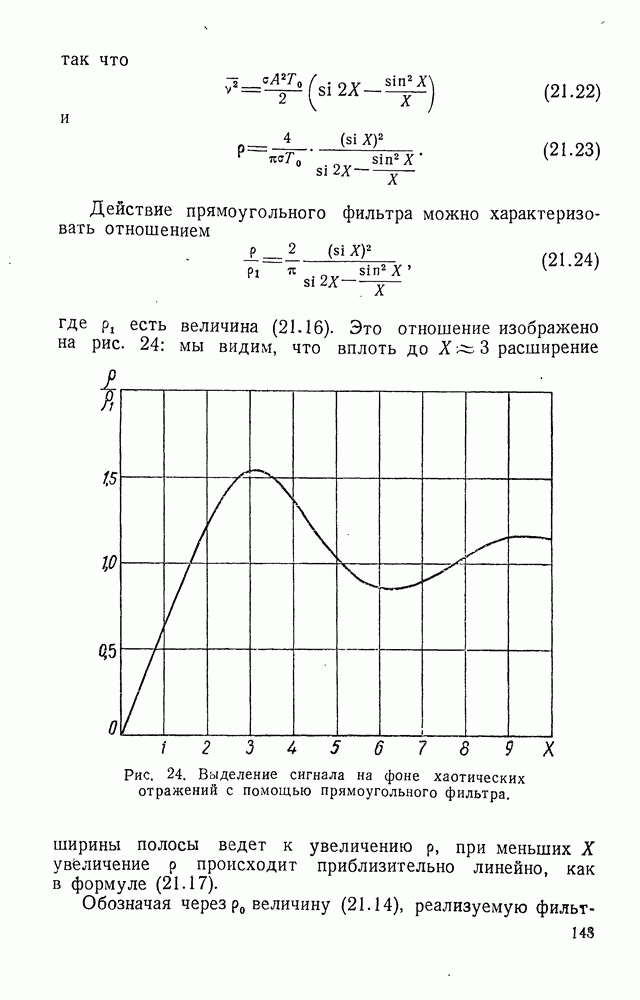
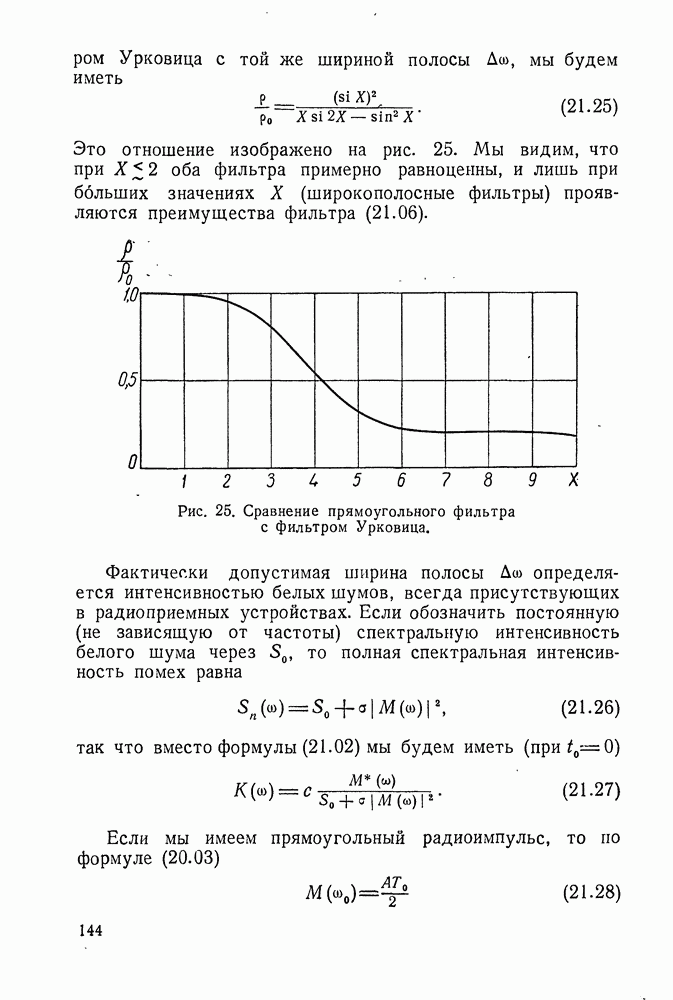
- § 21. ФИЛЬТР УРКОВИЦА
- § 22. О ФИЛЬТРАХ, ВЫДЕЛЯЮЩИХ СИГНАЛЫ ИЗВЕСТНОЙ ФОРМЫ
- ГЛАВА IV. СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 23. ФИЛЬТРАЦИЯ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- § 24. ТЕОРЕМА ХИНЧИНА ДЛЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ. НЕКОТОРЫЕ ВОПРОСЫ ФИЛЬТРАЦИИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- § 25. ФИЛЬТР ДЛЯ ВЫДЕЛЕНИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ИЗВЕСТНОЙ ФОРМЫ
- § 26. ФИЛЬТРАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ПРОЦЕССОВ I
- § 27. ФИЛЬТРАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ПРОЦЕССОВ. II
- ЧАСТЬ ВТОРАЯ. СТАТИСТИЧЕСКАЯ ТЕОРИЯ ОПТИМАЛЬНЫХ ПРИЕМНИКОВ
- § 28. ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ПРИЕМА
- § 29. АПОСТЕРИОРНЫЕ ВЕРОЯТНОСТИ И КОЭФФИЦИЕНТЫ ПРАВДОПОДОБИЯ
- § 30. АПРИОРНЫЕ ВЕРОЯТНОСТИ. РЕШАЮЩИЕ СХЕМЫ
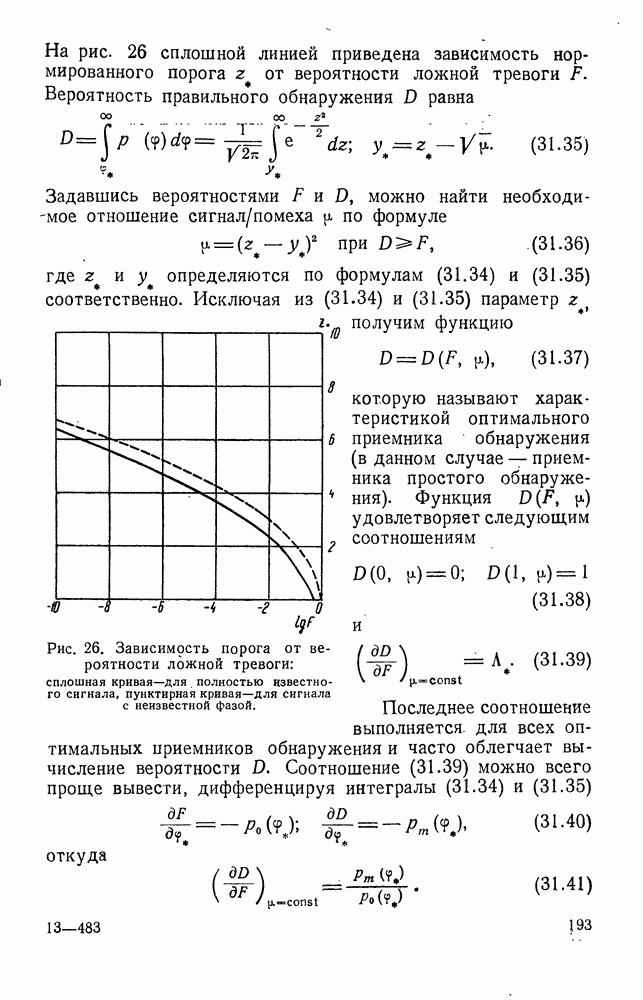
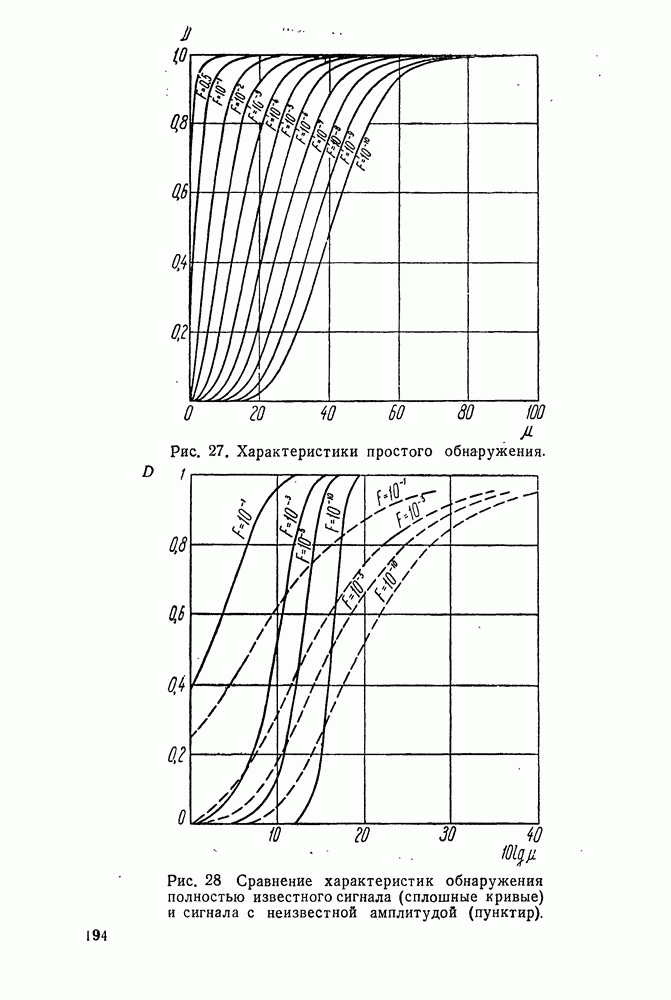
- § 31. ПРОСТОЕ ОБНАРУЖЕНИЕ СИГНАЛА НА ФОНЕ КОРРЕЛИРОВАННЫХ НОРМАЛЬНЫХ ПОМЕХ
- § 32. СЛОЖНОЕ ОБНАРУЖЕНИЕ СИГНАЛА С НЕИЗВЕСТНОЙ АМПЛИТУДОЙ
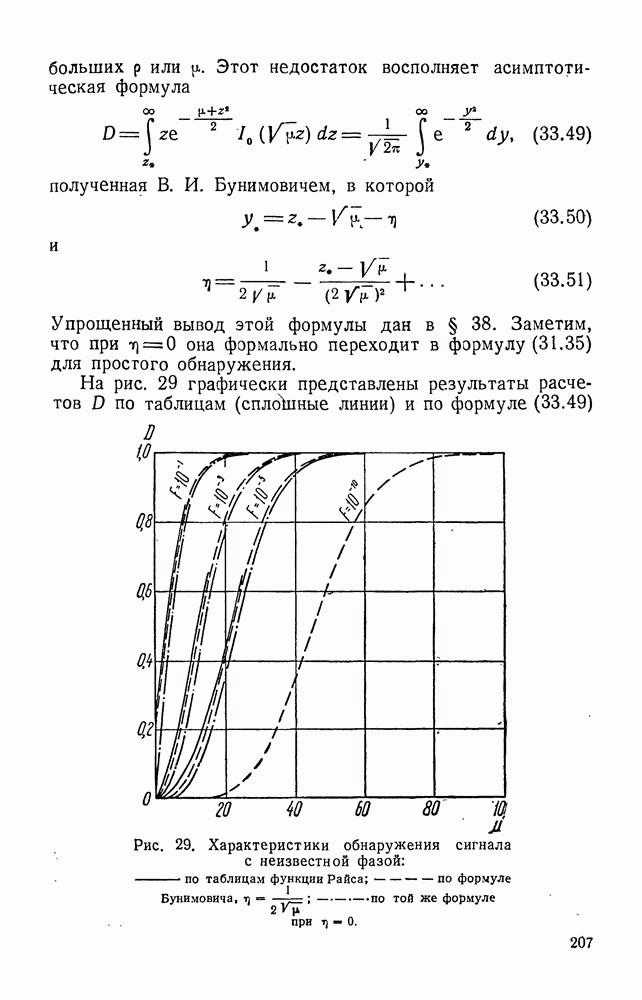
- § 33. ОБНАРУЖЕНИЕ СИГНАЛА С НЕИЗВЕСТНОЙ ФАЗОЙ
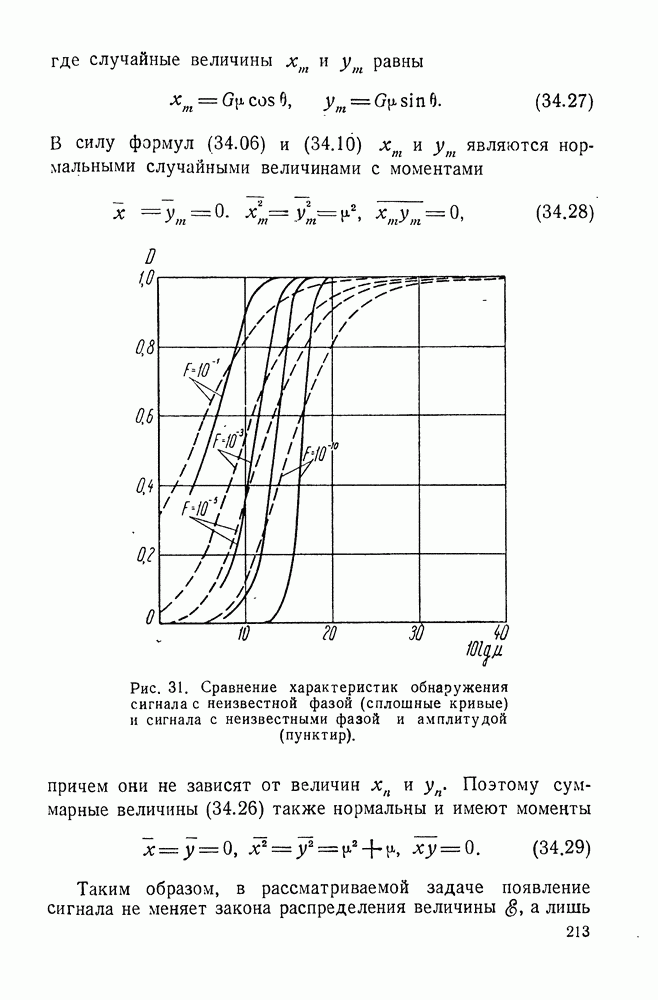
- § 34. ОБНАРУЖЕНИЕ СИГНАЛА С НЕИЗВЕСТНЫМИ ФАЗОЙ И АМПЛИТУДОЙ
- § 35. ОБНАРУЖЕНИЕ СЛУЧАЙНОГО ПРОЦЕССА (ПОЛЕЗНОГО СИГНАЛА) НА ФОНЕ ДРУГОГО СЛУЧАЙНОГО ПРОЦЕССА (ПОМЕХИ) ПРИ ЗАДАННЫХ КОРРЕЛЯЦИОННЫХ СВОЙСТВАХ ОБОИХ ПРОЦЕССОВ
- ГЛАВА VI. ОБНАРУЖЕНИЕ ПАЧКИ СИГНАЛОВ
- § 36. КОГЕРЕНТНАЯ И НЕКОГЕРЕНТНАЯ ПАЧКИ СИГНАЛОВ. О КОРРЕЛИРОВАННЫХ ПОМЕХАХ В РАДИОЛОКАЦИИ
- § 37. ОБНАРУЖЕНИЕ НЕКОГЕРЕНТНОЙ ПАЧКИ СИГНАЛОВ НА ФОНЕ НОРМАЛЬНЫХ ПОМЕХ
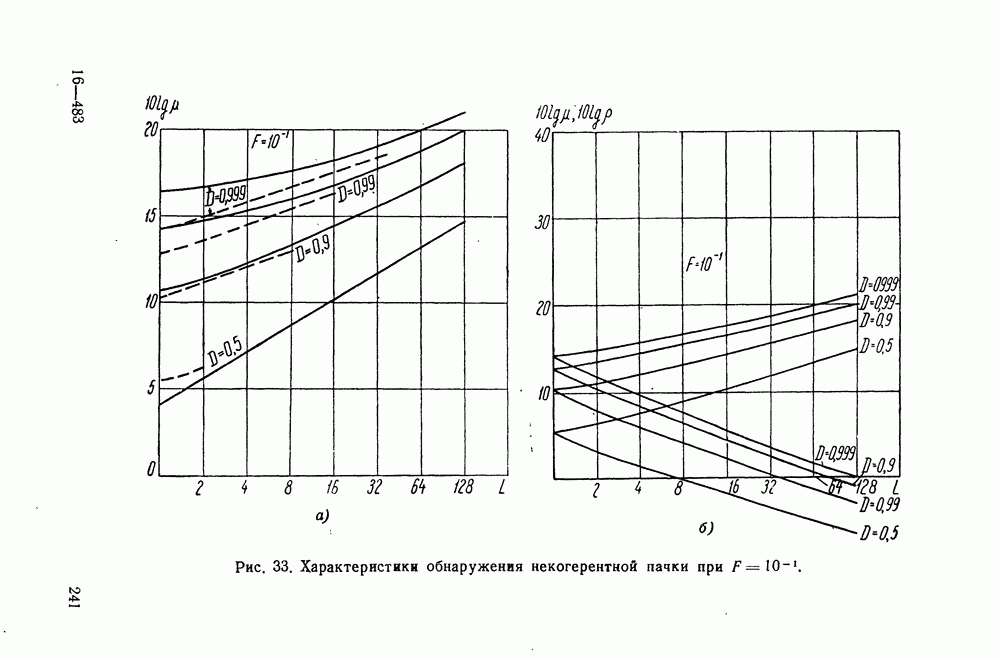
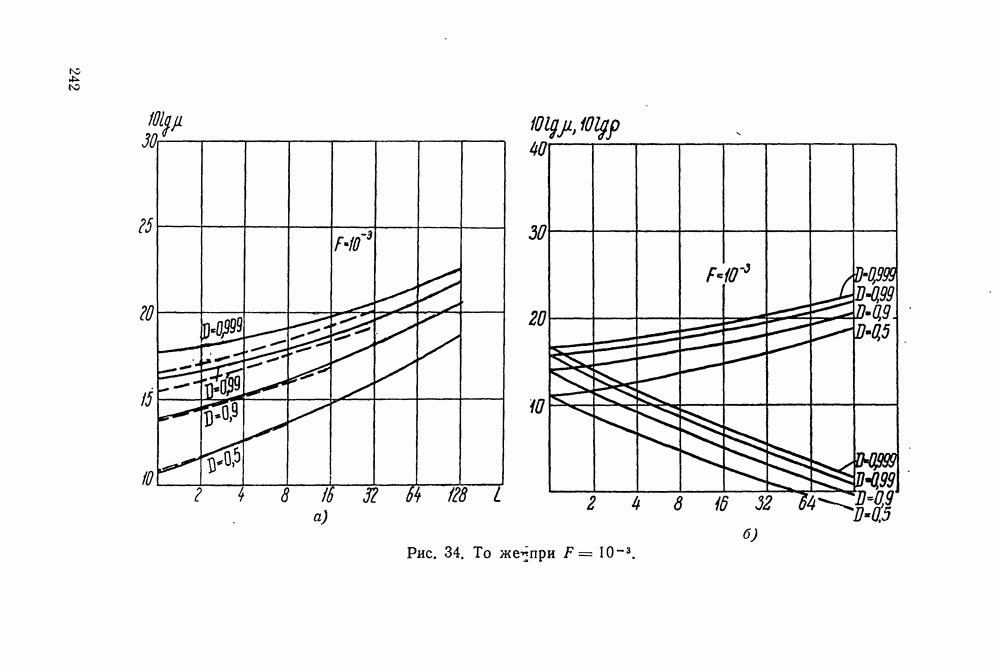
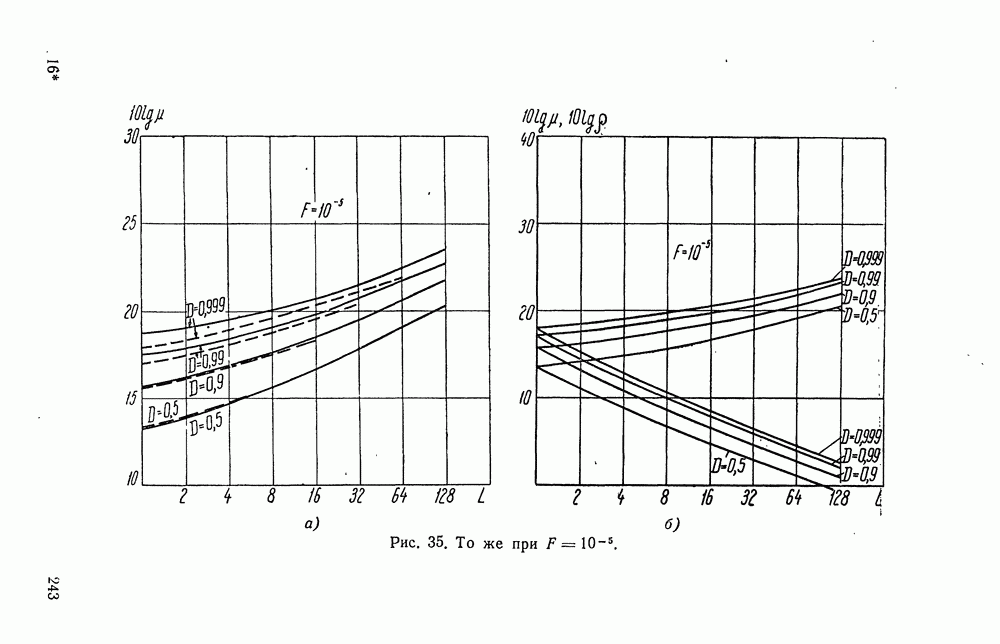
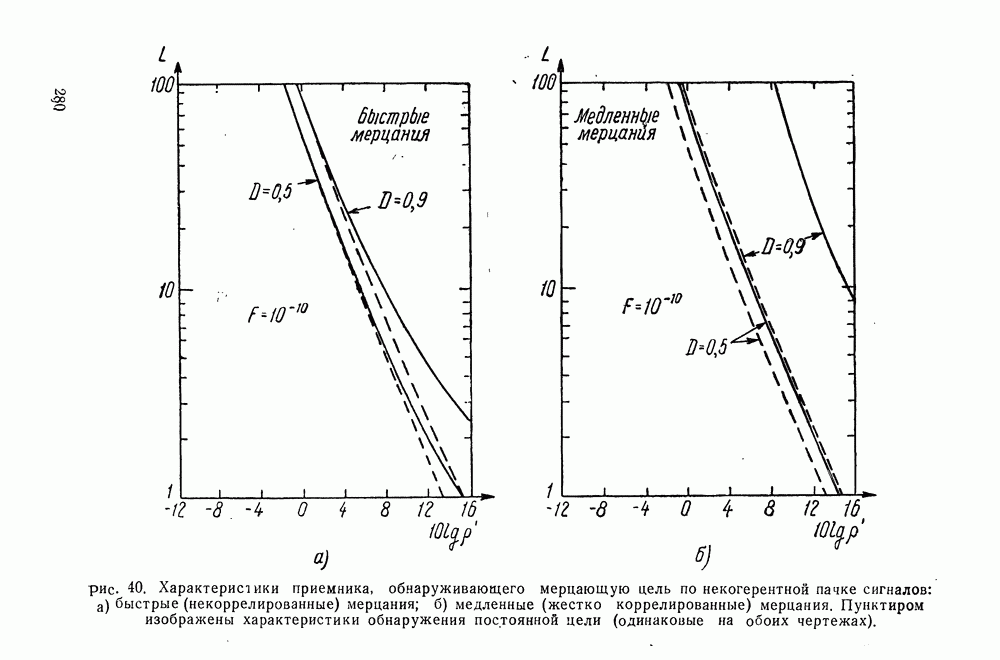
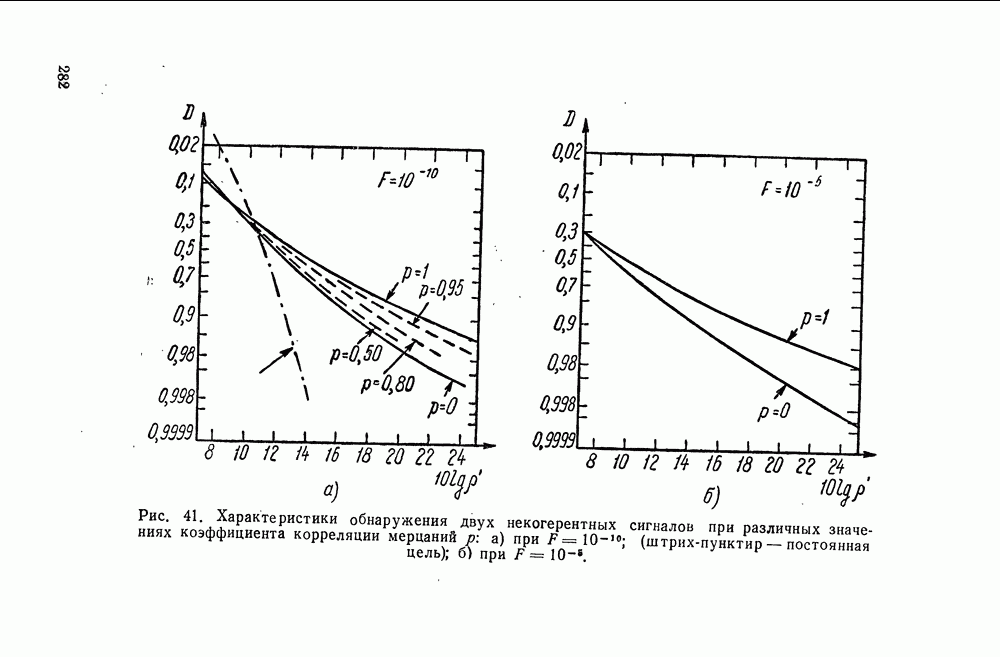
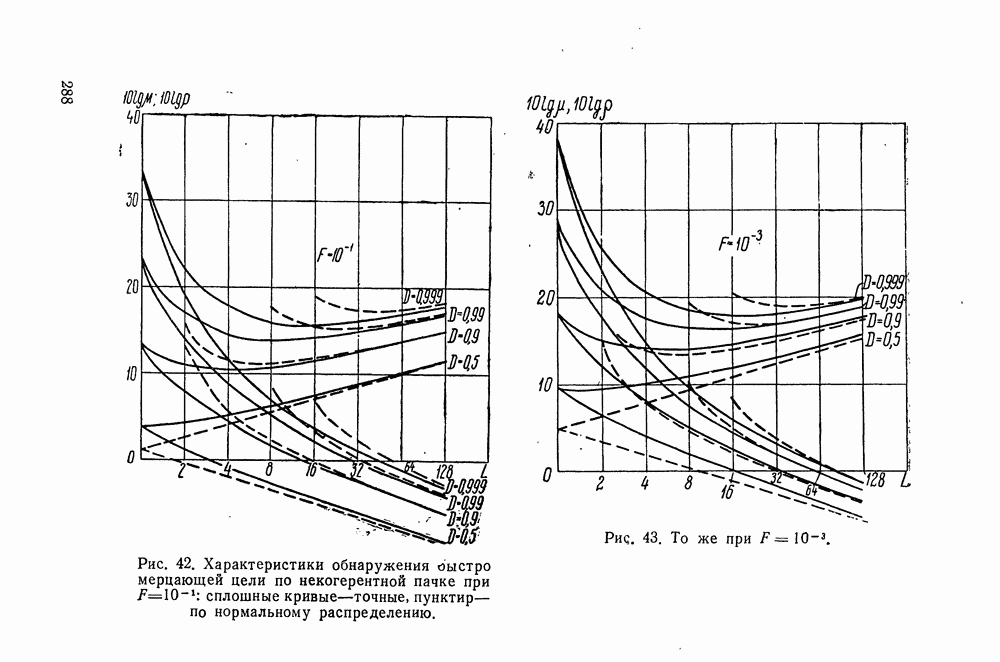
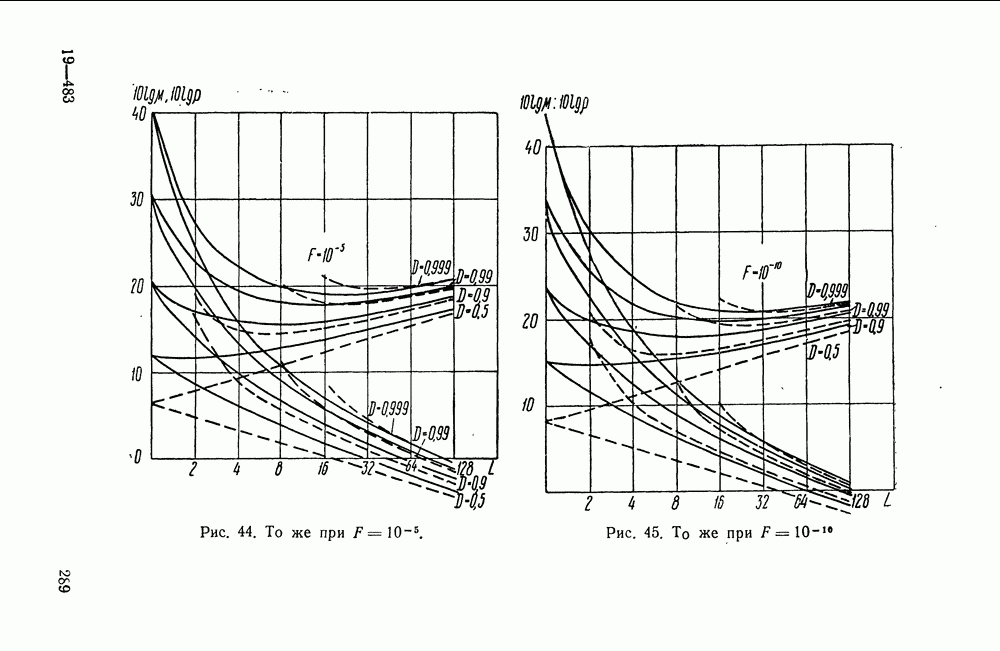
- § 38. ХАРАКТЕРИСТИКИ ПРИЕМНИКА, ОБНАРУЖИВАЮЩЕГО НЕКОГЕРЕНТНУЮ ПАЧКУ
- § 39. ОБНАРУЖЕНИЕ КОГЕРЕНТНОЙ ПАЧКИ НА ФОНЕ НОРМАЛЬНЫХ КОРРЕЛИРОВАННЫХ ПОМЕХ
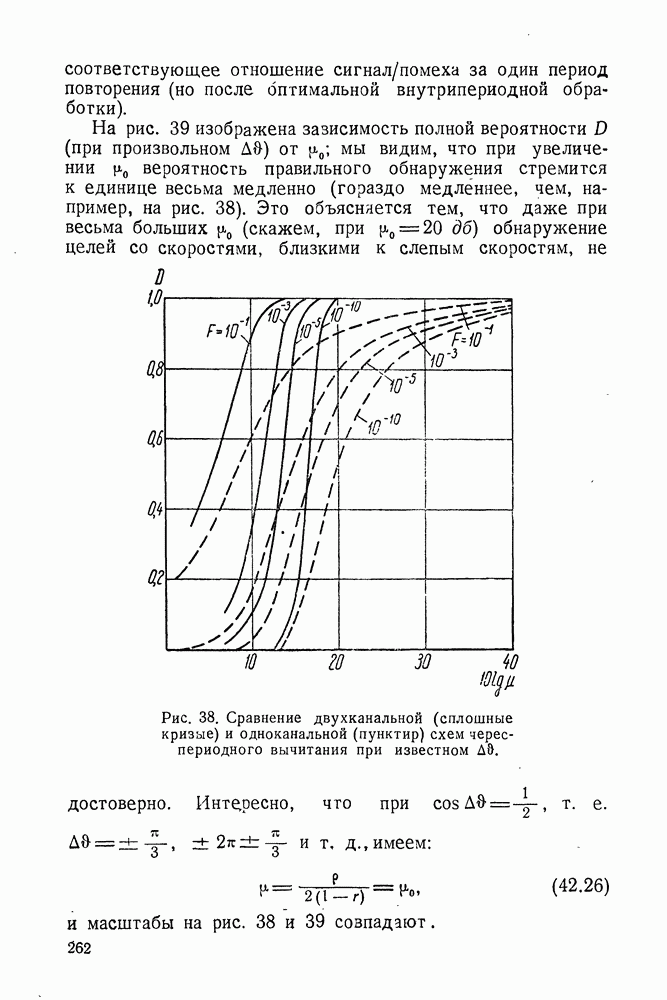
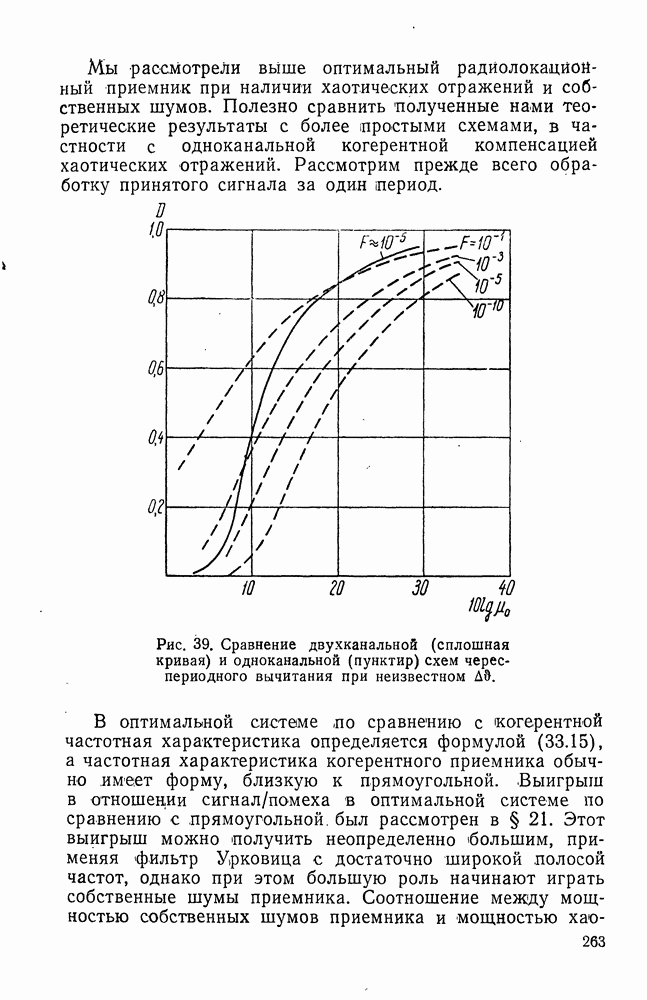
- § 40. ОПТИМАЛЬНОЕ ОБНАРУЖЕНИЕ КОГЕРЕНТНОЙ ПАЧКИ ПРИ РАЗЛИЧНЫХ СКОРОСТЯХ ЦЕЛИ
- § 41. ОБНАРУЖЕНИЕ КОГЕРЕНТНОЙ ПАЧКИ СИГНАЛОВ ЗА ДВА ПЕРИОДА ПОВТОРЕНИЯ ПРИ ИЗВЕСТНОМ И НЕИЗВЕСТНОМ СМЕЩЕНИИ ЧАСТОТЫ
- § 42. ВЕРОЯТНОСТИ F И D ПРИ ЧЕРЕСПЕРИОДНОМ ВЫЧИТАНИИ
- ГЛАВА VII. РАДИОЛОКАЦИОННОЕ ОБНАРУЖЕНИЕ «МЕРЦАЮЩЕЙ ЦЕЛИ»
- § 44. КОЭФФИЦИЕНТ ПРАВДОПОДОБИЯ ДЛЯ НЕКОГЕРЕНТНОЙ ПАЧКИ
- § 45. ХАРАКТЕРИСТИКИ ПРИЕМНИКА, ПРОИЗВОДЯЩЕГО КВАДРАТИЧНОЕ СУММИРОВАНИЕ
- § 46. РАЗЛИЧНЫЕ АППРОКСИМАЦИИ В ЗАДАЧАХ ОБ ОБНАРУЖЕНИИ НЕКОГЕРЕНТНОЙ ПАЧКИ
- § 47. КОЭФФИЦИЕНТ ПРАВДОПОДОБИЯ ДЛЯ КОГЕРЕНТНОЙ ПАЧКИ
- § 48. ОПТИМАЛЬНЫЙ ПРИЕМНИК В ЧАСТНЫХ СЛУЧАЯХ
- § 49. ХАРАКТЕРИСТИКИ ПРИЕМНИКА, ОБРАЗУЮЩЕГО ЧЕРЕСПЕРИОДНУЮ РАЗНОСТЬ
- ГЛАВА VIII. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ПОЛЕЗНОГО СИГНАЛА ПРИ НАЛИЧИИ ПОМЕХ
- § 50. ИЗМЕРЕНИЕ ПАРАМЕТРА ПО МАКСИМУМУ АПОСТЕРИОРНОЙ ВЕРОЯТНОСТИ
- § 51. ВЫДЕЛЕНИЕ СЛУЧАЙНОГО СИГНАЛА НА ФОНЕ СЛУЧАЙНЫХ ПОМЕХ
- § 52. ИЗМЕРЕНИЕ ПАРАМЕТРА СИГНАЛА ПРИ СЛАБЫХ И СИЛЬНЫХ ПОМЕХАХ
- § 53. ПРОСТОЕ ИЗМЕРЕНИЕ ВРЕМЕНИ ПРИХОДА СИГНАЛА ПРИ СЛАБЫХ ПОМЕХАХ
- § 54. СЛОЖНОЕ ИЗМЕРЕНИЕ ВРЕМЕНИ ПРИХОДА СИГНАЛА ПРИ СЛАБЫХ ПОМЕХАХ
- § 55. ИЗМЕРЕНИЕ МОМЕНТА ПРИХОДА СИГНАЛА ПРИ ПРОИЗВОЛЬНЫХ ПОМЕХАХ
- § 56. ЗАДАЧА О РАЗЛИЧЕНИИ M ОРТОГОНАЛЬНЫХ СИГНАЛОВ
- § 57. ОБНАРУЖЕНИЕ СИГНАЛА С ДИСКРЕТНЫМ ПАРАМЕТРОМ И ИЗМЕРЕНИЕ ЭТОГО ПАРАМЕТРА
- ЧАСТЬ ТРЕТЬЯ. ВСПОМОГАТЕЛЬНЫЕ ВОПРОСЫ
- ГЛАВА IX. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И СЛУЧАЙНЫЕ ПРОЦЕССЫ НОРМАЛЬНОГО ТИПА
- § 59. МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ГАУССА
- § 60. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ДЛЯ ОГИБАЮЩИХ
- § 61. ТЕПЛОВЫЕ И ДРОБОВЫЕ ШУМЫ КАК ПРИМЕРЫ НОРМАЛЬНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- ГЛАВА Х. ТЕОРИЯ ФЛЮКТУАЦИОННОЙ МОДУЛЯЦИИ
- § 63. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И СПЕКТР МОДУЛИРОВАННЫХ КОЛЕБАНИЙ
- § 64. МОДУЛЯЦИЯ С ПОМОЩЬЮ МОНОХРОМАТИЧЕСКИХ КОЛЕБАНИЙ (КВАЗИСИНУСОИДАЛЬНАЯ МОДУЛЯЦИЯ)
- § 65. ПРЕДЕЛЬНЫЕ СЛУЧАИ СПЕКТРАЛЬНЫХ РАСПРЕДЕЛЕНИЙ
- § 66. ЗАВИСИМОСТЬ ШИРИНЫ СПЕКТРА МОДУЛИРОВАННЫХ КОЛЕБАНИЙ ОТ ШИРИНЫ СПЕКТРА МОДУЛИРУЮЩИХ КОЛЕБАНИЙ
- ГЛАВА XI. ХАОТИЧЕСКИЕ ОТРАЖЕНИЯ
- § 67. ПОМЕХИ, ОБУСЛОВЛЕННЫЕ ХАОТИЧЕСКИМИ ОТРАЖЕНИЯМИ
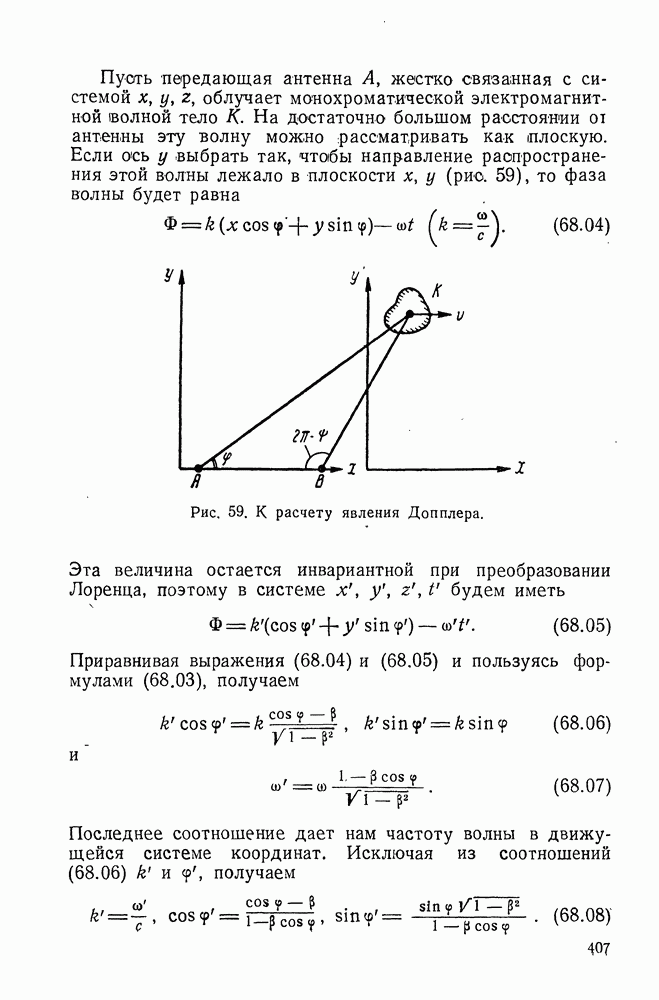
- § 68. ЯВЛЕНИЕ ДОППЛЕРА
- § 69. ФУНКЦИЯ КОРРЕЛЯЦИИ ПОМЕХИ, ОБУСЛОВЛЕННОЙ ХАОТИЧЕСКИМИ ОТРАЖЕНИЯМИ
- § 70. РАССЕЯНИЕ РАДИОВОЛН НА БЛУЖДАЮЩИХ ЧАСТИЦАХ
- § 71. ПРИМЕНЕНИЕ ТЕОРИИ ФЛЮКТУАЦИОННОИ МОДУЛЯЦИИ К ХАОТИЧЕСКИМ ОТРАЖЕНИЯМ
- ПРИЛОЖЕНИЕ I. ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ И ОПТИМАЛЬНЫЕ ПРИЕМНИКИ
- ПРИЛОЖЕНИЕ II. ОБ ОТНОШЕНИИ СИГНАЛ/ПОМЕХА ПРИ НЕОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ОБРАБОТКЕ ВХОДНЫХ ДАННЫХ
- ПРИЛОЖЕНИЕ III. О ПАРАДОКСАХ В ТЕОРИИ ОБНАРУЖЕНИЯ
- ПРИЛОЖЕНИЕ IV. ПРЕОБРАЗОВАНИЕ НЕМОНОХРОМАТИЧЕСКИХ СИГНАЛОВ ВСЛЕДСТВИЕ ЯВЛЕНИЯ ДОППЛЕРА
- ПРИЛОЖЕНИЕ V. О «СВЕТЯЩИХСЯ ТОЧКАХ»
- ЛИТЕРАТУРА