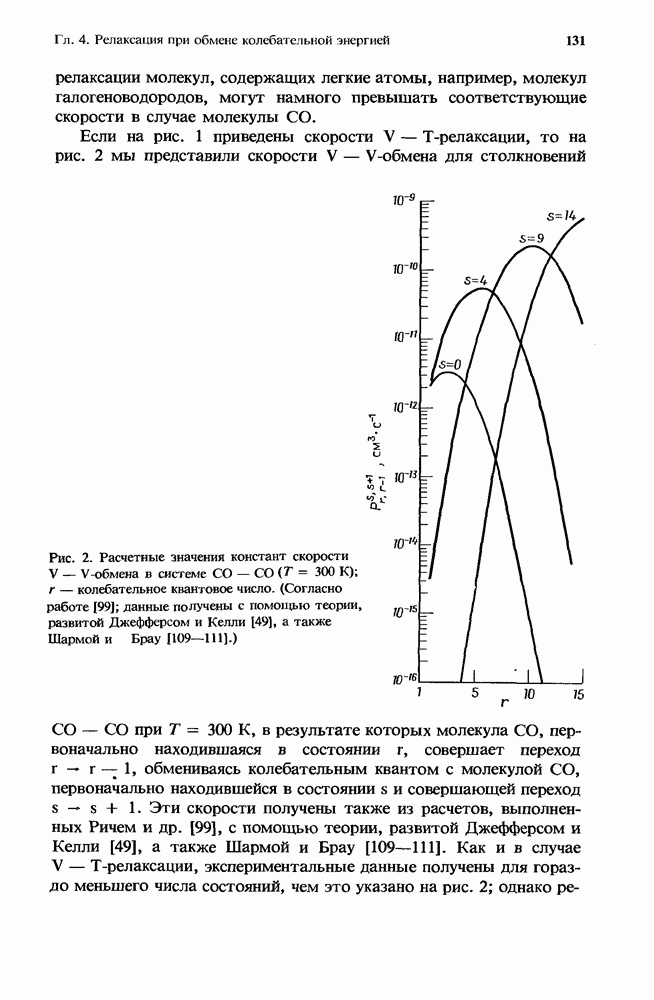
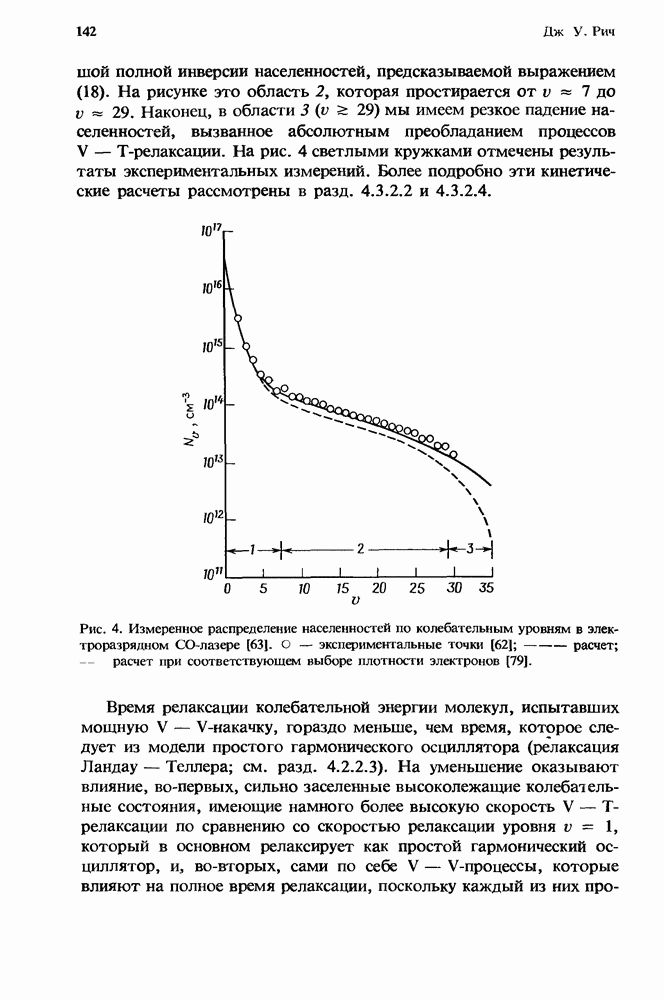
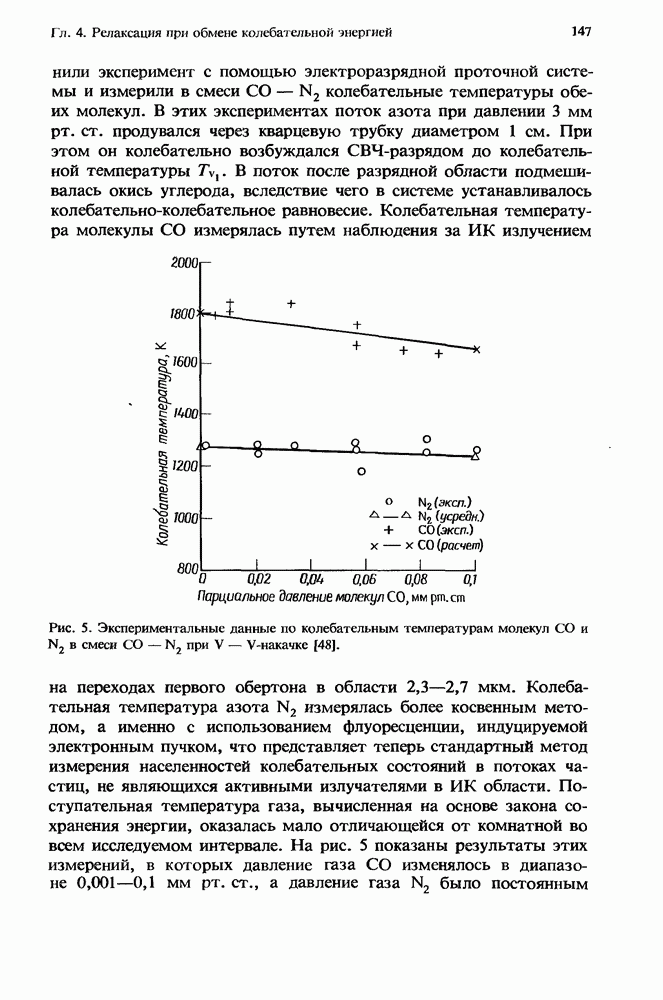
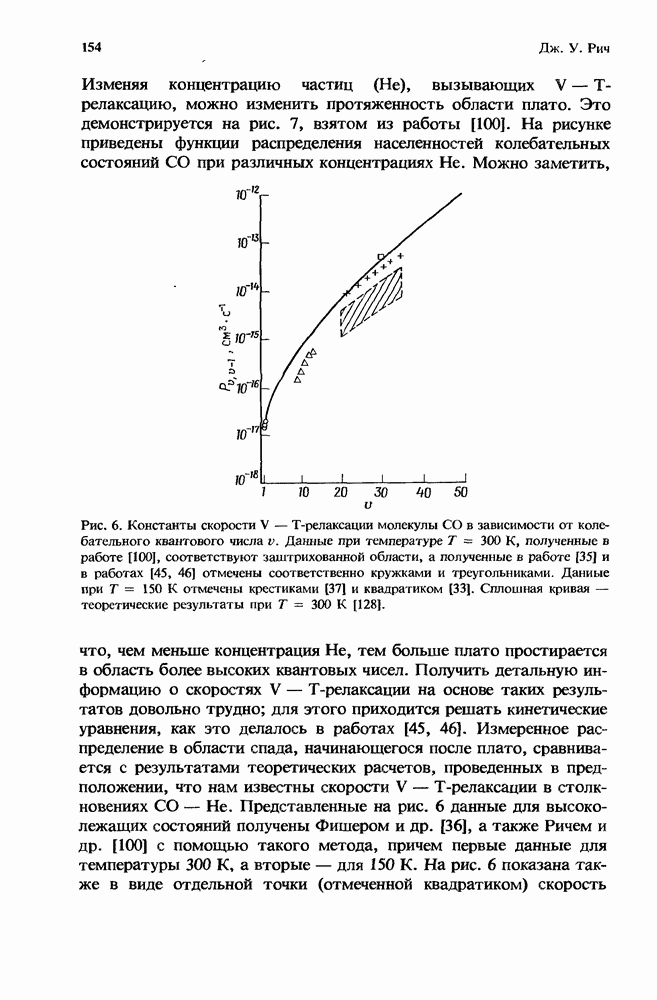
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
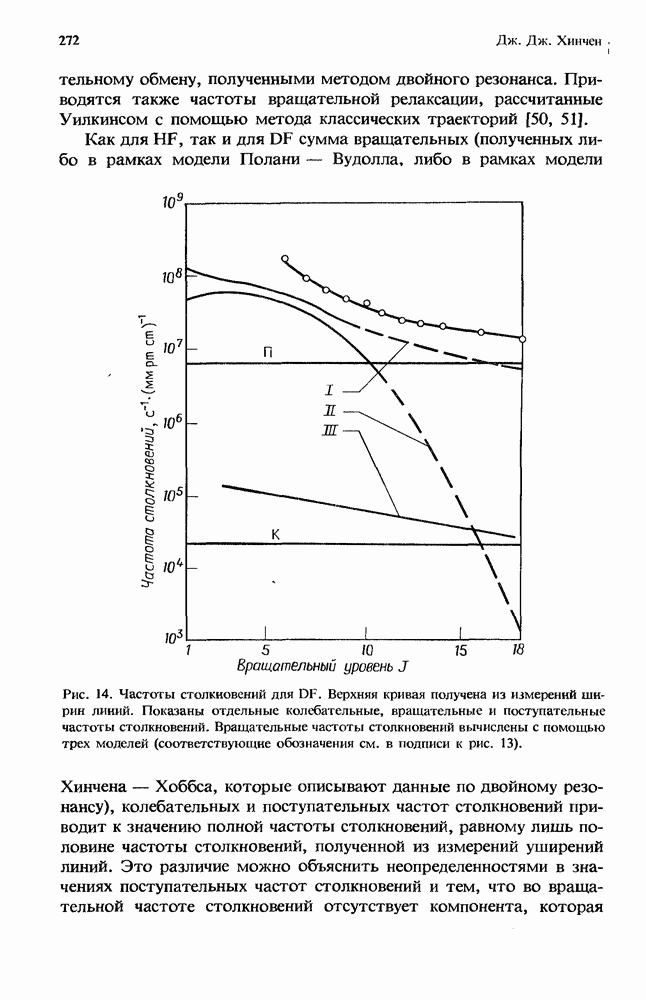
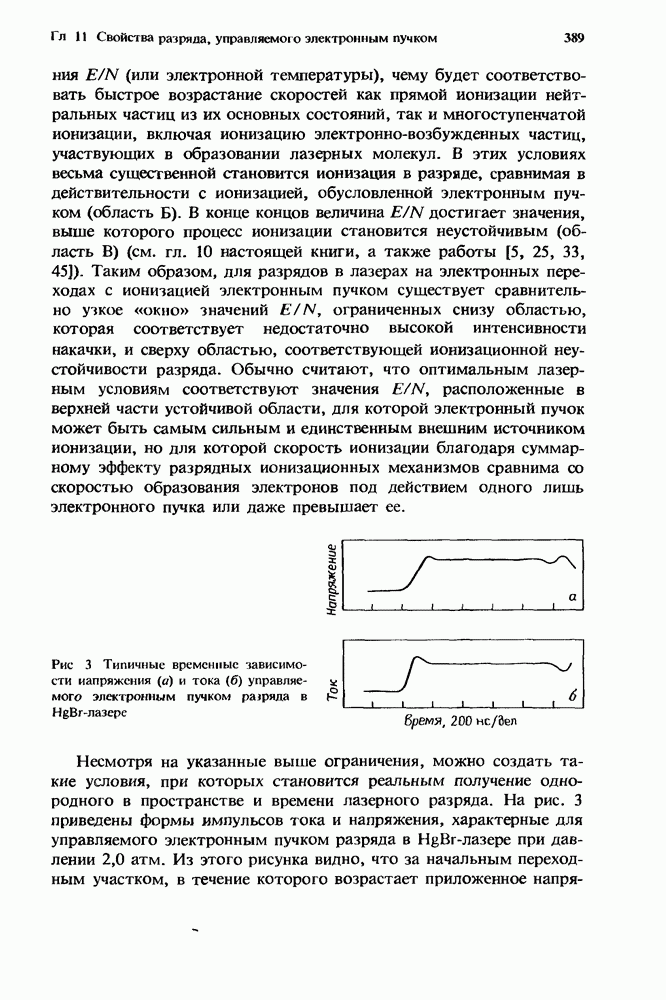
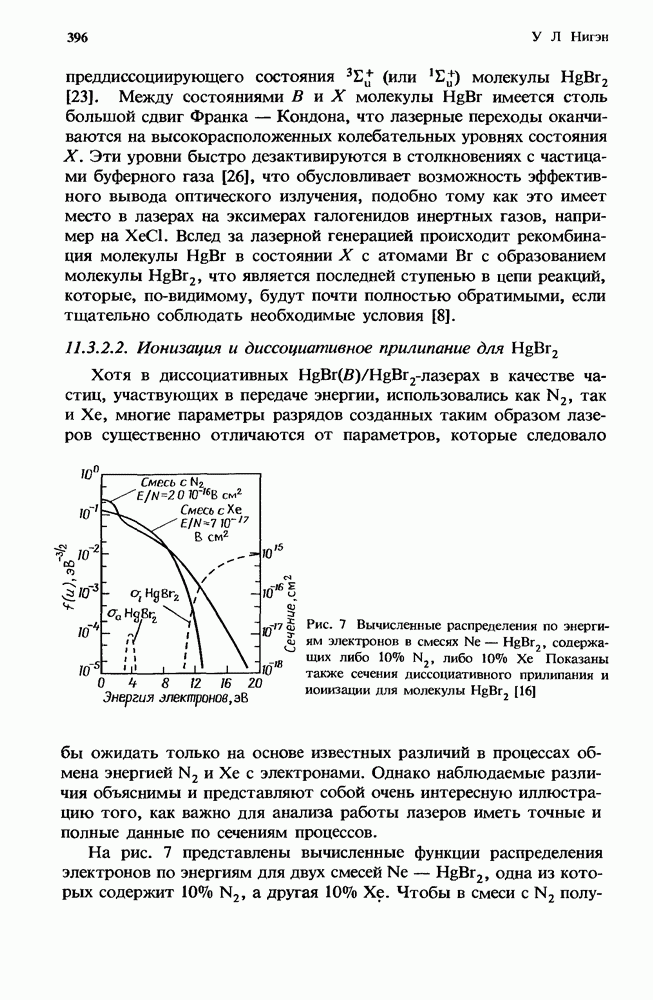
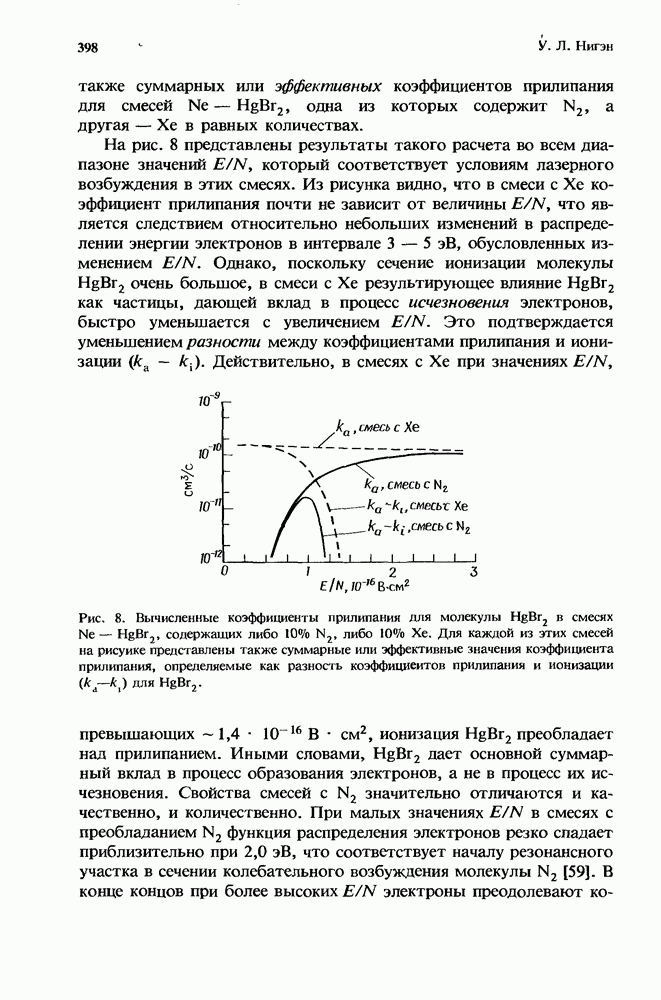
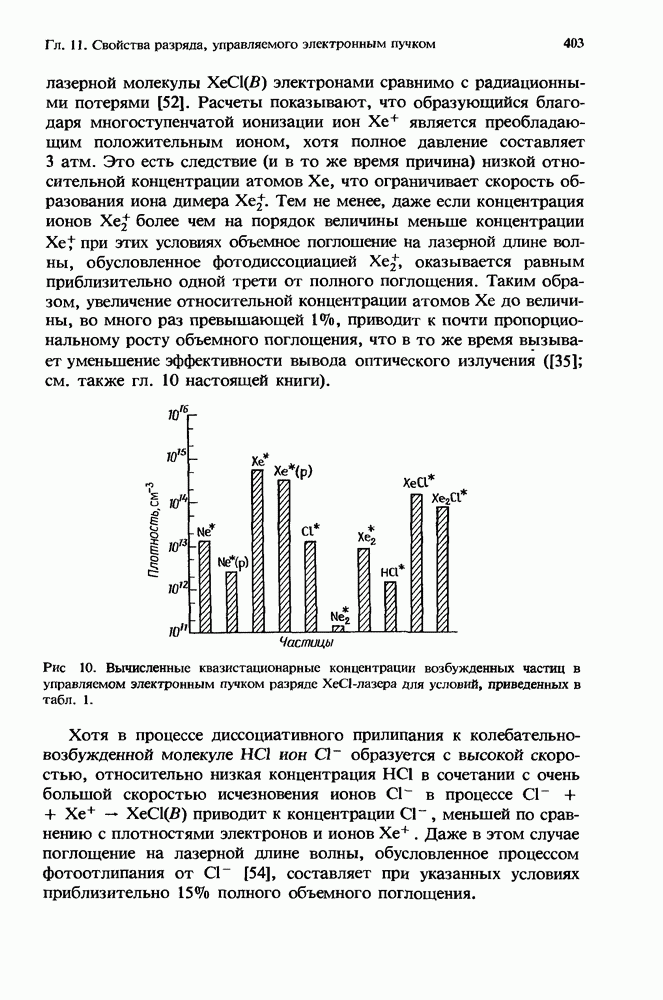
2. Образование отрицательных йодов в газовых лазерах
П. Дж. Чантри
2.1. Введение
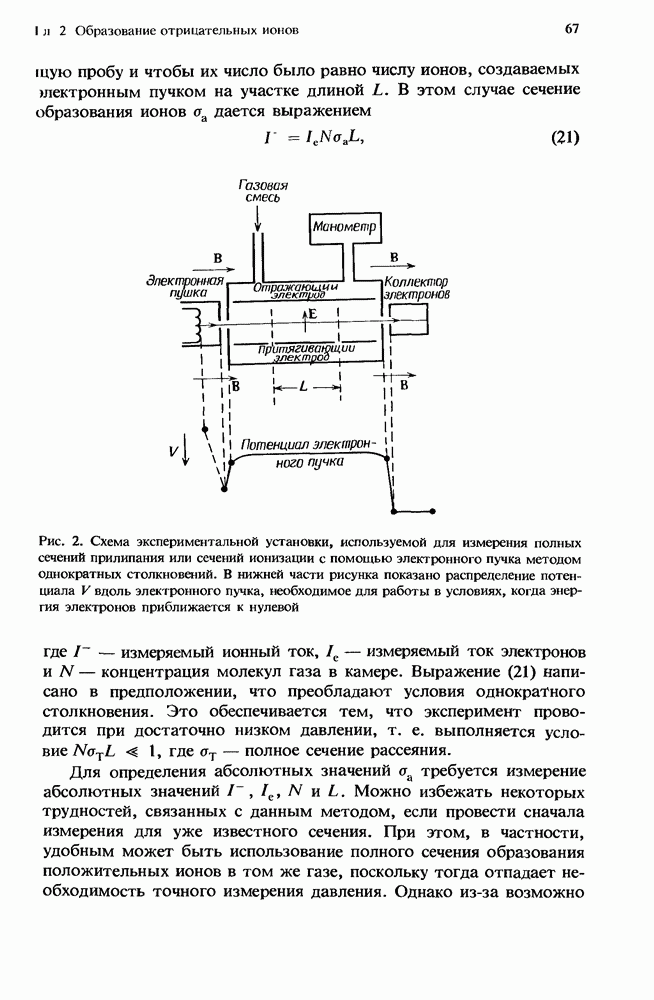
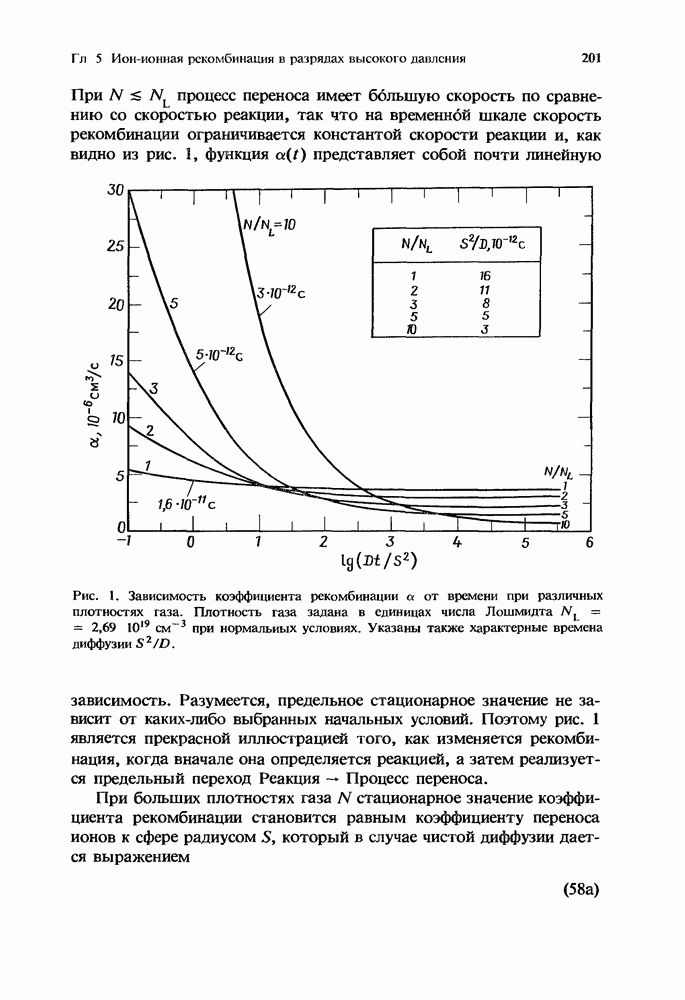
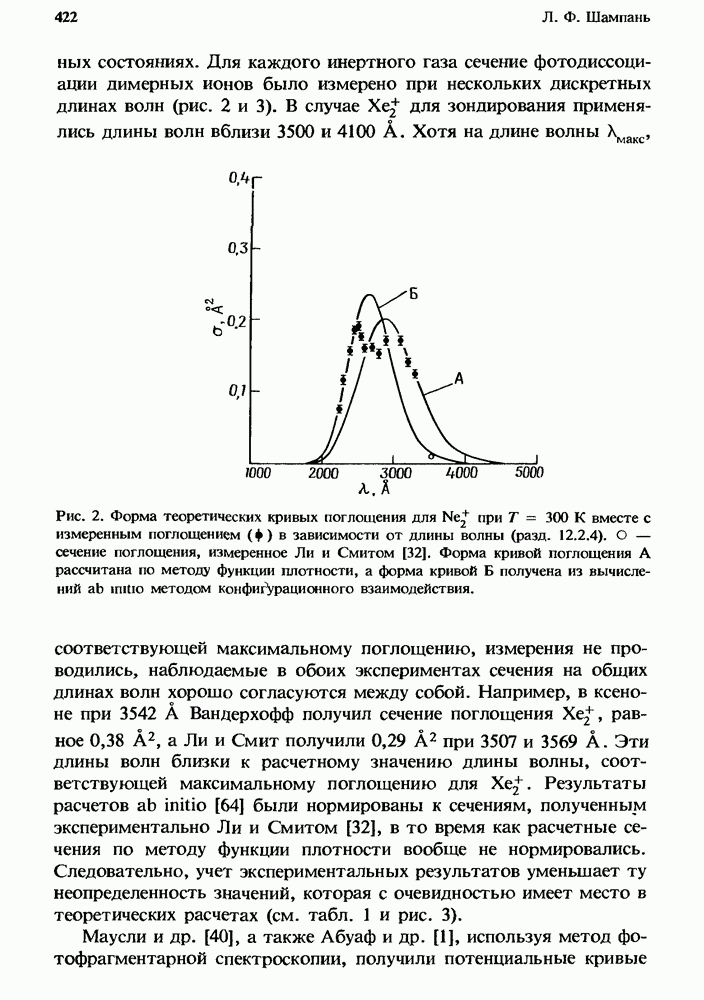
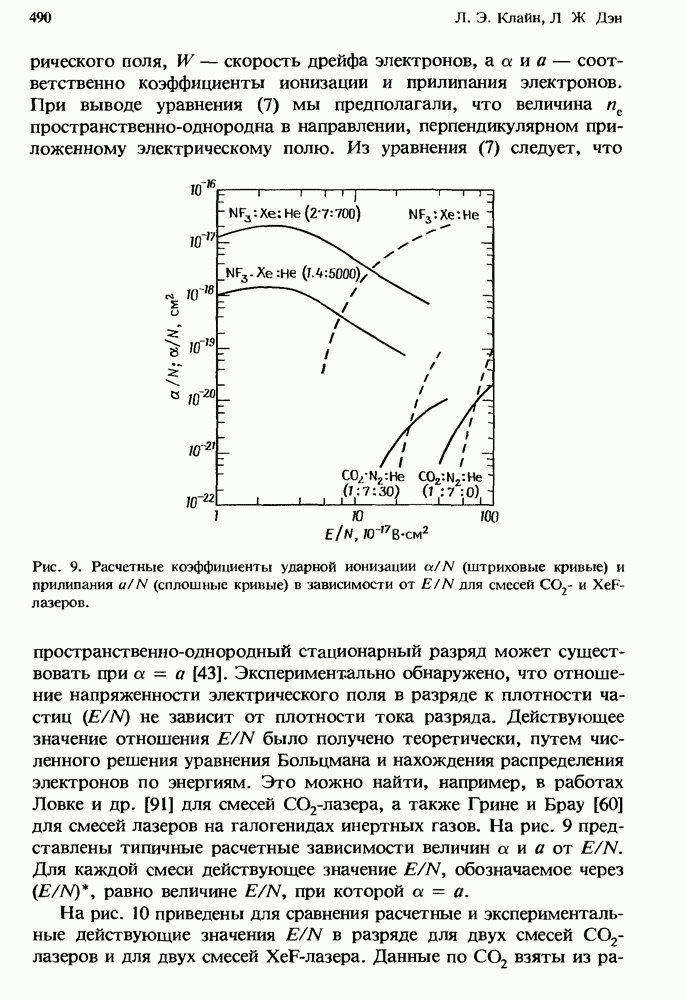
Данная глава посвящена рассмотрению газовых лазеров, в работе которых значительную роль играет образование отрицательных ионов. В большинстве газовых лазеров для реализации их оптимальной работы используются соответствующие смеси, и зачастую одна или более компонент этих смесей оказываются электроотрицательными газами. Так, например, в разряде высокого давления с поперечным возбуждением диффузия к стенкам оказывает относительно несущественное влияние на исчезновение электронов, в то время как роль других процессов возрастает. Даже в таком слабо электроотрицательном газе, как СО2, на потерю электронов сильно влияет процесс прилипания. Это впервые отметили Дэн и Ловке [38], которые показали, что величина E/N (отношение электрического поля к плотности частиц), требуемая для поддержания разряда, в конкретной смеси определяется балансом между процессом рождения электронов при ионизации прямым электронным ударом и их гибелью в процессе двухчастичного диссоциативного прилипания к 

В том же году Нигэн и др. [71] указали на то, что при достаточном количестве продукты реакции (1) могут стать важным источником электронов и причиной локальной неустойчивости плазмы вследствие протекания обратной реакции ассоциативного отлипания.
Как правило, образование отрицательных ионов с большей вероятностью происходит в тех газовых лазерных средах, в которых важную роль играют плотность и энергия электронов или сами по
себе отрицательные ионы. Главная цель этой главы состоит в том, чтобы перечислить и подробно обсудить различные эффекты, которые в настоящее время известны в связи с проблемой образования отрицательных ионов.
2.1.1. Некоторые определения
Процесс прилипания электронов количественно можно описать различными способами. Поэтому вначале полезно дать определения наиболее широко используемых величин. Для большинства случаев, связанных с газовыми лазерами, нам приходится иметь дело с ансамблем электронов, испытывающих многократные столкновения с частицами газа, причем, как правило, в присутствии приложенного электрического поля Е. В таких сложных условиях мы феноменологически имеем дело с усредненными характеристиками процесса прилипания. Во многих случаях удобно пользоваться понятием частоты прилипания  (измеряется в единицах
(измеряется в единицах  Таким образом, величина
Таким образом, величина  есть вероятность того, что за короткий интервал времени
есть вероятность того, что за короткий интервал времени  электрон подвергнется прилипанию. Если в отрицательном направлении оси
электрон подвергнется прилипанию. Если в отрицательном направлении оси  приложить электрическое поле Е, то мы получим результирующее движение электронов в положительном направлении оси
приложить электрическое поле Е, то мы получим результирующее движение электронов в положительном направлении оси  характеризуемое в среднем скоростью дрейфа
характеризуемое в среднем скоростью дрейфа  Во многих случаях пространственные эффекты прилипания описываются с помощью коэффициента прилипания
Во многих случаях пространственные эффекты прилипания описываются с помощью коэффициента прилипания  имеющего размерность
имеющего размерность  По определению, величина
По определению, величина  есть вероятность того, что электрон окажется прилипшим при смещении на небольшое расстояние
есть вероятность того, что электрон окажется прилипшим при смещении на небольшое расстояние 
Следует отметить, что  характеризуют эффективность прилипания в газовой смеси соответственно во времени и в пространстве. Однако они не несут информации о том, какова эффективность прилипания, присущая отдельным сортам частиц, ответственным за этот процесс. Такие величины получаются нормированием на концентрацию соответствующих частиц
характеризуют эффективность прилипания в газовой смеси соответственно во времени и в пространстве. Однако они не несут информации о том, какова эффективность прилипания, присущая отдельным сортам частиц, ответственным за этот процесс. Такие величины получаются нормированием на концентрацию соответствующих частиц 
Определенную таким образом величину  обычно обозначают символом
обычно обозначают символом  Это и есть широко используемая в кинетике лазеров константа скорости прилипания, имеющая размерность
Это и есть широко используемая в кинетике лазеров константа скорости прилипания, имеющая размерность  Константу
Константу  можно определить эквивалентным образом с помощью уравнения, описывающего потерю электронов:
можно определить эквивалентным образом с помощью уравнения, описывающего потерю электронов: 

Нормированная величина  имеет размерность
имеет размерность  Данные экспериментов с электронной дрейфовой трубкой часто описываются
Данные экспериментов с электронной дрейфовой трубкой часто описываются
при помощи этой величины. Связь между  определяется соотношением
определяется соотношением

причем скорость дрейфа электронов  при выбранных условиях считается известной.
при выбранных условиях считается известной.
Как  так и
так и  отражают усредненное по энергиям взаимодействие электронов с частицами газа в процессе прилипания. Эти величины обычно имеют вид функций от E/N или, особенно в случае
отражают усредненное по энергиям взаимодействие электронов с частицами газа в процессе прилипания. Эти величины обычно имеют вид функций от E/N или, особенно в случае  их представляют как функции от средней энергии электронов е. Вообще говоря, значения этих величин зависят также от состава газовой смеси, определяющего форму распределения электронов по энергиям. Таким образом,
их представляют как функции от средней энергии электронов е. Вообще говоря, значения этих величин зависят также от состава газовой смеси, определяющего форму распределения электронов по энергиям. Таким образом,  не могут характеризовать однозначно свойства прилипания. Дело в том, что, измерив их величину для одной смеси, мы не можем затем применить эти данные непосредственно к другой. Только введение понятия сечения прилипания
не могут характеризовать однозначно свойства прилипания. Дело в том, что, измерив их величину для одной смеси, мы не можем затем применить эти данные непосредственно к другой. Только введение понятия сечения прилипания  позволяет это сделать. Сечение прилипания описывает процесс двухчастичного взаимодействия электрона с изолированной молекулой, при котором образуется отрицательный ион. Эта величина имеет размерность площади и представляет собой эффективный размер молекулы, определяемый через вероятность прилипания электрона с энергией е. По определению, вероятность прилипания электрона, движущегося через среду, в единице объема которой содержится
позволяет это сделать. Сечение прилипания описывает процесс двухчастичного взаимодействия электрона с изолированной молекулой, при котором образуется отрицательный ион. Эта величина имеет размерность площади и представляет собой эффективный размер молекулы, определяемый через вероятность прилипания электрона с энергией е. По определению, вероятность прилипания электрона, движущегося через среду, в единице объема которой содержится  молекул, способных к захвату электрона, при смещении электрона на небольшое расстояние
молекул, способных к захвату электрона, при смещении электрона на небольшое расстояние  равна
равна  Отсюда следует, что для моноэнергетических электронов, имеющих скорость
Отсюда следует, что для моноэнергетических электронов, имеющих скорость  соответствующую энергии
соответствующую энергии  эквивалентная константа скорости прилипания будет равна
эквивалентная константа скорости прилипания будет равна  . В более общем случае с учетом взаимодействия со всей совокупностью электронов используется усредненное значение константы
. В более общем случае с учетом взаимодействия со всей совокупностью электронов используется усредненное значение константы  Это значение дается сверткой
Это значение дается сверткой

где  — вероятность того, что электрон имеет энергию между
— вероятность того, что электрон имеет энергию между  Данное соотношение позволяет сравнить измеренные значения
Данное соотношение позволяет сравнить измеренные значения  с измеренными или предварительно полученными значениями сечения
с измеренными или предварительно полученными значениями сечения  Это сравнение можно провести при условии, что мы знаем функцию распределения
Это сравнение можно провести при условии, что мы знаем функцию распределения  Вообще говоря, чтобы получить функцию распределения, требуется найти решение
Вообще говоря, чтобы получить функцию распределения, требуется найти решение
уравнения Больцмана [42]. Такую задачу можно решить, если известна вся совокупность соответствующих сечений столкновительных процессов обмена энергией. В заключение перепишем соотношение (3) в виде

откуда видно, что величина  хотя и имеет такую же размерность, как и сечение, но превосходит его на множитель, приблизительно равный отношению средней скорости электронов к их скорости дрейфа.
хотя и имеет такую же размерность, как и сечение, но превосходит его на множитель, приблизительно равный отношению средней скорости электронов к их скорости дрейфа.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
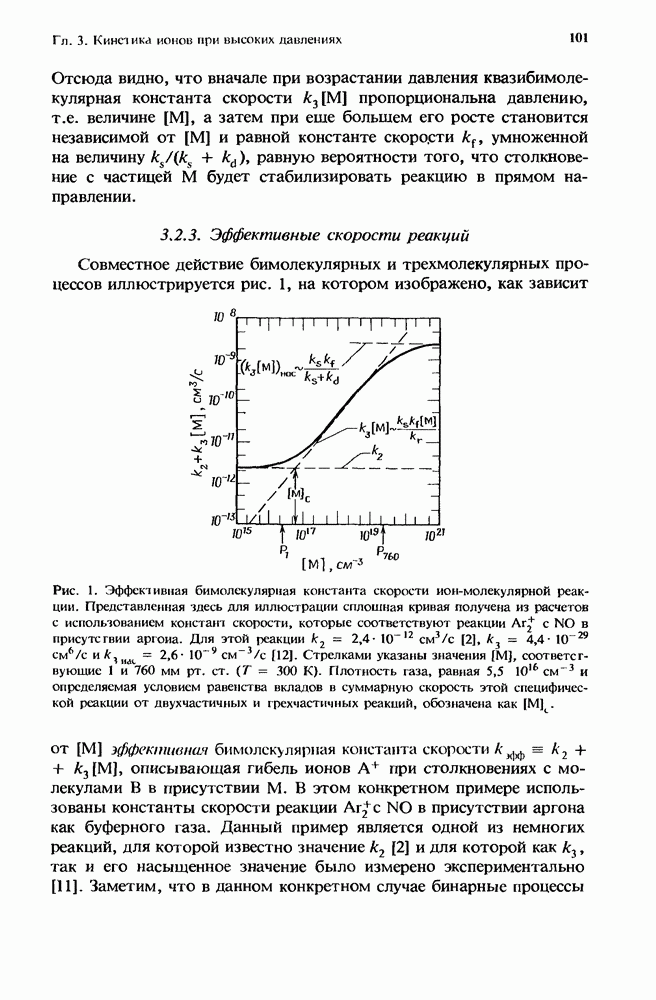
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
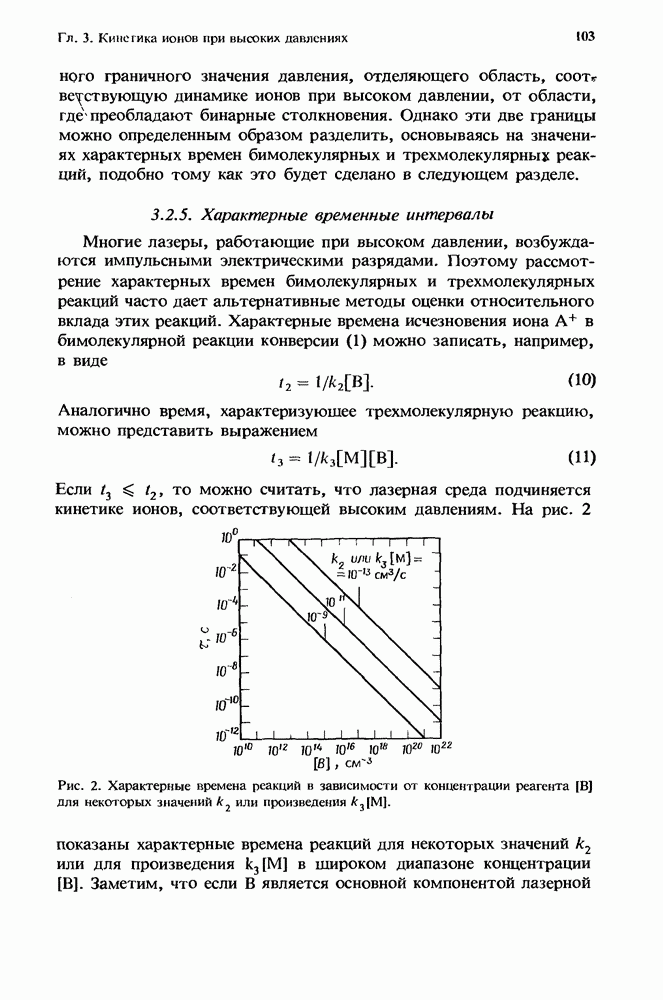
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
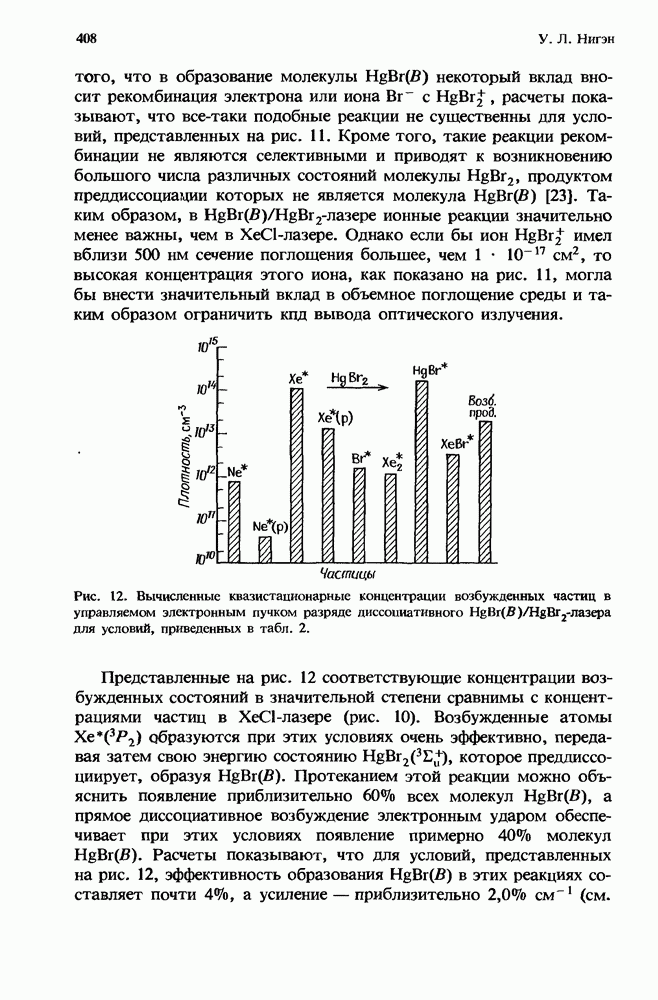
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
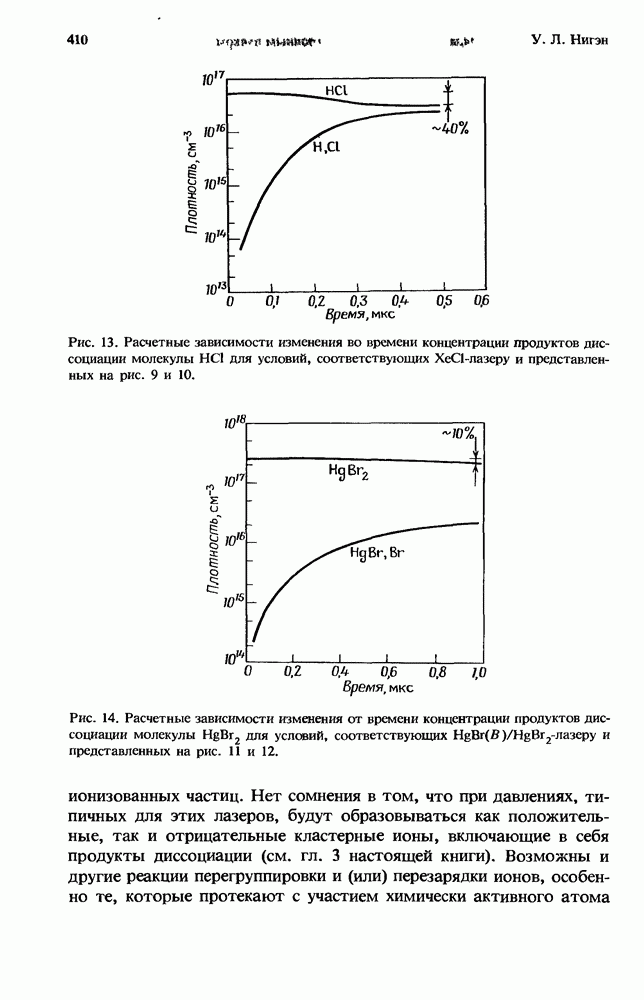
- 11.4.3. Диссоциация галогенидов
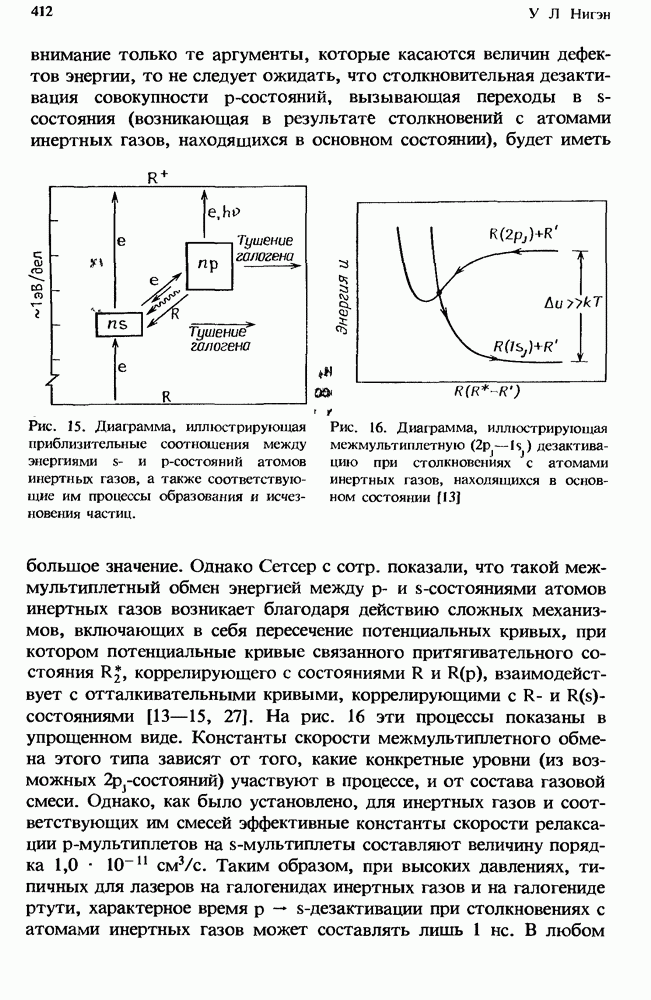
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
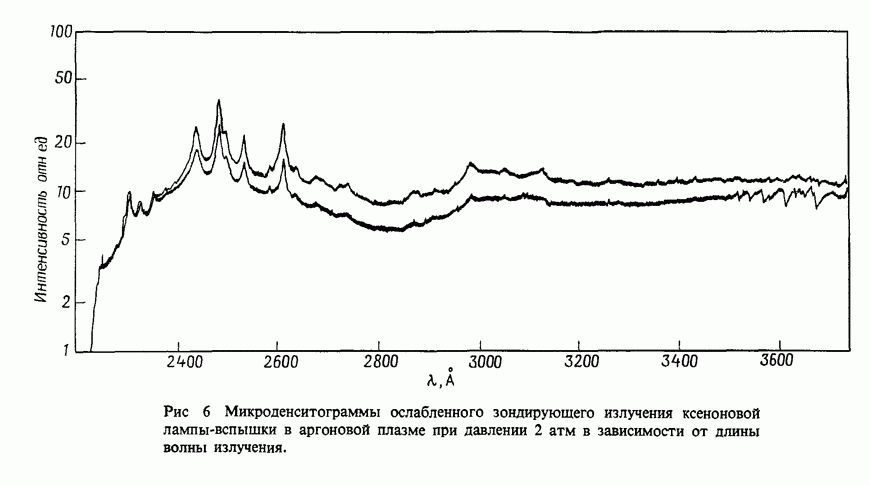
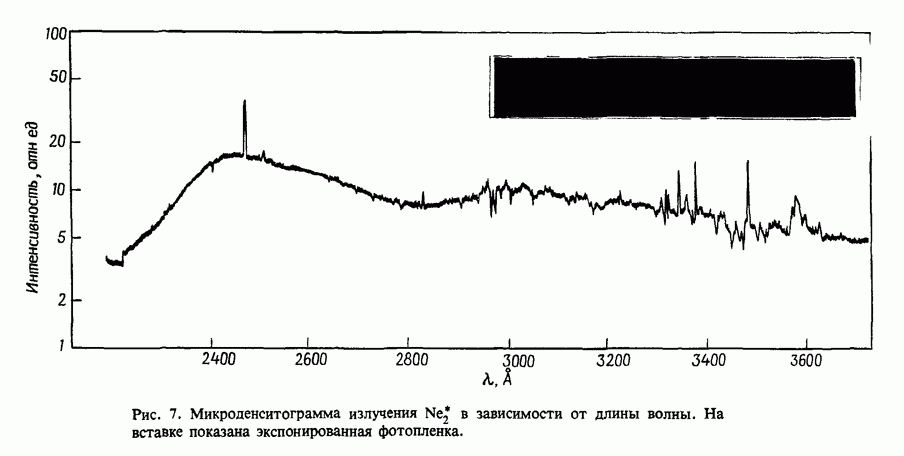
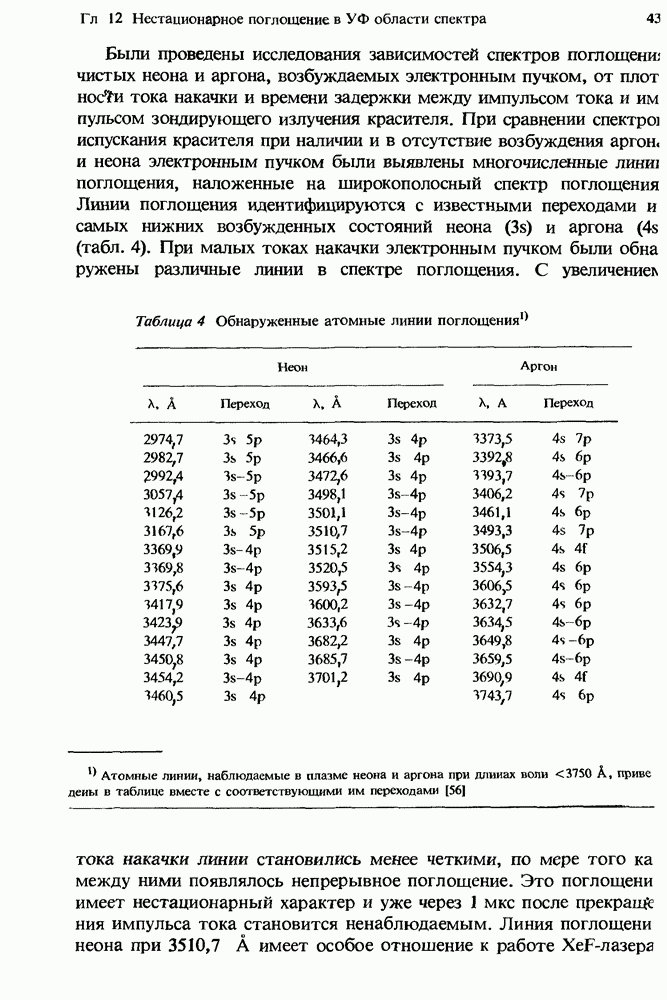
- 12. Нестационарное поглощение в УФ области спектра
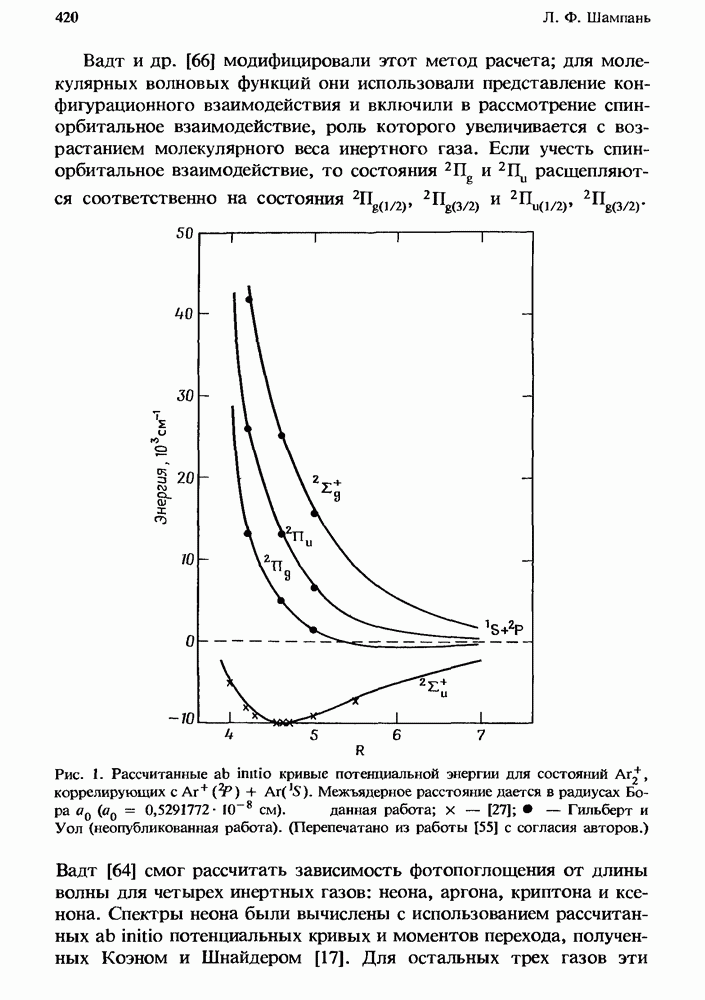
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
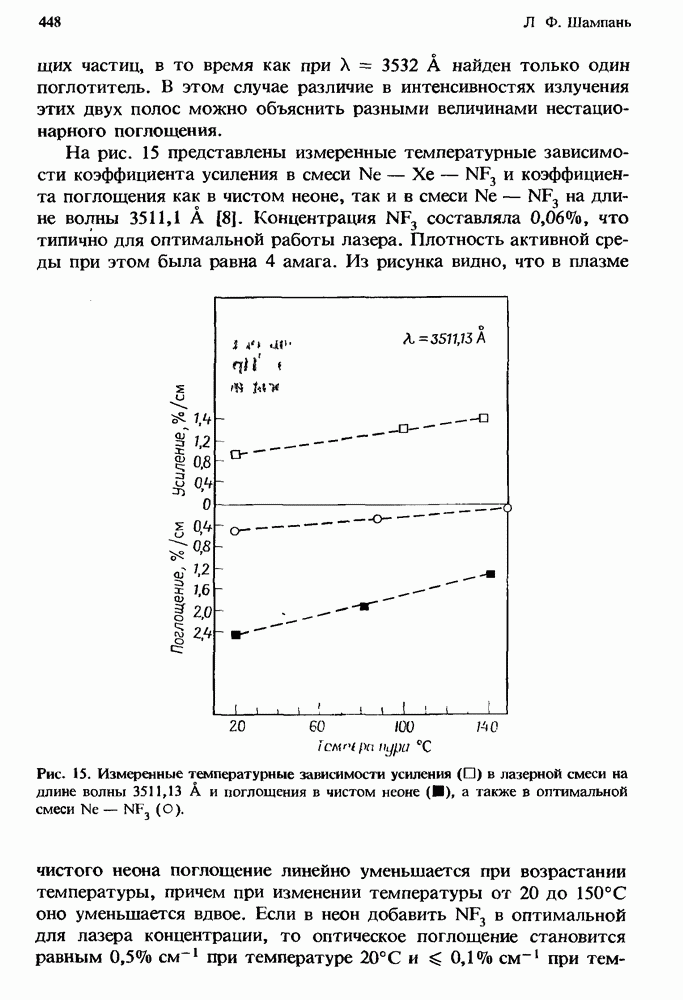
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
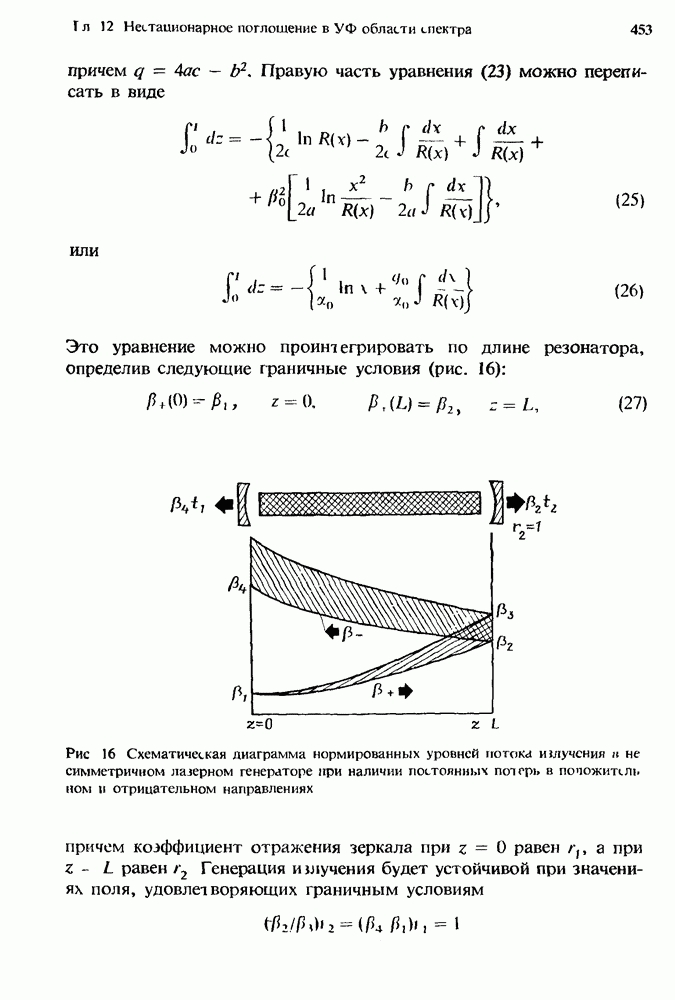
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
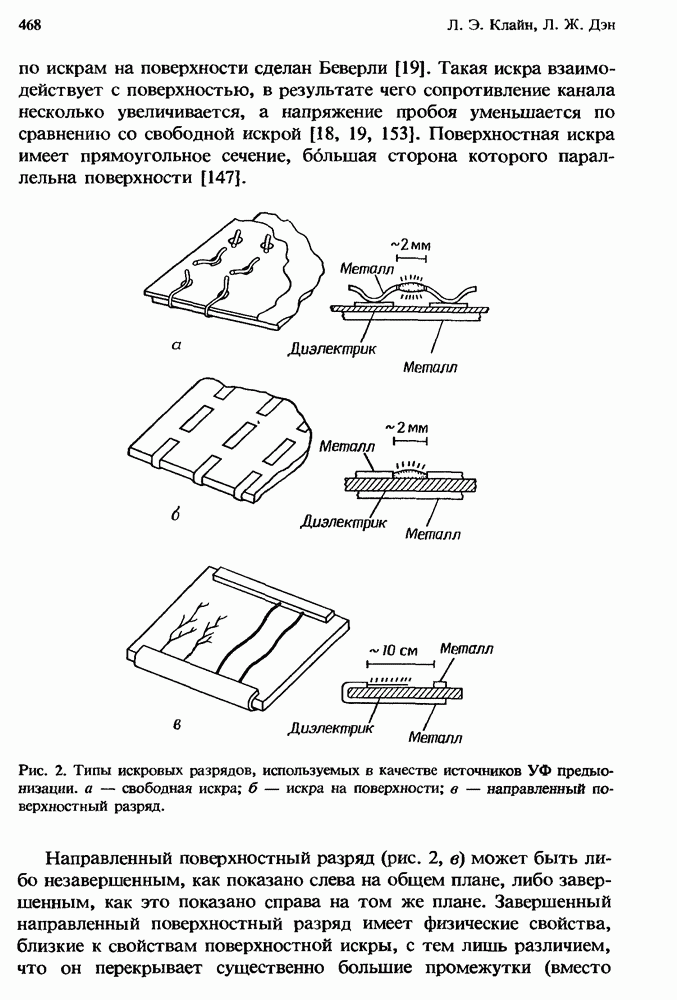
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
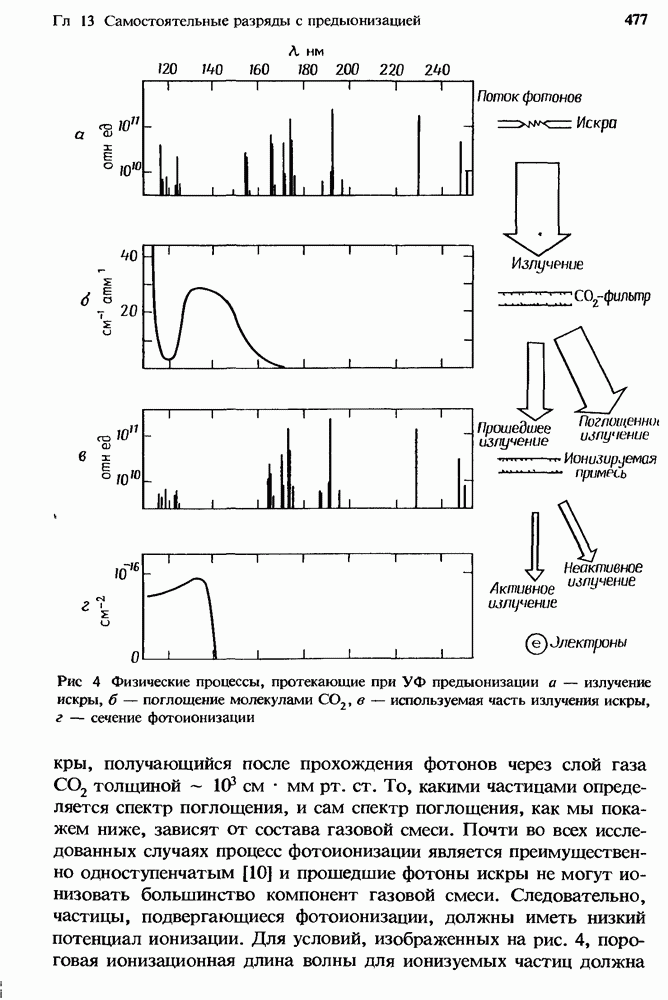
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации