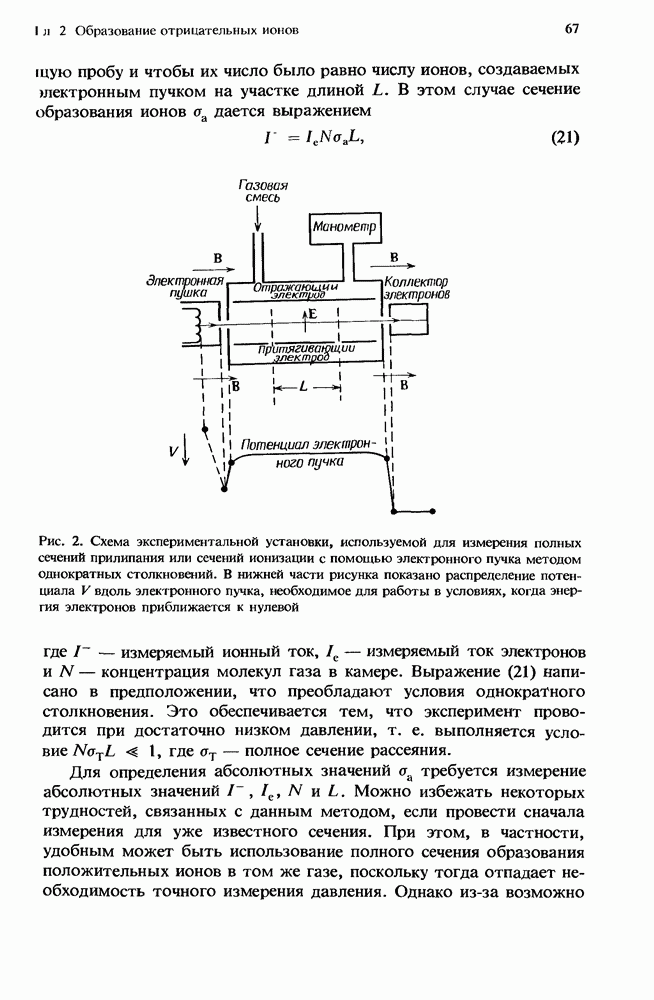
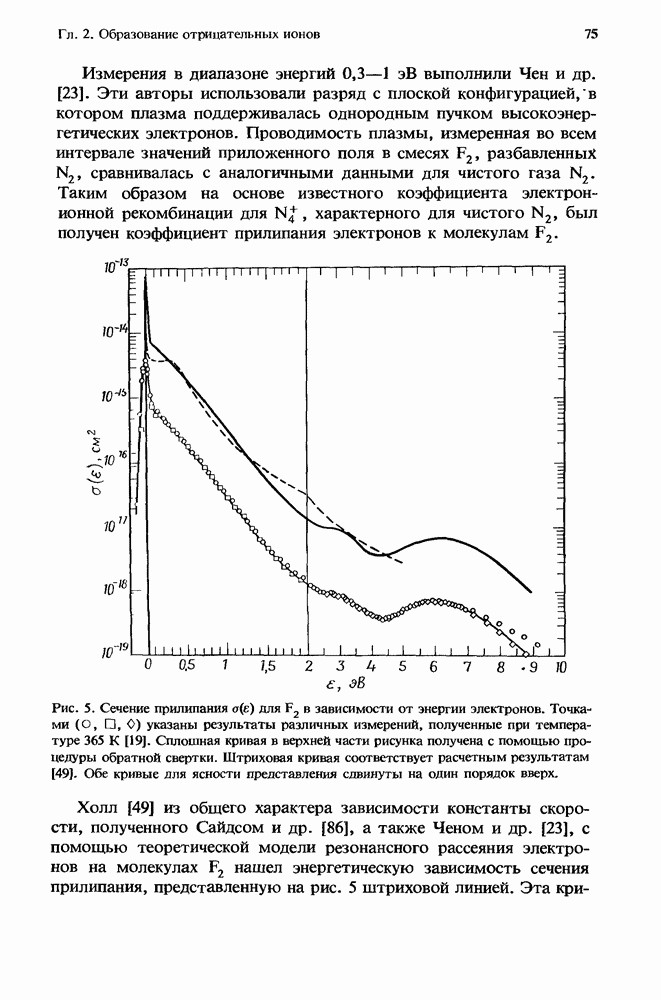
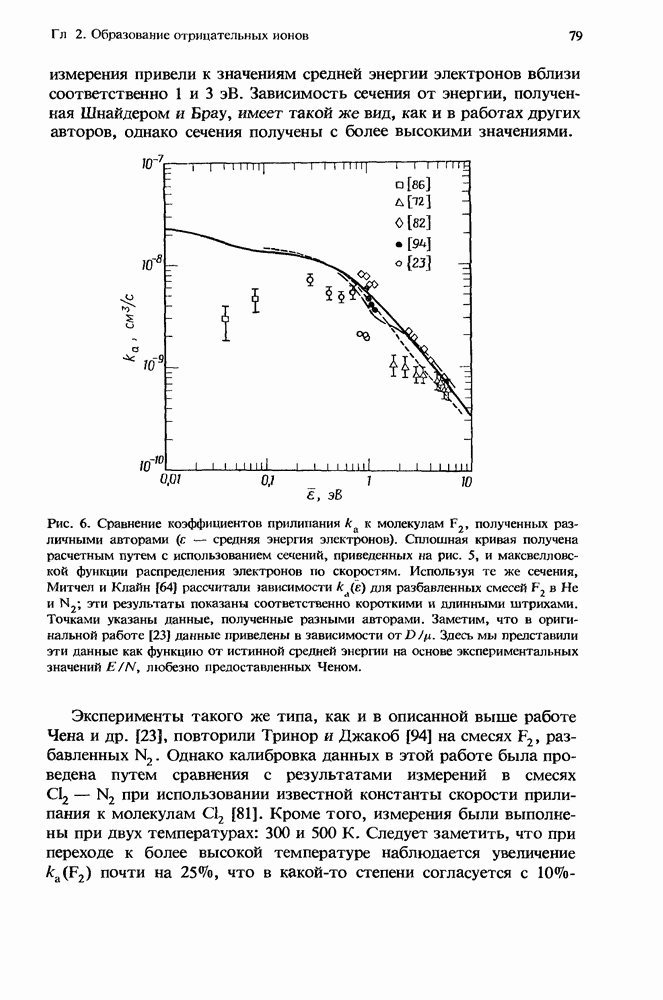
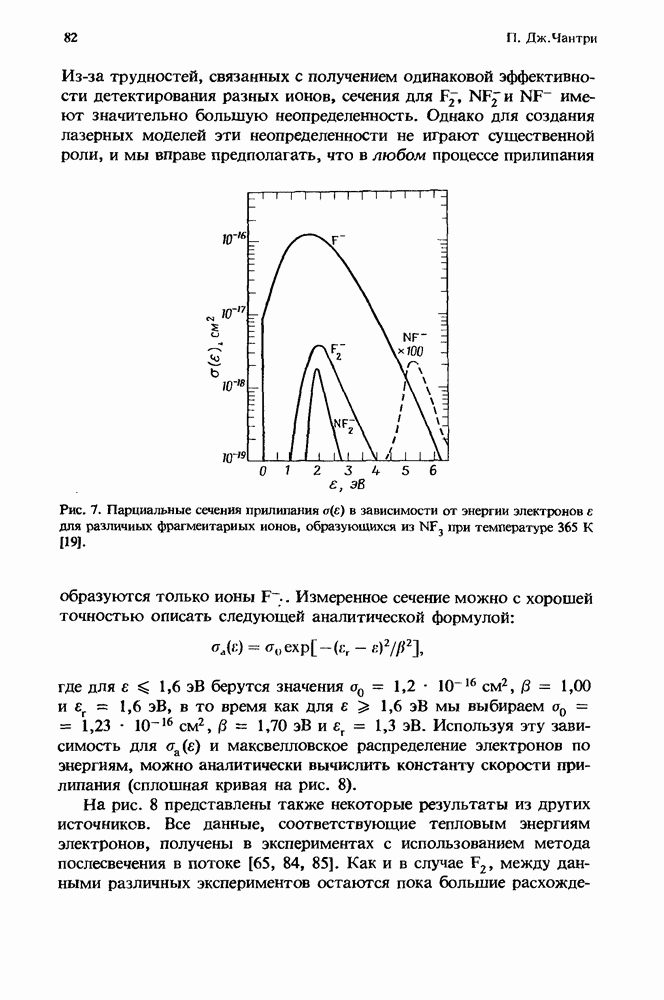
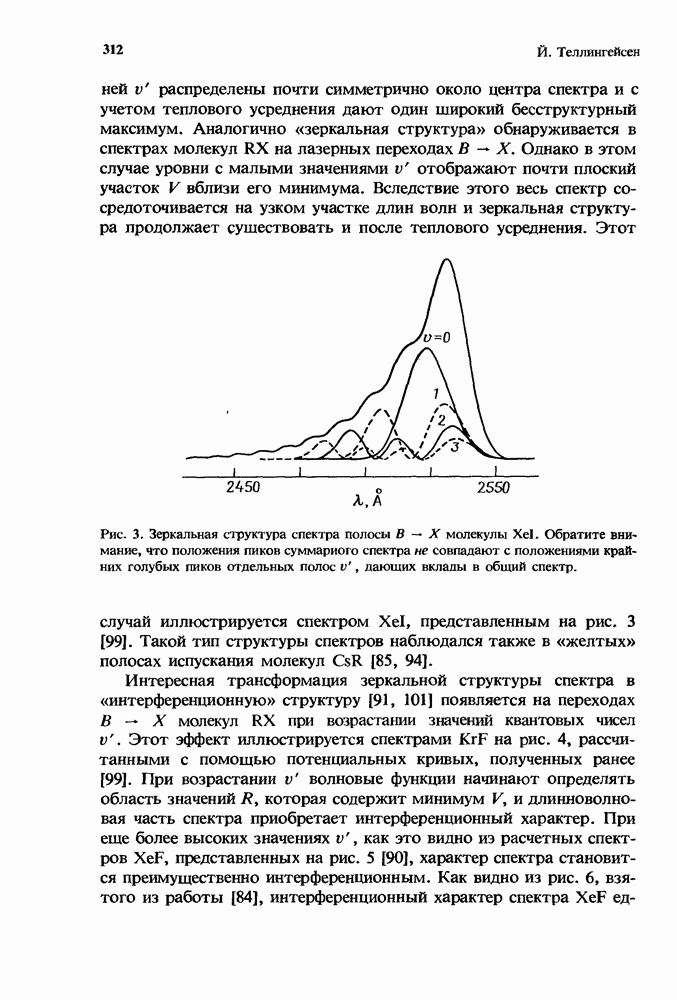
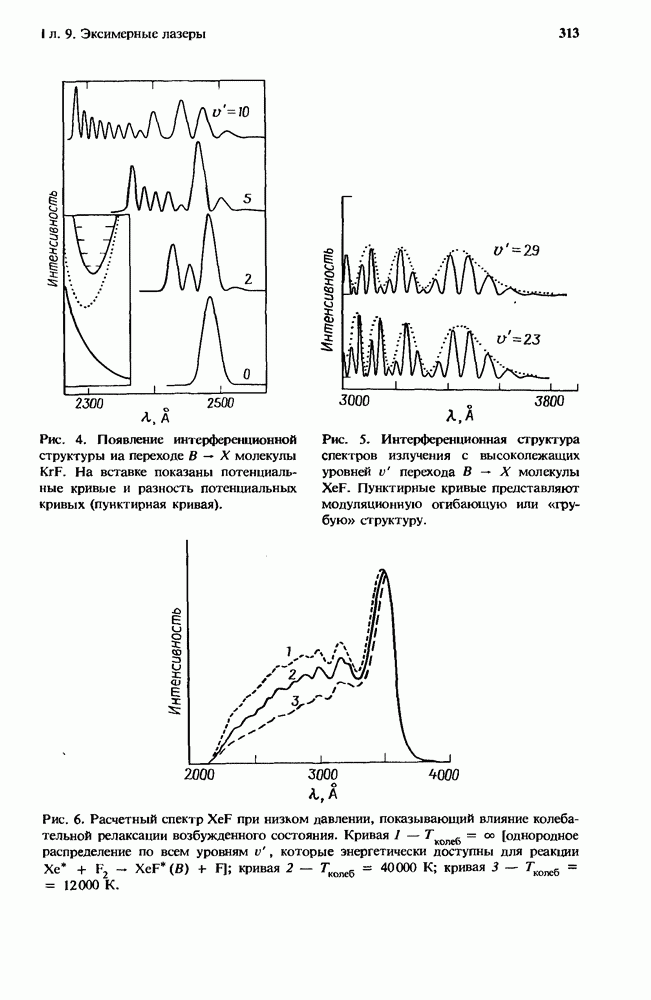
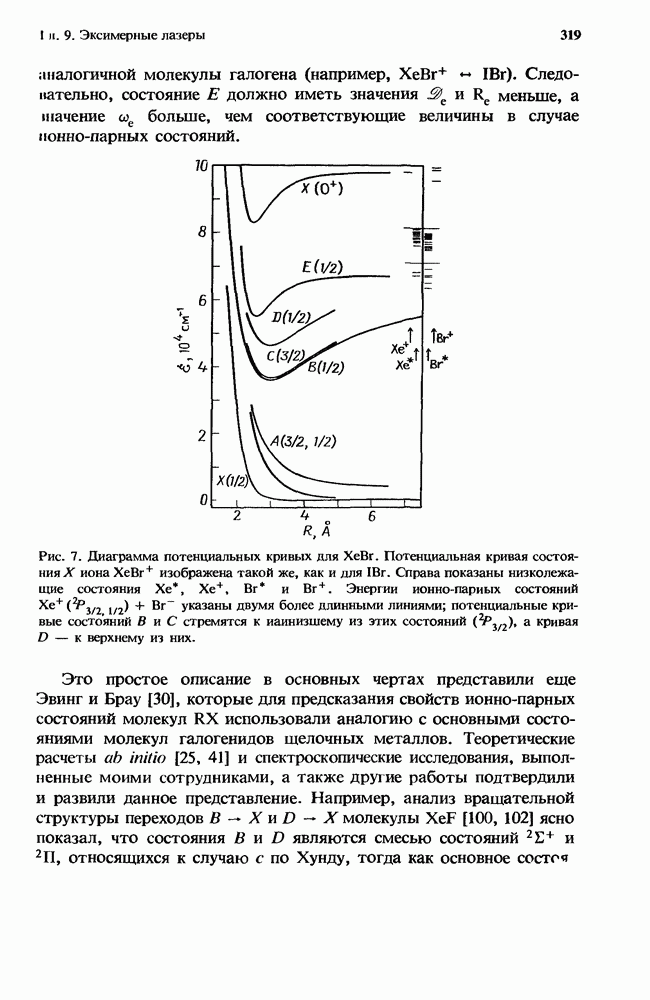
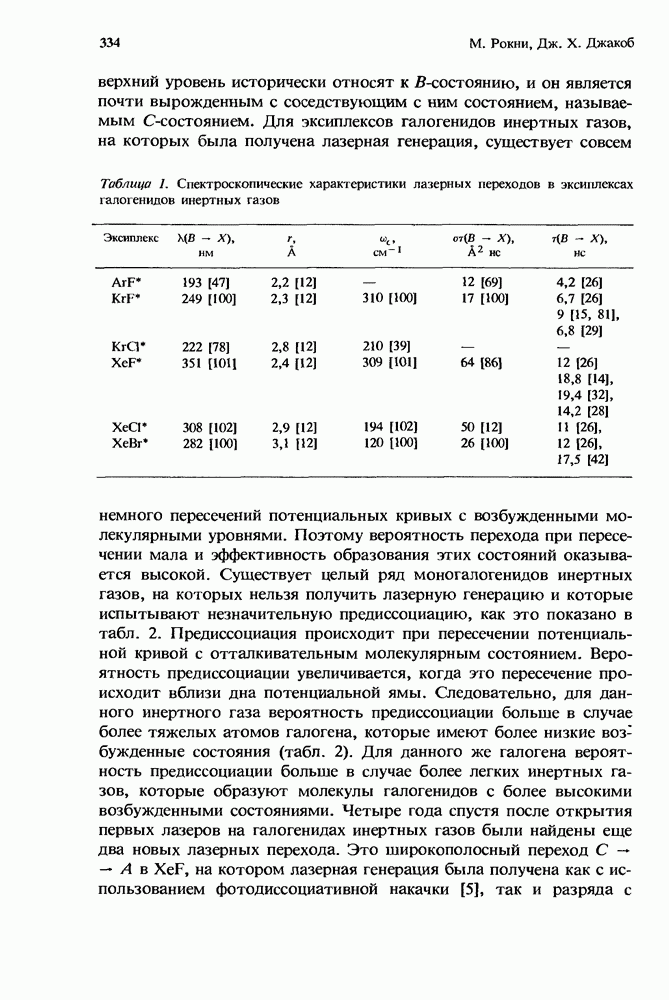
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
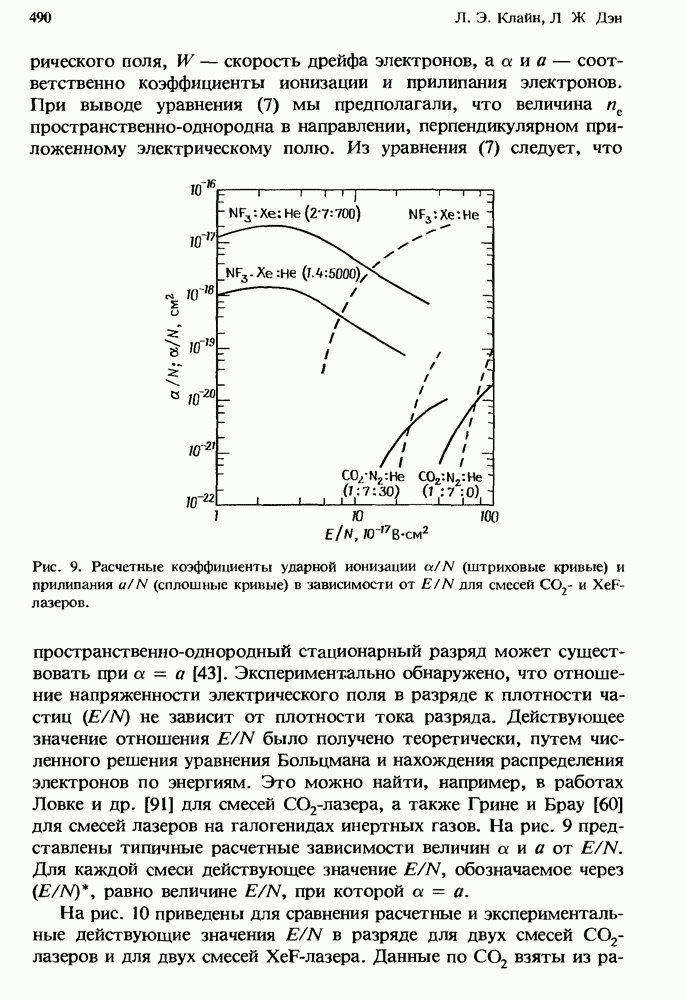
4.2.2. Модели релаксации
4.2.2.1. Скорости элементарных процессов
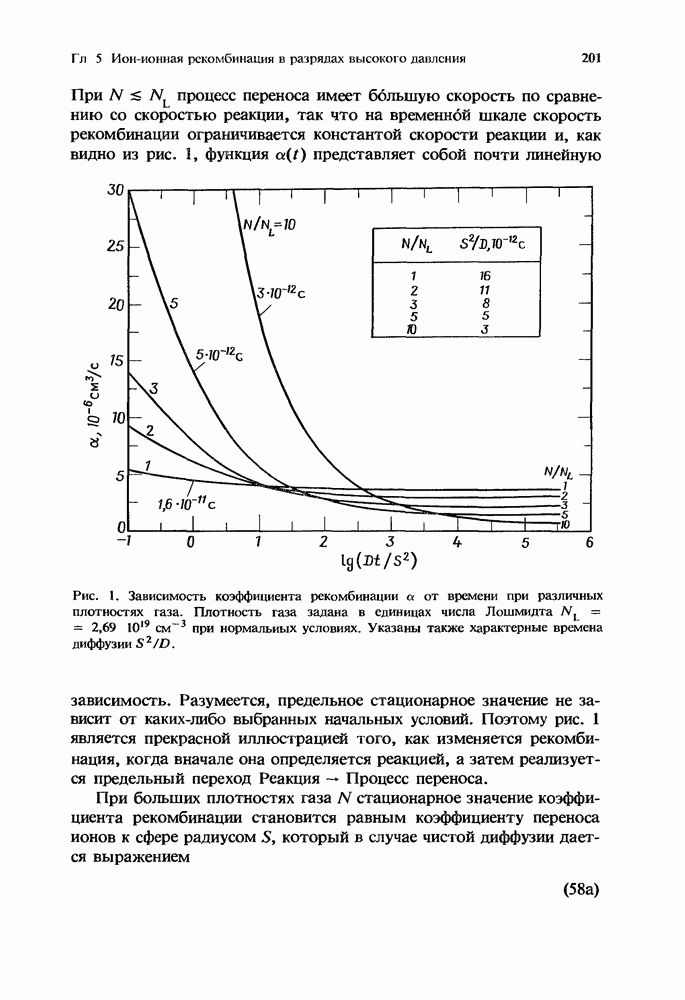
Для обсуждения некоторых хорошо известных приближенных решений кинетического уравнения (1) необходимо рассмотреть общую природу констант скорости элементарных процессов  Развитие методов лазерного возбуждения квантовых состояний позволило определить константы скорости элементарных процессов для ряда молекул. Вместе с тем большие надежды возлагаются и на теоретические расчеты этих скоростей, основанные на различных моделях неупругого молекулярного рассеяния. Существует обширная литература, в которой описываются такие расчеты, и мы отсылаем читателя к опубликованным в последнее время книгам и обзорным статьям [106, 75, 126, 95]. Для наших целей можно сделать несколько замечаний, касающихся следующих общих свойств процессов релаксации колебательной энергии:
Развитие методов лазерного возбуждения квантовых состояний позволило определить константы скорости элементарных процессов для ряда молекул. Вместе с тем большие надежды возлагаются и на теоретические расчеты этих скоростей, основанные на различных моделях неупругого молекулярного рассеяния. Существует обширная литература, в которой описываются такие расчеты, и мы отсылаем читателя к опубликованным в последнее время книгам и обзорным статьям [106, 75, 126, 95]. Для наших целей можно сделать несколько замечаний, касающихся следующих общих свойств процессов релаксации колебательной энергии:
1. За исключением случая очень высоких температур, среди рассматриваемых кинетических процессов в значительной степени преобладают одноквантовые процессы. Таким образом, уравнение (1) можно упростить, если записать стандартные условия

В моделях гармонического осциллятора, описывающих колебательные моды, эти правила отбора для столкновительных процессов колебательной релаксации являются строгими, если не предполагать, что потенциал межмолекулярного взаимодействия имеет чисто отталкивательный характер [47]; эти же правила отбора остаются хорошим приближением и в моделях ангармонического осциллятора [95].
2. Обычно наиболее быстрыми являются те процессы, в которых внешним поступательным и вращательным степеням свободы передается наименьшее количество энергии. Иными словами, наибольшей будет та константа скорости  для которой дефект резонанса
для которой дефект резонанса  будет наименьшим. Поэтому процессы, в которых происходит одновременное изменение колебательных квантов в каждом из сталкивающихся партнеров (коле-бательно-колебательный обмен, или V — V-обмен), обычно протекают намного быстрее, чем процессы, в которых колебательные
будет наименьшим. Поэтому процессы, в которых происходит одновременное изменение колебательных квантов в каждом из сталкивающихся партнеров (коле-бательно-колебательный обмен, или V — V-обмен), обычно протекают намного быстрее, чем процессы, в которых колебательные
кванты изменяются только у одной молекулы. [колебательнопоступательная (вращательная) релаксация, или V — Т-релаксация]. В случае V — V-обмена процессы могут протекать в условиях точного резонанса, что соответствует обмену квантами между идентичными состояниями, для которых  Возможно также протекание большого числа других процессов V — V-обмена, близких к резонансному. Для V — Т-процессов дефект резонанса, вообще говоря, велик; для самых низких колебательных квантовых состояний
Возможно также протекание большого числа других процессов V — V-обмена, близких к резонансному. Для V — Т-процессов дефект резонанса, вообще говоря, велик; для самых низких колебательных квантовых состояний  фундаментальная частота молекулярных колебаний). Чаще всего эти процессы являются более медленными, чем процессы V — V-обмена.
фундаментальная частота молекулярных колебаний). Чаще всего эти процессы являются более медленными, чем процессы V — V-обмена.

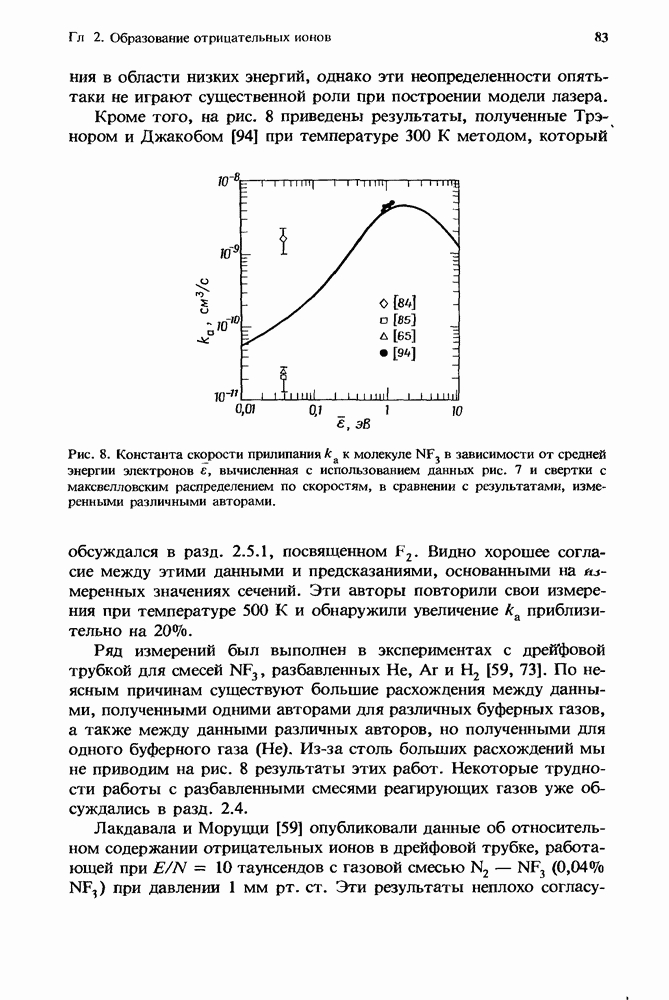
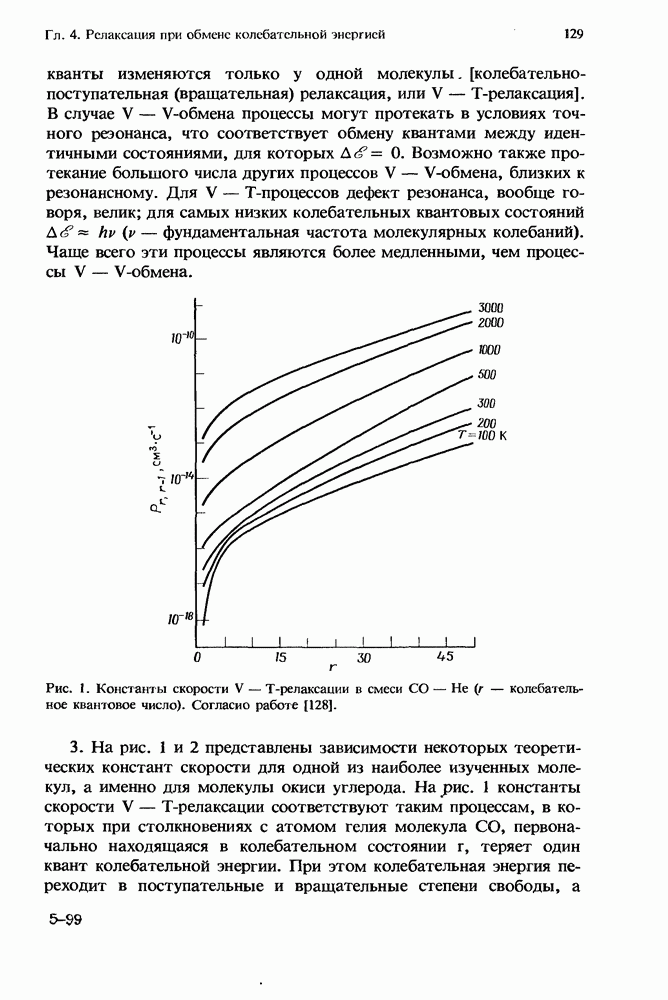
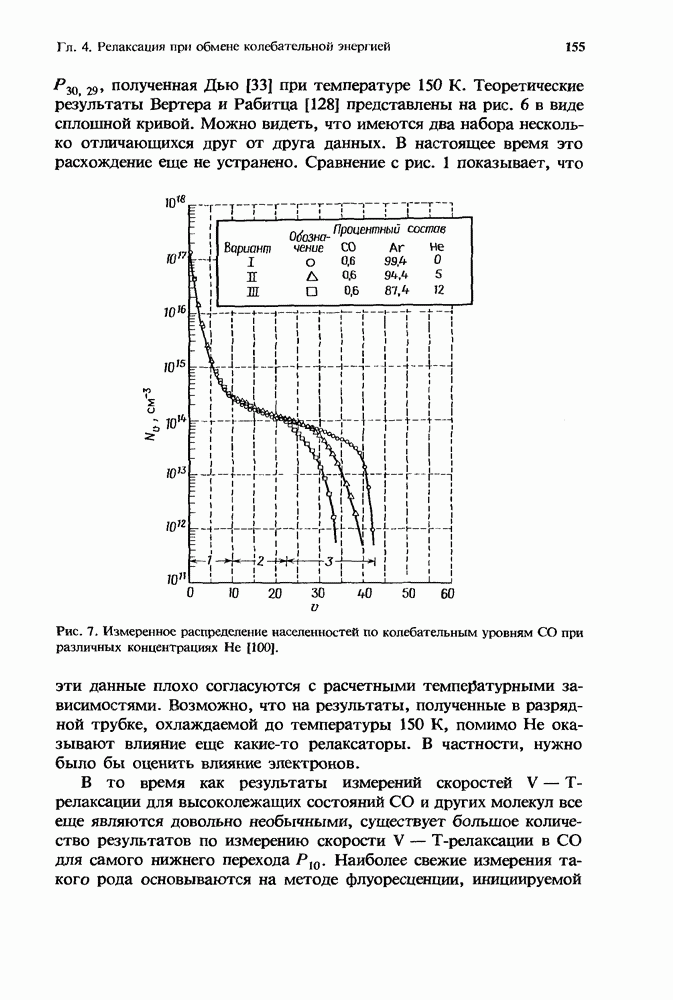
Рис. 1. Константы скорости V — Т-релаксации в смеси СО — Не ( — колебательное квантовое число). Согласно работе [128].
— колебательное квантовое число). Согласно работе [128].
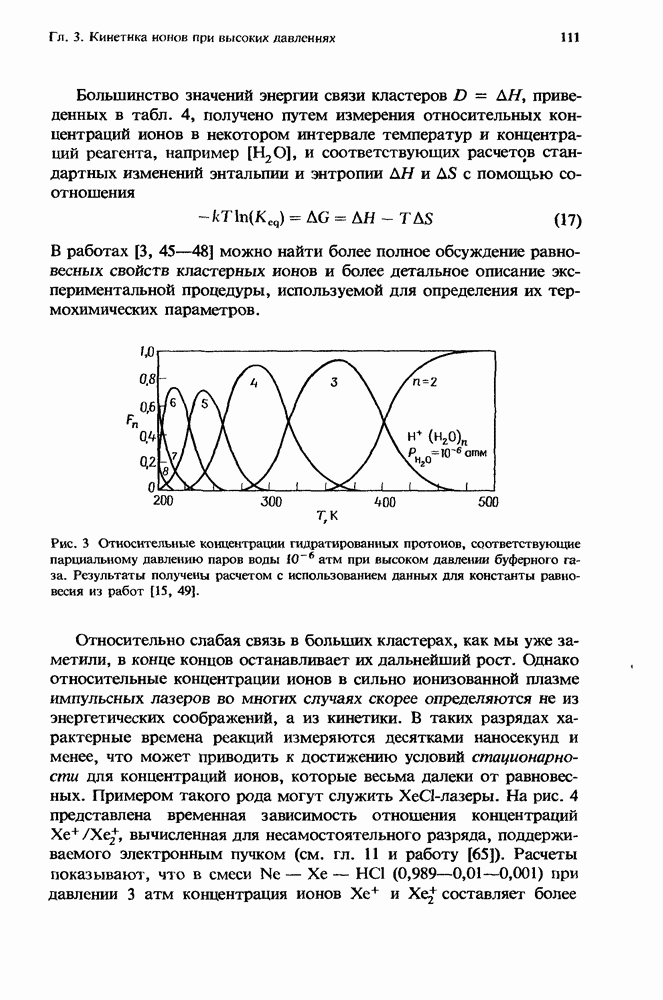
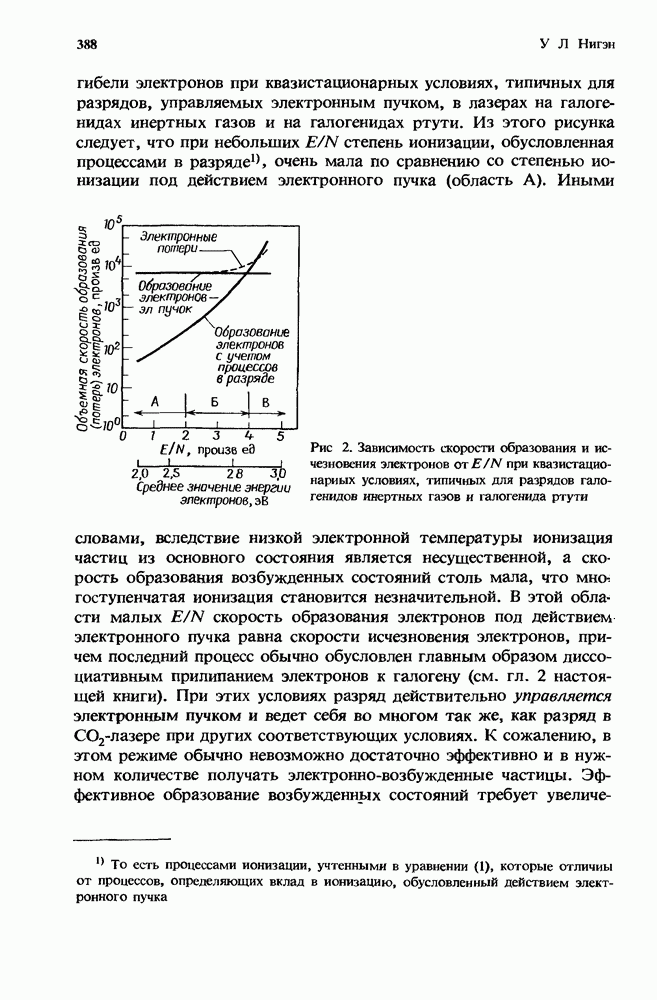
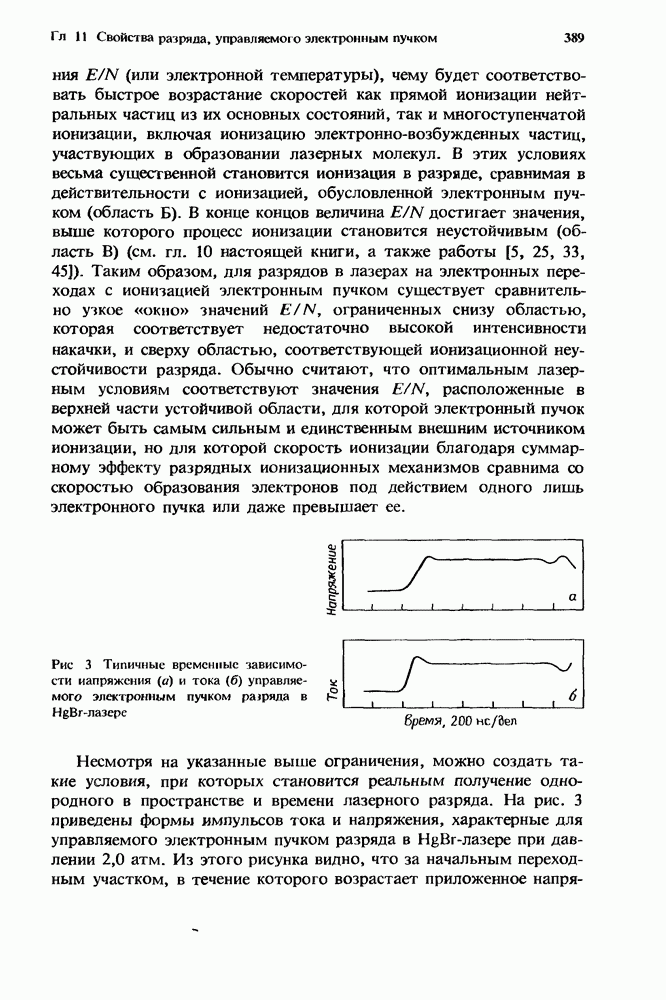
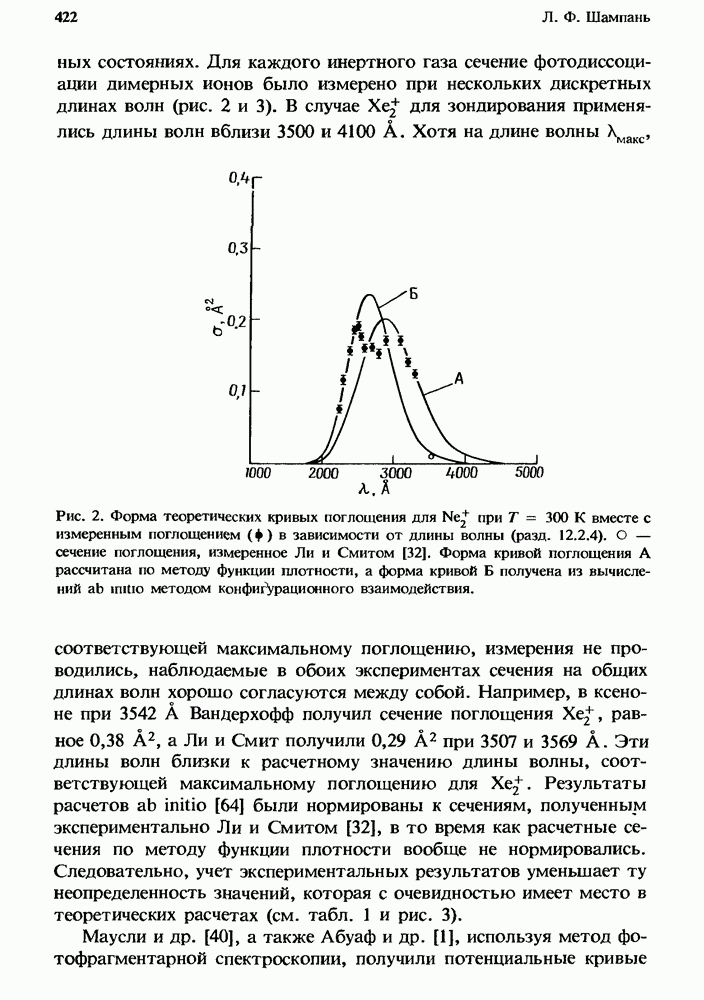
3. На рис. 1 и 2 представлены зависимости некоторых теоретических констант скорости для одной из наиболее изученных молекул, а именно для молекулы окиси углерода. На рис. 1 константы скорости V — Т-релаксации соответствуют таким процессам, в которых при столкновениях с атомом гелия молекула СО, первоначально находящаяся в колебательном состоянии  теряет один квант колебательной энергии. При этом колебательная энергия переходит в поступательные и вращательные степени свободы, а
теряет один квант колебательной энергии. При этом колебательная энергия переходит в поступательные и вращательные степени свободы, а
внутри молекулы происходит переход  Кривые на рис. 1 построены на основе теоретических расчетов Вертера и Рабитца [128] и демонстрируют поведение скорости релаксации в зависимости от квантового числа
Кривые на рис. 1 построены на основе теоретических расчетов Вертера и Рабитца [128] и демонстрируют поведение скорости релаксации в зависимости от квантового числа  и температуры вращательнопоступательных степеней свободы. Эти расчеты находятся в превосходном согласии с экспериментальными данными, полученными для отдельных колебательных состояний СО в смеси СО — Не. Однако эти экспериментальные результаты ограничены измерениями, проведенными лишь для нескольких колебательных состояний при низкой температуре. Обзор этих данных представлен в разд. 4.3.2.3.
и температуры вращательнопоступательных степеней свободы. Эти расчеты находятся в превосходном согласии с экспериментальными данными, полученными для отдельных колебательных состояний СО в смеси СО — Не. Однако эти экспериментальные результаты ограничены измерениями, проведенными лишь для нескольких колебательных состояний при низкой температуре. Обзор этих данных представлен в разд. 4.3.2.3.
Как видно из рис. 1, скорость V — Т-релаксации быстро увеличивается с ростом квантового числа и температуры. Такое поведение типично для широкого класса двухатомных молекул. Увеличение скорости релаксации с квантовым числом связано с уменьшением величины колебательного кванта высоколежащих ангармонических колебательных состояний, что приводит к уменьшению передачи энергии в поступательные степени свободы. Увеличение скорости релаксации с ростом температуры обусловлено возрастанием числа столкновений, соответствующих высоким скоростям относительного движения; такие столкновения приводят главным образом к неупругим процессам V — Т-релаксации [106].
Следует также отметить относительное снижение скоростей релаксации при уменьшении величины квантового числа и температуры. Для смеси СО — Не частота упругих столкновений в расчете на 1 молекулу при температуре 300 К составляет  Поэтому в среднем необходимо
Поэтому в среднем необходимо  столкновений молекул СО с атомом гелия, чтобы при температуре 300 К произошла V — Т-релаксация
столкновений молекул СО с атомом гелия, чтобы при температуре 300 К произошла V — Т-релаксация  с соответствующей константой скорости
с соответствующей константой скорости  Именно благодаря столь низкой скорости установления равновесия между колебательной модой и поступательно-врашательными степенями свободы мы сталкиваемся в молекулярной физике почти всюду с неравновесностью распределения колебательных мод. Заметим также, что скорости
Именно благодаря столь низкой скорости установления равновесия между колебательной модой и поступательно-врашательными степенями свободы мы сталкиваемся в молекулярной физике почти всюду с неравновесностью распределения колебательных мод. Заметим также, что скорости
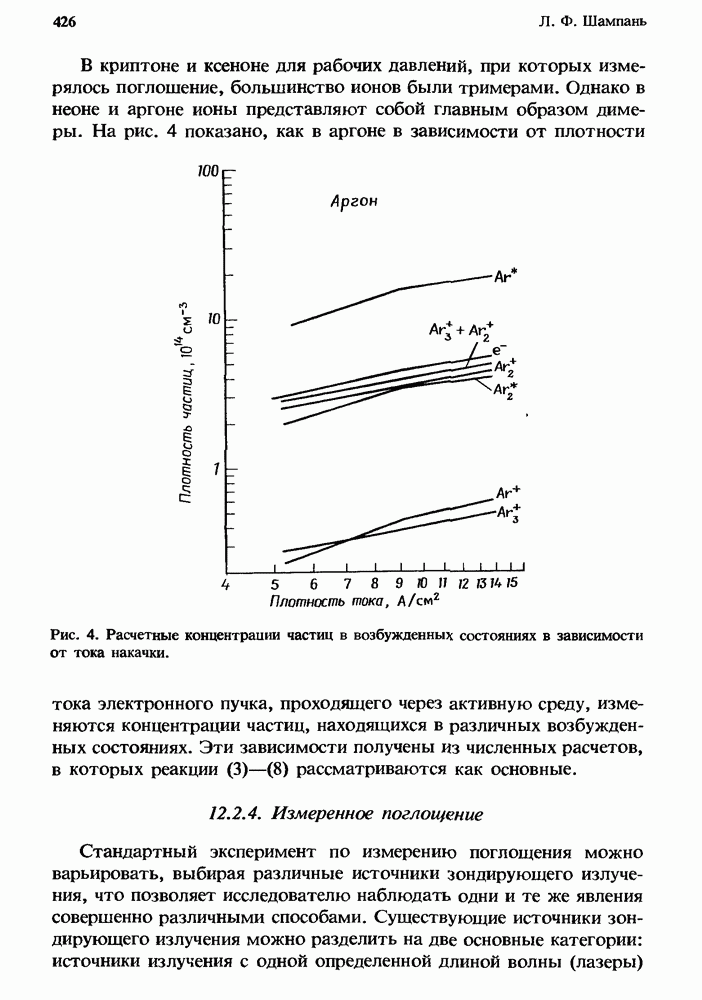
V — Т-релаксации больше, как правило, для более легких частиц, участвующих в столкновениях. Например, скорости V — Т-релаксации в смеси СО — Не (рис. 1) намного превышают соответствующие скорости для смесей  и
и  Скорости
Скорости
релаксации молекул, содержащих легкие атомы, например, молекул галогеноводородов, могут намного превышать соответствующие скорости в случае молекулы СО.
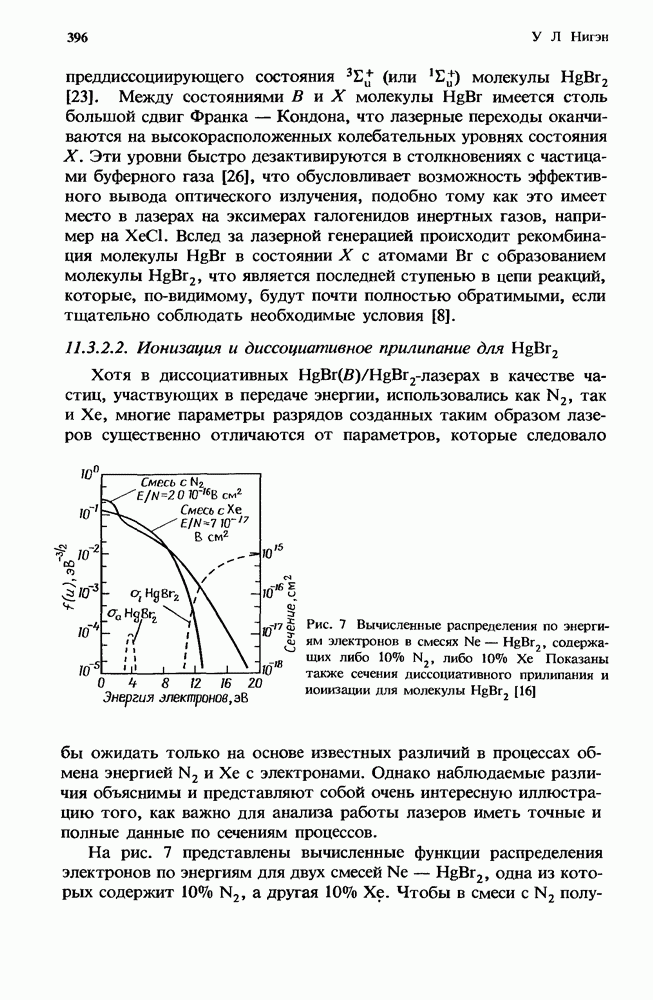
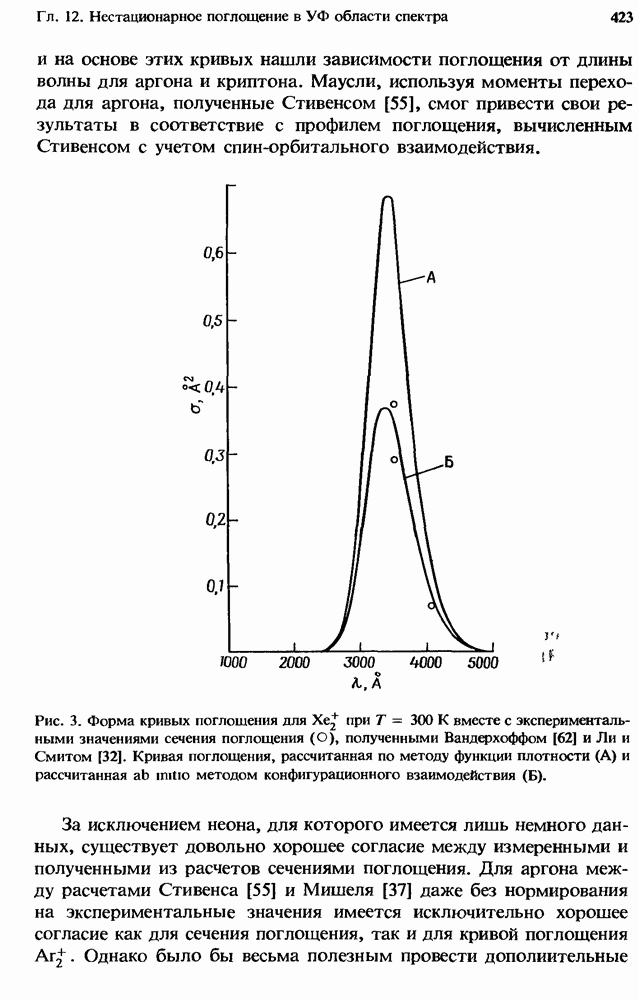
Если на рис. 1 приведены скорости V — Т-релаксации, то на рис. 2 мы представили скорости V — V-обмена для столкновений  при
при  в результате которых молекула
в результате которых молекула  первоначально находившаяся в состоянии
первоначально находившаяся в состоянии  совершает переход
совершает переход  обмениваясь колебательным квантом с молекулой
обмениваясь колебательным квантом с молекулой  первоначально находившейся в состоянии
первоначально находившейся в состоянии  и совершающей переход
и совершающей переход 

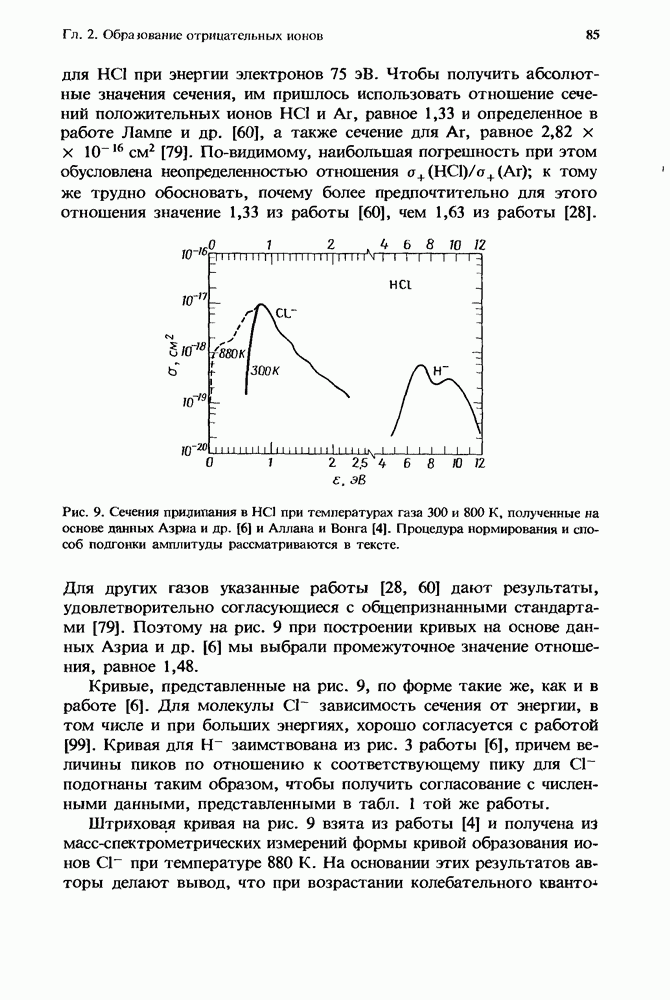
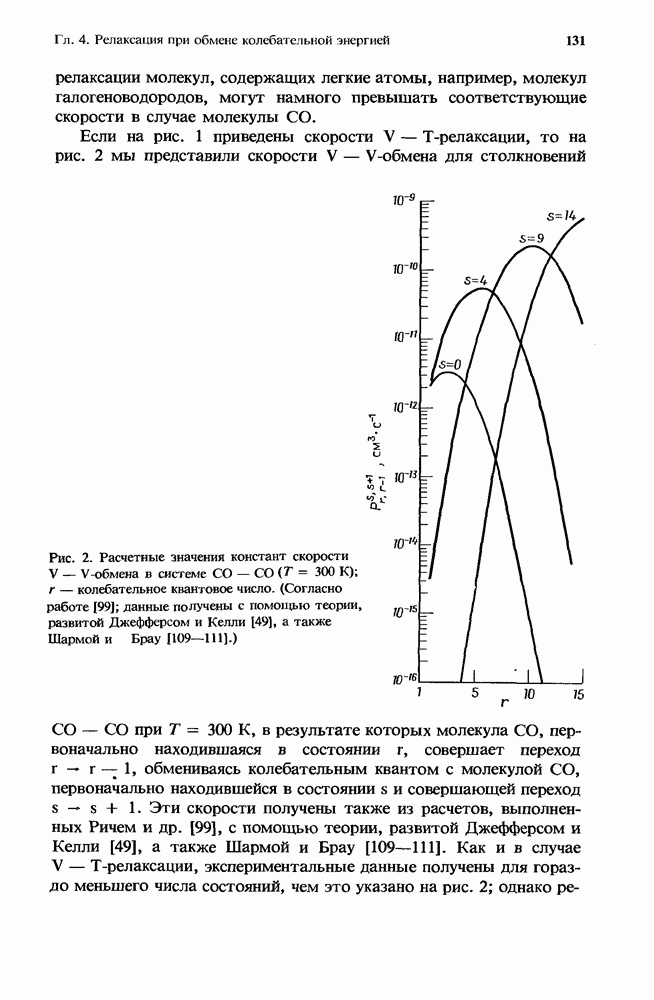
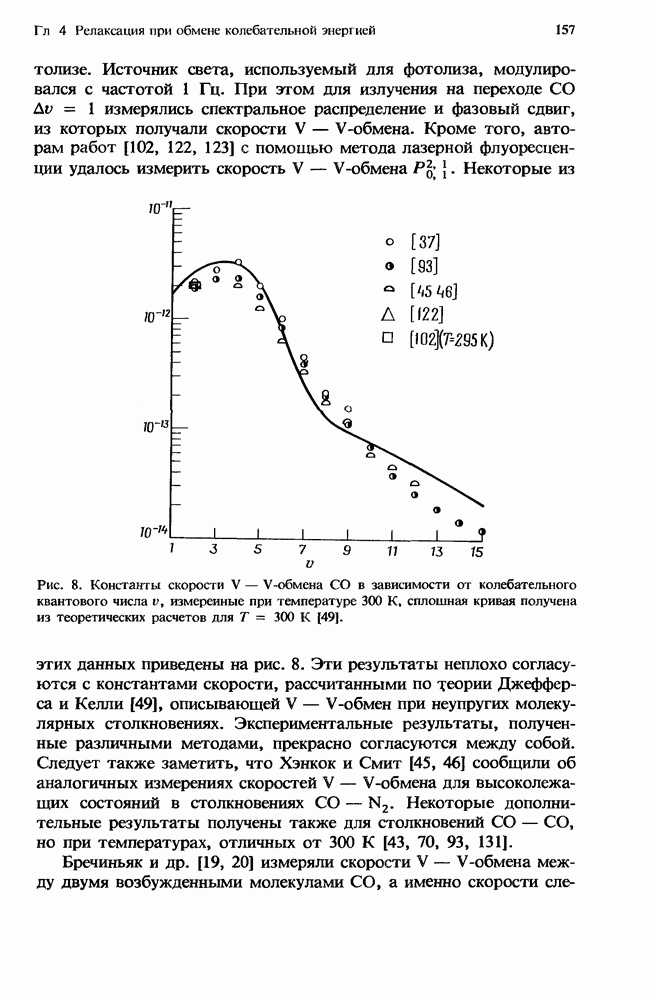
Рис. 2. Расчетные значения констант скорости V — V-обмена в системе  — колебательное квантовое число. (Согласно работе [99]; данные получены с помощью теории, развитой Джефферсом и Келли [49], а также Шармой и Брау
— колебательное квантовое число. (Согласно работе [99]; данные получены с помощью теории, развитой Джефферсом и Келли [49], а также Шармой и Брау 
Эти скорости получены также из расчетов, выполненных Ричем и др. [99], с помощью теории, развитой Джефферсом и Келли [49], а также Шармой и Брау [109—111]. Как и в случае
V — Т-релаксации, экспериментальные данные получены для гораздо меньшего числа состояний, чем это указано на рис. 2; однако
результаты измерений находятся в прекрасном согласии с расчетными данными (см. разд. 4.3.2.3). На рис. 2 можно заметить, что скорость V — V-обмена сильно зависит от дефекта резонанса. Как отмечалось выше, скорость V — V-обмена оказывается наибольшей для тех процессов, которые соответствуют наименьшему количеству энергии, передаваемому во внешние поступательные и вращательные степени свободы. Таковыми являются переходы, для которых начальные квантовые числа сталкивающихся молекул СО оказываются близкими  Вблизи такого резонанса скорости V — V-обмена намного превосходят скорости почти всех V — Т-процессов для столкновений СО — Не при
Вблизи такого резонанса скорости V — V-обмена намного превосходят скорости почти всех V — Т-процессов для столкновений СО — Не при  К (рис. 1). Только для очень высоколежащих квантовых уровней скорости V — Т-релаксации становятся сравнимыми со скоростями почти резонансного V — V-обмена.
К (рис. 1). Только для очень высоколежащих квантовых уровней скорости V — Т-релаксации становятся сравнимыми со скоростями почти резонансного V — V-обмена.
В заключение отметим, что в отличие от температурных зависимостей для V — Т-процессов, представленных на рис. 1, скорости почти резонансного V — V-обмена слабо зависят от температуры. В реальной ситуации скорость V — V-обмена имеет зависимость от температуры, пропорциональную  [110].
[110].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
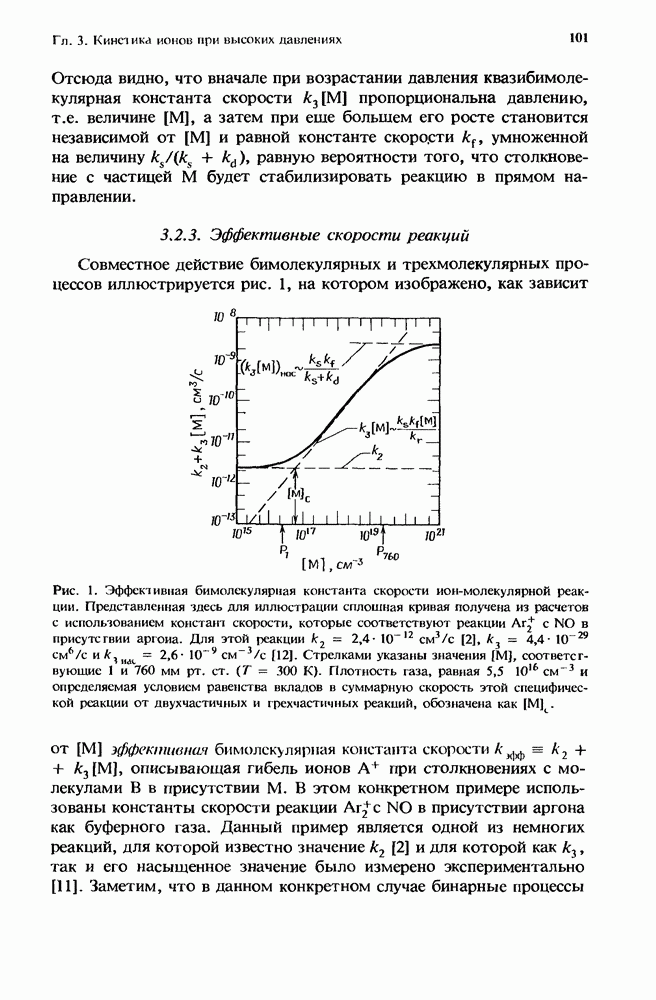
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
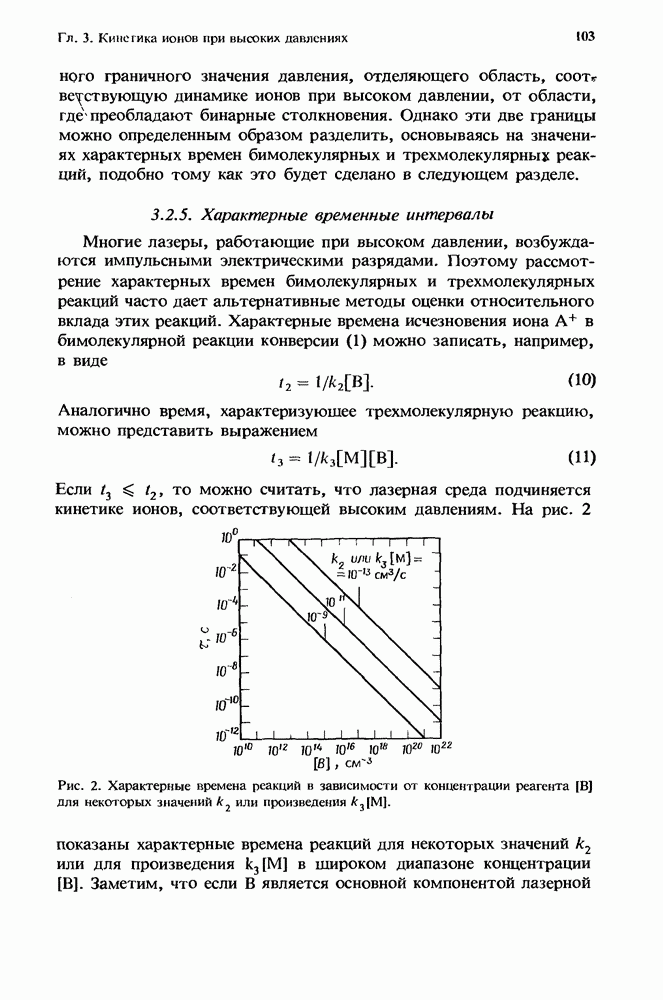
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
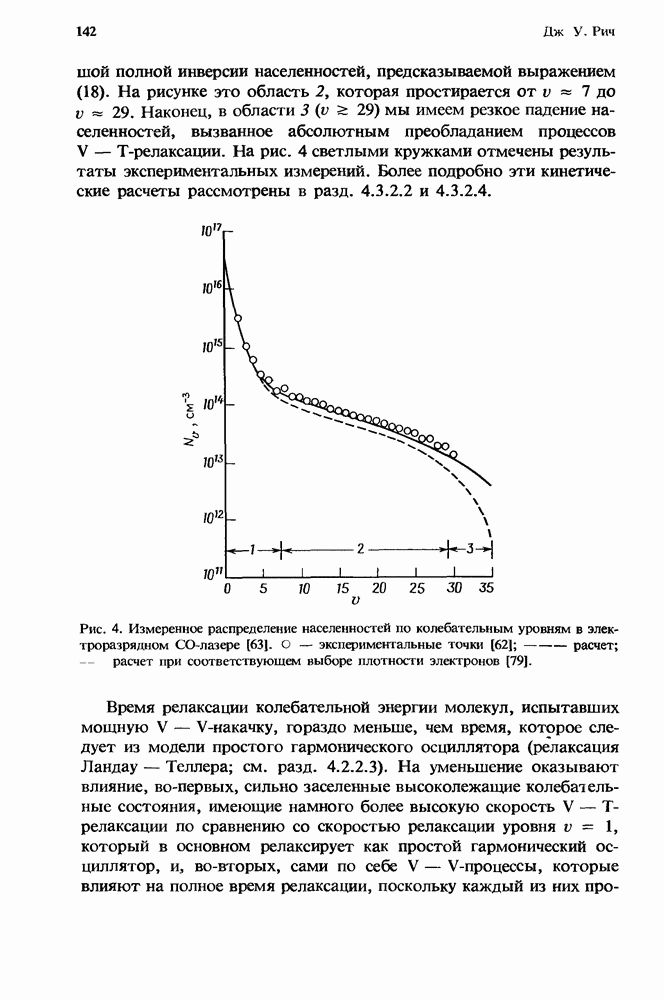
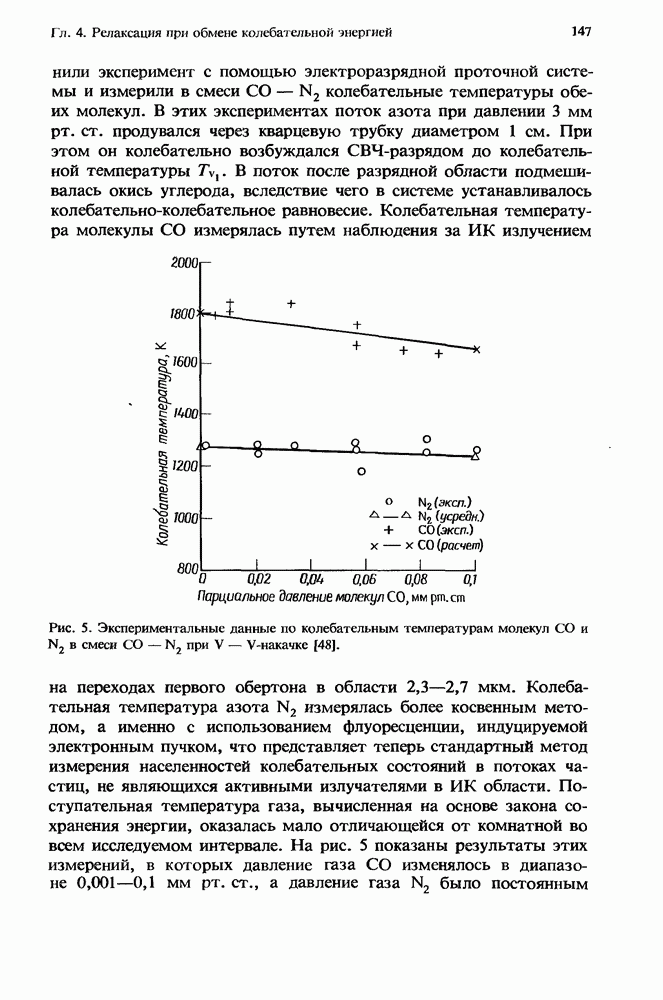
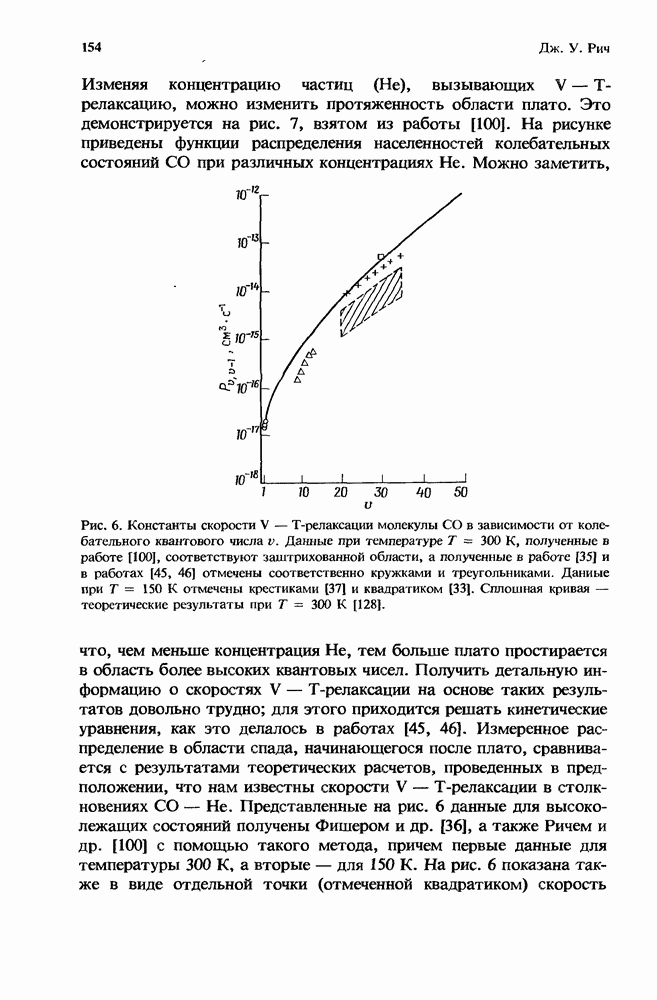
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
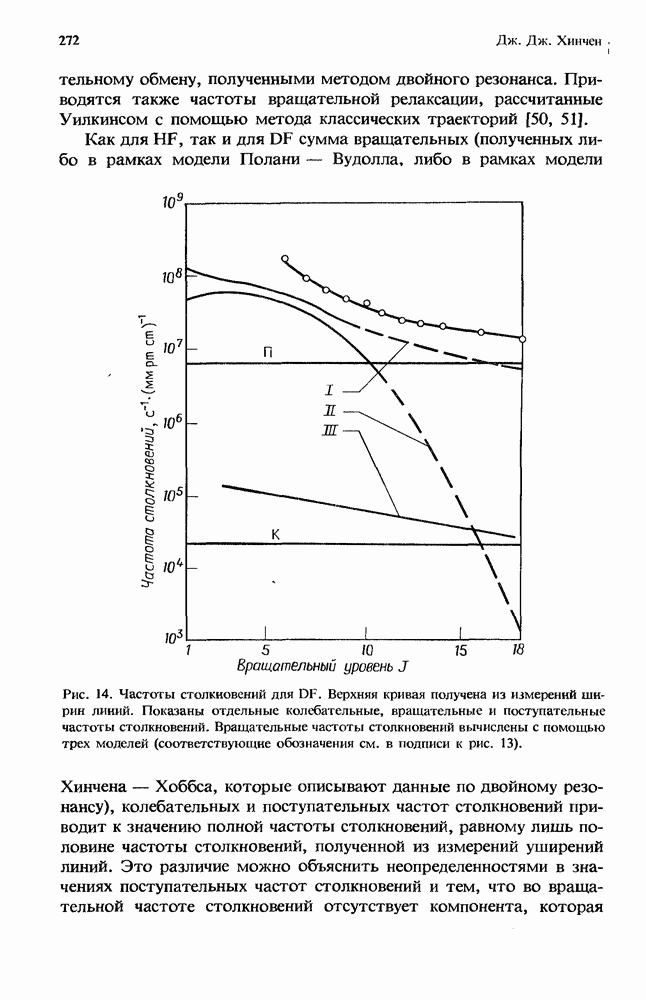
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
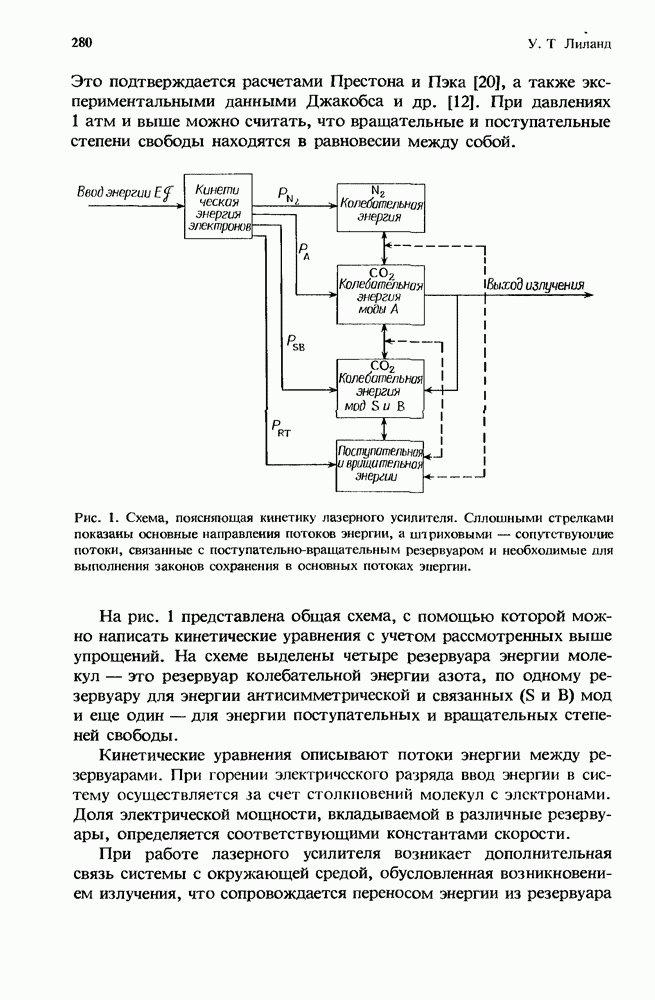
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
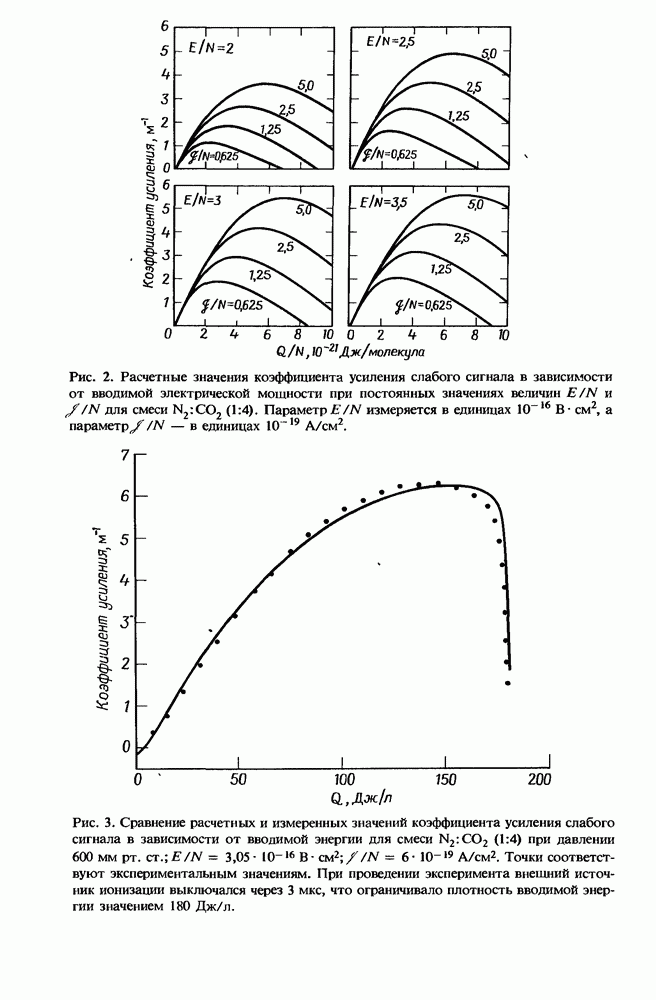
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
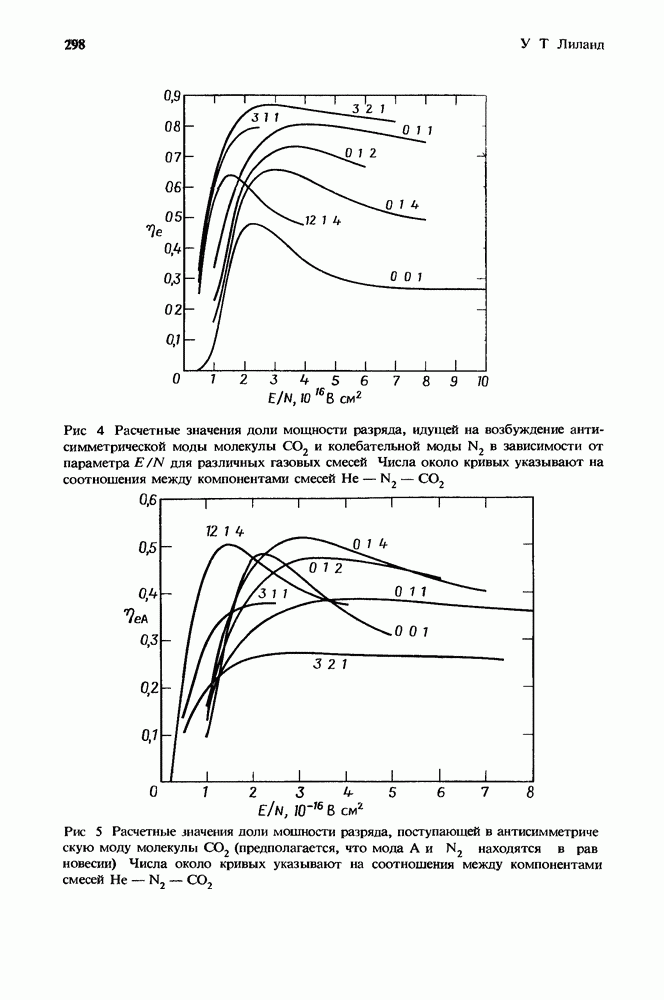
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
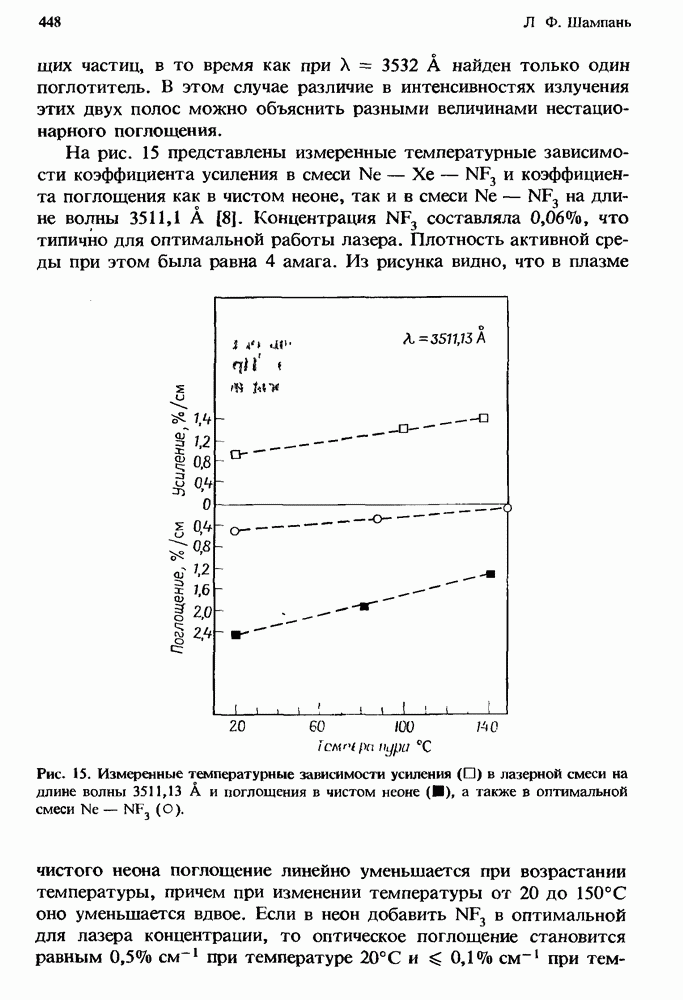
- 12.2.4. Измеренное поглощение
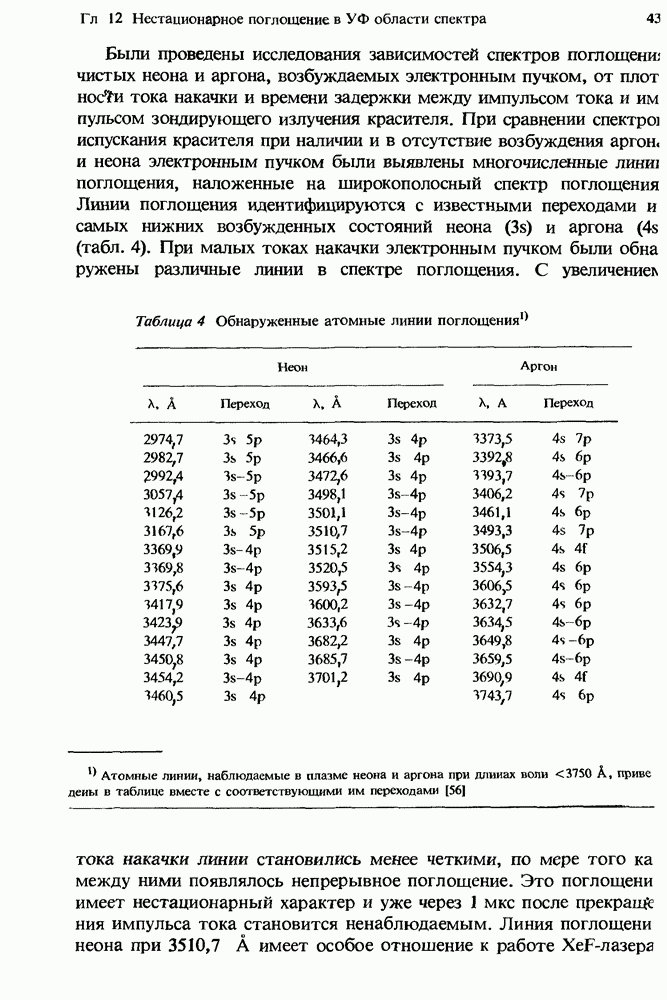
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
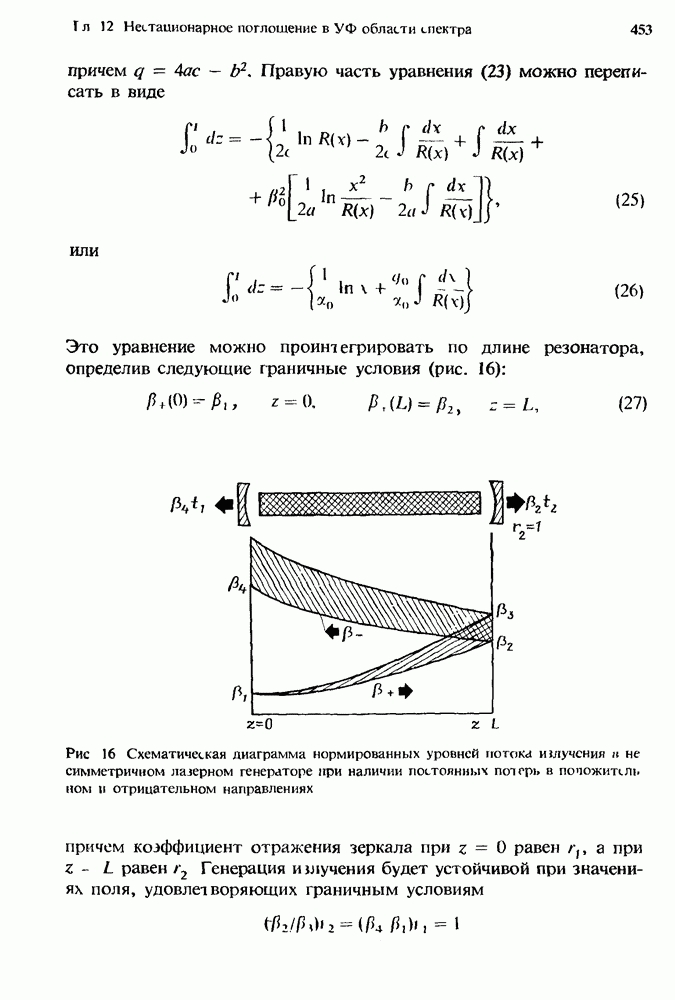
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
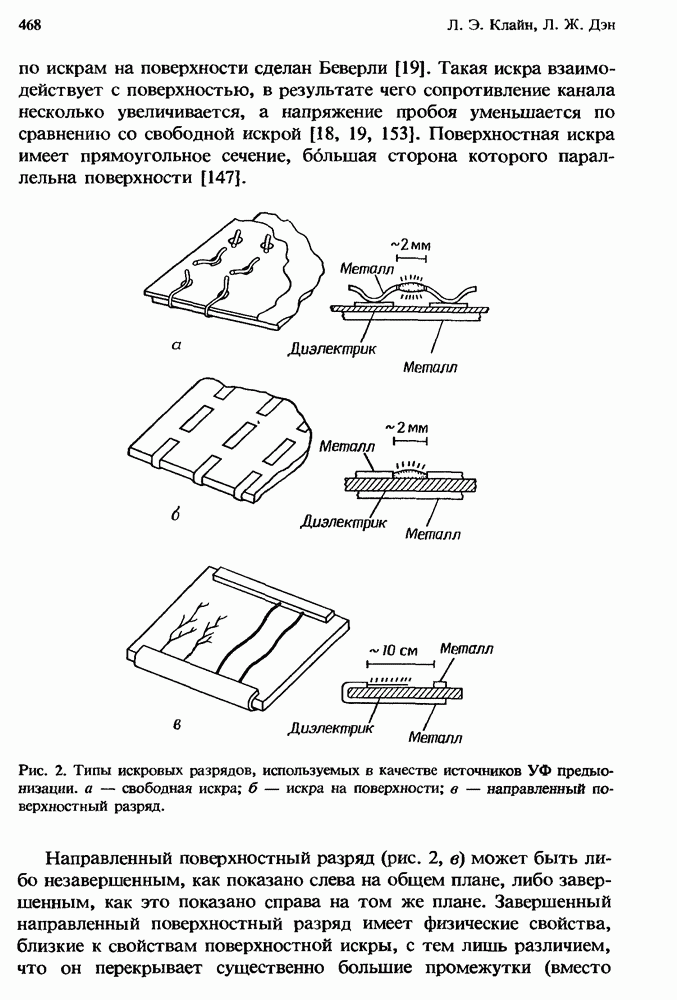
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
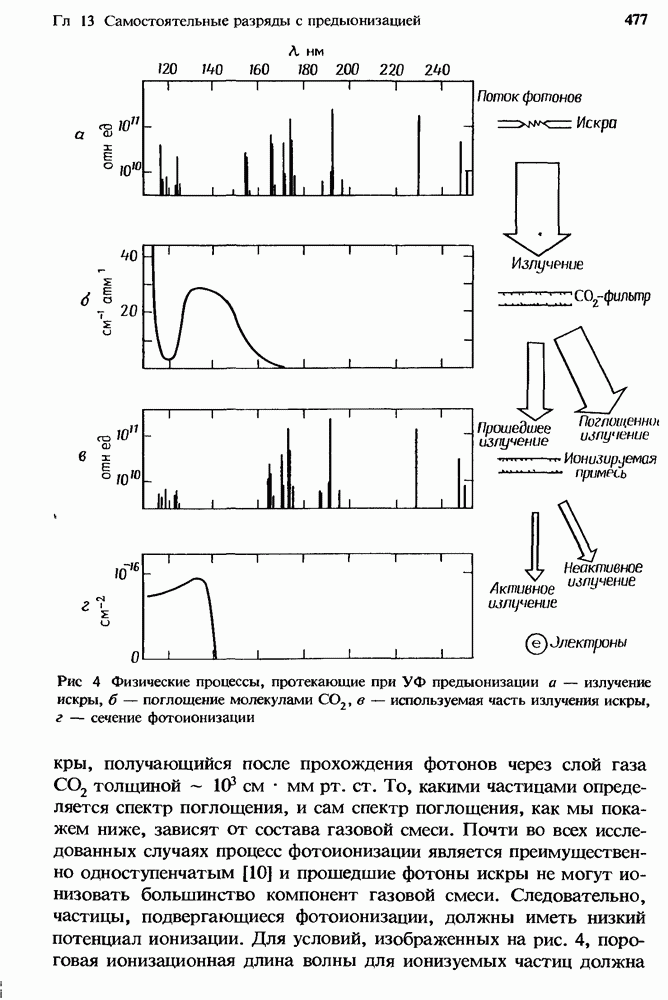
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации