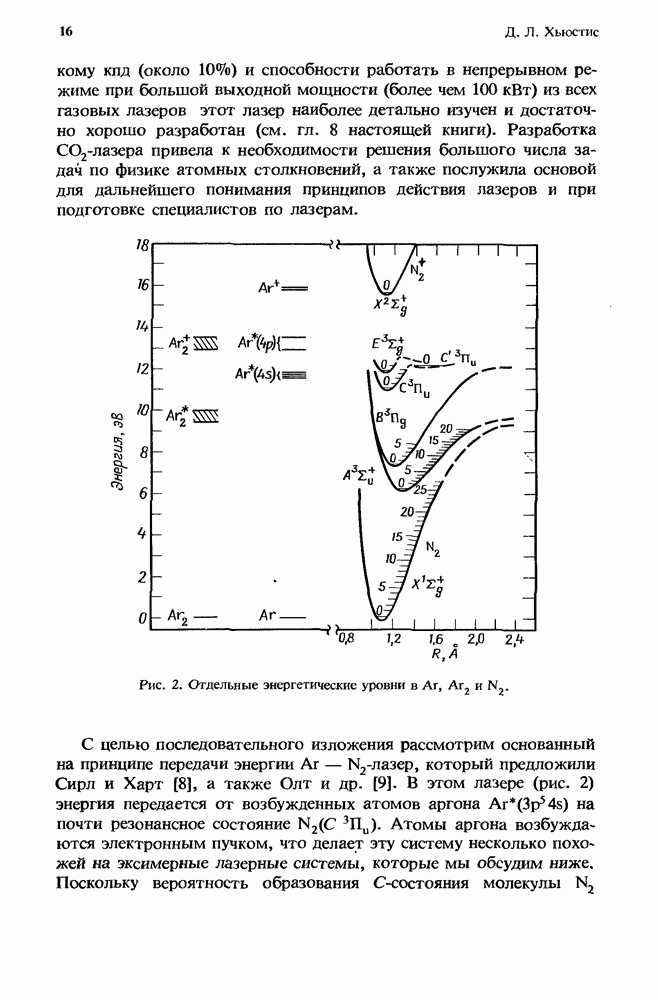
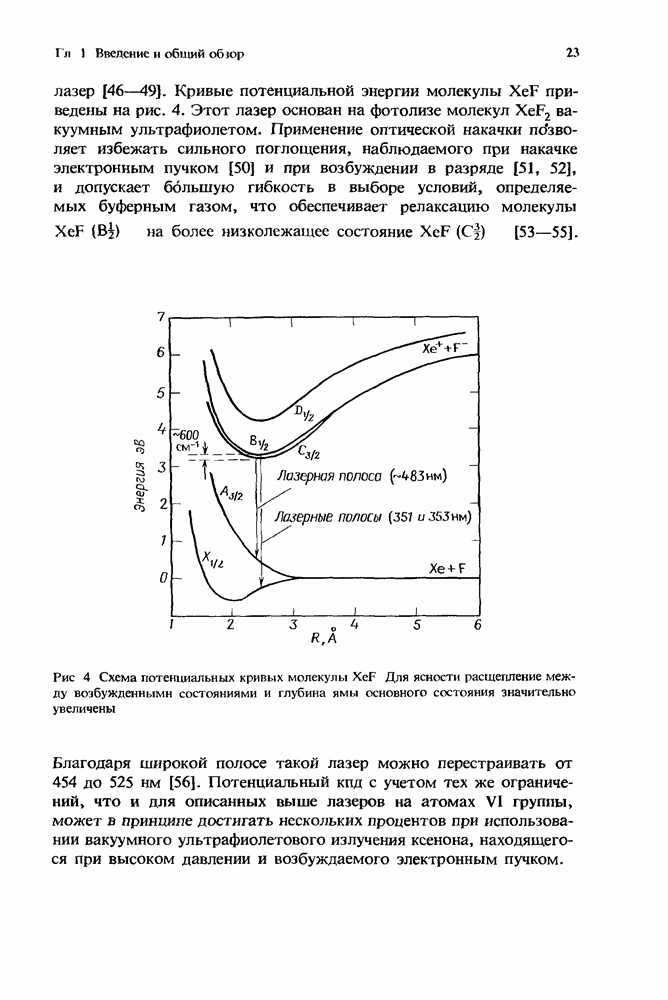
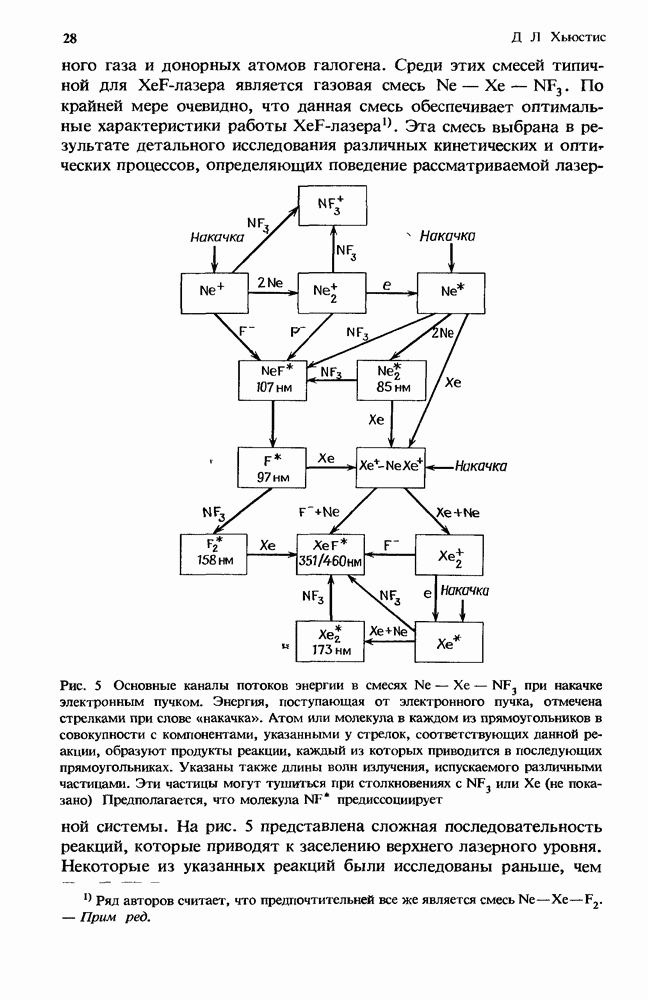
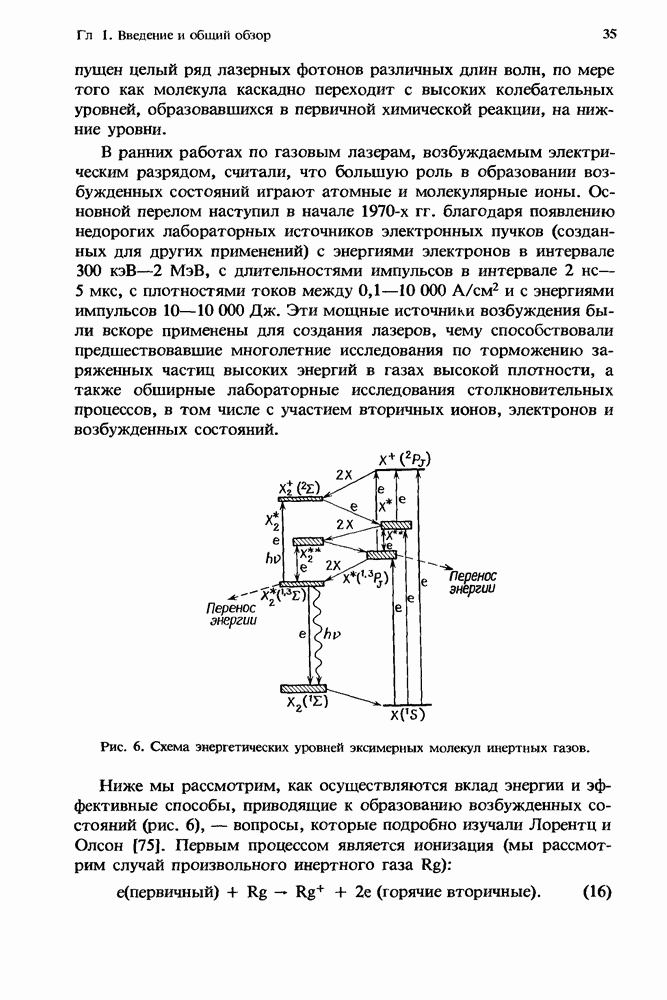
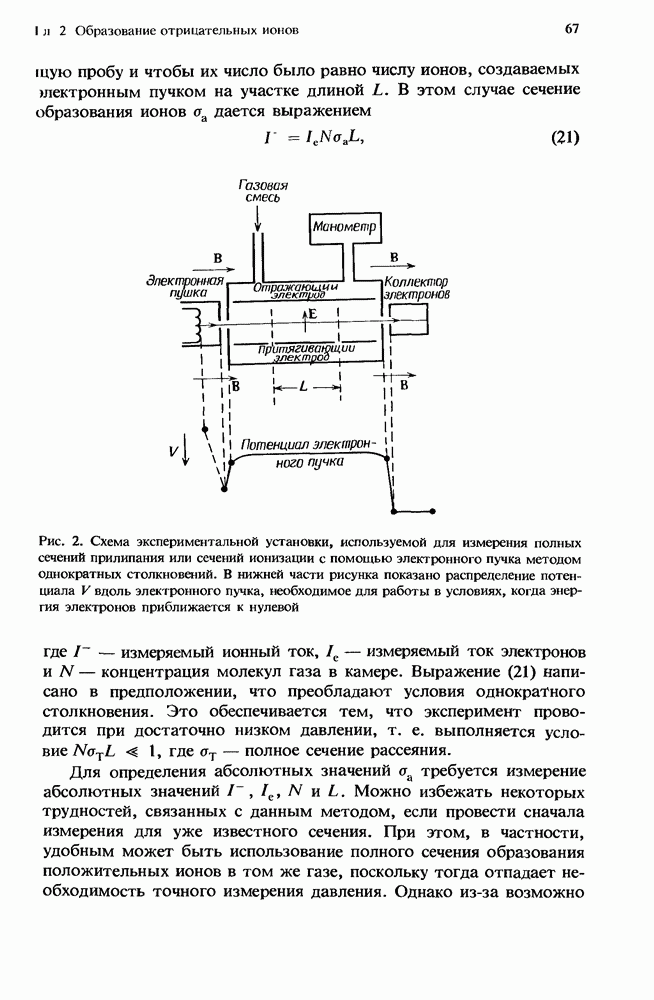
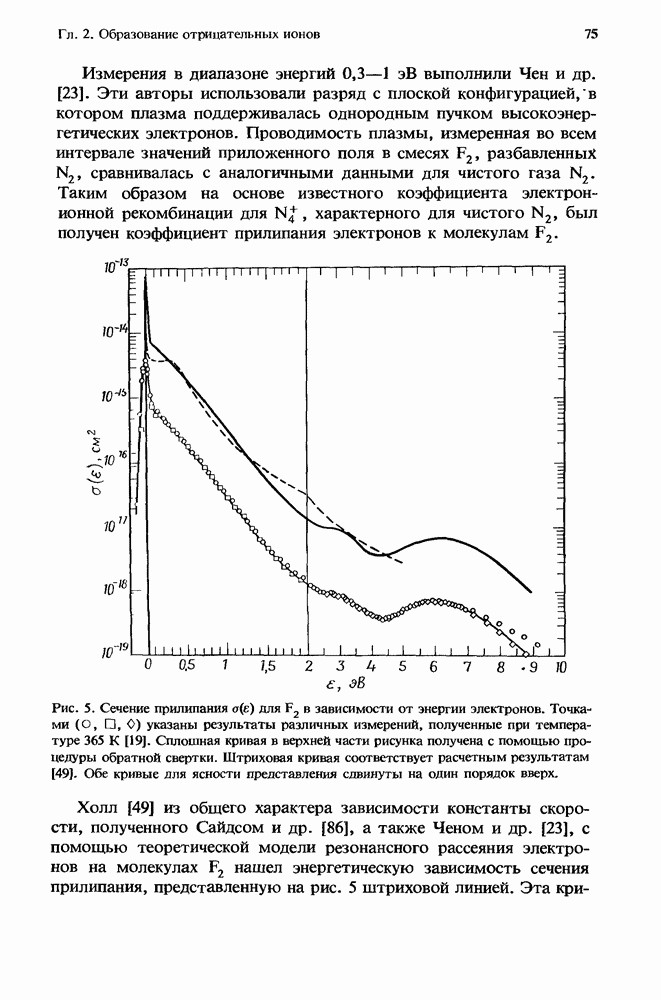
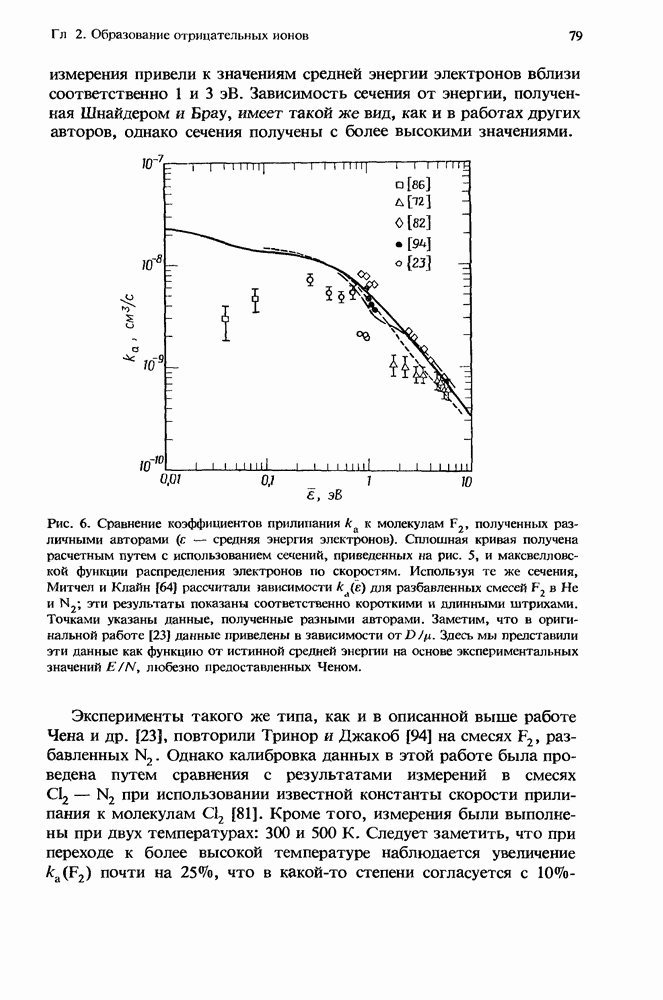
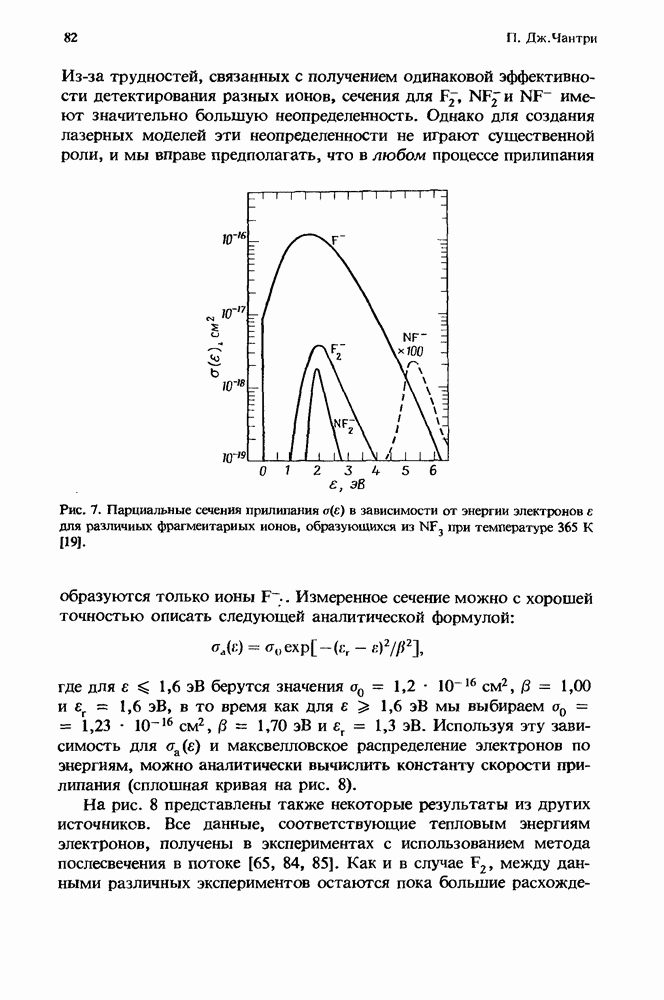
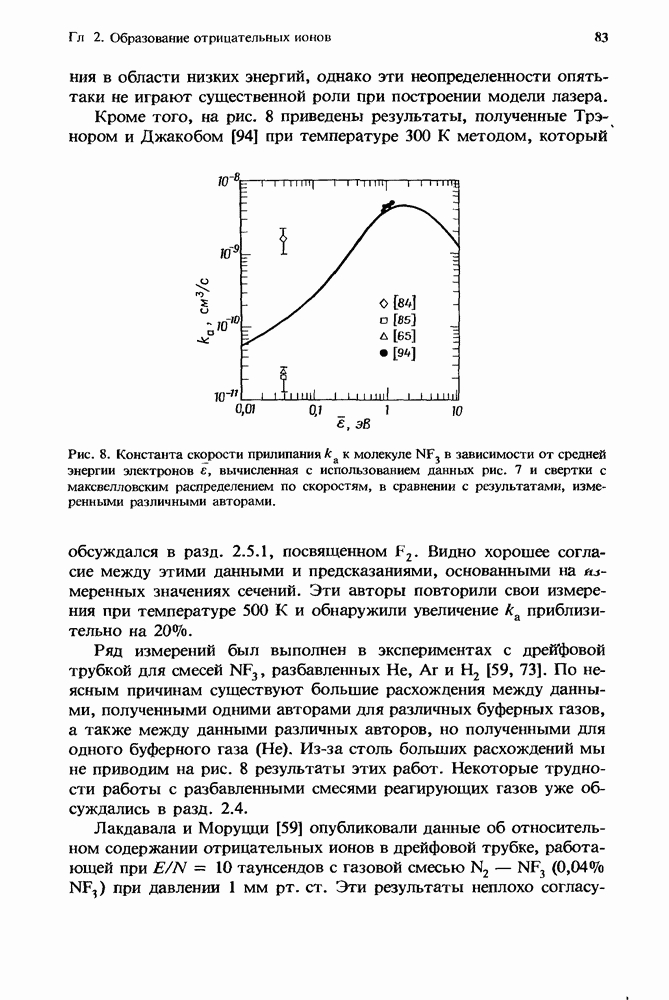
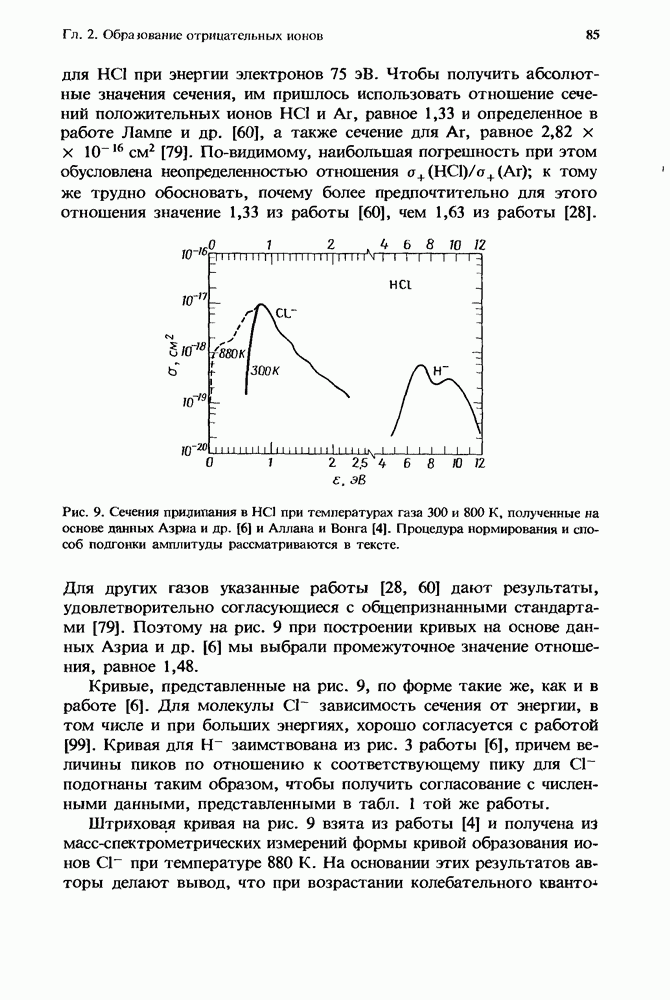
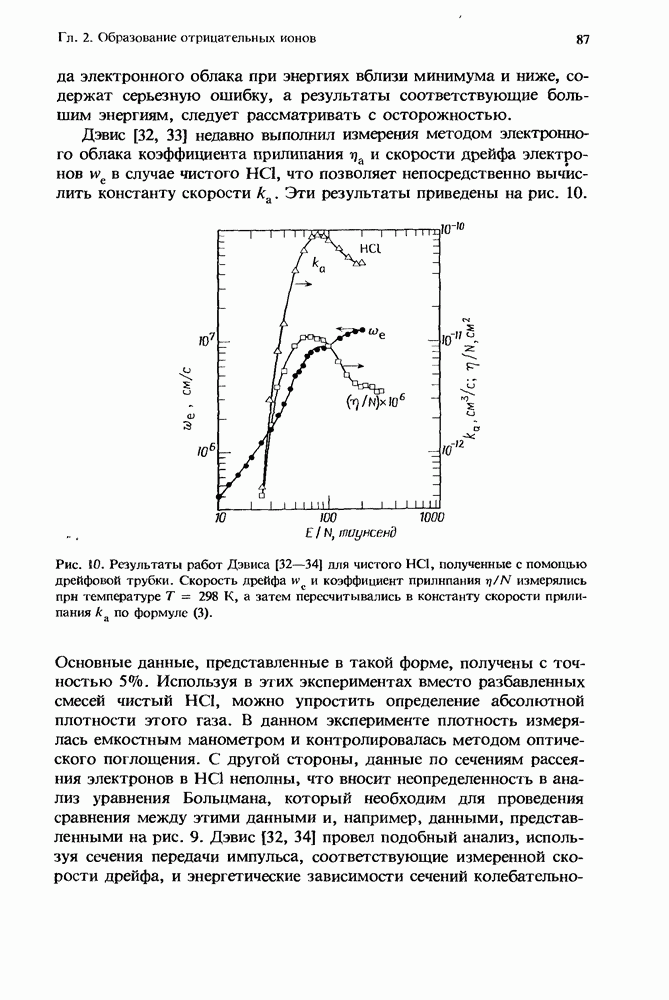
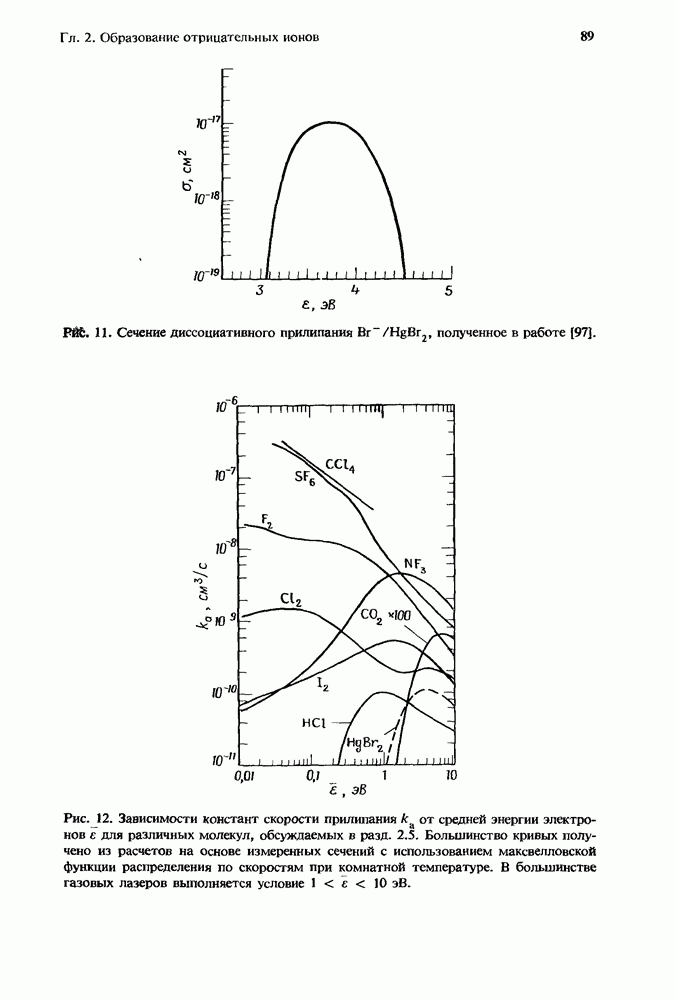
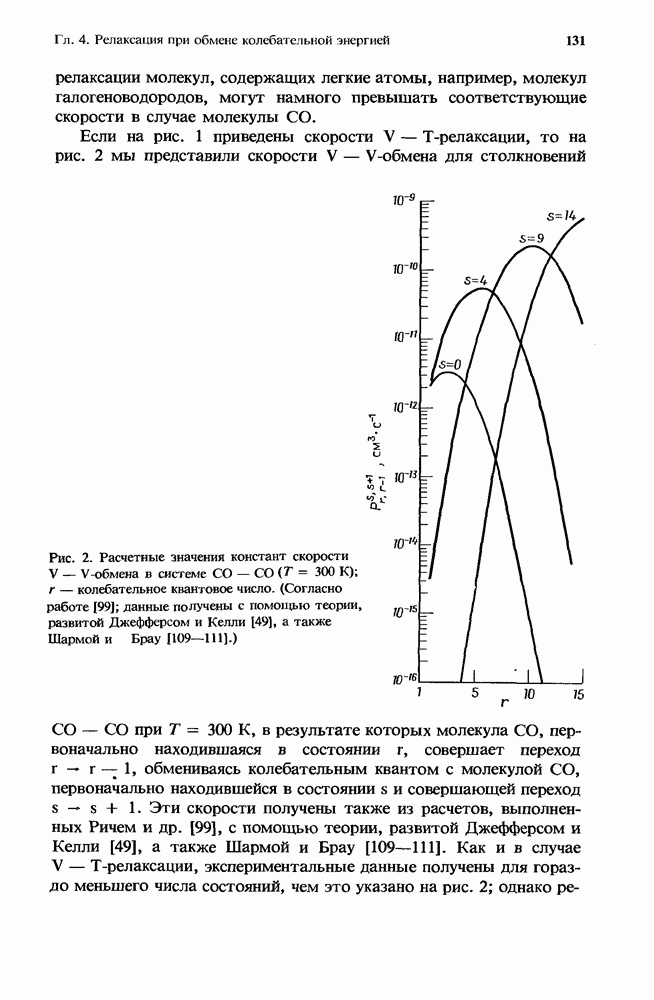
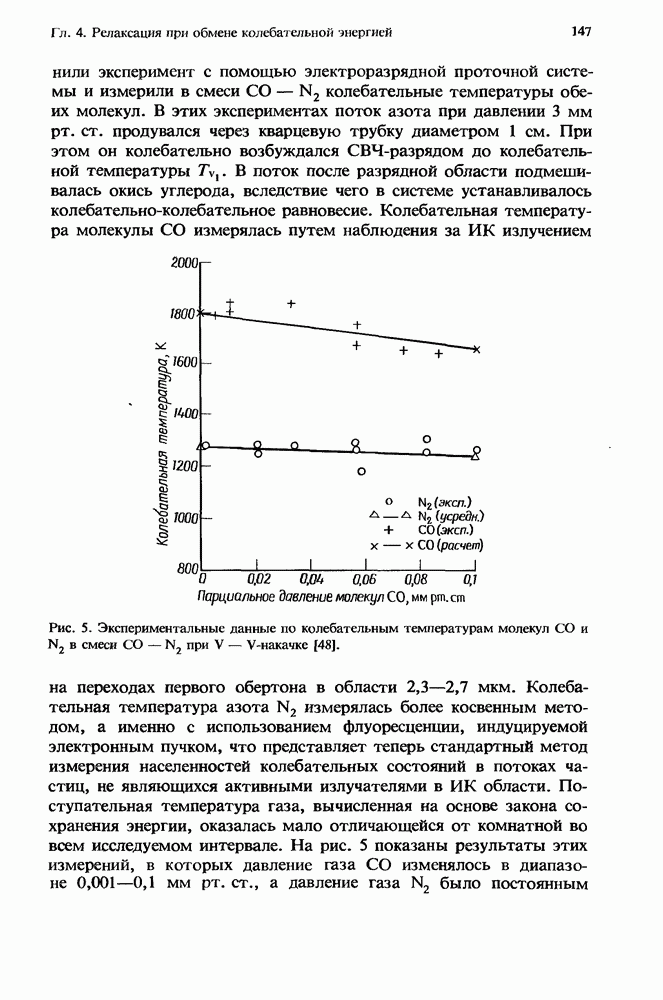
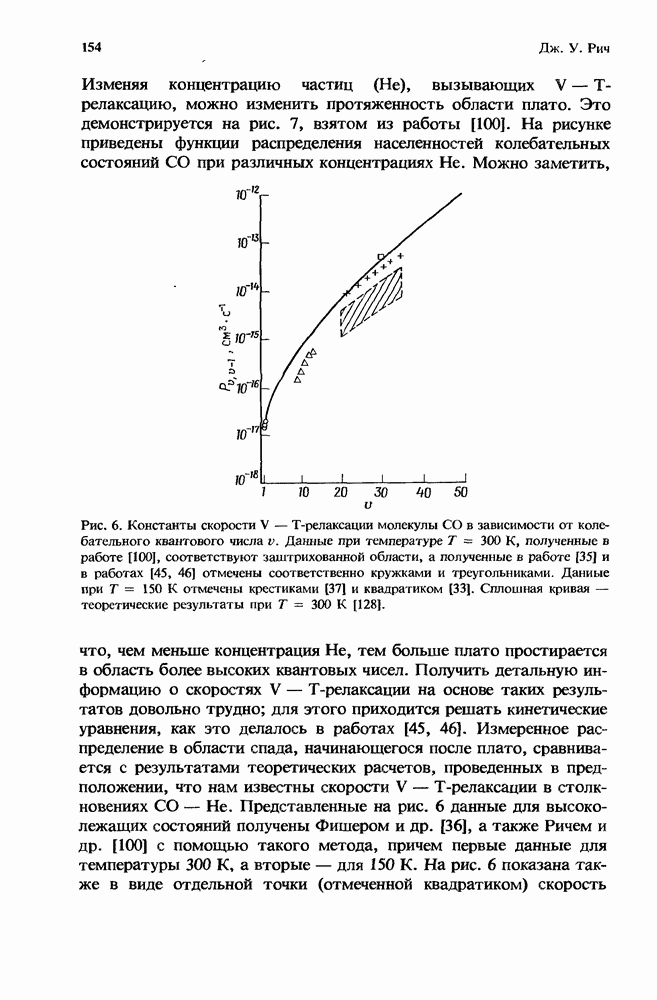
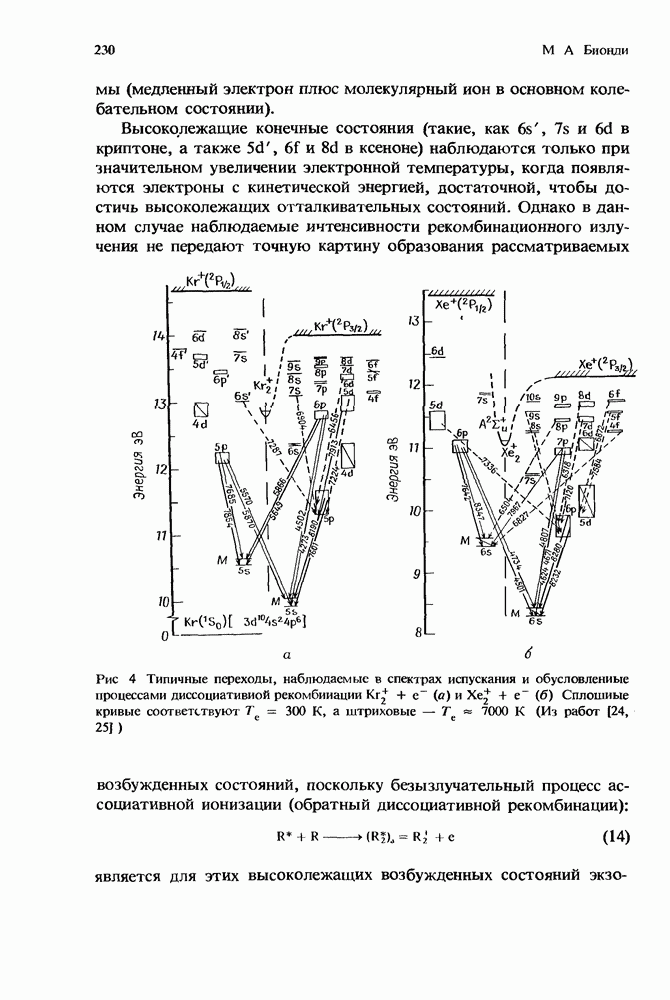
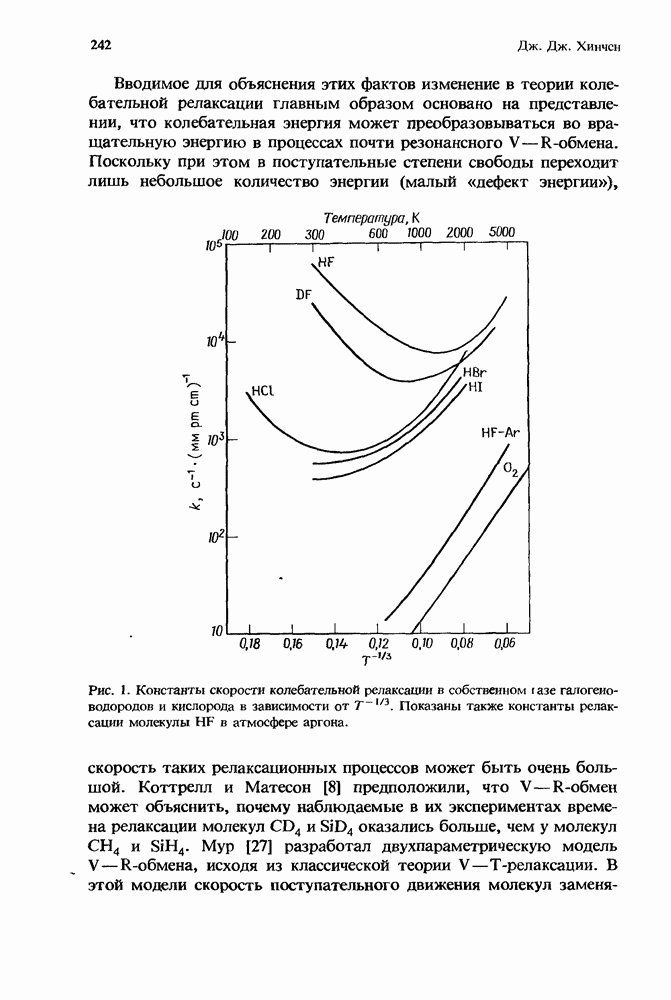
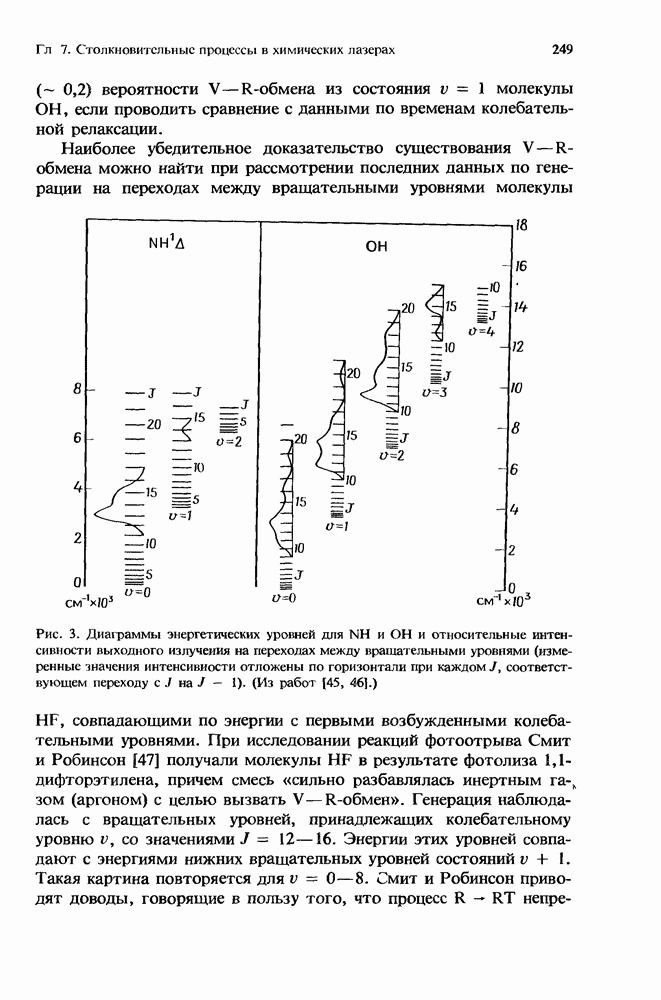
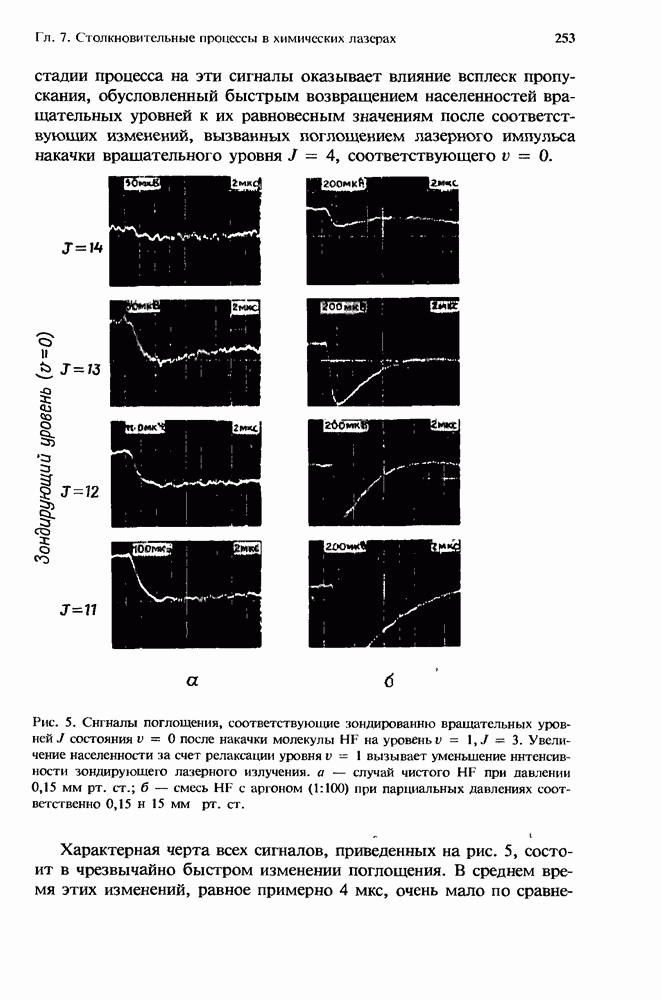
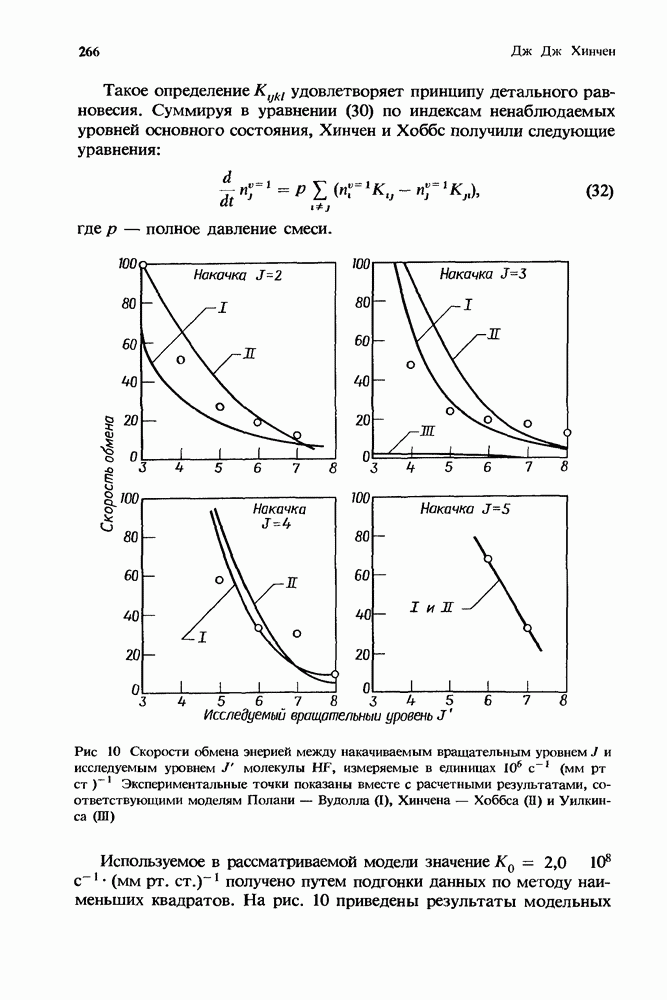
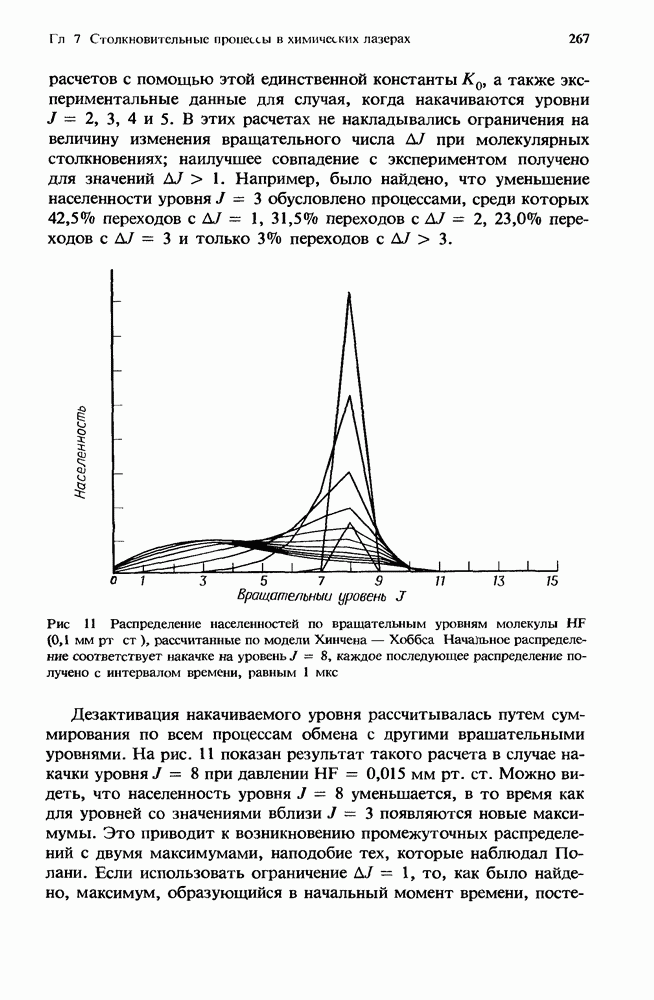
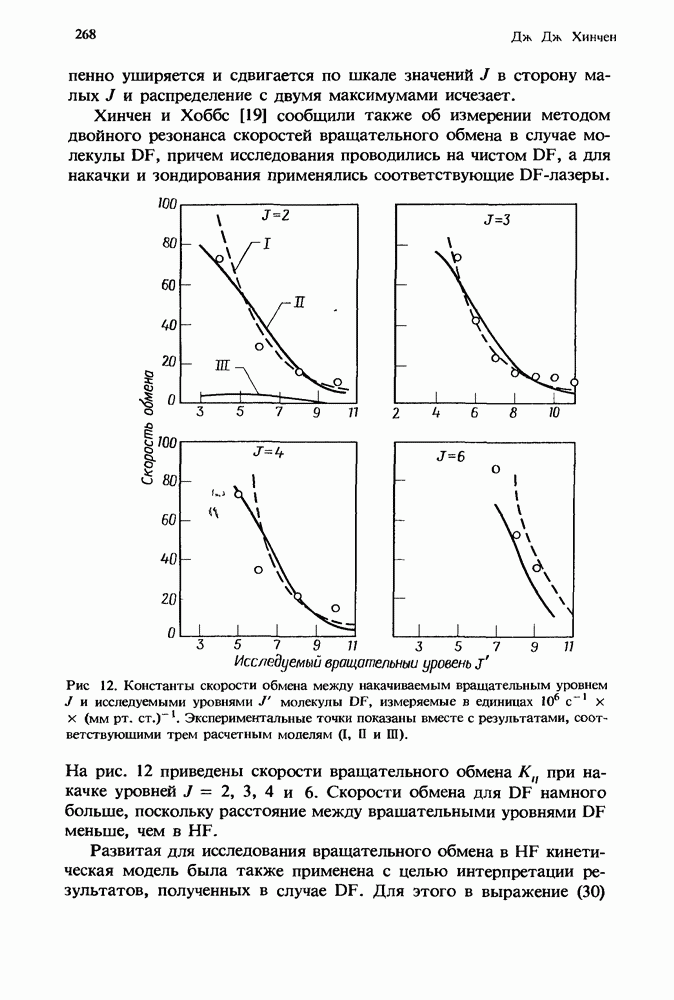
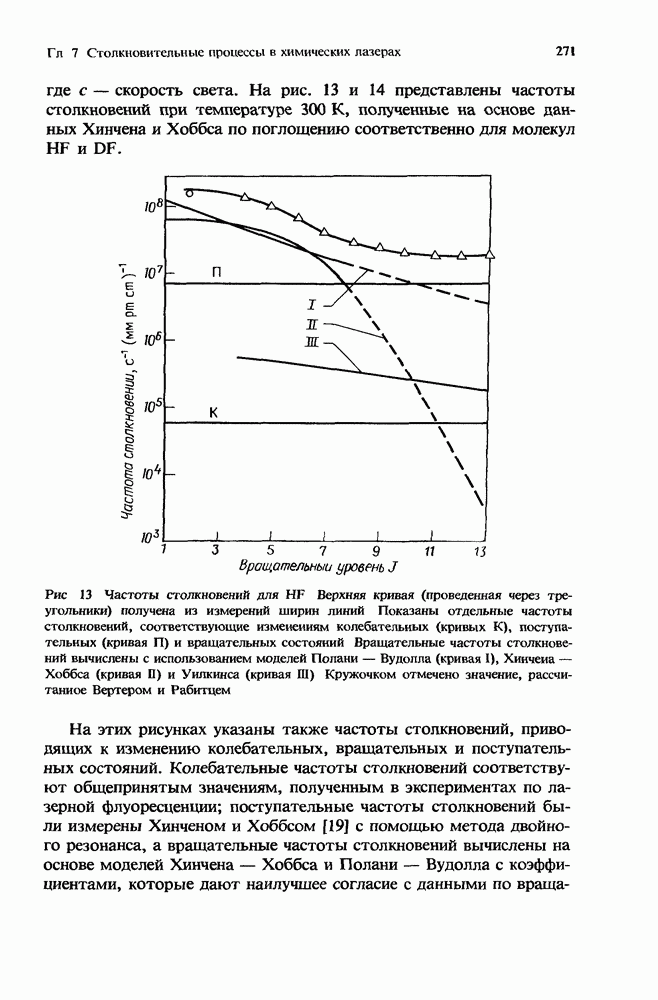
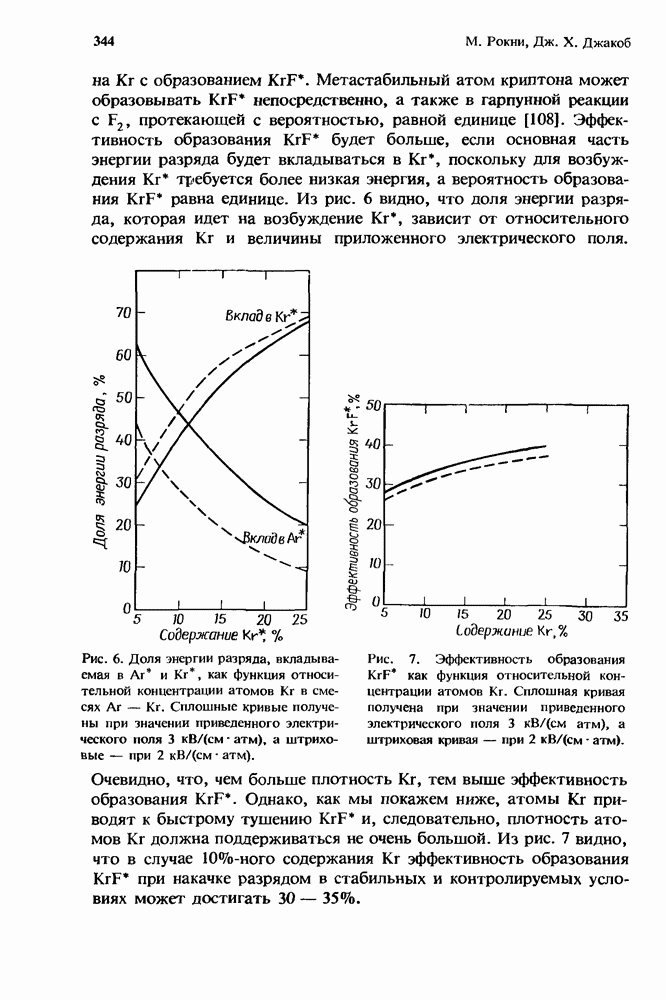
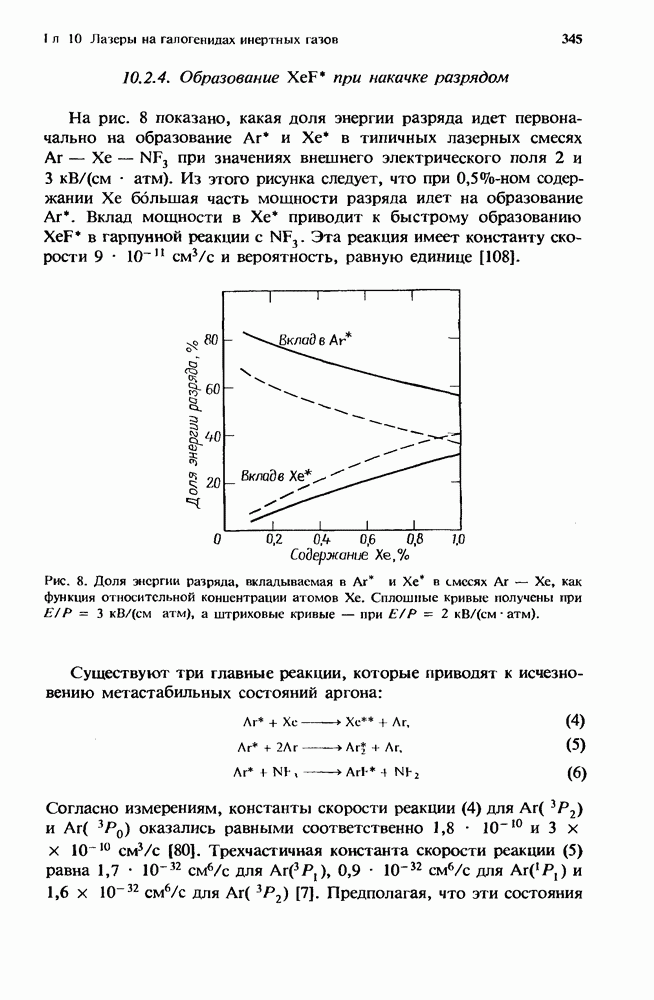
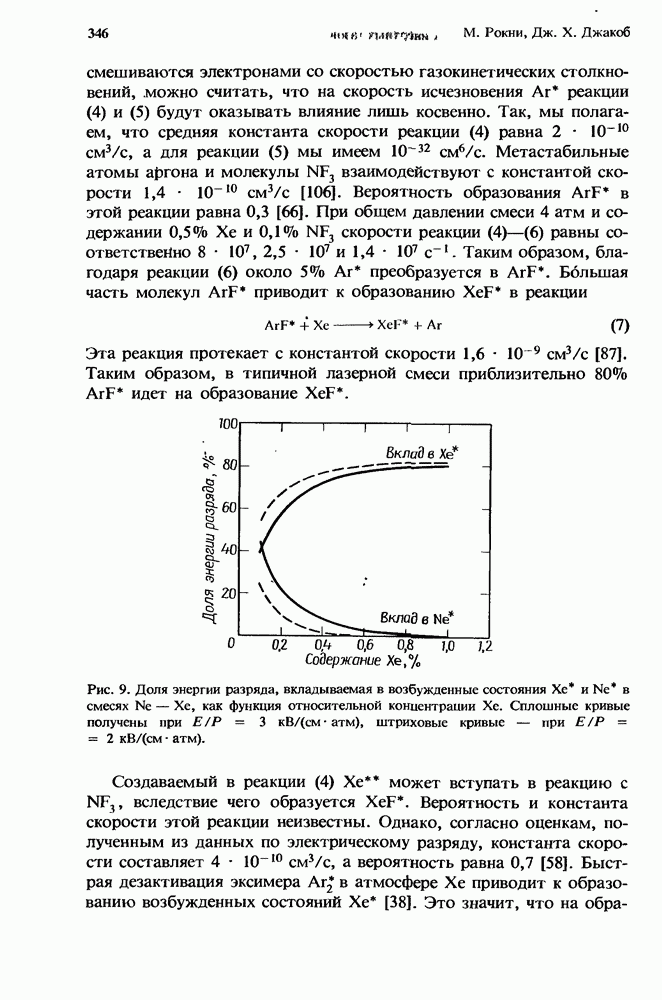
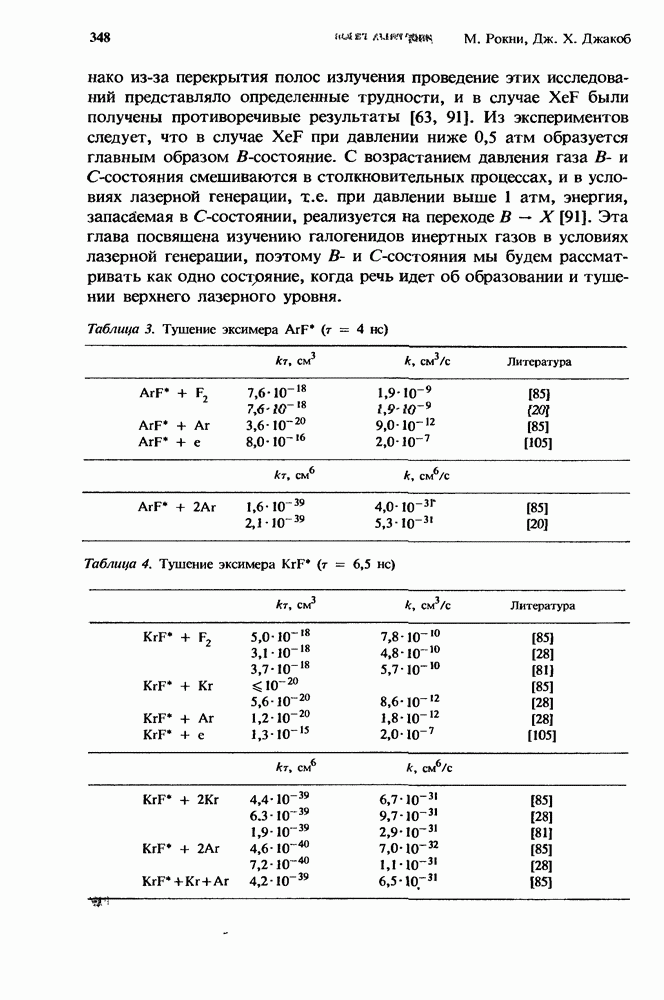
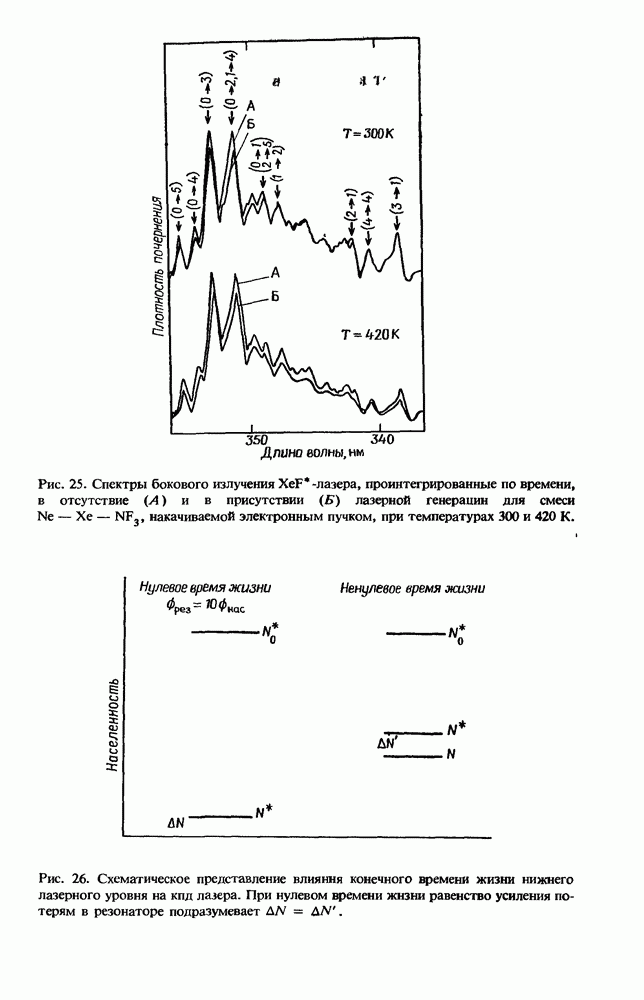
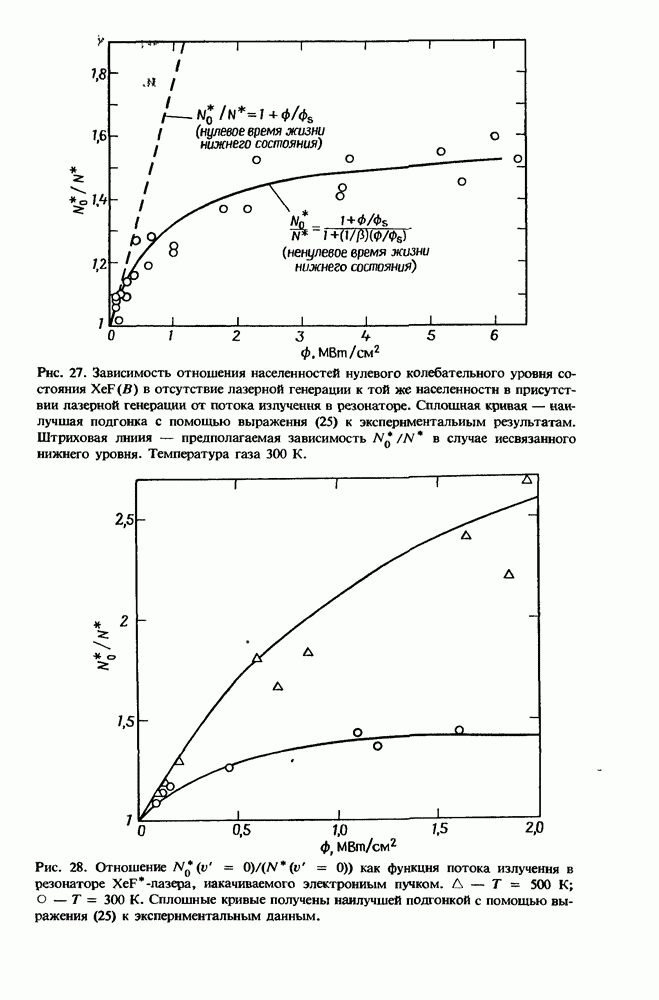
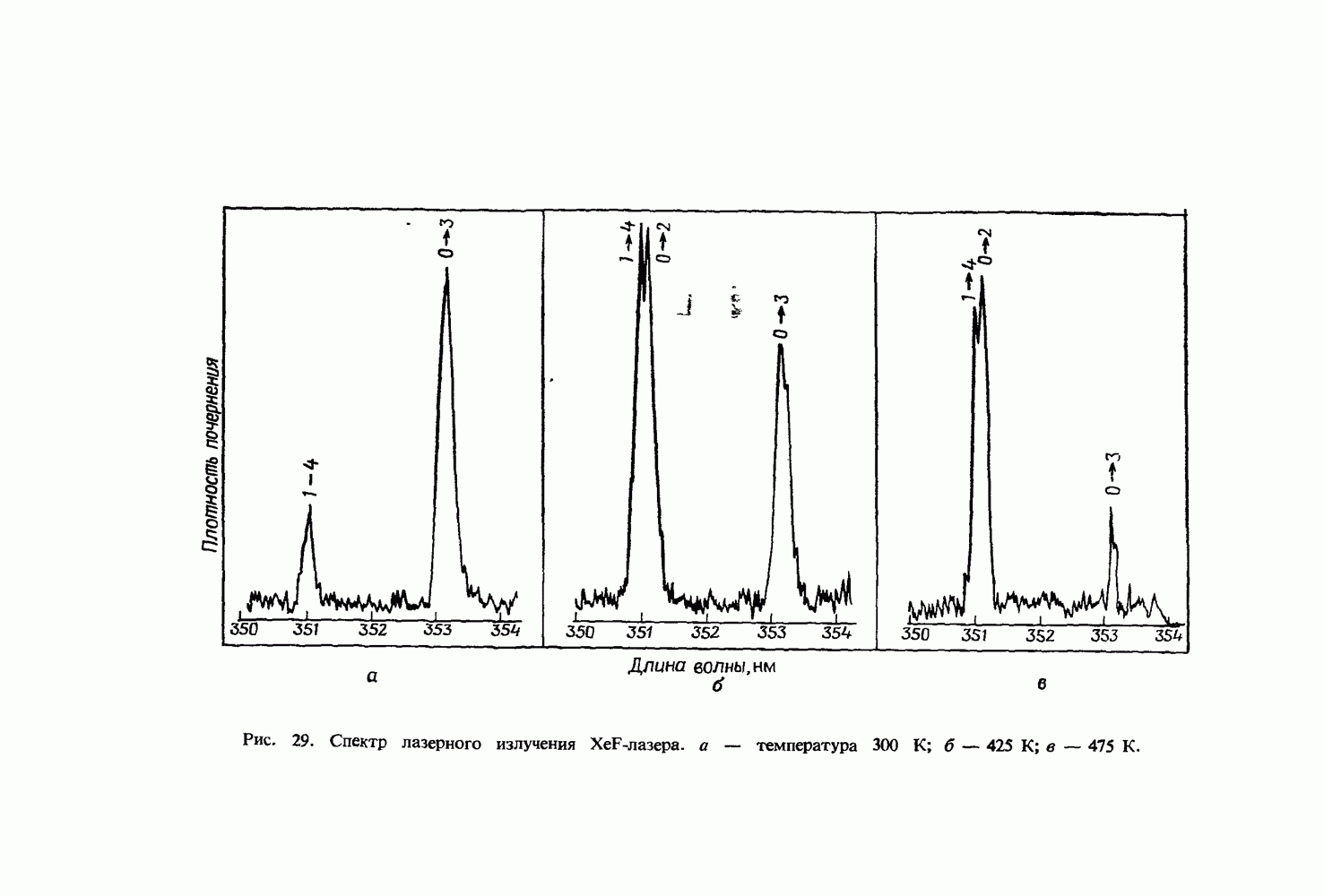
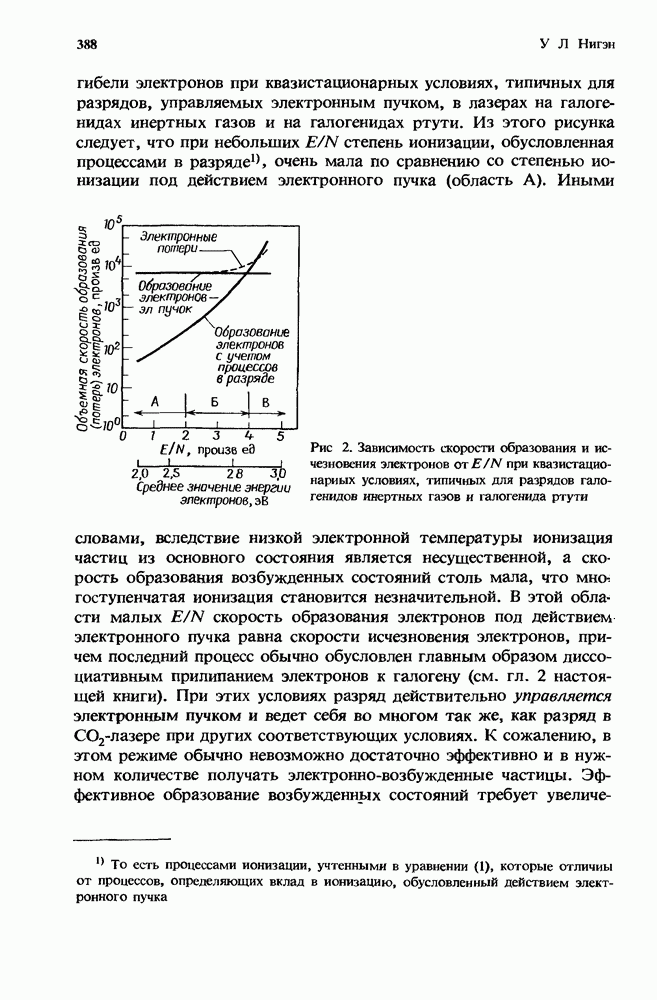
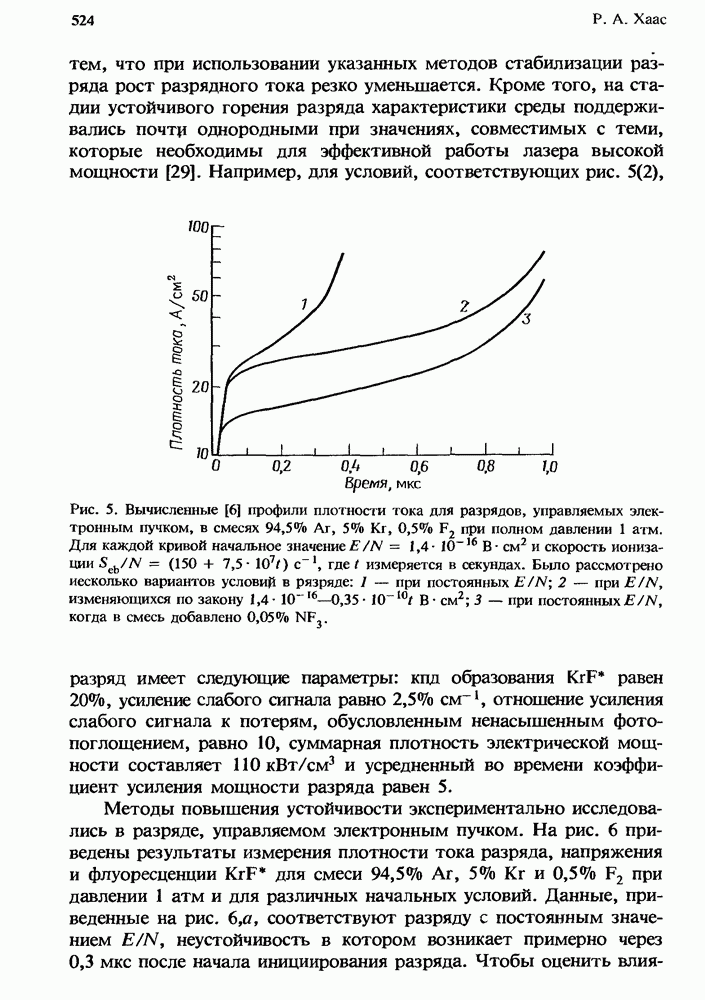
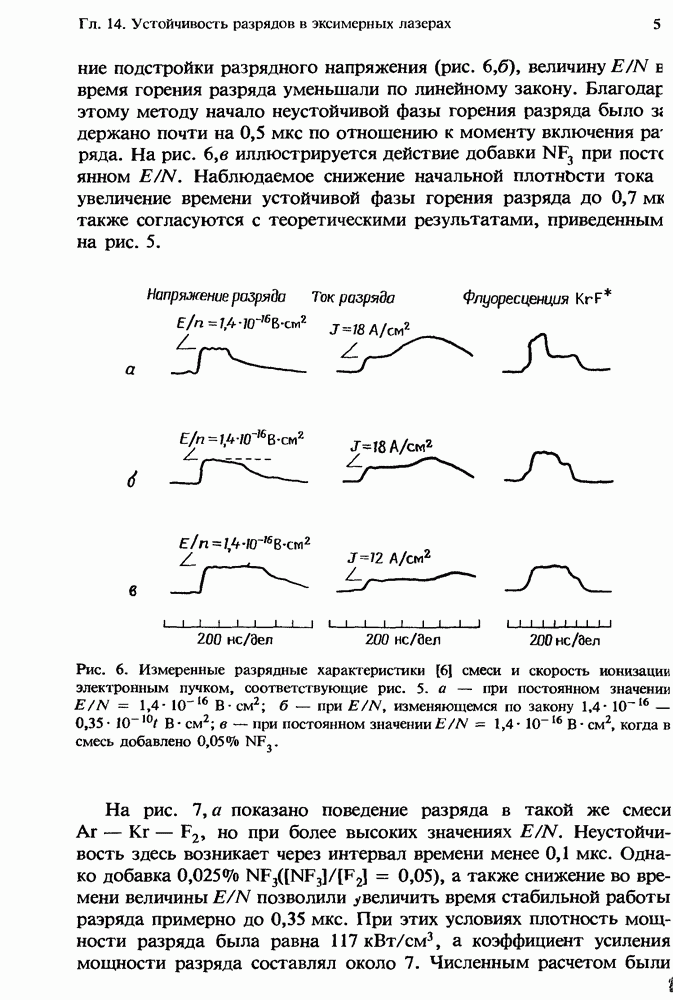
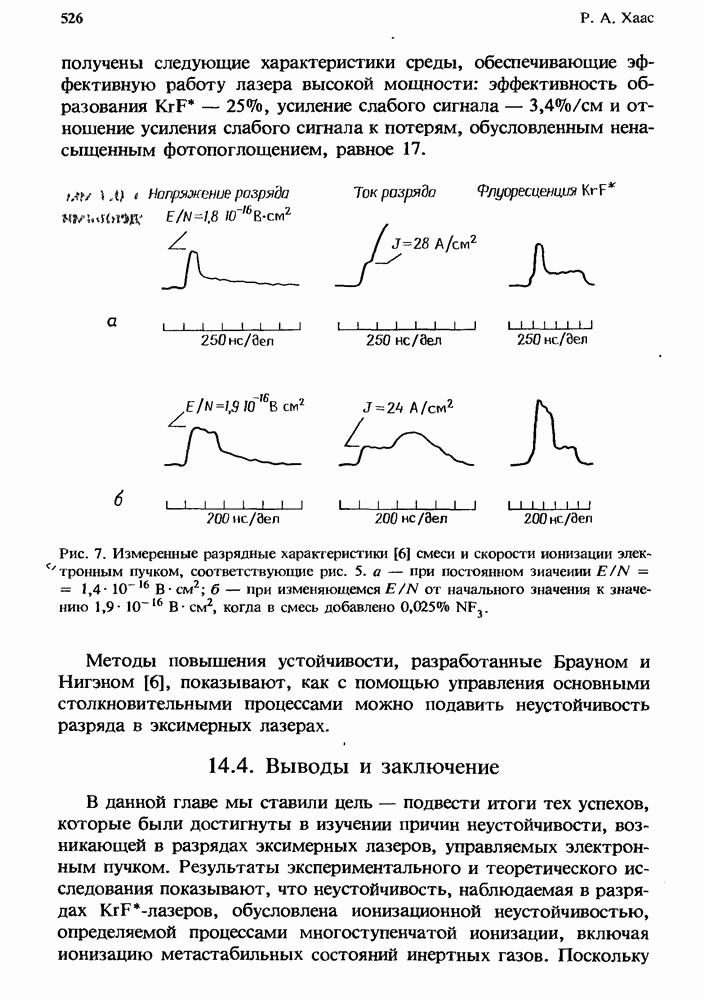
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2.2.5. Релаксация ангармонического осциллятора
Для того чтобы рассмотреть более общий случай, соответствующий релаксации ангармонического осциллятора, вернемся к кинетическому уравнению (4) для бинарной газовой смеси. В случае ангармонического молекулярного осциллятора константы элементарных процессов и энергии уровней уже не являются линейными функциями квантового числа и, следовательно, соотношения (8) и (13) неприменимы. Если в уравнении (4) оставить члены, описывающие как V - V-, так и V — Т-релаксацию, то простые аналитические решения для них найти не удается. Однако, как было отмечено выше, скорости V — V-обмена для всех квантовых состояний (кроме высоколежащих) намного выше скоростей V — Т-процессов (ср. рис. 1 и 2). Поэтому можно получить аналитическое стационарное решение только при учете V — V-процессов. Это решение имеет большое физическое значение и является хорошей аппроксимацией реального квазистационарного распределения колебательных населенностей квантовых уровней, обусловленного главным образом
V — V-обменом. Прямой подстановкой можно проверить, что благодаря распределению

3-й и 4-й члены в уравнении (4) обращаются в нуль. Именно это распределение устанавливается в процессе V — V-обмена при условии, что отсутствуют процессы другого вида. Оно аналогично больцмановскому распределению, которое образуется в гармоническом осцилляторе вследствие V — V-релаксации. Действительно, мы покажем, что в пределе гармонического осциллятора выражение (14) описывает больцмановское распределение. В общем случае
 является единственным параметром, который появляется в больцмановском распределении и заменяет в нем колебательную температуру
является единственным параметром, который появляется в больцмановском распределении и заменяет в нем колебательную температуру 
При высоких значениях энергии, запасенной в колебательной моде, и при низкой поступательной температуре газа распределение (14) начинает существенно отличаться от больцмановского. Это легче всего показать, если представить параметр у в виде, позволяющем сравнивать его непосредственно с температурой. Чтобы сделать это, заметим, что, хотя больше и не существует единой колебательной температуры, связывающей населенности всех уровней, можно ввести параметр в, определяемый выражением

Вообще говоря, для каждого из уровней имеется свое значение в. Приравнивая друг другу выражения (14) и (15), получаем следующее соотношение между у и в:

причем величина 0, связана с в соотношением

Подставляя это соотношение в выражение (15), получаем

Выражение (18) представляет собой искомую альтернативу распределения (14), в котором параметр у заменен на в.
Нетрудно проверить, что в пределе, соответствующем условию  распределение (18) сводится к больцмановскому. Этот предел соответствует равновесию между колебательной и поступательной степенями свободы, к которому стремится система. Однако в общем случае
распределение (18) сводится к больцмановскому. Этот предел соответствует равновесию между колебательной и поступательной степенями свободы, к которому стремится система. Однако в общем случае  распределение (18) все еще остается больцмановским для самых нижних гармонических колебательных уровней, для которых
распределение (18) все еще остается больцмановским для самых нижних гармонических колебательных уровней, для которых  Для этих состояний второй член в показателе экспоненты выражения (18) является малым и функция распределения оказывается очень близкой к распределению Больцмана с «колебательной температурой» в. В случае когда в
Для этих состояний второй член в показателе экспоненты выражения (18) является малым и функция распределения оказывается очень близкой к распределению Больцмана с «колебательной температурой» в. В случае когда в  , функция распределения остается почти больцмановской даже для высоколежащих уровней, поскольку при этом второй член в показателе экспоненты также довольно мал. Однако в противоположном случае, когда
, функция распределения остается почти больцмановской даже для высоколежащих уровней, поскольку при этом второй член в показателе экспоненты также довольно мал. Однако в противоположном случае, когда  распределение заметно отклоняется от больцмановского. Для данного в населенности высоких колебательных состояний оказываются большими, чем населенности, соответствующие распределению Больцмана с температурой
распределение заметно отклоняется от больцмановского. Для данного в населенности высоких колебательных состояний оказываются большими, чем населенности, соответствующие распределению Больцмана с температурой  . Этот эффект
. Этот эффект
проявляется тем сильнее, чем больше колебательное квантовое число, так что выше некоторого уровня должна образовываться инверсия населенностей. Такая накачка является прежде всего следствием связанных принципом детального равновесия [выражение (2)] соотношений между скоростями прямых и обратных процессов
V — V-обмена, определяемого соответствующими членами уравнения (4). Этому можно дать простое объяснение на примере четырехуровневой системы (рис. 3).

Рис. 3. Четырехуровневая схема колебательно-колебательной (V —  -накачки.
-накачки.
Рассмотрим молекулу А с двумя колебательными энергетическими состояниями 1 и 2, которая сталкивается с молекулой Б, имеющей также два колебательных состояния 5 и 4. Энергии этих состояний указаны на рис. 3. Дефект резонанса А Нравен разности энергий  Предположим, что первоначально молекула А находится в состоянии 2, а молекула Б в состоянии 3. В результате столкновения они обмениваются внутренней энергией, причем молекула А совершает переход
Предположим, что первоначально молекула А находится в состоянии 2, а молекула Б в состоянии 3. В результате столкновения они обмениваются внутренней энергией, причем молекула А совершает переход  молекула Б — переход
молекула Б — переход  На рис. 3 данный процесс указан сплошными стрелками. Скорость этого процесса равна а его протекание сопровождается передачей энергии во внешние (поступательные и врашательные) степени свободы. Если поступательные степени свободы находятся в равновесии при температуре Г, то, согласно принципу детального равновесия, скорость обратного процесса
На рис. 3 данный процесс указан сплошными стрелками. Скорость этого процесса равна а его протекание сопровождается передачей энергии во внешние (поступательные и врашательные) степени свободы. Если поступательные степени свободы находятся в равновесии при температуре Г, то, согласно принципу детального равновесия, скорость обратного процесса  указанного на рис. 3 штриховыми стрелками, связана со скоростью
указанного на рис. 3 штриховыми стрелками, связана со скоростью  соотношением
соотношением

Таким образом, при низких температурах, при которых отношение  велико, скорость процесса, обозначенного сплошными стрелками, может значительно превышать скорость обратного ему процесса, т. е. мы имеем
велико, скорость процесса, обозначенного сплошными стрелками, может значительно превышать скорость обратного ему процесса, т. е. мы имеем  При этих условиях система
При этих условиях система
Б с меньшей разностью энергии между конечным и начальным состояниями накачивается за счет системы А, т.е. появляется тенденция к образованию инверсии между уровнями 4 и 5. Возвращаясь к более общему случаю многоуровневой системы ангармонических колебательных уровней, описываемой выражением (18), мы видим, что указанный процесс накачки, возникающий при  соответствует ситуации, когда поступательные степени свободы системы являются «холодными», а большая часть энергии сосредоточена в колебательной моде.
соответствует ситуации, когда поступательные степени свободы системы являются «холодными», а большая часть энергии сосредоточена в колебательной моде.
Распределение (18) оказывается справедливым только для тех квантовых состояний, для которых можно пренебречь V — Т-релаксацией по сравнению с V - V-обменом. Как мы уже отмечали в разд. 4.2.2.1 (рис. 1 и 2), такое преобладание процессов V - V-обмена над другими, процессами характерно для нижних квантовых колебательных состояний. Для большинства изученных в настоящее время молекул существует некоторое колебательное квантовое число, начиная с которого скорость V — Т-процессов становится соизмеримой со скоростью V - V-обмена. Быстрый переход в поступательные и вращательные степени свободы возможен вследствие все более уменьшающегося расстояния между высоколежащими колебательными уровнями. Для этих высоколежащих состояний выражение (18) неприменимо, и, что более важно, утверждение о возникновении на них очень большой инверсии населенностей неверно. Действительно, для очень высоких квантовых состояний, для которых скорости V — Т-процессов велики и полностью определяют процесс релаксации, функция распределения, как следовало бы ожидать, будет иметь больцмановский вид с поступательной температурой Т. В соответствии с этим полное решение кинетического уравнения (4), учитывающего как V - Т-, так и V - V-процессы, для нижних состояний будет иметь вид, аналогичный выражению (18), а для очень высоких состояний будет аналогично распределению Больцмана с поступательной температурой.
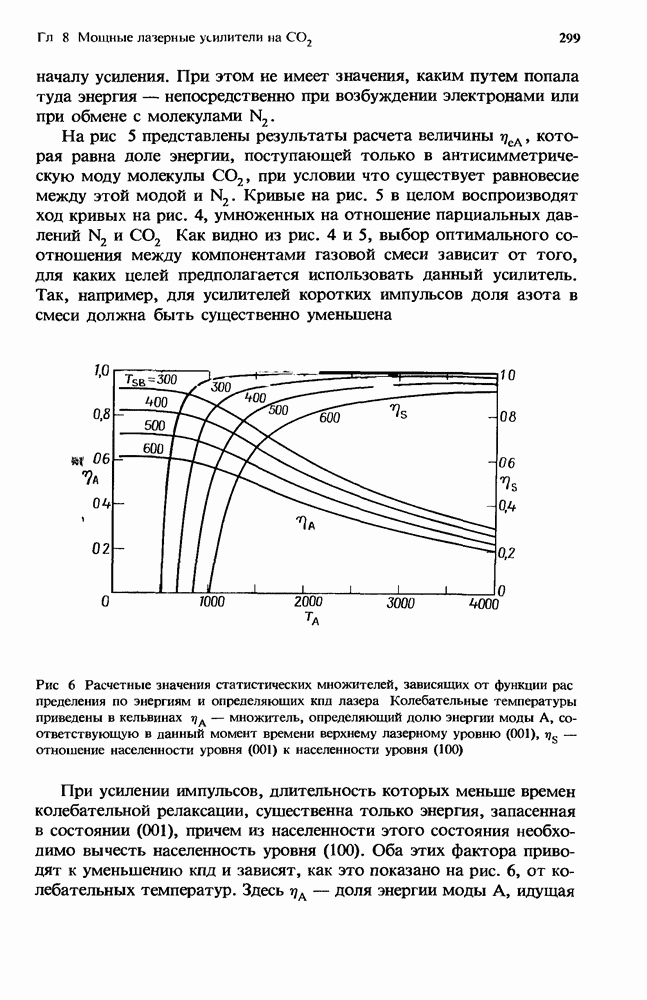
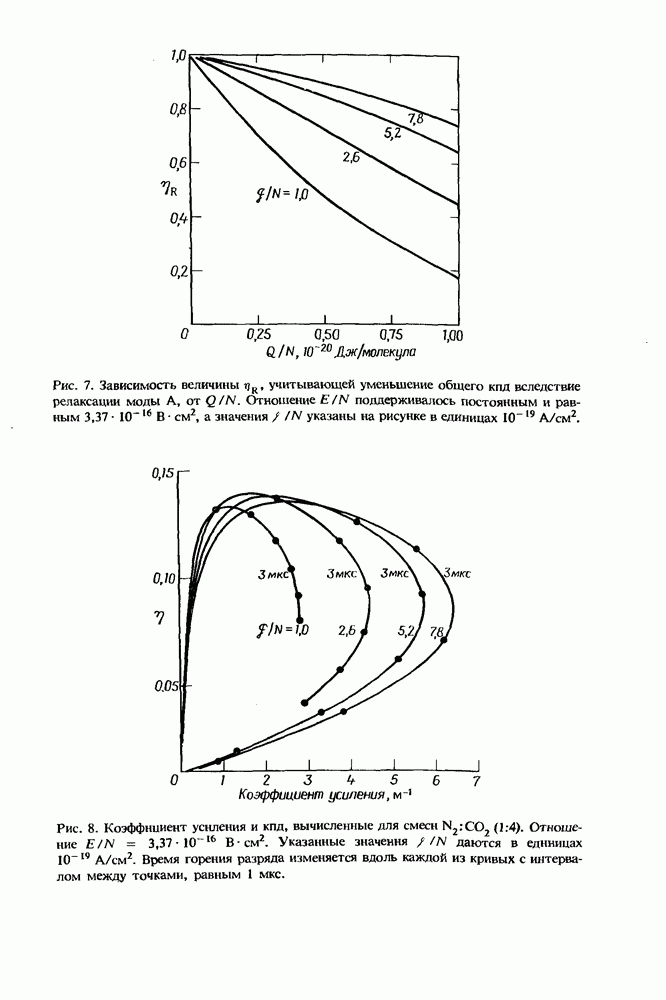
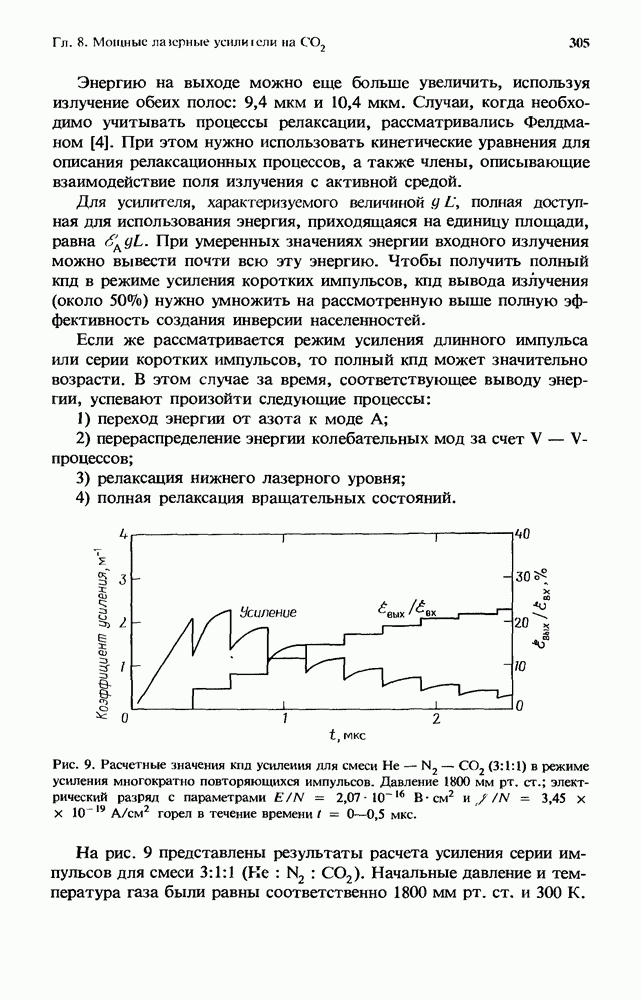
Проведенное рассмотрение релаксации ангармонического осциллятора показывает, что при некоторых условиях населенности колебательных уровней могут значительно отклониться от больцмановского распределения. Точнее говоря, высокие колебательные квантовые состояния могут достичь существенного перезаселения по сравнению с распределением Больцмана, если имеют место следующие условия:
1. Поступательная температура должна быть меньше, чем характеристическая колебательная температура газа, что обеспечивает преобладание механизма колебательного обмена:  где
где 
2. Параметр в, соответствующий колебательной температуре, должен по крайней мере составлять значительную часть характеристической колебательной температуры, чтобы оказывать какое-либо значительное влияние на возбужденные колебательные состояния:

3. Отношение параметра в к поступательной температуре должно значительно превосходить единицу: 
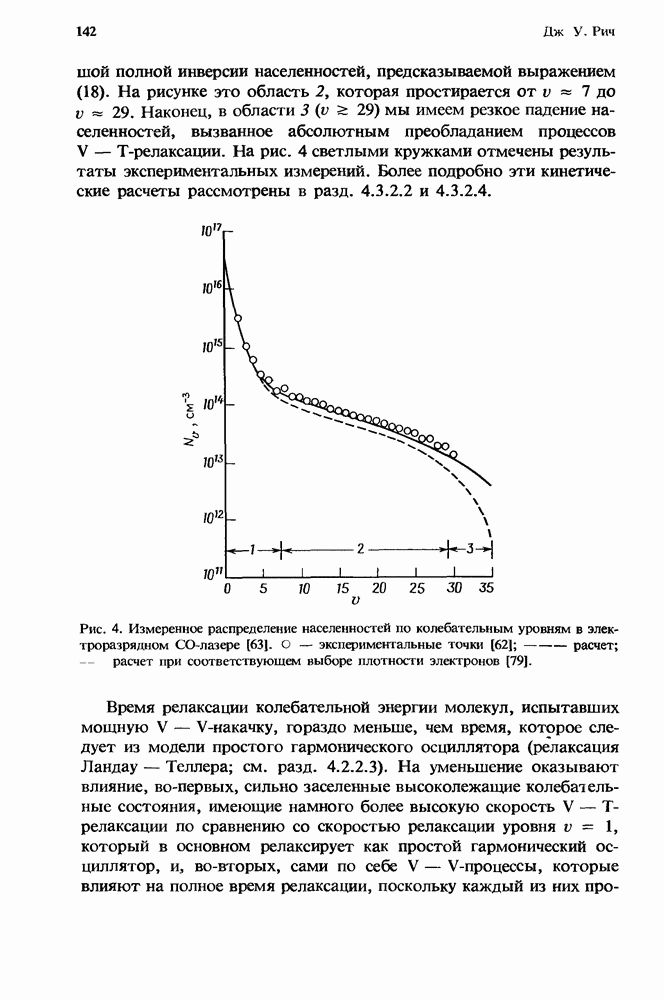
Такие условия, приводящие к существенному заселению высоко-лежащих колебательных квантовых состояний при низкой поступательной температуре, называют колебательно-колебательной (V — V) накачкой [127]. Дальнейший анализ населенностей колебательных состояний в газе ангармонических молекул требует полного решения кинетических уравнений [уравнение (4)] с учетом как V - V-, так и V — Т-процессов. Вообще говоря, такое решение нельзя получить аналитически для произвольной зависимости скорости релаксации от квантового числа. Первые решения были найдены численными методами в работах [18, 23, 72]. В последнее время было также проведено множество расчетов; некоторые из них мы рассмотрим в разд. 4.3.2.4. На рис. 4 приведен один из примеров функции распределения для окиси углерода, рассчитанной в условиях V — V-накачки (это распределение показано в виде штриховой кривой) [79]. На рисунке населенности колебательных состояний  представлены в зависимости от квантового чила
представлены в зависимости от квантового чила  Выло найдено, что функция распределения, полученная с учетом только
Выло найдено, что функция распределения, полученная с учетом только
V — V-накачки, является прекрасным приближением для реальной функции распределения вплоть до значений  соответствующих минимуму выражения (18). В конкретном случае, представленном на рис. 4, это соответствует указанной на рисунке области 1, которая простирается от
соответствующих минимуму выражения (18). В конкретном случае, представленном на рис. 4, это соответствует указанной на рисунке области 1, которая простирается от  до
до  Вне этой области реальная функция распределения обычно имеет вид сильно неравновесного «плато», где населенности слабо уменьшаются с ростом квантового числа, что приблизительно можно описать выражением
Вне этой области реальная функция распределения обычно имеет вид сильно неравновесного «плато», где населенности слабо уменьшаются с ростом квантового числа, что приблизительно можно описать выражением  . В области плато мощная V — V-накачка компенсируется V — Т-процессами, что предотвращает образование
. В области плато мощная V — V-накачка компенсируется V — Т-процессами, что предотвращает образование
большой полной инверсии населенностей, предсказываемой выражением (18). На рисунке это область 2, которая простирается от  до
до  Наконец, в области
Наконец, в области  мы имеем резкое падение населенностей, вызванное абсолютным преобладанием процессов V — Т-релаксации. На рис. 4 светлыми кружками отмечены результаты экспериментальных измерений. Более подробно эти кинетические расчеты рассмотрены в разд. 4.3.2.2 и 4.3.2.4.
мы имеем резкое падение населенностей, вызванное абсолютным преобладанием процессов V — Т-релаксации. На рис. 4 светлыми кружками отмечены результаты экспериментальных измерений. Более подробно эти кинетические расчеты рассмотрены в разд. 4.3.2.2 и 4.3.2.4.

Рис. 4. Измеренное распределение населенностей по колебательным уровням в электроразрядном СО-лазере [63]. О — экспериментальные точки [62];  - расчет;
- расчет;  расчет при соответствующем выборе плотности электронов [79].
расчет при соответствующем выборе плотности электронов [79].
Время релаксации колебательной энергии молекул, испытавших мощную V — V-накачку, гораздо меньше, чем время, которое следует из модели простого гармонического осциллятора (релаксация Ландау — Теллера; см. разд. 4.2.2.3). На уменьшение оказывают влияние, во-первых, сильно заселенные высоколежащие колебательные состояния, имеющие намного более высокую скорость V — Т-релаксации по сравнению со скоростью релаксации уровня  который в основном релаксирует как простой гармонический осциллятор, и, во-вторых, сами по себе V — V-процессы, которые влияют на полное время релаксации, поскольку каждый из них
который в основном релаксирует как простой гармонический осциллятор, и, во-вторых, сами по себе V — V-процессы, которые влияют на полное время релаксации, поскольку каждый из них
протекает с некоторым дефектом резонанса и, следовательно, должен приводить к обмену энергией с внешними поступательными и вращательными степенями свободы. Как мы видели, при высоких значениях колебательной энергии и при низкой поступательной энергии сталкивающихся частиц, что обусловливает мощную V — V-накачку, должны протекать главным образом V — V-процессы, соответствующие передаче энергии в поступательные степени свободы. Именно из-за существования этого дефекта резонанса процессы обмена колебательной энергией могут сами по себе иногда приводить к релаксации колебательной энергии системы. Такой механизм иногда называют  -релаксацией. Вновь отметим, что этот механизм совсем иной, чем механизм, вызывающий релаксацию нижнего колебательного состояния, описываемого уравнениями (9) и (11).
-релаксацией. Вновь отметим, что этот механизм совсем иной, чем механизм, вызывающий релаксацию нижнего колебательного состояния, описываемого уравнениями (9) и (11).
Для смеси двух или более двухатомных газов, соответствующих ангармоническим осцилляторам, можно также провести рассмотрение, аналогичное выполненному в разд. 4.2.2.4. Анализ кинетического уравнения (4) в случае бинарной смеси полностью совпадает с рассмотренным выше, и из него следует, что члены уравнения, отвечающие за обмен энергией, тождественно равны нулю, если распределения для населенностей каждого компонента газа записываются соответственно в виде

В этих выражениях в любой данный момент времени значение величины у является одним и тем же.
I Интересно отметить, что в упрощенном варианте, когда оба компонента газа рассматриваются как гармонические осцилляторы, каждый из них будет релаксирсвать, проходя последовательности больцмановских распределений с определенными колебательными температурами. Однако в любой данный момент времени эти колебательные температуры не равны друг другу. Таким образом, если первый газ представить в виде гармонического осциллятора с расстоянием между уровнями колебательной энергии, равным  (или с характеристической температурой
(или с характеристической температурой  то для него энергия
то для него энергия  колебательного уровня будет равна
колебательного уровня будет равна  а распределение (19) запишется в виде
а распределение (19) запишется в виде

где температура  связана с у соотношением
связана с у соотношением

Если второй газ можно представить также гармоническим осциллятором с характеристической температурой  то для него распределение (20) можно записать в виде
то для него распределение (20) можно записать в виде

где температура выражается через у следующим образом:

Поскольку величина у одинакова в уравнениях (22) и (24), колебательные температуры оказываются связанными соотношением

Рассмотрим, например, газ, состоящий из молекул N2 и СО, для которых соответственно имеем  Если теперь рассмотреть условия, соответствующие быстрому расширению, когда
Если теперь рассмотреть условия, соответствующие быстрому расширению, когда  а колебательная температура равна примерно 2000 К, то разность в колебательных температурах будет равна примерно 200 К, причем молекулы с ббльшим значением в будут иметь меньшие
а колебательная температура равна примерно 2000 К, то разность в колебательных температурах будет равна примерно 200 К, причем молекулы с ббльшим значением в будут иметь меньшие 
Соотношение (25) было выведено как частный случай более общего распределения для смеси двух газов, каждый из которых является ангармоническим осциллятором [127]; этот результат был получен одновременно и независимо в работе [125] и применен для описания релаксирующих смесей азота и окиси углерода.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
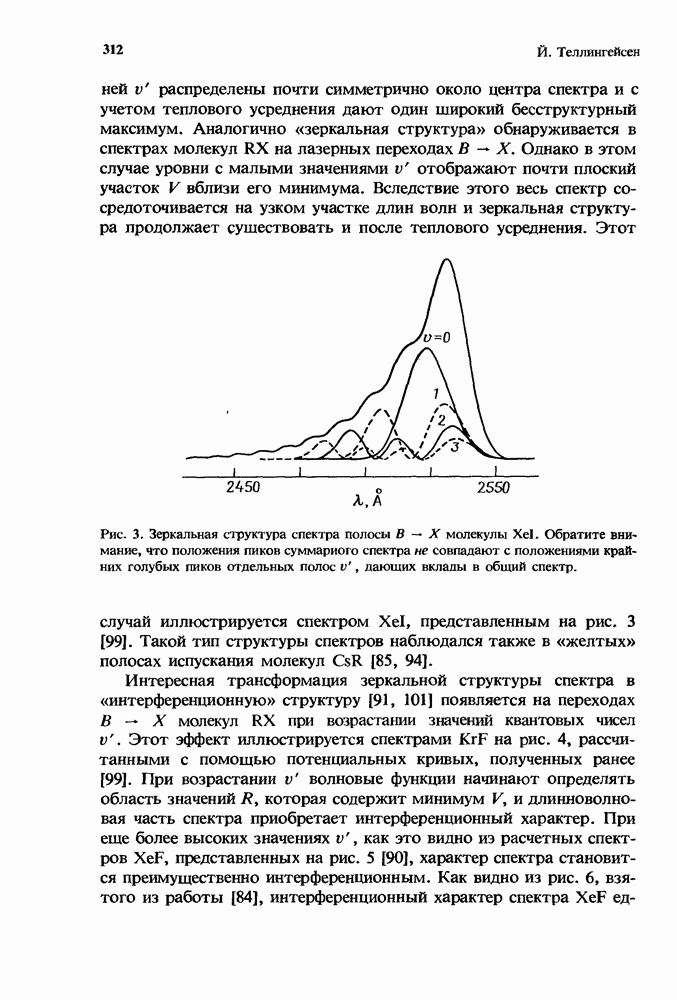
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
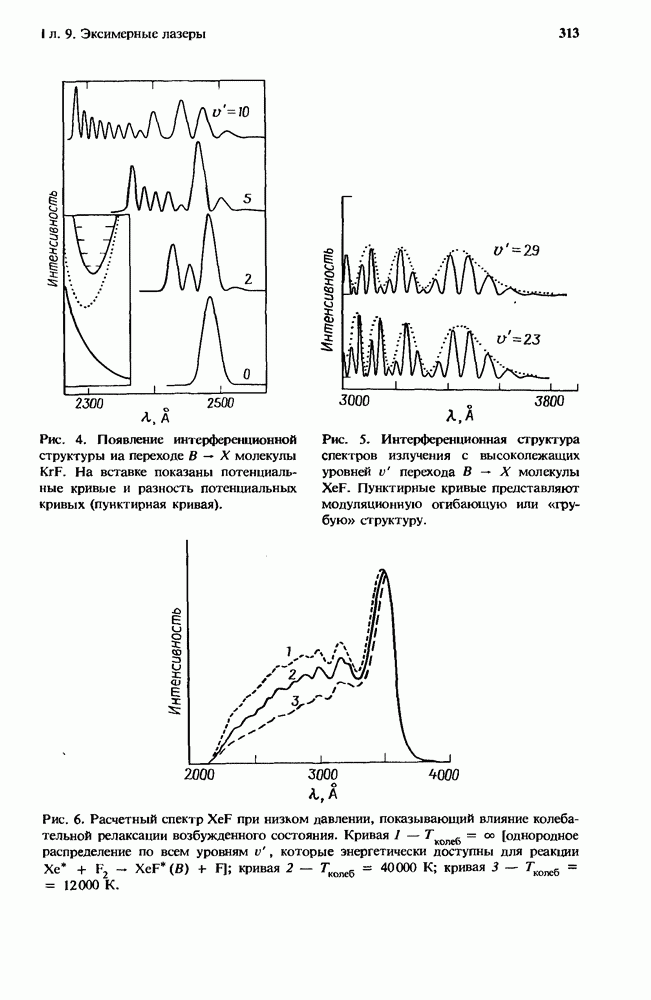
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
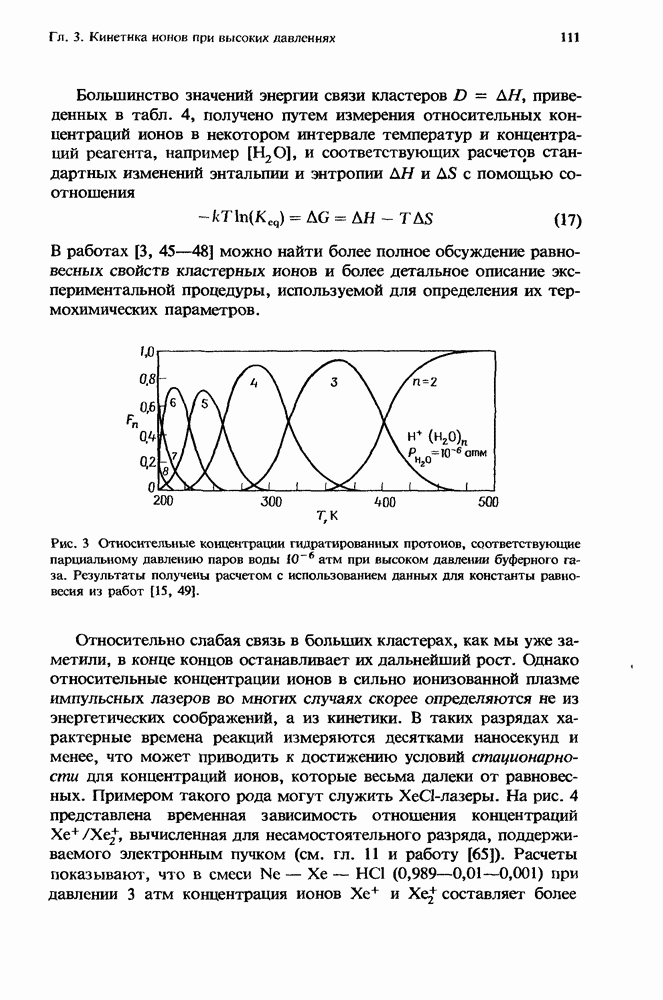
- 3. Кинетика ионов при высоких давлениях
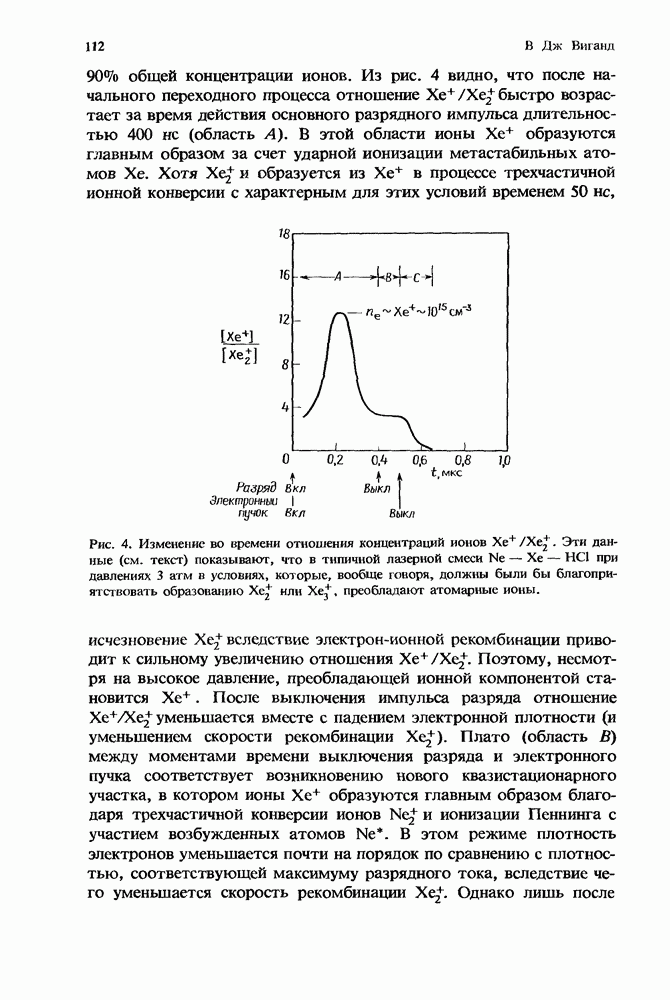
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
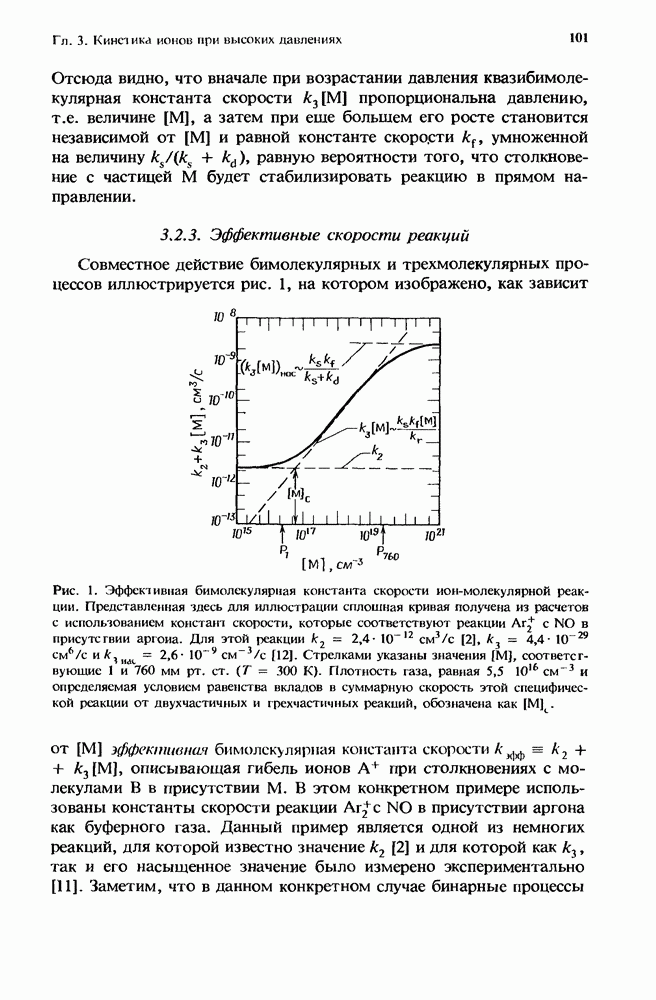
- 3.2.3. Эффективные скорости реакций
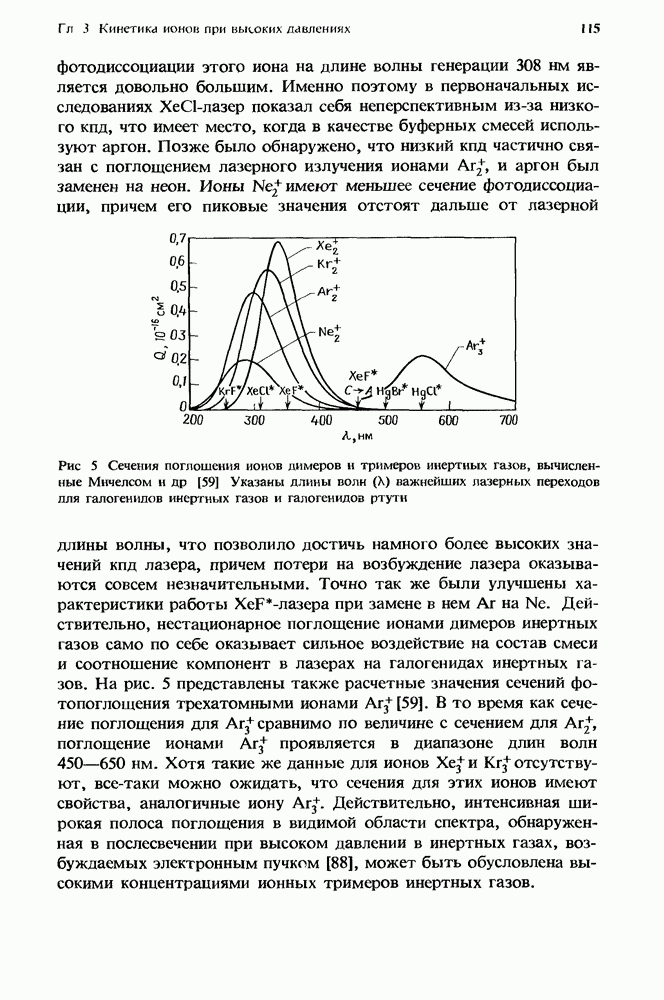
- 3.2.4. Зависимость от давления
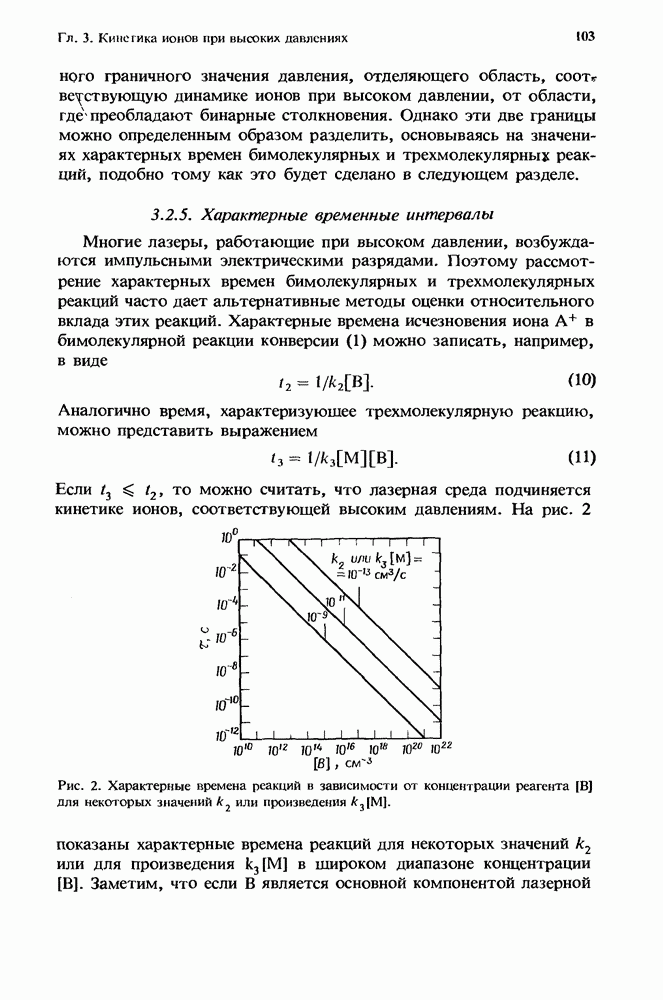
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
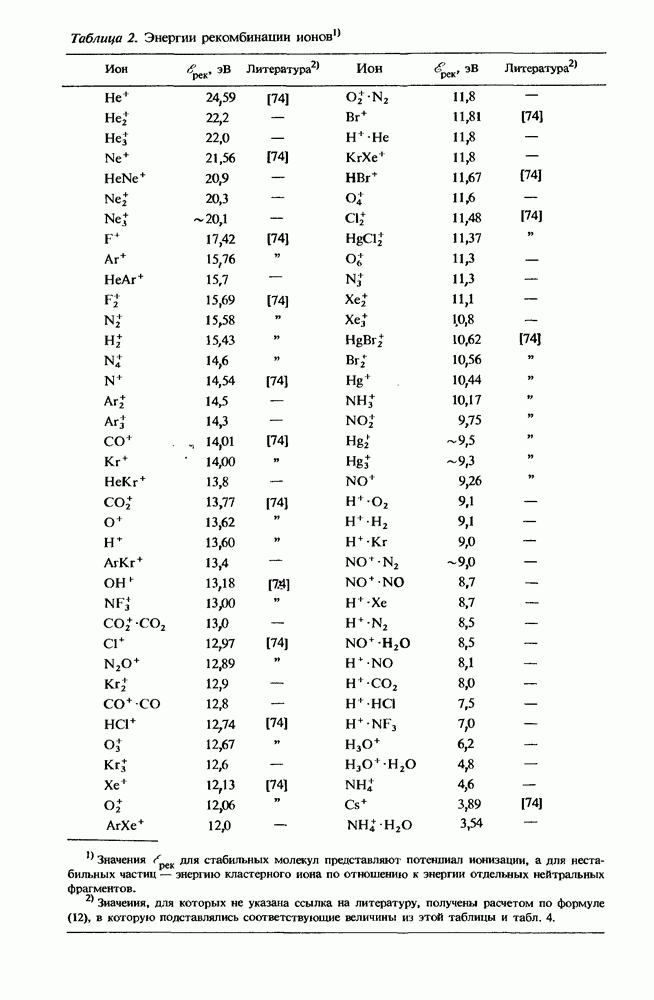
- 3.2.2. Энергетика отрицательных ионов
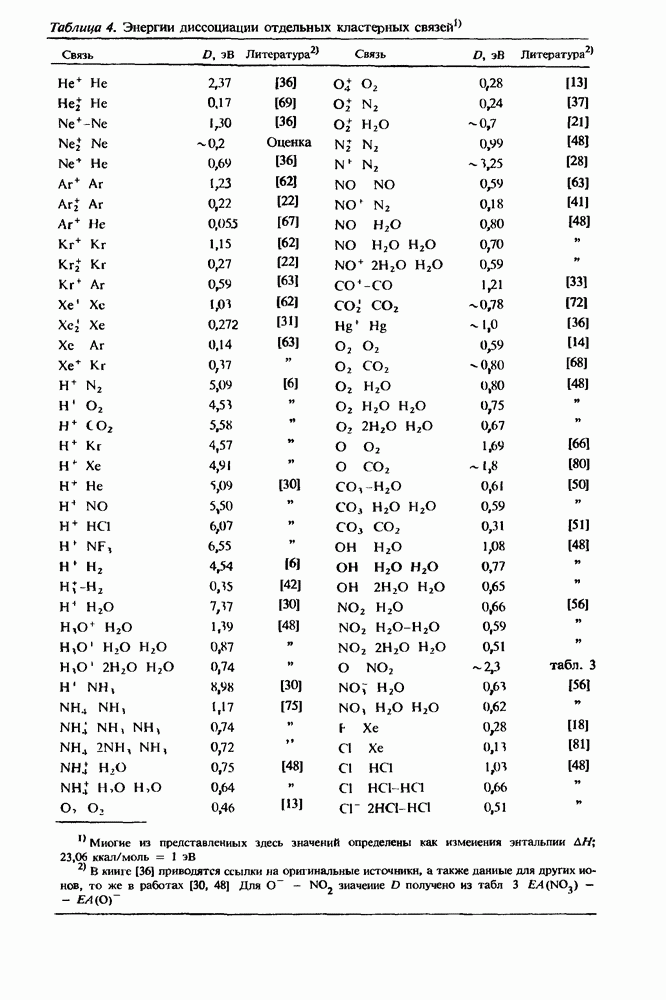
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
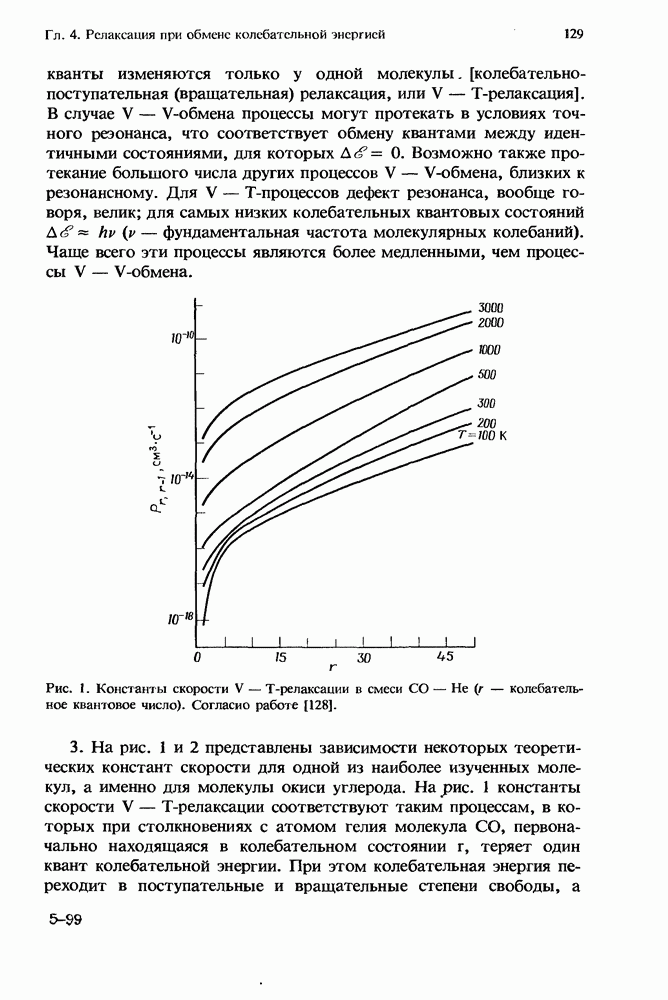
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
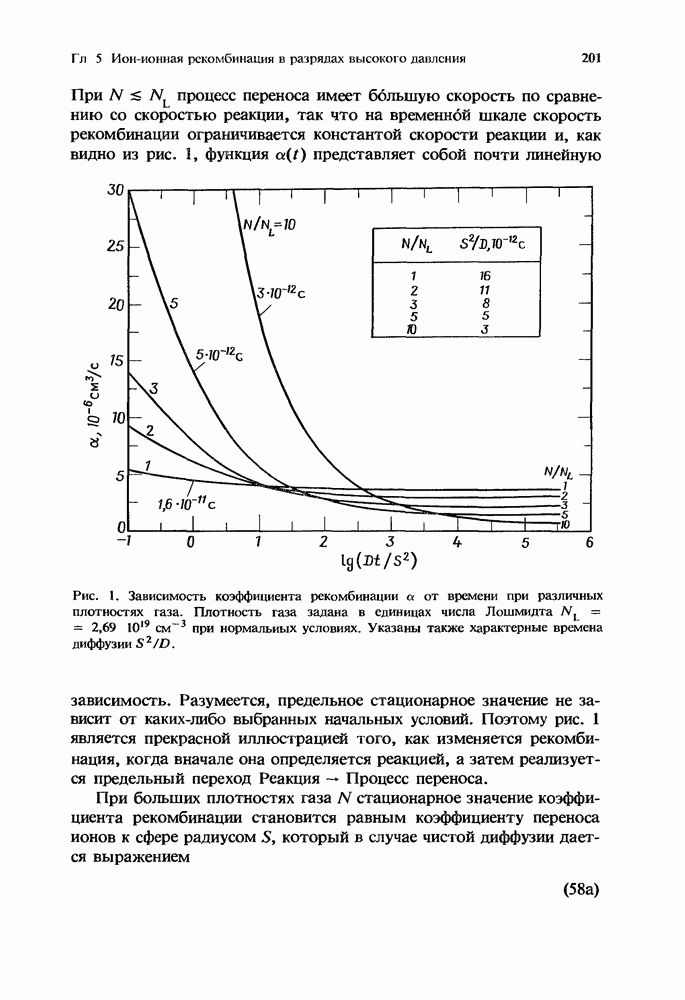
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
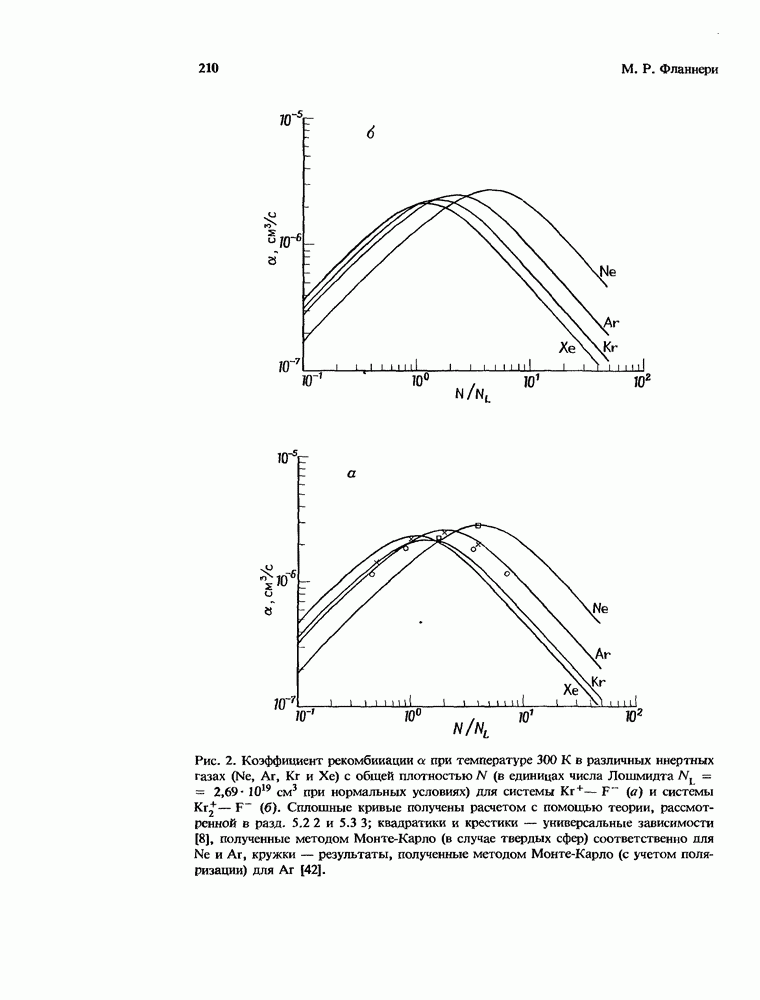
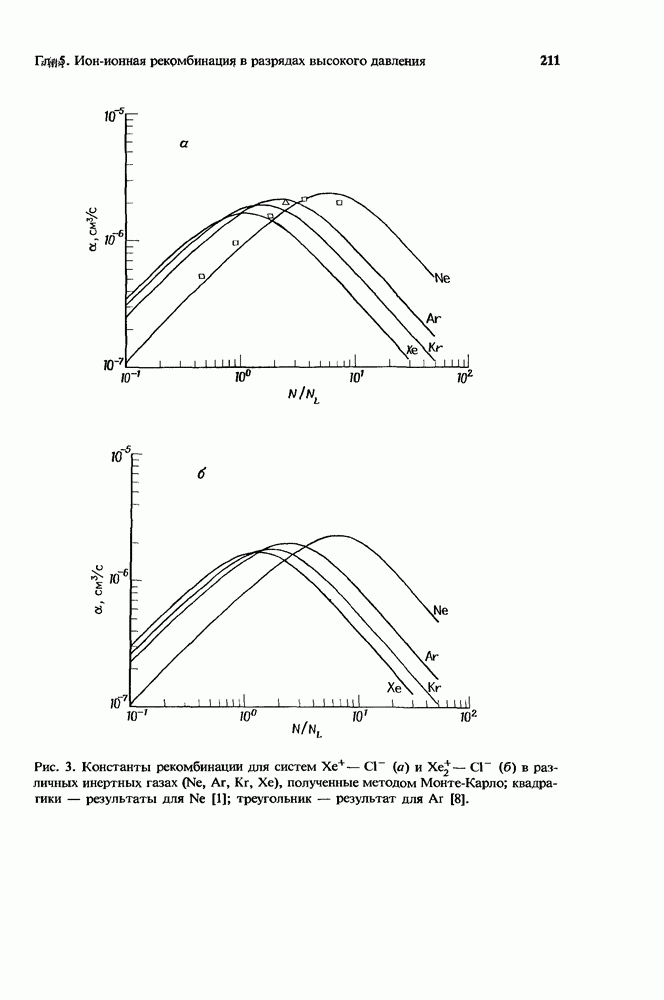
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
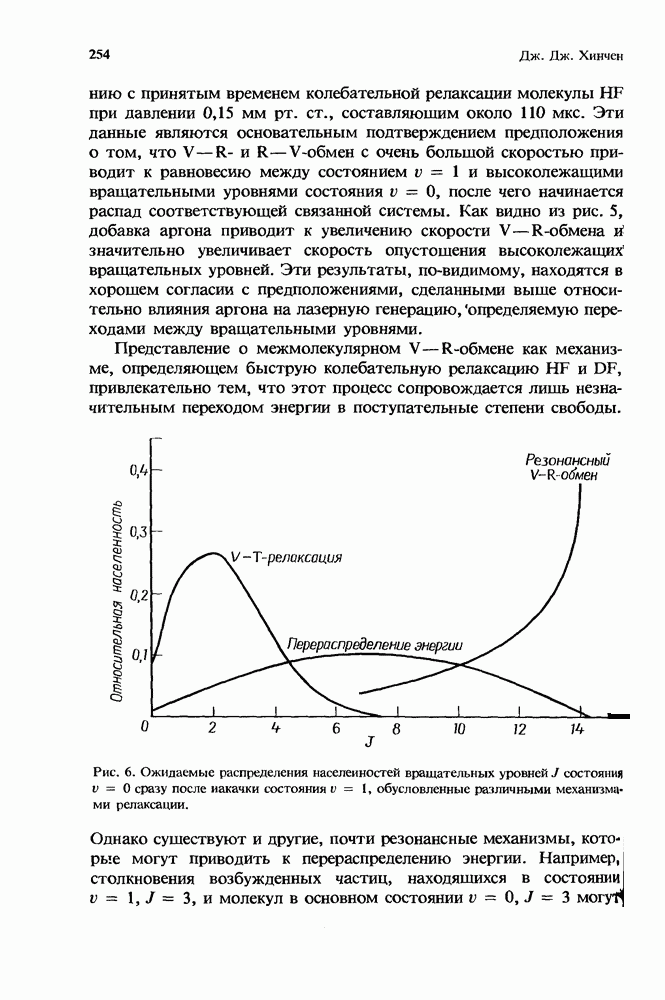
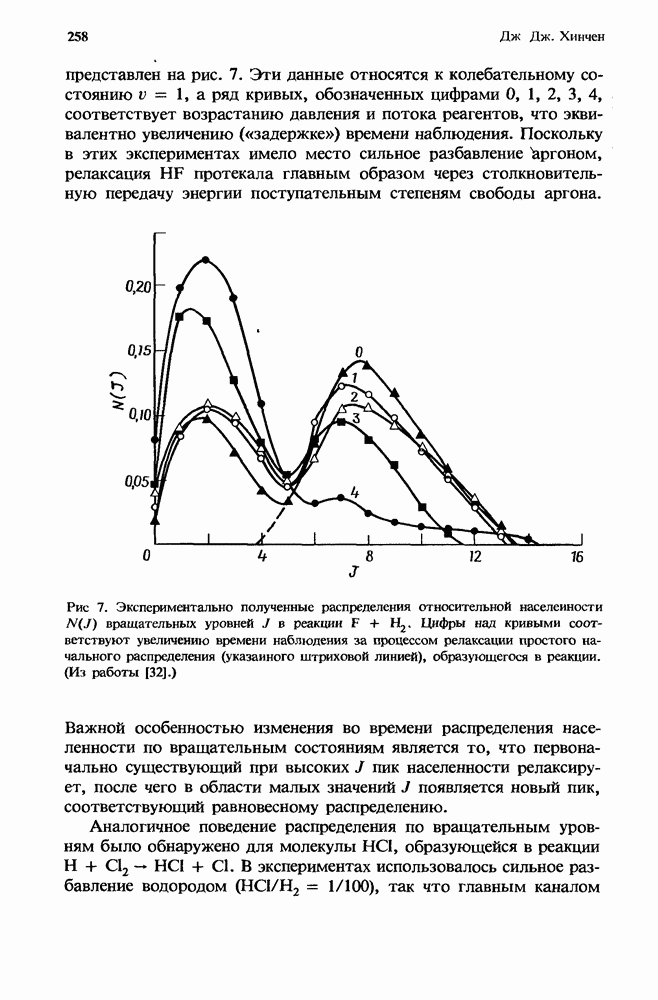
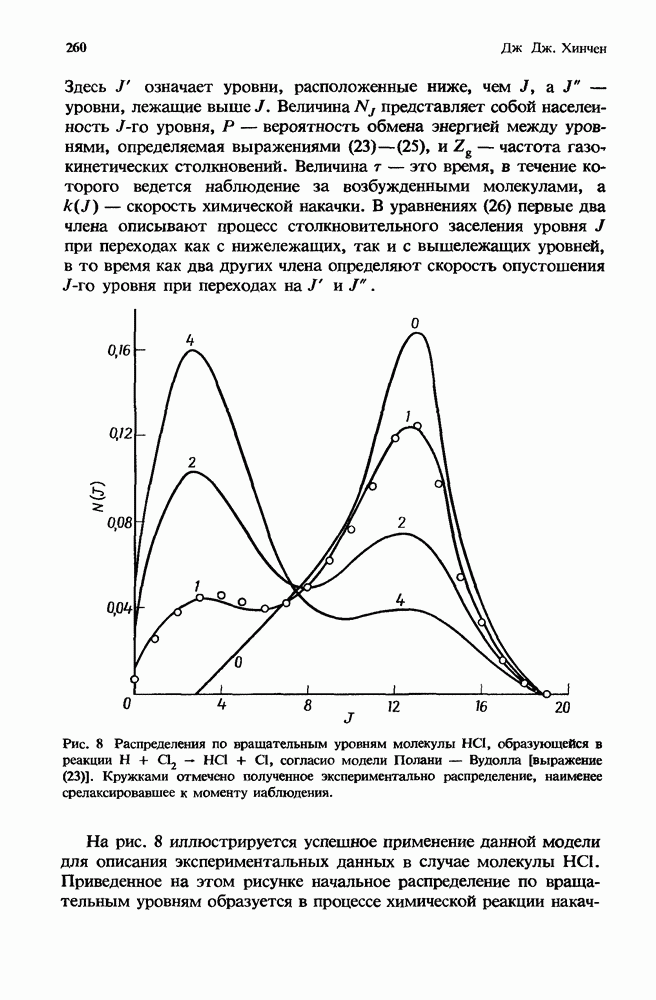
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
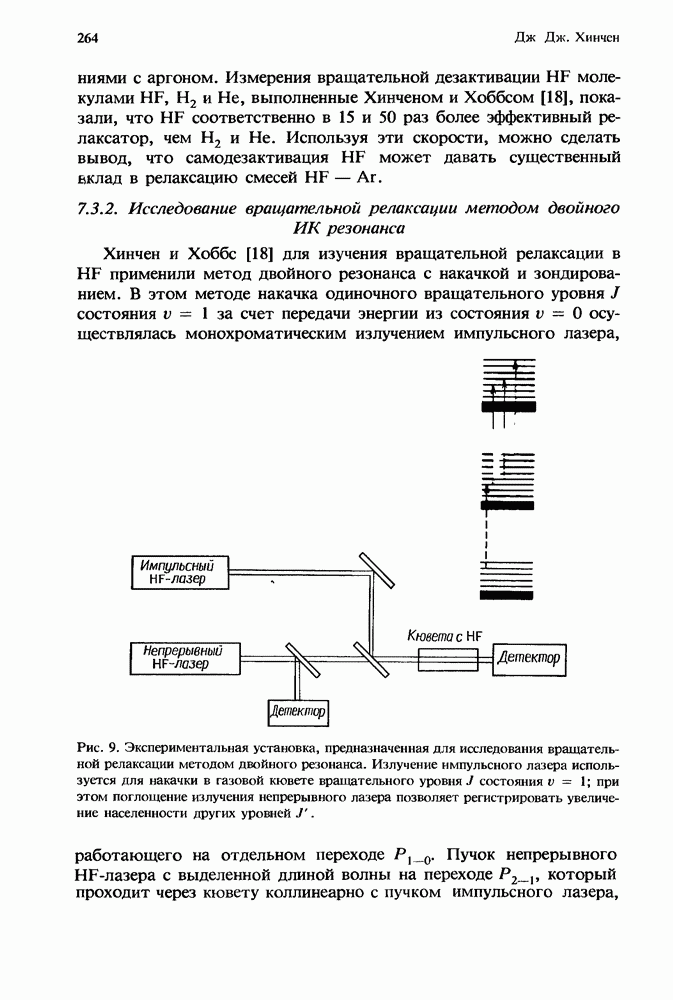
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
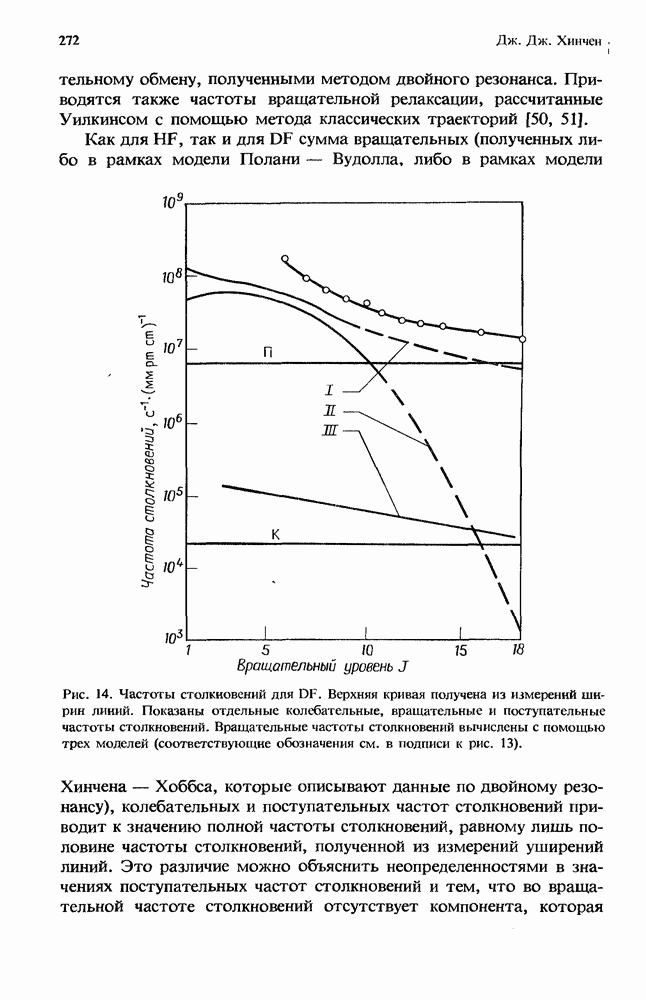
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
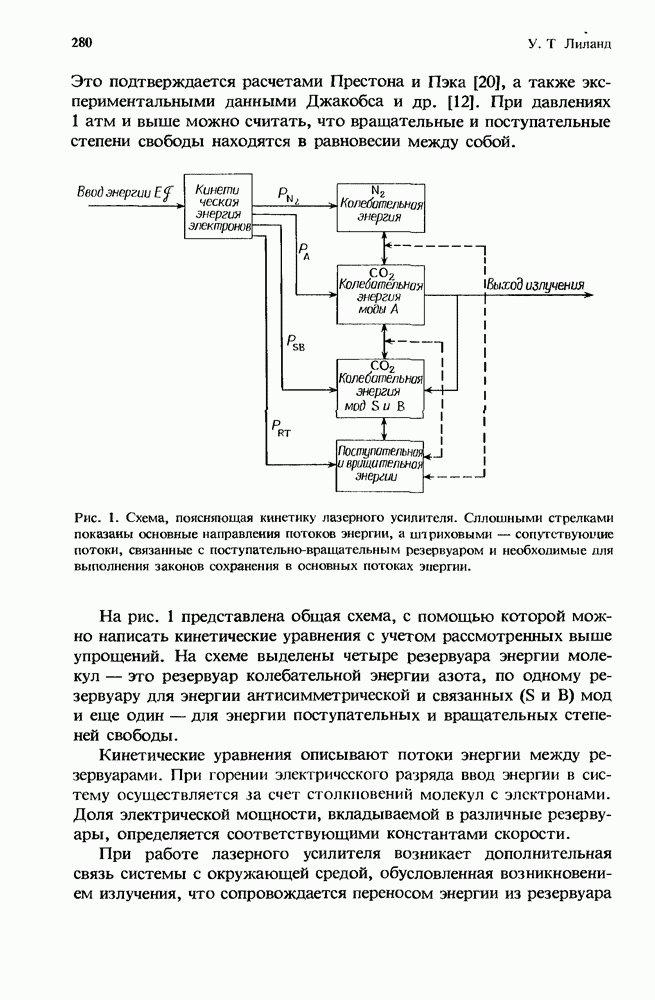
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
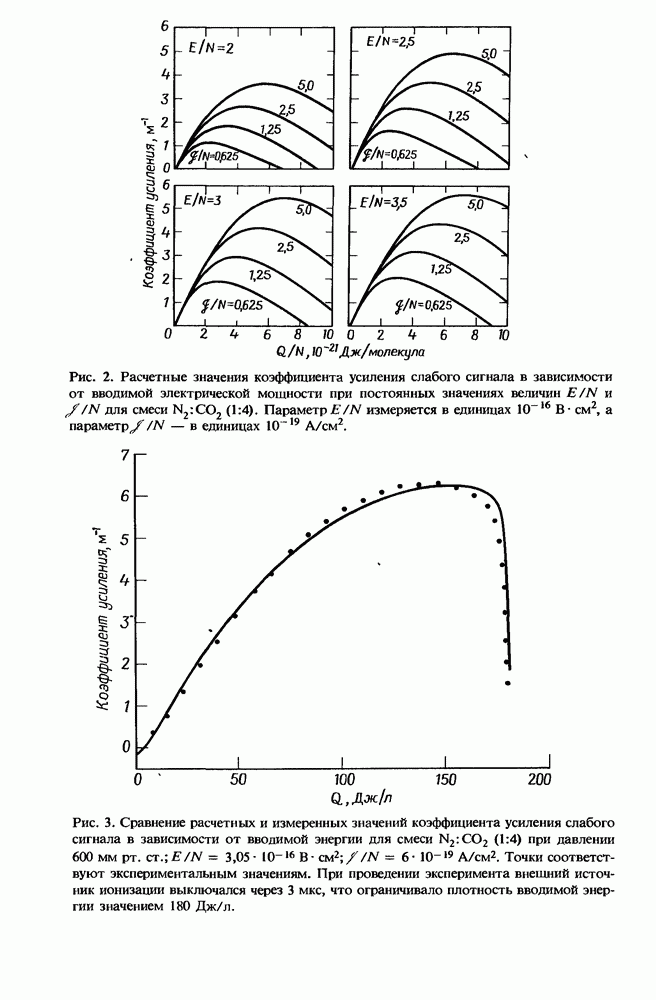
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
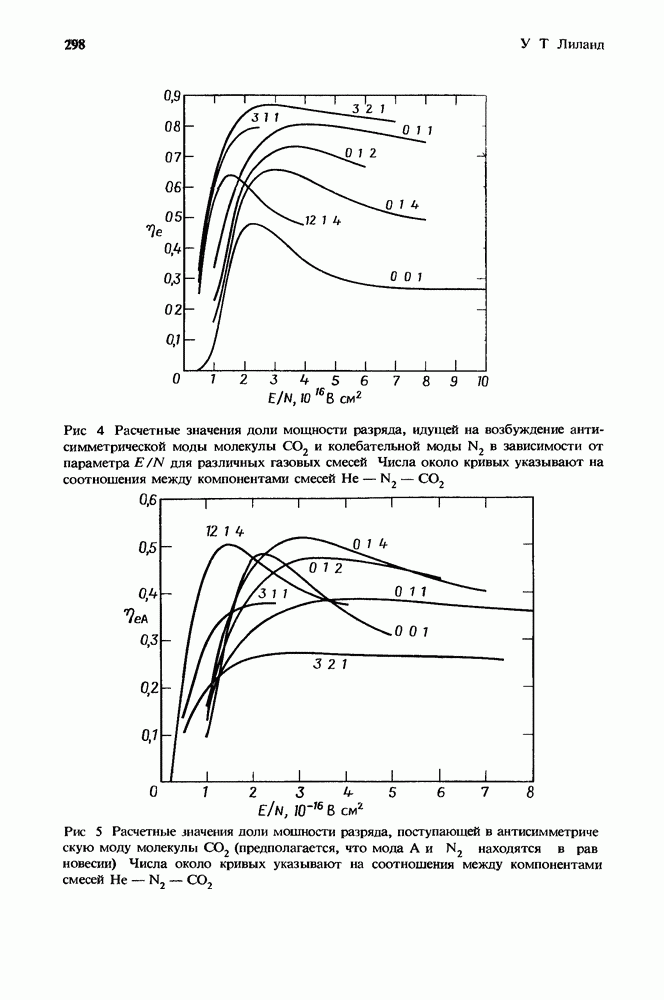
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
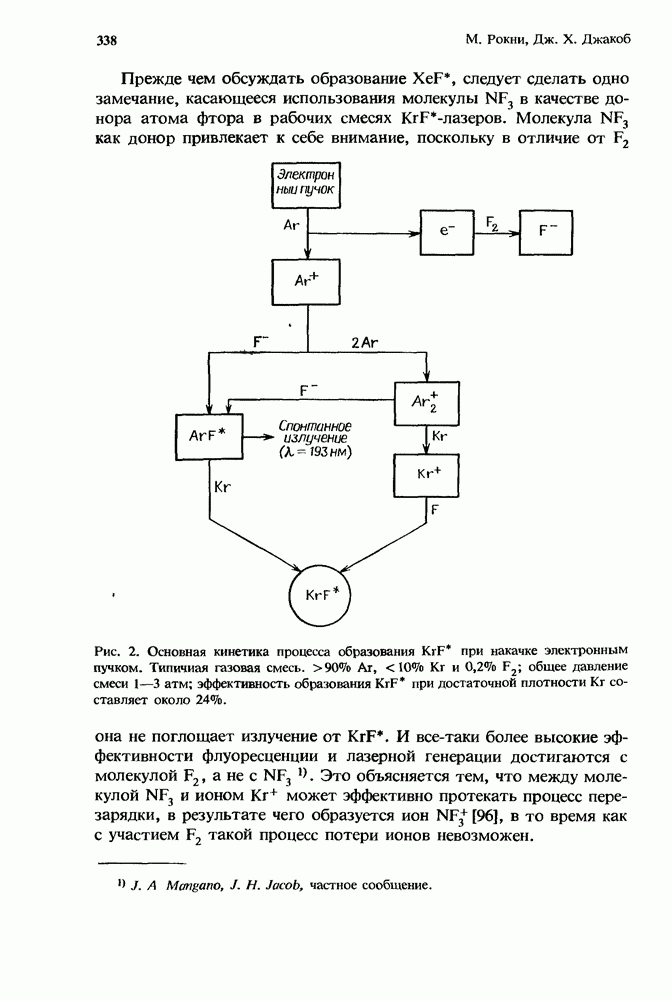
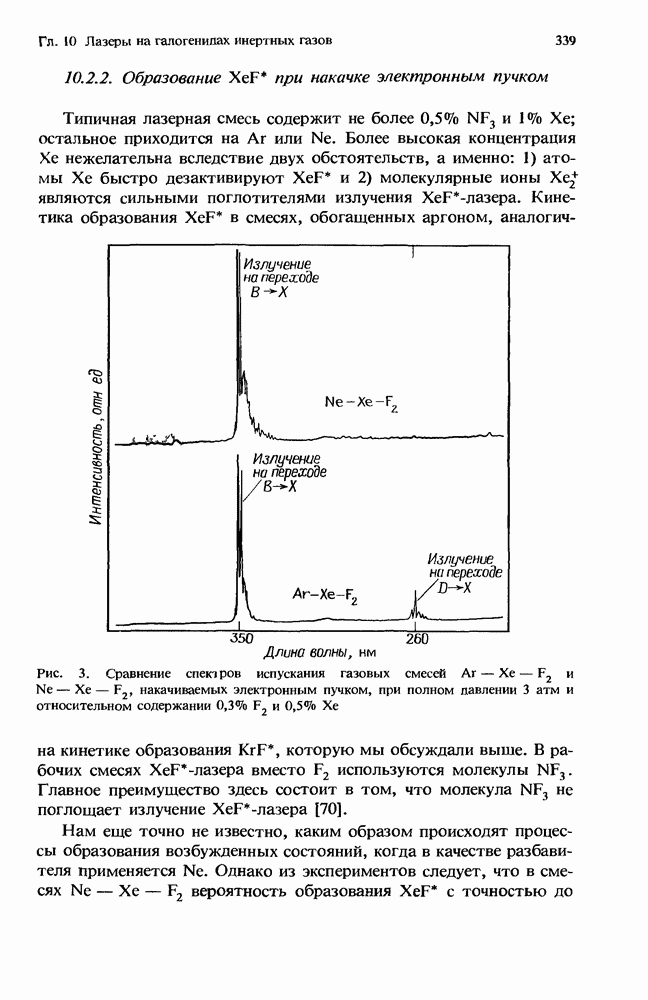
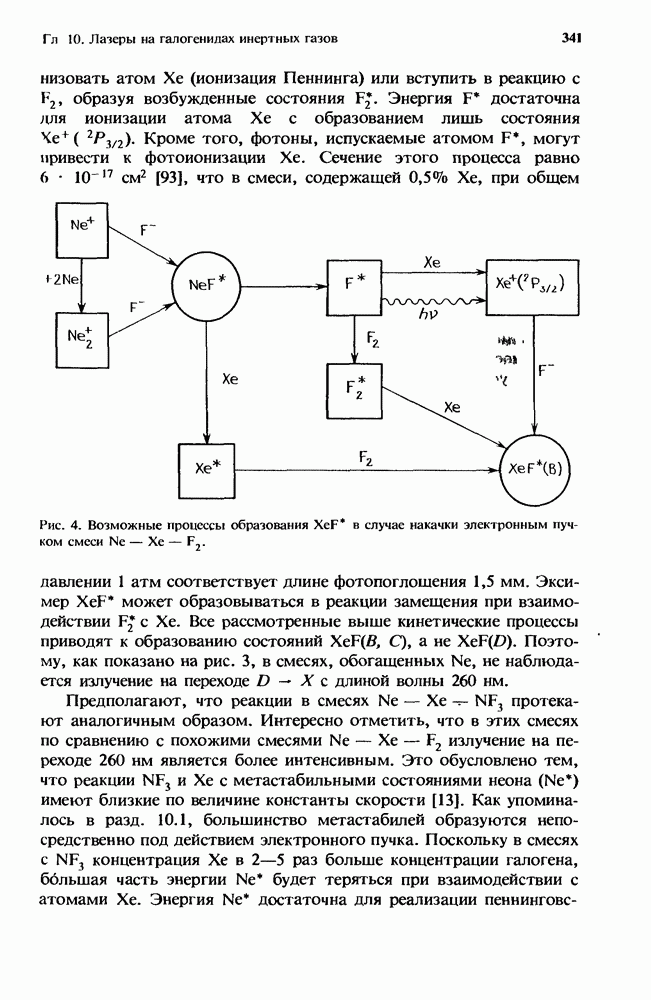
- 10.2. Кинетика образования верхнего лазерного уровня
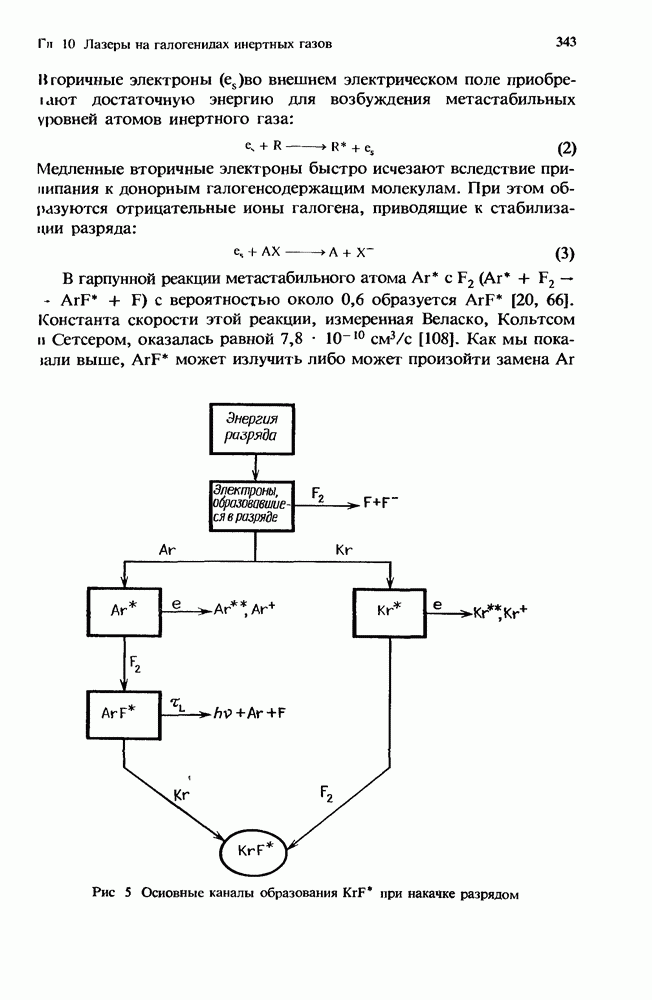
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
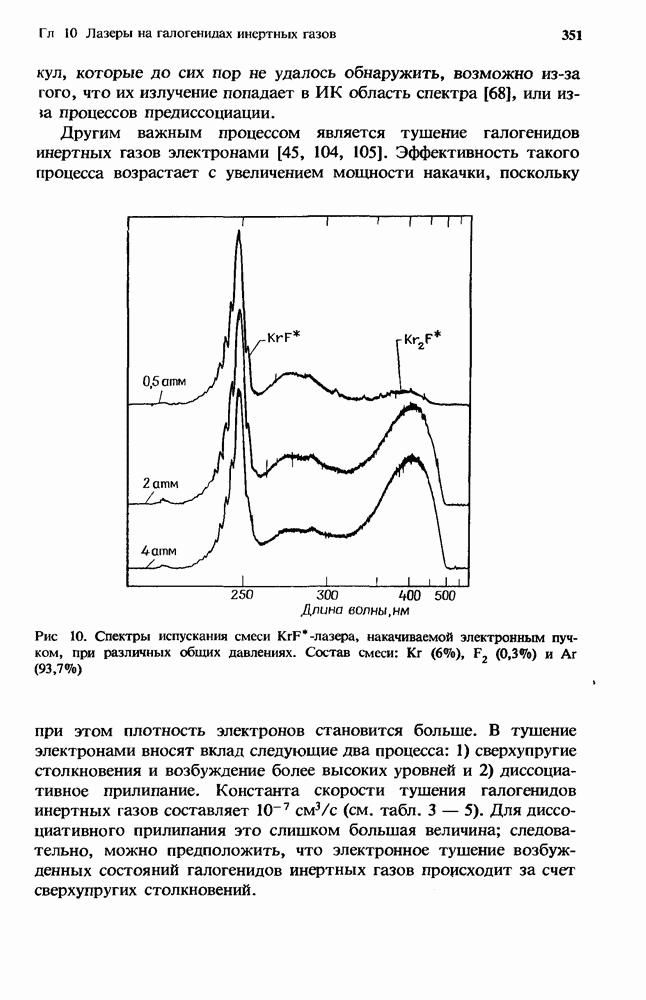
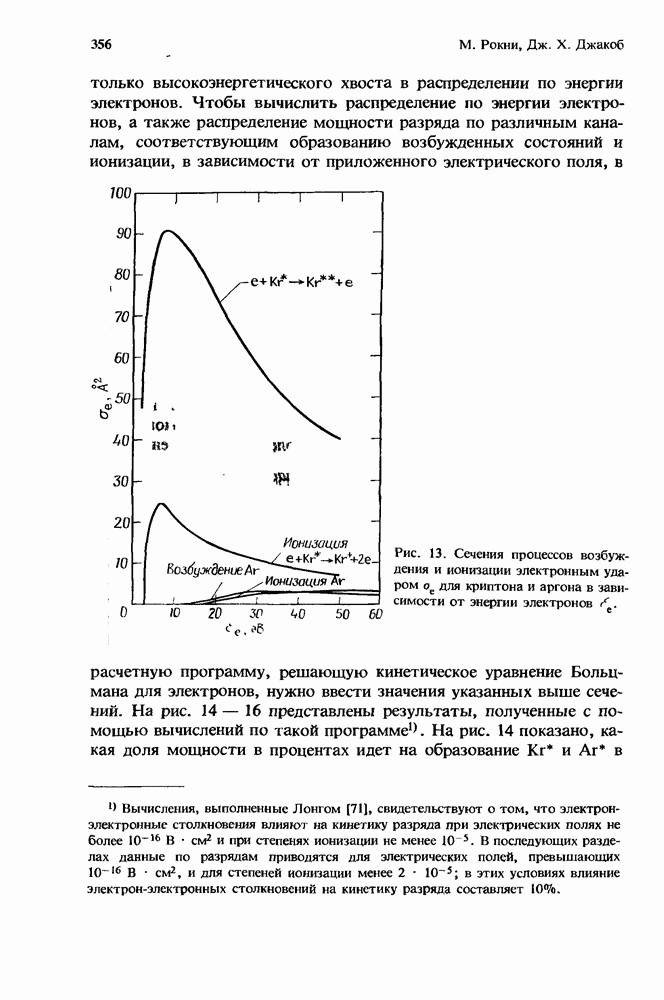
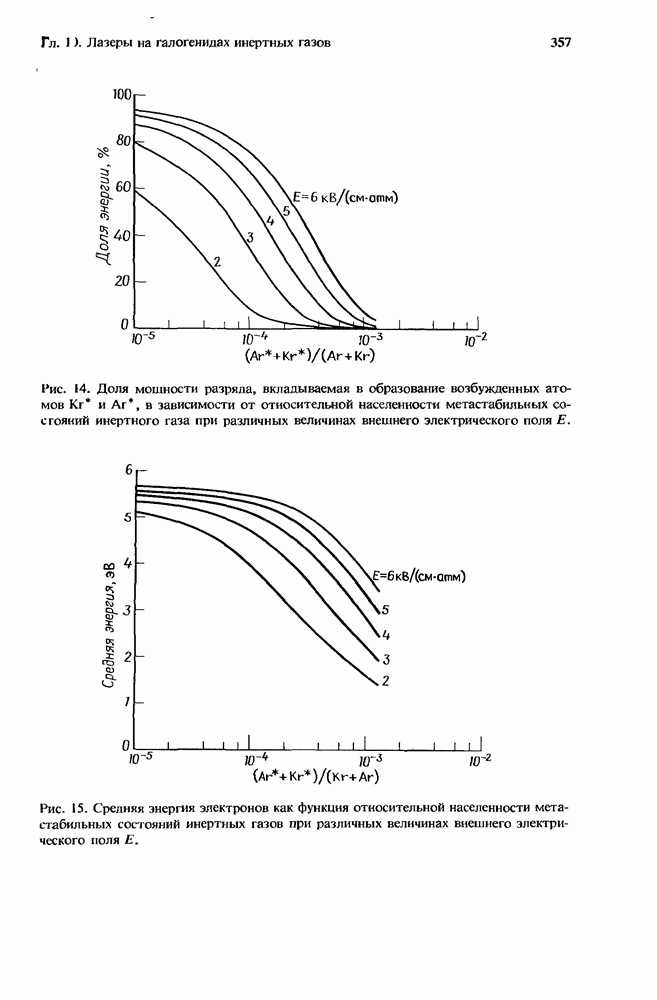
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
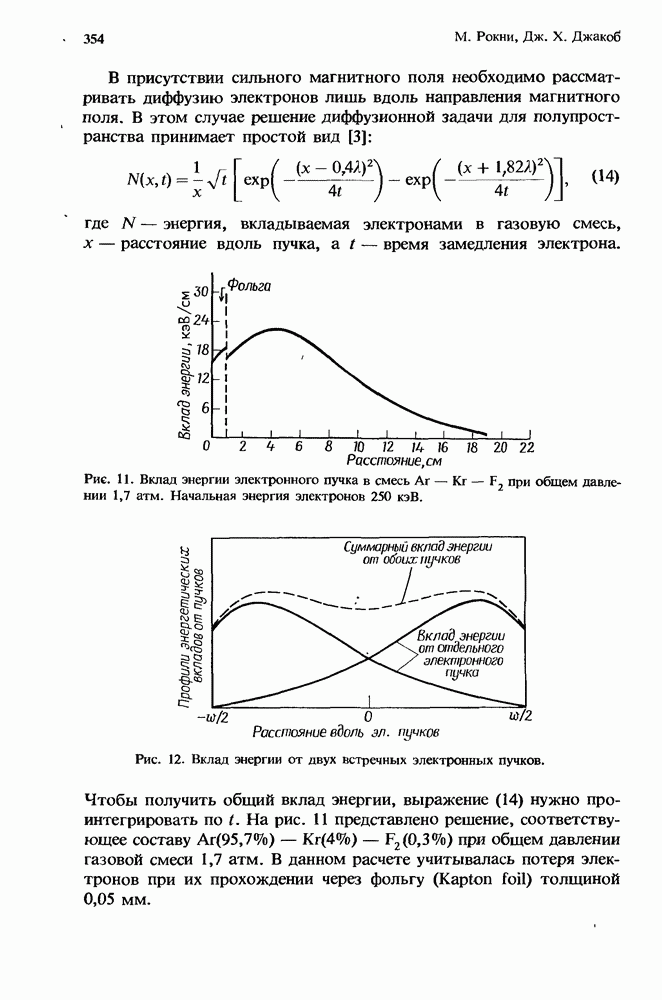
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
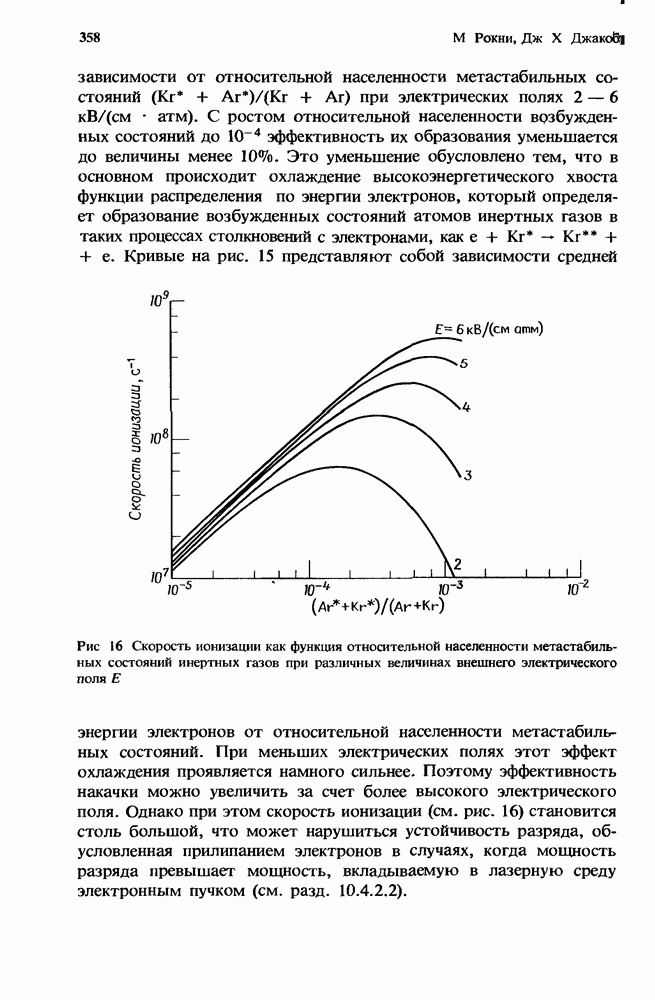
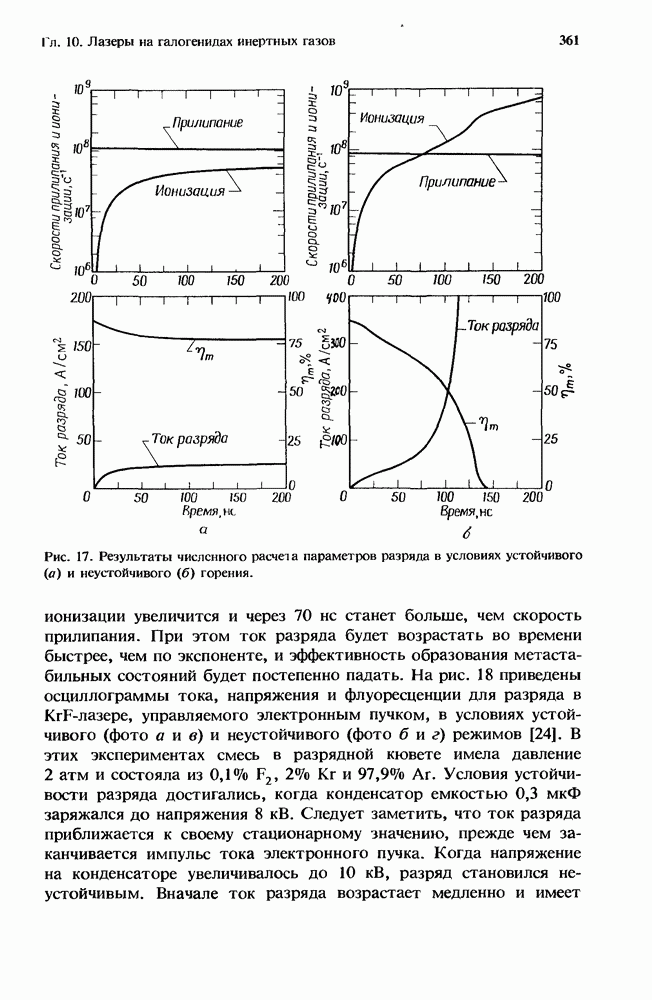
- 10.4.2.2. Устойчивость разряда
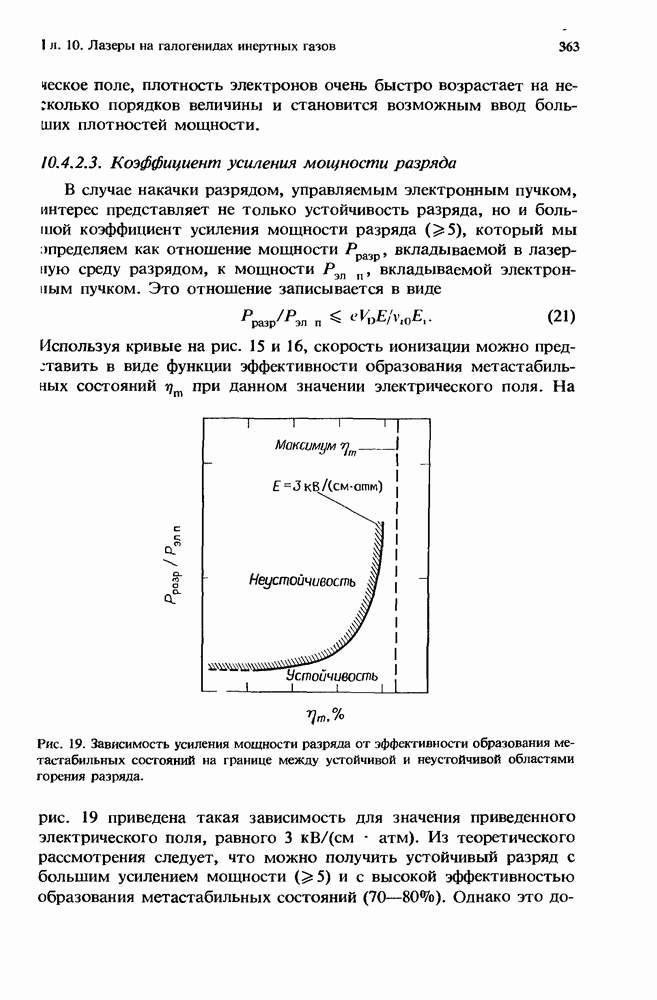
- 10.4.2.3. Коэффициент усиления мощности разряда
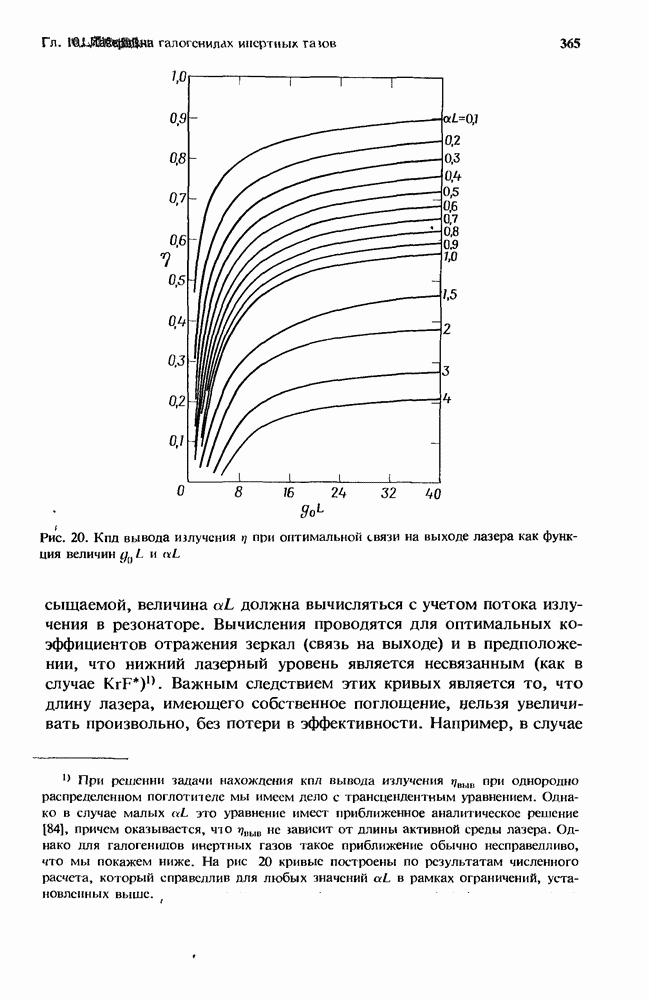
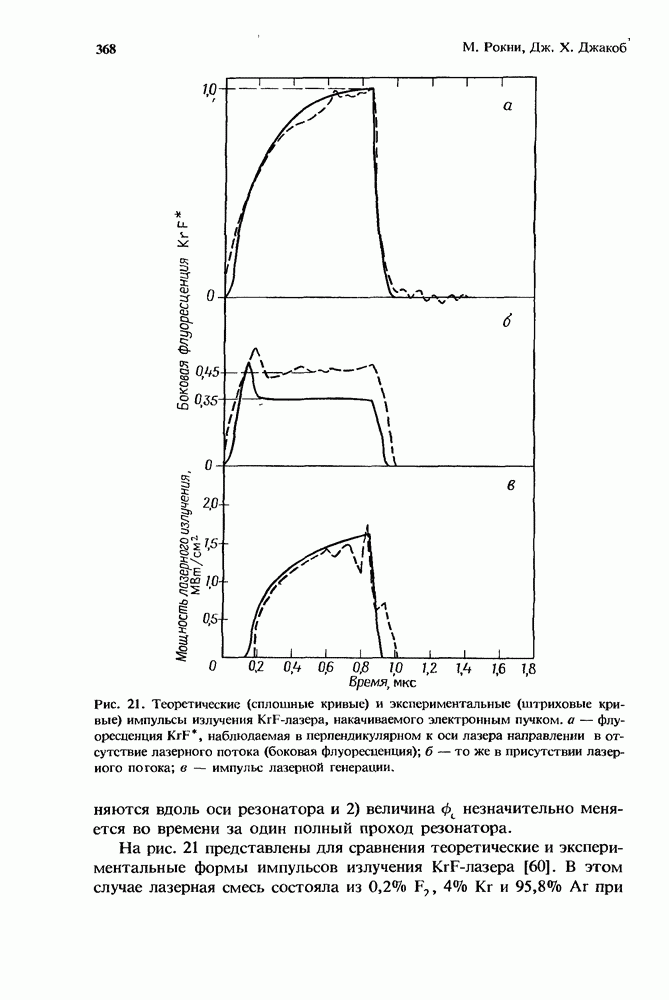
- 10. 5. Вывод мощности
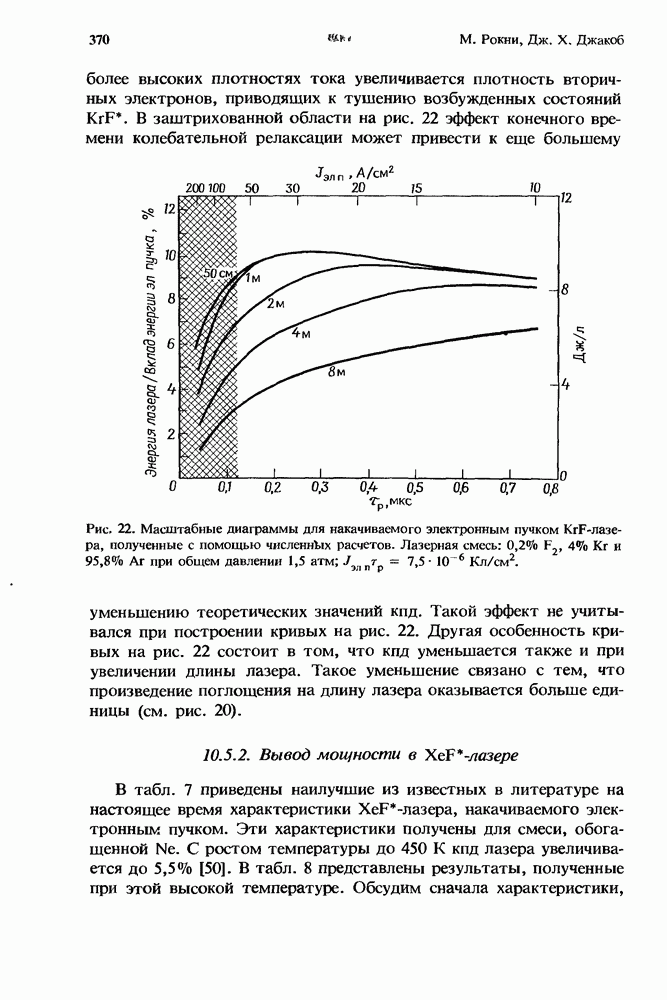
- 10.5.1. Вывод мощности в KrF*-лазере
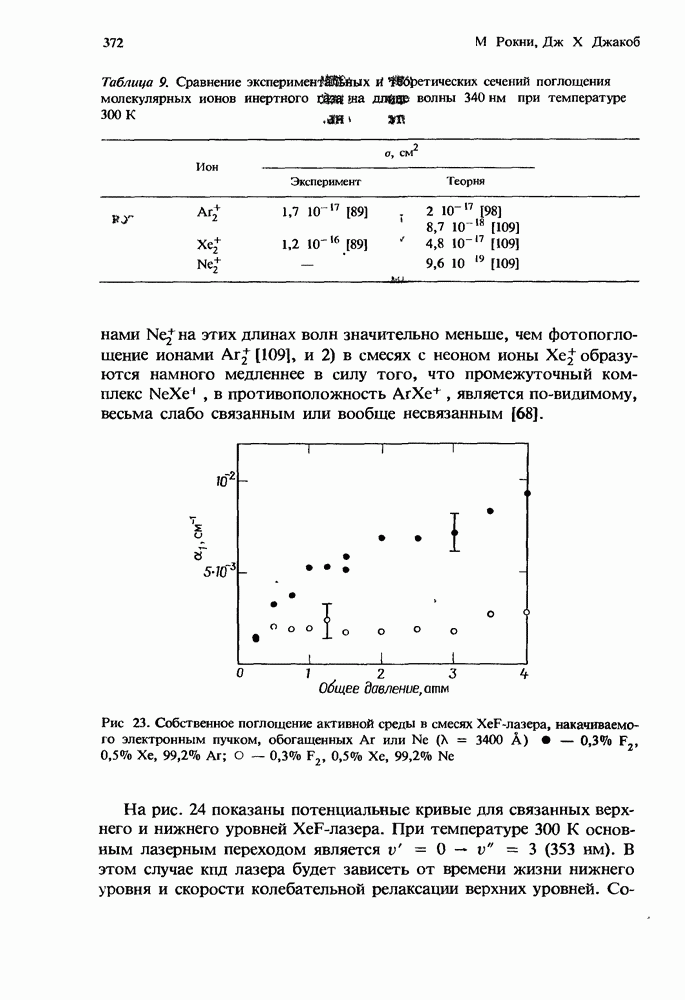
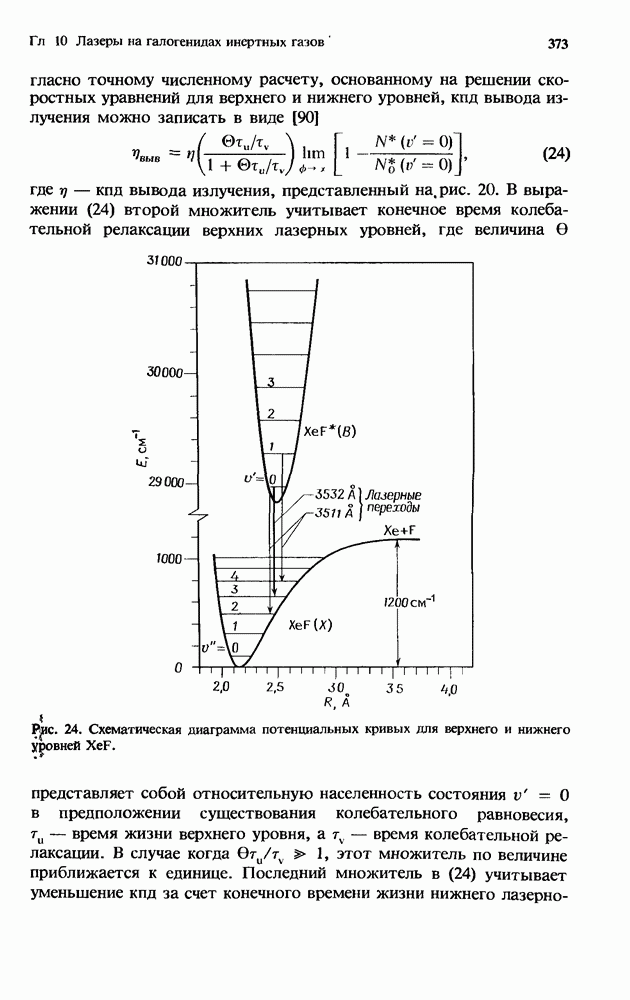
- 10.5.2. Вывод мощности в XcF*-лазере
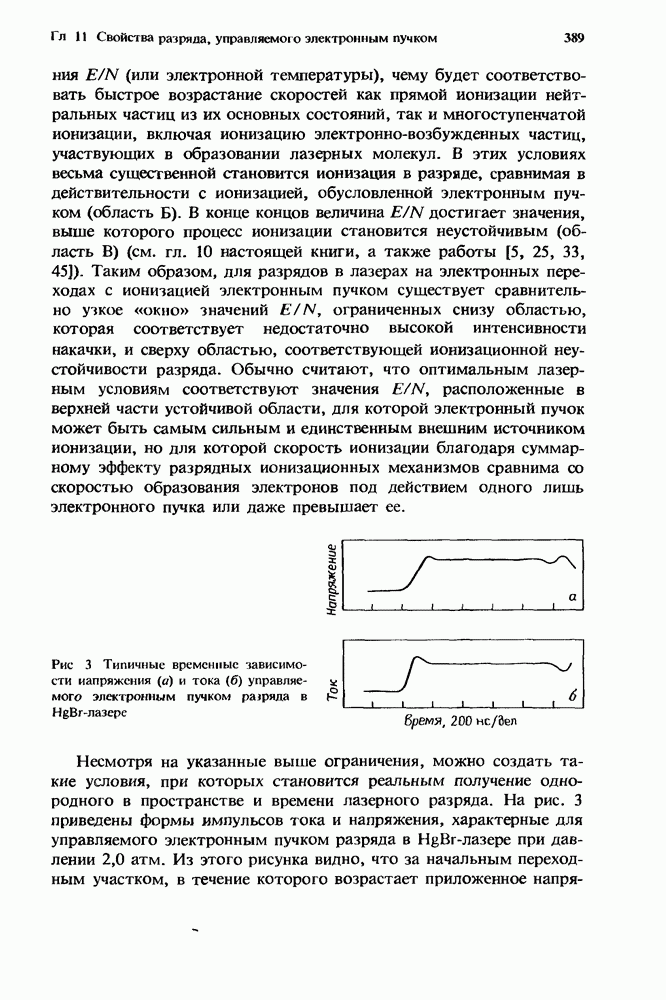
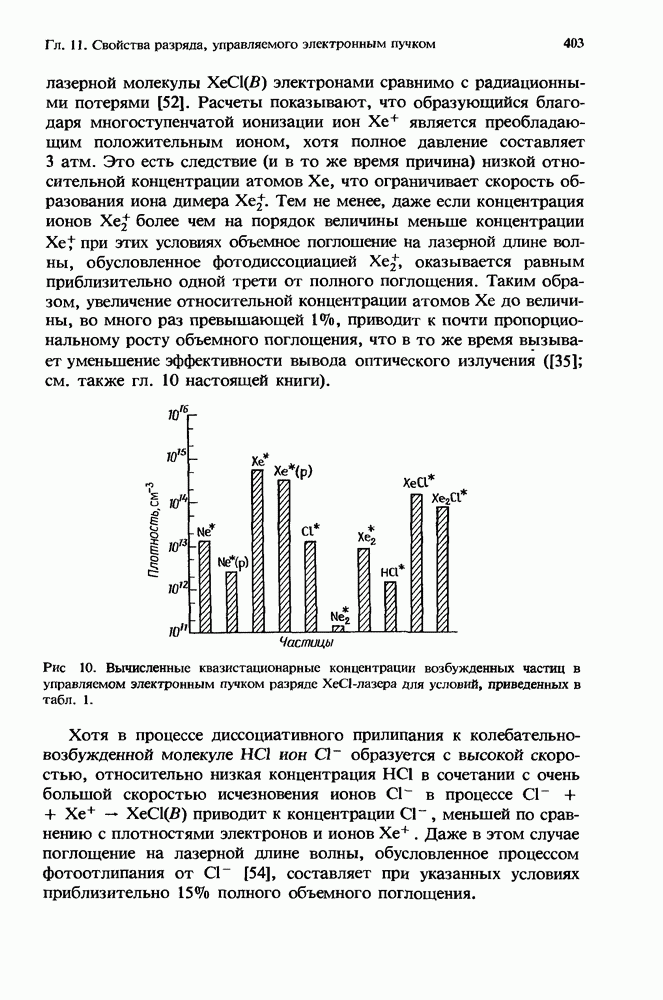
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
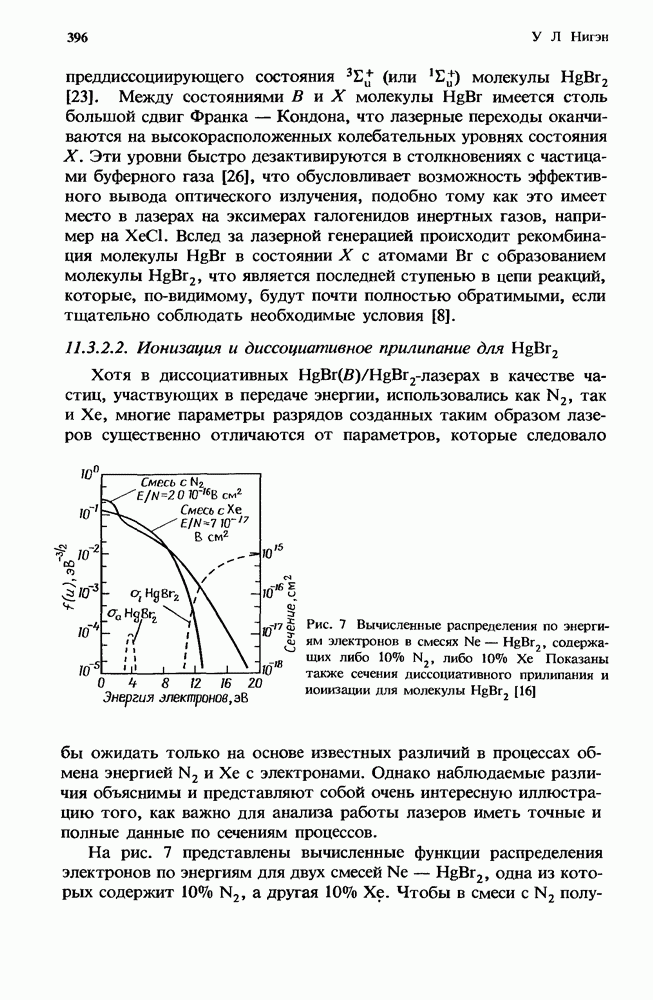
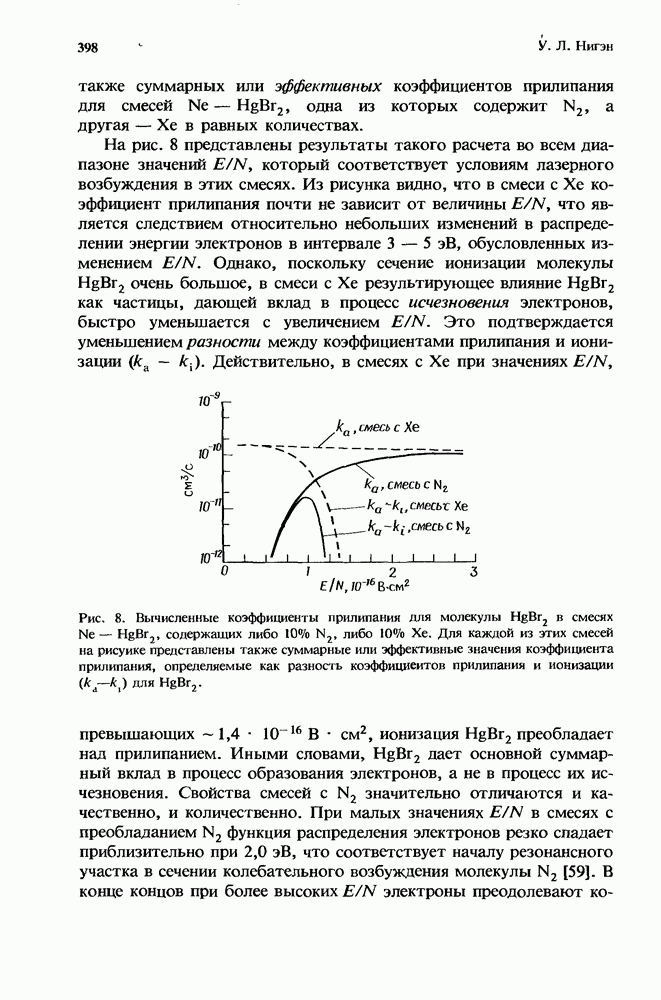
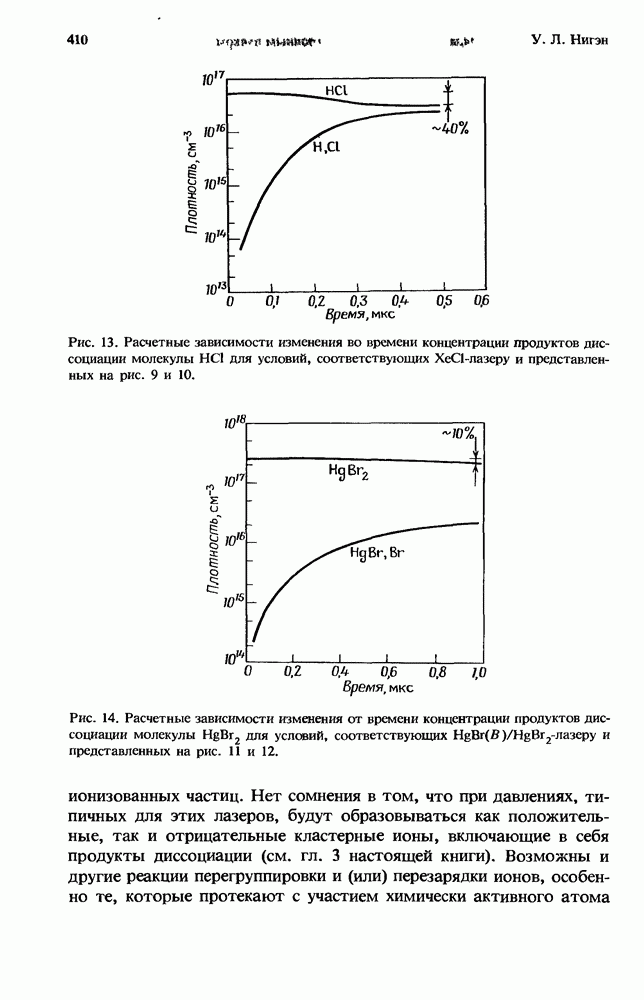
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
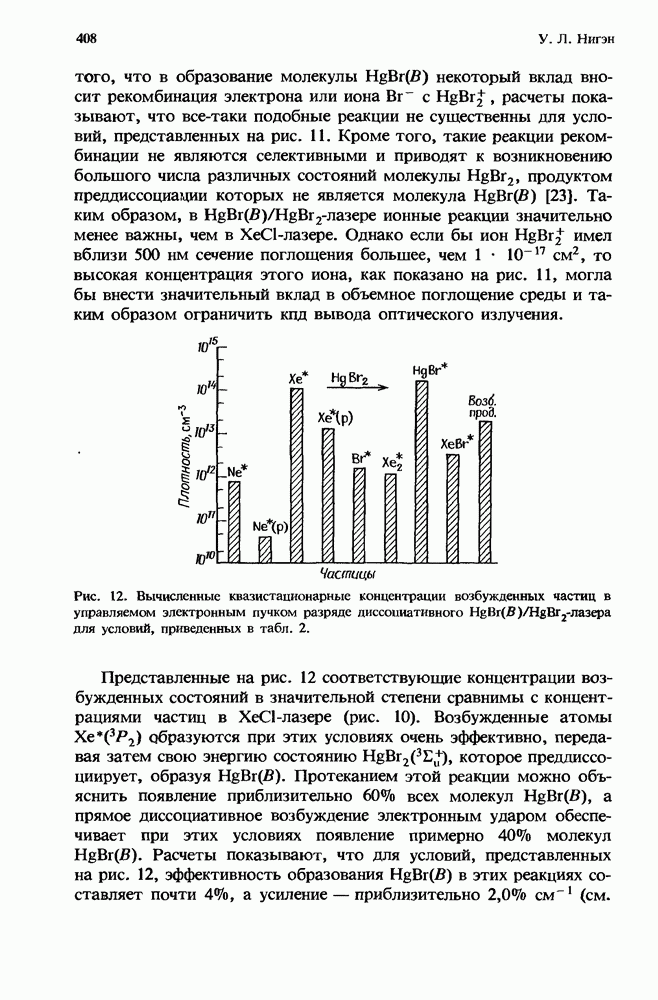
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
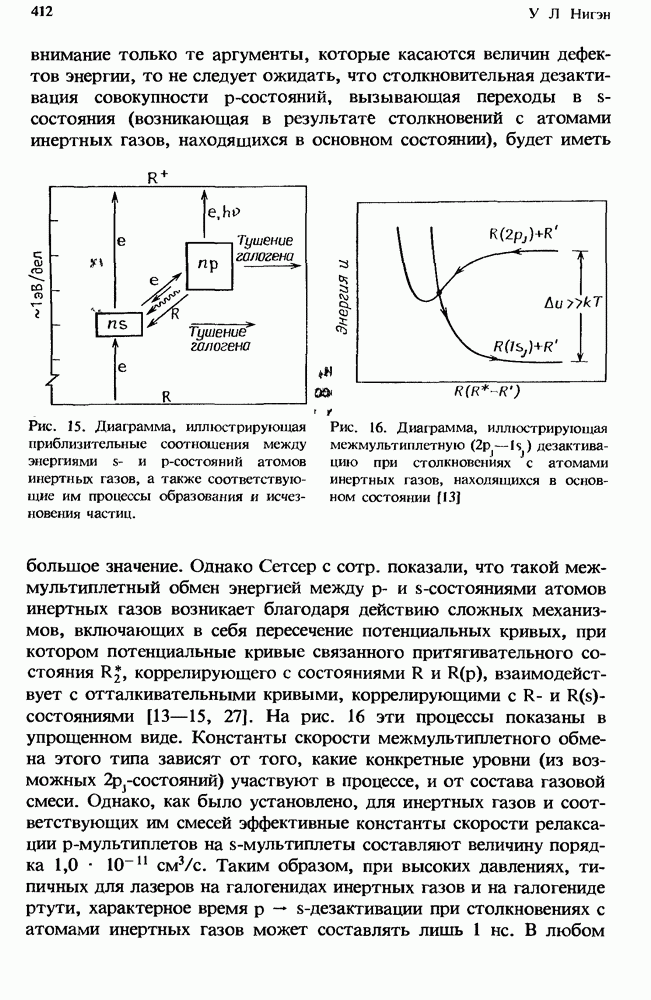
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
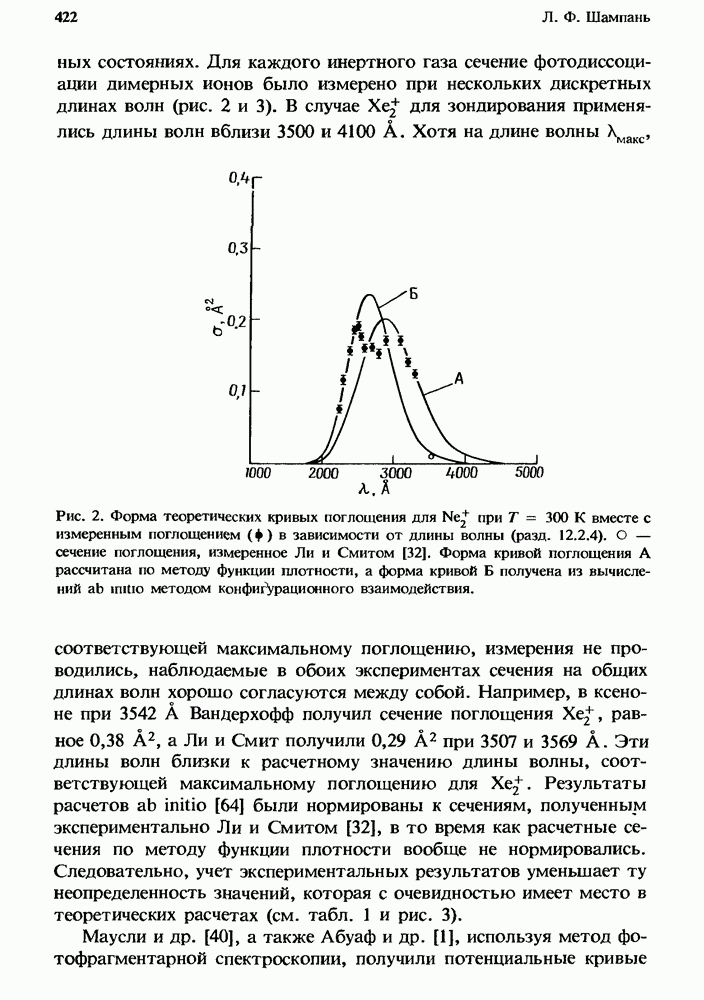
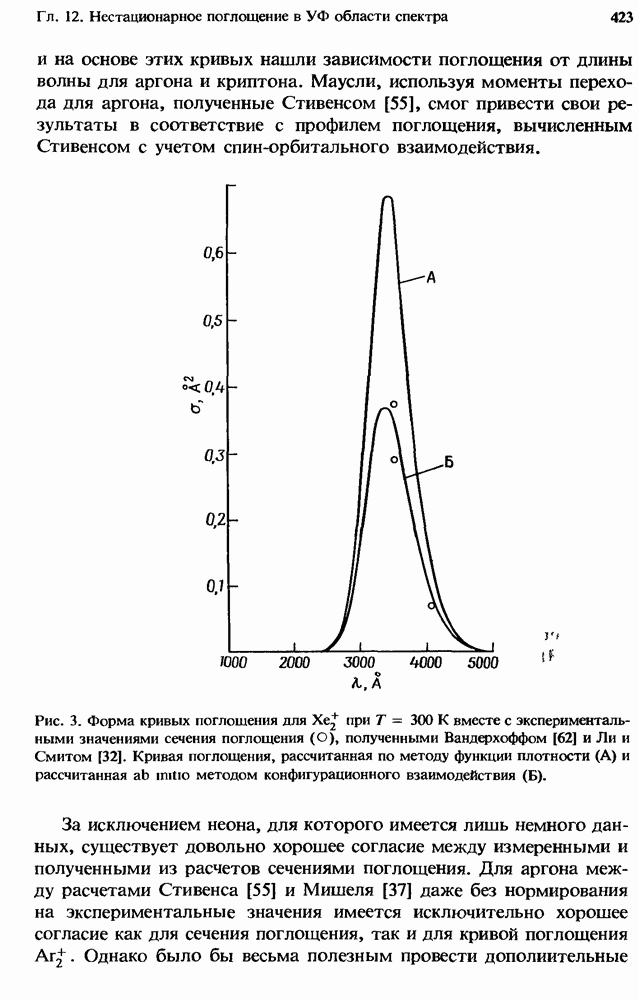
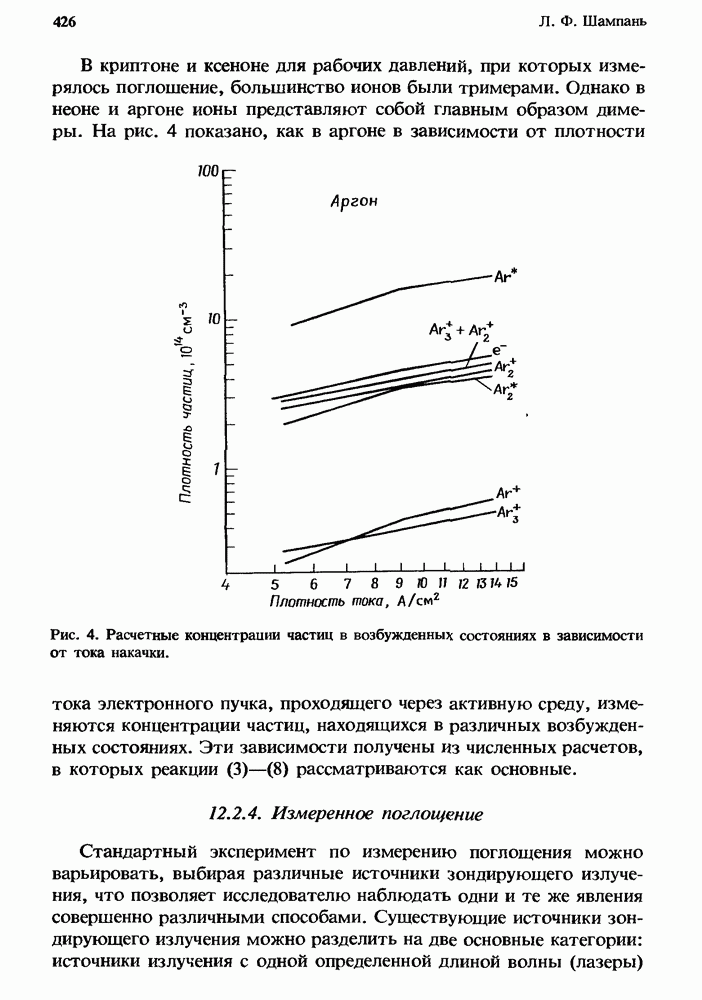
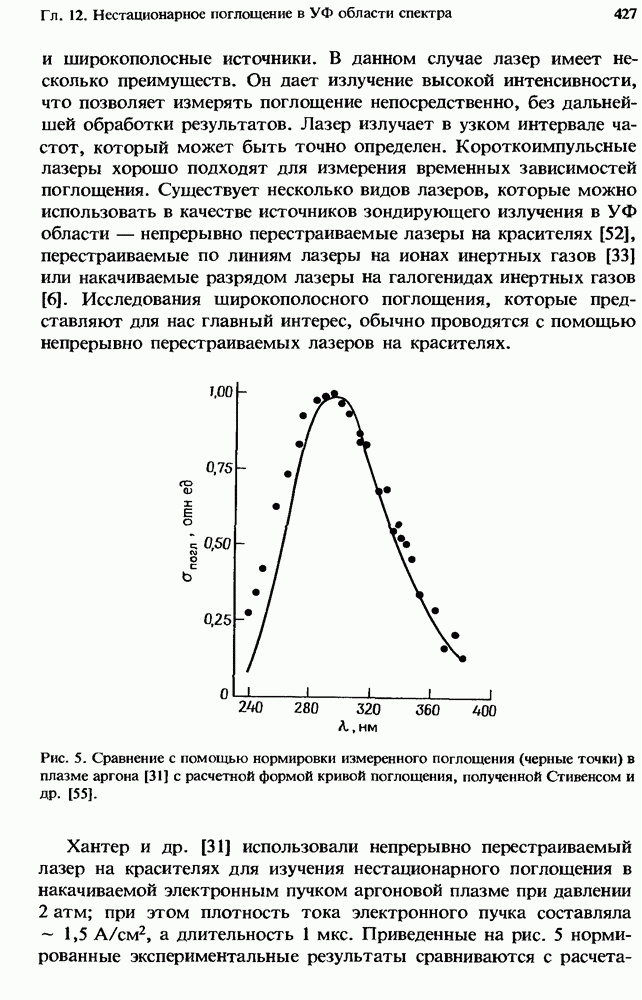
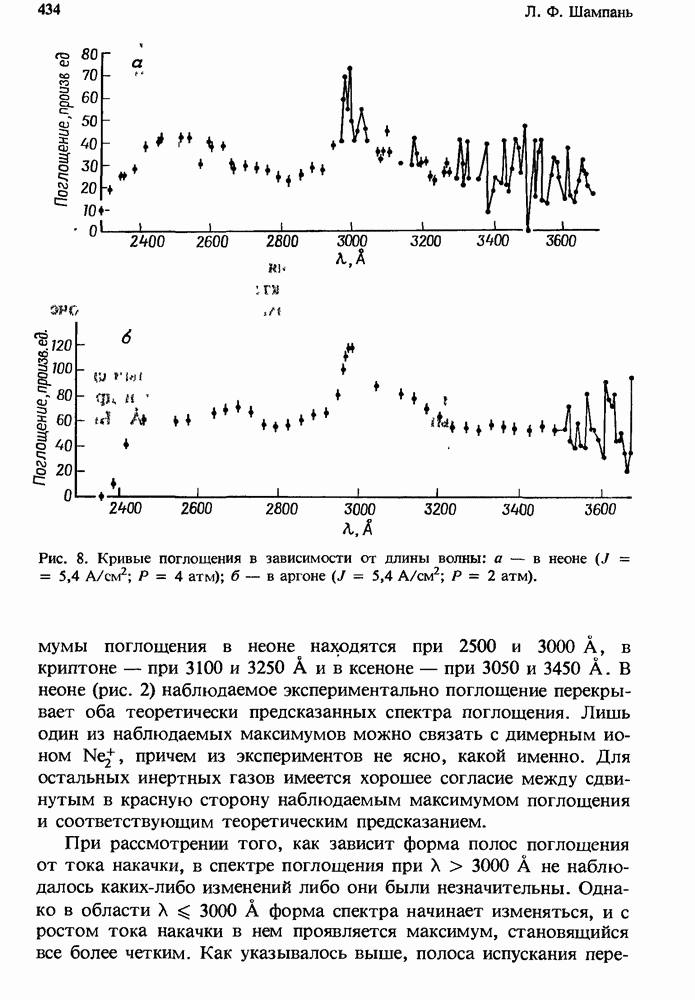
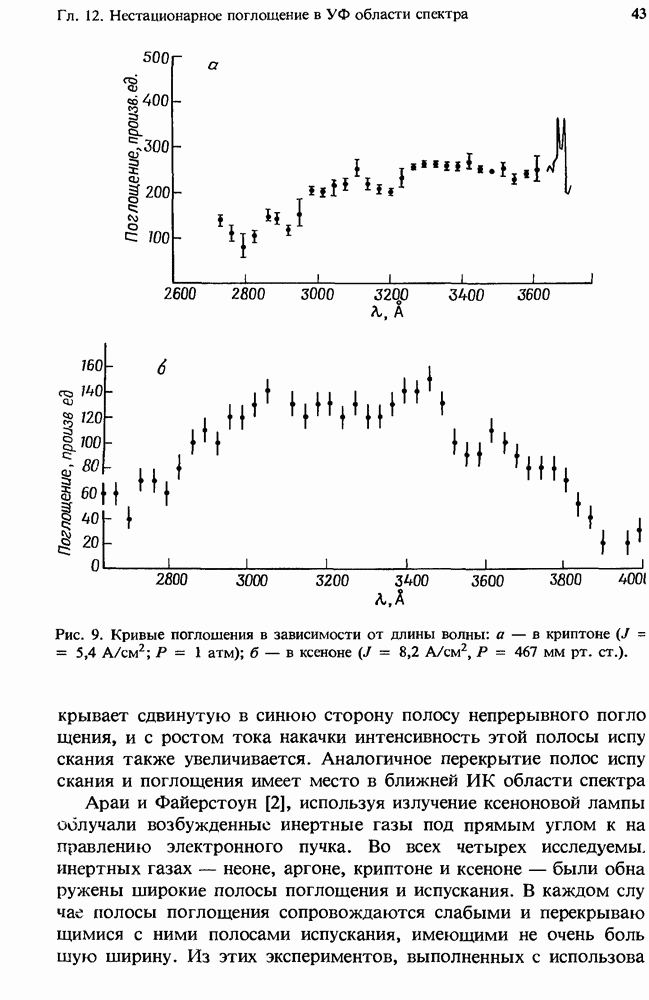
- 12.2.4. Измеренное поглощение
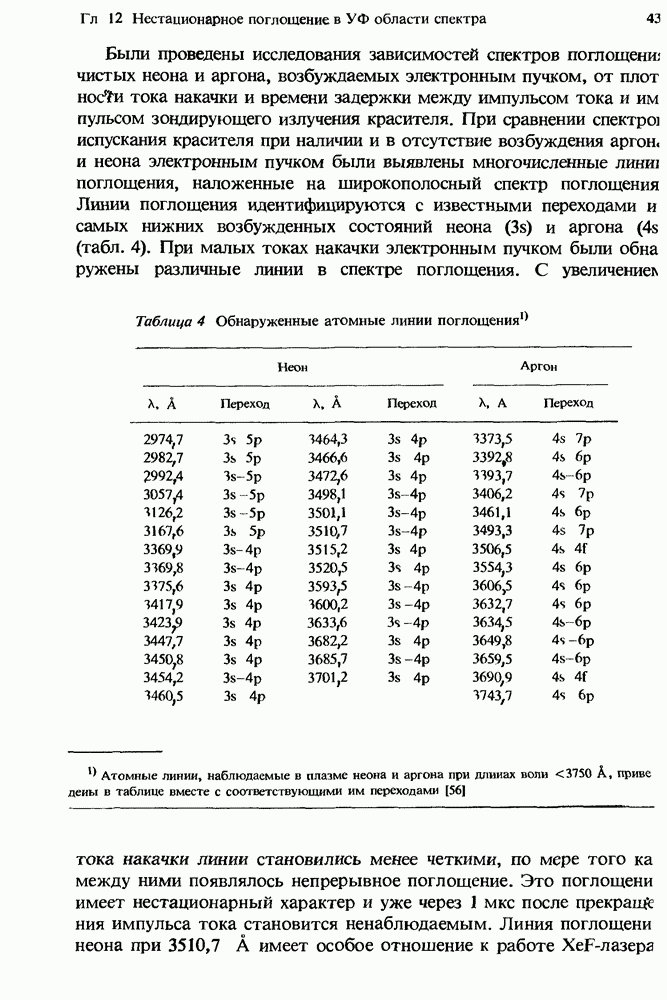
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
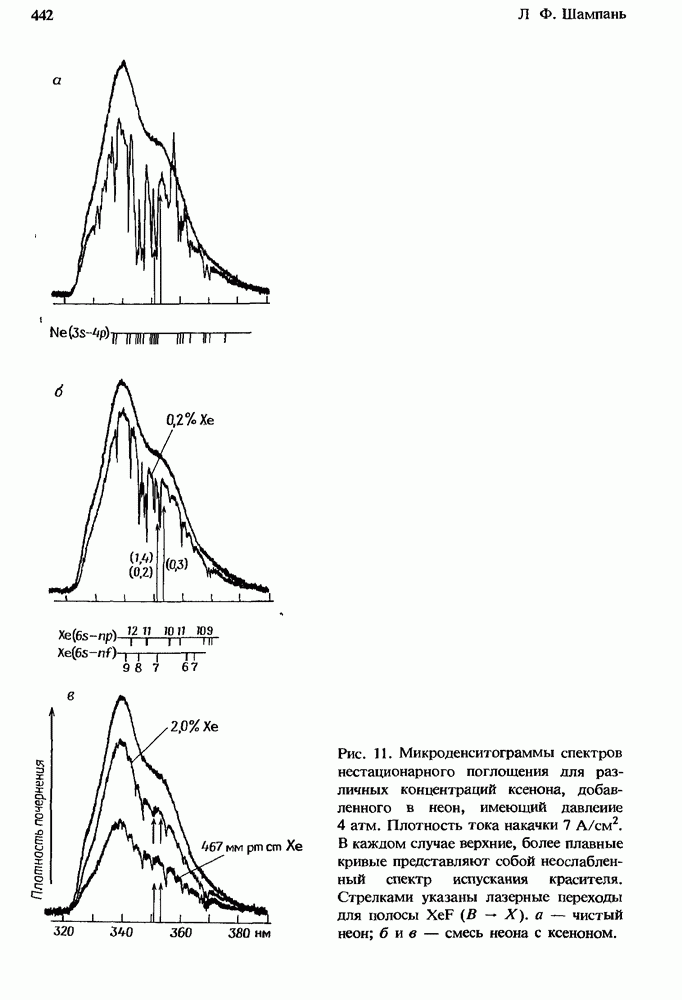
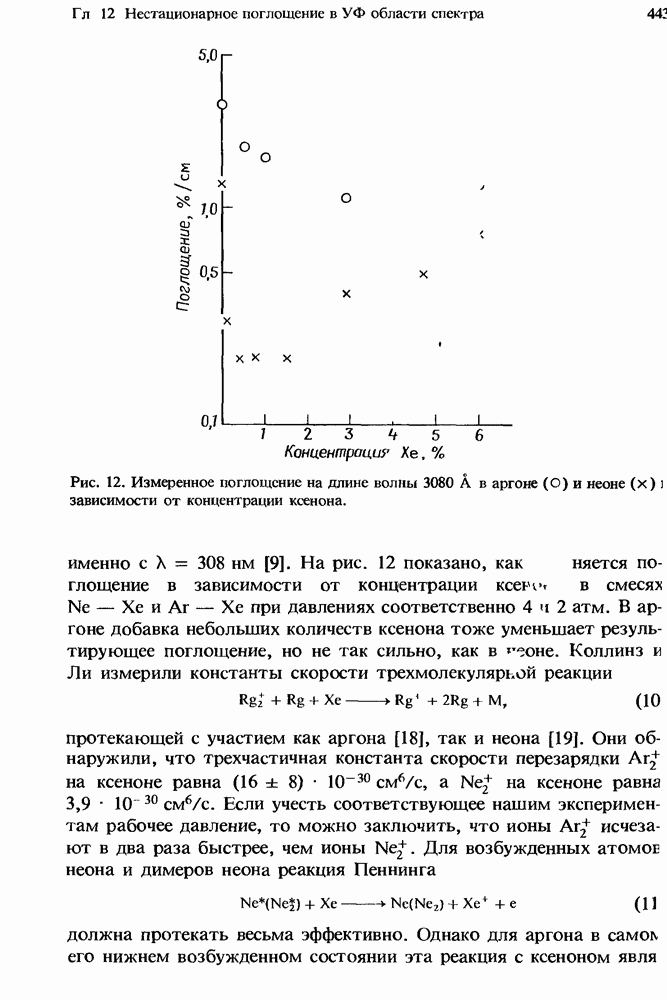
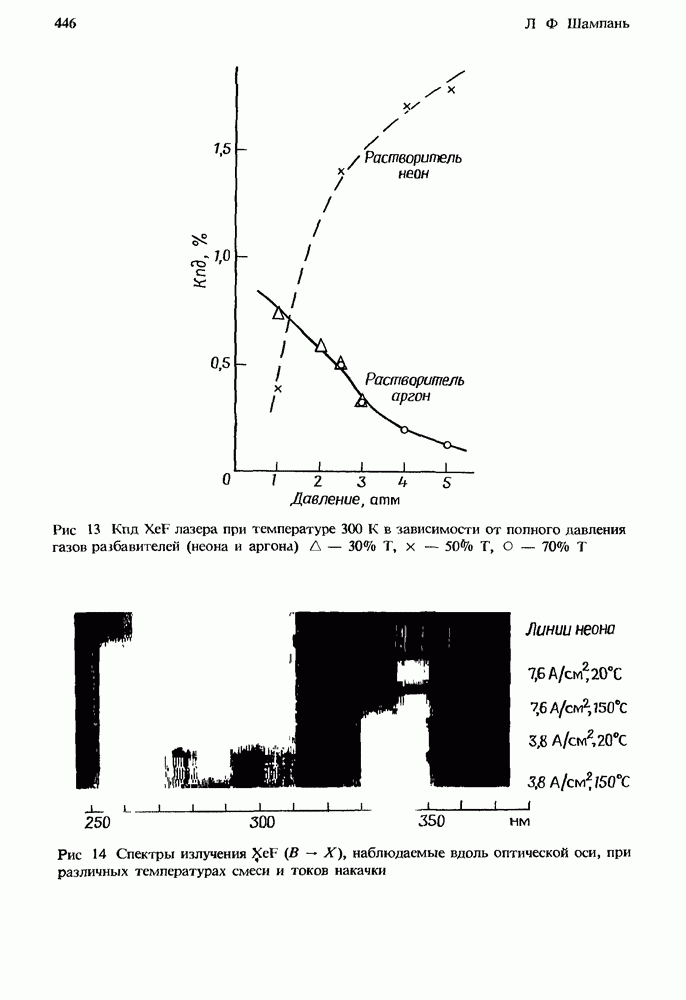
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
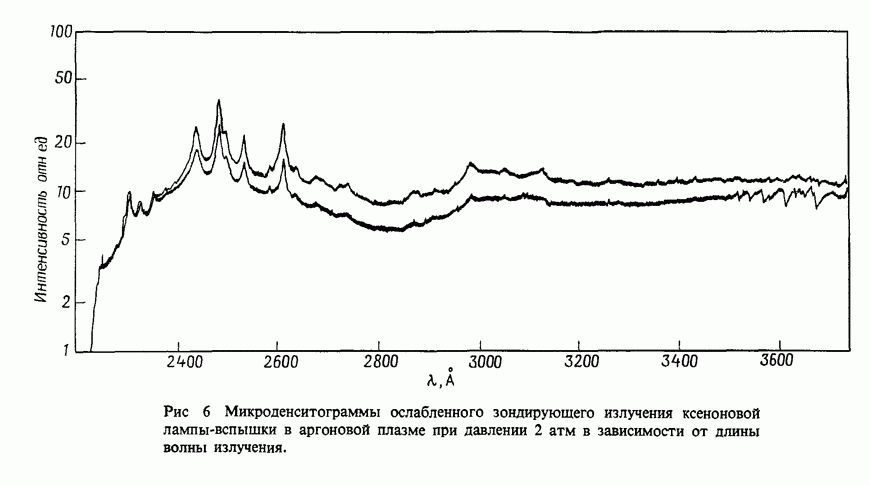
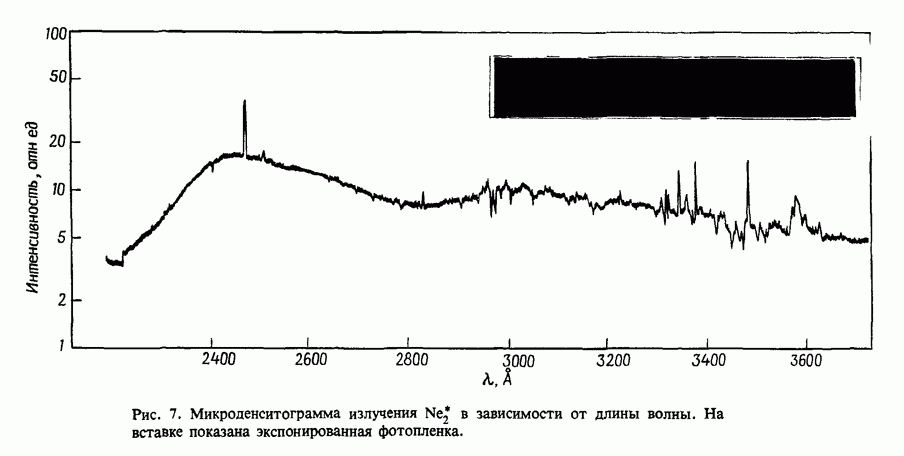
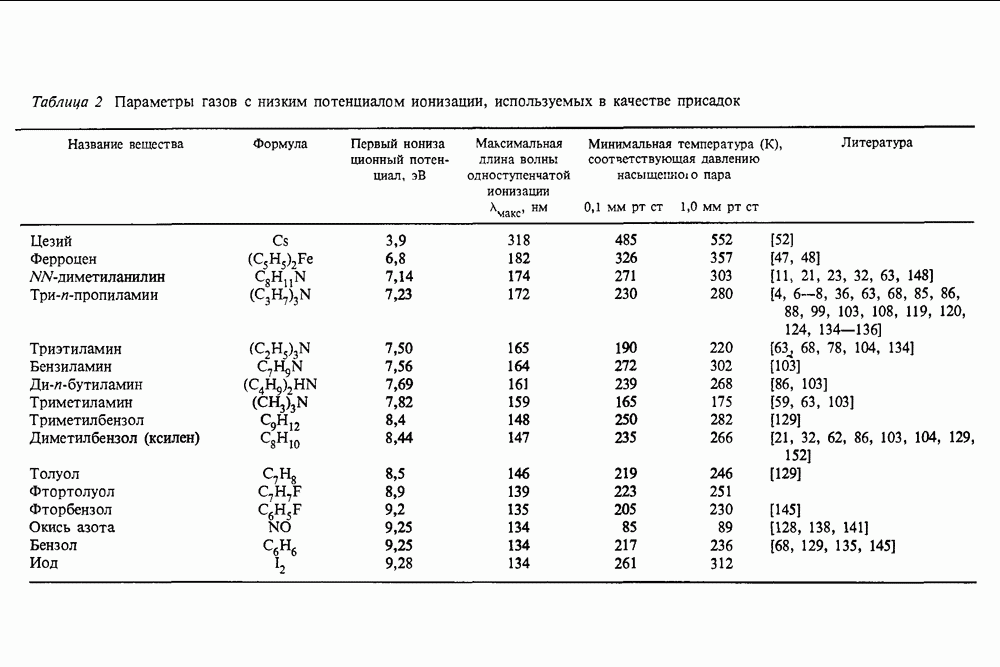
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
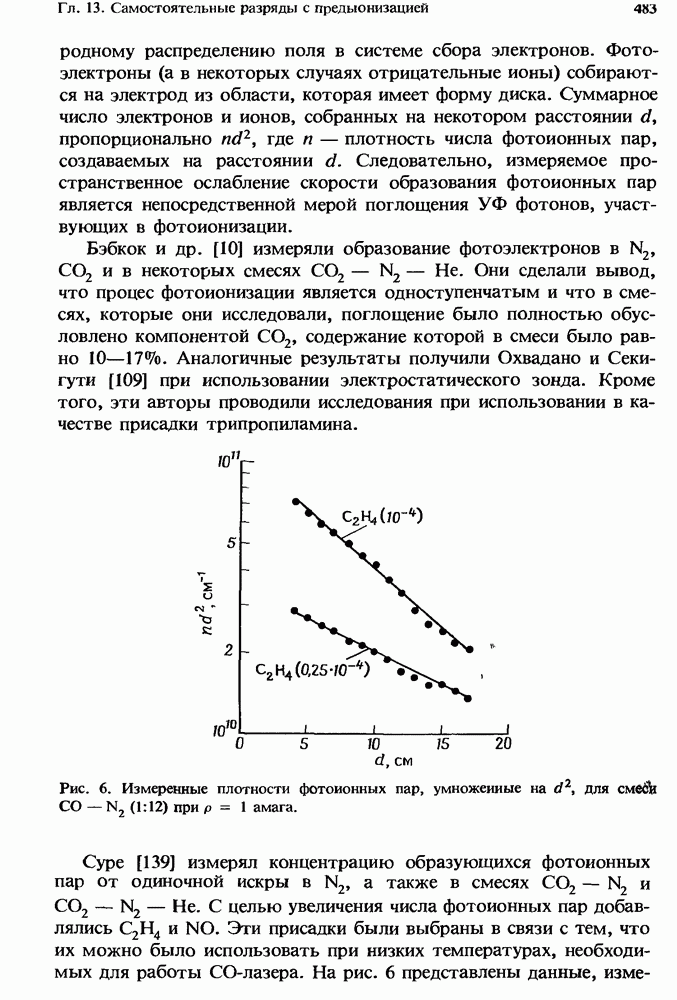
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
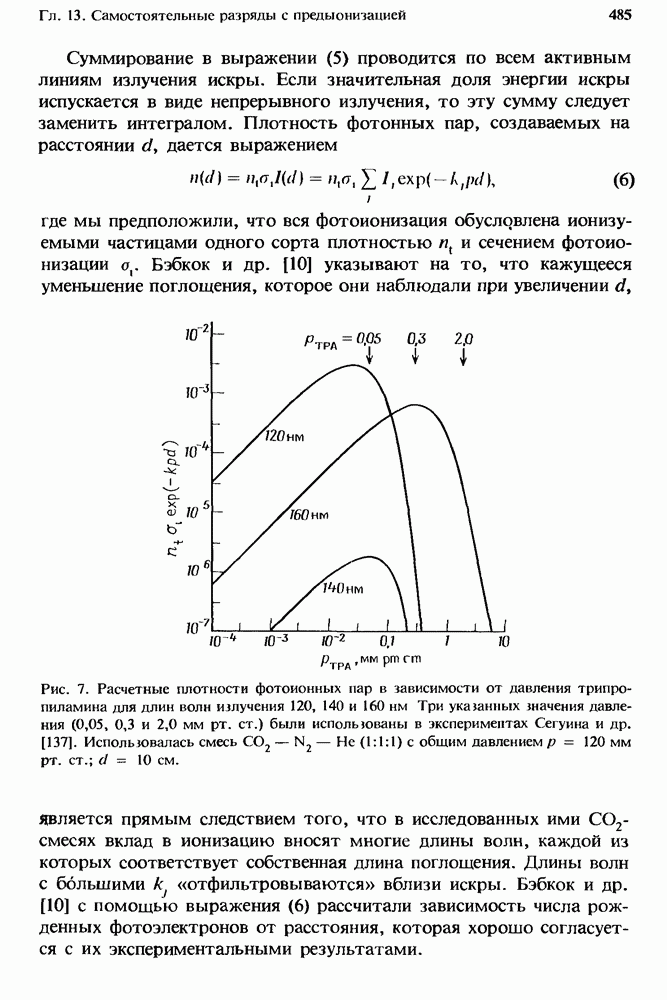
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
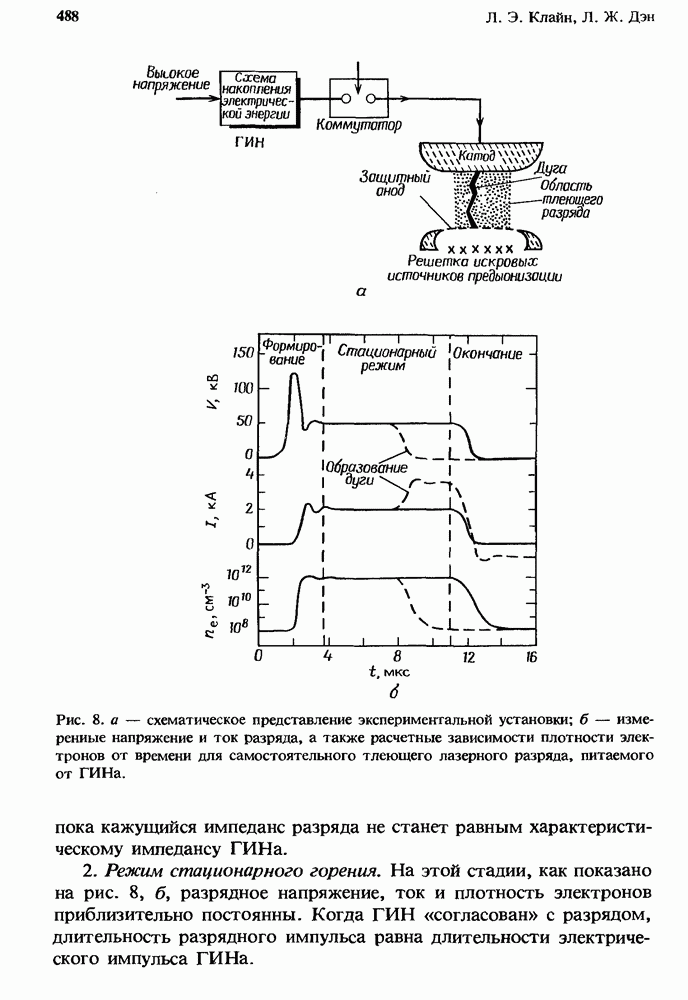
- 13.4. Физика самостоятельного тлеющего разряда
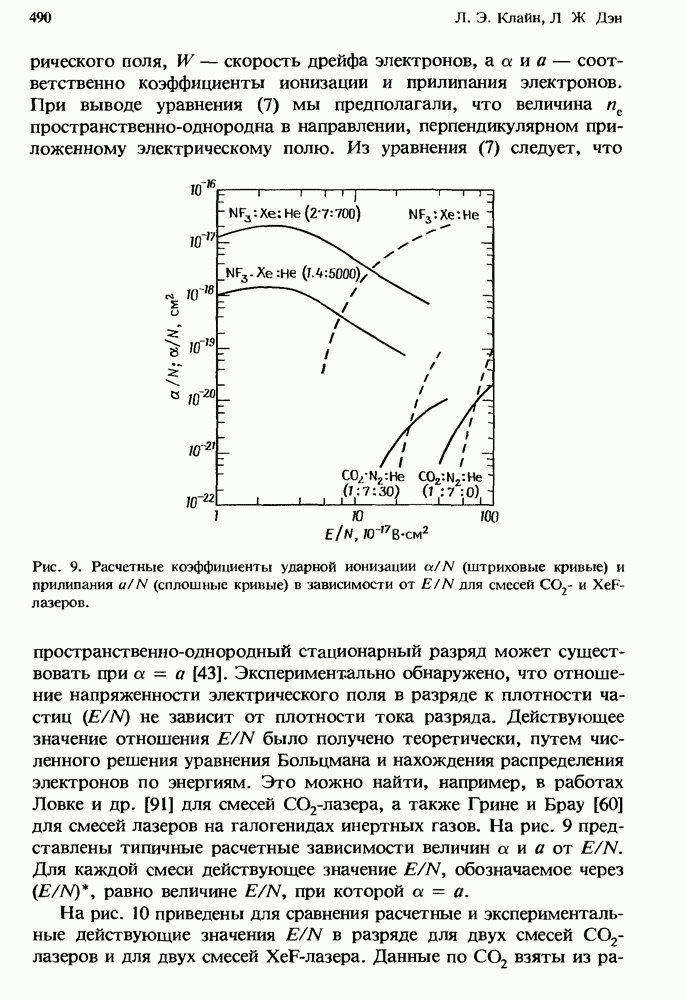
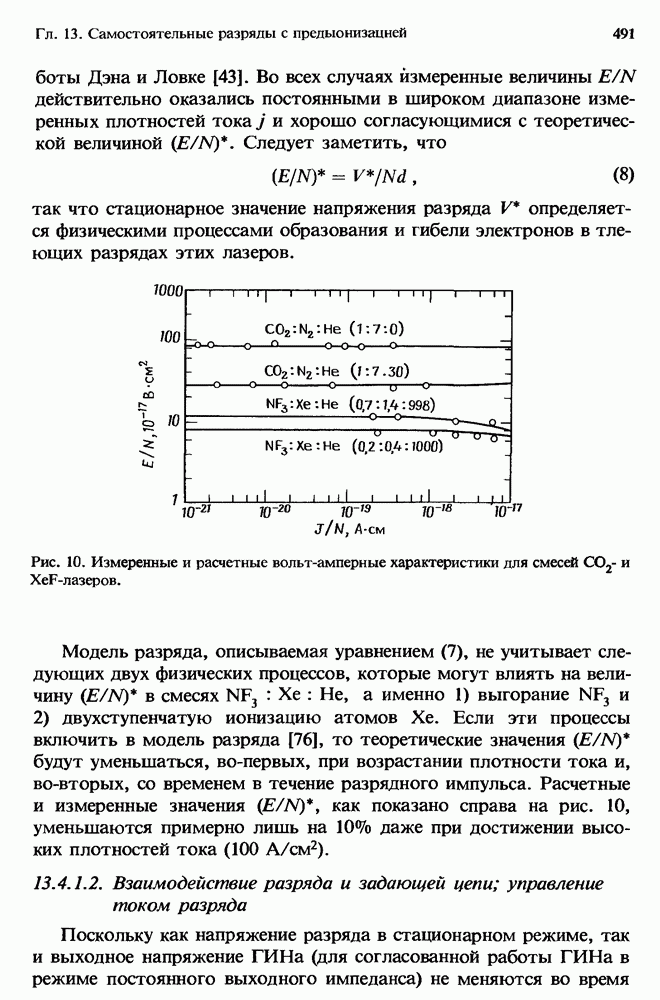
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
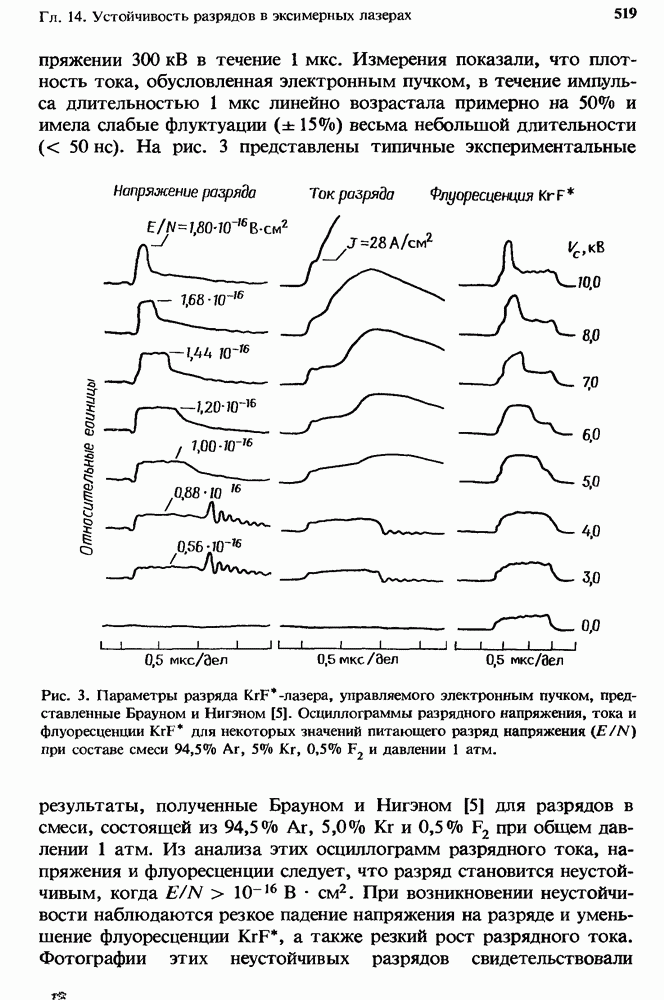
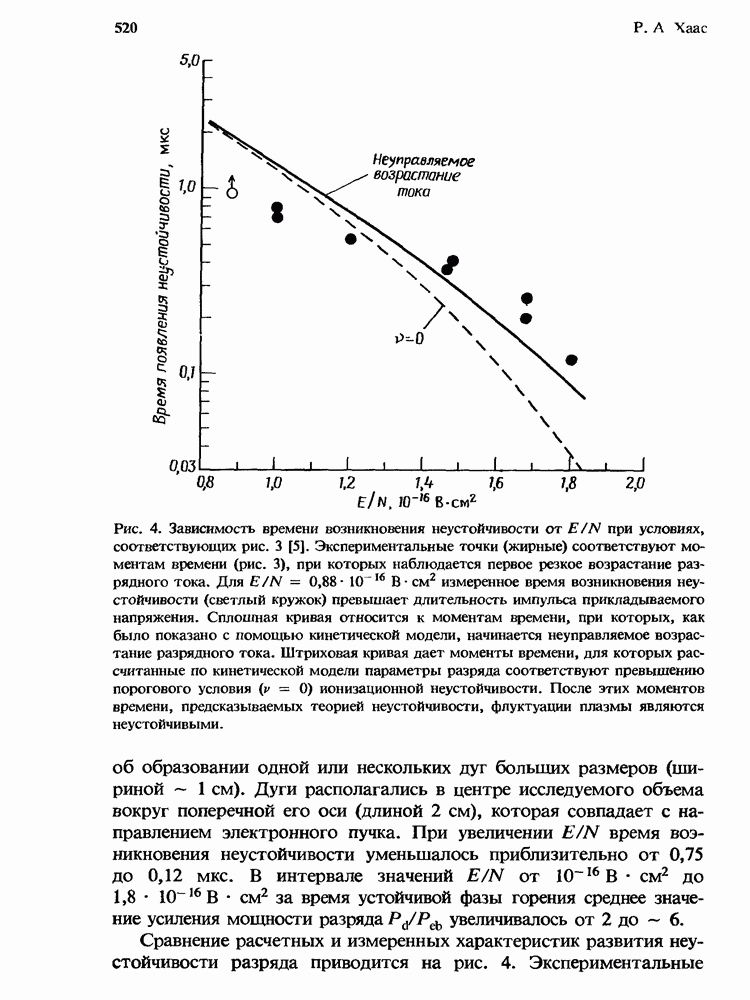
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации