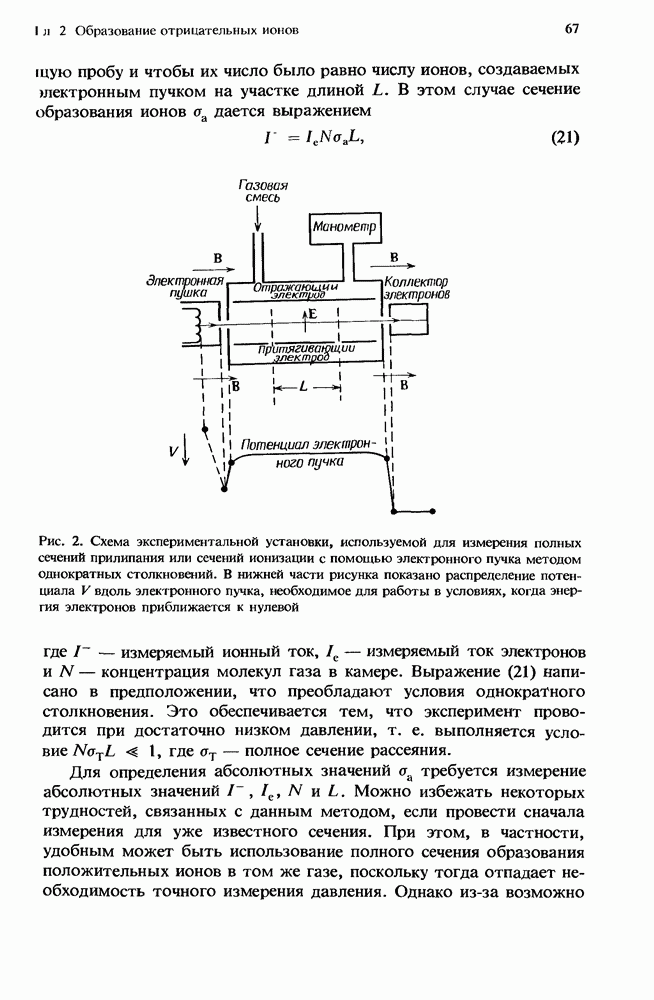
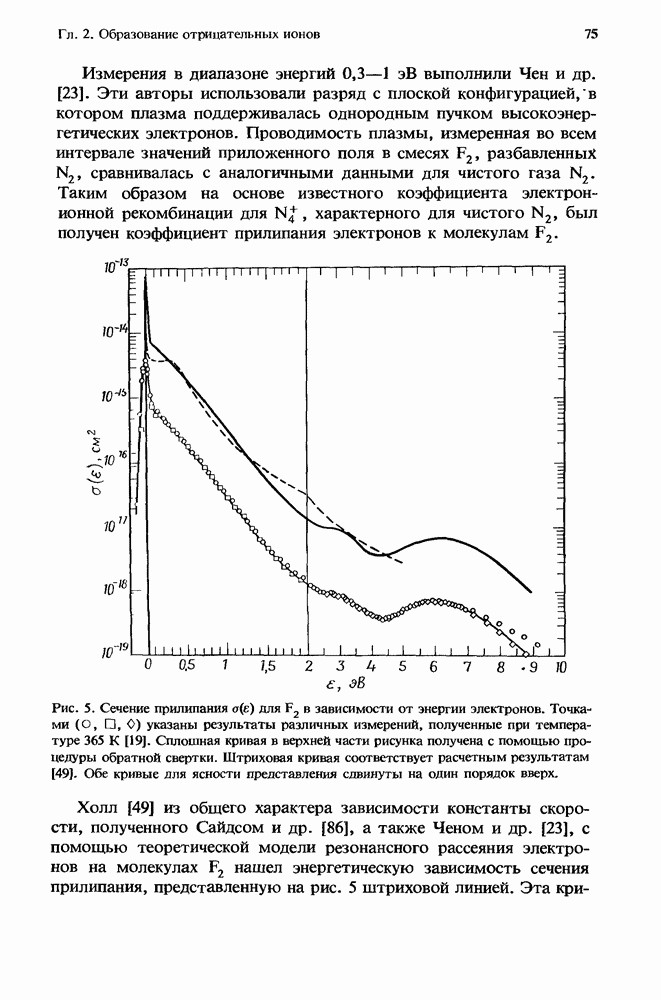
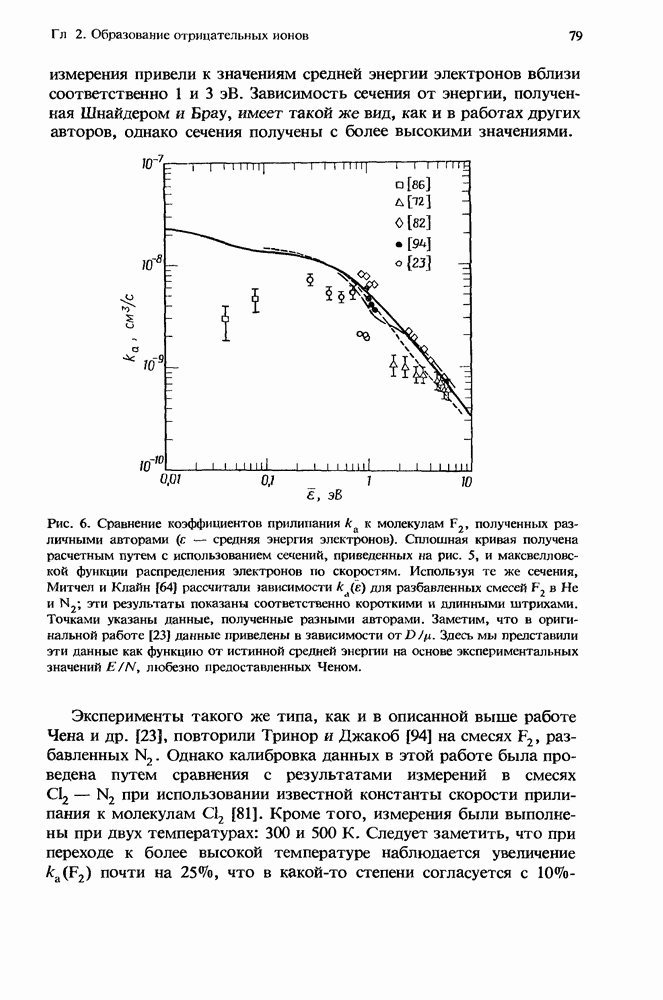
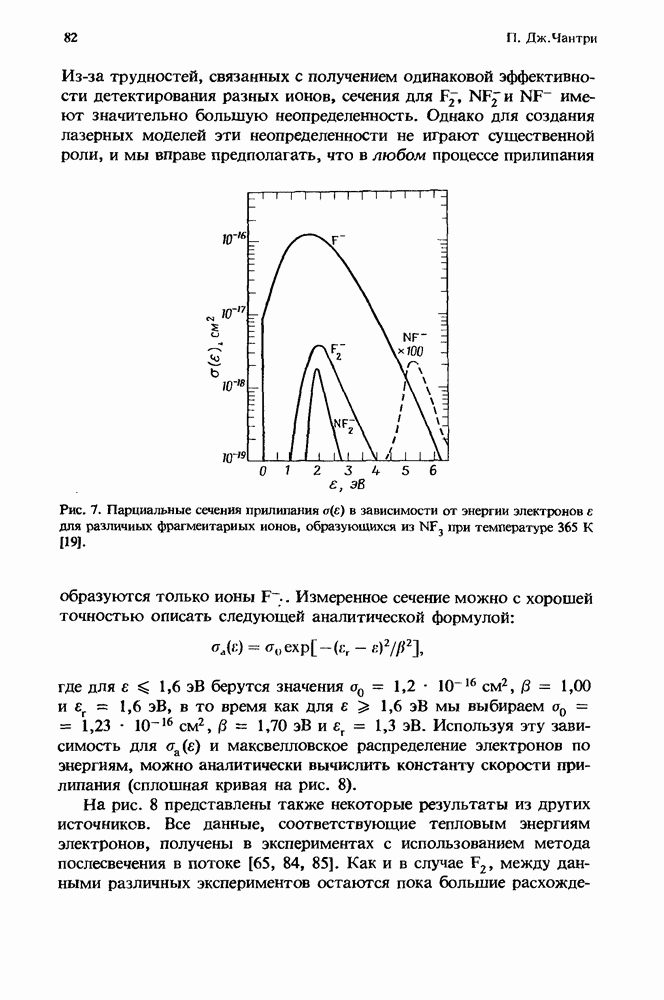
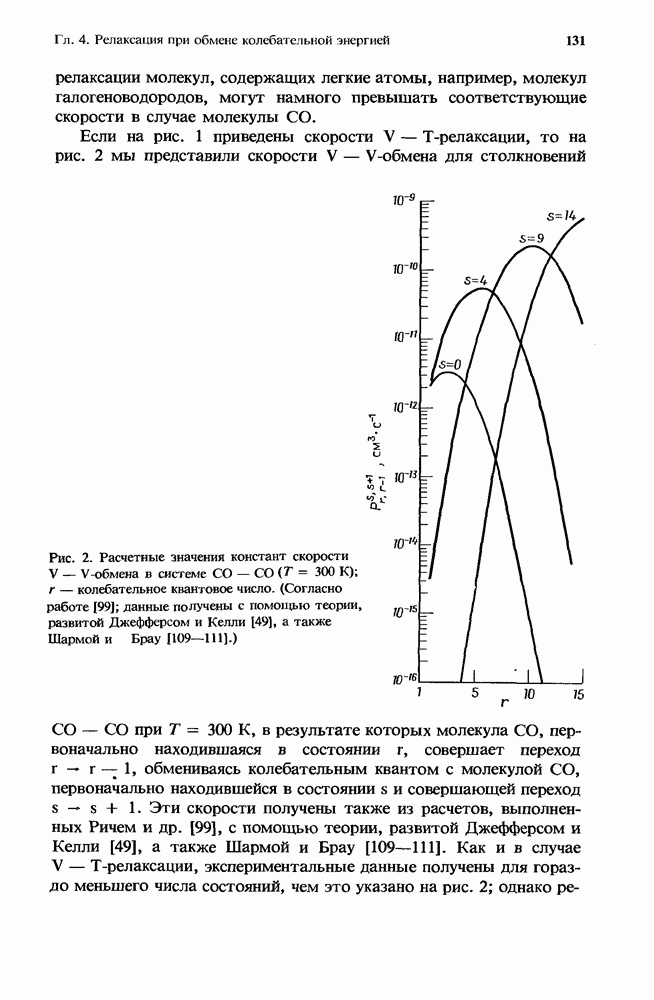
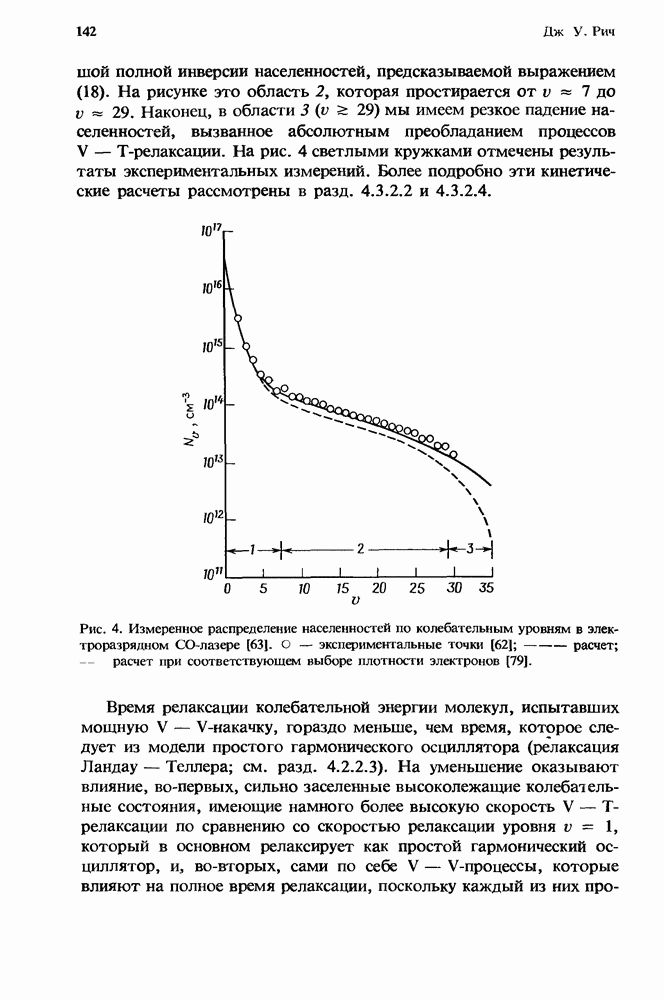
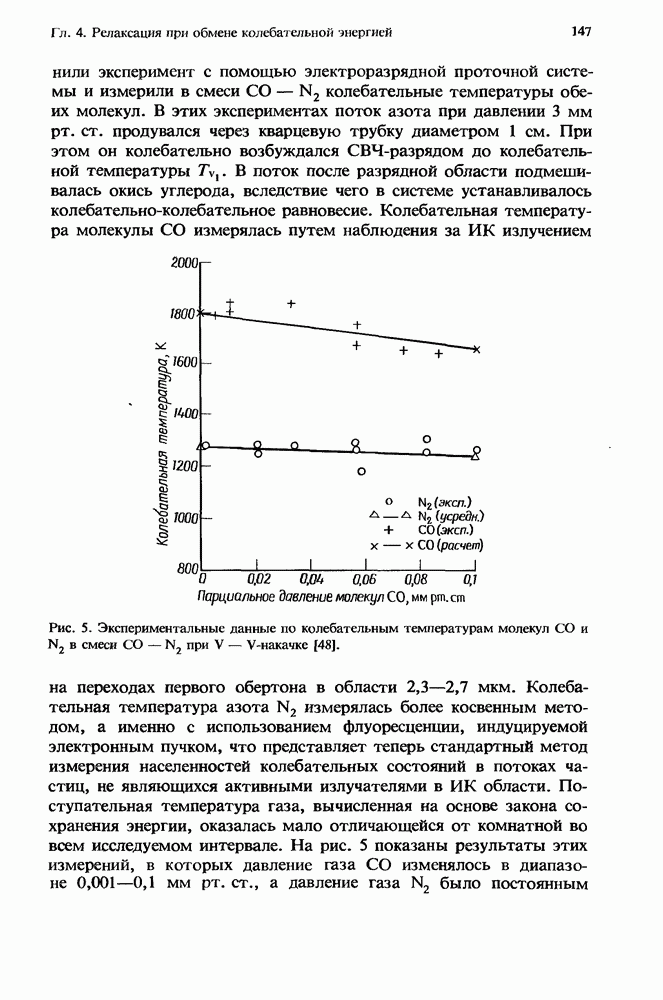
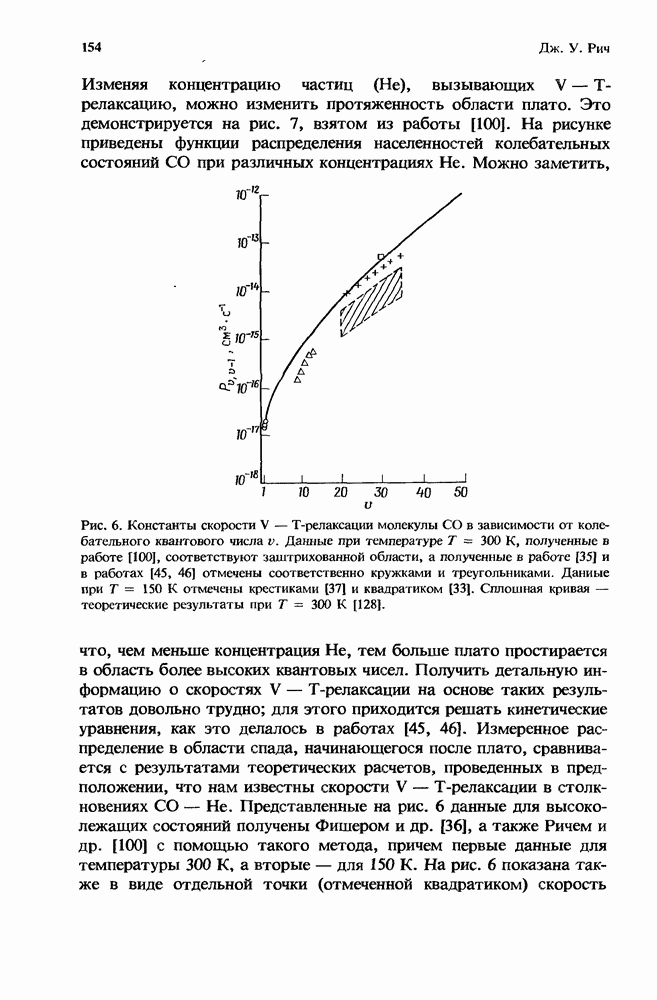
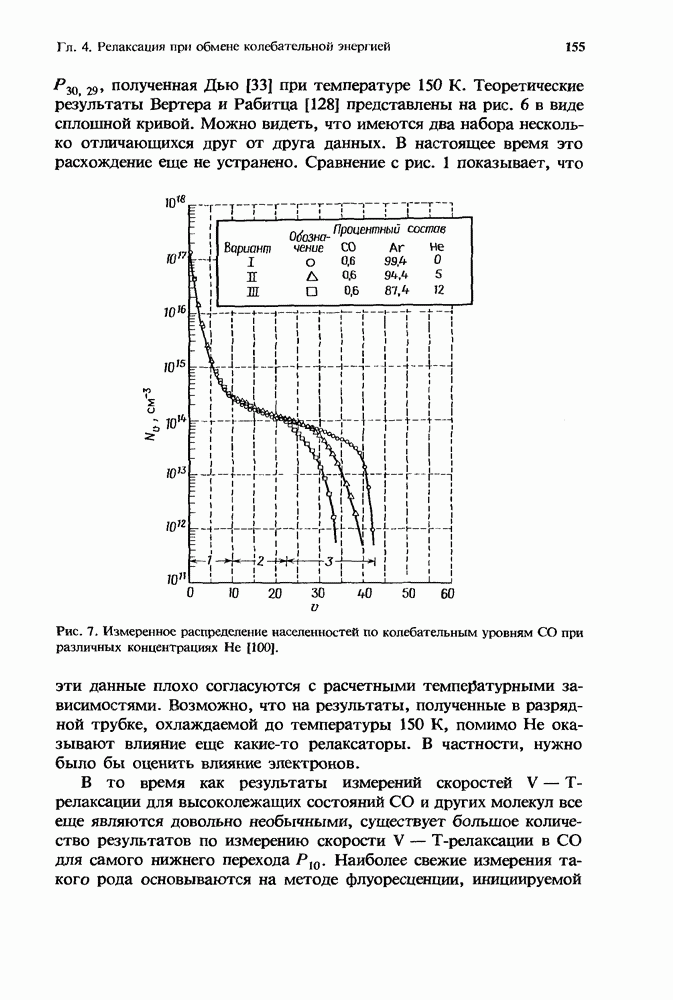
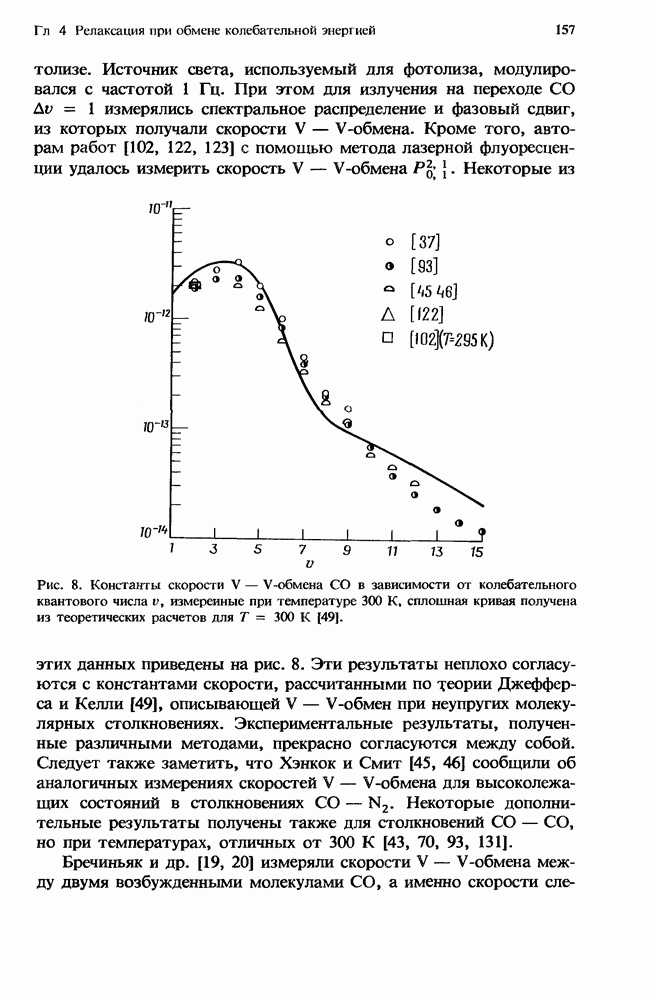
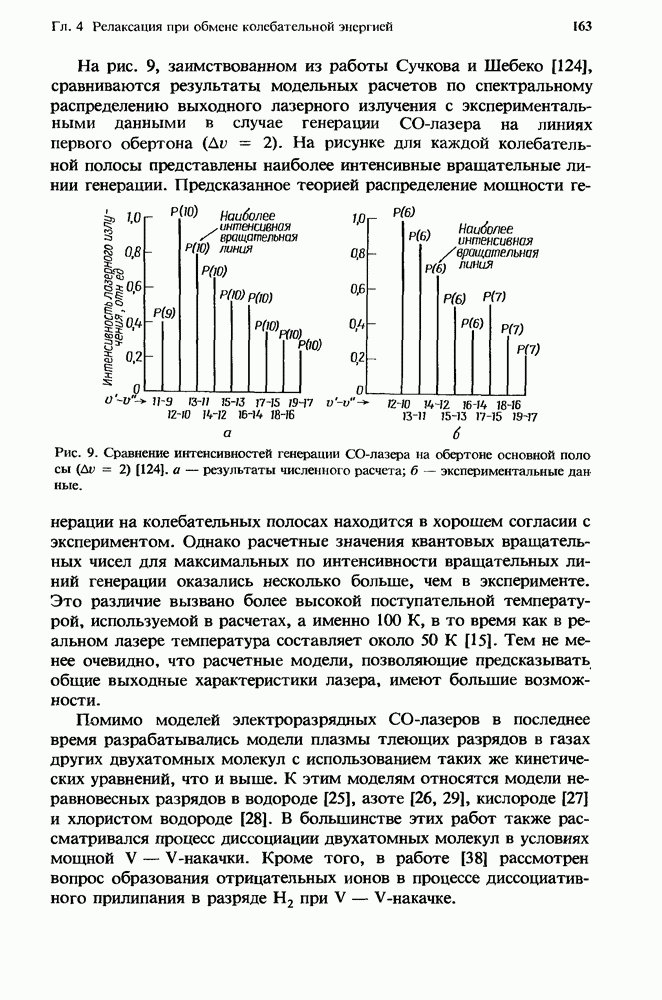
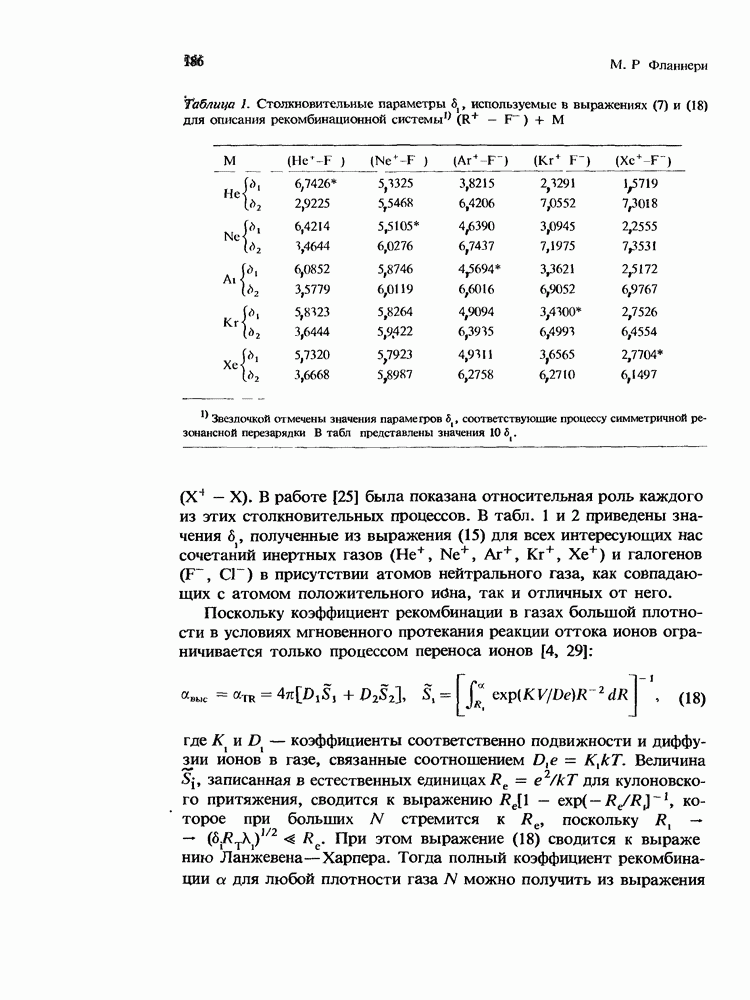
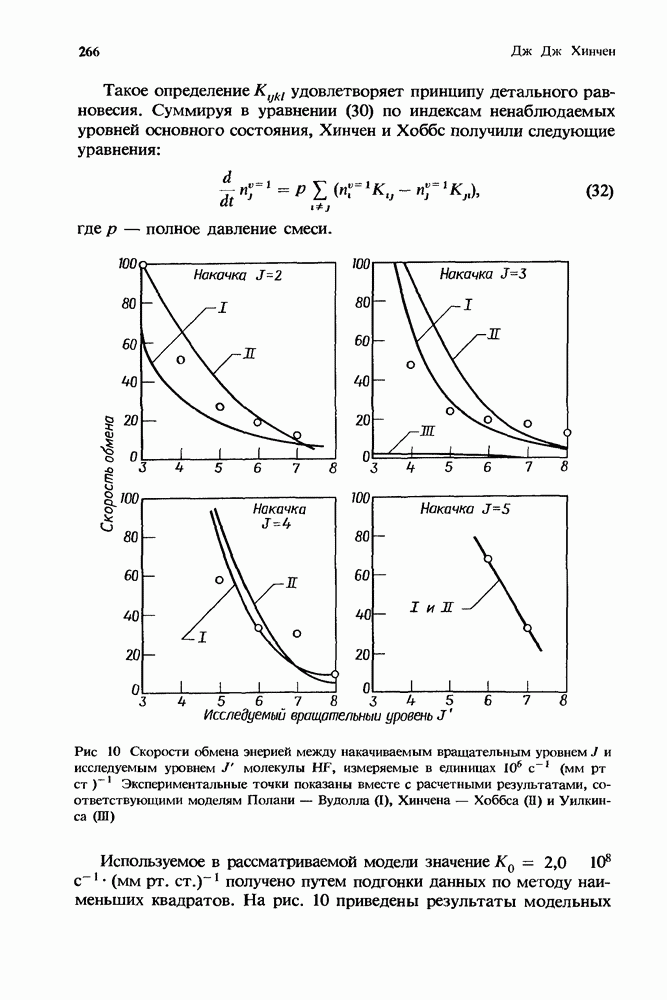
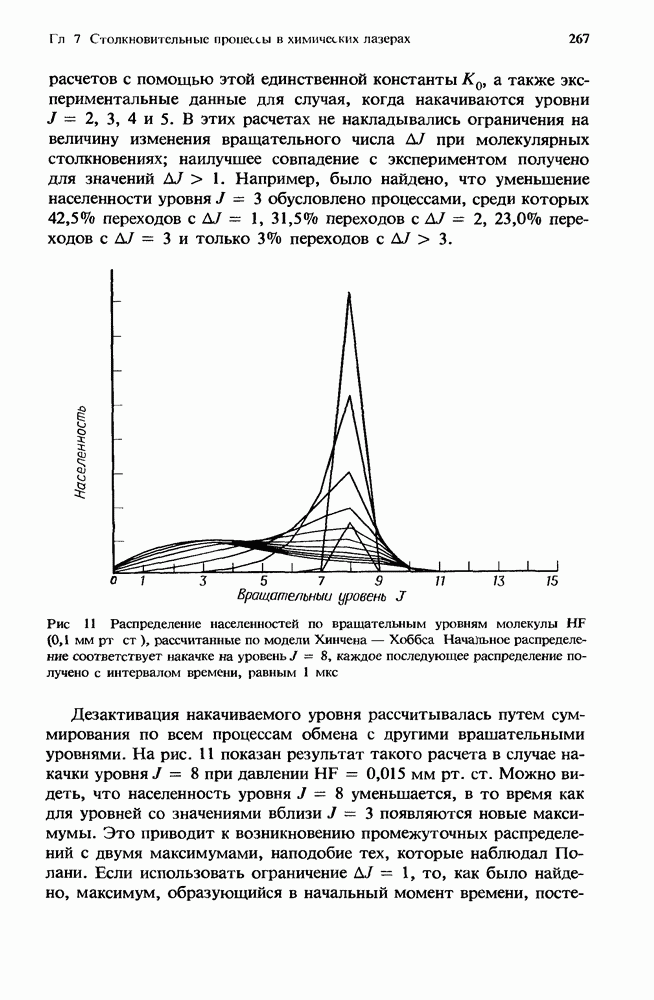
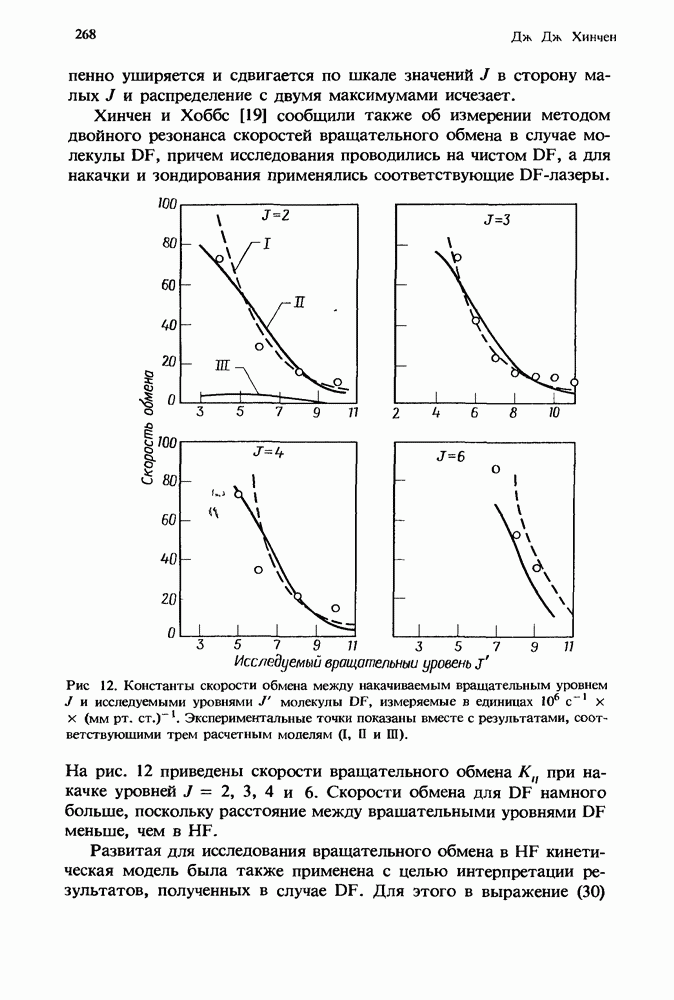
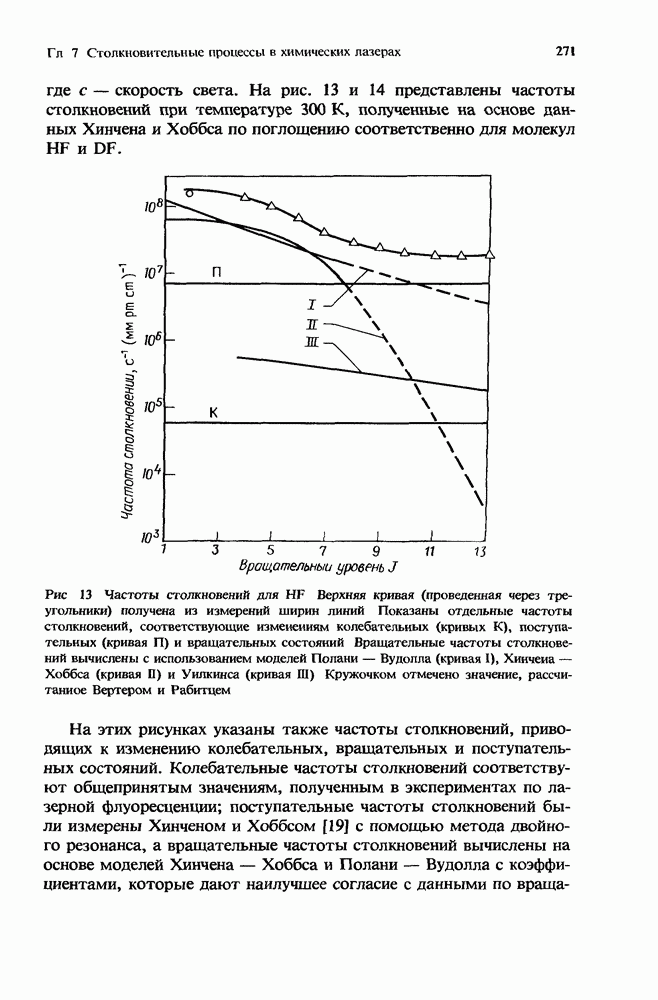
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
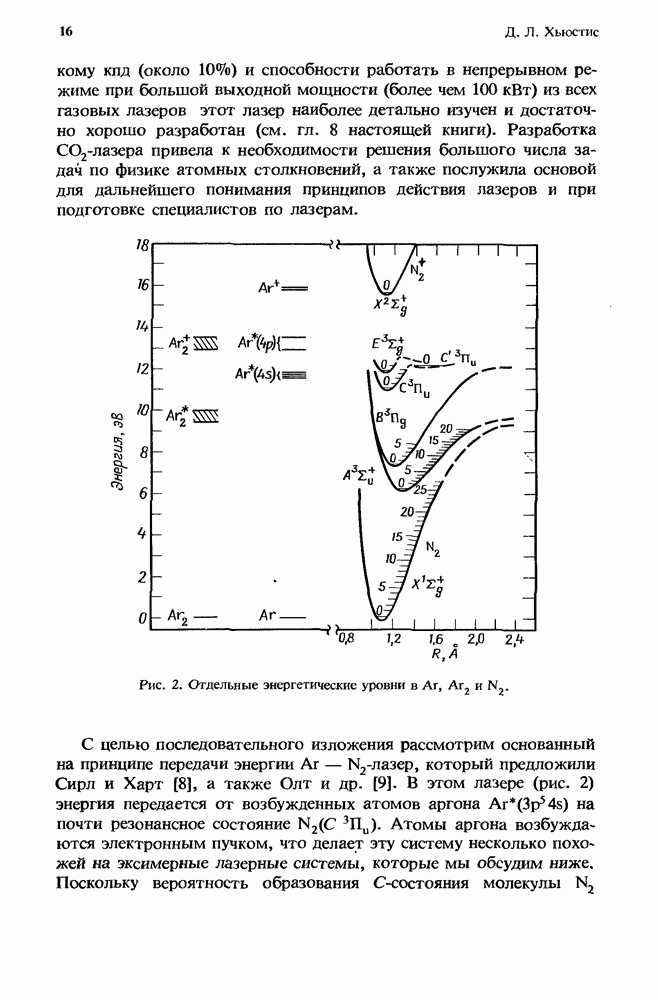
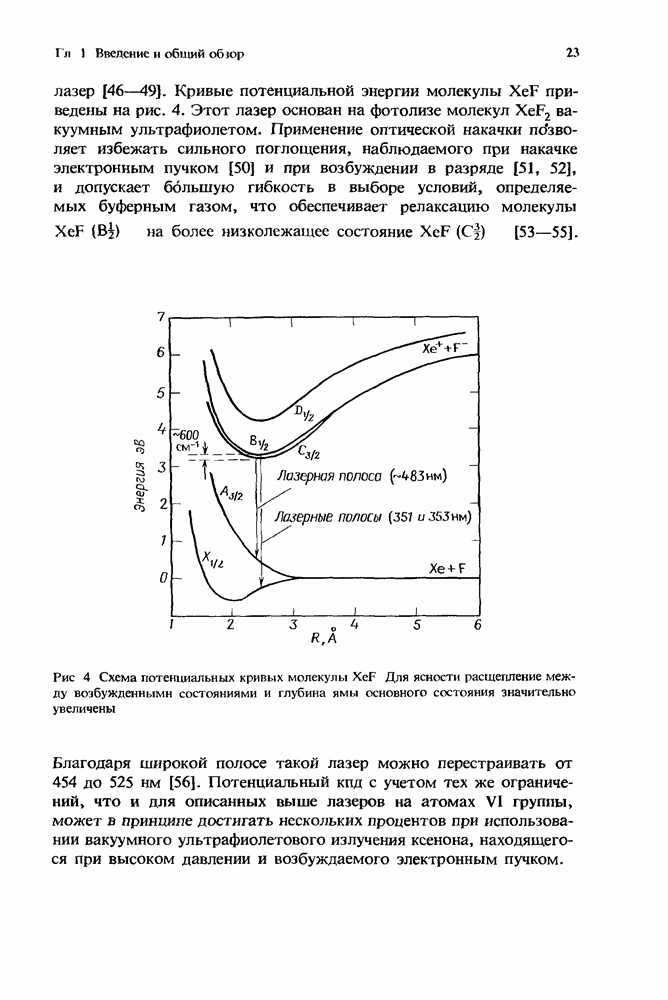
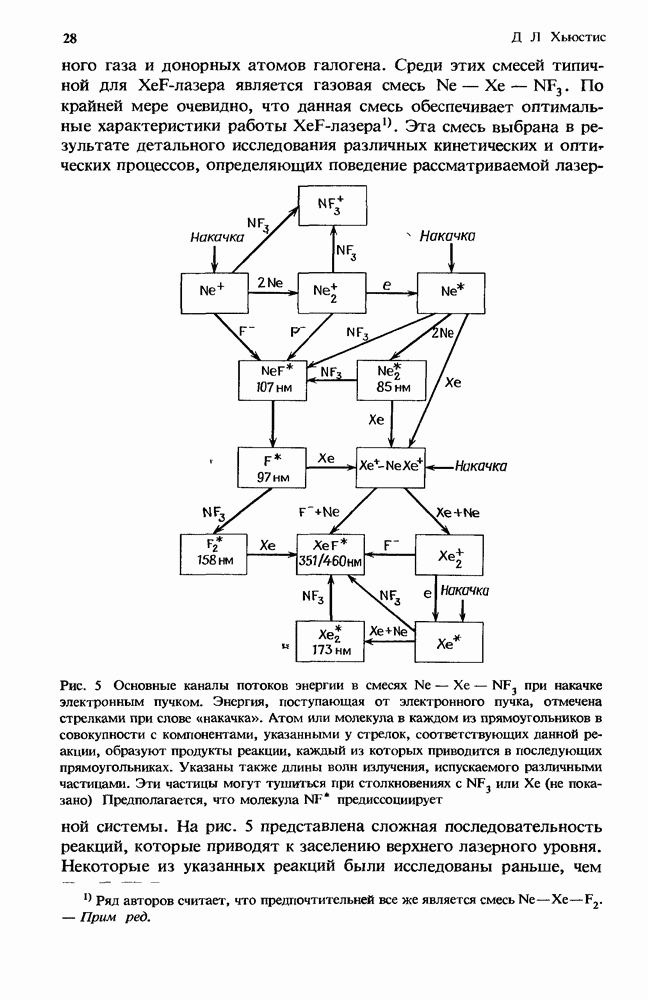
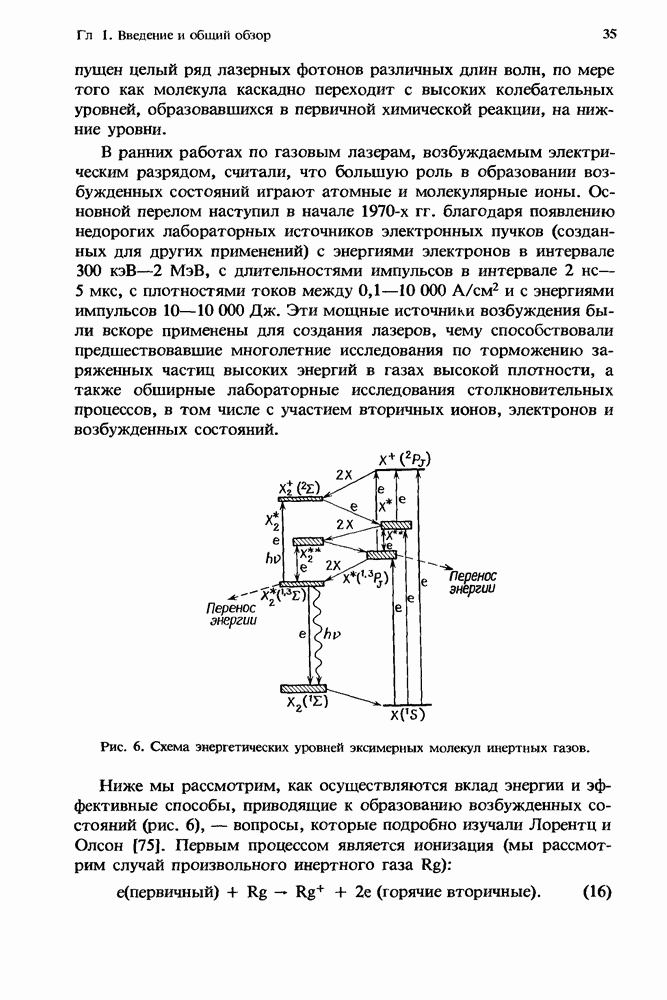
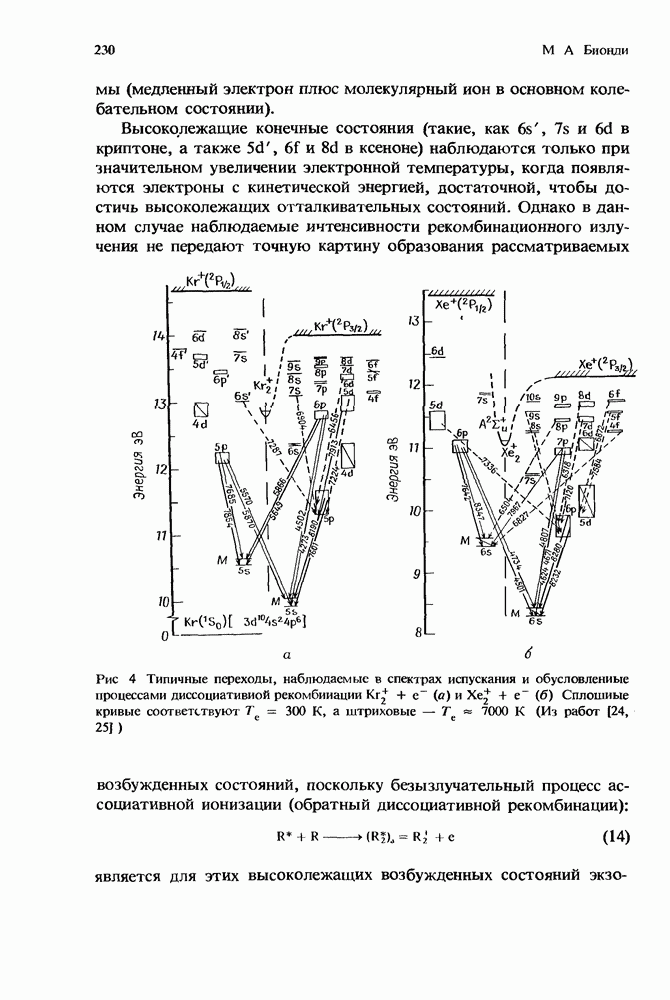
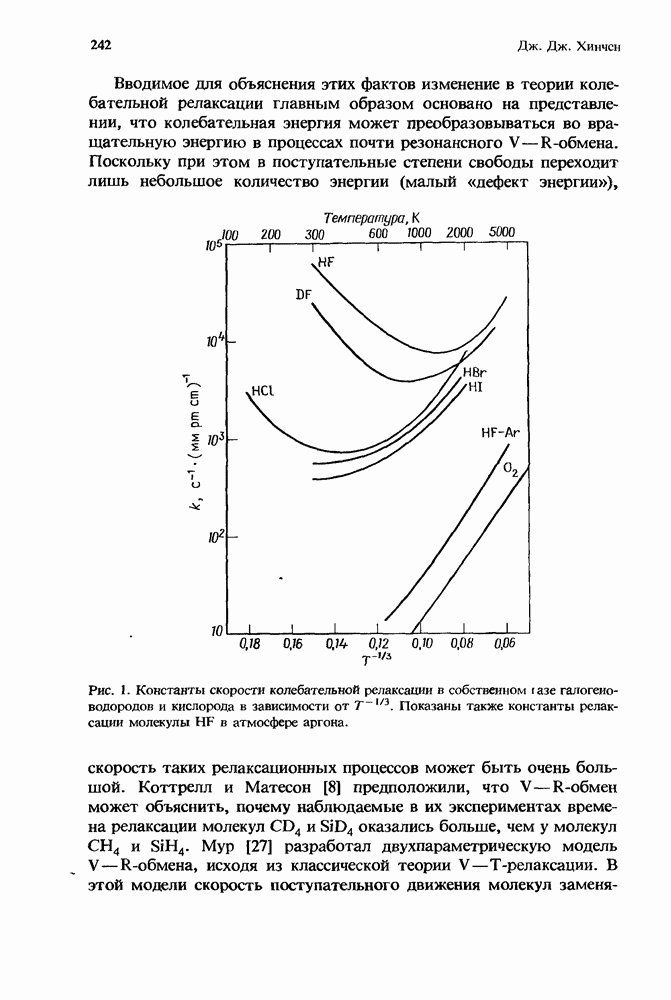
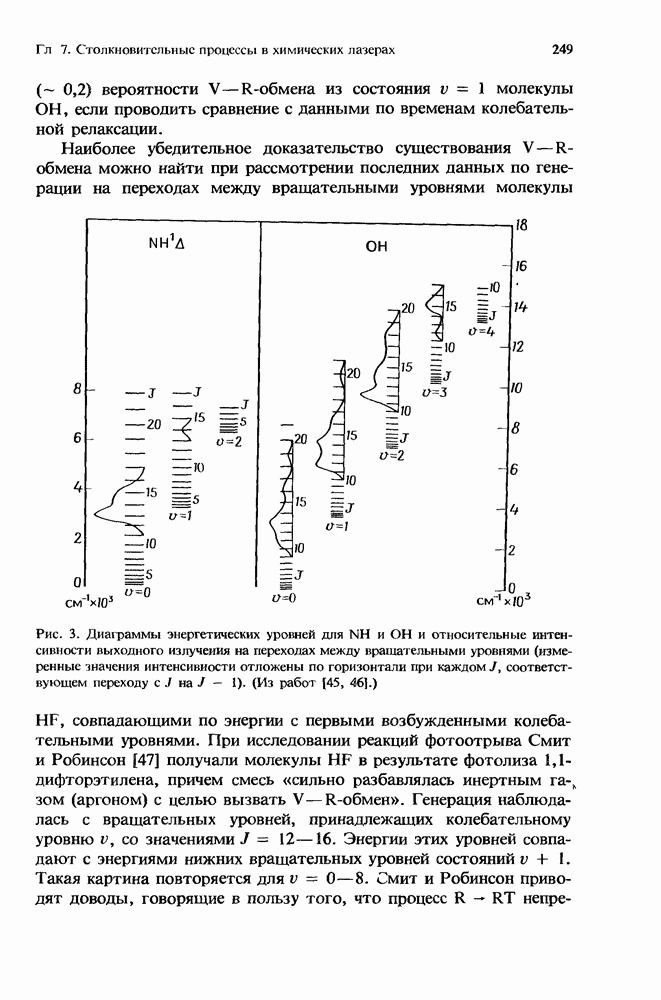
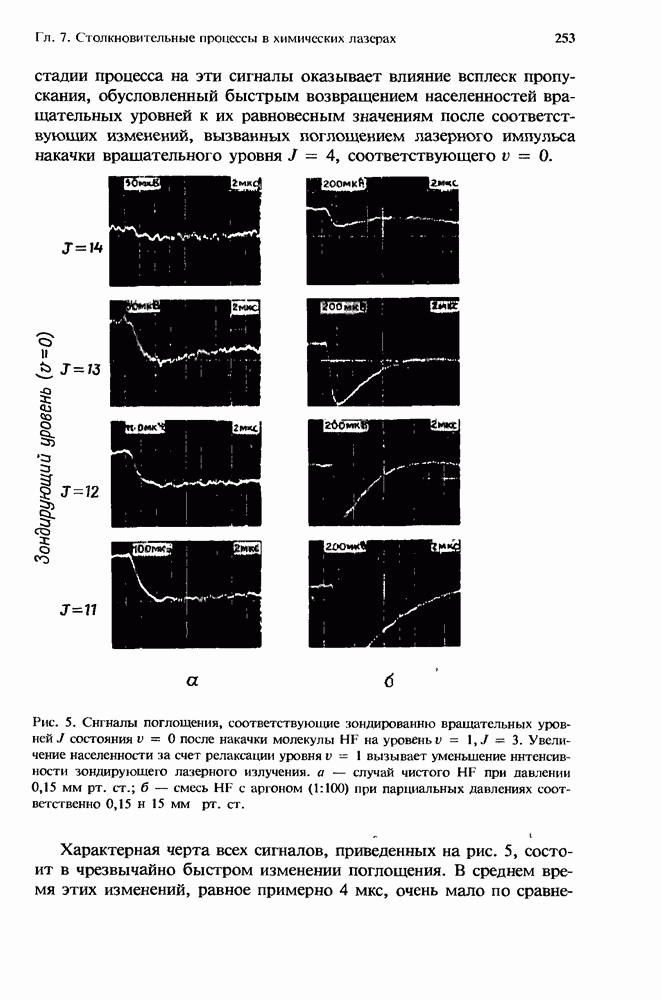
5. Ион-ионная рекомбинация в разрядах высокого давления
М. Р. Фланнери
5.1. Успехи современной теории
За последние несколько лет в теории процессов ион-ионной рекомбинации,

были выполнены важные фундаментальные разработки, которые представляют большой интерес. При этом изучалась зависимость реакции (1) не только от плотности буферного газа  но и от плотности ионов
но и от плотности ионов  рассматривалось также протекание этой реакции во времени. Экспериментальные исследования пока таких возможностей нам не дают. Полный обзор с подробным описанием состояния дел в исследованиях ион-ионной рекомбинации вплоть до
рассматривалось также протекание этой реакции во времени. Экспериментальные исследования пока таких возможностей нам не дают. Полный обзор с подробным описанием состояния дел в исследованиях ион-ионной рекомбинации вплоть до  представлен в работах [2, 20, 21, 40]. Поэтому здесь мы сконцентрируем внимание на основных результатах исследований, проведенных в последнее время.
представлен в работах [2, 20, 21, 40]. Поэтому здесь мы сконцентрируем внимание на основных результатах исследований, проведенных в последнее время.
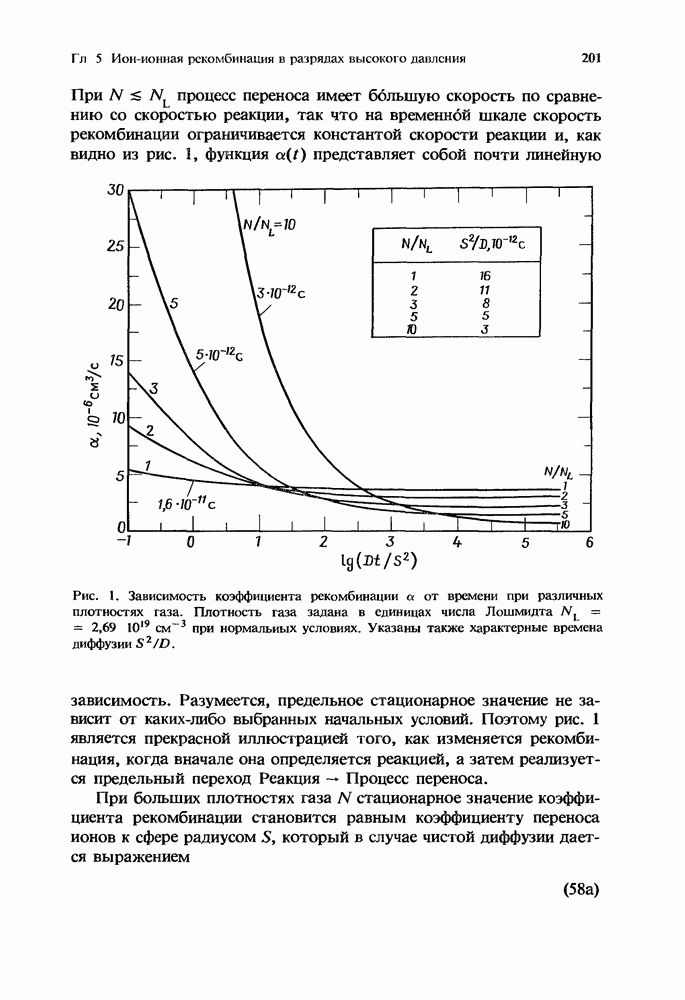
Современные теории рассматривают граничное значение коэффициента рекомбинации а при низких плотностях газа [11, 15, 24, 25, 34], а также то, как оно изменяется при переходе из этой линейной области, соответствующей трехчастичным процессам [47], в область нелинейной зависимости от плотности газа. При этом преследуется цель [12] — найти в конечном счете связь с областью Ланжевена — Харпера [4], которая соответствует высоким плотностям газа и в которой процесс рекомбинации определяется макроскопическими эффектами подвижности и диффузии.
Фундаментальные основы рассматриваемой теории и связь между поведением процессов рекомбинации при низких и высоких плотностях, базирующиеся полностью на микроскопических принципах, были построены лишь сравнительно недавно [29], поскольку ключевая теоретическая проблема является сложной и трудной, а различные феноменологические подходы затушевывают нередко роль серьезного теоретического рассмотрения. Из этой теории естественным образом следуют такие макроскопические эффекты, как отток частиц в процессе рекомбинации, подвижность и диффузия, причем они рассматриваются на языке соответствующих микроскопических процессов. Теория представляет коэффициент рекомбинации а как общую функцию плотности газа  плотности ионов
плотности ионов  и времени
и времени 
Далее, в работах [22, 31—33] был использован метод, являющийся существенной модификацией подхода Натансона [43], который с помощью обобщенного варианта метода Фукса [35], описывающего испарение капель воды в газовой среде, несколько прояснил вопрос о связи между рекомбинацией при низких и высоких плотностях газа  Все эти подходы, использующие понятие радиуса захвата при сильном столкновении, остаются феноменологическими, в духе тех методов, которые были развиты в пионерских работах Ланжевена [38], Харпера [36] и Томсона [47].
Все эти подходы, использующие понятие радиуса захвата при сильном столкновении, остаются феноменологическими, в духе тех методов, которые были развиты в пионерских работах Ланжевена [38], Харпера [36] и Томсона [47].
Весьма эффективным оказалось также применение в численных расчетах метода Монте-Карло [1, 6, 7, 14]. Однако этот метод, хотя и дает числовые значения а, не позволяет получить ясную теоретическую интерпретацию основных рассматриваемых вопросов. Тем не менее Бейтс и Мендаш [14] в своих расчетах методом Монте-Карло обнаружили эффект ускорения взаимной нейтрализации  при возрастании плотности газа
при возрастании плотности газа  Этот важный эффект получил впоследствии теоретическое объяснение в работе Бейтса [5]. Файбелмэн [19] ранее применил метод Монте-Карло с целью вычисления граничного значения а, соответствующего низким плотностям, однако его критерий получения стабильной молекулы в процессе рекомбинации основывался не на представлении о столкновительной дезактивации ионной пары на уровень, расположенный ниже некоторого определенного уровня с отрицательным значением энергии, а на представлении об определенном числе
Этот важный эффект получил впоследствии теоретическое объяснение в работе Бейтса [5]. Файбелмэн [19] ранее применил метод Монте-Карло с целью вычисления граничного значения а, соответствующего низким плотностям, однако его критерий получения стабильной молекулы в процессе рекомбинации основывался не на представлении о столкновительной дезактивации ионной пары на уровень, расположенный ниже некоторого определенного уровня с отрицательным значением энергии, а на представлении об определенном числе  актов столкновений иона с нейтралами.
актов столкновений иона с нейтралами.
Важный результат был получен Бейтсом [6—8], который из соображений размерности сделал вывод о существовании универсальной зависимости для коэффициента рекомбинации а, справедливой при любых газовых температурах, любых сочетаниях масс и
констант взаимодействия для любой рекомбинирующей системы. Эта зависимость была подтверждена расчетами, выполненными Бейтсом с использованием метода Монте-Карло.
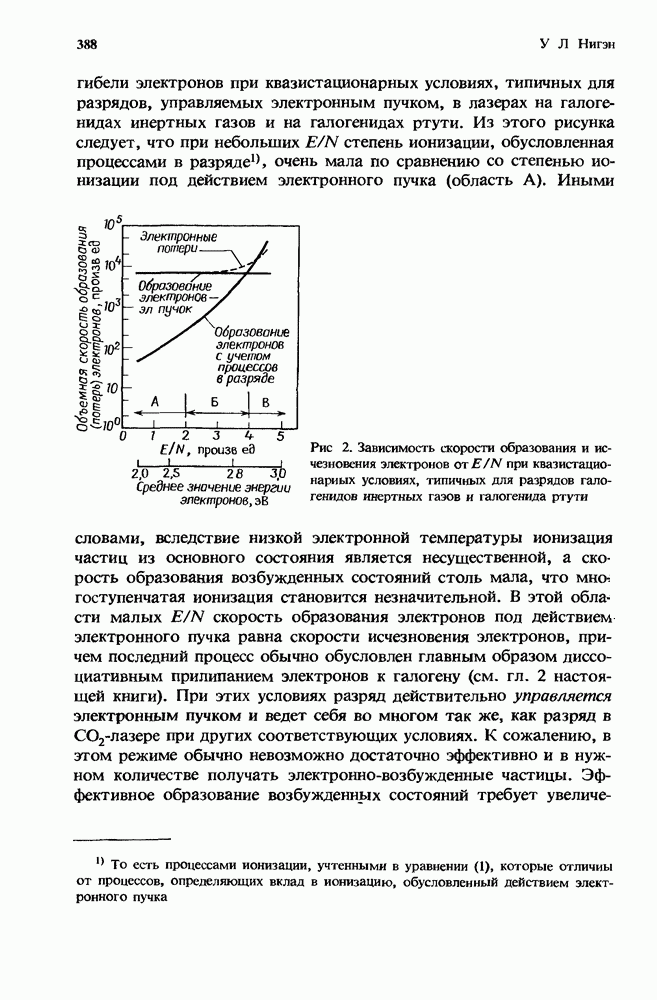
Активные действия в данной области в последнее время стимулировались главным образом классической природой рассматриваемой проблемы и до некоторой степени той главной ролью (см. [23] и гл. 3 и 10), которую ион-ионная рекомбинация играет в процессе заселения верхних молекулярных состояний в лазерах на галогенидах инертных газов, которые работают не только при высоких давлениях газа  атм), но также при умеренно высоких плотностях ионов
атм), но также при умеренно высоких плотностях ионов  Поскольку ионный состав меняется с ростом плотности газа
Поскольку ионный состав меняется с ростом плотности газа  то проведение соответствующих надежных лабораторных экспериментов даже при низких плотностях ионов
то проведение соответствующих надежных лабораторных экспериментов даже при низких плотностях ионов  и при высоких
и при высоких  является трудной задачей. За исключением общей фундаментальной теории, основанной на микроскопических принципах [29], все предшествующие теоретические рассмотрения и любые доступные экспериментальные результаты (см. разд. 5.4) неявно относятся к случаю, когда ионная компонента считается разбавленной
является трудной задачей. За исключением общей фундаментальной теории, основанной на микроскопических принципах [29], все предшествующие теоретические рассмотрения и любые доступные экспериментальные результаты (см. разд. 5.4) неявно относятся к случаю, когда ионная компонента считается разбавленной  см 3). Развитая в работе [29] теория раскрывает, каким образом потенциал ион-ионного взаимодействия
см 3). Развитая в работе [29] теория раскрывает, каким образом потенциал ион-ионного взаимодействия  который больше нельзя полагать ab initio чисто кулоновским, определяется через уравнение Пуассона плотностью числа ионов, связанной в свою очередь непосредственно и через V как с кинетикой рекомбинационного оттока частиц (сжимаемая часть), так и с токовыми членами, описывающими эффекты диффузии и подвижности (несжимаемая часть). При этом коэффициент рекомбинации а, являющийся функцией от
который больше нельзя полагать ab initio чисто кулоновским, определяется через уравнение Пуассона плотностью числа ионов, связанной в свою очередь непосредственно и через V как с кинетикой рекомбинационного оттока частиц (сжимаемая часть), так и с токовыми членами, описывающими эффекты диффузии и подвижности (несжимаемая часть). При этом коэффициент рекомбинации а, являющийся функцией от  и
и  определяется плотностями в самосогласованном фазовом пространстве (которые определяют соответствующее V) и скоростями элементарных столкновительных процессов обмена энергией в ионной паре.
определяется плотностями в самосогласованном фазовом пространстве (которые определяют соответствующее V) и скоростями элементарных столкновительных процессов обмена энергией в ионной паре.
Бейтс [9] доказал, что прямое использование Морганом и др. [42] потенциала взаимодействия Дебая — Хюккеля является ошибочным и что полученное Ланжевеном (разд. 5.2) выражение дает правильный результат при высоких значениях  для любых
для любых  Взаимодействие Дебая — Хюккеля допускает учет плазменной экранировки только в равновесных условиях, как в случае предельно низкой плотности
Взаимодействие Дебая — Хюккеля допускает учет плазменной экранировки только в равновесных условиях, как в случае предельно низкой плотности  (см. [26, 29], а также разд. 5.3), и, разумеется, при условии
(см. [26, 29], а также разд. 5.3), и, разумеется, при условии  При больших
При больших  использование потенциала взаимодействия, самосогласованного с плотностью, дает правильные результаты (разд. 5.3).
использование потенциала взаимодействия, самосогласованного с плотностью, дает правильные результаты (разд. 5.3).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
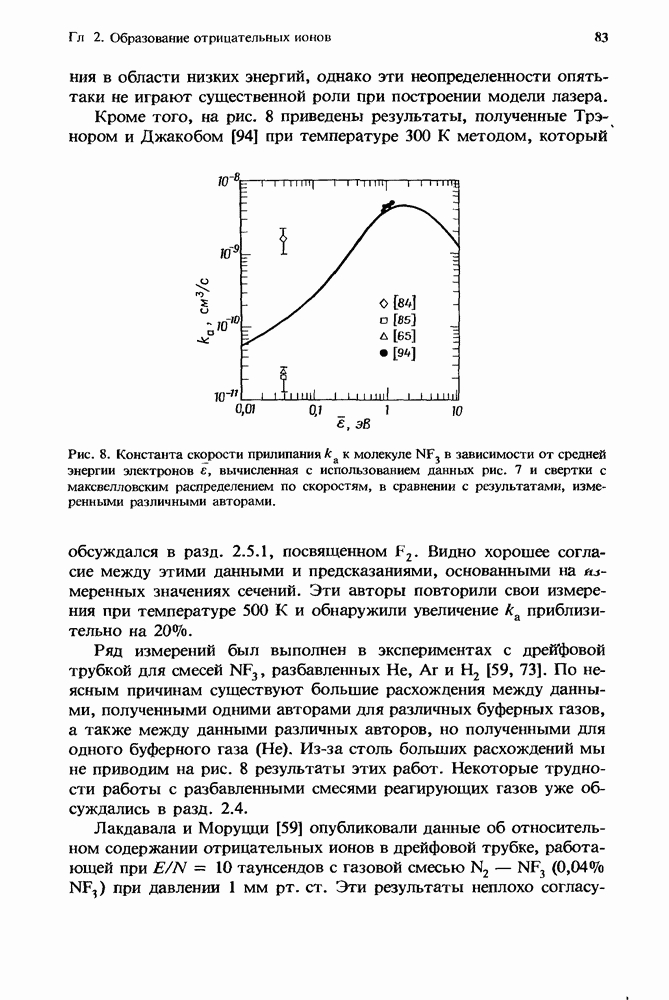
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
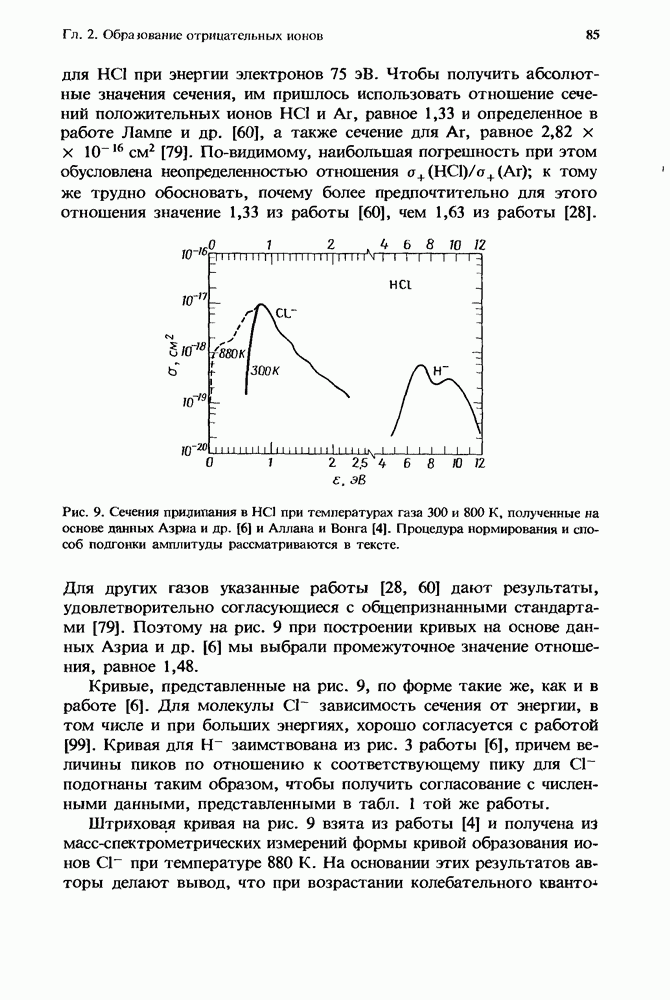
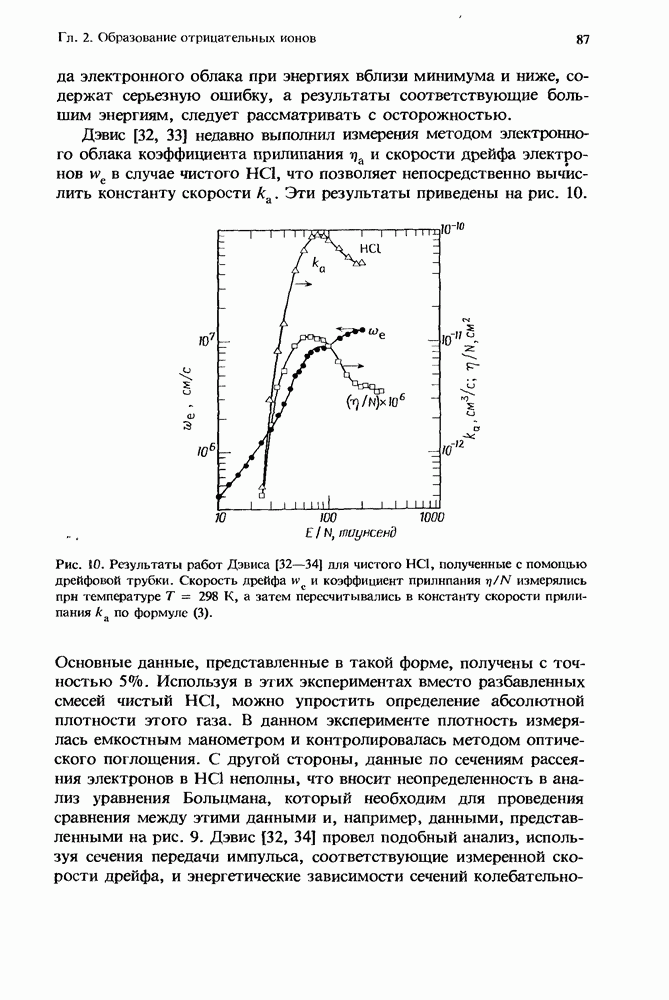
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
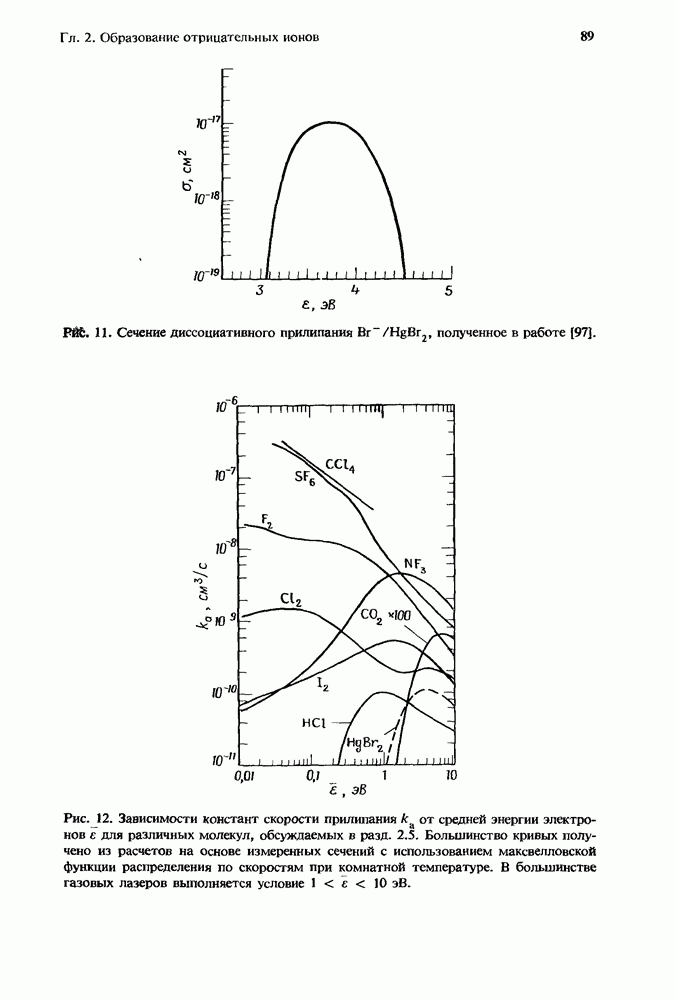
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
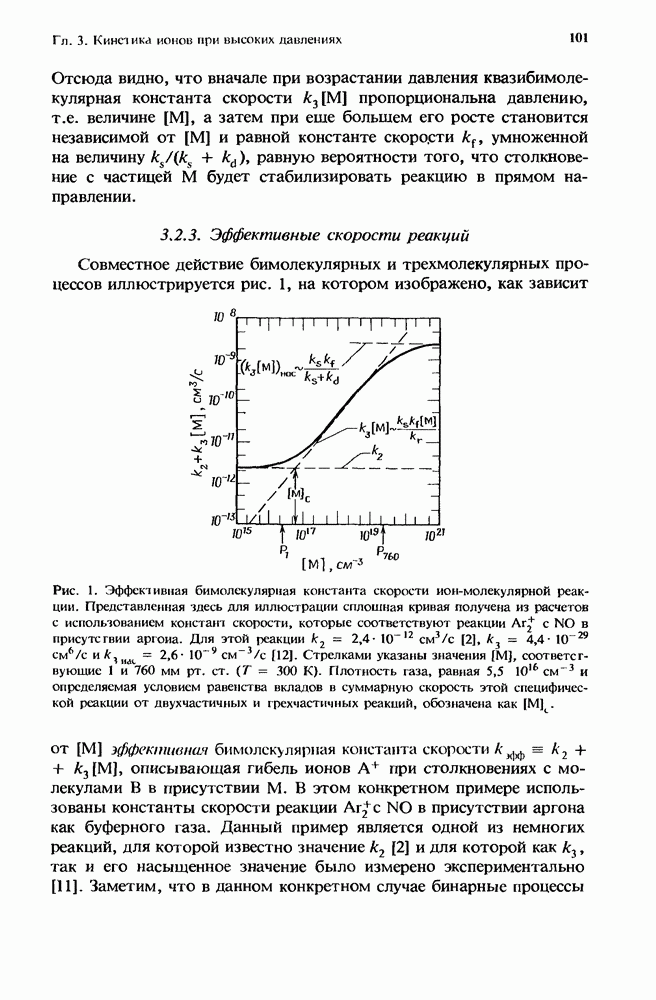
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
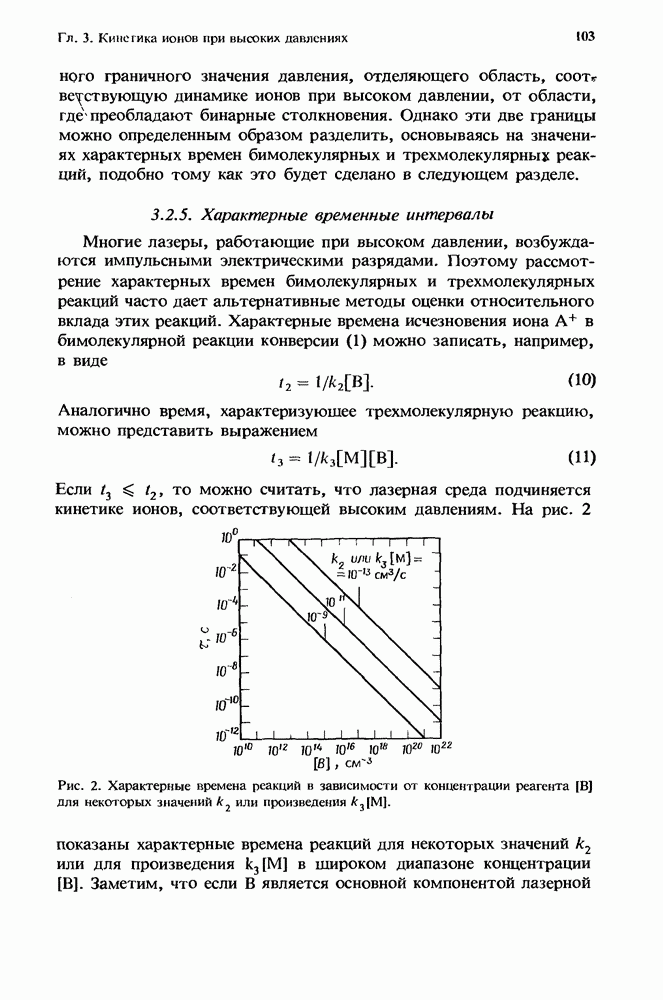
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
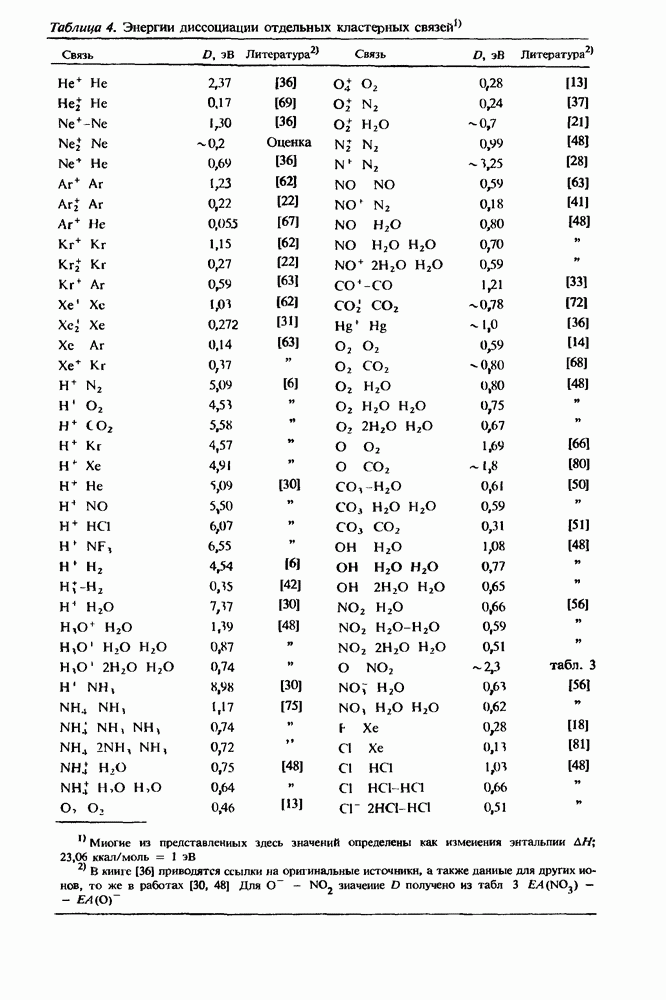
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
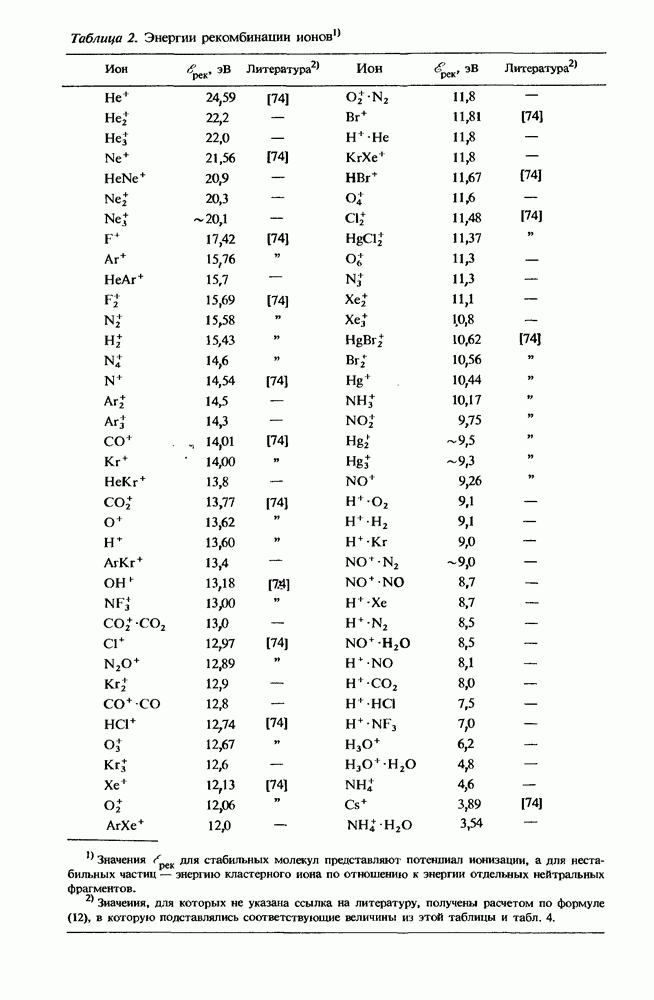
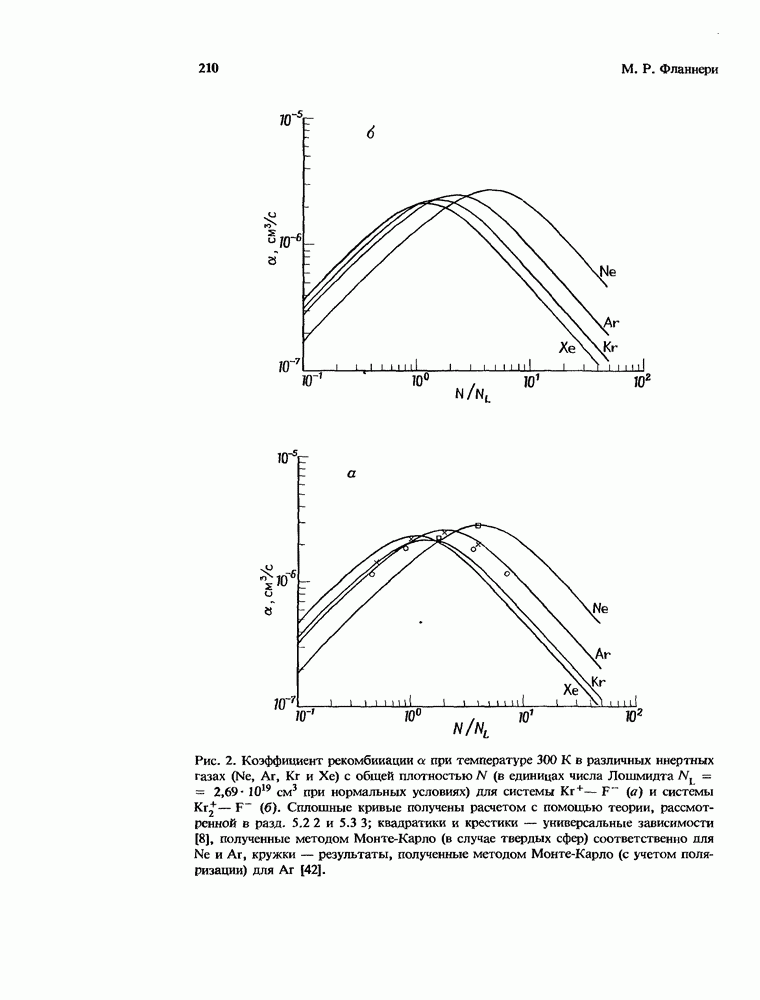
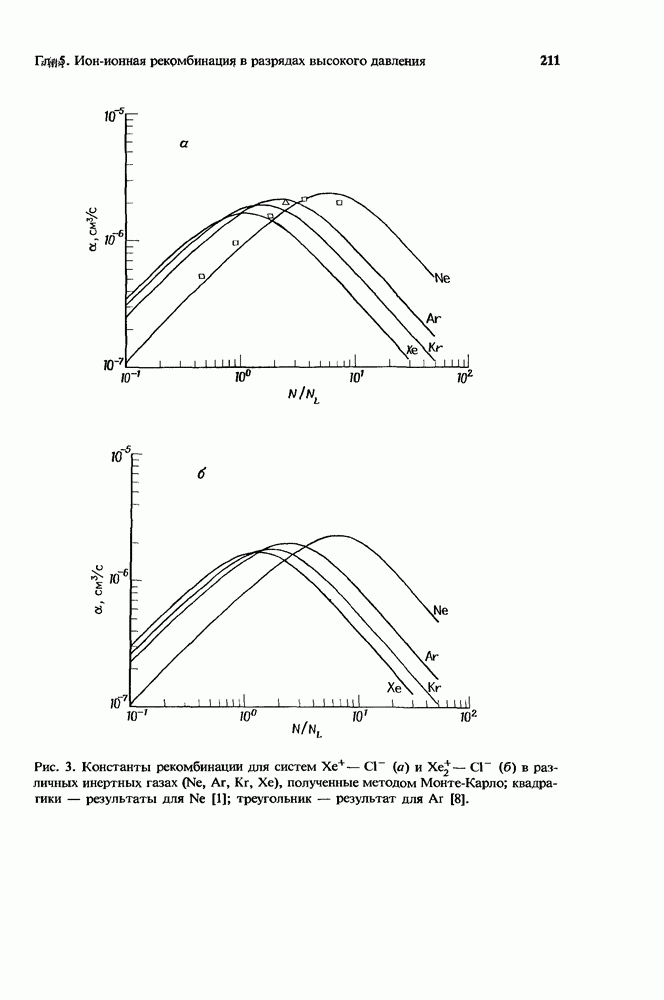
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
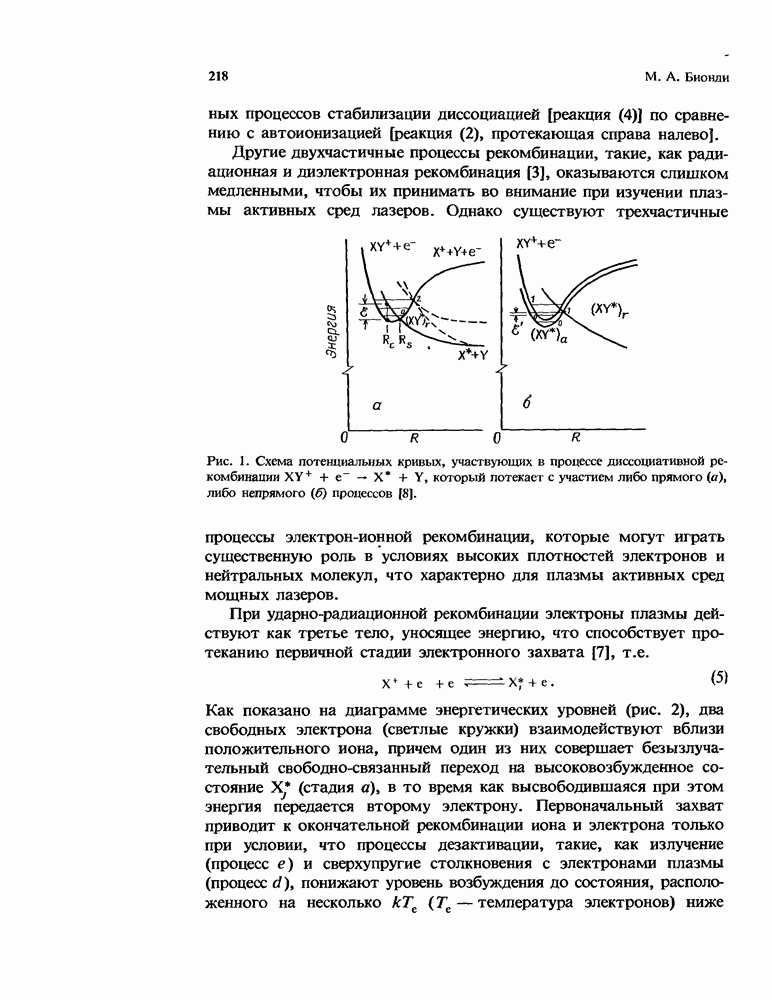
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
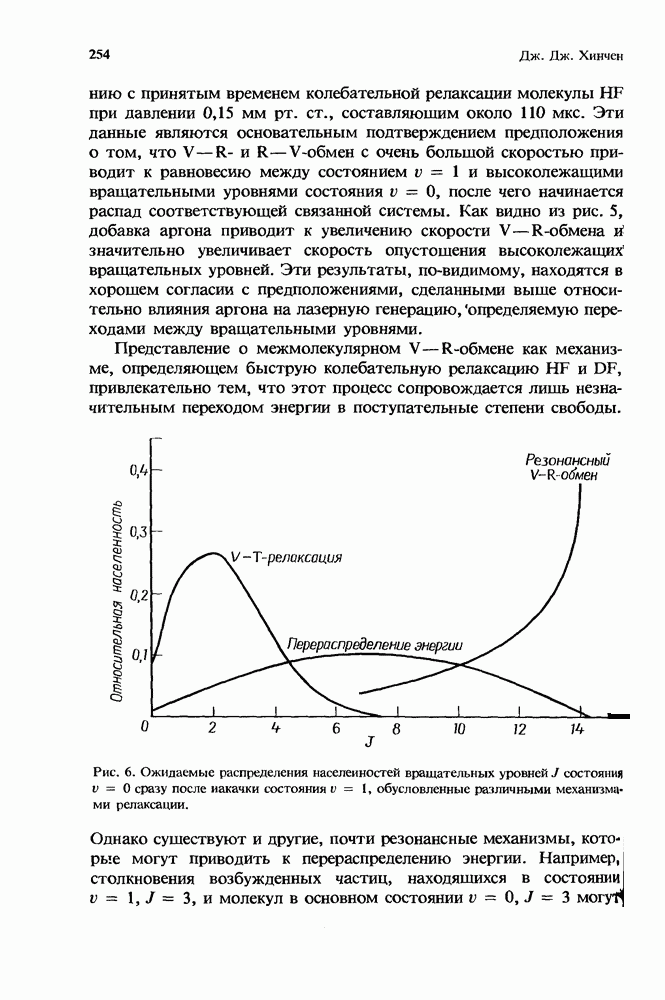
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
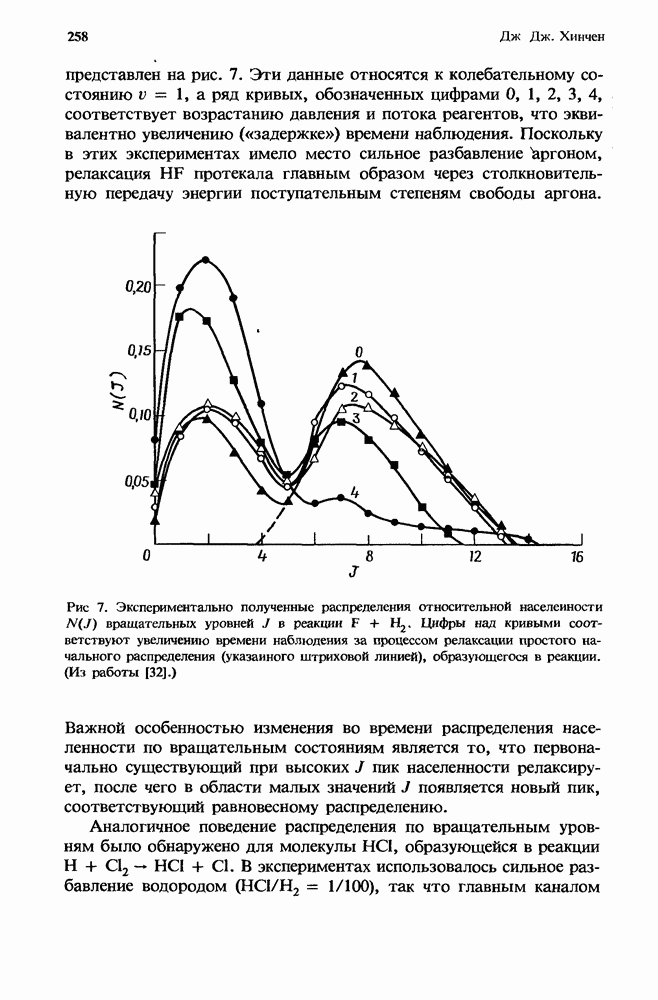
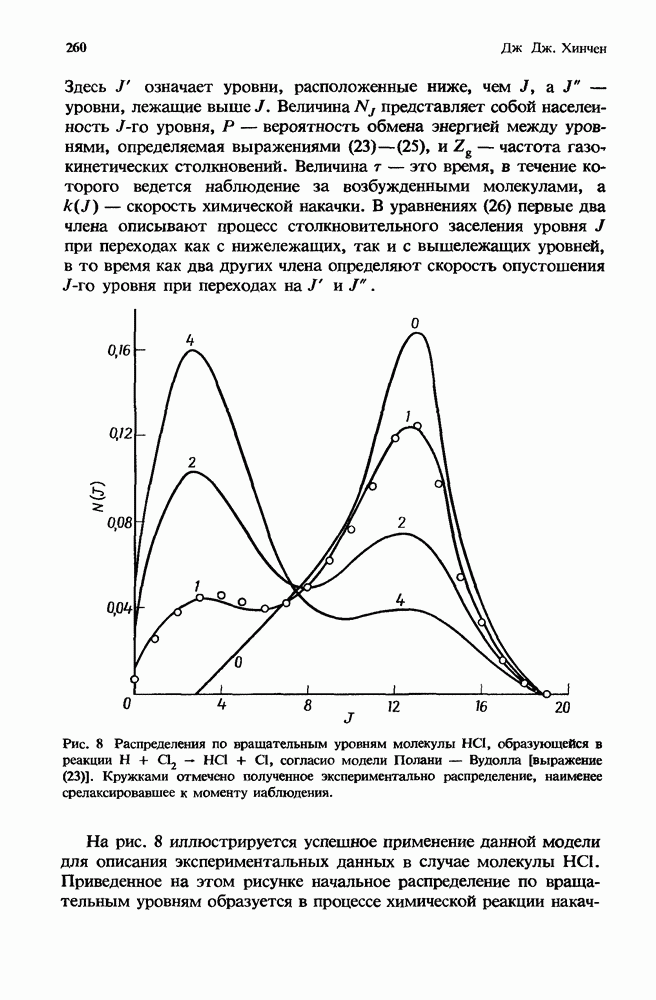
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
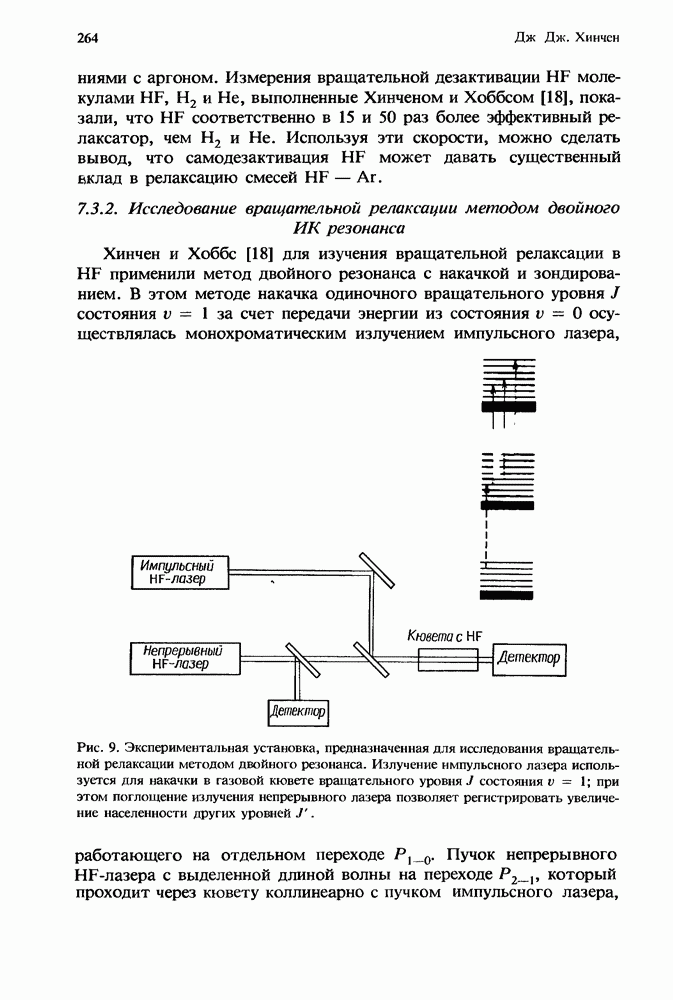
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
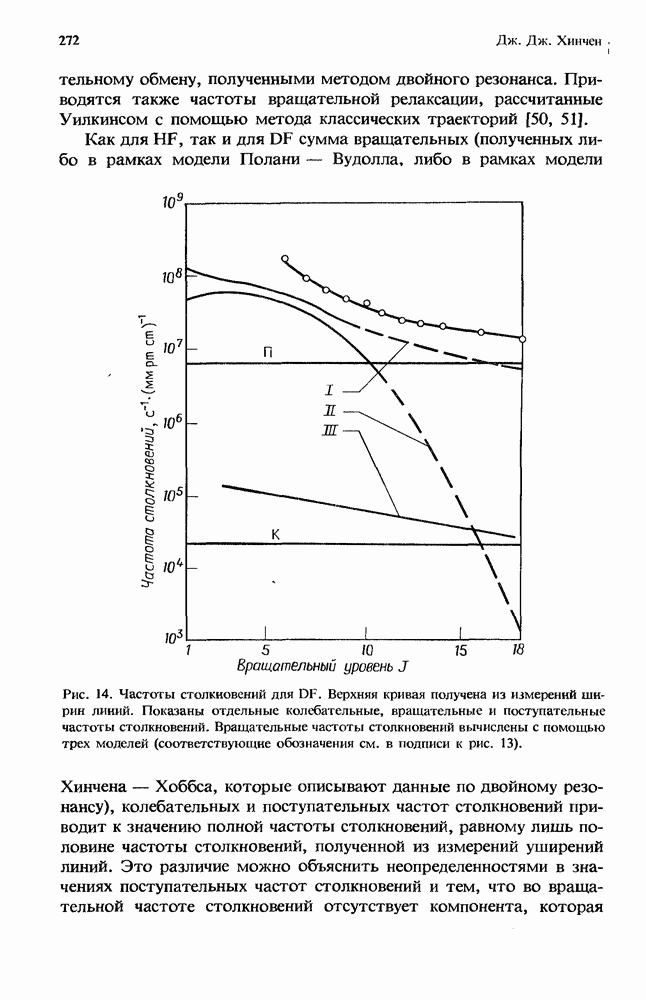
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
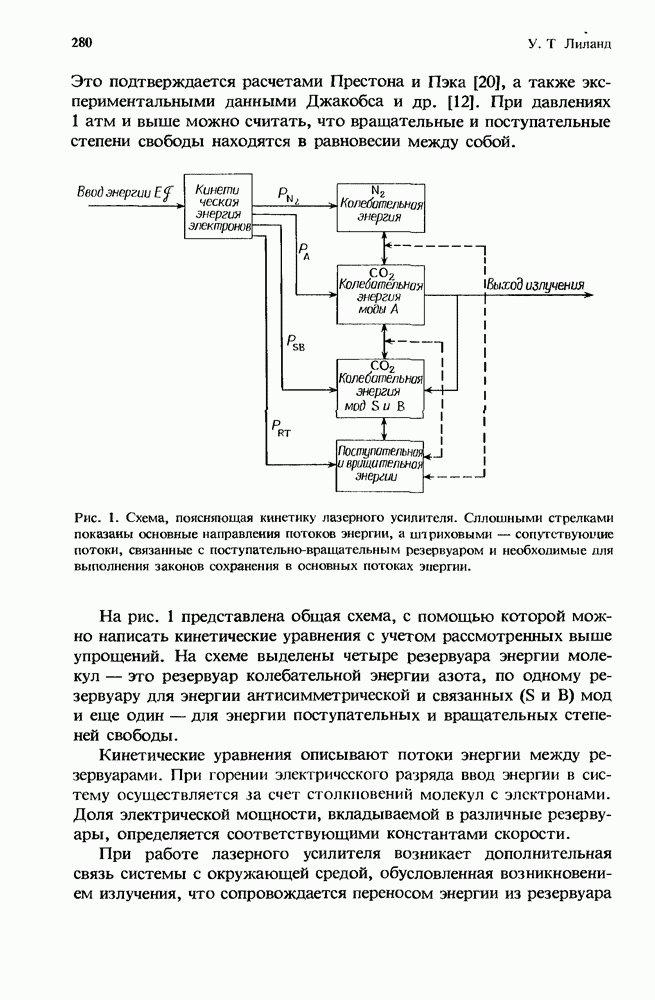
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
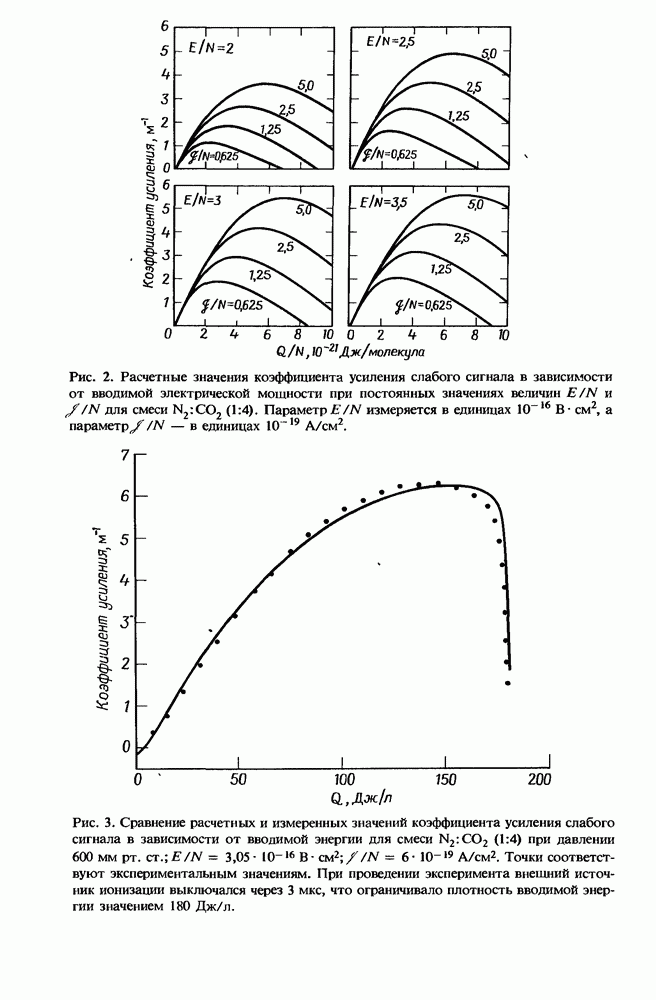
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
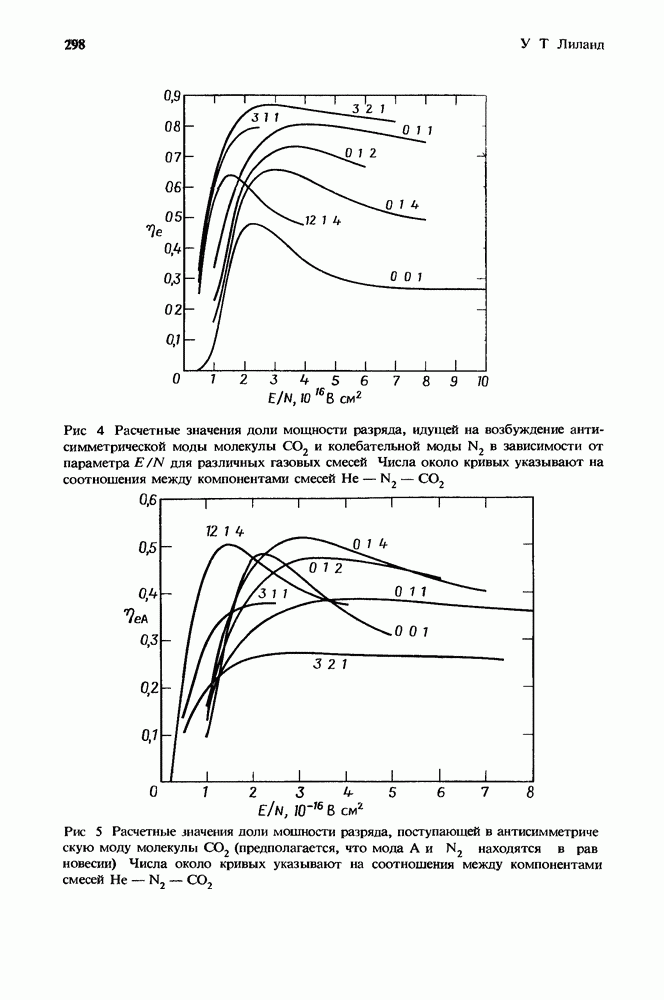
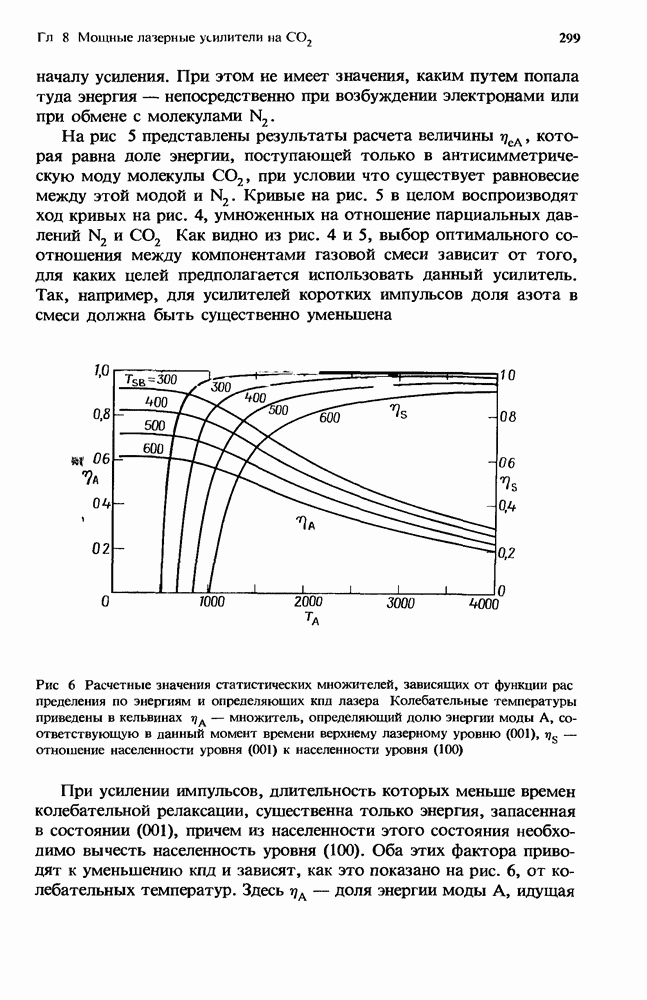
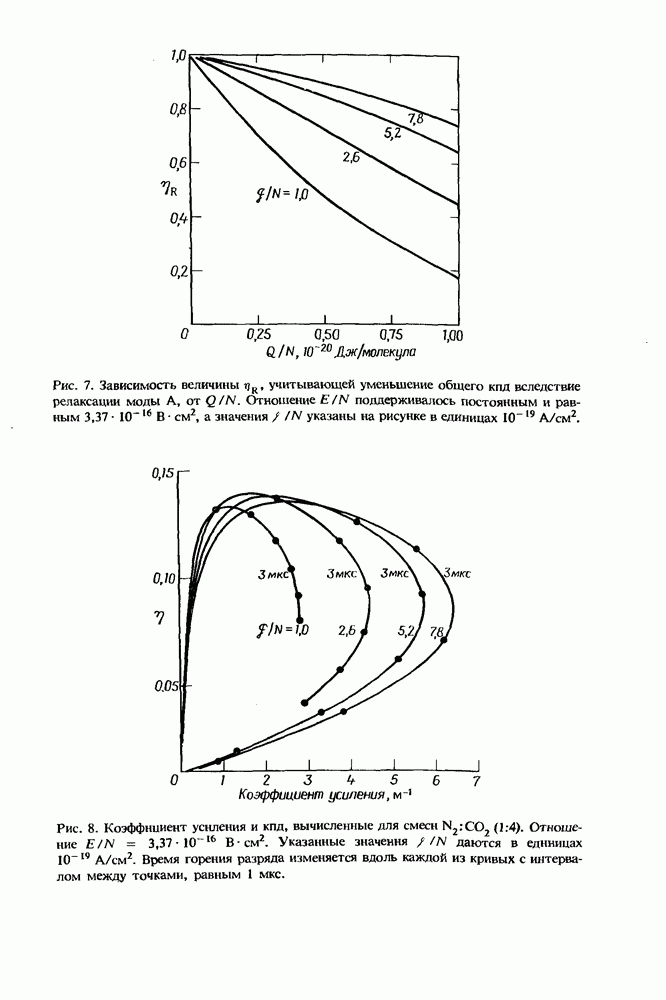
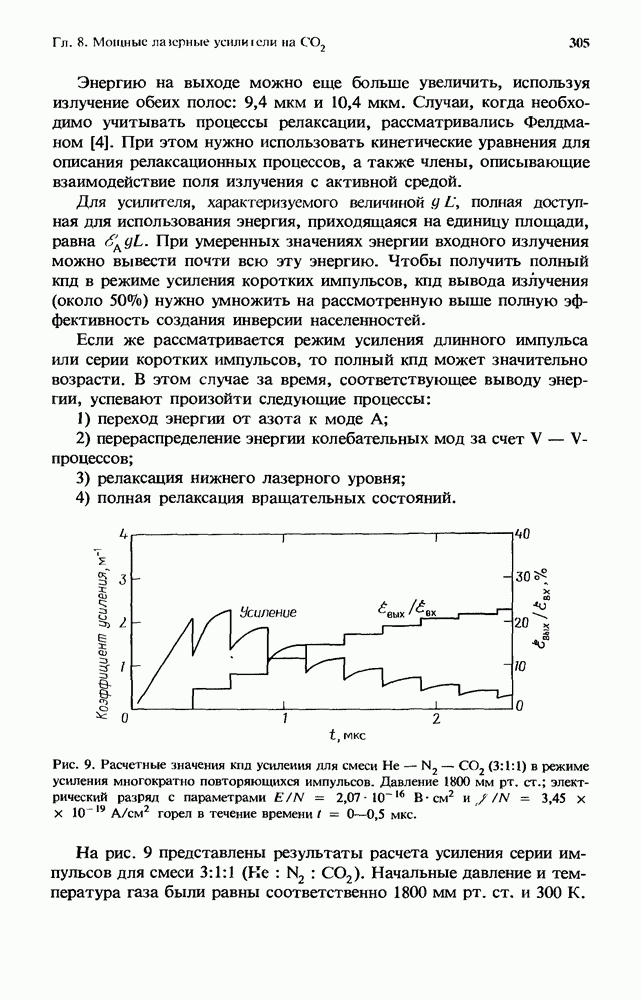
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
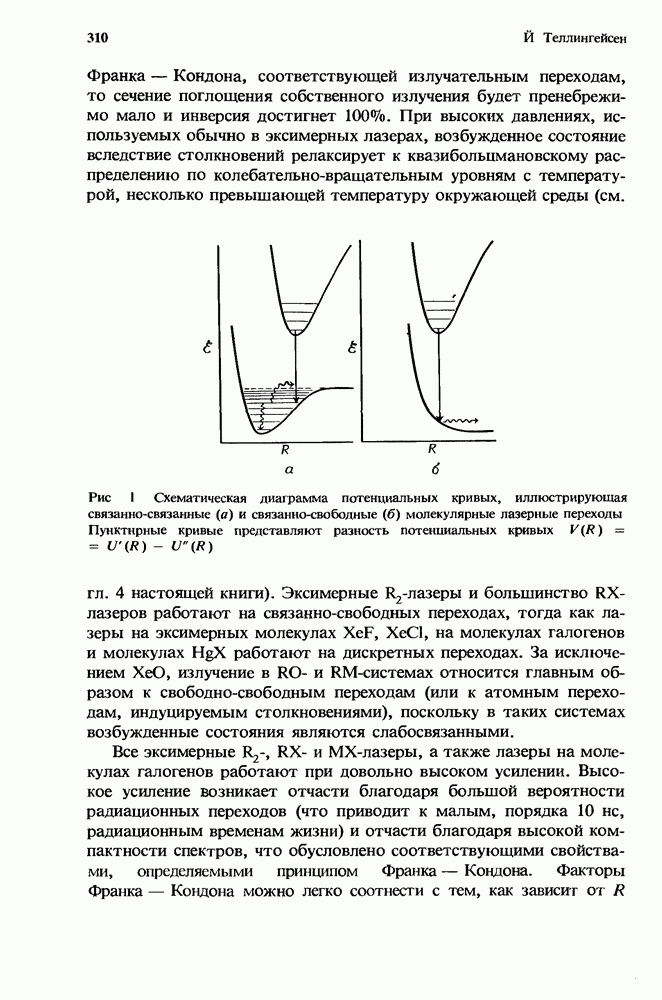
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
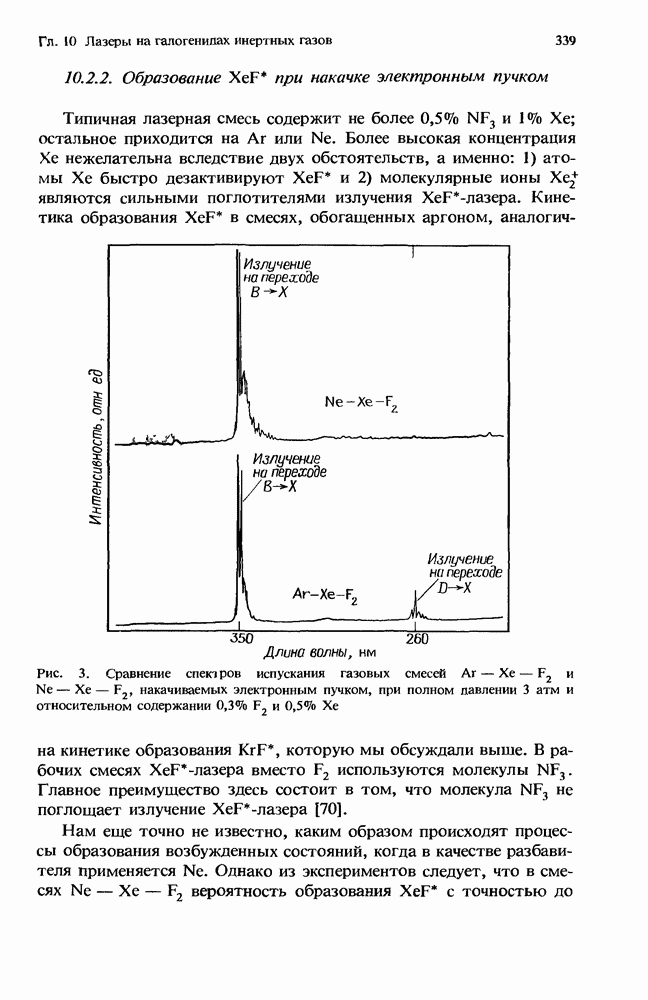
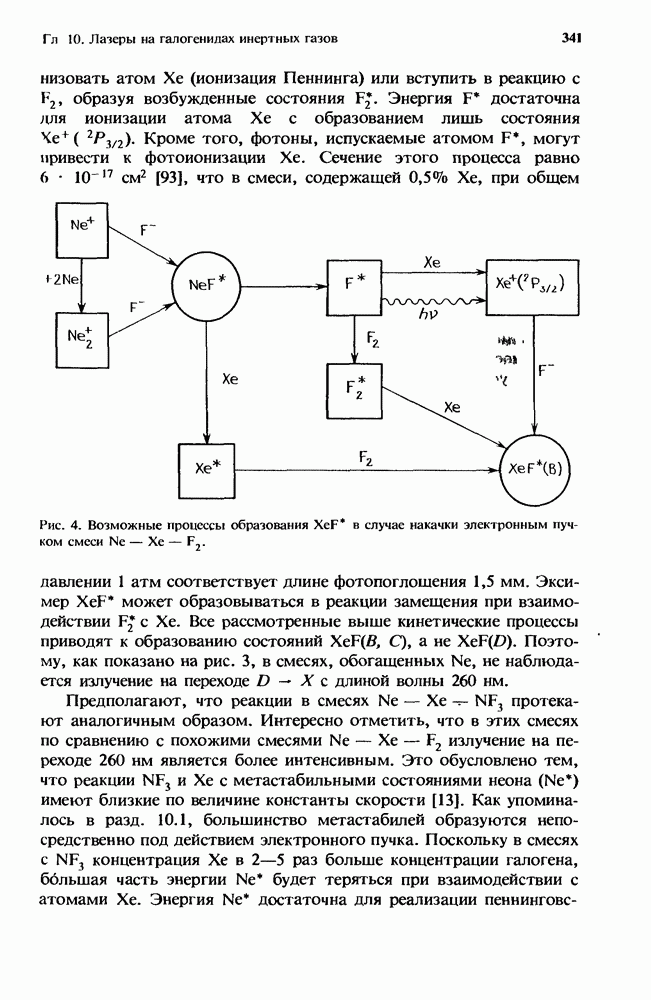
- 10.2. Кинетика образования верхнего лазерного уровня
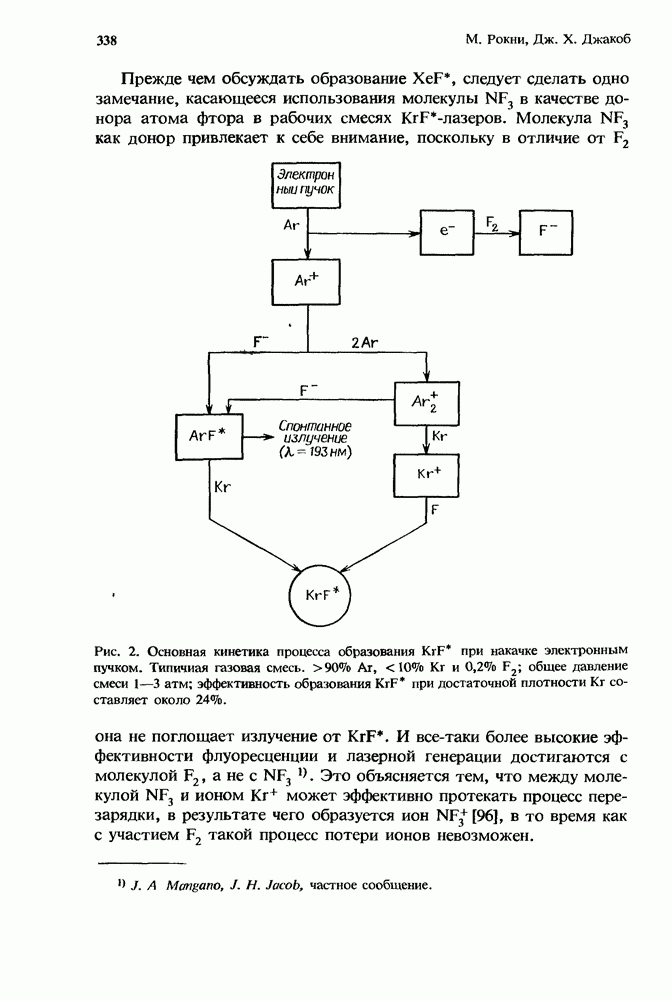
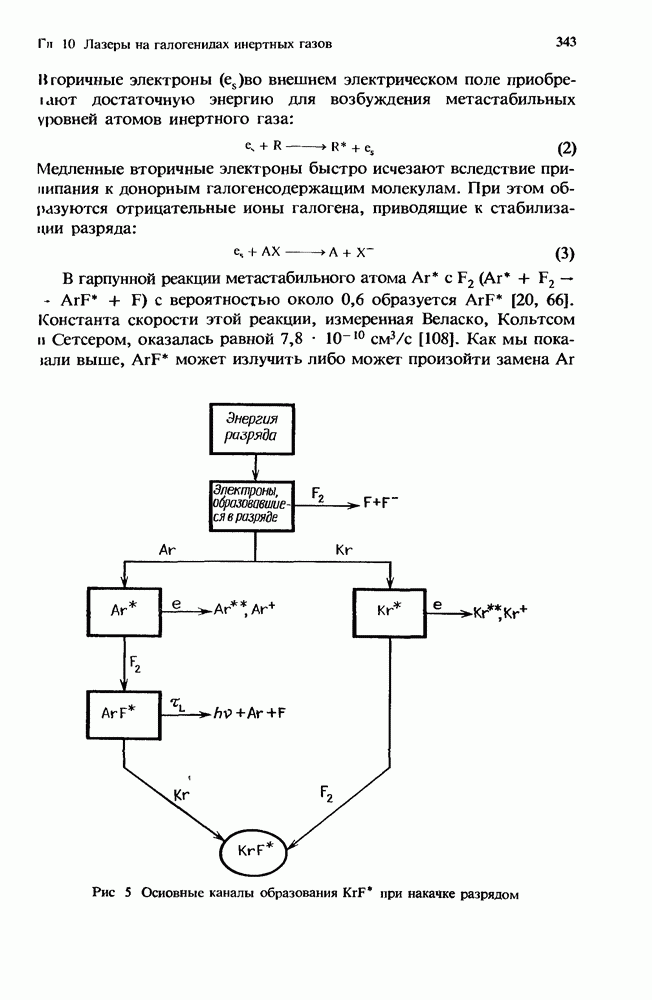
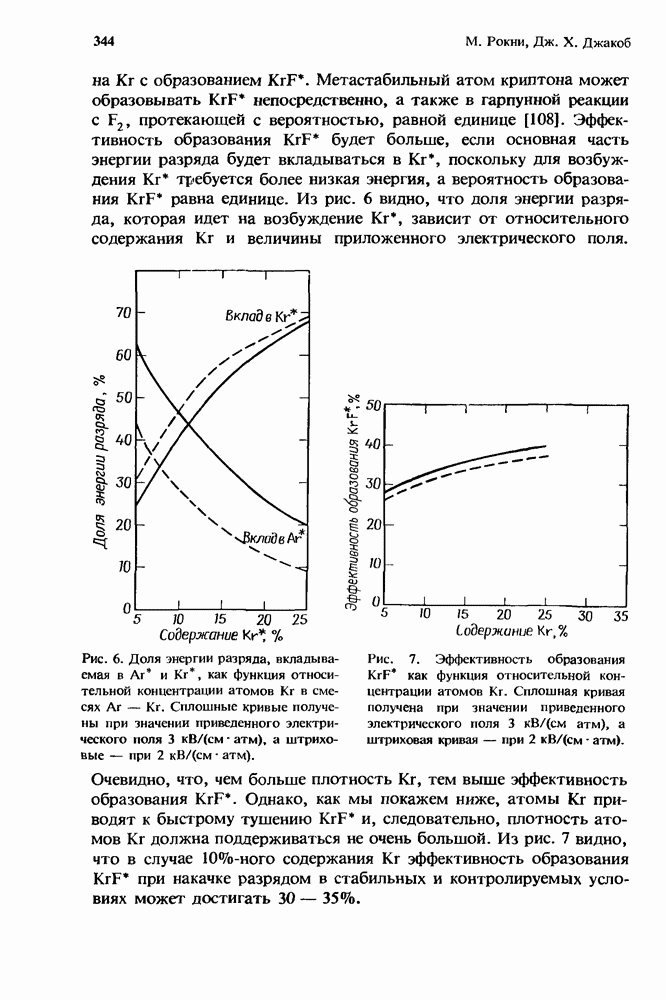
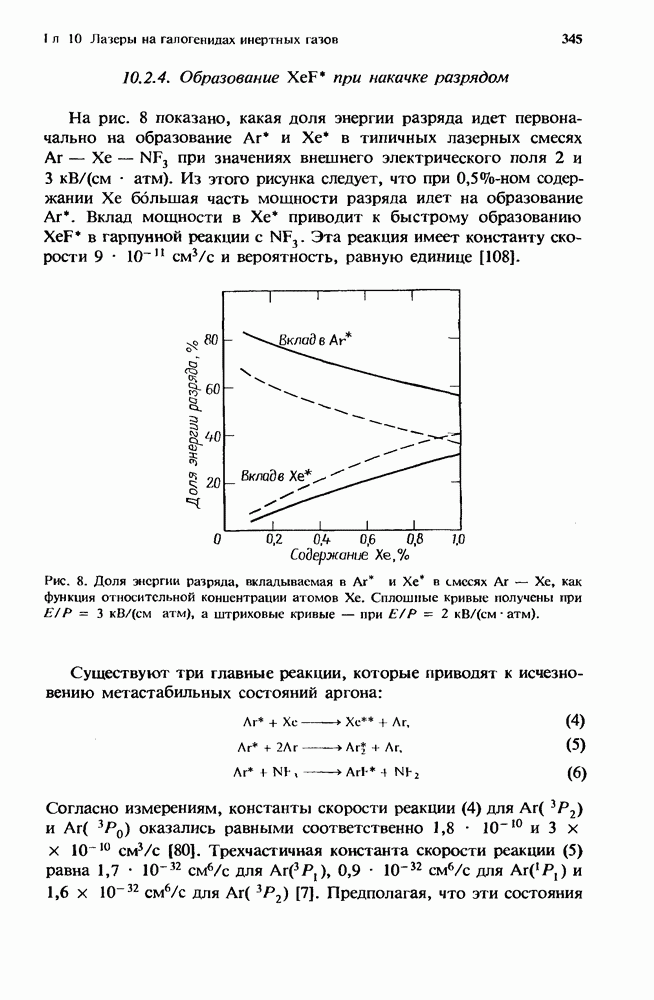
- 10.2.3. Образование KrF* в разряде
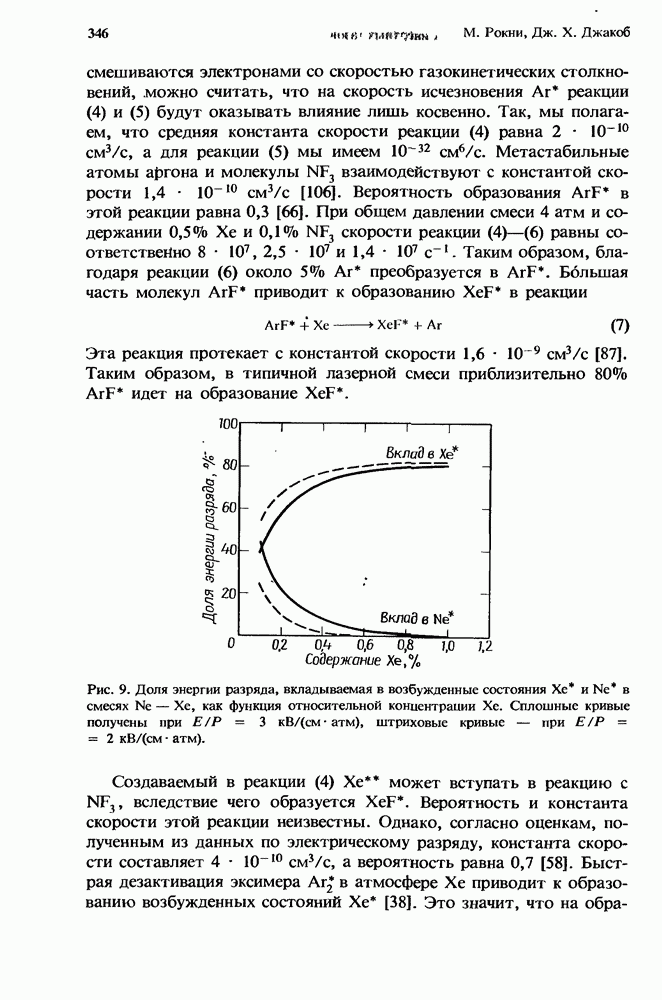
- 10.2.4. Образование XeF* при накачке разрядом
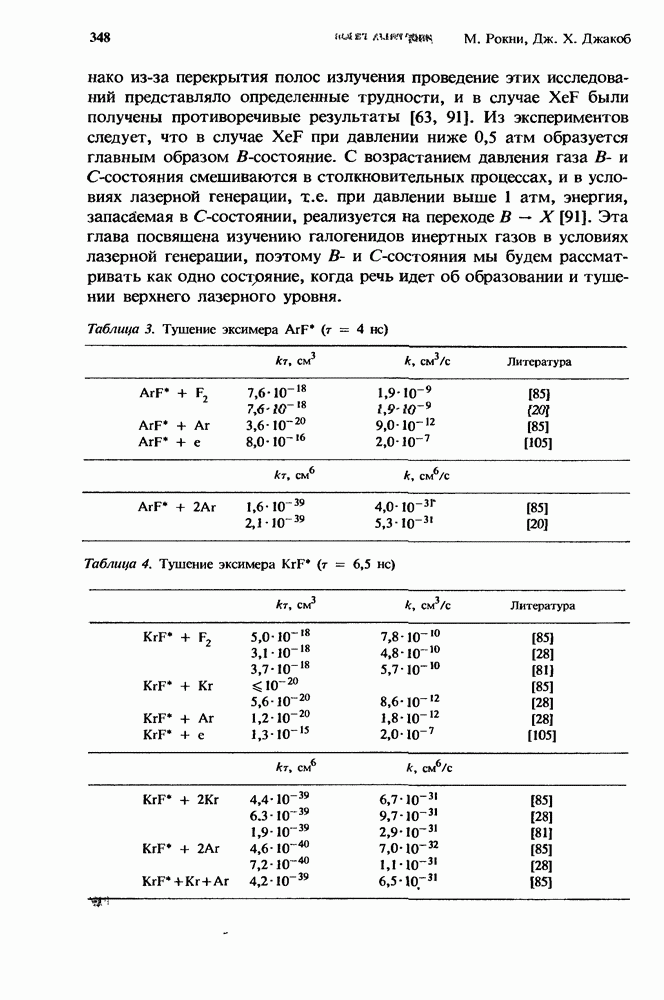
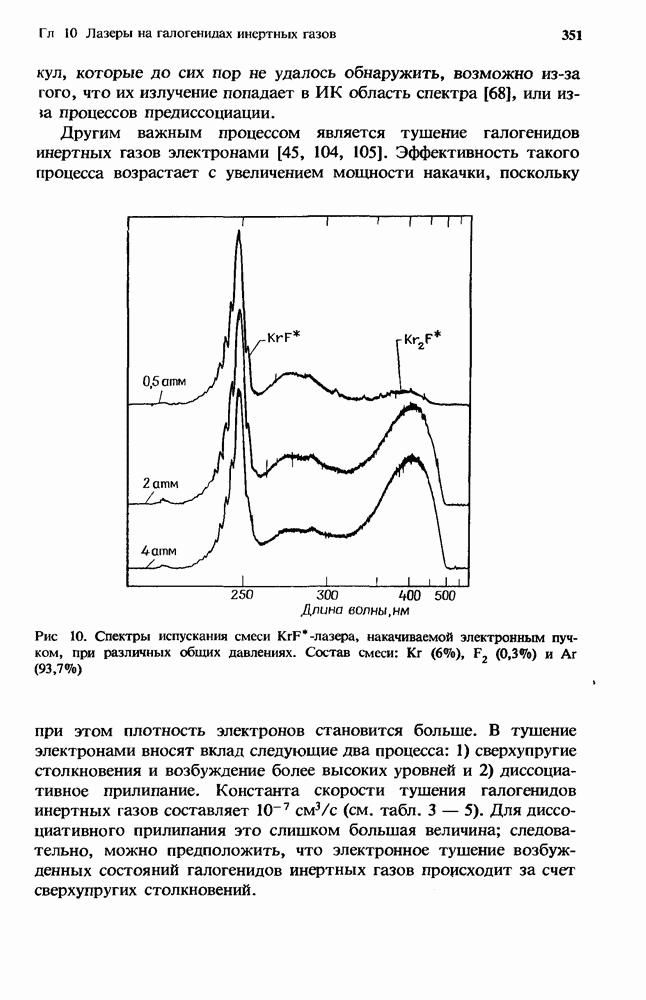
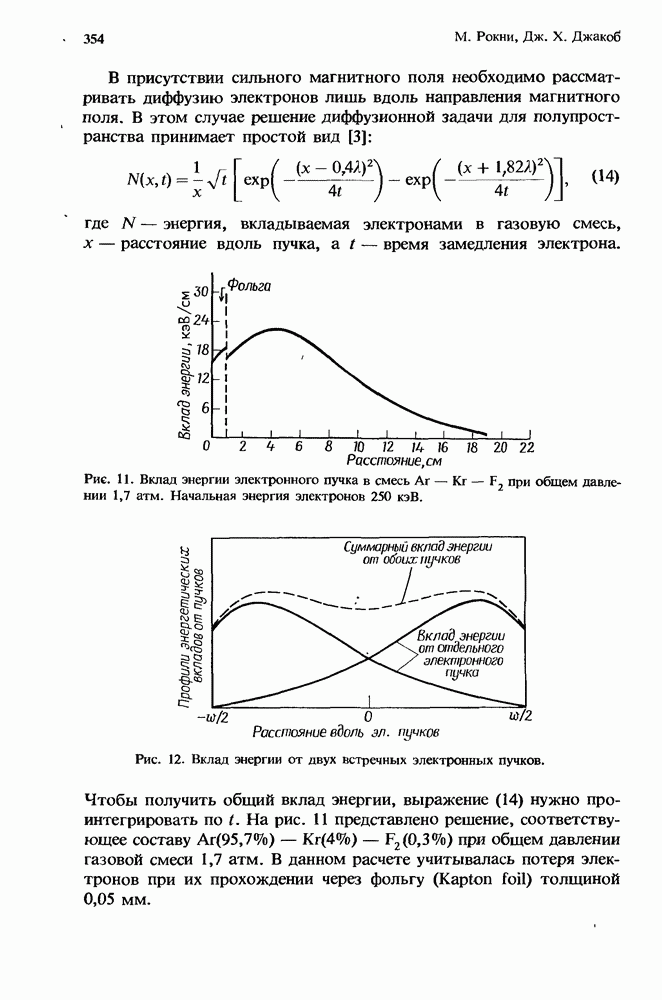
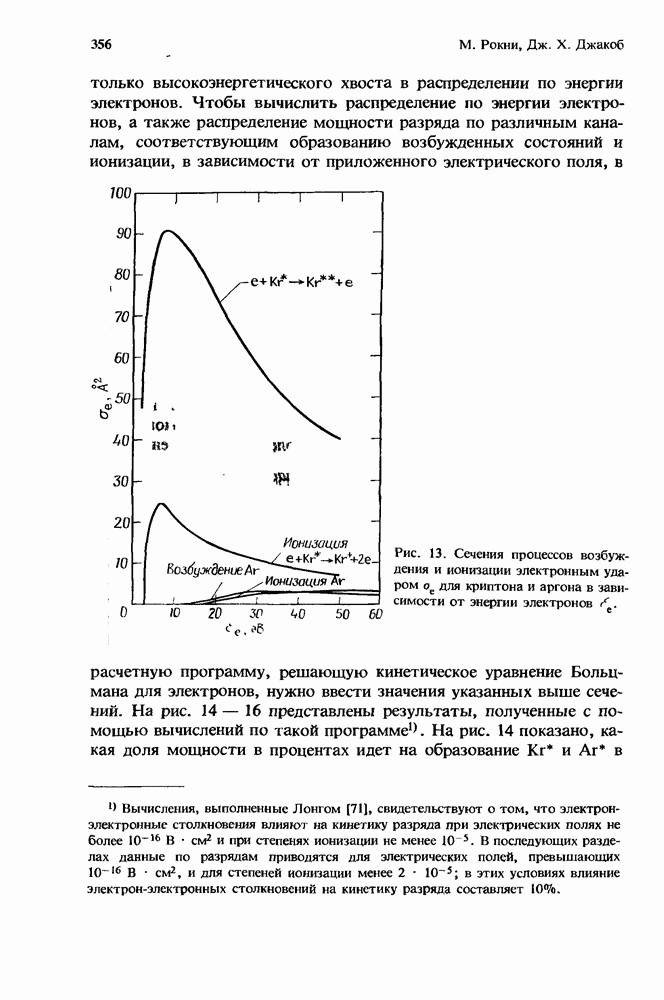
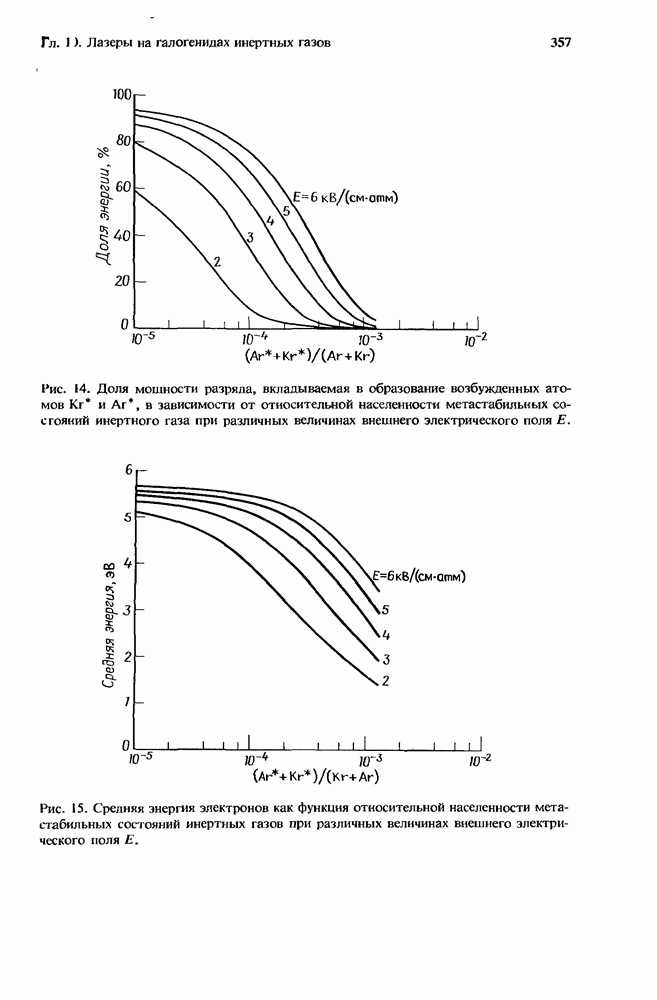
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
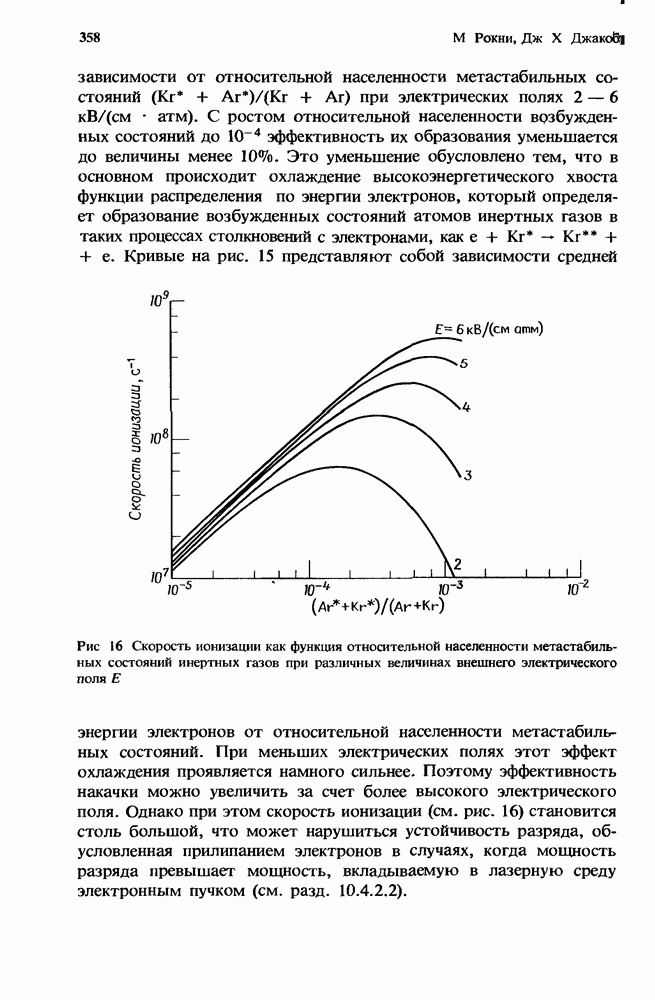
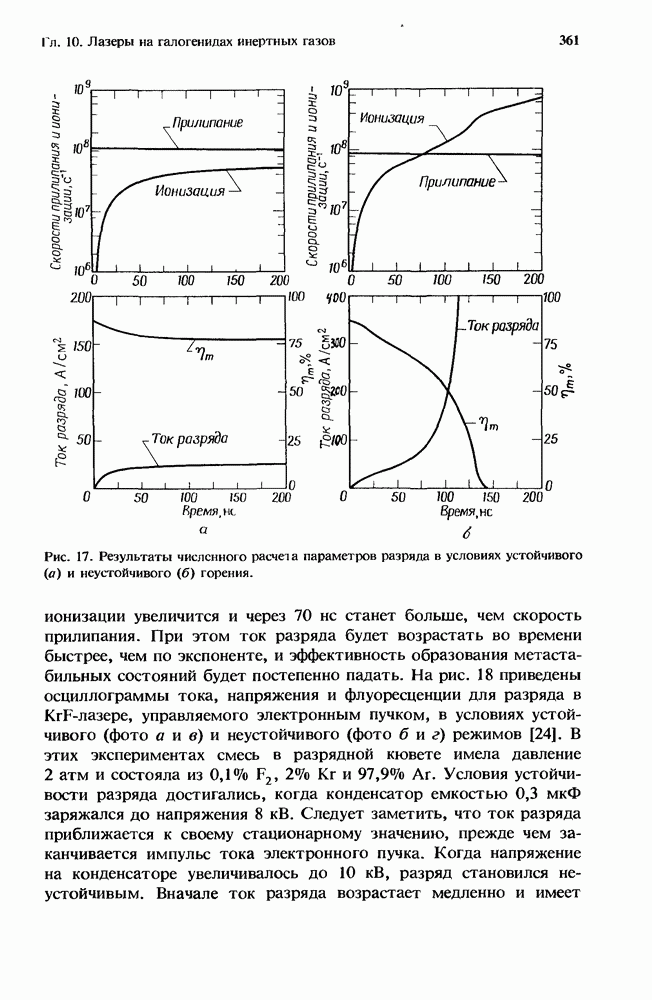
- 10.4.2.2. Устойчивость разряда
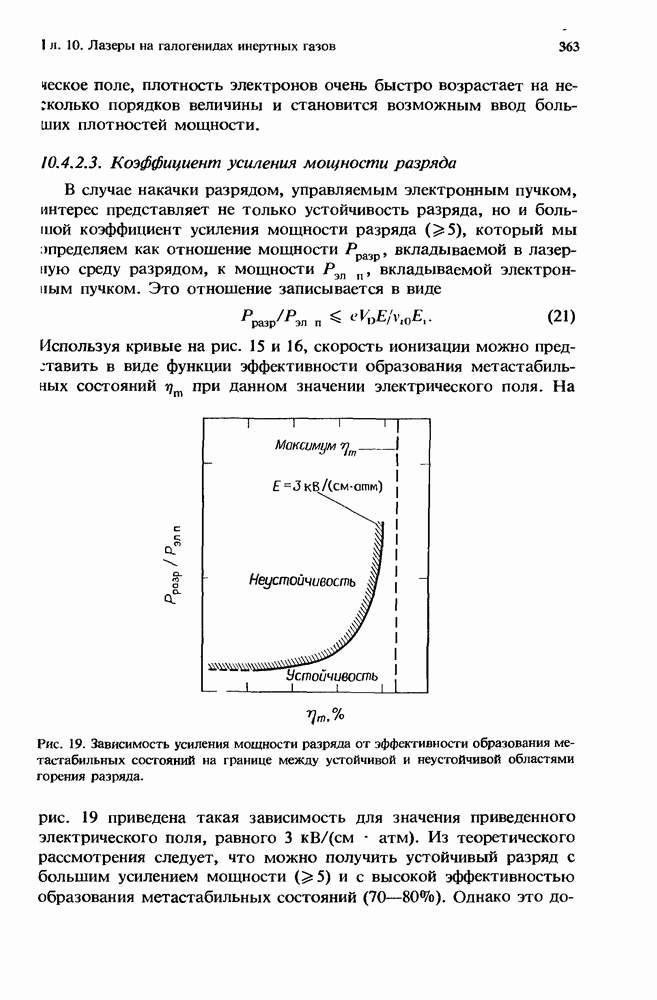
- 10.4.2.3. Коэффициент усиления мощности разряда
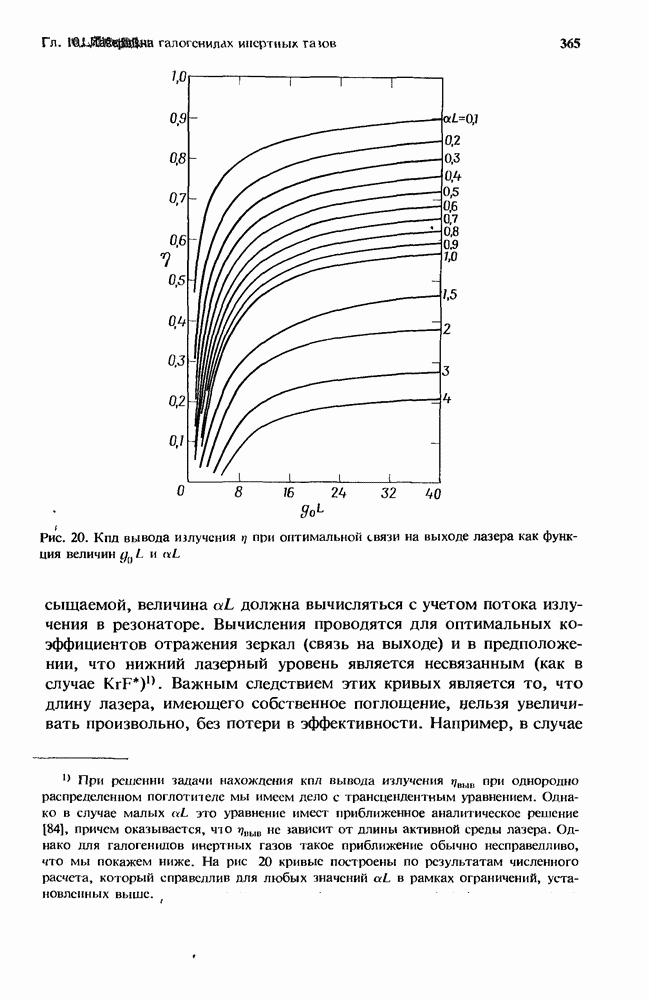
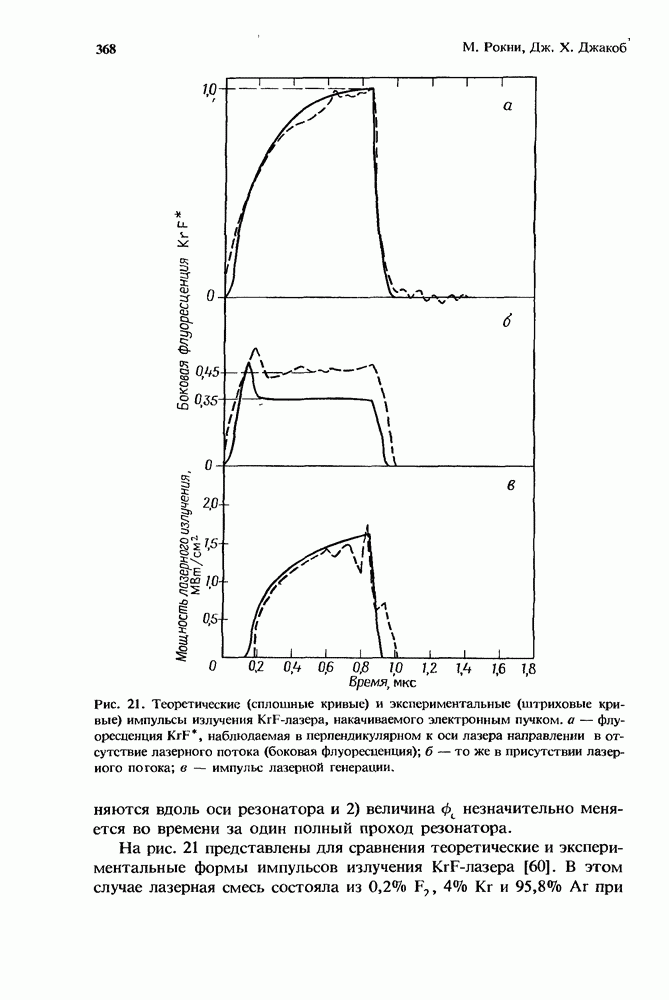
- 10. 5. Вывод мощности
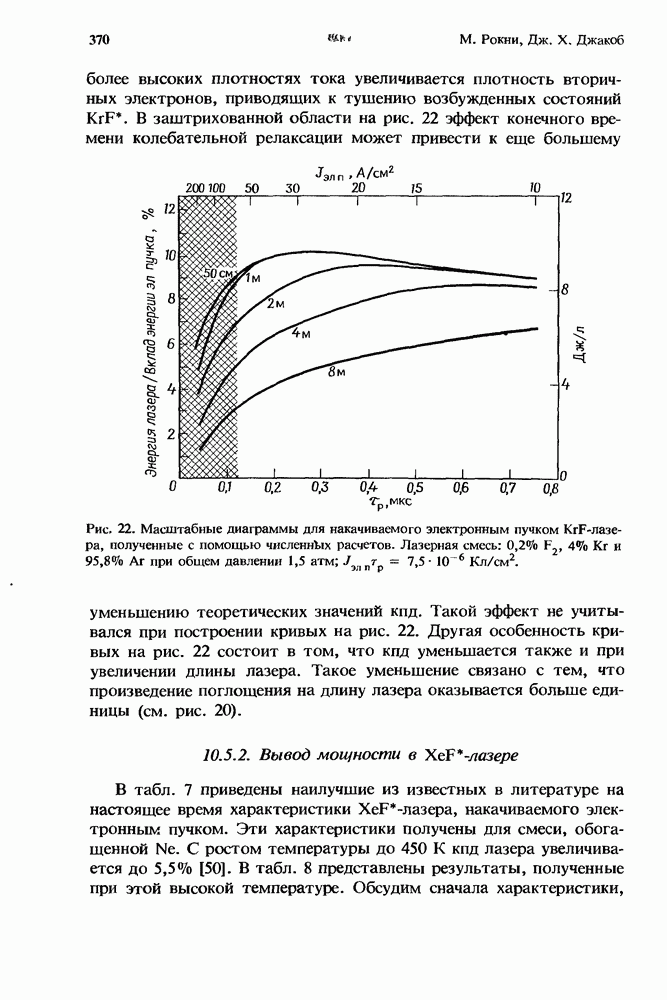
- 10.5.1. Вывод мощности в KrF*-лазере
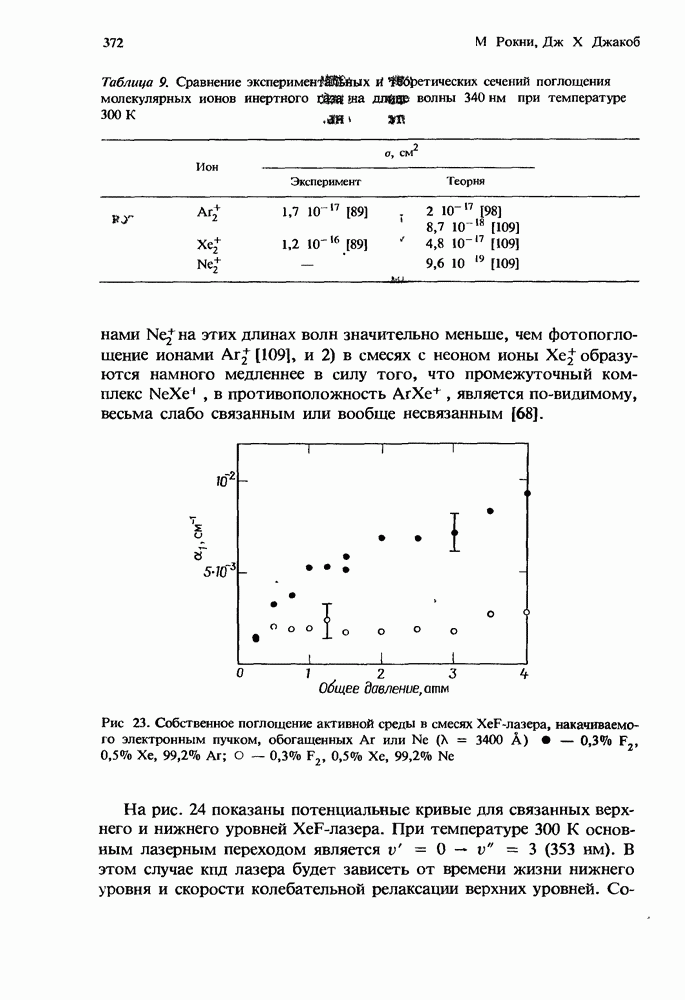
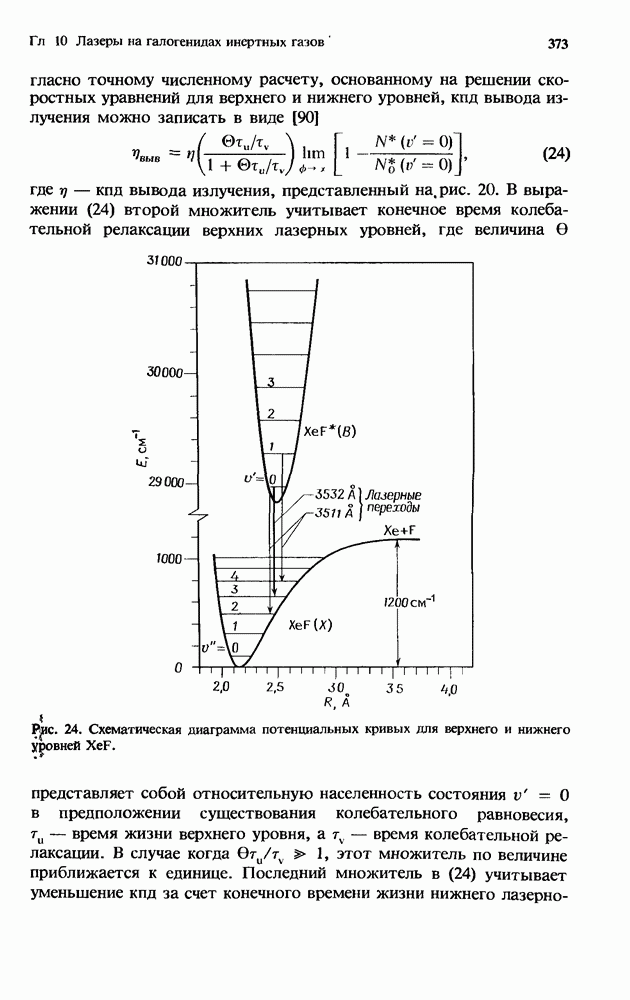
- 10.5.2. Вывод мощности в XcF*-лазере
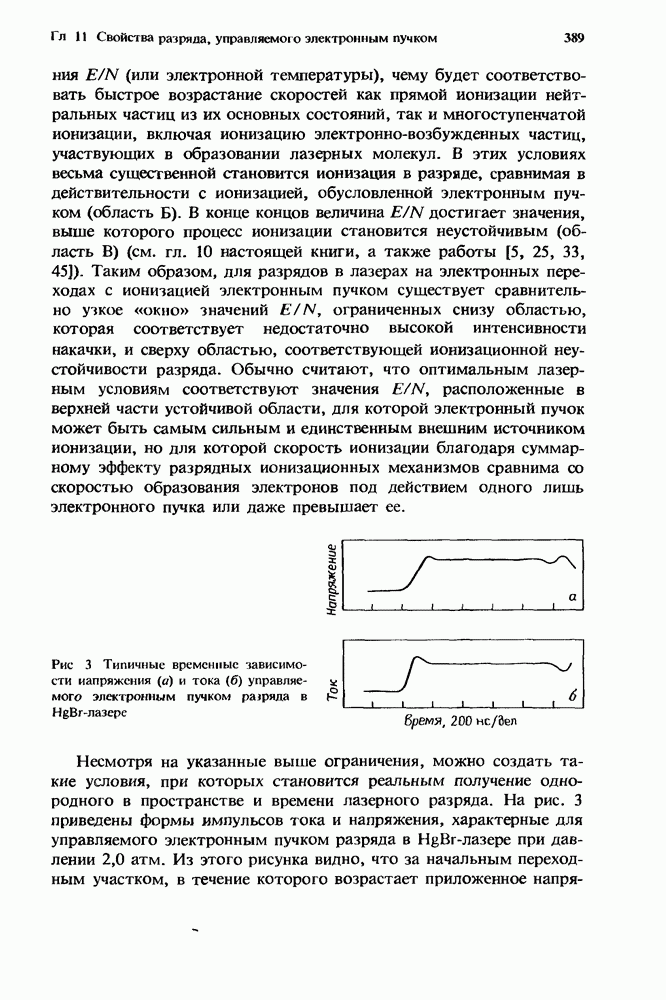
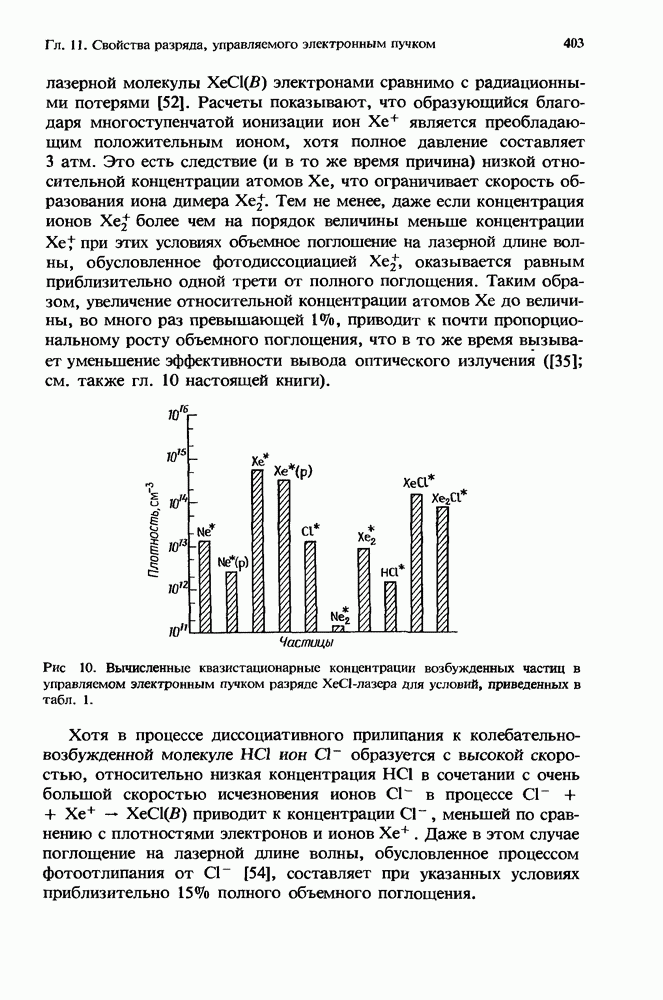
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
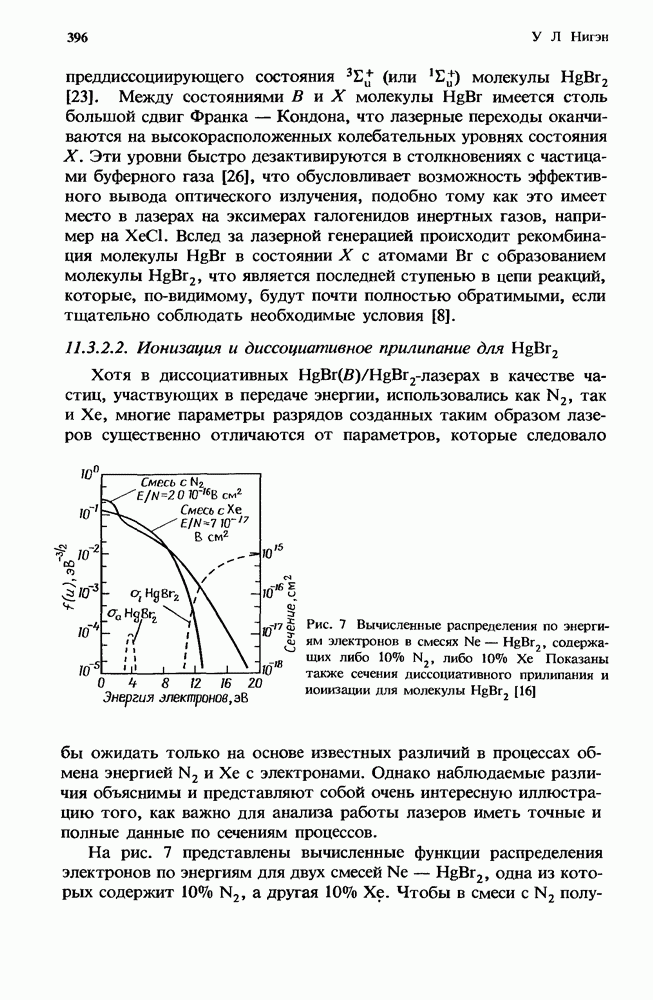
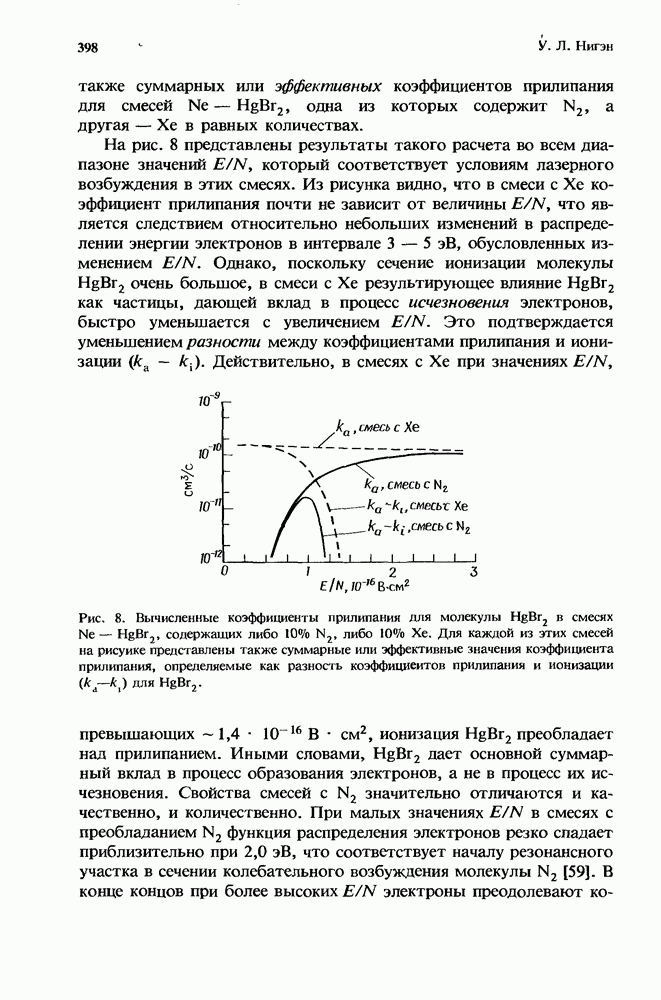
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
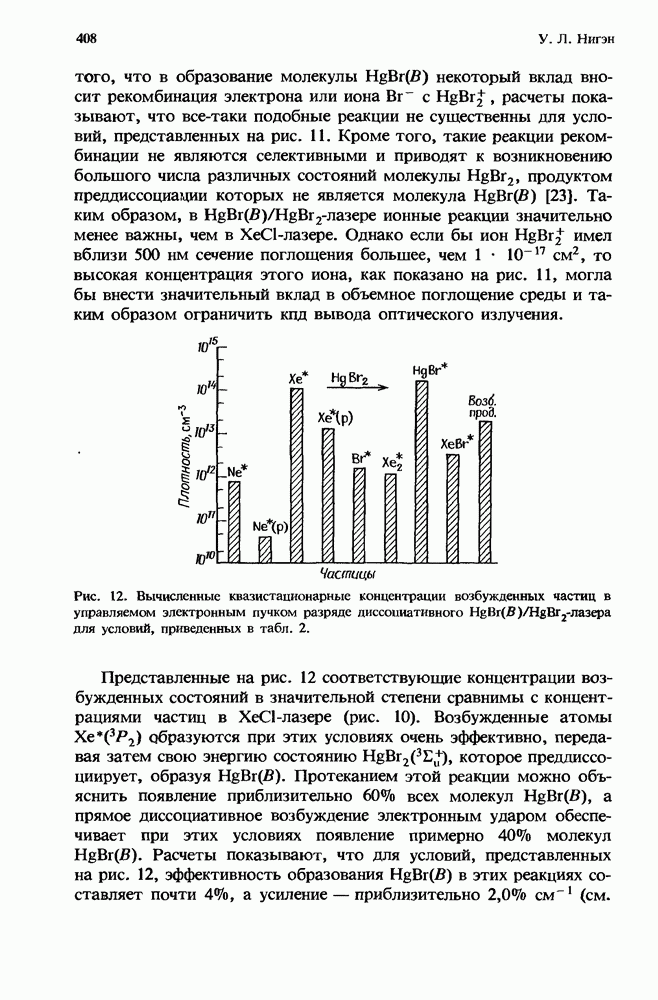
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
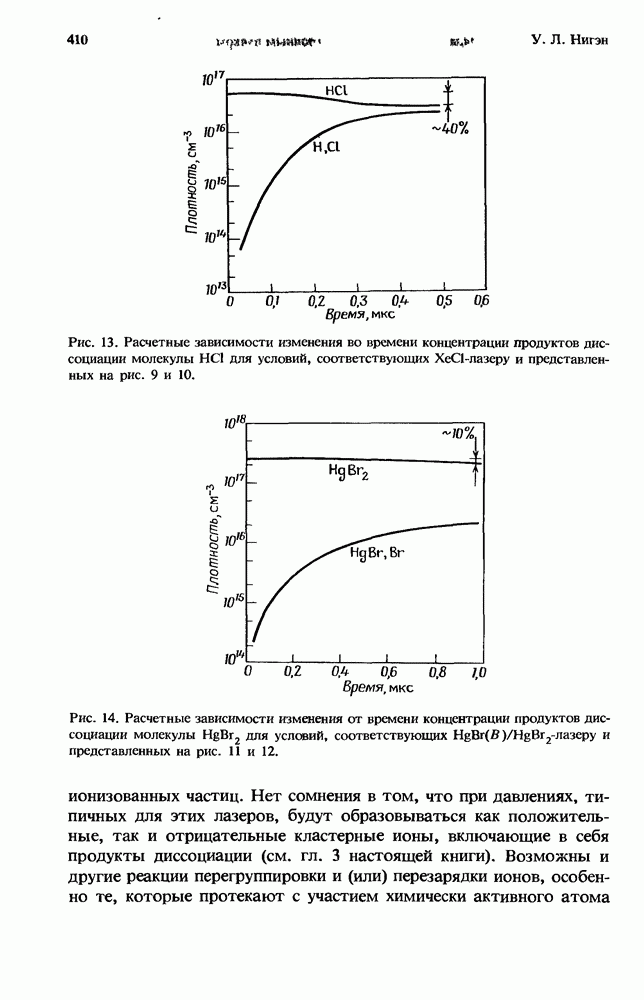
- 11.4.3. Диссоциация галогенидов
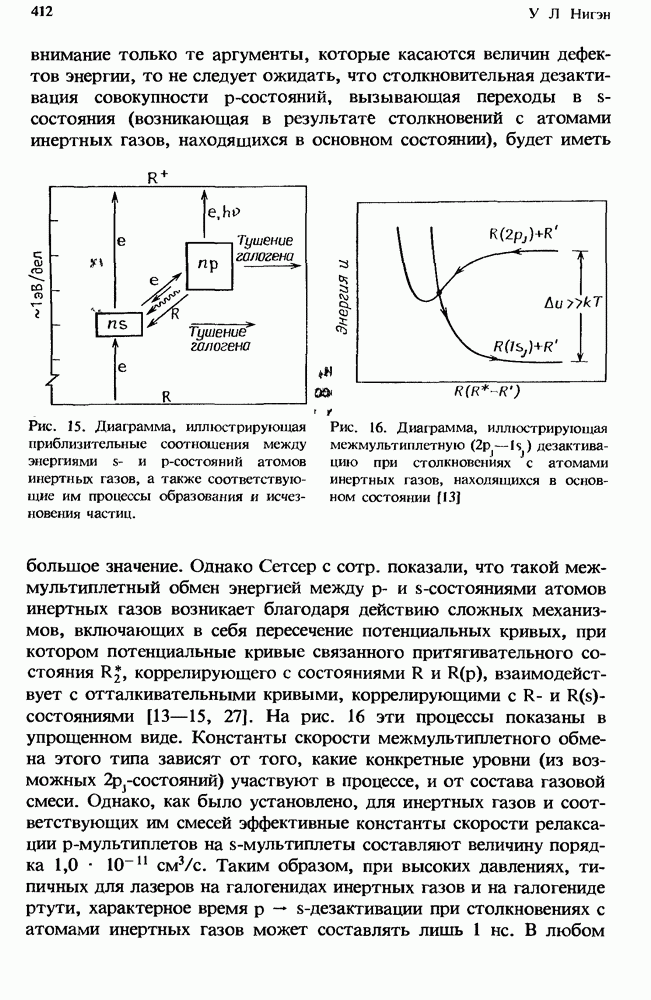
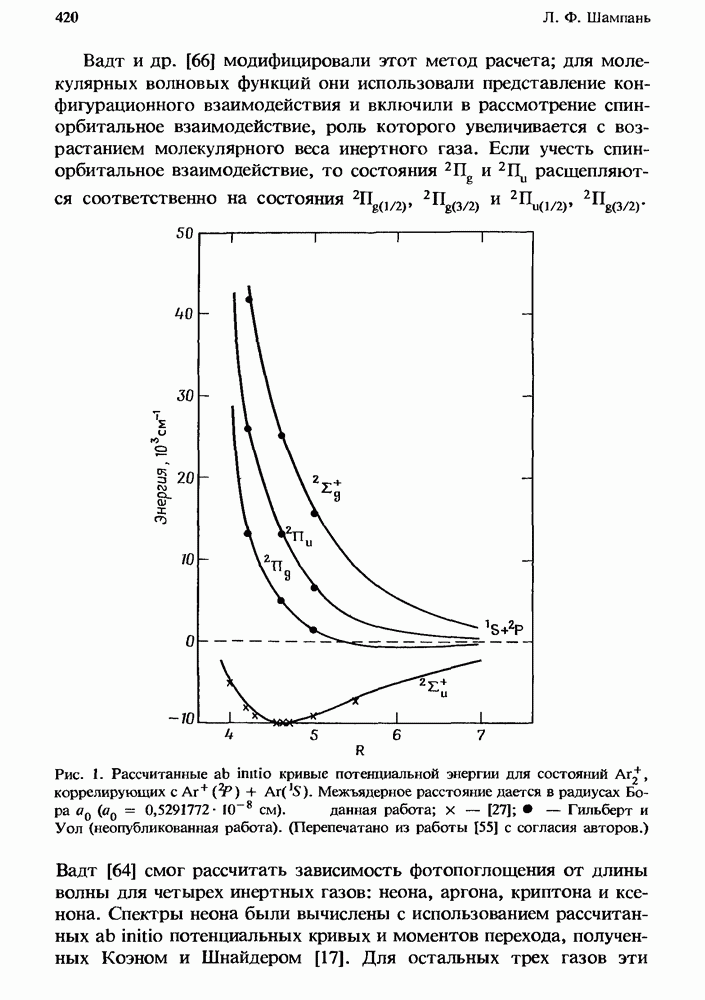
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
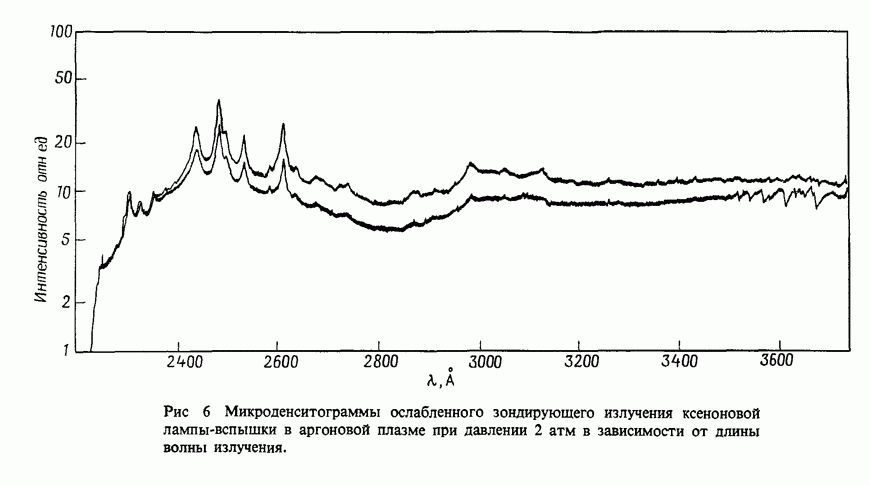
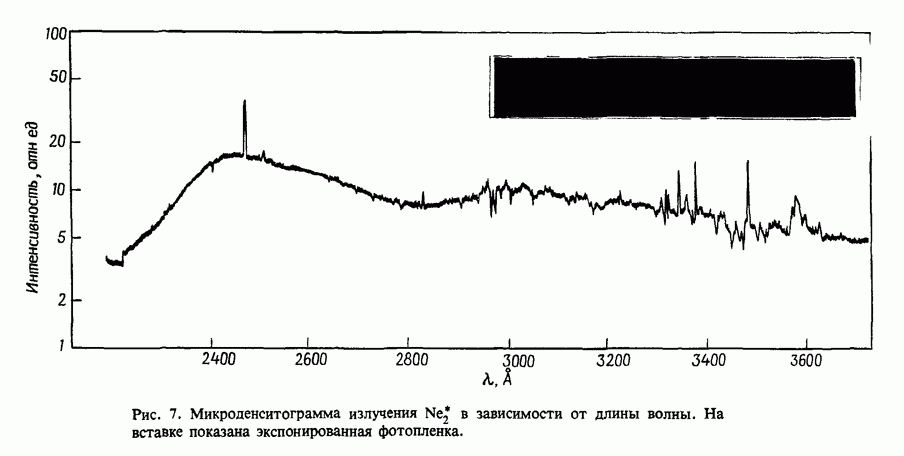
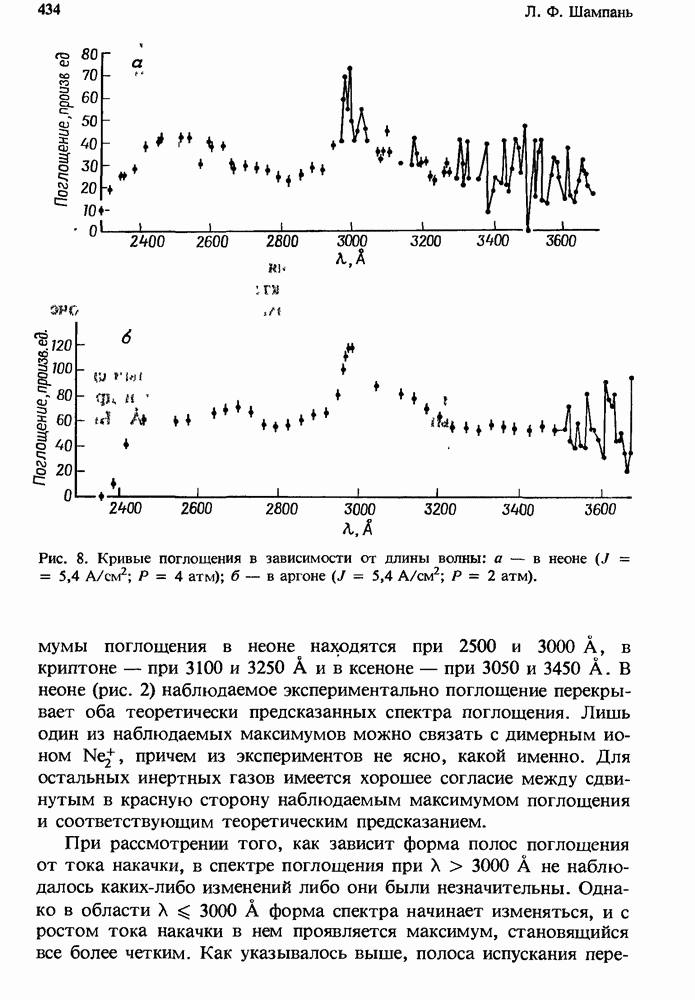
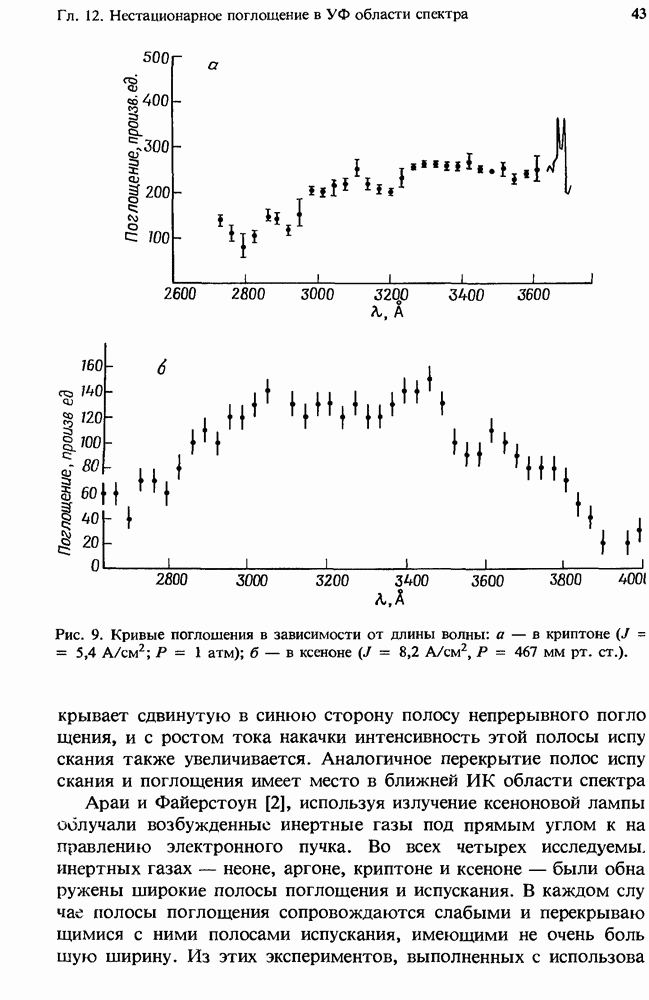
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
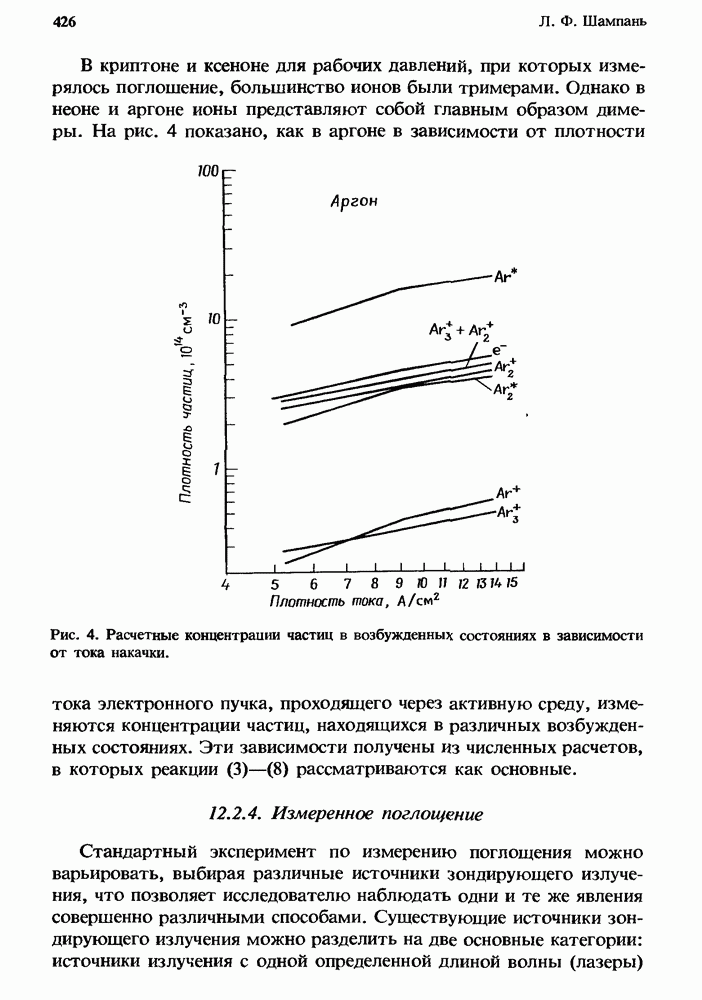
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
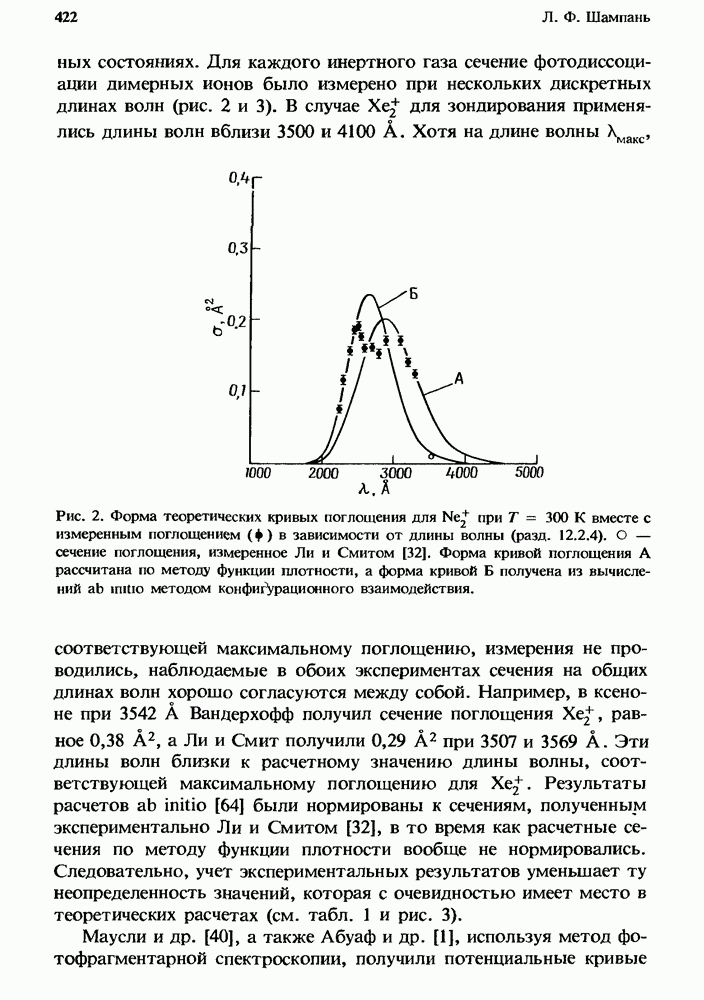
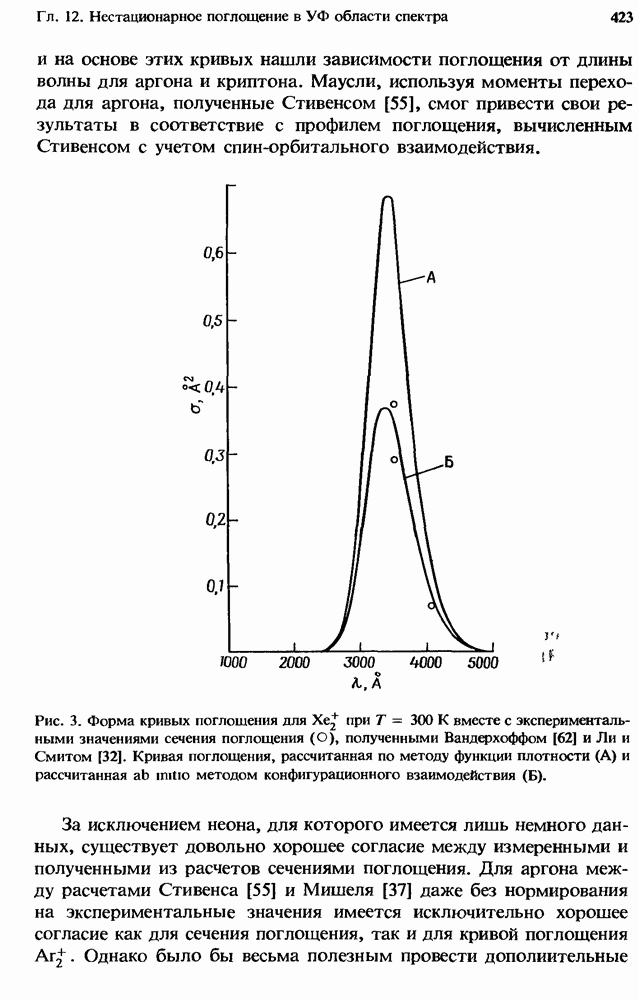
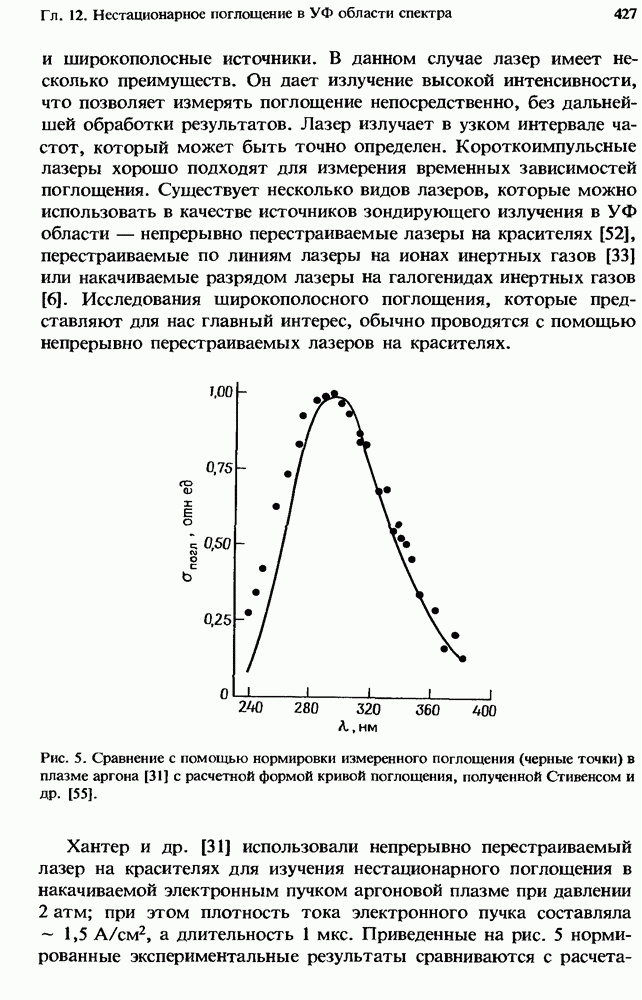
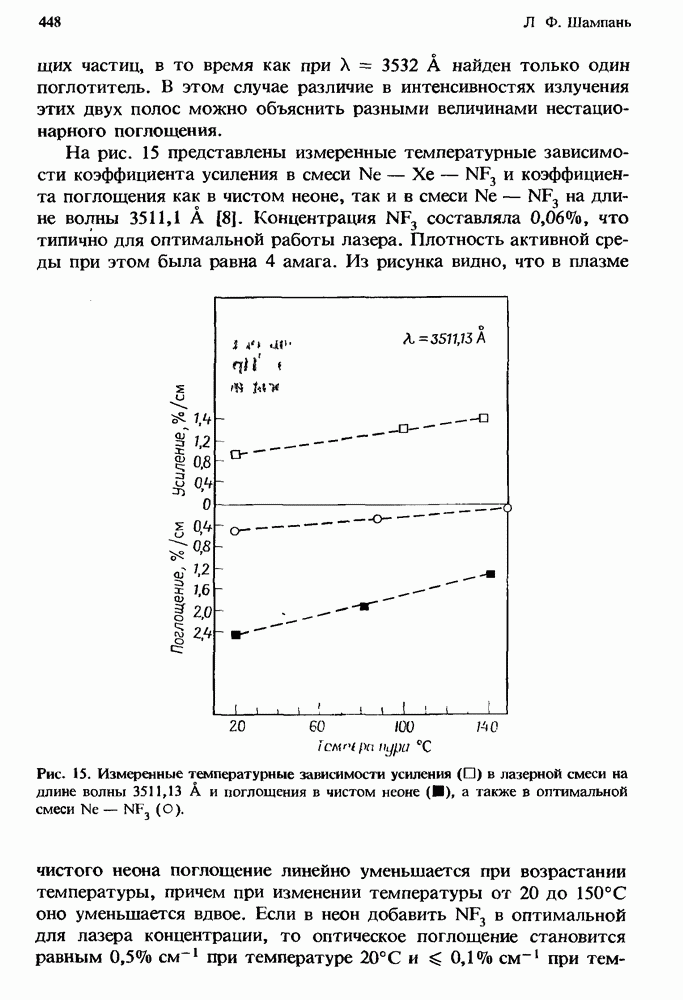
- 12.2.4. Измеренное поглощение
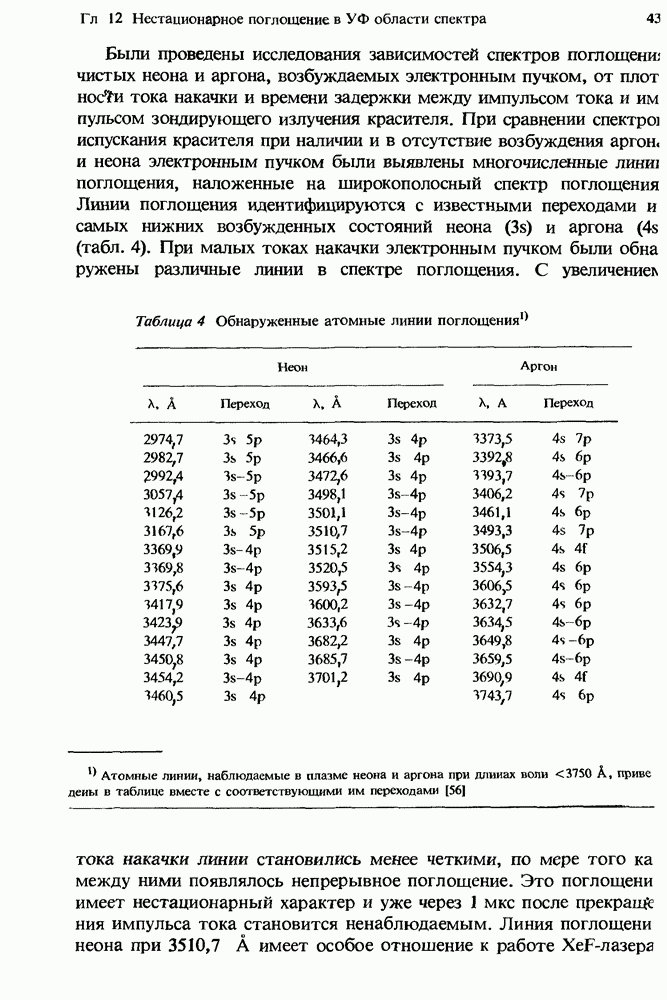
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
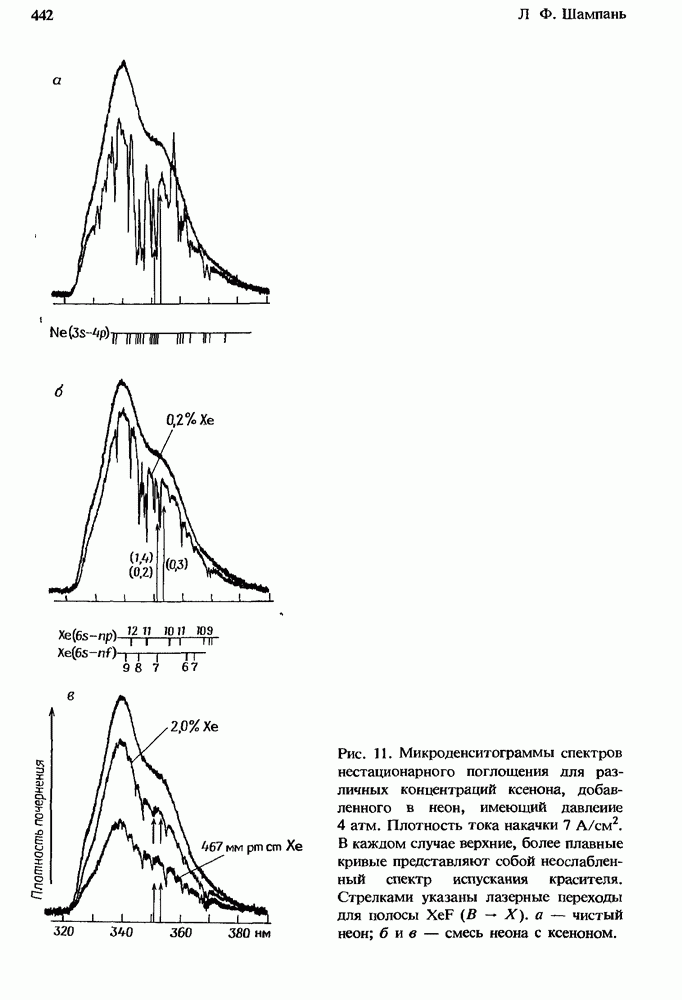
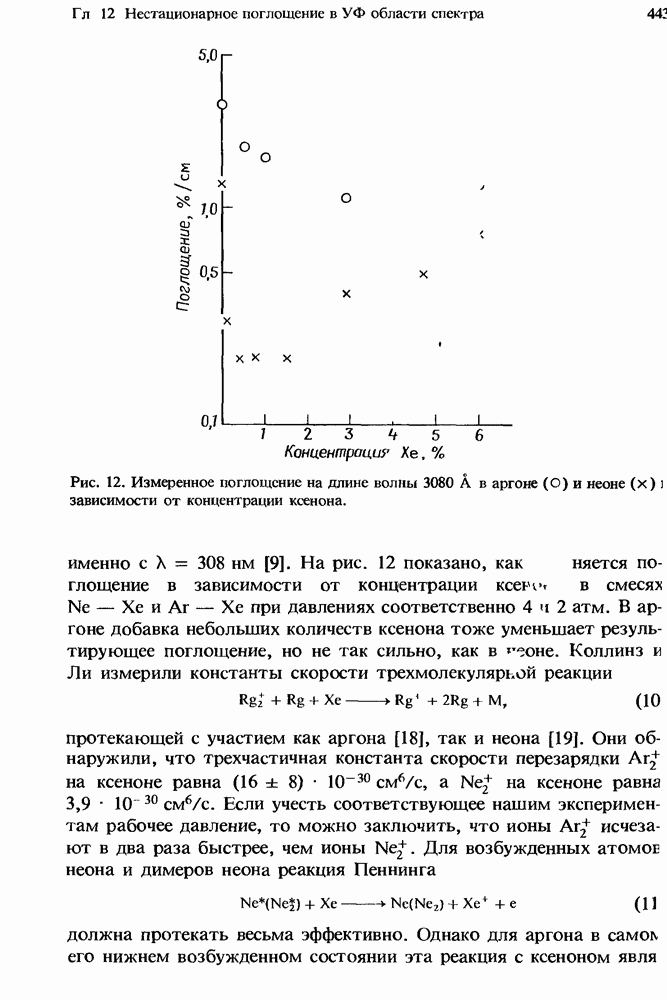
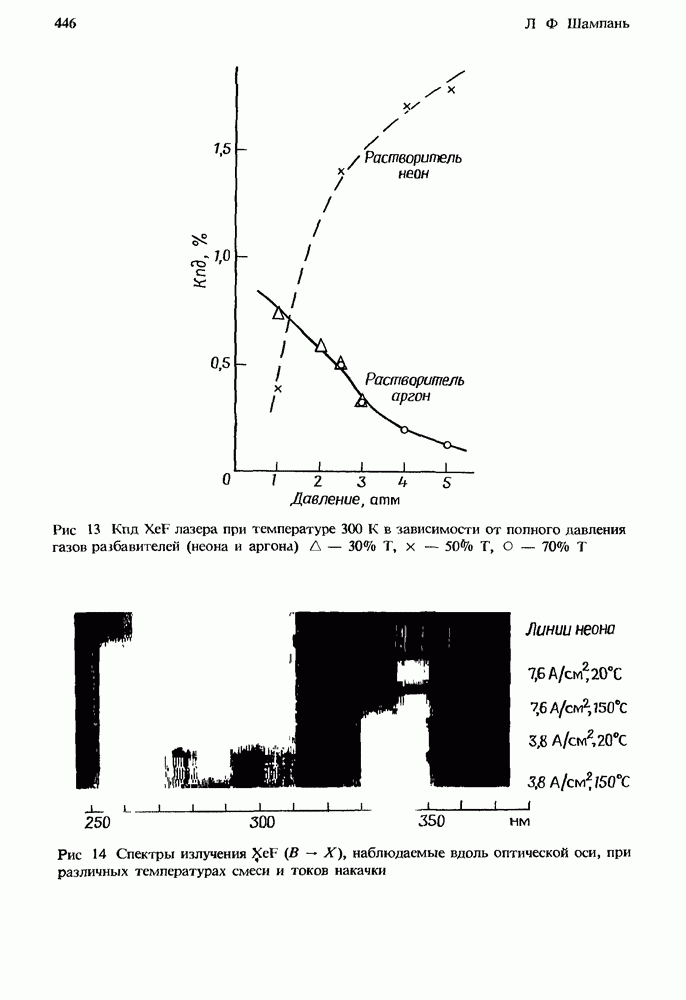
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
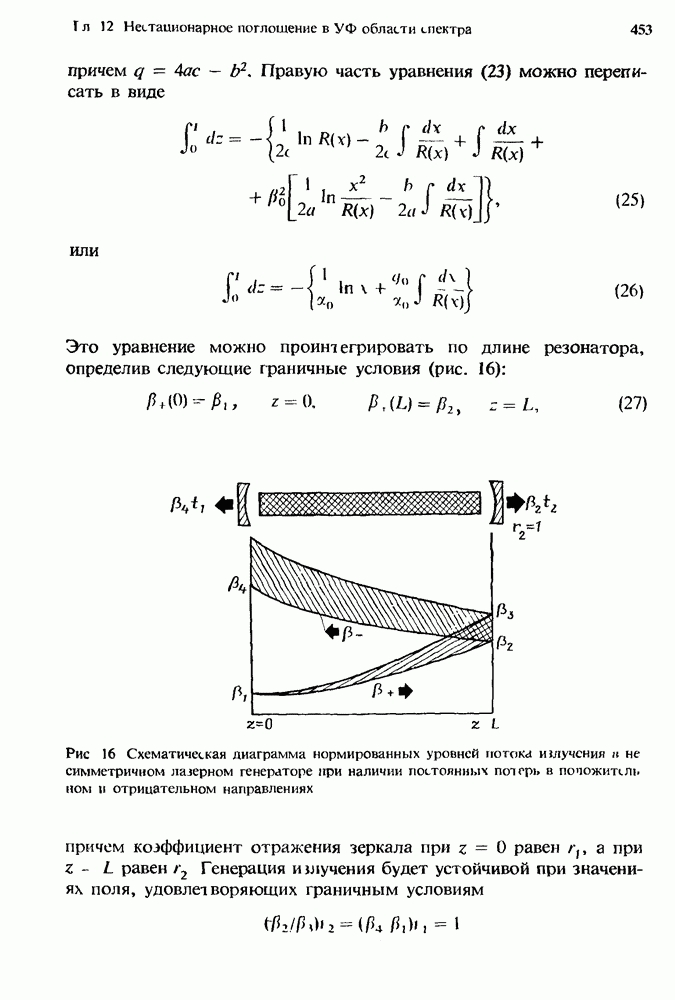
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
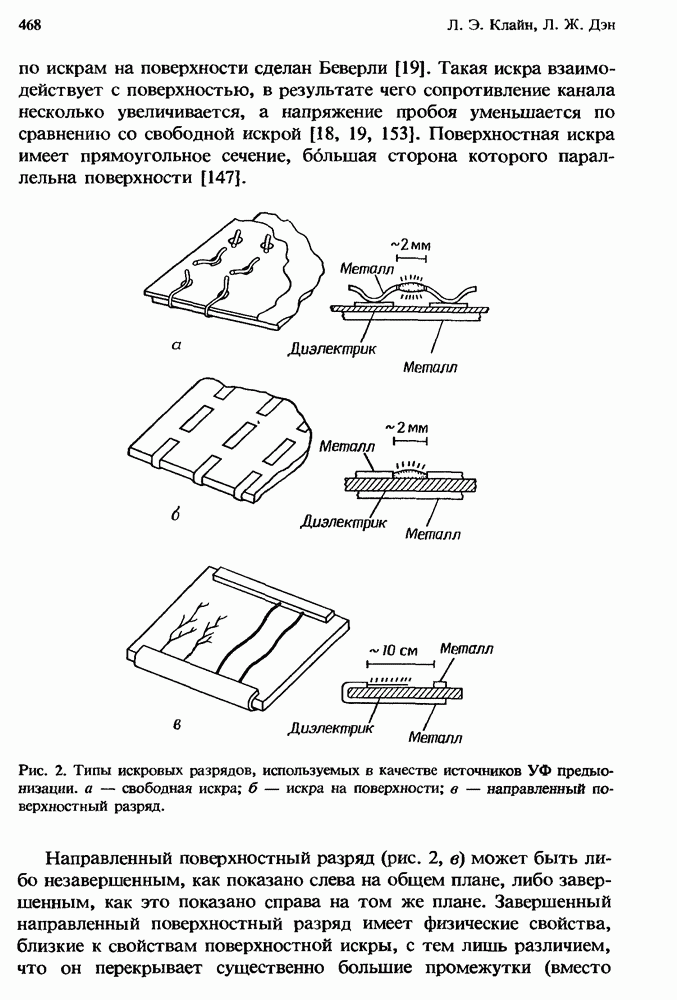
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
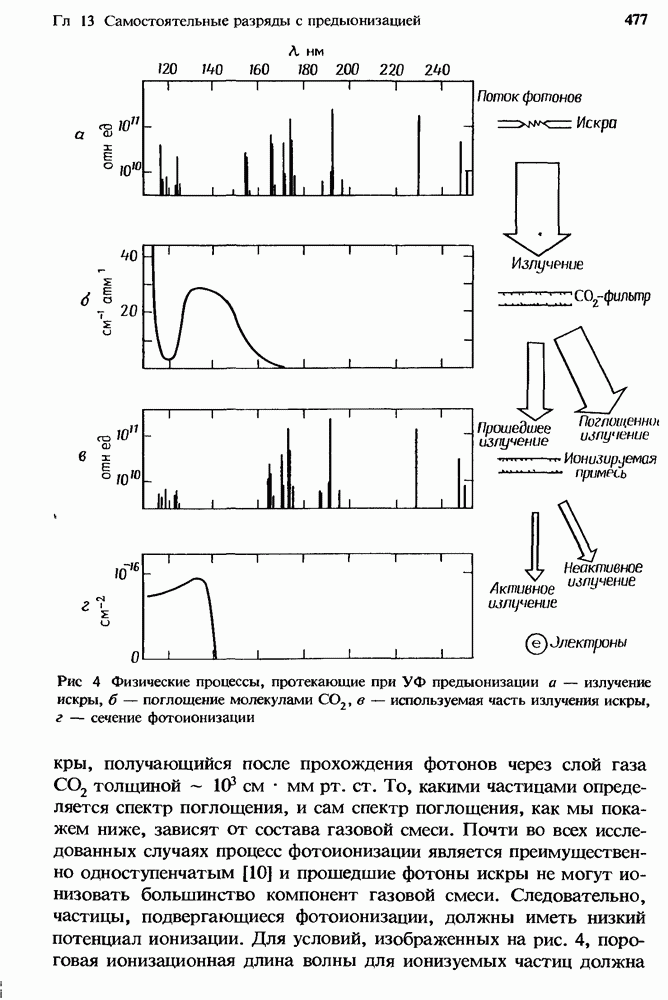
- 13.3.1. Спектр искрового разряда
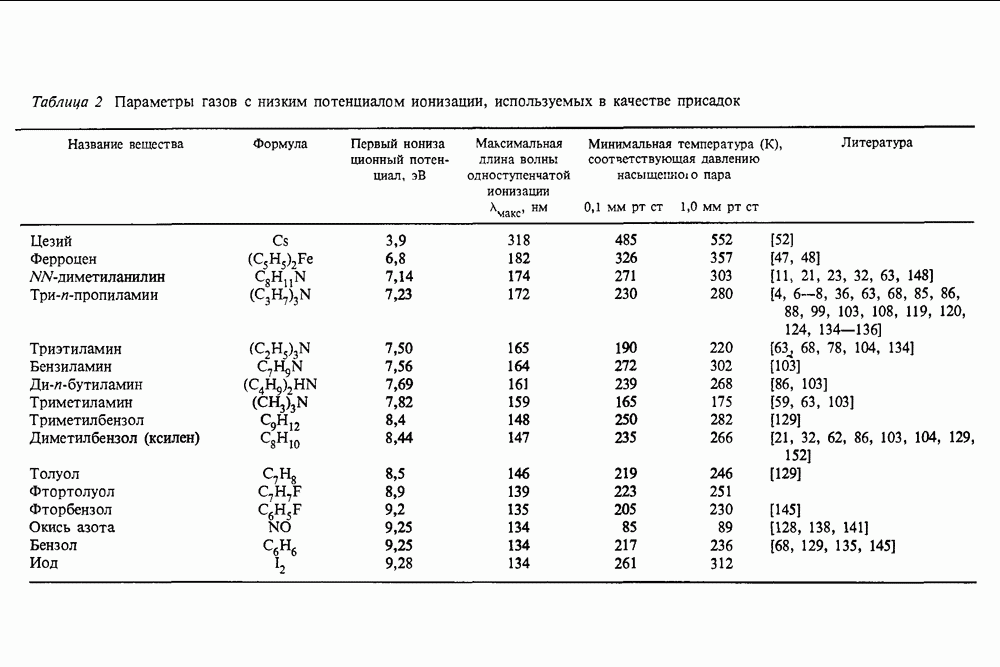
- 13.3.2. Фотоионизационные спектры
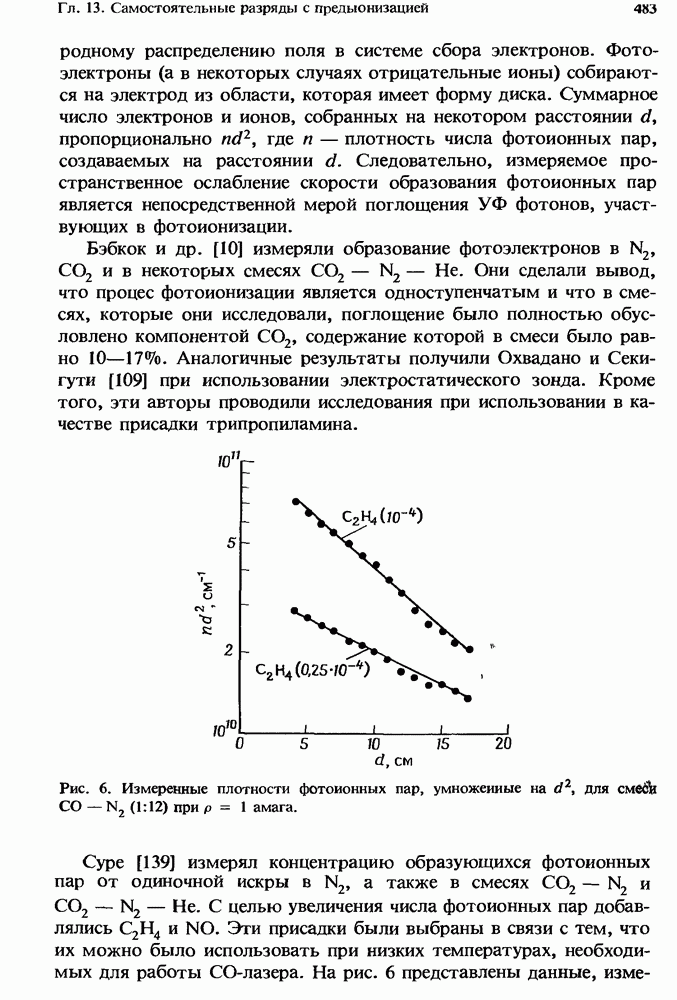
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
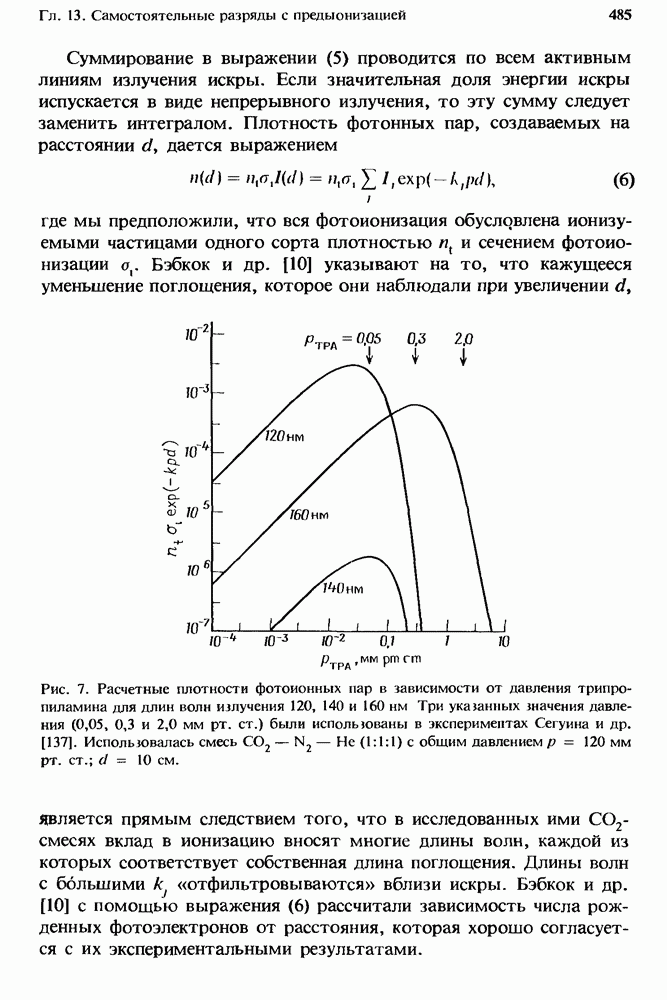
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
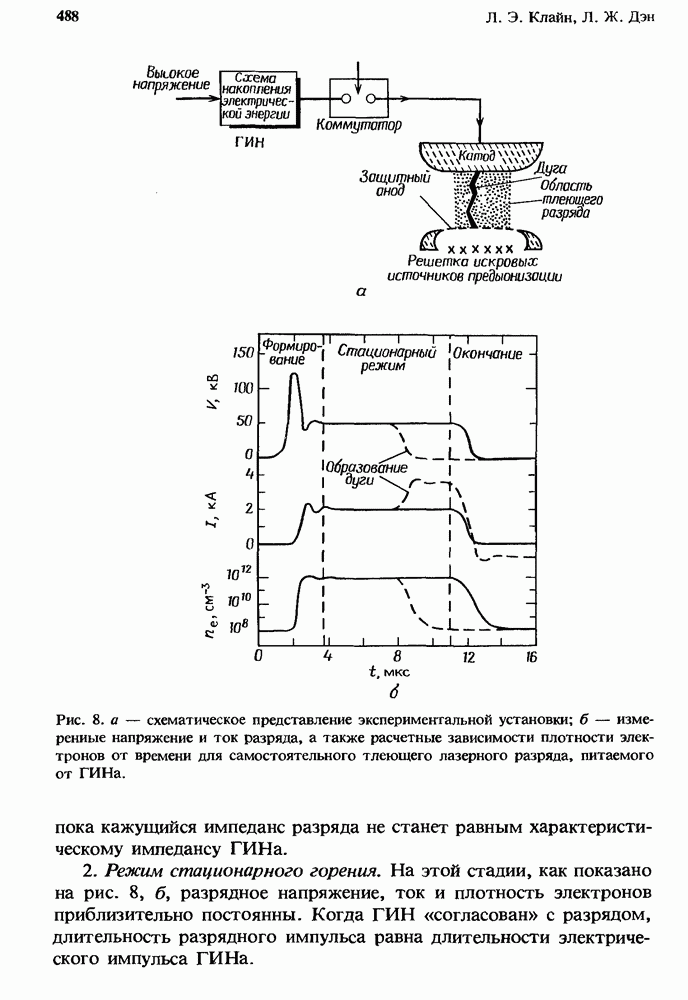
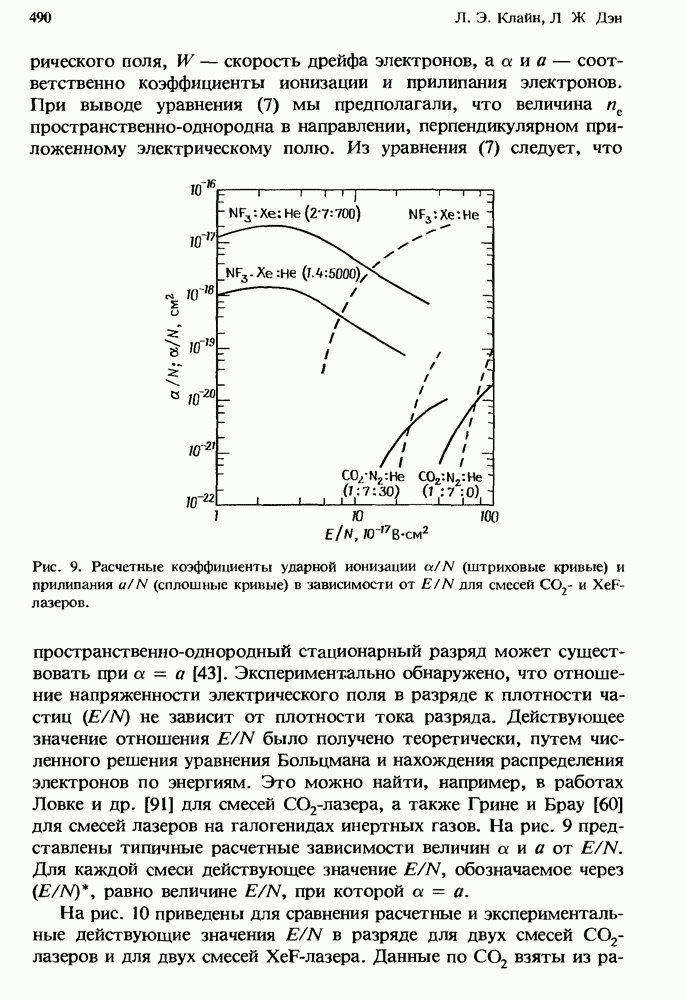
- 13.4. Физика самостоятельного тлеющего разряда
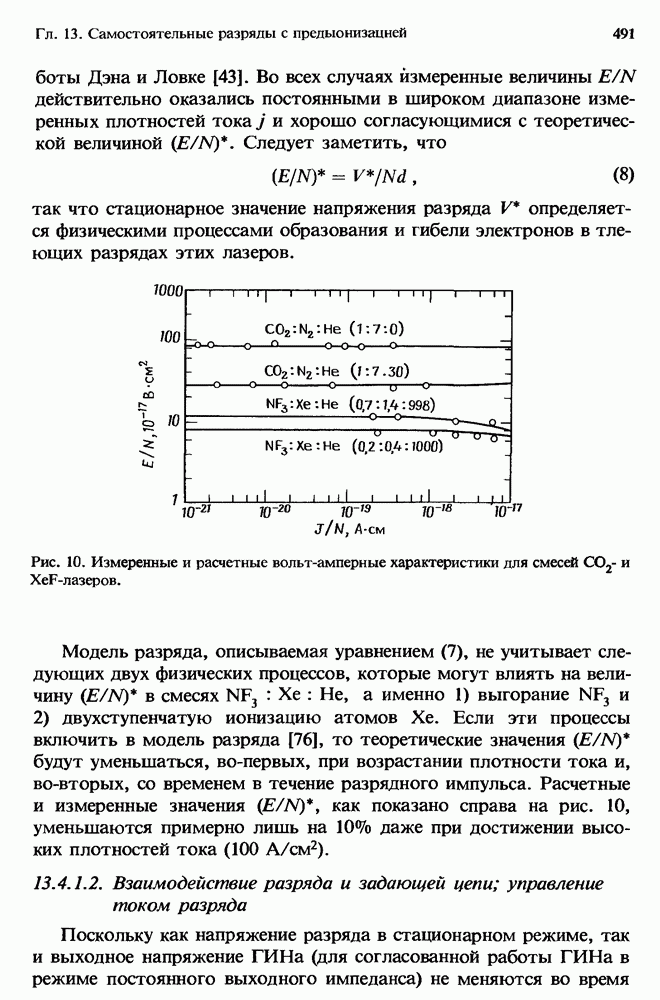
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
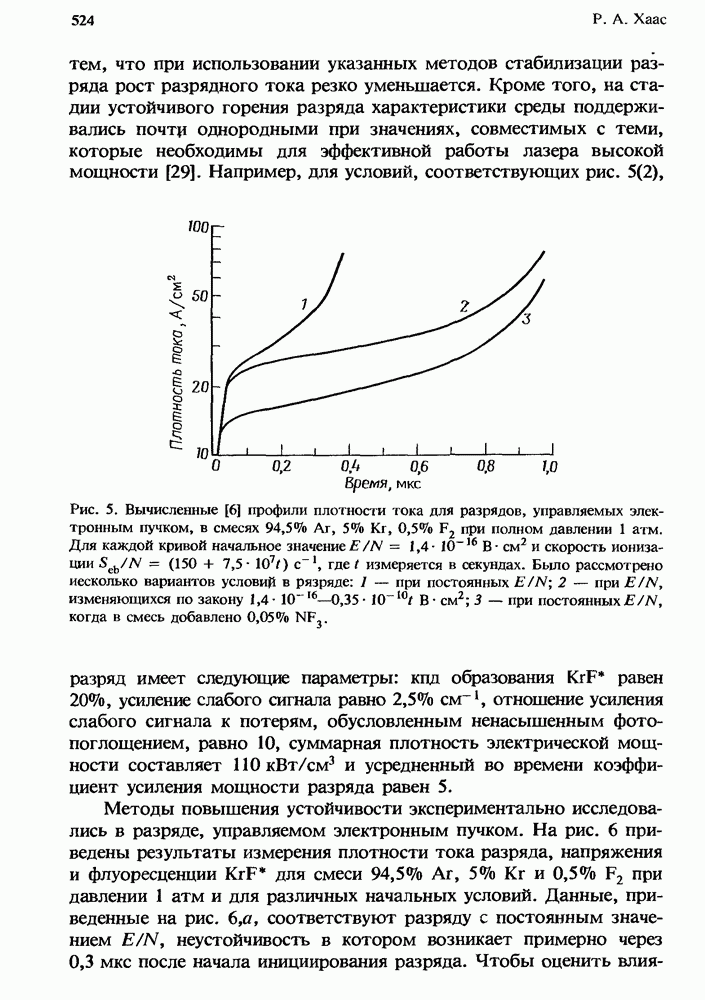
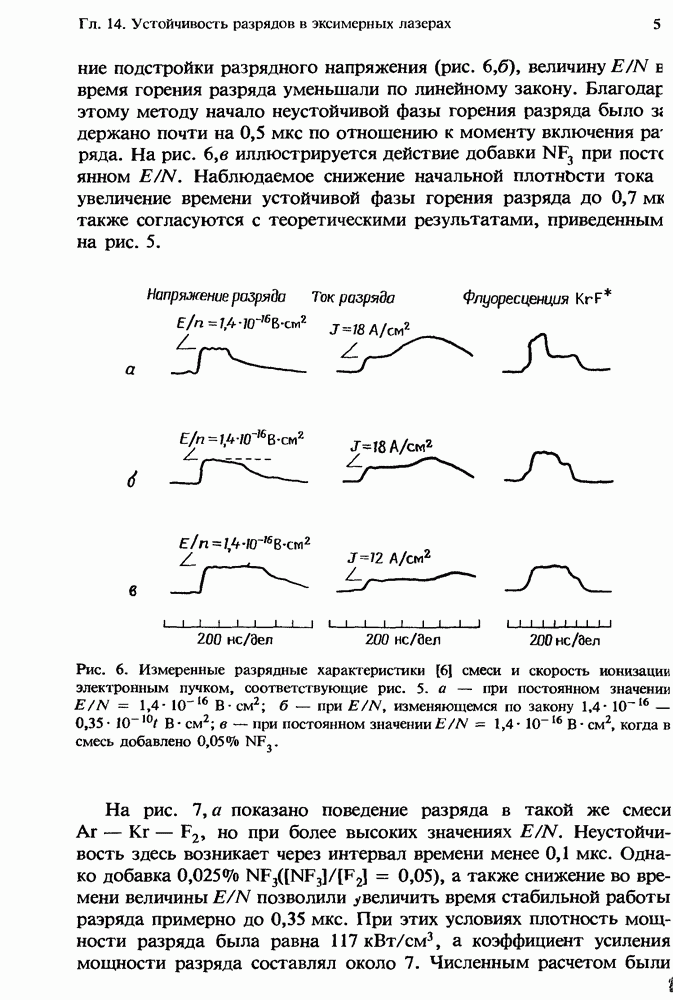
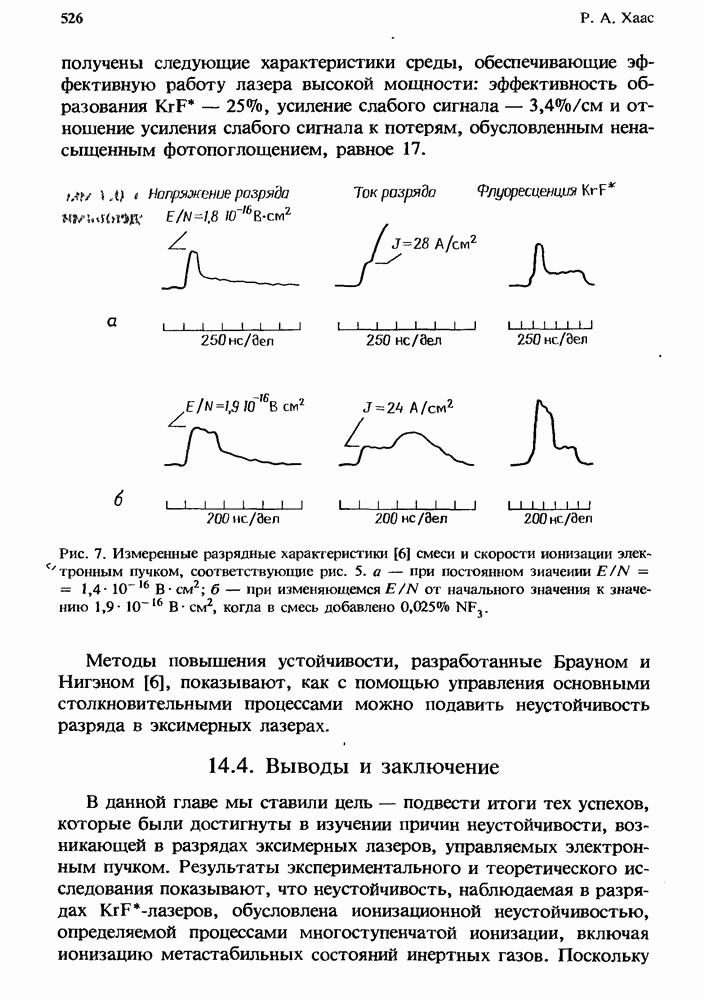
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
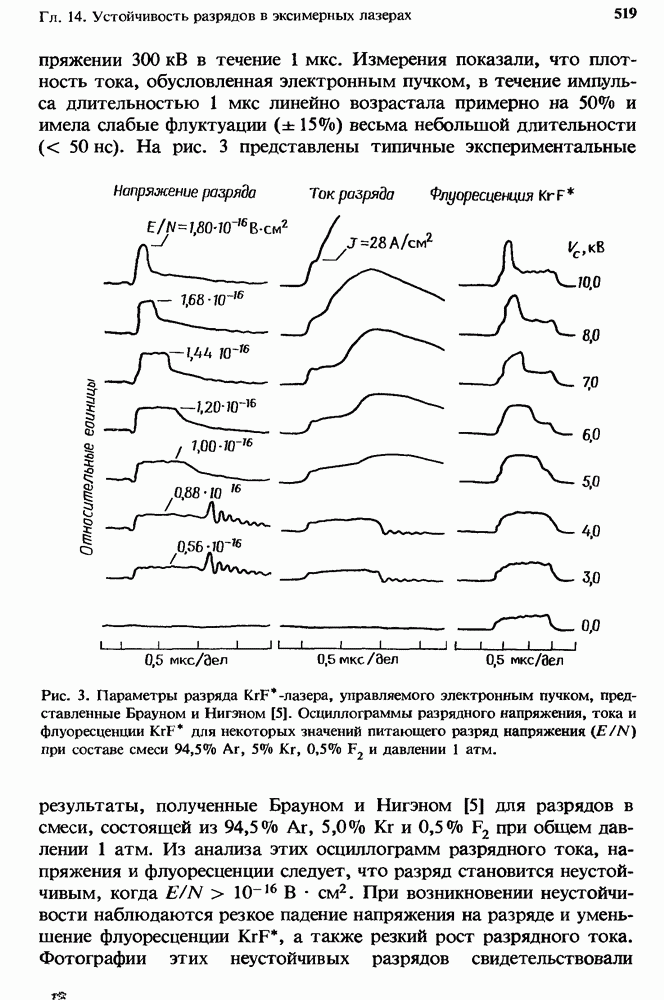
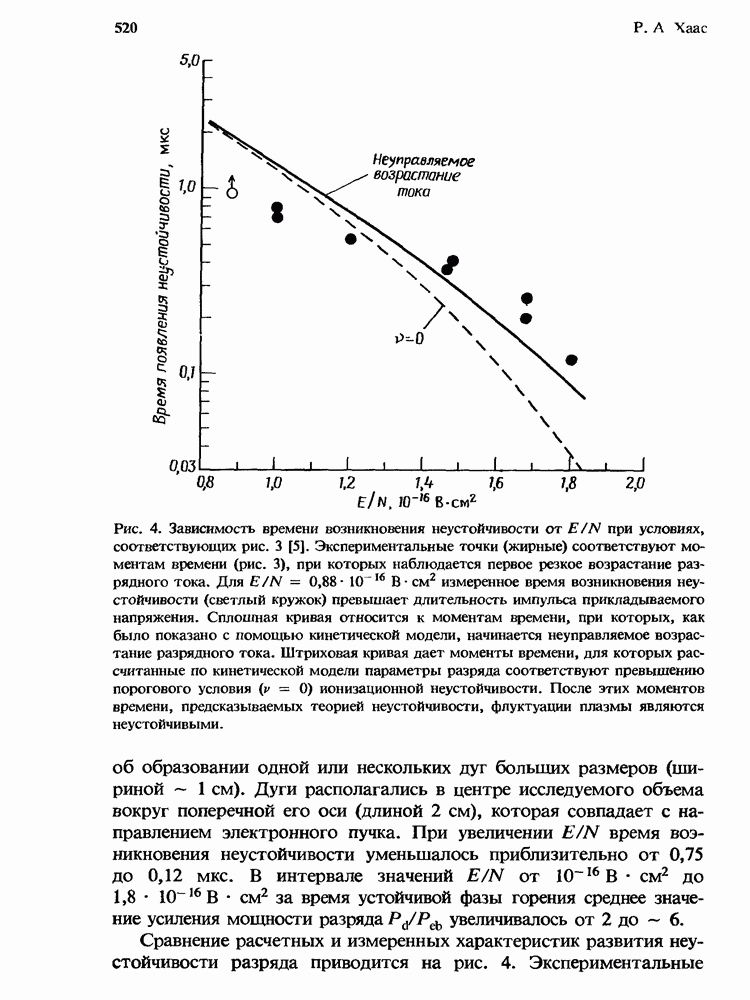
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации