| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.3.3. Зависимость от плотности ионов
Все ранее выполненные теоретические и экспериментальные исследования ион-ионной рекомбинации относятся к случаю низкой степени ионизации, соответствующей плотности ионов  Между тем ион-ионная рекомбинация играет одну из главных ролей [23] в процессе заселения уровней верхнего электронного состояния в лазерах на галогенидах инертных газов, которые работают не только при большой плотности газа
Между тем ион-ионная рекомбинация играет одну из главных ролей [23] в процессе заселения уровней верхнего электронного состояния в лазерах на галогенидах инертных газов, которые работают не только при большой плотности газа  , но также при относительно больших плотностях ионов
, но также при относительно больших плотностях ионов  При возрастании
При возрастании  взаимодействие между положительными и отрицательными ионами перестает быть чисто кулоновским и начинает зависеть от экранировки, что обусловлено действием соседних ионов вследствие влияния, оказываемого распределением плотности заряда, которое, в свою очередь, через а связано с рекомбинационным оттоком, явно зависящим от V. Большую роль могут также играть отталкивание одноименных ионов и конкуренция между соседними областями оттока за ионный поток.
взаимодействие между положительными и отрицательными ионами перестает быть чисто кулоновским и начинает зависеть от экранировки, что обусловлено действием соседних ионов вследствие влияния, оказываемого распределением плотности заряда, которое, в свою очередь, через а связано с рекомбинационным оттоком, явно зависящим от V. Большую роль могут также играть отталкивание одноименных ионов и конкуренция между соседними областями оттока за ионный поток.
При интегрировании выражения (42а), в котором явно пренебрегается конкуренцией между областями оттока [см. уравнение (75)] по объему сферы  в предположении, что
в предположении, что  можно видеть, что из граничного условия (45а) для излучения следует выполнение соотношения
можно видеть, что из граничного условия (45а) для излучения следует выполнение соотношения  Поэтому при нормальных условиях в сферической области рекомбинации радиусом
Поэтому при нормальных условиях в сферической области рекомбинации радиусом  должно присутствовать малое число стоков, и, следовательно, мы имеем
должно присутствовать малое число стоков, и, следовательно, мы имеем  что также согласуется с пренебрежением
что также согласуется с пренебрежением
в исходном уравнении Больцмана (21) ион-ионными столкновениями.
Теперь энергия взаимодействия V между ионами определяется из решения соответствующего уравнения Пуассона

где  — распределение плотности заряда
— распределение плотности заряда  выраженное через плотность положительных и отрицательных ионов,
выраженное через плотность положительных и отрицательных ионов,  диэлектрическая проницаемость буферного газа
диэлектрическая проницаемость буферного газа  В газе с плотностью
В газе с плотностью  и поляризуемостью молекул
и поляризуемостью молекул  мы имеем
мы имеем  так что в случае Хе при
так что в случае Хе при  эта величина равна
эта величина равна  т.е. близка к единице. Суммарный внутренний стационарный поток
т.е. близка к единице. Суммарный внутренний стационарный поток  положительных ионов в направлении к данному положительному иону можно написать в виде
положительных ионов в направлении к данному положительному иону можно написать в виде

где  — коэффициент диффузии, а
— коэффициент диффузии, а  — подвижность положительных ионов, обозначаемых индексом 1. Суммарный внутренний поток отрицательных ионов (обозначаемых нижним индексом 2) в направлении к положительному иону 1, как и в предыдущем случае, дается выражением
— подвижность положительных ионов, обозначаемых индексом 1. Суммарный внутренний поток отрицательных ионов (обозначаемых нижним индексом 2) в направлении к положительному иону 1, как и в предыдущем случае, дается выражением

где  — коэффициенты диффузии,
— коэффициенты диффузии,  подвижности отрицательных ионов 2). В системе координат, связанной с положительными ионами, величина обращается в нуль и интегрирование выражения (65) дает
подвижности отрицательных ионов 2). В системе координат, связанной с положительными ионами, величина обращается в нуль и интегрирование выражения (65) дает

Здесь  если соотношение Эйнштейна больше не выполняется. Следовательно, уравнение Пуассона для радиально-симметричного распределения можно написать в виде
если соотношение Эйнштейна больше не выполняется. Следовательно, уравнение Пуассона для радиально-симметричного распределения можно написать в виде

где плотность отрицательных ионов  определяется уравнением непрерывности (27) для квазистапионарного потока через
определяется уравнением непрерывности (27) для квазистапионарного потока через
поверхность радиусом  т.е. уравнением
т.е. уравнением

Решение уравнения (68) для потенциала V связано с решением уравнения (69) для плотности  которая в свою очередь с помощью выражения (28) для
которая в свою очередь с помощью выражения (28) для  связана с решением интегродифференциального уравнения (21), описывающего распределение отрицательных ионов
связана с решением интегродифференциального уравнения (21), описывающего распределение отрицательных ионов  в фазовом пространстве. Применение рассмотренной выше теории для решения нашей проблемы представляет собой трудную, но все-таки разрешимую задачу. С помощью выражения (38) самосогласованный потенциал взаимодействия V, представляющий собой функцию от
в фазовом пространстве. Применение рассмотренной выше теории для решения нашей проблемы представляет собой трудную, но все-таки разрешимую задачу. С помощью выражения (38) самосогласованный потенциал взаимодействия V, представляющий собой функцию от  и
и  можно найти в виде соответствующего решения уравнения
можно найти в виде соответствующего решения уравнения

Здесь радиус «экранировки» дается выражением

где  В уравнении (70) член в квадратных скобках зависит от
В уравнении (70) член в квадратных скобках зависит от  и R и в случае малых
и R и в случае малых  стремится к единице при любом значении
стремится к единице при любом значении  а в случае больших
а в случае больших  он возрастает от нуля при
он возрастает от нуля при  до единицы при
до единицы при  Если
Если  то в уравнении (70) взаимодействие
то в уравнении (70) взаимодействие  становится чисто кулоновским.
становится чисто кулоновским.
При выполнении условия  уравнение (70) имеет точное решение [27, 29] вида
уравнение (70) имеет точное решение [27, 29] вида

Отсюда следует, что при малых  когда а
когда а  «к (где
«к (где  — ланжевеновская скорость дрейфа), мы имеем взаимодействие Дебая — Хюккеля:
— ланжевеновская скорость дрейфа), мы имеем взаимодействие Дебая — Хюккеля:

в то время как при больших  получаем нечто среднее между кулоновским взаимодействием и взаимодействием Дебая — Хюккеля:
получаем нечто среднее между кулоновским взаимодействием и взаимодействием Дебая — Хюккеля:

которое согласуется с выбором а 
Прямое численное решение уравнения (70) с граничным условием в виде (72) при асимптотических значениях  когда
когда  показывает, что выражение (72) остается справедливым с высокой степенью точности для любых
показывает, что выражение (72) остается справедливым с высокой степенью точности для любых  При малых
При малых  условие
условие  выполняется в важной области
выполняется в важной области  когда
когда  Последнее неравенство с учетом соотношения (71) означает, что внутри сферы
Последнее неравенство с учетом соотношения (71) означает, что внутри сферы  находится много ионов и
находится много ионов и  С увеличением
С увеличением  радиус реакционной зоны
радиус реакционной зоны  уменьшается как
уменьшается как  и при больших
и при больших  мы имеем
мы имеем  так что потенциал, определяемый выражением (74), при
так что потенциал, определяемый выражением (74), при  становится чисто кулоновским.
становится чисто кулоновским.
С увеличением  ионные пары распределяются по всему пространству. Связь между парной и гомогенной рекомбинациями становится существенной и может быть выражена следующим уравнением:
ионные пары распределяются по всему пространству. Связь между парной и гомогенной рекомбинациями становится существенной и может быть выражена следующим уравнением:

для концентрации ионных пар  (в единицах
(в единицах  Таким образом, величина
Таким образом, величина  равна концентрации ионных пар с внутренними расстояниями между ионами
равна концентрации ионных пар с внутренними расстояниями между ионами  лежащими в интервале
лежащими в интервале  В уравнении (75) средняя плотность непрореагировавших ионных пар
В уравнении (75) средняя плотность непрореагировавших ионных пар  равна
равна

а величина представляет собой суммарный внутренний поток ионов  за счет диффузионного дрейфа, определяемый выражением (426). Два последних члена в правой части уравнения (75) описывают соответственно парную и гомогенную рекомбинации. Подставляя в уравнение (75) выражение
за счет диффузионного дрейфа, определяемый выражением (426). Два последних члена в правой части уравнения (75) описывают соответственно парную и гомогенную рекомбинации. Подставляя в уравнение (75) выражение

где С удовлетворяет уравнению

находим, что плотность вероятности, или парная корреляционная  функция
функция  удовлетворяет уравнению Дебая — Смолуховского для изолированного стока:
удовлетворяет уравнению Дебая — Смолуховского для изолированного стока:

Таким образом, получаем следующее выражение:

которое описывает временной распад всех ионных пар вследствие рекомбинации; здесь  — начальная концентрация ионных пар, а функция
— начальная концентрация ионных пар, а функция  дает пространственное распределение ионных пар с длиной
дает пространственное распределение ионных пар с длиной  Отсюда следует, что коэффициент рекомбинации
Отсюда следует, что коэффициент рекомбинации

удовлетворяет уравнению

где  — функция, полученная как соответствующее решение уравнения (76) для изолированного стока (или постоянного значения С) при условии, что внутри области рекомбинации находится малое число ионов, как и в случае квазистационарных условий,
— функция, полученная как соответствующее решение уравнения (76) для изолированного стока (или постоянного значения С) при условии, что внутри области рекомбинации находится малое число ионов, как и в случае квазистационарных условий,  Если начальная концентрация
Если начальная концентрация  и время парной рекомбинации
и время парной рекомбинации  достаточно малы, так что выполняется следующее неравенство:
достаточно малы, так что выполняется следующее неравенство:

то решения (60) и (82) сводятся к случаю изолированного стока и связанного с ним значения 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
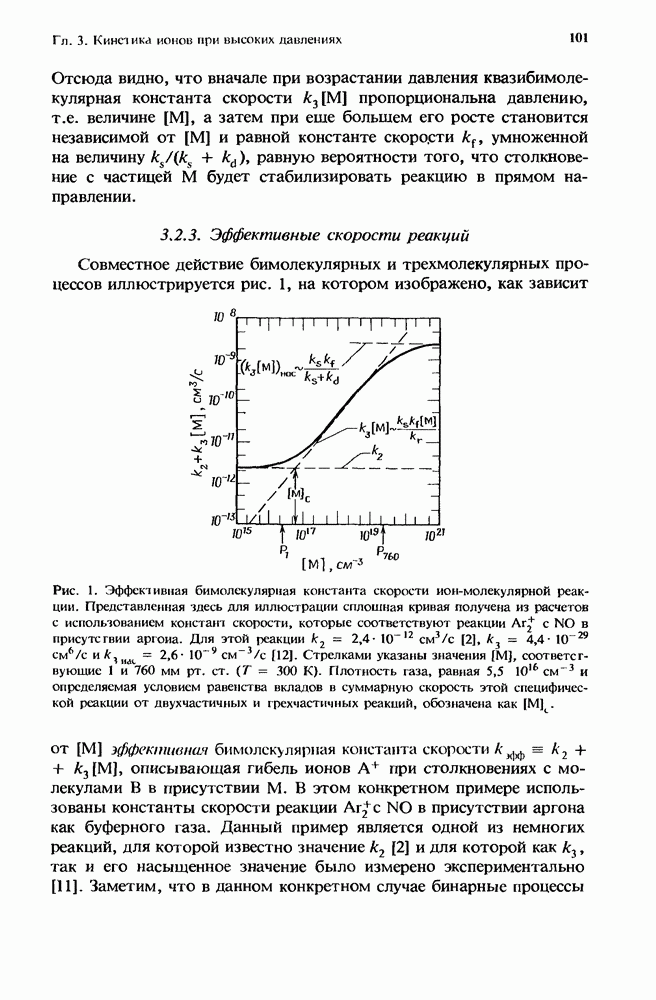
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
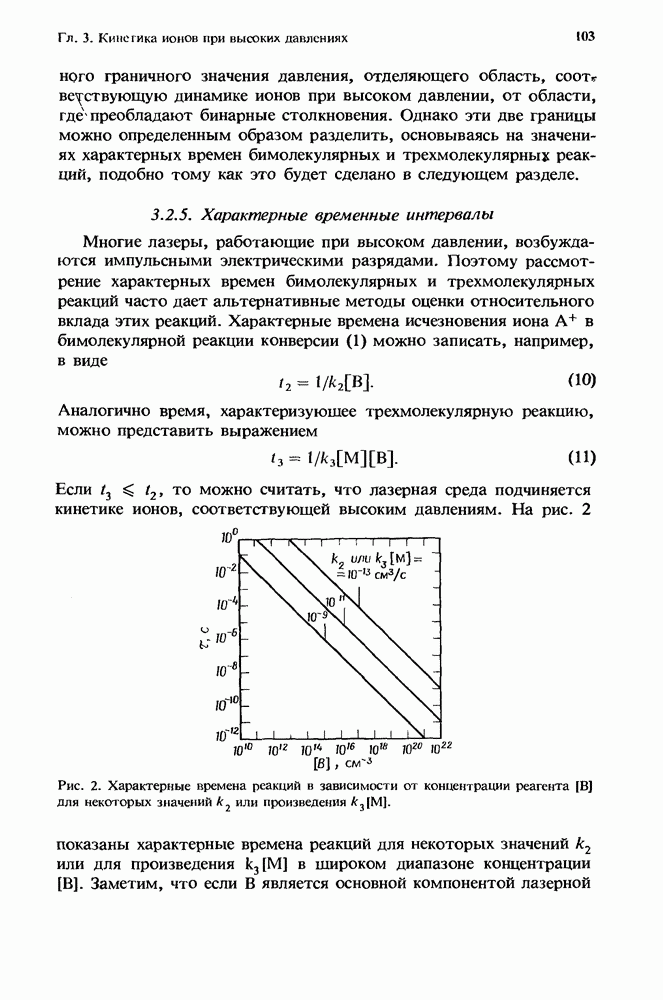
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
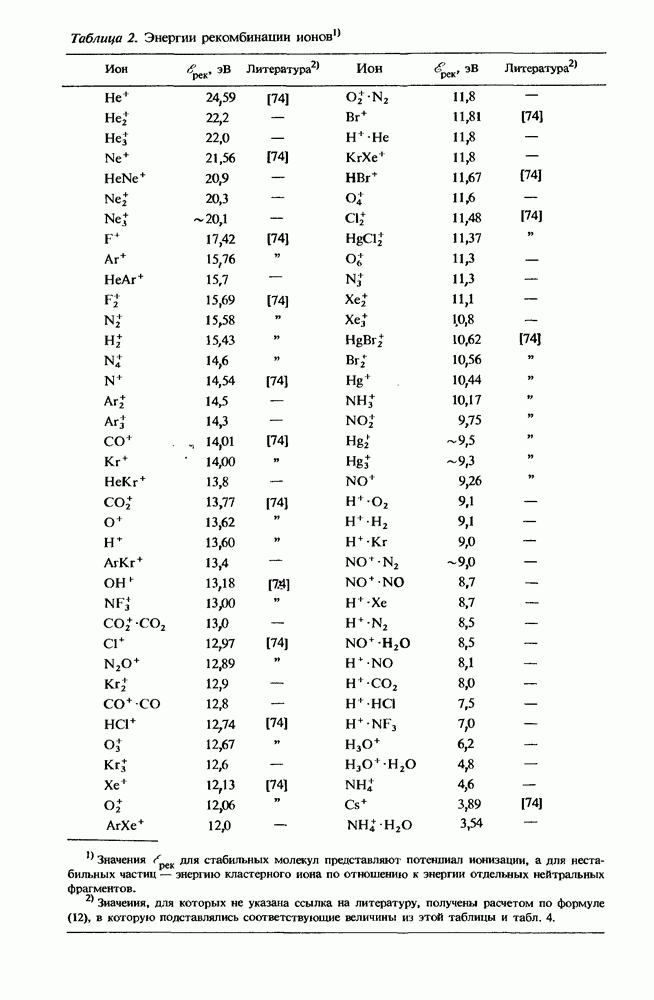
- 3.2.2. Энергетика отрицательных ионов
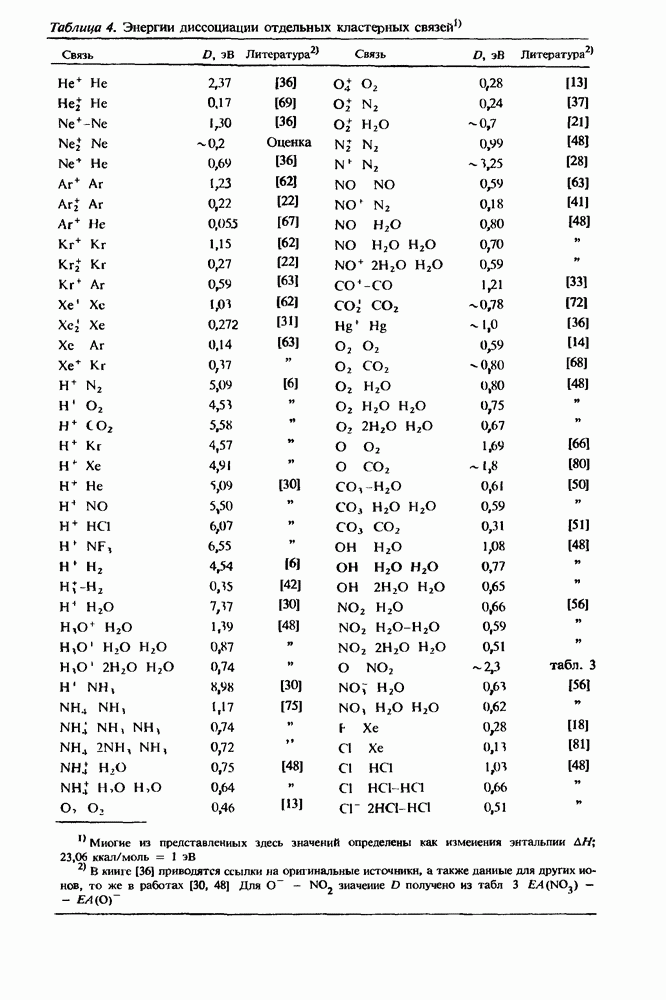
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
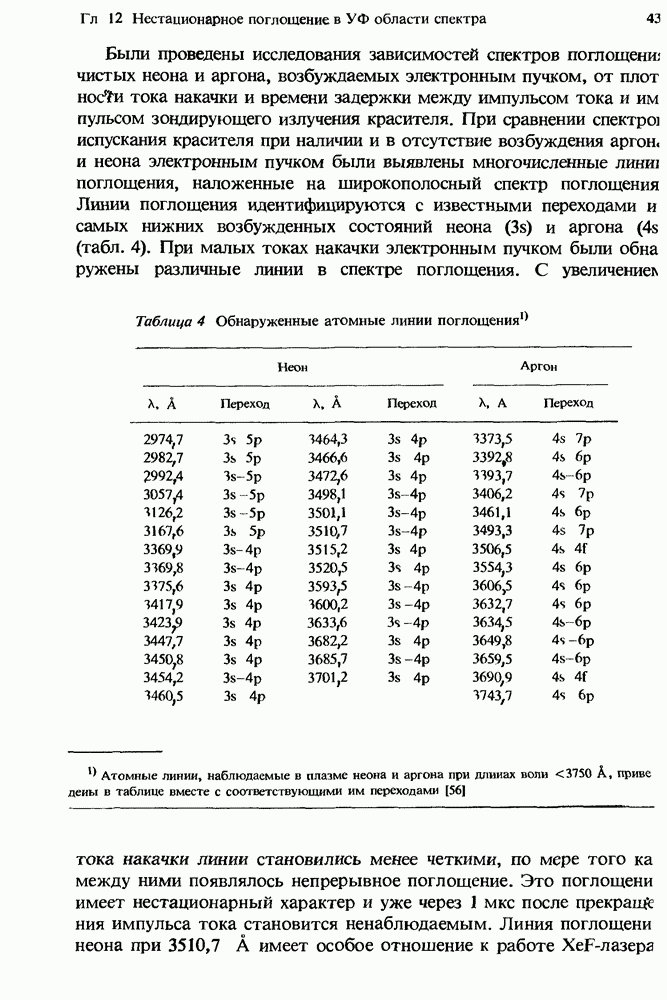
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
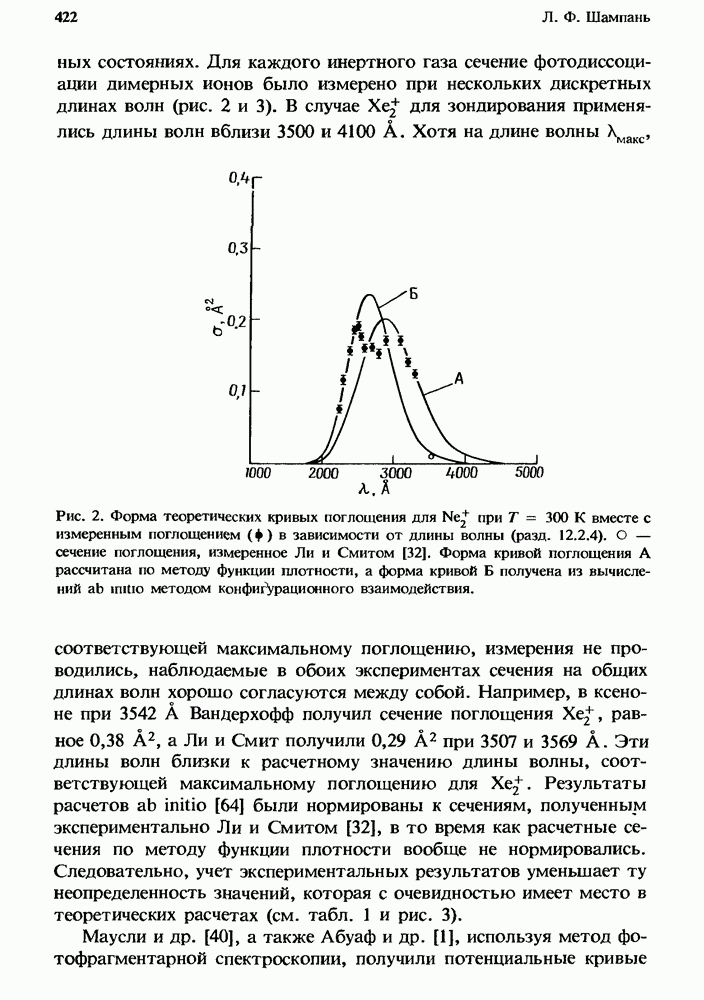
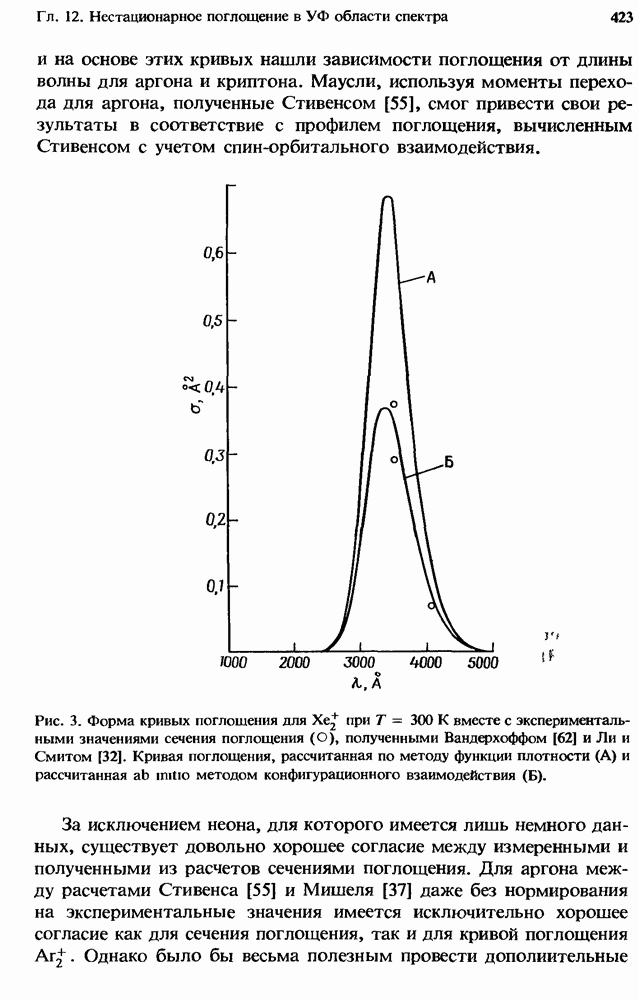
- 12.2.2. Сечение фотопоглощения
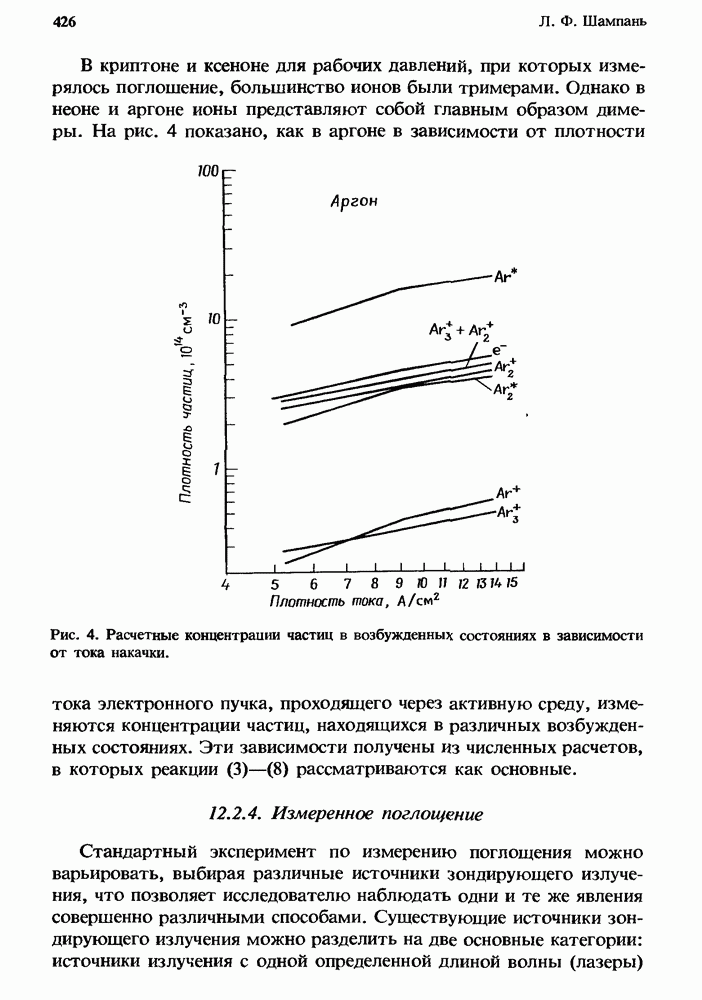
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
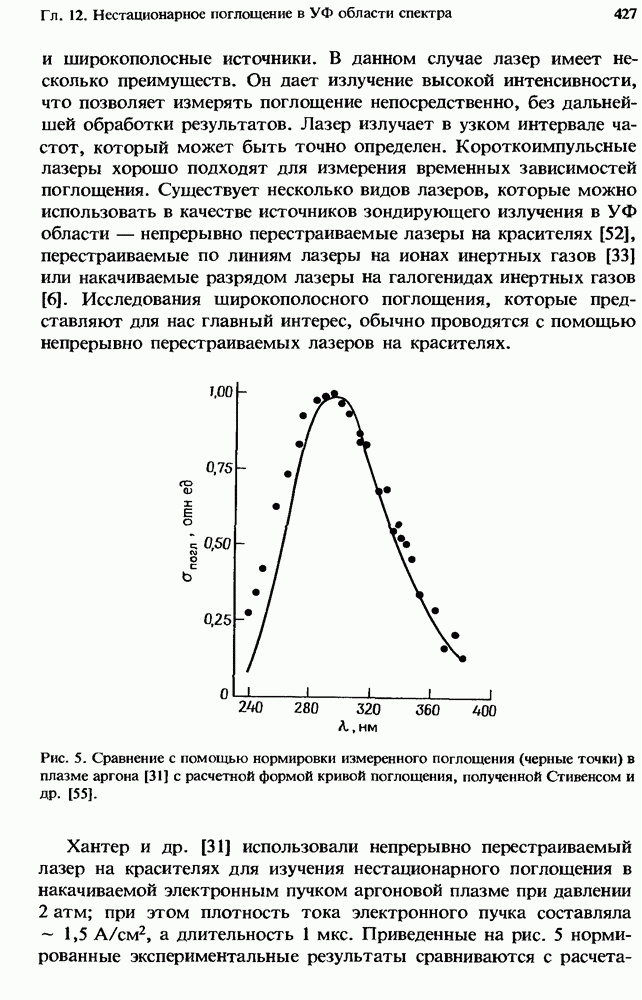
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации