| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Критический обзор экспериментальных данных
В этом разделе представлен обзор данных по прилипанию электронов к различным молекулам, используемым в газовых лазерах. В разд.  мы подробно обсудим данные по
мы подробно обсудим данные по  . В разд. 2.5.5 приведены отдельные результаты для
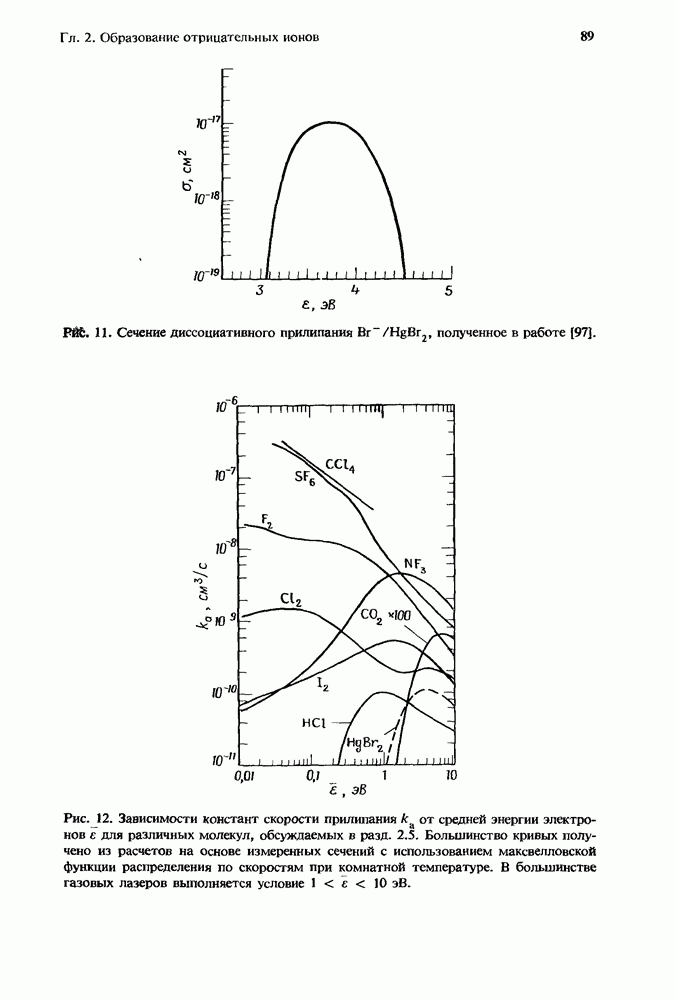
. В разд. 2.5.5 приведены отдельные результаты для  Па рис. 12 построены характерные для каждого газа зависимости
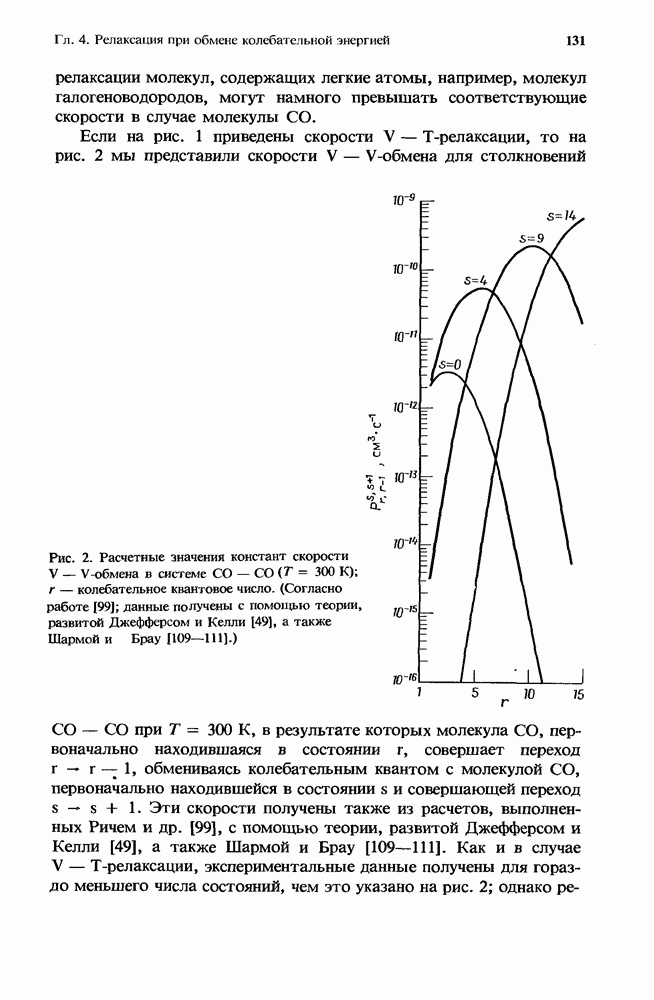
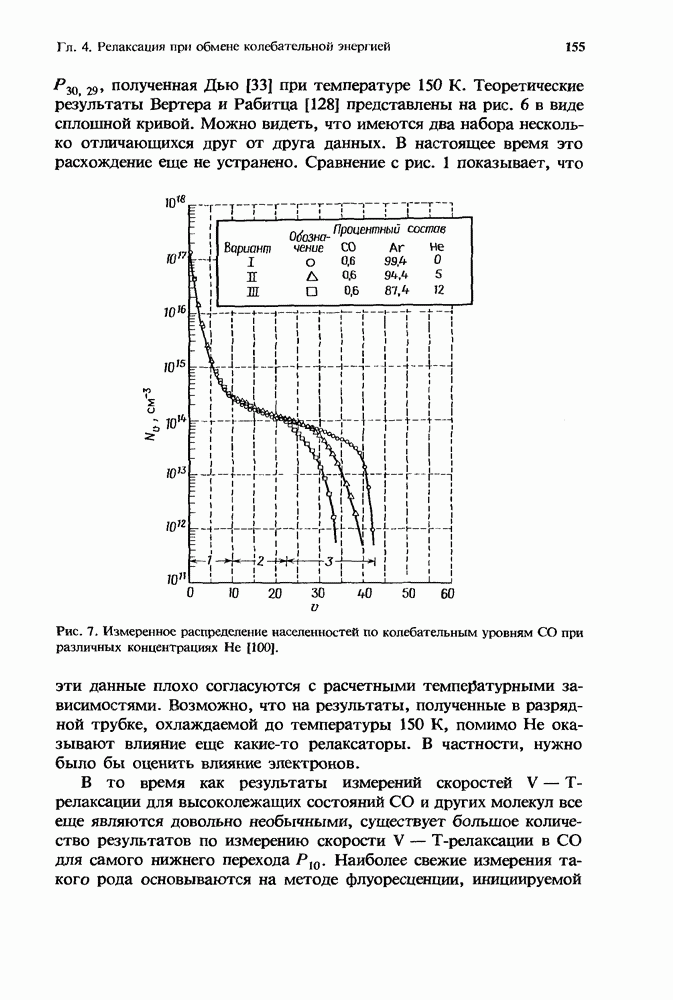
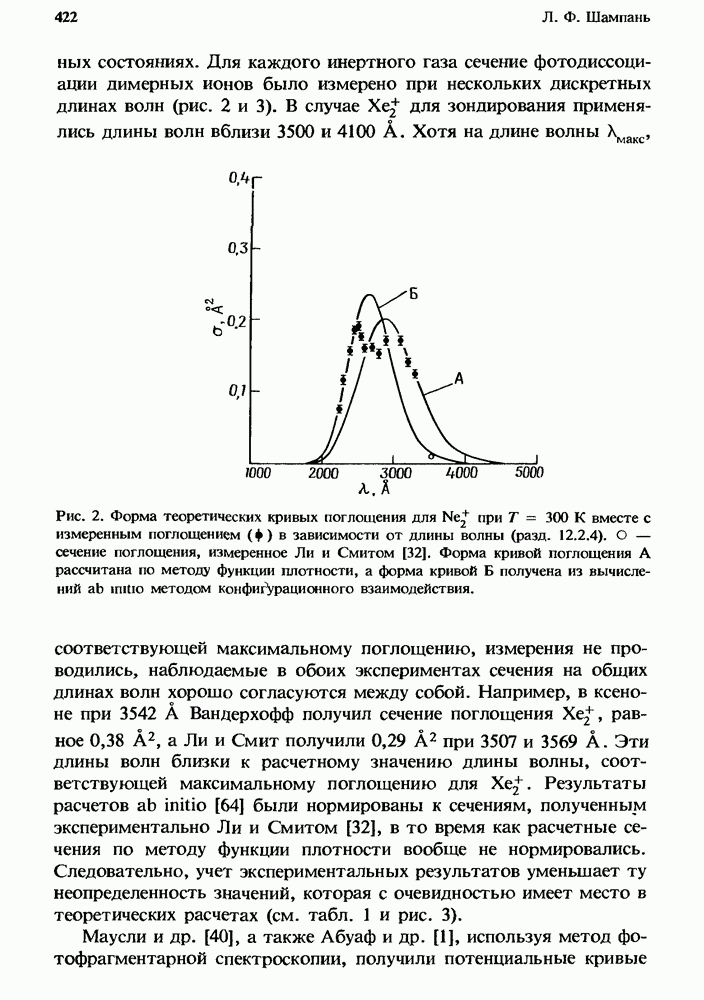
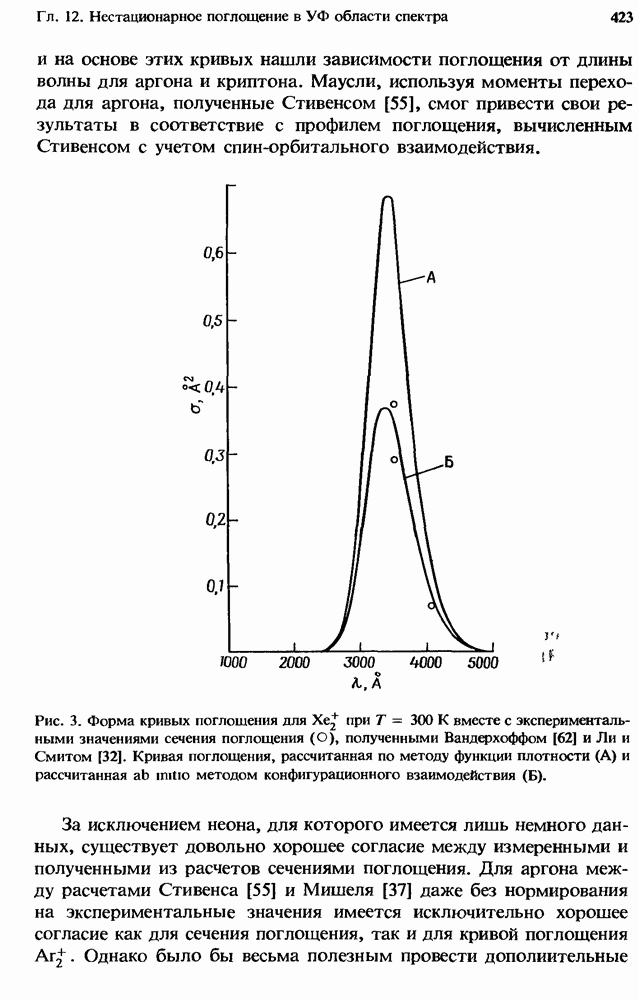
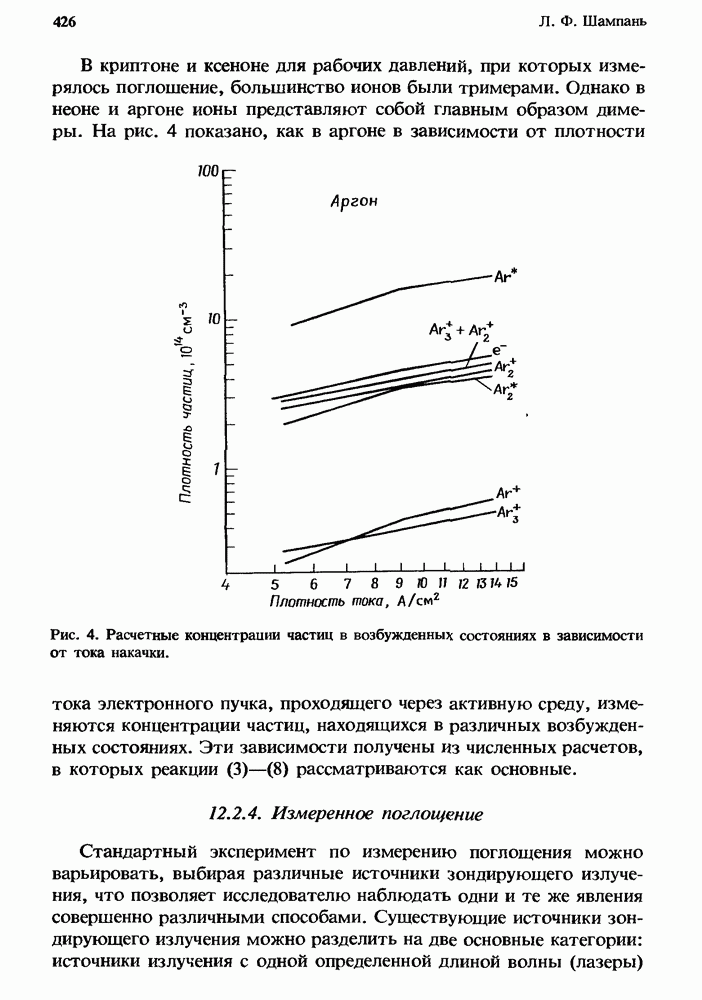
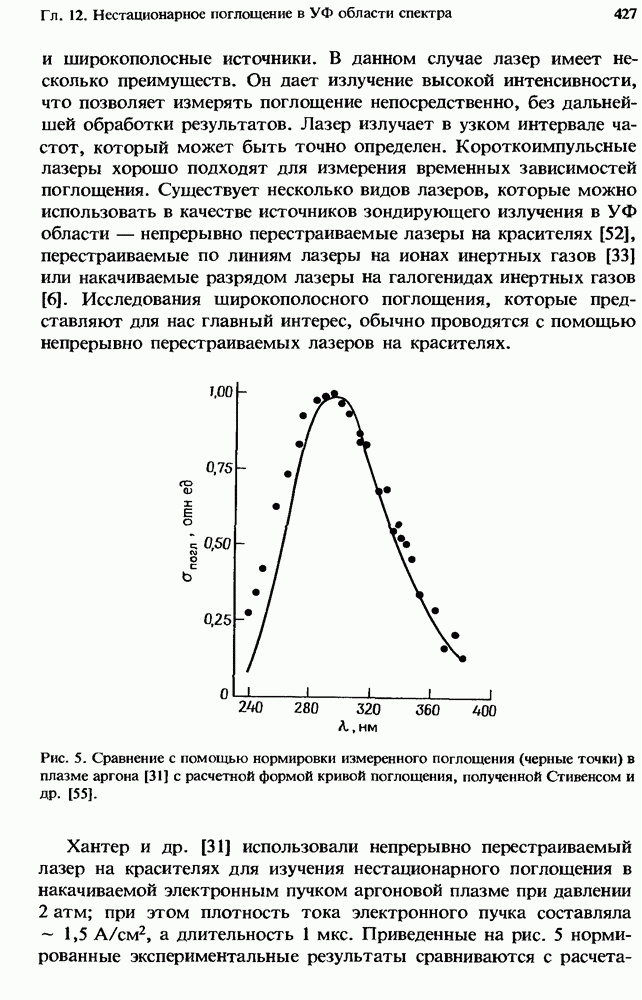
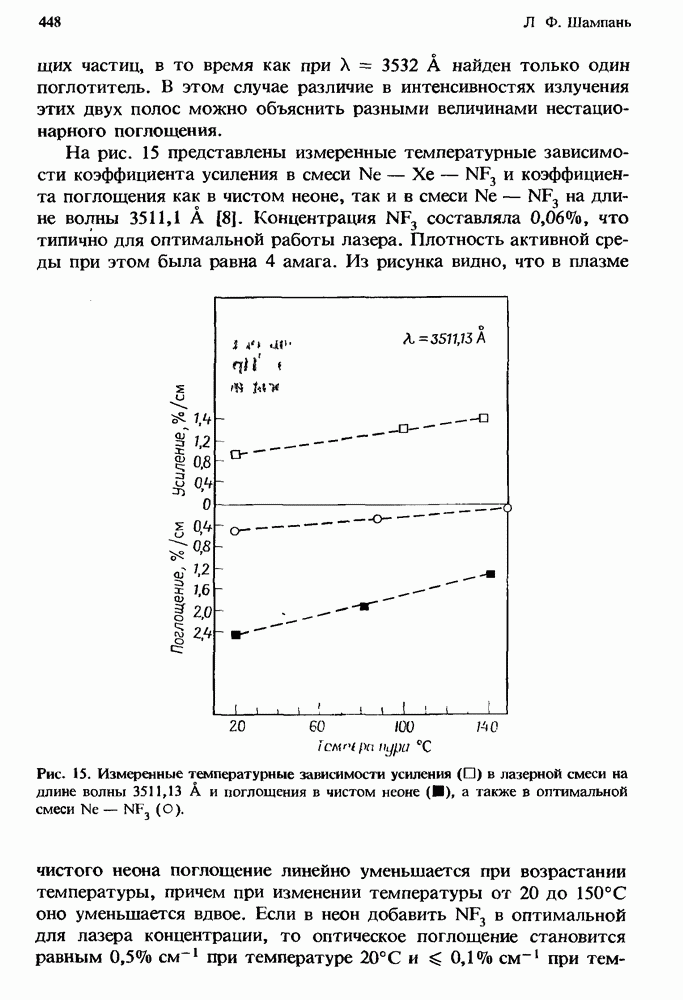
Па рис. 12 построены характерные для каждого газа зависимости  полученные путем интегрирования сечения совместно с максвелловской функцией распределения электронов по скоростям. Поэтому, хотя при рассмотрении какого-либо конкретного практического случая эти кривые можно использовать лишь для качественной оценки, они позволяют провести удобное сравнение относительных эффективностей прилипания для этих молекул в широком диапазоне средних энергий электронов.
полученные путем интегрирования сечения совместно с максвелловской функцией распределения электронов по скоростям. Поэтому, хотя при рассмотрении какого-либо конкретного практического случая эти кривые можно использовать лишь для качественной оценки, они позволяют провести удобное сравнение относительных эффективностей прилипания для этих молекул в широком диапазоне средних энергий электронов.
2.5.1. Фтор (F2)
До тех пор пока фтор не стали использовать в лазерах на молекулах фторидов инертных газов, имелись лишь данные по прилипанию электронов к этой молекуле, полученные в масс-спектрометрических измерениях, выполненных Де Корпо и др. [36], которые указали на то, что в этом случае процесс прилипания имеет место при низких энергиях. В этой работе, по-видимому, из-за трудностей, связанных с проведением экспериментов с электронным пучком при низких энергиях, форма кривой появления ионов  существенно отличается от тех, которые были получены в более поздних работах, рассматриваемых ниже. Аналогичные трудности, по-видимому, свели на нет измерения сечений, выполненные Махадеваном и Хофлендом [62], которым впоследствии пришлось пересмотреть свои заключения [63]. Сайдс и др. [86] для измерения коэффициентов прилипания использовали послесвечение в потоке при электронных температурах 350 и 600 К. Однако данные, полученные при этих электронных температурах, не имеют прямого
существенно отличается от тех, которые были получены в более поздних работах, рассматриваемых ниже. Аналогичные трудности, по-видимому, свели на нет измерения сечений, выполненные Махадеваном и Хофлендом [62], которым впоследствии пришлось пересмотреть свои заключения [63]. Сайдс и др. [86] для измерения коэффициентов прилипания использовали послесвечение в потоке при электронных температурах 350 и 600 К. Однако данные, полученные при этих электронных температурах, не имеют прямого  ношения к условиям, которые реализуются в разрядах, применяем
ношения к условиям, которые реализуются в разрядах, применяем  для накачки лазеров. Дело в том, что в таких разрядах
для накачки лазеров. Дело в том, что в таких разрядах  энергия электронов равна приблизительно 1 эВ и больше.
энергия электронов равна приблизительно 1 эВ и больше.
Измерения в диапазоне энергий  эВ выполнили Чен и др. [23]. Эти авторы использовали разряд с плоской конфигурацией, в котором плазма поддерживалась однородным пучком высокоэнергетических электронов. Проводимость плазмы, измеренная во всем интервале значений приложенного поля в смесях F2, разбавленных N2, сравнивалась с аналогичными данными для чистого газа N2. Таким образом на основе известного коэффициента электрон-ионной рекомбинации для
эВ выполнили Чен и др. [23]. Эти авторы использовали разряд с плоской конфигурацией, в котором плазма поддерживалась однородным пучком высокоэнергетических электронов. Проводимость плазмы, измеренная во всем интервале значений приложенного поля в смесях F2, разбавленных N2, сравнивалась с аналогичными данными для чистого газа N2. Таким образом на основе известного коэффициента электрон-ионной рекомбинации для  характерного для чистого N2, был получен коэффициент прилипания электронов к молекулам
характерного для чистого N2, был получен коэффициент прилипания электронов к молекулам 

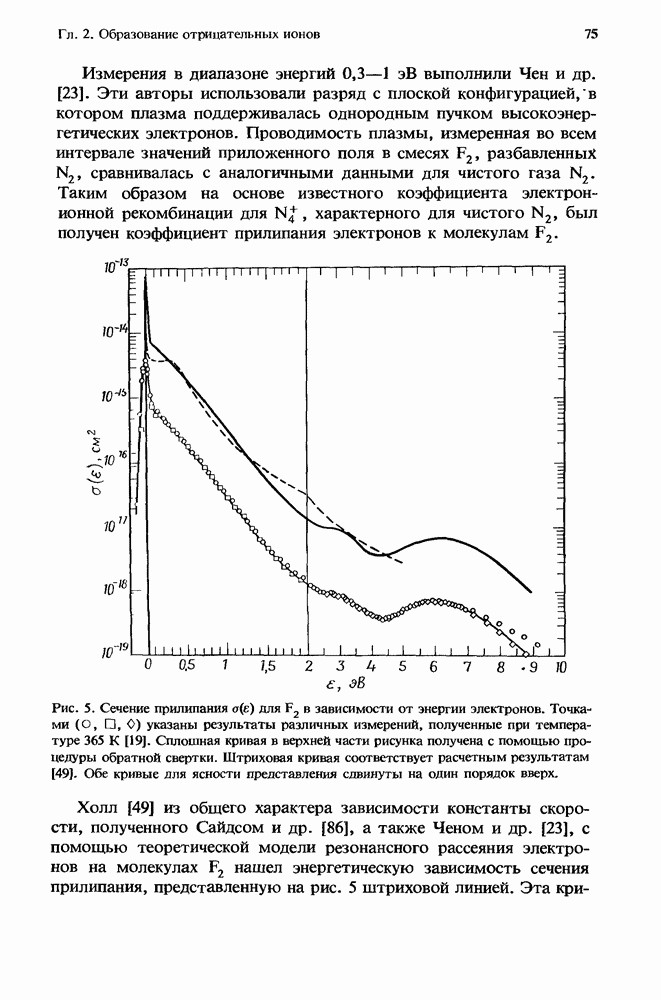
Рис. 5. Сечение прилипания  для F2 в зависимости от энергии электронов. Точками
для F2 в зависимости от энергии электронов. Точками  указаны результаты различных измерений, полученные при температуре 365 К [19]. Сплошная кривая в верхней части рисунка получена с помощью процедуры обратной свертки. Штриховая кривая соответствует расчетным результатам [49]. Обе кривые для ясности представления сдвинуты на один порядок вверх.
указаны результаты различных измерений, полученные при температуре 365 К [19]. Сплошная кривая в верхней части рисунка получена с помощью процедуры обратной свертки. Штриховая кривая соответствует расчетным результатам [49]. Обе кривые для ясности представления сдвинуты на один порядок вверх.
Холл [49] из общего характера зависимости константы скорости, полученного Сайдсом и др. [86], а также Ченом и др. [23], с помощью теоретической модели резонансного рассеяния электронов на молекулах F2 нашел энергетическую зависимость сечения прилипания, представленную на рис. 5 штриховой линией. Эта
кривая, как было показано, более или менее удовлетворительно согласуется с последующими измерениями.
Нигаард и др. [72] в экспериментах с дрейфовой трубкой, проведенных для разбавленных смесей F2 в Не, измеряли коэффициент прилипания  и скорость дрейфа электронов
и скорость дрейфа электронов  Произведение этих величин дает константу скорости
Произведение этих величин дает константу скорости  для конкретной газовой смеси, которая содержит такое количество F2, что это уже начинает оказывать влияние на функцию распределения электронов по энергиям. Трудности получения строгой интерпретации этих данных мы обсуждали в разд. 2.4. В данном случае авторы [72] имели возможность провести лишь качественное сравнение с результатами других измерений, причем им пришлось предположить, что средняя энергия электронов в смеси дается выражением
для конкретной газовой смеси, которая содержит такое количество F2, что это уже начинает оказывать влияние на функцию распределения электронов по энергиям. Трудности получения строгой интерпретации этих данных мы обсуждали в разд. 2.4. В данном случае авторы [72] имели возможность провести лишь качественное сравнение с результатами других измерений, причем им пришлось предположить, что средняя энергия электронов в смеси дается выражением  которое справедливо для чистого гелия. Эти авторы заметили, что на самом деле значение средней энергии почти наверняка меньше того, которое дается выражением
которое справедливо для чистого гелия. Эти авторы заметили, что на самом деле значение средней энергии почти наверняка меньше того, которое дается выражением 
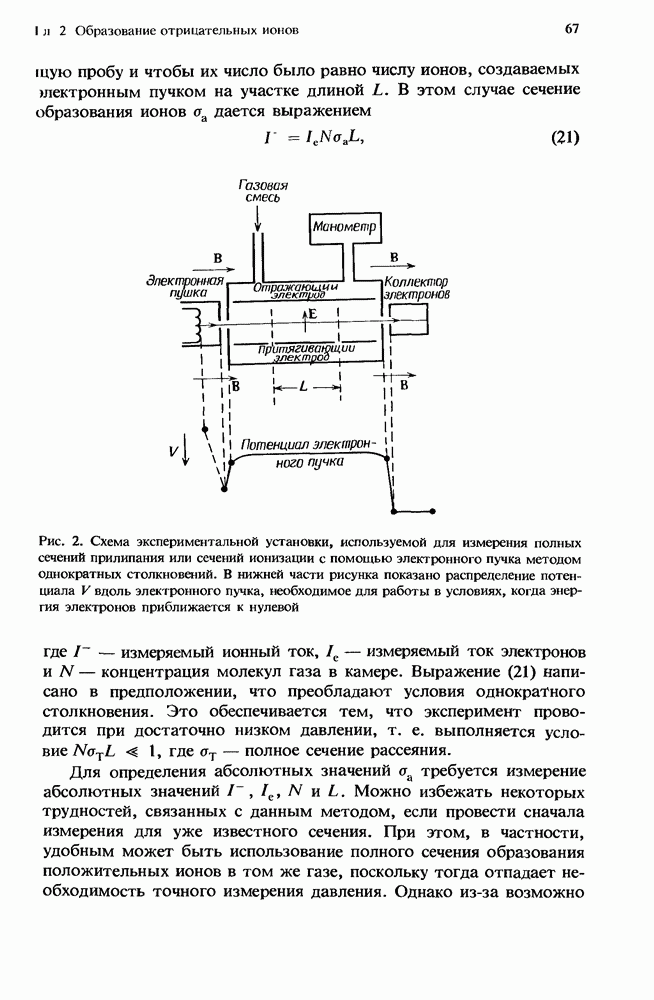
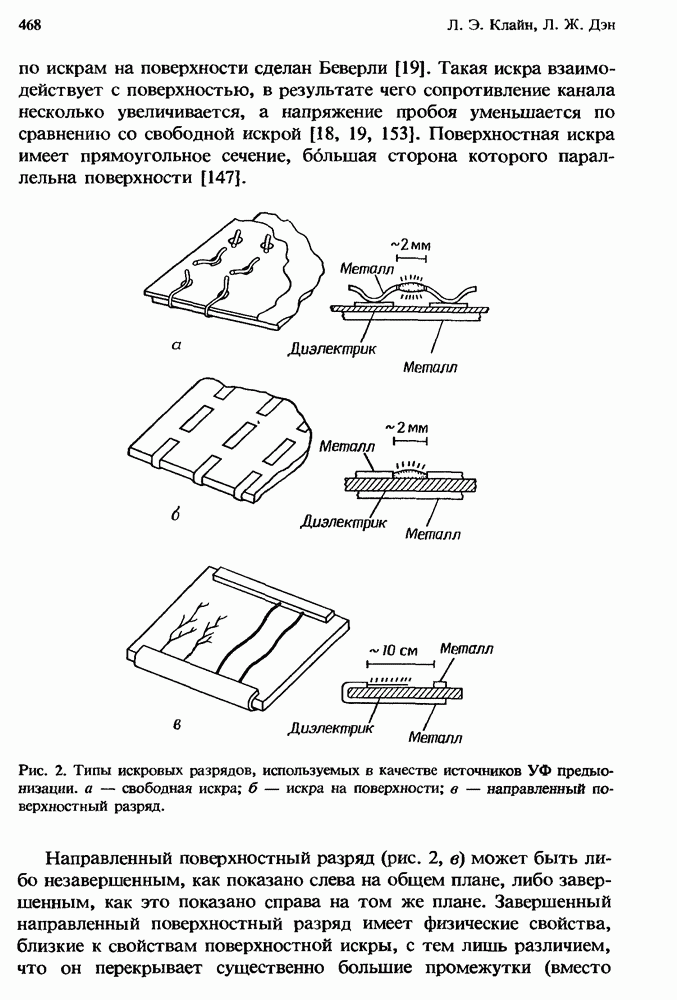
Там и Вонг [91], используя масс-спектрометр с хорошим разрешением, получили кривые появления отрицательных ионов в газообразном F2 (а также в других галогенах). Они обнаружили одиночный пик для иона F при энергиях, очень близких к нулевым, с «хвостом», простирающимся до 2 эВ. Такая особенность была подтверждена Чантри [19], который использовал метод полного собирания ионов на коллекторе с помощью камеры типа показанной на рис. 2. Метод задерживающего потенциала [47, 15] обеспечивал разрешение по энергиям около 0,08 эВ (полная ширина на полувысоте). Как форма, так и величина сечения измерялись в интервале энергий  эВ. Некоторые результаты измерений приведены на рис. 5, на котором различные данные, полученные в разных экспериментах, обозначены различными точками.
эВ. Некоторые результаты измерений приведены на рис. 5, на котором различные данные, полученные в разных экспериментах, обозначены различными точками.
Энергетическая шкала на рис. 5 откалибрована с использованием кривой задержек электронного пучка и положения пика, измеренного с хорошей точностью и соответствующего образованию ионов О- из  при энергии электронов 2,25 эВ [16]. Согласие результатов для этих двух калибровок подтверждает то, что пространственное распределение потенциала в столкновительной камере относительно апертуры пучка было выбрано правильно, так что отражение электронного пучка происходило внутри камеры. При этом установлено, что энергетическая шкала прокалибрована с точностью не хуже ±0,1 эВ, а пик, соответствующий области низких энергий, появляется при нулевой энергии. V
при энергии электронов 2,25 эВ [16]. Согласие результатов для этих двух калибровок подтверждает то, что пространственное распределение потенциала в столкновительной камере относительно апертуры пучка было выбрано правильно, так что отражение электронного пучка происходило внутри камеры. При этом установлено, что энергетическая шкала прокалибрована с точностью не хуже ±0,1 эВ, а пик, соответствующий области низких энергий, появляется при нулевой энергии. V
Полное измерение энергетической зависимости сечения проводилось при разных давлениях с различными значениями поля,
вытягивающего ионы. Эти данные проверялись с помощью масс-спектрометрических измерений ионов  отбираемых щелью в электроде, собирающем ионы. Величина сечения была получена путем сравнения ионного сигнала, измеренного при данной энергии, с пиковыми сигналами, соответствующими реакциям образования
отбираемых щелью в электроде, собирающем ионы. Величина сечения была получена путем сравнения ионного сигнала, измеренного при данной энергии, с пиковыми сигналами, соответствующими реакциям образования
О из  имеющими известные сечения [78]. Оказалось, что результаты различаются в два раза. Это объясняется разной эффективностью собирания ионов вследствие существенного различия в кинетических энергиях ионов
имеющими известные сечения [78]. Оказалось, что результаты различаются в два раза. Это объясняется разной эффективностью собирания ионов вследствие существенного различия в кинетических энергиях ионов  , образующихся из
, образующихся из  и ионов
и ионов  , образующихся из
, образующихся из  Поскольку в важной для лазеров области энергий электронов ионы
Поскольку в важной для лазеров области энергий электронов ионы  образующиеся из F2, имеют промежуточное значение энергии, для окончательной калибровки использовалось среднее между калибровками для случаев
образующиеся из F2, имеют промежуточное значение энергии, для окончательной калибровки использовалось среднее между калибровками для случаев  Результатам, соответствующим интервалу энергий
Результатам, соответствующим интервалу энергий  эВ, был приписан доверительный интервал ±30%. При более высоких энергиях значение сечения может оказаться заниженным вследствие трудностей собирания ионов, связанных с возрастанием их кинетической энергии.
эВ, был приписан доверительный интервал ±30%. При более высоких энергиях значение сечения может оказаться заниженным вследствие трудностей собирания ионов, связанных с возрастанием их кинетической энергии.
Область энергий ниже 0,1 эВ требует специального рассмотрения. Полученные данные явно свидетельствуют в пользу того, что ширина исследуемого пика определяется тем, какое мы имеем разрешение по энергиям электронов. В этом случае полученные результаты дают лишь верхнюю границу реальной ширины пика и оценку интегрального сечения. Указанная оценка может быть получена только при условии, что точно известно положение минимума энергии электронного пучка в столкновительной камере. Если этот минимум расположен близко к выходному концу камеры, то, отражаясь при очень низких энергиях, электроны в среднем дважды проходят через область взаимодействия. Кроме того, электроны, прошедшие назад через входное отверстие, могут вновь отразиться потенциалом электронной пушки и еще раз пройти через столкновительную камеру. Опыт [17] показал, что это приводит к увеличению эффективного пути более чем в  раза. Представленная на рис. 5 кривая, построенная по экспериментальным точкам, дает значение интегрального сечения в области энергий ниже 0,1 эВ, равное
раза. Представленная на рис. 5 кривая, построенная по экспериментальным точкам, дает значение интегрального сечения в области энергий ниже 0,1 эВ, равное  эВ. Если это значение поправить с учетом указанного выше множителя, то сечение оказывается равным
эВ. Если это значение поправить с учетом указанного выше множителя, то сечение оказывается равным  эВ. Однако при этом нужно отдавать себе отчет в том, что мы можем занизить величину интегрального сечения, но ни в коем случае не завысить. Приведенные в табл. 1 числовые данные
эВ. Однако при этом нужно отдавать себе отчет в том, что мы можем занизить величину интегрального сечения, но ни в коем случае не завысить. Приведенные в табл. 1 числовые данные  для энергий меньше 0,1 эВ соответствуют указанной выше поправке и графически представлены сплошной кривой в верхней
для энергий меньше 0,1 эВ соответствуют указанной выше поправке и графически представлены сплошной кривой в верхней
Таблица 1. (см. скан) Сечения прилипания для F2
части рис. 5, где для сравнения приведена также теоретическая кривая Холла [49]. Мы считаем, что при энергиях электронов больше — 0,25 эВ согласие очень хорошее. При построении сплошной кривой на рис. 5 была сделана попытка выделить в сечении резкий пик при нулевой энергии. Используемая при этом для сечения функция  выбрана из соображений удобства и является чисто умозрительной, однако соответствующее ей интегральное еечение совпадает с ранее полученным значением.
выбрана из соображений удобства и является чисто умозрительной, однако соответствующее ей интегральное еечение совпадает с ранее полученным значением.
На рис. 6 приведена в виде сплошной кривой зависимость константы скорости прилипания от средней энергии электронов  полученная сверткой сечений, приведенных на рис. 5 и в табл. 1, с максвелловской функцией распределения электронов по энергиям. Там же для сравнения приведены данные, взятые из других источников. Шнайдер и Брау [82] получили результаты путем измерения проводимости в распадающейся плазме между двумя параллельными плоскими электродами в смесях F2, разбавленных
полученная сверткой сечений, приведенных на рис. 5 и в табл. 1, с максвелловской функцией распределения электронов по энергиям. Там же для сравнения приведены данные, взятые из других источников. Шнайдер и Брау [82] получили результаты путем измерения проводимости в распадающейся плазме между двумя параллельными плоскими электродами в смесях F2, разбавленных  Эти
Эти
измерения привели к значениям средней энергии электронов вблизи соответственно 1 и 3 эВ. Зависимость сечения от энергии, полученная Шнайдером и Брау, имеет такой же вид, как и в работах других авторов, однако сечения получены с более высокими значениями.

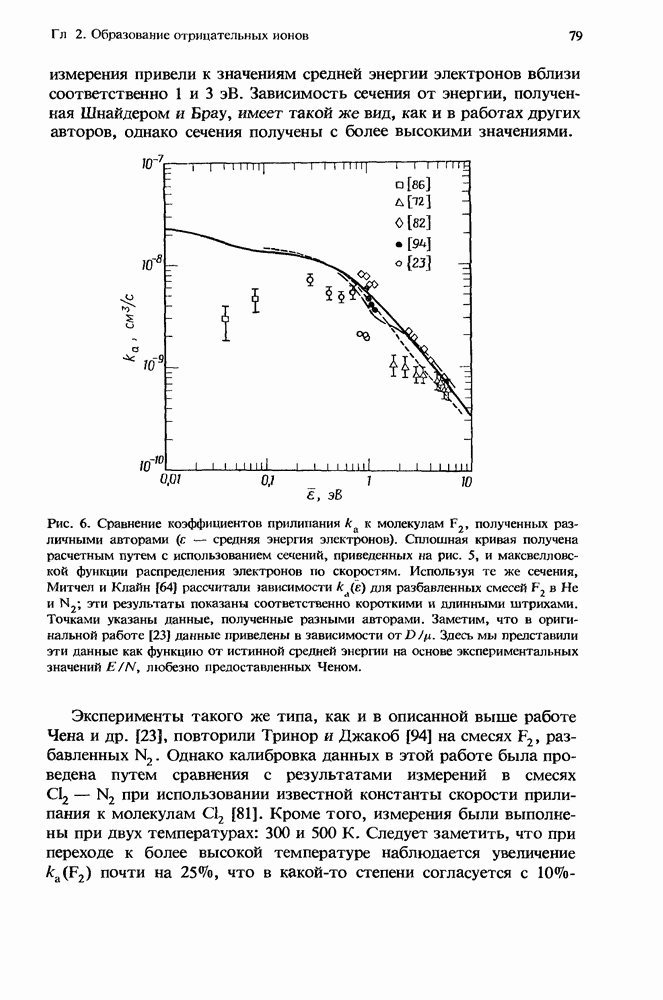
Рис. 6. Сравнение коэффициентов прилипания к а к молекулам F2, полученных различными авторами (с — средняя энергия электронов). Сплошная кривая получена расчетным путем с использованием сечений, приведенных на рис. 5, и максвелловской функции распределения электронов по скоростям. Используя те же сечения, Митчел и Клайн [64] рассчитали гависимости  для разбавленных смесей F2 в Не и
для разбавленных смесей F2 в Не и  эти результаты показаны соответственно короткими и длинными штрихами. Точками указаны данные, полученные разными авторами. Заметим, что в оригинальной работе [23] данные приведены в зависимости от
эти результаты показаны соответственно короткими и длинными штрихами. Точками указаны данные, полученные разными авторами. Заметим, что в оригинальной работе [23] данные приведены в зависимости от  Здесь мы представили эти данные как функцию от истинной средней энергии на основе экспериментальных значений E/N, любезно предоставленных Ченом.
Здесь мы представили эти данные как функцию от истинной средней энергии на основе экспериментальных значений E/N, любезно предоставленных Ченом.
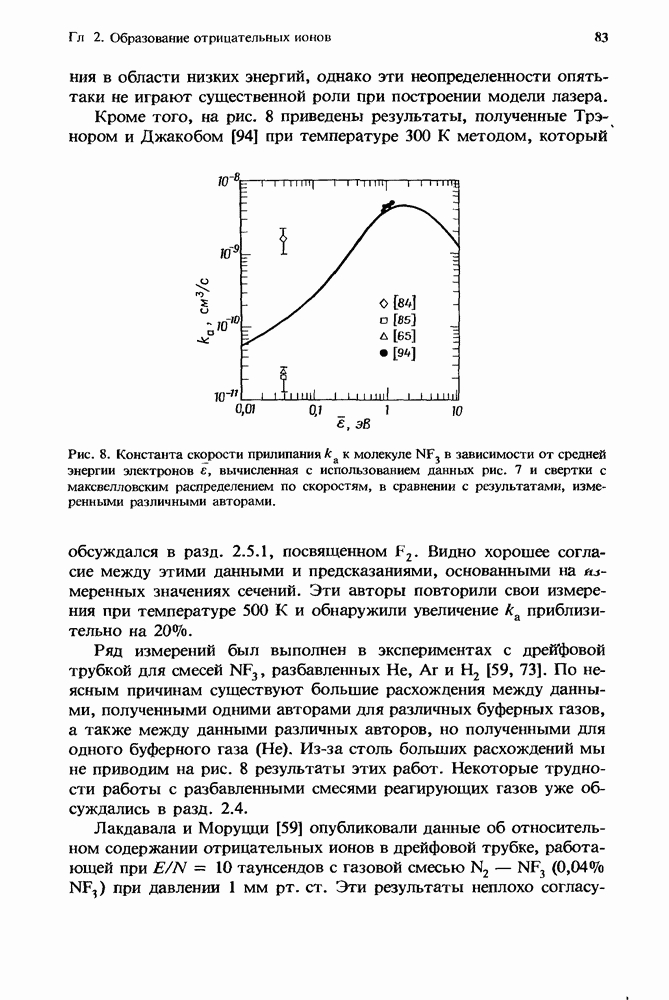
Эксперименты такого же типа, как и в описанной выше работе Чена и др. [23], повторили Тринор и Джакоб [94] на смесях F2, разбавленных N2. Однако калибровка данных в этой работе была проведена путем сравнения с результатами измерений в смесях  при использовании известной константы скорости прилипания к молекулам
при использовании известной константы скорости прилипания к молекулам  Кроме того, измерения были выполнены при двух температурах: 300 и 500 К. Следует заметить, что при переходе к более высокой температуре наблюдается увеличение
Кроме того, измерения были выполнены при двух температурах: 300 и 500 К. Следует заметить, что при переходе к более высокой температуре наблюдается увеличение  почти на 25%, что в какой-то степени согласуется с 10%-ным
почти на 25%, что в какой-то степени согласуется с 10%-ным
возрастанием этой величины, предсказываемым теоретической моделью Холла [49].
На рис. 6 представлены фактически все имеющиеся количественные данные для  в случае
в случае  Каждая из трех кривых построена на основе сечений, измеренных Чантри [17] и приведенных в табл. 1 и на рис. 5. Сплошная кривая соответствует максвелловскому распределению электронов по скоростям. Кривая с длинными штрихами отвечает дрейфу электронов в N2, а кривая с короткими штрихами — дрейфу электронов в Не [64].
Каждая из трех кривых построена на основе сечений, измеренных Чантри [17] и приведенных в табл. 1 и на рис. 5. Сплошная кривая соответствует максвелловскому распределению электронов по скоростям. Кривая с длинными штрихами отвечает дрейфу электронов в N2, а кривая с короткими штрихами — дрейфу электронов в Не [64].
Для энергий электронов выше примерно 0,5 эВ согласие между различными данными оказывается вполне удовлетворительным, что позволяет выделить по крайней мере общую тенденцию увеличения  с ростом средней энергии, причем разница в значениях
с ростом средней энергии, причем разница в значениях  находится в пределах множителя 2. Однако при тепловых энергиях наблюдается серьезное расхождение в результатах. По соображениям, первоначально высказанным по поводу измерений при энергиях ниже 0,1 эВ в связи с рис. 5, можно сформулировать общее правило, согласно которому скорости прилипания, полученные в прямых измерениях при тепловых энергиях [86], следует рассматривать как более надежные по сравнению с экспериментами, в которых используются электронные пучки очень низкой энергии. Заметим, однако, что Сайдс и др. [86] измерили также
находится в пределах множителя 2. Однако при тепловых энергиях наблюдается серьезное расхождение в результатах. По соображениям, первоначально высказанным по поводу измерений при энергиях ниже 0,1 эВ в связи с рис. 5, можно сформулировать общее правило, согласно которому скорости прилипания, полученные в прямых измерениях при тепловых энергиях [86], следует рассматривать как более надежные по сравнению с экспериментами, в которых используются электронные пучки очень низкой энергии. Заметим, однако, что Сайдс и др. [86] измерили также  для молекул
для молекул  причем они получили значения, которые в 5—8 раз меньше общепринятых значений этой величины. Как видно из рис. 6, характер расхождения между данными по скоростям прилипания для F2, полученными этими авторами, и данными, предсказываемыми на основе измеренных сечений, такой же.
причем они получили значения, которые в 5—8 раз меньше общепринятых значений этой величины. Как видно из рис. 6, характер расхождения между данными по скоростям прилипания для F2, полученными этими авторами, и данными, предсказываемыми на основе измеренных сечений, такой же.
Бэрдсли и др. [11], а также Хази и др. [51] недавно выполнили дополнительные теоретические расчеты сечений прилипания. Полученные теми и другими авторами результаты неплохо согласуются с данными, приведенными на рис. 5, при энергиях  эВ. Однако эти авторы указывают на то, что при
эВ. Однако эти авторы указывают на то, что при  сечение прямого диссоциативного прилипания, протекающего с участием состояния
сечение прямого диссоциативного прилипания, протекающего с участием состояния  должно быть равно нулю. Следовательно, на рис. 5 зависимость сечения для энергий, меньших 0,15 эВ, нельзя объяснить только этим процессом. Ясно, что для уменьшения неопределенности в значениях сечений прилипания при низких энергиях электронов должны быть проведены дополнительные эксперименты с использованием электронного облака или метода послесвечения. Следует заметить, что в области энергий, используемых в лазерной среде, величина
должно быть равно нулю. Следовательно, на рис. 5 зависимость сечения для энергий, меньших 0,15 эВ, нельзя объяснить только этим процессом. Ясно, что для уменьшения неопределенности в значениях сечений прилипания при низких энергиях электронов должны быть проведены дополнительные эксперименты с использованием электронного облака или метода послесвечения. Следует заметить, что в области энергий, используемых в лазерной среде, величина  малочувствительна к значениям сечений при
малочувствительна к значениям сечений при  эВ.
эВ.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
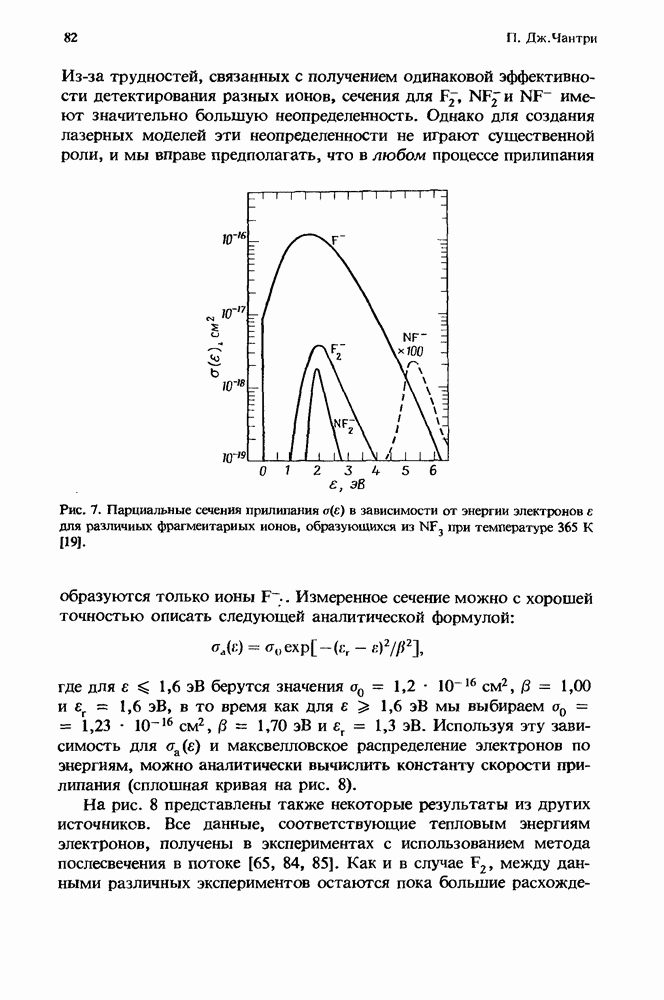
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
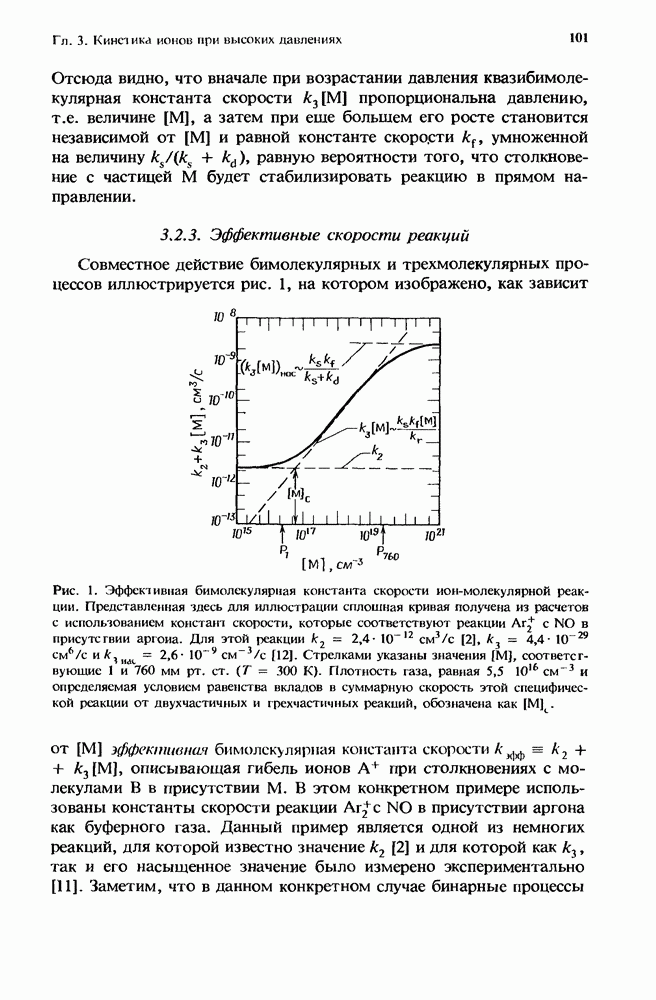
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
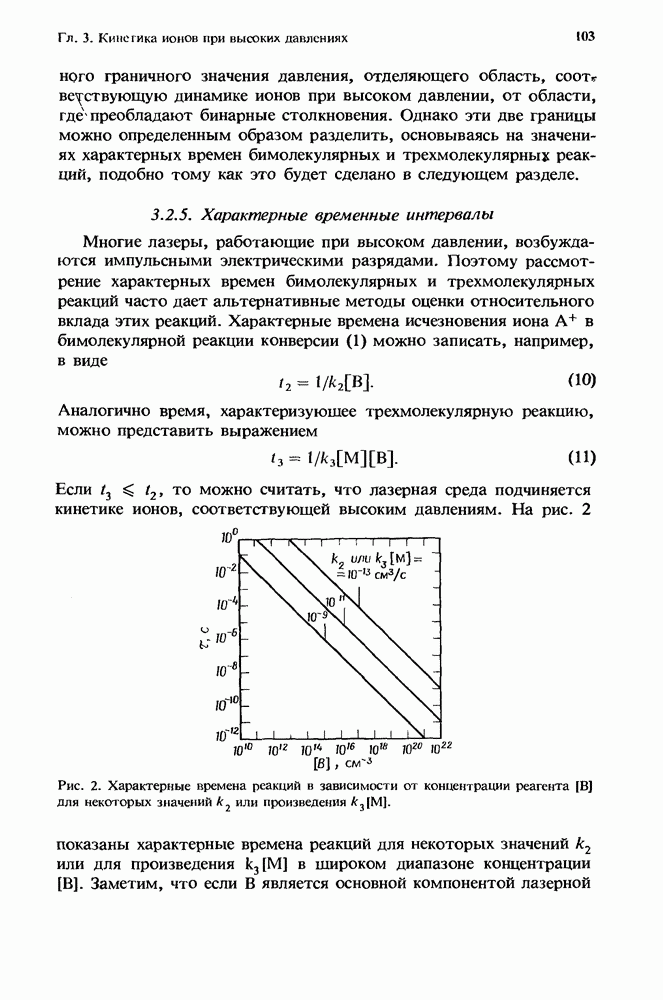
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
- 12.2.4. Измеренное поглощение
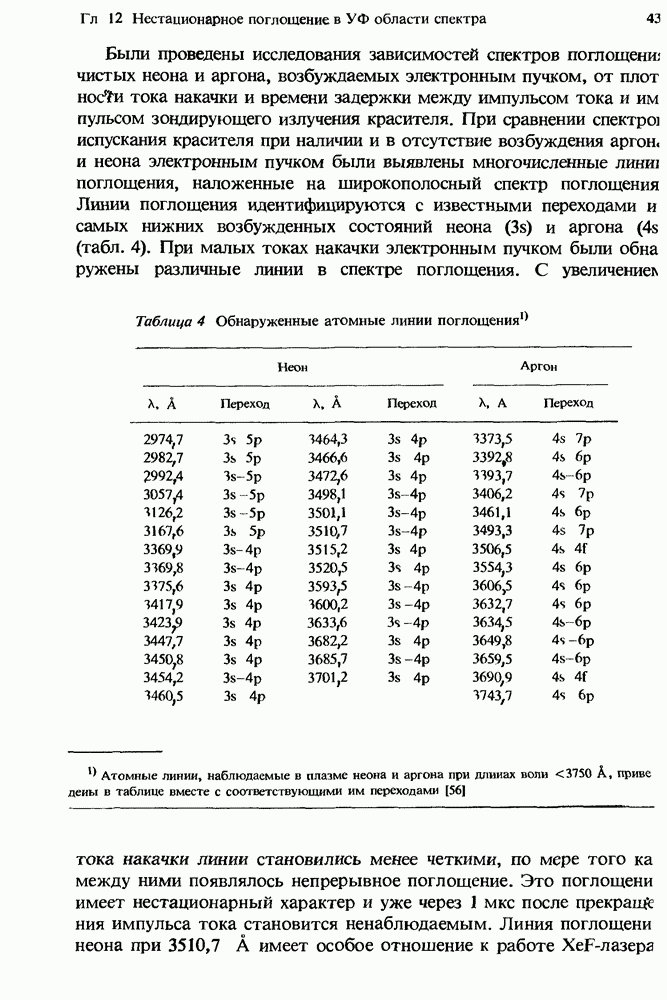
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации