5.2.2. Промежуточные значения плотности газа

В настоящее время обсуждаются два метода, базирующиеся на использовании соответственно точных граничных квазиравновесных значений при низких плотностях и граничных значений при высоких плотностях газа. Следствием каждого из этих методов, применяемых в рамках теории, основанной на рассмотрении процесса переноса ионов, является либо конечное значение константы скорости [29], либо универсальная кривая Бейтса. Эти методы можно рекомендовать для определения зависимости а от Из фундаментальной теории следует, что для коэффициента рекомбинации а можно получить следующее точное соотношение (разд. 5.3):

где и — соответственно константа скорости и коэффициент переноса, связанные с микроскопическими трехчастичными столкновениями и с диффузионным дрейфом. При малых плотностях газа имеет место предельный переход а причем ионы находятся в состоянии квазибольцмановского равновесия. Большие плотности газа соответствуют предельному переходу и в этом случае распределение ионов существенно отклоняется от больцмановского. Таким образом, фундаментальная теория дает прочное теоретическое обоснование выражению (6), которое следует из (см. [12]) выражения для а, данного в работе Натансона [43] и имеющего поразительную аналогию с формулами теории электрических цепей [3].

5.2.2.1. Константы скорости и коэффициенты переноса

Коэффициент рекомбинации ионов равен константе скорости при условии, что, как и в случае малой плотности, в системе ионов поддерживается больцмановское распределение [29]. Предположим, что реакция обусловлена сильными столкновениями с газом каждого из ионов составляющих ионную пару с внутренним расстоянием между ядрами Таким образом, для ионов со средней длиной свободного пробега X можно написать следующее выражение:

где — некоторая усредненная скорость сближения ионов; — наименьшее из и Коэффициент фокусировки

определяет траекторию относительного движения ионов в поле потенциала в отличие от прямолинейных траекторий, которые учитывались при выводе выражения (5), описывающего вероятность столкновения ионов с нейтралами. Входящая в выражение (7) величина

учитывает больцмановское возрастание плотности ионов в поле, действующем на расстоянии ., на котором происходит последнее (неэффективное) столкновение иона с нейтральной частицей непосредственно перед входом иона в область рекомбинации радиусом Если в выражении (8) взять среднее, а не среднекгадратичное значение скорости, как это сделано здесь, то мы получим . Вероятность одновременного столкновения в области радиусом равна и из простых геометрических соображений следует, что множитель в выражении (7) равен либо либо в зависимости от того, равен ли радиус величине или соответственно. Поскольку в среднем прерывание движения ионов не происходит только для расстояний между ионами в интервале между , и начальную кинетическую энергию относительного движения ионов можно записать в виде

Если конечная кинетическая энергия Т ионной пары недостаточна для преодоления силы ион-ионного притяжения, действующего между столкновениями, соответствующими средней длине свободного пробега, т.е. при выполнении неравенства

которое при в пределе исчезающе малых сводится к томсоновскому условию, то расстояние R между двумя ионами при столкновении ионной пары с нейтралом не может увеличиться до . Параметр столкновения 6. таков, что разность равна В этом случае для чисто кулоновского притяжения критерий (11) дает следующее значение радиуса захвата:

Этот радиус монотонно уменьшается с X. и удовлетворяет условию Томсоновский радиус равен Следует заметить, что внутри сферы радиусом существенной для процесса рекомбинации, потенциал ион-ионного взаимодействия удовлетворяет условию , следовательно, при больших становится невозможной линеаризация уравнения Пуассона для V, для которой необходимо выполнение условия разд. 5.3.3), за исключением асимптотически малых значений фактически несущественных для протекания реакции. При малых плотностях предельным значением является так что в этом случае коэффициент рекомбинации (7) принимает предельное значение

где величина

представляет собой парциальный томсоновский коэффициент рекомбинации, соответствующий Таким образом, если известно отношение точных квазиравновесных предельных значений соответствующих малым плотностям, то для различных интересующих нас систем можно получить параметр столкновений , решая уравнение

Следовательно, величину входящую в выражение (6), можно определить непосредственно из выражений и (15). В ранних работах [31—33] было выведено и использовано выражение для 6., построенное на принципах классической механики в зависимости от масс М ионов и частиц нейтрального газа Недавно на основе рассмотрения условий точного квазиравновесия была получена [24, 25] зависимость отношения 3? от масс частиц, участвующих в процессе, для двух следующих реакций:

В реакции (16) переходы между энергетическими уровнями обусловлены упругими столкновениями ионов с нейтралами, а в реакции (17) помимо упругих столкновений происходят также столкновения, соответствующие симметричной резонансной перезарядке

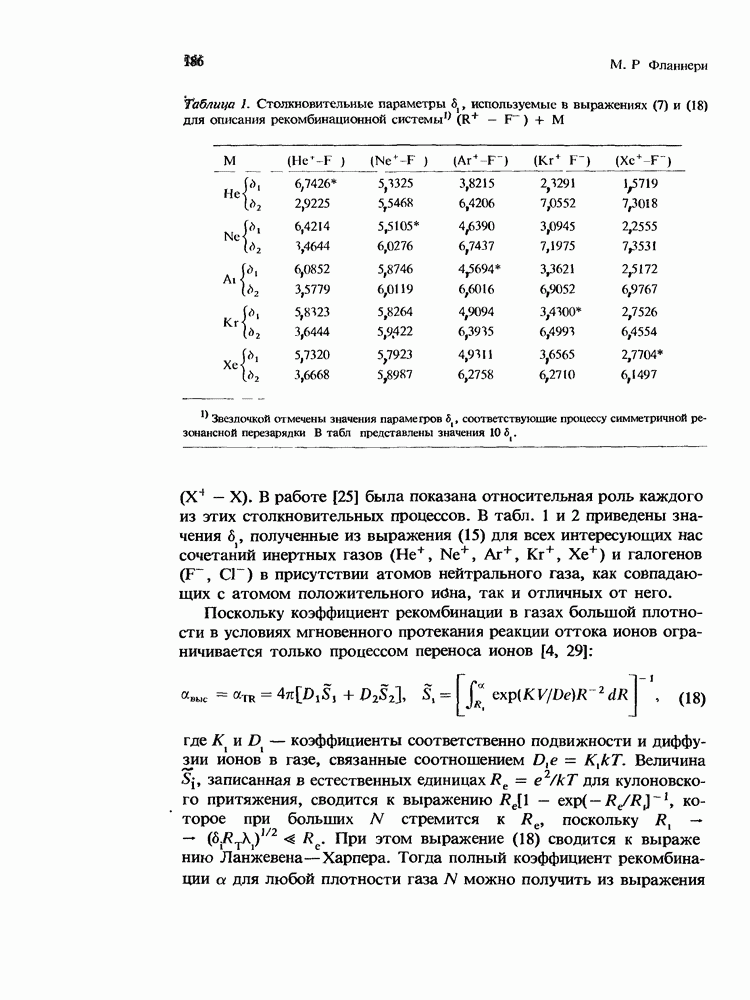
Таблица I. Столкновительные параметры используемые в выражениях (7) и (18) для описания рекомбинационной системы

. В работе [25] была показана относительная роль каждого из этих столкновительных процессов. В табл. 1 и 2 приведены значения 6, полученные из выражения (15) для всех интересующих нас сочетаний инертных газов и галогенов в присутствии атомов нейтрального газа, как совпадающих с атомом положительного ийна, так и отличных от него.

Поскольку коэффициент рекомбинации в газах большой плотности в условиях мгновенного протекания реакции оттока ионов ограничивается только процессом переноса ионов [4, 29]:

где К и — коэффициенты соответственно подвижности и диффузии ионов в газе, связанные соотношением Величина записанная в естественных для кулоновского притяжения, сводится к выражению которое при больших стремится к поскольку

При этом выражение (18) сводится к выраже Ланжевена—Харпера. Тогда полный коэффициент рекомбинации а для любой плотности газа можно получить из выражения

Таблица 2. Столкновительные параметры 6, используемые в выражениях (7) и (18) для описания рекомбинационной системы

(6), в котором первое из предельных значений с соответствует малым а второе — большим. Зависимости полученные на основании данных, приведенных в табл. 1 и 2, мы рассмотрим в разд. 5.4.

5.2.2.2. Универсальная кривая Бейтса

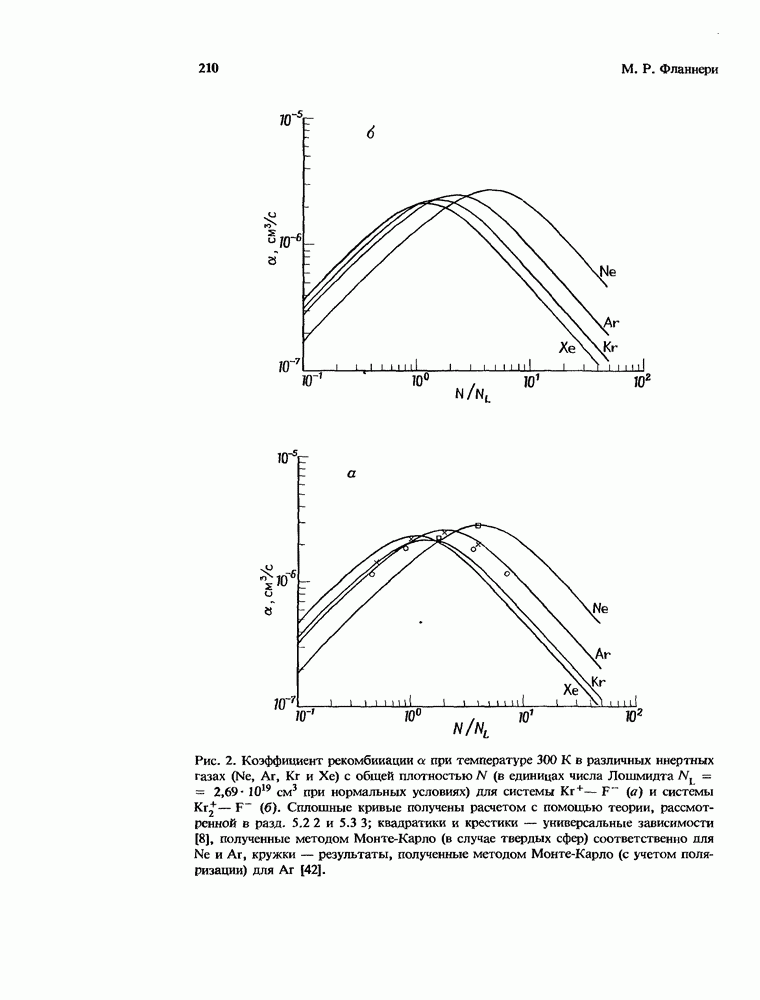
Бейтс [7] разработал метод, с помощью которого можно получить зависимость для некоторых неизвестных условий, обозначаемых нижним индексом по известной зависимости соответствующей некоторым стандартным условиям, обозначаемым нижним индексом Бейтс [6] выполнил наиболее полные расчеты методом Монте-Карло для системы которая рассматривается как стандартный случай. Именно эта система случайно оказалась той относительно простой системой, для которой имеются достаточно точные измерения [41] вплоть до давлений газа 1 атм. Учитывая то, что предельные значения а, соответствующие малым [выражение (2)] и большим [выражение (3)] плотностям, имеют следующие зависимости от

где А и В — константы, характеризующие рекомбинационную систему, Бейтс [7] из соображений размерности, обозначая нижним индексом неизвестный случай, стандартный случай, сделал вывод, что безразмерные пересчетные параметры

обладают таким свойством, что зависимость величины от представляет собой универсальную кривую. Входящая в эти выражения температурная зависимость записана также в универсальном вйде, где в случае, соответствующем взаимодействию твердых сфер, и в случае, соответствующем чисто поляризационному взаимодействию ионов с нейтралами [8]. Это мощная теорема, для применения которой необходимо знать лишь то, как ведет себя а при стандартных условиях а также каковы при малых и больших плотностях соответствующие предельные значения а для случаев и Эти предельные значения анизк и сивыс определяются соответственно по наклону кривой при полученной в условиях квазиравновесия, и из измерений подвижности. При определенных условиях эта теорема является точной. Бейтс [7] предложил также различные методы, учитывающие влияние асимметрии масс. Соответствующие результаты мы обсудим в разд. 5.4.