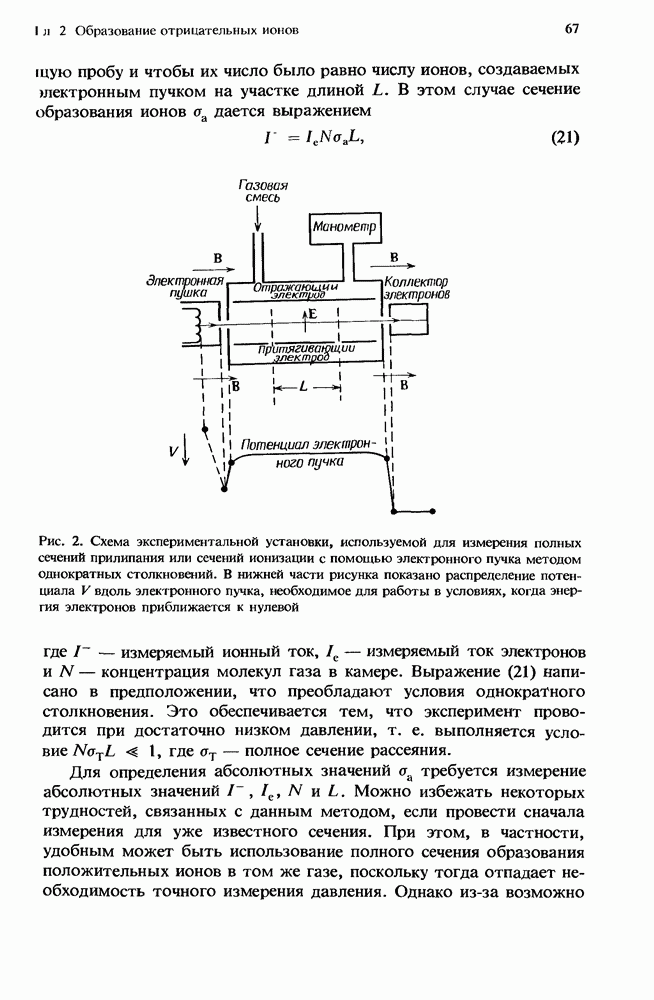
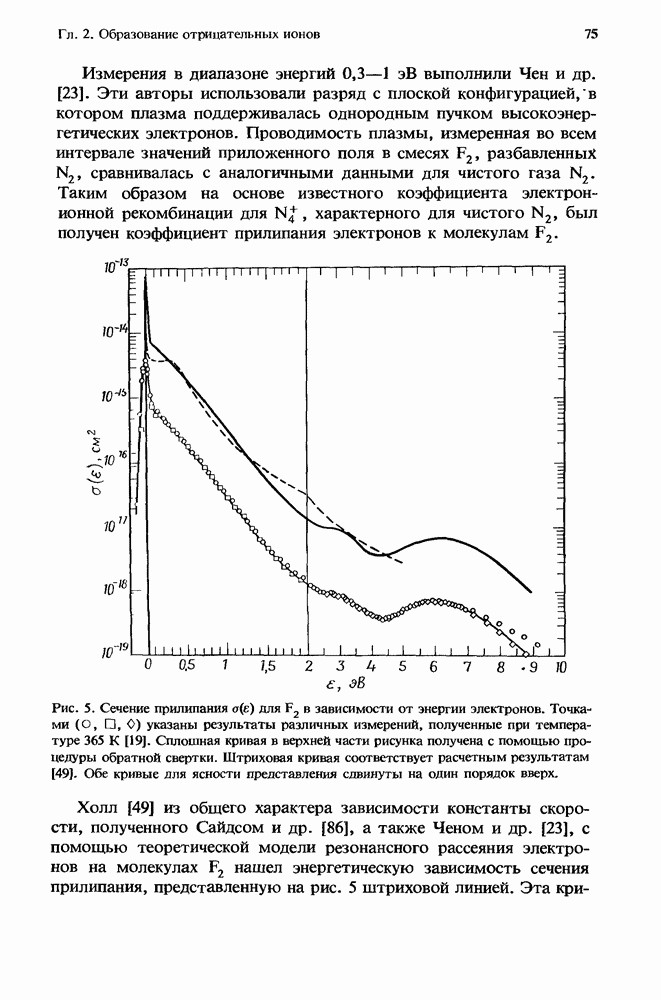
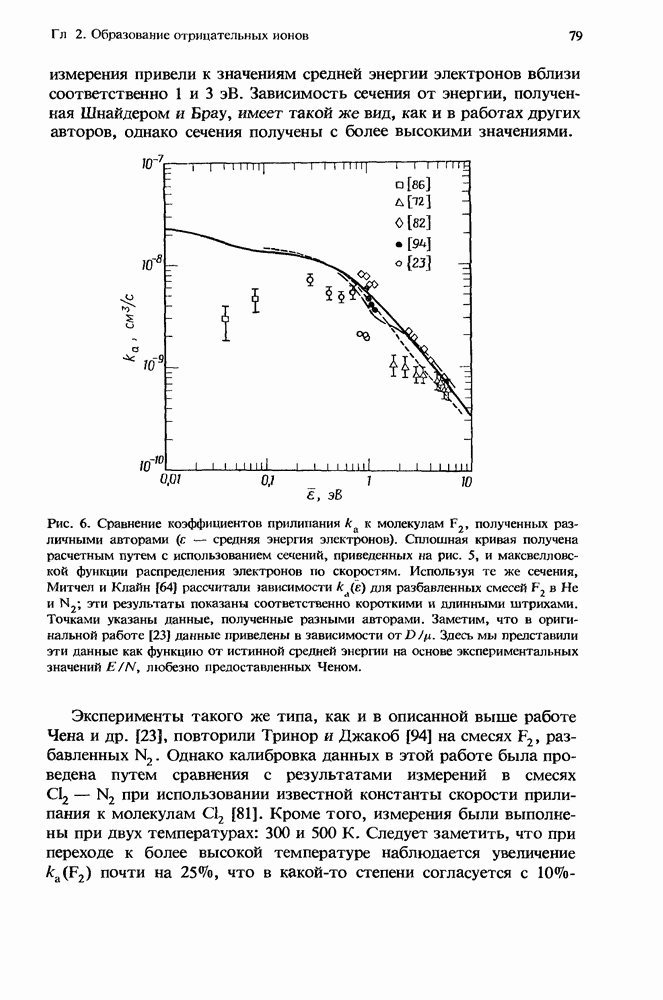
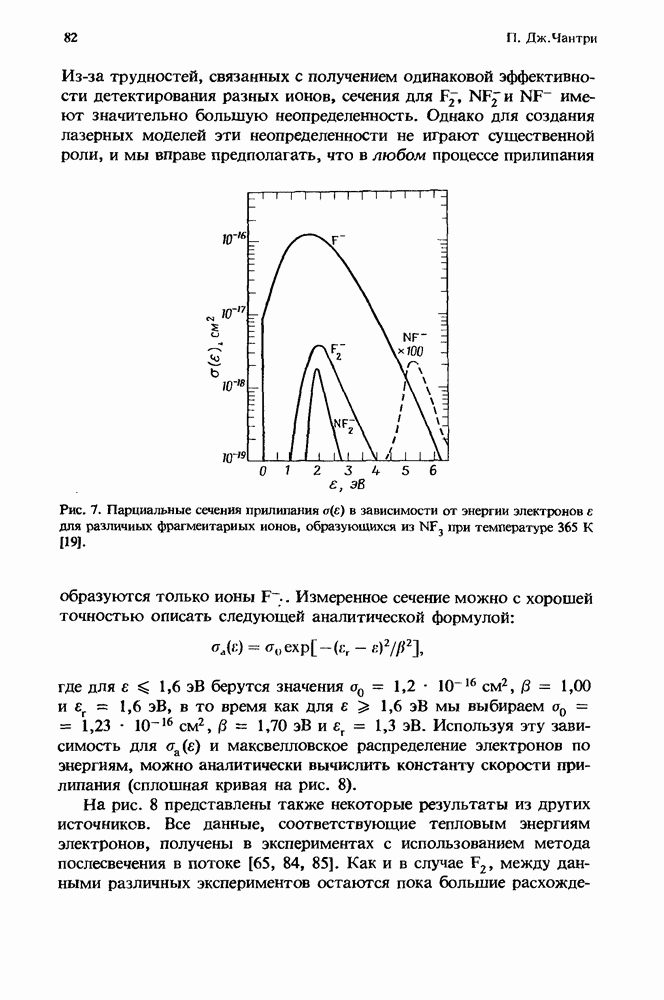
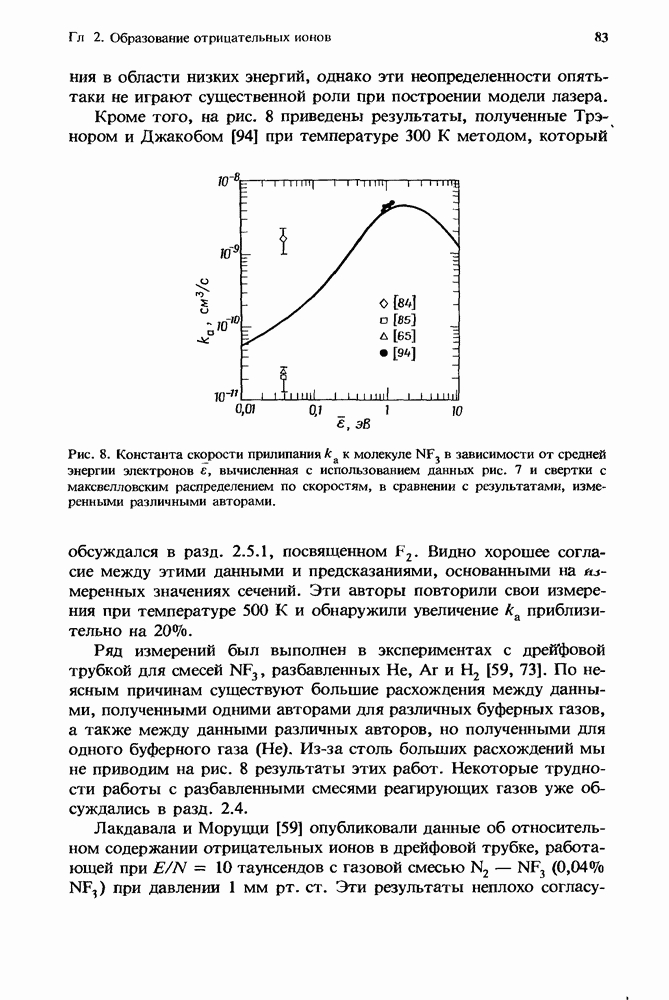
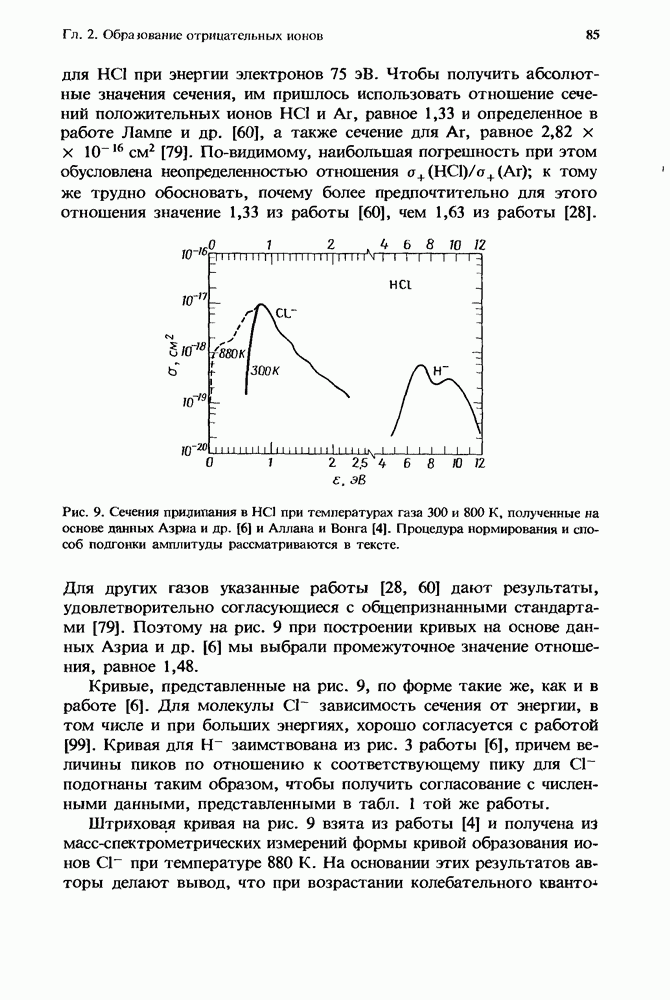
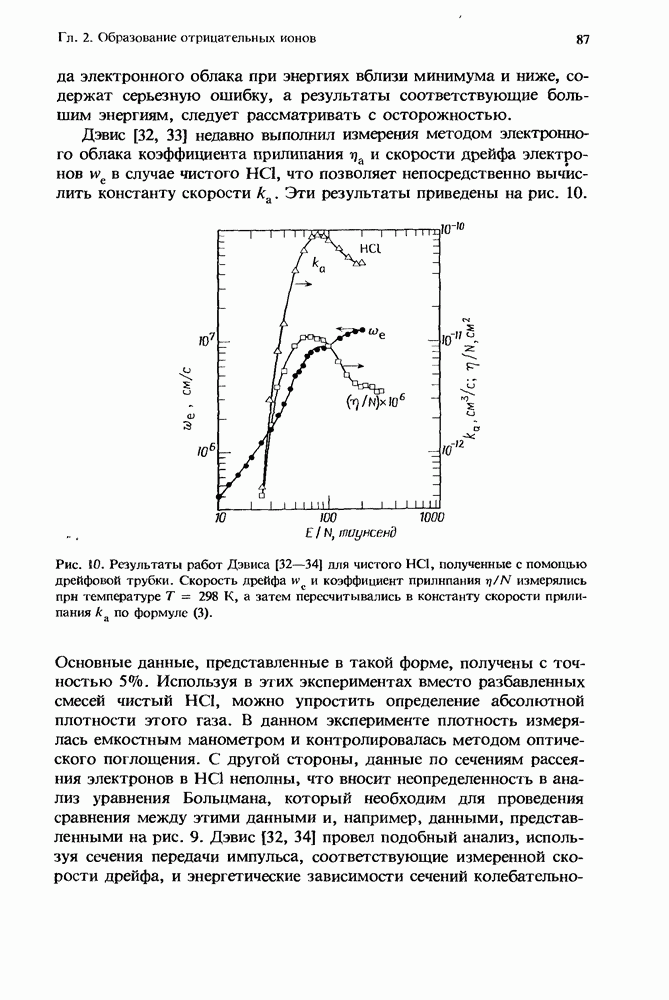
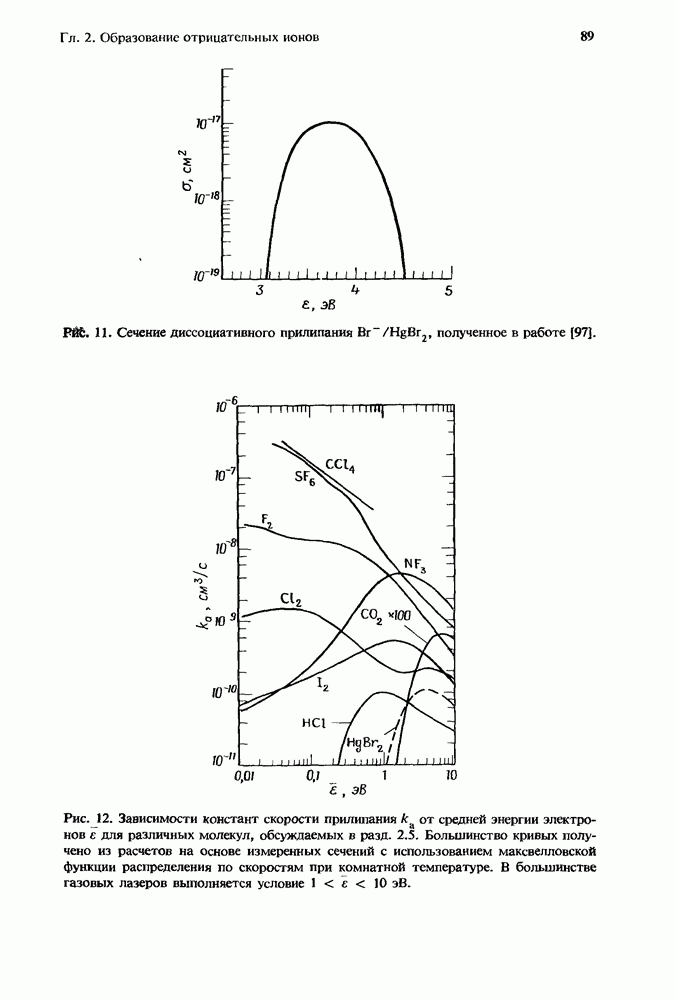
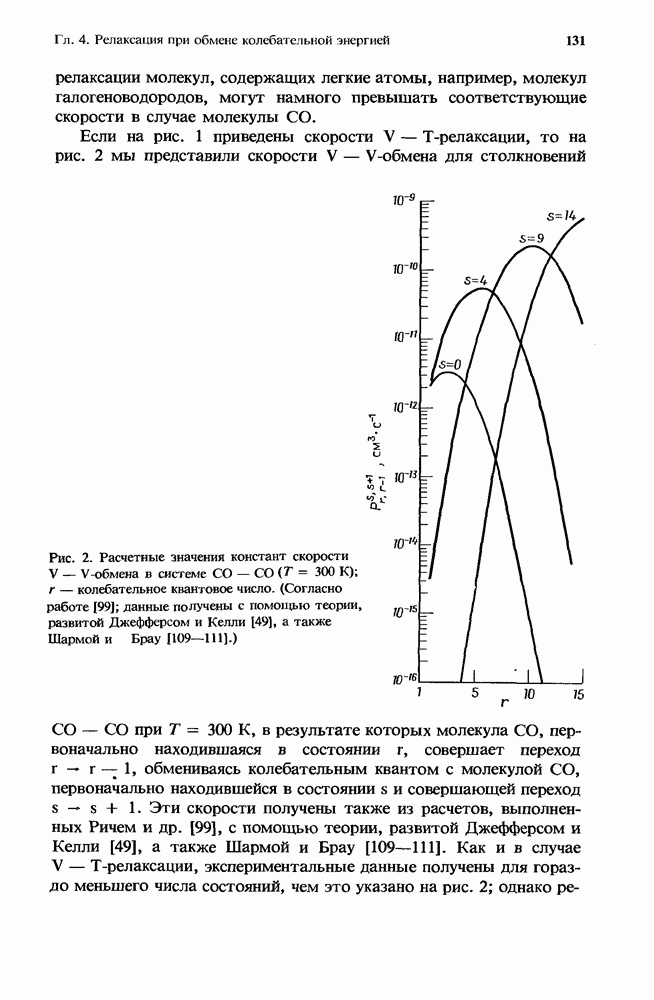
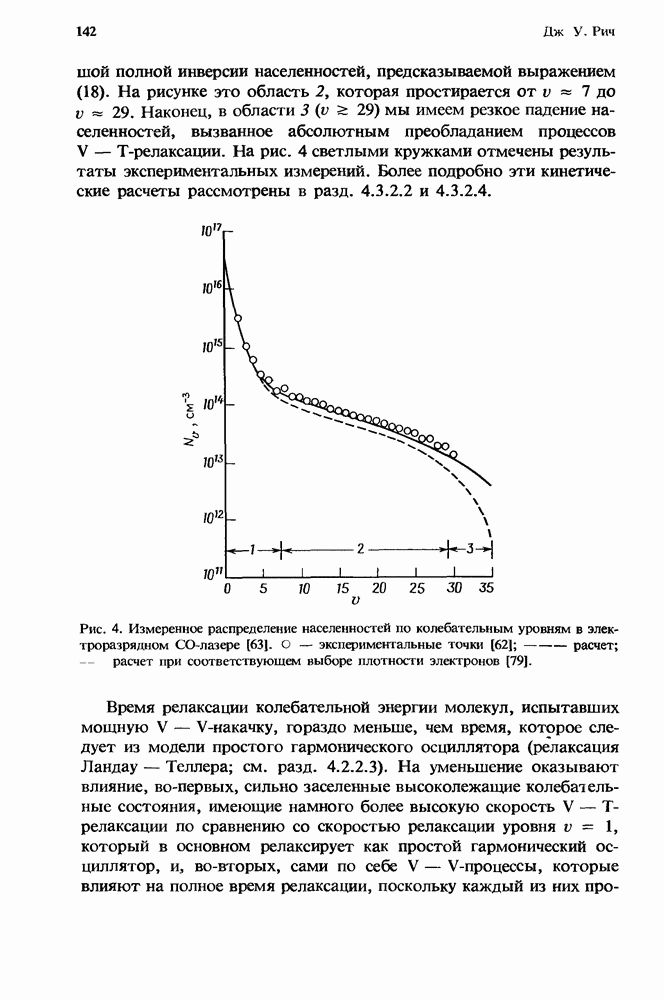
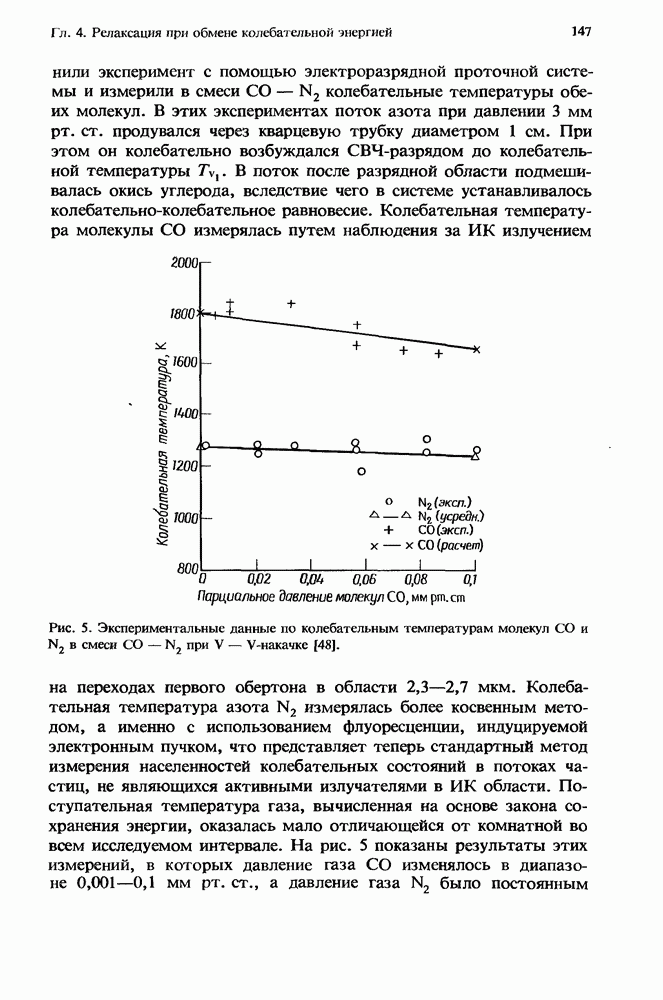
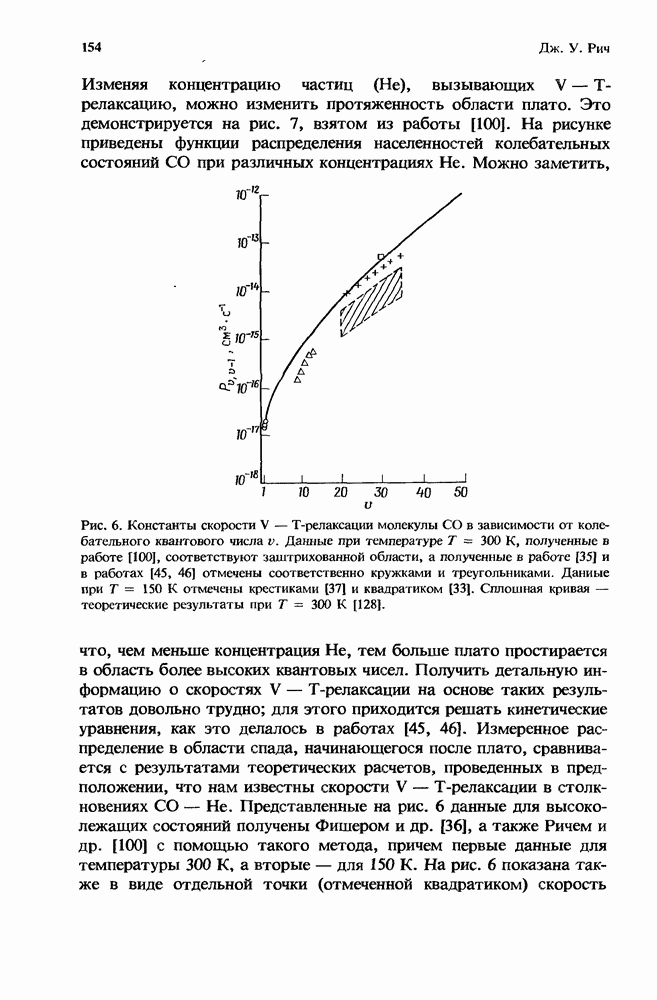
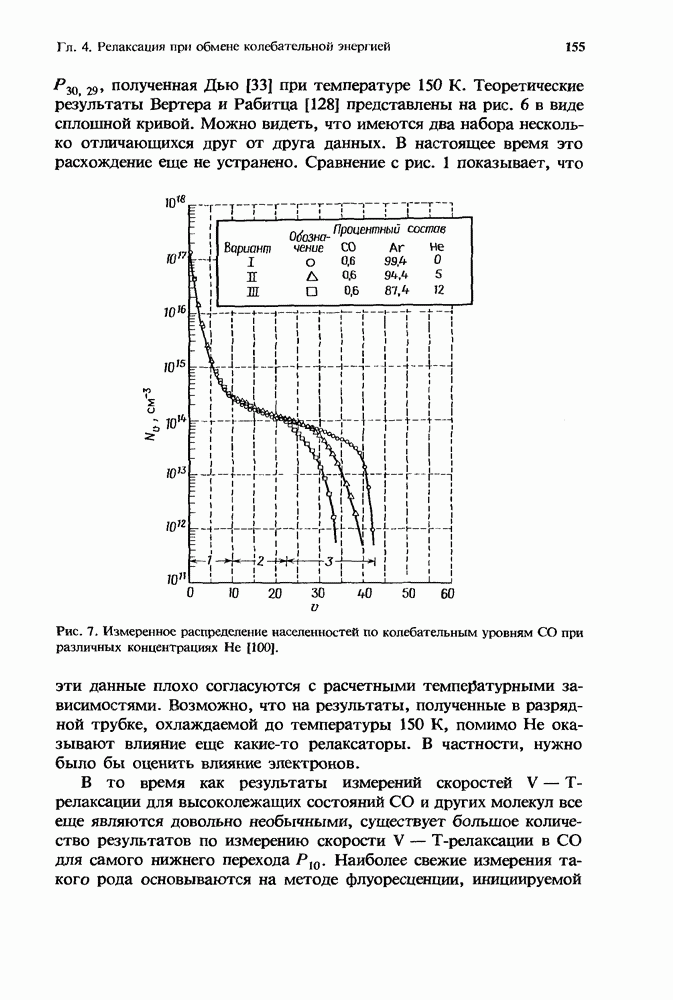
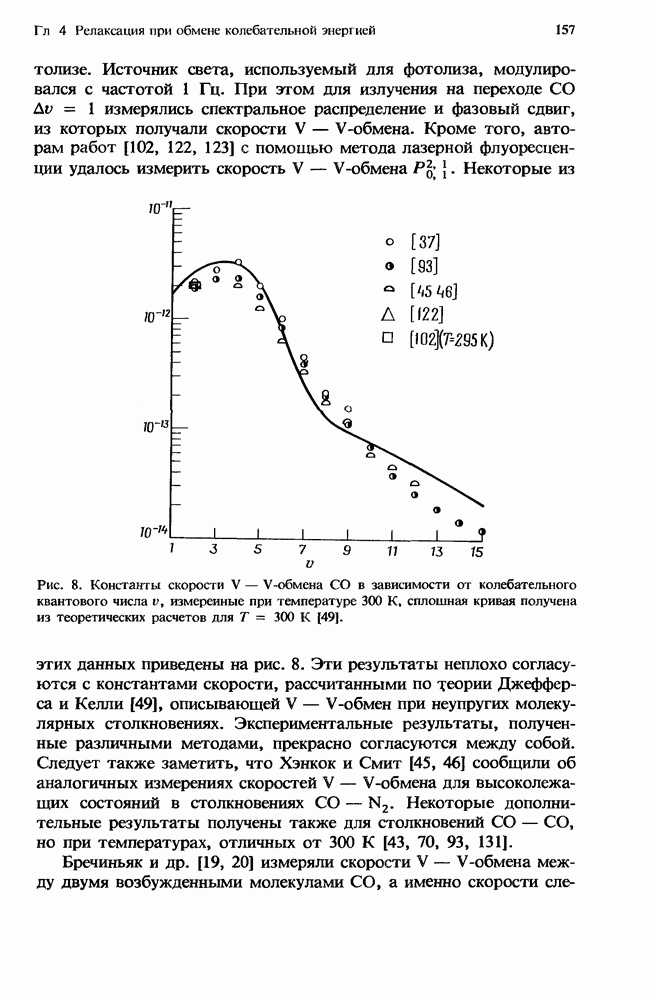
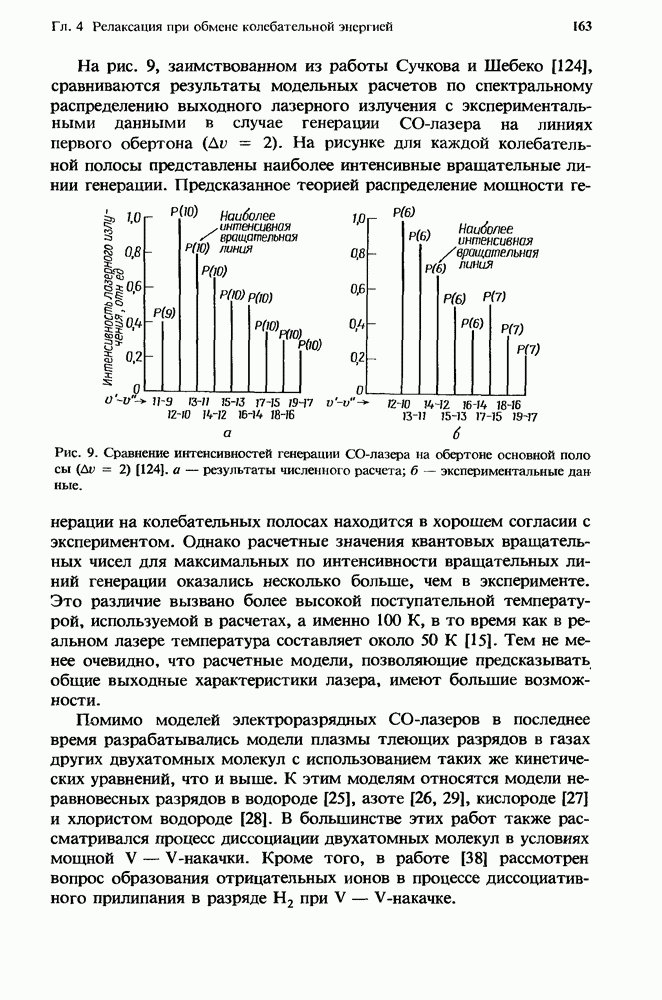
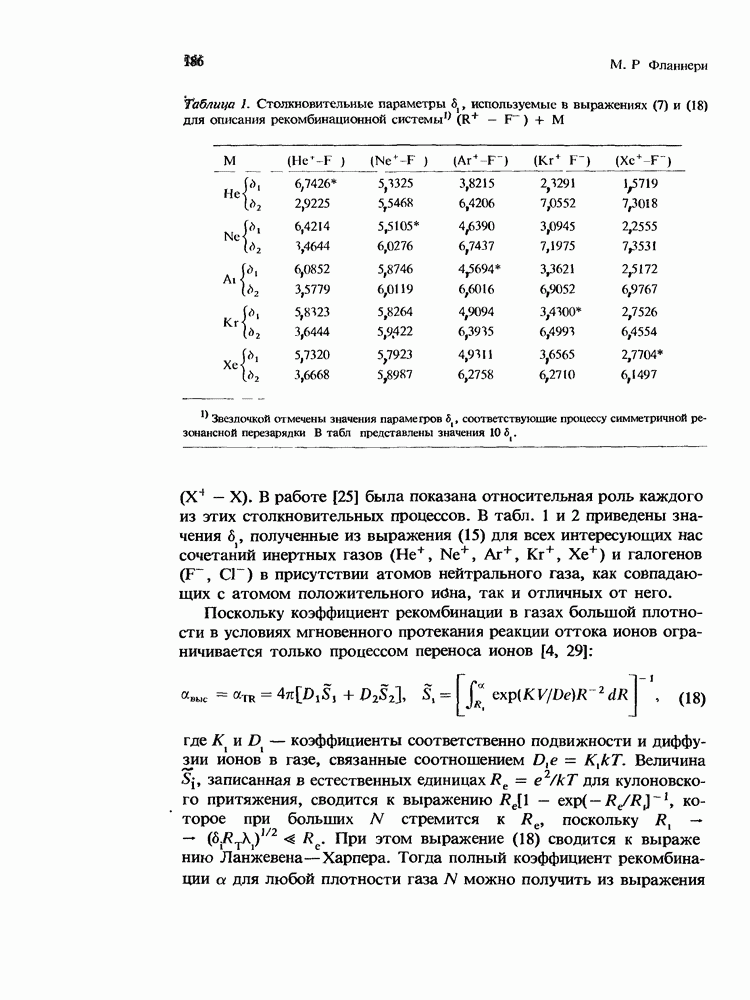
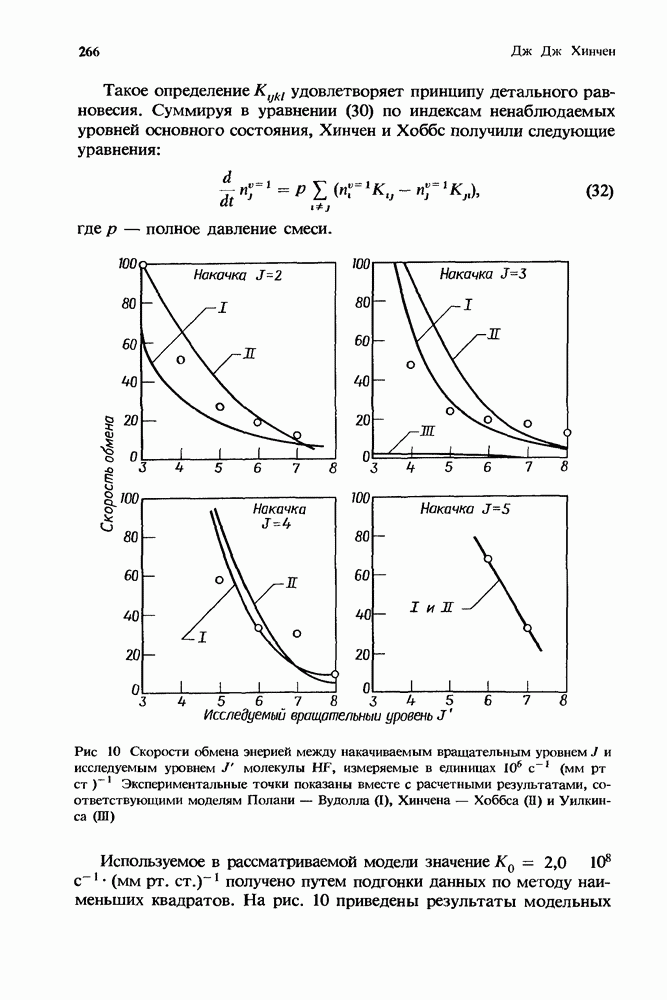
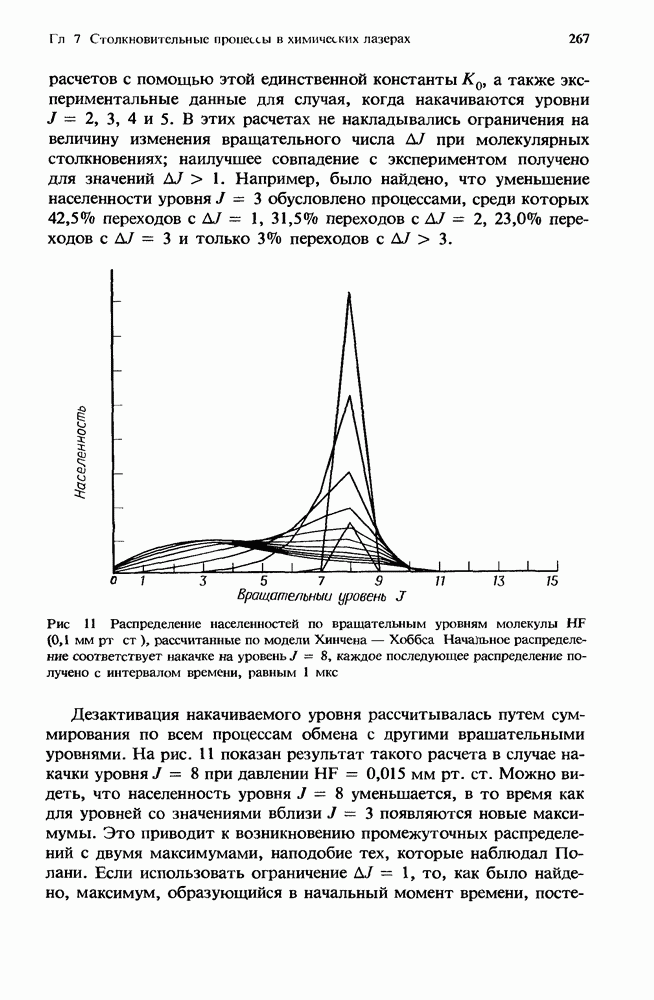
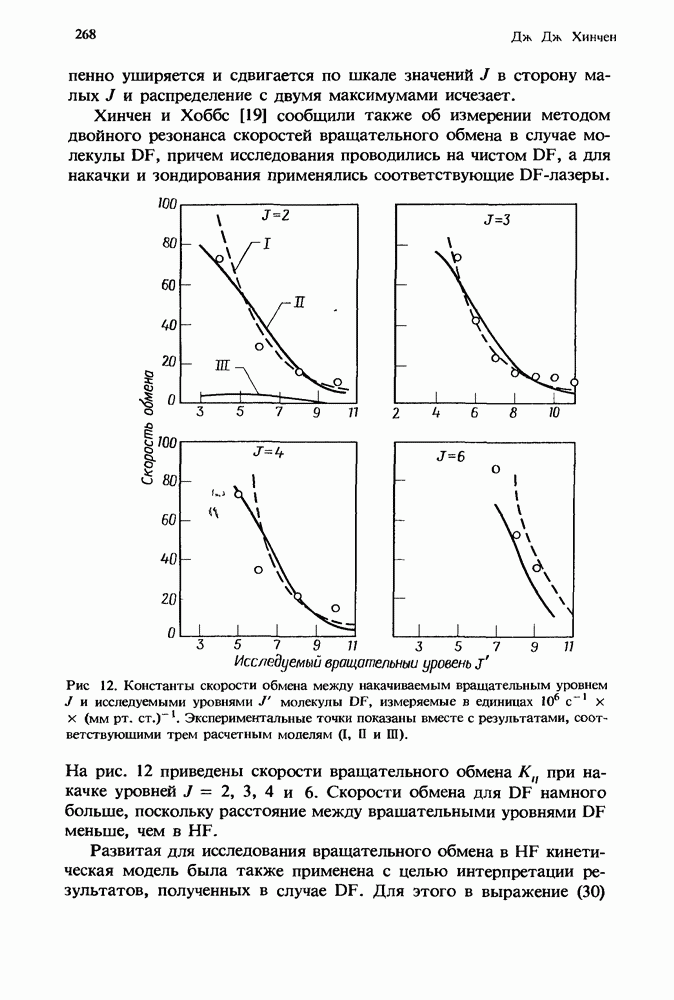
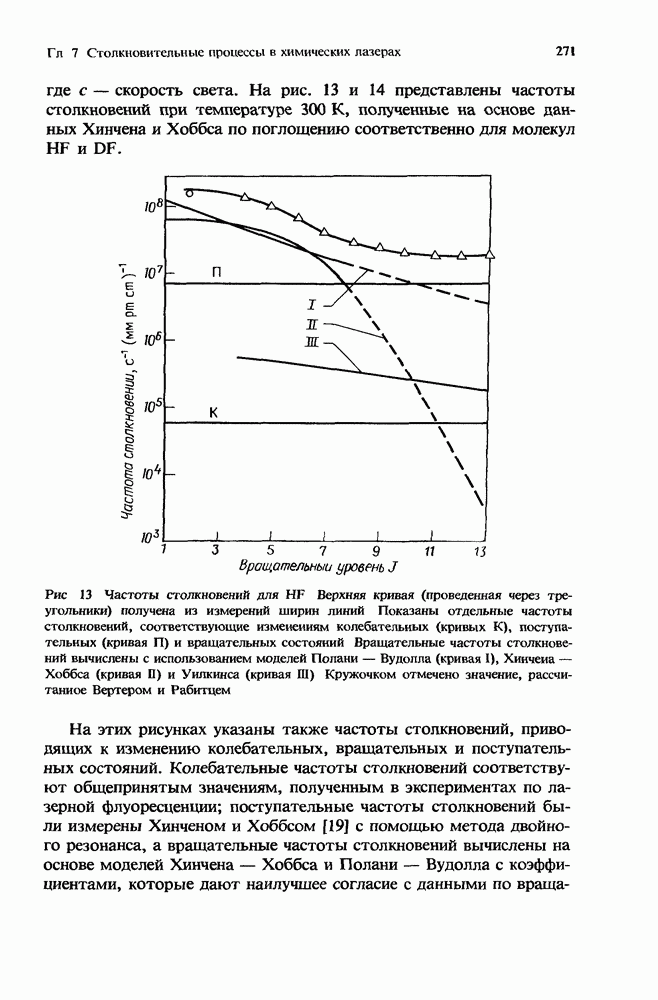
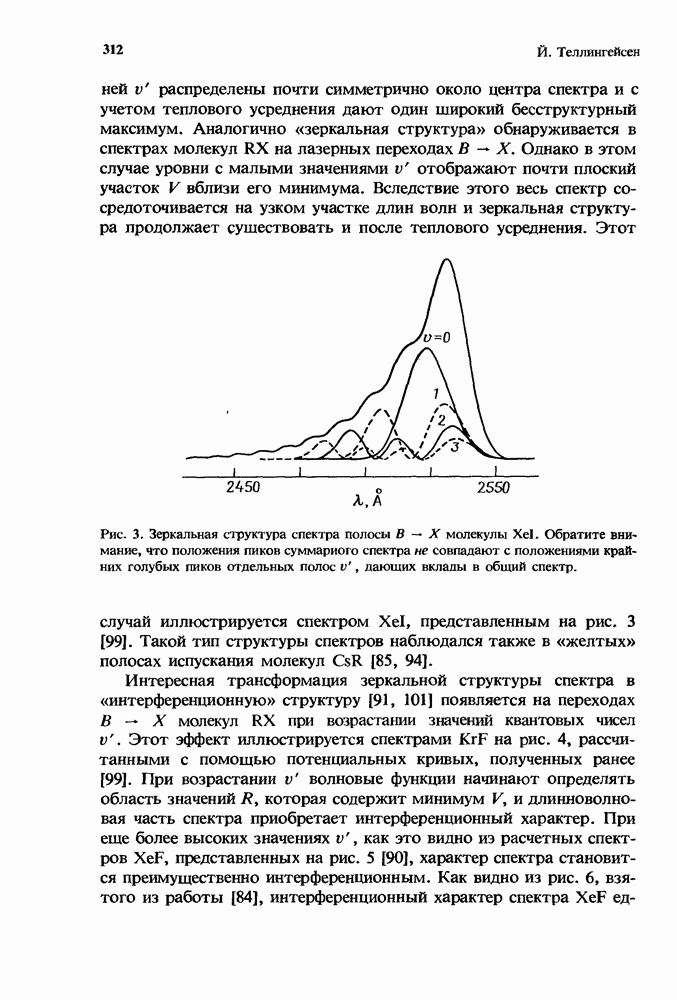
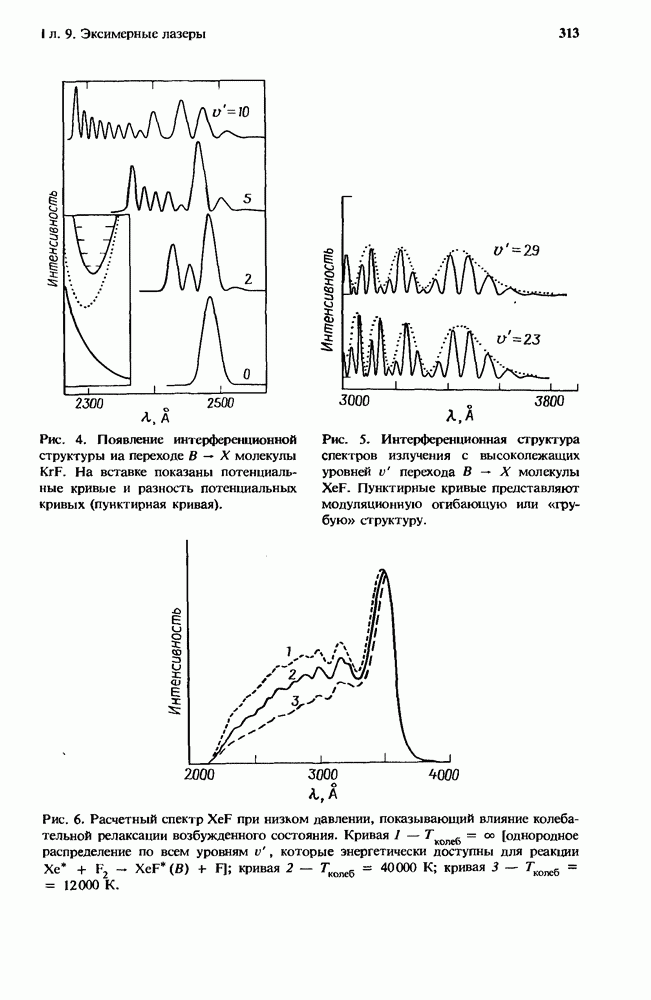
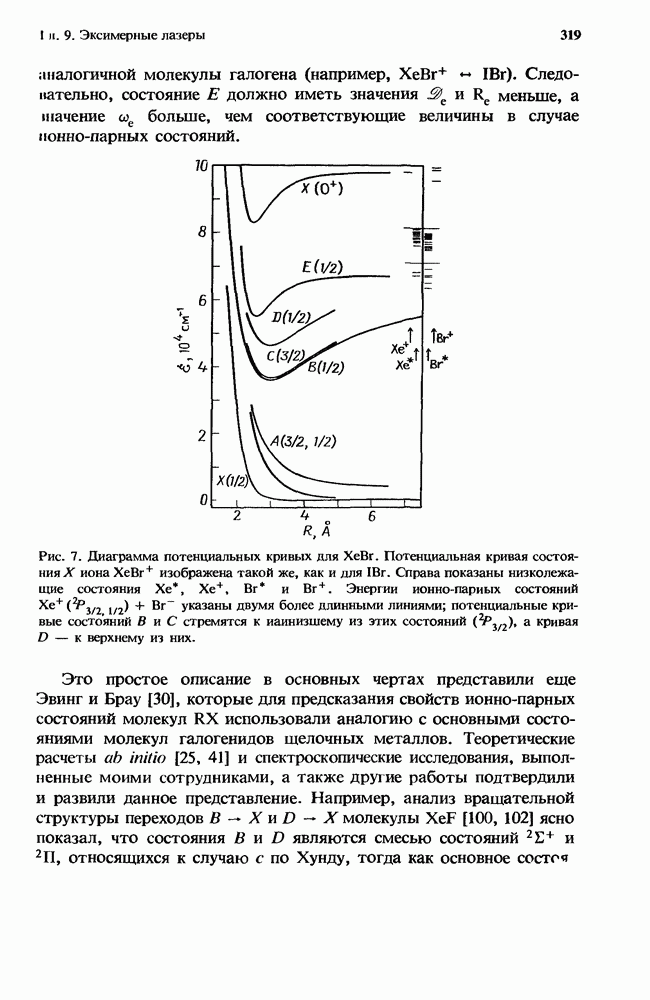
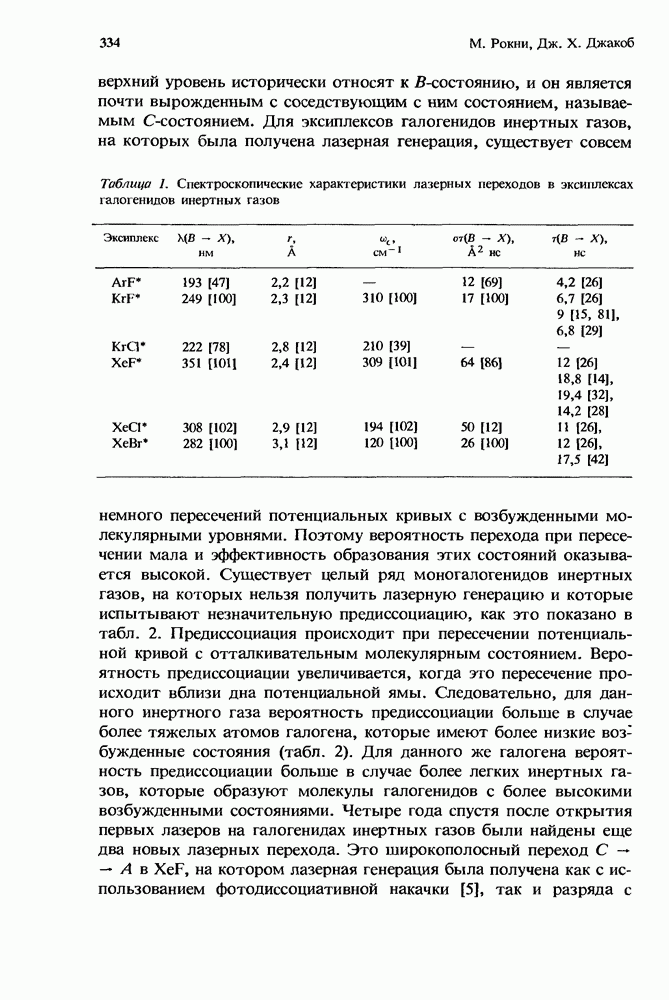
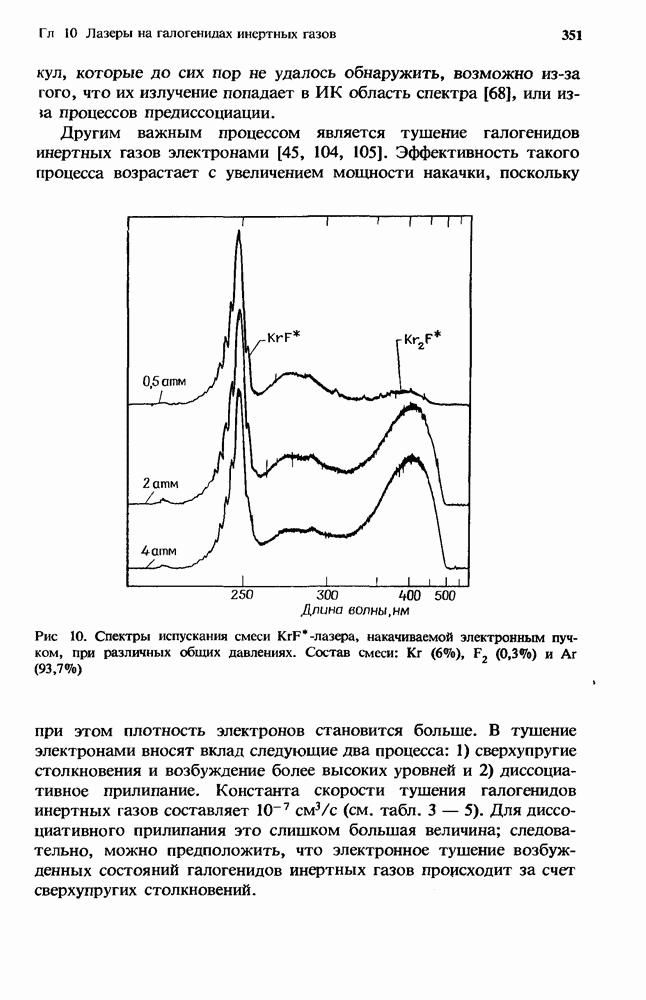
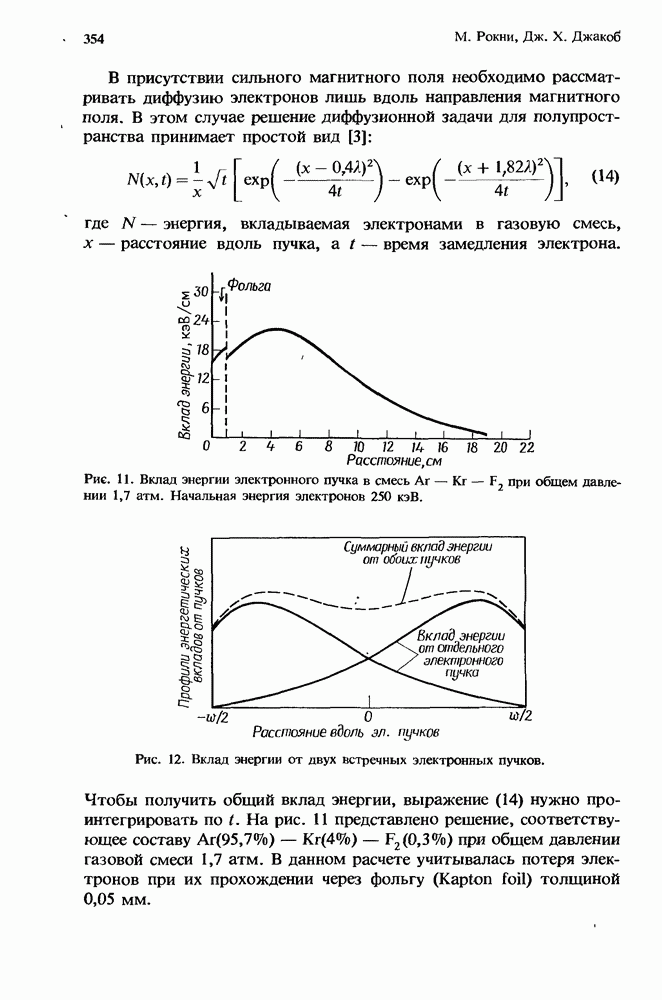
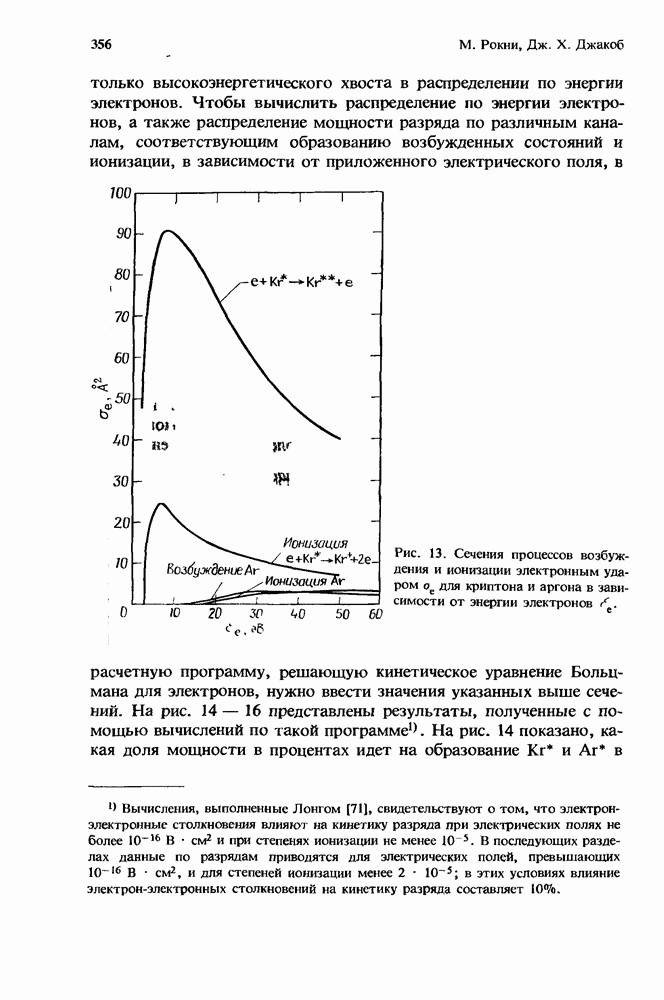
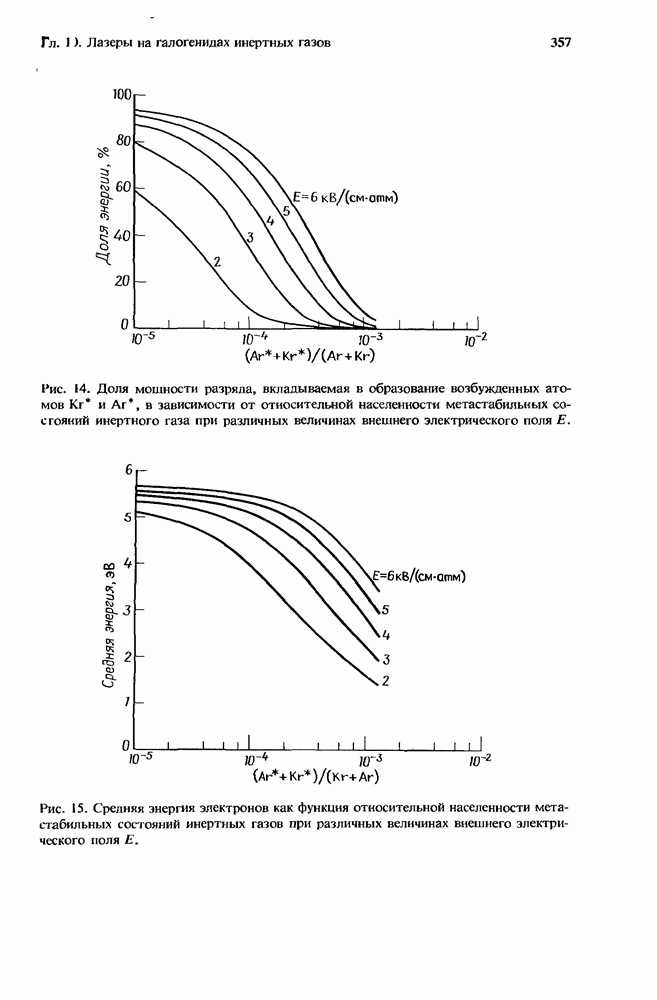
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
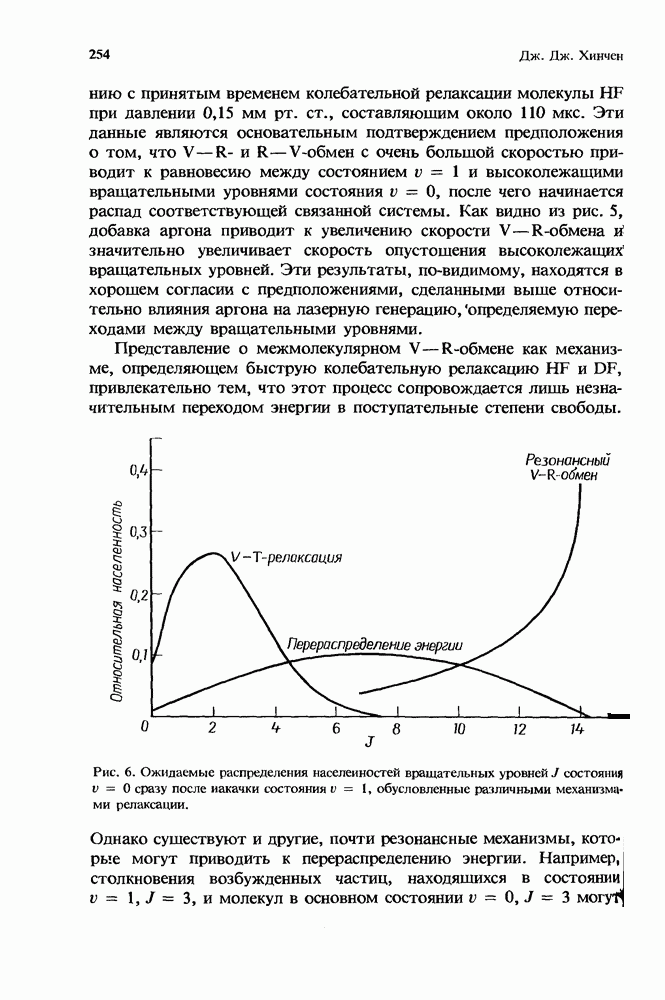
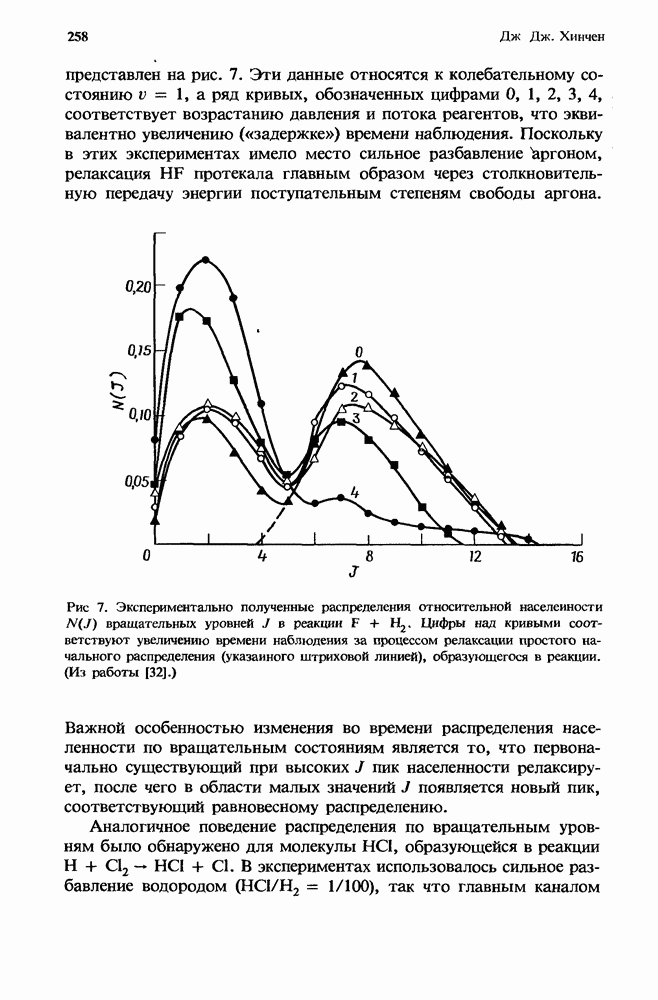
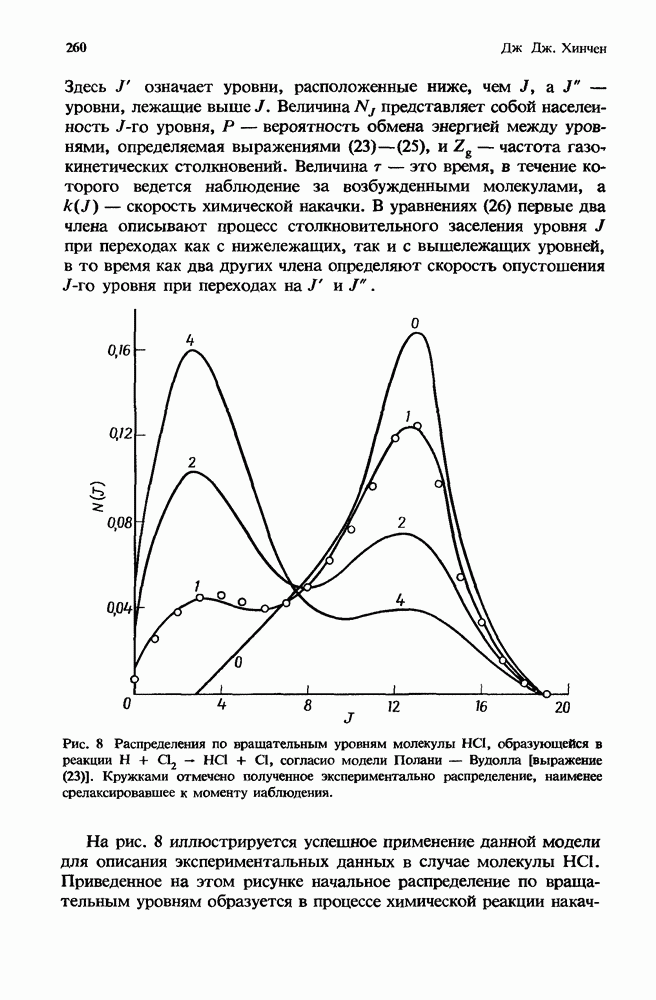
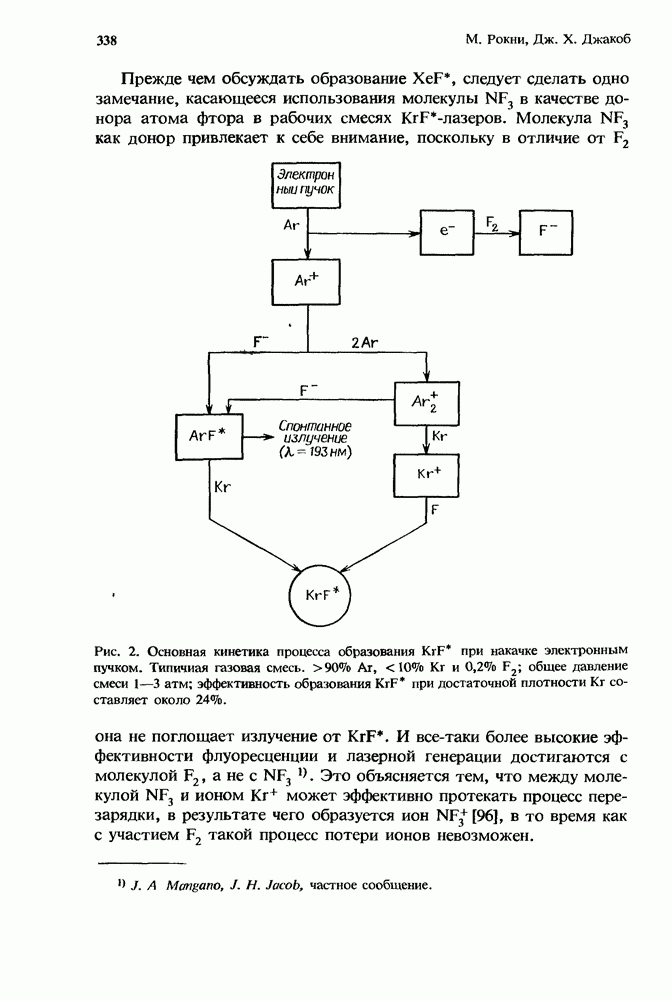
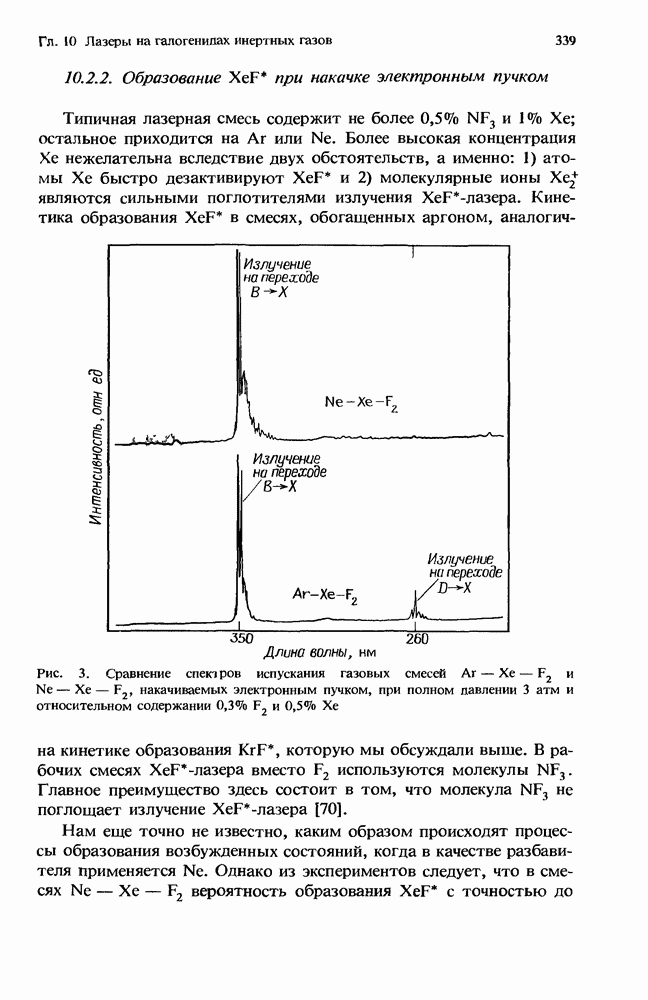
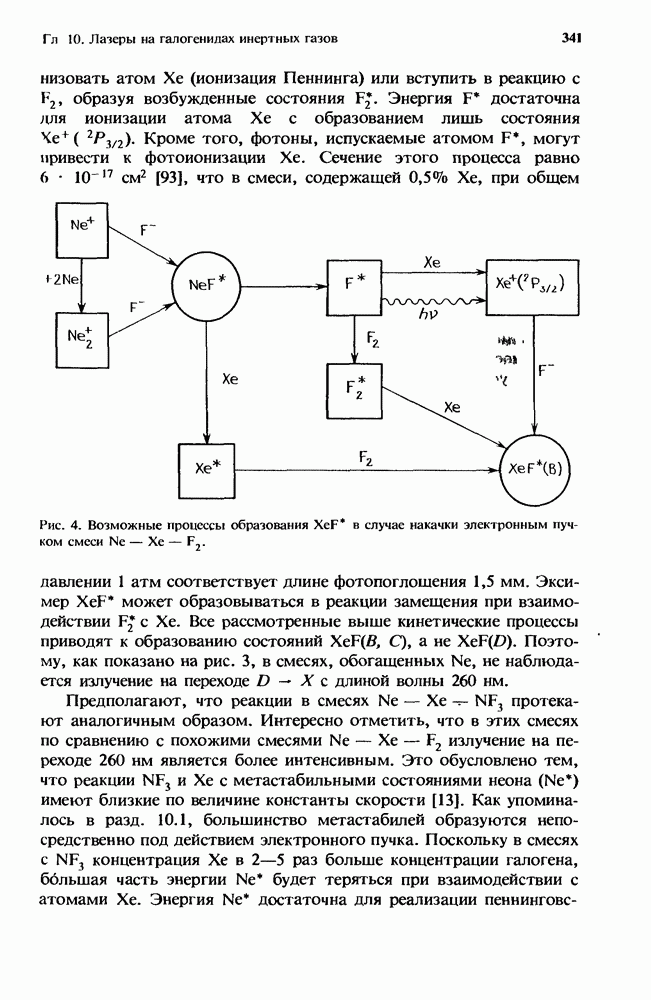
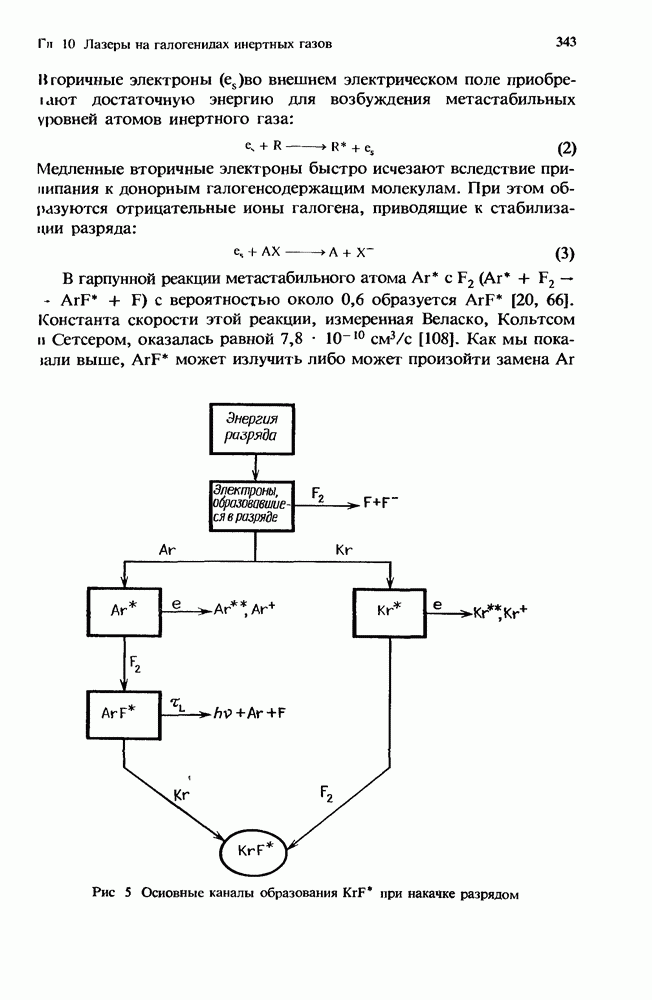
8.2.5. Межмолекулярные взаимодействия
В дополнение к процессам, вызванным электрон-молекулярными столкновениями, в кинетике СО2-лазера важную роль играют межмолекулярные взаимодействия. Наиболее важные из них следующие:
1. Передача энергии колебательной моды В врашательным и поступательным степеням свободы.
2. Обмен колебательной энергией между азотом и колебательной модой А.
3. Переход энергии моды А в энергию мод S и В.
Обзор данных о константах скорости этих процессов представлен Тейлором и Биттерманом [25], а также Мак-Даниелем и др. [16]. Все эти константы скорости зависят от газовой температуры. Значения этих скоростей могут также измениться в условиях, когда значительная доля молекул находится в возбужденном состоянии. Для моделирования взаимодействий между возбужденными состояниями будем считать, что молекулярные колебания описываются гармоническими осцилляторами.
Рассмотрим случай, когда две аналогичные молекулы (гармонические осцилляторы) вступают в реакцию вида

Молекула А, находясь в колебательном состоянии к, сталкивается с молекулой В и переходит в состояние к  Молекула В теряет возбуждение и переходит из состояния
Молекула В теряет возбуждение и переходит из состояния  в состояние
в состояние  Энергетический обмен с внешней средой отсутствует.
Энергетический обмен с внешней средой отсутствует.
Вероятность конкретной реакции зависит от того, какие колебательные состояния в ней участвуют, и от конкретных особенностей
процесса столкновения. Детальное описание столкновений подразумевает знание относительной скорости молекул, их взаимной ориентации и т. п. Здесь предполагается, что соответствующее усреднение по всевозможным столкновениям проведено и что результирующая «средняя» вероятность столкновения зависит только от газовой температуры. Для однотипных процессов теория гармонического осциллятора дает

где Р — вероятности процессов, в которых колебательные квантовые числа меняются так, как это указано с помощью индексов. Соотношения (17) и (18) остаются верными и после усреднения по всем возможным столкновениям. Число столкновений пропорционально произведению плотностей сталкивающихся частиц. Таким образом, используя выражения (16)-(18) и приравнивая скорости прямых и обратных процессов, получаем следующее соотношение:

где  — плотность возбужденных состояний с указанными в скобках значениями соответствующих колебательных квантовых чисел.
— плотность возбужденных состояний с указанными в скобках значениями соответствующих колебательных квантовых чисел.
Из (19) следует, что отношение плотностей молекул, находящихся на соседних колебательных уровнях, сохраняется постоянным. Константу  можно выразить либо через отношение населенностей двух любых выбранных уровней, либо через полное число колебательных квантов. Таким образом,
можно выразить либо через отношение населенностей двух любых выбранных уровней, либо через полное число колебательных квантов. Таким образом,

Полное число молекул  дается выражением
дается выражением

Объединяя выражения (20) и (21), имеем

или

Связь с колебательной температурой получим по аналогии с теорией Больцмана, положив 
Как отмечалось выше, обоснованием для введения понятия «колебательная температура» является преобладающая роль реакций резонансного V — V-обмена, описываемых уравнением (16). Однако определенную роль играют также процессы вида

Выделение или поглощение кинетической энергии  в этих процессах сильно уменьшает вероятность их протекания. Процессы такого типа в конечном счете ответственны за установление равновесия между колебательными и вращательно-поступательными степенями свободы. Скорость изменения числа квантов можно записать через константы
в этих процессах сильно уменьшает вероятность их протекания. Процессы такого типа в конечном счете ответственны за установление равновесия между колебательными и вращательно-поступательными степенями свободы. Скорость изменения числа квантов можно записать через константы  посредством суммирования по возбужденным состояниям:
посредством суммирования по возбужденным состояниям:

В условиях равновесия имеем  так что при газовой температуре Т получаем следующее соотношение:
так что при газовой температуре Т получаем следующее соотношение:

При этом уравнение (25) принимает вид

Величина, равная числу квантов, приходящихся на одну молекулу, релаксирует к своему равновесному значению  по экспоненциальному закону с характерным временем
по экспоненциальному закону с характерным временем  Если в процессерелаксации участвуют молекулы разного сорта, то нужно просуммировать по всем сортам молекул М:
Если в процессерелаксации участвуют молекулы разного сорта, то нужно просуммировать по всем сортам молекул М:

где  — доля молекул сорта М.
— доля молекул сорта М.
Переходя к рассмотрению кинетики молекул СО2, заметим, что уравнение (27) соответствует передаче энергии мод  во вращательно-поступательные степени свободы. В основном процесс релаксации протекает между уровнями моды В, так как соответст
во вращательно-поступательные степени свободы. В основном процесс релаксации протекает между уровнями моды В, так как соответст
вукяцие ей значения колебательного кванта и требуемые изменения кинетической энергии меньше, чем для моды  Таким образом, скорость изменения числа квантов в моде
Таким образом, скорость изменения числа квантов в моде  за счет ухода энергии в поступательные степени свободы можно записать в виде
за счет ухода энергии в поступательные степени свободы можно записать в виде

Процесс колебательного обмена между модой молекулы N2 и модой А молекулы СО2 характеризуется числами  соответственно. Уравнение реакции обмена в этом случае имеет вид
соответственно. Уравнение реакции обмена в этом случае имеет вид

Применяя к этому процессу теорию гармонического осциллятора, необходимо провести суммирование по всем состояниям каждого из двух осцилляторов. При этом скорость передачи колебательной энергии от N2 к моде А дается выражением

где  — константы скорости соответственно прямого и обратного процессов, описываемых уравнением (29) для
— константы скорости соответственно прямого и обратного процессов, описываемых уравнением (29) для 
При полном равновесии, соответствующем газовой температуре Т, суммарное изменение числа квантов в каждой из мод равно нулю и, следовательно,

Подставляя соотношения (22), (23) и (31) в уравнение (30), получаем следующее уравнение:

Поскольку уход каждого кванта из колебательной моды азота соответствует одновременному появлению одного кванта в моде А, мы имеем

или, если пренебречь всеми другими процессами,

Если  то из соотношения (31) следует
то из соотношения (31) следует

а также

Поскольку  то в равновесии из условия
то в равновесии из условия  Тследует
Тследует 
Уравнение (32) показывает, что релаксация к равновесию между N2 и модой А носит сложный характер. Подставляя выражения (34) — (36) в уравнение (32), получаем

где

причем

Здесь через  обозначены решения системы уравнений
обозначены решения системы уравнений

Величина  численно равна 25,62 К, так что
численно равна 25,62 К, так что

Обычно величины  малы по сравнению с единицей, что дает
малы по сравнению с единицей, что дает

Таким образом, система стремится к равновесию по закону, мало чем отличающемуся от простой экспоненты, и релаксационный
процесс можно описать достаточно точно с помощью одной постоянной времени, равной  т.е.
т.е.

Эта величина обратно пропорциональна суммарной плотности молекул 
Приток и отток энергии из колебательной моды А молекулы СО2, обусловлен также процессами колебательного обмена с модами  и с прямым преобразованием колебательной энергии в энергию кинетического движения. Однако из-за большой величины колебательного кванта
и с прямым преобразованием колебательной энергии в энергию кинетического движения. Однако из-за большой величины колебательного кванта  обычно предполагают, что преобладающими процессами являются процессы обмена энергией с другими колебательными модами. Соотношение фундаментальных частот таково, что при переносе возбуждения каждый квант, теряемый антисимметрическим типом колебаний, приводит к возникновению трех квантов в деформационной моде. Рассматриваемая реакция имеет вид
обычно предполагают, что преобладающими процессами являются процессы обмена энергией с другими колебательными модами. Соотношение фундаментальных частот таково, что при переносе возбуждения каждый квант, теряемый антисимметрическим типом колебаний, приводит к возникновению трех квантов в деформационной моде. Рассматриваемая реакция имеет вид

В рамках теории гармонического осциллятора ее можно описать уравнением

Измерение соответствующей этому процессу константы скорости обычно проводят при соблюдении условия  Тогда уравнение (48) принимает вид
Тогда уравнение (48) принимает вид

Это уравнение используется для вычисления величины  из экспериментальных данных, которую затем можно подставить в уравнение (48). Реакцию, описываемую уравнением (47), можно выбрать произвольным образом. Другие реакции, по-видимому, также вносят свой вклад в релаксацию антисимметрического типа колебаний. Наблюдаемые экспериментально и предсказываемые теорией характеристики работы СО2-усилителя хорошо согласуются между собой при умеренных степенях возбуждения, однако при высокой степени возбуждения появляются значительные расхождения. Наблюдаемые значения колебательной температуры Т ниже, чем
из экспериментальных данных, которую затем можно подставить в уравнение (48). Реакцию, описываемую уравнением (47), можно выбрать произвольным образом. Другие реакции, по-видимому, также вносят свой вклад в релаксацию антисимметрического типа колебаний. Наблюдаемые экспериментально и предсказываемые теорией характеристики работы СО2-усилителя хорошо согласуются между собой при умеренных степенях возбуждения, однако при высокой степени возбуждения появляются значительные расхождения. Наблюдаемые значения колебательной температуры Т ниже, чем
это предсказывает теория, что может указывать на наличие других реакций, возможно более резонансных и протекающих с участием более высоковозбужденных состояний.
Из вышесказанного следует, что поступательные и вращательные степени свободы нагреваются не только непосредственно электронами, но и вследствие всей совокупности молекулярных процессов, которые не обладают точным резонансом.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
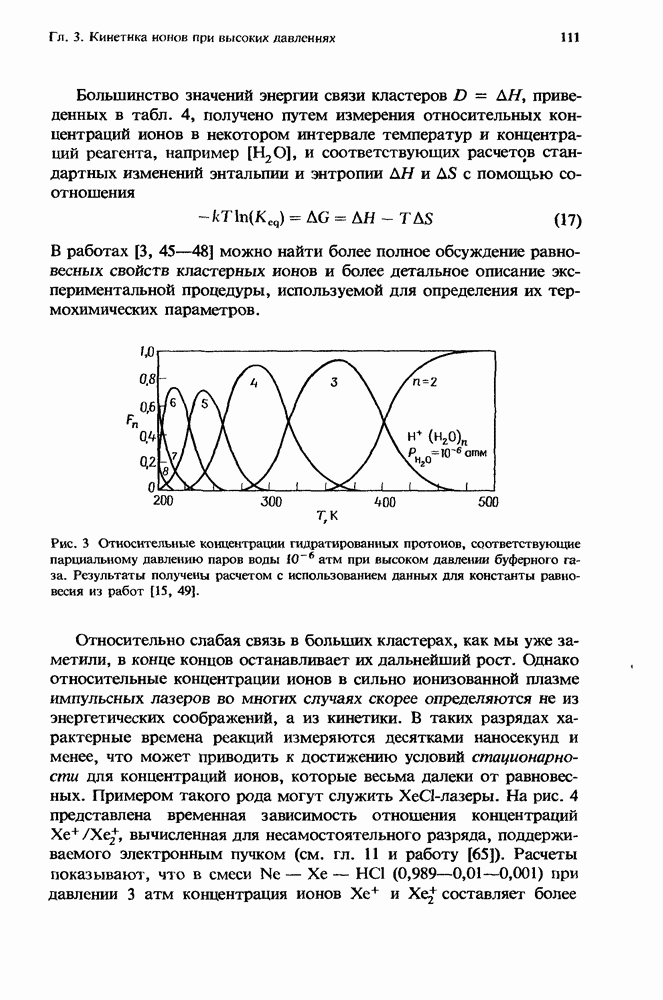
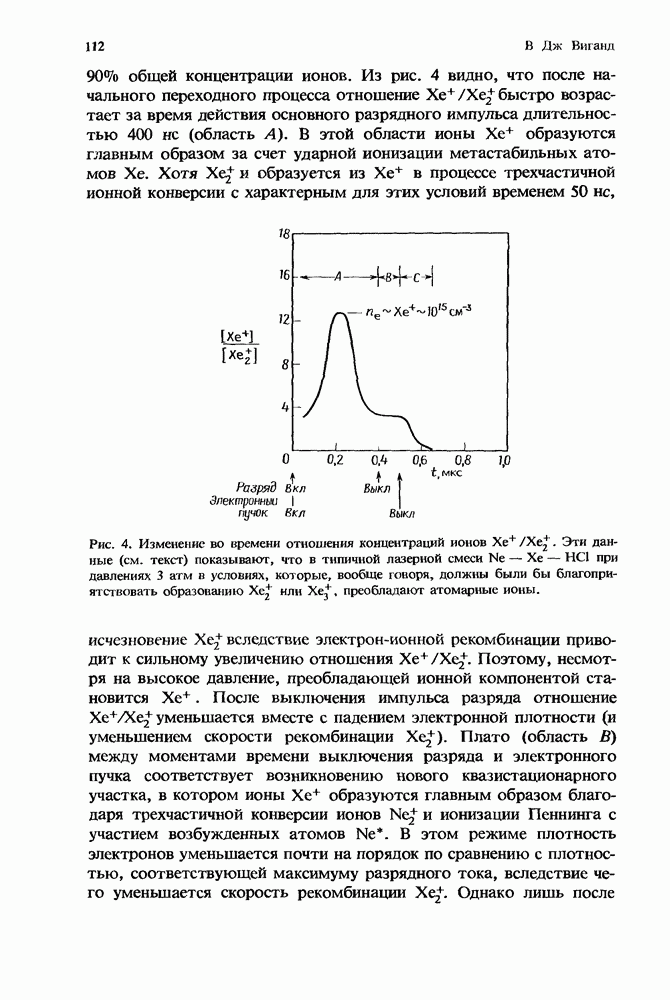
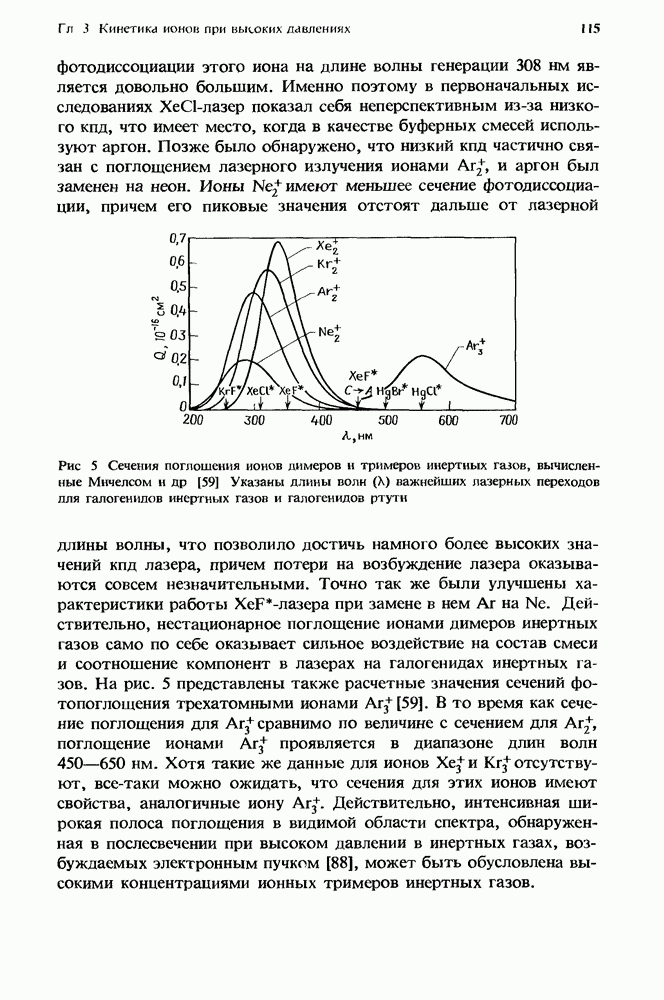
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
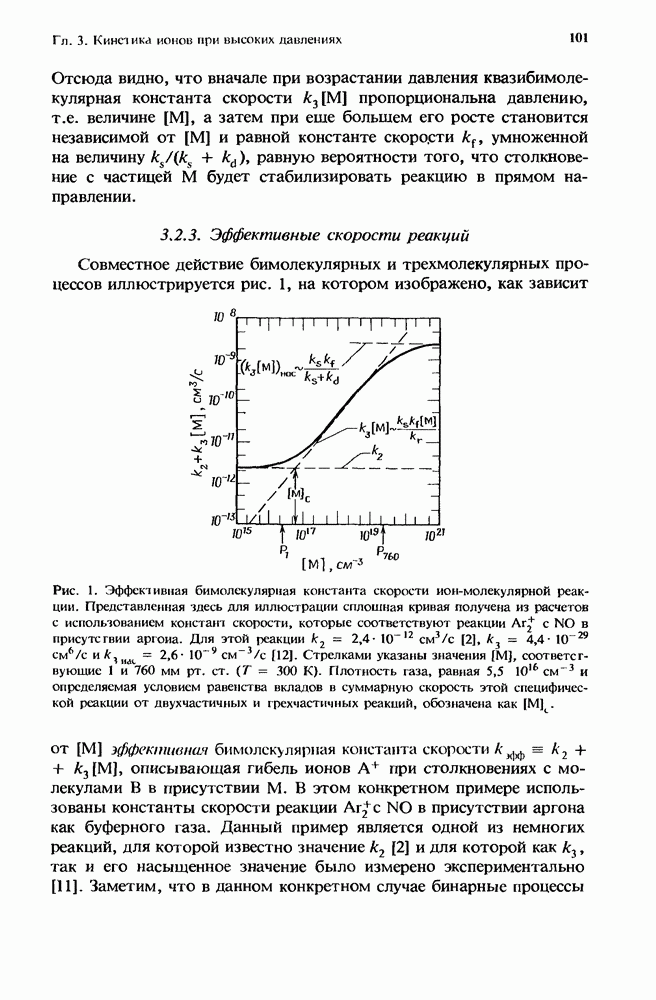
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
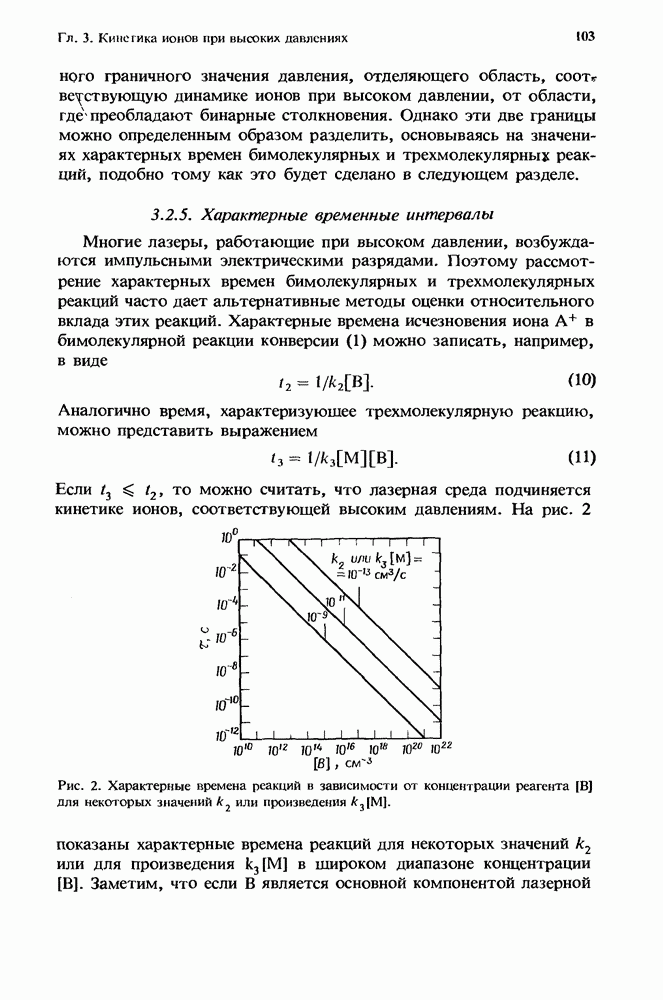
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
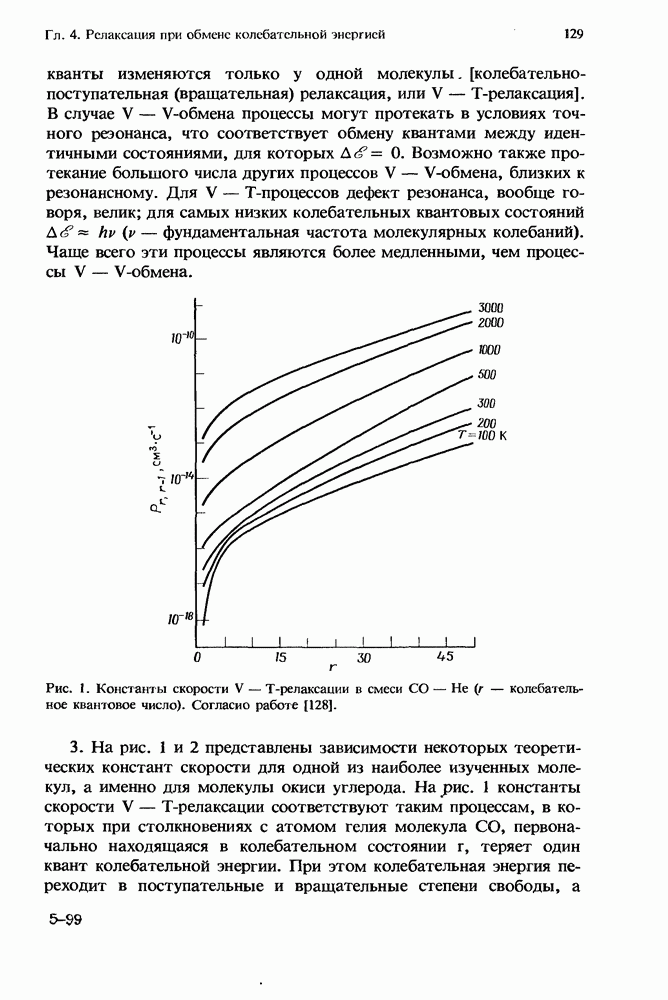
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
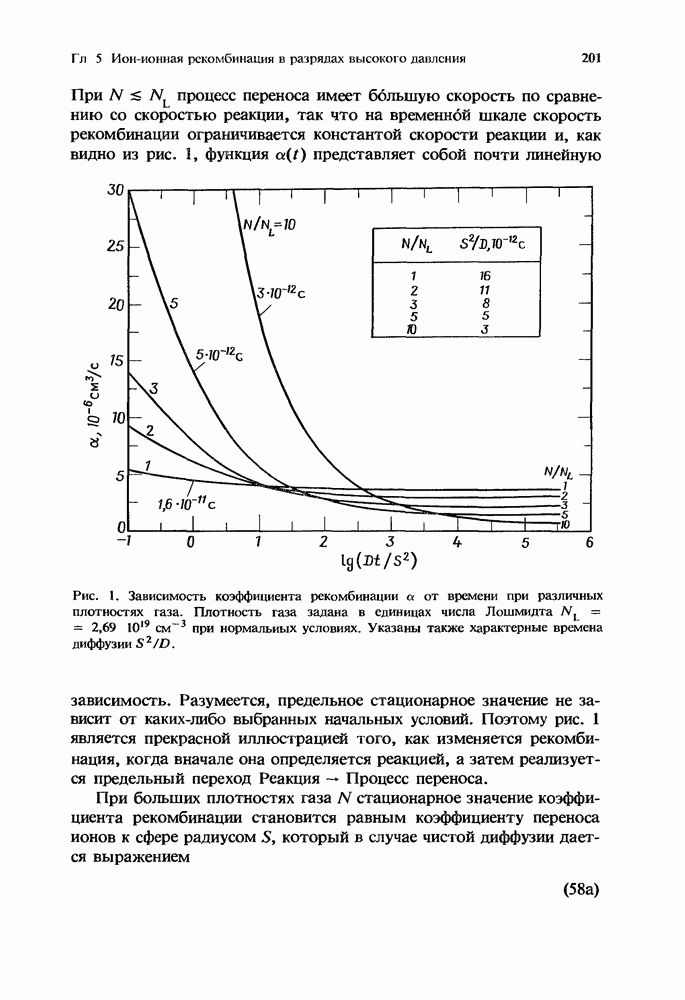
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
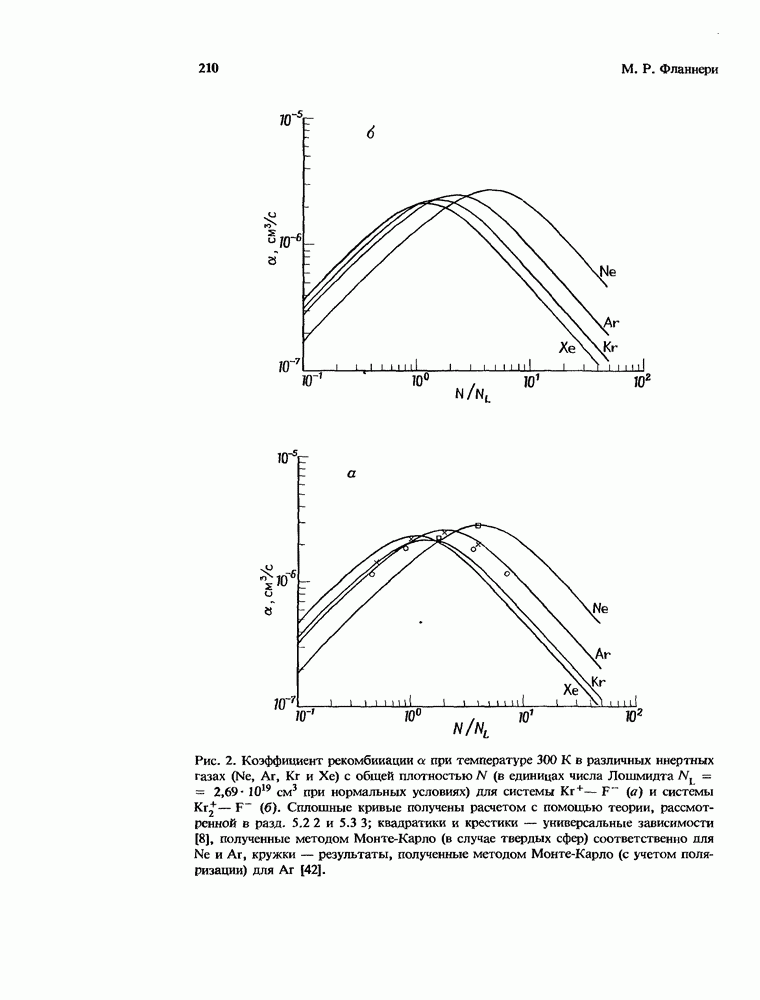
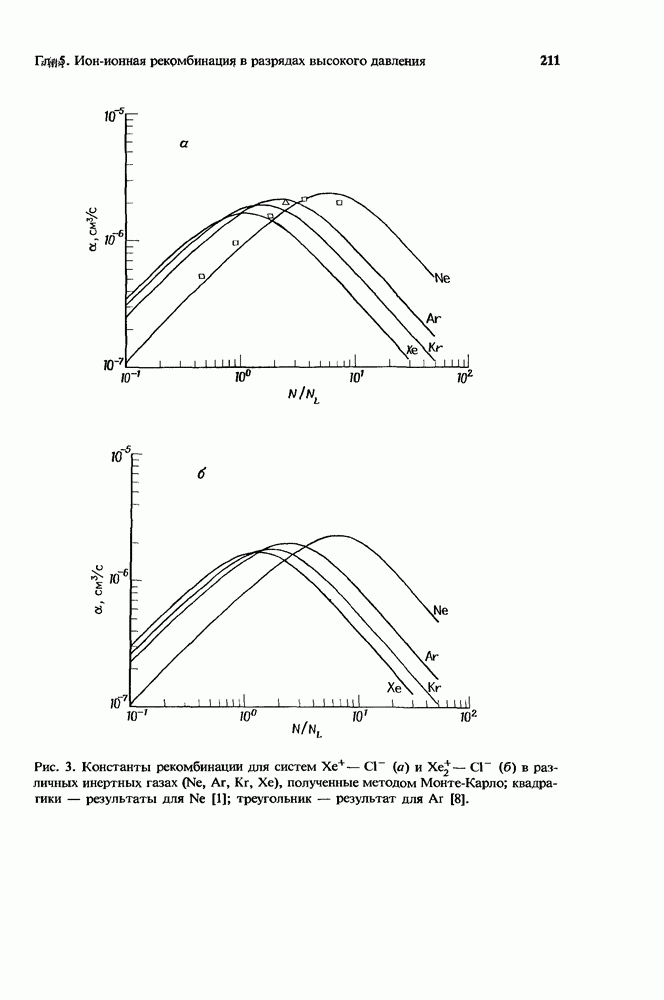
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
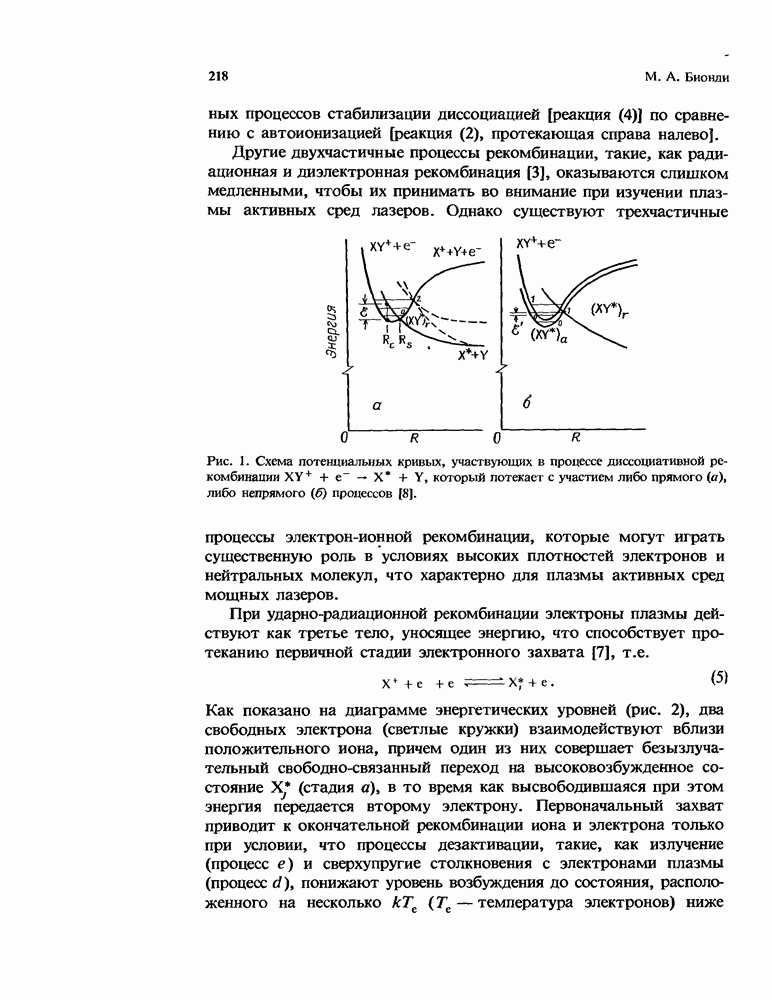
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
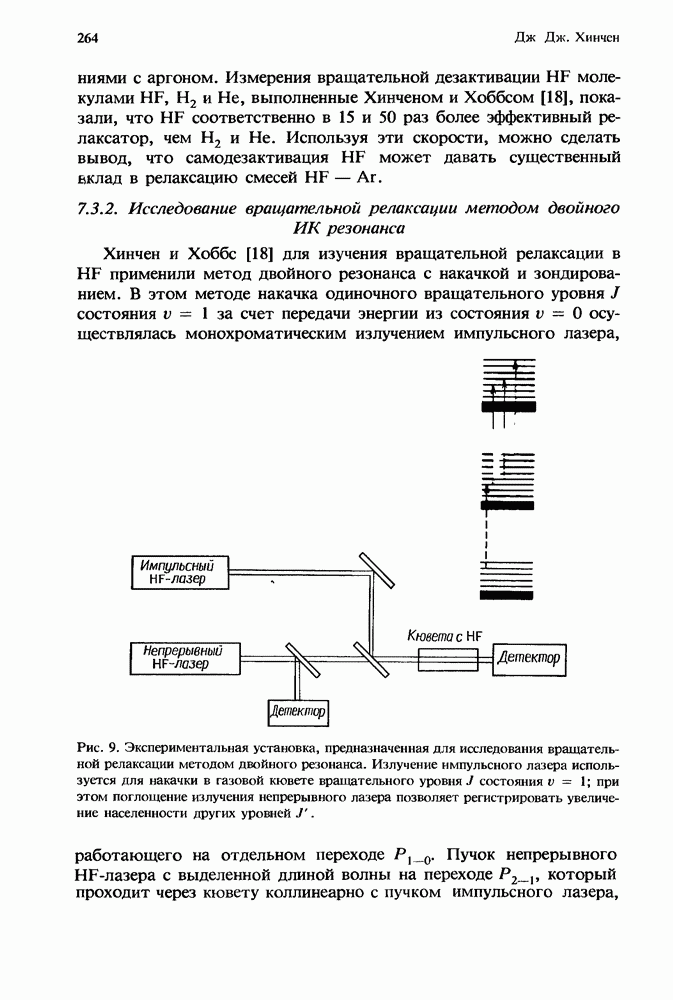
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
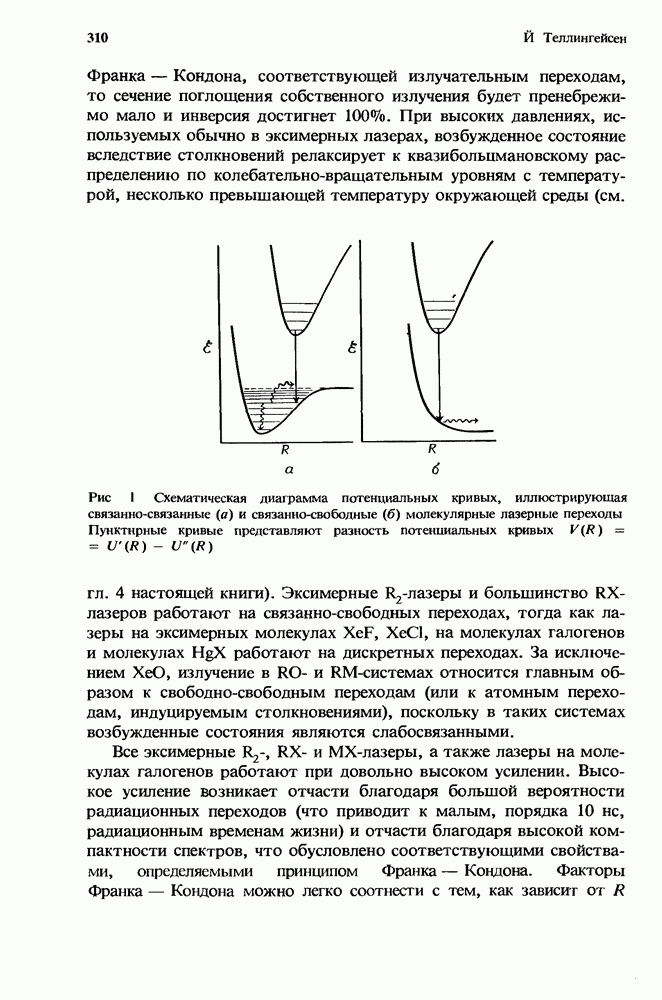
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
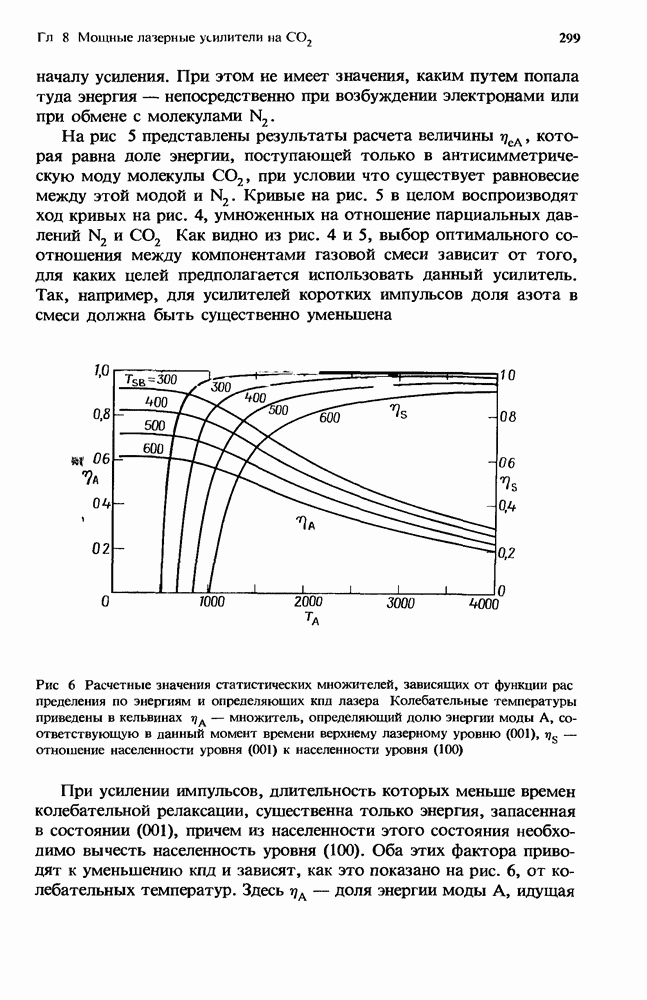
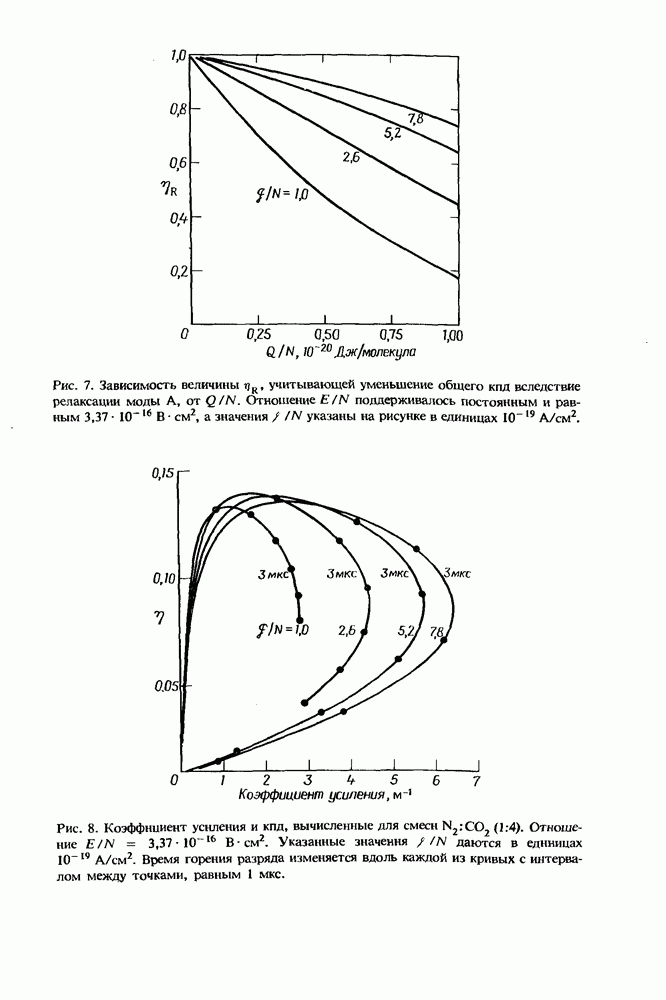
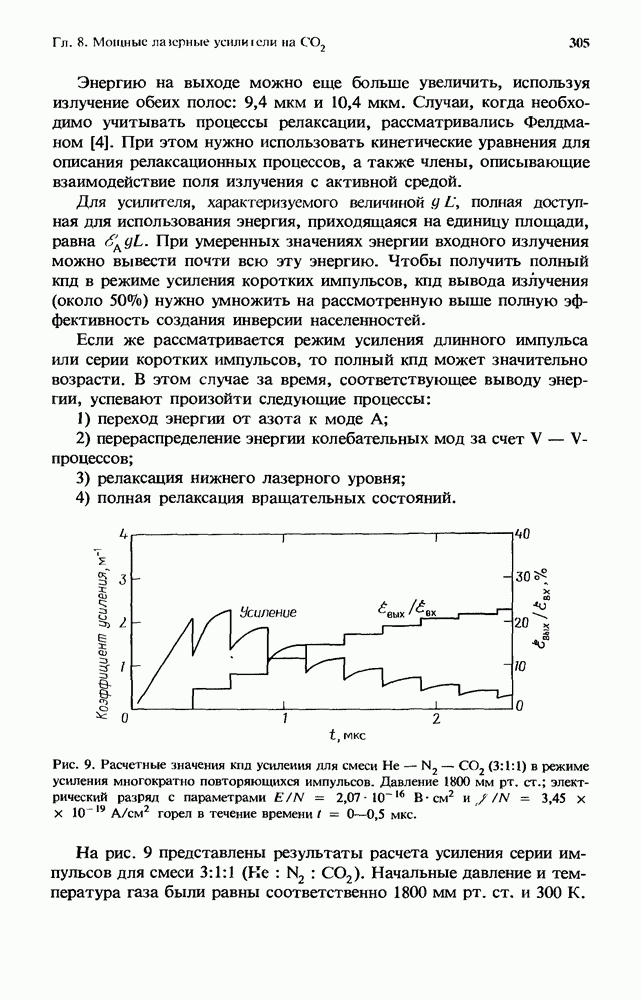
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
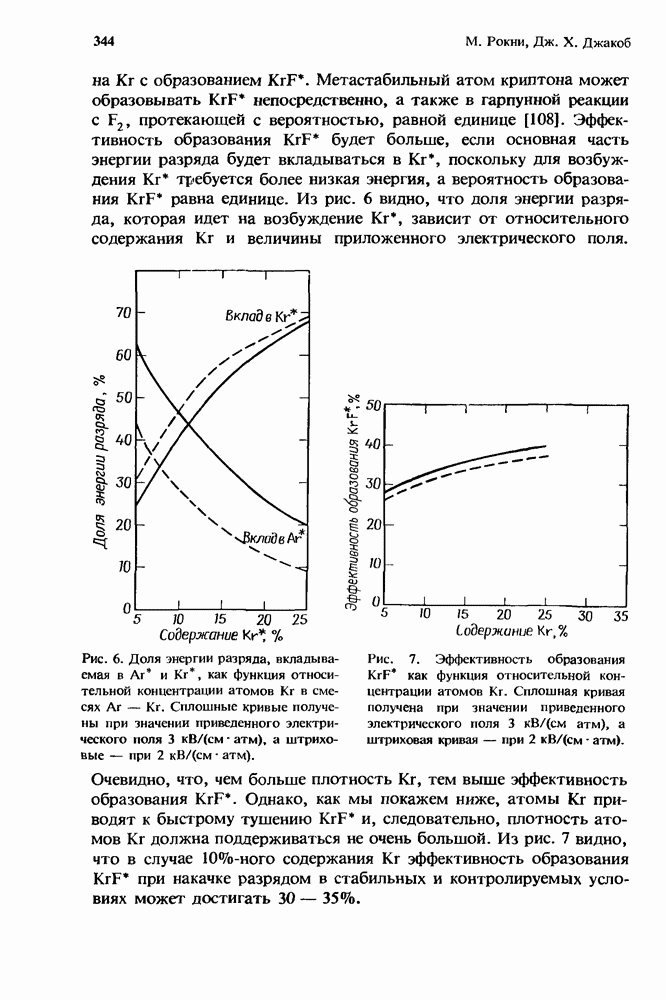
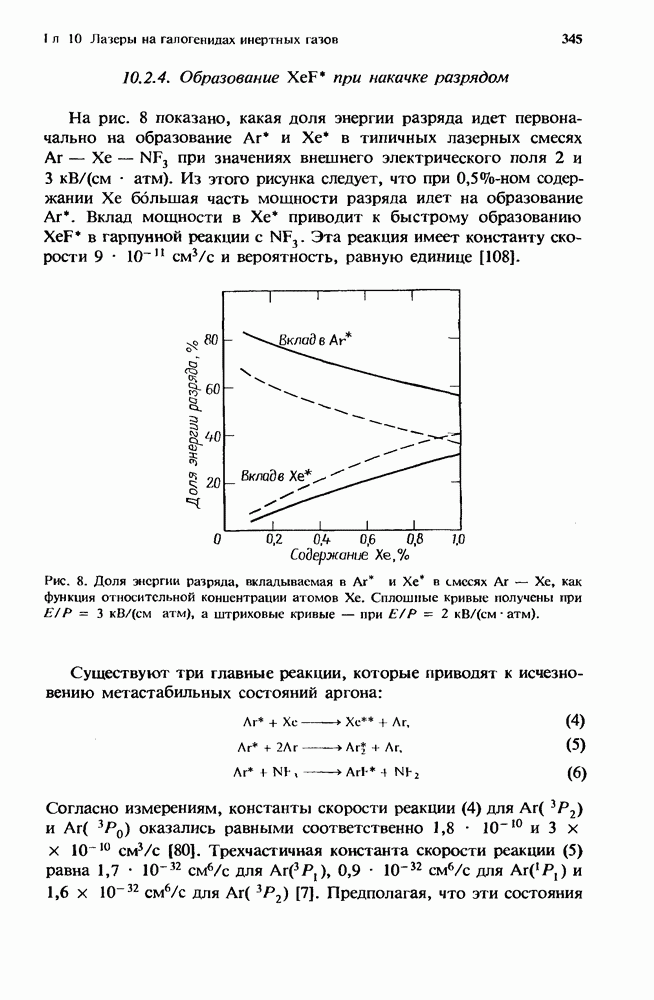
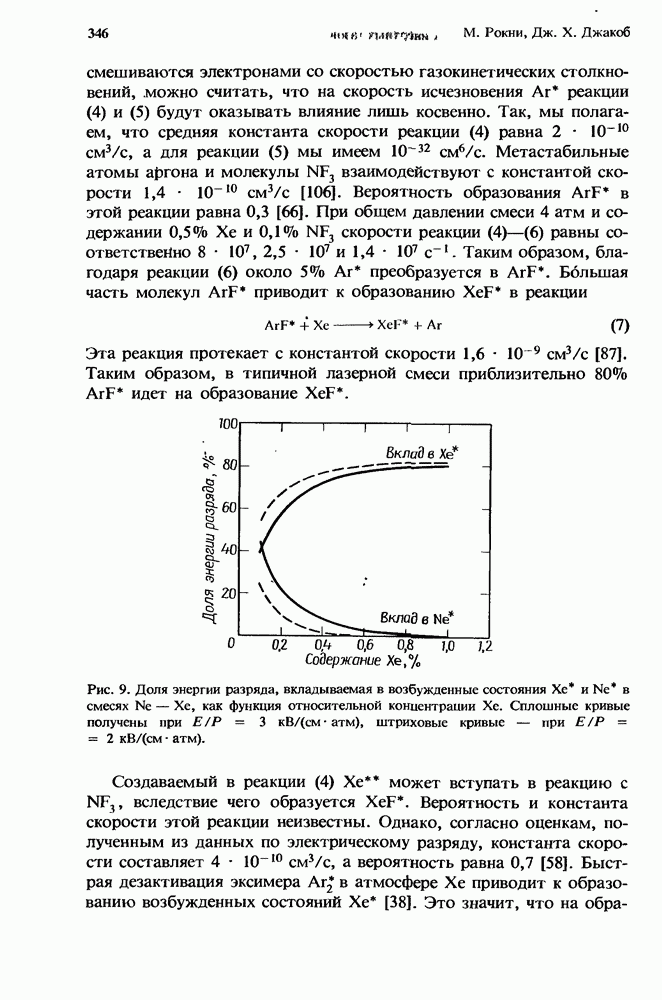
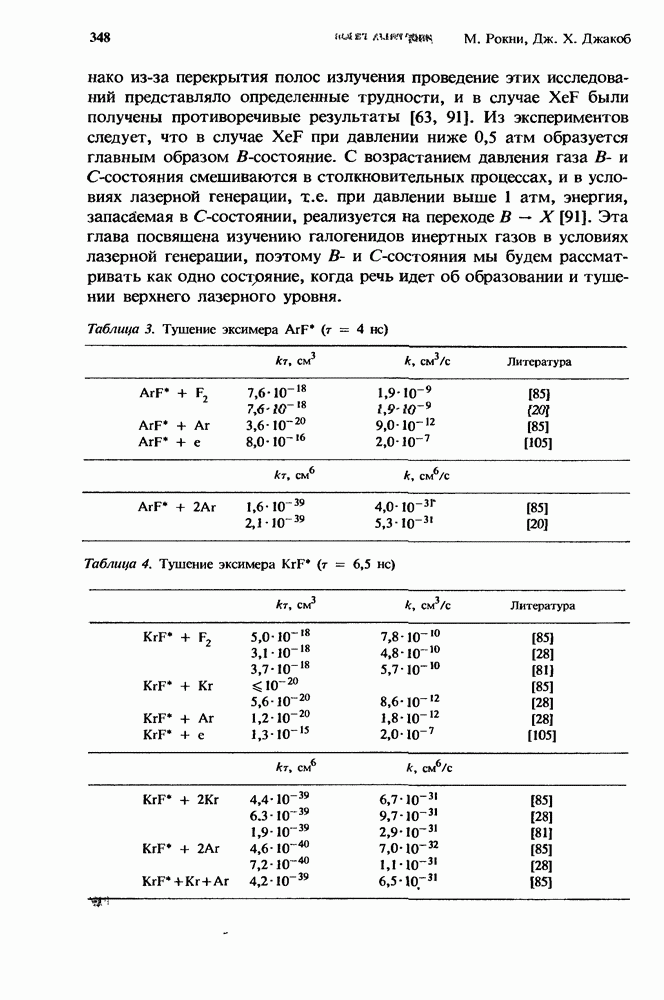
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
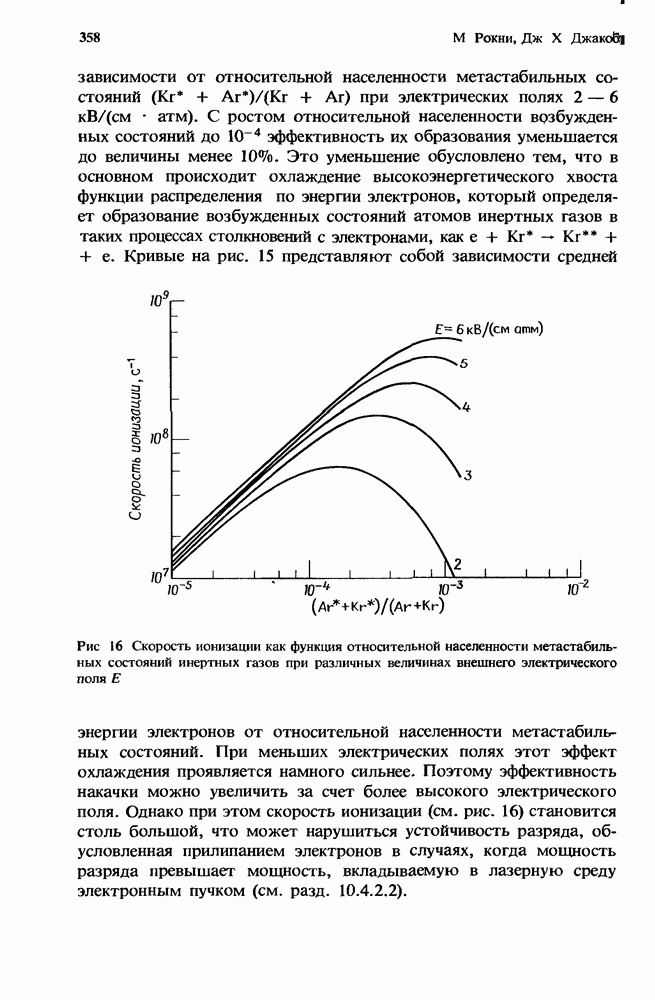
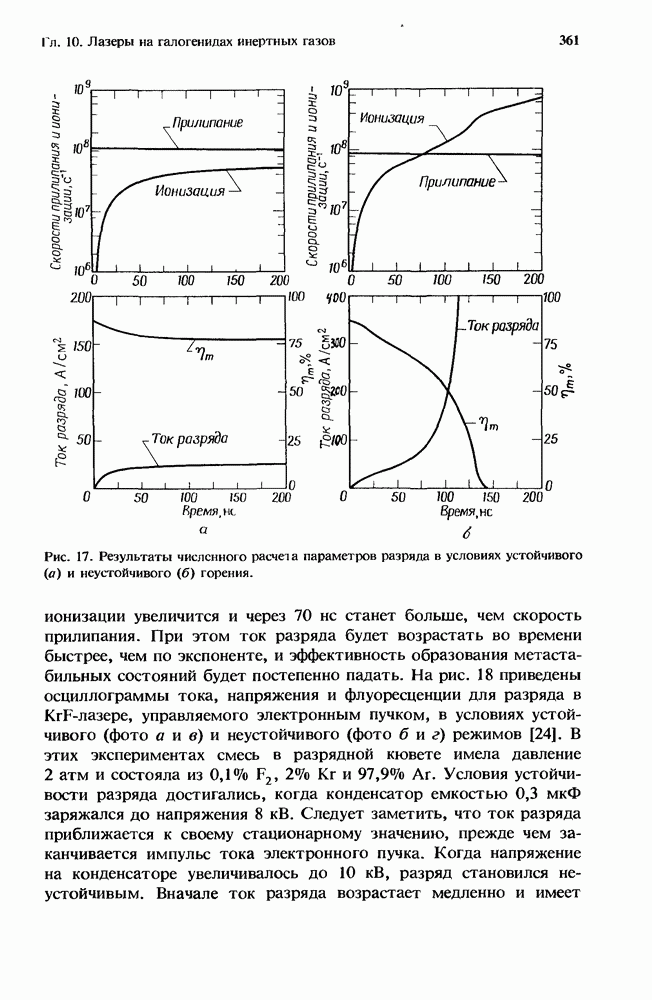
- 10.4.2.2. Устойчивость разряда
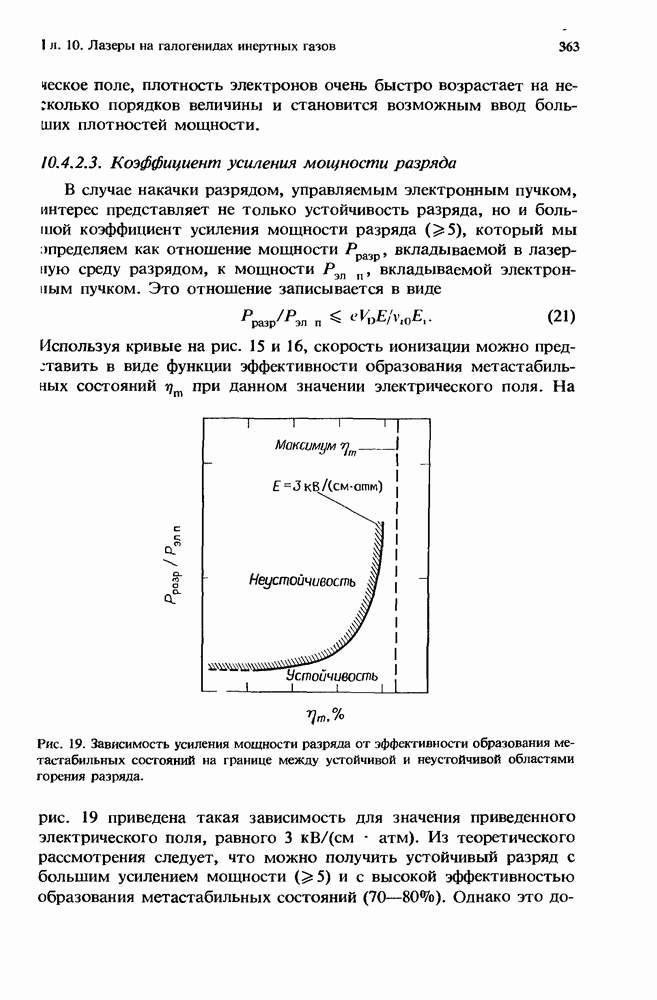
- 10.4.2.3. Коэффициент усиления мощности разряда
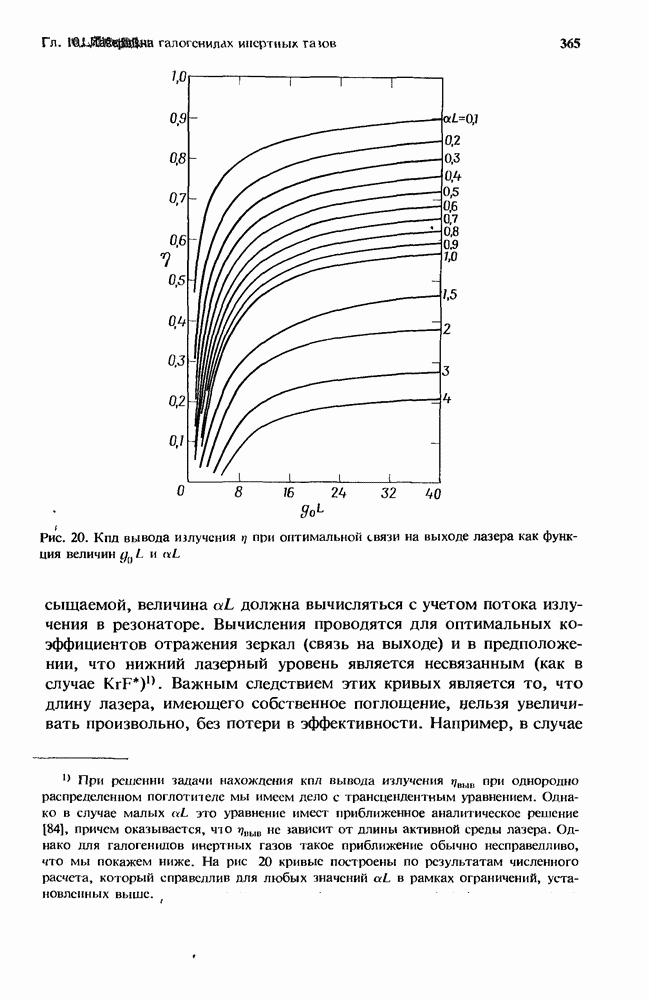
- 10. 5. Вывод мощности
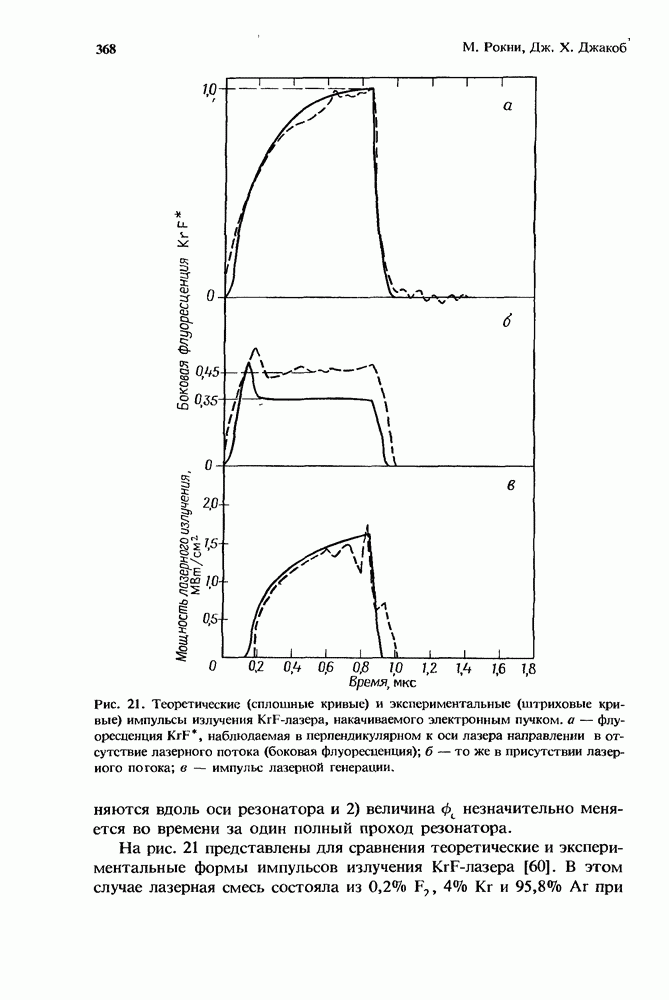
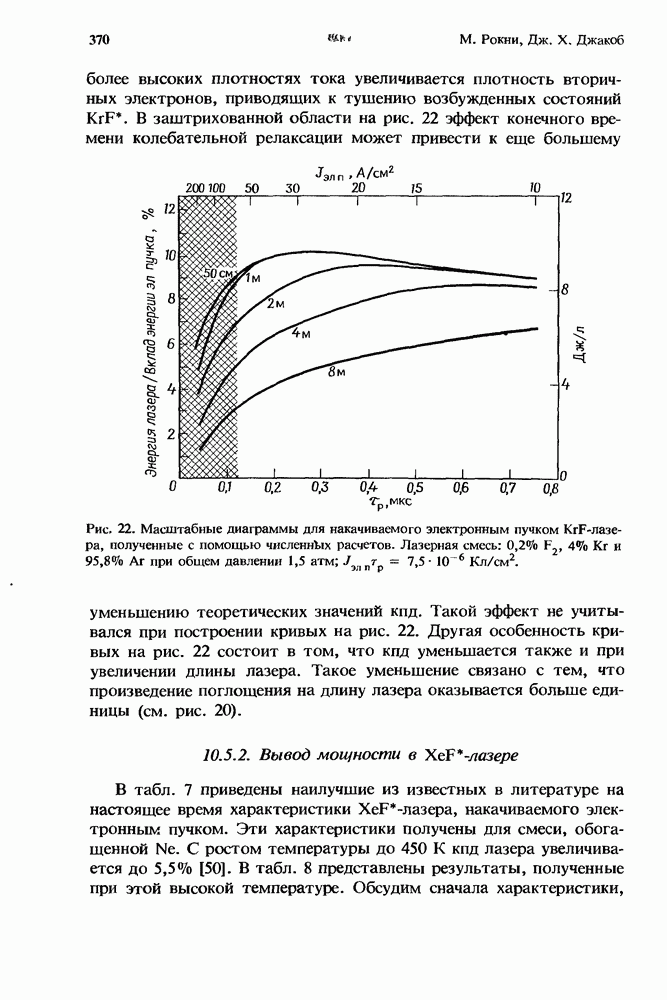
- 10.5.1. Вывод мощности в KrF*-лазере
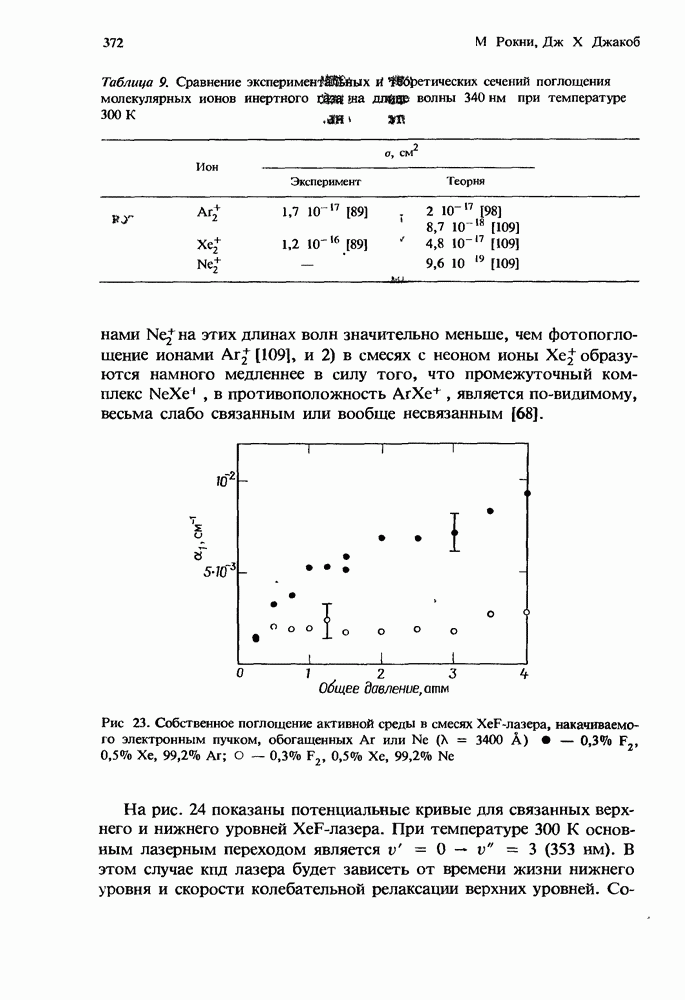
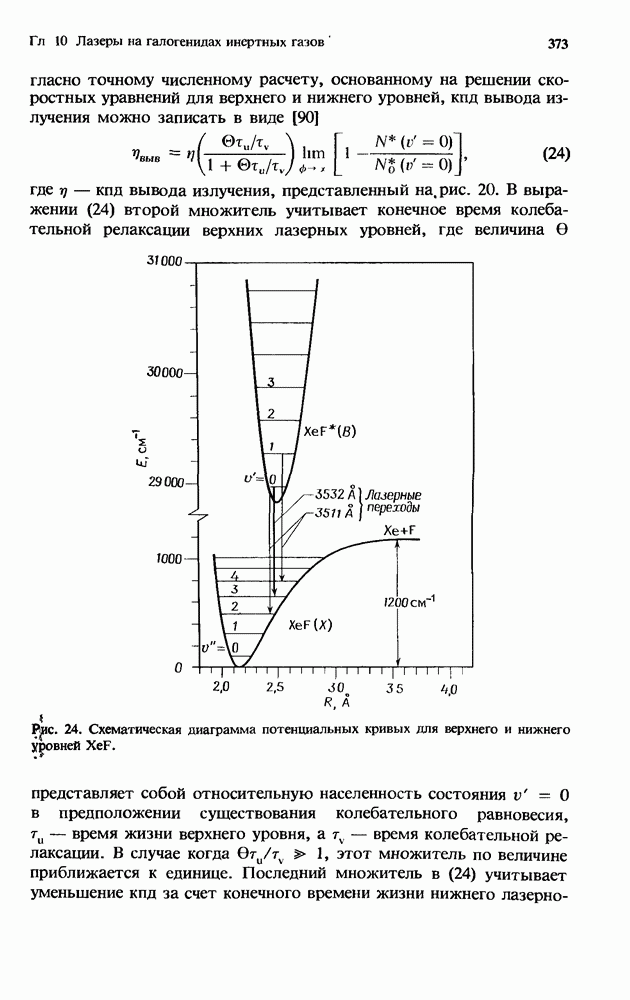
- 10.5.2. Вывод мощности в XcF*-лазере
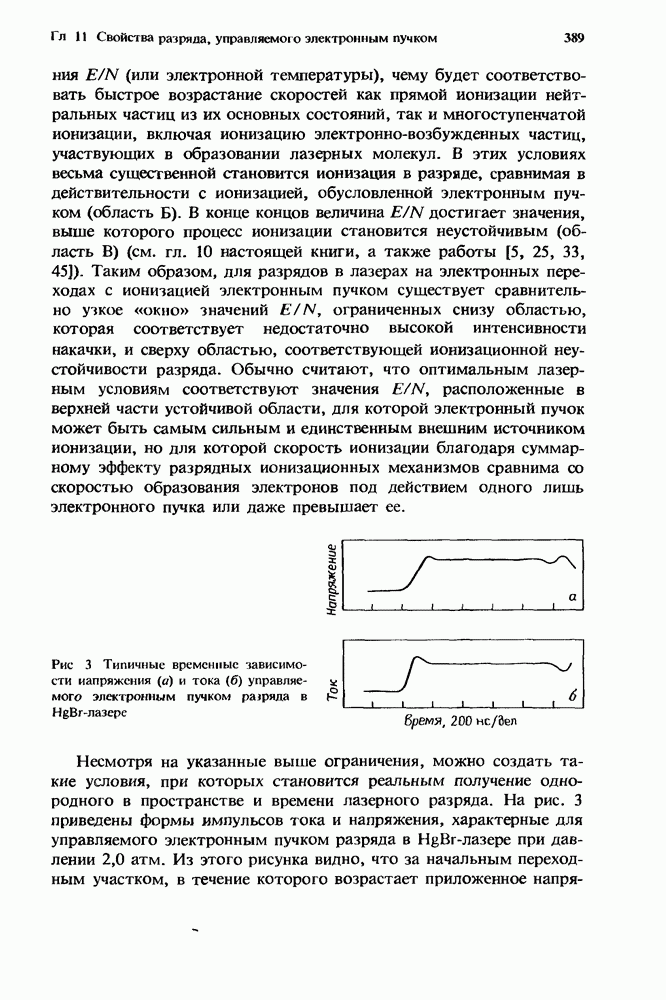
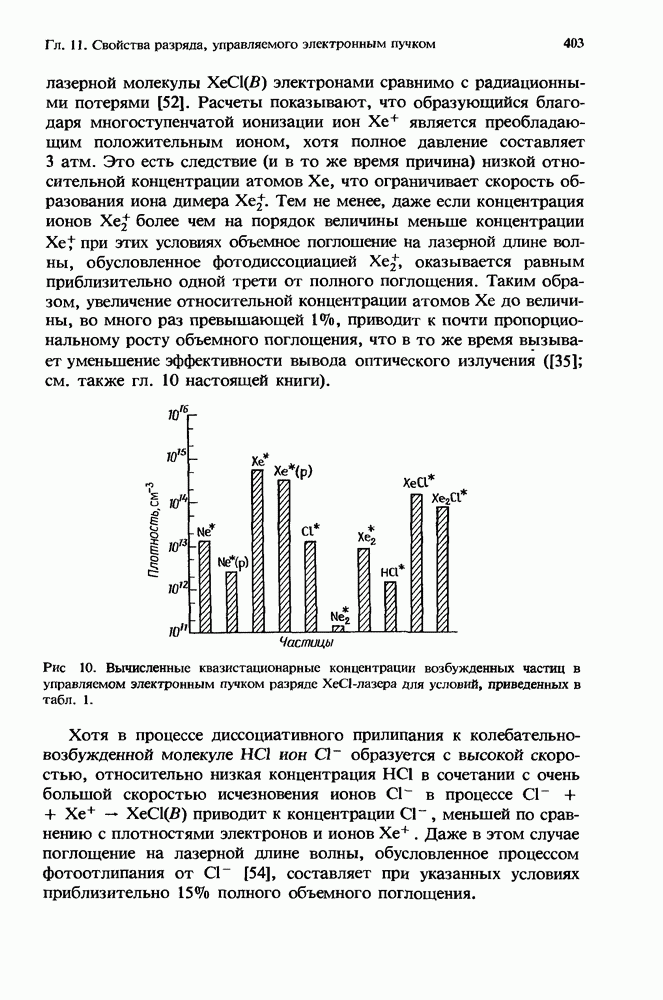
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
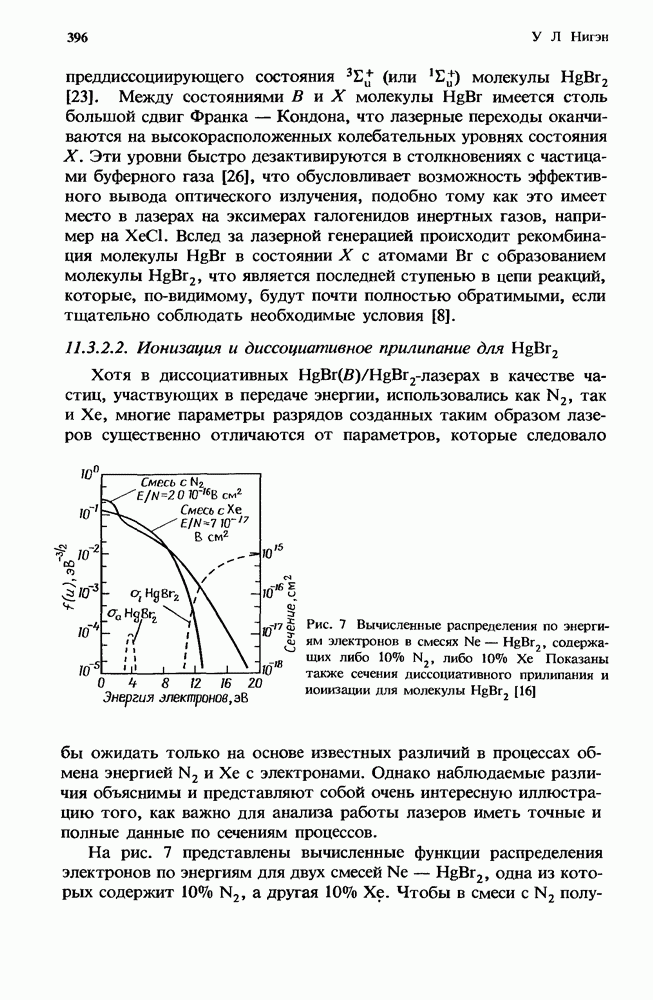
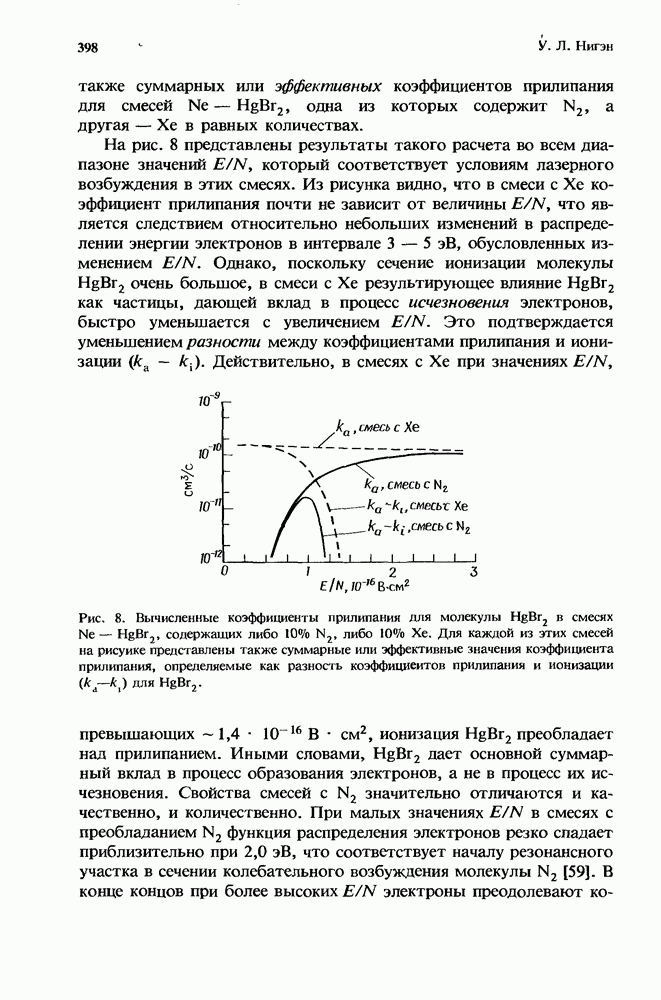
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
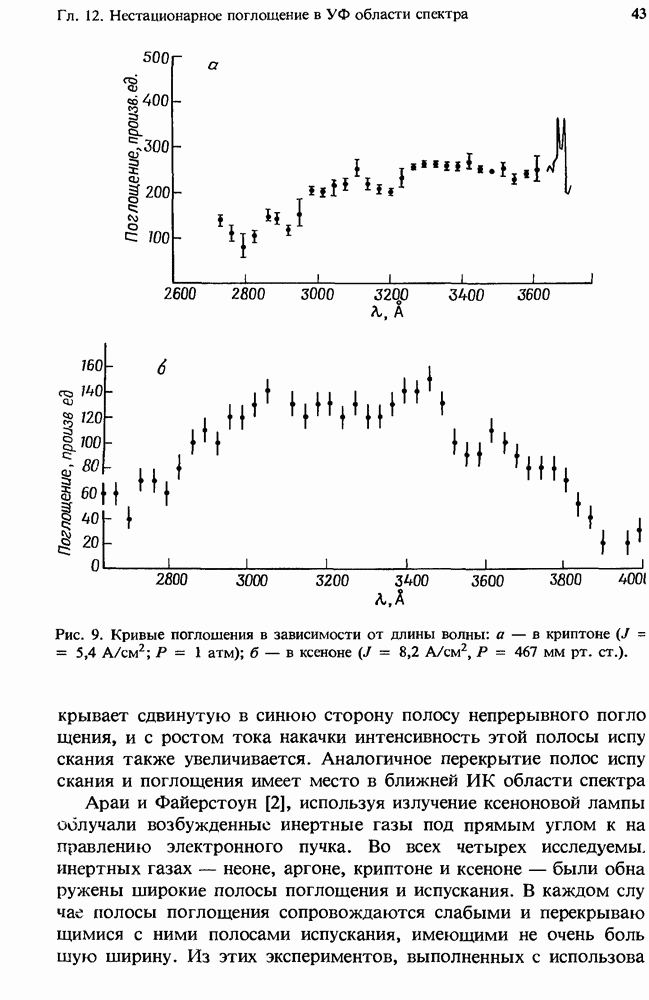
- 12. Нестационарное поглощение в УФ области спектра
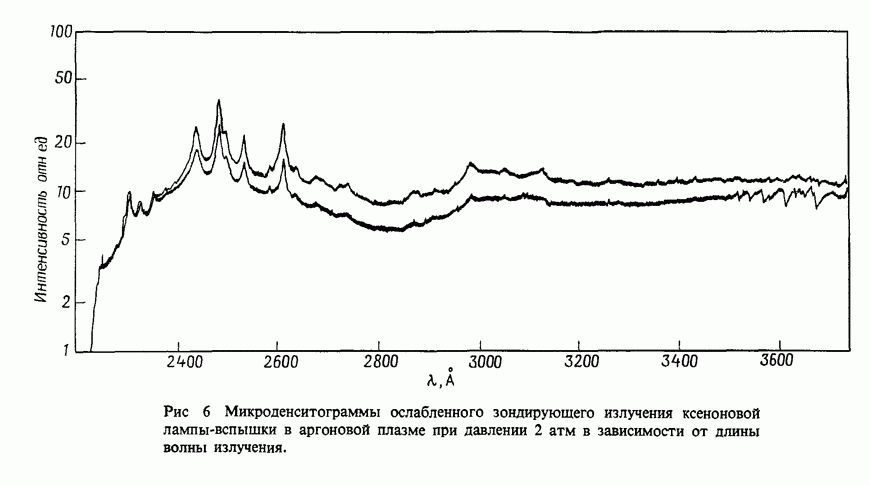
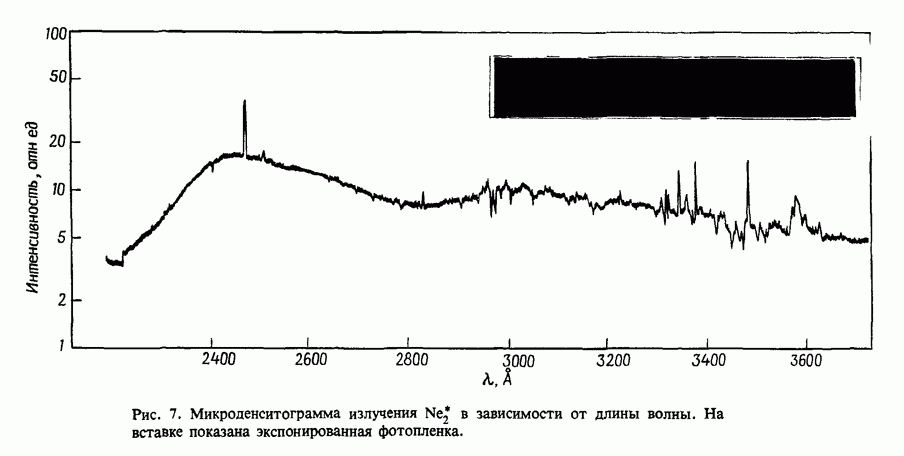
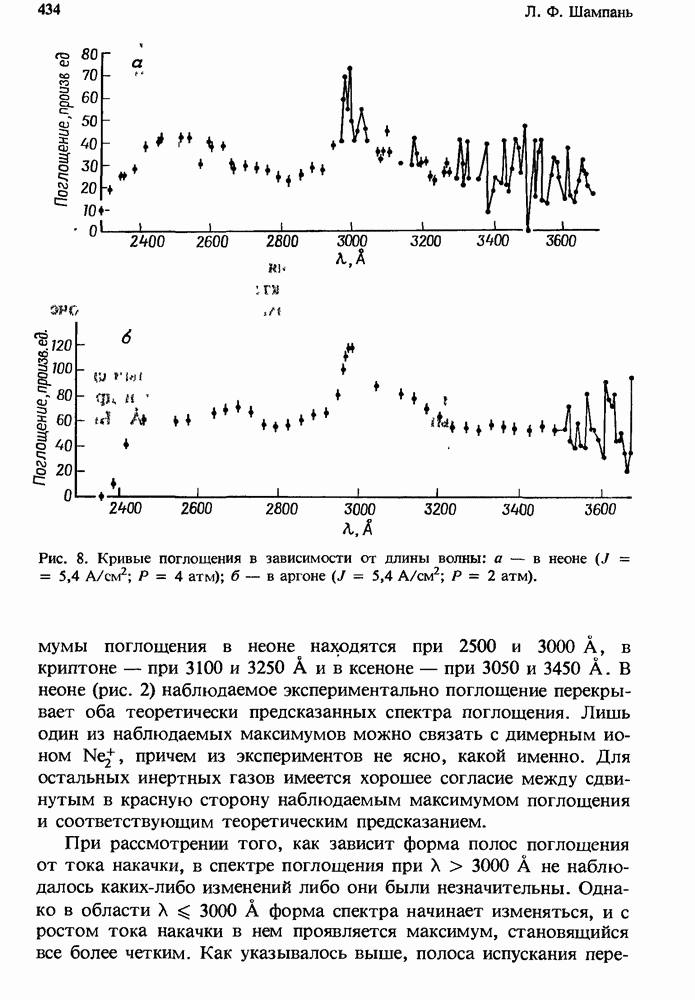
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
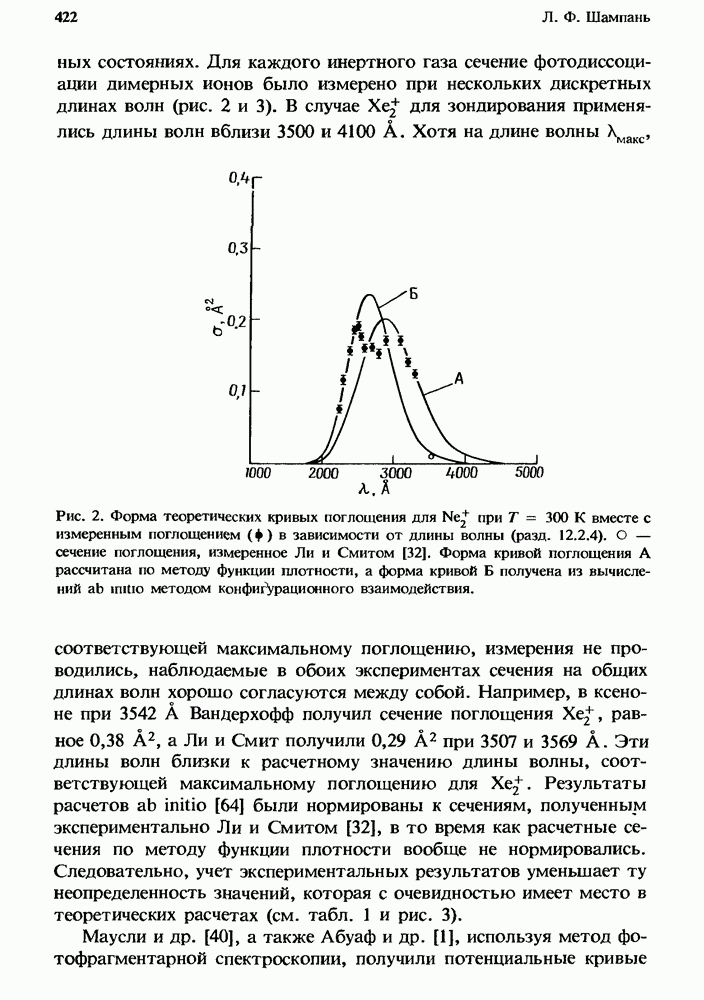
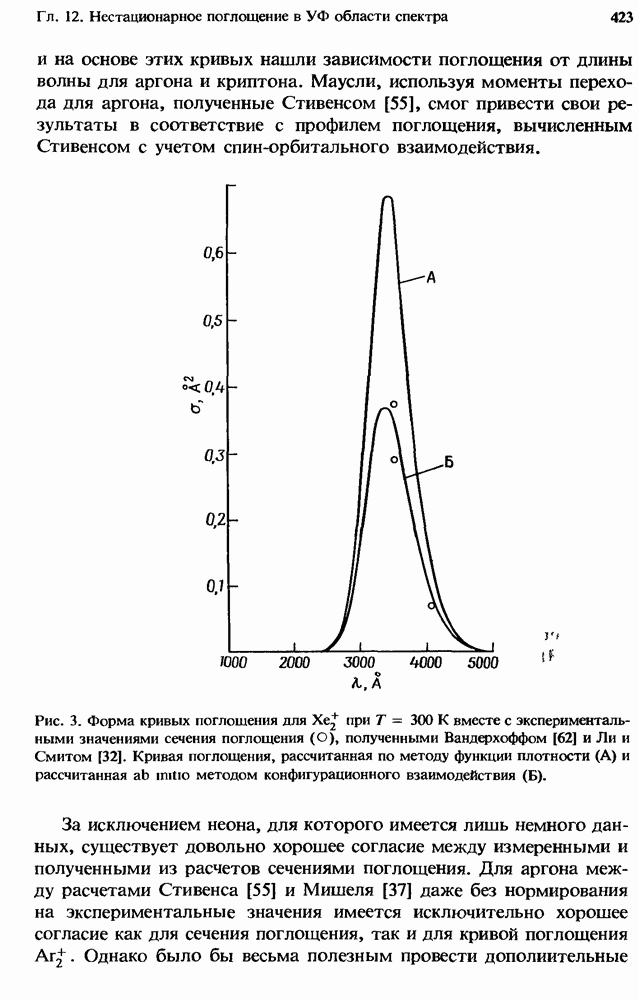
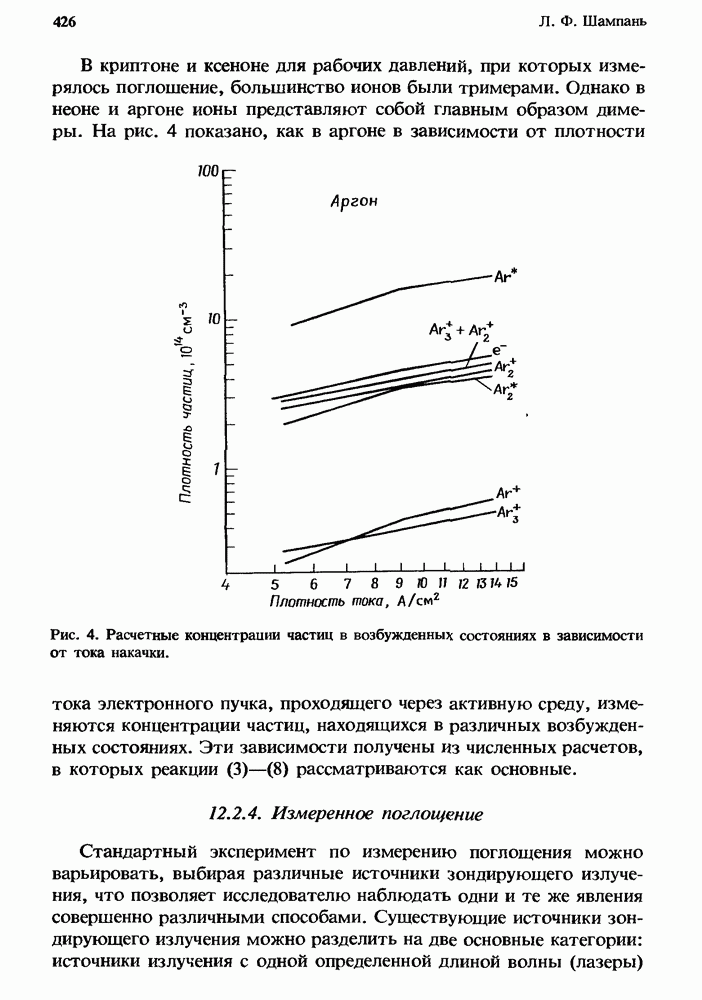
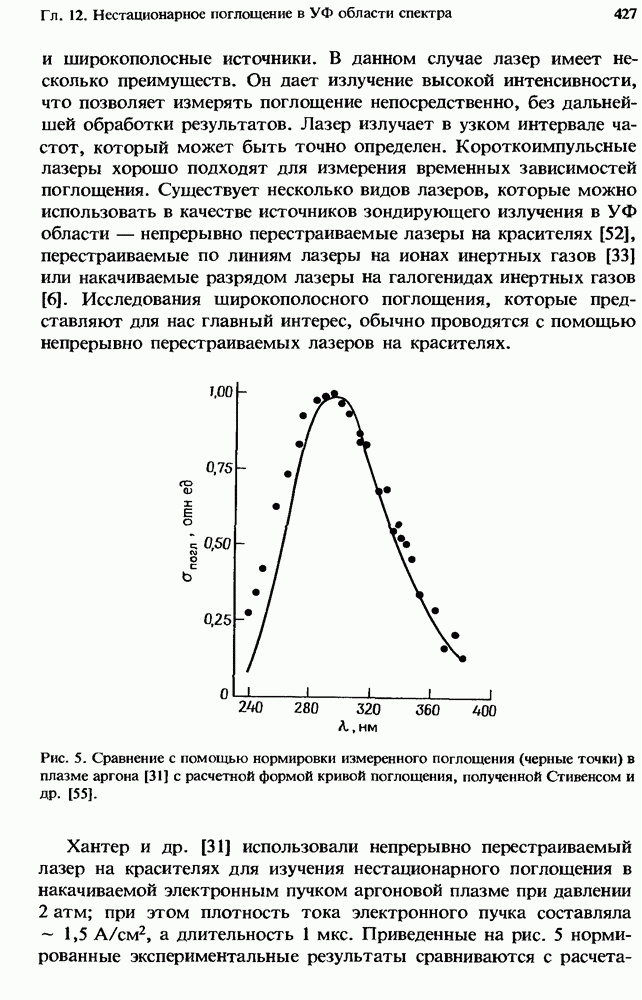
- 12.2.4. Измеренное поглощение
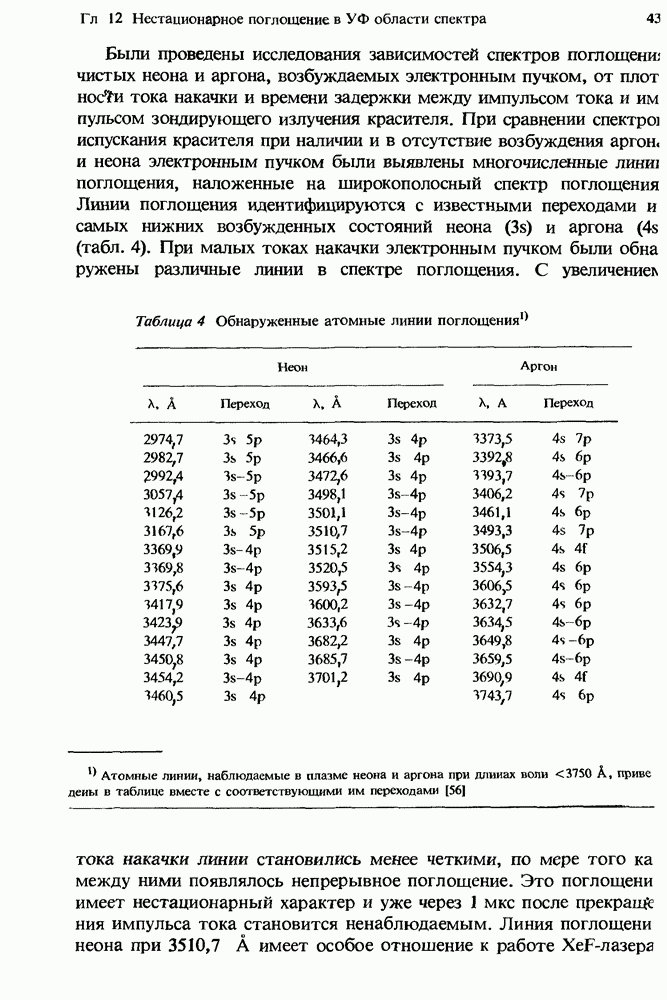
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
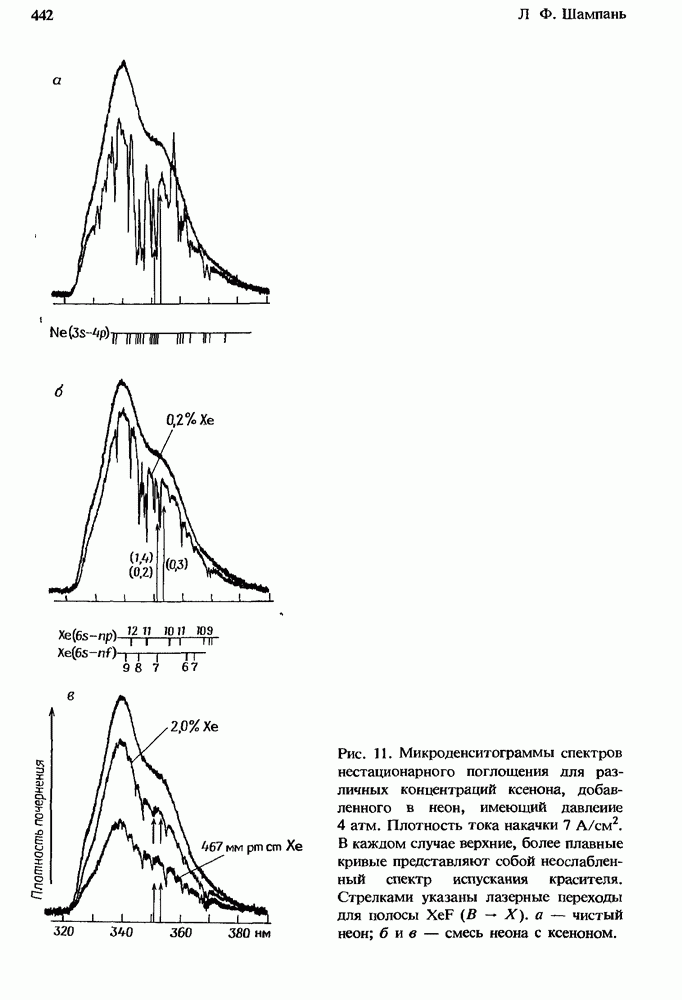
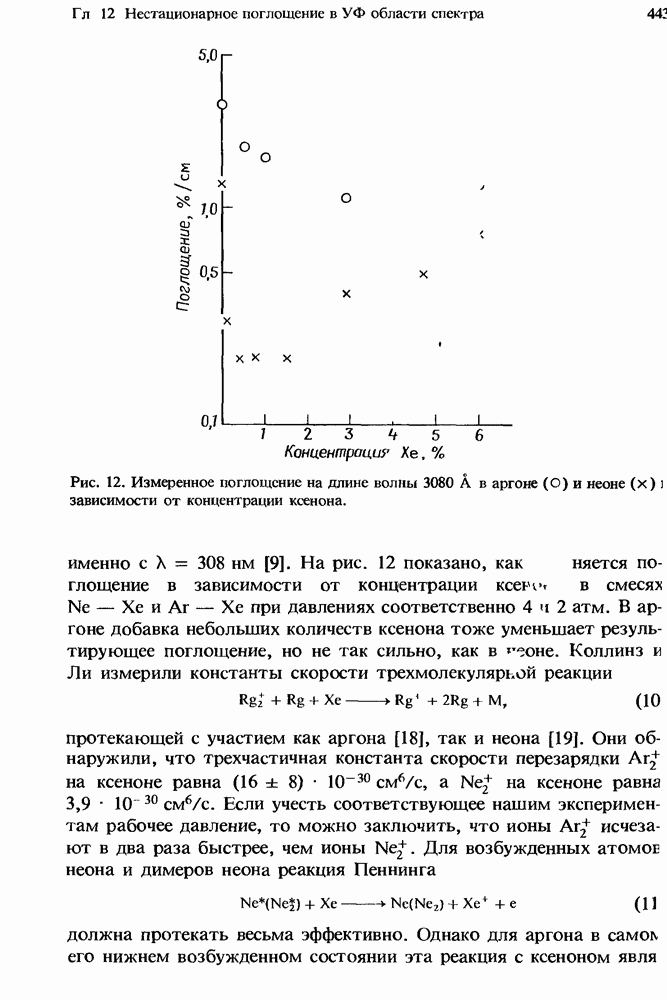
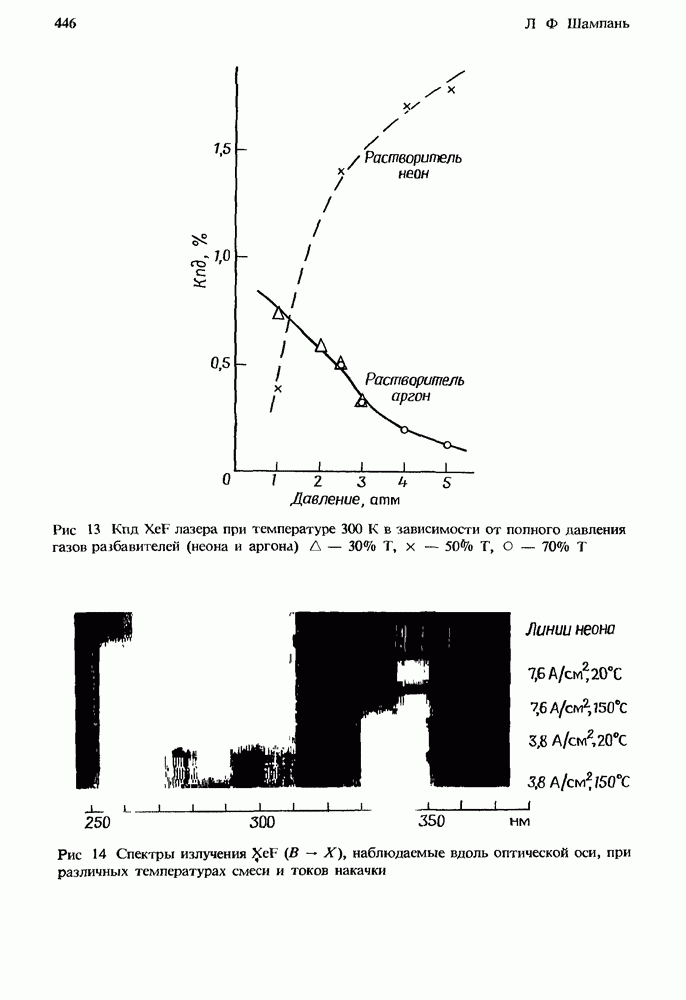
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
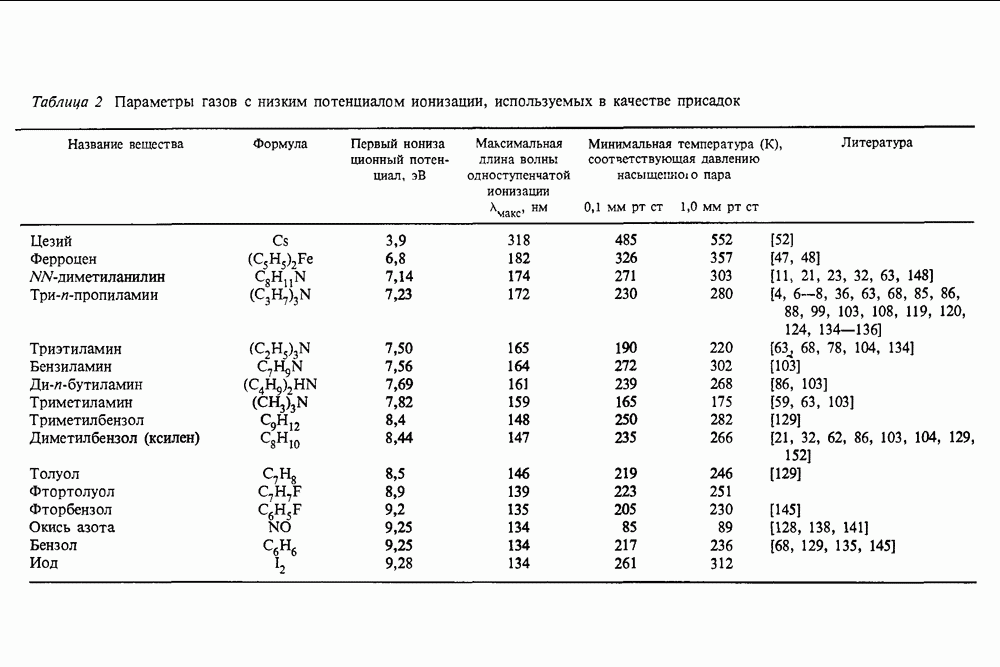
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
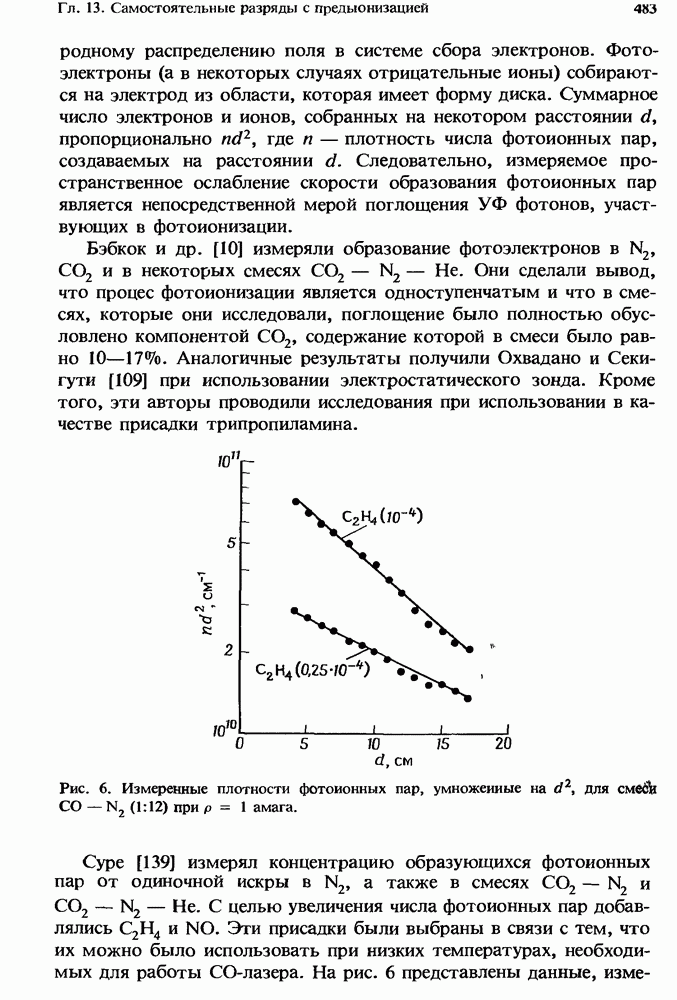
- 13.3.4. Измерения плотности предыонизации от отдельной искры
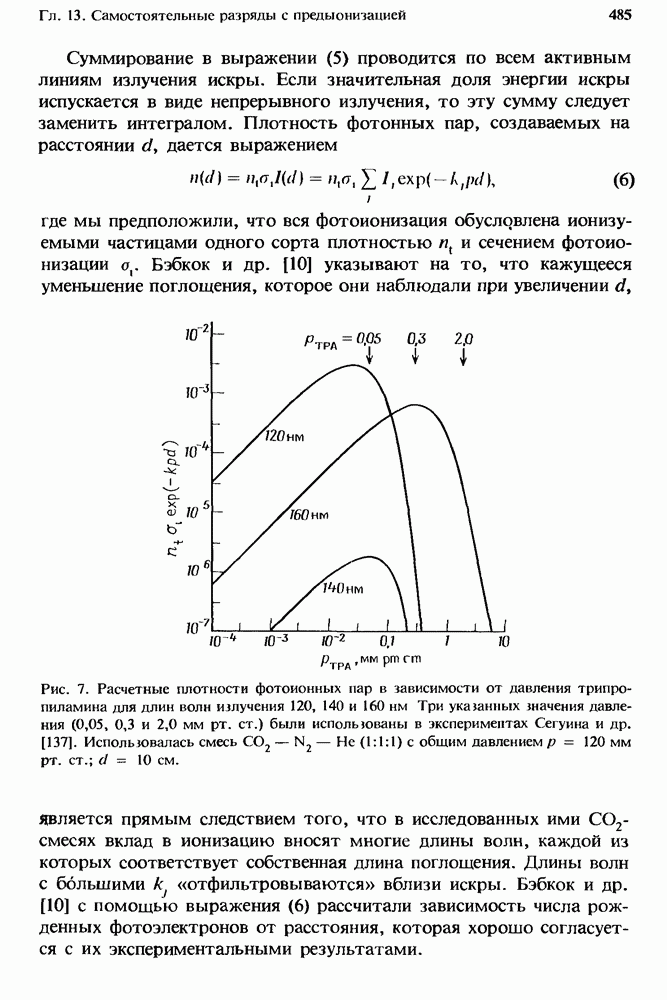
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
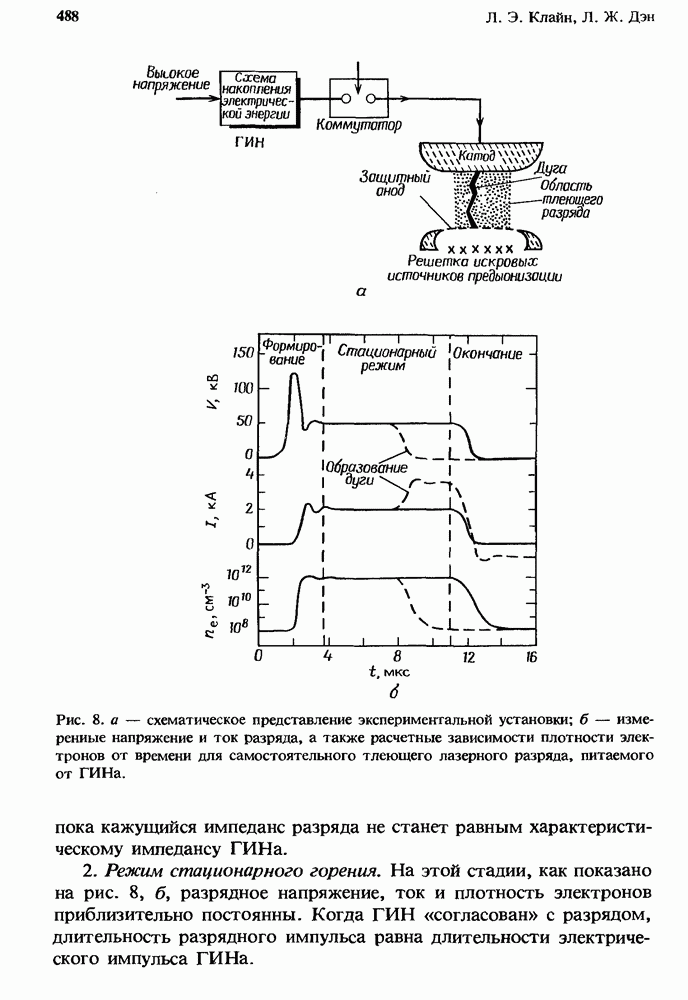
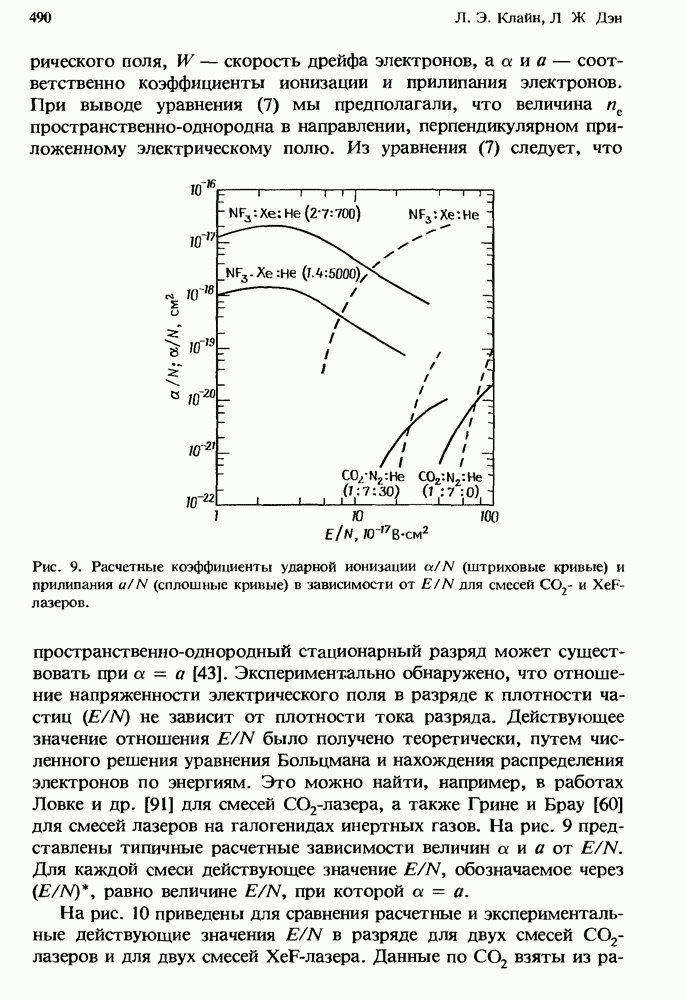
- 13.4. Физика самостоятельного тлеющего разряда
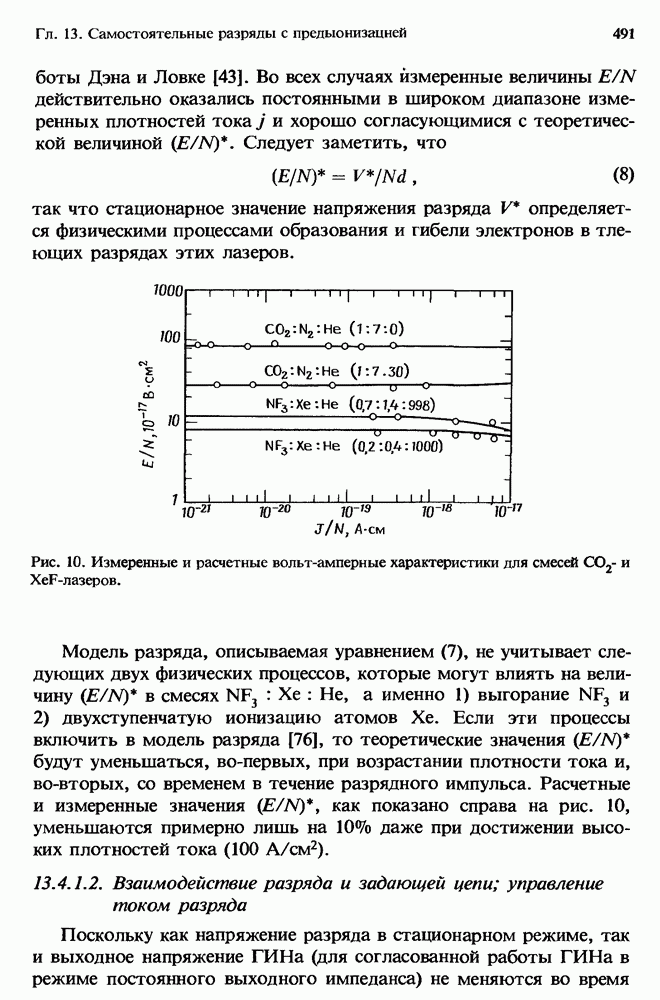
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
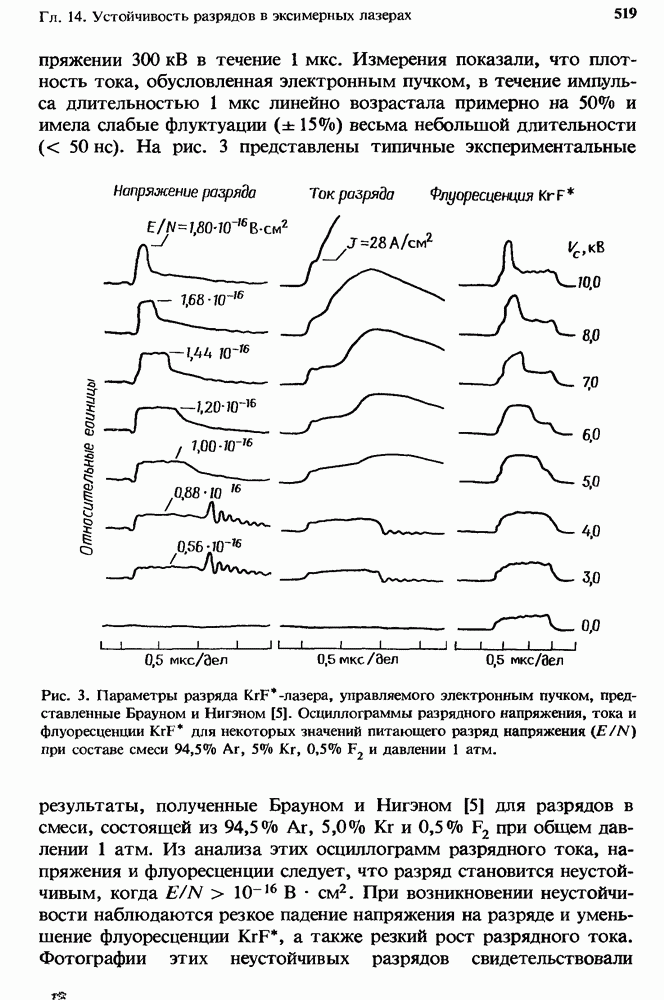
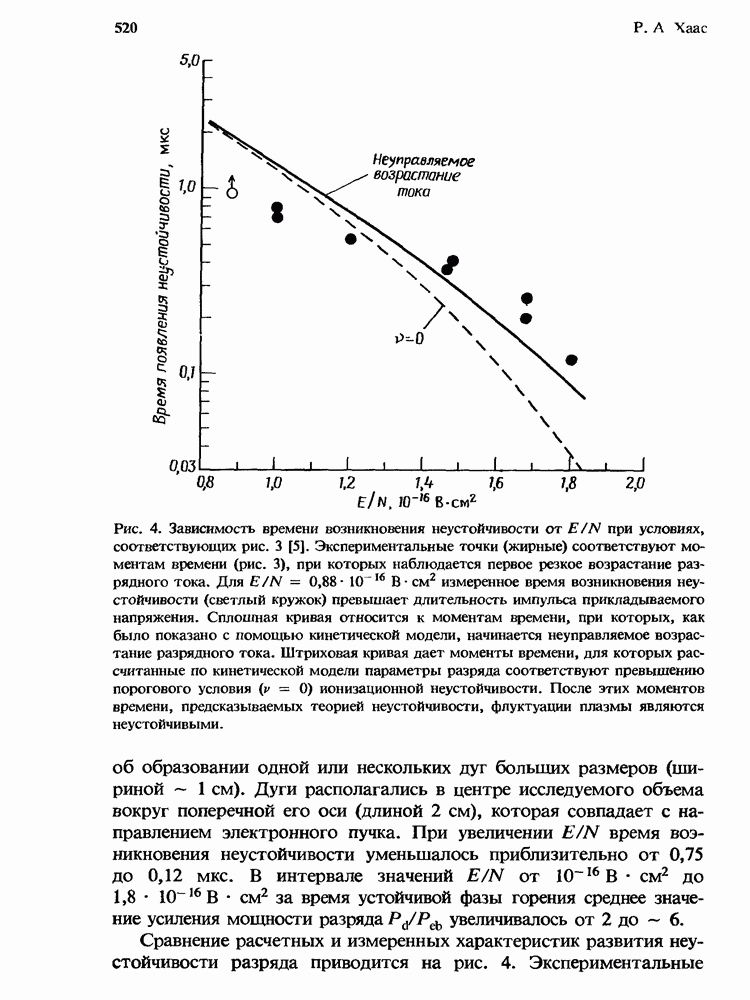
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
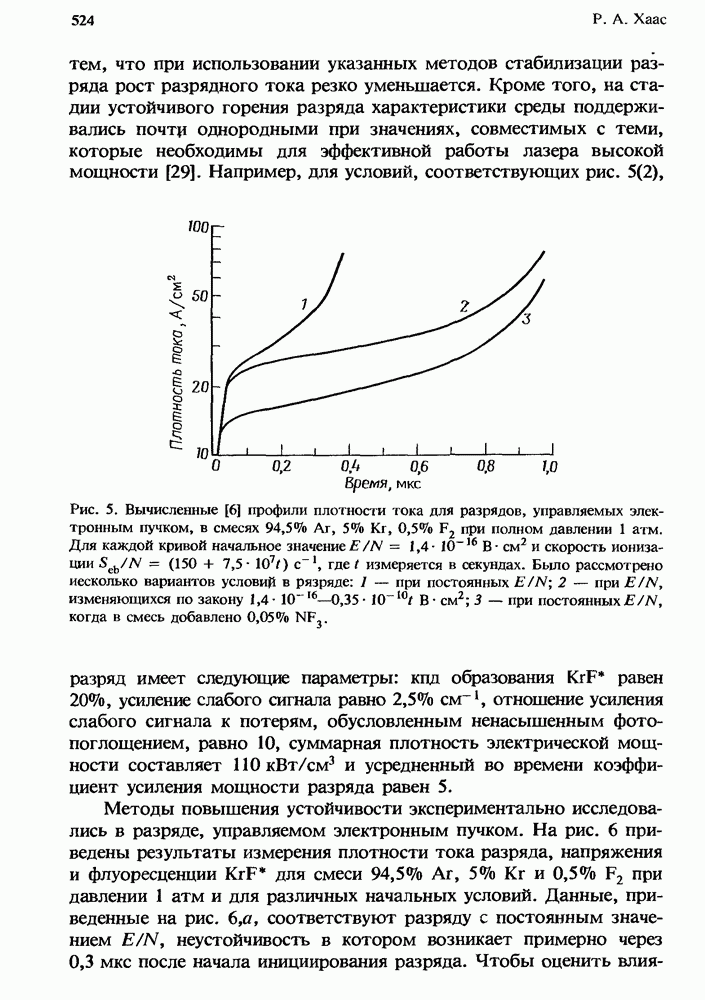
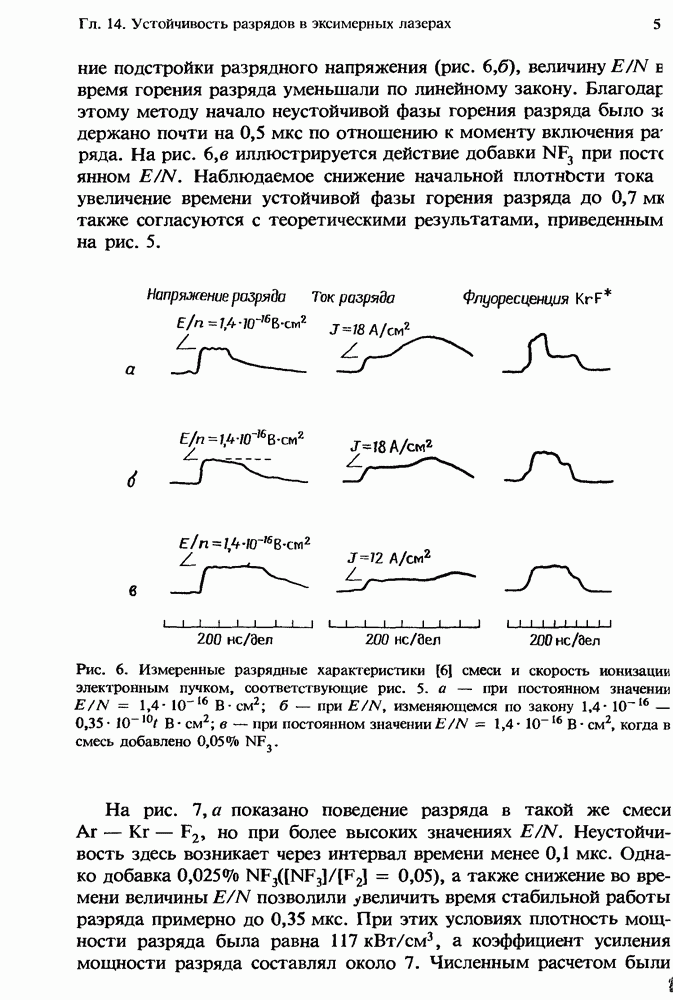
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
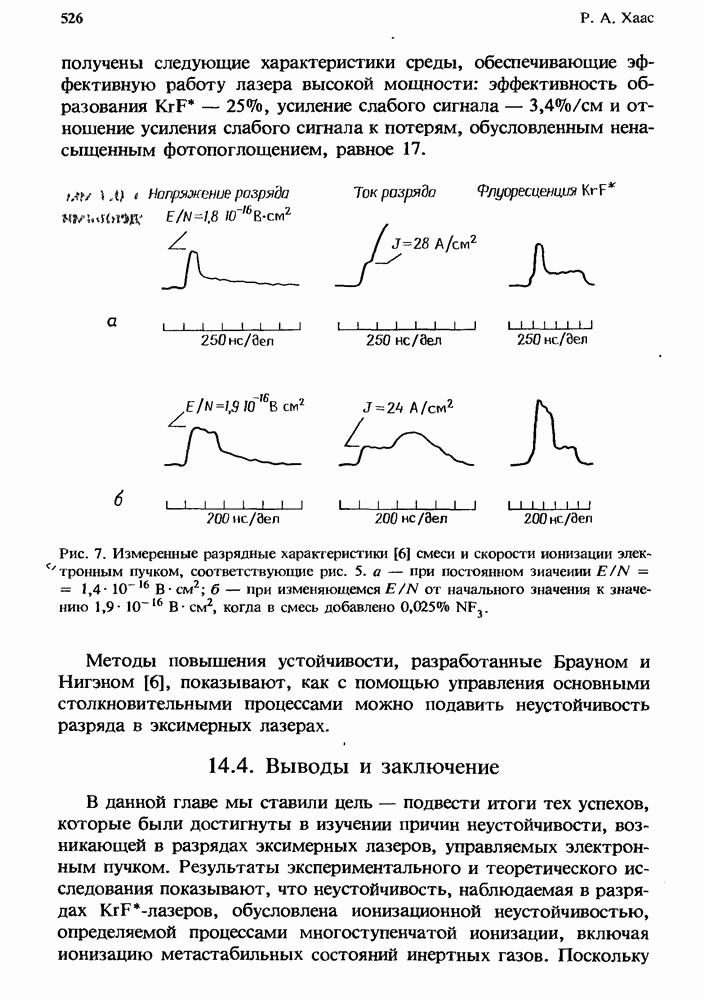
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации