| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
Существует ряд превосходных обзоров, посвященных теории обмена колебательной энергией. Среди них наиболее часто ссылаются на работы Херцфельда и Литовица [17], Котрелла и Мак-Кубри [9], Бернетта и Норта [6]. Из более последних обзоров можно назвать работы Такаянаги [48], Секреста [38], Херцфельда [16], Рэппа и Кессэла [34], а также Амми [1]. Проводимое нами рассмотрение не является исчерпывающим, а представляет собой краткий обзор и анализ применения теории колебательной релаксации к молекулам галогеноводородов.
Классическая теория рассматривает обмен между колебательными и поступательными степенями свободы как процесс столкновения между двухатомным гармоническим осциллятором и налетающим атомом или молекулой. В рамках простейшей теории сталкивающиеся частицы сближаются по оси, соединяющей атомы двухатомной молекулы, а соударение происходит между максимально сблизившимися атомами. При этом взаимодействие определяется отталкивательным потенциалом V, который представляет собой отрицательную экспоненту от расстояния между молекулой и налетающей частицей  Это расстояние определяется как поступательным, так и колебательным движением молекулы. Предполагается, что осциллятор не вращается. Необходимо решить дифференциальное уравнение, описывающее совместное движение налетающей частицы и осциллятора. Ландау и Теллер [25] показали, что вероятность
Это расстояние определяется как поступательным, так и колебательным движением молекулы. Предполагается, что осциллятор не вращается. Необходимо решить дифференциальное уравнение, описывающее совместное движение налетающей частицы и осциллятора. Ландау и Теллер [25] показали, что вероятность  обмена энергией можно вычислить с помощью адиабатического принципа. Соответствующее выражение имеет вид
обмена энергией можно вычислить с помощью адиабатического принципа. Соответствующее выражение имеет вид

где  — время столкновения,
— время столкновения,  — период колебаний осциллятора и С — константа. Усредняя по максвелловскому распределению, получаем среднее при данной температуре Т значение вероятности, равное
— период колебаний осциллятора и С — константа. Усредняя по максвелловскому распределению, получаем среднее при данной температуре Т значение вероятности, равное

где  — приведенная масса осциллятора и налетающей частицы. Ландау и Теллер показали [25], что этот интеграл можно записать в приближенном виде:
— приведенная масса осциллятора и налетающей частицы. Ландау и Теллер показали [25], что этот интеграл можно записать в приближенном виде:

откуда следует, что для большинства газов вероятность релаксации пропорциональна  Существует следующее соотношение между вероятностью обмена энергией Р и временем релаксации
Существует следующее соотношение между вероятностью обмена энергией Р и временем релаксации 

где  — частота колебаний,
— частота колебаний,  — частота столкновений,
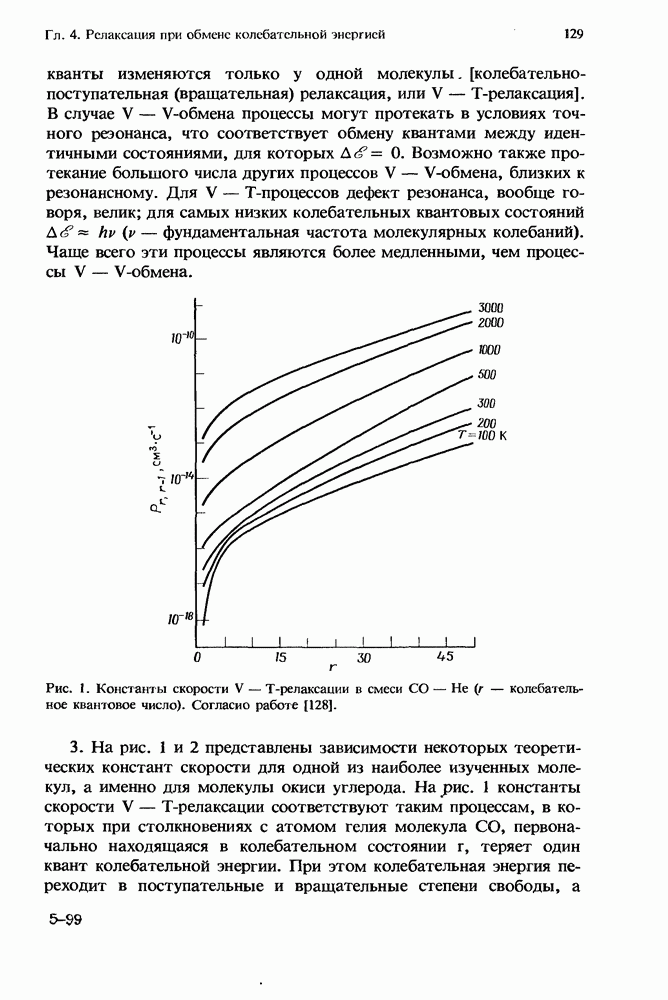
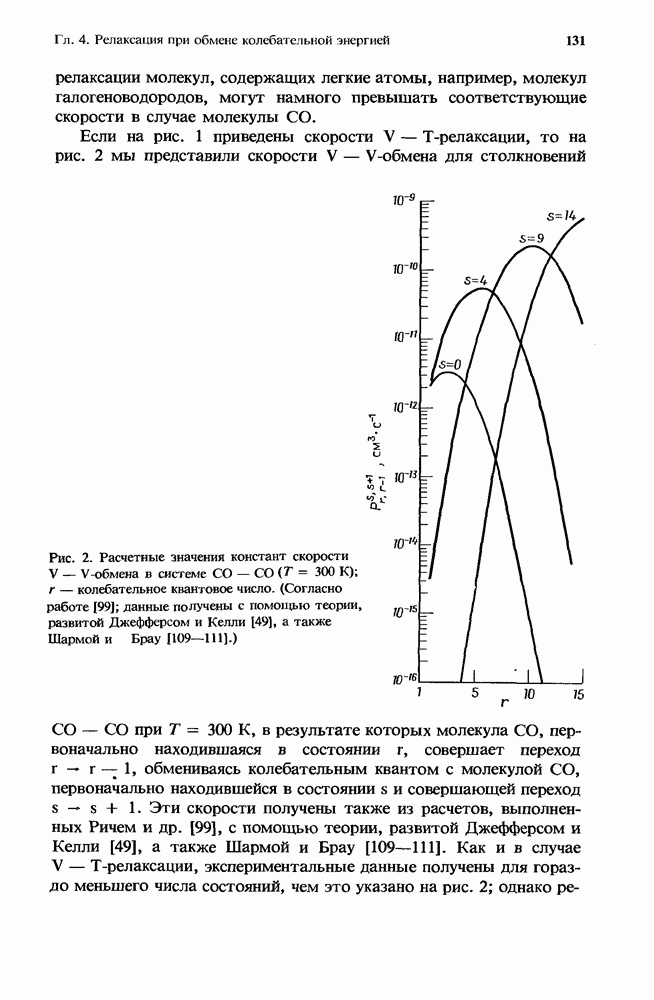
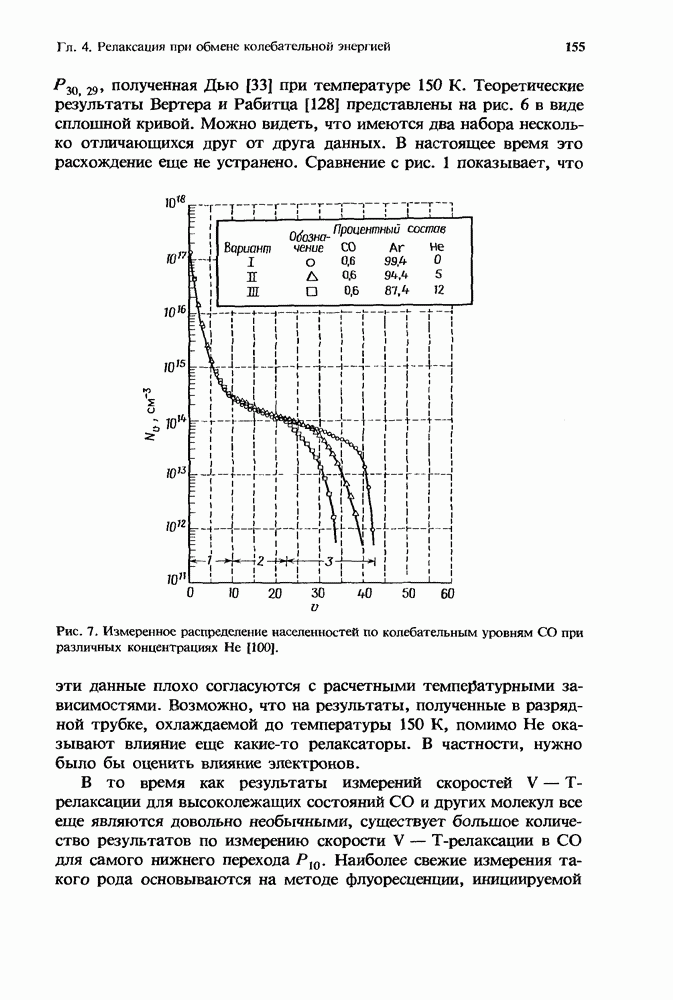
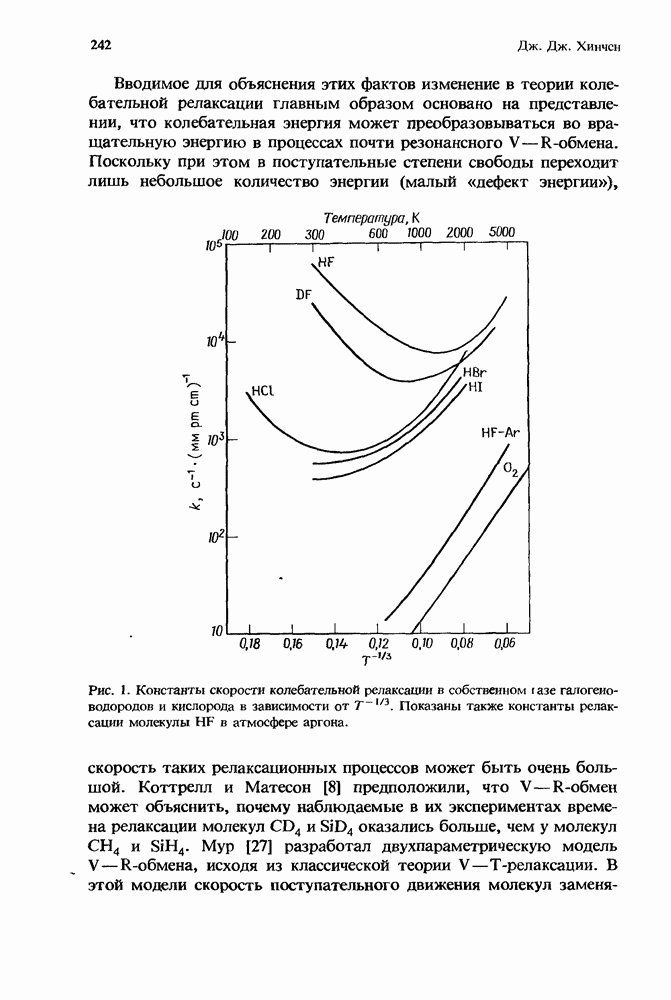
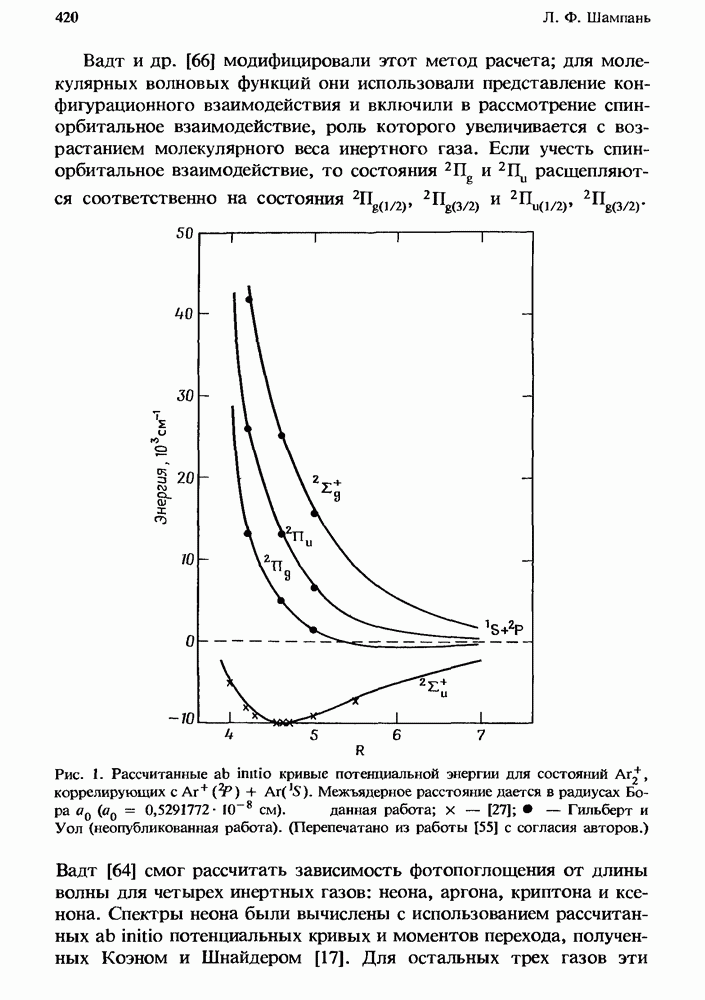
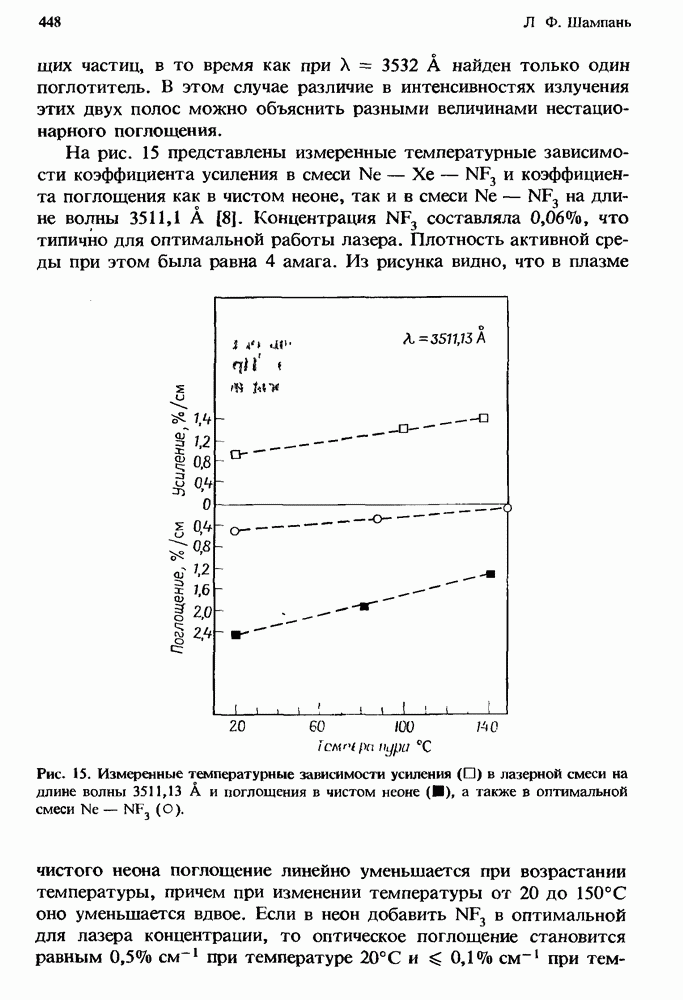
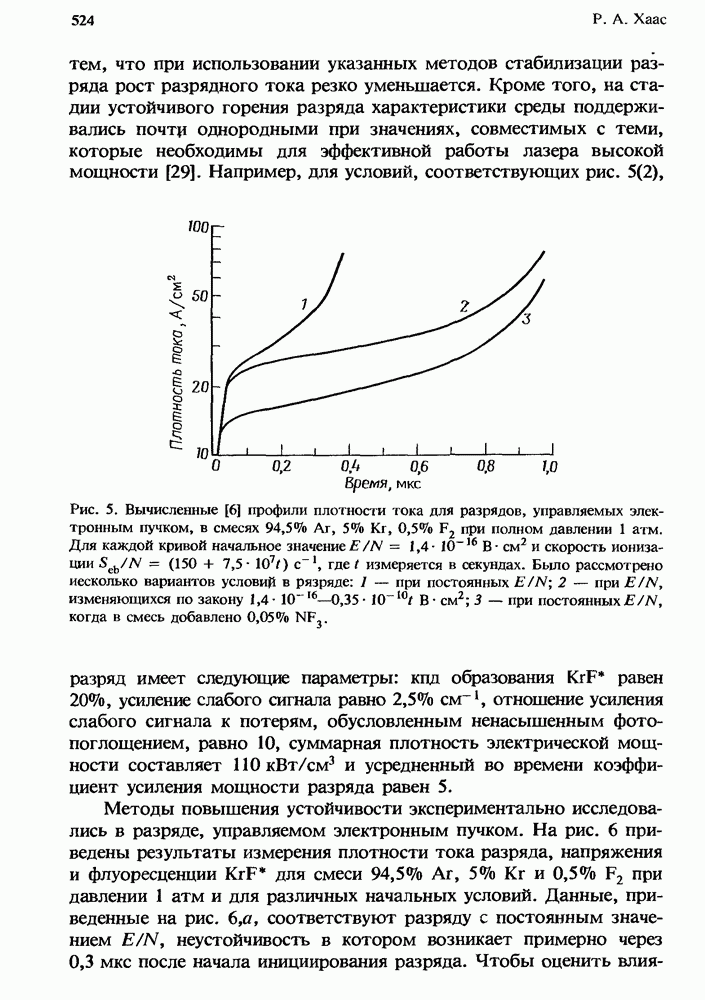
— частота столкновений,  газокинетическое сечение столкновений. Именно такая функциональная зависимость продемонстрирована на рис. 1 для кислорода. Галогеноводороды проявляют значительное отклонение от этой зависимости.
газокинетическое сечение столкновений. Именно такая функциональная зависимость продемонстрирована на рис. 1 для кислорода. Галогеноводороды проявляют значительное отклонение от этой зависимости.
В более детализированных классических теориях получают решение уравнений, которое дает непосредственно координаты относительного движения сталкивающихся частиц. В рассмотрении участвуют также ангармонические осцилляторы и учитываются как отталкивательная, так и притягивательная части потенциала взаимодействия. В частности, используется потенциал Леннарда-Джонса (потенциал 6-12). При этом вычисляются траектории налетающих частиц с последующим усреднением по начальным скоростям, прицельным параметрам, фазам и ориентациям осциллятора.
В полуклассической теории осциллятор квантуется, в то время как поступательное движение налетающей частицы рассматривается классически. Во время столкновения осциллятор, испытывающий зависящее от времени возмущение, переходит из колебательного состояния  в колебательное состояние
в колебательное состояние  Классические уравнения движения позволяют получать решения при зависящей от времени силе возмущения.
Классические уравнения движения позволяют получать решения при зависящей от времени силе возмущения.
В квантовомеханической теории пучок налетающих атомов рассматривается в виде плоской волны, взаимодействующей с квантовым осциллятором. Метод искаженных волн позволяет вычислять фазовые сдвиги, обусловленные V — Т-обменом энергией, для однородных последовательностей сталкивающихся частиц. Вероятность перехода определяется отношением амплитуд упруго и неупруго рассеянных волн.
Из упомянутых выше трех теоретических подходов наибольшее  распространение получила квантовомеханическая теория
распространение получила квантовомеханическая теория
колебательной релаксации. Для расчета времени V-Т-релаксации большого числа двухатомных газов с успехом применялась хорошо известная теория Шварца — Славского — Херцфельда (теория  Шварц и Херцфельд [36] обобщили эту теорию на трехмерный случай столкновений и использовали потенциал Леннарда-Джонса. Полученную ими вероятность перехода можно приближённо записать в виде
Шварц и Херцфельд [36] обобщили эту теорию на трехмерный случай столкновений и использовали потенциал Леннарда-Джонса. Полученную ими вероятность перехода можно приближённо записать в виде

где  а характеристическая колебательная температура равна
а характеристическая колебательная температура равна

 — глубина потенциальной ямы.
— глубина потенциальной ямы.
Как и теория Ландау — Теллера, теория  дает температурную зависимость вида
дает температурную зависимость вида  Выражение (10) было использовано Милликеном и Уайтом [29] для получения полуэмпирической температурной зависимости времени V-Т-релаксации
Выражение (10) было использовано Милликеном и Уайтом [29] для получения полуэмпирической температурной зависимости времени V-Т-релаксации 

где  — давление газа. С помощью этой функции Милликену и Уайту удалось согласовать данные по скоростям релаксации для многих газов в диапазоне температур 300—8000 К.
— давление газа. С помощью этой функции Милликену и Уайту удалось согласовать данные по скоростям релаксации для многих газов в диапазоне температур 300—8000 К.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации