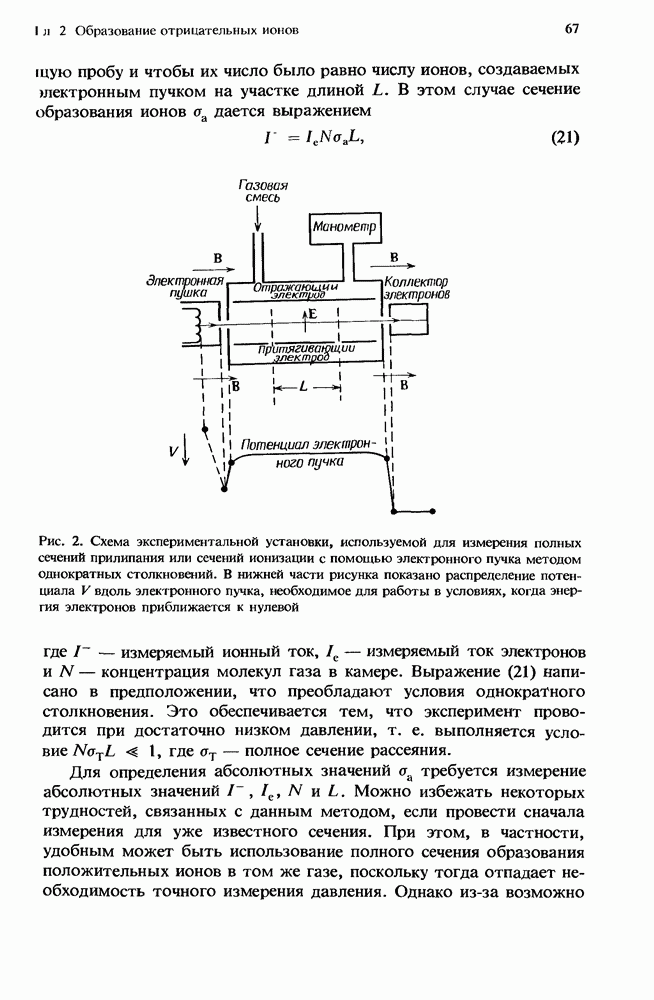
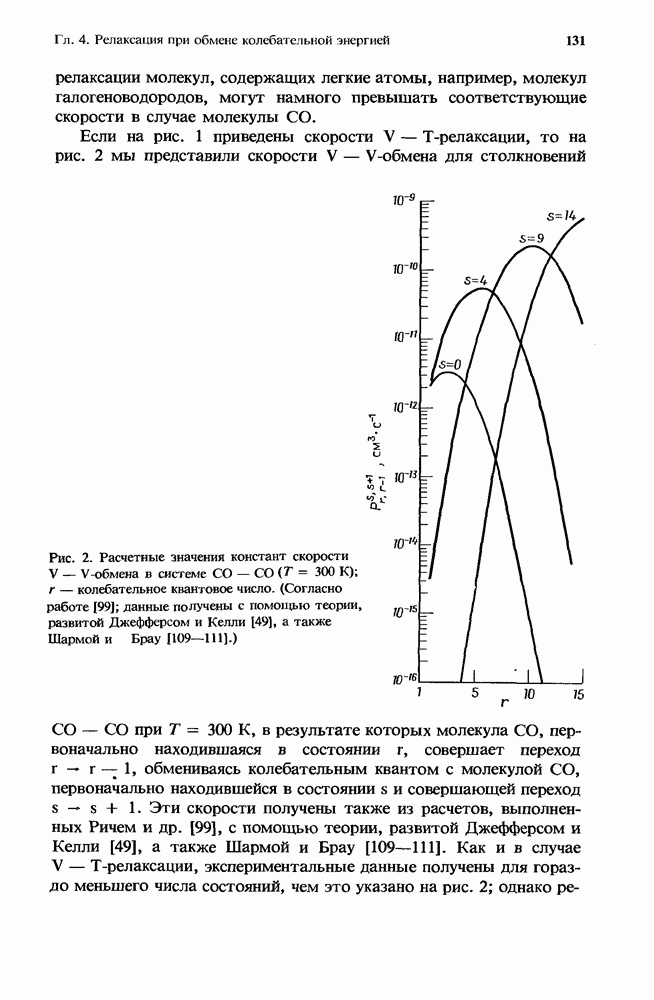
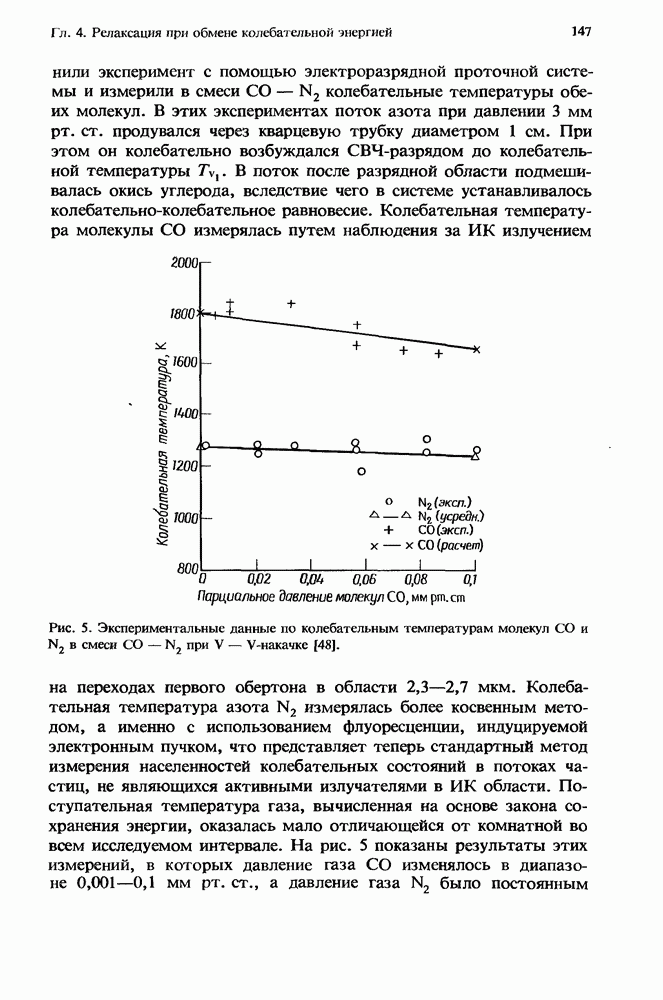
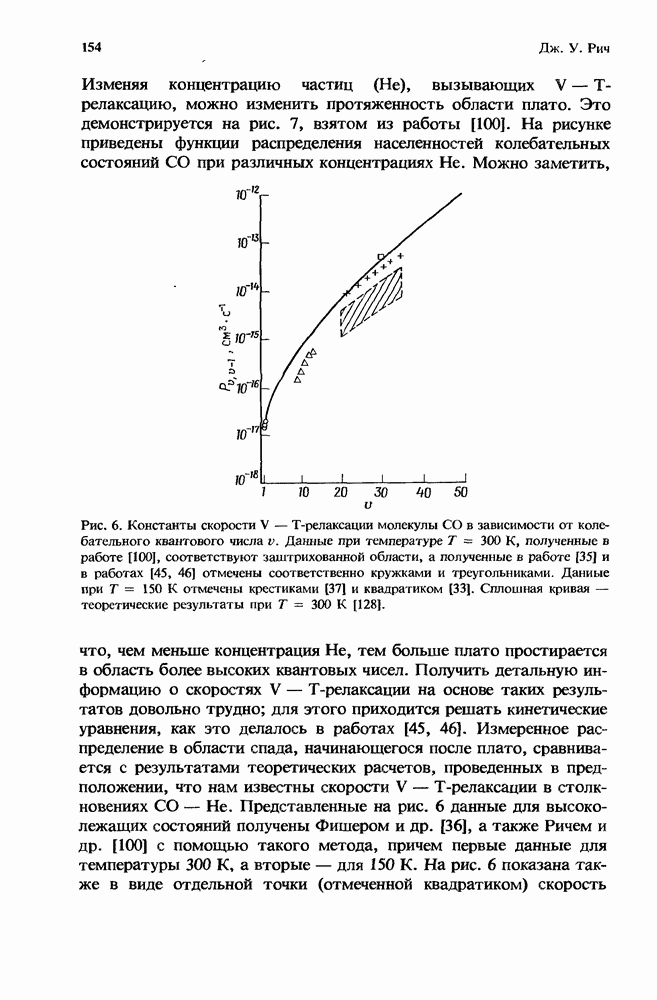
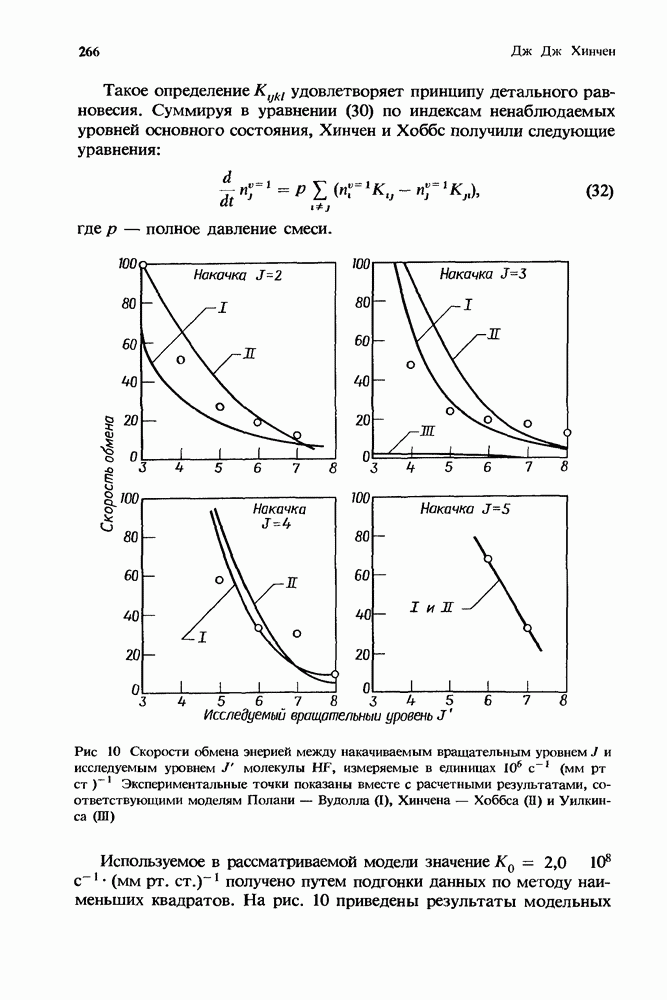
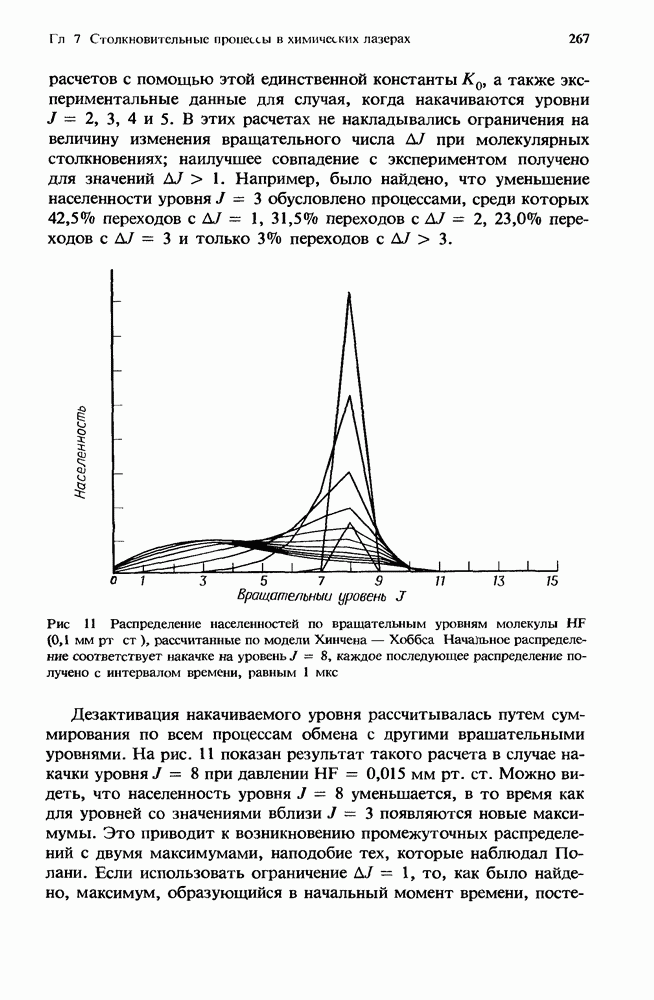
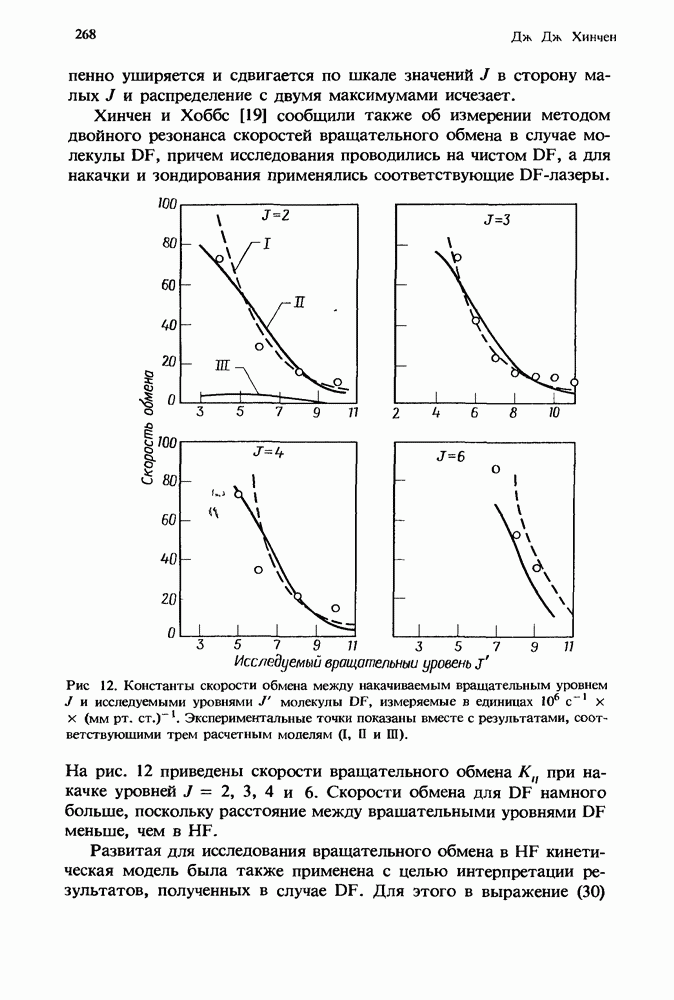
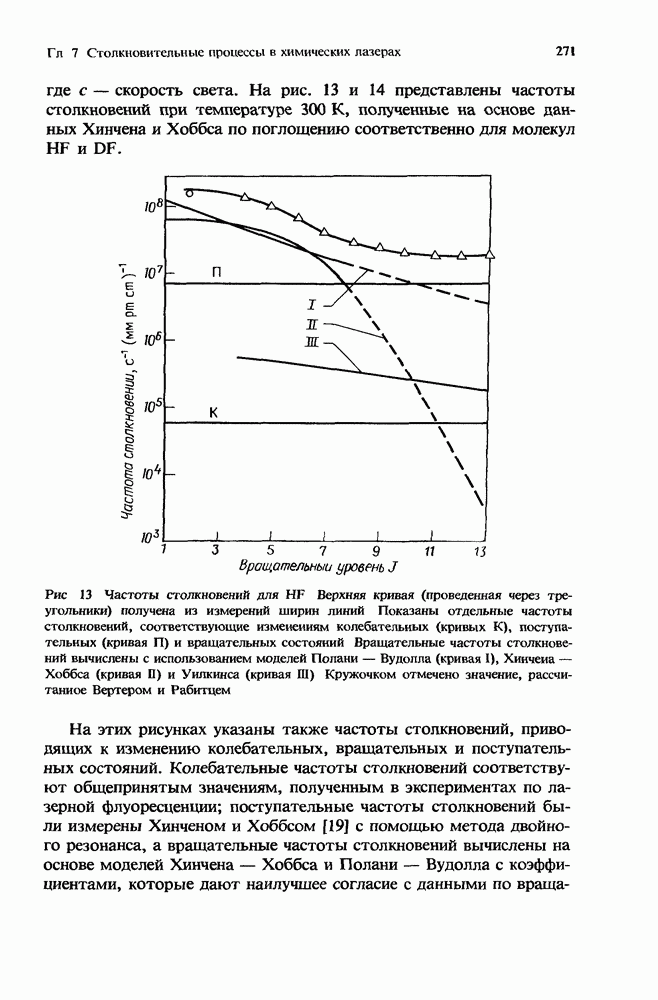
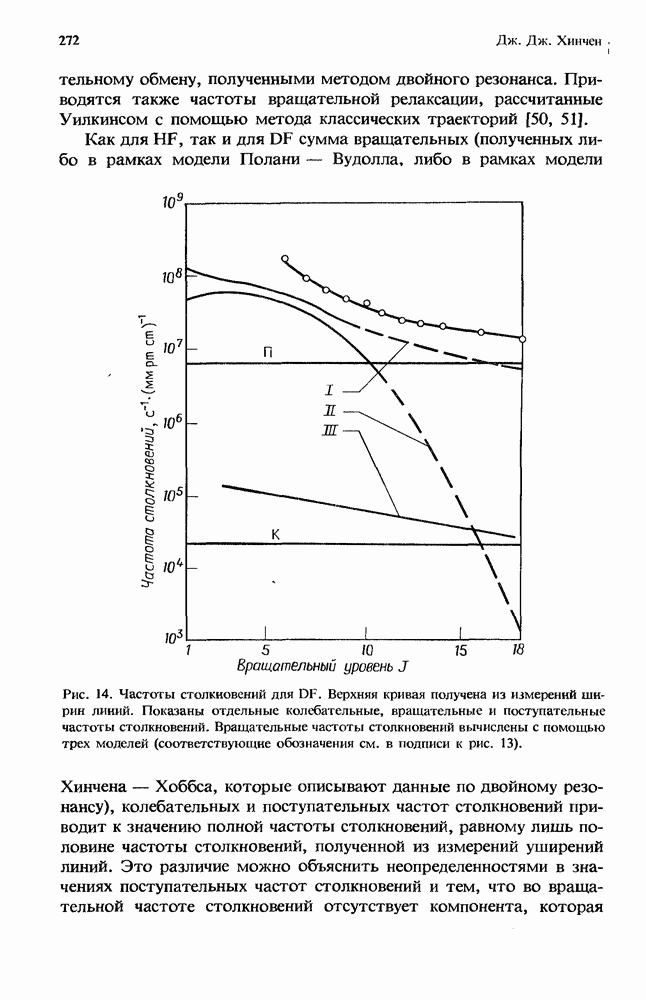
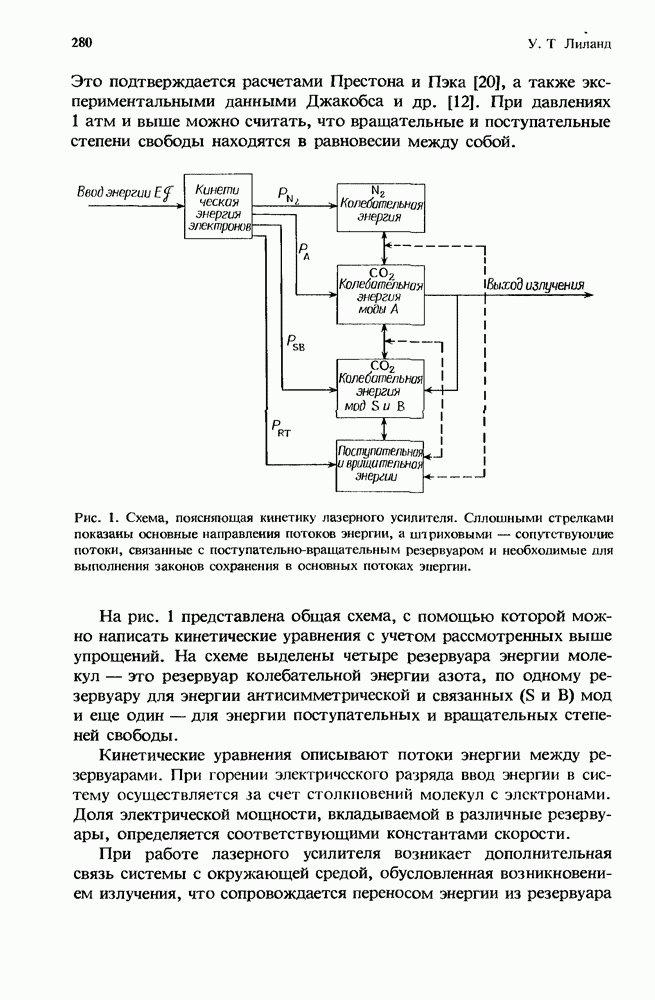
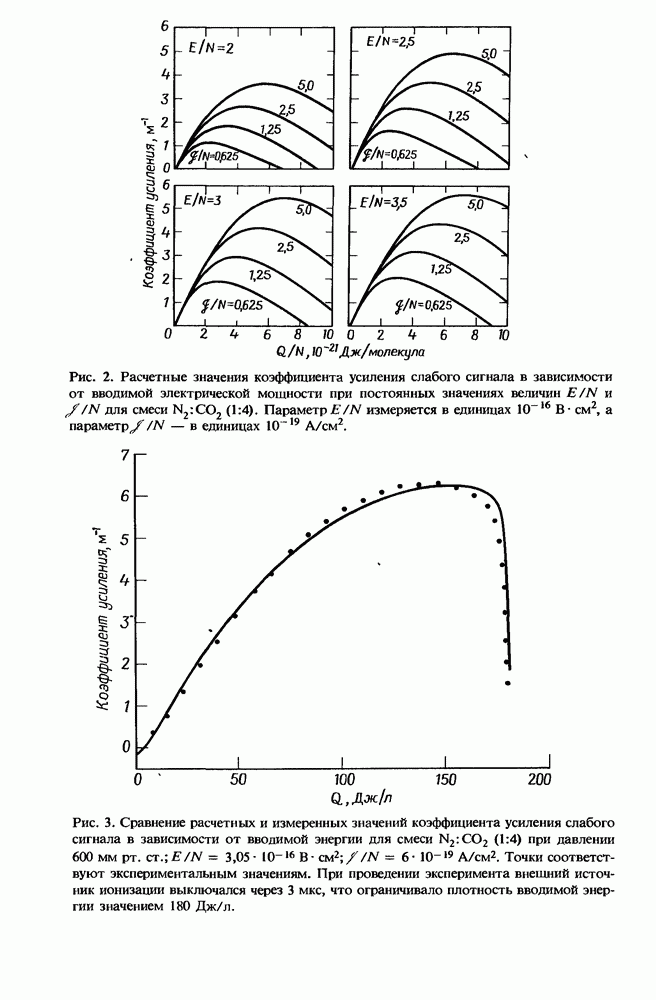
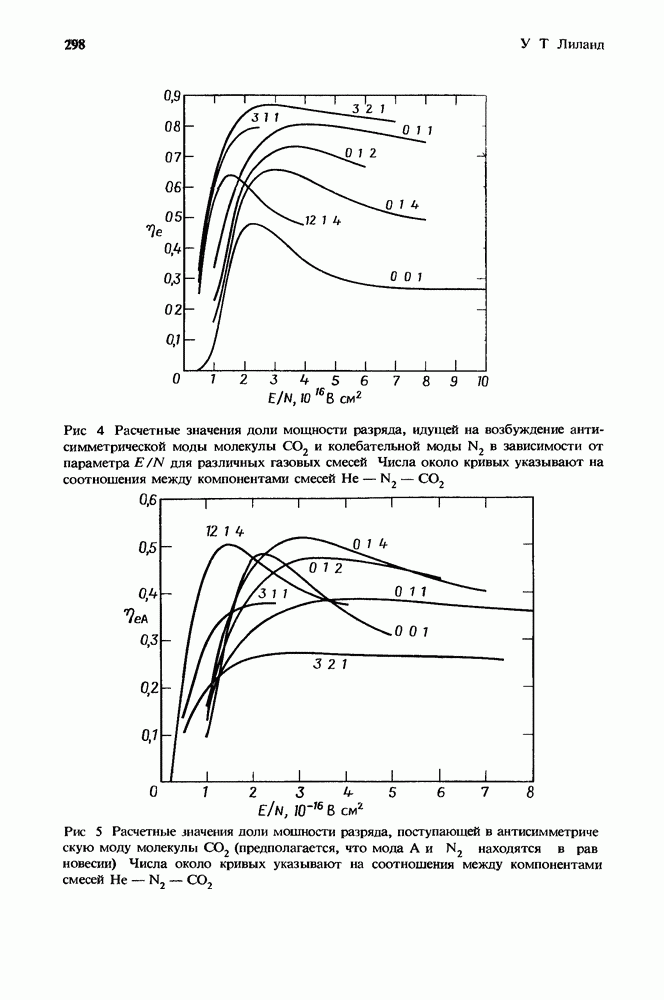
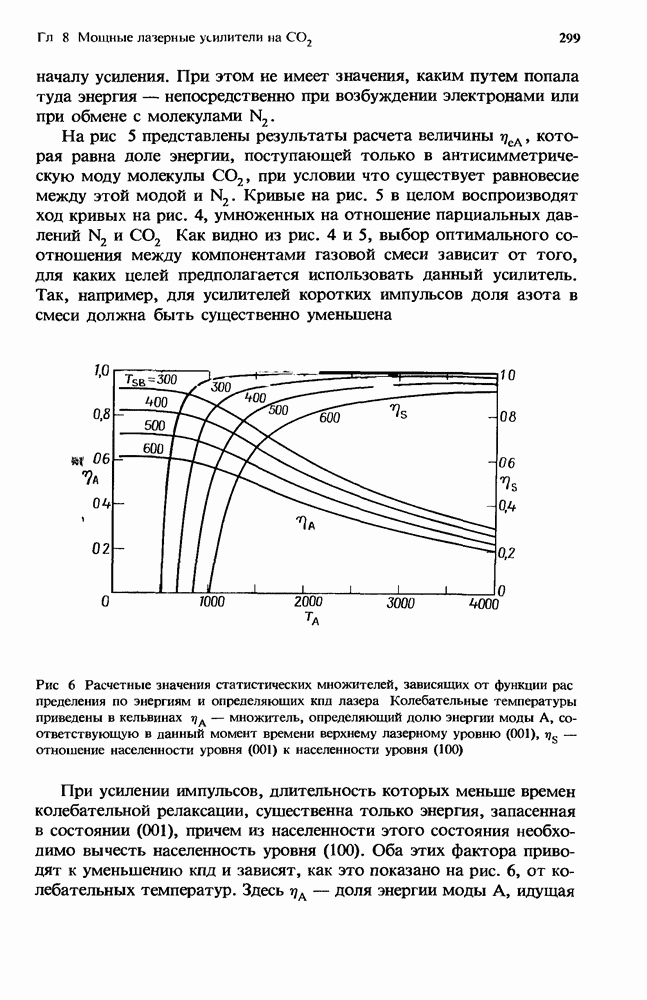
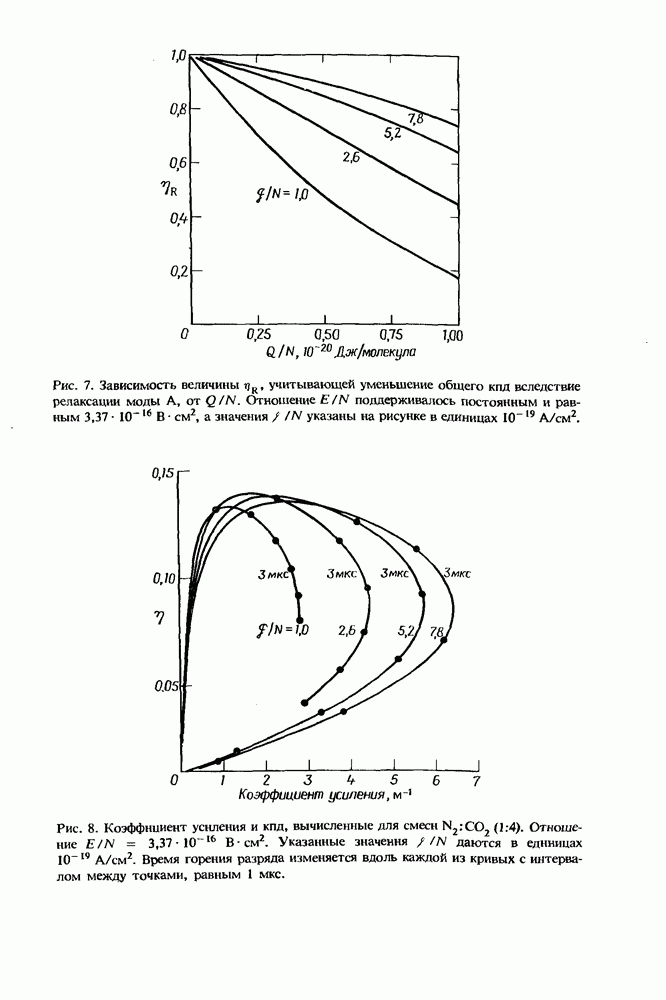
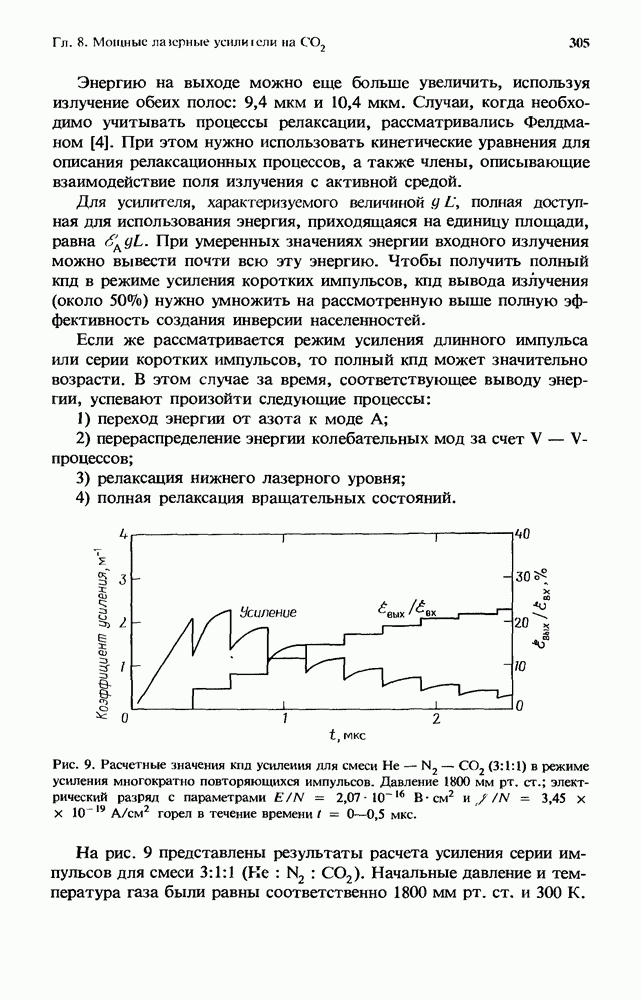
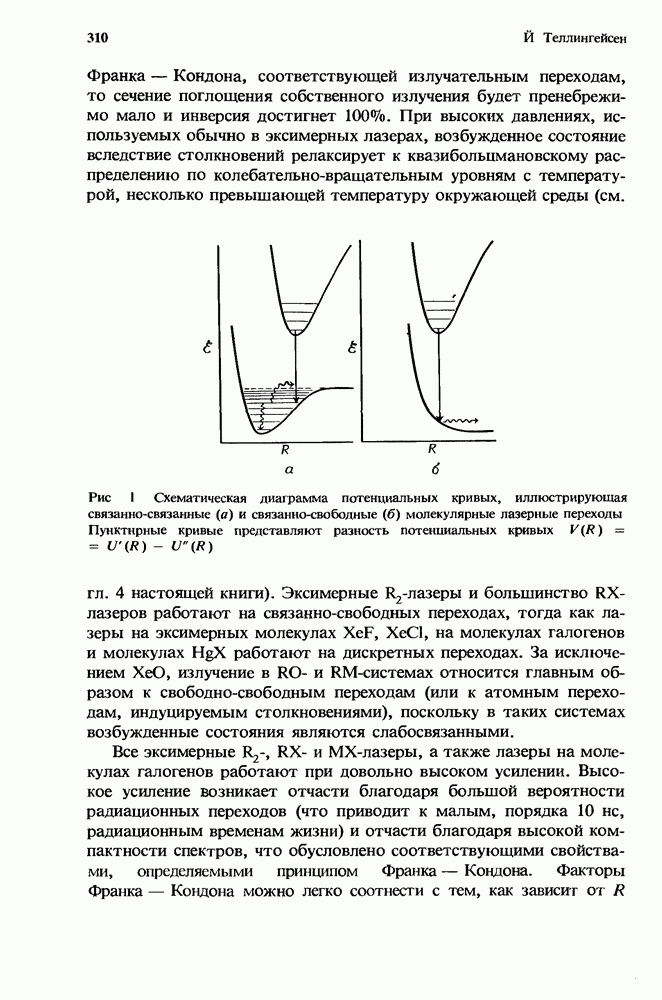
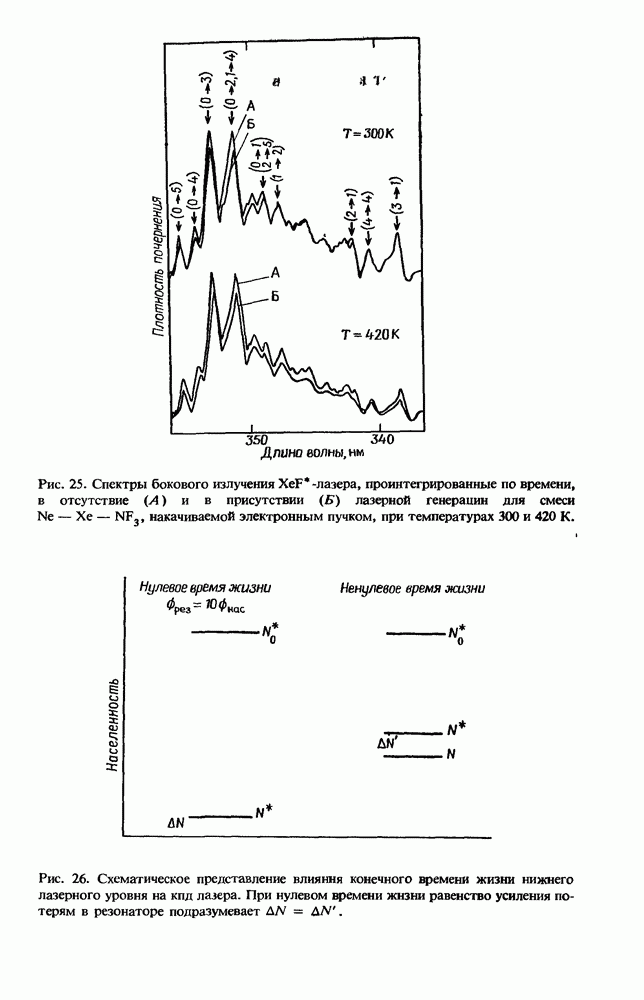
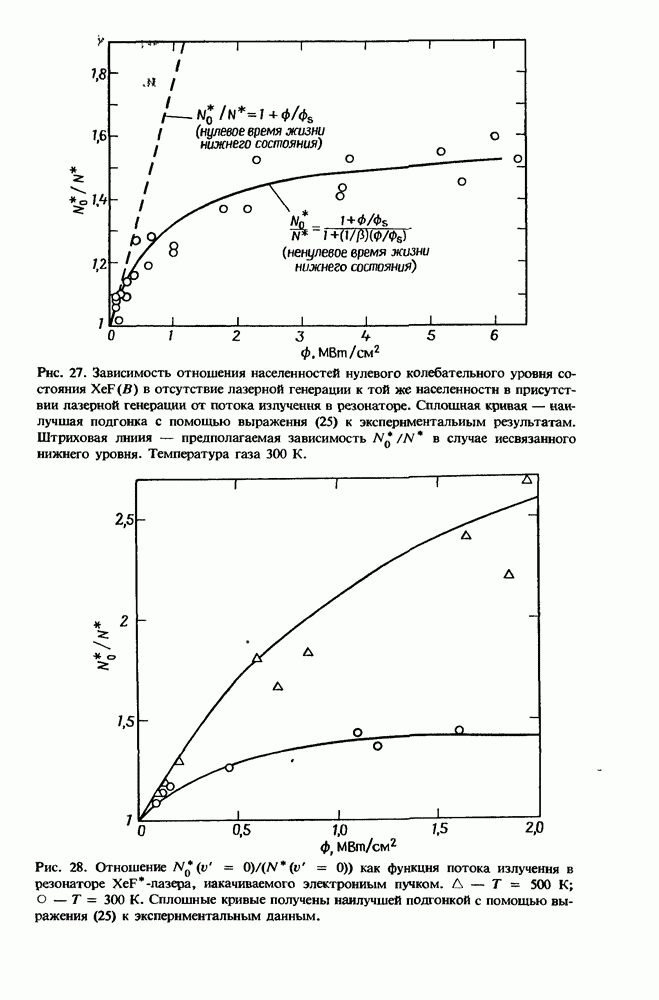
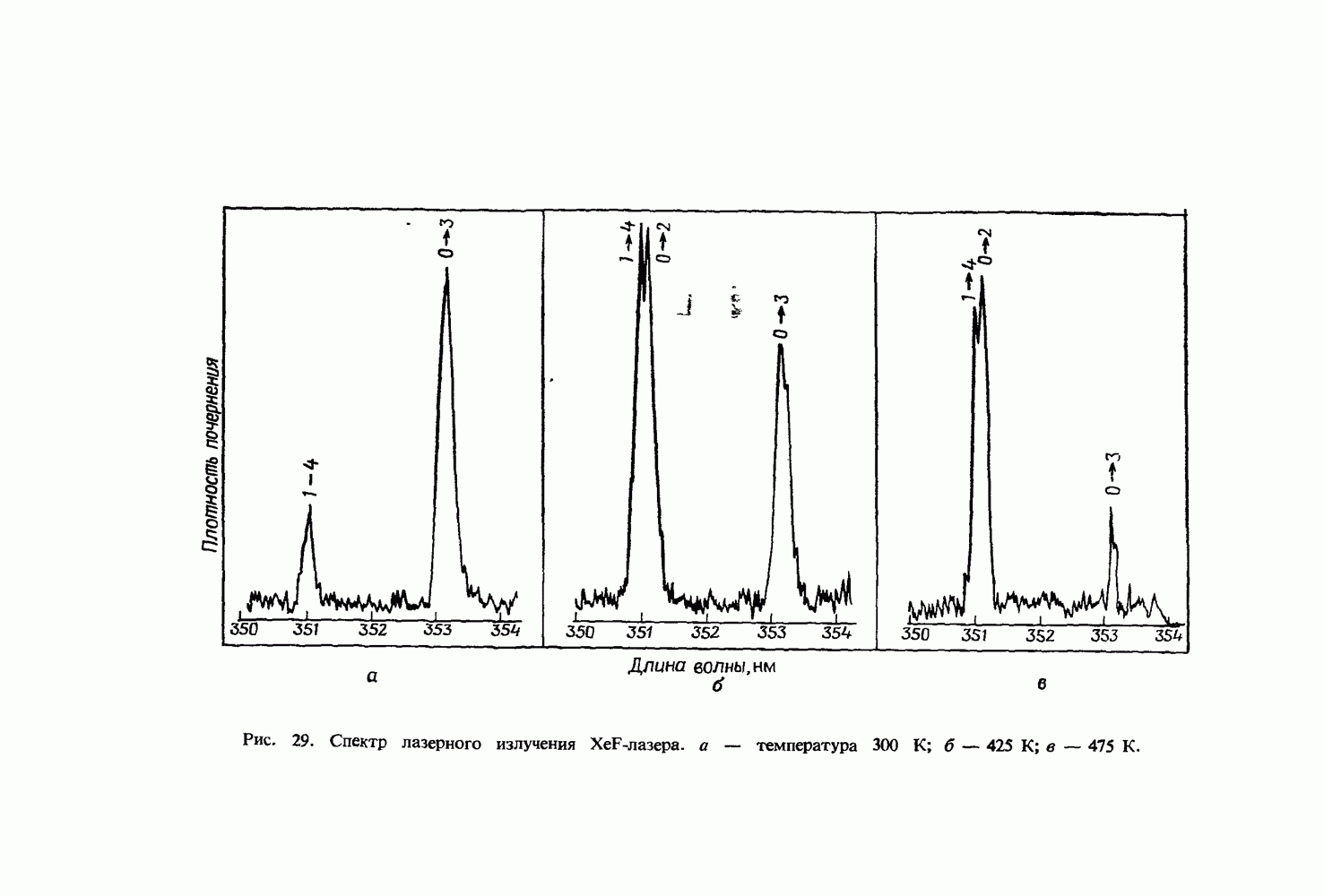
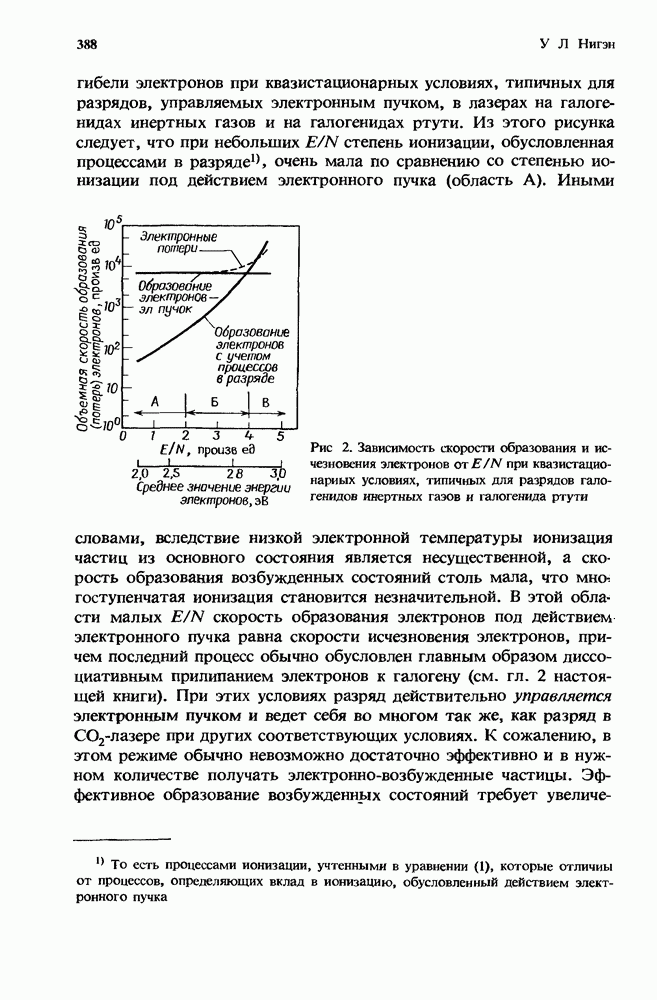
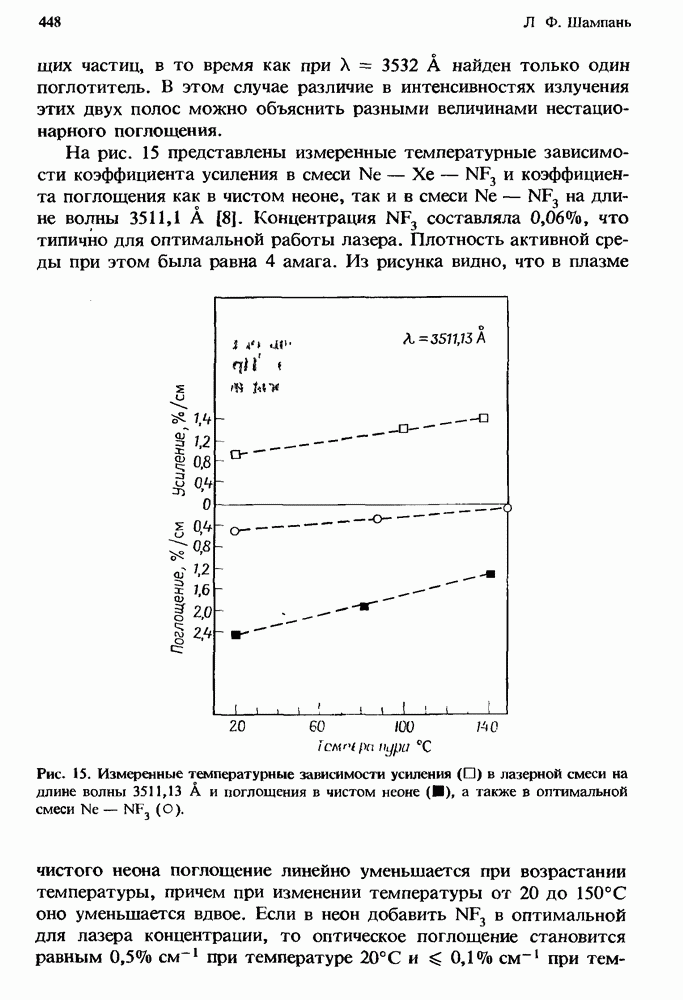
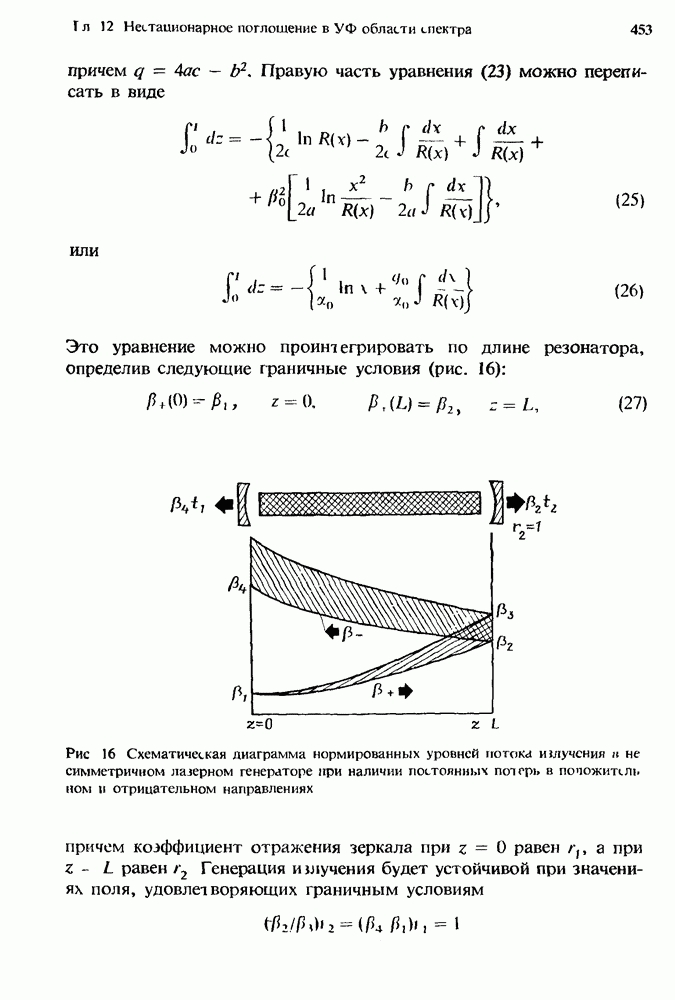
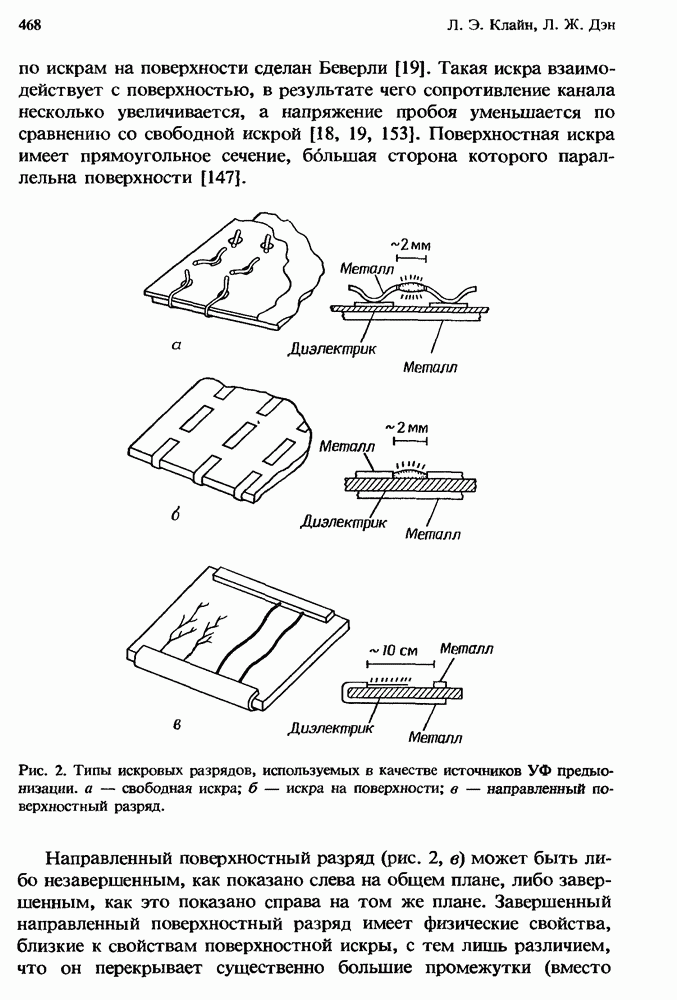
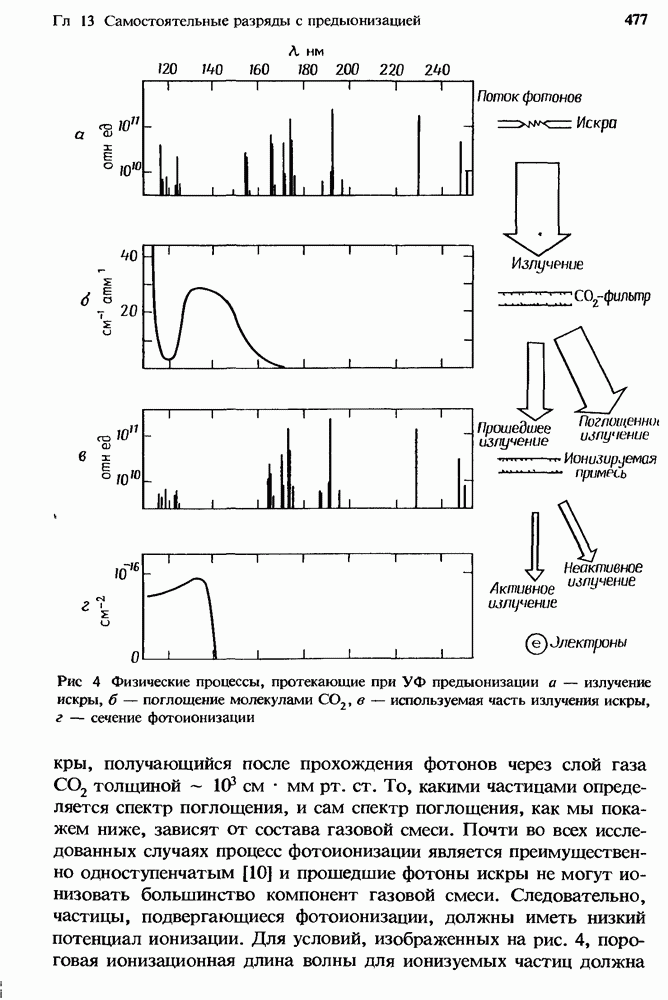
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3.2.4. Кинетическая модель СО-лазеров
В течение последних десяти лет были развиты довольно полные кинетические модели, описывающие работу СО-лазеров различного типа. Все эти модели описываются кинетическими уравнениями, аналогичными уравнению (4), но с добавочными членами в правых частях, учитывающих вклад и потери энергии в исследуемой системе. Для проточных систем, таких, как рассмотренные в разд. 4.2.2.1 газодинамические СО-лазеры, уравнение (4) должно решаться совместно с уравнениями сохранения, описывающими изменение плотности газа, поступательно-вращательной температуры и давления газодинамического потока в лазере. При разработке модели такого газодинамического лазера в кинетическое уравнение (4) обычно добавляют члены, описывающие только одноквантовые переходы  фундаментальная полоса) и двухквантовые переходы
фундаментальная полоса) и двухквантовые переходы  первый обертон), связанные с процессом спонтанного излучения СО. Необходимые для расчетов коэффициенты Эйнштейна А, определяющие скорости таких радиационных переходов, в настоящее время известны вплоть до самых высоких колебательных квантовых чисел, которые только необходимо учитывать при моделировании СО-лазеров. Значения коэффициента А получены в теоретической работе [134] и подтверждены экспериментально в работе [62]. Система уравнений для этого случая решается путем численного интегрирования на ЭВМ. При заданных начальных концентрациях газовых компонентов, значениях температуры и давления в форкамере газодинамического лазера, а также с учетом
первый обертон), связанные с процессом спонтанного излучения СО. Необходимые для расчетов коэффициенты Эйнштейна А, определяющие скорости таких радиационных переходов, в настоящее время известны вплоть до самых высоких колебательных квантовых чисел, которые только необходимо учитывать при моделировании СО-лазеров. Значения коэффициента А получены в теоретической работе [134] и подтверждены экспериментально в работе [62]. Система уравнений для этого случая решается путем численного интегрирования на ЭВМ. При заданных начальных концентрациях газовых компонентов, значениях температуры и давления в форкамере газодинамического лазера, а также с учетом
известной геометрии сверхзвукового сопла можно в результате численного решения получить населенности колебательных уровней, газовую поступательную температуру и коэффициент усиления слабого сигнала в зависимости от расстояния до критического сечения сопла. Как мы уже отмечали, самую первую кинетическую модель газодинамического СО-лазера разработал Мак-Кензи [72, 73]. Впоследствии появились сообщения о создании других моделей [31, 52, 135].
Моделирование электроразрядного СО-лазера является более сложной задачей. Различные процессы, протекающие в разряде с участием электронов, связаны, разумеется, с кинетикой колебательной релаксации. Хорошо известно, что основная энергетическая связь между электронной компонентой тлеющего разряда в активной лазерной среде и колебательной модой СО обусловлена главным образом большими сечениями неупругих процессов возбуждения низколежащих колебательных состояний электронами с энергией, лежащей в интервале 1—3 эВ [105]. Сечения возбуждения первых восьми колебательных уровней СО при столкновениях с электронами, энергия которых лежит в указанном интервале, достигают значений от  до
до 
При моделировании электроразрядного СО-лазера не всегда проводят совместное решение полной совокупности уравнений, описывающих как колебательное, так и электронное распределение энергий. Самые первые кинетические модели электроразрядного СО-лазера [98] основывались на предположении, что электроны имеют больцмановское распределение по энергиям с соответствующей температурой электронов  которая использовалась как входной параметр расчетной модели. Предположение, что распределение электронов по энергиям является равновесным, позволяет избежать решения кинетических уравнений для электронов и получить (в грубой форме) желаемое разделение электронных и колебательных степеней свободы. В более современных моделях, предложенных Нигэном [80—82], учитывается кинетика электронов в СО-лазере. Расчеты этой кинетики выполняются численным решением кинетического уравнения Больцмана для электронного газа в положительном столбе тлеющего разряда СО-лазера, причем в уравнении Больцмана учитываются как члены, ответственные за обмен энергией между электронными и молекулярными поступательными, вращательными и колебательными степенями свободы, так и члены, описывающие возбуждение электронных состояний и ионизацию молекул. В этих расчетах кинетику колебательной релаксации можно отделить от кинетики электронов, если задать
которая использовалась как входной параметр расчетной модели. Предположение, что распределение электронов по энергиям является равновесным, позволяет избежать решения кинетических уравнений для электронов и получить (в грубой форме) желаемое разделение электронных и колебательных степеней свободы. В более современных моделях, предложенных Нигэном [80—82], учитывается кинетика электронов в СО-лазере. Расчеты этой кинетики выполняются численным решением кинетического уравнения Больцмана для электронного газа в положительном столбе тлеющего разряда СО-лазера, причем в уравнении Больцмана учитываются как члены, ответственные за обмен энергией между электронными и молекулярными поступательными, вращательными и колебательными степенями свободы, так и члены, описывающие возбуждение электронных состояний и ионизацию молекул. В этих расчетах кинетику колебательной релаксации можно отделить от кинетики электронов, если задать
определенное больцмановское распределение по колебательным энергиям. Следует заметить, что пренебрежение небольцмановским характером реальной функции распределения по колебательным состояниям не вносит серьезных ошибок, поскольку электронные и колебательные степени свободы взаимодействуют главным образом на самых нижних колебательных состояниях, имеющих больцмановское распределение даже в условиях сильной накачки (см. рис. 4). Полученные Нигэном результаты показывают, что распределение электронов по энергиям сильно отличается от больцмановского. Для каждого из колебательных переходов, вызываемых столкновениями с электронами, константу скорости можно вычислить путем усреднения сечений возбуждения колебательных состояний СО при электронном ударе по функции распределения электронов. Полученные таким образом константы скорости используются затем в уравнении (4). Каждый из членов уравнения (4), ответственных за протекание рассматриваемых процессов, имеет вид

где  — усредненная указанным выше способом константа скорости процесса обмена энергией между электронами и колебательными степенями свободы, приводящего к переходу между колебательными уровнями
— усредненная указанным выше способом константа скорости процесса обмена энергией между электронами и колебательными степенями свободы, приводящего к переходу между колебательными уровнями  — плотность электронов и
— плотность электронов и  — населенность
— населенность  колебательного состояния. Хотя сечения, определяющие
колебательного состояния. Хотя сечения, определяющие  очень большие, сами члены
очень большие, сами члены  относительно невелики по сравнению с членами, ответственными за V — V-обмен. Это обусловлено тем, что в типичном тлеющем разряде плотность электронов довольно мала
относительно невелики по сравнению с членами, ответственными за V — V-обмен. Это обусловлено тем, что в типичном тлеющем разряде плотность электронов довольно мала  по сравнению с плотностью молекулярных частиц. Поэтому существенной является лишь величина полной энергии, поступающей в колебательную степень свободы вследствие протекания процессов с участием электронов; вид функции распределения по колебательным состояниям определяется более быстрыми процессами V — V-обмена, перераспределяющими населенности колебательных состояний. Важно, что на возбуждение колебательной моды СО может пойти более 90% всей энергии разряда, горящего в активной среде лазера [81], что подтверждается высоким электрическим кпд рассматриваемых лазеров.
по сравнению с плотностью молекулярных частиц. Поэтому существенной является лишь величина полной энергии, поступающей в колебательную степень свободы вследствие протекания процессов с участием электронов; вид функции распределения по колебательным состояниям определяется более быстрыми процессами V — V-обмена, перераспределяющими населенности колебательных состояний. Важно, что на возбуждение колебательной моды СО может пойти более 90% всей энергии разряда, горящего в активной среде лазера [81], что подтверждается высоким электрическим кпд рассматриваемых лазеров.
Можно также рассчитать реальные выходные спектральные характеристики СО-лазеров. Для этого в уравнение (4) необходимо добавить члены, описывающие скорости вынужденных излучательных переходов между колебательными уровнями. Такие расчеты обычно базируются на модели, в которой оптическим резонатором является резонатор Фабри — Перо (два плоских зеркала), а вывод
энергии описывается упрощенной схемой, в которой интенсивность выходного излучения определяется из условия, что возрастание интенсивности за счет вынужденного излучения при проходе через резонатор уравновешивается выходом излучения из резонатора или потерями на зеркалах. Если пренебречь пространственными изменениями поля, то такая схема позволяет непосредственно проинтегрировать кинетические уравнения. Однако Милонни и Пэкстон [76] предложили модель электроразрядного СО-лазера с неустойчивым резонатором, которая учитывает эффекты изменения амплитуды и фазы лазерного поля. Решения в этой модели получаются методом итераций.
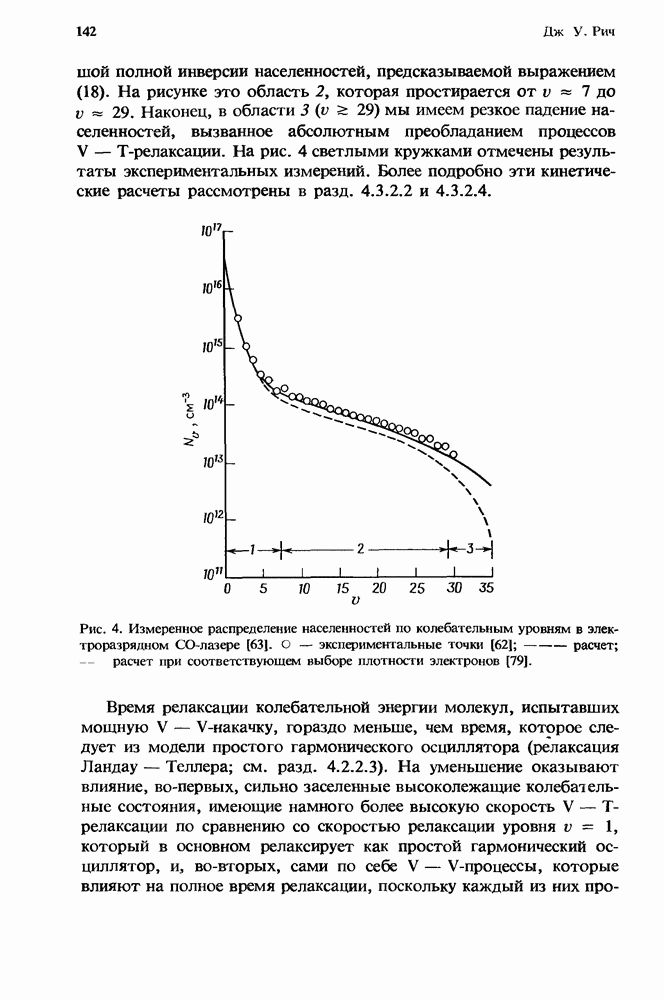
К 1980 г. появилось много работ, посвященных численному моделированию СО-лазеров, например работы [9, 31, 44, 50, 53—55, 76, 79, 92, 96, 101, 116—118, 120, 121, 124]. Некоторые из этих численных моделей (см., например, [53]) дают решения полностью связанных уравнений, описывающих кинетику колебательных и электронных степеней свободы. Учитываются также эффекты, обусловленные сверхупругими процессами электрон-молекулярных столкновений, благодаря которым электроны черпают энергию из колебательной моды. Задавая концентрацию и температуру газа, величину внешнего электрического поля и коэффициенты отражения лазерных зеркал, с помощью таких моделей можно с хорошей точностью рассчитать спектр выходного излучения и распределение энергии на выходе СО-лазера, особенно если в модели учесть значения скоростей V — V-обмена, рассмотренные в разд. 4.3.2.3. Мы уже приводили два примера, демонстрирующих возможности этих расчетных моделей. На рис. 4, согласно работе Лайтмана и Фишера [62], сравниваются измеренное стационарное распределение по колебательным уровням с распределением, полученным расчетным путем [79] с помощью разработанной этими авторами модели небольшого электроразрядного лазера, охлаждаемого жидким азотом; этот лазер мы рассматривали в разд. 4.3.2.2. На рисунке штриховая кривая соответствует результатам предварительных расчетов, в которых использовались значения электронной плотности, вычисленные по измеренным значениям тока и приложенного напряжения. За исключением высоколежащих состояний, наблюдается неплохое согласие с экспериментом. Если выбрать несколько большее значение плотности электронов (которое, по-видимому, соответствует реальным условиям в плазме), то, как показывает на рис. 4 сплошная кривая, расчет очень хорошо согласуется с экспериментом.
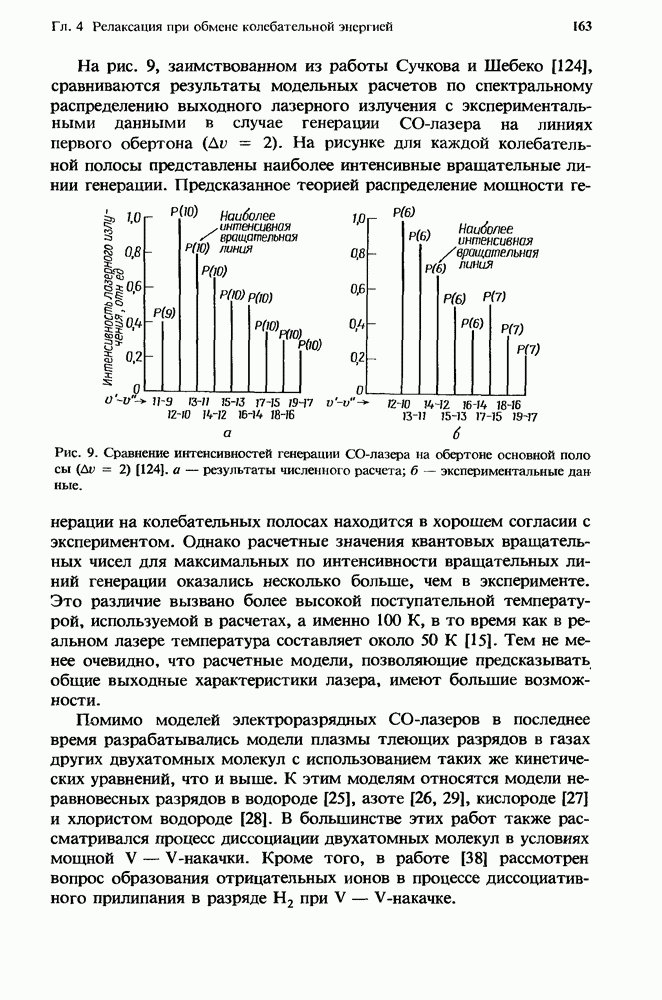
На рис. 9, заимствованном из работы Сучкова и Шебеко [124], сравниваются результаты модельных расчетов по спектральному распределению выходного лазерного излучения с экспериментальными данными в случае генерации СО-лазера на линиях первого обертона  На рисунке для каждой колебательной полосы представлены наиболее интенсивные вращательные линии генерации. Предсказанное теорией распределение мощности генерации на колебательных полосах находится в хорошем согласии с экспериментом.
На рисунке для каждой колебательной полосы представлены наиболее интенсивные вращательные линии генерации. Предсказанное теорией распределение мощности генерации на колебательных полосах находится в хорошем согласии с экспериментом.

Рис. 9. Сравнение интенсивностей генерации СО-лазера на обертоне основной полосы  а — результаты численного расчета; б — экспериментальные данные.
а — результаты численного расчета; б — экспериментальные данные.
Однако расчетные значения квантовых вращательных чисел для максимальных по интенсивности вращательных линий генерации оказались несколько больше, чем в эксперименте. Это различие вызвано более высокой поступательной температурой, используемой в расчетах, а именно 100 К, в то время как в реальном лазере температура составляет около 50 К [15]. Тем не менее очевидно, что расчетные модели, позволяющие предсказывать общие выходные характеристики лазера, имеют большие возможности.
Помимо моделей электроразрядных СО-лазеров в последнее время разрабатывались модели плазмы тлеющих разрядов в газах других двухатомных молекул с использованием таких же кинетических уравнений, что и выше. К этим моделям относятся модели неравновесных разрядов в водороде [25], азоте [26, 29], кислороде [27] и хлористом водороде [28]. В большинстве этих работ также рассматривался процесс диссоциации двухатомных молекул в условиях мощной V — V-накачки. Кроме того, в работе [38] рассмотрен вопрос образования отрицательных ионов в процессе диссоциативного прилипания в разряде  при V — V-накачке.
при V — V-накачке.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
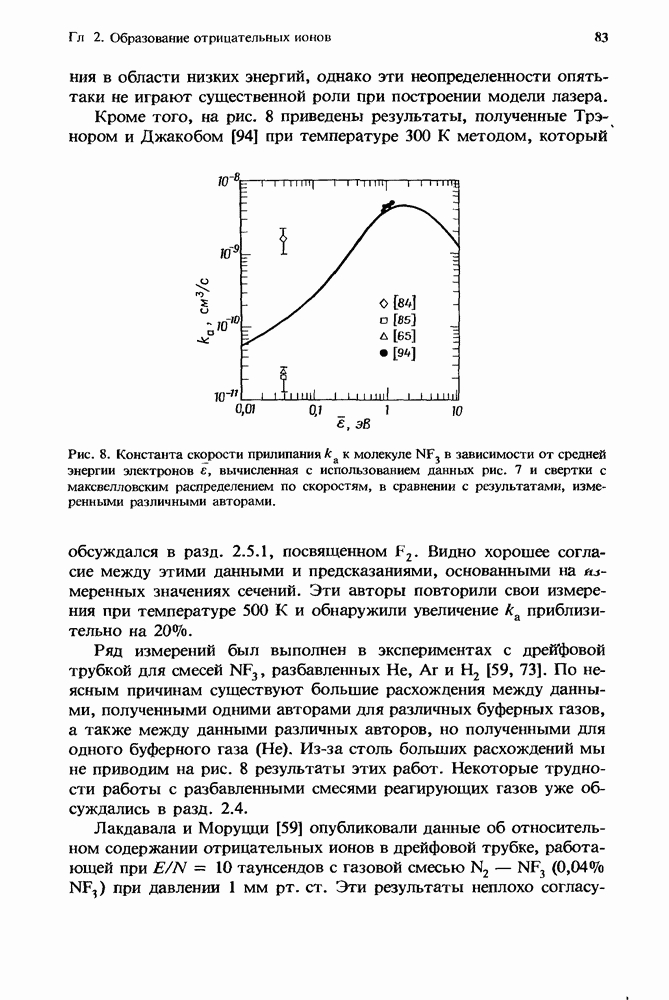
- 2.5.2. Трифторид азота (NF3)
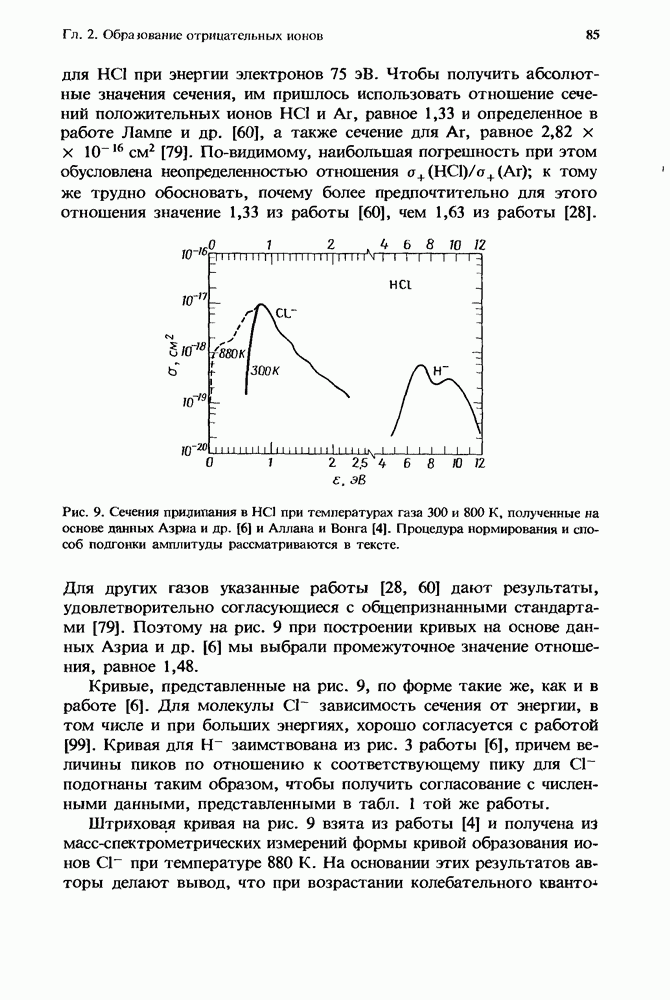
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
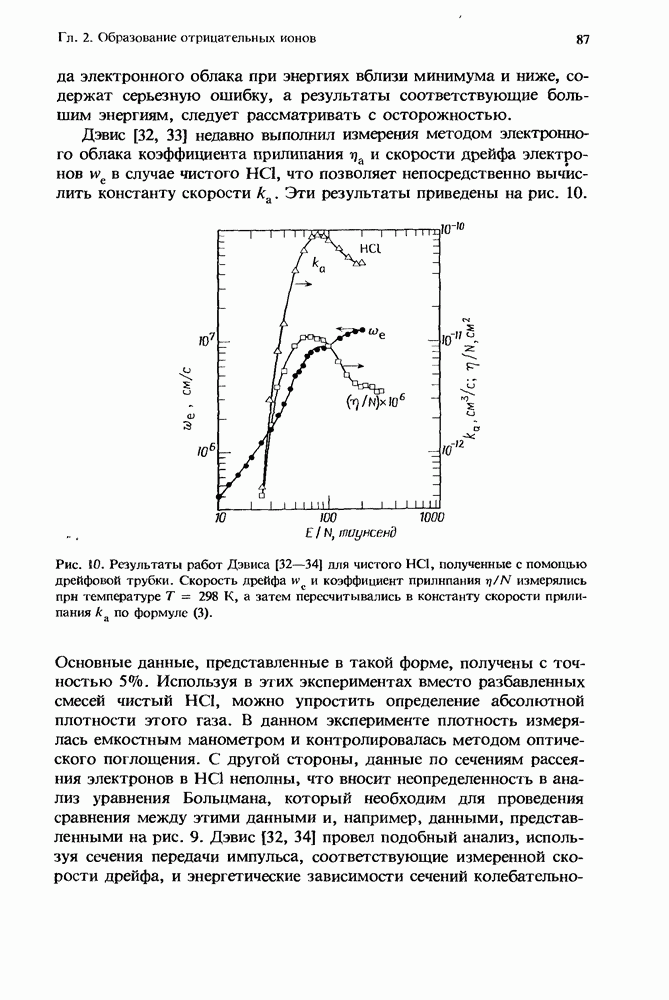
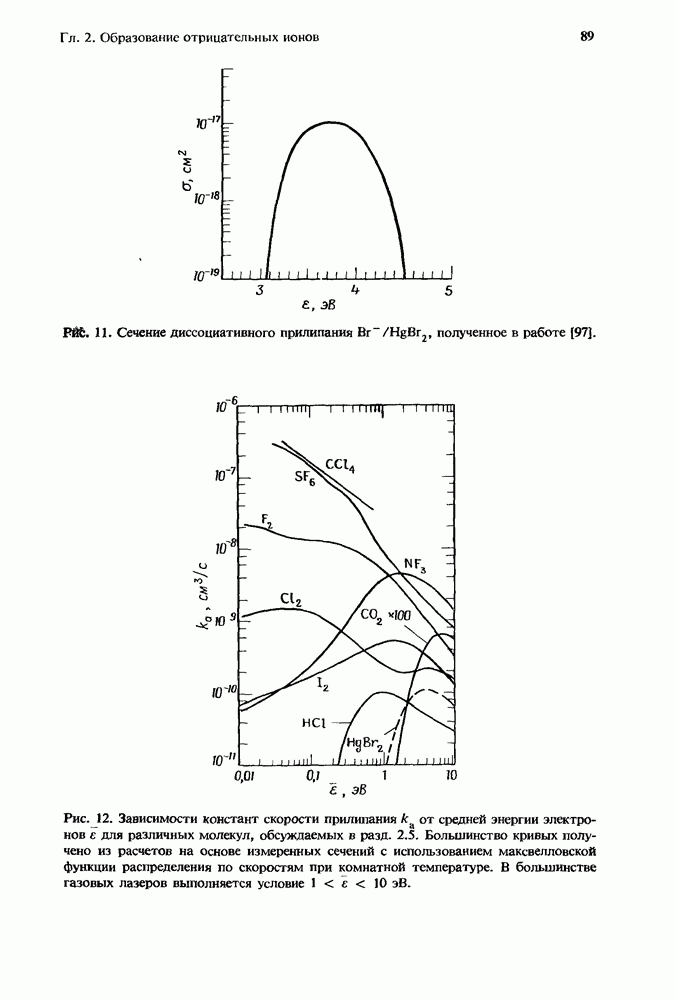
- 2.5.5. Другие газы, представляющие интерес
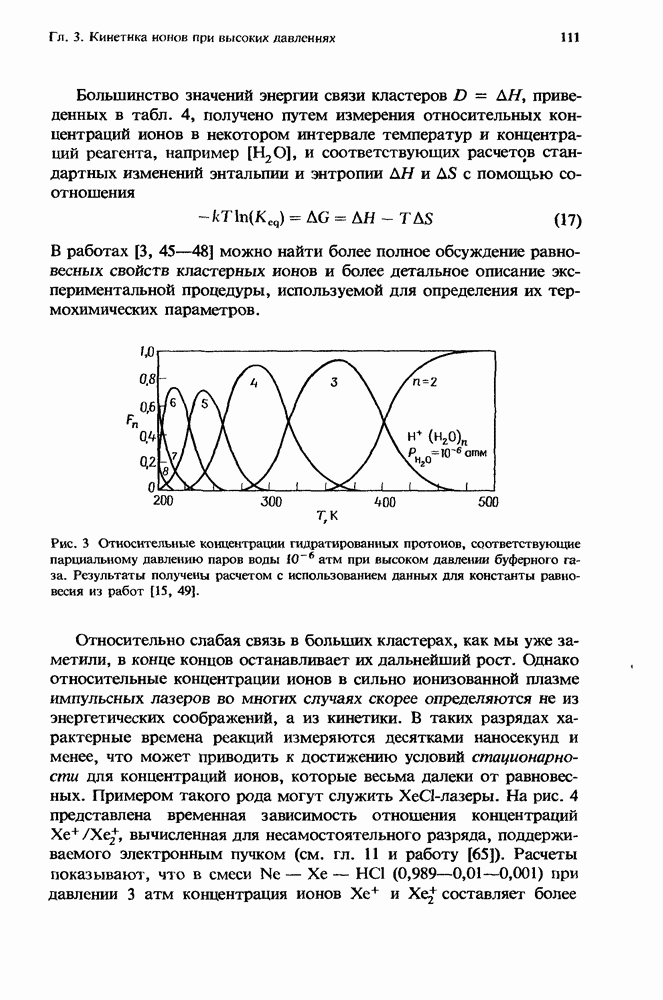
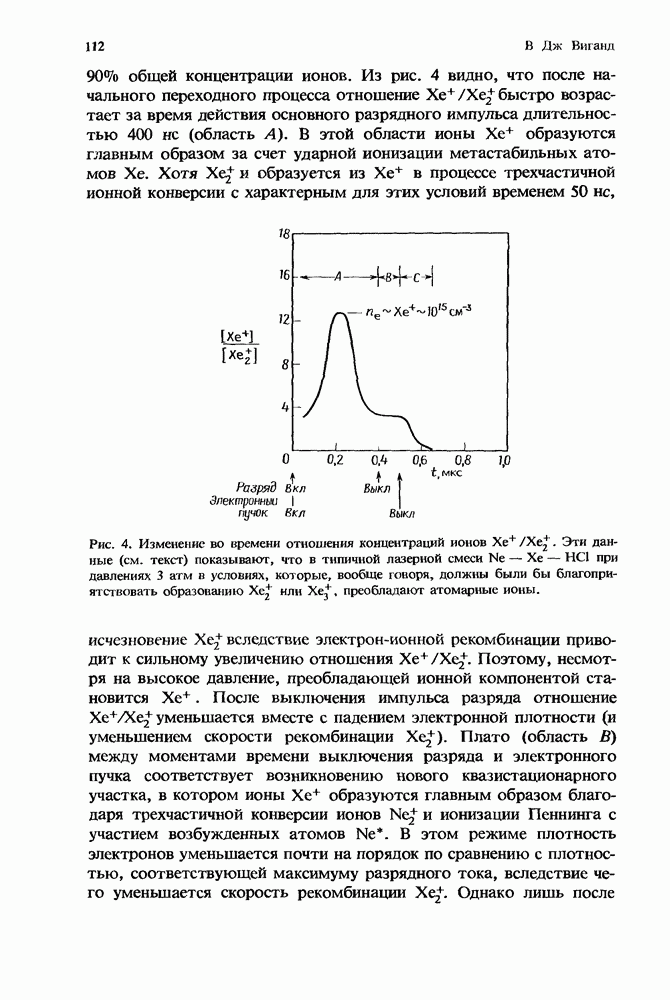
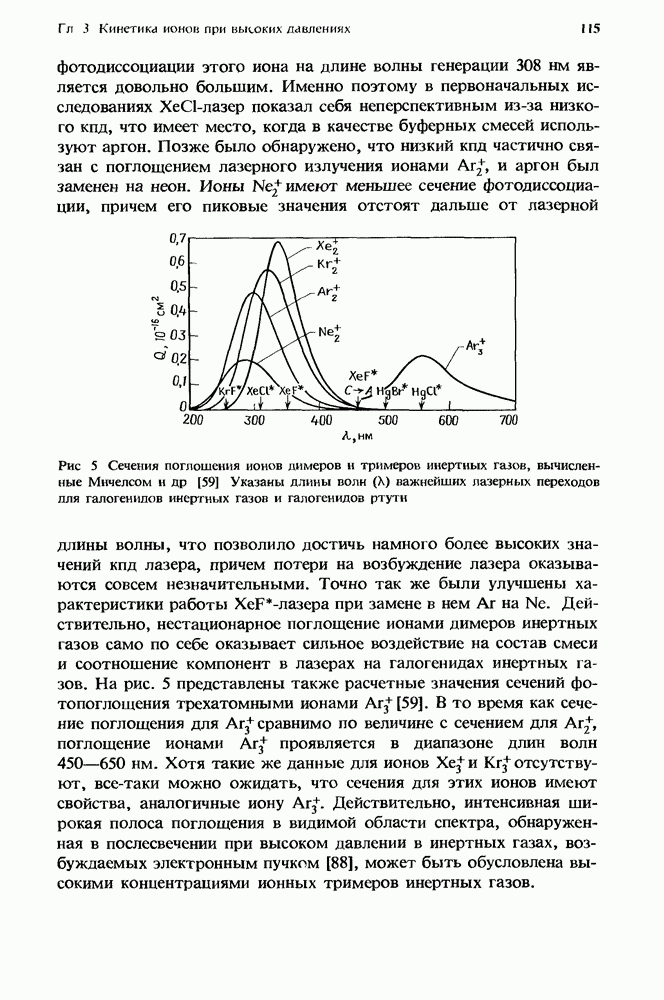
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
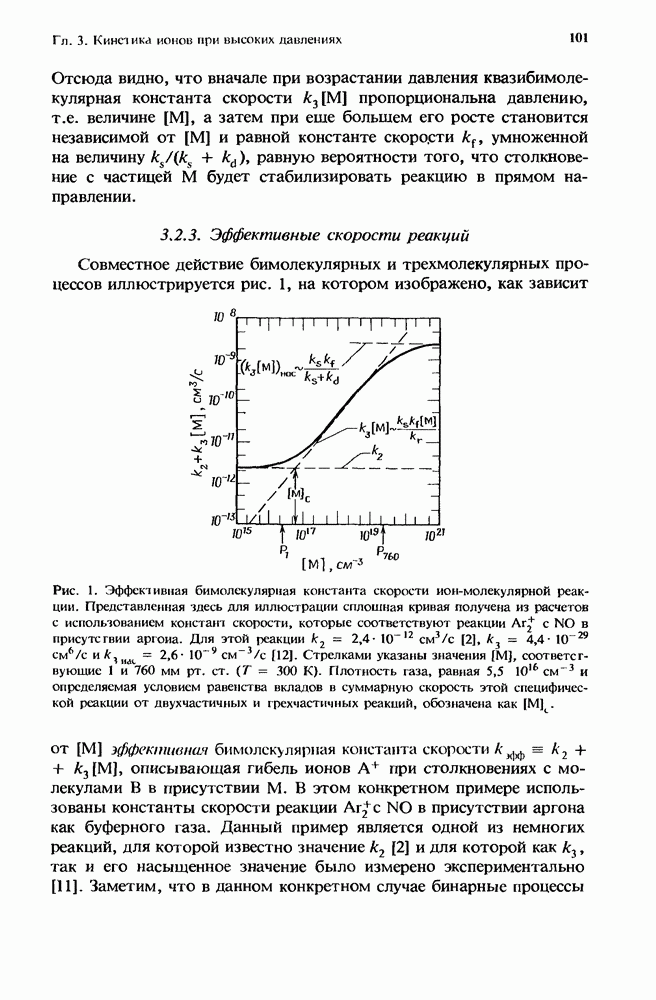
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
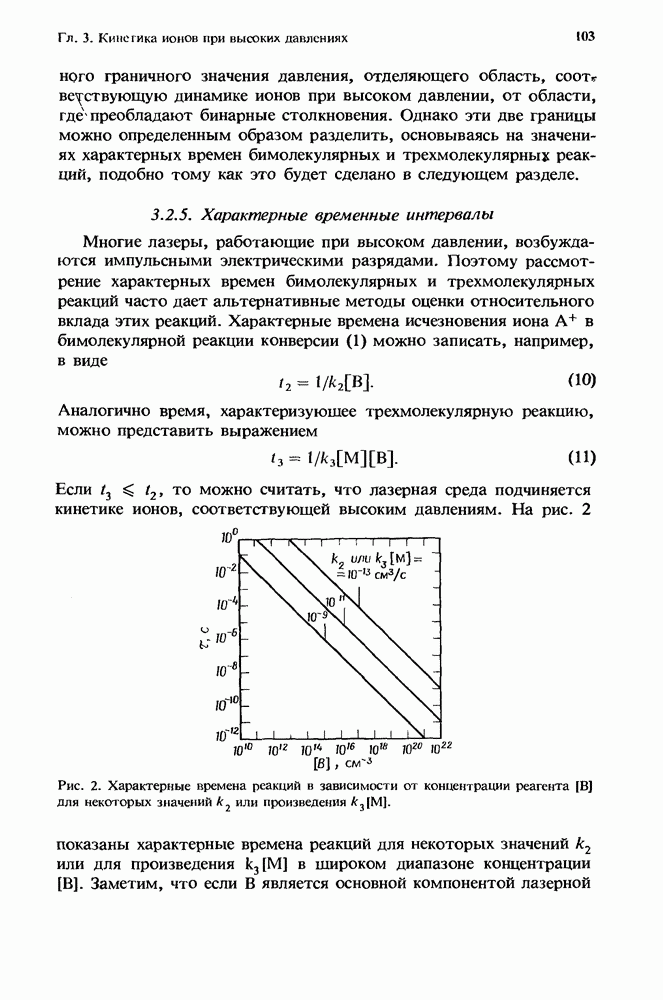
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
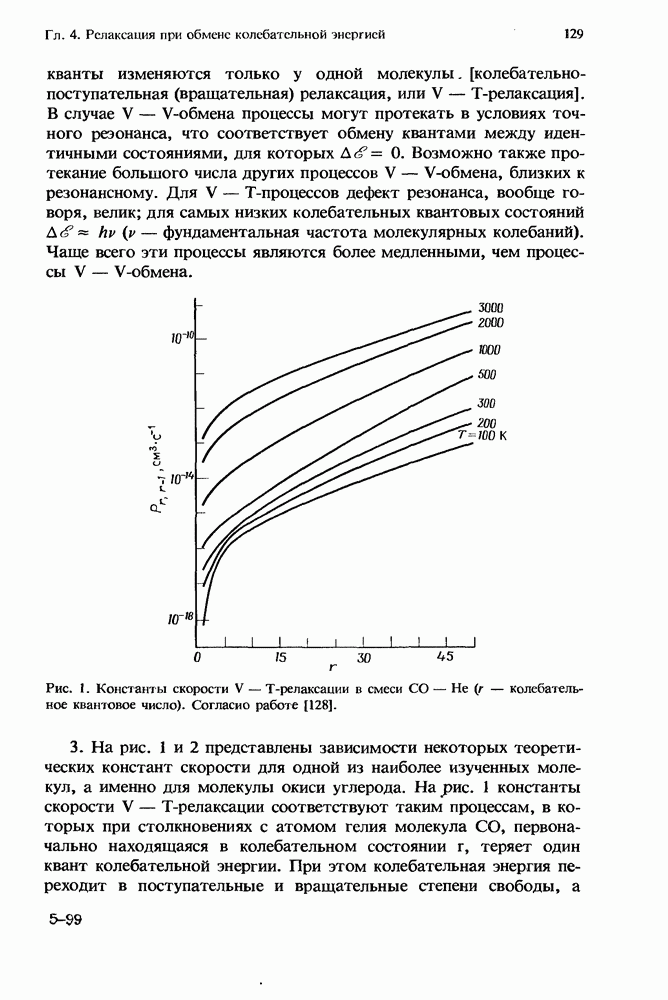
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
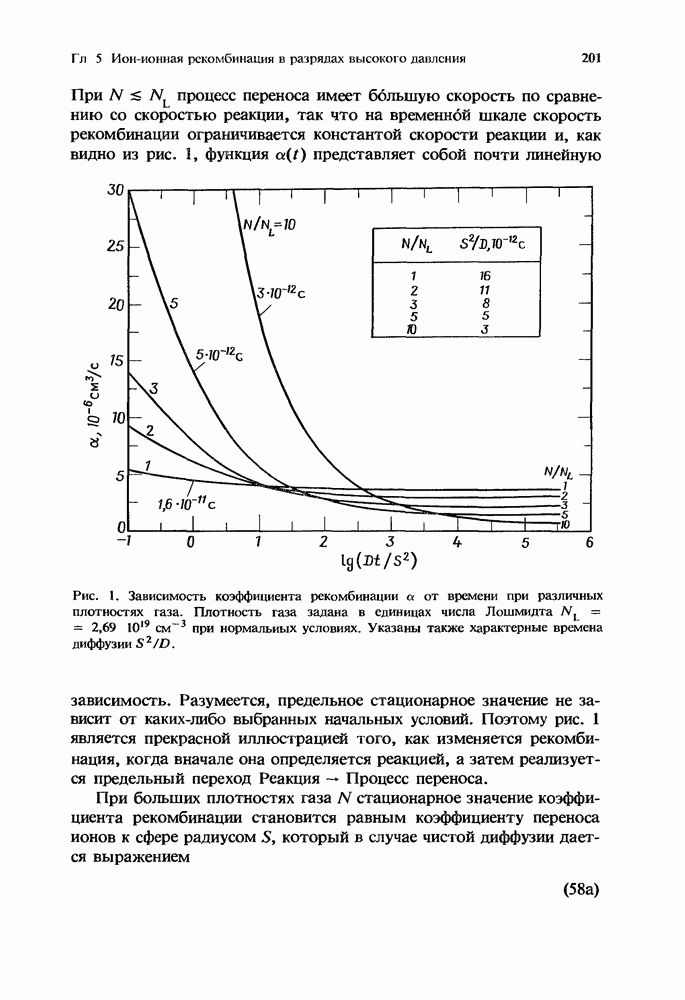
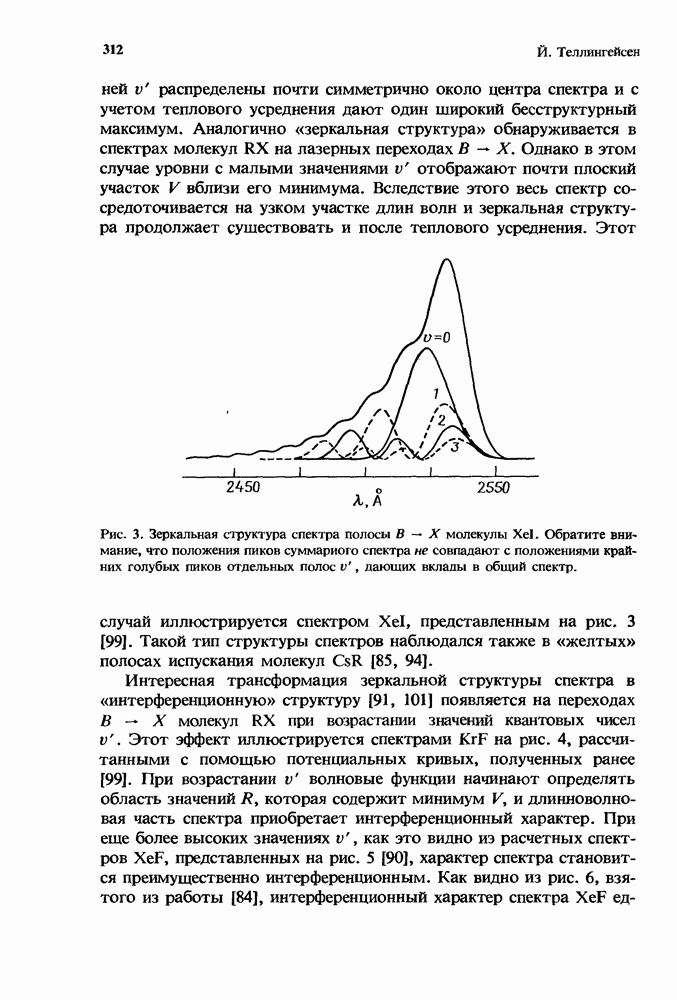
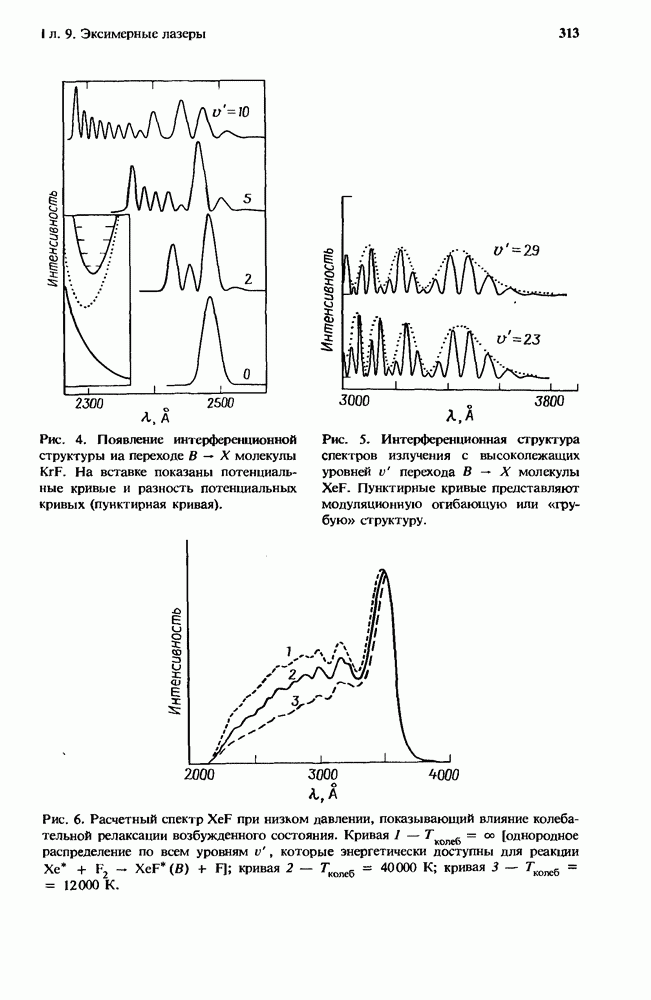
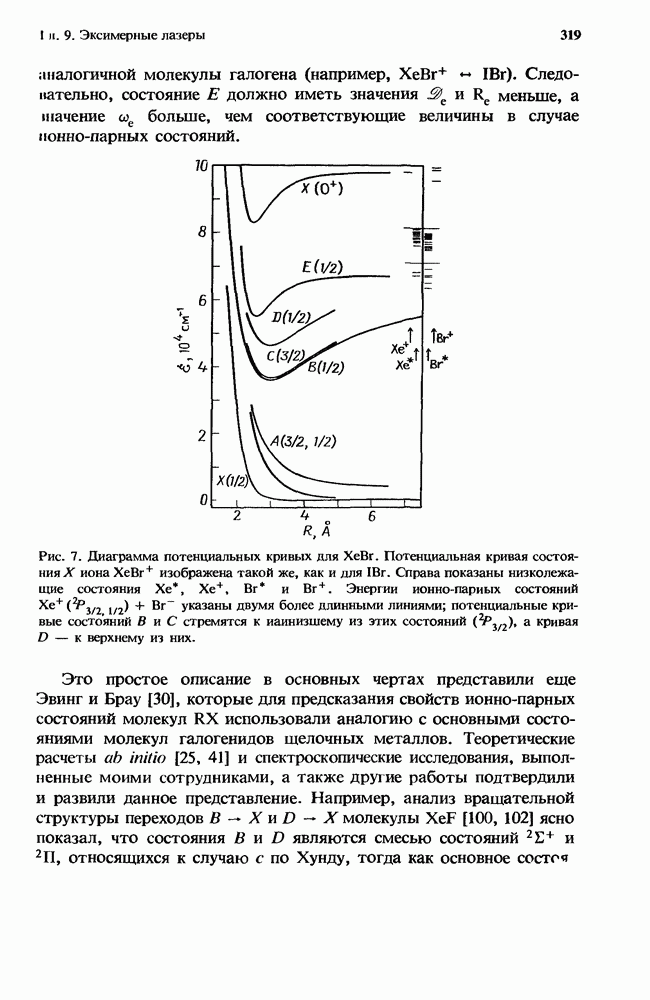
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
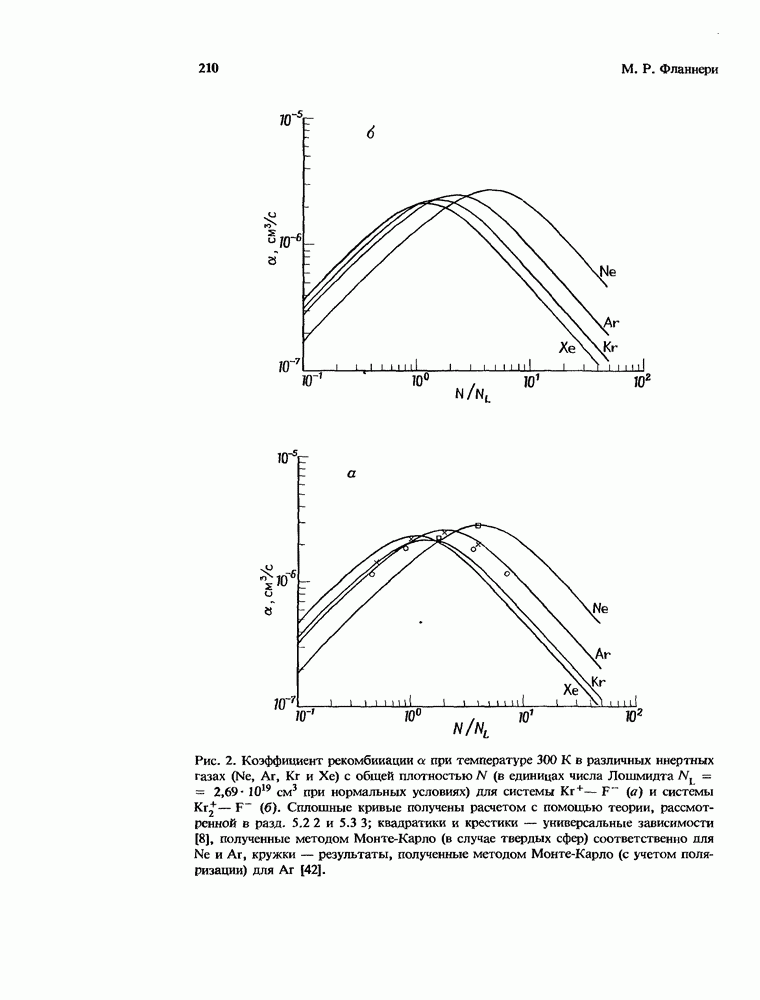
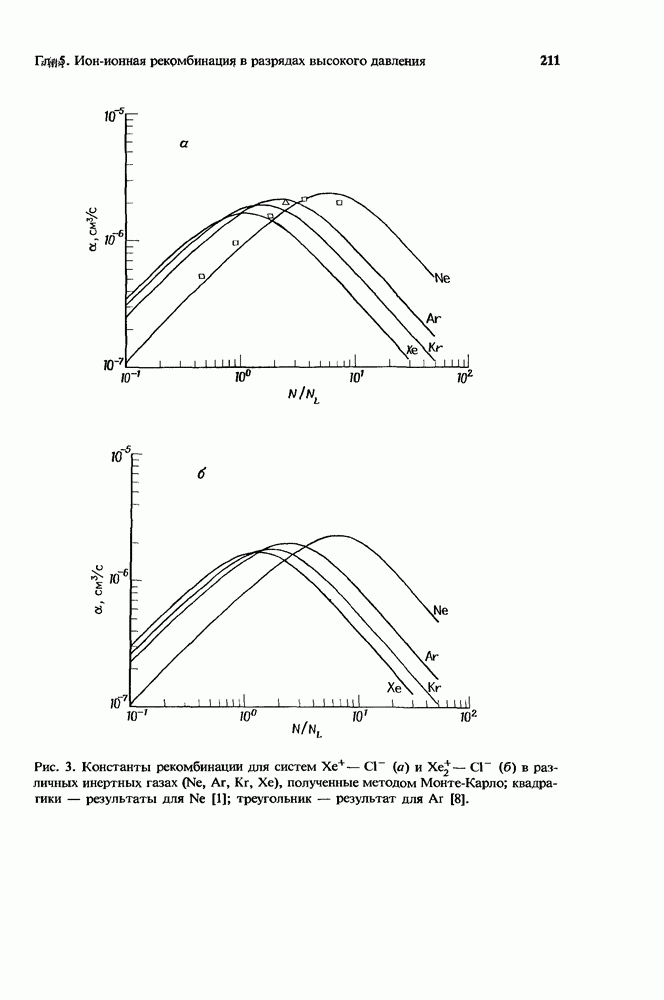
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
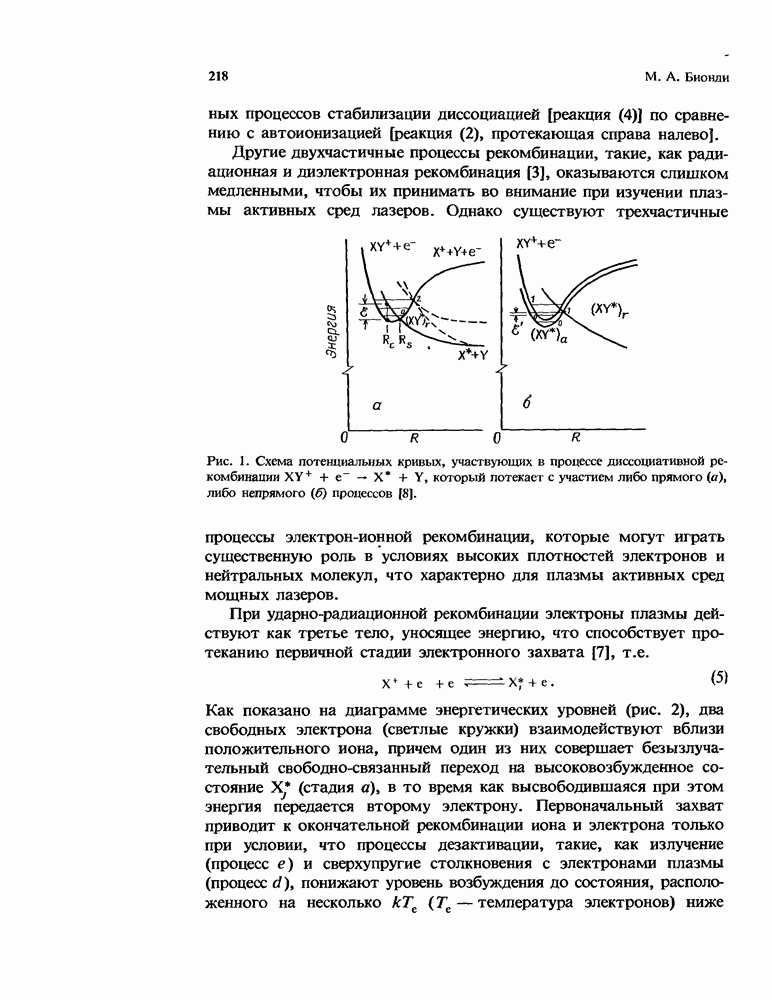
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
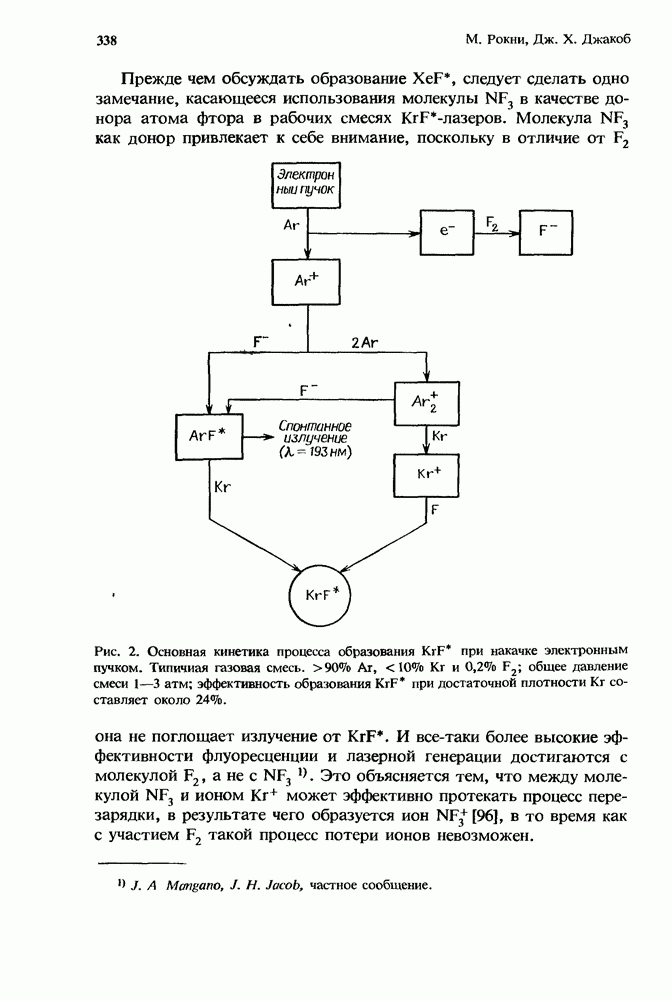
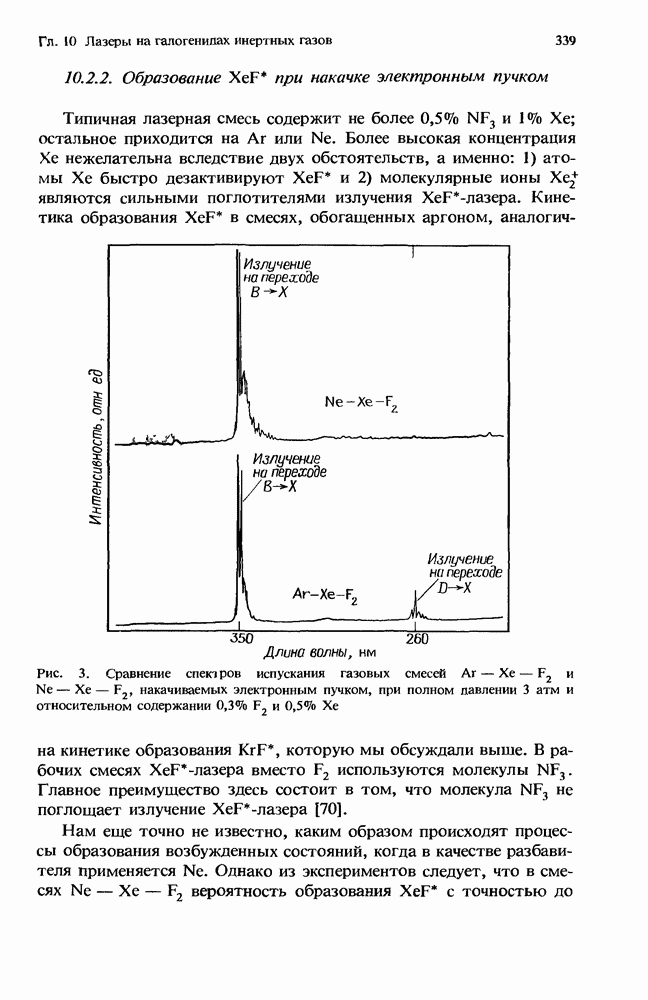
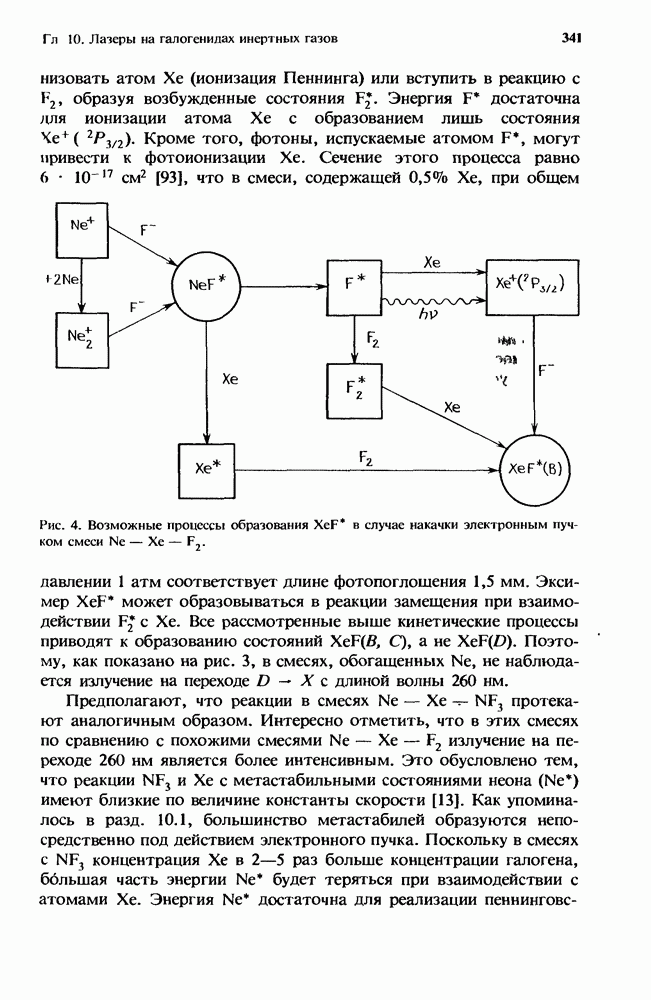
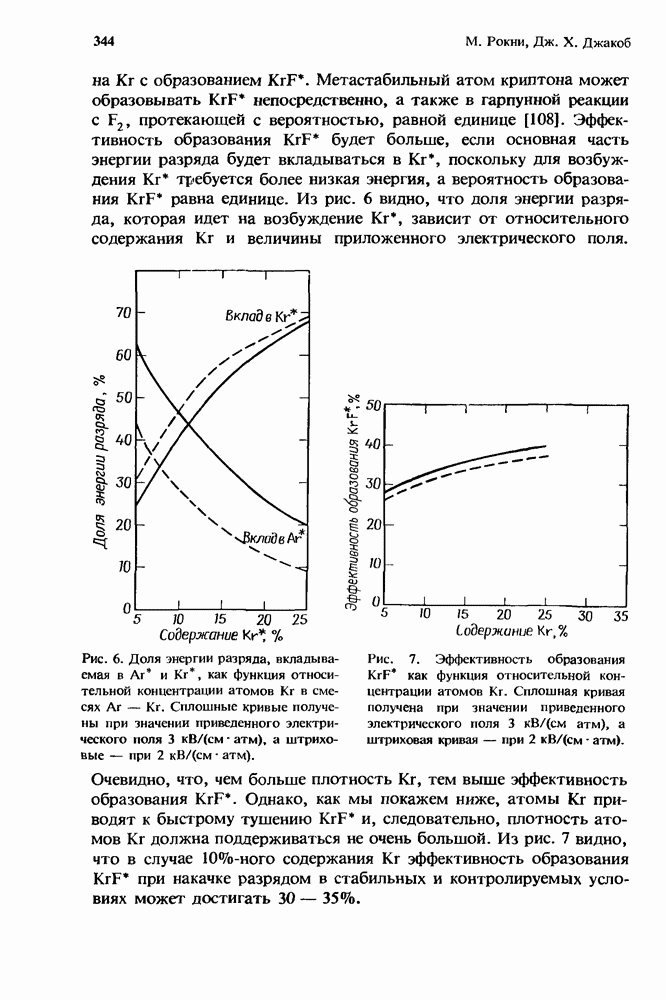
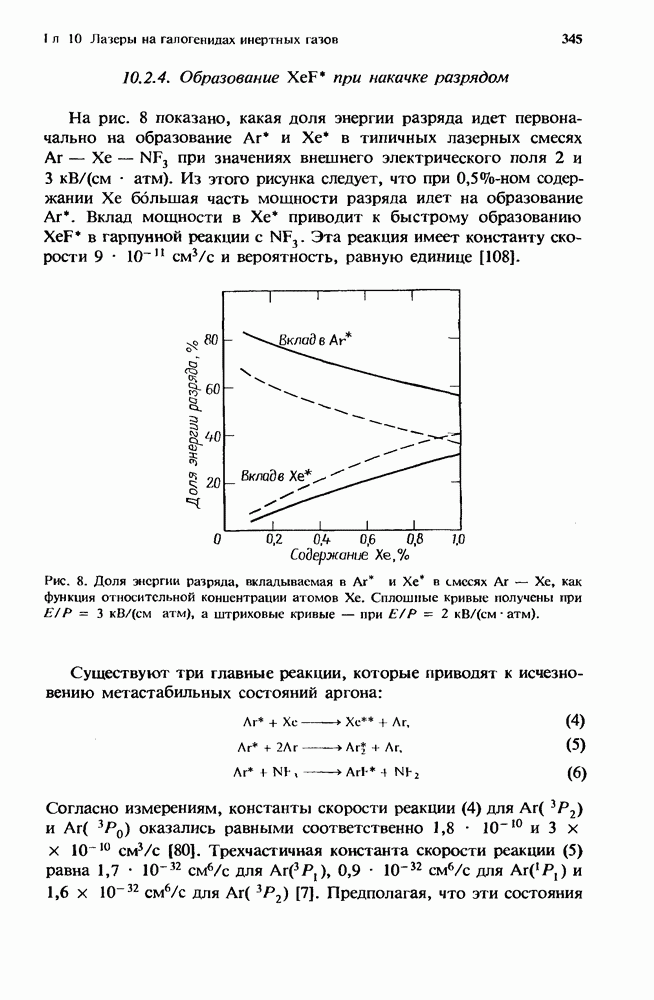
- 10.2. Кинетика образования верхнего лазерного уровня
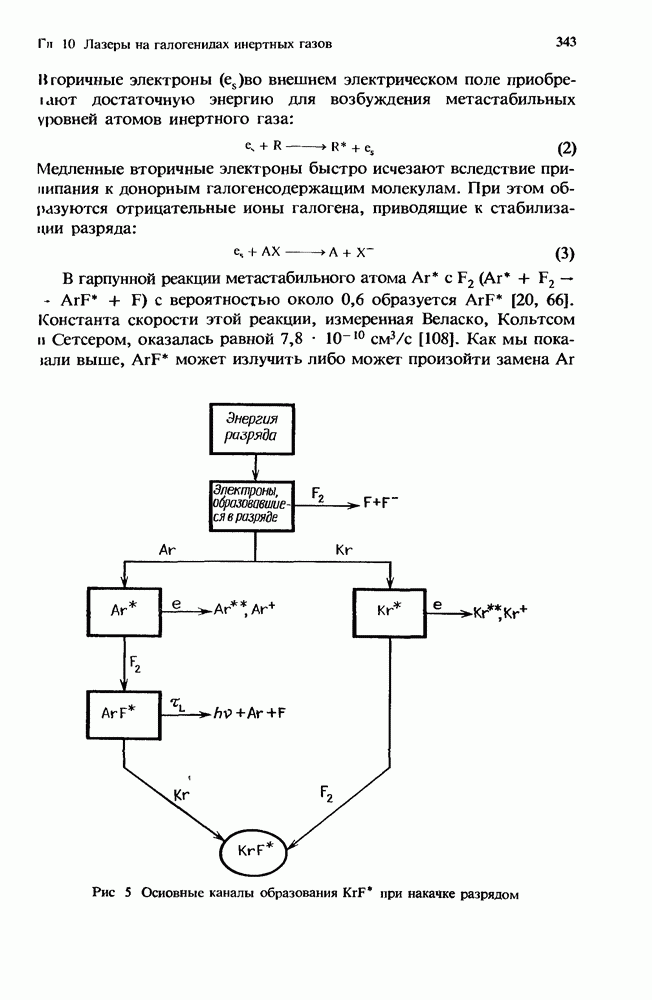
- 10.2.3. Образование KrF* в разряде
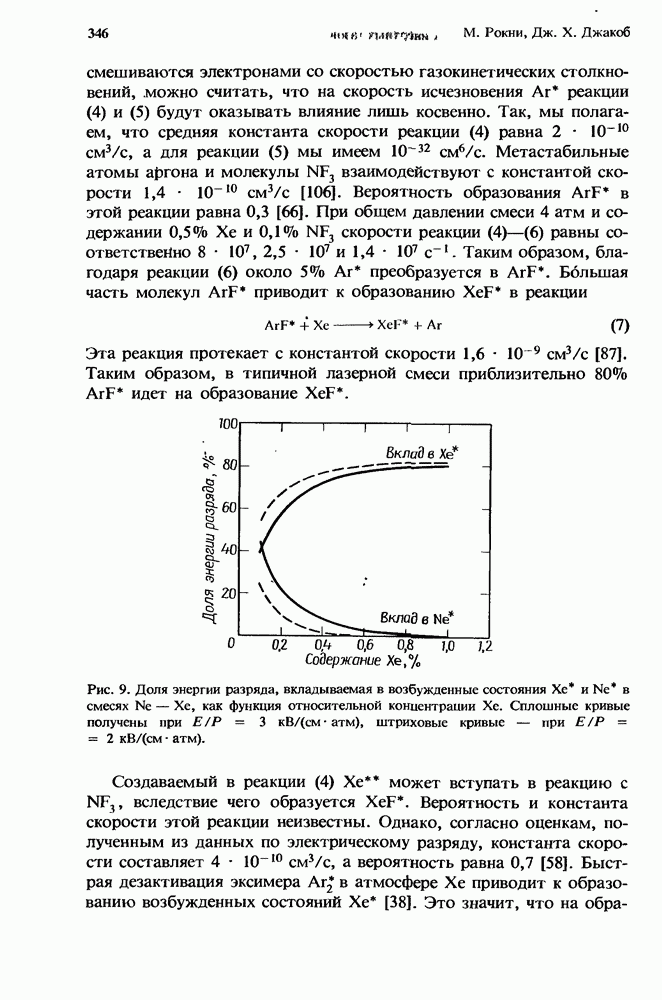
- 10.2.4. Образование XeF* при накачке разрядом
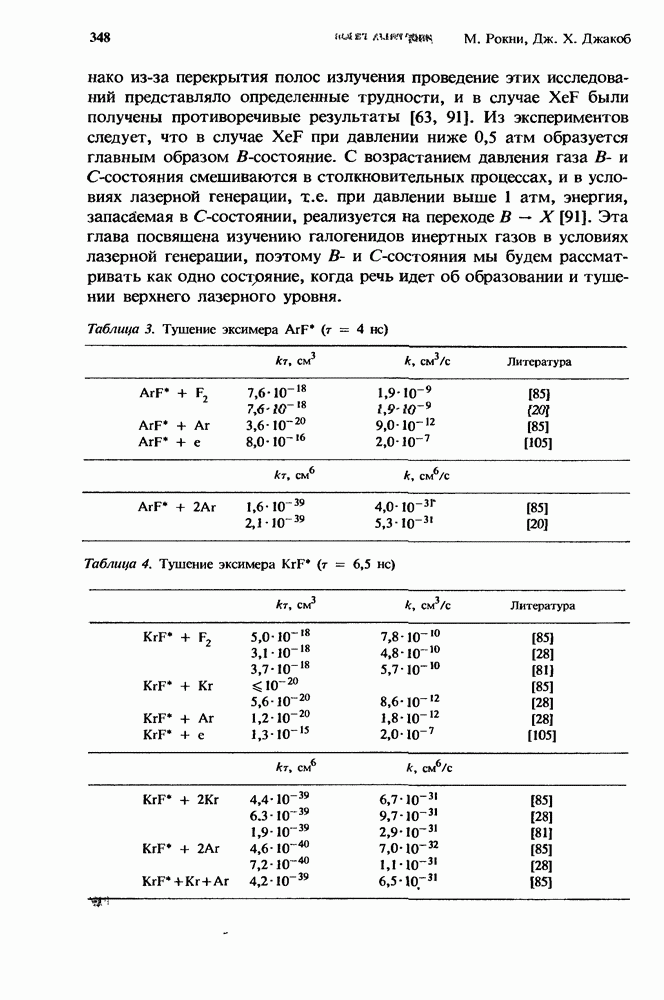
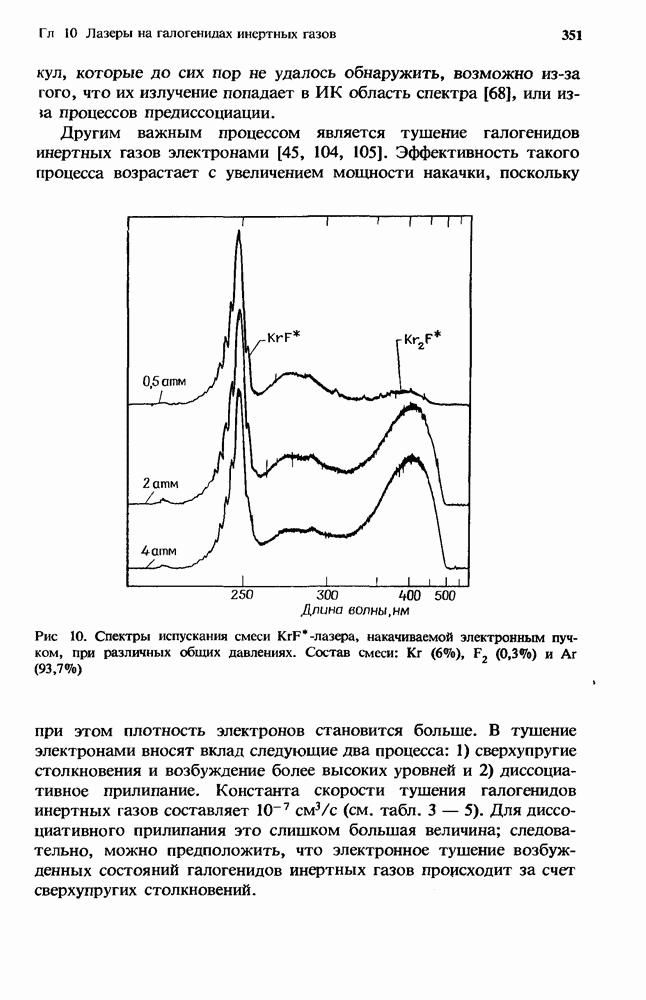
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
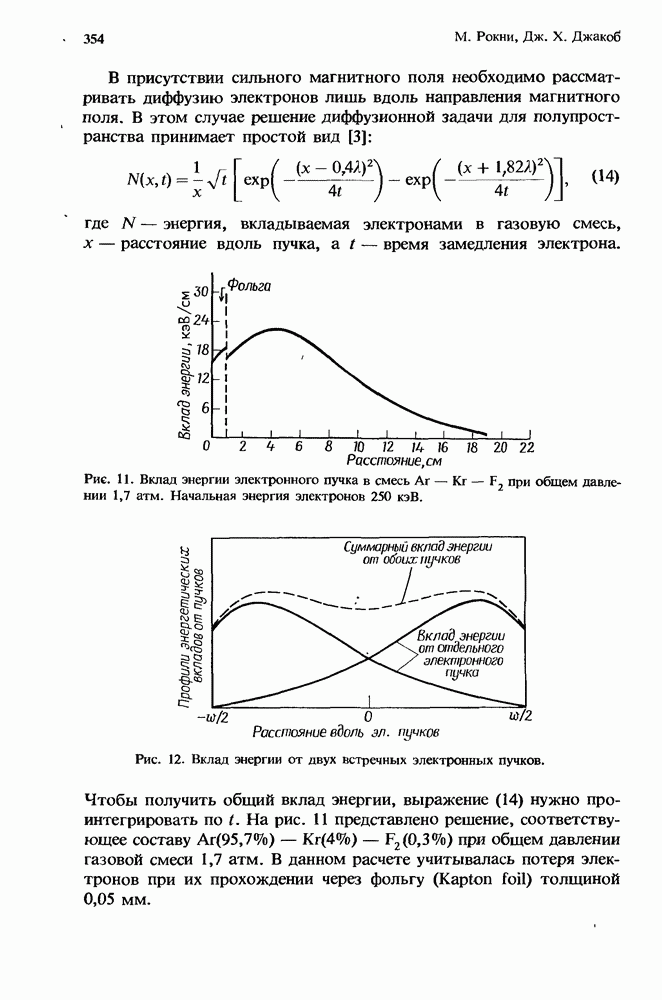
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
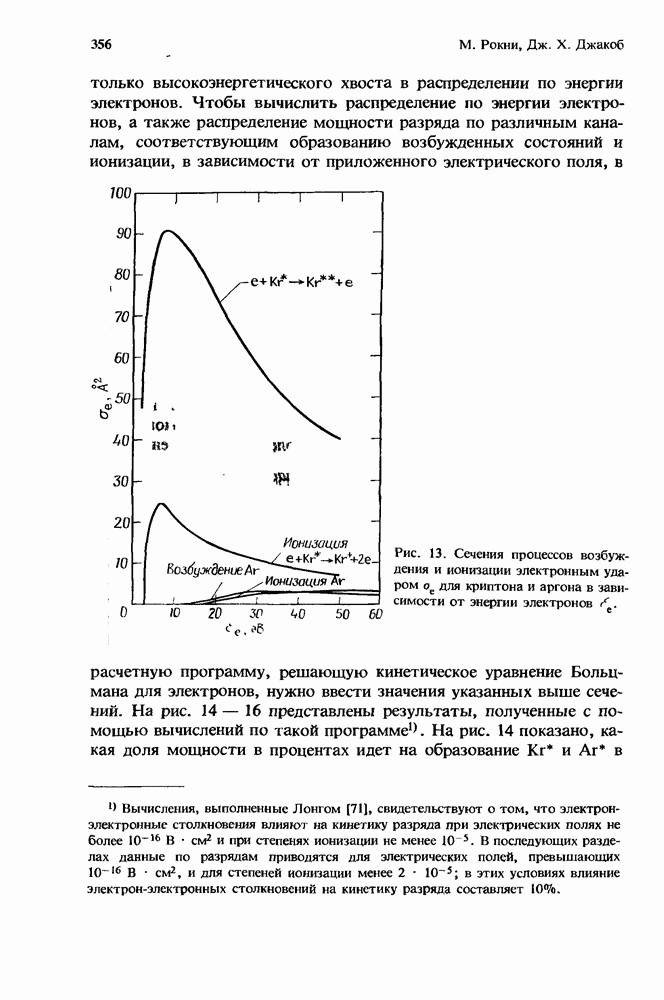
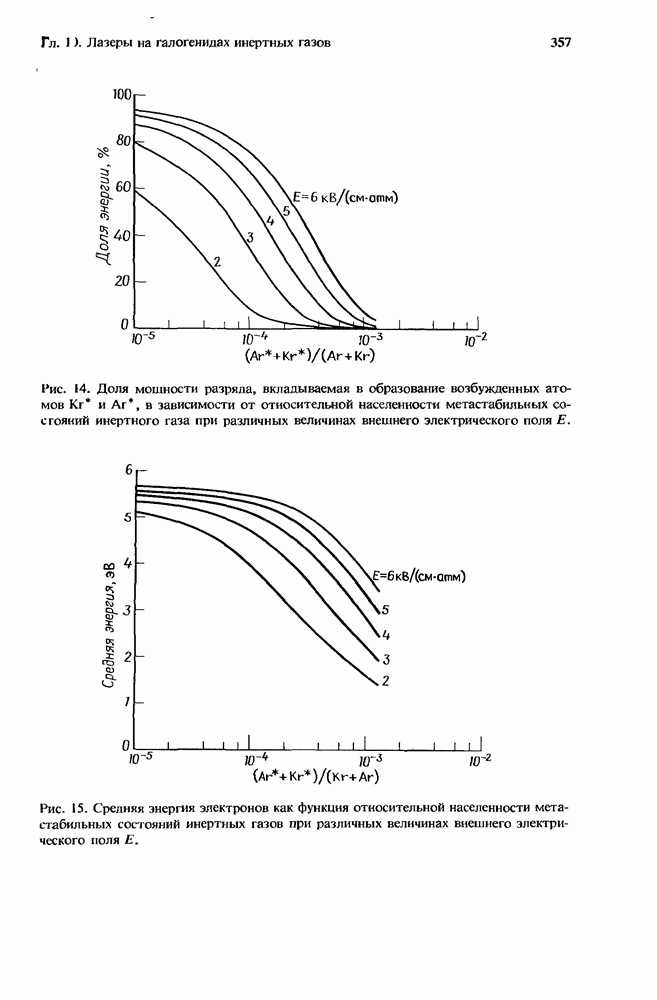
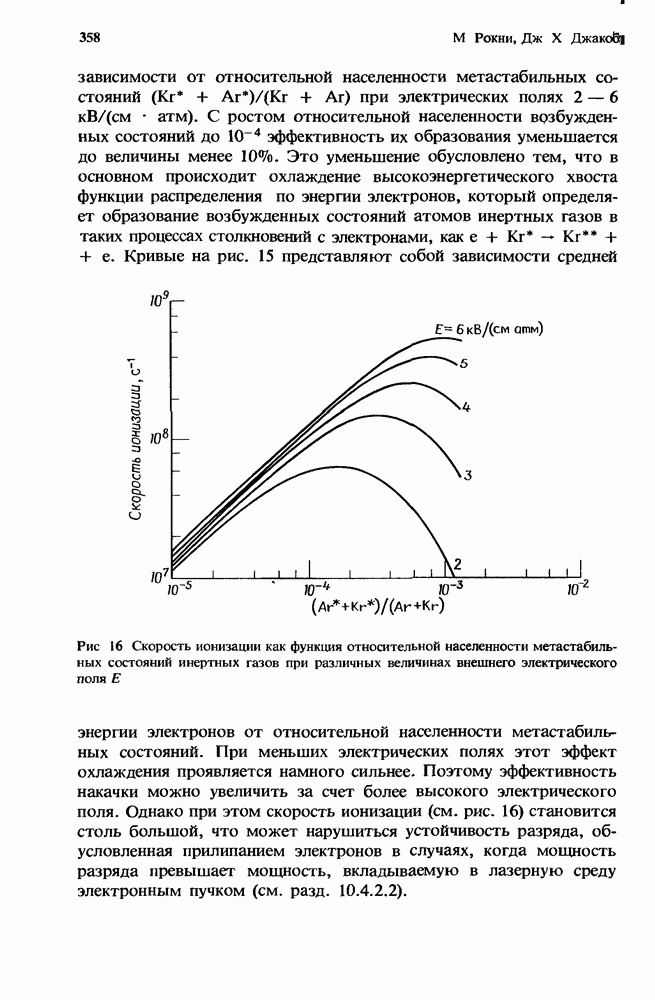
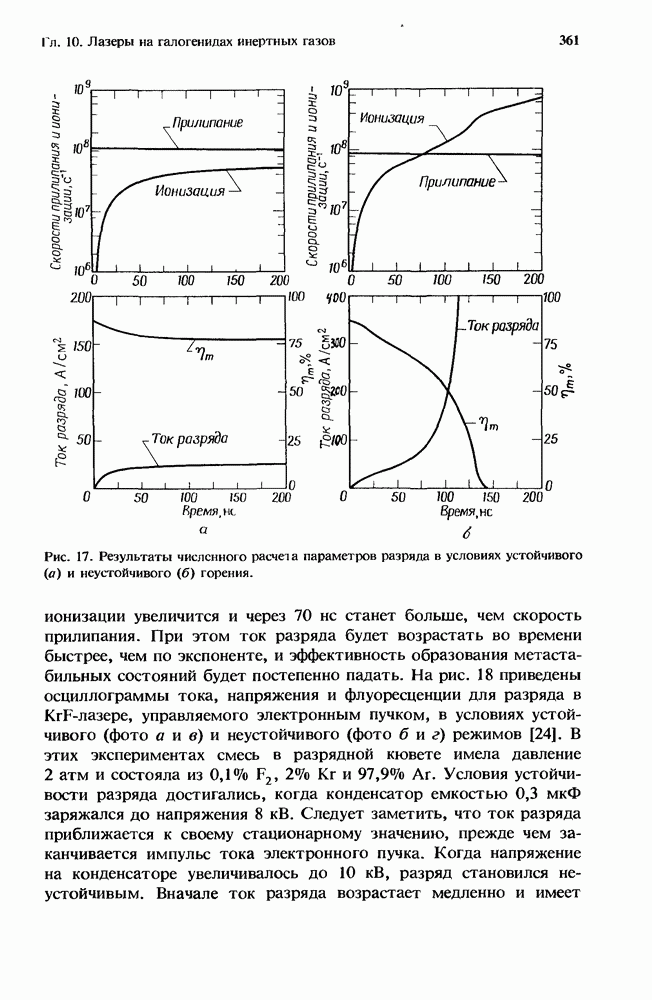
- 10.4.2.2. Устойчивость разряда
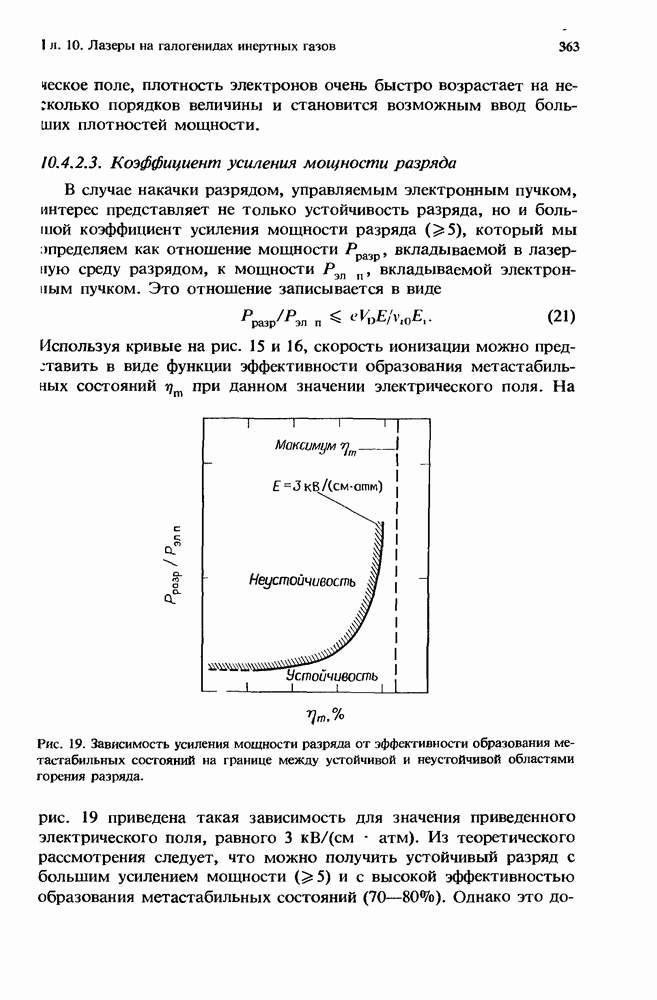
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
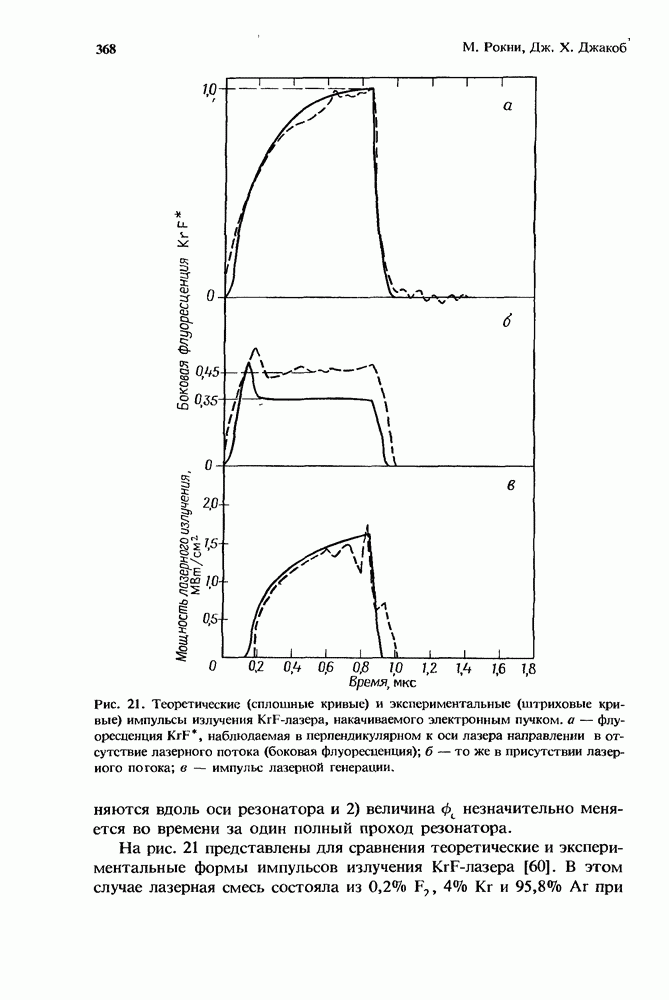
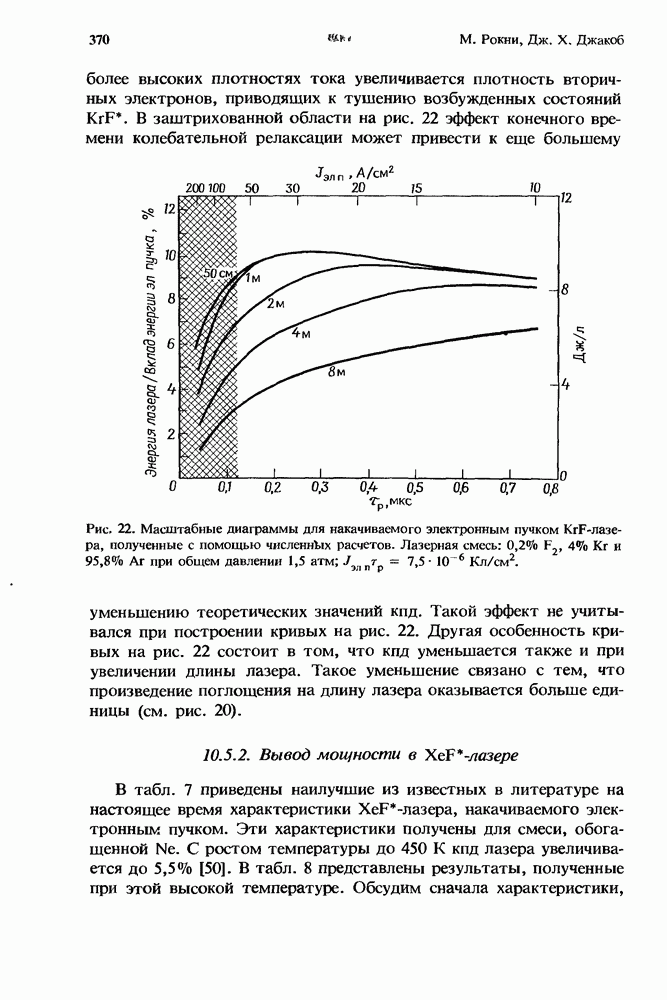
- 10.5.1. Вывод мощности в KrF*-лазере
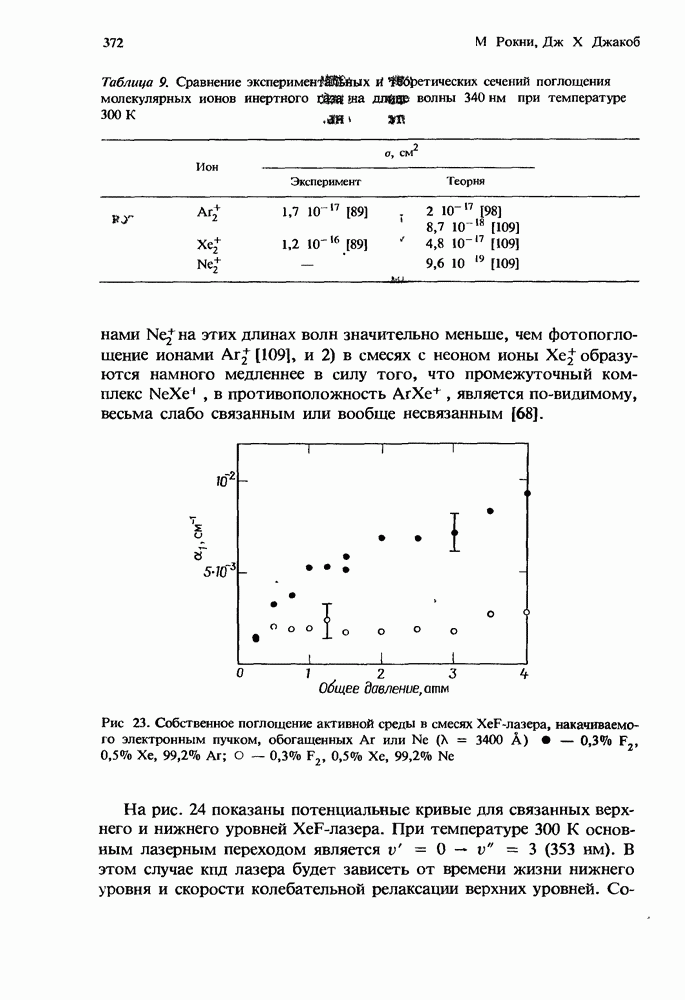
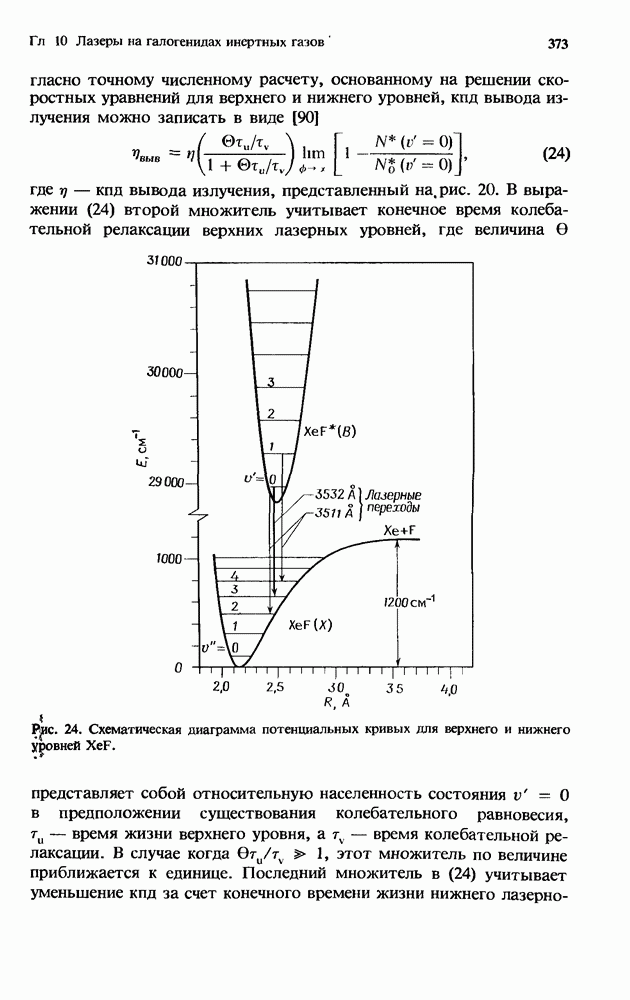
- 10.5.2. Вывод мощности в XcF*-лазере
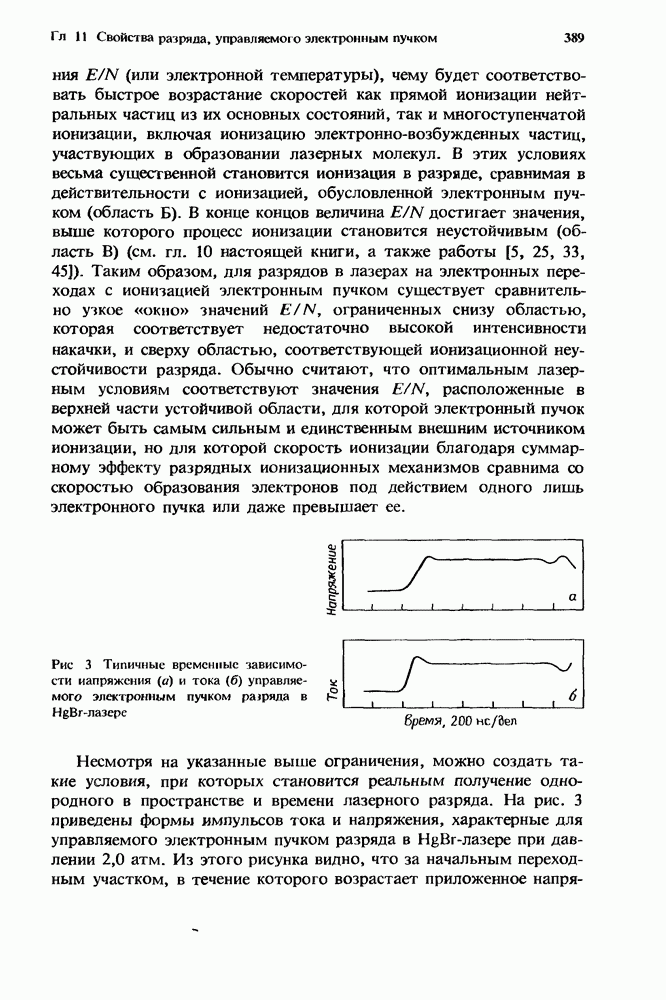
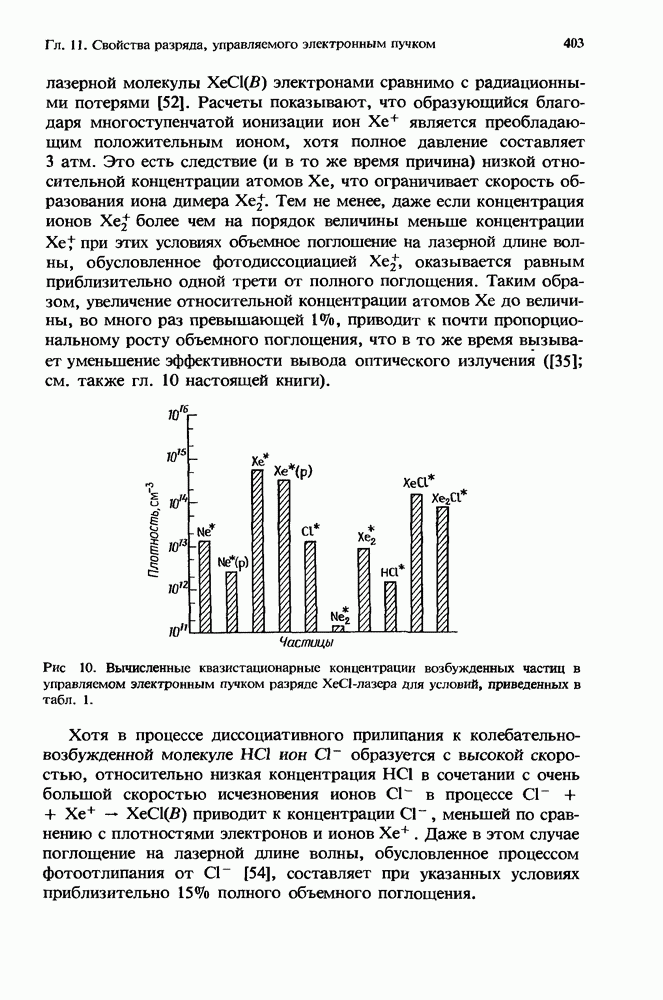
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
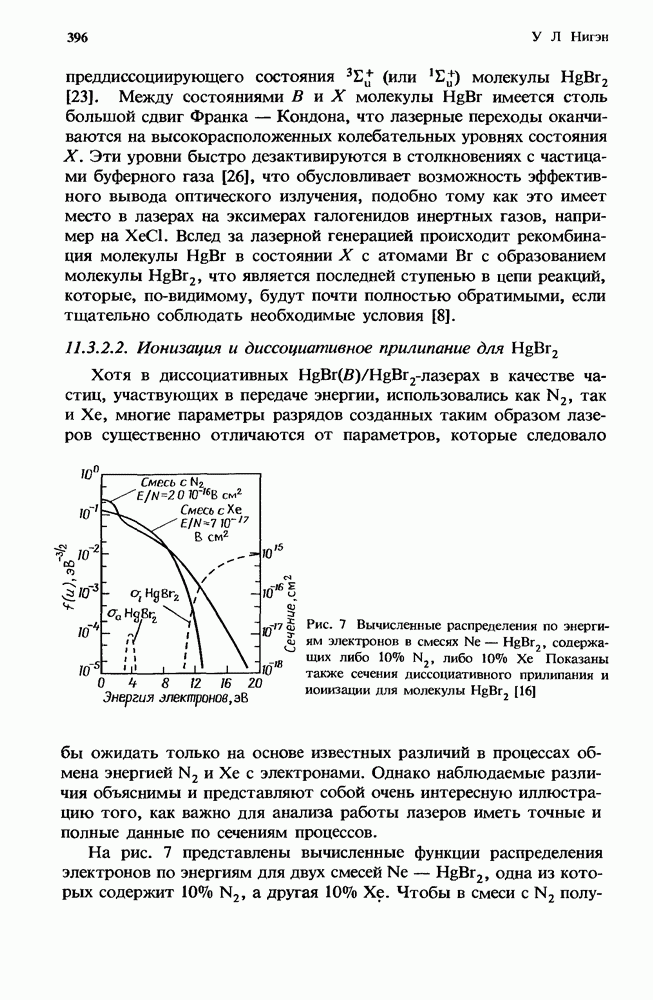
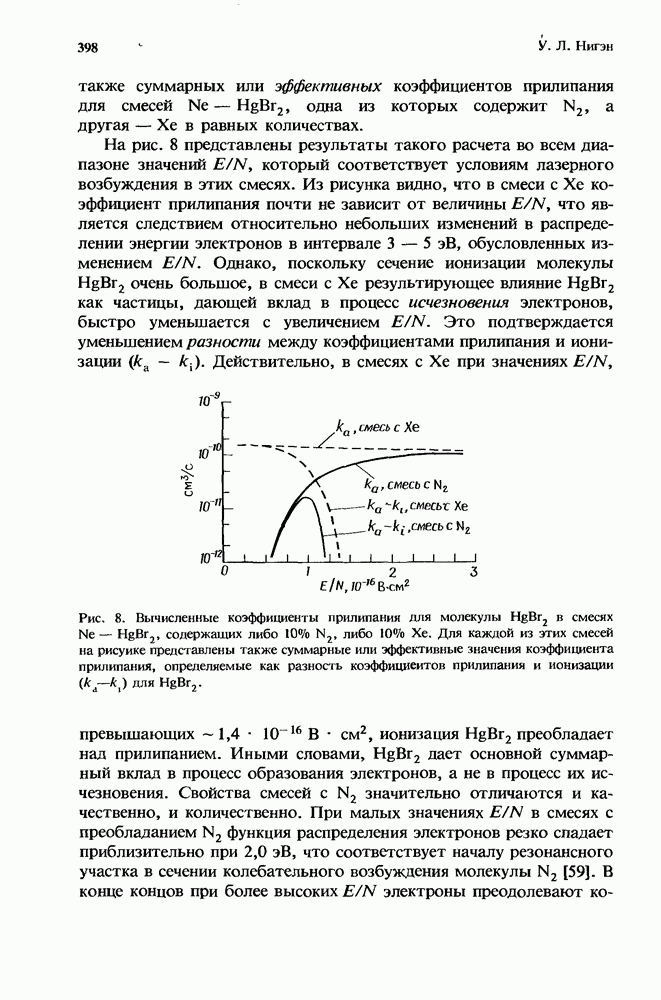
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
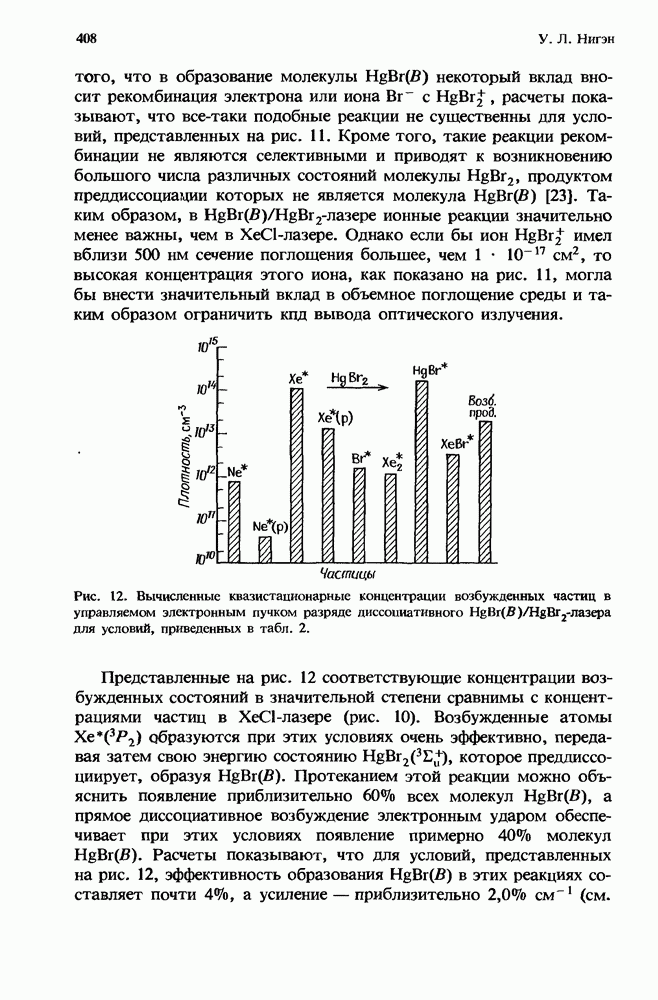
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
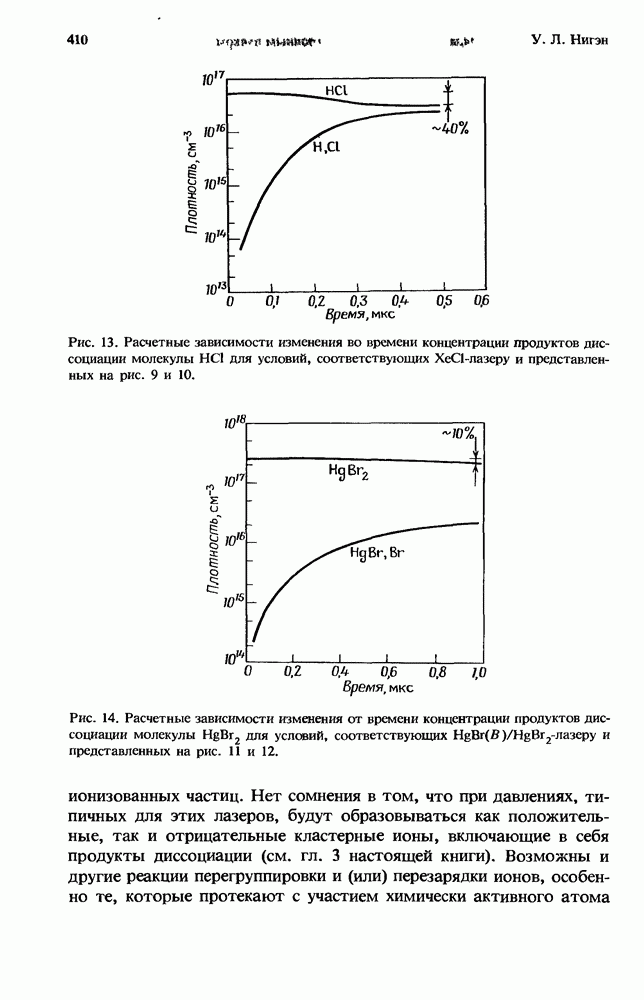
- 11.4.3. Диссоциация галогенидов
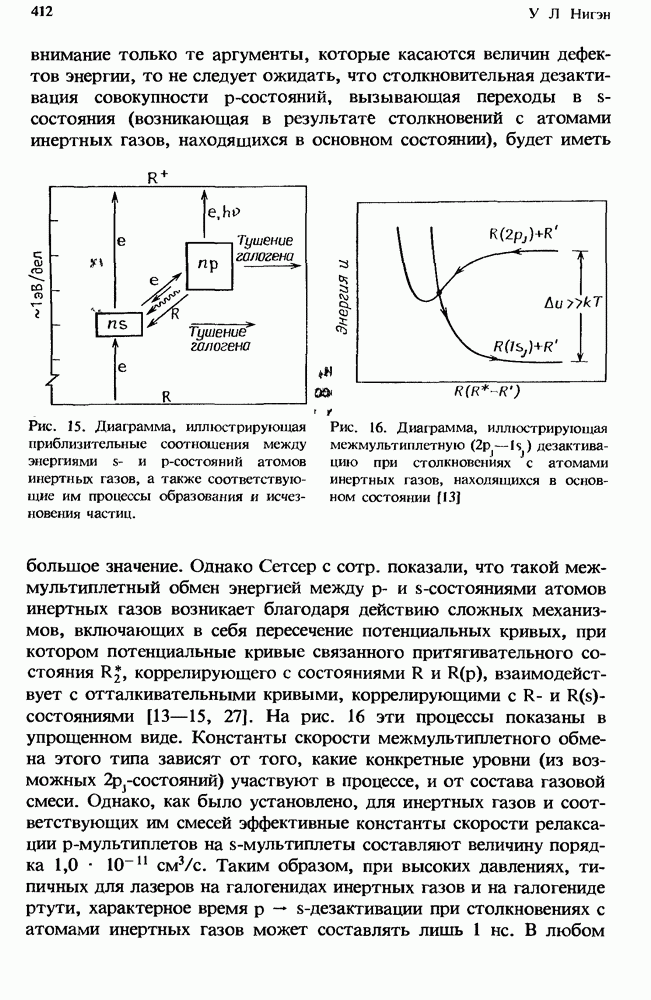
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
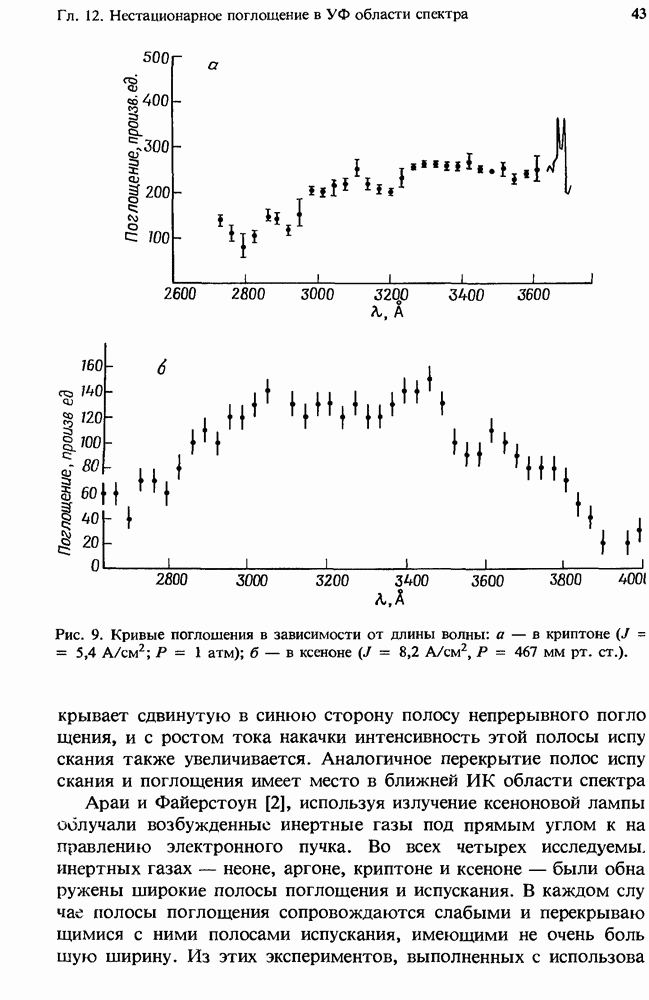
- 12. Нестационарное поглощение в УФ области спектра
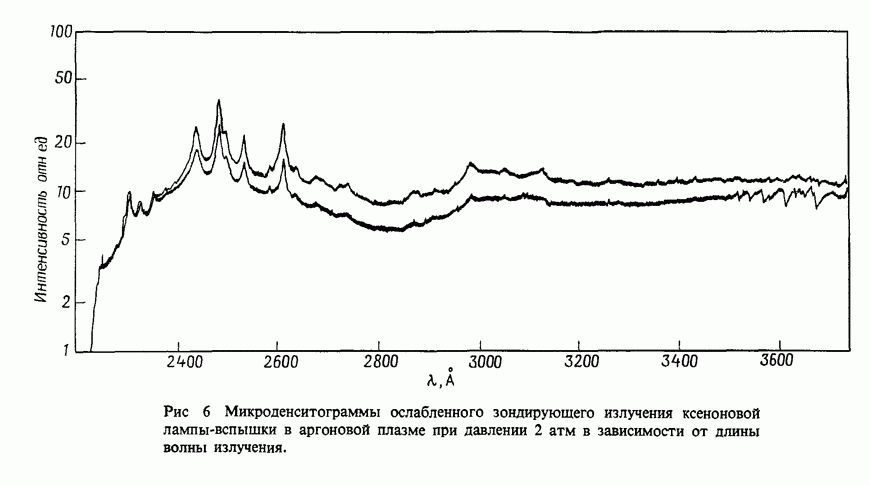
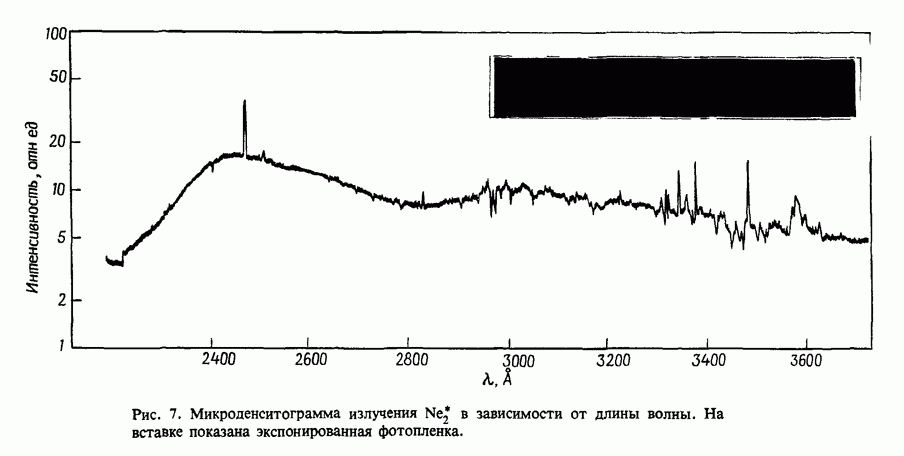
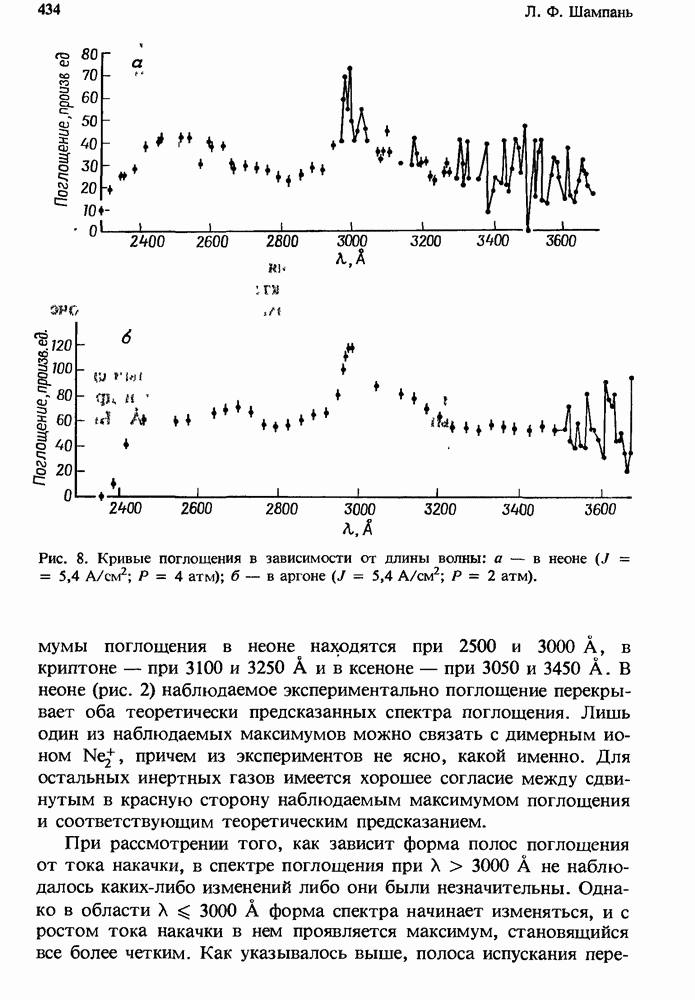
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
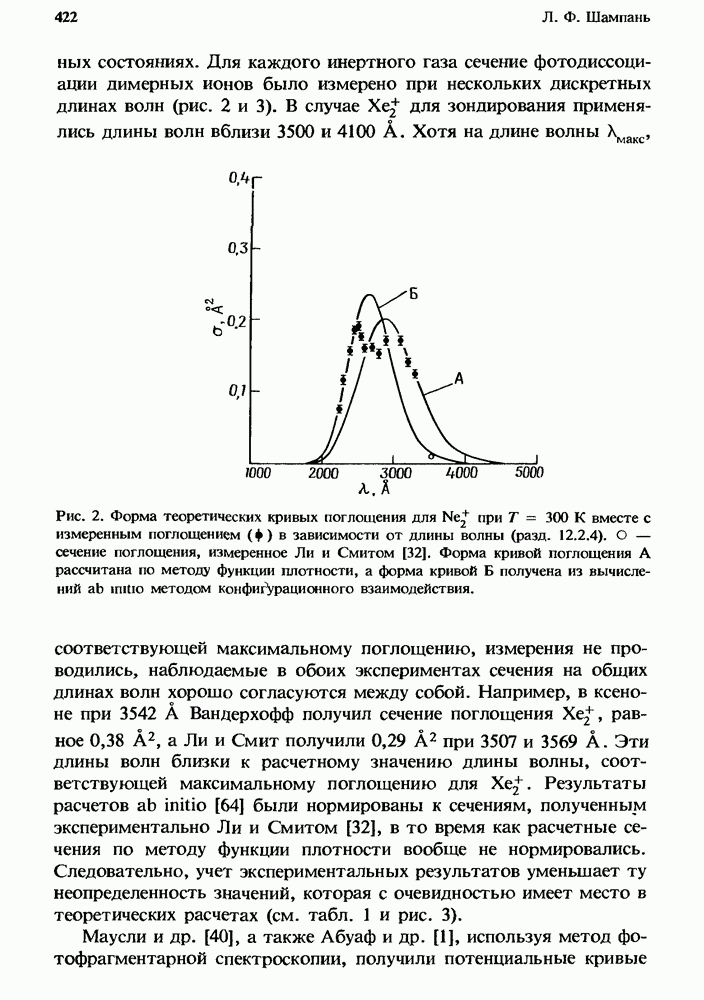
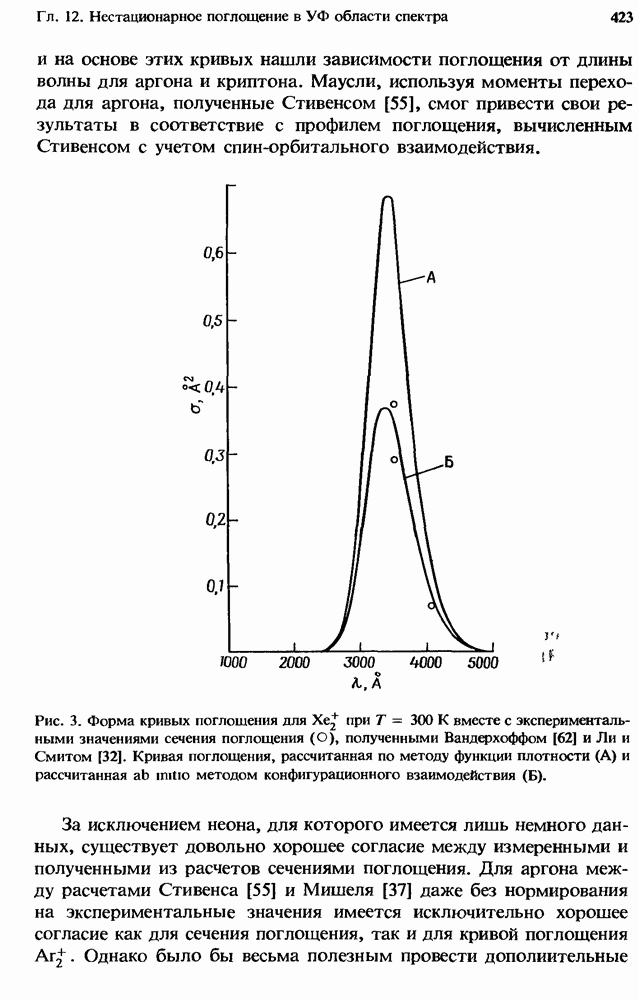
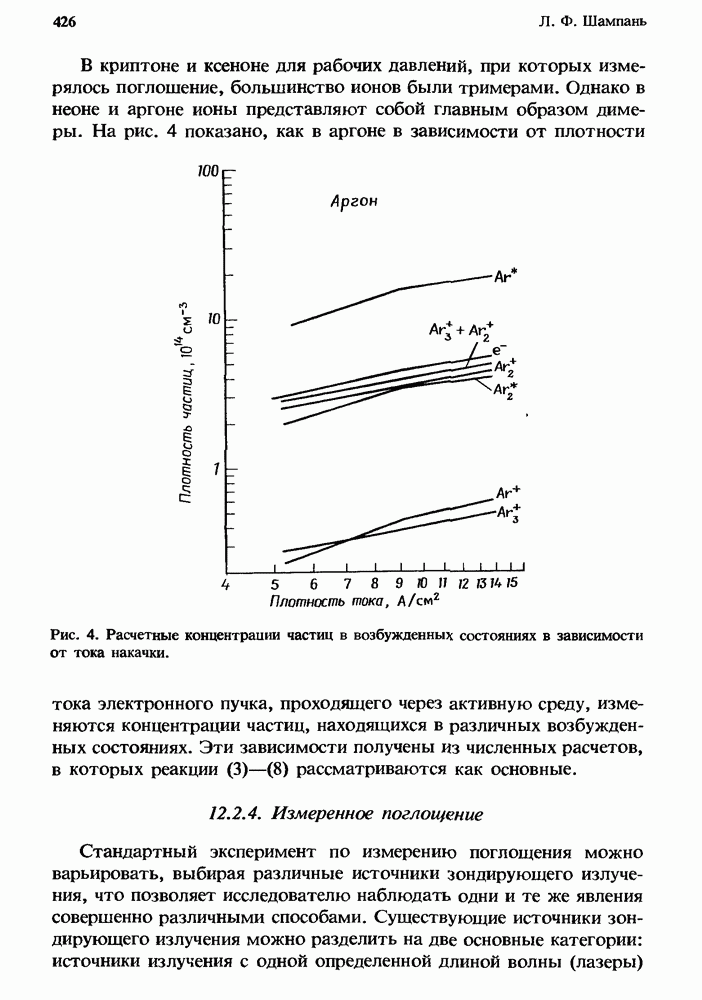
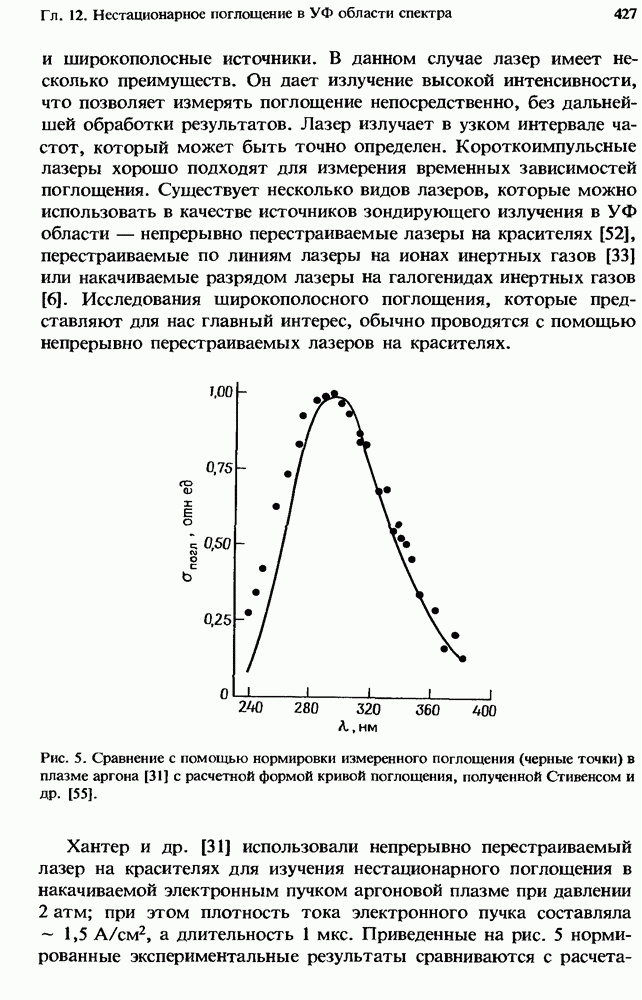
- 12.2.4. Измеренное поглощение
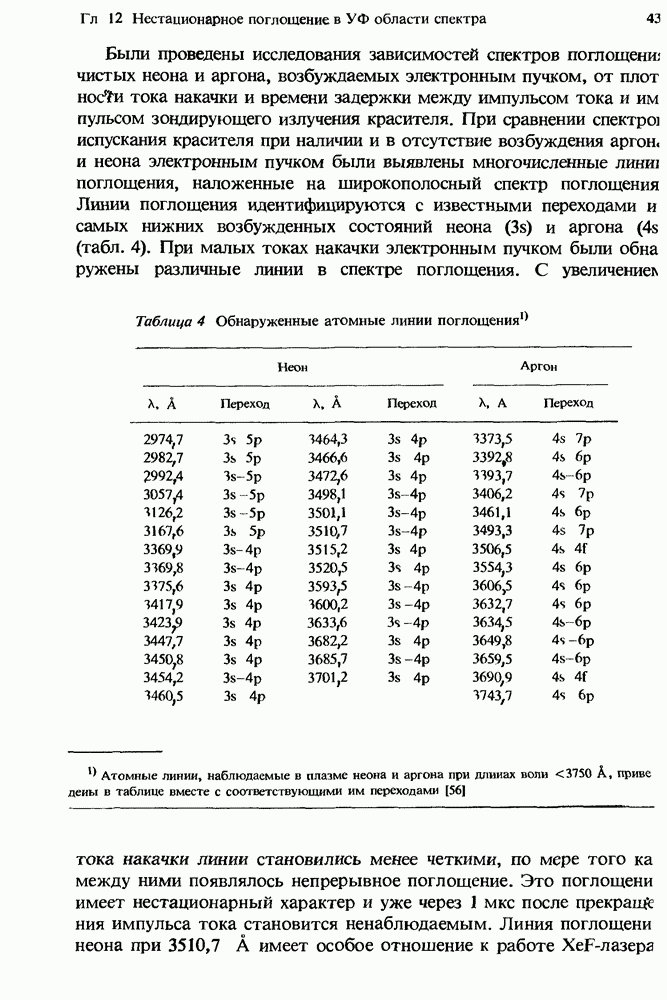
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
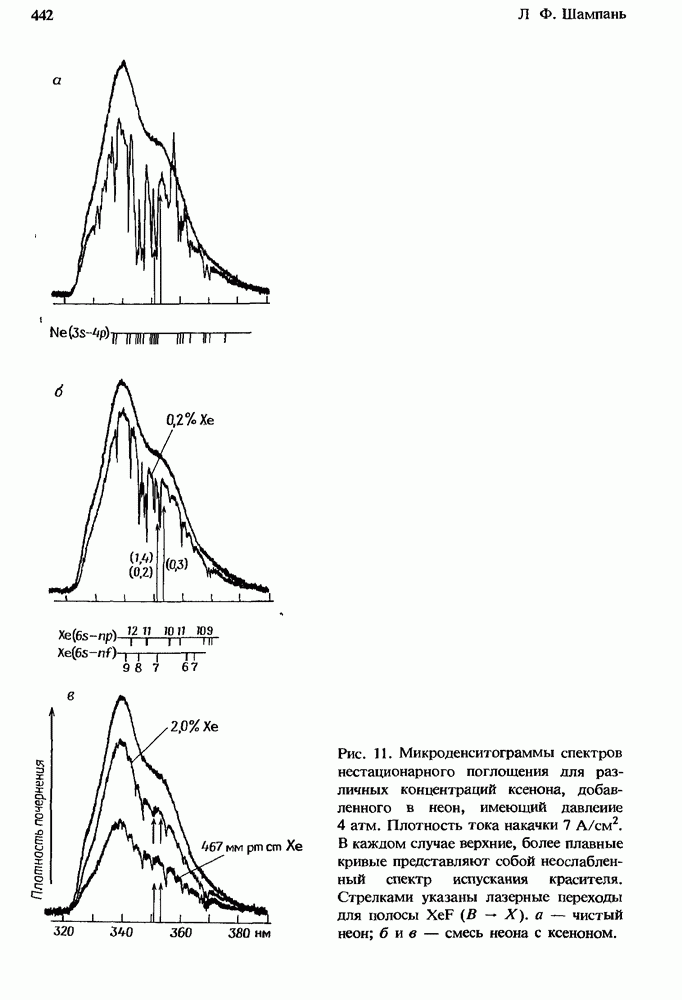
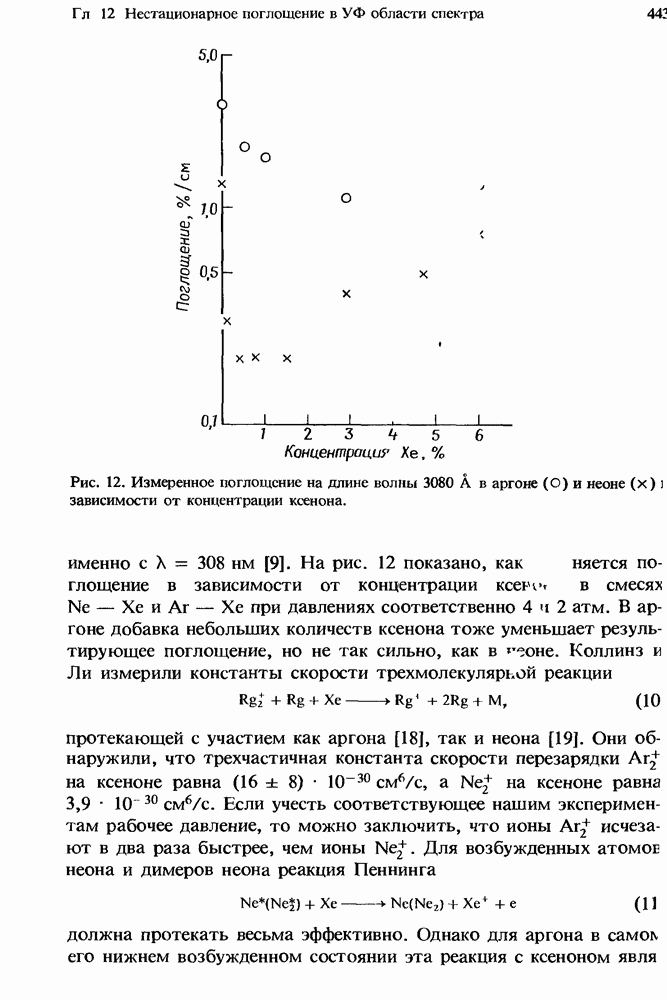
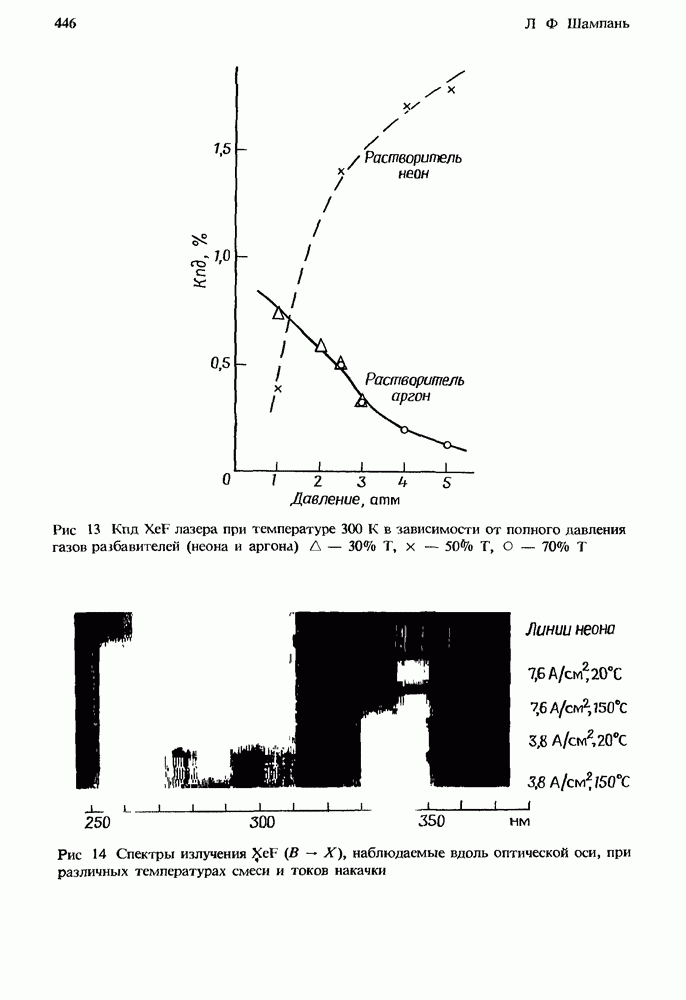
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
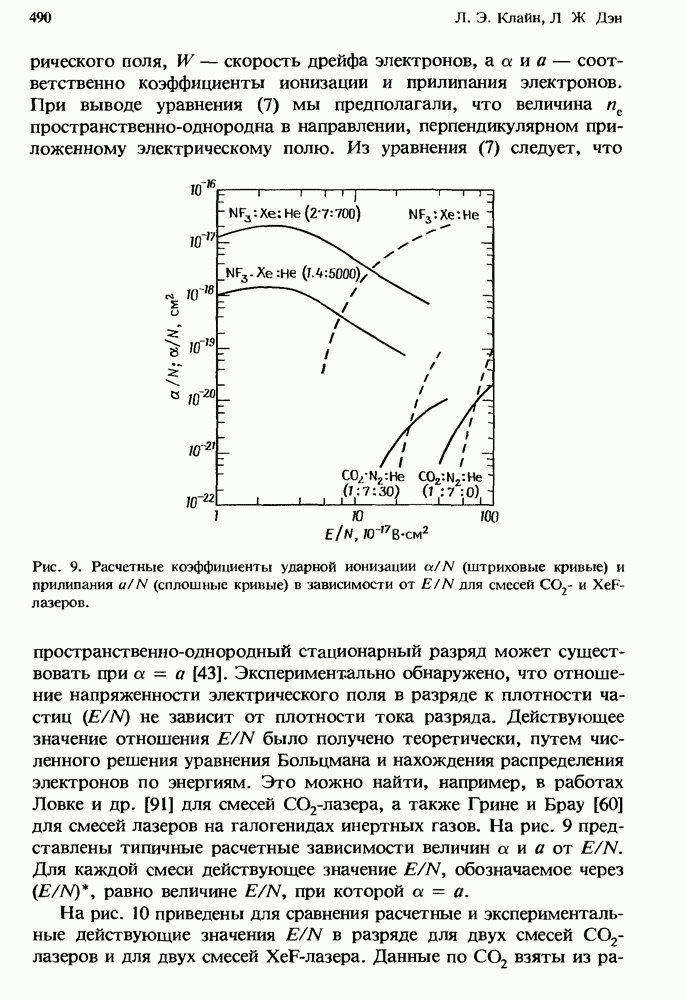
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
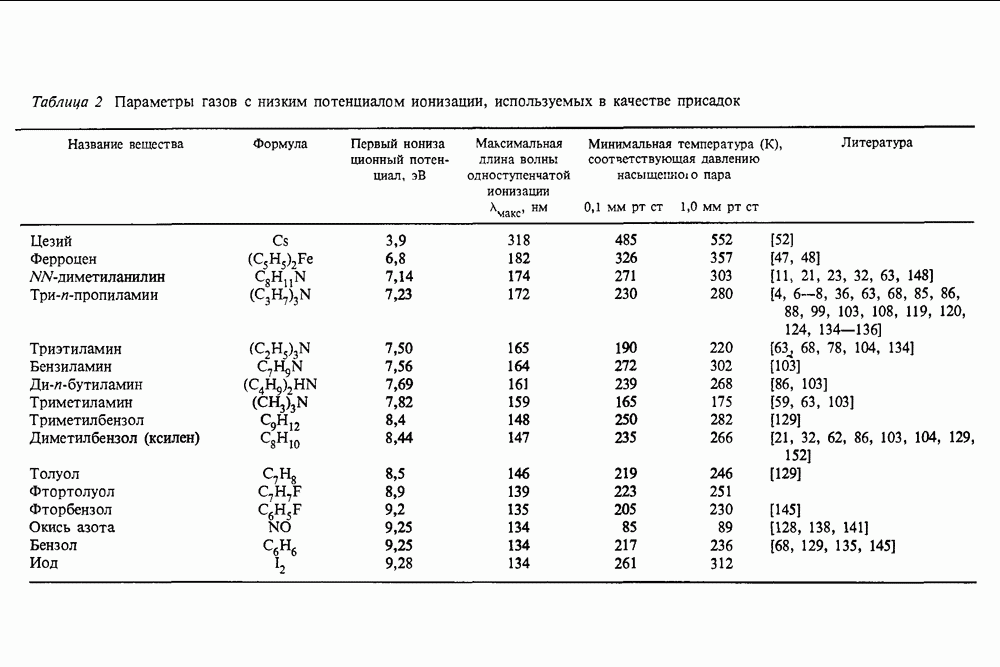
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
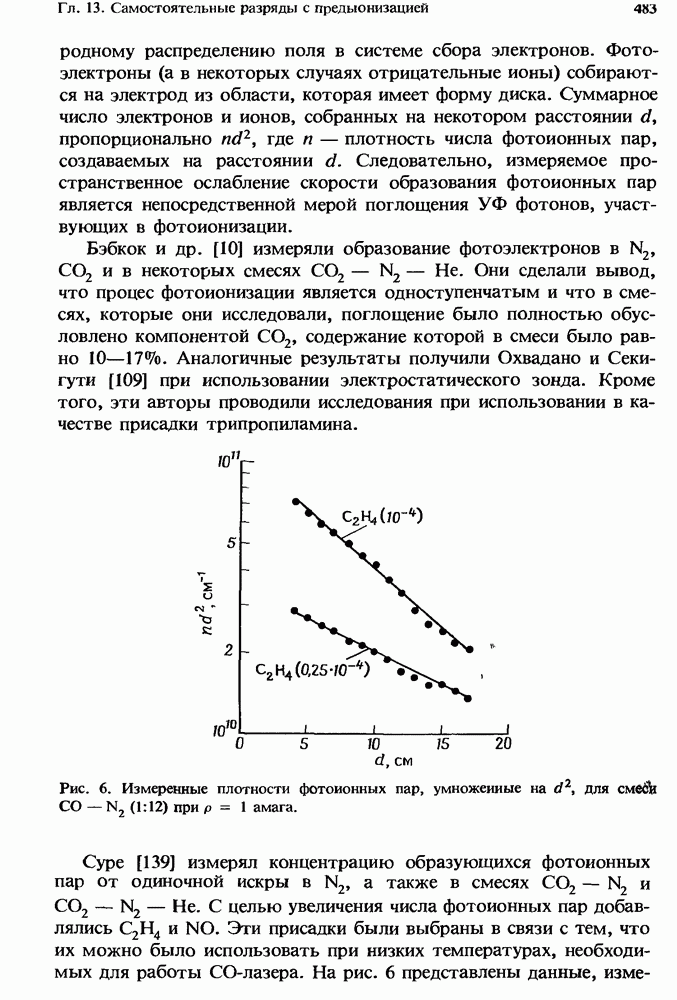
- 13.3.4. Измерения плотности предыонизации от отдельной искры
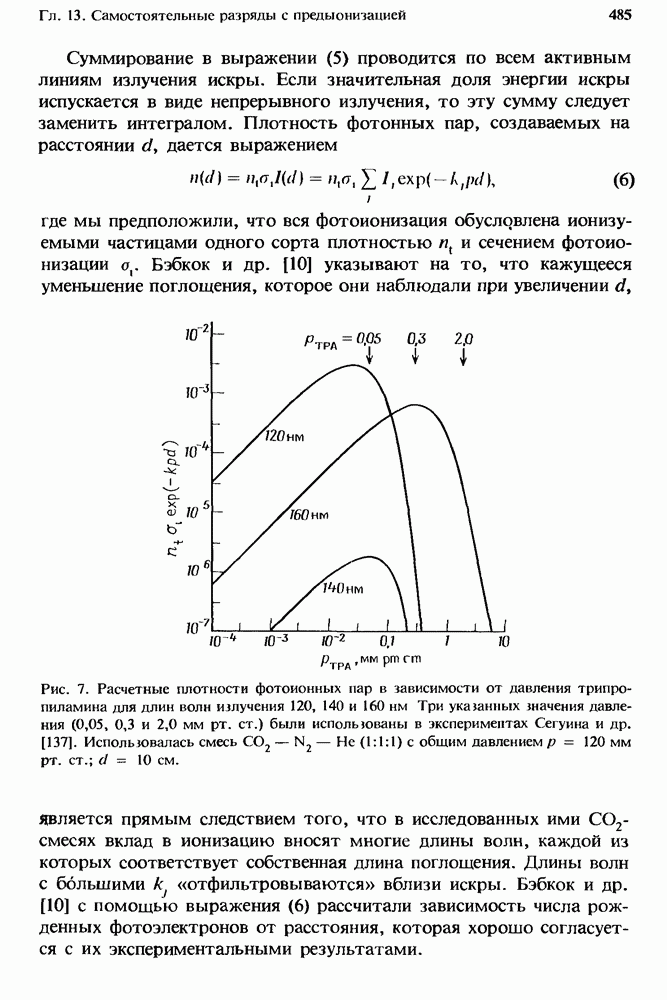
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
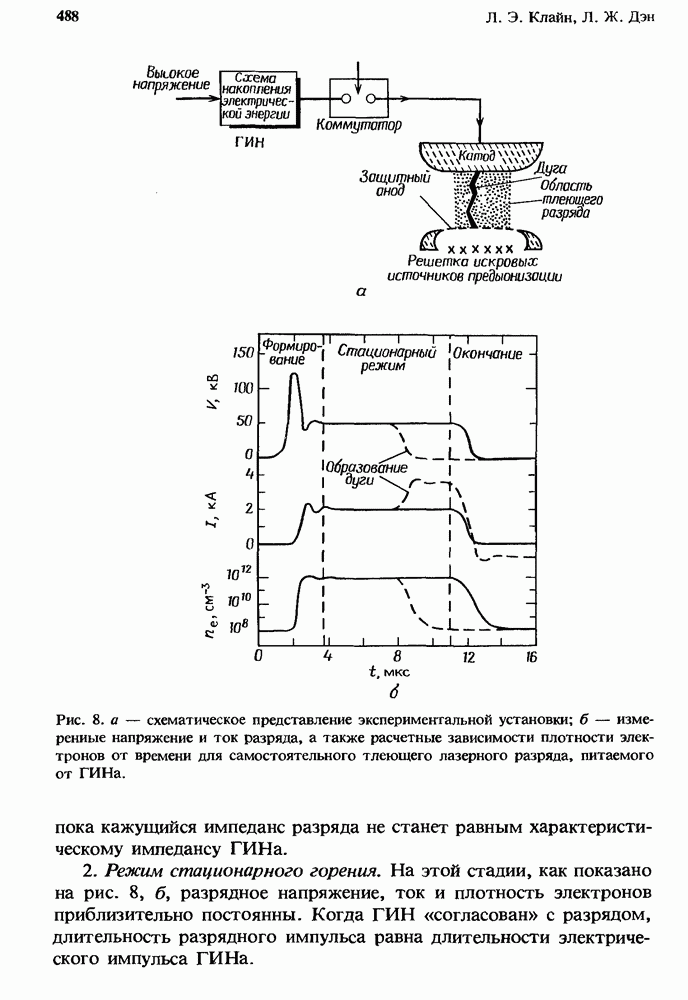
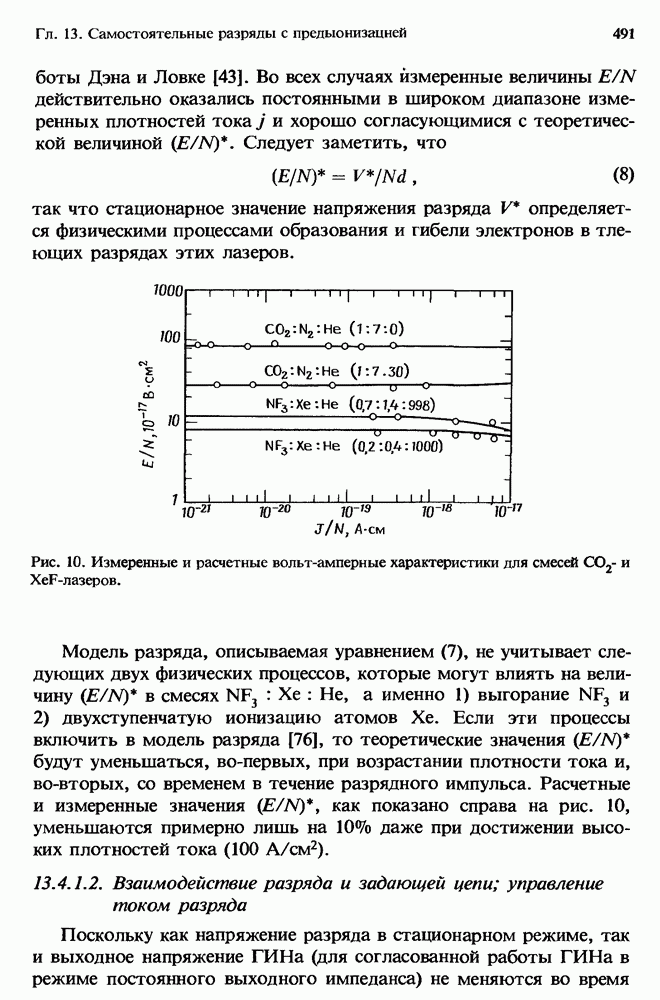
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
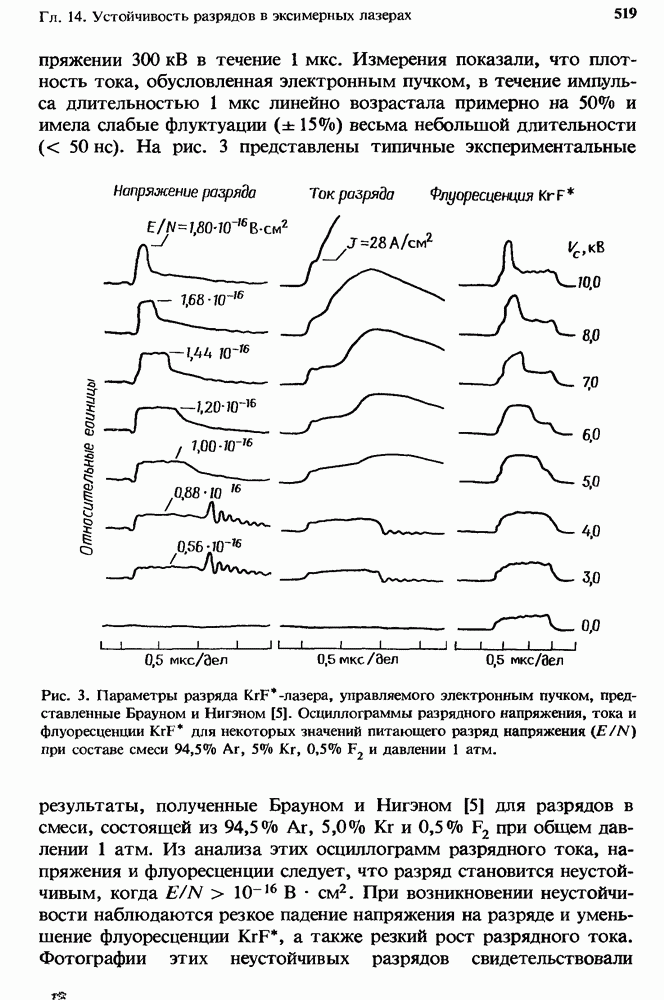
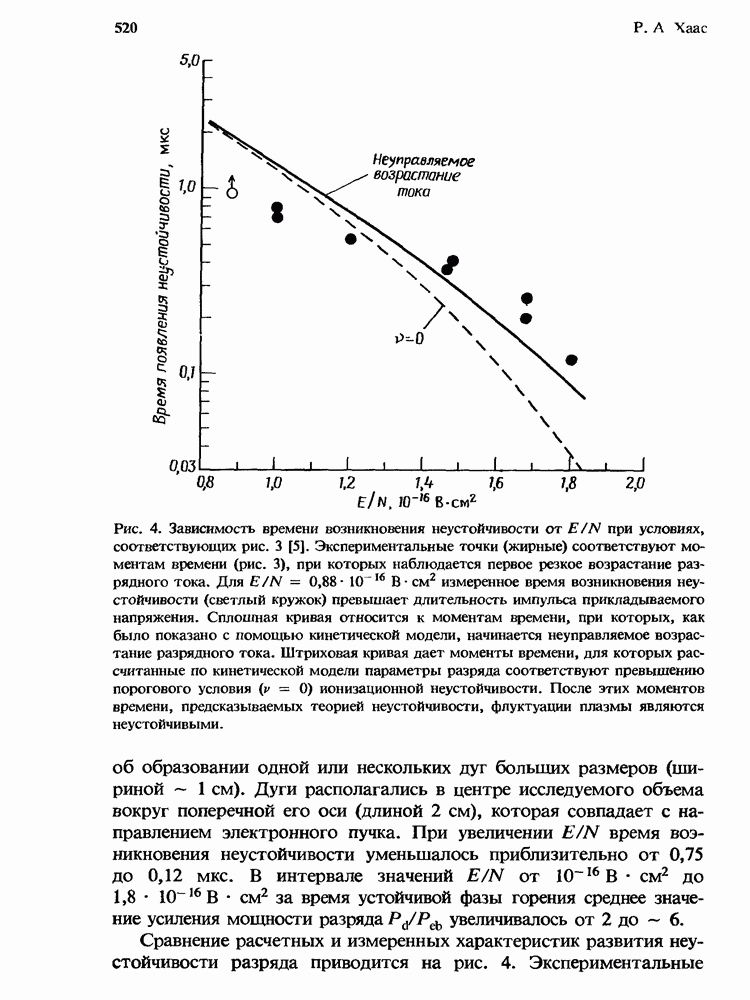
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
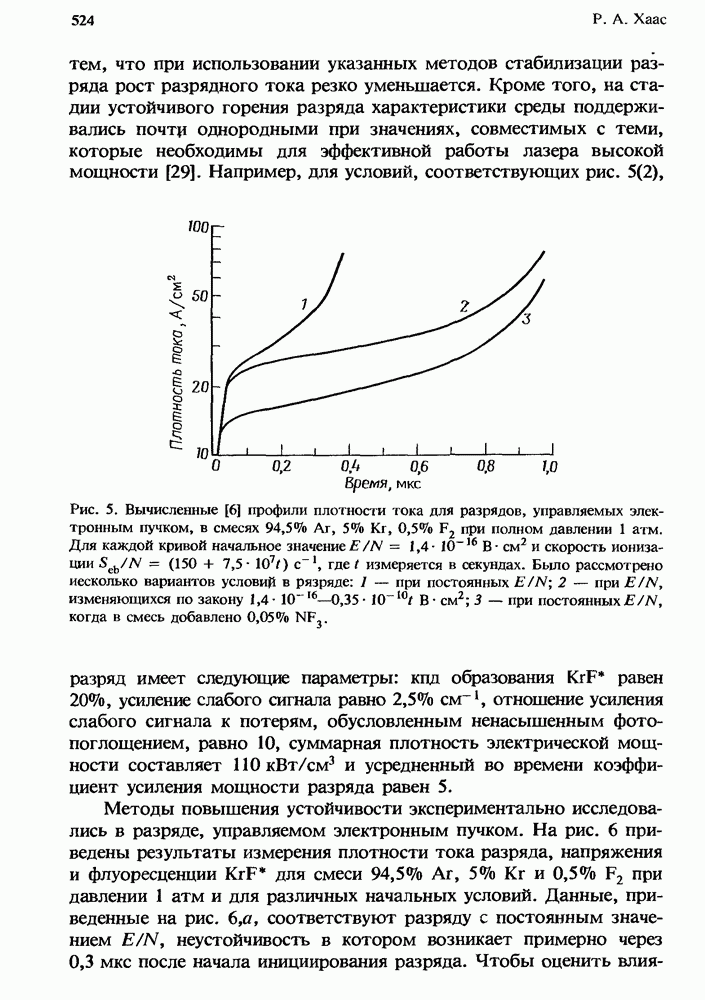
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
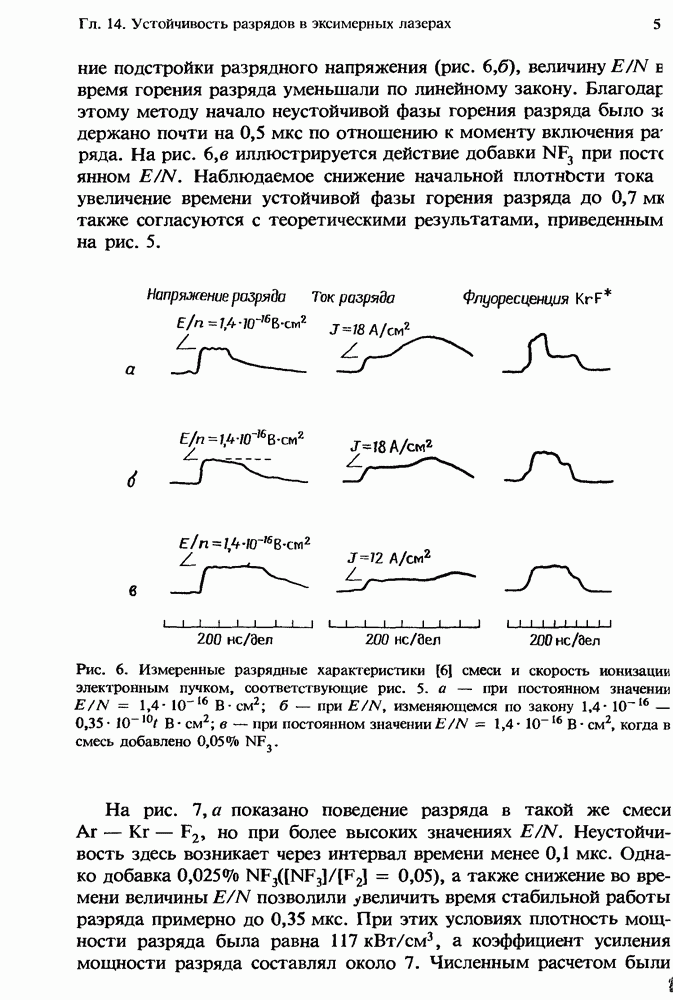
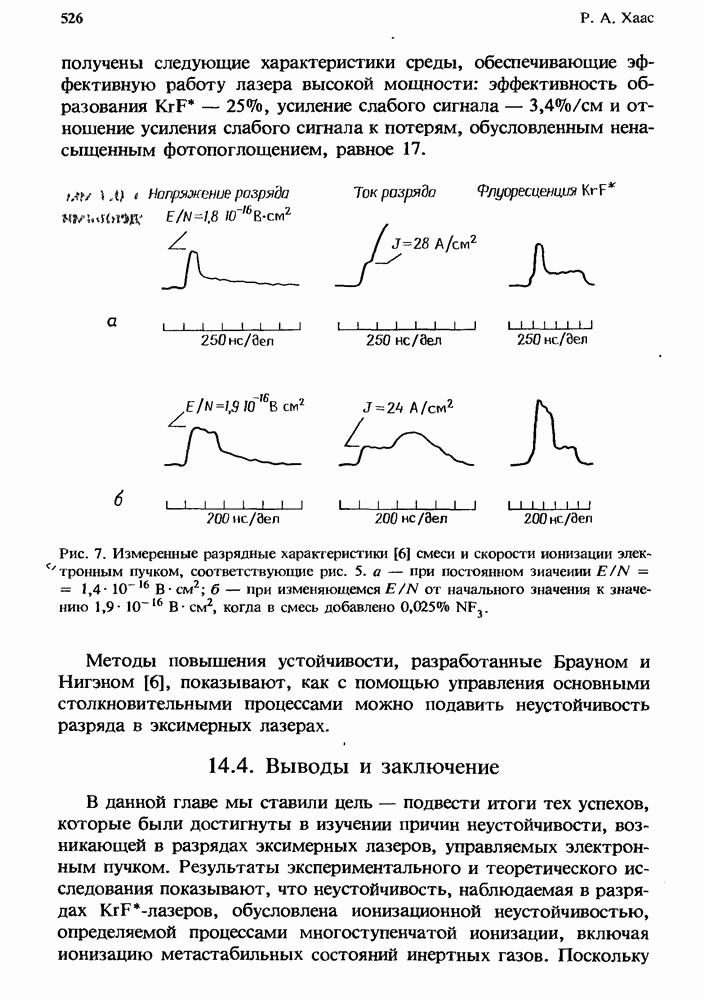
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации