| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.2. Коэффициент рекомбинации как функция плотности газа
5.2.1. Случаи высоких и низких плотностей газа
При высоких плотностях газа  средние длины свободного пробега положительных и отрицательных ионов
средние длины свободного пробега положительных и отрицательных ионов  для положительных ионов и
для положительных ионов и  для отрицательных) исчезающие малы и частота столкновений ионов с нейтралами достаточно высока, так что скорость ион-ионного диффузионного дрейфа
для отрицательных) исчезающие малы и частота столкновений ионов с нейтралами достаточно высока, так что скорость ион-ионного диффузионного дрейфа  находится в равновесии с электростатическим полем и скорость реакции между положительными и отрицательными ионами
находится в равновесии с электростатическим полем и скорость реакции между положительными и отрицательными ионами  ) в газе
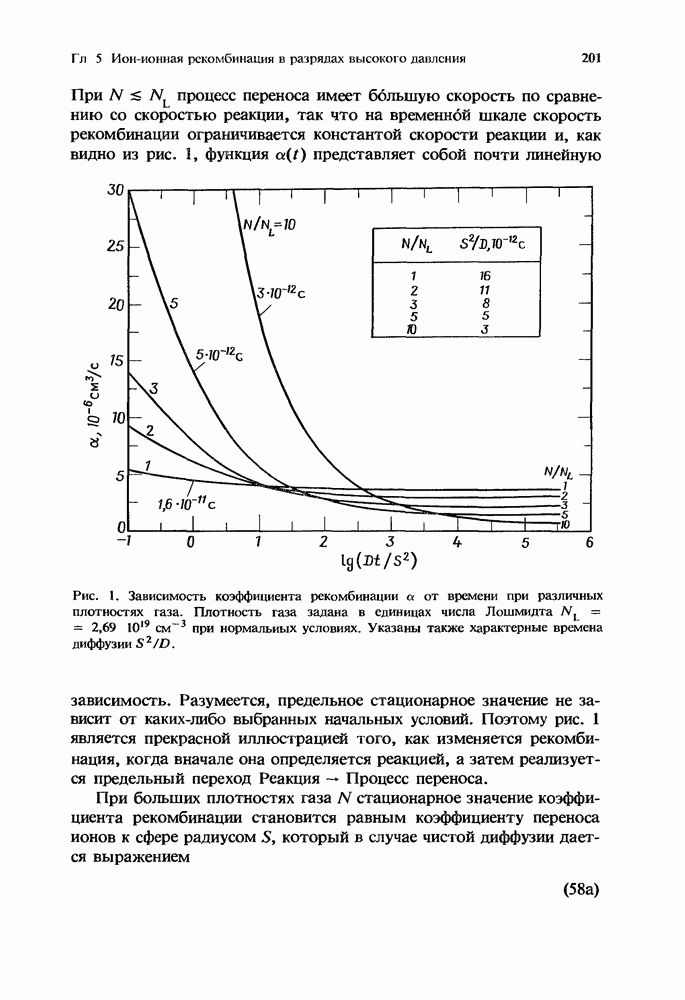
) в газе  можно рассматривать бесконечно большой по сравнению со скоростью переноса ионов. Следовательно, скорость рекомбинации ограничивается скоростью относительного переноса ионов 1 и 2 на расстояние R друг от друга, при котором возникает реакция. Ланжевен [38] связывал процесс переноса исключительно с дрейфом ионов в их собственном кулоновском поле V, что приводит к коэффициенту рекомбинации
можно рассматривать бесконечно большой по сравнению со скоростью переноса ионов. Следовательно, скорость рекомбинации ограничивается скоростью относительного переноса ионов 1 и 2 на расстояние R друг от друга, при котором возникает реакция. Ланжевен [38] связывал процесс переноса исключительно с дрейфом ионов в их собственном кулоновском поле V, что приводит к коэффициенту рекомбинации

где  — относительная подвижность ионов 1 и 2, равная сумме подвижностей каждого из иолов в газе. Харпер [36] считал, что перенос определяется исключительно диффузией, откуда следует коэффициент рекомбинации
— относительная подвижность ионов 1 и 2, равная сумме подвижностей каждого из иолов в газе. Харпер [36] считал, что перенос определяется исключительно диффузией, откуда следует коэффициент рекомбинации

Это выражение с помощью соотношения Эйнштейна  связывающего К и коэффициент взаимной диффузии
связывающего К и коэффициент взаимной диффузии  сводится к выражению (2а) только при
сводится к выражению (2а) только при  Объединив процессы диффузии и дрейфа, Бейтс [4] получил следующее выражение для полного коэффициента рекомбинации:
Объединив процессы диффузии и дрейфа, Бейтс [4] получил следующее выражение для полного коэффициента рекомбинации:

которое при  что соответствует большим значениям
что соответствует большим значениям  совпадает с выражением (2а). В случае потенциала взаимодействия
совпадает с выражением (2а). В случае потенциала взаимодействия  общего вида полный коэффициент переноса с учетом диффузии и дрейфа запишется в виде
общего вида полный коэффициент переноса с учетом диффузии и дрейфа запишется в виде

Отсюда следует, что это выражение совпадает при данном V с выражением (26), полученным Харпером, если в нем заменить R на 
Метод Ланжевена, используемый для вывода выражения (2а), является несовершенным в том смысле, что для очень малых R он дает правильное предельное значение полного коэффициента переноса только для кулоновского взаимодействия, а для всех остальных дальнодействующих потенциалов притяжения он приводит к расходящемуся пределу (см. разд. 5.3.2).
При малых  частота столкновений ионов с нейтралами становится исчезающе малой, так что скорость
частота столкновений ионов с нейтралами становится исчезающе малой, так что скорость  относительного движения становится больше, чем тепловая, и большая часть близких столкновений не приводит к нейтрализации. Если предположить, что рекомбинация возникает в результате отдельных сильных столкновений (когда ион
относительного движения становится больше, чем тепловая, и большая часть близких столкновений не приводит к нейтрализации. Если предположить, что рекомбинация возникает в результате отдельных сильных столкновений (когда ион  сталкивается с нейтралом), происходящих внутри некоторой области захвата с радиусом
сталкивается с нейтралом), происходящих внутри некоторой области захвата с радиусом  и центром, расположенным на другом ионе, то а оказывается линейной функцией от
и центром, расположенным на другом ионе, то а оказывается линейной функцией от  Таким образом, мы имеем
Таким образом, мы имеем

где  — константа равновесия, усредненная по всем энергиям ион-ионных взаимодействий, соответствующих образованию ион-ионных пар с внутренним расстоянием между ионами
— константа равновесия, усредненная по всем энергиям ион-ионных взаимодействий, соответствующих образованию ион-ионных пар с внутренним расстоянием между ионами  — сумма сечений передачи импульса для каждого из столкновений иона с нейтралом. При подходящем выборе величины
— сумма сечений передачи импульса для каждого из столкновений иона с нейтралом. При подходящем выборе величины  выражение (3) будет совпадать с предельным значением а, полученным Томсоном [47] в случае низкой плотности газа. Бейтс, Моффетт и Фланнери [11, 15] первыми разразработали строгую теорию рекомбинации в газе низкой плотности, основанную на микроскопических принципах энергетического обмена. Эта теория на базе рассмотрения квазиравновесной кинетики определила основные пути преобразования внутренней энергии рекомбинирующих ионных пар и дала строгое теоретическое обоснование тому факту, что при низких плотностях величина а, согласно выражению (3), линейно зависит от
выражение (3) будет совпадать с предельным значением а, полученным Томсоном [47] в случае низкой плотности газа. Бейтс, Моффетт и Фланнери [11, 15] первыми разразработали строгую теорию рекомбинации в газе низкой плотности, основанную на микроскопических принципах энергетического обмена. Эта теория на базе рассмотрения квазиравновесной кинетики определила основные пути преобразования внутренней энергии рекомбинирующих ионных пар и дала строгое теоретическое обоснование тому факту, что при низких плотностях величина а, согласно выражению (3), линейно зависит от  Эта теория была далее развита Фланнери [24, 25], в результате чего были получены точные предельные значения а для случая низких плотностей газа [нормированные на значения, найденные с помощью выражения Томсона (3)] и для широкого диапазона масс ионов и нейтралов.
Эта теория была далее развита Фланнери [24, 25], в результате чего были получены точные предельные значения а для случая низких плотностей газа [нормированные на значения, найденные с помощью выражения Томсона (3)] и для широкого диапазона масс ионов и нейтралов.
При увеличении  скорость ионного оттока, описываемая выражением (3), возрастает до такой степени, что ее влияние на плотность ионов
скорость ионного оттока, описываемая выражением (3), возрастает до такой степени, что ее влияние на плотность ионов  находящихся на расстоянии R от центра, становится существенным и должно быть согласовано с
находящихся на расстоянии R от центра, становится существенным и должно быть согласовано с  посредством некоторого уравнения, описывающего диффузионный
посредством некоторого уравнения, описывающего диффузионный
дрейф, который уменьшает время жизни сближающихся ионов. Это приводит к более слабой, чем линейная, общей зависимости а от  и к возможному уменьшению а. Следовательно, при возрастании
и к возможному уменьшению а. Следовательно, при возрастании  константа скорости реакции увеличивается и становится сравнимой в конечном счете с коэффициентом переноса или больше его. Напротив, Томсон [47] предположил, что с ростом
константа скорости реакции увеличивается и становится сравнимой в конечном счете с коэффициентом переноса или больше его. Напротив, Томсон [47] предположил, что с ростом  вероятность
вероятность  эффективных столкновений ионов с нейтралами для ионных пар с
эффективных столкновений ионов с нейтралами для ионных пар с  увеличивается в конечном счете до единицы:
увеличивается в конечном счете до единицы:

где вероятность отдельных столкновений иона с нейтралом (для прямолинейных ион-ионных траекторий) равна

Это выражение сводится к выражению (3) при  однако оно несправедливо при больших
однако оно несправедливо при больших  Бейтс и Мендаш [14] обобщили микроскопический квазиравновесный подход на область нелинейной зависимости от
Бейтс и Мендаш [14] обобщили микроскопический квазиравновесный подход на область нелинейной зависимости от  посредством строгого учета уменьшения числа эффективных столкновений ионов с нейтральными частицами при возрастании плотности среды и получили нелинейный закон для а в соответствии с начальным нелинейным поведением, определяемым выражением (5). Коэффициент рекомбинации а, определяемый выражением (3), представляет собой по существу константу скорости реакции.
посредством строгого учета уменьшения числа эффективных столкновений ионов с нейтральными частицами при возрастании плотности среды и получили нелинейный закон для а в соответствии с начальным нелинейным поведением, определяемым выражением (5). Коэффициент рекомбинации а, определяемый выражением (3), представляет собой по существу константу скорости реакции.
Несостоятельность модели Томсона при больших  обусловлена тем, что в ней пренебрегается [29] как уменьшающимся влиянием ускорений, возникающих в промежутках времени между часто происходящими столкновениями ионов с нейтралами и вызванных межионным полем, так и эффектами, связанными с подвижностью и определяемыми требованием сохранения термодинамического равновесия в отсутствие источников и стоков. Кроме того, модель Томсона при больших
обусловлена тем, что в ней пренебрегается [29] как уменьшающимся влиянием ускорений, возникающих в промежутках времени между часто происходящими столкновениями ионов с нейтралами и вызванных межионным полем, так и эффектами, связанными с подвижностью и определяемыми требованием сохранения термодинамического равновесия в отсутствие источников и стоков. Кроме того, модель Томсона при больших  не справедлива также и потому, что в ней явно пренебрегается диффузией ионов в области, примыкающей к реакционной сфере радиусом
не справедлива также и потому, что в ней явно пренебрегается диффузией ионов в области, примыкающей к реакционной сфере радиусом  хотя в выражении (5) подразумевается неявное влияние диффузии на протекание реакций энергетического обмена. Оба этих эффекта, которые определяют процесс переноса ионов в фазовом пространстве, естественным образом вытекают из фундаментальной теории Фланнери [27, 29], изложенной кратко в разд. 5.3.
хотя в выражении (5) подразумевается неявное влияние диффузии на протекание реакций энергетического обмена. Оба этих эффекта, которые определяют процесс переноса ионов в фазовом пространстве, естественным образом вытекают из фундаментальной теории Фланнери [27, 29], изложенной кратко в разд. 5.3.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
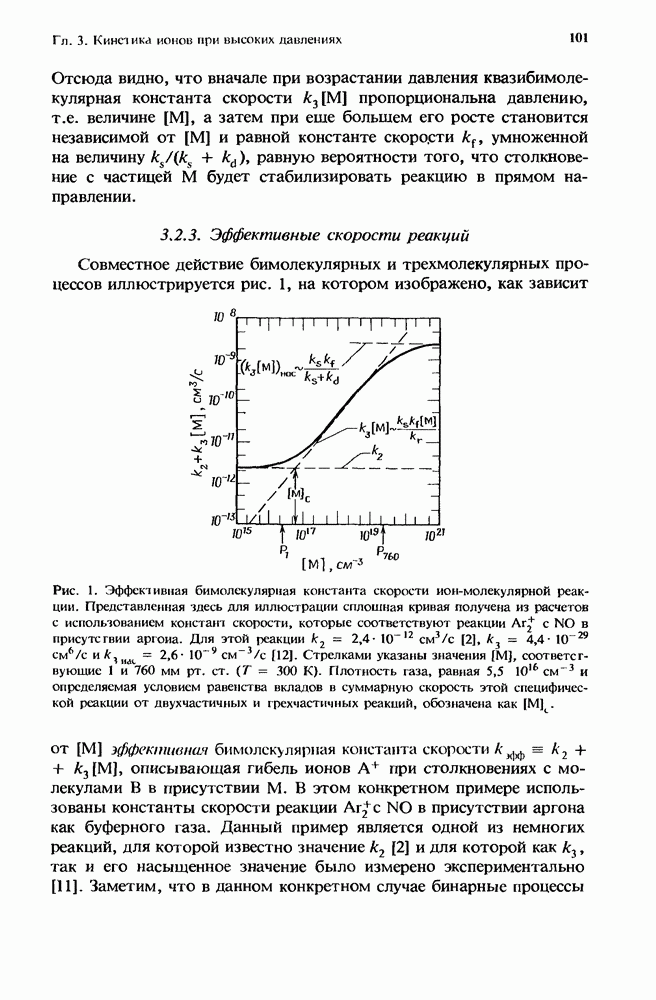
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
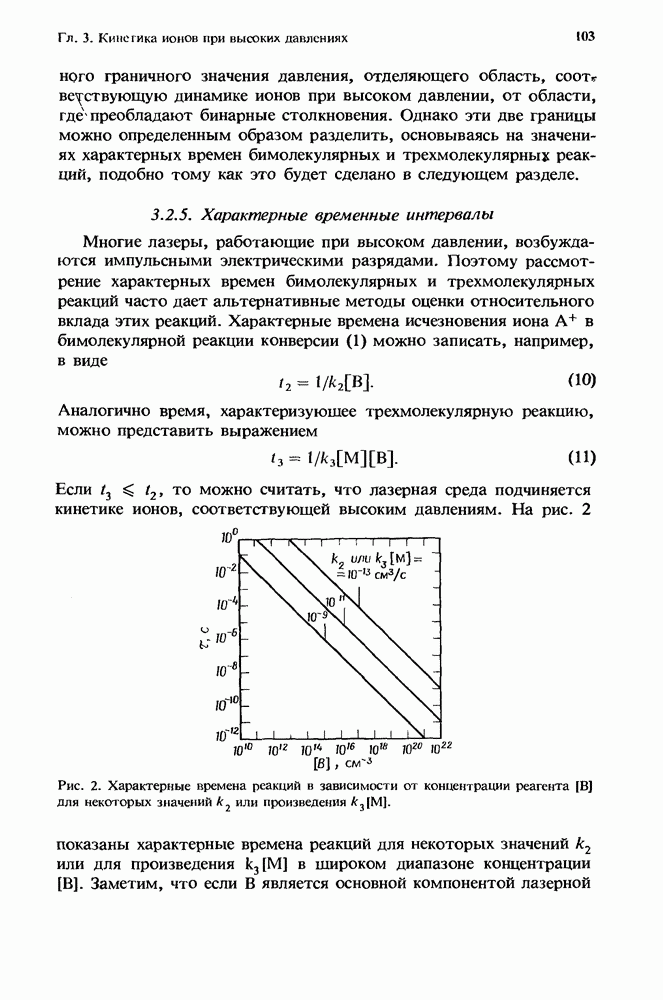
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации