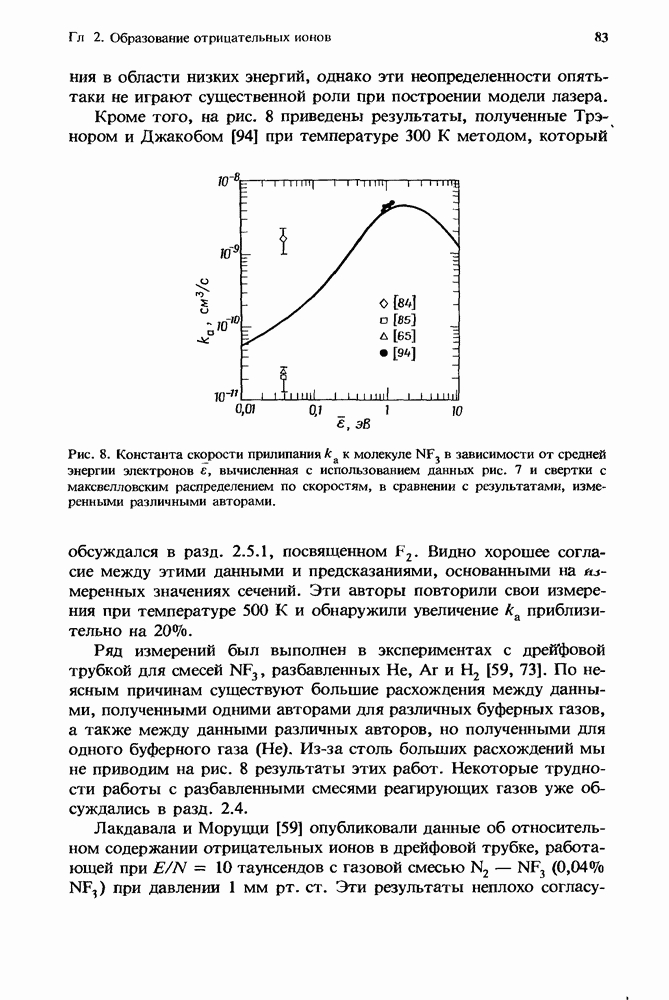
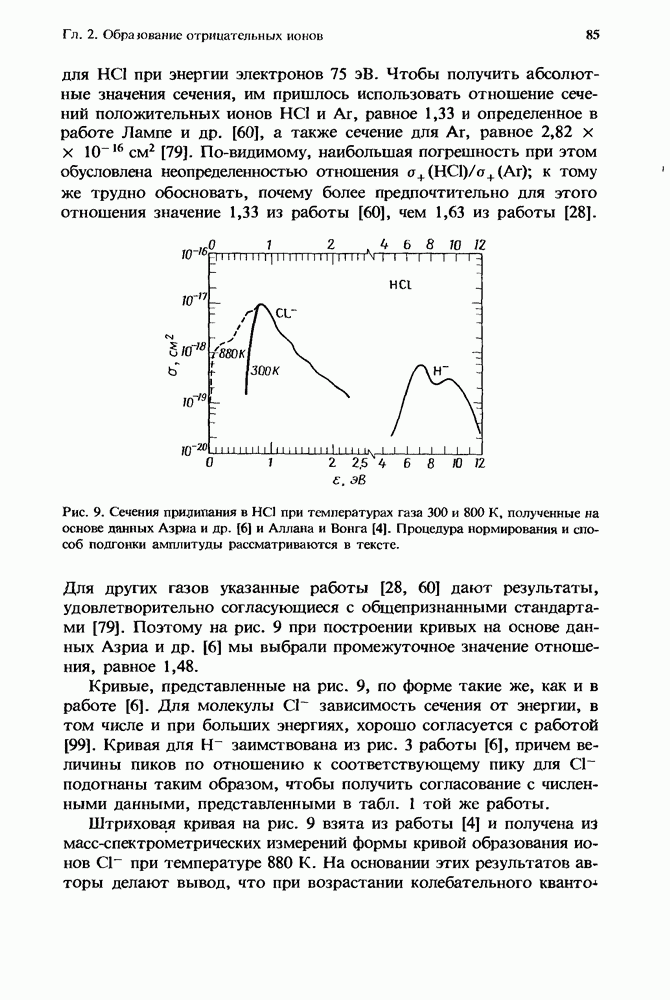
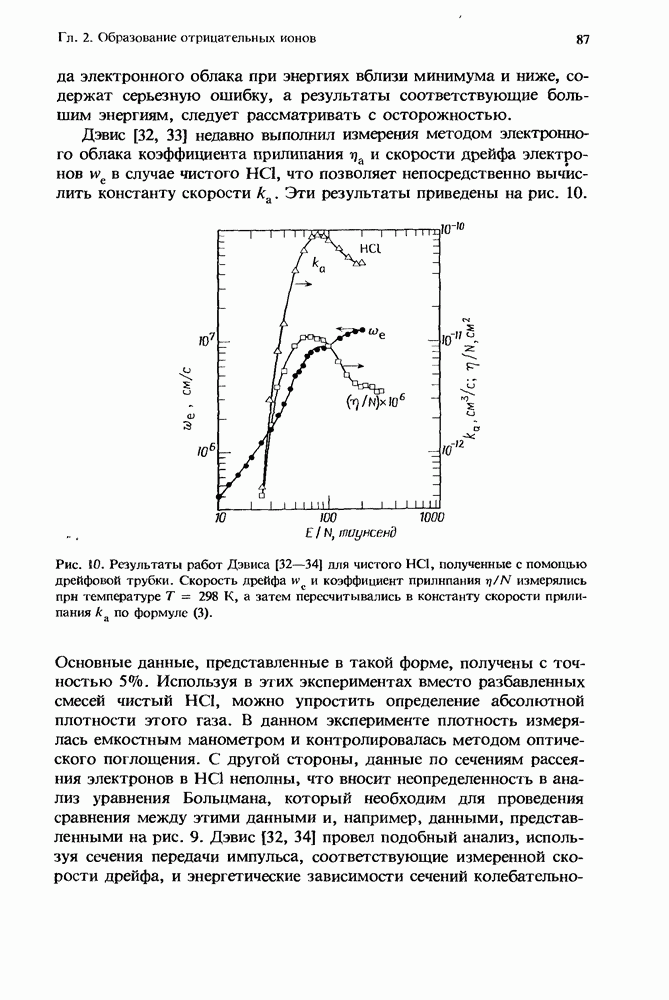
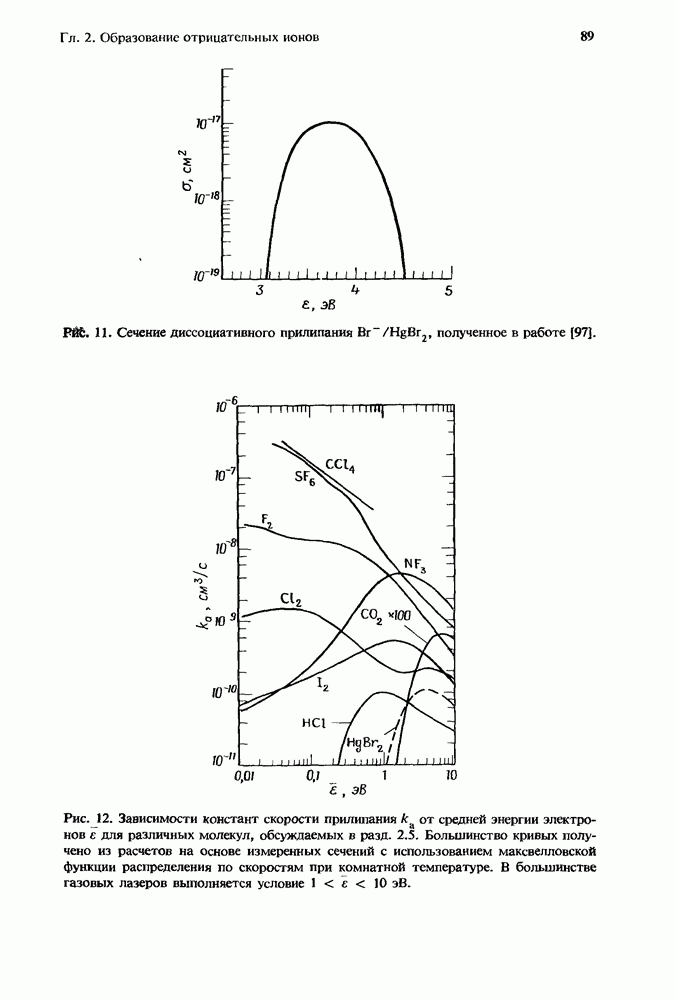
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
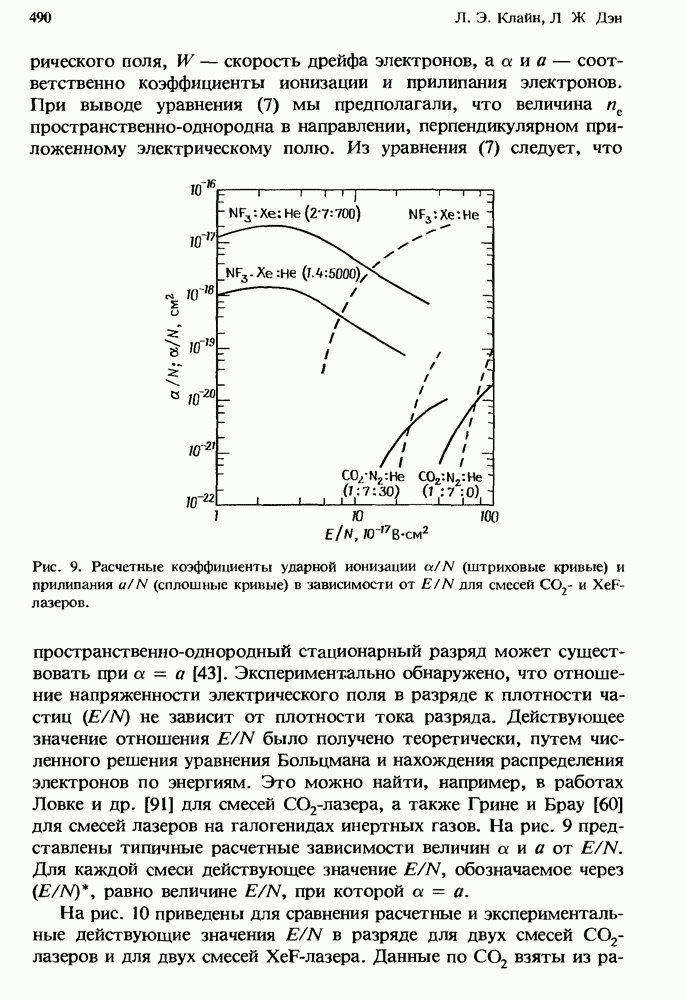
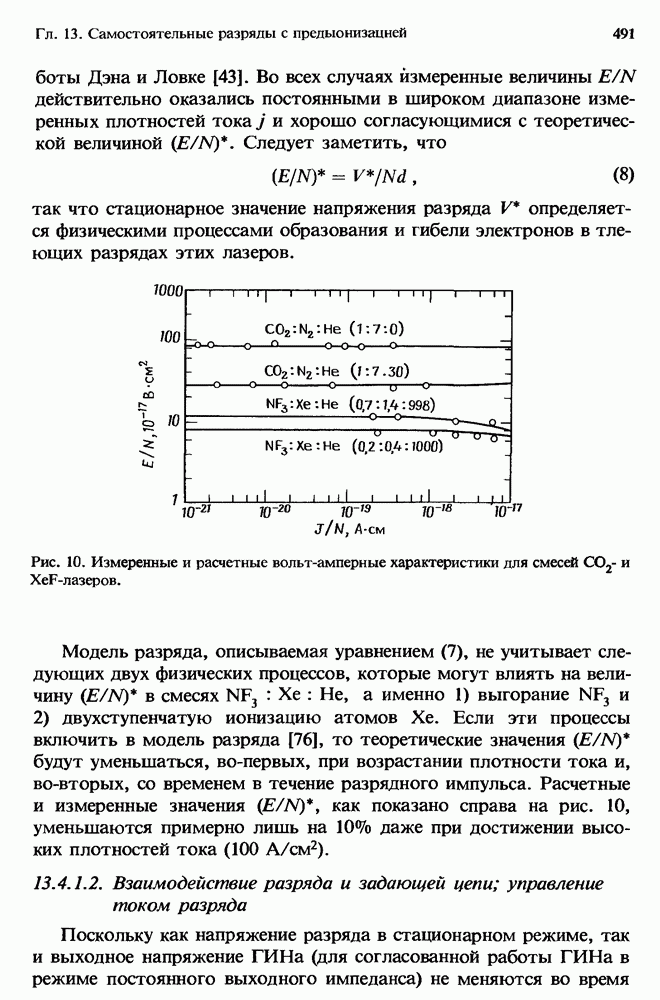
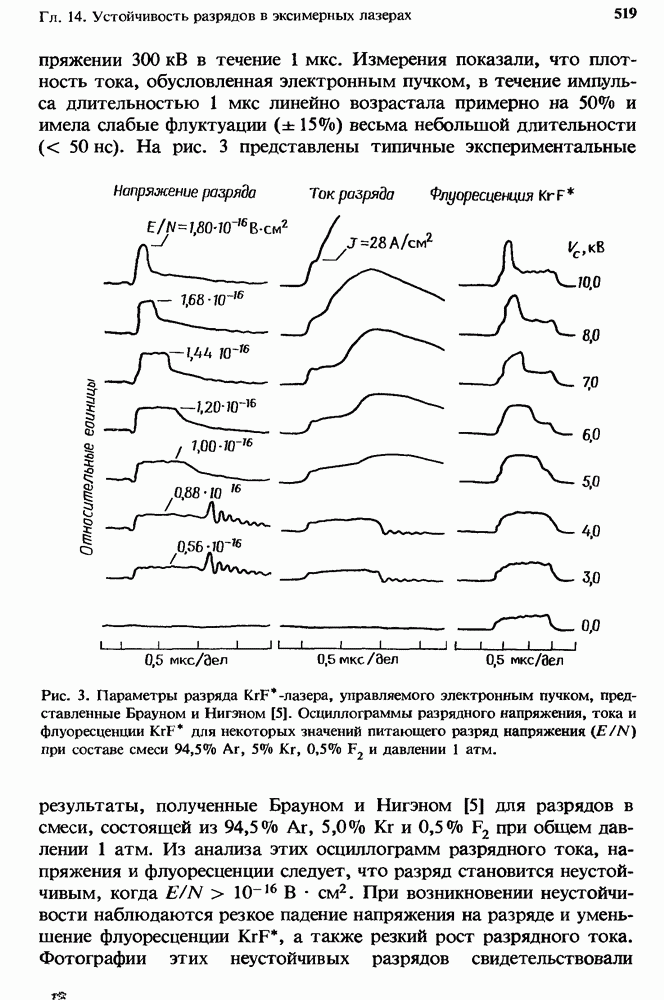
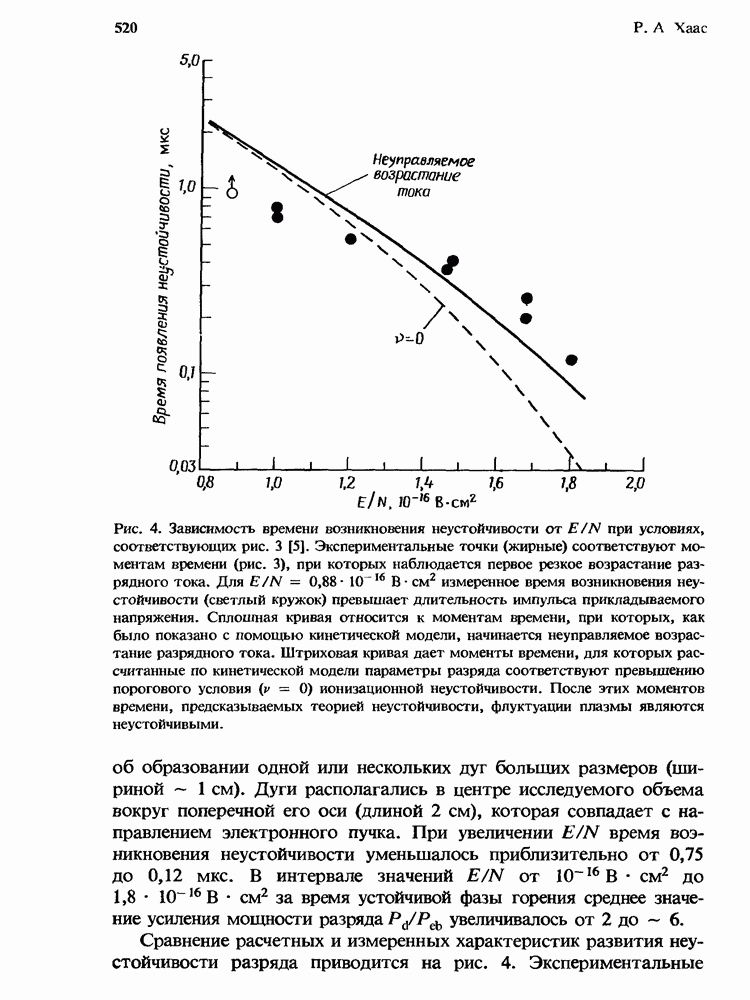
12.5. Однородно распределенные потери
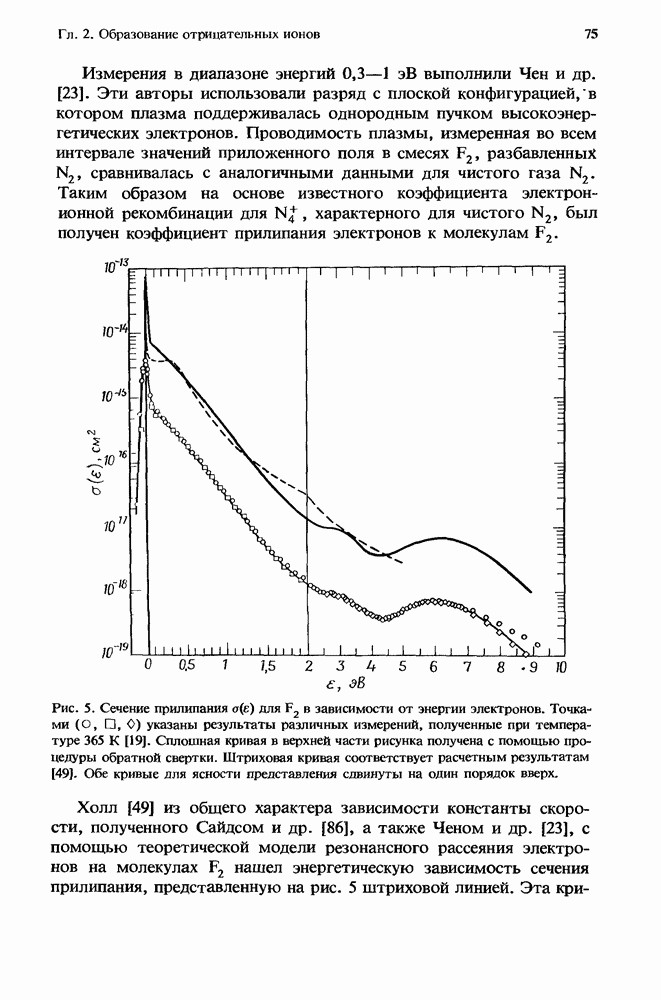
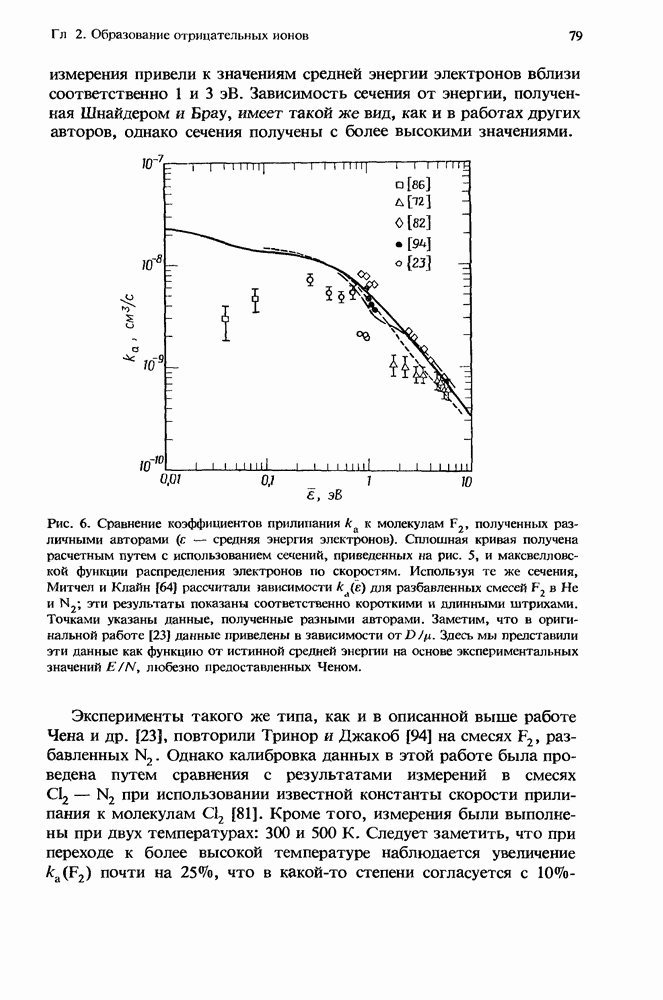
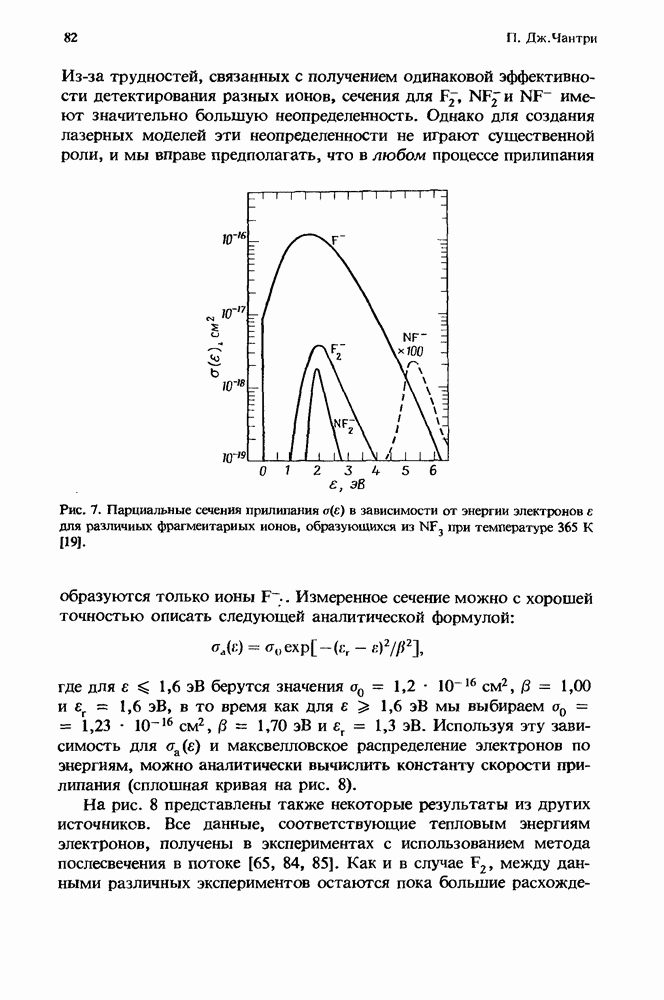
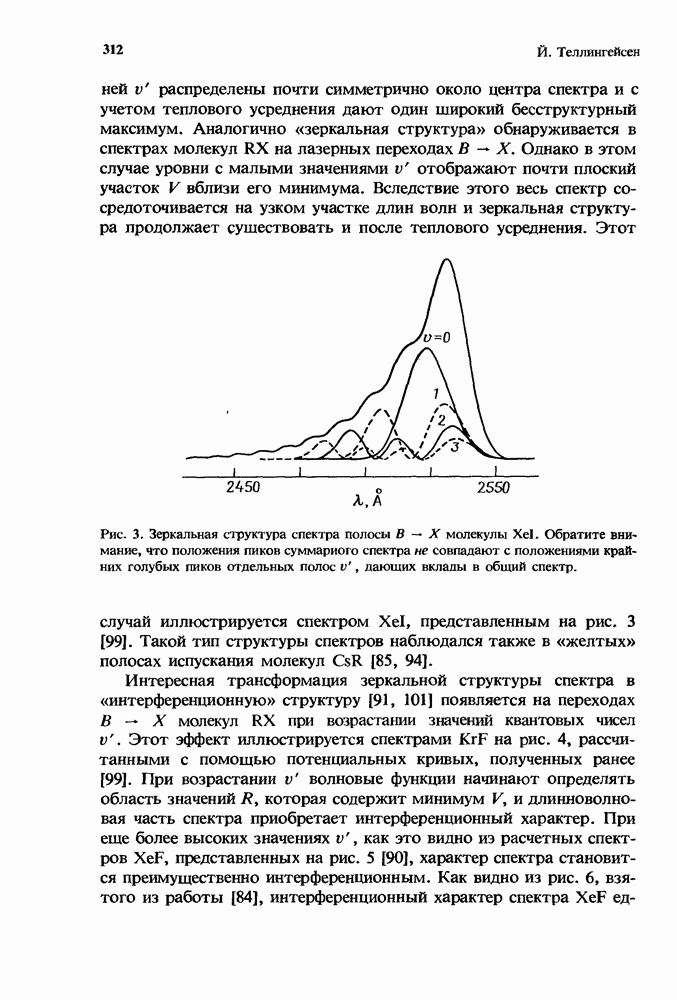
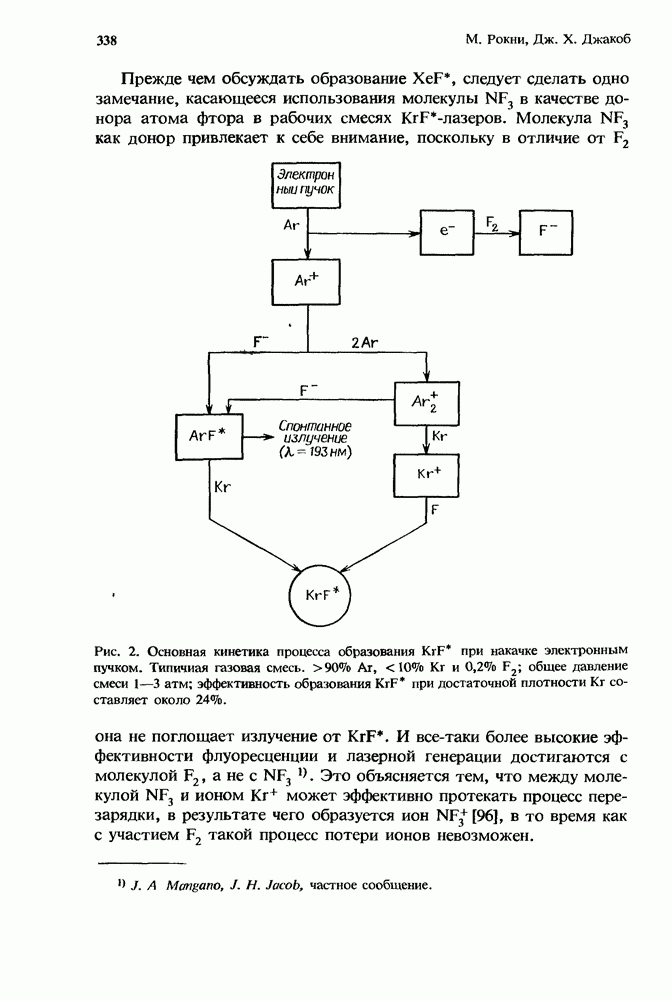
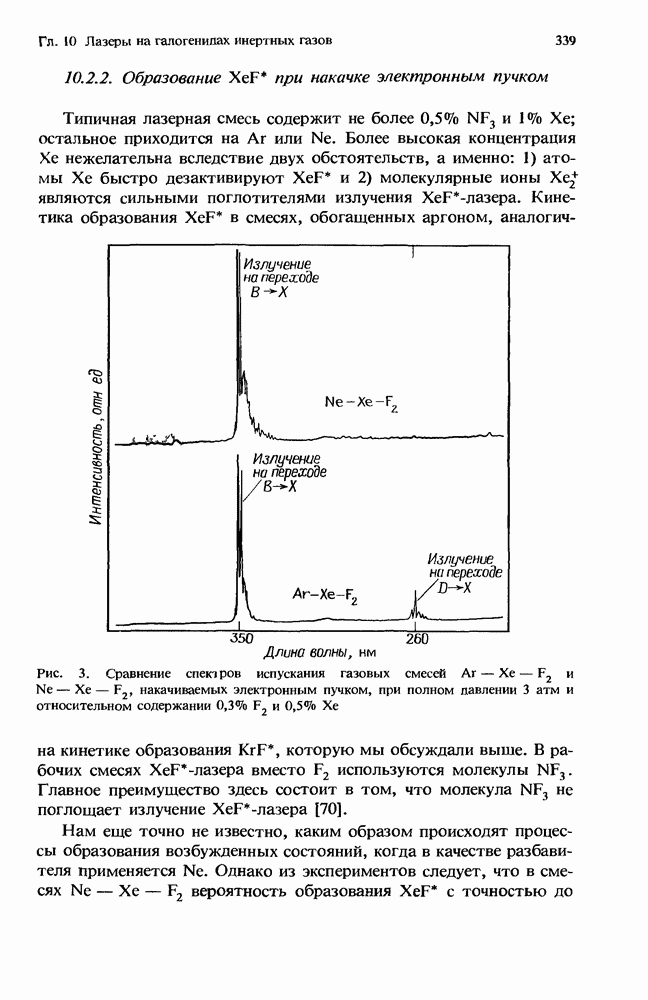
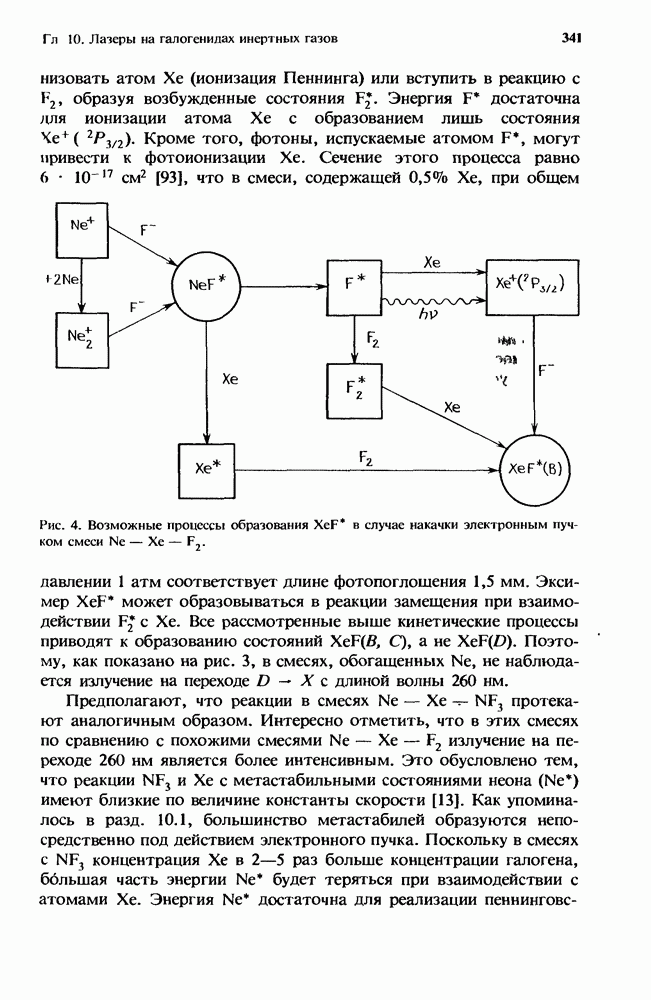
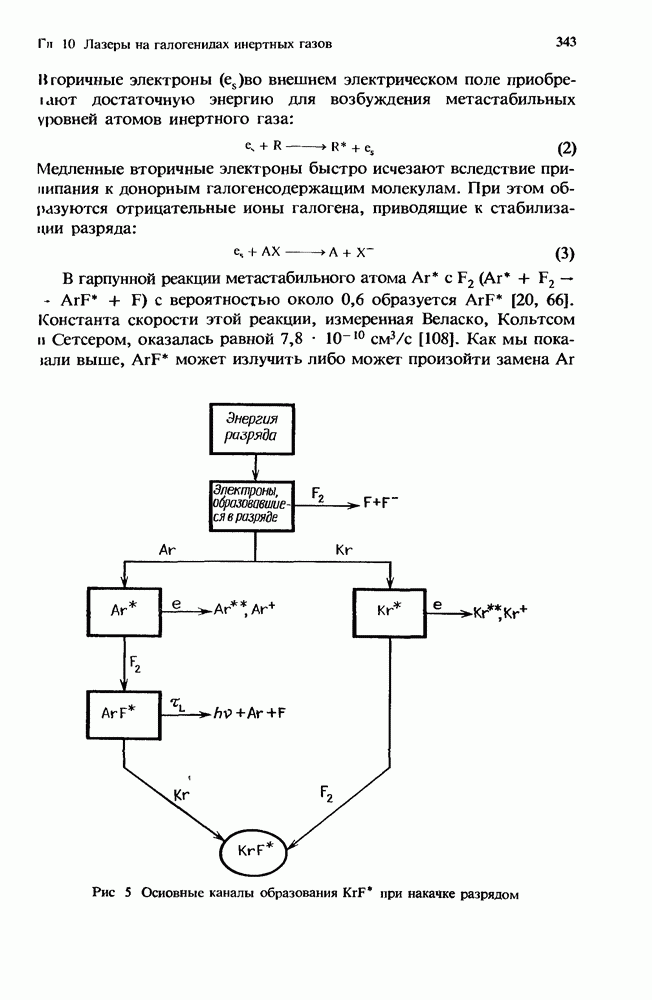
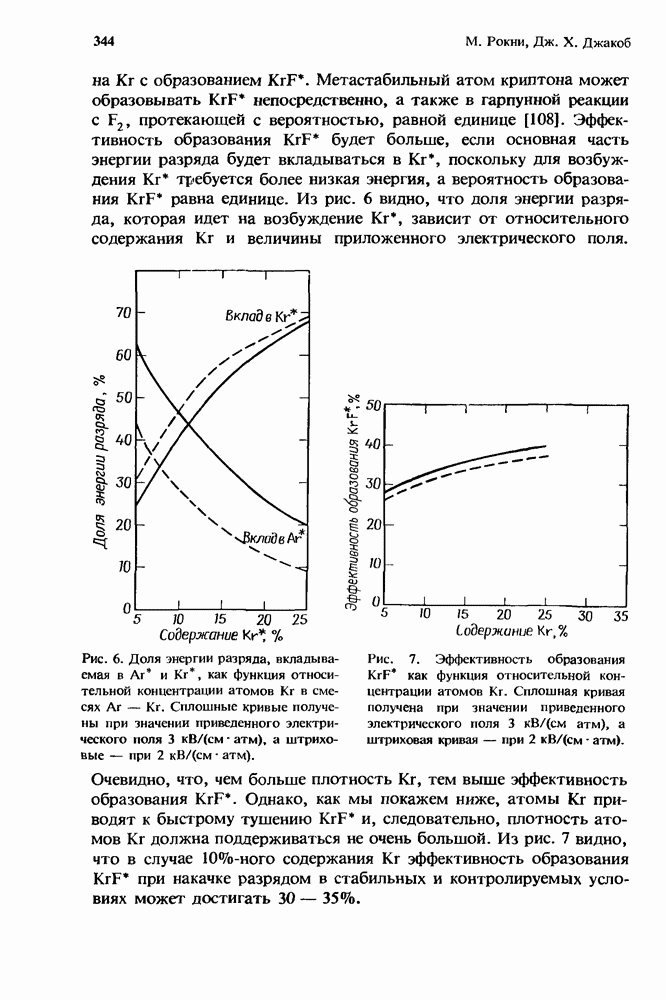
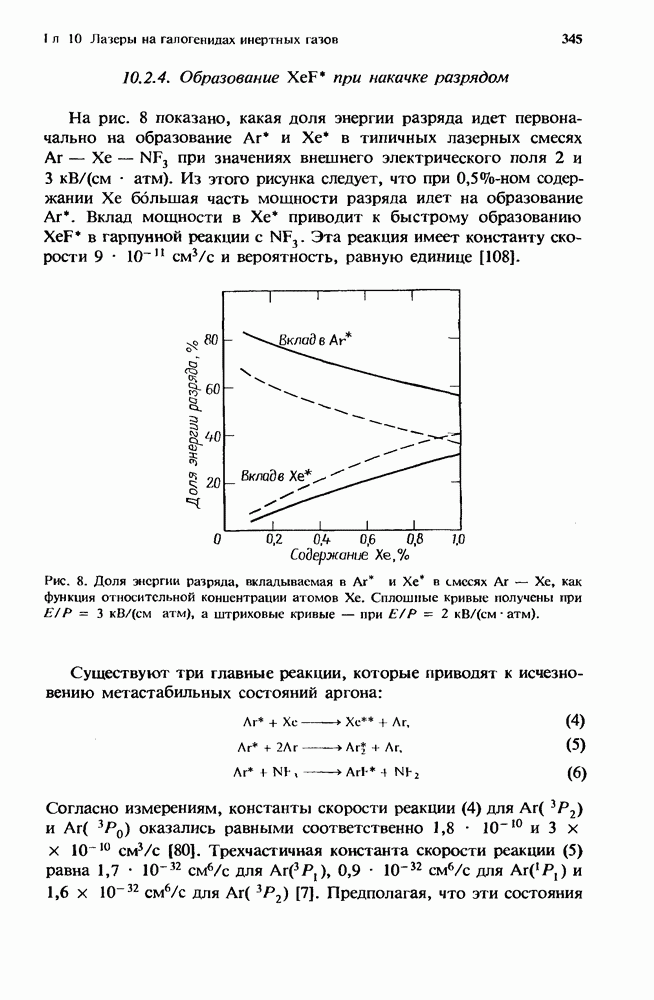
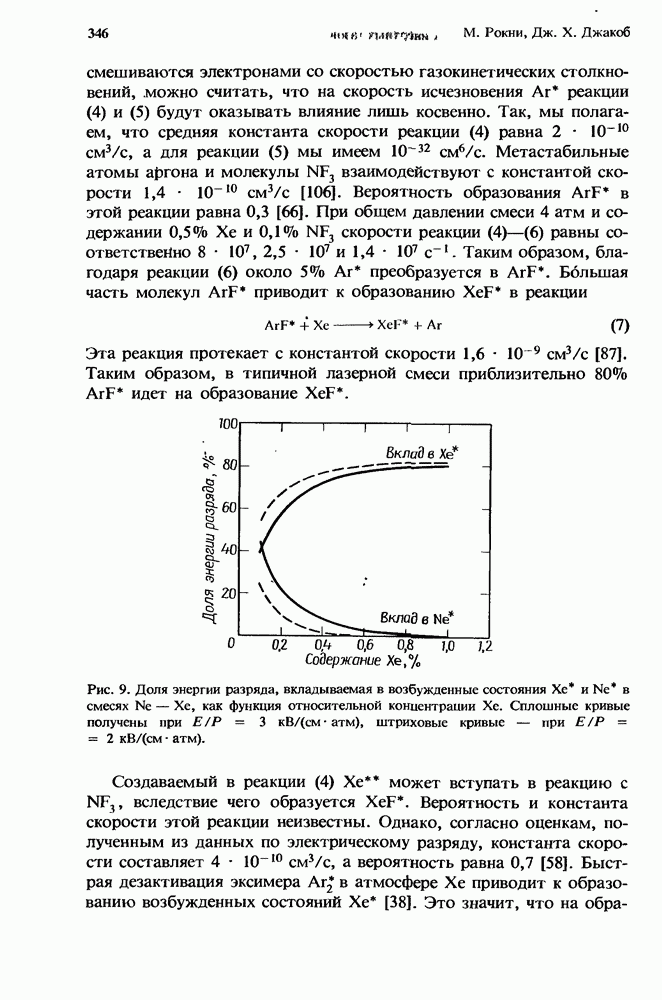
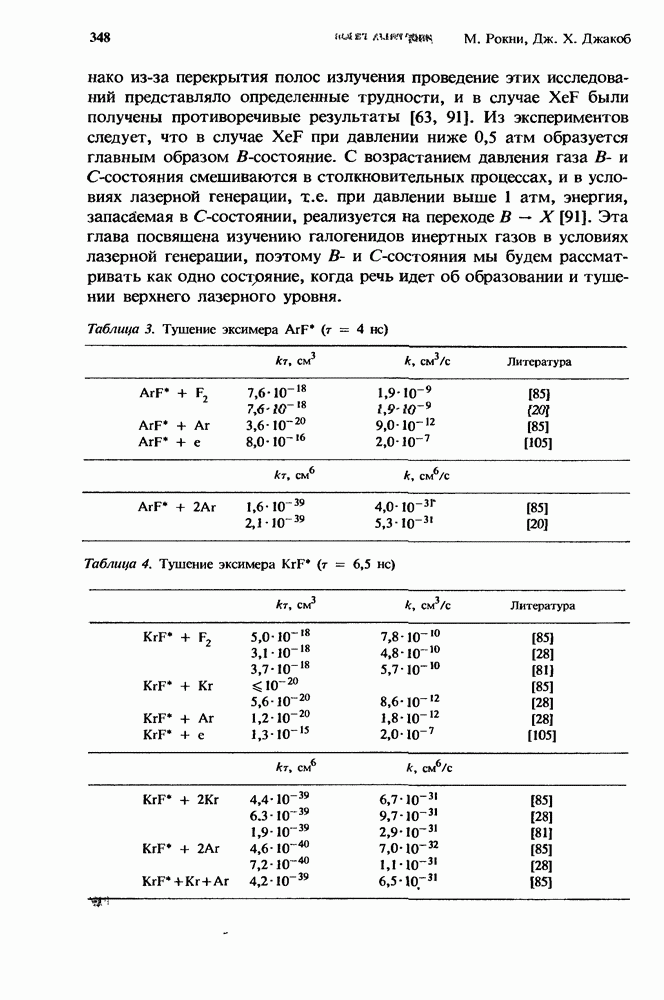
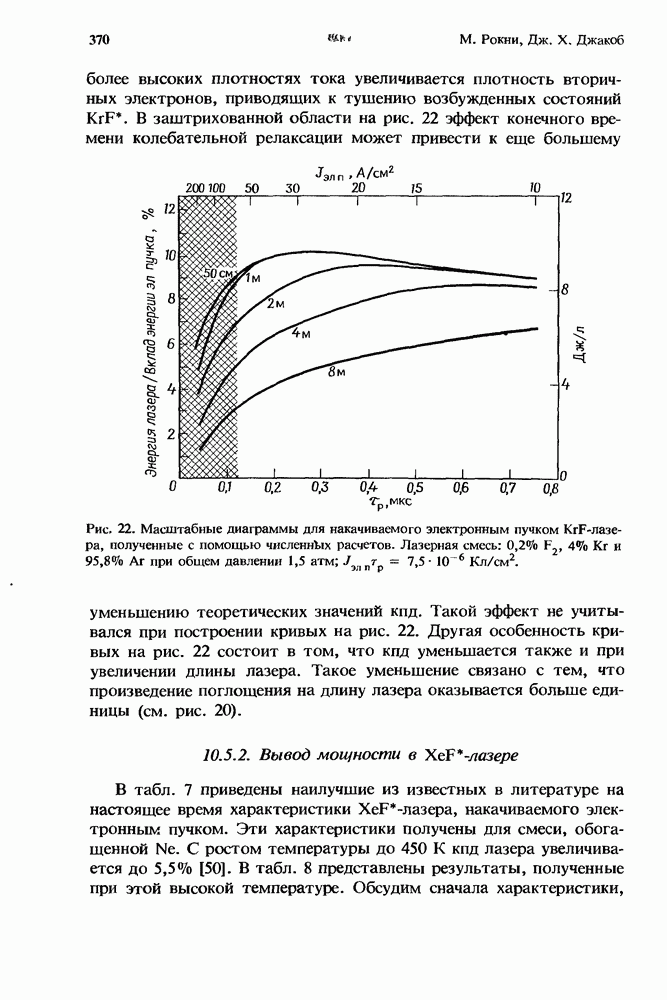
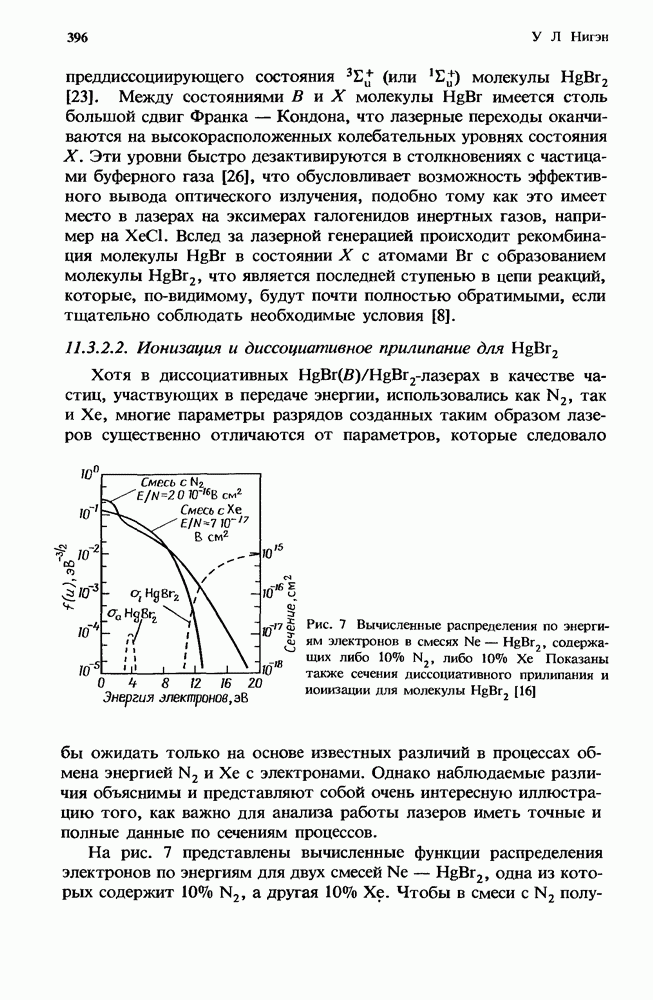
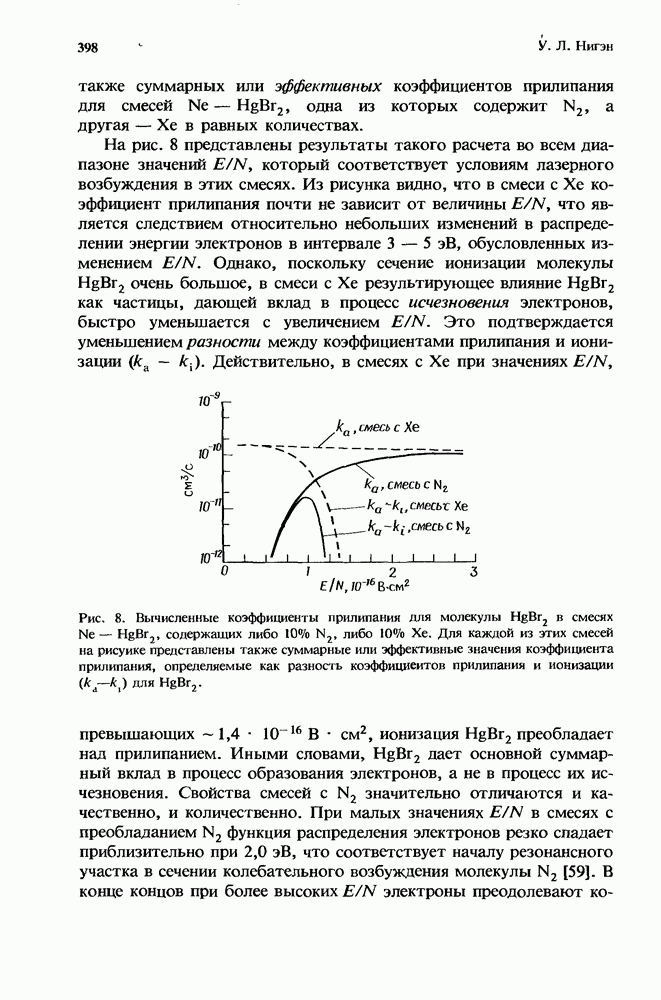
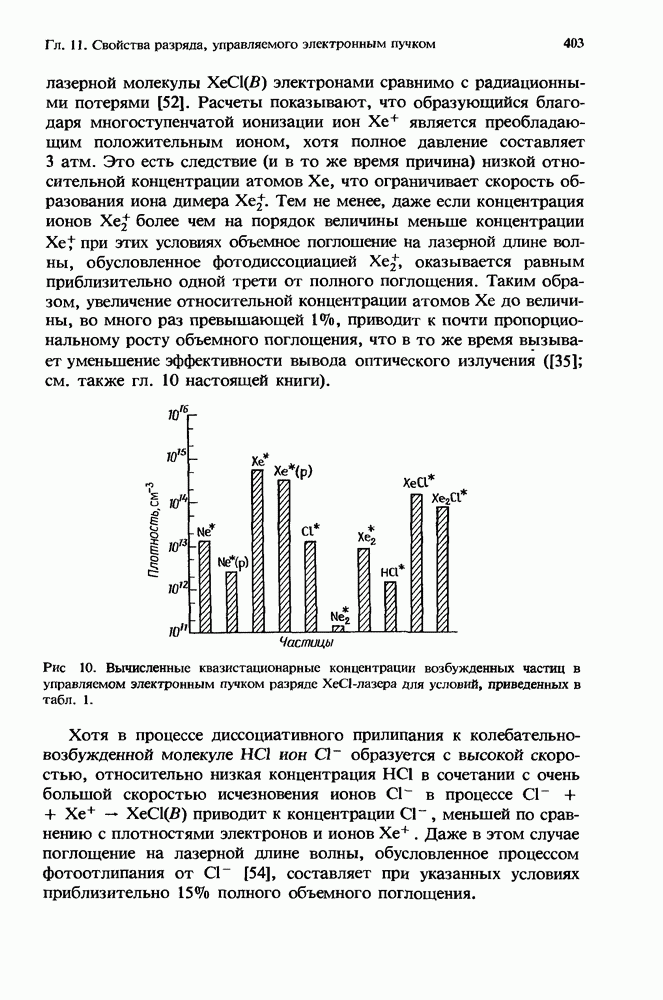
Первый грубый расчет [13] характеристик лазера с высоким усилением в присутствии нестационарного поглощения уже давно заменен простым, но все же достаточно точным приближением, справедливым для систем небольших размеров (разд. 12.5.2). Эта модель позволяет получить решение как аналитически, так и численными методами (разд. 12.5.3). При масштабировании лазеров с целью перехода к высоким средним мощностям (разд. 12.5.4) применяются сложные, но более точные численные модели.
Ригрод [48] вывел выражения, которые описывают эффекты насыщения в лазерах (как с низким, так и с высоким усилением [49]), имеющих однородно уширенные спектры. Шульц-Дюбуа [54] получил точное решение для лазера с однородным уширением, который имеет как высокое усиление, так и однородно распределенные потери. Однако трансцендентное решение трудно получить в аналитической форме, и эта задача представляет собой значительную проблему при преобразовании ее к форме, подходящей для проведен и  численного решения с помощью ЭВМ.
численного решения с помощью ЭВМ.
12.5.1. Точное решение
Пусть в одномерном лазере с однородно уширенной линией, имеющем ненасыщенный коэффициент усиления с) 0 и постоянный коэффициент потерь «0, нормированные интенсивности поля излучения, распространяющегося в направлениях  и
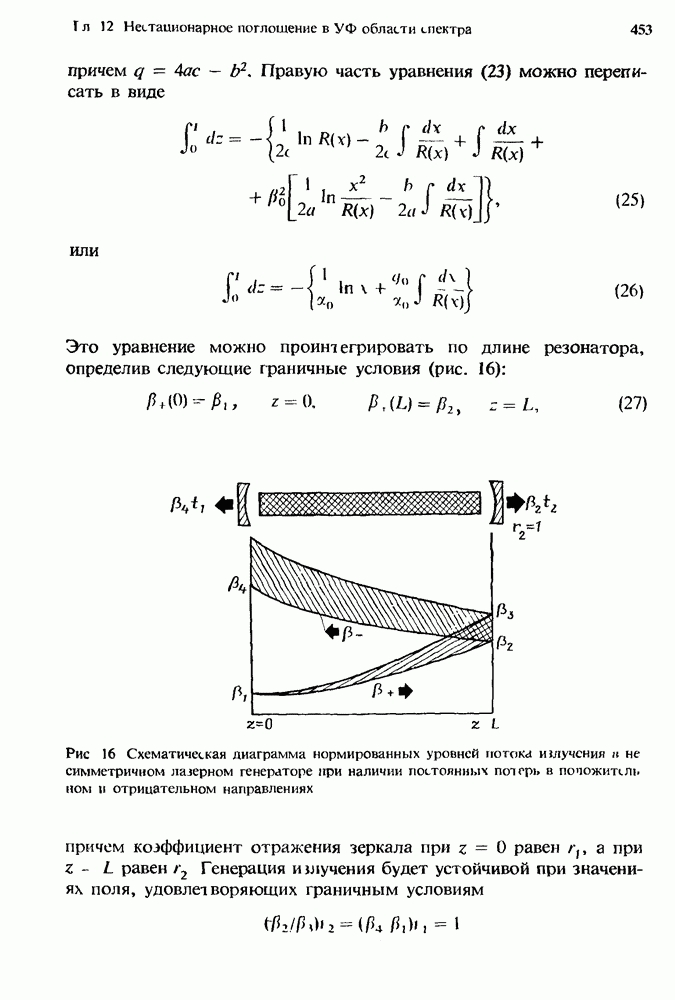
и  лазерного генератора, равны соответственно (рис. 16)
лазерного генератора, равны соответственно (рис. 16)

Здесь  — насыщающая интенсивность поля. Насыщенный коэффициент усиления связан с ненасыщенным коэффициентом усиления
— насыщающая интенсивность поля. Насыщенный коэффициент усиления связан с ненасыщенным коэффициентом усиления  постоянным коэффициентом потерь «0 соотношением
постоянным коэффициентом потерь «0 соотношением

Коэффициент усиления является изотропным:

откуда следует, что

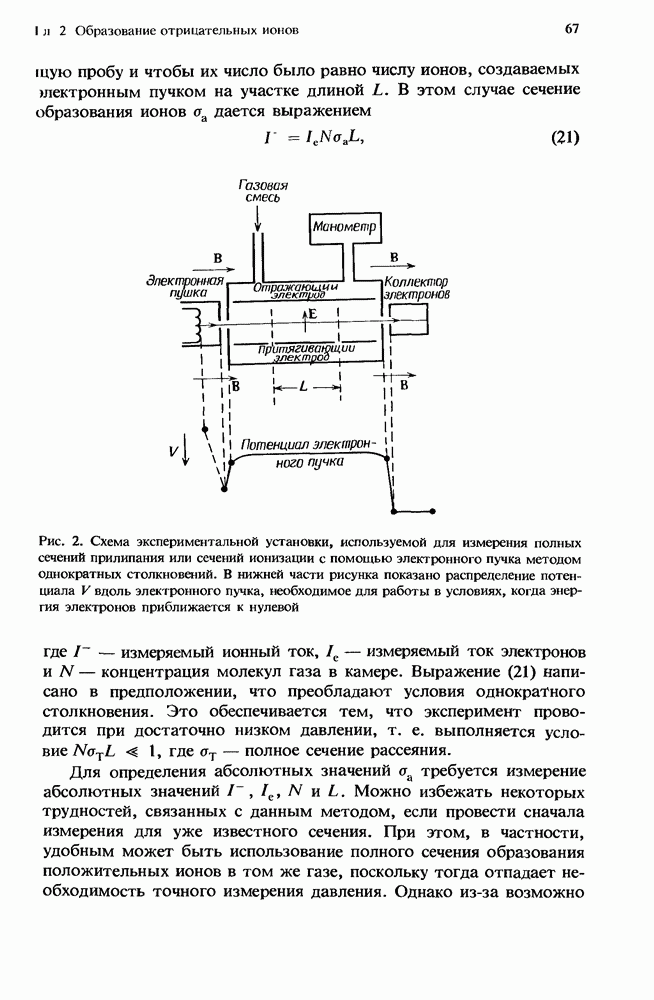
Подставляя в (15) выражение (16), получаем

Разделяя переменные, находим

или

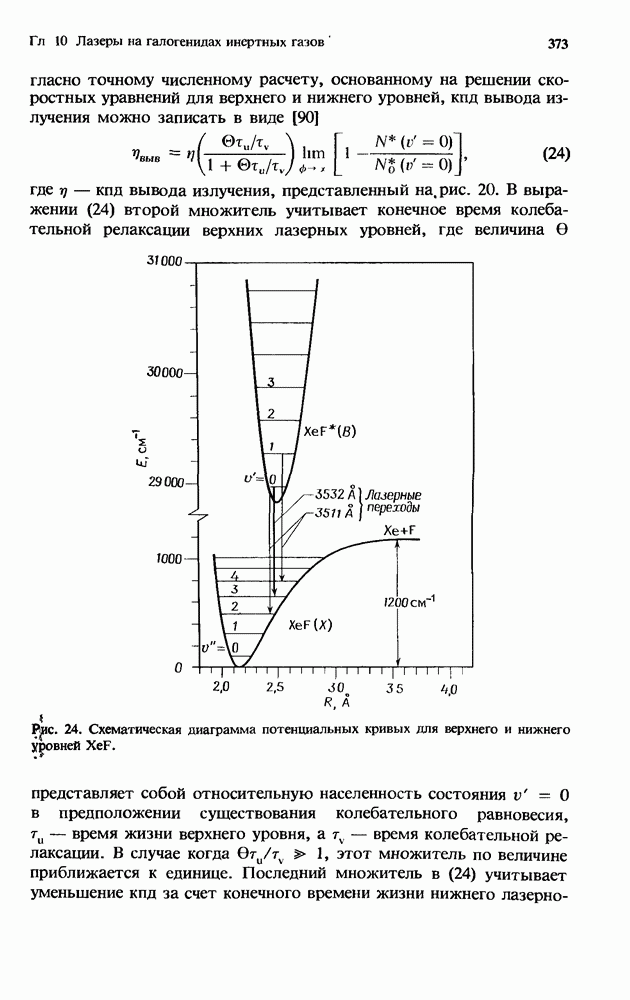
Уравнение (20) можно упростить, используя следующие подстановки:

Подставляя эти выражения в (20), имеем

Интегрируя по длине резонатора, уравнение (22) можно переписать в виде

Эти интегралы содержат члены  в которых
в которых  имеет вид
имеет вид

причем  Правую часть уравнения (23) можно переписать в виде
Правую часть уравнения (23) можно переписать в виде

или


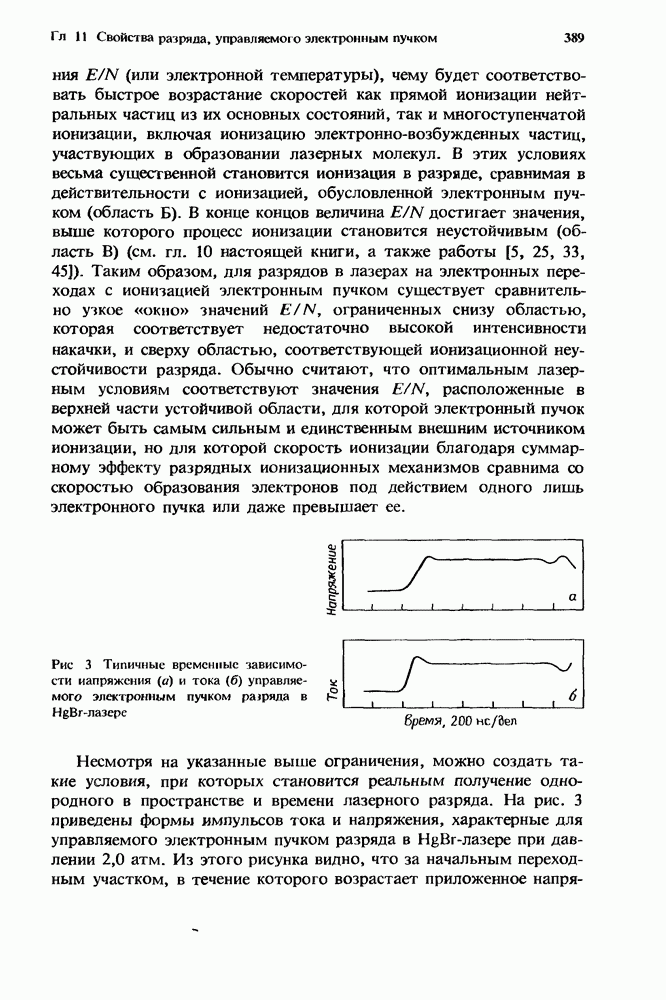
Рис. 16 Схематическая диаграмма нормированных уровней потока излучения  не симметричном лазерном генераторе при наличии постоянных потерь в положительном и отрицательном направлениях
не симметричном лазерном генераторе при наличии постоянных потерь в положительном и отрицательном направлениях
Это уравнение можно проинтегрировать по длине резонатора, определив следующие граничные условия (рис. 16):

причем коэффициент отражения зеркала при  равен
равен  а при
а при  равен
равен  Генерация излучения будет устойчивой при значениях поля, удовлетворяющих граничным условиям
Генерация излучения будет устойчивой при значениях поля, удовлетворяющих граничным условиям

Заметив 

получим

Интеграл

Имеет несколько значений, которые зависят от выбора величины  Потребуем, чтобы выполнялось условие
Потребуем, чтобы выполнялось условие

Интегрирование уравнения (26) приводит к выражению

здесь

Точное решение, задаваемое уравнением (31), трудно получить в аналитической форме; его нельзя свести к простому выражению, которое бы описывало работу лазера, имеющего однородно уширенную линию, в отсутствие поглощения средой  Само собой не очевидно, что выражение (31) сводится к пороговому условию возникновения генерации
Само собой не очевидно, что выражение (31) сводится к пороговому условию возникновения генерации

Макроскопические параметры, используемые для описания работы лазера, такие, как мощность, выводимая из лазерного резонатора  или приведенная интенсивность излучения
или приведенная интенсивность излучения  довольно трудно получить из уравнения (31).
довольно трудно получить из уравнения (31).
Мощность пучка, выводимого из резонатора и имеющего площадь А, определяется выражением

где приведенная полная интенсивность излучения (30 равна (рис. 16)

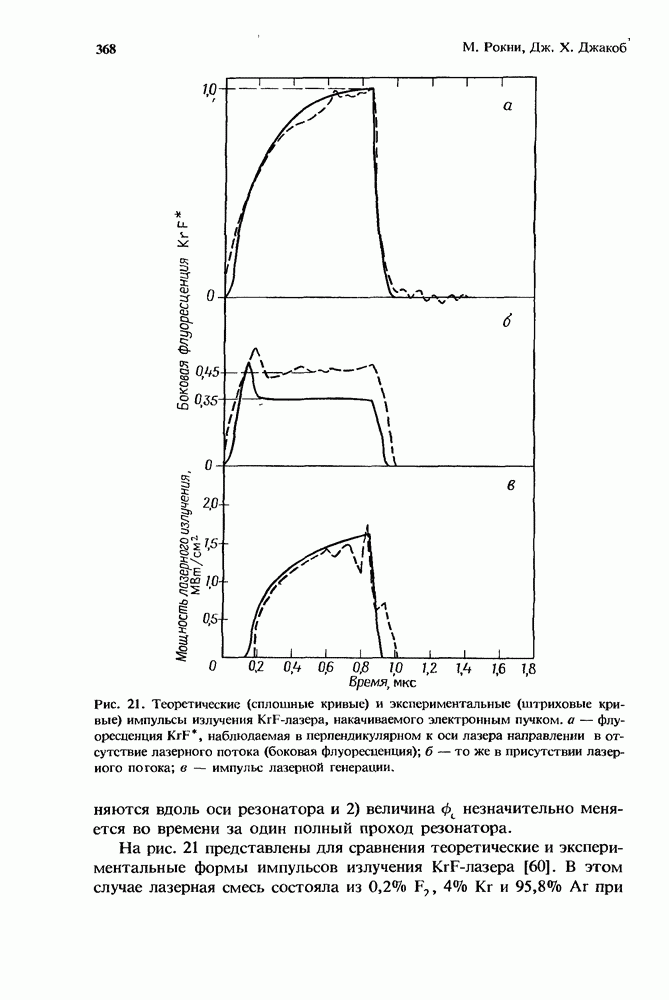
Кпд лазера определяется как отношение реальной выходной мощности (34) к максимальному возможному значению выходной мощности. Вспомним, что, как было указано в разд. 12.4, флуоресценция, наблюдаемая вдоль оптической оси, сравнима по величине с флуоресценцией в боковом направлении. Флуоресценция вдоль оптической оси соответствует реальной выходной мощности. Наблюдение флуоресценции сбоку — это способ регистрации, при котором проявления всех процессов радиационных потерь, таких, как рассеяние и поглощение, сводится до минимума. В идеальном эксперименте все потери должны быть исключены из рассмотрения, так что выходную мощность излучения, испускаемого объемом V, в этом случае можно записать в виде

где I — интенсивность. При отсутствии всех видов поглощения, кроме тех, которые связаны с самим лазерным переходом, имеем

В идеальном случае максимальная выходная мощность реализуется, когда все потери (радиационные и нерадиационные) близки к нулю. В этом случае интенсивность I стремится к бесконечности и мы можем напигать следующее выражение:

Таким образом, кпд лазера  запишется в виде
запишется в виде

где  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
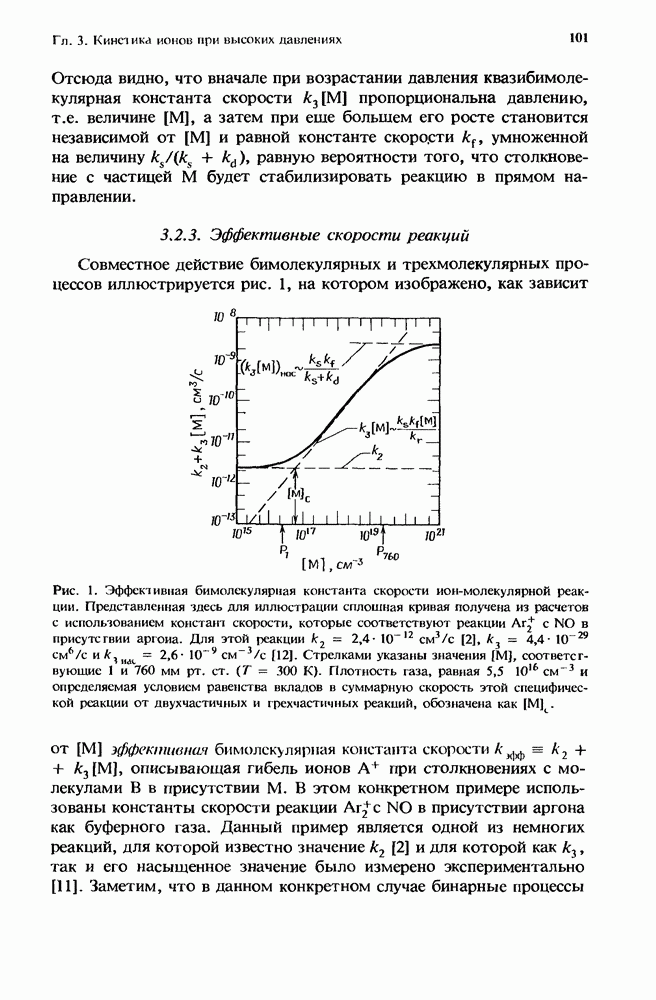
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
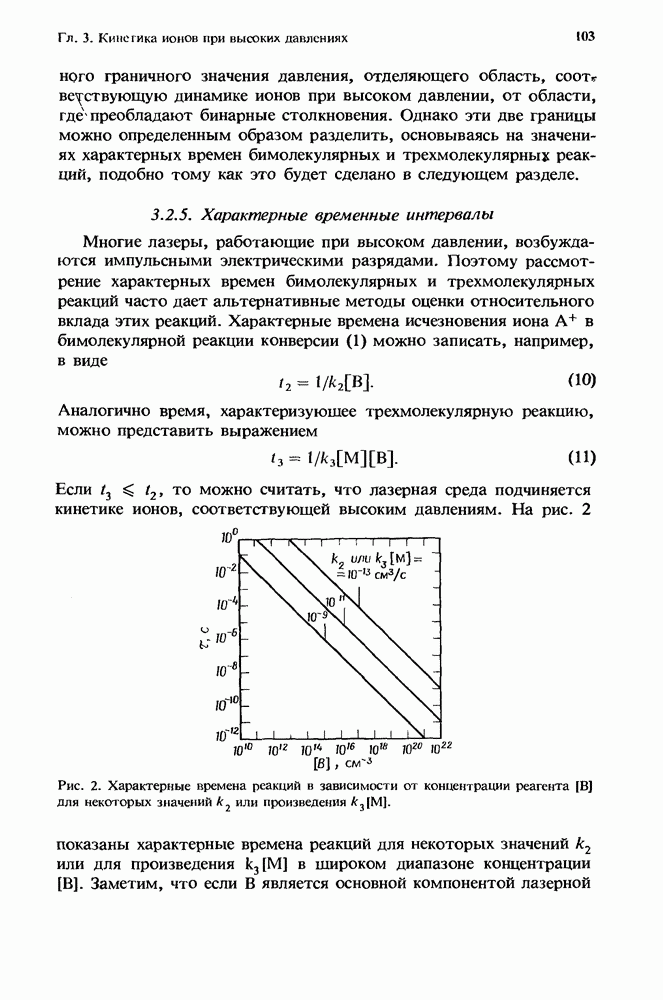
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
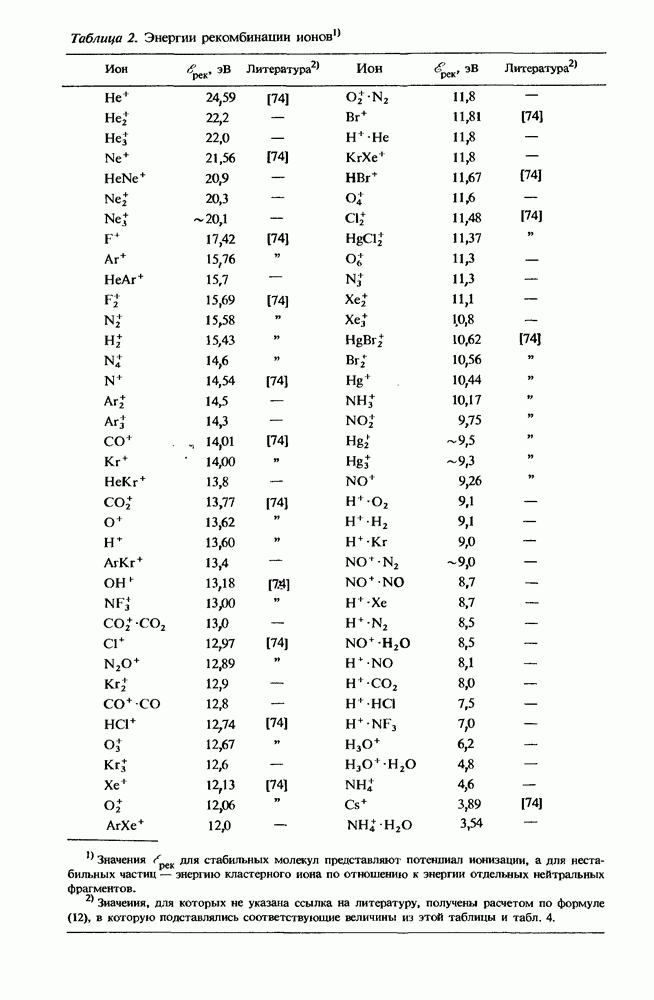
- 3.2.2. Энергетика отрицательных ионов
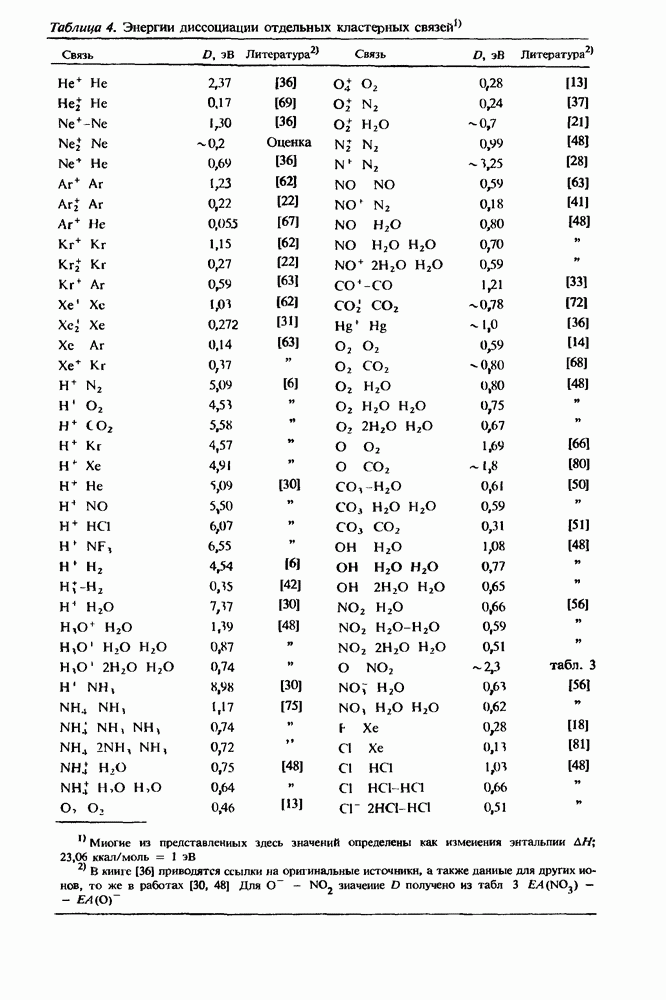
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
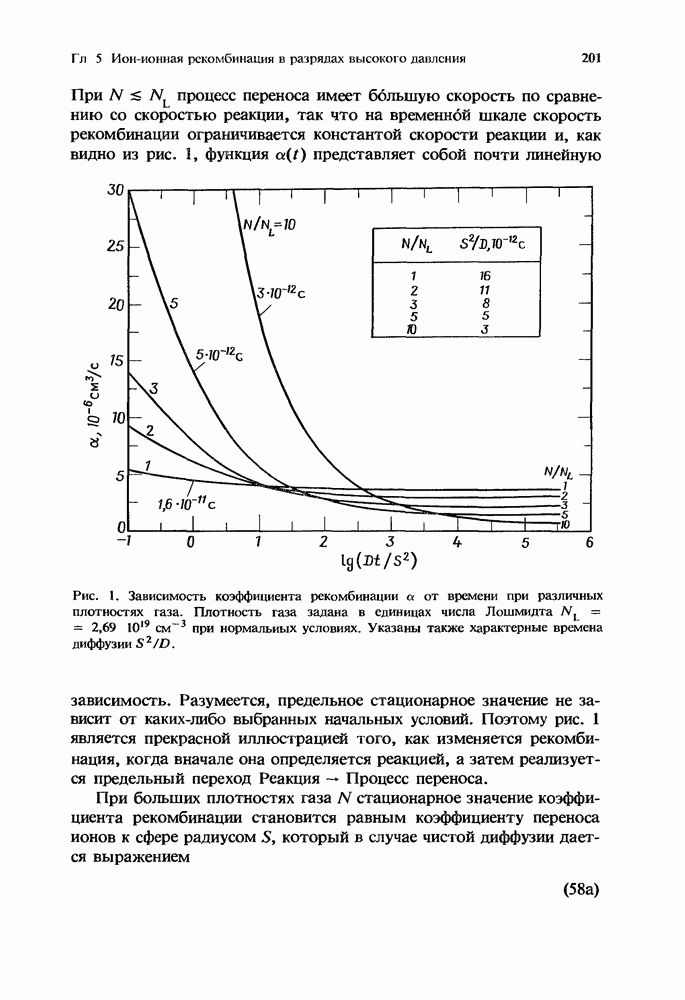
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
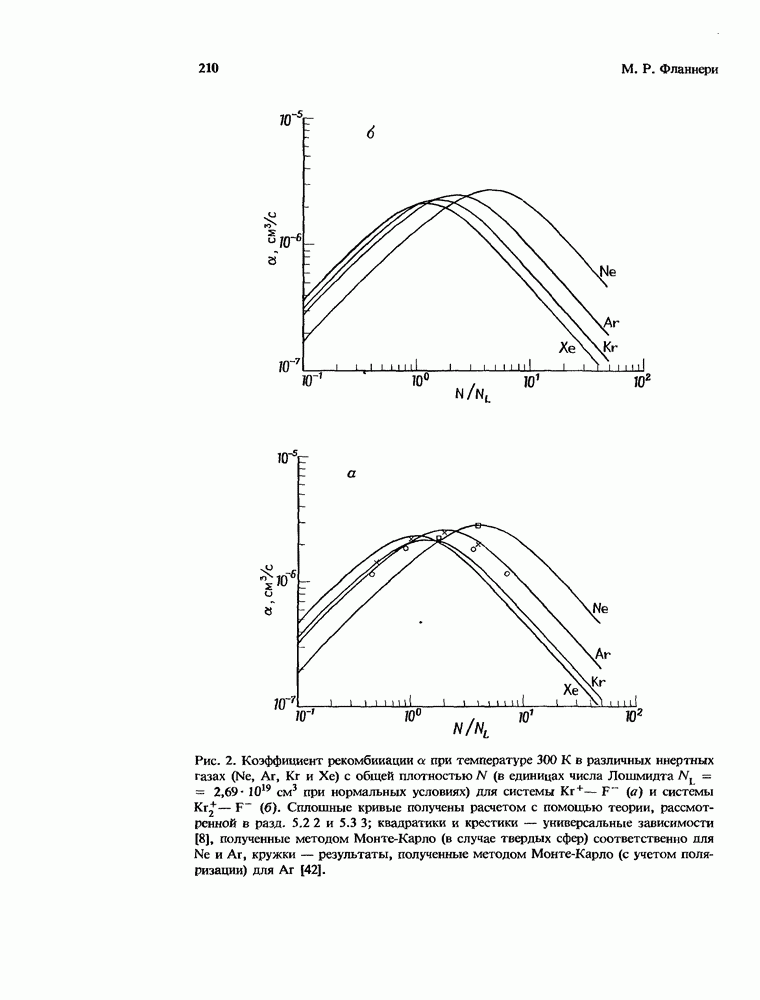
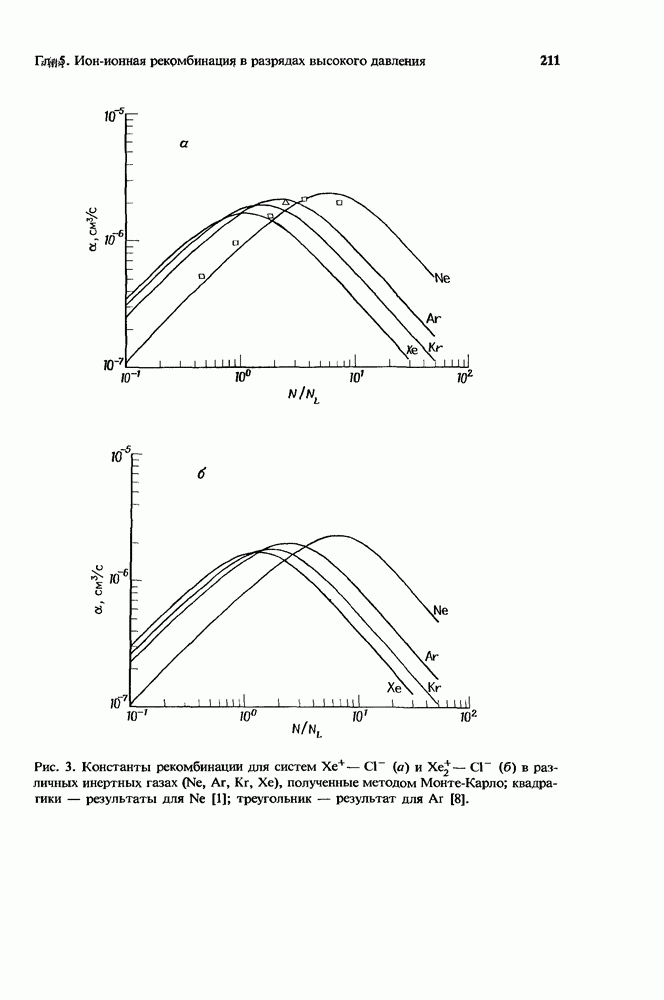
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
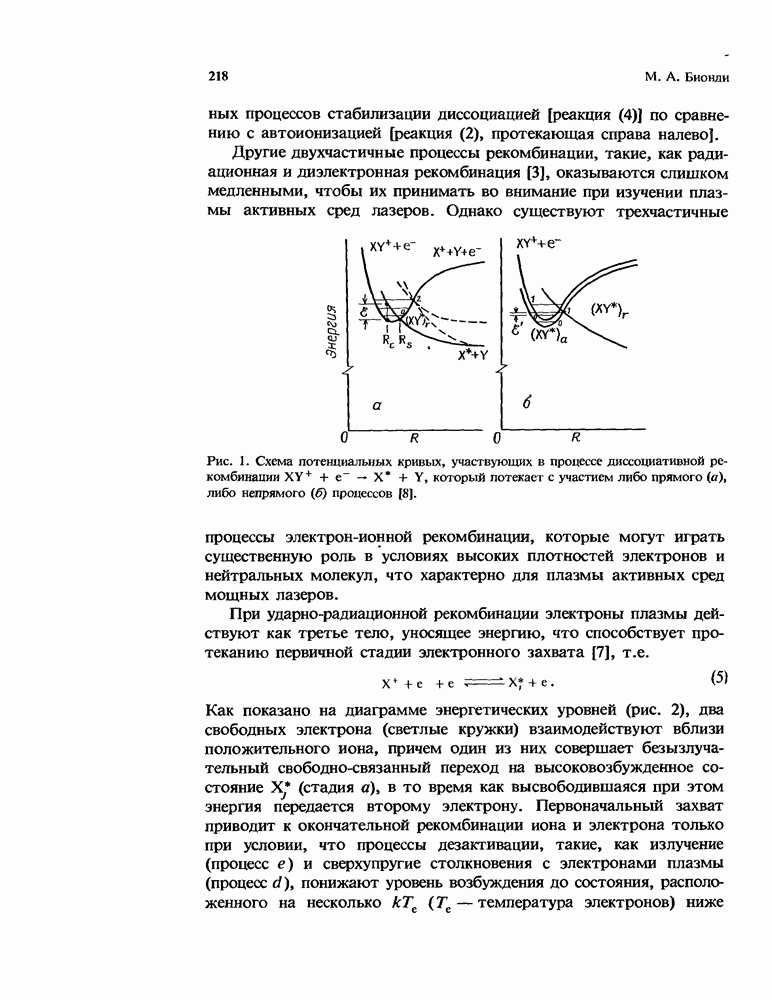
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
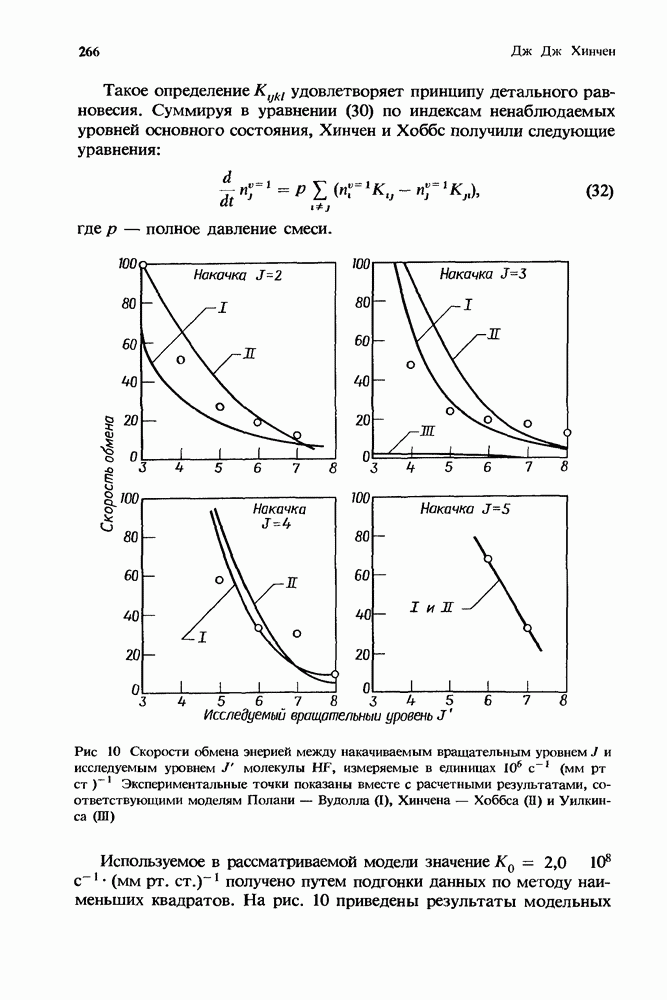
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
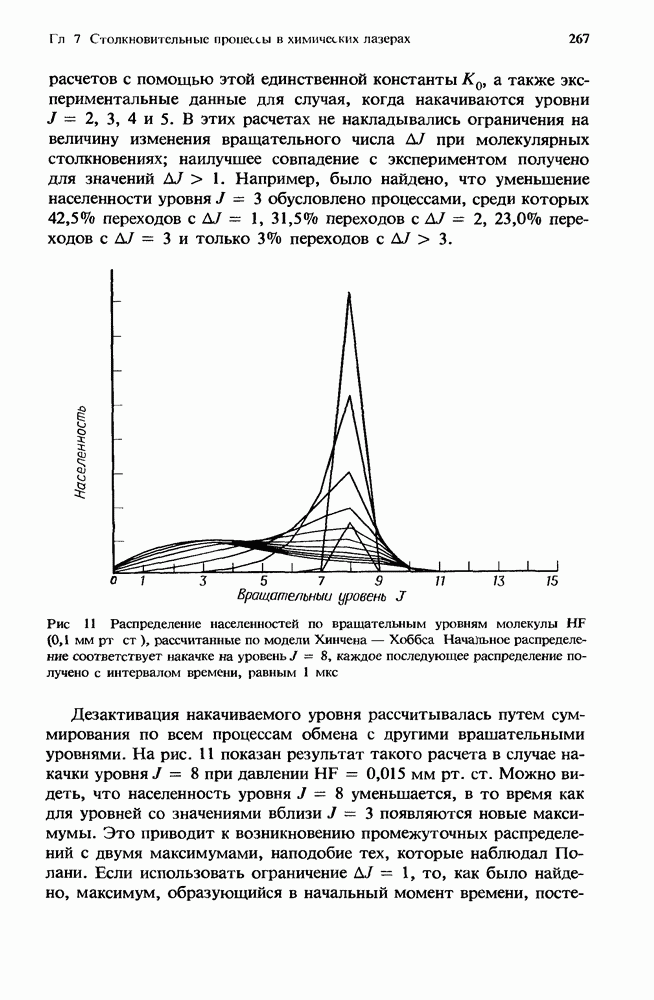
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
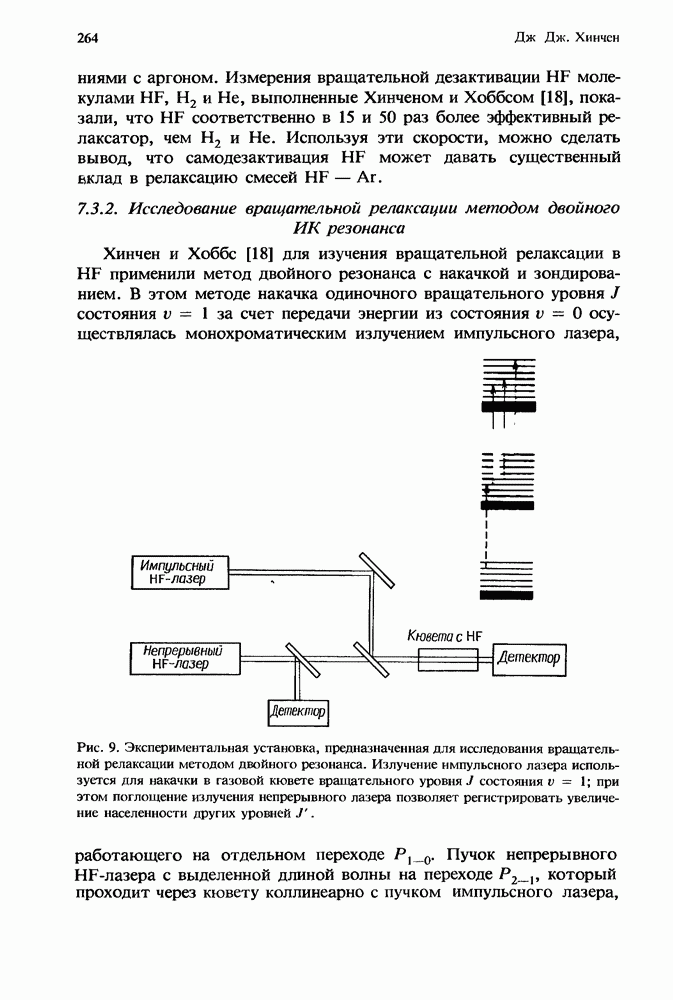
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
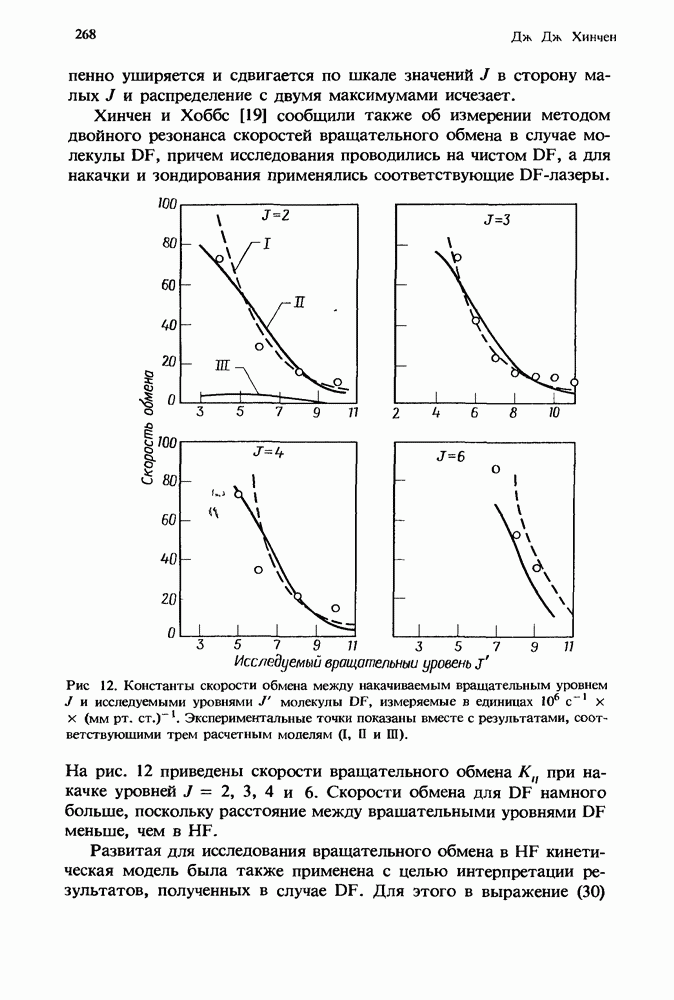
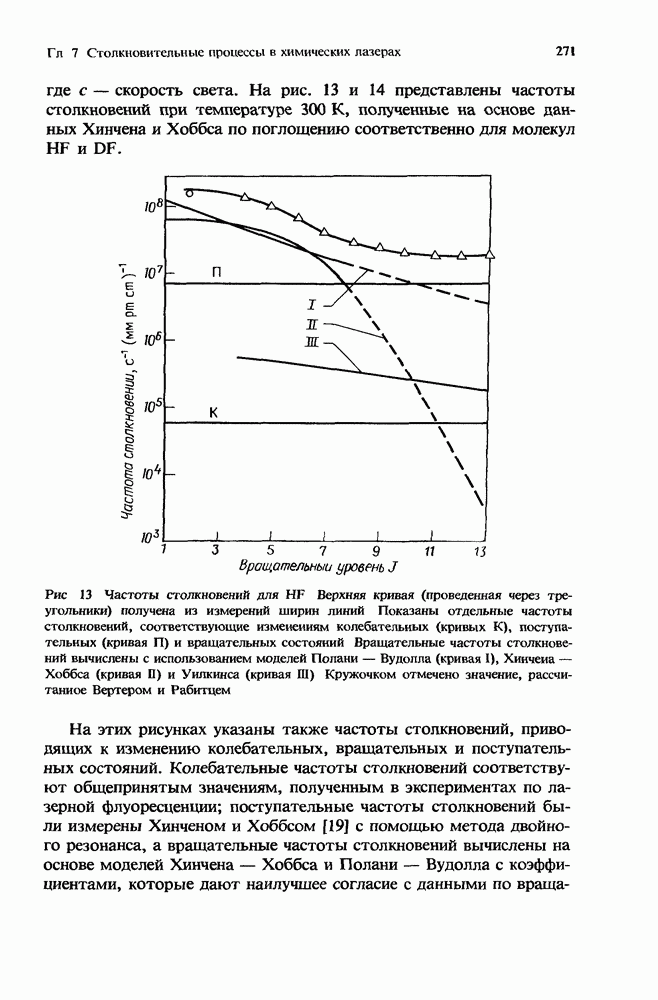
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
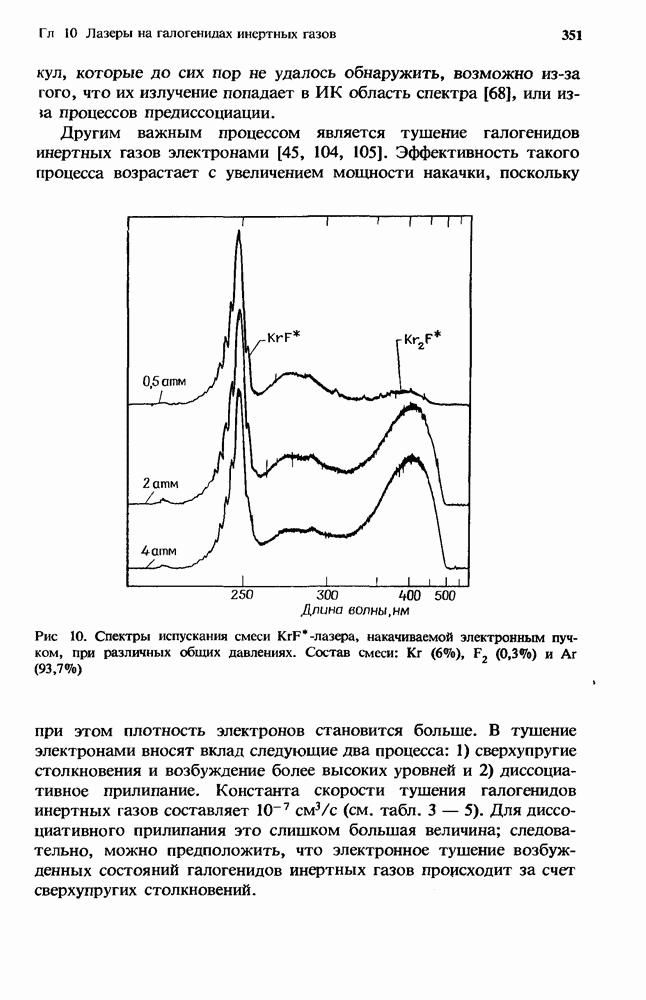
- 10.3. Кинетика тушения галогенидов инертных газов
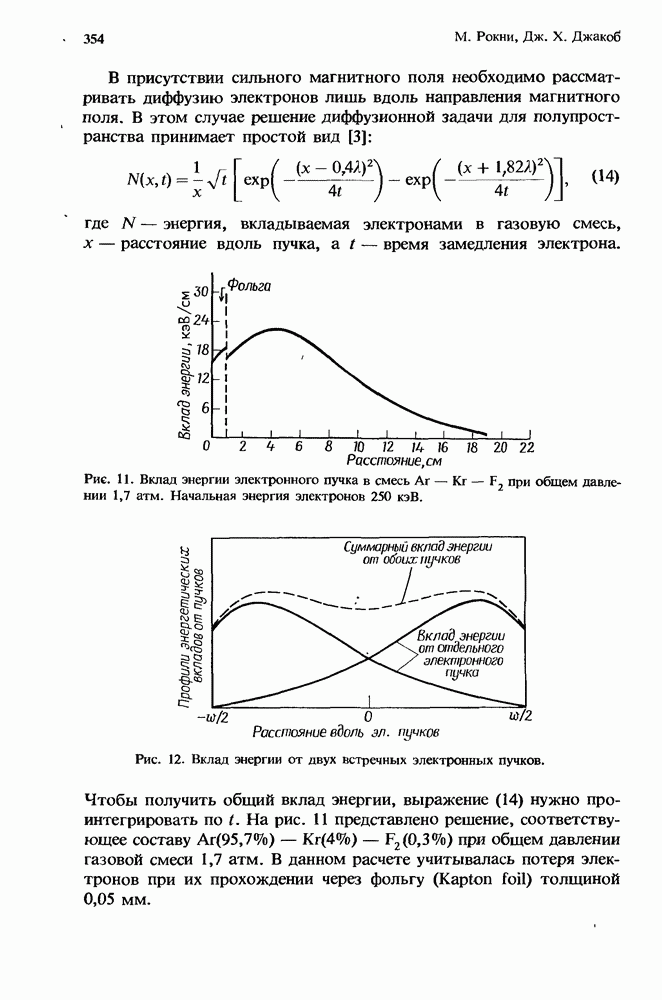
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
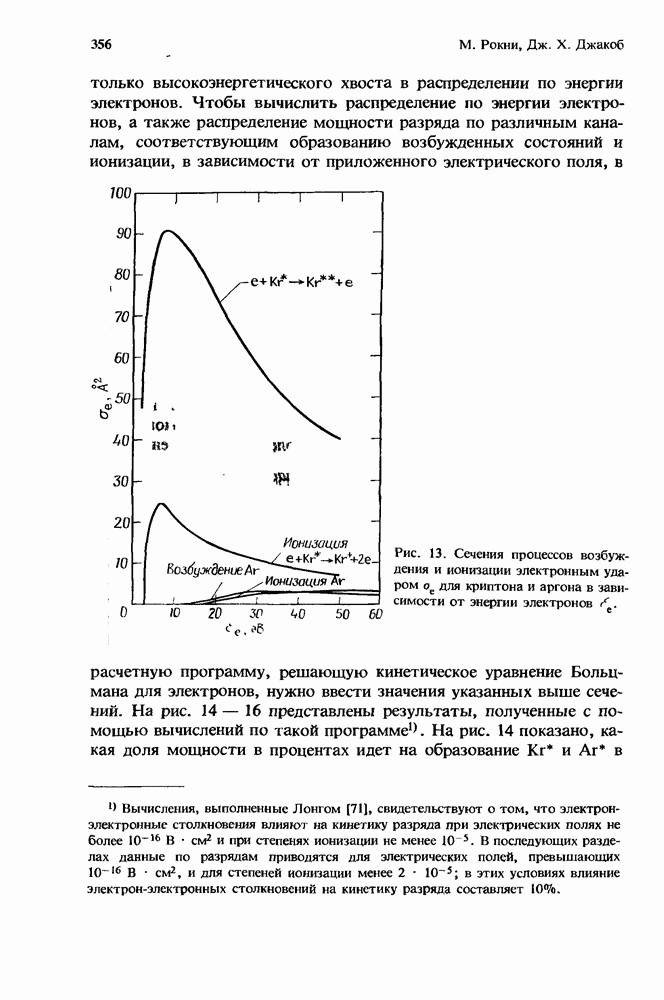
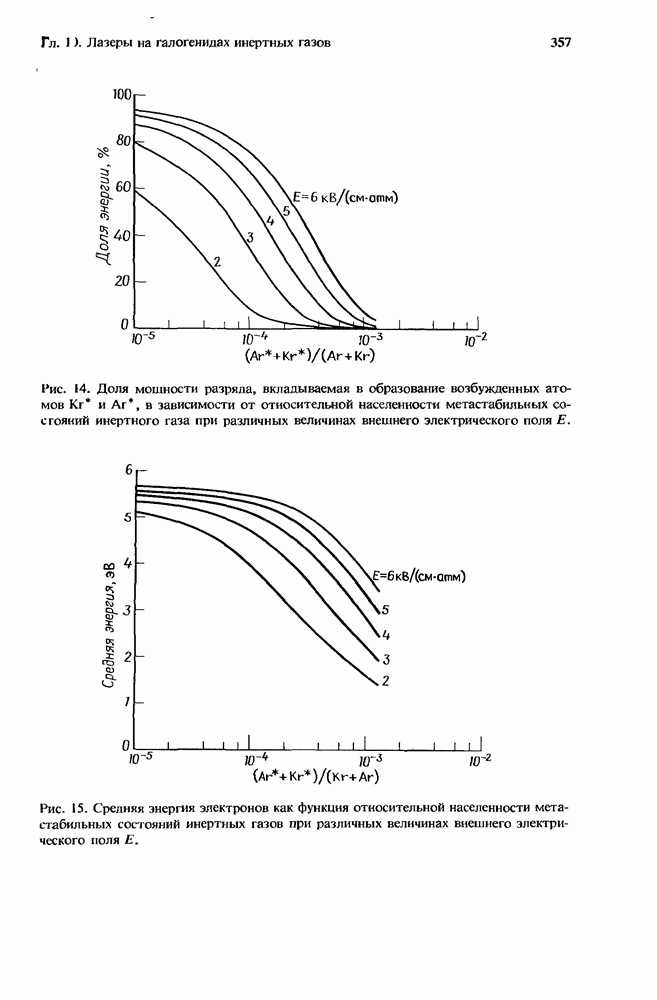
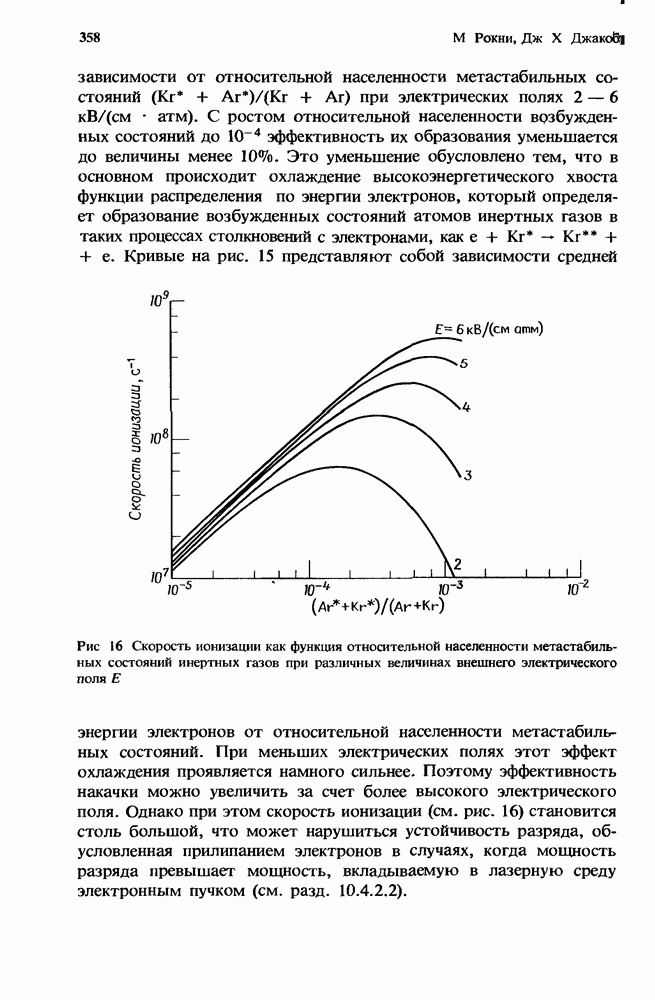
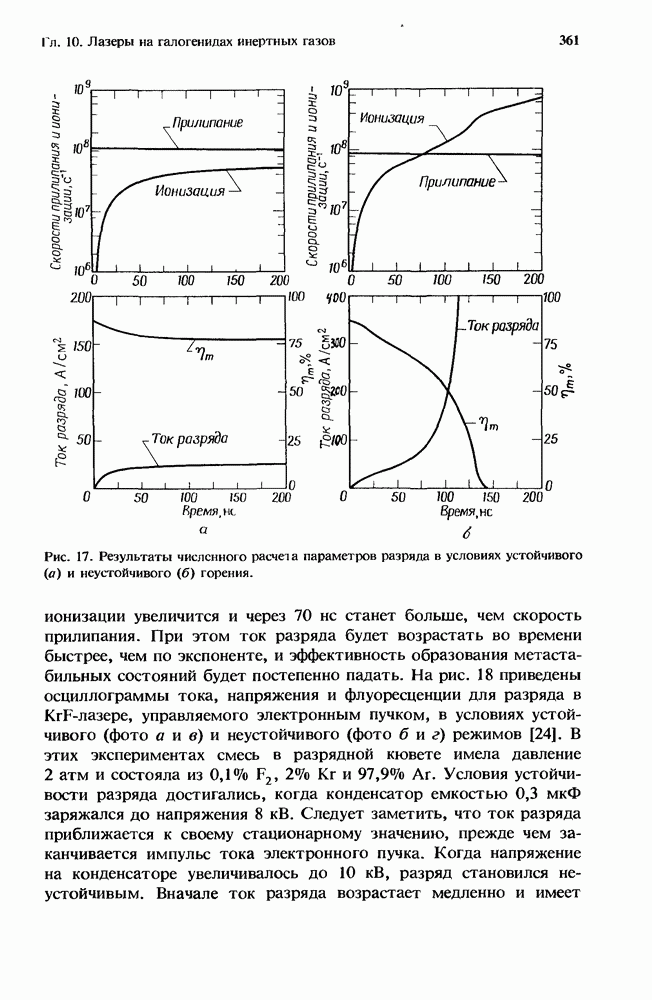
- 10.4.2.2. Устойчивость разряда
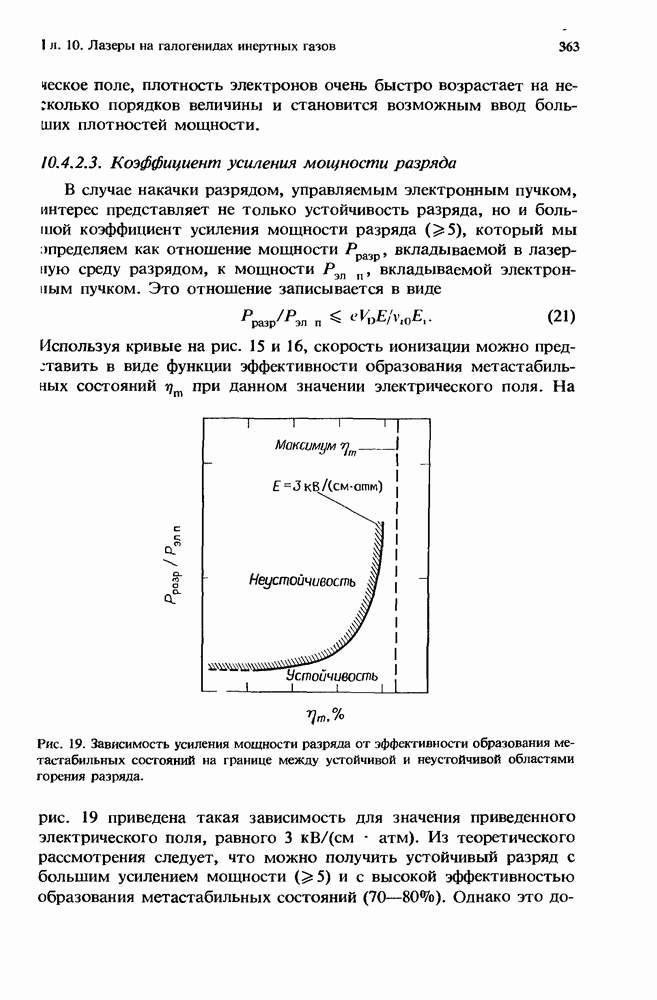
- 10.4.2.3. Коэффициент усиления мощности разряда
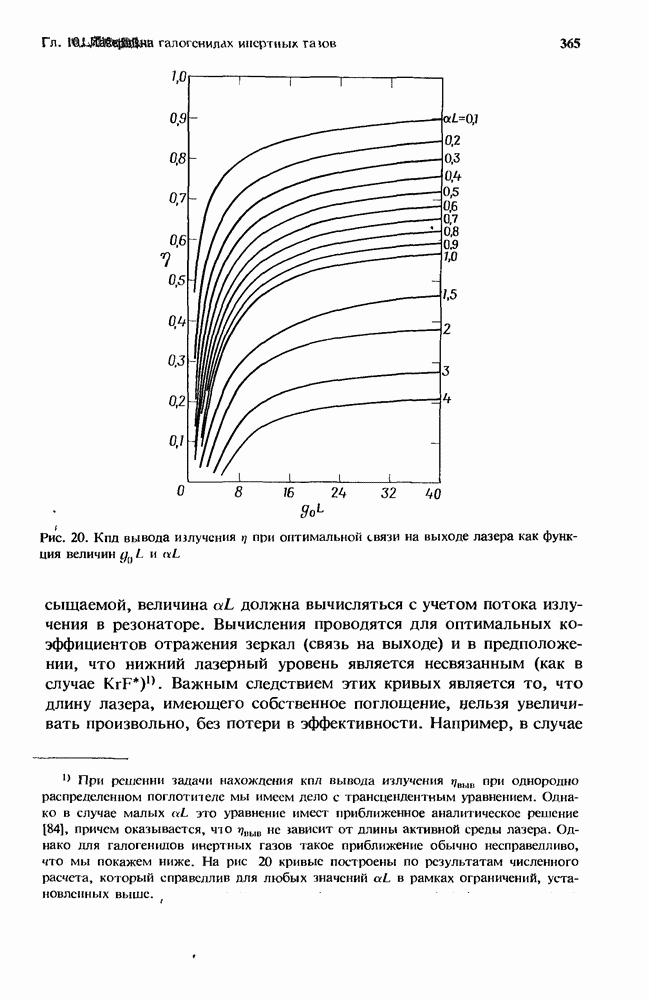
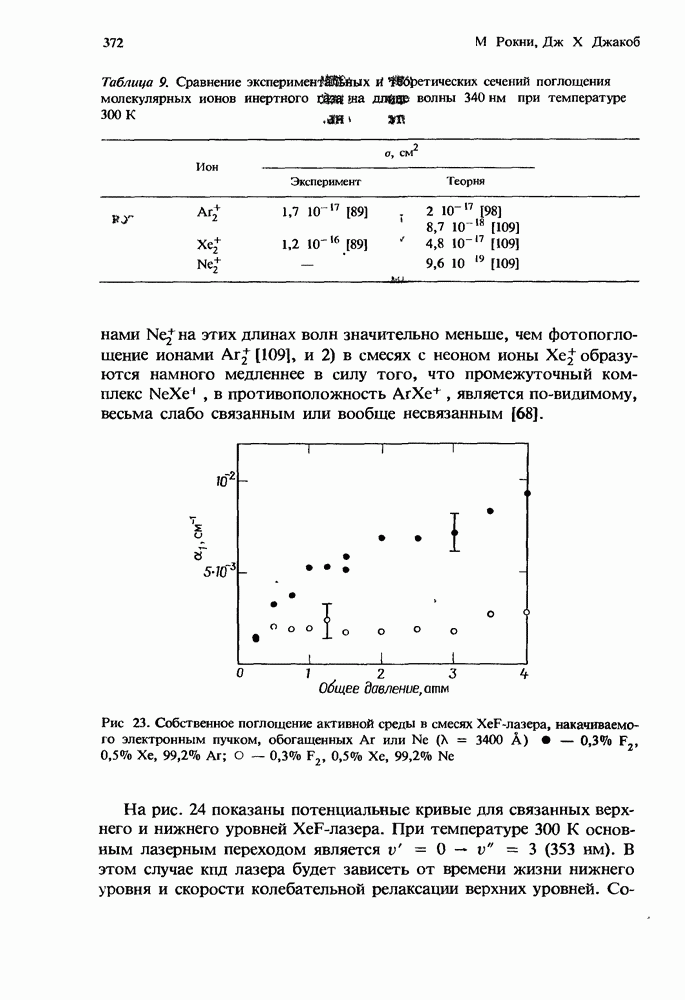
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
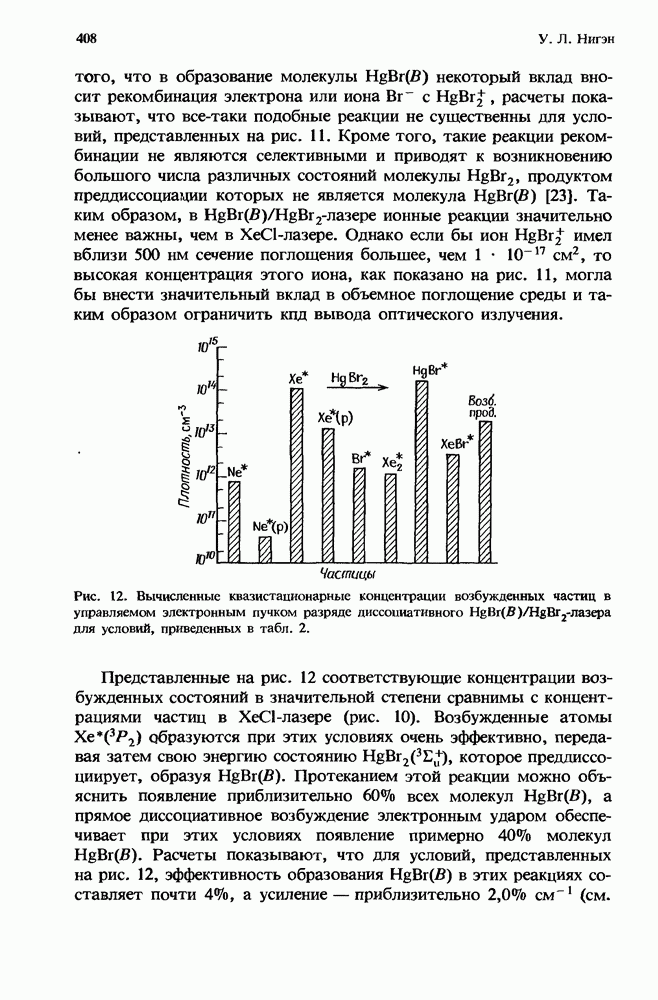
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
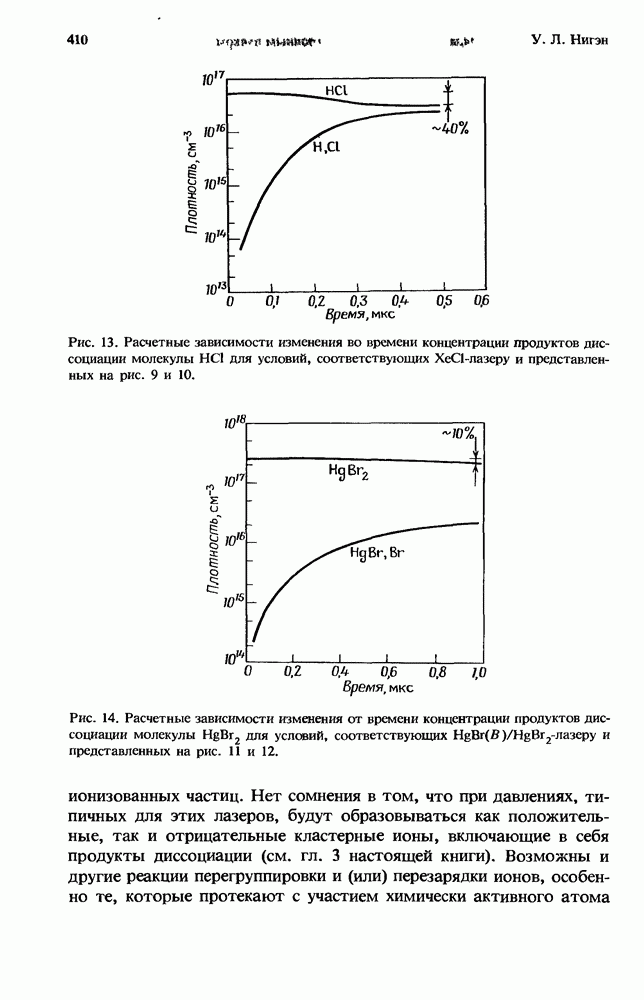
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
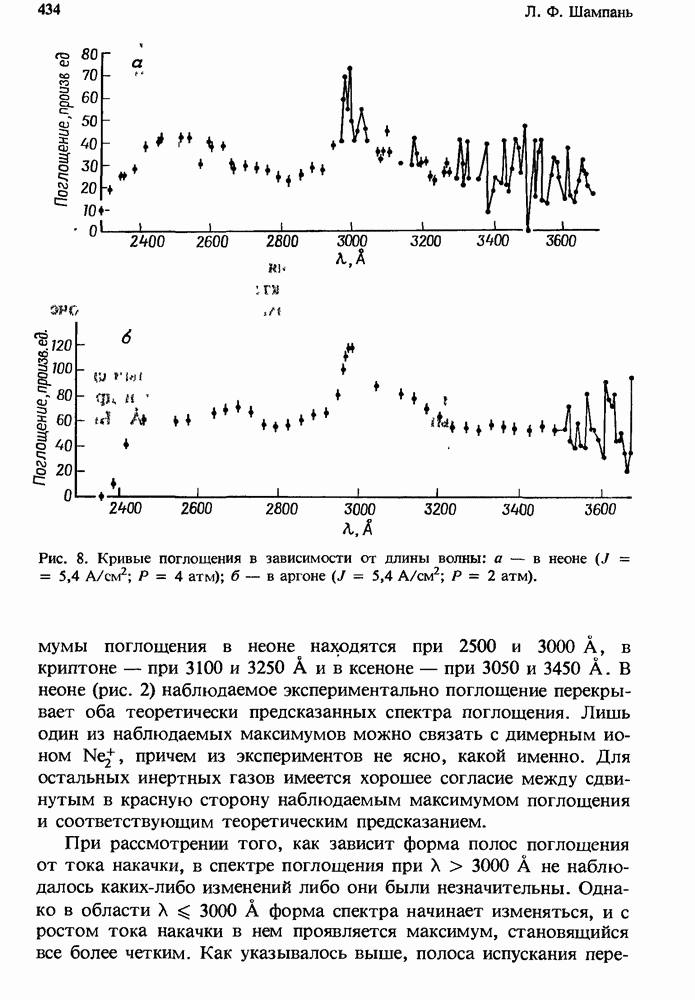
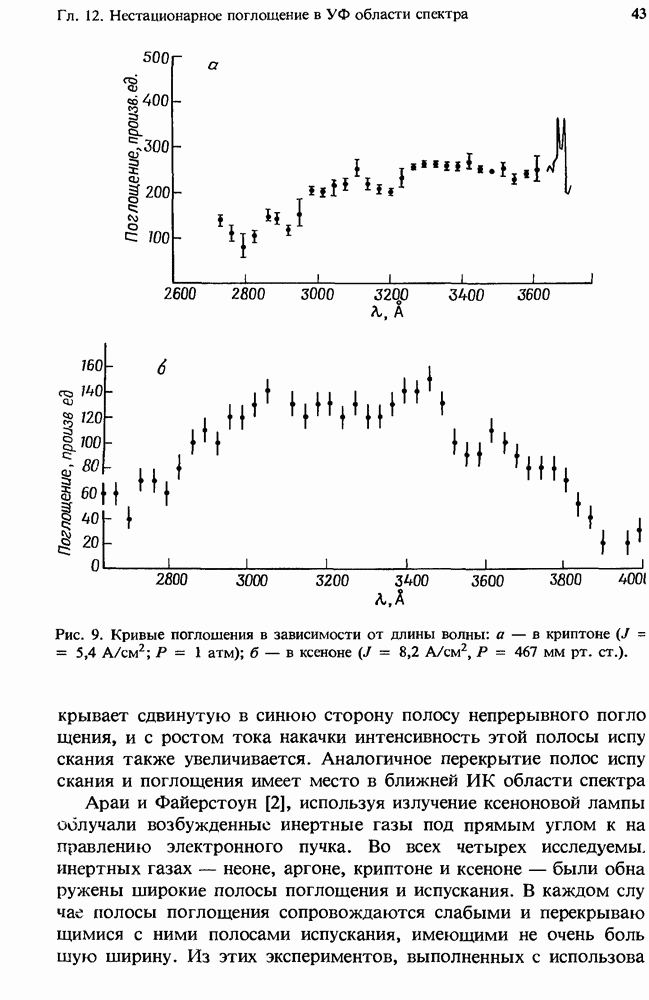
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
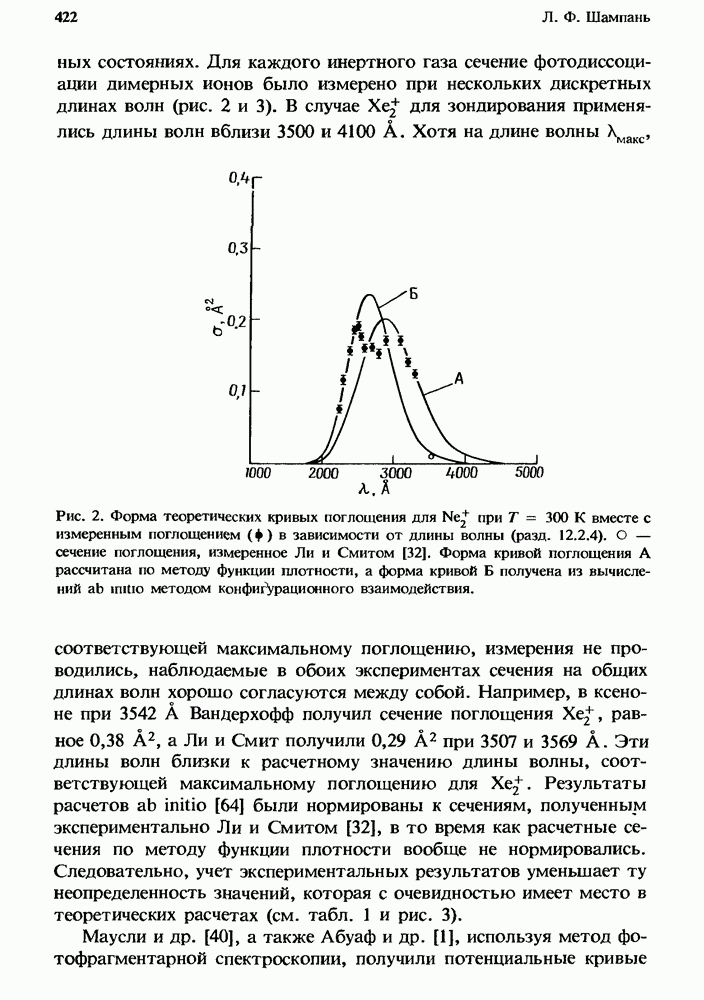
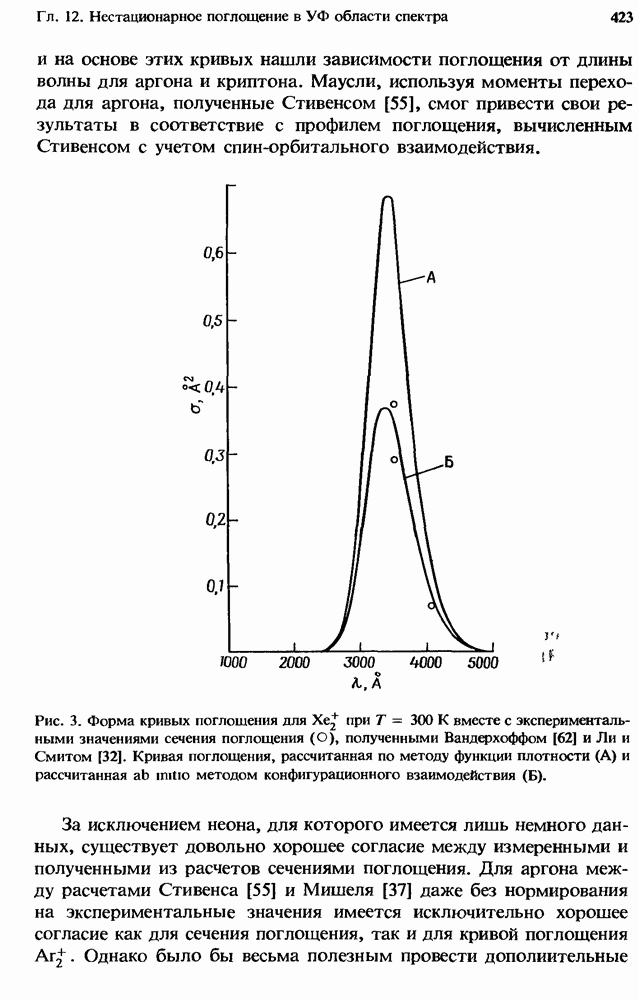
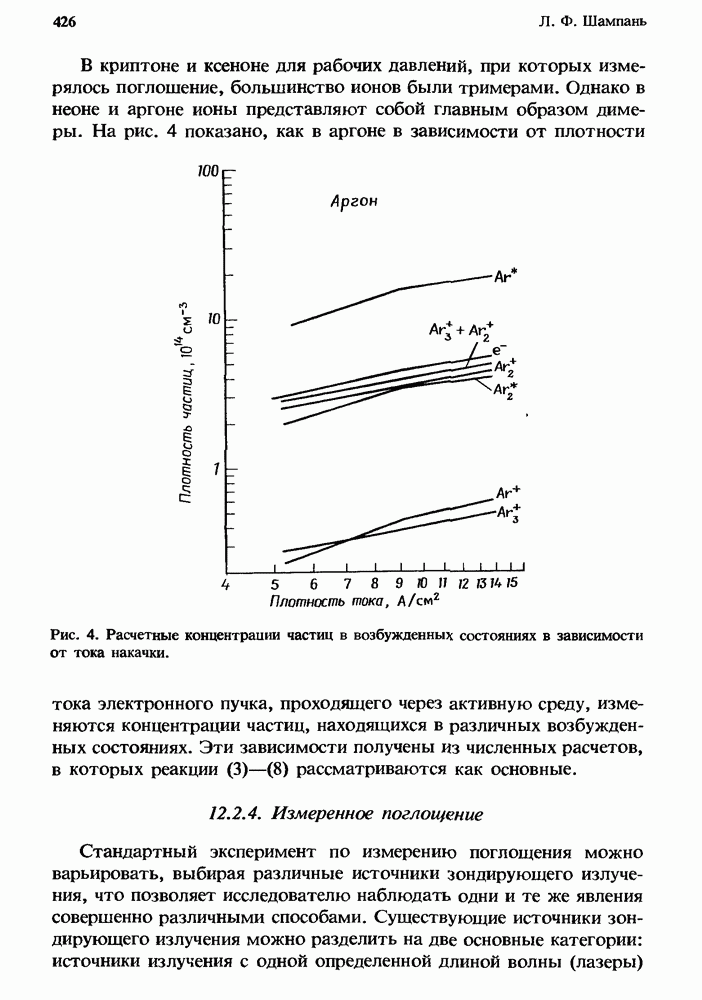
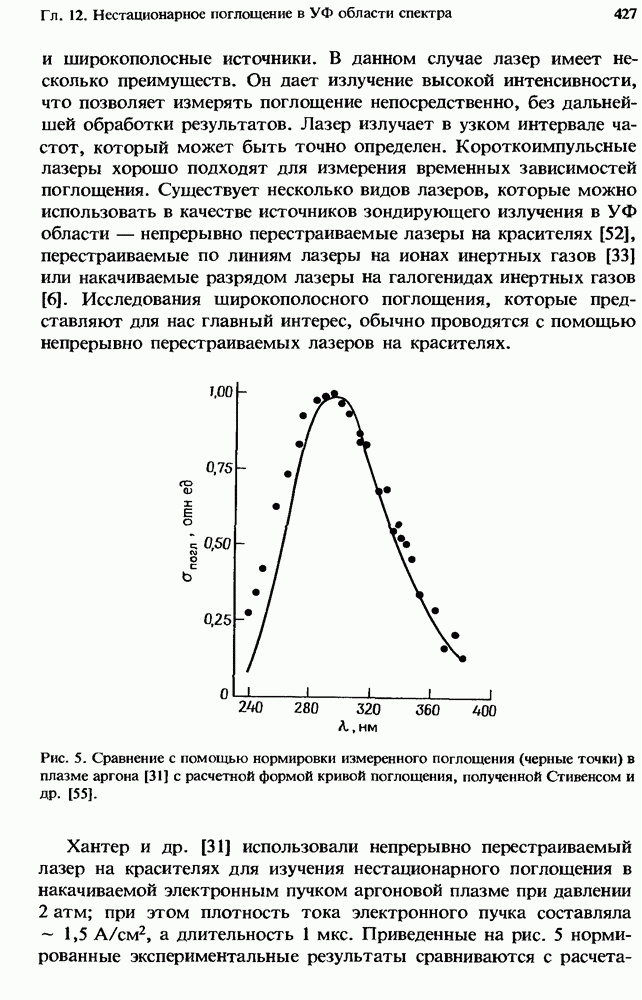
- 12.2.4. Измеренное поглощение
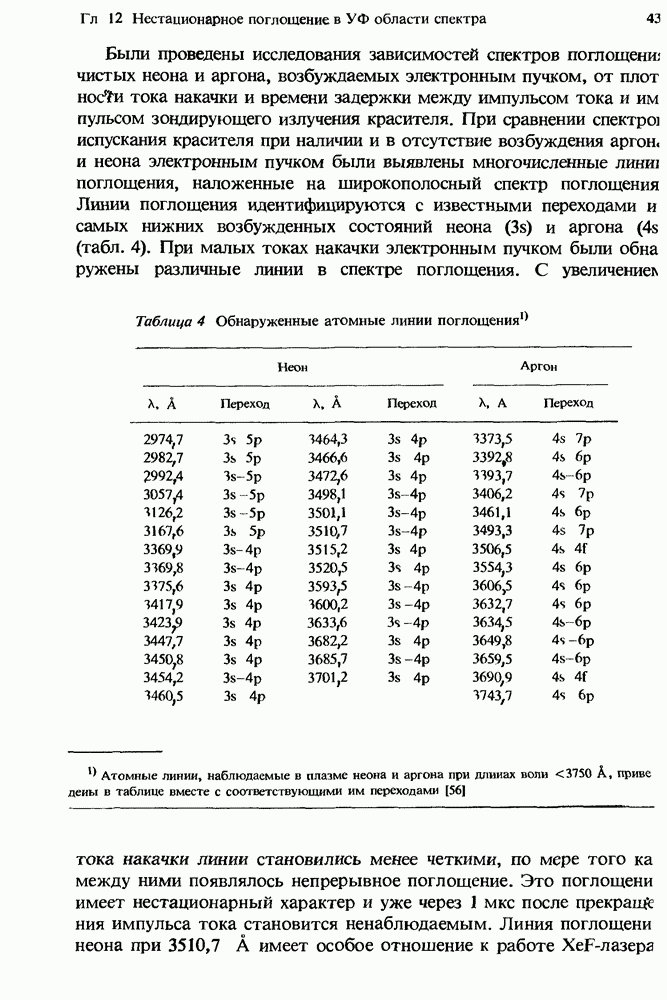
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
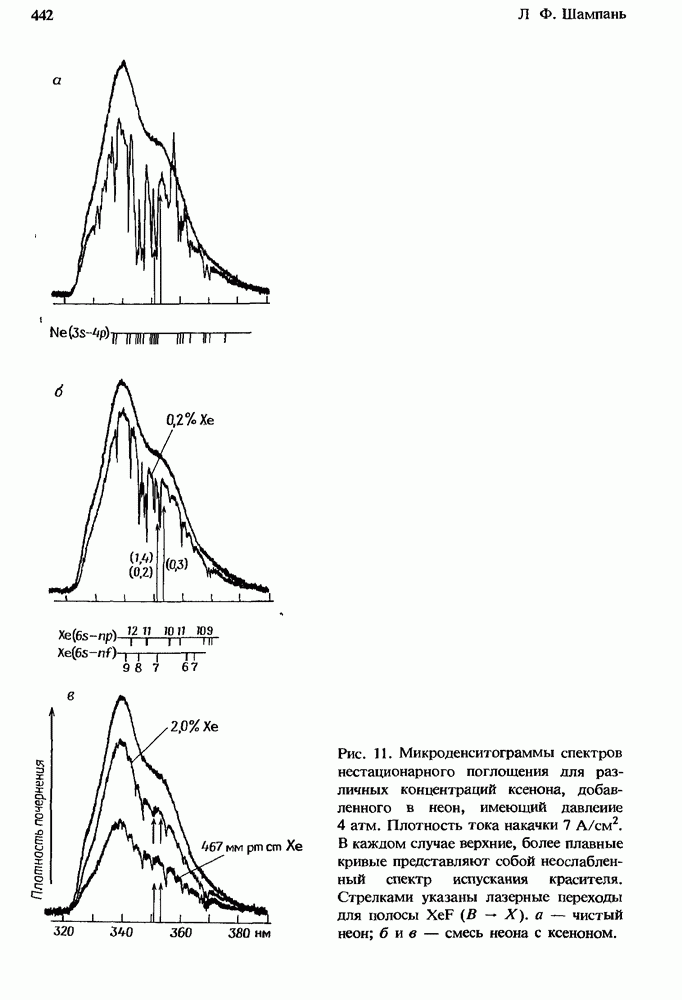
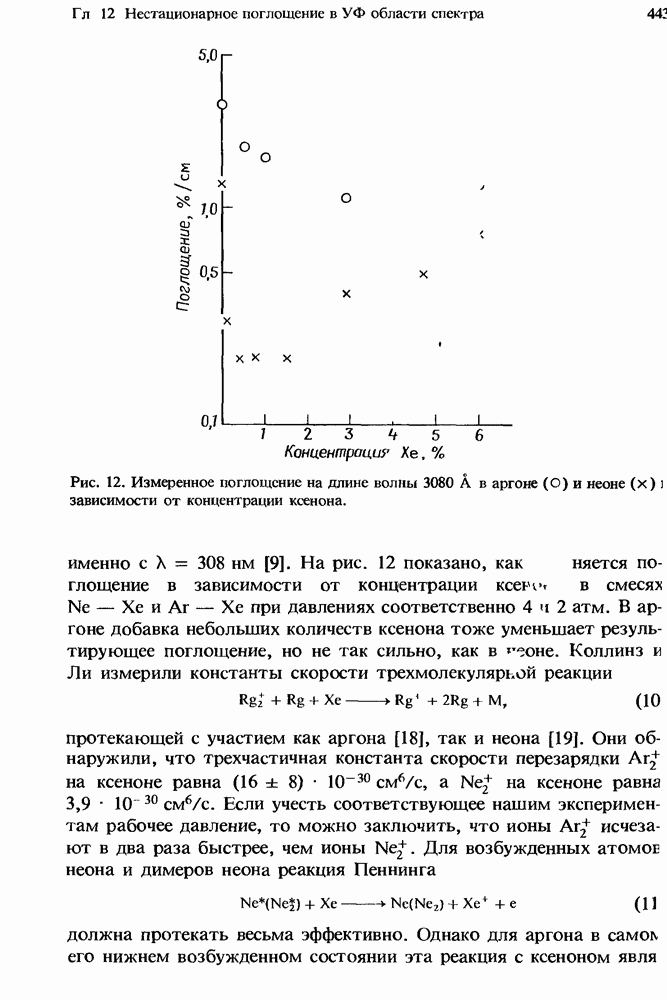
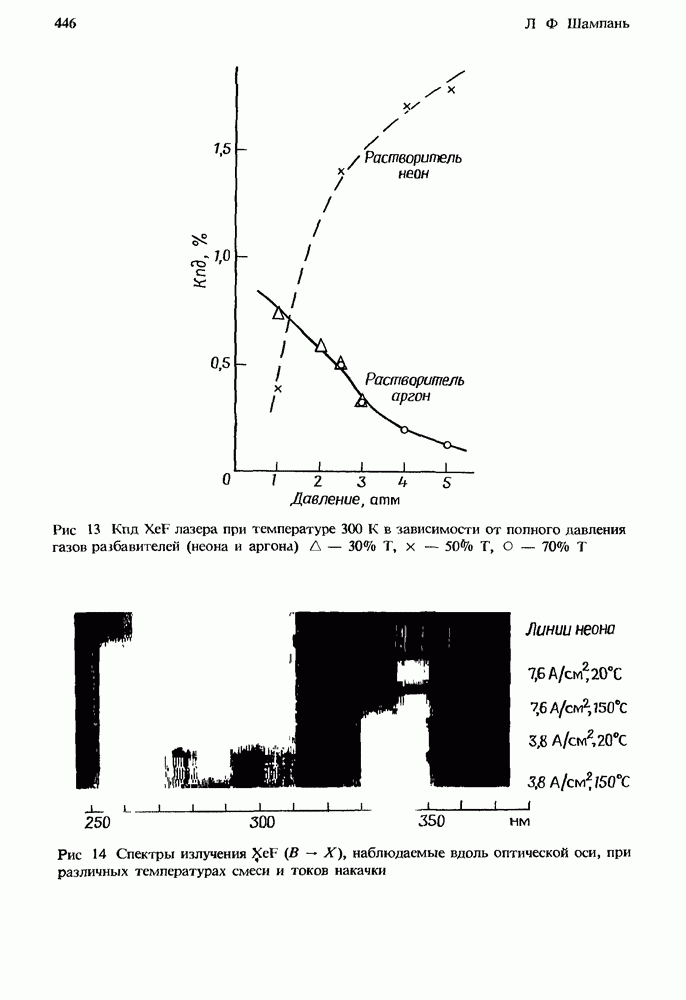
- 12.3. Двухкомпонентные смеси
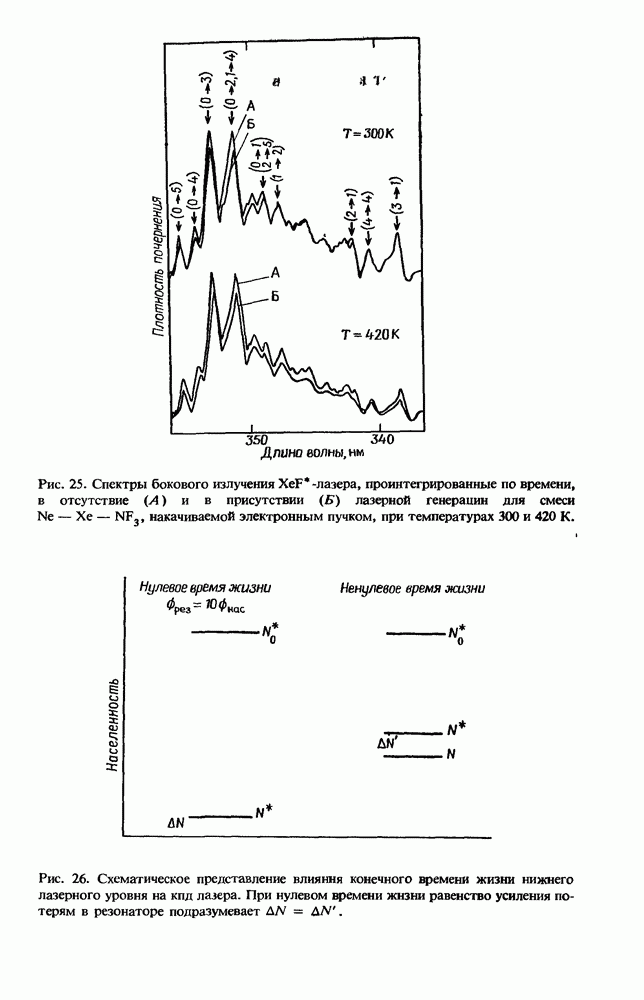
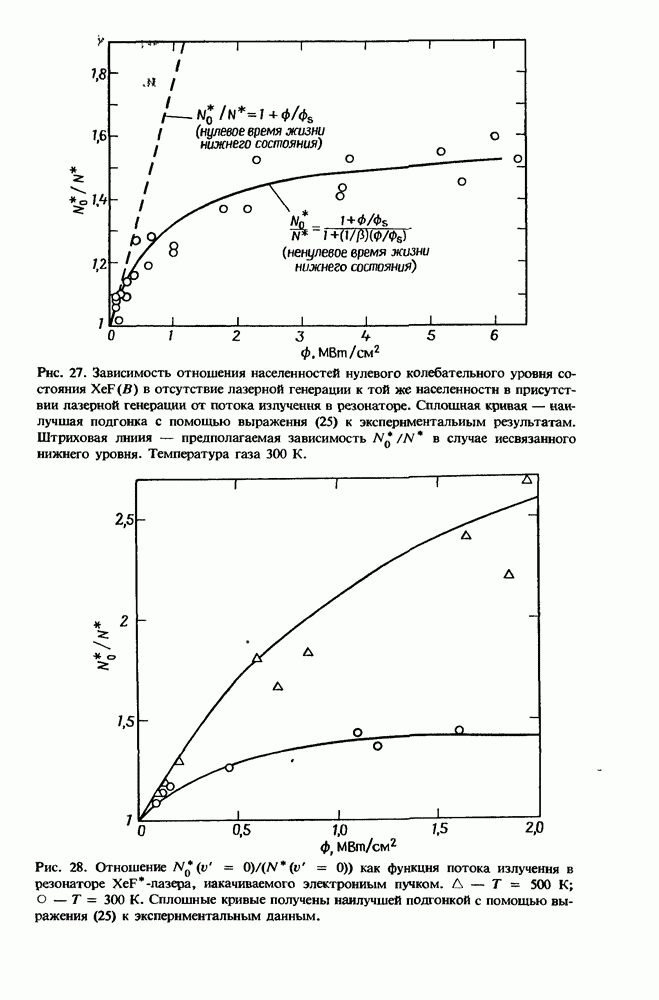
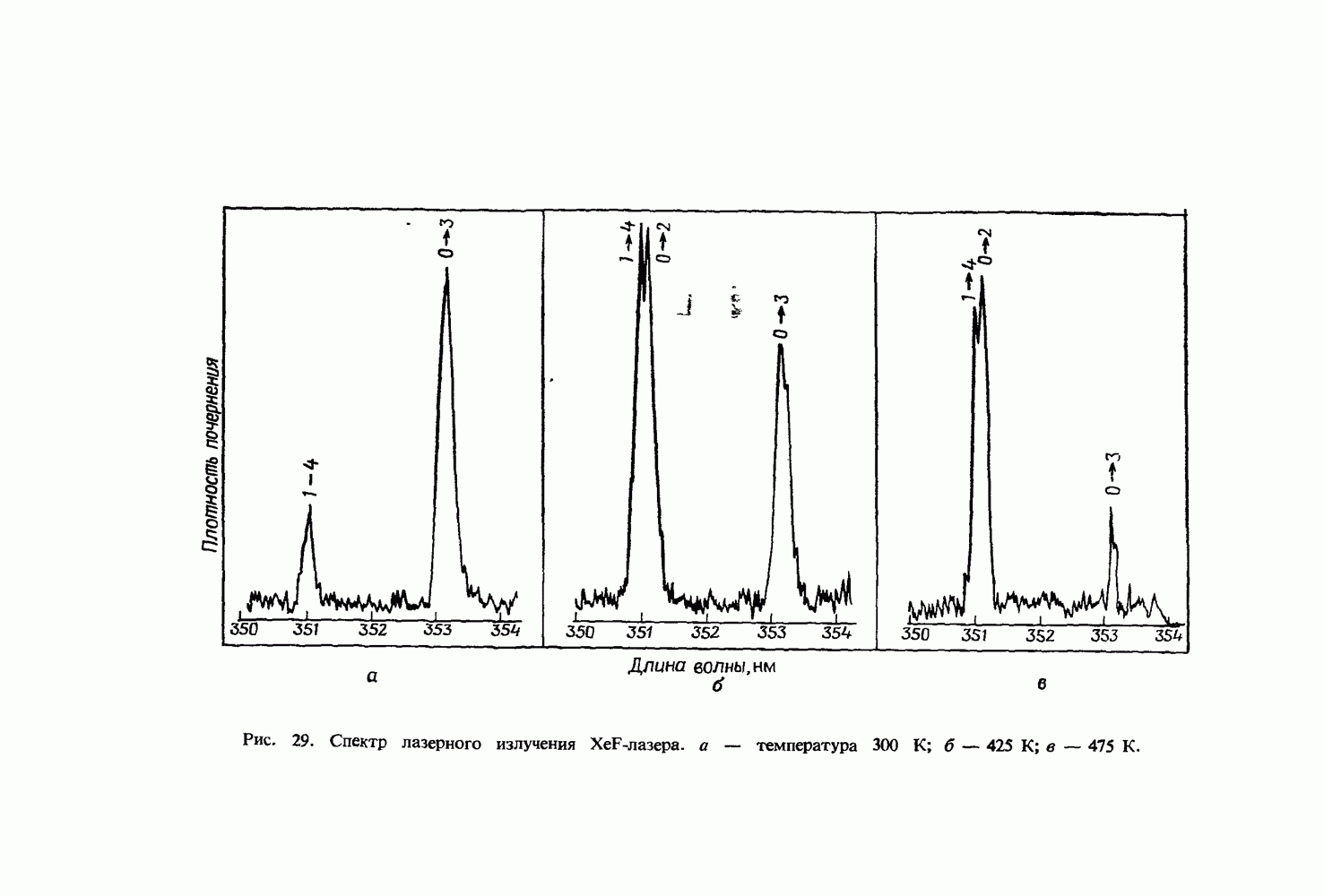
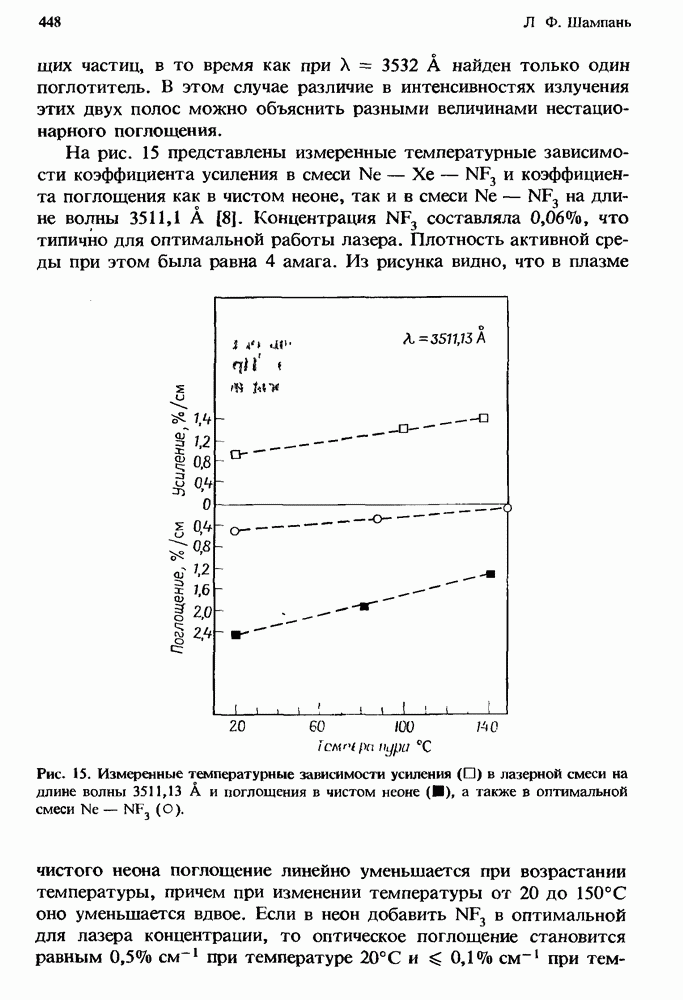
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
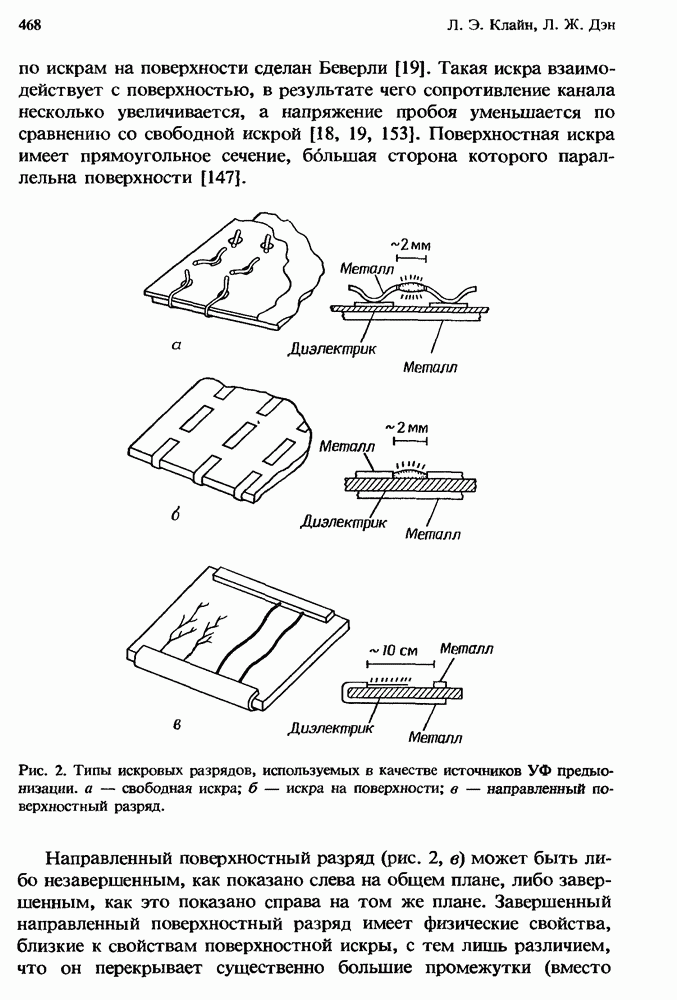
- 13.3. Физические механизмы предыонизации УФ излучением
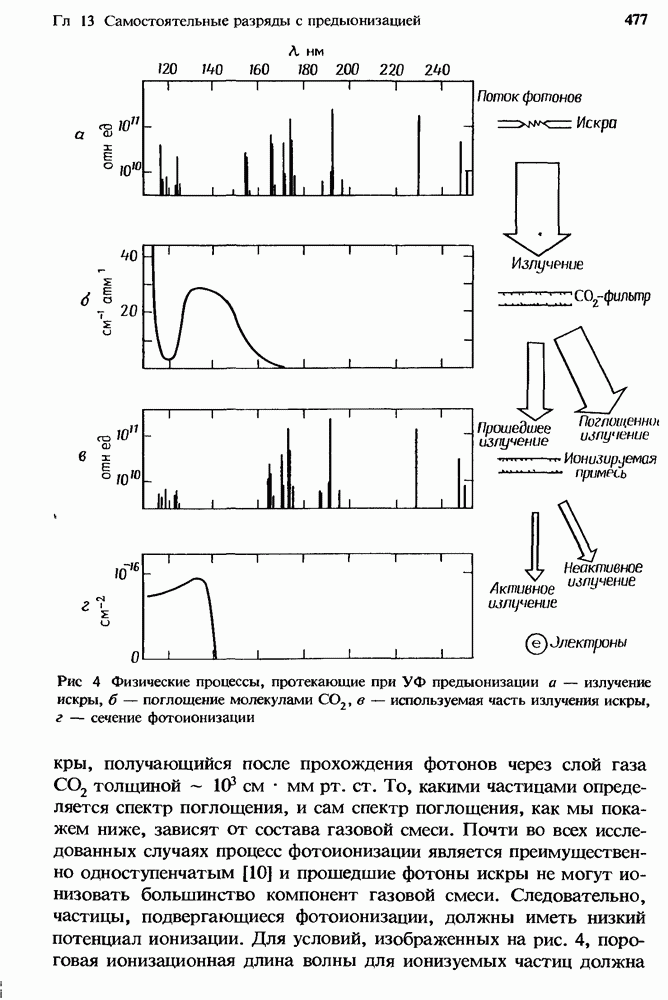
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
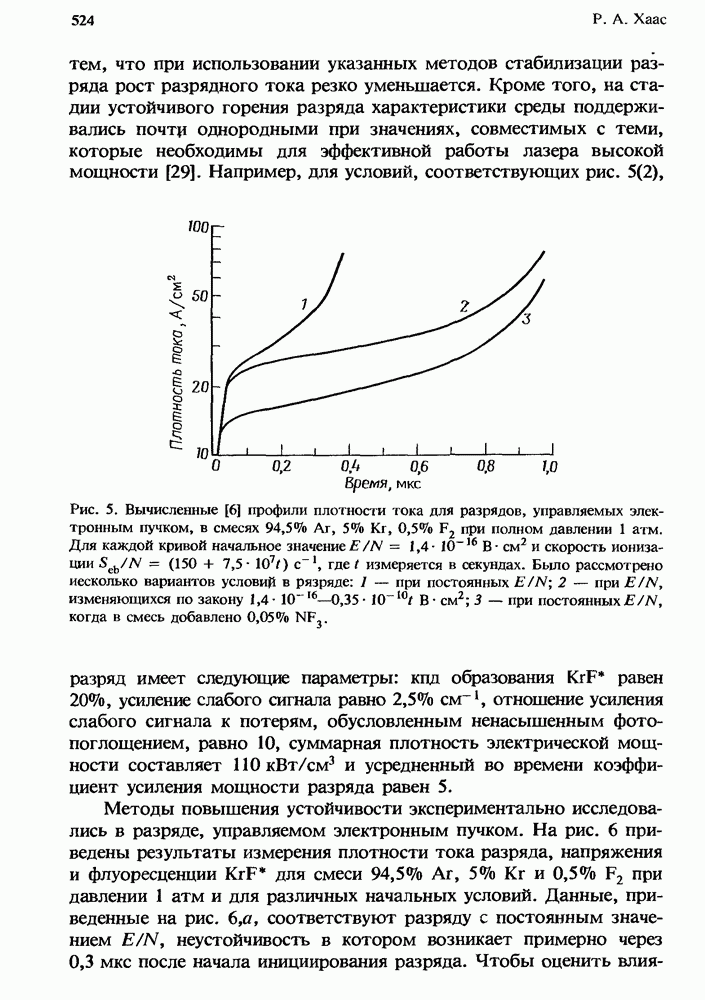
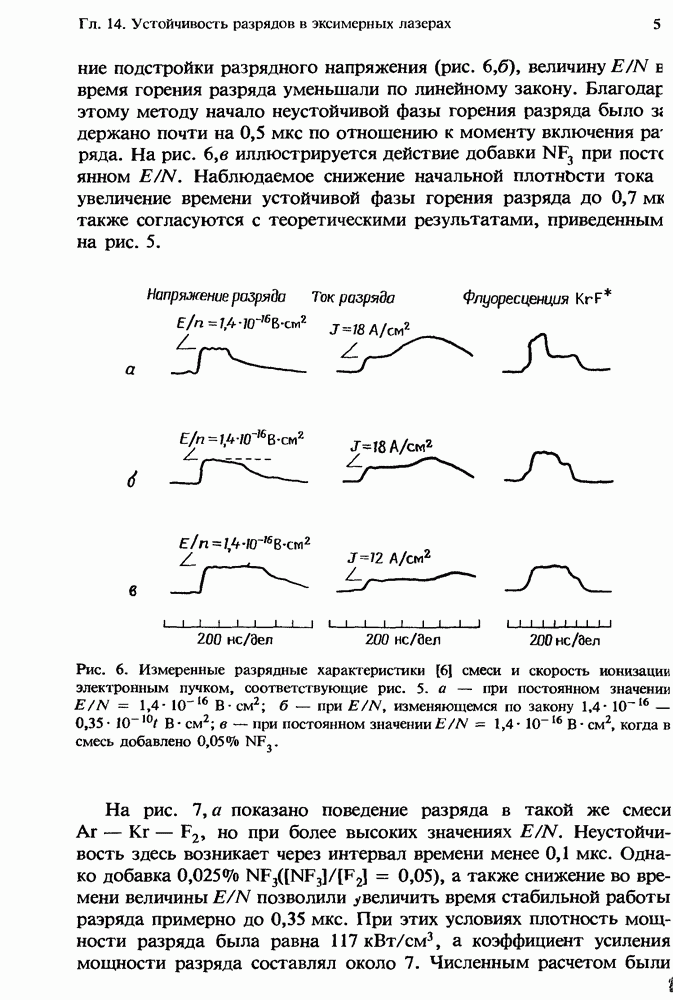
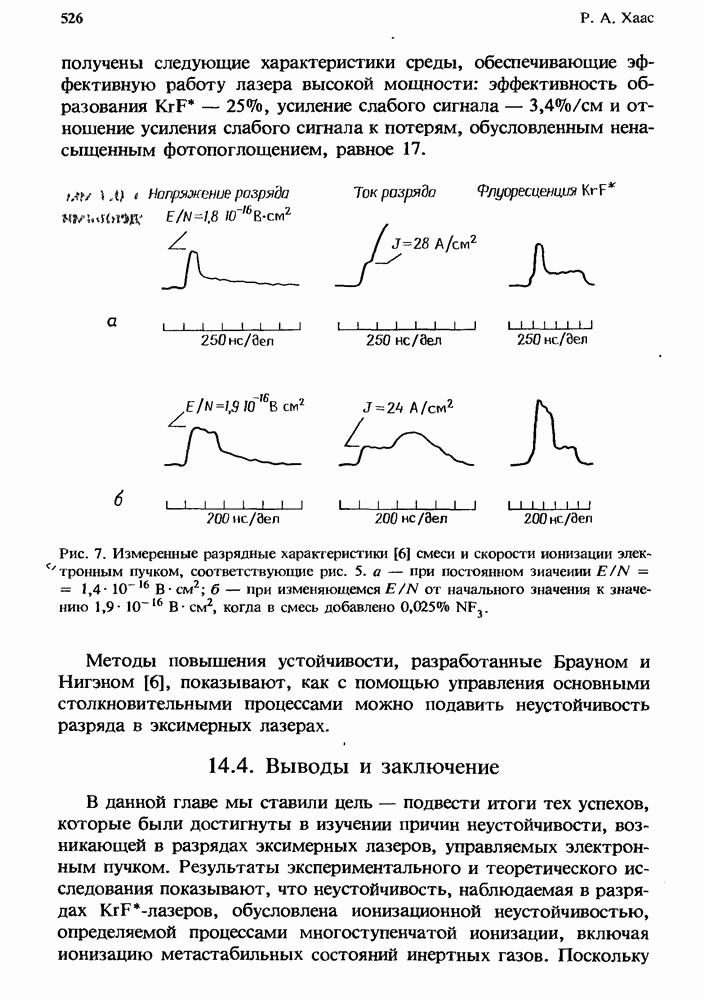
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации