| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
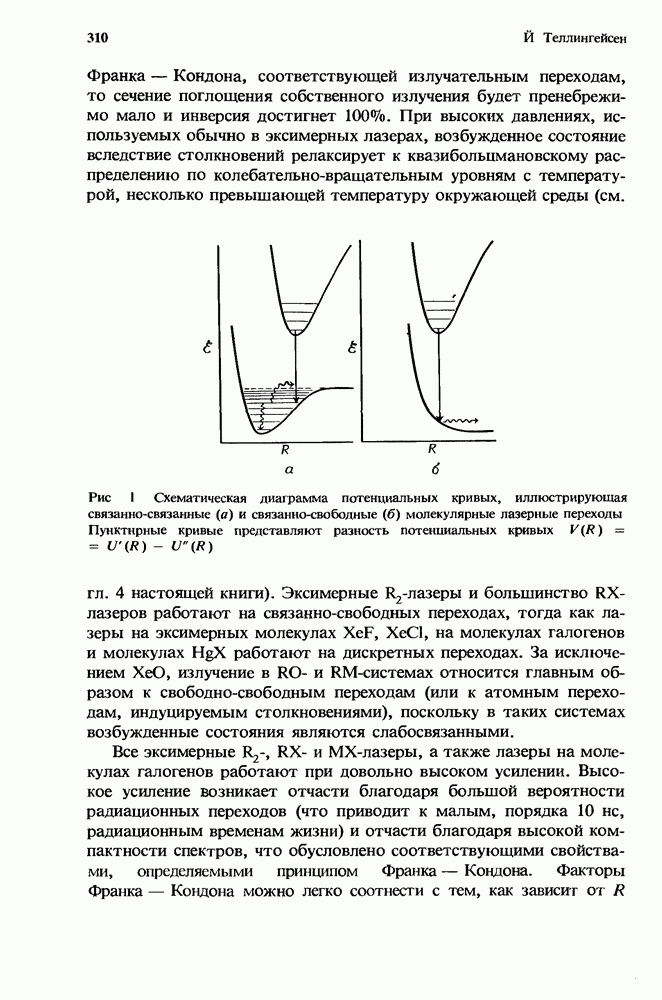
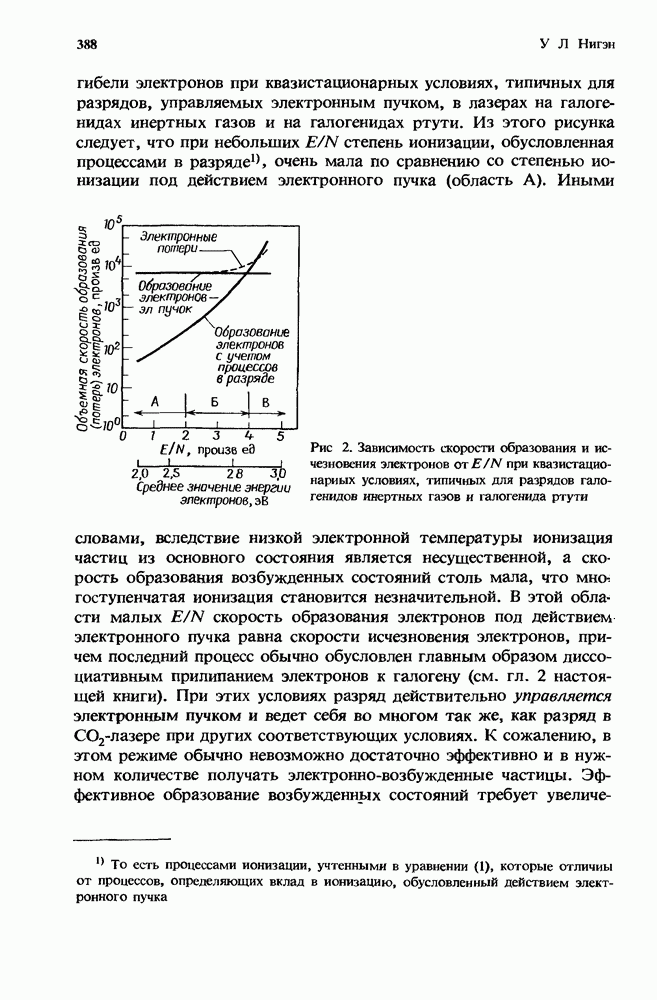
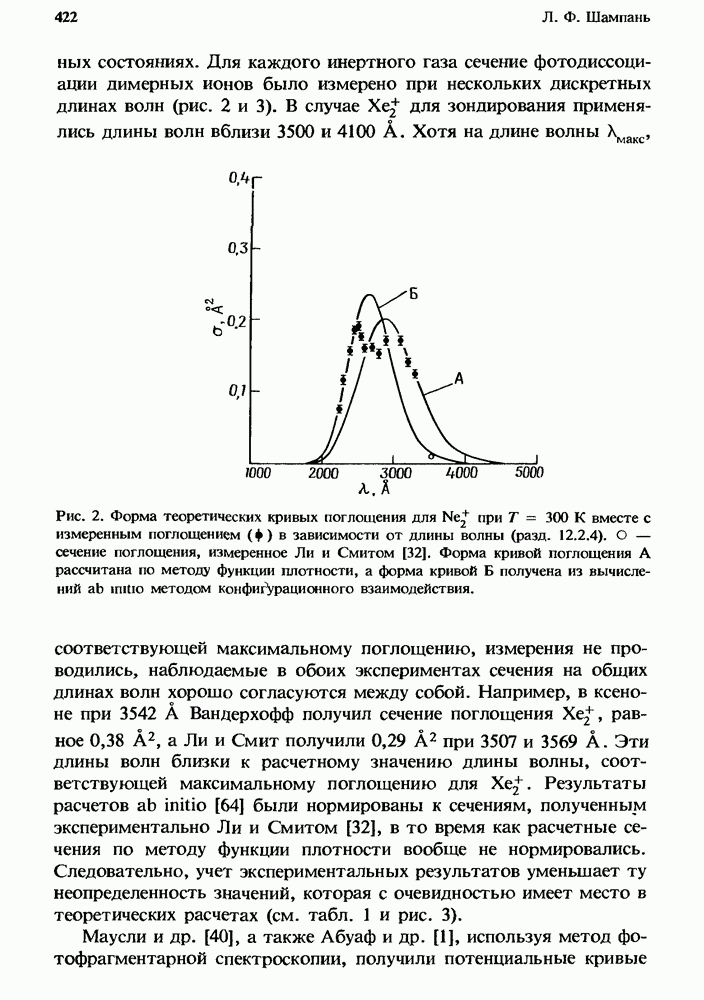
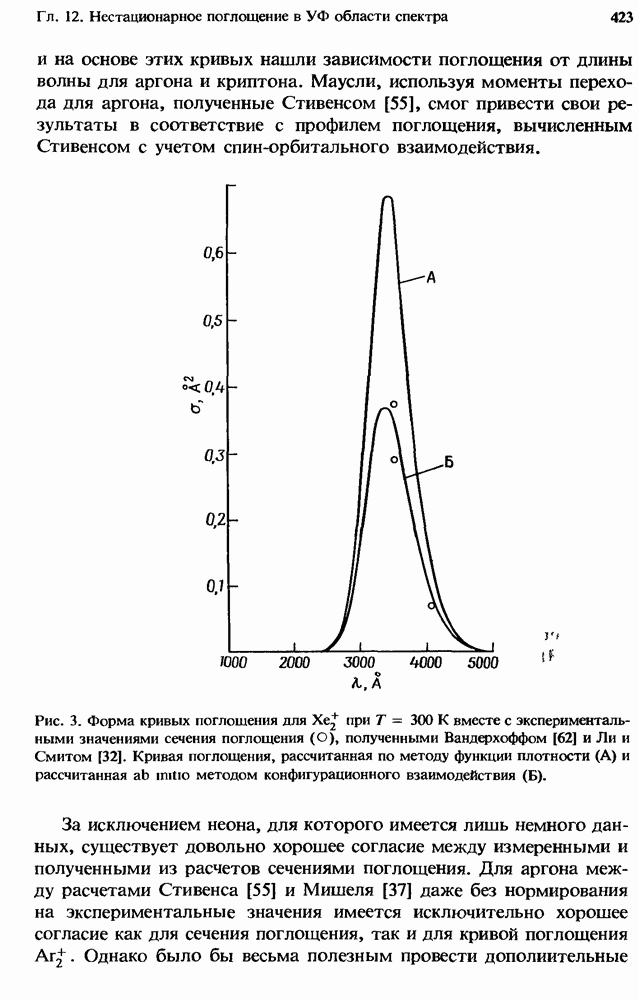
Обычно в разряде эксимерных лазеров давление составляет 1 атм или превышает это значение. На рис. 1 приведена схема типичного эксимерного лазера с разрядом, управляемым электронным пучком. Плазма, создаваемая разрядом, имеет степень ионизации в интервале  и среднюю энергию электронов порядка нескольких электронвольт. Лазерные эксимерные молекулы обычно образуются в столкновительных процессах, включая ионную рекомбинацию и/или столкновительное тушение электронновозбужденных атомов инертных газов или паров металла [3, 12]. Создаваемые при этом относительные плотности электронновозбужденных состояний превышают обычно величину
и среднюю энергию электронов порядка нескольких электронвольт. Лазерные эксимерные молекулы обычно образуются в столкновительных процессах, включая ионную рекомбинацию и/или столкновительное тушение электронновозбужденных атомов инертных газов или паров металла [3, 12]. Создаваемые при этом относительные плотности электронновозбужденных состояний превышают обычно величину  Общее поведение такой плазмы определяется сложной цепью процессов переноса энергии и взаимодействий, при которых сохраняются
Общее поведение такой плазмы определяется сложной цепью процессов переноса энергии и взаимодействий, при которых сохраняются
частицы (см. гл. 10 и 11 настоящей книги). Вследствие сильно не равновесной природы разрядной плазмы существует несколько типов неустойчивости [14], относящихся к различным степеням свободы лазерной среды. Анализ этих различных типов неустойчивосп разряда в эксимерных лазерах показывает, что только ионизацион ной неустойчивости свойственны условия возникновения и высока скорость нарастания, которые приводят к разрушению разряда за времена, наблюдаемые экспериментально. Кроме того, скорост) нарастания этой неустойчивости сравнима с общей скоростью ионизации, обусловленной электронным ударом.

Рис. 1. Схематическое представление электроразрядного лазера, управляемого электронным пучком. Обшие характеристики этих устройств рассматривали Брау [6 Эуинг [12] и Догерти [8]. 1 — источник питания разряда (+); 2 — возбужденная среда; 3 — катод разряда; 4 — катод для электронного пучка; 5 — высокое напряжена (—); 6 — проходной изолятор; 7 — анод для электронного пучка и фольга; 8 — анод разряда.
Хотя электрические разряды, создающие активную среду экси мерных лазеров больших объемов, по своей природе являются не стационарными, их локальные свойства изменяются за существен но большие временные интервалы по сравнению с характерным) временами столкновительных процессов. При стабильном горени разряда выполняются условия локального квазистационарного со стояния и средняя плотность электронов  удовлетворяет уравнению непрерывности
удовлетворяет уравнению непрерывности

где  — константа полной скорости ионизации под действием при ложенного электрического поля, а — коэффициент потерь электронов и
— константа полной скорости ионизации под действием при ложенного электрического поля, а — коэффициент потерь электронов и  — скорость ионизации, обусловленная электронным
— скорость ионизации, обусловленная электронным  ком высокой энергии. В общем случае константа скорости
ком высокой энергии. В общем случае константа скорости  является функцией электронной плотности и кинетической температуры
является функцией электронной плотности и кинетической температуры
электронов  . Она представляет собой сумму вкладов в полную скорость ионизации, обусловленных ионизацией из электронно-возбужденных состояний, а именно
. Она представляет собой сумму вкладов в полную скорость ионизации, обусловленных ионизацией из электронно-возбужденных состояний, а именно

здесь  — плотность
— плотность  электронно-возбужденного состояния и
электронно-возбужденного состояния и  — константа скорости ионизации
— константа скорости ионизации  состояния электронами, нагретыми разрядом. Величина
состояния электронами, нагретыми разрядом. Величина  представляет собой общую плотность газа. Константа скорости
представляет собой общую плотность газа. Константа скорости  зависит главным образом от кинетической температуры электронов. Зависимость
зависит главным образом от кинетической температуры электронов. Зависимость  от плотности электронов определяется, как правило, зависимостью плотностей, электронно-возбужденных состояний
от плотности электронов определяется, как правило, зависимостью плотностей, электронно-возбужденных состояний  - от
- от  .
.
В приложении А показано, что величина прикладываемого электрического поля, необходимая для поддержания кинетической температуры электронов Т, определяется сохранением энергии при джоулевом нагреве совместно с процессами, связанными с потерями энергии электронов при столкновениях. В условиях разряда, характерных для большинства эксимерных лазеров, вклад энергии электронного пучка в нагрев электронов весьма мал  Основная часть энергии электронного пучка идет на ионизацию
Основная часть энергии электронного пучка идет на ионизацию  образование электронно-возбужденных состояний
образование электронно-возбужденных состояний  а также на диссоциацию молекул и образование отрицательных ионов или на диссоциативную рекомбинацию
а также на диссоциацию молекул и образование отрицательных ионов или на диссоциативную рекомбинацию  Котя электронный пучок и вносит вклад в формирование возбужденных состояний, плотности электронно-возбужденных состояний
Котя электронный пучок и вносит вклад в формирование возбужденных состояний, плотности электронно-возбужденных состояний  в разряде эксимерных лазеров главным образом определяются возбуждением электронами, нагретыми (джоулев нагрев) в разряде. Исчезновение этих электронно-возбужденных частиц обусловлено лавным образом тушением их тяжелыми частицами, что в большинстве случаев приводит непосредственно к образованию эксимерных молекул.
в разряде эксимерных лазеров главным образом определяются возбуждением электронами, нагретыми (джоулев нагрев) в разряде. Исчезновение этих электронно-возбужденных частиц обусловлено лавным образом тушением их тяжелыми частицами, что в большинстве случаев приводит непосредственно к образованию эксимерных молекул.
Моделирование разряда эксимерных лазеров [16, 23, 29] показано, что мощность разряда можно с большой эффективностью использовать для создания электронно-возбужденных состояний, из которых затем в процессах тушения этих состояний нейтральными частицами образуются эксимеры. Например, из модельных исследований в случае KrF [16] следует, что, до тех пор пока относительная концентрация метастабильных состояний поддерживается  уровне
уровне  на образование метастабильных состояний инертного газа может расходоваться 70 — 80% мощности разряда. Такая эффективность образования метастабилей может
на образование метастабильных состояний инертного газа может расходоваться 70 — 80% мощности разряда. Такая эффективность образования метастабилей может
привести к образованию эксимеров KrF с кпд до 35%. Моделирование показало также, что в этих условиях электроны в разряде возникают главным образом вследствие ионизации метастабилей. При этом разряд оказывается существенно менее устойчивым, поскольку скорость образования электронов становится сильно возрастающей функцией электронной плотности. В отсутствие управления соответствующими параметрами разряда возникает ионизационная неустойчивость, которая ведет к образованию дуги или шнурованию разряда, что быстро заканчивается прекращением лазерной генерации [9].
В работах [5, 6, 9, 18] показано, что стационарное состояние, определяемое уравнением (1), будет неустойчивым (т. е. будет разрушаться благодаря росту флуктуаций малой амплитуды) при выполнении следующего условия (см. приложение 1 к настоящей главе);

Если в неравенстве (3) знак «больше» заменить на «меньше», то стационарное состояние разряда, определяемое выражением (1), будет стабильным. Начальная скорость нарастания флуктуаций малой амплитуды, ведущих к неустойчивости, дается выражением (см. приложение 1 к настоящей главе)

Частные производные в (3) и (4) вычисляются при постоянной кинетической температуре электронов. Электрическое поле и джоулев нагрев возмущаются таким образом, что в первый момент развития ионизационной неустойчивости возмущения электронной кинетической температуры остаются малыми по сравнению с возмущениями плотности электронов. Поэтому условие неустойчивости [соотношение (3)] и начальная скорость нарастания возмущений с малой амплитудой [соотношение (4)] зависят в первом приближении лишь от того, как меняется плотность электронов в процессе их образования и гибели.
Соотношение (3) показывает, что состояние разряда в чистом виде  будет неустойчивым, если с ростом плотности электронов константа суммарной скорости ионизации
будет неустойчивым, если с ростом плотности электронов константа суммарной скорости ионизации  увеличивается быстрее, чем коэффициент потерь электронов а (т. е.
увеличивается быстрее, чем коэффициент потерь электронов а (т. е.  ). Когда это условие выполняется, то за счет многоступенчатой ионизации с участием возбужденных состояний за
). Когда это условие выполняется, то за счет многоступенчатой ионизации с участием возбужденных состояний за
время флуктуации образуется больше электронов, чем их теряется в процессе рекомбинации. Таким образом, как только электронная плотность начала возрастать, скорость образования электронов увеличивается быстрее, чем скорость их исчезновения, и увеличение электронной плотности уже не сдерживается более процессом гибели электронов. Характерное время роста неустойчивости  равно времени ионизации
равно времени ионизации  Эта неустойчивость может быть подавлена с помощью ионизующего электронного пучка
Эта неустойчивость может быть подавлена с помощью ионизующего электронного пучка  Скорость ионизации электронным пучком
Скорость ионизации электронным пучком  необходимую для стабилизации разряда, можно определить, обратив знак неравенства в выражении (3).
необходимую для стабилизации разряда, можно определить, обратив знак неравенства в выражении (3).
Обычно в разрядах эксимерных лазеров преобладает один из двух процессов гибели электронов — это диссоциативное прилипание или диссоциативная рекомбинация. В разрядах галогенидов инертных газов (см. гл. 10 настоящей книги) и большинства галогенидов металлов (см. гл. 11 настоящей книги) электроны исчезают благодаря диссоциативному прилипанию, причем  где
где  — плотность электроотрицательных частиц (как правило, это молекулы галогенов), а
— плотность электроотрицательных частиц (как правило, это молекулы галогенов), а  — константа скорости прилипания. В этом случае условие для порога неустойчивости [см. выражение (3)] принимает более простой вид
— константа скорости прилипания. В этом случае условие для порога неустойчивости [см. выражение (3)] принимает более простой вид

Соответствующая скорость нарастания неустойчивости [см. выражение (4)] записывается в виде

Для разрядов в парах металлов гибель электронов в основном определяется диссоциативной рекомбинацией и  где
где  — константа скорости диссоциативной рекомбинации. В случае таких разрядов пороговое условие (3) для возникновения неустойчивости имеет вид
— константа скорости диссоциативной рекомбинации. В случае таких разрядов пороговое условие (3) для возникновения неустойчивости имеет вид

Соответствующая скорость нарастания неустойчивости [выражение (4)] равна

В разрядах, в которых диссоциативная рекомбинация преобладает над диссоциативным прилипанием, неустойчивость возникает при ббльших значениях  . В этом смысле разряды эксимерных лазеров, в которых гибель электронов обусловлена образованием отрицательных ионов при диссоциативном прилипании, значительно менее устойчивы, чем те, в которых гибель электронов определяется диссоциативной рекомбинацией. Однако в обоих случаях устойчивость разряда существенно зависит от того, как функционально зависит константа суммарной скорости к, ионизации от плотности электронов.
. В этом смысле разряды эксимерных лазеров, в которых гибель электронов обусловлена образованием отрицательных ионов при диссоциативном прилипании, значительно менее устойчивы, чем те, в которых гибель электронов определяется диссоциативной рекомбинацией. Однако в обоих случаях устойчивость разряда существенно зависит от того, как функционально зависит константа суммарной скорости к, ионизации от плотности электронов.
В равновесной плазме плотности возбужденных состояний подчиняются распределению Больцмана

и являются функциями только электронной температуры. Таким образом, в равновесной и квазиравновесной плазме константа суммарной скорости ионизации [выражение (2)] не зависит от плотности электронов, т. е. мы имеем  и в соответствии с условием (3) разряд оказывается устойчивым. Ротуэлл и др. [30], Шуман и др. [7], а также Шукер и др. [24] получили экспериментально устойчивый стационарный разряд с высокой плотностью мощности
и в соответствии с условием (3) разряд оказывается устойчивым. Ротуэлл и др. [30], Шуман и др. [7], а также Шукер и др. [24] получили экспериментально устойчивый стационарный разряд с высокой плотностью мощности  в ксеноне с добавками металла без использования источника предыонизации или электронного пучка. В этих разрядах степень ионизации определялась конкуренцией между процессом образования электронов в процессе столкновительного многоступенчатого возбуждения с последующей ионизацией возбужденных атомов металла и процессом гибели электронов за счет диссоциативной рекомбинации с двухатомными ионами металла. Изменения показали, что в таких разрядах распределения населенностей электронных состояний атомов металла близки к больцмановскому распределению с температурой
в ксеноне с добавками металла без использования источника предыонизации или электронного пучка. В этих разрядах степень ионизации определялась конкуренцией между процессом образования электронов в процессе столкновительного многоступенчатого возбуждения с последующей ионизацией возбужденных атомов металла и процессом гибели электронов за счет диссоциативной рекомбинации с двухатомными ионами металла. Изменения показали, что в таких разрядах распределения населенностей электронных состояний атомов металла близки к больцмановскому распределению с температурой  [см. выражение (9)]. К сожалению, в разрядах эксимерных лазеров квазистационарные состояния, как правило, не реализуются. Напротив, как прямое следствие механизма образования лазерных эксимерных молекул, населенности электронно-возбужденных состояний
[см. выражение (9)]. К сожалению, в разрядах эксимерных лазеров квазистационарные состояния, как правило, не реализуются. Напротив, как прямое следствие механизма образования лазерных эксимерных молекул, населенности электронно-возбужденных состояний  отклоняются от равновесных вследствие конкуренции столкновительных процессов с участием электронов и тяжелых частиц. В столкновениях с тяжелыми частицами населенность возбужденных состояний уменьшается, в то время как в столкновениях с электронами она увеличивается. Следовательно, с ростом плотности электронов при постоянной кинетической температуре Те плотности возбужденных состояний должны возрастать. Поскольку константа суммарной скорости ионизации
отклоняются от равновесных вследствие конкуренции столкновительных процессов с участием электронов и тяжелых частиц. В столкновениях с тяжелыми частицами населенность возбужденных состояний уменьшается, в то время как в столкновениях с электронами она увеличивается. Следовательно, с ростом плотности электронов при постоянной кинетической температуре Те плотности возбужденных состояний должны возрастать. Поскольку константа суммарной скорости ионизации
[выражение (2)] пропорциональна населенностям возбужденных состояний, она увеличивается с ростом плотности электронов, т. е. в общем случае мы имеем  Причины неустойчивости можно понять лучше, если рассмотреть несколько простых моделей кинетики ионизации в разрядах эксимерных лазеров.
Причины неустойчивости можно понять лучше, если рассмотреть несколько простых моделей кинетики ионизации в разрядах эксимерных лазеров.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
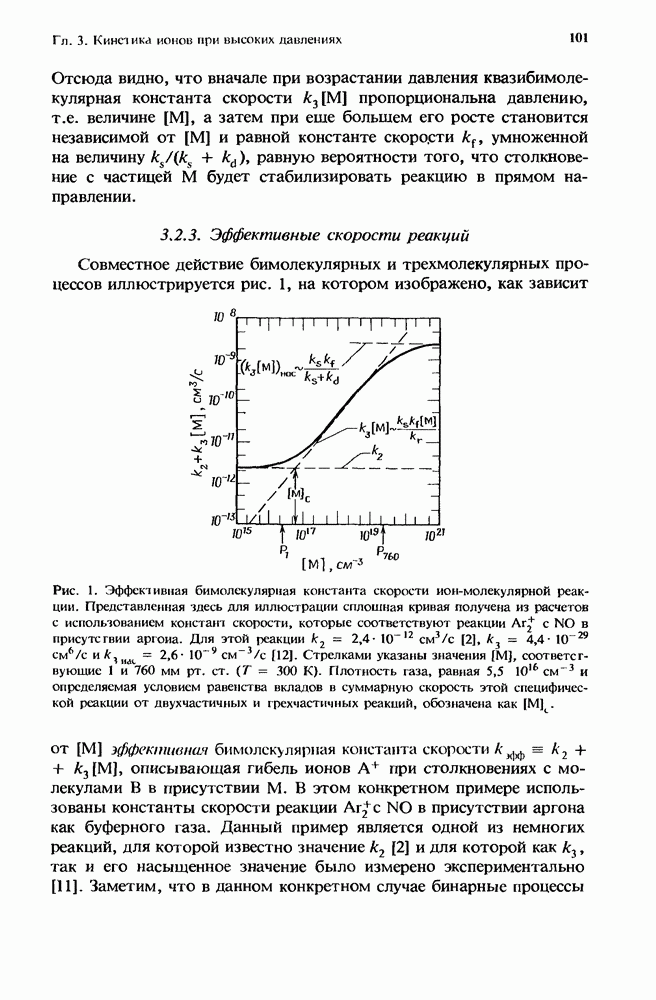
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
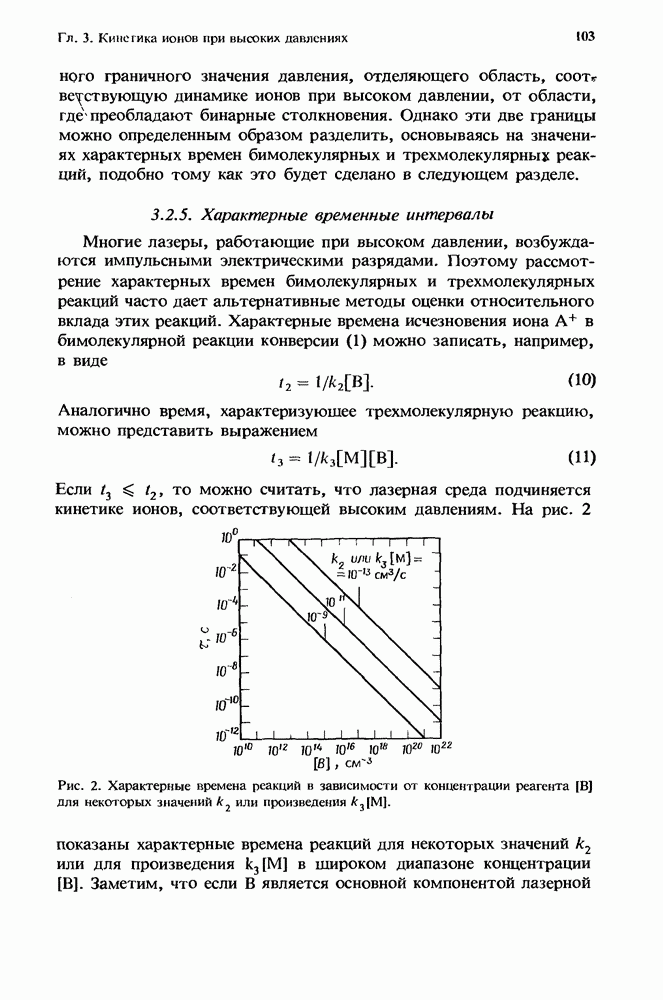
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
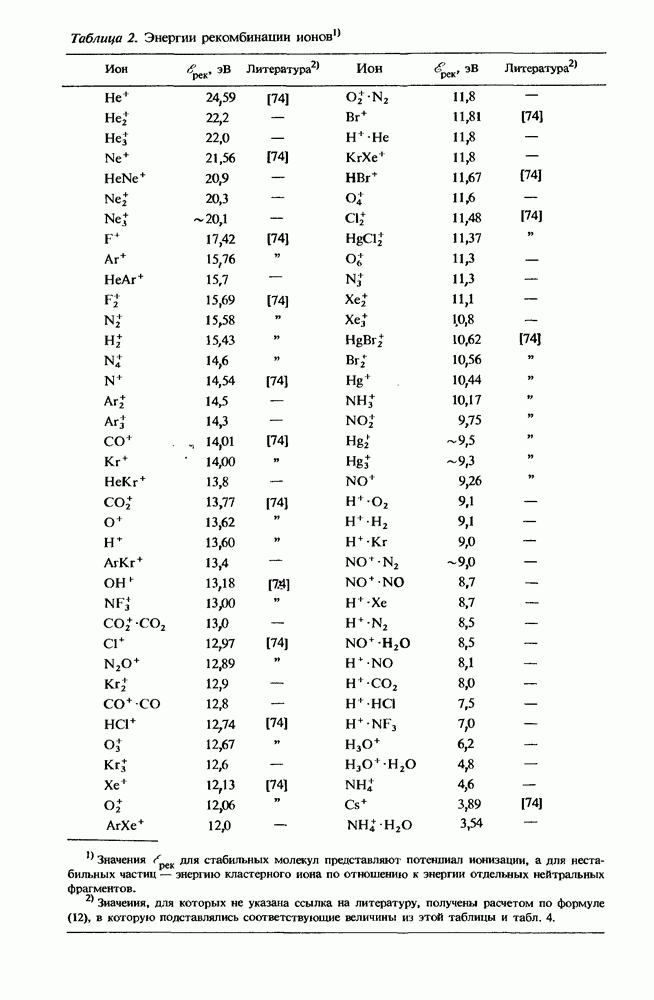
- 3.2.2. Энергетика отрицательных ионов
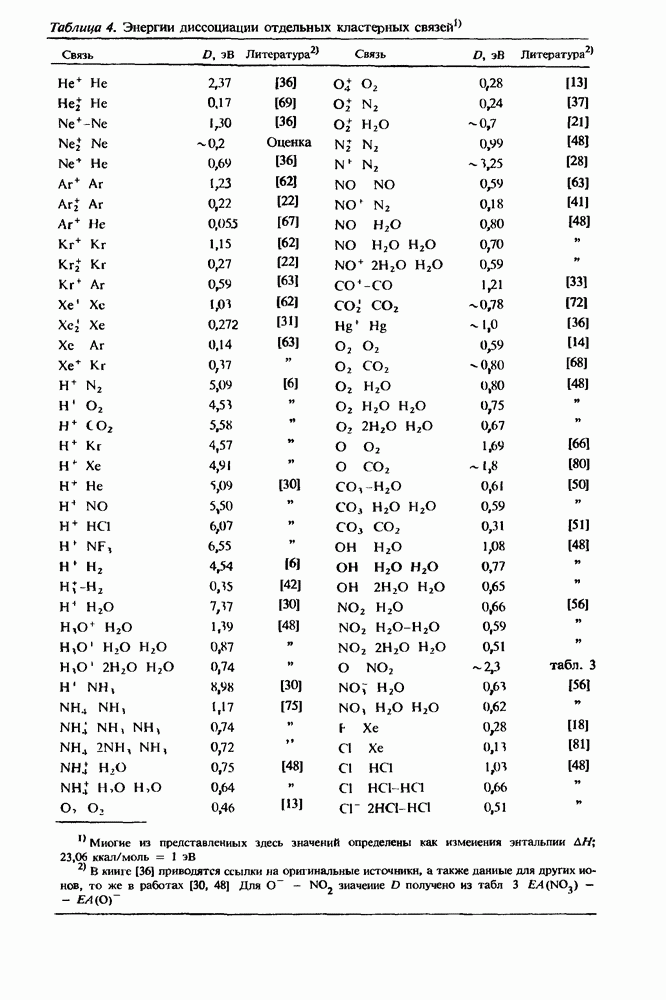
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
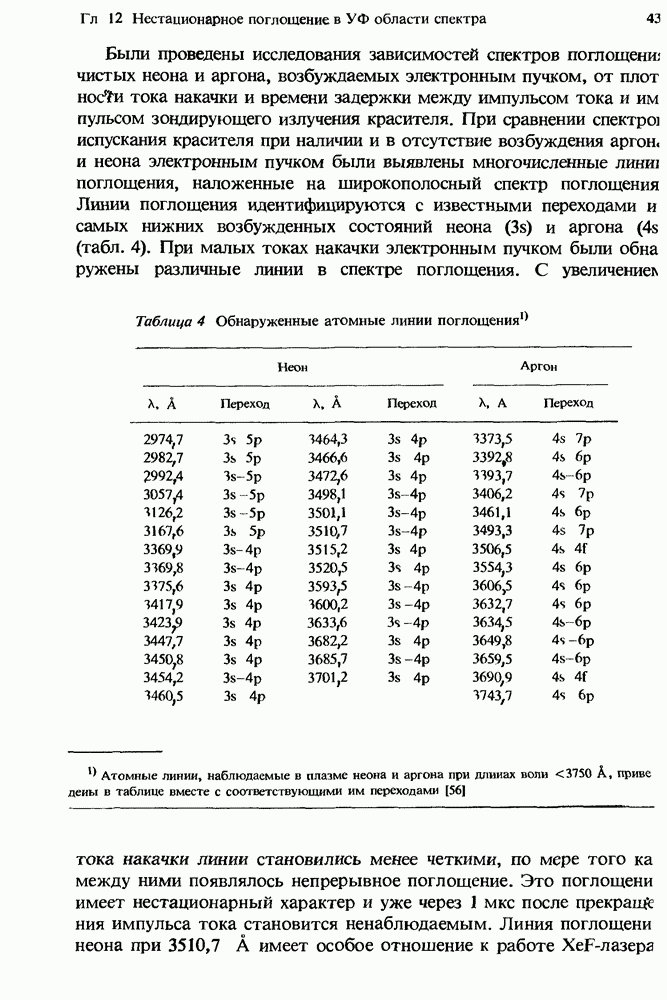
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации