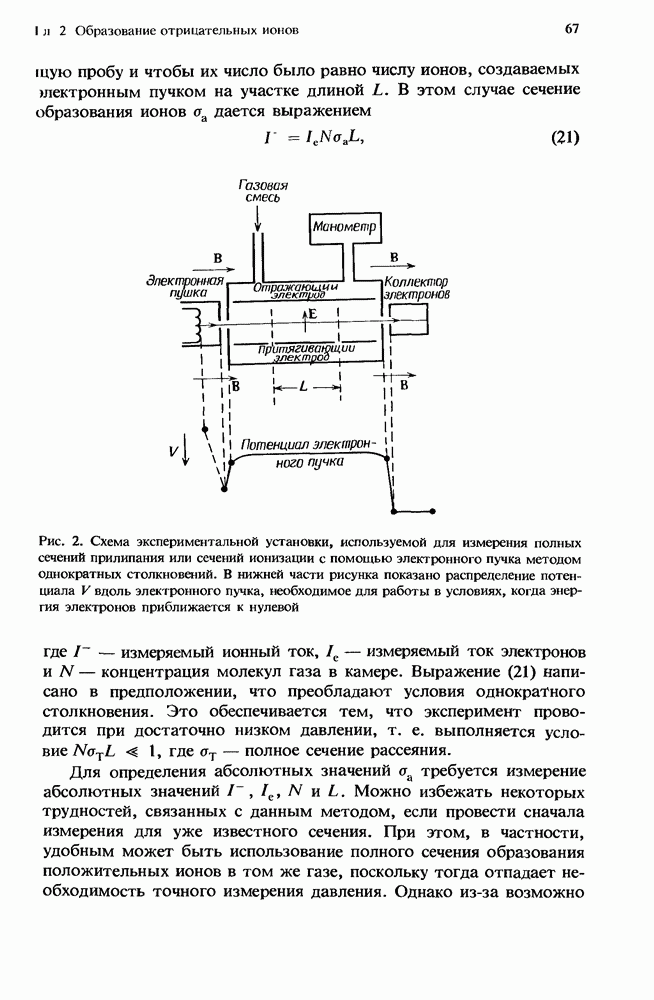
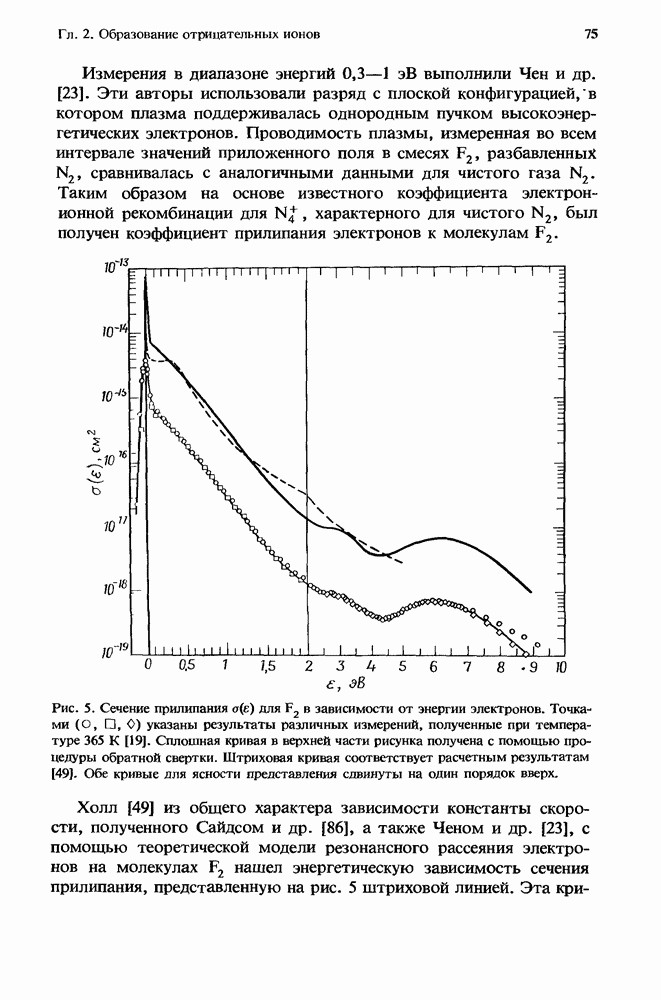
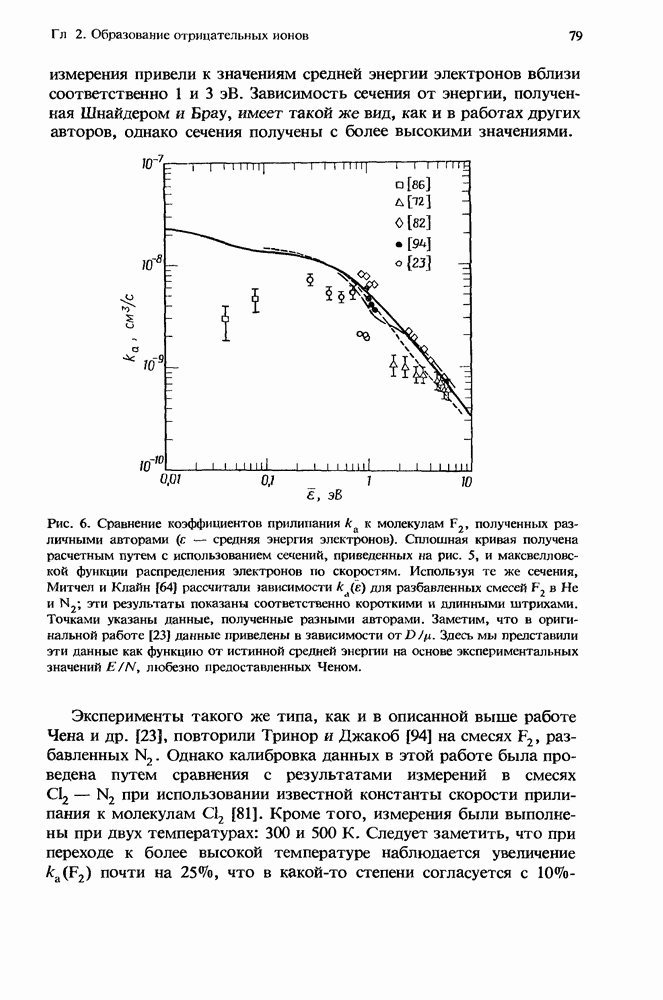
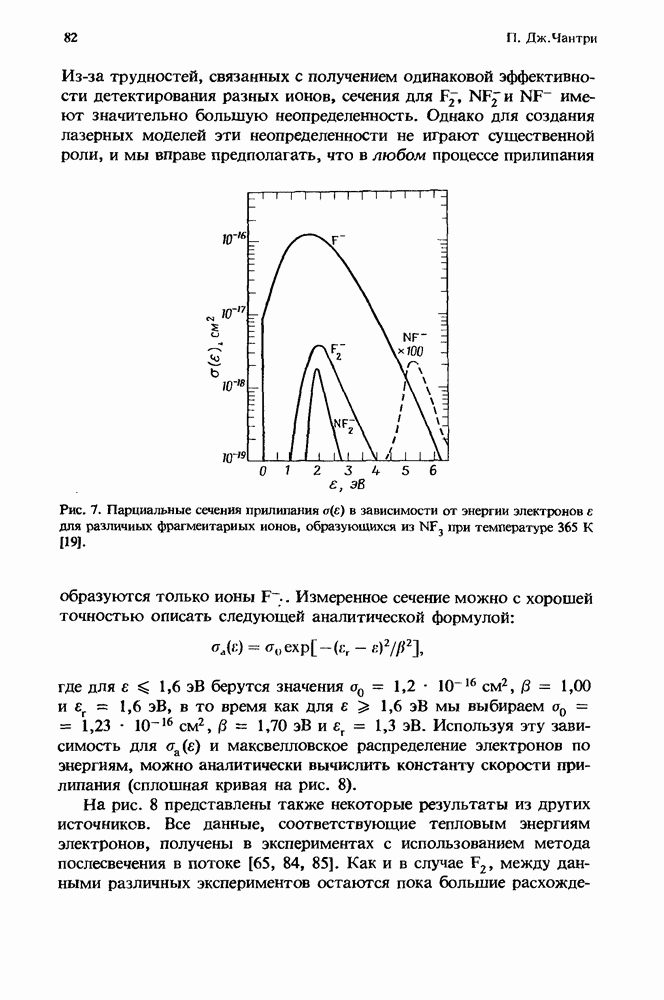
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8.2.3. Кинетическая модель
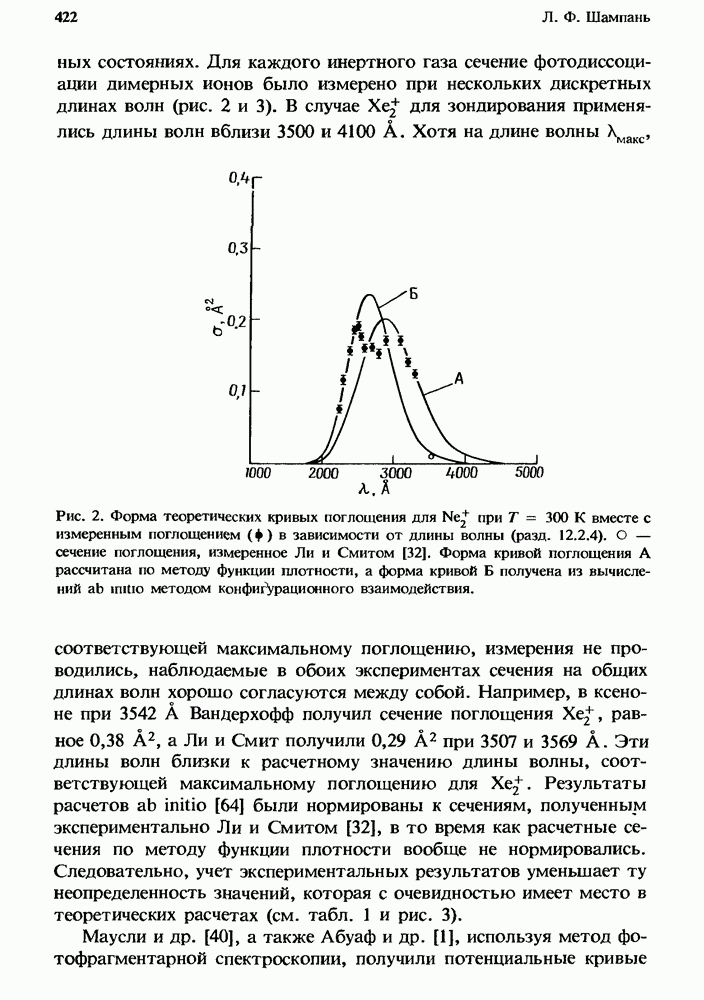
Электрические разряды в газовых смесях, содержащих Не,  приводят к огромному числу различных взаимодействий между образующимися в разряде электронами, ионами и молекулами, находящимися в различных возбужденных состояниях. Для достаточно простого описания процессов, протекающих в плазме газового разряда, необходимо иметь конечное число переменных, которые бы соответствовали поставленным задачам и позволяли бы
приводят к огромному числу различных взаимодействий между образующимися в разряде электронами, ионами и молекулами, находящимися в различных возбужденных состояниях. Для достаточно простого описания процессов, протекающих в плазме газового разряда, необходимо иметь конечное число переменных, которые бы соответствовали поставленным задачам и позволяли бы
провести соответствующее усреднение по всевозможным взаимодействиям и состояниям.
Задачу можно существенно упростить, если заметить, что в интересующем нас масштабе времени (микросекунды) межмолекуляр-ные столкновения определенного класса происходят столь часто, что для энергетических состояний, связанных взаимодействиями, возникающими при этих столкновениях, реализуются квазиравновесные условия.
Обмен колебательной энергией внутри любой колебательной моды протекает с небольшим изменением кинетической энергии молекул. Пэк [19] предсказал очень высокую скорость таких «почти резонансных» процессов V — V-обмена. При моделировании квазиравновесное состояние, устанавливаемое внутри каждой колебательной моды, можно получить, если каждую моду рассматривать как гармонический осциллятор и использовать статистику Больцмана. Колебательную температуру можно определить через полную энергию, запасенную в колебательной моде. В принципе внутримодовое квазиравновесное распределение зависит от температуры газа  поскольку при протекании реакций V —
поскольку при протекании реакций V —  -обмена происходит хотя и незначительное, но все же отличное от нуля изменение кинетической энергии. Необходимо также учитывать обмен с резервуаром поступательной энергии молекул, даже если рассматриваются столкновения только квазиравновесного V — V-обмена.
-обмена происходит хотя и незначительное, но все же отличное от нуля изменение кинетической энергии. Необходимо также учитывать обмен с резервуаром поступательной энергии молекул, даже если рассматриваются столкновения только квазиравновесного V — V-обмена.
Еще одно упрощение можно сделать, предполагая существование процесса быстрого, почти резонансного V — V-обмена:

Экспериментальные данные Джакобса и др. [13] указывают на то, что этому процессу при нормальных условиях соответствуют времена релаксации порядка нескольких наносекунд. Это приводит к кинетической связи между симметрической  и деформационной
и деформационной  колебательными модами. Таким образом, если не интересоваться изменением населенностей уровней за время порядка наносекунд, то совокупность
колебательными модами. Таким образом, если не интересоваться изменением населенностей уровней за время порядка наносекунд, то совокупность  и В мод можно рассматривать как сильносвязанную изолированную систему, характеризуемую единственной переменной, а именно колебательной температурой.
и В мод можно рассматривать как сильносвязанную изолированную систему, характеризуемую единственной переменной, а именно колебательной температурой.
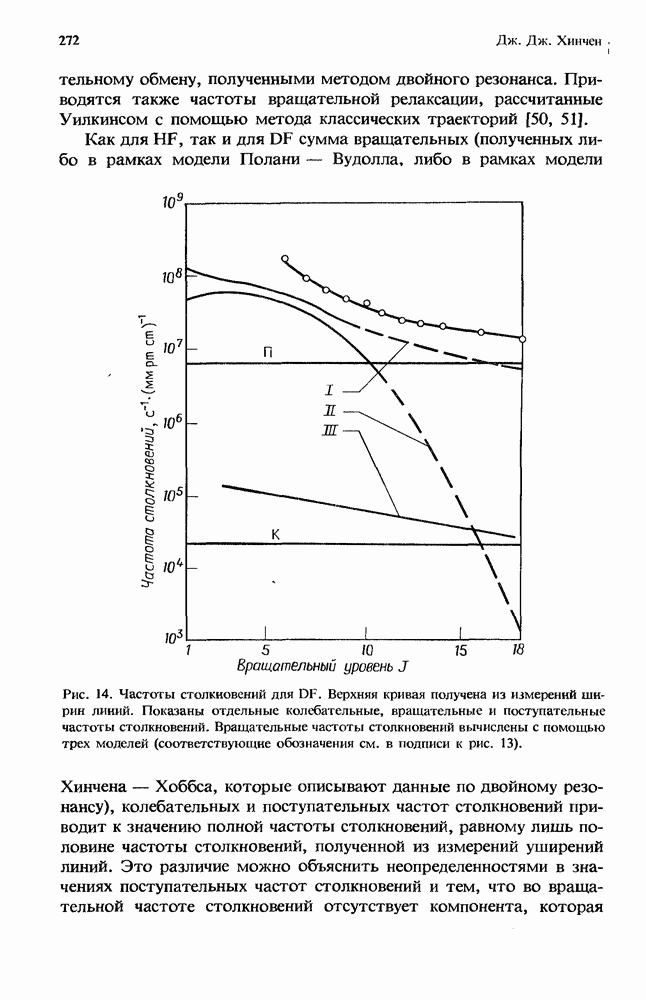
Поскольку величина вращательных квантов мала, при столкновениях вращательная энергия легко переходит в поступательную.
Это подтверждается расчетами Престона и Пэка [20], а также экспериментальными данными Джакобса и др. [12]. При давлениях 1 атм и выше можно считать, что вращательные и поступательные степени свободы находятся в равновесии между собой.

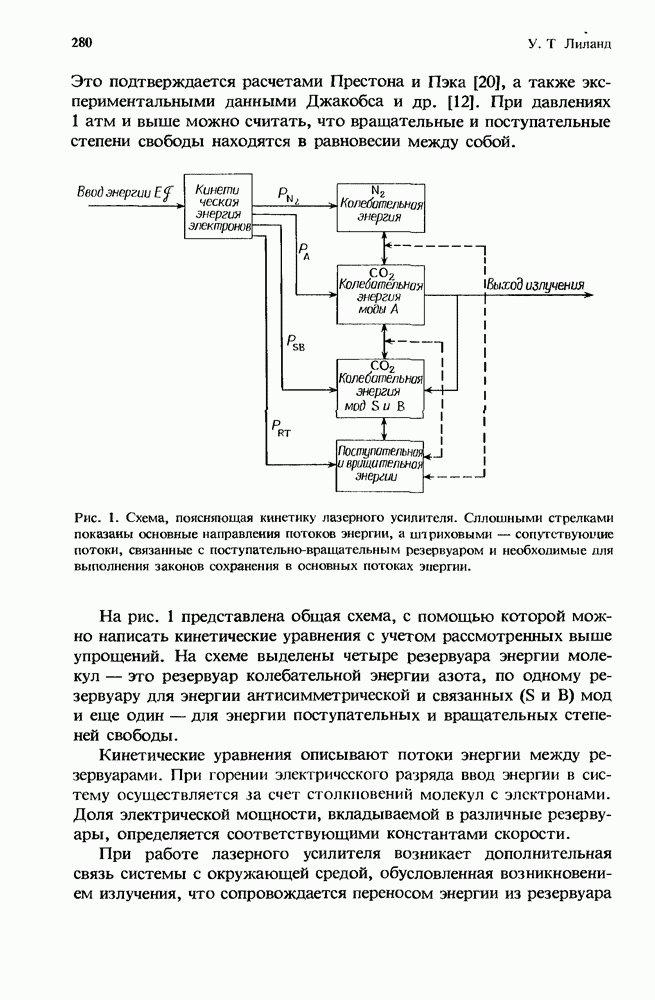
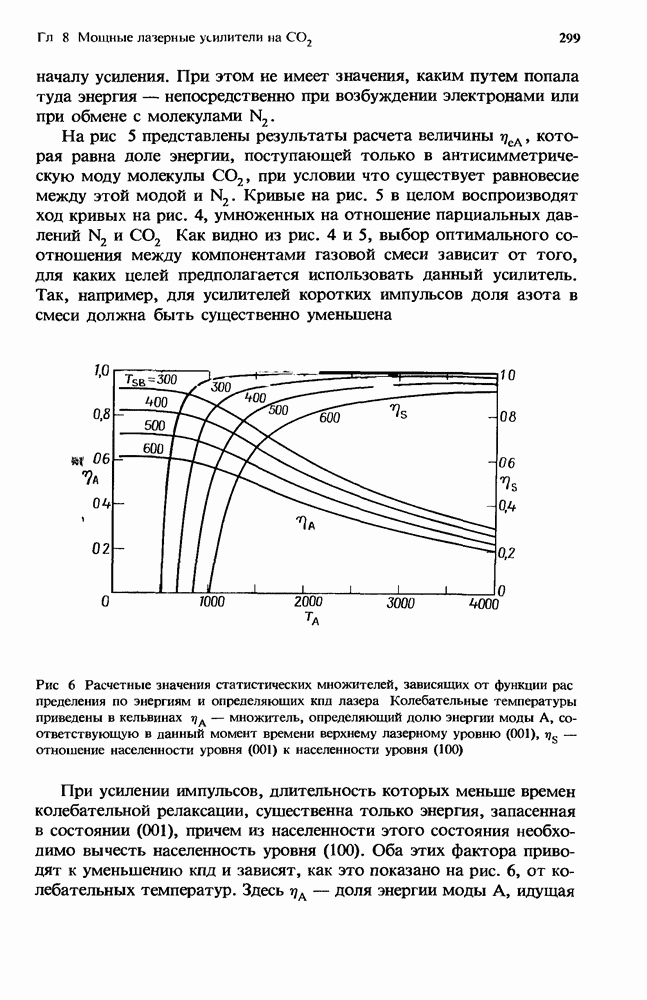
Рис. I. Схема, поясняющая кинетику лазерного усилителя. Сплошными стрелками показаны основные направления потоков энергии, а штриховыми — сопутствующие потоки, связанные с поступательно-вращательным резервуаром и необходимые для выполнения законов сохранения в основных потоках энергии.
На рис. 1 представлена общая схема, с помощью которой можно написать кинетические уравнения с учетом рассмотренных выше упрощений. На схеме выделены четыре резервуара энергии молекул — это резервуар колебательной энергии азота, по одному резервуару для энергии антисимметрической и связанных  мод и еще один — для энергии поступательных и вращательных степеней свободы.
мод и еще один — для энергии поступательных и вращательных степеней свободы.
Кинетические уравнения описывают потоки энергии между резервуарами. При горении электрического разряда ввод энергии в систему осуществляется за счет столкновений молекул с электронами. Доля электрической мощности, вкладываемой в различные резервуары, определяется соответствующими константами скорости.
При работе лазерного усилителя возникает дополнительная связь системы с окружающей средой, обусловленная возникновением излучения, что сопровождается переносом энергии из резервуара
А в резервуар SB. В процессе усиления приблизительно 40% энергии, отбираемой из резервуара А, выделяется в виде энергии излучения, а около 60% переходит в резервуар  Необходимо помнить, что интересующая нас молекула СО2 не может принадлежать к какому-либо отдельному резервуару; ее энергия распределена между всеми резервуарами.
Необходимо помнить, что интересующая нас молекула СО2 не может принадлежать к какому-либо отдельному резервуару; ее энергия распределена между всеми резервуарами.
После того как из кинетических уравнений будет определена величина полной энергии, запасенной в каждом из резервуаров, можно ответить на вопрос о значениях населенностей отдельных уровней. Предполагая, что внутри каждого резервуара реализуется равновесное распределение, плотность населенности колебательного состояния  можно записать через колебательные температуры соответствующих мод
можно записать через колебательные температуры соответствующих мод  следующим образом:
следующим образом:

где индекс X обозначает типы колебаний S, В или  — плотность молекул СО2. Величина
— плотность молекул СО2. Величина

представляет собой долю молекул СО2, находящихся в основном состоянии. Отметим, что существует  состояний с квантовым числом
состояний с квантовым числом  каждое из которых имеет населенность, определяемую выражением (3).
каждое из которых имеет населенность, определяемую выражением (3).
Колебательная температура — это не самая подходящая переменная для записи кинетических уравнений. В качестве переменных более удобно использовать либо полное число квантов в моде  либо плотности квантов (число квантов в моде, приходящееся на одну молекулу:
либо плотности квантов (число квантов в моде, приходящееся на одну молекулу:  . Эти переменные связаны с колебательной температурой и полной энергией, запасенной в моде, соотношением
. Эти переменные связаны с колебательной температурой и полной энергией, запасенной в моде, соотношением

где  — плотности энергии соответственно в модах S, В и А. Аналогичные соотношения можно записать и для молекулы азота:
— плотности энергии соответственно в модах S, В и А. Аналогичные соотношения можно записать и для молекулы азота:

Для отдельного колебательного состояния доля  молекул СО2, находящихся во вращательном состоянии
молекул СО2, находящихся во вращательном состоянии  задается выражением
задается выражением

где В соответствует величине В, в выражении (1) и имеет значения, которые лишь слегка отличаются друг от друга для различных наборов чисел  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
- 12.2.2. Сечение фотопоглощения
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации