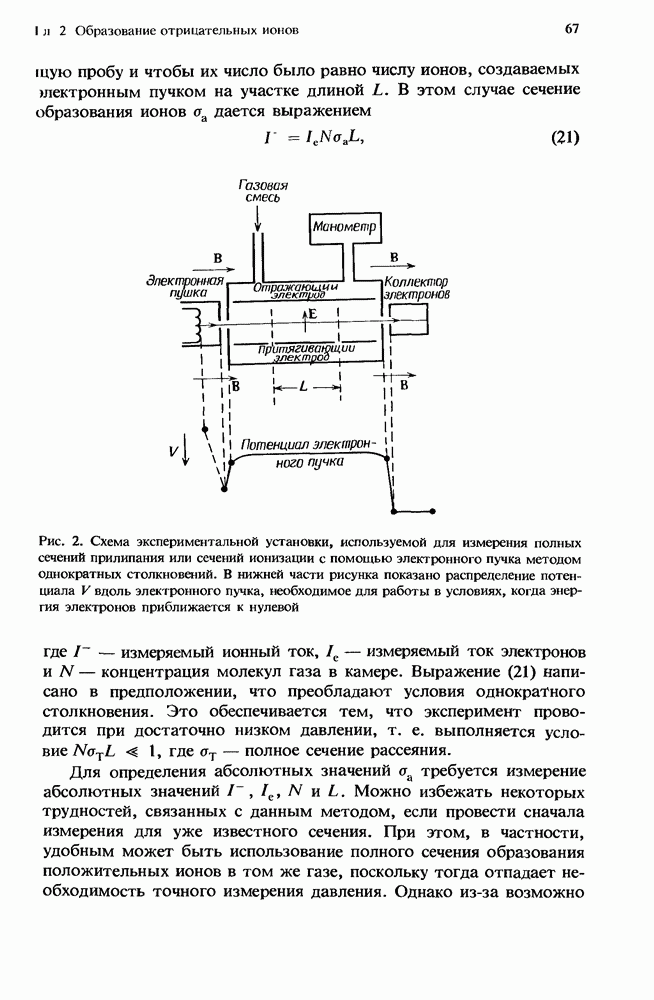
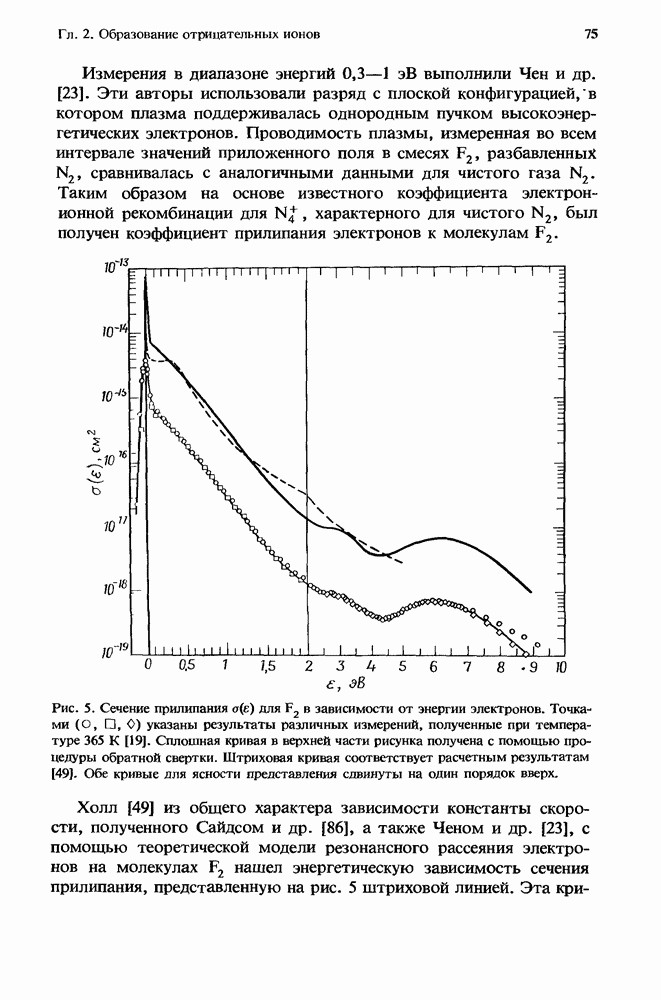
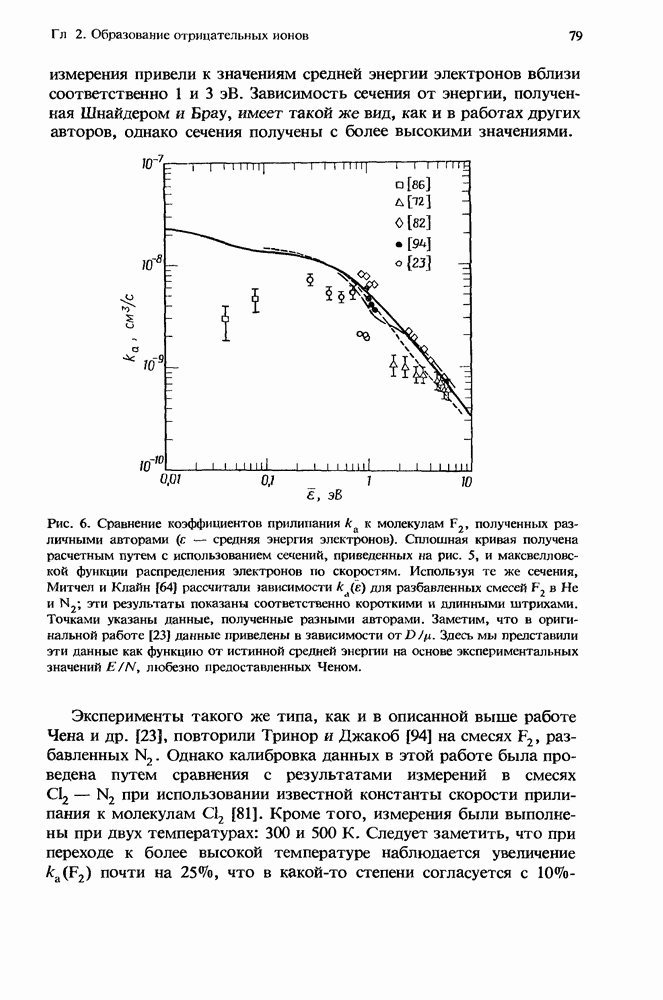
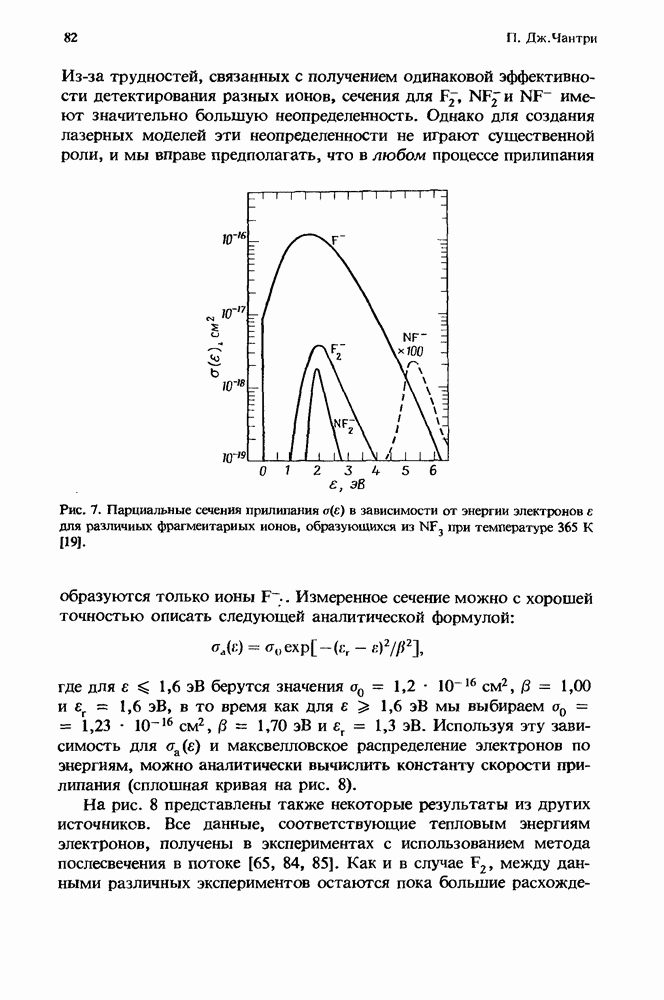
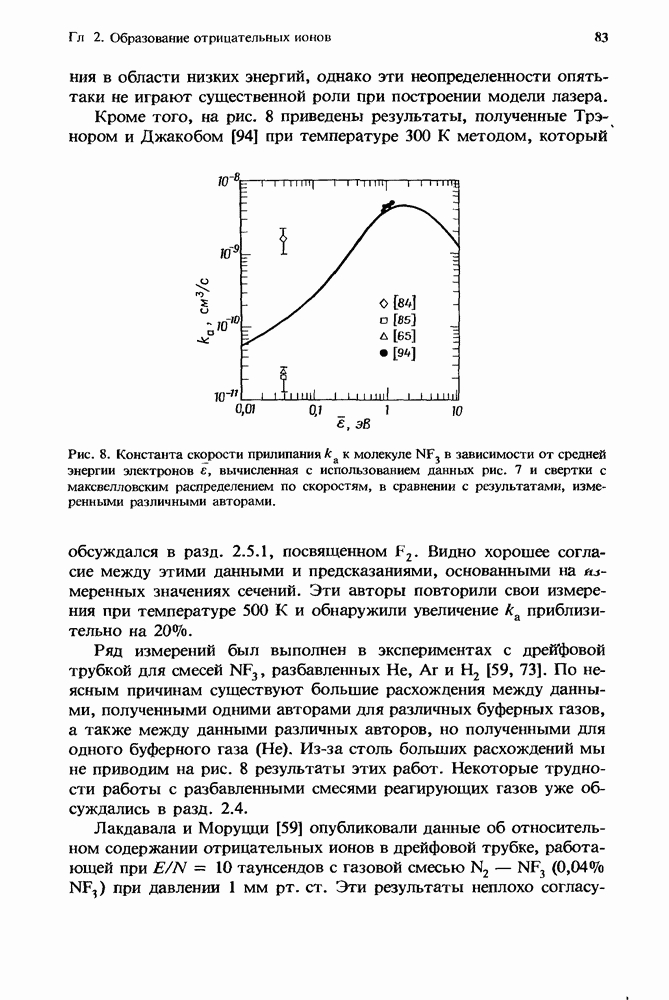
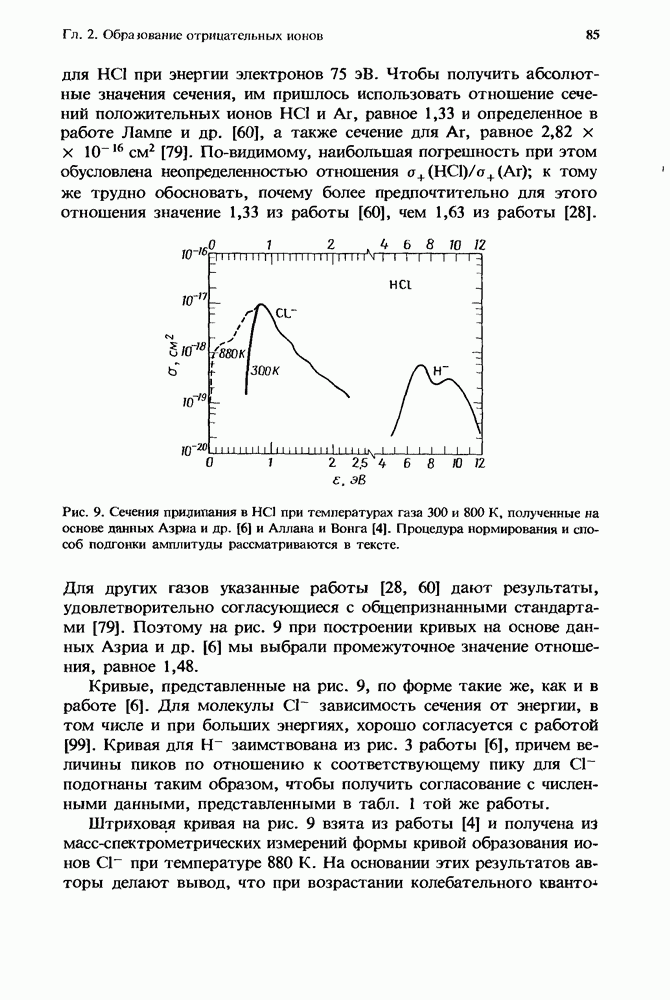
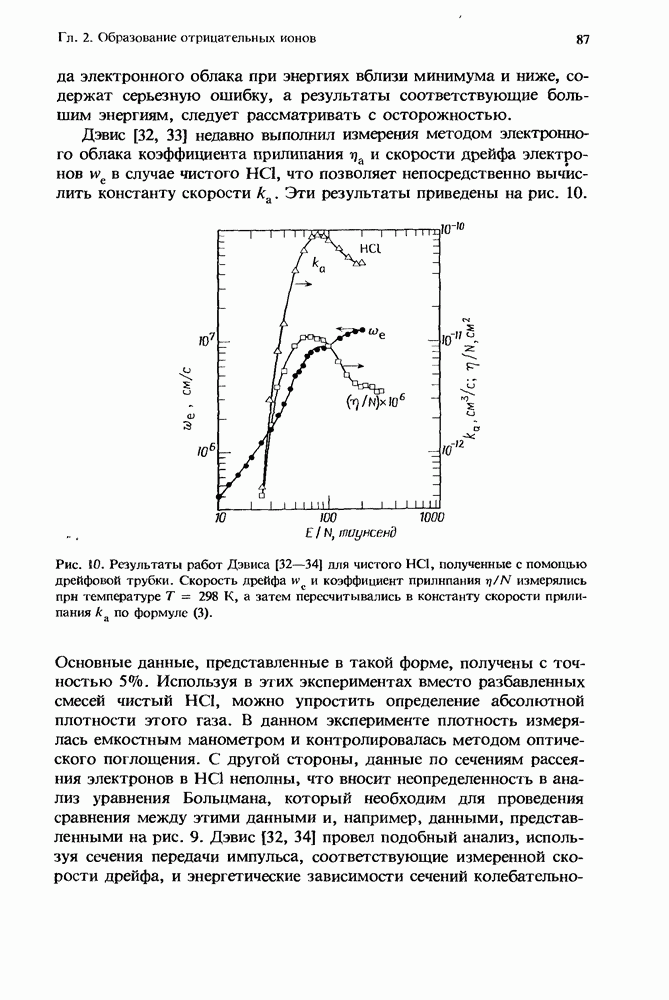
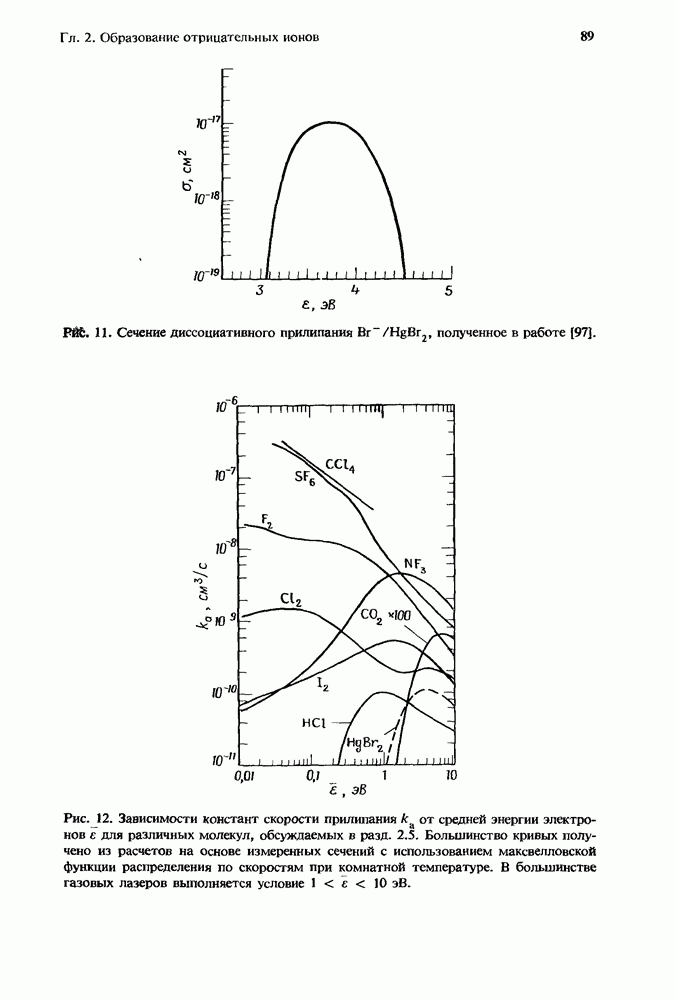
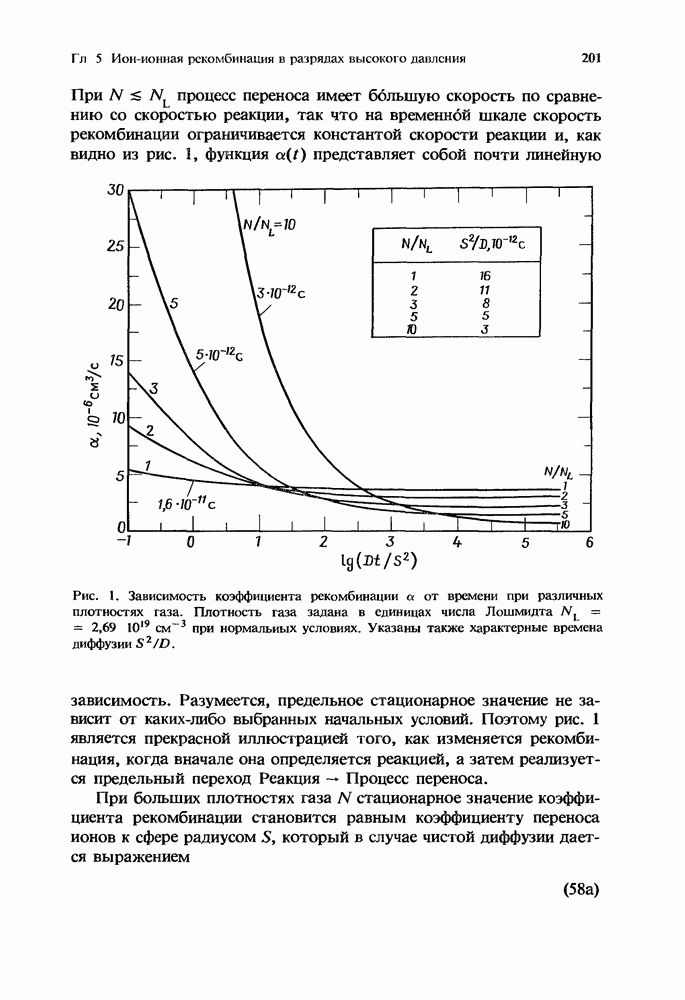
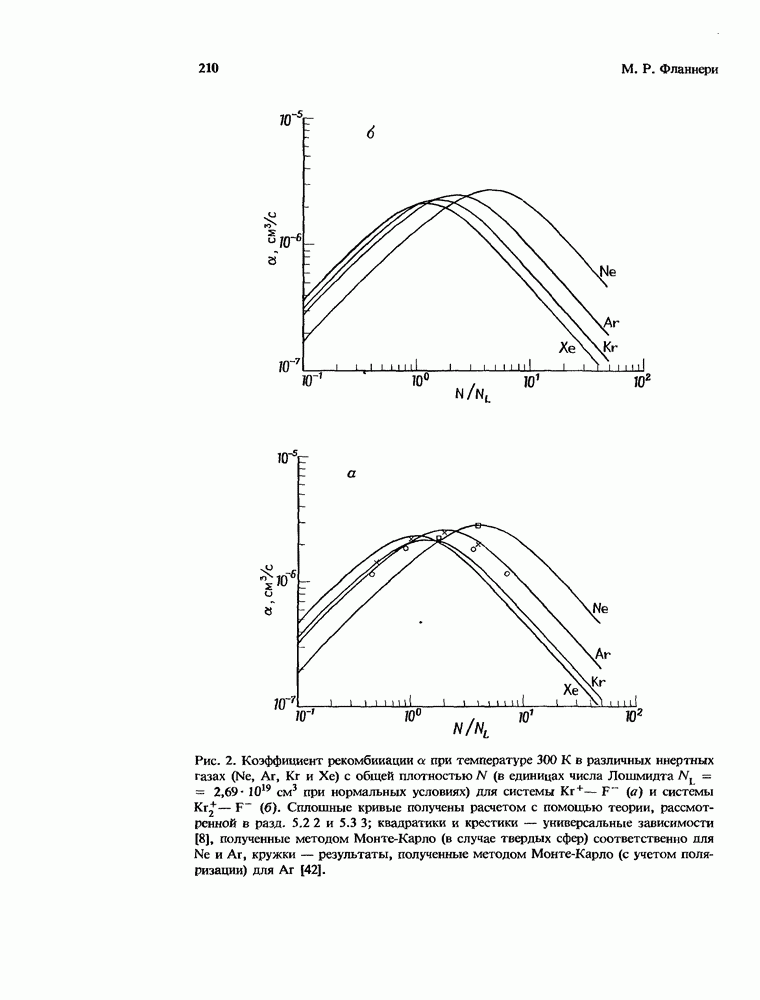
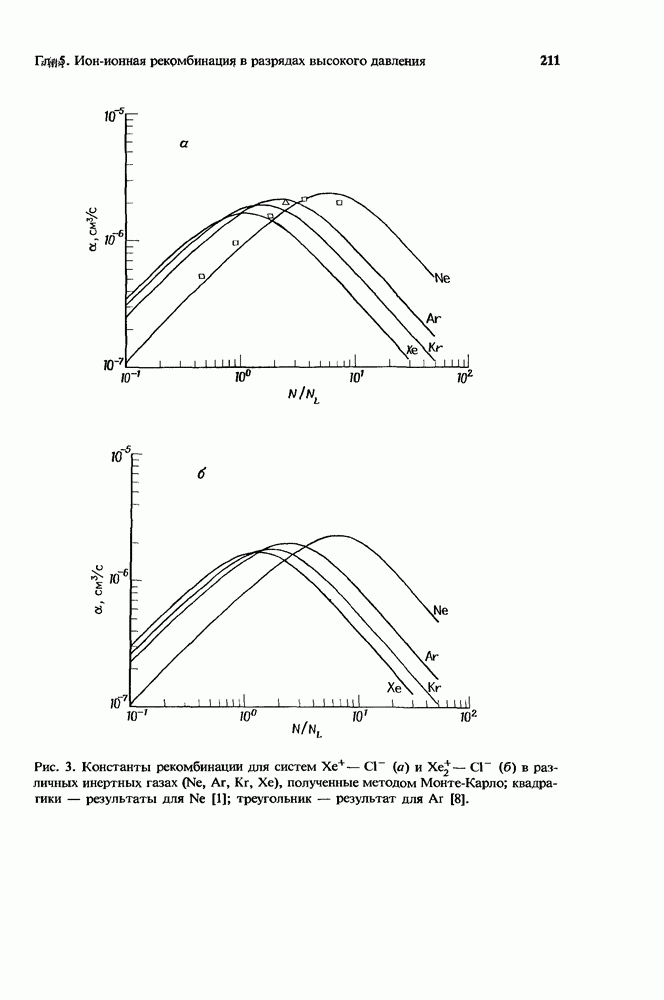
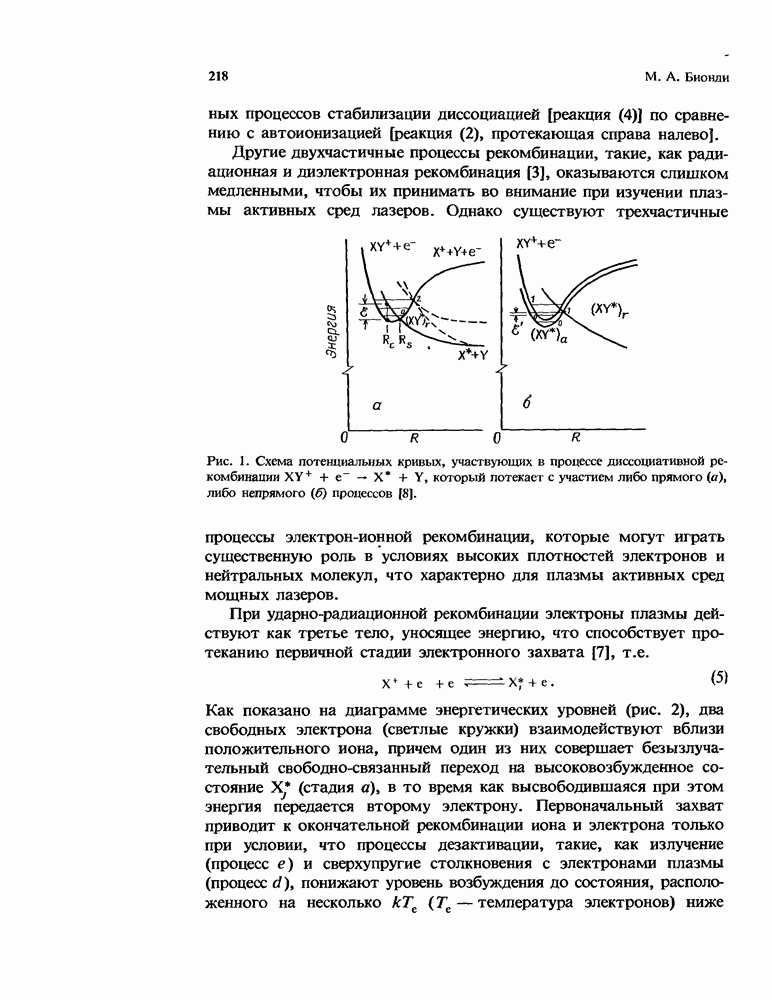
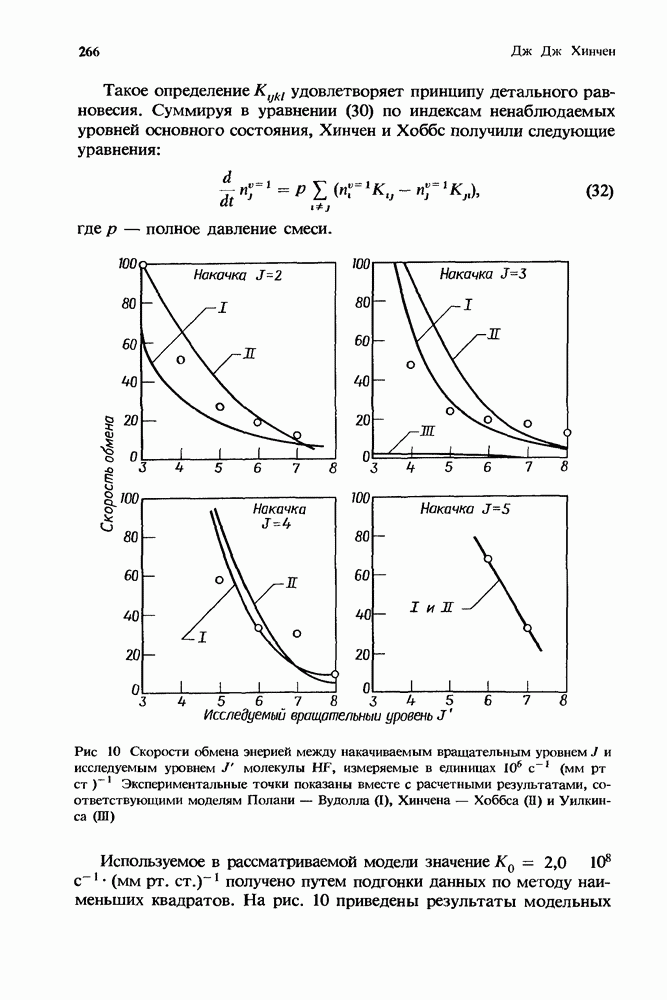
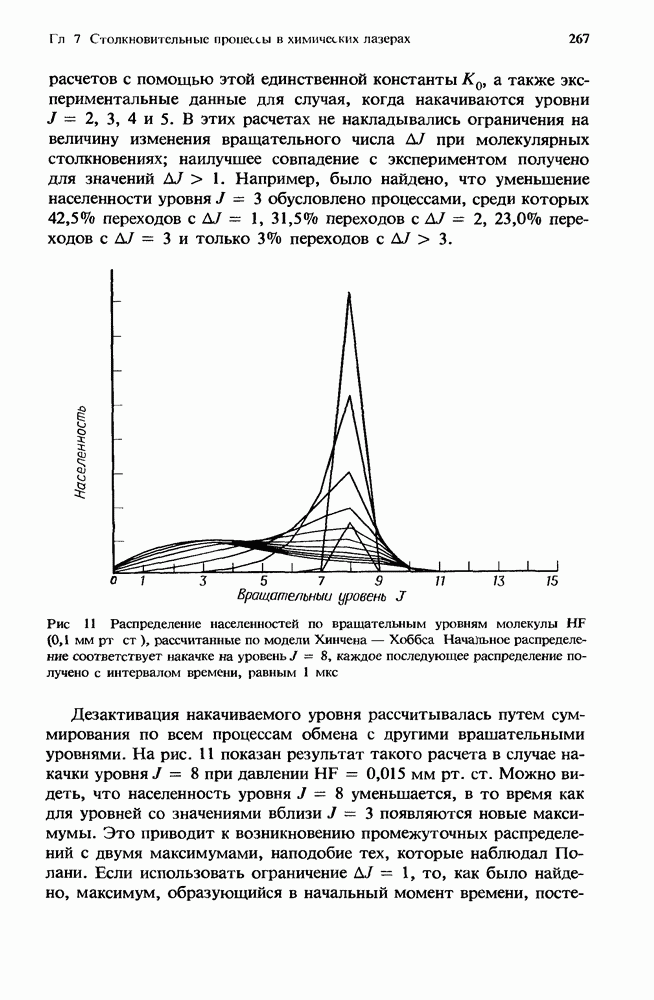
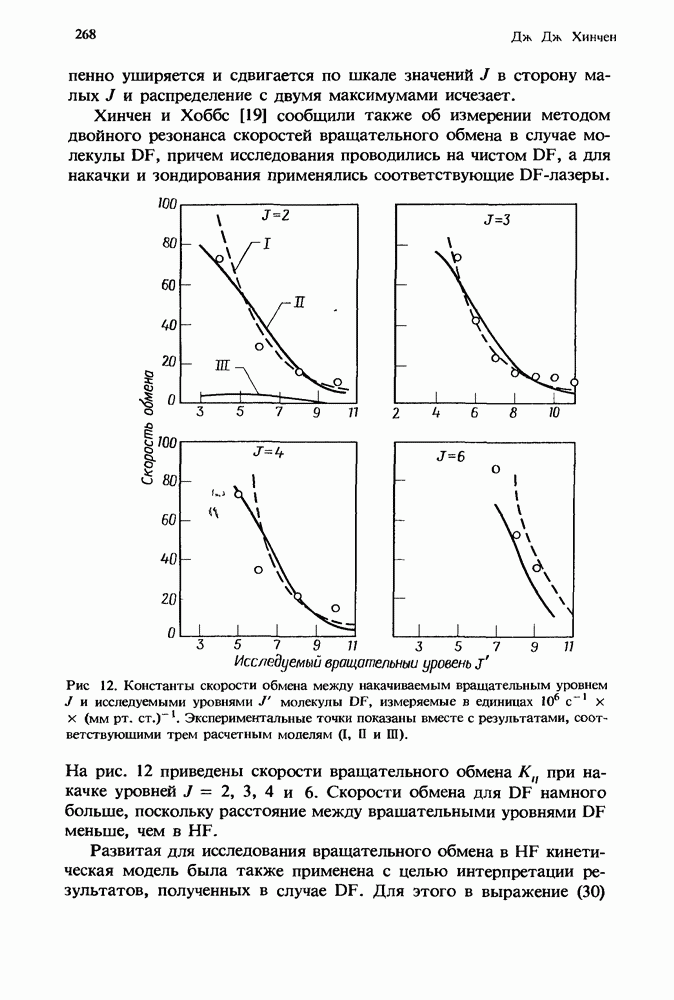
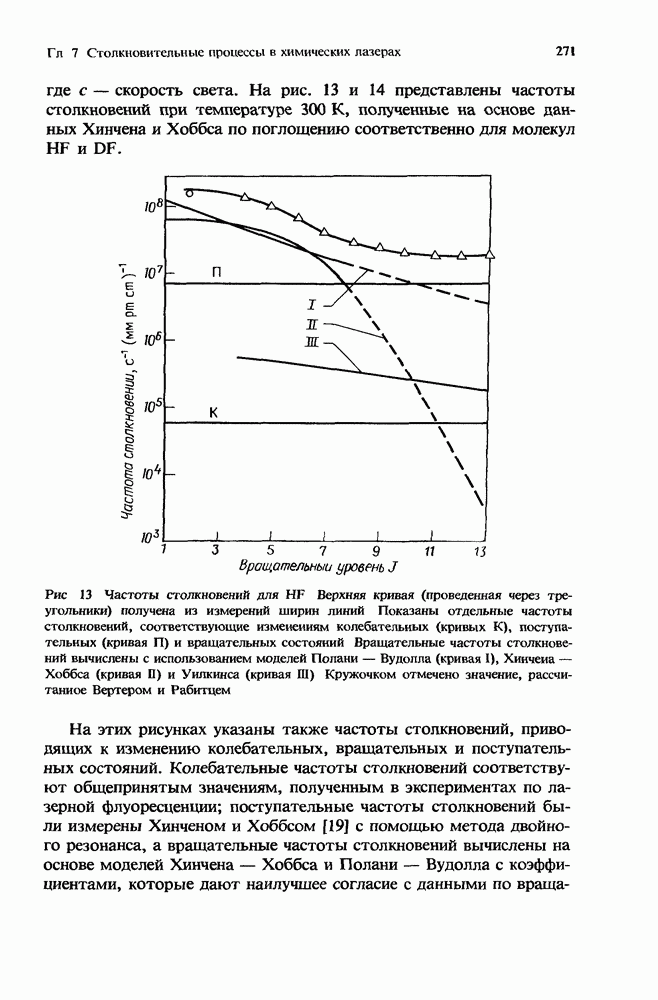
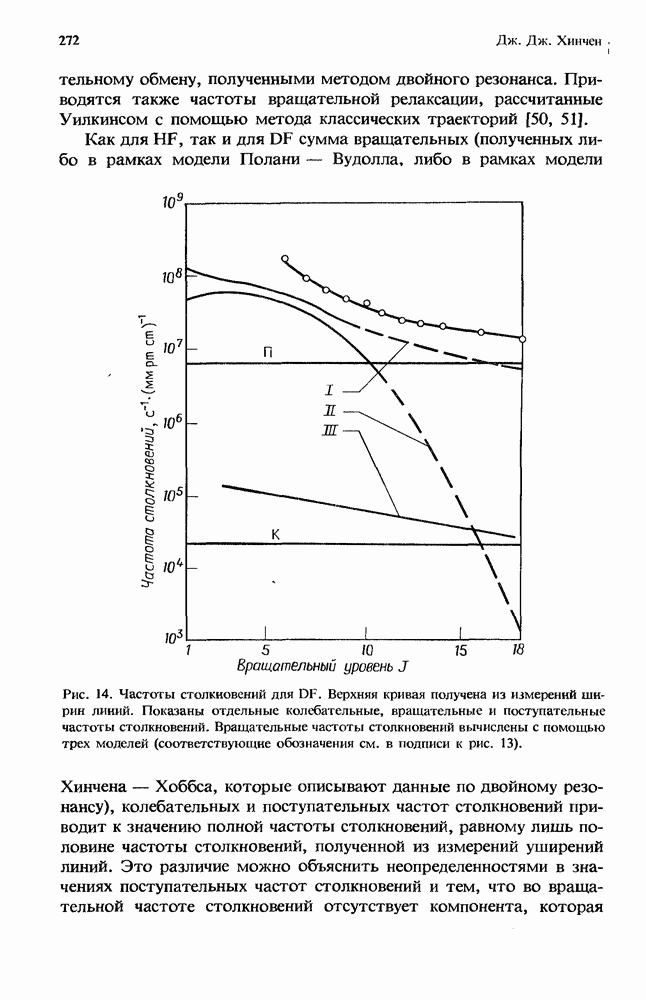
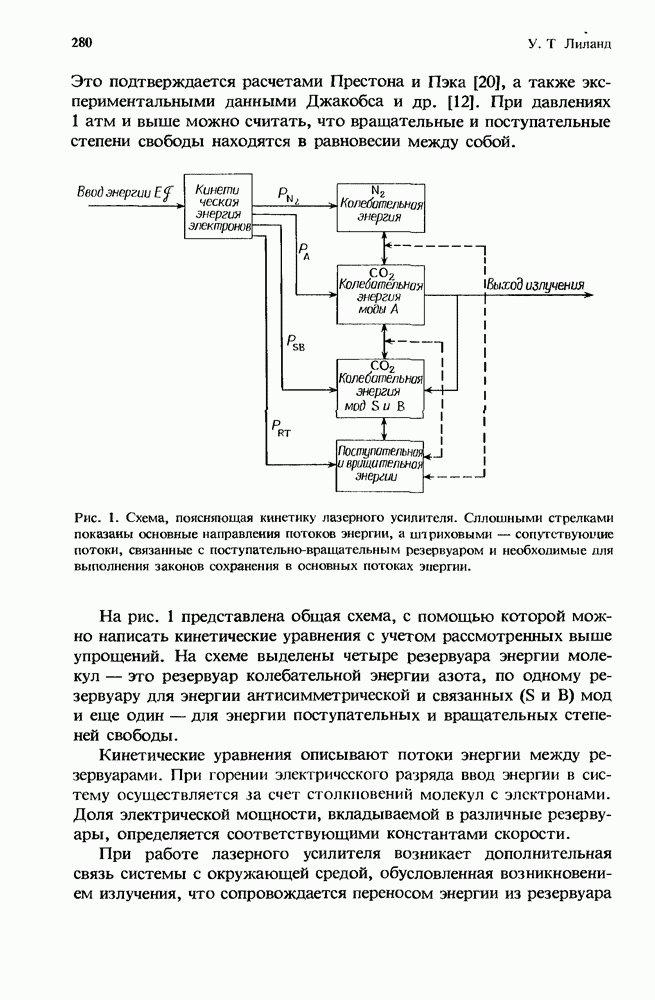
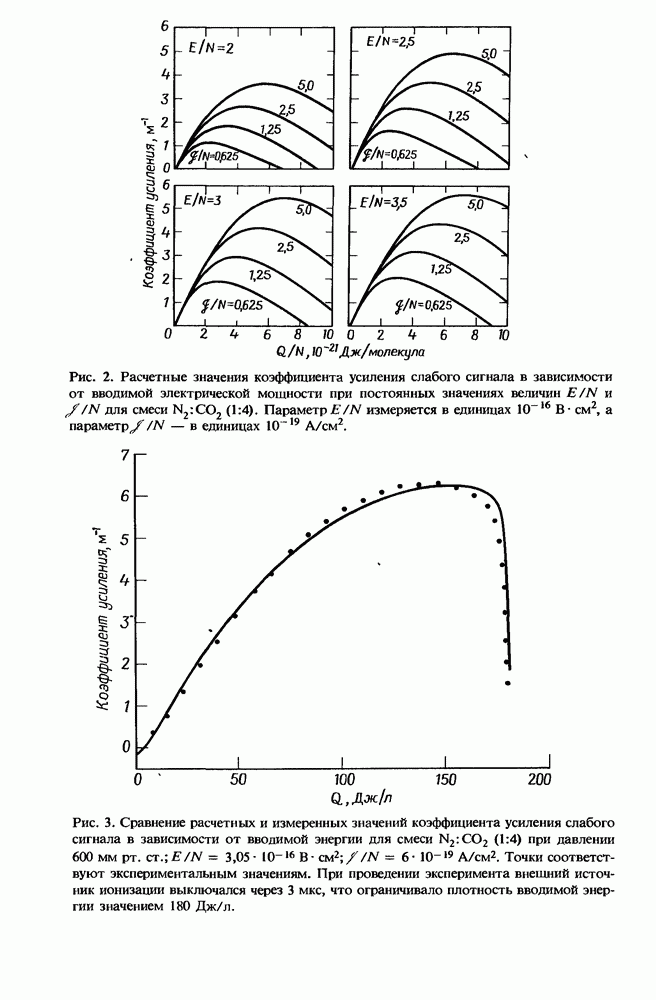
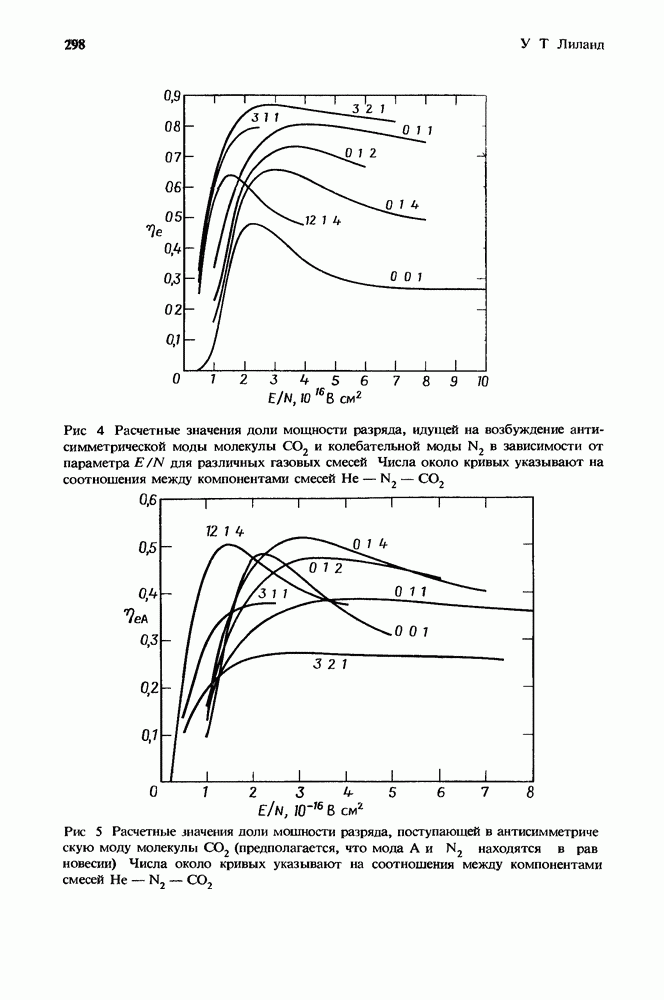
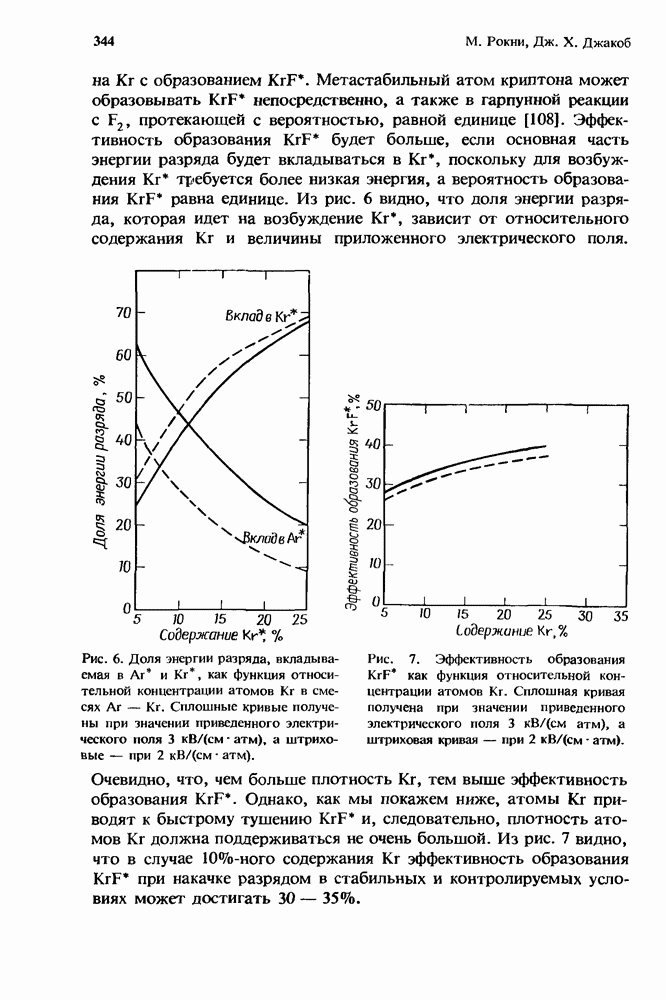
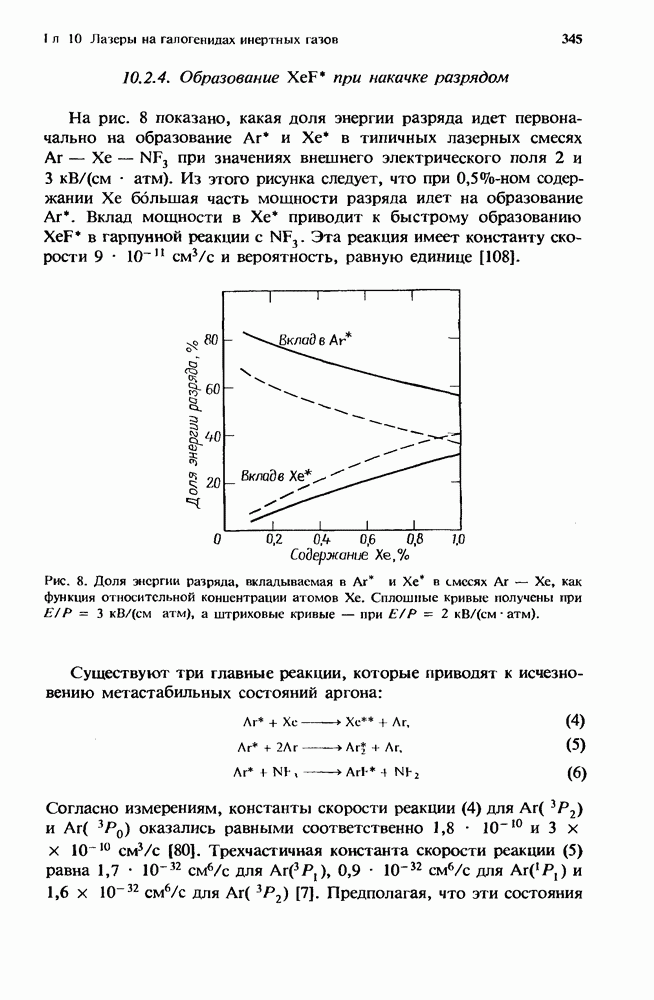
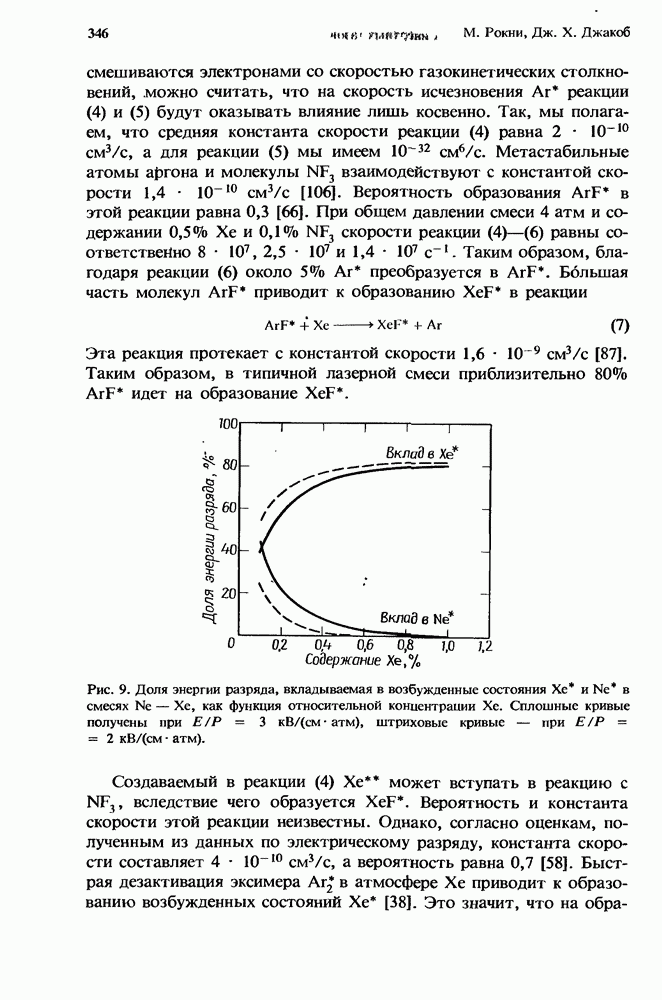
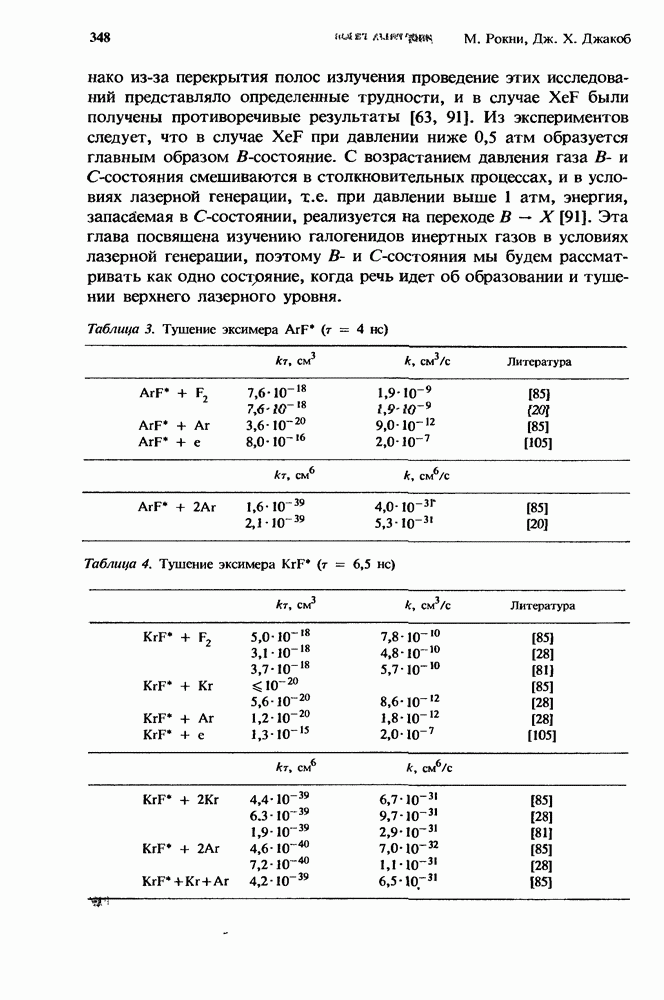
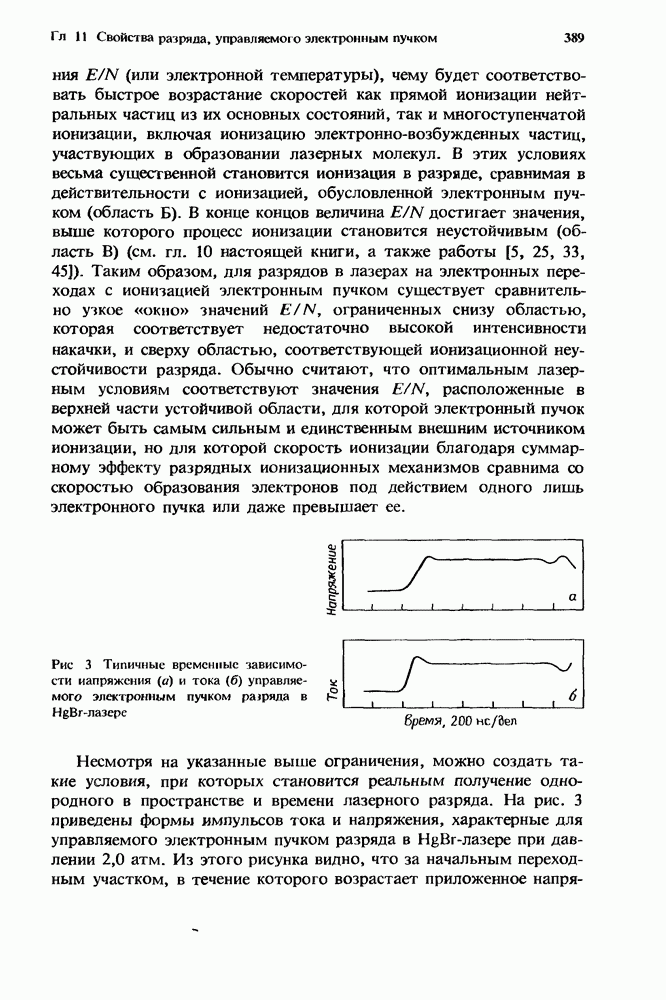
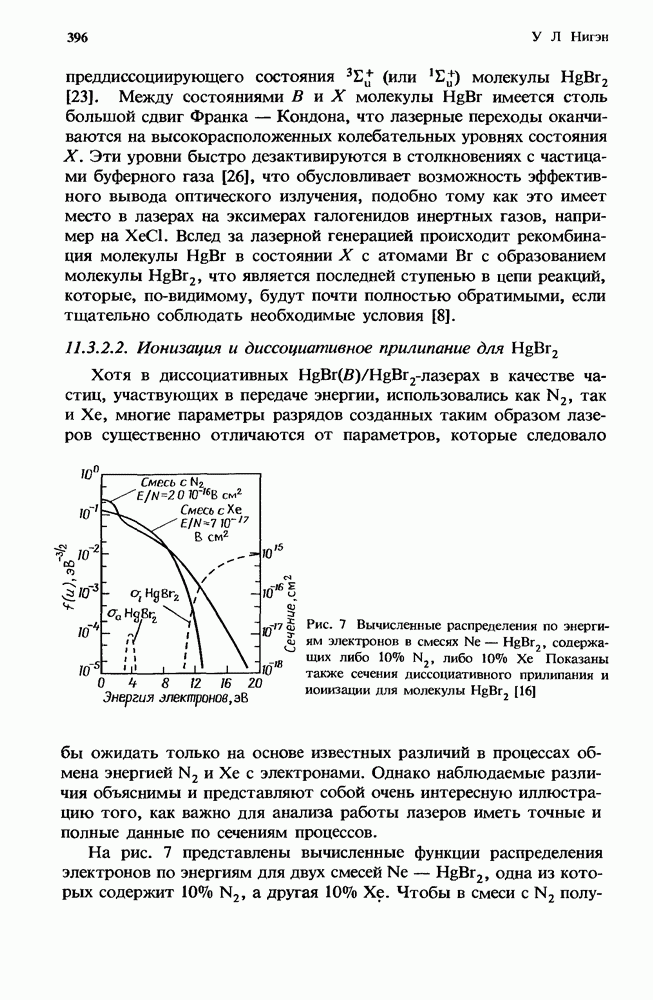
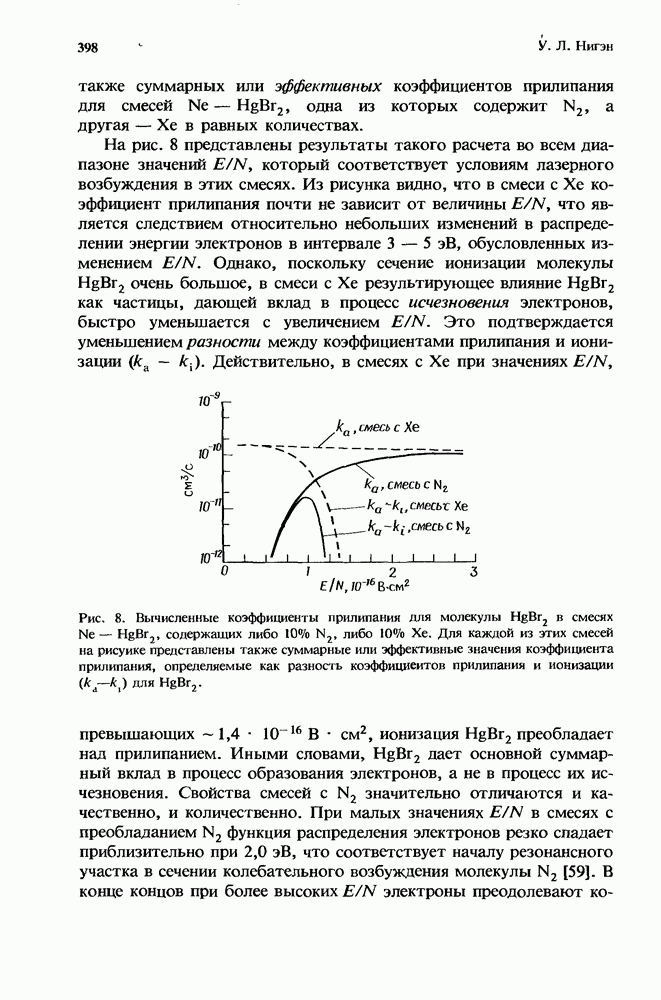
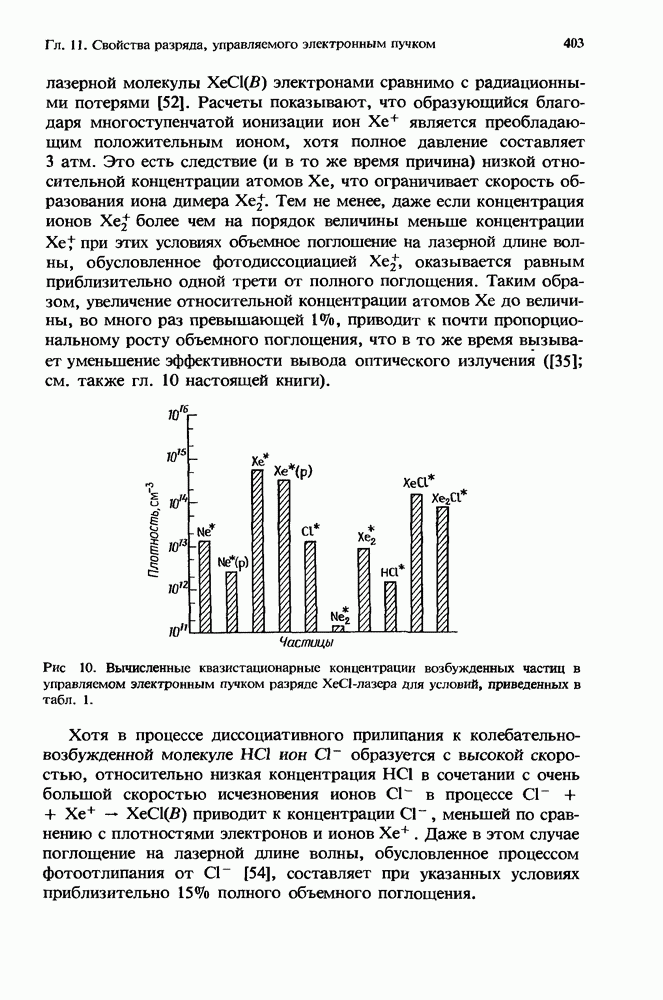
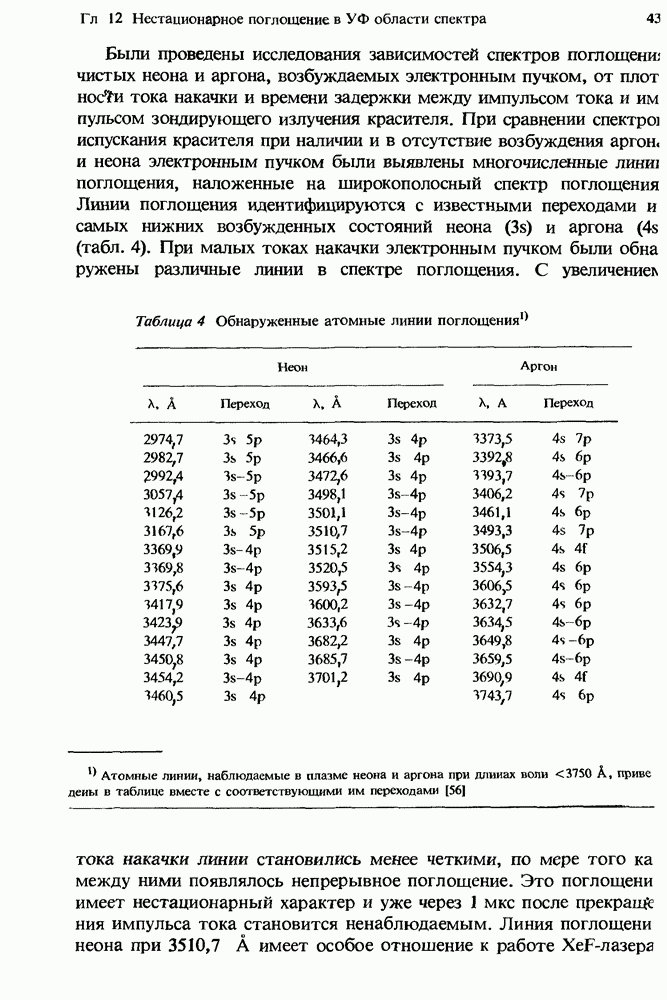
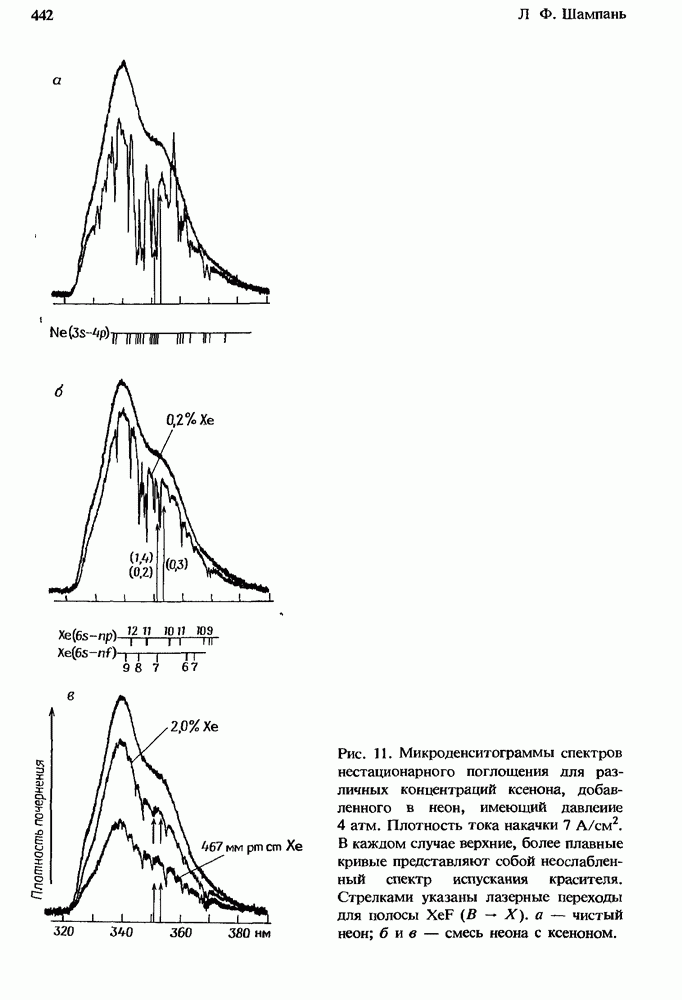
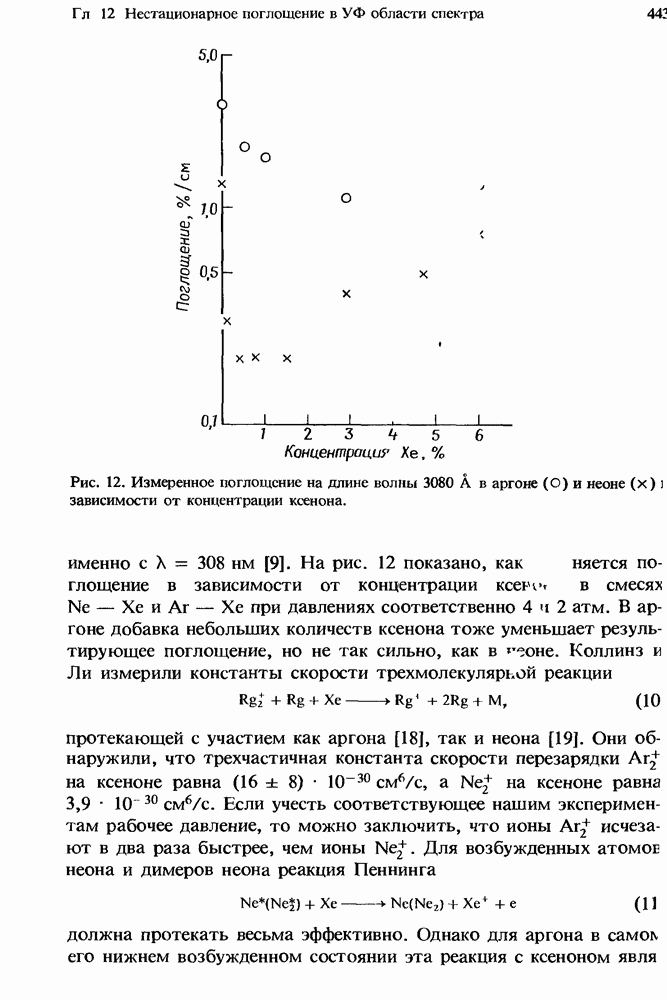
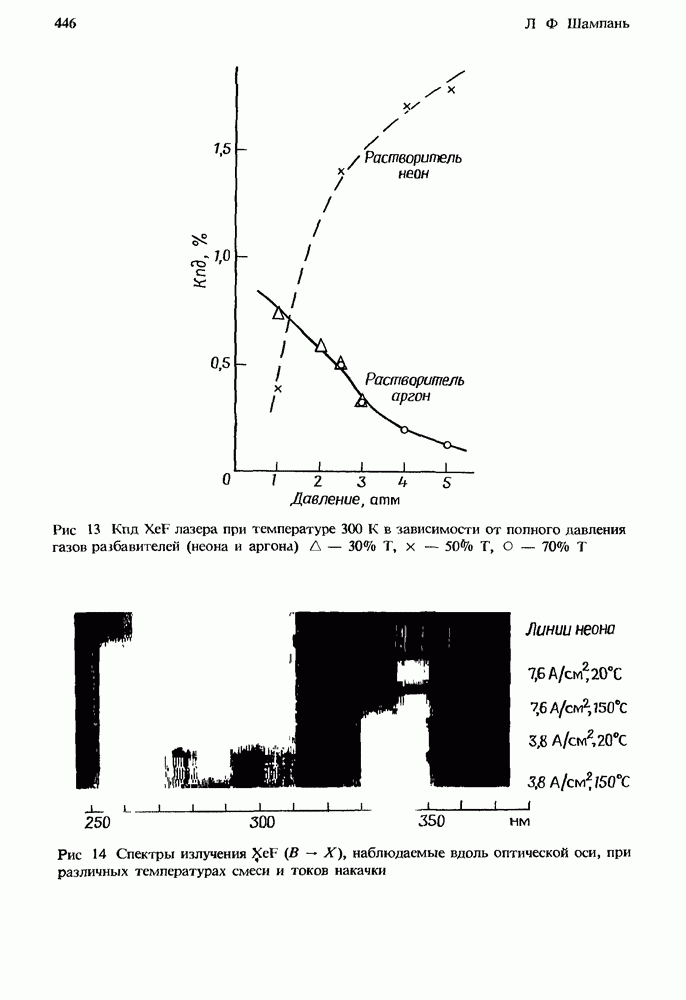
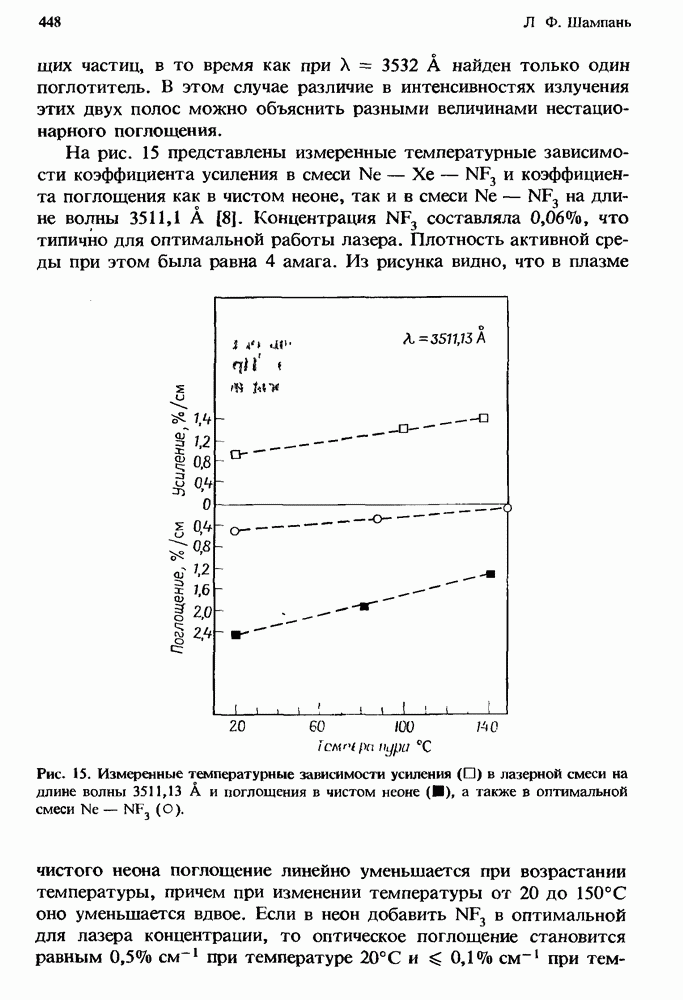
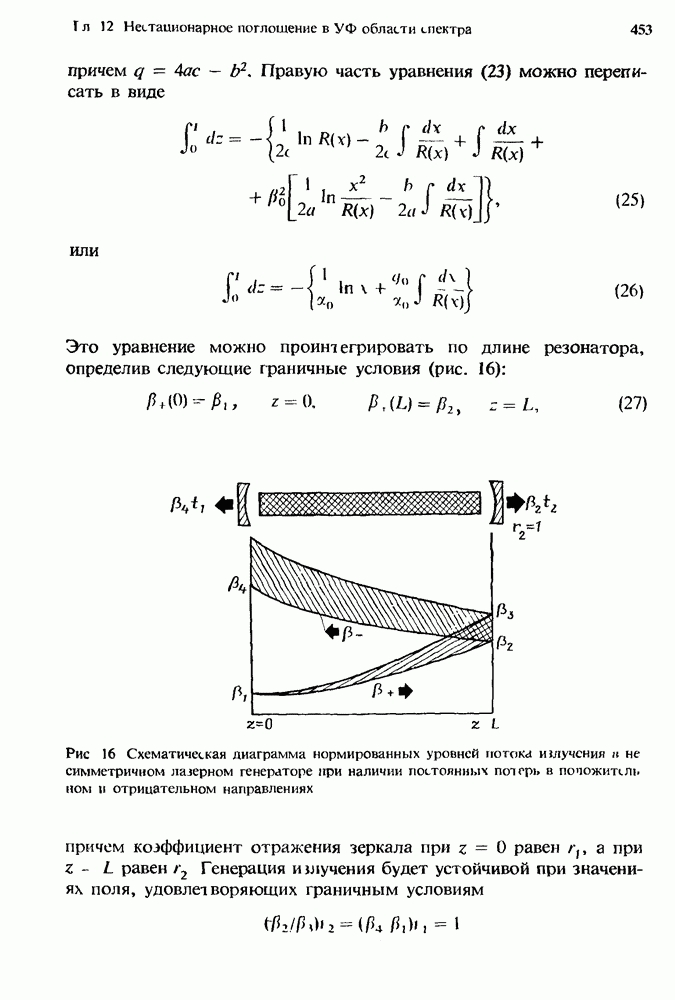
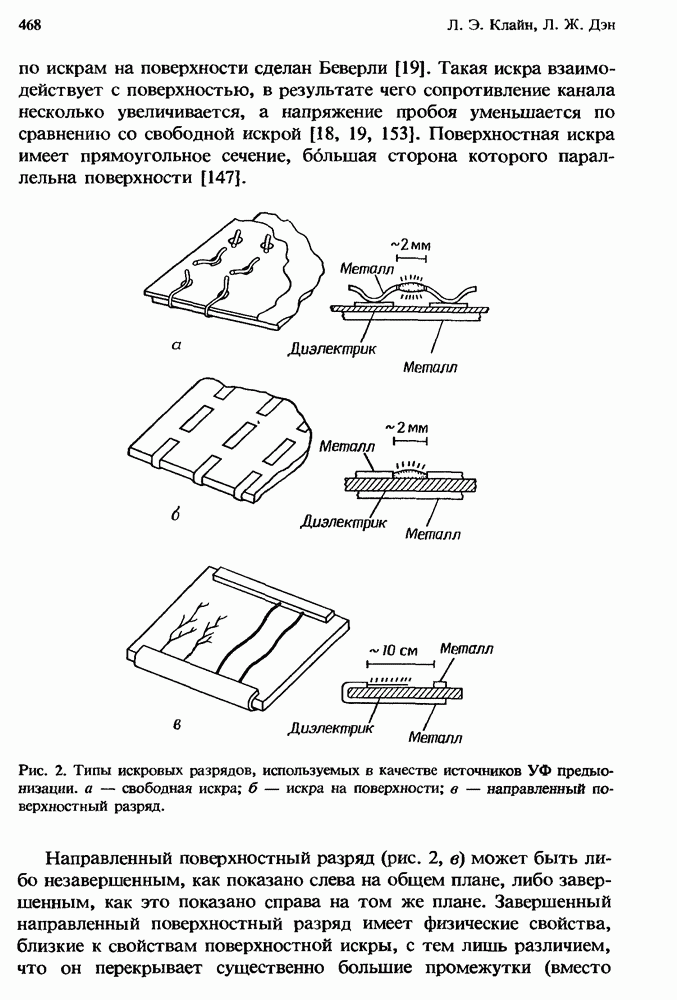
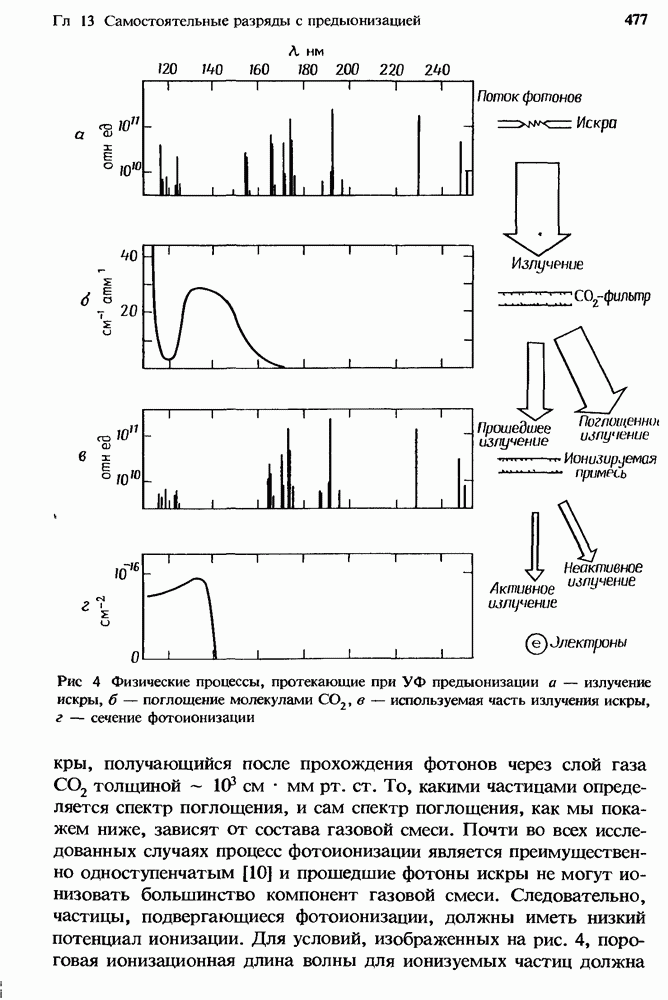
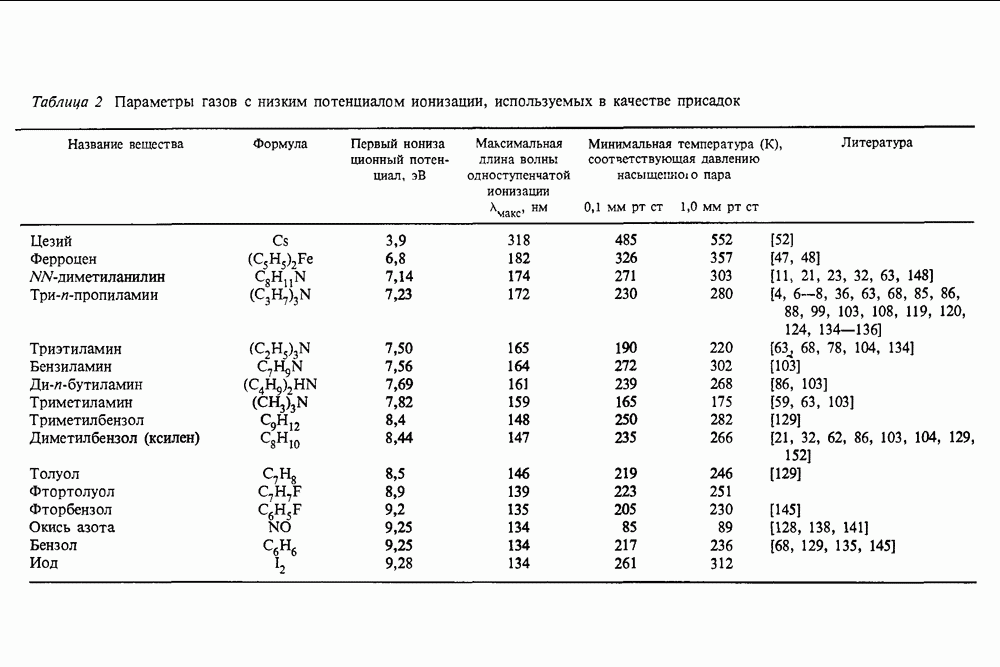
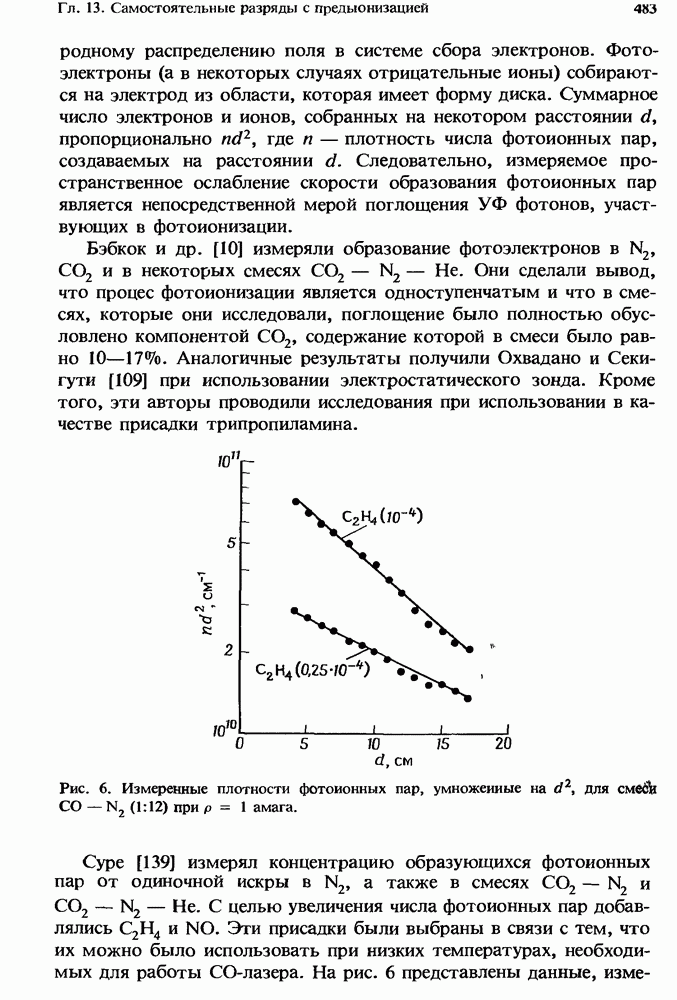
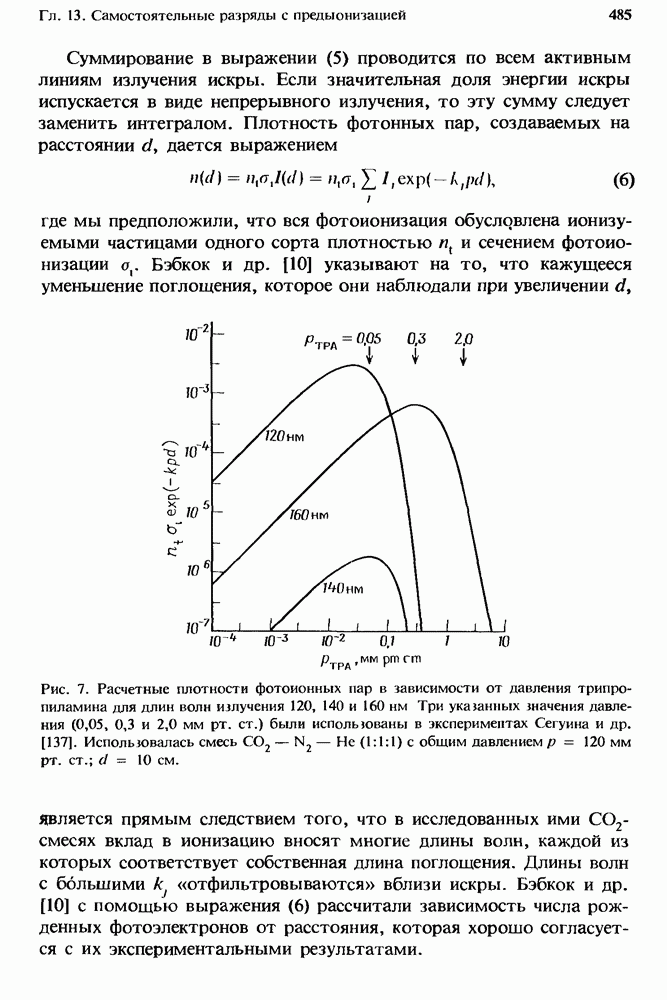
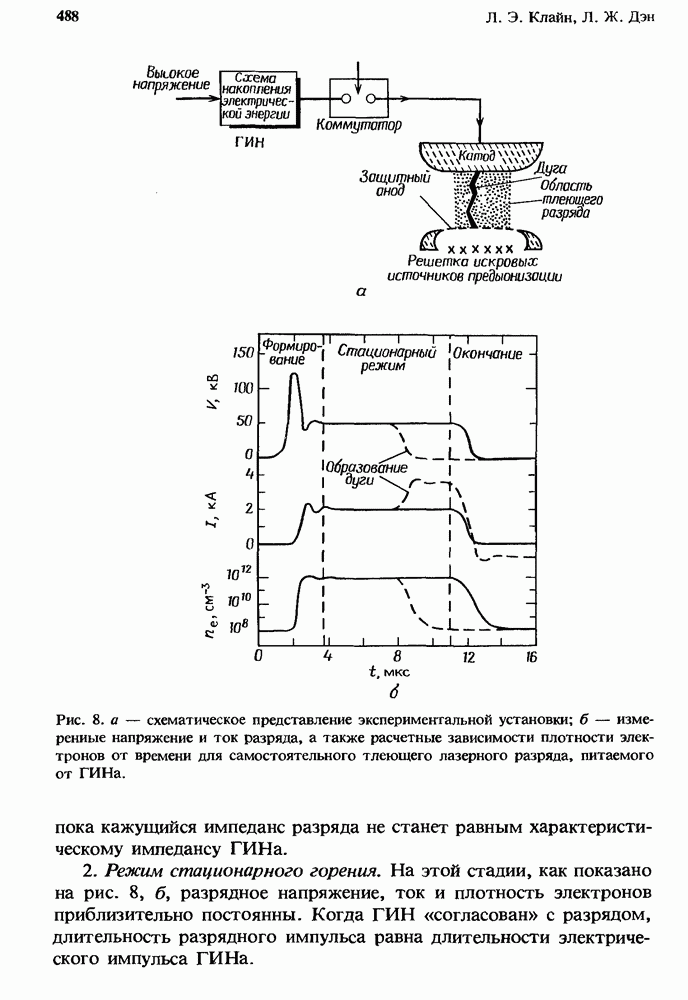
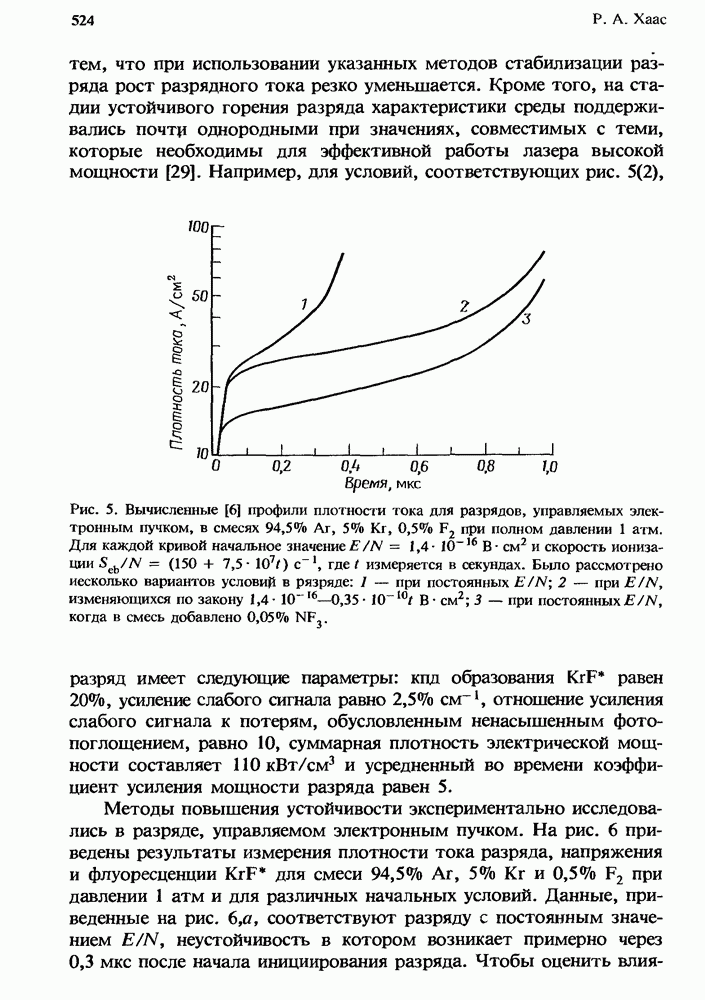
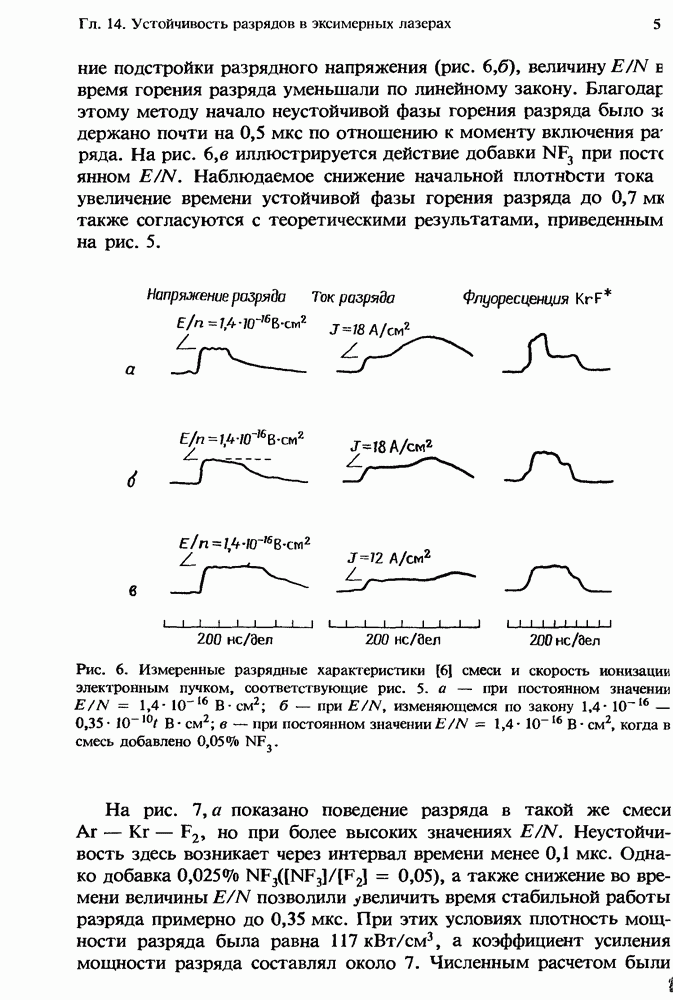
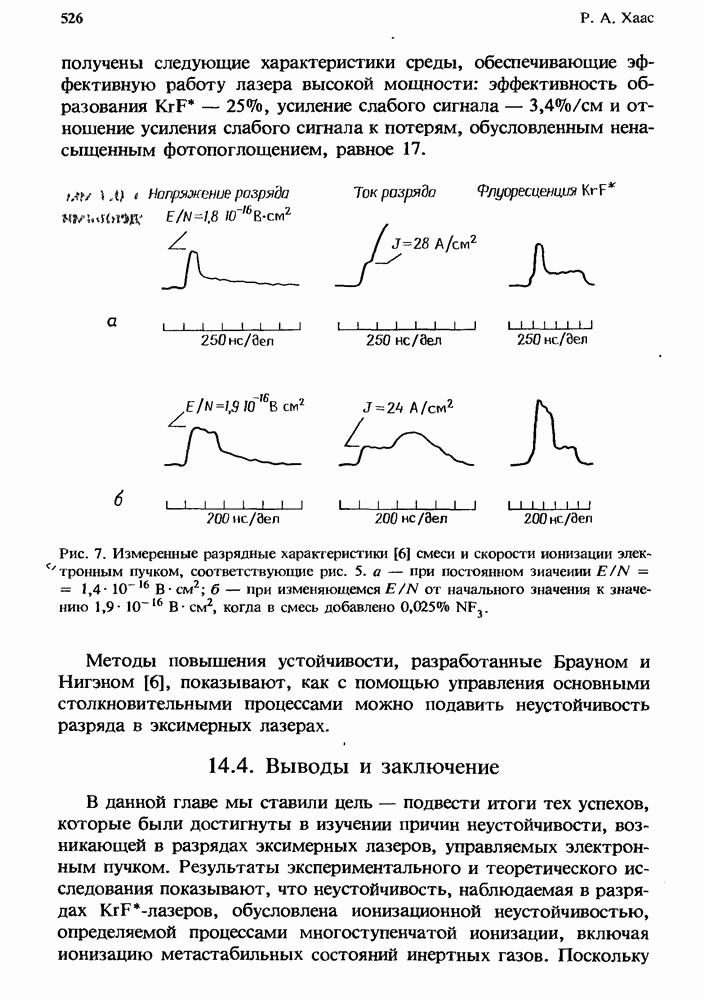
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение 1. Теория ионизационной неустойчивости
В этом разделе выводятся основные уравнения, описывающие ионизационные колебания в разрядах эксимерных лазеров. Условие возникновения неустойчивости и ее начальная скорость роста получены с использованием стандартных методов [14].
П.1.1. Модель плазмы
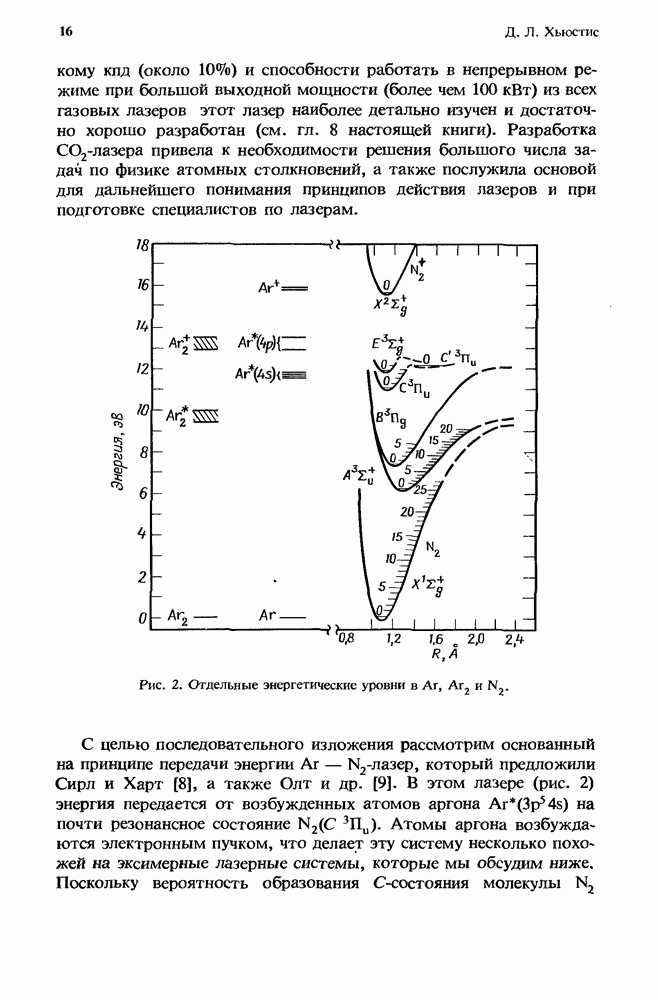
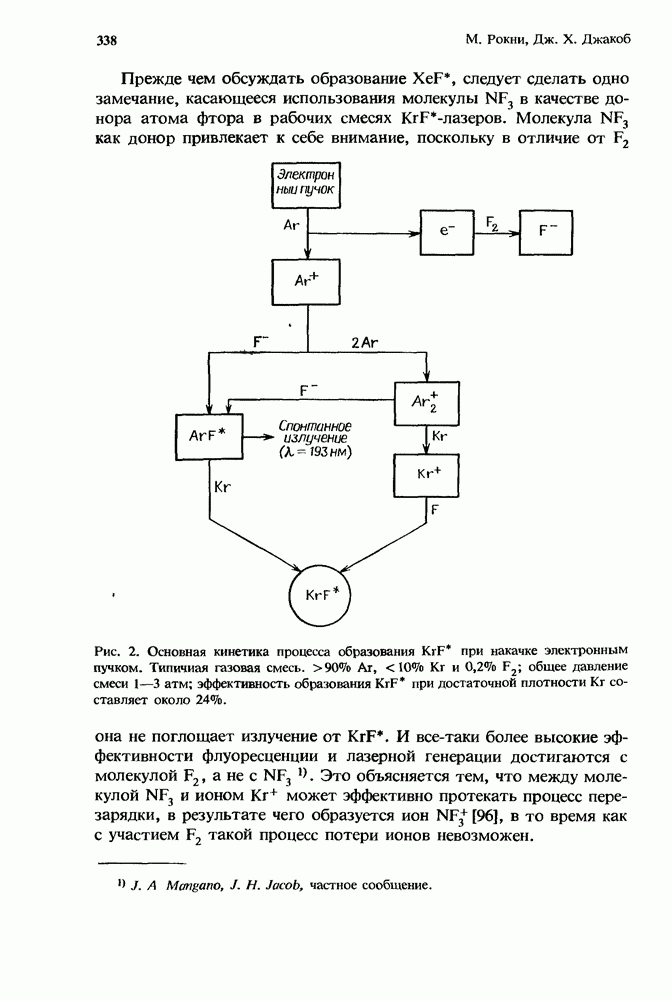
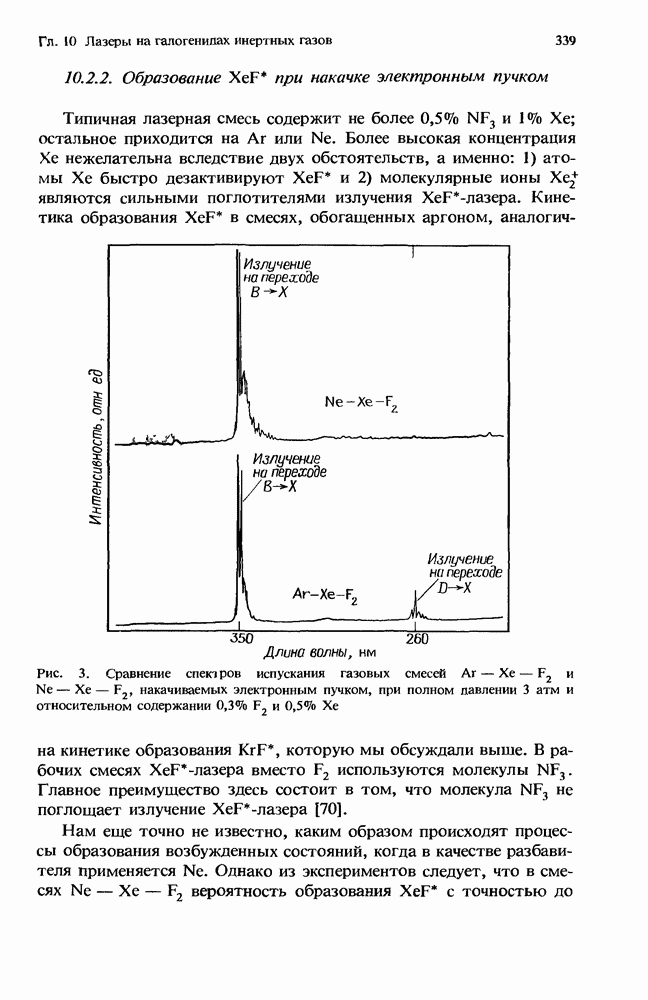
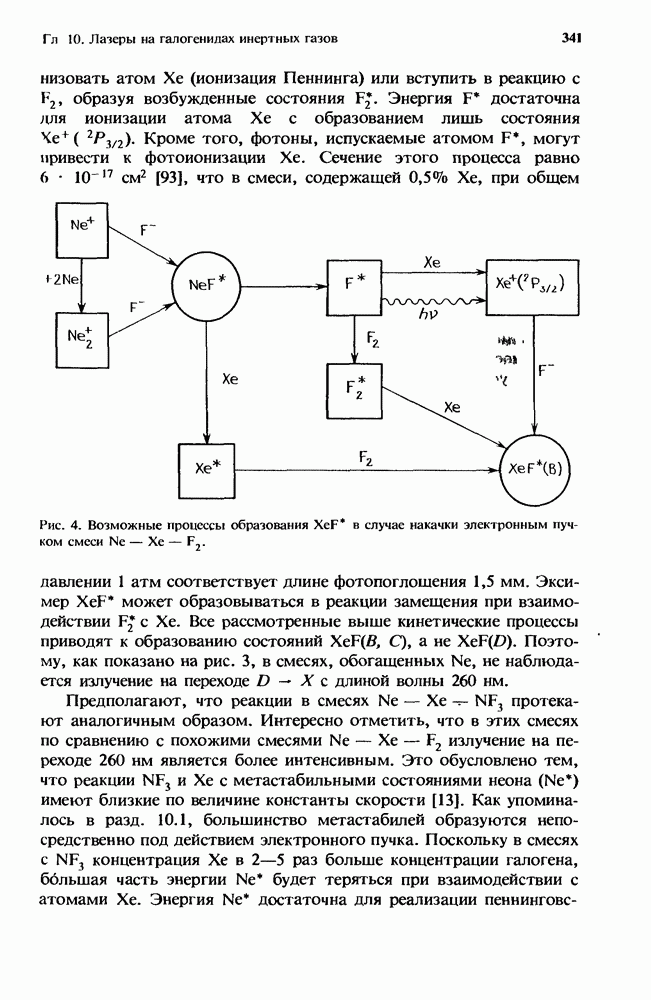
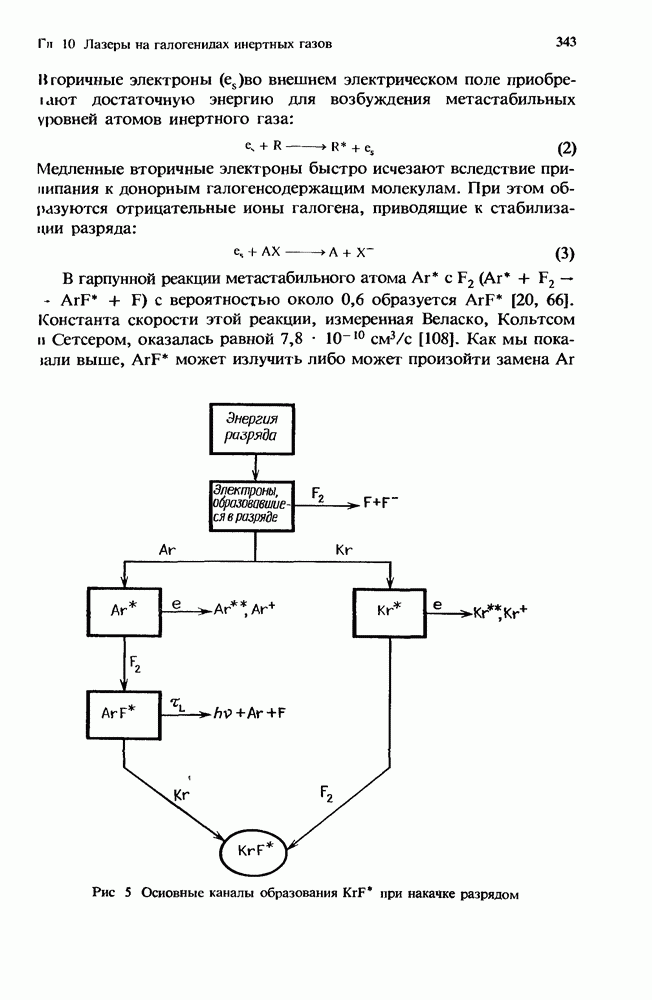
Разряды эксимерных лазеров высокого давления  атм) создают высокоионизованную
атм) создают высокоионизованную  и сильно возбужденную
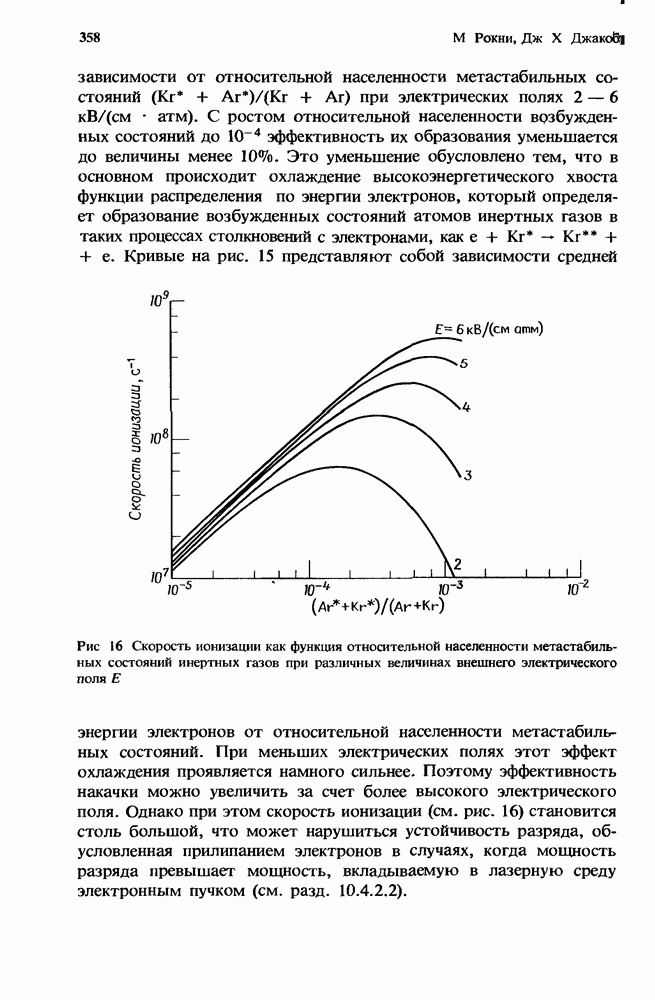
и сильно возбужденную  плазму со средней энергией электронов в несколько электронвольт. В установках с разрядом большого объема поведение плазмы определяется не процессами переноса, а столкновительными процессами. Ионизационная неустойчивость возникает локально, когда во время флуктуации процессы многоступенчатой ионизации создают больше электронов, чем их исчезает за счет столкновений. Разобраться в микроскопических физических механизмах, управляющих ионизационной неустойчивостью, можно с помощью простой модели, описывающей плазму разряда эксимерного лазера. В последующих разделах мы приведем и обсудим уравнения, описывающие локальную эволюцию плазменных флуктуаций в рамках этой модели разрядной плазмы. Кроме того, запишем условие возникновения ионизационной неустойчивости, обусловленное усилением этих флуктуаций, а также представим выражение, описывающее поведение во времени начального усиления или скорость роста неустойчивости.
плазму со средней энергией электронов в несколько электронвольт. В установках с разрядом большого объема поведение плазмы определяется не процессами переноса, а столкновительными процессами. Ионизационная неустойчивость возникает локально, когда во время флуктуации процессы многоступенчатой ионизации создают больше электронов, чем их исчезает за счет столкновений. Разобраться в микроскопических физических механизмах, управляющих ионизационной неустойчивостью, можно с помощью простой модели, описывающей плазму разряда эксимерного лазера. В последующих разделах мы приведем и обсудим уравнения, описывающие локальную эволюцию плазменных флуктуаций в рамках этой модели разрядной плазмы. Кроме того, запишем условие возникновения ионизационной неустойчивости, обусловленное усилением этих флуктуаций, а также представим выражение, описывающее поведение во времени начального усиления или скорость роста неустойчивости.
П.1.2. Динамика тяжелых частиц
При условиях, соответствующих развитию ионизационной неустойчивости, электроны образуются главным образом благодаря процессам многоступенчатой ионизации электронно-возбужденных частиц. Процессы возбуждения и дезактивации отдельных состояний протекают со скоростью большей, чем суммарная скорость ионизации [1, 2]. Суммарной скоростью ионизации определяется скорость развития неустойчивости. Кроме того, на временах, соответствующих развитию неустойчивости, процессы переноса частиц и газовой динамики можно считать замороженными. В квазистаци-онарном процессе плотность электронов связана с плотностями электронно-возбужденных частиц  следующим уравнением:
следующим уравнением:

где  — константа скорости возбуждения электронами электронного перехода
— константа скорости возбуждения электронами электронного перехода  — константа скорости тушения тяжелыми частицами
— константа скорости тушения тяжелыми частицами  электронного состояния и
электронного состояния и  — константа скорости ионизации электронами из 1-го электронного состояния. В уравнении (П. 1.1) не учтен вклад процесса образования возбужденных состояний непосредственно электронным пучком, поскольку разряды эксимерных лазеров, как правило, работают в режиме, при котором этот эффект пренебрежимо мал. Число
— константа скорости ионизации электронами из 1-го электронного состояния. В уравнении (П. 1.1) не учтен вклад процесса образования возбужденных состояний непосредственно электронным пучком, поскольку разряды эксимерных лазеров, как правило, работают в режиме, при котором этот эффект пренебрежимо мал. Число  возбужденных состояний, участвующих в ионизационном процессе, зависит от конкретных свойств среды. Для разрядов в галогенидах инертных газов [9] основную роль играют первые метастабильные электронные состояния и
возбужденных состояний, участвующих в ионизационном процессе, зависит от конкретных свойств среды. Для разрядов в галогенидах инертных газов [9] основную роль играют первые метастабильные электронные состояния и  В случае галогенидов металлов и паров металлов [28] в разрядах возбуждаются несколько электронных состояний атомов металла и
В случае галогенидов металлов и паров металлов [28] в разрядах возбуждаются несколько электронных состояний атомов металла и  В разрядах эксимерных лазеров плотности возбужденных состояний атомов
В разрядах эксимерных лазеров плотности возбужденных состояний атомов  определяются, как правило, столкновительными, а не излучательными процессами. Тушение возбужденных состояний за счет столкновений с тяжелыми частицами, определяемое в уравнении (П. 1.1) членами
определяются, как правило, столкновительными, а не излучательными процессами. Тушение возбужденных состояний за счет столкновений с тяжелыми частицами, определяемое в уравнении (П. 1.1) членами  обычно с вероятностью порядка единицы приводит к образованию эксимерных молекул [3, 12].
обычно с вероятностью порядка единицы приводит к образованию эксимерных молекул [3, 12].
П.1.3. Динамика электронов и электромагнитного поля
Пренебрегая процессами переноса для рассматриваемой модели кинетики плазмы, можно написать следующее уравнение непрерывности
для электронов:

где  — коэффициент потерь электронов, а
— коэффициент потерь электронов, а  - констант скорости ионизации электронами
- констант скорости ионизации электронами  электронного состояния. Диссоциативная рекомбинация или прилипание электронов представлю
электронного состояния. Диссоциативная рекомбинация или прилипание электронов представлю  собой, как правило, основные процессы потерь электронов.
собой, как правило, основные процессы потерь электронов.  случае диссоциативного прилипания коэффициент потерь электрс нов а дается выражением
случае диссоциативного прилипания коэффициент потерь электрс нов а дается выражением

где  — плотность числа электроотрицательных частиц, а
— плотность числа электроотрицательных частиц, а  — константа скорости диссоциативного прилипания. Из выражени (П. 1.3) следует, что коэффициент потерь электронов не зависит
— константа скорости диссоциативного прилипания. Из выражени (П. 1.3) следует, что коэффициент потерь электронов не зависит  плотности электронов. Хотя диссоциативное прилипание приводи к образованию отрицательных ионов, их плотность обычно значи тельно меньше, чем плотность электронов. Аналогично для случа) диссоциативной рекомбинации, если
плотности электронов. Хотя диссоциативное прилипание приводи к образованию отрицательных ионов, их плотность обычно значи тельно меньше, чем плотность электронов. Аналогично для случа) диссоциативной рекомбинации, если  — константа скорости этогс процесса, коэффициент потерь электронов запишется в виде
— константа скорости этогс процесса, коэффициент потерь электронов запишется в виде

т.е. в этом случае мы имеем линейную зависимость от плотностг электронов. Величина  есть суммарная скорость образованш электронов под действием инжектируемого пучка электронов высо кой энергии. Так как кинетика возбужденных состояний являете» квазистационарной, мы можем решить (см. приложение 2) связанные между собой уравнения непрерывности для возбужденных состояний [уравнения (П. 1.1)]. В результате для любого момента времени получим плотность каждого возбужденного состояния
есть суммарная скорость образованш электронов под действием инжектируемого пучка электронов высо кой энергии. Так как кинетика возбужденных состояний являете» квазистационарной, мы можем решить (см. приложение 2) связанные между собой уравнения непрерывности для возбужденных состояний [уравнения (П. 1.1)]. В результате для любого момента времени получим плотность каждого возбужденного состояния  в виде функции локальной плотности электронов и кинетической температуры [14], т. е.
в виде функции локальной плотности электронов и кинетической температуры [14], т. е.  При этом уравнение непрерывности для электронов можно записать следующим образом:
При этом уравнение непрерывности для электронов можно записать следующим образом:

где суммарная скорость ионизации

является функцией плотности электронов и температуры.
Поскольку в разрядах эксимерных лазеров время передачи энергии электронами значительно меньше времени ионизации, можно написать следующее выражение для энергии электронов:

где  — частота столкновений с передачей энергии электронами,
— частота столкновений с передачей энергии электронами,  — вектор плотности электронного тока и Е — электрическое поле в разряде. В выражении (П. 1.7) не учитывается непосредственный вклад энергии от электронного пучка, поскольку он обычно мал по сравнению с омическим нагревом электронов в электрическом поле. Кроме того, в этом выражении зависимость величины
— вектор плотности электронного тока и Е — электрическое поле в разряде. В выражении (П. 1.7) не учитывается непосредственный вклад энергии от электронного пучка, поскольку он обычно мал по сравнению с омическим нагревом электронов в электрическом поле. Кроме того, в этом выражении зависимость величины  от плотности возбужденных состояний устранена с помощью уравнения (П. 1.1). Плотность электронного тока и электрическое поле связаны законом Ома:
от плотности возбужденных состояний устранена с помощью уравнения (П. 1.1). Плотность электронного тока и электрическое поле связаны законом Ома:

где а — электронная проводимость,  — эффективная частота столкновений с передачей импульса.
— эффективная частота столкновений с передачей импульса.
В данном случае для интересующих нас относительно медленных возмущений, связанных с ионизационной неустойчивостью, плазма является квазинейтральной, а электромагнитное поле — квазистатическим. Таким образом, электрическое поле определяется уравнениями

П.1.4. Анализ устойчивости
П. 1.4.1. Флуктуации малой амплитуды
Уравнения движения, приведенные в данном приложении, описывают развитие локальных возмущений в случае, когда динамика плазмы определяется процессами столкновений, а не процессами переноса. Из-за флуктуаций плазмы, шума, генерируемого турбулентностями потока, из-за пульсаций источника питания и т.д. внутренний объем разряда высокой энергии вообще не может быть локально стационарным или однородным. Если амплитуда флуктуаций достаточно мала, то полезно представить свойства плазмы в виде суммы пространственно почти однородной стационарной величины  и изменяющейся во времени и пространстве флуктуации
и изменяющейся во времени и пространстве флуктуации  нормипованной на
нормипованной на 

Через  мы обозначили набор основных свойств плазмы, необходимых для описания ее поведения:
мы обозначили набор основных свойств плазмы, необходимых для описания ее поведения:  Представляя возмущение в таком виде, основные уравнения
Представляя возмущение в таком виде, основные уравнения  можно разложить на компоненты нулевого и первого порядка, описывающие соответственно стационарные и флуктуирующие величины. Анализом устойчивости этих флуктуаций малой амплитуды мы и займемся ниже
можно разложить на компоненты нулевого и первого порядка, описывающие соответственно стационарные и флуктуирующие величины. Анализом устойчивости этих флуктуаций малой амплитуды мы и займемся ниже
П.1.4.2. Условия существования стационарного состояния
Условия существования стационарного состояния плазмы определяются уравнениями

Протекание в разряде реакций может вызвать уменьшение концентрации некоторых частиц, что приводит к появлению характерных времен разряда. Однако ионизационная неустойчивость развивается за характерные времена, которые намного меньше, чем времена указанных реакций, и поэтому уравнения  обеспечивают неплохое описание соотношений между основными характеристиками стационарной плазмы, такими, как
обеспечивают неплохое описание соотношений между основными характеристиками стационарной плазмы, такими, как  .
.
П.1.4.3. Условие возникновения неустойчивости
Подставляя выражение  в уравнения
в уравнения  с последующей их линеаризацией с помощью
с последующей их линеаризацией с помощью  можно получить систему линейных уравнений, которая описывает эволюцию флуктуаций малой амплитуды. Чтобы решить эти уравнения, необходимо найти зависимость начальных возмущений от пространственных координат и времени. Если источник возмущения 0 удовлетворяет условию
можно получить систему линейных уравнений, которая описывает эволюцию флуктуаций малой амплитуды. Чтобы решить эти уравнения, необходимо найти зависимость начальных возмущений от пространственных координат и времени. Если источник возмущения 0 удовлетворяет условию  для
для  то с помощью преобразования Фурье — Лапласа общий отклик плазмы на эту начальную флуктуацию можно записать в виде
то с помощью преобразования Фурье — Лапласа общий отклик плазмы на эту начальную флуктуацию можно записать в виде

где величина  выбирается таким образом, чтобы для обеспечения однозначности контур на плоскости со располагался ниже всех
выбирается таким образом, чтобы для обеспечения однозначности контур на плоскости со располагался ниже всех
особых точек подынтегрального выражения. Функция  полученная из уравнений
полученная из уравнений  имеет вид
имеет вид

где

Величина в представляет собой угол между волновым вектором возмущения к и направлением электрического поля в разряде Е. В общем случае для локализованного начального возмущения функция  является аналитической. В выражении
является аналитической. В выражении  нетрудно вычислить интеграл по со, что дает
нетрудно вычислить интеграл по со, что дает

Исследование асимптотического поведения соотношений, аналогичных  показывает [4, 15, 27], что необходимым и достаточным условием неустойчивости является выполнение неравенства
показывает [4, 15, 27], что необходимым и достаточным условием неустойчивости является выполнение неравенства  записанного для некоторого действительного значения комплексной величины к. Исследование рассматриваемых в нашем случае выражений
записанного для некоторого действительного значения комплексной величины к. Исследование рассматриваемых в нашем случае выражений  показывает, что неустойчивость возникает, если для некоторого значения в мы имеем
показывает, что неустойчивость возникает, если для некоторого значения в мы имеем  Кроме того, скорость роста неустойчивости определяется неравенством
Кроме того, скорость роста неустойчивости определяется неравенством  Из выражения
Из выражения  также следует, что, хотя неустойчивыми могут быть отдельные фурье-компоненты, неустойчивость при ее развитии не обязательно должна иметь форму волны.
также следует, что, хотя неустойчивыми могут быть отдельные фурье-компоненты, неустойчивость при ее развитии не обязательно должна иметь форму волны.
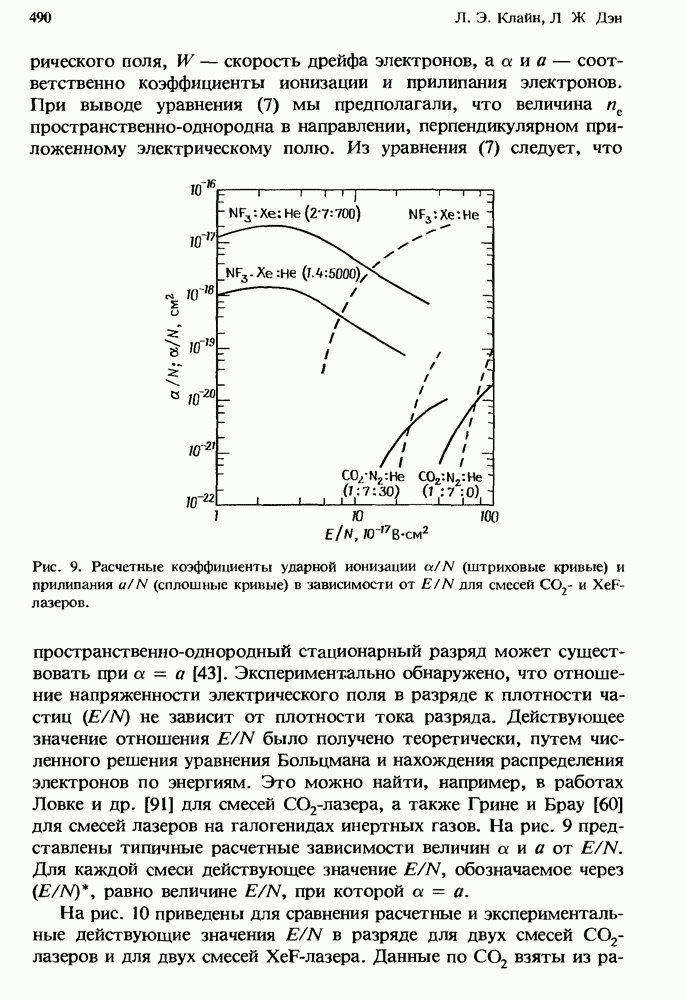
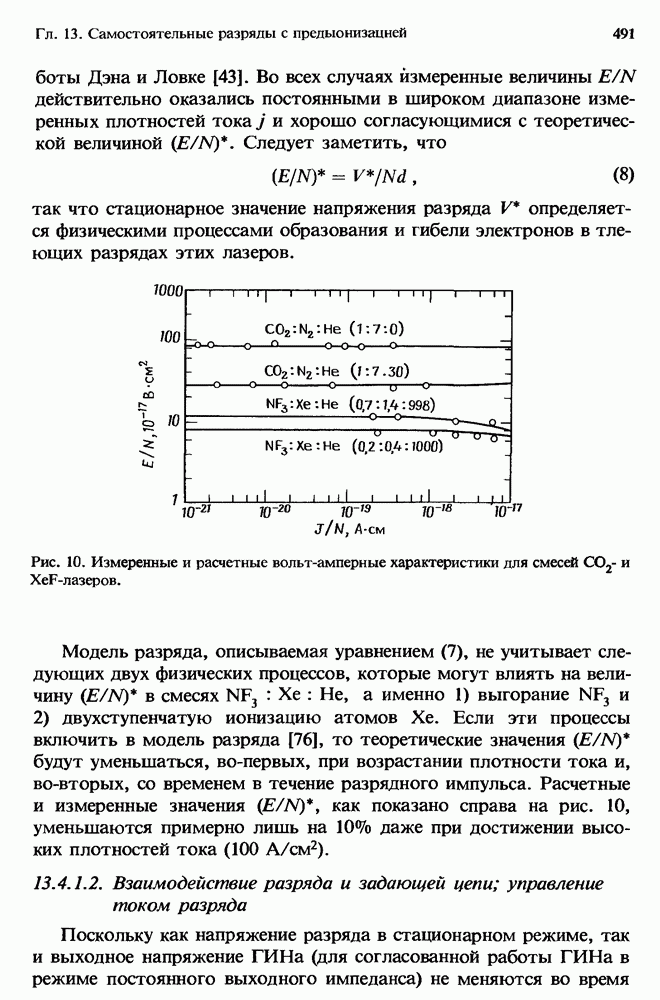
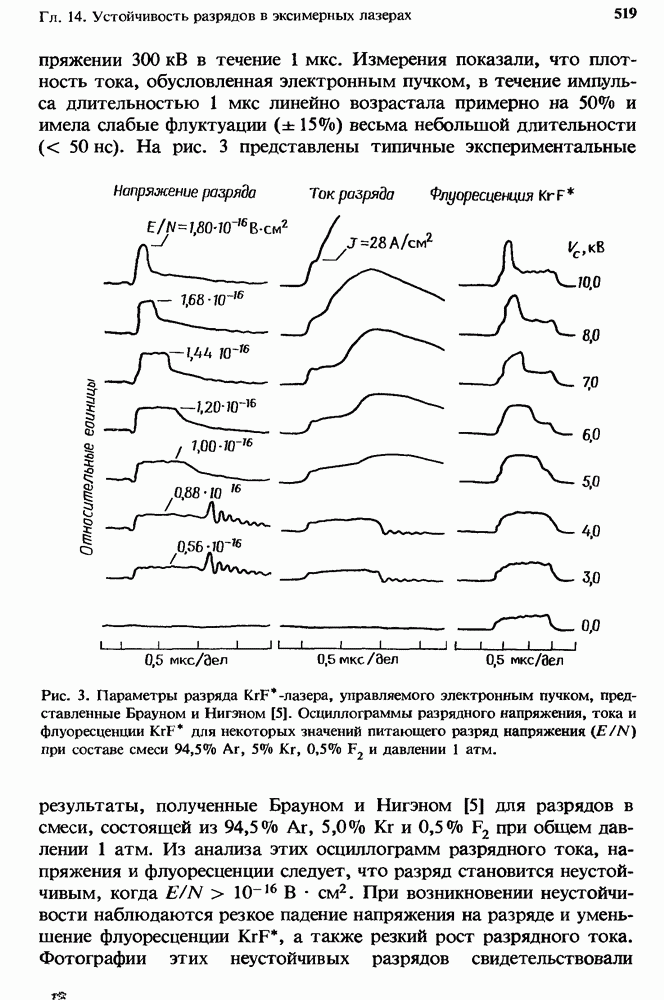
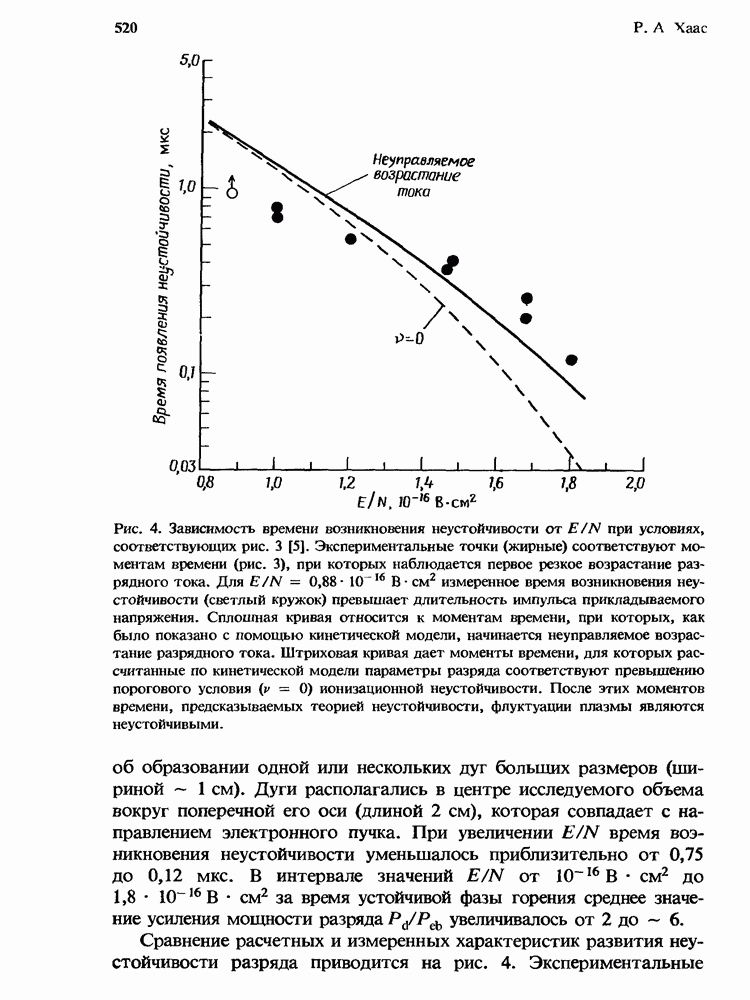
Обычно условия возникновения ионизационной неустойчивости получают с помощью выражений  определяя угол в, при котором
определяя угол в, при котором  впервые станет больше нуля, т. е. впервые возникнет рост неустойчивости. Как можно видеть из следующих нестрогих рассуждений, для многих интересующих нас случаев условие
впервые станет больше нуля, т. е. впервые возникнет рост неустойчивости. Как можно видеть из следующих нестрогих рассуждений, для многих интересующих нас случаев условие  в первую очередь выполняется для величин в, близких к 0 или
в первую очередь выполняется для величин в, близких к 0 или  . Для условий, типичных в случае разрядов эксимерных лазеров, зависимость и от плотности электронов является слабой, знаменатель в выражении
. Для условий, типичных в случае разрядов эксимерных лазеров, зависимость и от плотности электронов является слабой, знаменатель в выражении  оказывается
оказывается
положительным и  в. В этом случае условия возникновения и окончательные характеристики неустойчивости [стратифицирование
в. В этом случае условия возникновения и окончательные характеристики неустойчивости [стратифицирование  или схлопывание
или схлопывание  разряда зависят от знака величины
разряда зависят от знака величины

В случае когда  разряд будет неустойчивым, если выполняется неравенство
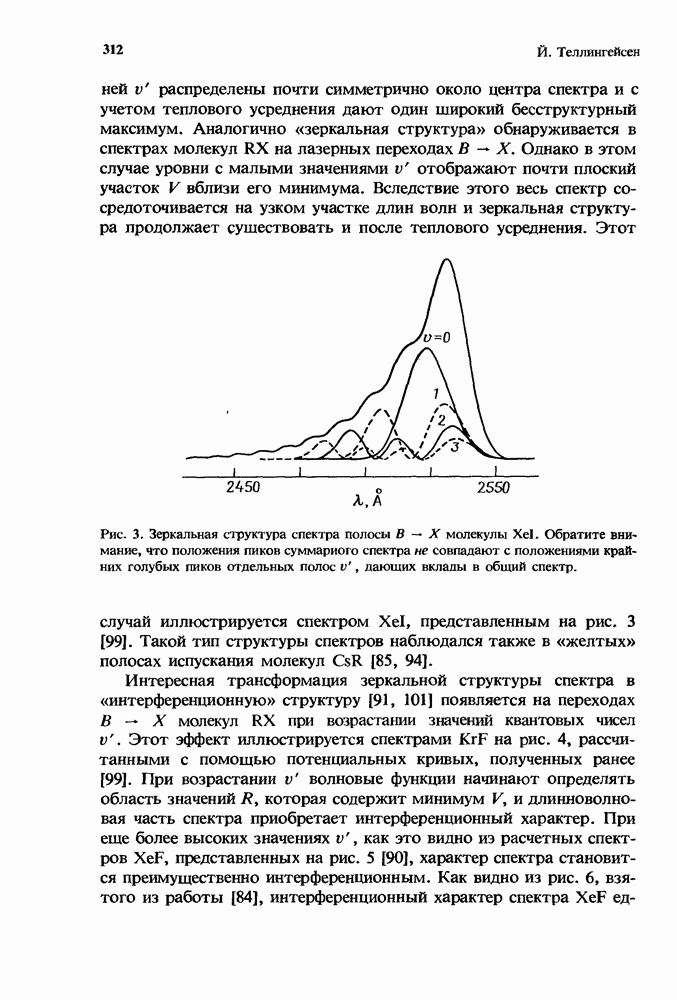
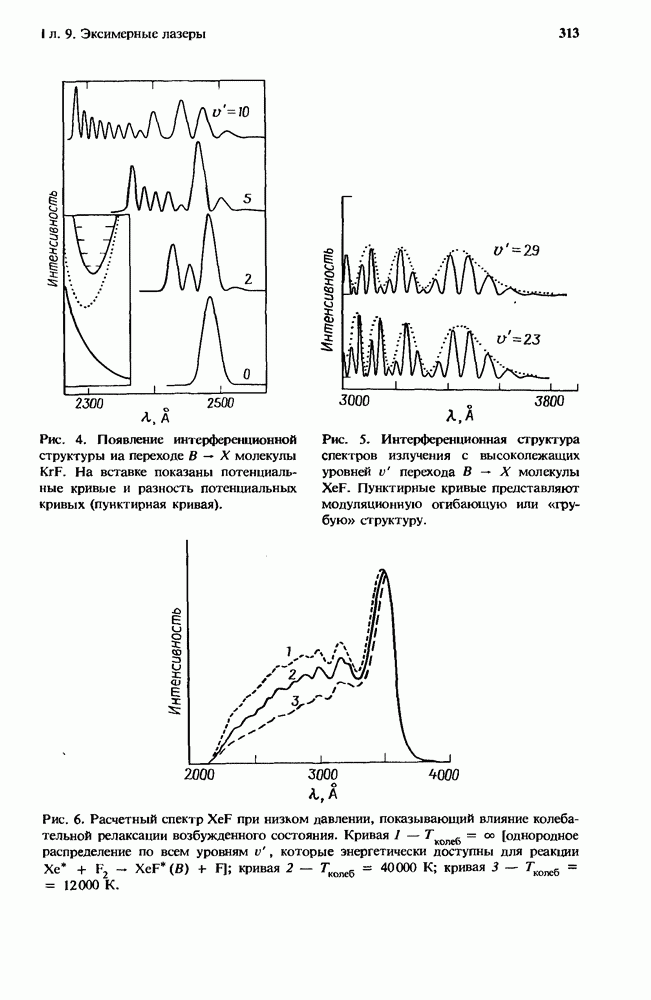
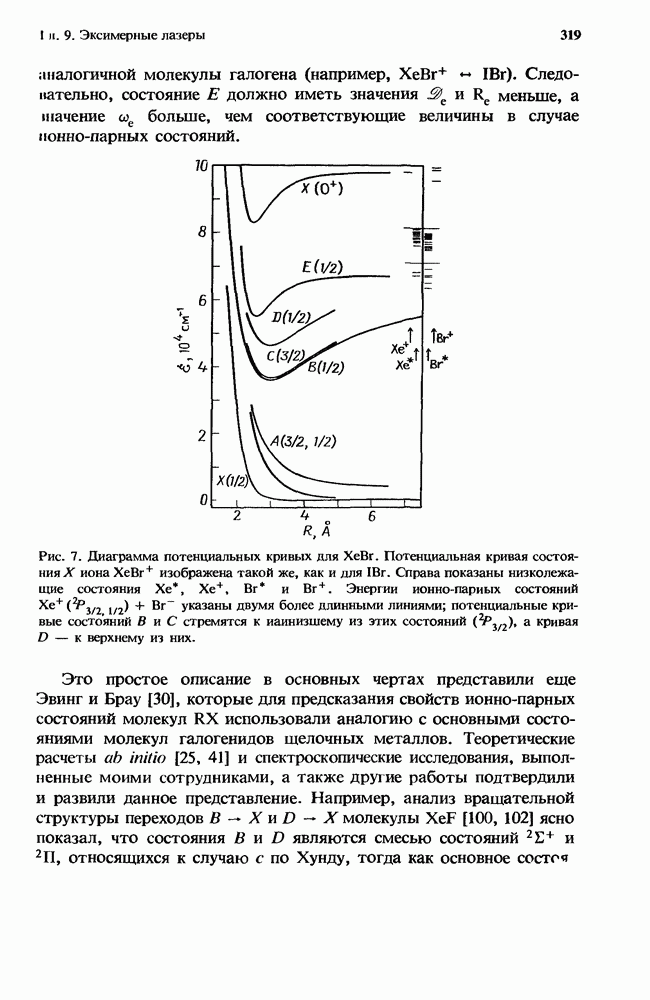
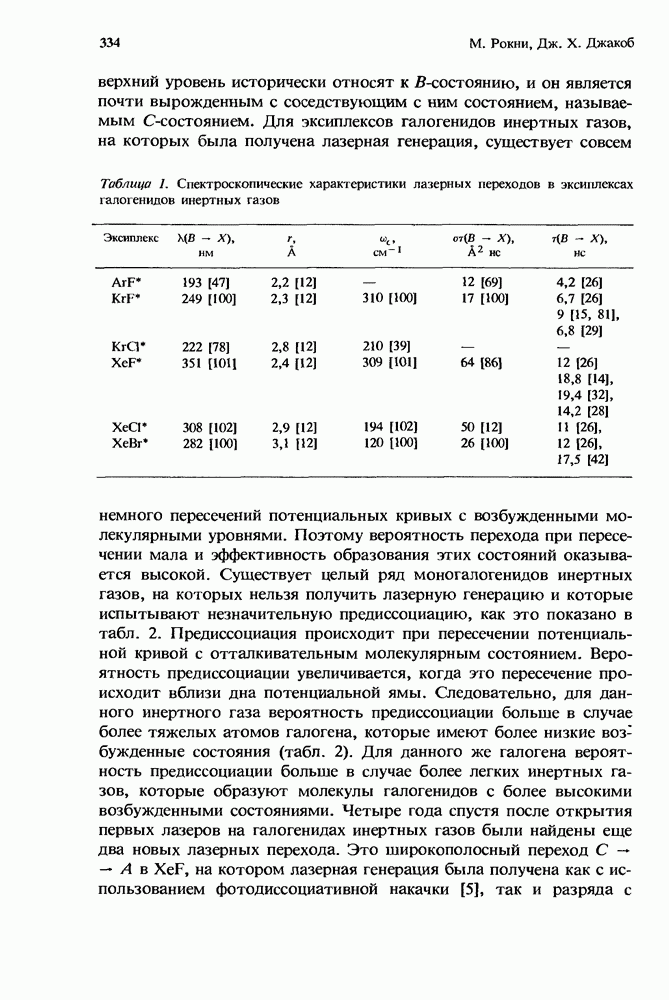
разряд будет неустойчивым, если выполняется неравенство

Эта ионизационная неустойчивость ведет к формированию страт  разряде. Такая неустойчивость возникает в разрядах
разряде. Такая неустойчивость возникает в разрядах  -лазеров (см. гл. 2 настоящей книги, а также работы [10, 13, 14, 20, 26, 27]). Для известных разрядов эксимерных лазеров удовлетворяется условие
-лазеров (см. гл. 2 настоящей книги, а также работы [10, 13, 14, 20, 26, 27]). Для известных разрядов эксимерных лазеров удовлетворяется условие  и разряд будет неустойчив, если выполняется неравенство
и разряд будет неустойчив, если выполняется неравенство

Эта ионизационная неустойчивость ведет к схлопыванию и шнурованию разряда. Она является преобладающей неустойчивостью в разрядах KrF-лазеров [5, 6, 8]. Для многих, но не обязательно для всех интересующих нас ситуаций условие ионизационной неустойчивости в разрядах эксимерных лазеров можно с хорошей степенью точности записать в виде

или

Скорость нарастания неустойчивости при условиях, когда имеют место неравенства  записывается приближенно
записывается приближенно
в виде

Характерное время нарастания неустойчивости приблизительно равно времени ионизации 
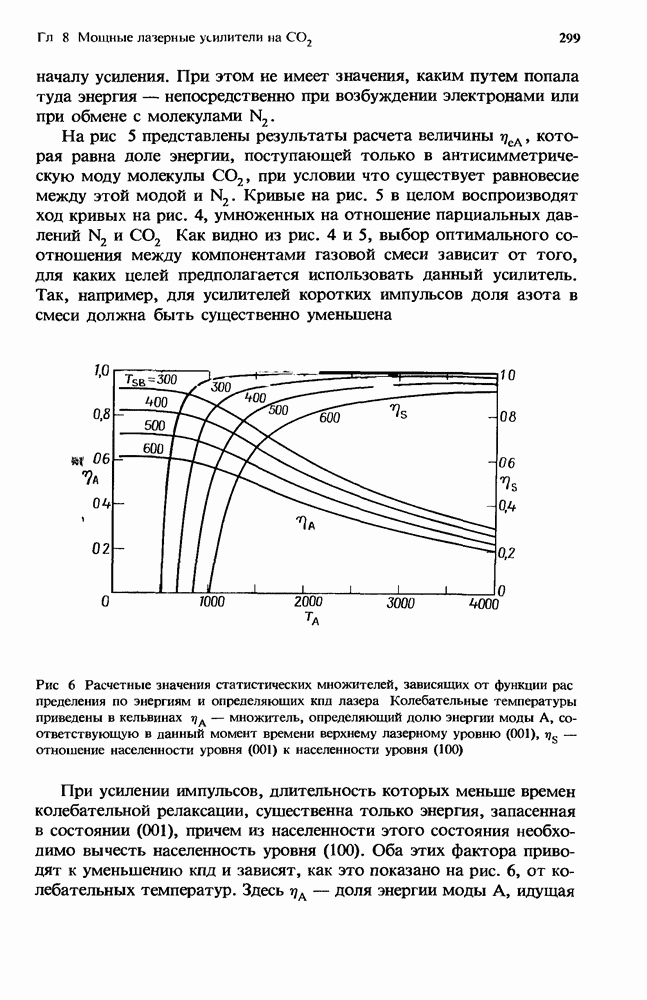
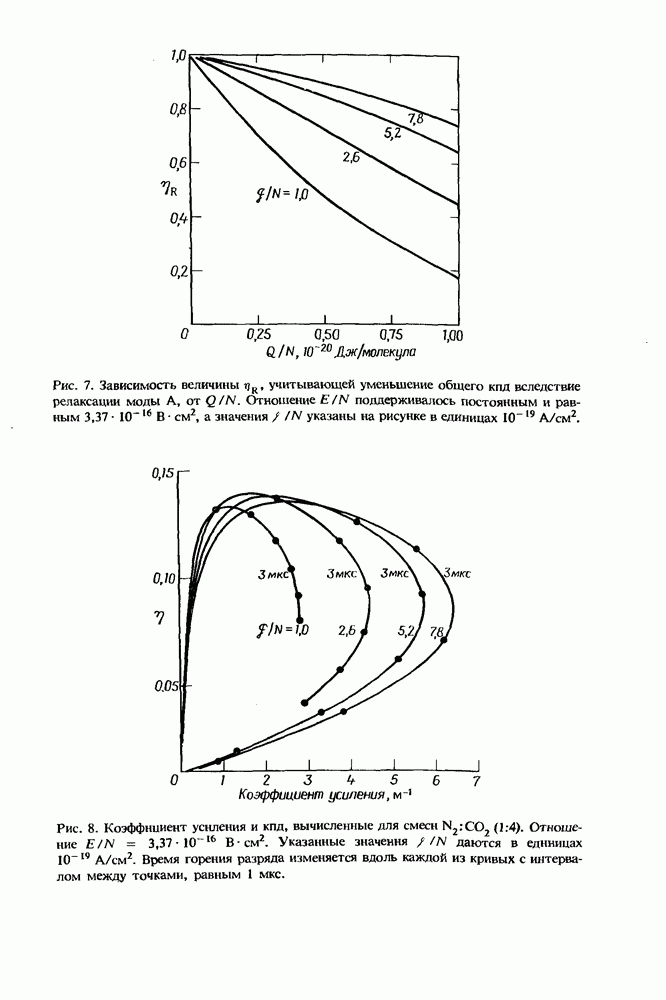
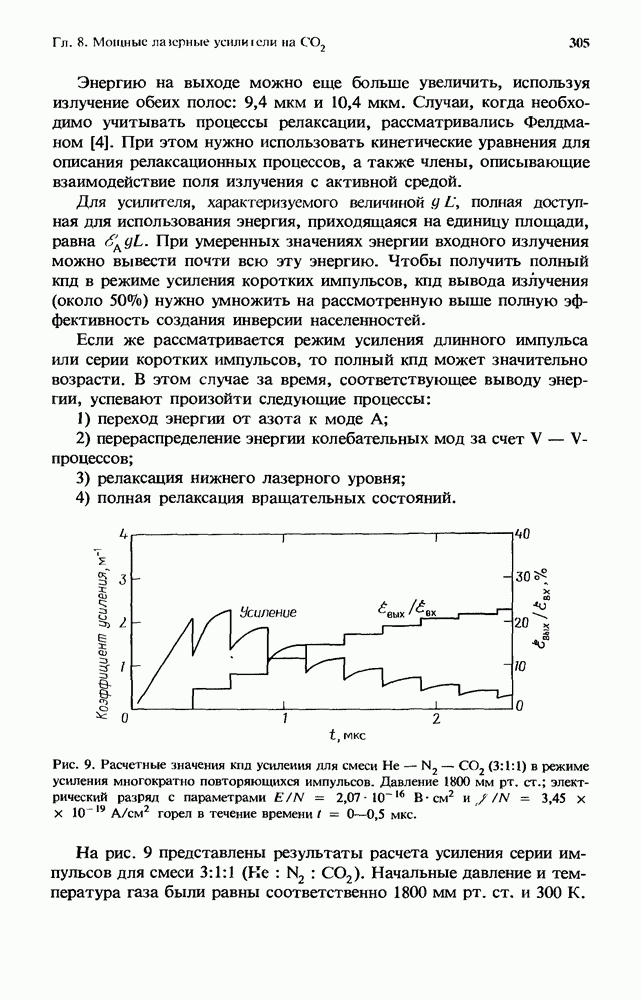
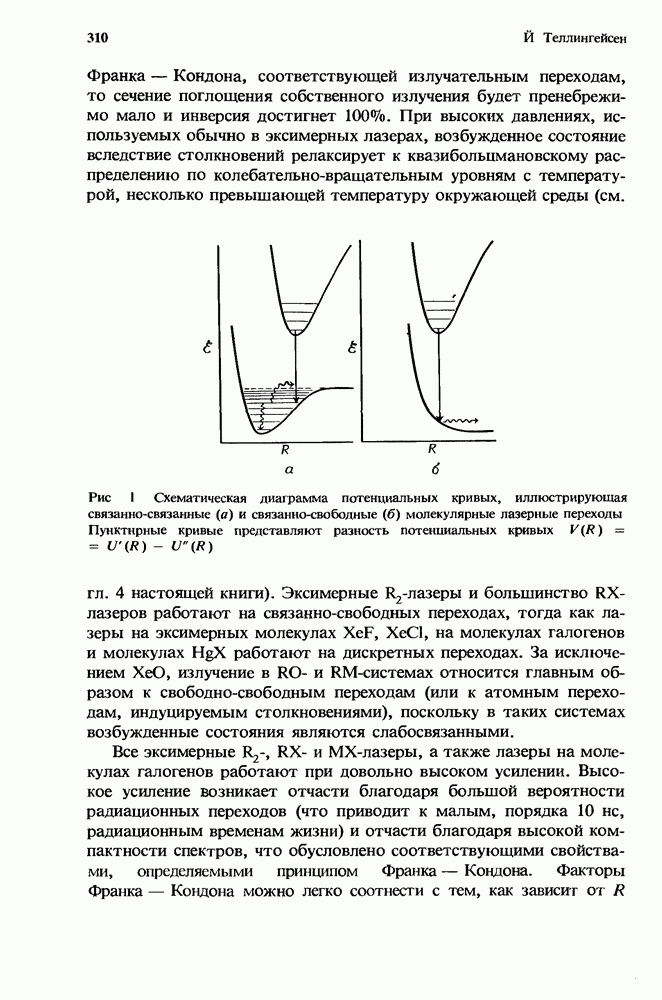
В настоящей главе мы детально исследовали условия возникновения ионизационной неустойчивости, приводящей к схлопыванию разряда в эксимерных лазерах. Мы показали, что такая ионизационная неустойчивость преобладает в разрядах эксимерных лазеров, изученных к настоящему времени. Вообще говоря, в практических приложениях каждую ситуацию следует рассматривать индивидуально. В первую очередь следует определить основные кинетические процессы, протекающие в разряде. Затем, анализируя выражения  необходимо правильно определить условия возникновения ионизационной неустойчивости и ее свойства (приводит ли она к стратифицированию или схлопыванию разряда).
необходимо правильно определить условия возникновения ионизационной неустойчивости и ее свойства (приводит ли она к стратифицированию или схлопыванию разряда).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
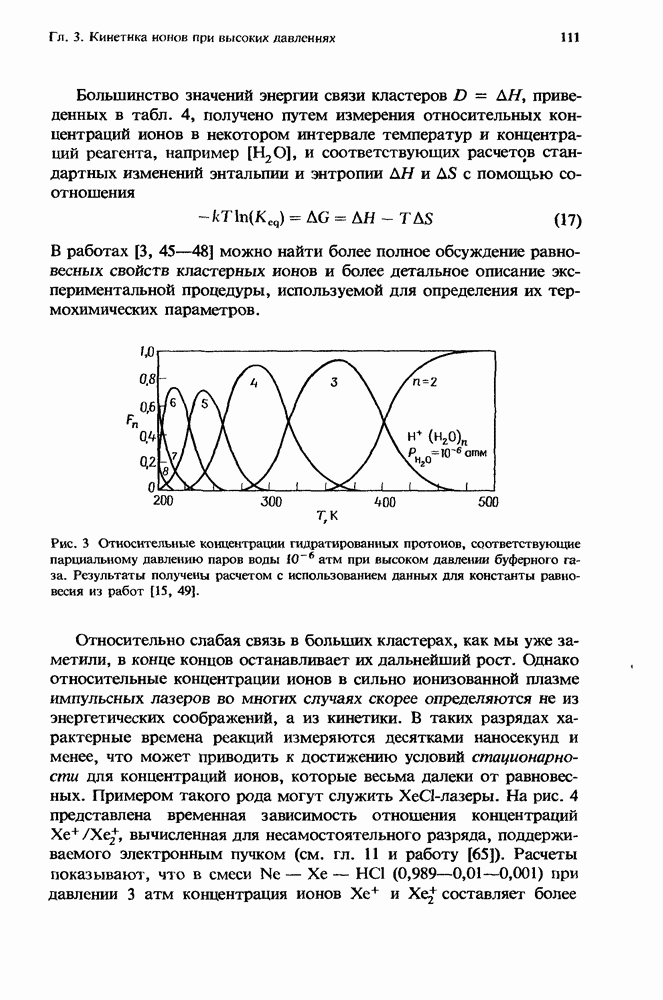
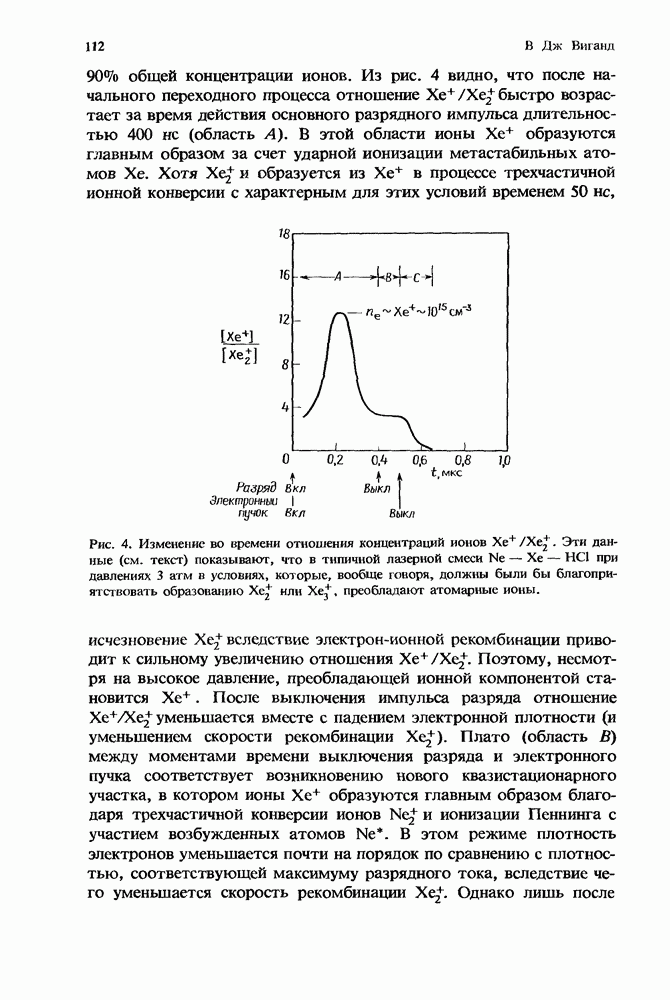
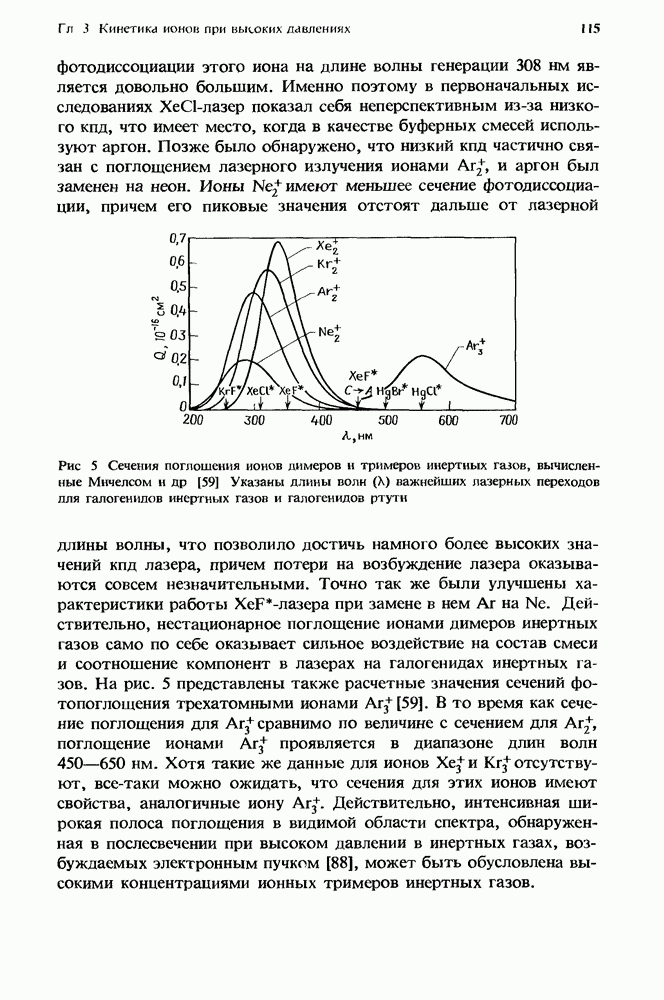
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
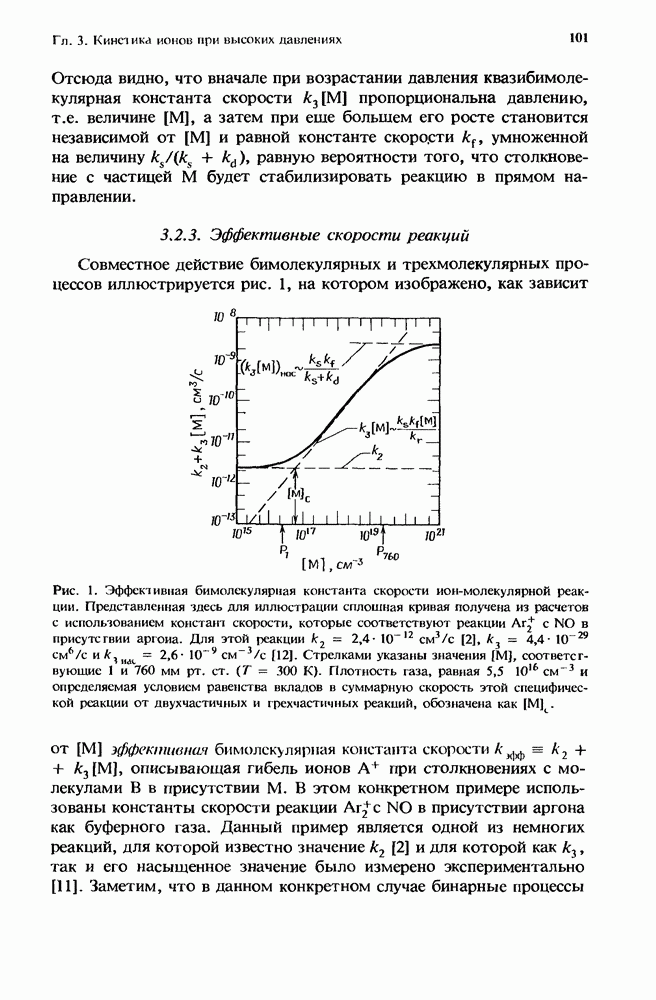
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
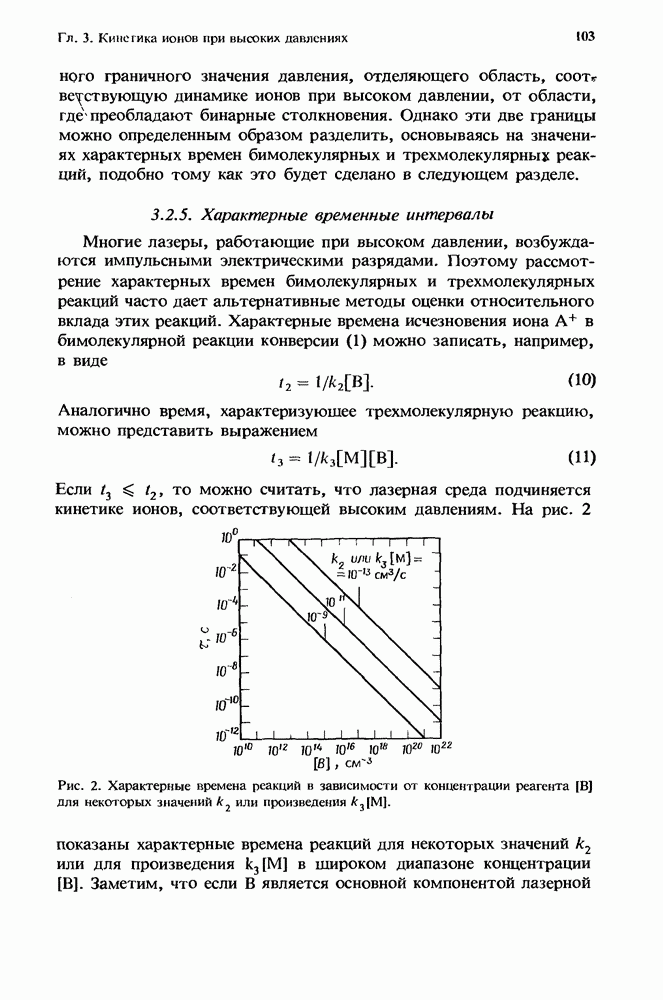
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
- 3.2.2. Энергетика отрицательных ионов
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
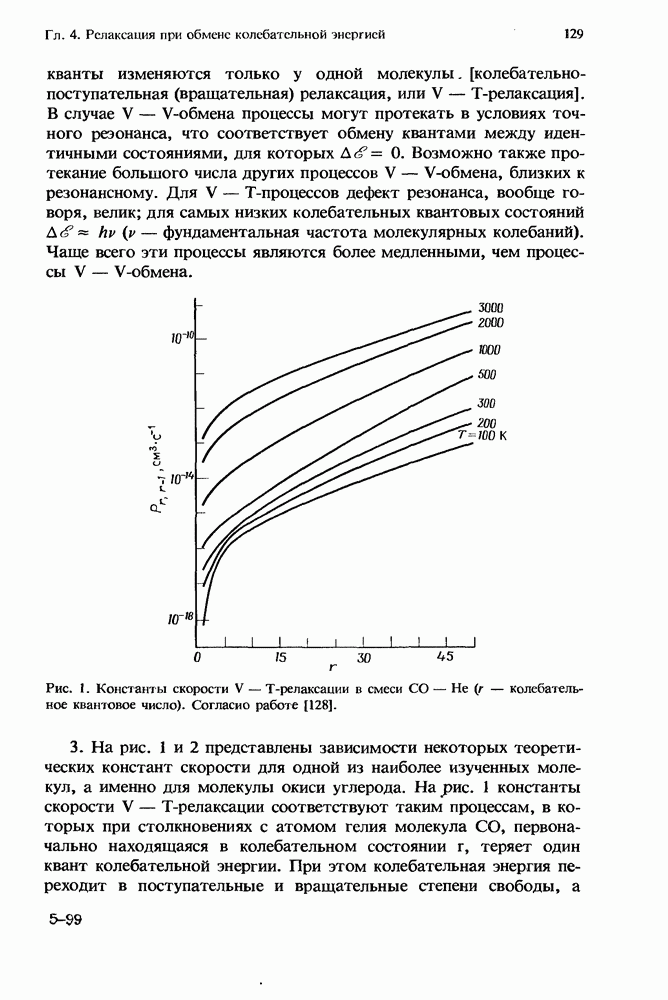
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
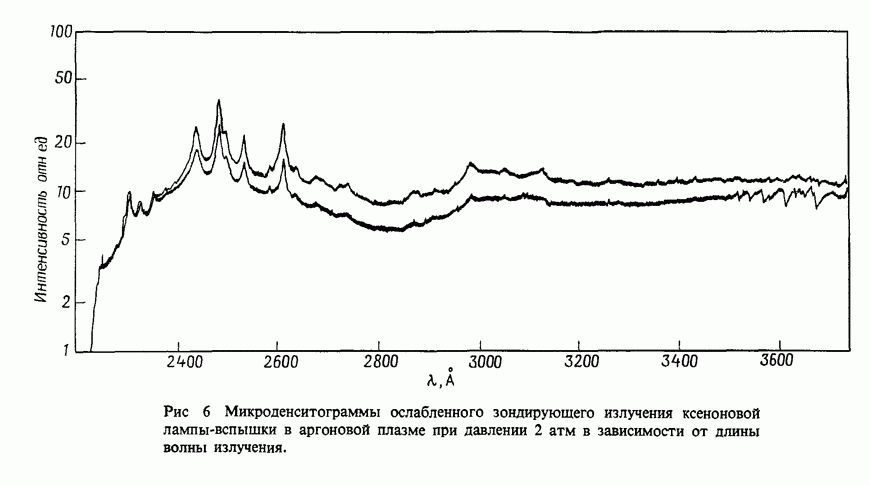
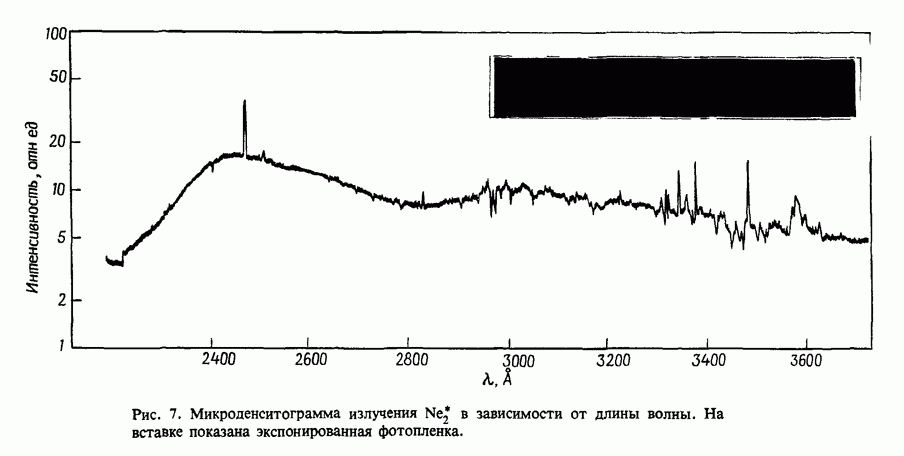
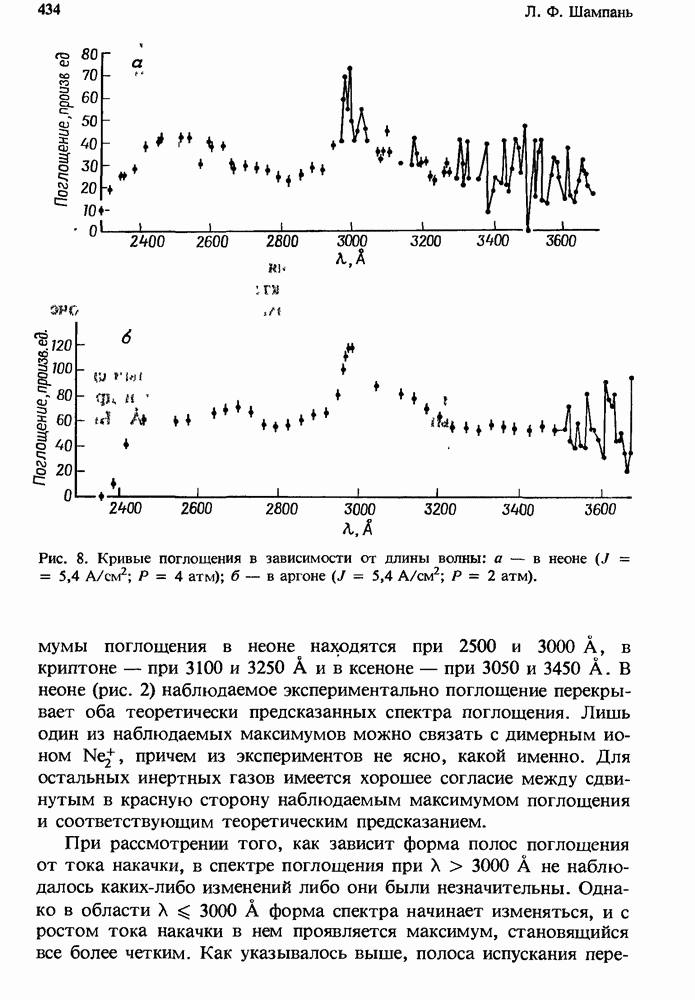
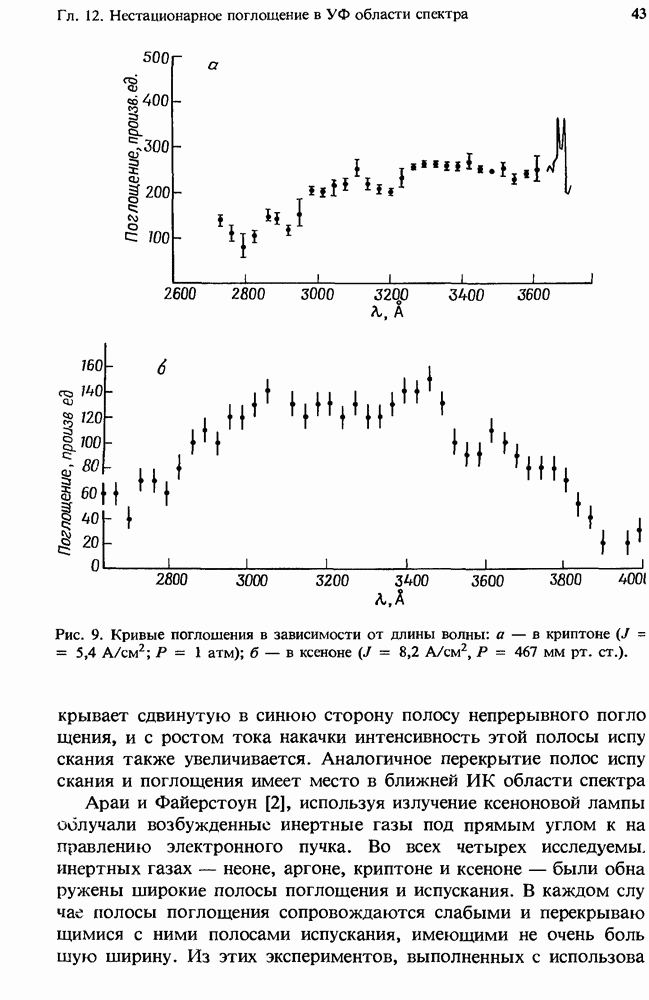
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
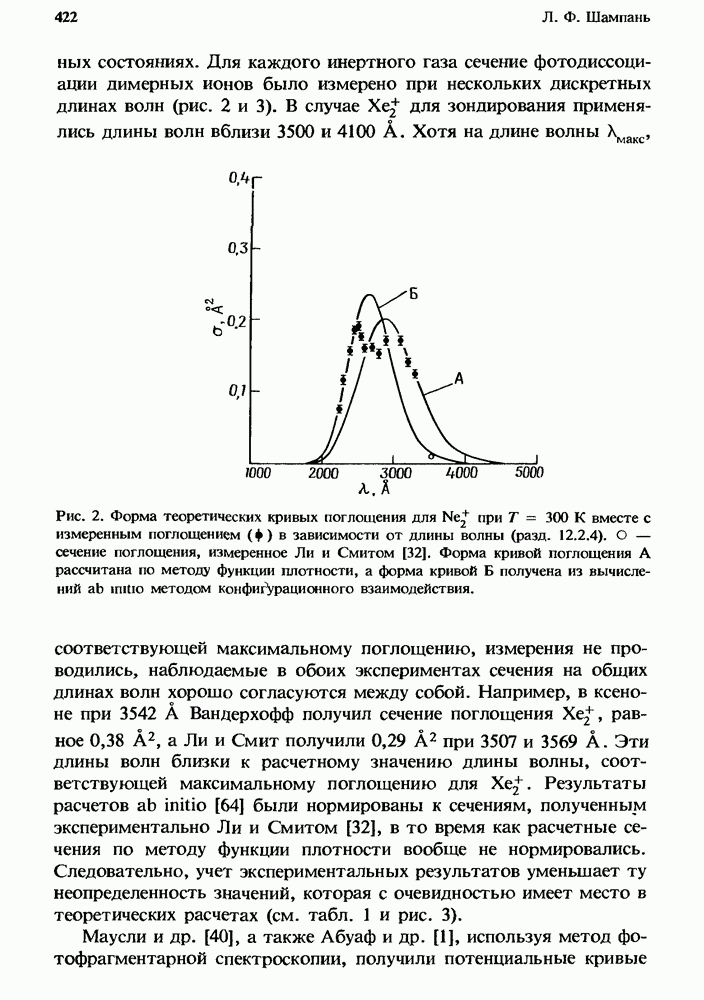
- 12.2.2. Сечение фотопоглощения
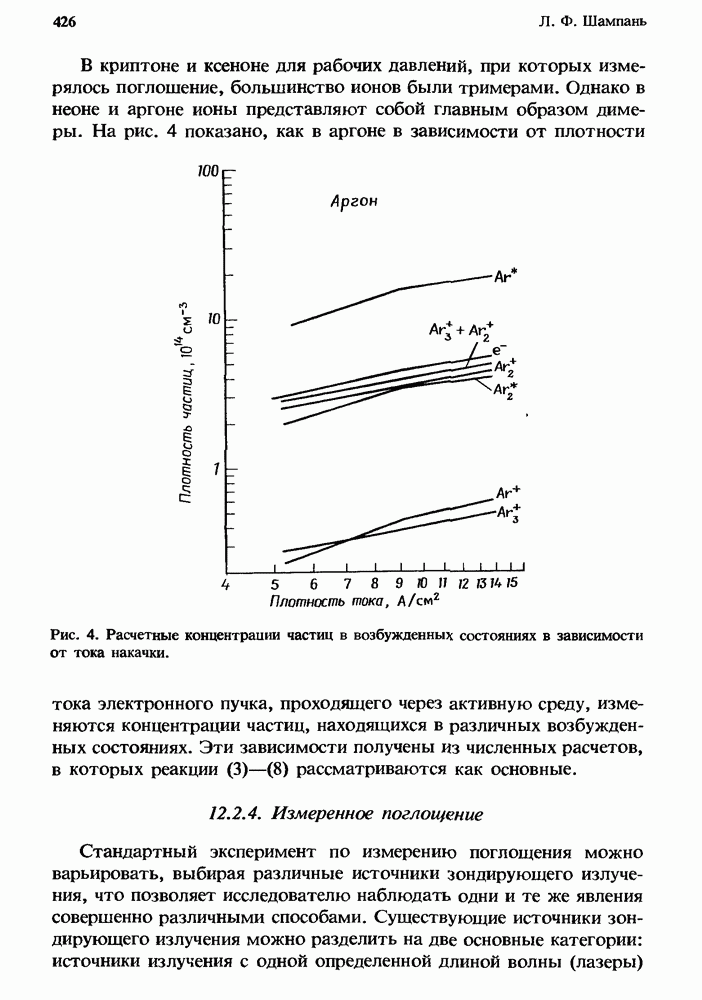
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
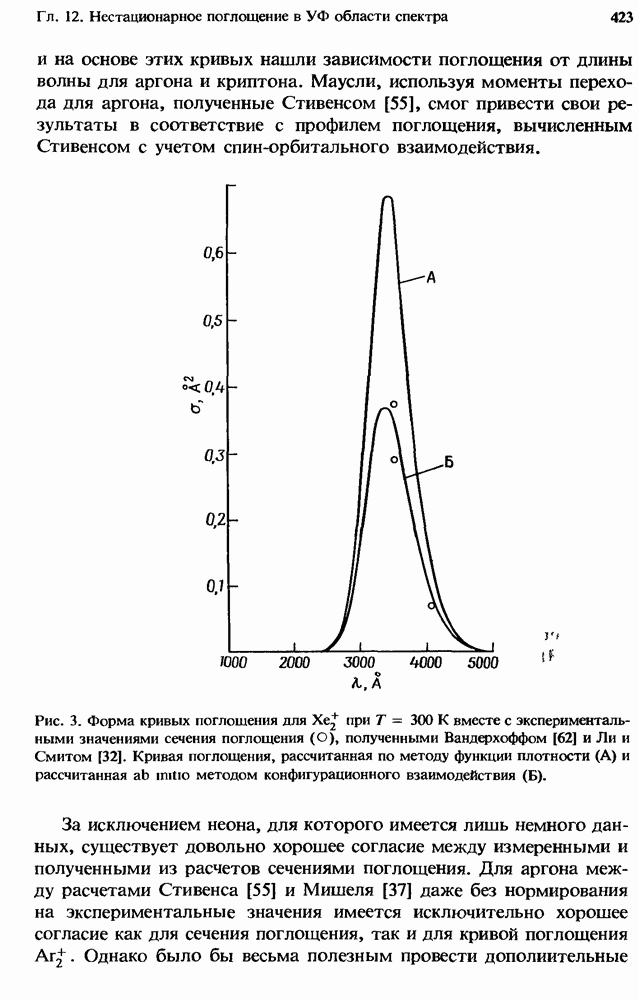
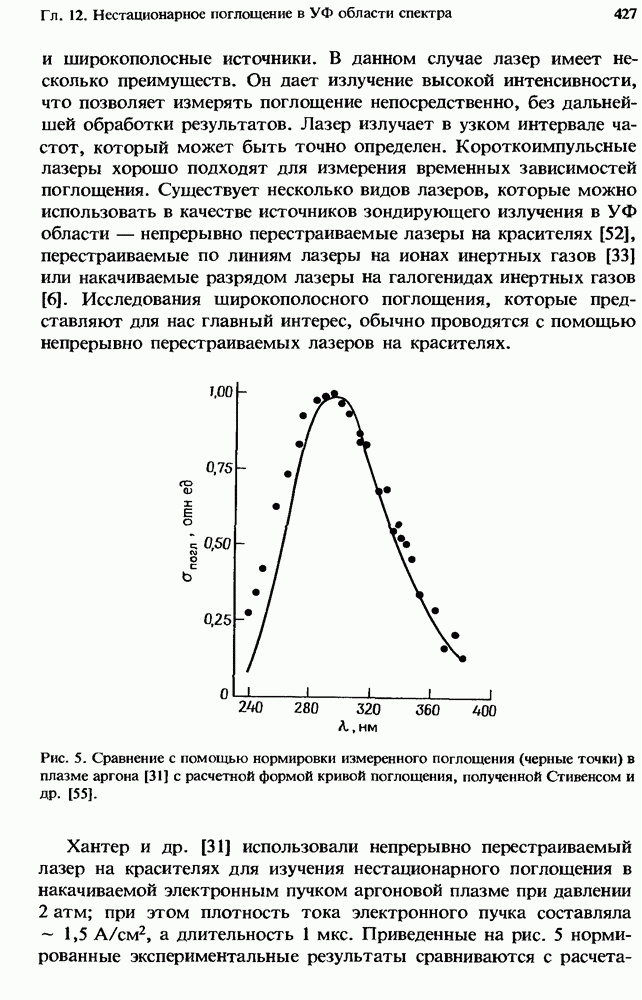
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации