§ 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний

1. Пусть

- все возможные состояния системы в однородной цепи Маркова, а  - определяющая эту цепь стохастическая матрица, составленная из переходных вероятностей   (см. стр. 381).

Обозначим через  вероятность нахождения системы в состоянии  в момент времени  если известно, что в момент времени  система находилась в состоянии  (, ). Очевидно,  . Пользуясь теоремами о сложении и умножении вероятностей, мы легко найдем:

или в матричной записи

Отсюда, давая  последовательно значения , получим важную формулу

Если существуют пределы

или в матричной записи

то величины   называются предельными или финальными переходными вероятностями.

Для выяснения, в каких случаях существуют предельные переходные вероятности, и для вывода соответствующих формул введем следующую терминологию.

Мы будем стохастическую матрицу  и соответствующую ой однородную цепь Маркова называть правильной, если у матрицы  нет характеристических чисел, отличных от единицы и равных по модулю единице, и регулярной, если дополнительно единица является простым корнем характеристического уравнения матрицы .

Правильная матрица  характеризуется том, что в ее нормальной форме (69) (стр. 373) матрицы  являются примитивными. Для регулярной матрицы дополнительно .

Кроме того, однородная цепь Маркова называется неразложимой, разложимой, ациклической, циклической, если для этой цепи стохастическая матрица  является соответственно неразложимой, разложимой, примитивной, импримитивной.

Поскольку примитивная стохастическая матрица является частным видом правильной матрицы, постольку ациклическая цепь Маркова является частным видом правильной цепи.

Мы покажем, что предельные переходные вероятности существуют только у правильных однородных цепей Маркова.

Действительно, пусть  - минимальный многочлен правильной матрицы . Тогда

 (, )    (95)

Согласно теореме 10 можно принять, что

,                                                       (95')

На основании формулы (24) гл. V (стр. 113)

         (96)

где  - приведенная присоединенная матрица и

при этом

 и

Если  - правильная матрица, то

 ,

и потому в правой части формулы (96) все слагаемые, кроме первого, при  стремится к нулю. Поэтому для правильной матрицы  существует матрица , составленная из предельных переходных вероятностей, и

                                                         (97)

Обратное положение очевидно. Если существует продел

                                                     (97')

то матрица  не может иметь характеристического числа , для которого , а , так как тогда не существовал бы предел  [Этот же предел должен существовать в силу существования предела (97').]

Мы доказали, что для правильной (и только для правильной) однородной цепи Маркова существует матрица . Эта матрица определяется формулой (97).

Покажем, как можно выразить матрицу  через характеристический многочлен

            (98)

и присоединенную матрицу .

Из тождества

в силу (95), (95') и (98) вытекает:

Поэтому формулу (97) можно заменить формулой

                                                (97)

Для регулярной цепи Маркова, поскольку она является частным видом правильной цепи, матрица существует и определяется любой из формул (97), (97'). В этом случае  и формула (97') имеет вид

                                                         (99)

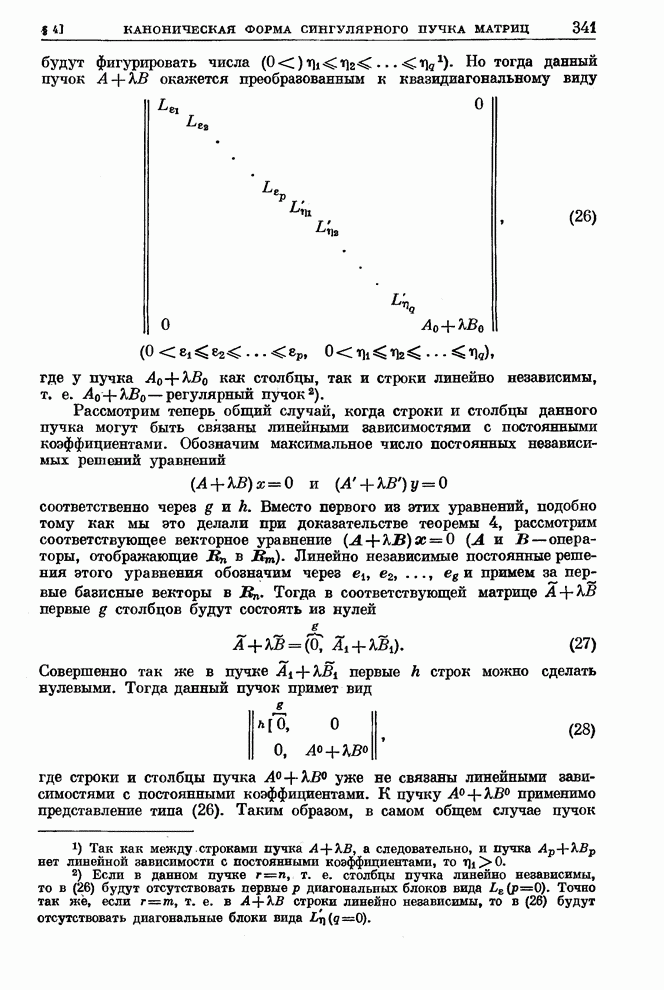
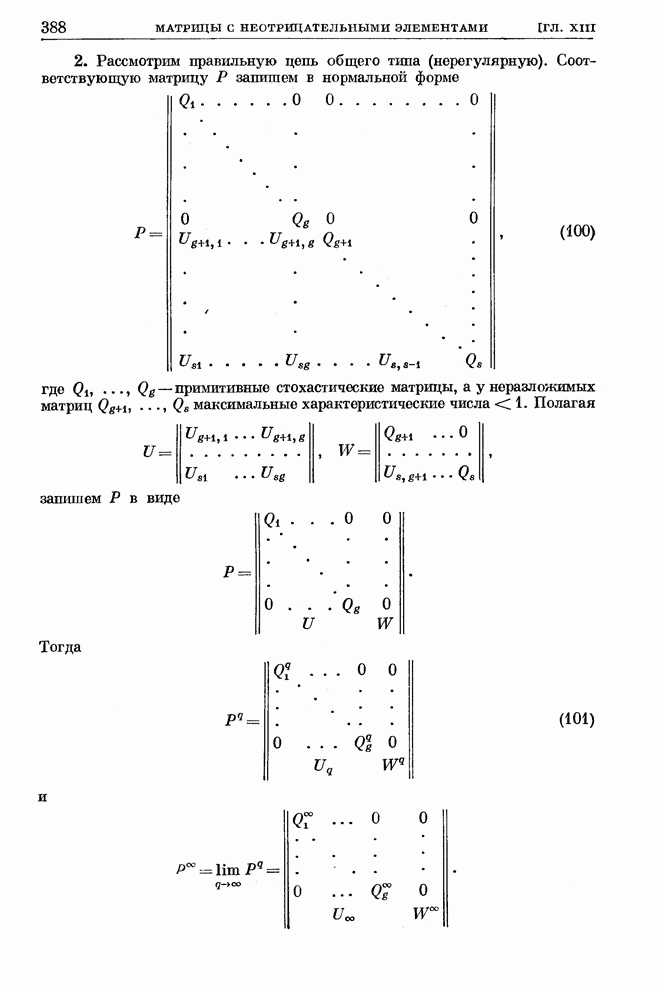
2. Рассмотрим правильную цепь общего типа (нерегулярную). Соответствующую матрицу   запишем в нормальной форме

    (100)

где  - примитивные стохастические матрицы, а у неразложимых матриц  максимальные характеристические числа . Полагая

,

запишем  в виде

Тогда

                                (101)

и

Но , поскольку все характеристические числа матрицы  по модулю меньше единицы. Поэтому

                                  (102)

Поскольку  - примитивные стохастические матрицы, то матрицы  согласно формулам (99) и (35) (стр. 362) положительны

и в каждом столбце любой из этих матриц все элементы равны между собой:

.

Заметим, что нормальному виду (100) стохастической матрицы  соответствует разбиение состояний системы  на группы:

                                  (103)

Каждой группе  в (104) соответствует своя группа рядов в (101). По терминологии Л. Н. Колмогорова состояния системы, входящие в , называются существенными, а состояния, входящие в остальные группы  - несущественными.

Из вида (101) матрицы  следует, что при любом коночном числе шагов  (от момента  к моменту ) возможен только переход системы а) из существенного состояния в существенное состояние той же группы, б) из несущественного состояния в существенное состояние и в) из несущественного состояния в несущественное состояние той же или предшествующей группы.

Из вида (102) матрицы  следует, что в продело при  переход возможен только из любого состояния в существенное состояние, т. е. вероятность перехода в любое несущественное состояние при числе шагов  стремится к нулю. Поэтому существенные состояния иногда называются и предельными состояниями.

3. Из формулы (97) следует:

.

Отсюда видно, что каждый столбец матрицы  является собственным вектором стохастической матрицы  для характеристического числа .

Для регулярной матрицы  число 1 является простым корнем характеристического уравнения и этому числу соответствует только один (с точностью до скалярного множителя) собственный вектор  матрицы . Поэтому в любом -м столбце матрицы  все элементы равны одному и тому же неотрицательному числу :

 (, )            (104)

Таким образом, в регулярной цепи предельные переходные вероятности но зависят от начального состояния.

Обратно, если в некоторой правильной однородной цепи Маркова продельные переходные вероятности не зависят от начального состояния, т. е. имеют место формулы (104), то в схеме (102) для матрицы  обязательно . Но тогда  и цепь является регулярной.

Для ациклической цепи, которая является частным случаем регулярной цепи,  - примитивная матрица. Поэтому при некотором   (см. теорему 8 на стр. 377). Но тогда и .

Обратно, из  следует, что при некотором  , а это по теореме 8 означает примитивность матрицы  и, следовательно, ацикличность данной однородной цепи Маркова.

Полученные результаты мы сформулируем в виде следующей теоремы:

Теорема 11. 1 .Для того чтобы в однородной цепа Маркова существовали все предельные переходные вероятности, необходимо и достаточно, чтобы цепь была правильной. В этом случае матрица , составленная из предельных переходных вероятностей, определяется формулой (95) или (98).

2. Для того чтобы в правильной однородной цепи Маркова предельные переходные вероятности не зависели от начального состояния, необходимо и достаточно, чтобы цепь была регулярной. В этом случае матрица  определяется формулой (99).

3. Для того чтобы в правильной однородной цепи Маркова все предельные переходные вероятности были отличны от нуля, необходимо и достаточно, чтобы цепь была ациклической.

4. Введем в рассмотрение столбцы из абсолютных вероятностей

                      (105)

где  - вероятность нахождения системы в момент  в состоянии  (,). Пользуясь теоремами сложения и умножения вероятностей, найдем:

 (,),

или в матричной записи

 ,                                   (106)

где  - транспонированная матрица для матрицы .

Все абсолютные вероятности (105) определяются из формулы (106), если известны начальные вероятности  и матрица переходных вероятностей  

Введем в рассмотрение предельные абсолютные вероятности

или

Переходя в обоих частях равенства (106) к пределу при , получим:

                                                           (107)

Заметим, что существование матрицы предельных переходных вероятностей  влечет существование предельных абсолютных вероятностей  при любых начальных вероятностях  и наоборот.

Из формулы (107) и из вида (102) матрицы  вытекает, что предельные абсолютные вероятности, соответствующие несущественным состояниям, равны нулю.

Умножая обе части матричного равенства

справа на , мы в силу (107) получим:

,

т. е. столбец предельных абсолютных вероятностей  является собственным вектором матрицы  для характеристического числа .

Если данная цепь Маркова регулярна, то  является простым корнем характеристического уравнения матрицы . В этом случае столбец предельных абсолютных вероятностей однозначно определяется из (108) (поскольку   и ).

Пусть дана регулярная цепь Маркова. Тогда из (104) и из (107) следует:

     (109)

В этом случае предельные абсолютные вероятности  не зависят от начальных вероятностей .

Обратно,  может не зависеть от  при наличии формулы (107) тогда и только тогда, когда все строки матрицы  одинаковы, т. е.

 ,

и потому (согласно теореме 11)  - регулярная матрица.

Если  — примитивная матрица, то , а отсюда в силу (109)

 .

Наоборот, если все   и не зависят от начальных вероятностен, то в каждом столбце матрицы  все элементы одинаковы и согласно (109) , а это по теореме 11 означает, что  - примитивная матрица, т. е. данная цепь ациклична.

Из изложенного вытекает, что теорему 11 можно сформулировать так:

Теорема 11'. 1. Для того чтобы в однородной цепи Маркова существовали все предельные абсолютные вероятности при любых начальных вероятностях, необходимо и достаточно, чтобы цепь была правильной.

2. Для того чтобы в однородной цепи Маркова существовали предельные абсолютные вероятности при любых начальных вероятностях и не зависели от этих начальных вероятностей, необходимо и достаточно, чтобы цепь была регулярной.

3. Для того чтобы в однородной цепи Маркова при любых начальных вероятностях существовали положительные предельные абсолютные вероятности и эти предельные вероятности не зависели от начальных, необходимо и достаточно, чтобы цепь была ациклической.

5. Рассмотрим теперь однородную цепь Маркова общего типа с матрицей переходных вероятностей .

Возьмем нормальную форму (69) матрицы  и обозначим через  индексы импримитивности матриц  в (69). Пусть  - наименьшее общее кратное целых чисел . Тогда матрица  не имеет характеристических чисел, равных по модулю единице, но отличных от единицы, т. е.  - правильная матрица; при этом  - наименьший показатель, при котором  - правильная матрица. Число  назовем периодом данной однородной цепи Маркова

Поскольку  - правильная матрица, то существуют предел

,

а значит, и пределы

Таким образом, в общем случае последовательность матриц

разбивается на  подпоследовательностей с пределами  .

Переходя от переходных вероятностей к абсолютным при помощи формулы (106), мы получим, что последовательность

распадается на  подпоследовательностей с пределами

 .

Для произвольной однородной цепи Маркова с коночным числом состояний всегда существуют пределы средних арифметических

   (110)

и

                                      (110')

Здесь  и . Величины   и   называются соответственно средними предельными переходными и средними предельными абсолютными вероятностями.

Поскольку

то

и, следовательно, в силу (110')

,                    (111)

т. е.  - собственный вектор матрицы  для .

Заметим, что по формулам (69) и (110) мы можем матрицу  представить в виде

где

 ,

Поскольку все характеристические числа матрицы  по модулю меньше единицы, то

и, следовательно .

Поэтому

Поскольку  — стохастическая матрица, то стохастическими являются здесь и матрицы .

Из полученного представления для  и из (107) следует, что средние предельные абсолютные вероятности, соответствующие несущественным состояниям, всегда равны нулю.

Если в нормальной форме матрицы  число , то для матрицы ' число  является простым характеристическим числом.

В этом случае  однозначно определяется из (111), и средние предельные вероятности  не зависят от начальных вероятностей . Обратно, если  не зависит от , то в силу (110') матрица  имеет ранг 1. Но матрица (112) может иметь ранг 1 только тогда, когда .

Полученные результаты мы сформулируем в виде следующей теоремы:

Теорема 12. Для произвольной однородной цепи Маркова с периодом  матрицы вероятностей  и  при  стремятся к периодическому повторению с периодом ; при этом всегда существуют средние предельные переходные и абсолютные вероятности  и , определяемые формулами (110) и (110').

Средние предельные абсолютные вероятности, соответствующие несущественным состояниям, всегда равны нулю.

Если в нормальной форме матрицы  число  (и только в этом случае), средние предельные абсолютные вероятности  не зависят от начальных вероятностей  и однозначно определяются из уравнения (111).