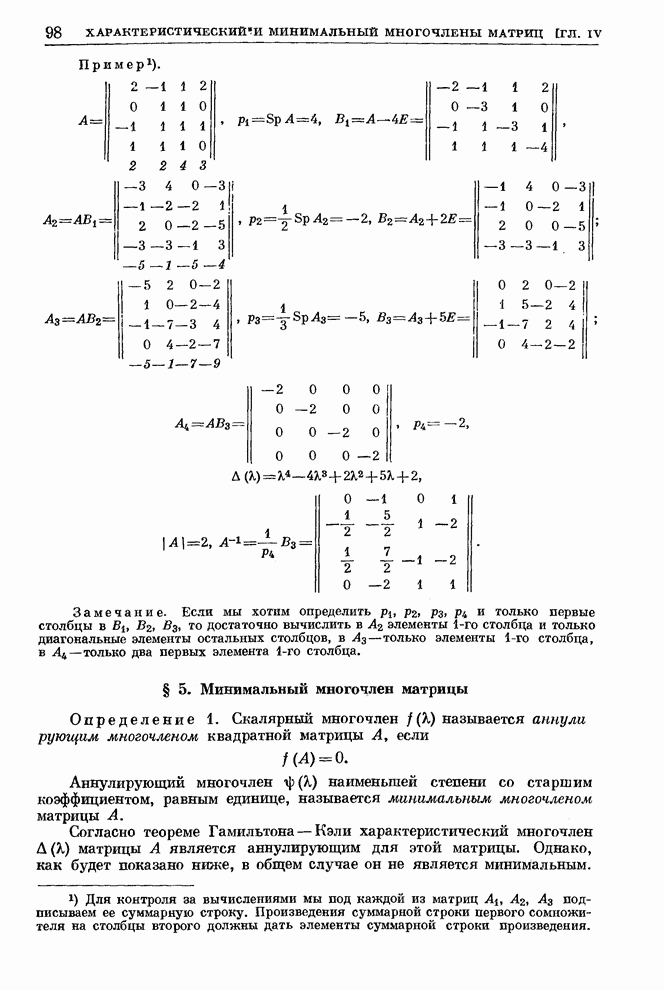
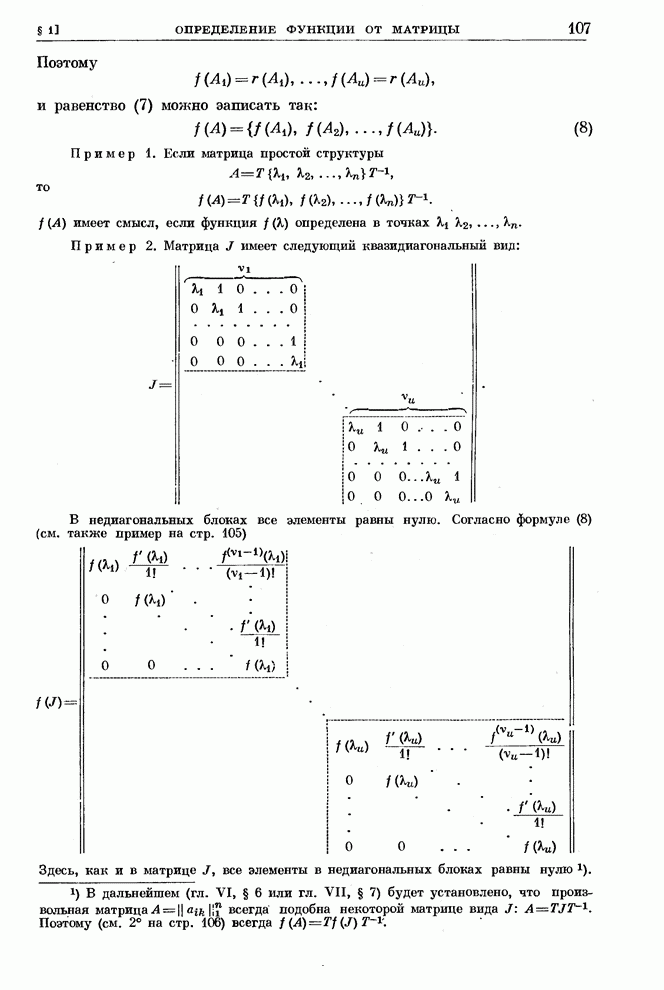
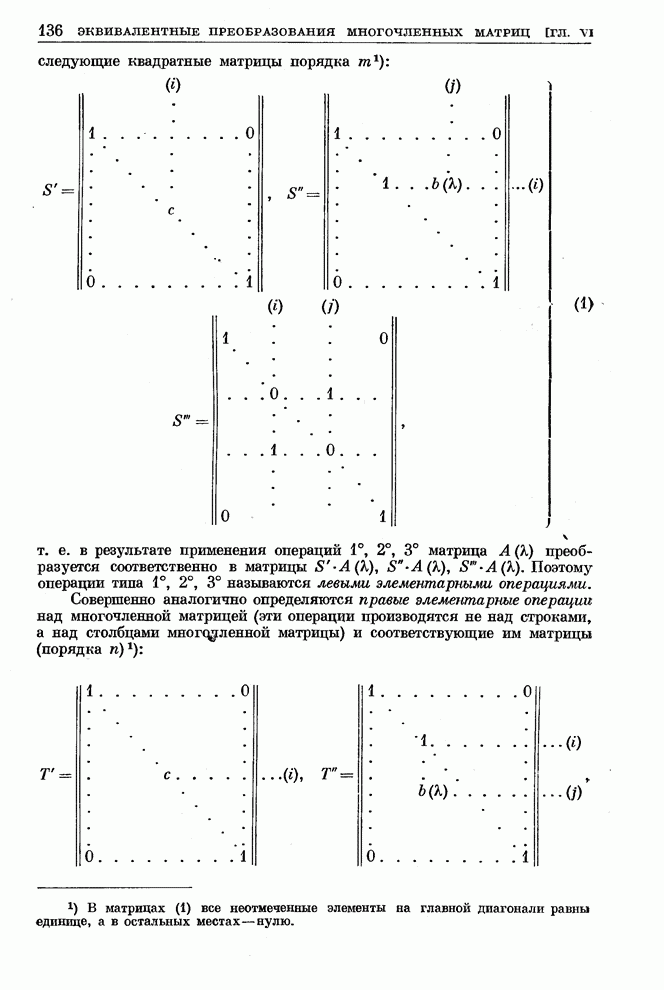
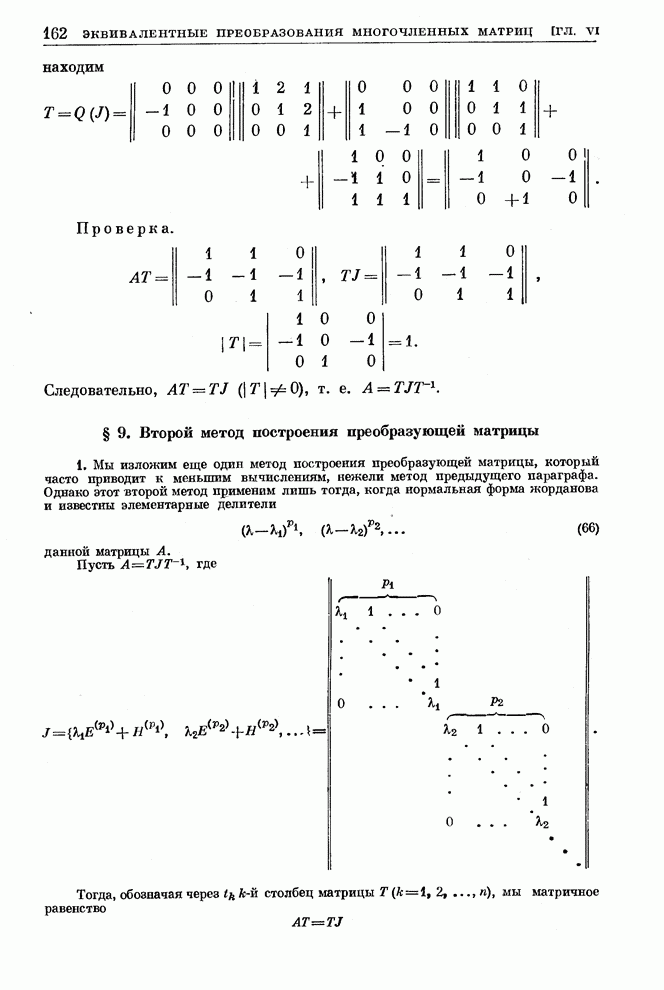
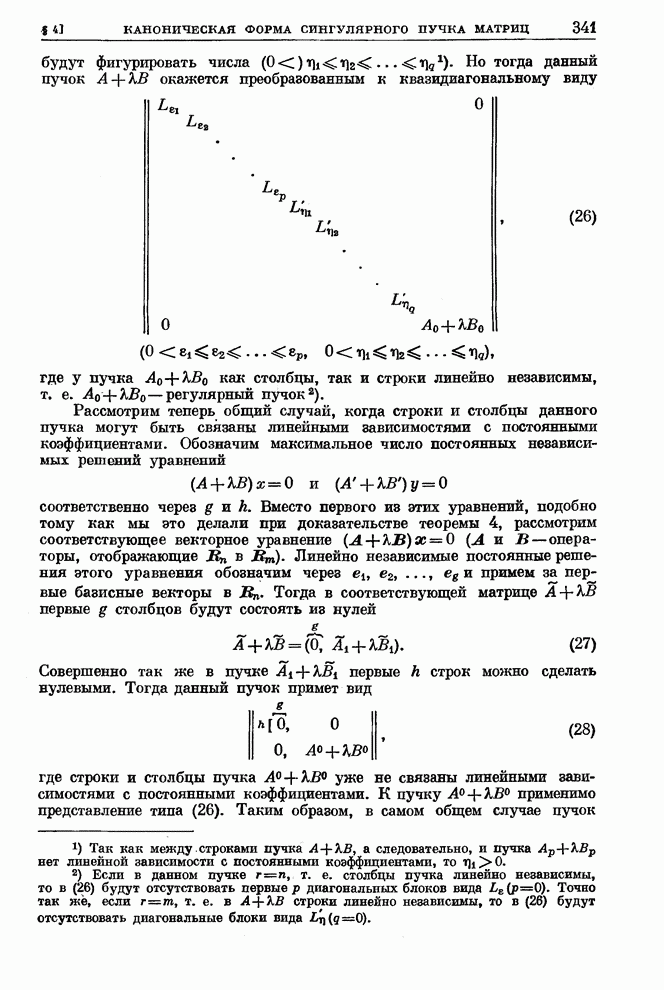
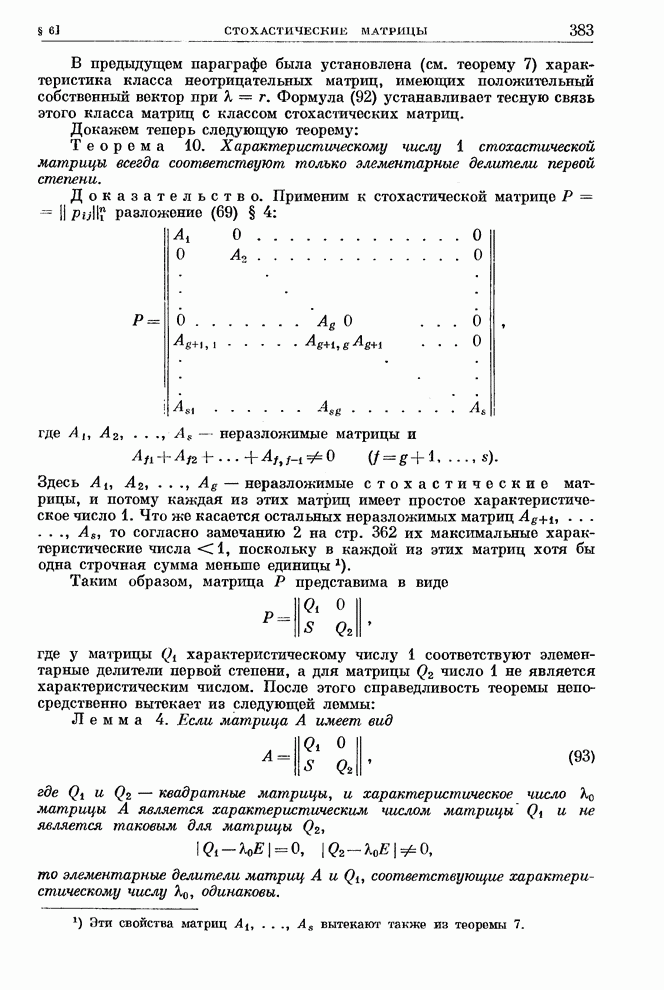
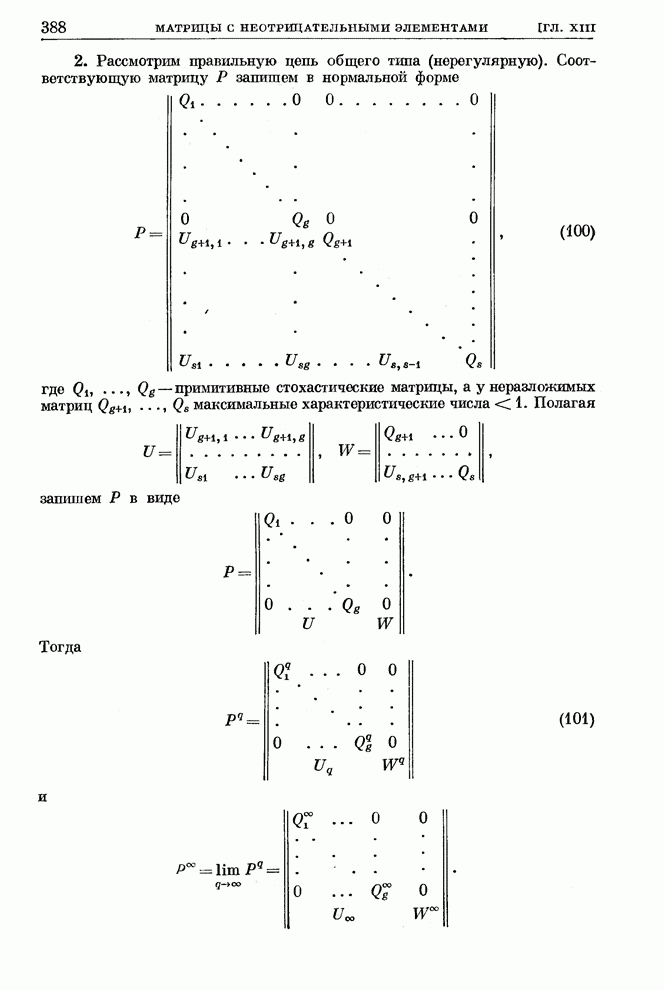
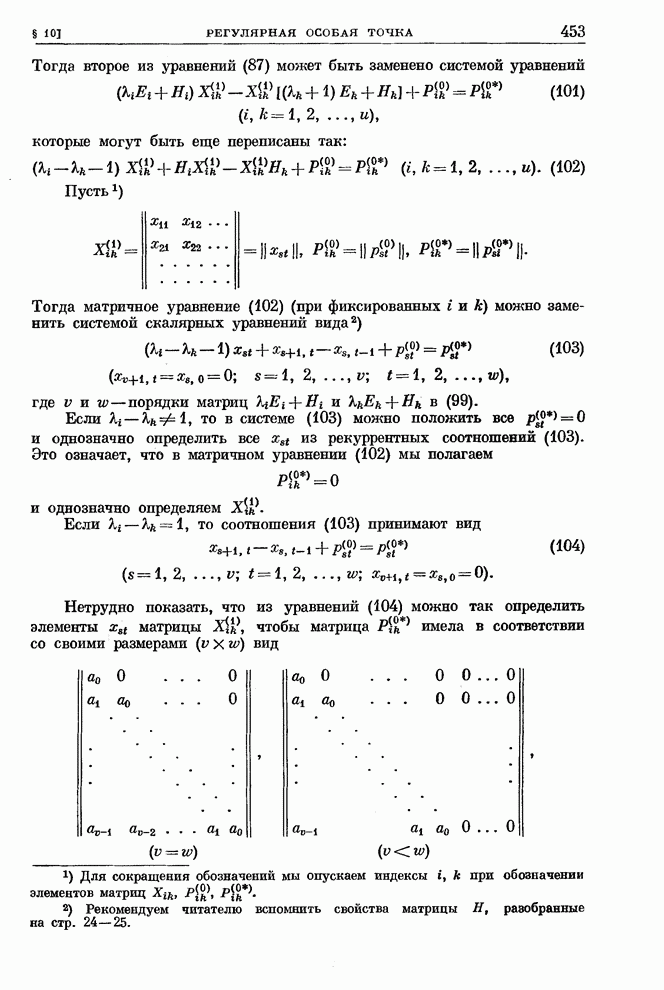
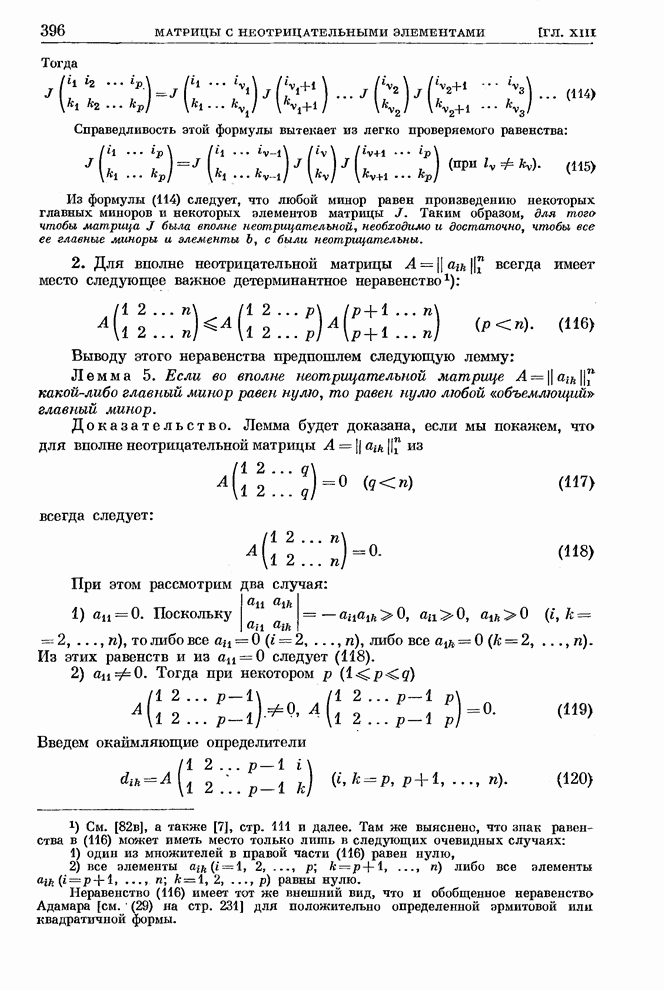| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. Регулярный пучок матриц
1.
Рассмотрим частный случай, когда пучки ![]() и
и ![]() состоят из квадратных матриц (
состоят из квадратных матриц (![]() ) и
) и ![]() ,
, ![]() . В
этом случае, как
было доказано в главе VI (стр. 140), два понятия «эквивалентность» и «строгая
эквивалентность» пучков совпадают. Поэтому, применяя к пучкам общий критерий
эквивалентности
. В
этом случае, как
было доказано в главе VI (стр. 140), два понятия «эквивалентность» и «строгая
эквивалентность» пучков совпадают. Поэтому, применяя к пучкам общий критерий
эквивалентности ![]() -матриц
(стр. 148), приходим к теореме:
-матриц
(стр. 148), приходим к теореме:
Теорема 1. Два пучка
квадратных матриц одного и того же порядка ![]() и
и ![]() , у которых
, у которых ![]() и
и ![]() , являются строго
эквивалентными в том и только в том случае, когда эти пучки имеют одни и те же
элементарные делители в поле
, являются строго
эквивалентными в том и только в том случае, когда эти пучки имеют одни и те же
элементарные делители в поле ![]() .
.
Пучок
квадратных матриц
![]() с
с ![]() в
главе VI называется регулярным, поскольку он представляет собой частный случай
регулярного матричного многочлена относительно
в
главе VI называется регулярным, поскольку он представляет собой частный случай
регулярного матричного многочлена относительно ![]() (см. гл. IV, стр. 87). В предыдущем
параграфе настоящей главы мы дали более широкое определение регулярного пучка.
Согласно этому определению в регулярном пучке возможно равенство
(см. гл. IV, стр. 87). В предыдущем
параграфе настоящей главы мы дали более широкое определение регулярного пучка.
Согласно этому определению в регулярном пучке возможно равенство ![]() (и даже
(и даже ![]() ).
).
Для того чтобы выяснить, сохранится ли теорема 1 для регулярных пучков (при расширенном определении 1), рассмотрим следующий пример:
 ,
,  (3)
(3)
Нетрудно видеть, что здесь каждый из
пучков ![]() и
и ![]() имеет только
один элементарный делитель
имеет только
один элементарный делитель ![]() . В то же время эти пучки не являются
строго эквивалентными, так как матрицы
. В то же время эти пучки не являются
строго эквивалентными, так как матрицы ![]() и
и ![]() имеют
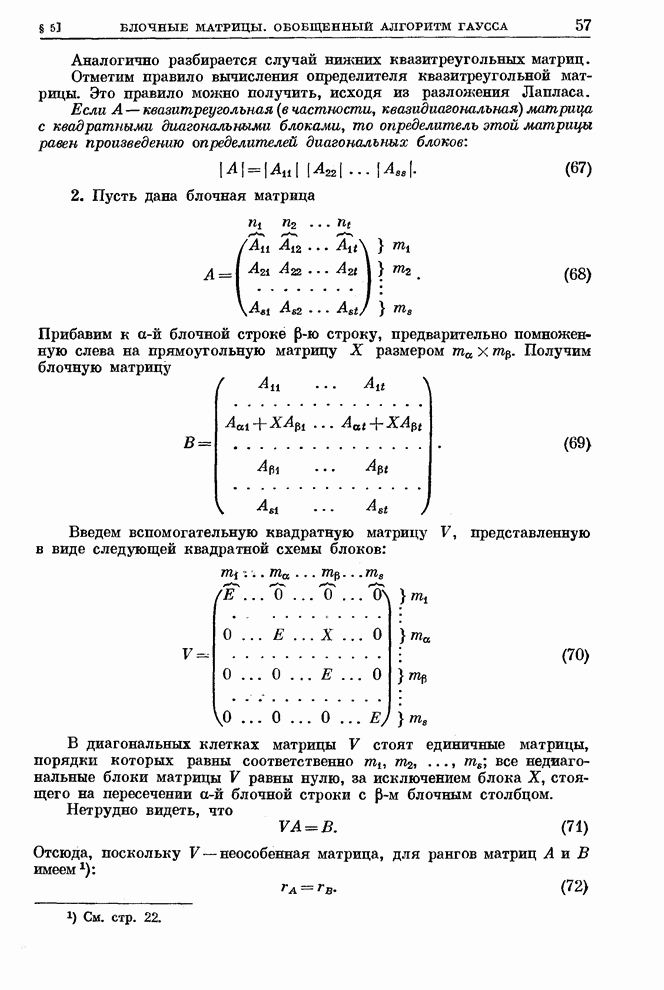
соответственно ранги 2 и 1, а из равенства (2), если бы оно имело место,
следовало бы, что ранги матриц
имеют
соответственно ранги 2 и 1, а из равенства (2), если бы оно имело место,
следовало бы, что ранги матриц
![]() и
и ![]() равны
между собой. При этом пучки (3) являются регулярными согласно определению 1,
так как
равны
между собой. При этом пучки (3) являются регулярными согласно определению 1,
так как
![]() .
.
Разобранный пример показывает, что теорема 1 неверна при расширенном определении регулярного пучка.
2. Для того чтобы сохранить теорему 1,
нам придется ввести понятие о «бесконечных» элементарных делителях пучка.
Будем пучок ![]() задавать
при помощи «однородных» параметров
задавать
при помощи «однородных» параметров ![]() . Тогда определитель
. Тогда определитель ![]() будет однородной функцией от
будет однородной функцией от ![]() . Определяя
наибольший общий делитель
. Определяя
наибольший общий делитель ![]() всех миноров
всех миноров ![]() -го порядка матрицы
-го порядка матрицы ![]()
![]() , получим
инвариантные многочлены по известным формулам
, получим
инвариантные многочлены по известным формулам
![]() ;
;
при этом все ![]() и
и ![]() - однородные
относительно
- однородные
относительно ![]() и
и
![]() многочлены.
Разлагая инвариантные многочлены на степени неприводимых в поле
многочлены.
Разлагая инвариантные многочлены на степени неприводимых в поле ![]() однородных
многочленов, получим элементарные делители
однородных
многочленов, получим элементарные делители ![]()
![]() пучка
пучка ![]() в поле
в поле ![]() .
.
Совершенно
очевидно, что, полагая ![]() в
в ![]() , мы вернемся к элементарным делителям
, мы вернемся к элементарным делителям
![]() пучка
пучка ![]() . Обратно, из
каждого элементарного делителя
. Обратно, из
каждого элементарного делителя ![]() степени
степени
![]() пучка
пучка ![]() мы получим
соответствующий элементарный делитель
мы получим
соответствующий элементарный делитель ![]() по формуле
по формуле
![]() . Таким способом
могут быть получены все элементарные делители пучка
. Таким способом
могут быть получены все элементарные делители пучка ![]() за исключением элементарных
делителей вида
за исключением элементарных
делителей вида ![]() .
.
Элементарные делители вида ![]() существуют в том и
только в том случае, когда
существуют в том и
только в том случае, когда ![]() , и носят название «бесконечных» элементарных
делителей для пучка
, и носят название «бесконечных» элементарных
делителей для пучка ![]() .
.
Поскольку из строгой эквивалентности
пучков ![]() и
и ![]() следует строгая эквивалентность пучков
следует строгая эквивалентность пучков ![]() и
и ![]() то у строго
эквивалентных пучков
то у строго
эквивалентных пучков
![]() и
и ![]() должны
совпадать не только «конечные», но и «бесконечные» элементарные делители.
должны
совпадать не только «конечные», но и «бесконечные» элементарные делители.
Пусть теперь даны два регулярных пучка ![]() и
и ![]() , у которых
соответственно совпадают все (в том числе и бесконечные) элементарные
делители. Введем однородные параметры:
, у которых
соответственно совпадают все (в том числе и бесконечные) элементарные
делители. Введем однородные параметры: ![]() ,
, ![]() . Преобразуем параметры:
. Преобразуем параметры:

![]()
В
новых параметрах пучки запишутся так: ![]() ,
, ![]() где
где ![]() ,
, ![]() . Из регулярности пучков
. Из регулярности пучков ![]() и
и ![]() вытекает, что
можно подобрать числа
вытекает, что
можно подобрать числа ![]() и
и ![]() так, чтобы
так, чтобы ![]() и
и ![]() .
.
Поэтому согласно теореме 1 пучки ![]() и
и ![]() , а следовательно,
и исходные пучки
, а следовательно,
и исходные пучки ![]() и
и
![]() (или, что
то же
(или, что
то же ![]() и
и ![]() ) строго
эквивалентны. Таким образом, мы пришли к следующему обобщению теоремы 1.
) строго
эквивалентны. Таким образом, мы пришли к следующему обобщению теоремы 1.
Теорема 2.
Для
того чтобы два регулярных пучка ![]() и
и
![]() были строго
эквивалентны, необходимо и достаточно, чтобы эти пучки имели одни и те же
(«конечные» и «бесконечные») элементарные делители.
были строго
эквивалентны, необходимо и достаточно, чтобы эти пучки имели одни и те же
(«конечные» и «бесконечные») элементарные делители.
В разобранном ранее примере пучки (3)
имели один и тот же «конечный» элементарный делитель ![]() , но отличались
«бесконечными» элементарными делителями (первый пучок имеет один «бесконечный»
элементарный делитель
, но отличались
«бесконечными» элементарными делителями (первый пучок имеет один «бесконечный»
элементарный делитель ![]() , а второй - два:
, а второй - два: ![]() ,
,![]() ). Поэтому эти пучки и не
оказались строго эквивалентными.
). Поэтому эти пучки и не
оказались строго эквивалентными.
3. Пусть теперь дан произвольный
регулярный пучок
![]() . Тогда существует
такое число
. Тогда существует
такое число ![]() ,
что
,
что ![]() .
Данный пучок представим в виде
.
Данный пучок представим в виде ![]() , где
, где ![]() и
потому
и
потому ![]() .
Умножим пучок слева на
.
Умножим пучок слева на ![]() . Преобразованием подобия приводим этот пучок к виду
. Преобразованием подобия приводим этот пучок к виду
![]() (4)
(4)
где ![]() - квазидиагональная нормальная форма
матрицы
- квазидиагональная нормальная форма
матрицы ![]() ,
, ![]() - жорданова
нильпотентная матрица, а
- жорданова
нильпотентная матрица, а ![]() .
.
Первый диагональный блок правой части
(4) умножим на
![]() . Получим:
. Получим: ![]() . Здесь коэффициент
при
. Здесь коэффициент
при ![]() -
нильпотентная матрица. Поэтому преобразованием подобия этот пучок можно
привести к виду
-
нильпотентная матрица. Поэтому преобразованием подобия этот пучок можно
привести к виду
 (5)
(5)
Второй диагональный блок в правой части
(4) умножением на ![]() , а затем преобразованием подобия
может быть приведен к виду
, а затем преобразованием подобия
может быть приведен к виду
![]() , где
, где ![]() - матрица, имеющая
нормальную форму, а
- матрица, имеющая
нормальную форму, а ![]() - единичная матрица. Мы пришли к
теореме
- единичная матрица. Мы пришли к
теореме
Теорема 3. Произвольный
регулярный пучок ![]() может
быть приведен к (строго эквивалентному) каноническому квазидиагональному виду
может
быть приведен к (строго эквивалентному) каноническому квазидиагональному виду
 (6)
(6)
где
первые ![]() диагональных
блоков соответствуют бесконечным элементарным делителям
диагональных
блоков соответствуют бесконечным элементарным делителям ![]() пучка
пучка ![]() , а нормальная
форма последнего диагонального блока
, а нормальная
форма последнего диагонального блока ![]() однозначно определяется конечными элементарными
делителями данного пучка.
однозначно определяется конечными элементарными
делителями данного пучка.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие автора к первому изданию
- Предисловие автора ко второму изданию
- ЧАСТЬ I. ОСНОВЫ ТЕОРИИ
- Глава I. Матрицы и действия над ними
- § 1. Матрицы. Основные обозначения
- § 2. Сложение и умножение прямоугольных матриц
- § 3. Квадратные матрицы
- § 4. Ассоциированные матрицы. Миноры обратной матрицы
- § 5. Обращение прямоугольных матриц. Псевдообратная матрица
- Глава II. Алгоритм Гаусса и некоторые его применения
- § 1. Метод исключения Гаусса
- § 2. Механическая интерпретация алгоритма Гаусса
- § 3. Детерминантное тождество Сильвестра
- § 4. Разложение квадратной матрицы на треугольные множители
- § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса
- Глава III. Лииейиые операторы в n-мерном векторном пространстве
- § 1. Векторное пространство
- § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное
- § 3. Сложение и умножение линейных операторов
- § 4. Преобразование координат
- § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра
- § 6. Линейные операторы, отображающие n-мерное пространство само в себя
- § 7. Характеристические числа и собственные векторы линейного оператора
- § 8. Линейные операторы простой структуры
- Глава IV. Характеристический и минимальный многочлены матрицы
- § 1. Сложение и умножение матричных многочленов
- § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу
- § 3. Характеристический многочлен матрицы. Присоединенная матрица
- § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы
- § 5. Минимальный многочлен матрицы
- Глава V. Функции от матрицы
- § 1. Определение функции от матрицы
- § 2. Интерполяционный многочлен Лагранжа–Сильвестра
- § 3. Другие формы определения f(A). Компоненты матрицы A
- § 4. Представление функций от матриц рядами
- § 5. Некоторые свойства функций от матриц
- § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 7. Устойчивость движения в случае линейной системы
- Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей
- § 1. Элементарные преобразования многочленной матрицы
- § 2. Канонический вид матрицы
- § 3. Инвариантные многочлены и элементарные делители многочленной матрицы
- § 4. Эквивалентность линейных двучленов
- § 5. Критерий подобия матриц
- § 6. Нормальные формы матрицы
- § 7. Элементарные делители матрицы f(A)
- § 8. Общий метод построения преобразующей матрицы
- § 9. Второй метод построения преобразующей матрицы
- Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей)
- § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора)
- § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами
- § 3. Сравнения. Надпространство
- § 4. Расщепление пространства на циклические инвариантные подпространства
- § 5. Нормальная форма матрицы
- § 6. Инвариантные многочлены. Элементарные делители
- § 7. Нормальная жорданова форма матрицы
- § 8. Метод акад. А. Н. Крылова преобразования векового уравнения
- Глава VIII. Матричные уравнения
- § 1. Уравнение AX=XB
- § 2. Частный случай: A=B. Перестановочные матрицы
- § 3. Уравнение AX-XB=C
- § 4. Скалярное уравнение f(X)=0
- § 5. Матричное многочленное уравнение
- § 6. Извлечение корня m-й степени из неособенной матрицы
- § 7. Извлечение корня m-й степени из особенной матрицы
- § 8. Логарифм матрицы
- Глава IX. Линейные операторы в унитарном пространстве
- § 1. Общие соображения
- § 2. Метризация пространства
- § 3. Критерий Грама линейной зависимости векторов
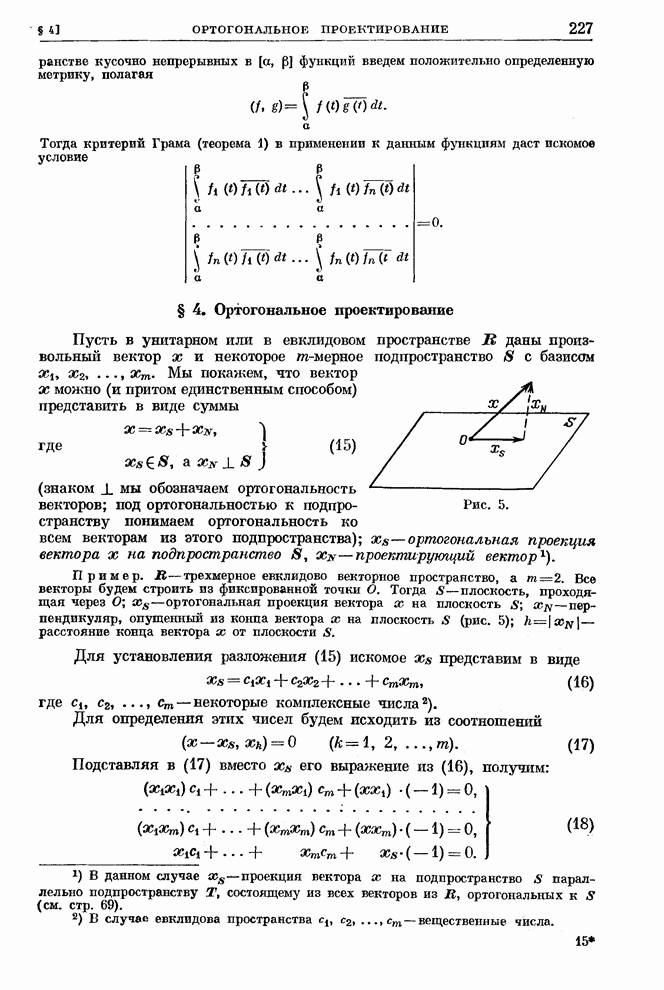
- § 4. Ортогональное проектирование
- § 5. Геометрический смысл определителя Грама и некоторые неравенства
- § 6. Ортогонализация ряда векторов
- § 7. Ортонормированный базис
- § 8. Сопряженный оператор
- § 9. Нормальные операторы в унитарном пространстве
- § 10. Спектр нормальных, эрмитовых, унитарных операторов
- § 11. Неотрицательные и положительно определенные эрмитовы операторы
- § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли
- § 13. Линейные операторы в евклидовом пространстве
- § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве
- § 15. Коммутирующие нормальные операторы
- § 16. Псевдообратный оператор
- Глава X. Квадратичные и эрмитовы формы
- § 1. Преобразование переменных в квадратичной форме
- § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции
- § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби
- § 4. Положительные квадратичные формы
- § 5. Приведение квадратичной формы к главным осям
- § 6. Пучок квадратичных форм
- § 7. Экстремальные свойства характеристических чисел регулярного пучка форм
- § 8. Малые колебания системы с n степенями свободы
- § 9. Эрмитовы формы
- § 10. Ганкелевы формы
- ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ
- Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы
- § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц
- § 2. Полярное разложение комплексной матрицы
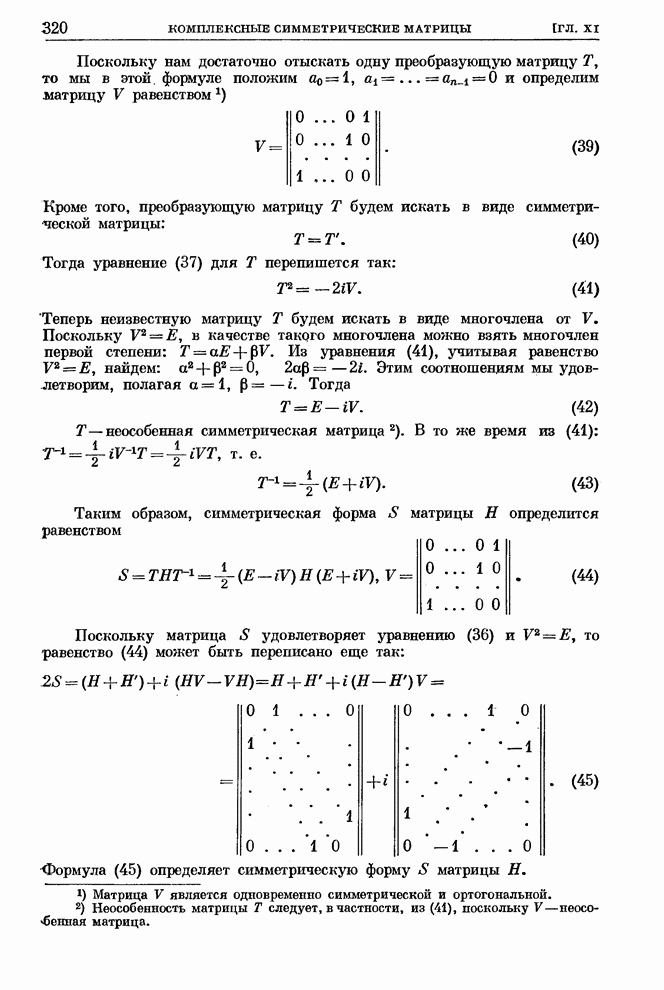
- § 3. Нормальная форма комплексной симметрической матрицы
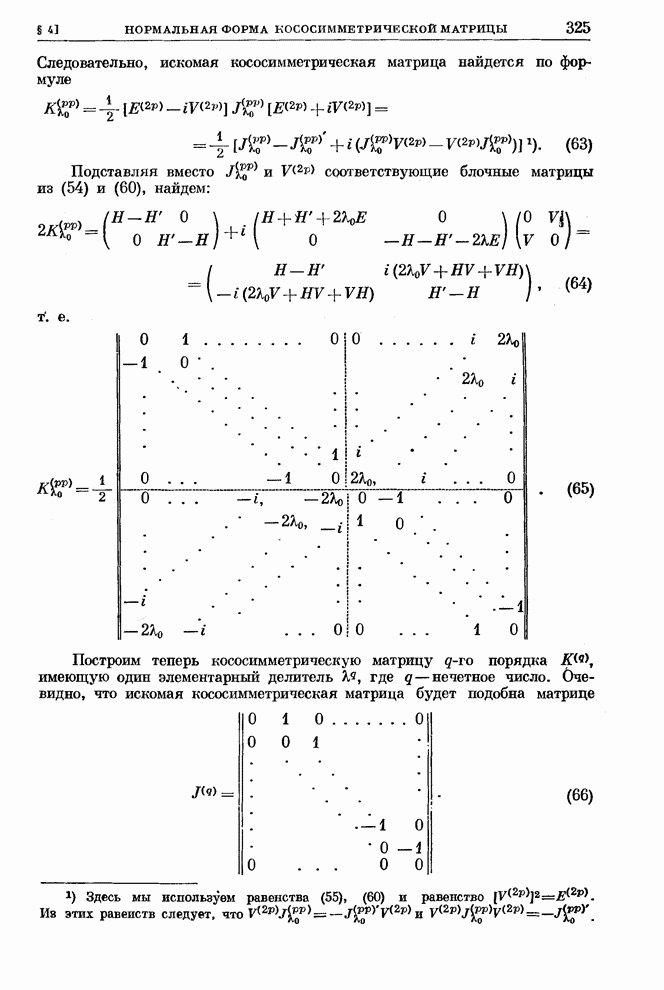
- § 4. Нормальная форма комплексной кососимметрической матрицы
- § 5. Нормальная форма комплексной ортогональной матрицы
- ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ
- § 1. Введение
- § 2. Регулярный пучок матриц
- § 3. Сингулярные пучки. Теорема о приведении
- § 4. Каноническая форма сингулярного пучка матриц
- § 5. Минимальные индексы пучка
- § 6. Сингулярные пучки квадратичных форм
- § 7. Приложения к дифференциальным уравнениям
- ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- § 1. Общие свойства
- § 2. Спектральные свойства неразложимых неотрицательных матриц
- § 3. Разложимые матрицы
- § 4. Нормальная форма разложимой матрицы
- § 5. Примитивные и импримитивные матрицы
- § 6. Стохастические матрицы
- § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний
- § 8. Вполне неотрицательные матрицы
- § 9. Осцилляционные матрицы
- Глава XIV. Различные критерии регулярности и локализации собственных значений
- § 1. Критерий регулярности Адамара и его обобщения
- § 2. Норма матрицы
- § 3. Распространение критерия Адамара на блочные матрицы
- § 4. Критерий регулярности Фидлера
- § 5. Круги Гершгорина и другие области локализации
- Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений
- § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия
- § 2. Преобразование Ляпунова
- § 3. Приводимые системы
- § 4. Каноническая форма приводимой системы. Теорема Еругина
- § 5. Матрицант
- § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра
- § 7. Дифференциальные системы в комплексной области. Общие свойства
- § 8. Мультипликативный интеграл в комплексной области
- § 9. Изолированная особая точка
- § 10. Регулярная особая точка
- § 11. Приводимые аналитические системы
- § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского
- ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ
- § 1. Введение
- § 2. Индексы Коши
- § 3. Алгоритм Рауса
- § 4. Особые случаи. Примеры
- § 5. Теорема Ляпунова
- § 6. Теорема Рауса-Гурвица
- § 7. Формула Орландо
- § 8. Особые случаи в теореме Рауса — Гурвица
- § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена
- § 10. Бесконечные ганкелевы матрицы конечного ранга
- § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя
- § 12. Второе доказательство теоремы Рауса—Гурвица
- § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара
- § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей
- § 15. Область устойчивости. Параметры Маркова
- § 16. Связь с проблемой моментов
- § 17. Связь между определителями Гурвица и определителями Маркова
- § 18. Теоремы Маркова и Чебышева
- § 19. Обобщенная задача Рауса-Гурвица
- ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ
- § 1. Мажорирующие последовательности
- § 2. Неравенства Неймана-Хорна
- § 3. Неравенства Вейля
- § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов
- § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов
- § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов
- ЛИТЕРАТУРА