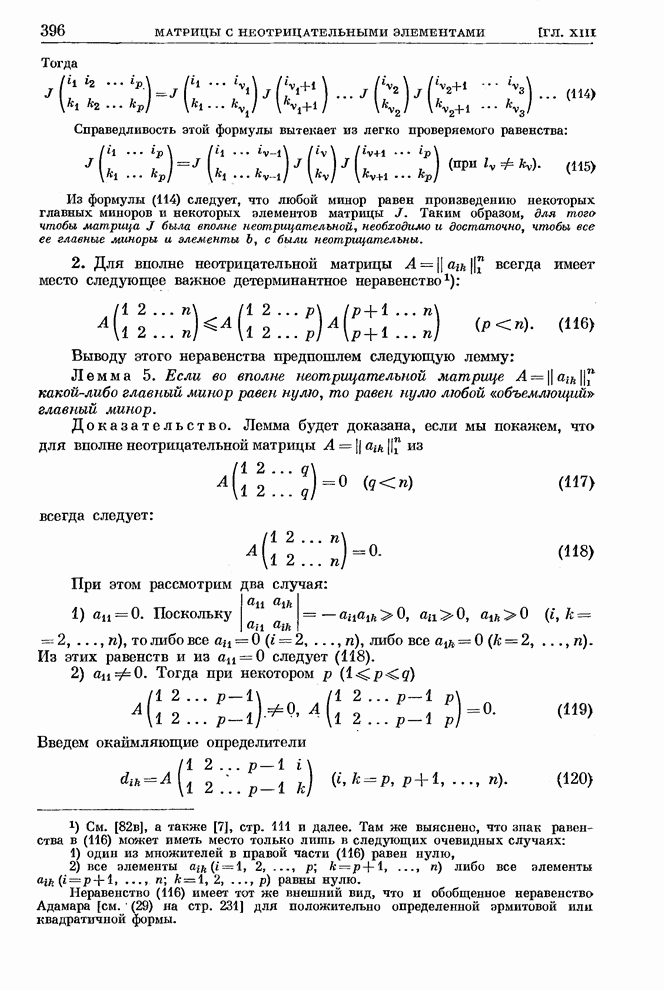| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
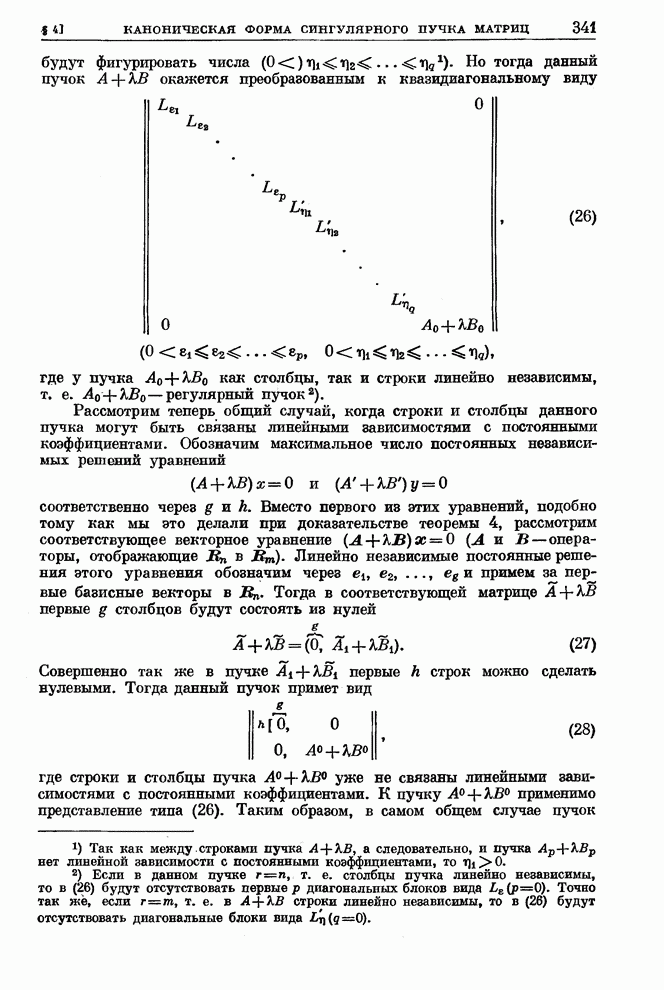
§ 3. Сингулярные пучки. Теорема о приведении
Переходим к рассмотрению сингулярного
пучка матриц ![]() с
размерами
с
размерами ![]() . Обозначим через
. Обозначим через ![]() ранг
пучка, т. е. наибольший из порядков миноров, не равных
тождественно нулю. Из сингулярности пучка следует, что всегда имеет место по
крайней мере одно из неравенств
ранг
пучка, т. е. наибольший из порядков миноров, не равных
тождественно нулю. Из сингулярности пучка следует, что всегда имеет место по
крайней мере одно из неравенств ![]() или
или ![]() . Пусть
. Пусть ![]() . Тогда столбцы
. Тогда столбцы ![]() -матрицы
-матрицы ![]() линейно зависимы,
т. е. уравнение
линейно зависимы,
т. е. уравнение
![]() (7)
(7)
где ![]() - искомый столбец, имеет ненулевое
решение. Каждое ненулевое решение этого уравнения определяет некоторую линейную
зависимость между столбцами
- искомый столбец, имеет ненулевое
решение. Каждое ненулевое решение этого уравнения определяет некоторую линейную
зависимость между столбцами ![]() -матрицы
-матрицы ![]() . Мы ограничимся только теми решениями
. Мы ограничимся только теми решениями
![]() уравнения
(7), которые являются многочленами относительно
уравнения
(7), которые являются многочленами относительно ![]() , и среди этих решений
возьмем решение наименьшей степени
, и среди этих решений
возьмем решение наименьшей степени ![]()
![]()
![]() (8)
(8)
Подставляя это решение в (7) и
приравнивая нулю коэффициенты при степенях ![]() , получим:
, получим:
![]() (9)
(9)
Рассматривая
эту систему равенств как систему линейных однородных уравнений относительно
элементов столбцов ![]() , заключаем, что матрица
коэффициентов этой системы
, заключаем, что матрица
коэффициентов этой системы
 (10)
(10)
имеет
ранг![]() . В
то же время в силу минимального свойства числа
. В
то же время в силу минимального свойства числа ![]() для рангов
для рангов ![]() матриц
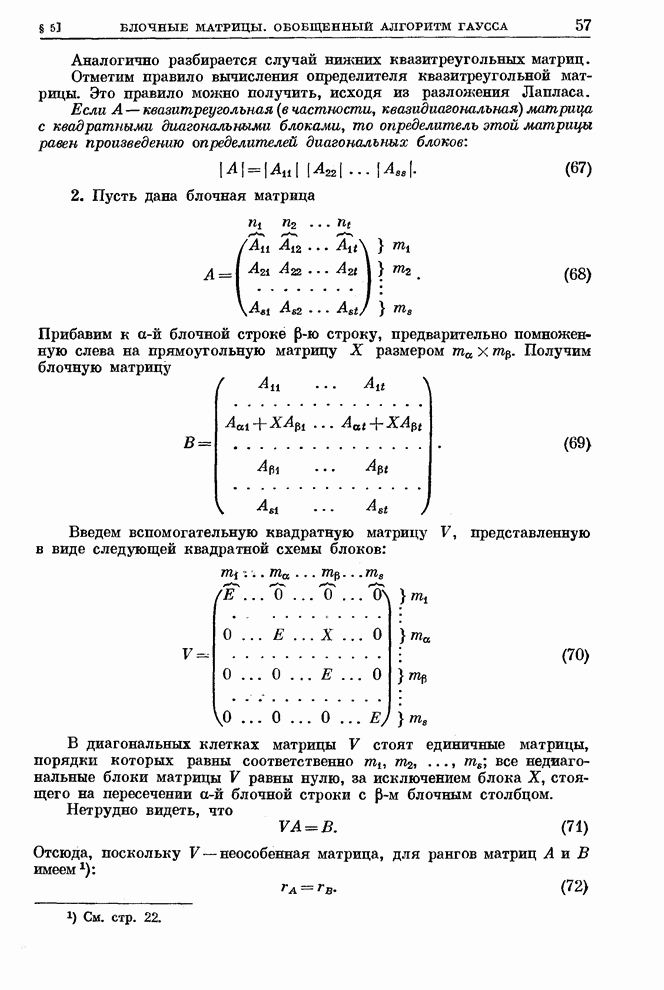
матриц
 (10’)
(10’)
имеют
место равенства ![]() .
.
Таким
образом, число ![]() есть
наименьшее значение индекса
есть
наименьшее значение индекса ![]() , при котором в соотношении
, при котором в соотношении ![]() имеет мести знак <.
имеет мести знак <.
Теперь мы сформулируем и докажем следующую фундаментальную теорему:
Теорема
4: Если уравнение (7) имеет решение минимальной степени ![]() и
и ![]() , то данный пучок
, то данный пучок ![]() строго
эквивалентен пучку вида
строго
эквивалентен пучку вида
 (11)
(11)
где
 (12)
(12)
а
![]() - пучок
матриц, для которого уравнение, аналогичное (7), имеет
решений степени
- пучок
матриц, для которого уравнение, аналогичное (7), имеет
решений степени ![]() .
.
Доказательство теоремы
разобьем на три этапа. Сначала докажем, что данный пучок ![]() строго
эквивалентен пучку вида
строго
эквивалентен пучку вида
 (13)
(13)
где
![]() ,
,
![]() ,
, ![]() ,
, ![]() -
постоянные прямоугольные матрицы соответственных размеров. Затем установим, что
уравнение
-
постоянные прямоугольные матрицы соответственных размеров. Затем установим, что
уравнение ![]() не
имеет решений
не
имеет решений ![]() степени
степени
![]() . После
этого мы покажем, что дальнейшими преобразованиями пучок (13) может быть
приведен к квазидиагональному виду (11).
. После
этого мы покажем, что дальнейшими преобразованиями пучок (13) может быть
приведен к квазидиагональному виду (11).
1. Первую часть доказательства облечем в
геометрическую форму. Вместо пучка матриц ![]() рассмотрим пучок
операторов
рассмотрим пучок
операторов ![]() отображающих
отображающих
![]() в
в ![]() , и покажем, что
при надлежащем выборе базисов в этих пространствах матрица, соответствующая
оператору
, и покажем, что
при надлежащем выборе базисов в этих пространствах матрица, соответствующая
оператору ![]() ,
будет иметь форму (13).
,
будет иметь форму (13).
Вместо, уравнения (7) возьмем векторное уравнение
![]() (14)
(14)
с векторным решением
![]() (15)
(15)
равенства (9) заменятся векторными равенствами
![]() (16)
(16)
Ниже мы докажем, что векторы
![]() (17)
(17)
линейно независимы. Отсюда легко будет следовать линейная независимость векторов
![]() (18)
(18)
Действительно, поскольку![]() , из
, из ![]() находим:
находим:
![]() ,
откуда в силу линейной независимости векторов (17)
,
откуда в силу линейной независимости векторов (17) ![]() . Но
. Но ![]() , поскольку в противном случае
, поскольку в противном случае
![]() было бы
решением уравнения (14) степени
было бы
решением уравнения (14) степени ![]() , что невозможно.
Поэтому и
, что невозможно.
Поэтому и ![]() .
.
Если теперь принять векторы (17) и (18)
в качестве первых базисных векторов для новых базисов соответственно в ![]() и
и ![]() , то в новых
базисах операторам
, то в новых
базисах операторам ![]() и
и ![]() в
силу (16) будут соответствовать матрицы
в
силу (16) будут соответствовать матрицы
 ,
, 
тогда
![]() -матрица
-матрица
![]() будет
иметь вид (13). Все предыдущие рассуждения будут обоснованными, если мы
докажем, что векторы (17) линейно независимы. Допустим противное, и пусть
будет
иметь вид (13). Все предыдущие рассуждения будут обоснованными, если мы
докажем, что векторы (17) линейно независимы. Допустим противное, и пусть
![]() -
первый в ряду (17) вектор, линейно зависящий от предыдущих векторов
-
первый в ряду (17) вектор, линейно зависящий от предыдущих векторов
![]()
В силу (16) это равенство может быть переписано так:
![]()
т. е.
![]() ,
,
где
![]()
Далее, опять в силу (16)
![]() ,
,
где
![]()
Продолжая этот, процесс далее и вводя еще векторы
![]() ,
,
мы получим цепочку равенств
![]() (19)
(19)
Из (19) следует, что
![]()
![]()
есть ненулевое решение уравнения (14)
степени ![]() ,
что невозможно. Таким образом, векторы (17) линейно независимы.
,
что невозможно. Таким образом, векторы (17) линейно независимы.
2. Докажем теперь, что уравнение
![]() не
имеет решений степени
не
имеет решений степени ![]() .
Сначала обратим внимание на то, что уравнение
.
Сначала обратим внимание на то, что уравнение ![]() , как
и уравнение (7), имеет ненулевое решение наименьшей степени
, как
и уравнение (7), имеет ненулевое решение наименьшей степени ![]() . В этом можно убедиться
непосредственно, если матричное уравнение
. В этом можно убедиться
непосредственно, если матричное уравнение ![]() заменить
системой обыкновенных уравнений
заменить
системой обыкновенных уравнений
![]()
![]() , откуда
, откуда ![]()
![]()
С другой стороны, если пучок имеет
«треугольный» вид (13), то соответствующие этому пучку матрицы ![]() [см. (10) и (10')
на стр. 335] после надлежащей перестановки строк и столбцов также могут быть
приведены к треугольному виду
[см. (10) и (10')
на стр. 335] после надлежащей перестановки строк и столбцов также могут быть
приведены к треугольному виду
 (20)
(20)
При ![]() все столбцы этой матрицы, а значит, и
столбцы матрицы
все столбцы этой матрицы, а значит, и
столбцы матрицы ![]() ,
линейно независимы. Но
,
линейно независимы. Но ![]() - квадратная матрица порядка
- квадратная матрица порядка ![]() . Поэтому и в
матрице
. Поэтому и в
матрице ![]() все
столбцы линейно независимы, а это, как было выяснено в начале параграфа,
означает, что уравнение
все
столбцы линейно независимы, а это, как было выяснено в начале параграфа,
означает, что уравнение ![]() не имеет решений степени
не имеет решений степени ![]() , что и требовалось
доказать.
, что и требовалось
доказать.
3. Заменим пучок (13) строго эквивалентным ему пучком
 (21)
(21)
где
![]() -
квадратные единичные матрицы соответственно порядков
-
квадратные единичные матрицы соответственно порядков ![]() и
и![]() , а
, а ![]() - произвольные постоянные
прямоугольные матрицы соответствующих размеров. Наша теорема будет полностью
доказана, если мы покажем, что матрицы
- произвольные постоянные
прямоугольные матрицы соответствующих размеров. Наша теорема будет полностью
доказана, если мы покажем, что матрицы ![]() и
и ![]() могут быть выбраны так,
чтобы имело место матричное равенство
могут быть выбраны так,
чтобы имело место матричное равенство
![]() (22)
(22)
Введем обозначения для элементов матриц ![]() ,
,![]() ,
,![]() а также для строк
матрицы
а также для строк
матрицы ![]() и
для столбцов матриц
и
для столбцов матриц ![]() ,
, ![]() :
:
![]() ,
, ![]() ,
, ![]() (
(![]() ;
; ![]() ;
; ![]() ),
),
 ,
, ![]() ,
, ![]()
Тогда матричное уравнение (22) можно
заменить системой скалярных уравнений, записывая, что элементы ![]() -го
столбца в левой и правой частях равенства (22) соответственно равны друг другу
-го
столбца в левой и правой частях равенства (22) соответственно равны друг другу ![]() :
:
 (23)
(23)
В левых частях этих равенств стоят
линейные двучлены относительно ![]() . Свободный член каждого из первых
. Свободный член каждого из первых ![]() этих двучленов
равен коэффициенту при
этих двучленов
равен коэффициенту при ![]() в следующем двучлене. Но тогда и
правые части должны удовлетворять этому условию. Поэтому
в следующем двучлене. Но тогда и
правые части должны удовлетворять этому условию. Поэтому
 (24)
(24)
Если равенства (24) имеют место, то,
очевидно, из (23) можно определить искомые элементы матрицы ![]() .
.
Теперь осталось показать, что система
уравнений (24) относительно элементов матрицы ![]() всегда имеет решение при любых
всегда имеет решение при любых ![]() и
и ![]() (
(![]() ;
; ![]() ).
Действительно, матрица, составленная из коэффициентов при неизвестных
элементах строк
).
Действительно, матрица, составленная из коэффициентов при неизвестных
элементах строк ![]() , может
быть записана после транспонирования в виде
, может
быть записана после транспонирования в виде

Но
эта матрица является матрицей ![]() для пучка прямоугольных матриц
для пучка прямоугольных матриц ![]() [см. (10') на стр.
335]. Ранг же этой матрицы равен
[см. (10') на стр.
335]. Ранг же этой матрицы равен ![]() , поскольку по доказанному уравнение
, поскольку по доказанному уравнение ![]() не
имеет решений степени
не
имеет решений степени ![]() . Таким образом, ранг системы
уравнений (24) равен числу уравнений, а такая система при любых свободных
членах является совместной (непротиворечивой).
. Таким образом, ранг системы
уравнений (24) равен числу уравнений, а такая система при любых свободных
членах является совместной (непротиворечивой).
Теорема доказана полностью.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие автора к первому изданию
- Предисловие автора ко второму изданию
- ЧАСТЬ I. ОСНОВЫ ТЕОРИИ
- Глава I. Матрицы и действия над ними
- § 1. Матрицы. Основные обозначения
- § 2. Сложение и умножение прямоугольных матриц
- § 3. Квадратные матрицы
- § 4. Ассоциированные матрицы. Миноры обратной матрицы
- § 5. Обращение прямоугольных матриц. Псевдообратная матрица
- Глава II. Алгоритм Гаусса и некоторые его применения
- § 1. Метод исключения Гаусса
- § 2. Механическая интерпретация алгоритма Гаусса
- § 3. Детерминантное тождество Сильвестра
- § 4. Разложение квадратной матрицы на треугольные множители
- § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса
- Глава III. Лииейиые операторы в n-мерном векторном пространстве
- § 1. Векторное пространство
- § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное
- § 3. Сложение и умножение линейных операторов
- § 4. Преобразование координат
- § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра
- § 6. Линейные операторы, отображающие n-мерное пространство само в себя
- § 7. Характеристические числа и собственные векторы линейного оператора
- § 8. Линейные операторы простой структуры
- Глава IV. Характеристический и минимальный многочлены матрицы
- § 1. Сложение и умножение матричных многочленов
- § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу
- § 3. Характеристический многочлен матрицы. Присоединенная матрица
- § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы
- § 5. Минимальный многочлен матрицы
- Глава V. Функции от матрицы
- § 1. Определение функции от матрицы
- § 2. Интерполяционный многочлен Лагранжа–Сильвестра
- § 3. Другие формы определения f(A). Компоненты матрицы A
- § 4. Представление функций от матриц рядами
- § 5. Некоторые свойства функций от матриц
- § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 7. Устойчивость движения в случае линейной системы
- Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей
- § 1. Элементарные преобразования многочленной матрицы
- § 2. Канонический вид матрицы
- § 3. Инвариантные многочлены и элементарные делители многочленной матрицы
- § 4. Эквивалентность линейных двучленов
- § 5. Критерий подобия матриц
- § 6. Нормальные формы матрицы
- § 7. Элементарные делители матрицы f(A)
- § 8. Общий метод построения преобразующей матрицы
- § 9. Второй метод построения преобразующей матрицы
- Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей)
- § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора)
- § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами
- § 3. Сравнения. Надпространство
- § 4. Расщепление пространства на циклические инвариантные подпространства
- § 5. Нормальная форма матрицы
- § 6. Инвариантные многочлены. Элементарные делители
- § 7. Нормальная жорданова форма матрицы
- § 8. Метод акад. А. Н. Крылова преобразования векового уравнения
- Глава VIII. Матричные уравнения
- § 1. Уравнение AX=XB
- § 2. Частный случай: A=B. Перестановочные матрицы
- § 3. Уравнение AX-XB=C
- § 4. Скалярное уравнение f(X)=0
- § 5. Матричное многочленное уравнение
- § 6. Извлечение корня m-й степени из неособенной матрицы
- § 7. Извлечение корня m-й степени из особенной матрицы
- § 8. Логарифм матрицы
- Глава IX. Линейные операторы в унитарном пространстве
- § 1. Общие соображения
- § 2. Метризация пространства
- § 3. Критерий Грама линейной зависимости векторов
- § 4. Ортогональное проектирование
- § 5. Геометрический смысл определителя Грама и некоторые неравенства
- § 6. Ортогонализация ряда векторов
- § 7. Ортонормированный базис
- § 8. Сопряженный оператор
- § 9. Нормальные операторы в унитарном пространстве
- § 10. Спектр нормальных, эрмитовых, унитарных операторов
- § 11. Неотрицательные и положительно определенные эрмитовы операторы
- § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли
- § 13. Линейные операторы в евклидовом пространстве
- § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве
- § 15. Коммутирующие нормальные операторы
- § 16. Псевдообратный оператор
- Глава X. Квадратичные и эрмитовы формы
- § 1. Преобразование переменных в квадратичной форме
- § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции
- § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби
- § 4. Положительные квадратичные формы
- § 5. Приведение квадратичной формы к главным осям
- § 6. Пучок квадратичных форм
- § 7. Экстремальные свойства характеристических чисел регулярного пучка форм
- § 8. Малые колебания системы с n степенями свободы
- § 9. Эрмитовы формы
- § 10. Ганкелевы формы
- ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ
- Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы
- § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц
- § 2. Полярное разложение комплексной матрицы
- § 3. Нормальная форма комплексной симметрической матрицы
- § 4. Нормальная форма комплексной кососимметрической матрицы
- § 5. Нормальная форма комплексной ортогональной матрицы
- ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ
- § 1. Введение
- § 2. Регулярный пучок матриц
- § 3. Сингулярные пучки. Теорема о приведении
- § 4. Каноническая форма сингулярного пучка матриц
- § 5. Минимальные индексы пучка
- § 6. Сингулярные пучки квадратичных форм
- § 7. Приложения к дифференциальным уравнениям
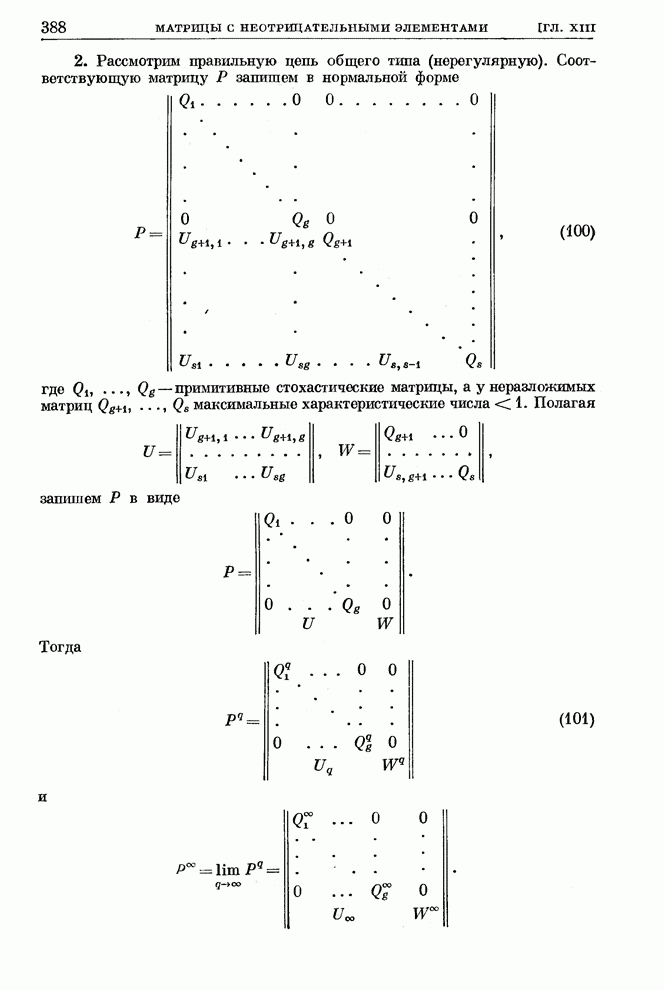
- ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- § 1. Общие свойства
- § 2. Спектральные свойства неразложимых неотрицательных матриц
- § 3. Разложимые матрицы
- § 4. Нормальная форма разложимой матрицы
- § 5. Примитивные и импримитивные матрицы
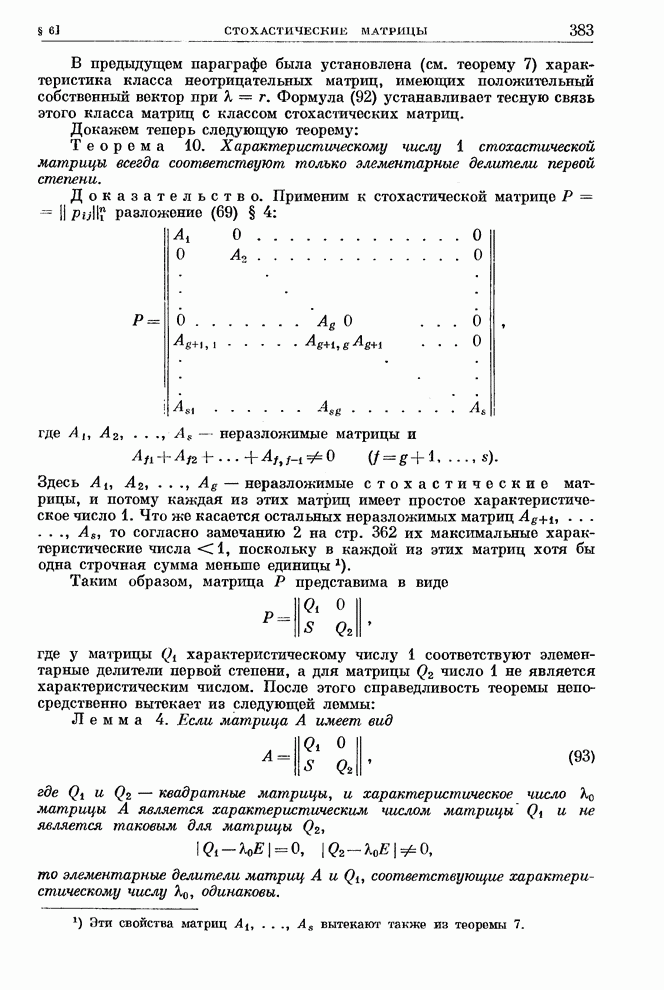
- § 6. Стохастические матрицы
- § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний
- § 8. Вполне неотрицательные матрицы
- § 9. Осцилляционные матрицы
- Глава XIV. Различные критерии регулярности и локализации собственных значений
- § 1. Критерий регулярности Адамара и его обобщения
- § 2. Норма матрицы
- § 3. Распространение критерия Адамара на блочные матрицы
- § 4. Критерий регулярности Фидлера
- § 5. Круги Гершгорина и другие области локализации
- Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений
- § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия
- § 2. Преобразование Ляпунова
- § 3. Приводимые системы
- § 4. Каноническая форма приводимой системы. Теорема Еругина
- § 5. Матрицант
- § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра
- § 7. Дифференциальные системы в комплексной области. Общие свойства
- § 8. Мультипликативный интеграл в комплексной области
- § 9. Изолированная особая точка
- § 10. Регулярная особая точка
- § 11. Приводимые аналитические системы
- § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского
- ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ
- § 1. Введение
- § 2. Индексы Коши
- § 3. Алгоритм Рауса
- § 4. Особые случаи. Примеры
- § 5. Теорема Ляпунова
- § 6. Теорема Рауса-Гурвица
- § 7. Формула Орландо
- § 8. Особые случаи в теореме Рауса — Гурвица
- § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена
- § 10. Бесконечные ганкелевы матрицы конечного ранга
- § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя
- § 12. Второе доказательство теоремы Рауса—Гурвица
- § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара
- § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей
- § 15. Область устойчивости. Параметры Маркова
- § 16. Связь с проблемой моментов
- § 17. Связь между определителями Гурвица и определителями Маркова
- § 18. Теоремы Маркова и Чебышева
- § 19. Обобщенная задача Рауса-Гурвица
- ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ
- § 1. Мажорирующие последовательности
- § 2. Неравенства Неймана-Хорна
- § 3. Неравенства Вейля
- § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов
- § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов
- § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов
- ЛИТЕРАТУРА