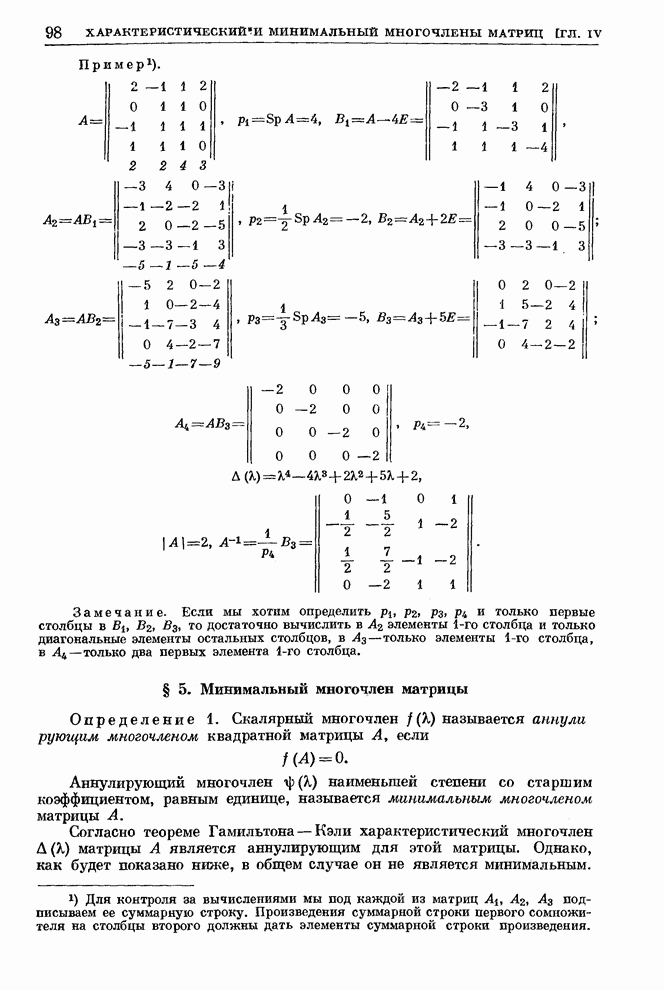
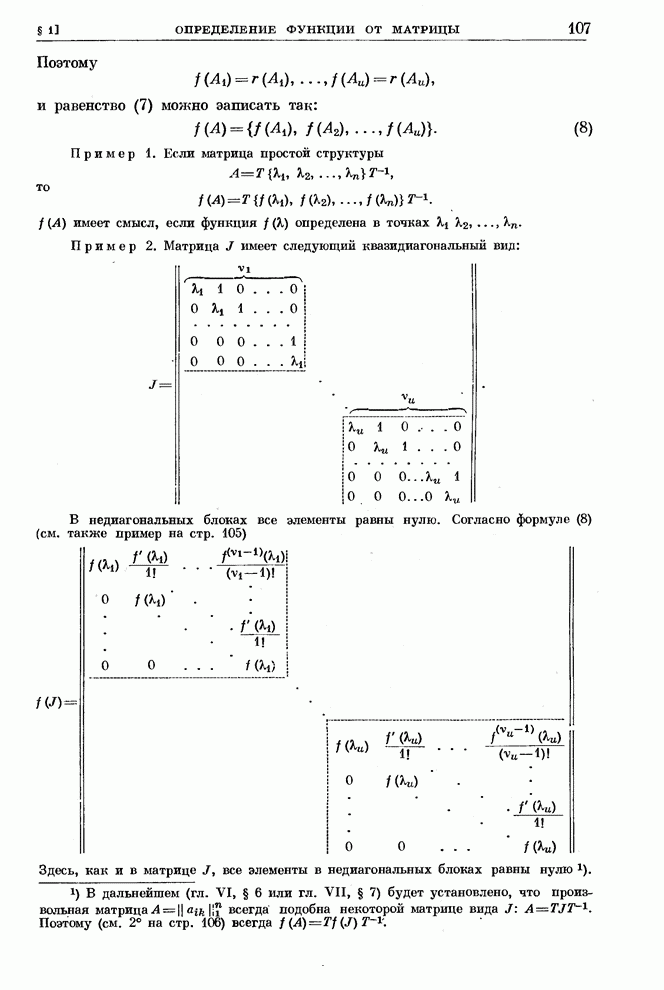
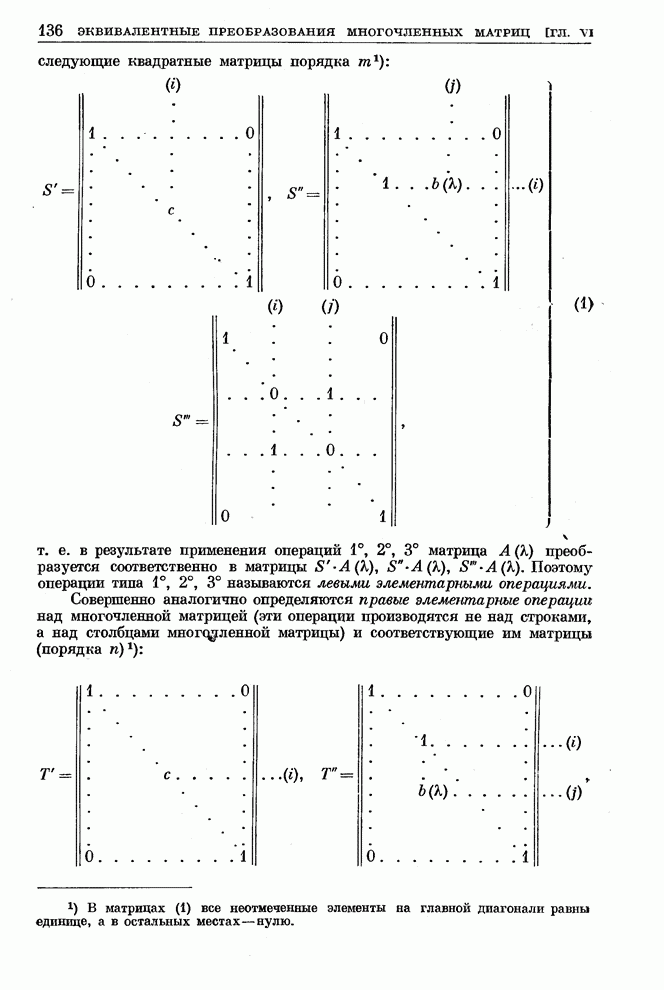
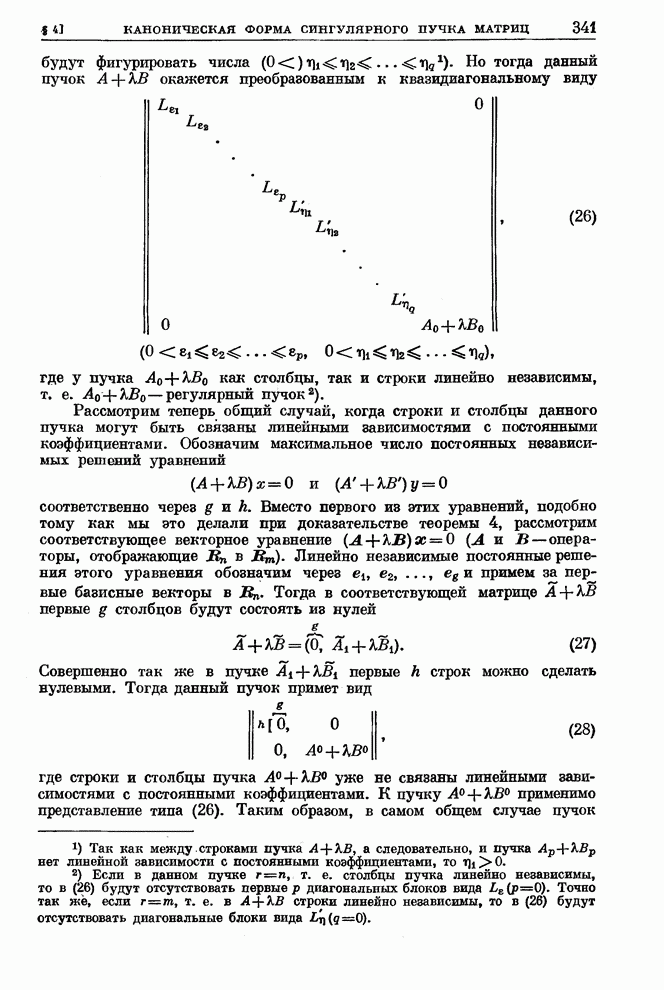
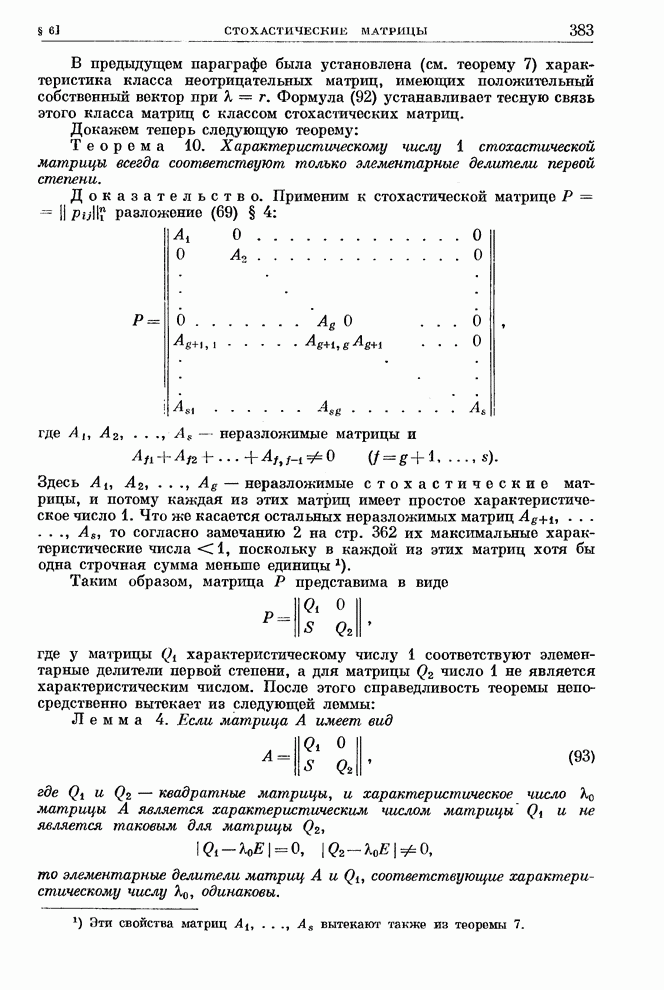
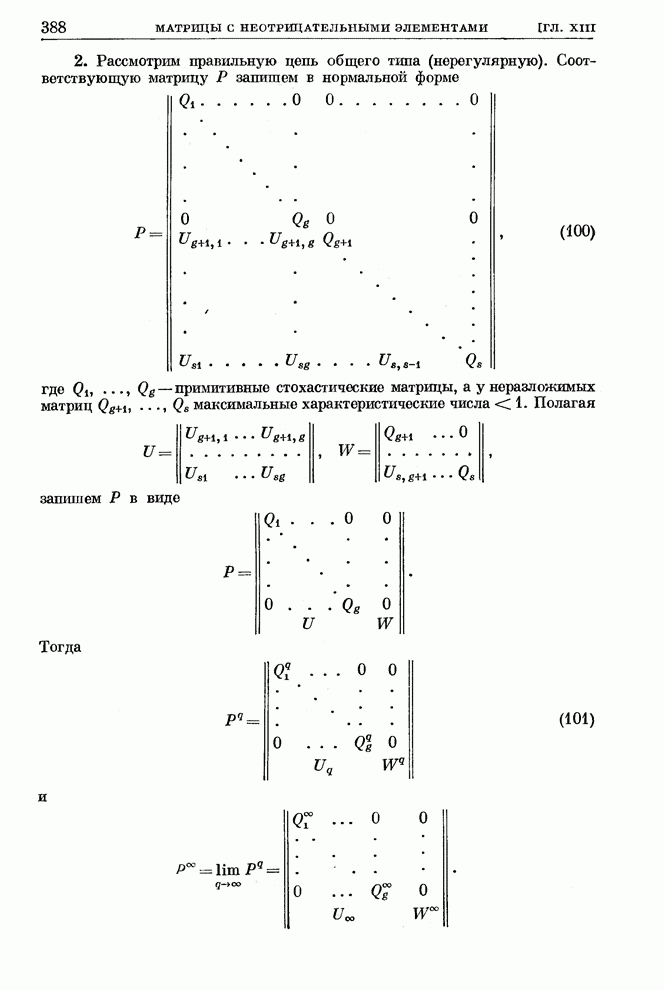
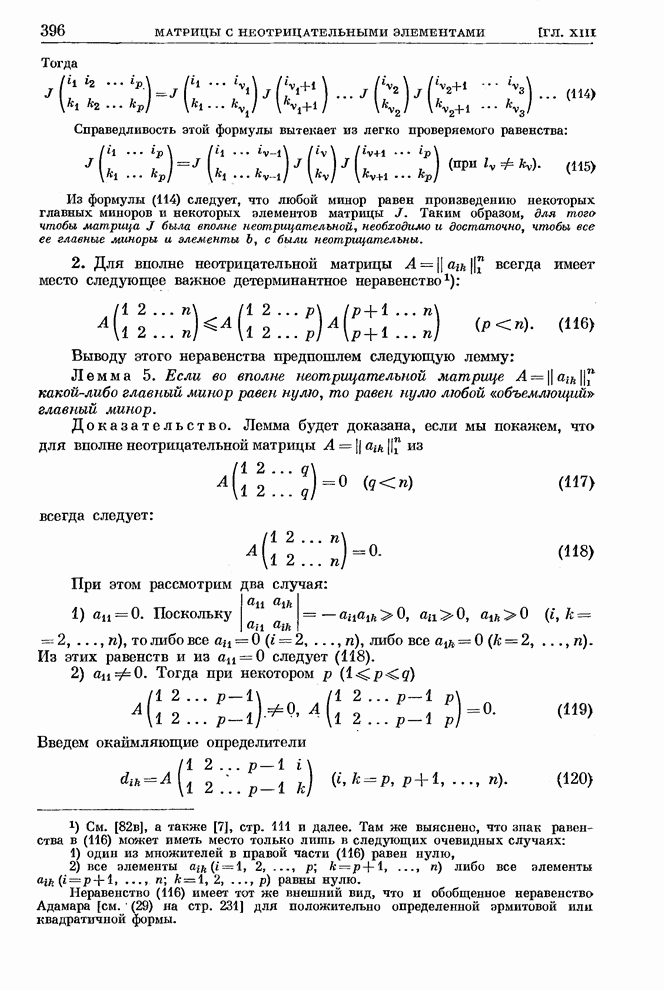| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА VIII. МАТРИЧНЫЕ УРАВНЕНИЯ
В этой главе мы рассмотрим некоторые типы матричных уравнений, встречающиеся в разнообразных вопросах теории матриц и ее приложений.
§ 1. Уравнение AX=XB
Пусть дано уравнение
![]() , (1)
, (1)
где
![]() и
и ![]() – две заданные
квадратные матрицы (вообще говоря, разных порядков)
– две заданные
квадратные матрицы (вообще говоря, разных порядков)
![]() ,
,
а
![]() – искомая
прямоугольная матрица размером
– искомая
прямоугольная матрица размером ![]() :
:
![]() .
.
Выпишем
элементарные делители матриц ![]() и
и ![]() (в поле комплексных чисел):
(в поле комплексных чисел):
 .
.
В
соответствии с этими элементарными делителями приведем матрицы ![]() и
и ![]() к нормальной
жордановой форме
к нормальной
жордановой форме
![]() , (2)
, (2)
где
![]() и
и ![]() – квадратные
неособенные матрицы соответственно порядка
– квадратные
неособенные матрицы соответственно порядка ![]() и
и ![]() , а
, а ![]() и
и ![]() – жордановы матрицы:
– жордановы матрицы:
 (3)
(3)
Подставляя
в уравнение (1) вместо ![]() и
и ![]() их выражения (2), получим:
их выражения (2), получим:
![]() .
.
Умножим
обе части этого равенства слева на ![]() , а справа – на
, а справа – на ![]() :
:
![]() . (4)
. (4)
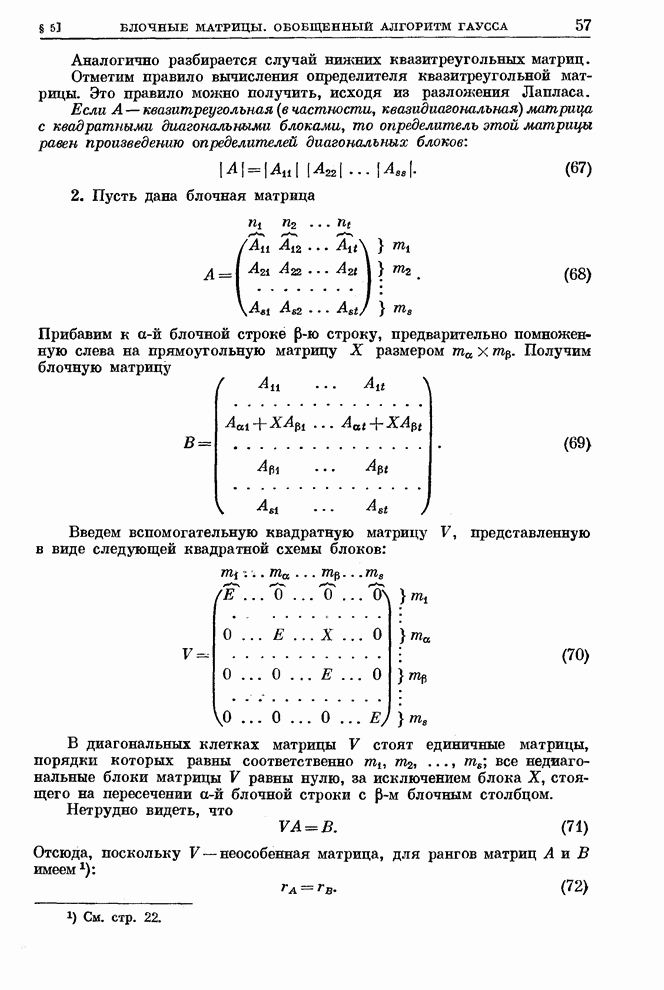
Вводя
вместо искомой матрицы ![]() новую искомую матрицу
новую искомую матрицу ![]() (тех же размеров
(тех же размеров ![]() )
)
![]() , (5)
, (5)
мы уравнение (4) запишем так:
![]() . (6)
. (6)
Мы заменили матричное уравнение (1) уравнением (6) того же вида, но в котором заданные матрицы имеют нормальную жорданову форму.
В
соответствии с квазидиагональным видом матриц ![]() и
и ![]() разобьем матрицу
разобьем матрицу ![]() на блоки:
на блоки:
![]()
(здесь
![]() – прямоугольная
матрица размером
– прямоугольная
матрица размером ![]() ).
).
Используя
правило умножения блочной матрицы на квазидиагональную (см. стр. 56),
произведем умножение матриц в левой и правой частях уравнения (6). Тогда это
уравнение распадается на ![]() матричных уравнений
матричных уравнений
![]() ,
,
которые перепишем еще так:
![]() ; (7)
; (7)
при этом мы ввели сокращенные обозначения
![]() . (8)
. (8)
Возьмем какое-нибудь из уравнений (7). Могут представиться два случая:
1.
![]() . Проитерируем
. Проитерируем
![]() раз
равенство (7):
раз
равенство (7):
![]() . (9)
. (9)
Заметим, что в силу (8)
![]() . (10)
. (10)
Если
в (9) взять ![]() ,
то в каждом члене суммы, стоящей в правой части равенства (9), выполняется по
крайней мере одно из соотношений
,
то в каждом члене суммы, стоящей в правой части равенства (9), выполняется по
крайней мере одно из соотношений
![]() ,
,
и
потому в силу (10) либо ![]() , либо
, либо ![]() . Так как, кроме того, в
рассматриваемом случае
. Так как, кроме того, в
рассматриваемом случае ![]() , то из (9) находим:
, то из (9) находим:
![]() . (11)
. (11)
2.
![]() . В этом
случае уравнение (7) принимает вид
. В этом
случае уравнение (7) принимает вид
![]() . (12)
. (12)
В
матрицах ![]() и
и
![]() элементы
первой наддиагонали равны единице, а все остальные элементы равны нулю.
Учитывая эту специфичную структуру матриц
элементы
первой наддиагонали равны единице, а все остальные элементы равны нулю.
Учитывая эту специфичную структуру матриц ![]() и
и ![]() и полагая
и полагая
![]() ,
,
мы заменим матричное уравнение (12) следующей эквивалентной ему системой скалярных соотношении:
![]() . (13)
. (13)
Равенства (13) означают:
1)
В матрице ![]() на
каждой линии, параллельной главной диагонали, стоят равные между собой
элементы,
на
каждой линии, параллельной главной диагонали, стоят равные между собой
элементы,
2)
![]() .
.
Пусть
![]() . В этом
случае
. В этом
случае ![]() –
квадратная матрица. Из 1), 2) следует, что в матрице
–
квадратная матрица. Из 1), 2) следует, что в матрице ![]() все элементы, расположенные
под главной диагональю, равны нулю, все элементы главной диагонали равны
некоторому числу
все элементы, расположенные
под главной диагональю, равны нулю, все элементы главной диагонали равны
некоторому числу ![]() ,
все элементы первой наддиагонали равны некоторому числу
,
все элементы первой наддиагонали равны некоторому числу ![]() и т. д., т. е.
и т. д., т. е.
 ; (14)
; (14)
![]()
здесь
![]() –
произвольные параметры (уравнения (12) не накладывают никаких ограничений на
значения этих параметров).
–
произвольные параметры (уравнения (12) не накладывают никаких ограничений на
значения этих параметров).
Легко
видеть, что при ![]()
![]() , (15)
, (15)
а
при ![]()
 . (16)
. (16)
Про
матрицы (14), (15) и (16) мы будем говорить, что они имеют правильную верхнюю
треугольную форму. Число произвольных параметров в ![]() равно наименьшему из чисел
равно наименьшему из чисел ![]() и
и ![]() . Приведенная ниже
схема показывает структуру матрицы
. Приведенная ниже
схема показывает структуру матрицы ![]() при
при ![]() (произвольные параметры здесь
обозначены через
(произвольные параметры здесь
обозначены через ![]() ):
):

Для
того чтобы при подсчете произвольных параметров в матрице ![]() охватить и случай 1,
обозначим через
охватить и случай 1,
обозначим через ![]() наибольший
общий делитель элементарных делителей
наибольший
общий делитель элементарных делителей ![]() и
и ![]() , а через
, а через ![]() – степень многочлена
– степень многочлена ![]()
![]() . В случае 1
. В случае 1 ![]() ; в случае 2 имеем:
; в случае 2 имеем:
![]() . Таким
образом, в обоих случаях число произвольных параметров в
. Таким
образом, в обоих случаях число произвольных параметров в ![]() равно
равно ![]() . Число произвольных
параметров в
. Число произвольных
параметров в ![]() определяется
формулой
определяется
формулой
 .
.
В
дальнейшем нам удобно будет общее решение уравнения (6) обозначить через ![]() (до сих пор мы это
решение обозначали буквой
(до сих пор мы это
решение обозначали буквой ![]() ).
).
Полученные в этом параграфе результаты можно сформулировать в виде следующей теоремы:
Теорема 1. Общее решение матричного уравнения
![]() ,
,
где

задается формулой
![]() . (17)
. (17)
Здесь
![]() – общее
решение уравнения
– общее
решение уравнения ![]() – имеет следующую структуру:
– имеет следующую структуру: ![]() разбивается на
блоки
разбивается на
блоки
 ;
;
если
![]() , то на
месте
, то на
месте ![]() стоит
нулевая матрица, если же
стоит
нулевая матрица, если же ![]() , то на месте
, то на месте ![]() стоит произвольная
правильная верхняя треугольная матрица.
стоит произвольная
правильная верхняя треугольная матрица.
![]() ,
а следовательно, и
,
а следовательно, и ![]() зависят линейно от
зависят линейно от ![]() произвольных
параметров
произвольных
параметров ![]() :
:
![]() , (18)
, (18)
где
![]() определяется
формулой
определяется
формулой
 (19)
(19)
[здесь
![]() обозначает
степень наибольшего общего делителя
обозначает
степень наибольшего общего делителя ![]() и
и ![]() ].
].
Заметим,
что матрицы ![]() ,
фигурирующие в формуле (18), суть решения исходного уравнения (1) (матрица
,
фигурирующие в формуле (18), суть решения исходного уравнения (1) (матрица ![]() получается из
получается из ![]() , если параметру
, если параметру ![]() дать значение
единицы, а остальным параметрам – нулевые значения;
дать значение
единицы, а остальным параметрам – нулевые значения; ![]() ). Эти решения линейно
независимы, так как в противном случае при некоторых значениях параметров
). Эти решения линейно
независимы, так как в противном случае при некоторых значениях параметров ![]() , не равных
одновременно нулю, матрица
, не равных
одновременно нулю, матрица ![]() , а следовательно, и
, а следовательно, и ![]() равнялись бы нулю,
что невозможно. Таким образом, равенство (19) показывает, что любое решение
исходного уравнения представляет собой линейную комбинацию
равнялись бы нулю,
что невозможно. Таким образом, равенство (19) показывает, что любое решение
исходного уравнения представляет собой линейную комбинацию ![]() линейно независимых
решений.
линейно независимых
решений.
Если
матрицы ![]() и
и
![]() не имеют
общих характеристических чисел (характеристические многочлены
не имеют
общих характеристических чисел (характеристические многочлены ![]() и
и ![]() взаимно просты),
то
взаимно просты),
то  и,
следовательно,
и,
следовательно, ![]() ,
т. е. в этом случае уравнение (1) имеет только тривиальное нулевое решение
,
т. е. в этом случае уравнение (1) имеет только тривиальное нулевое решение ![]() .
.
Замечание.
Пусть элементы матриц ![]() и
и ![]() принадлежат некоторому числовому полю
принадлежат некоторому числовому полю
![]() . Тогда
нельзя утверждать, что элементы матриц
. Тогда
нельзя утверждать, что элементы матриц ![]() фигурирующих в формуле (17), также
принадлежат полю
фигурирующих в формуле (17), также
принадлежат полю ![]() .
Элементы этих матриц можно выбрать в расширенном поле
.
Элементы этих матриц можно выбрать в расширенном поле ![]() , которое получается из поля
, которое получается из поля
![]() путем
приобщения к последнему корней характеристических уравнений
путем
приобщения к последнему корней характеристических уравнений ![]() и
и ![]() . С такого рода расширением
основного поля всегда приходится иметь дело, когда пользуются приведением
заданных матриц к нормальной жордановой форме.
. С такого рода расширением
основного поля всегда приходится иметь дело, когда пользуются приведением
заданных матриц к нормальной жордановой форме.
Однако
матричное уравнение (1) эквивалентно системе ![]() линейных однородных уравнении, где
неизвестными служат элементы
линейных однородных уравнении, где
неизвестными служат элементы ![]()
![]() искомой матрицы
искомой матрицы ![]() :
:
 . (20)
. (20)
Нами
доказано, что эта система имеет ![]() линейно независимых решений, где
линейно независимых решений, где ![]() определяется
формулой (19). Но известно, что базисные линейно независимые решения можно
выбрать в основном поле
определяется
формулой (19). Но известно, что базисные линейно независимые решения можно
выбрать в основном поле ![]() , которому принадлежат коэффициенты
уравнений (20). Таким образом, в формуле (18) матрицы
, которому принадлежат коэффициенты
уравнений (20). Таким образом, в формуле (18) матрицы ![]() можно выбрать так, чтобы их
элементы принадлежали полю
можно выбрать так, чтобы их
элементы принадлежали полю ![]() . Тогда, придавая в формуле (18)
произвольным параметрам всевозможные значения из поля
. Тогда, придавая в формуле (18)
произвольным параметрам всевозможные значения из поля ![]() , мы получим все матрицы
, мы получим все матрицы ![]() с элементами из
с элементами из ![]() , удовлетворяющие
уравнению (1).
, удовлетворяющие
уравнению (1).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие автора к первому изданию
- Предисловие автора ко второму изданию
- ЧАСТЬ I. ОСНОВЫ ТЕОРИИ
- Глава I. Матрицы и действия над ними
- § 1. Матрицы. Основные обозначения
- § 2. Сложение и умножение прямоугольных матриц
- § 3. Квадратные матрицы
- § 4. Ассоциированные матрицы. Миноры обратной матрицы
- § 5. Обращение прямоугольных матриц. Псевдообратная матрица
- Глава II. Алгоритм Гаусса и некоторые его применения
- § 1. Метод исключения Гаусса
- § 2. Механическая интерпретация алгоритма Гаусса
- § 3. Детерминантное тождество Сильвестра
- § 4. Разложение квадратной матрицы на треугольные множители
- § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса
- Глава III. Лииейиые операторы в n-мерном векторном пространстве
- § 1. Векторное пространство
- § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное
- § 3. Сложение и умножение линейных операторов
- § 4. Преобразование координат
- § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра
- § 6. Линейные операторы, отображающие n-мерное пространство само в себя
- § 7. Характеристические числа и собственные векторы линейного оператора
- § 8. Линейные операторы простой структуры
- Глава IV. Характеристический и минимальный многочлены матрицы
- § 1. Сложение и умножение матричных многочленов
- § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу
- § 3. Характеристический многочлен матрицы. Присоединенная матрица
- § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы
- § 5. Минимальный многочлен матрицы
- Глава V. Функции от матрицы
- § 1. Определение функции от матрицы
- § 2. Интерполяционный многочлен Лагранжа–Сильвестра
- § 3. Другие формы определения f(A). Компоненты матрицы A
- § 4. Представление функций от матриц рядами
- § 5. Некоторые свойства функций от матриц
- § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 7. Устойчивость движения в случае линейной системы
- Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей
- § 1. Элементарные преобразования многочленной матрицы
- § 2. Канонический вид матрицы
- § 3. Инвариантные многочлены и элементарные делители многочленной матрицы
- § 4. Эквивалентность линейных двучленов
- § 5. Критерий подобия матриц
- § 6. Нормальные формы матрицы
- § 7. Элементарные делители матрицы f(A)
- § 8. Общий метод построения преобразующей матрицы
- § 9. Второй метод построения преобразующей матрицы
- Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей)
- § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора)
- § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами
- § 3. Сравнения. Надпространство
- § 4. Расщепление пространства на циклические инвариантные подпространства
- § 5. Нормальная форма матрицы
- § 6. Инвариантные многочлены. Элементарные делители
- § 7. Нормальная жорданова форма матрицы
- § 8. Метод акад. А. Н. Крылова преобразования векового уравнения
- Глава VIII. Матричные уравнения
- § 1. Уравнение AX=XB
- § 2. Частный случай: A=B. Перестановочные матрицы
- § 3. Уравнение AX-XB=C
- § 4. Скалярное уравнение f(X)=0
- § 5. Матричное многочленное уравнение
- § 6. Извлечение корня m-й степени из неособенной матрицы
- § 7. Извлечение корня m-й степени из особенной матрицы
- § 8. Логарифм матрицы
- Глава IX. Линейные операторы в унитарном пространстве
- § 1. Общие соображения
- § 2. Метризация пространства
- § 3. Критерий Грама линейной зависимости векторов
- § 4. Ортогональное проектирование
- § 5. Геометрический смысл определителя Грама и некоторые неравенства
- § 6. Ортогонализация ряда векторов
- § 7. Ортонормированный базис
- § 8. Сопряженный оператор
- § 9. Нормальные операторы в унитарном пространстве
- § 10. Спектр нормальных, эрмитовых, унитарных операторов
- § 11. Неотрицательные и положительно определенные эрмитовы операторы
- § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли
- § 13. Линейные операторы в евклидовом пространстве
- § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве
- § 15. Коммутирующие нормальные операторы
- § 16. Псевдообратный оператор
- Глава X. Квадратичные и эрмитовы формы
- § 1. Преобразование переменных в квадратичной форме
- § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции
- § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби
- § 4. Положительные квадратичные формы
- § 5. Приведение квадратичной формы к главным осям
- § 6. Пучок квадратичных форм
- § 7. Экстремальные свойства характеристических чисел регулярного пучка форм
- § 8. Малые колебания системы с n степенями свободы
- § 9. Эрмитовы формы
- § 10. Ганкелевы формы
- ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ
- Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы
- § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц
- § 2. Полярное разложение комплексной матрицы
- § 3. Нормальная форма комплексной симметрической матрицы
- § 4. Нормальная форма комплексной кососимметрической матрицы
- § 5. Нормальная форма комплексной ортогональной матрицы
- ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ
- § 1. Введение
- § 2. Регулярный пучок матриц
- § 3. Сингулярные пучки. Теорема о приведении
- § 4. Каноническая форма сингулярного пучка матриц
- § 5. Минимальные индексы пучка
- § 6. Сингулярные пучки квадратичных форм
- § 7. Приложения к дифференциальным уравнениям
- ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- § 1. Общие свойства
- § 2. Спектральные свойства неразложимых неотрицательных матриц
- § 3. Разложимые матрицы
- § 4. Нормальная форма разложимой матрицы
- § 5. Примитивные и импримитивные матрицы
- § 6. Стохастические матрицы
- § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний
- § 8. Вполне неотрицательные матрицы
- § 9. Осцилляционные матрицы
- Глава XIV. Различные критерии регулярности и локализации собственных значений
- § 1. Критерий регулярности Адамара и его обобщения
- § 2. Норма матрицы
- § 3. Распространение критерия Адамара на блочные матрицы
- § 4. Критерий регулярности Фидлера
- § 5. Круги Гершгорина и другие области локализации
- Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений
- § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия
- § 2. Преобразование Ляпунова
- § 3. Приводимые системы
- § 4. Каноническая форма приводимой системы. Теорема Еругина
- § 5. Матрицант
- § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра
- § 7. Дифференциальные системы в комплексной области. Общие свойства
- § 8. Мультипликативный интеграл в комплексной области
- § 9. Изолированная особая точка
- § 10. Регулярная особая точка
- § 11. Приводимые аналитические системы
- § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского
- ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ
- § 1. Введение
- § 2. Индексы Коши
- § 3. Алгоритм Рауса
- § 4. Особые случаи. Примеры
- § 5. Теорема Ляпунова
- § 6. Теорема Рауса-Гурвица
- § 7. Формула Орландо
- § 8. Особые случаи в теореме Рауса — Гурвица
- § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена
- § 10. Бесконечные ганкелевы матрицы конечного ранга
- § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя
- § 12. Второе доказательство теоремы Рауса—Гурвица
- § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара
- § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей
- § 15. Область устойчивости. Параметры Маркова
- § 16. Связь с проблемой моментов
- § 17. Связь между определителями Гурвица и определителями Маркова
- § 18. Теоремы Маркова и Чебышева
- § 19. Обобщенная задача Рауса-Гурвица
- ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ
- § 1. Мажорирующие последовательности
- § 2. Неравенства Неймана-Хорна
- § 3. Неравенства Вейля
- § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов
- § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов
- § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов
- ЛИТЕРАТУРА