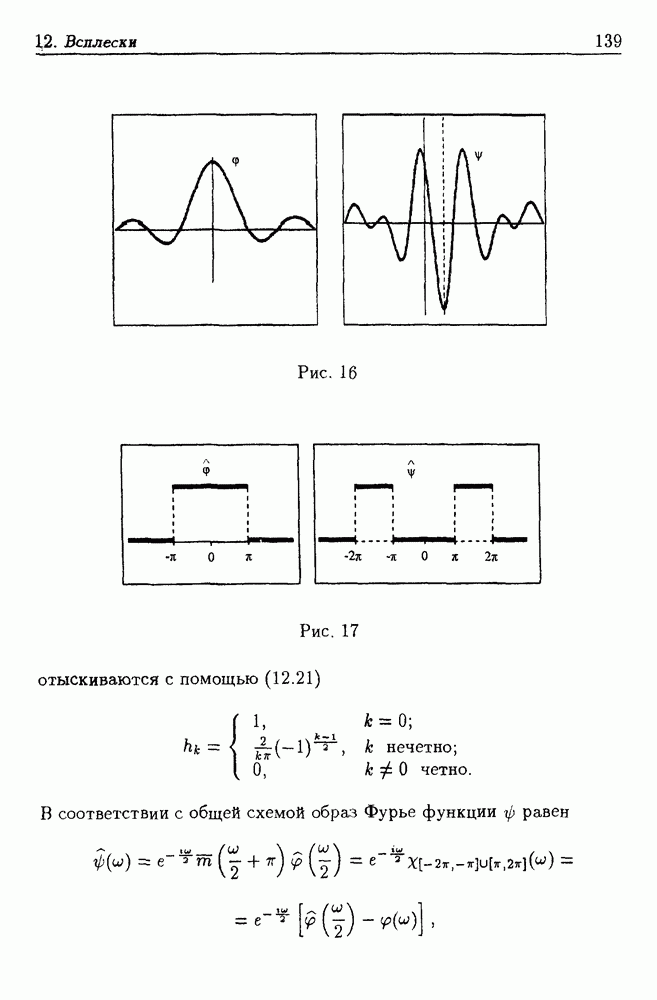
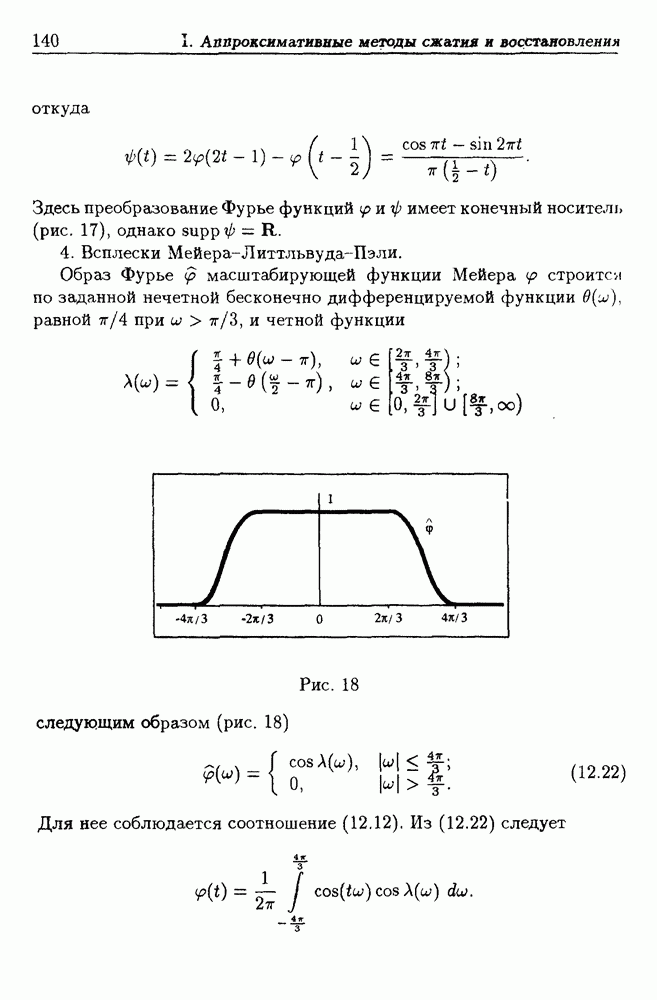
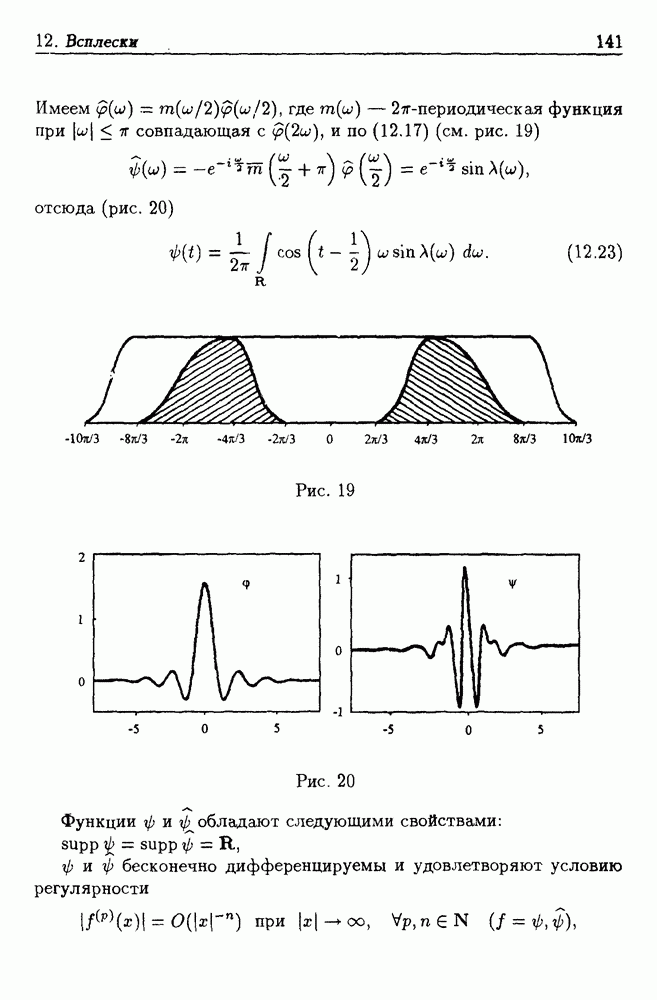
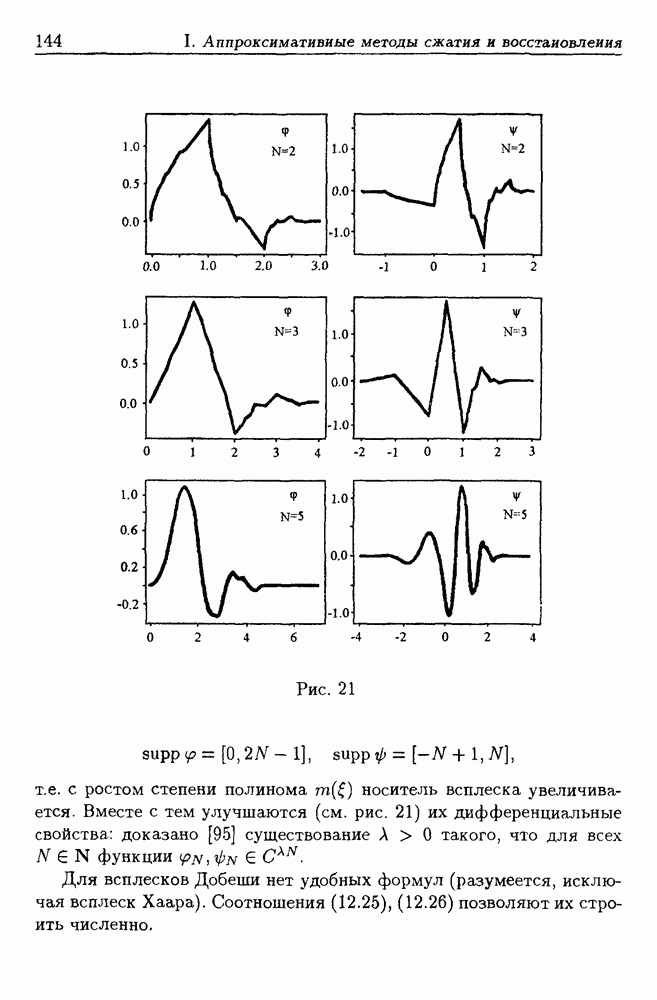
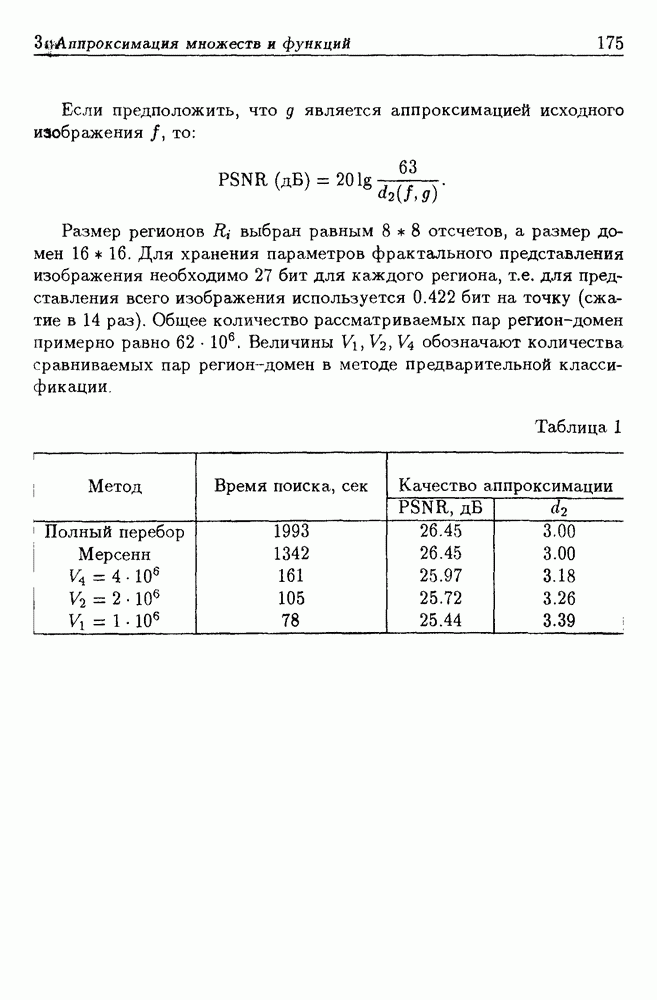
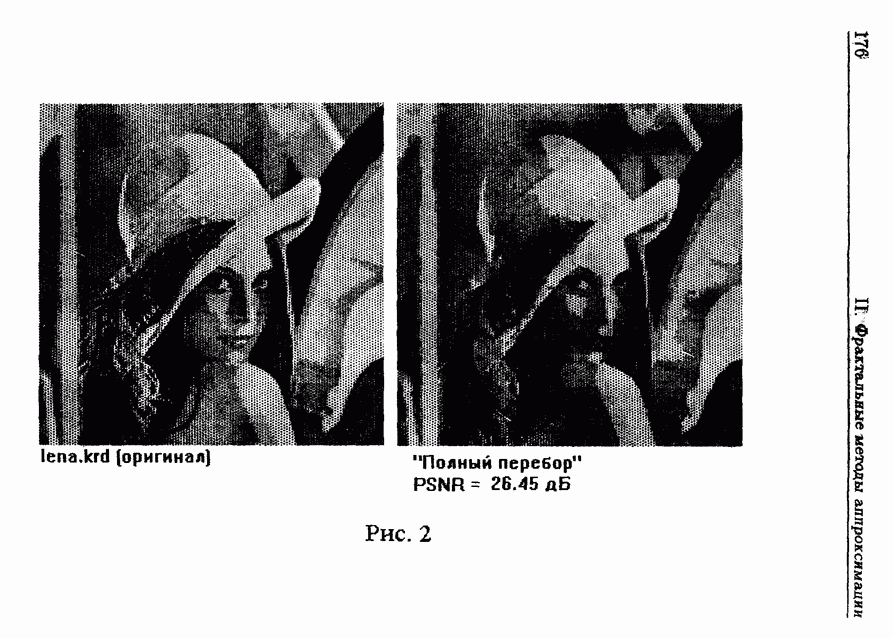
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Аппроксимация полиномами в метрике, связанной с задачей навигации
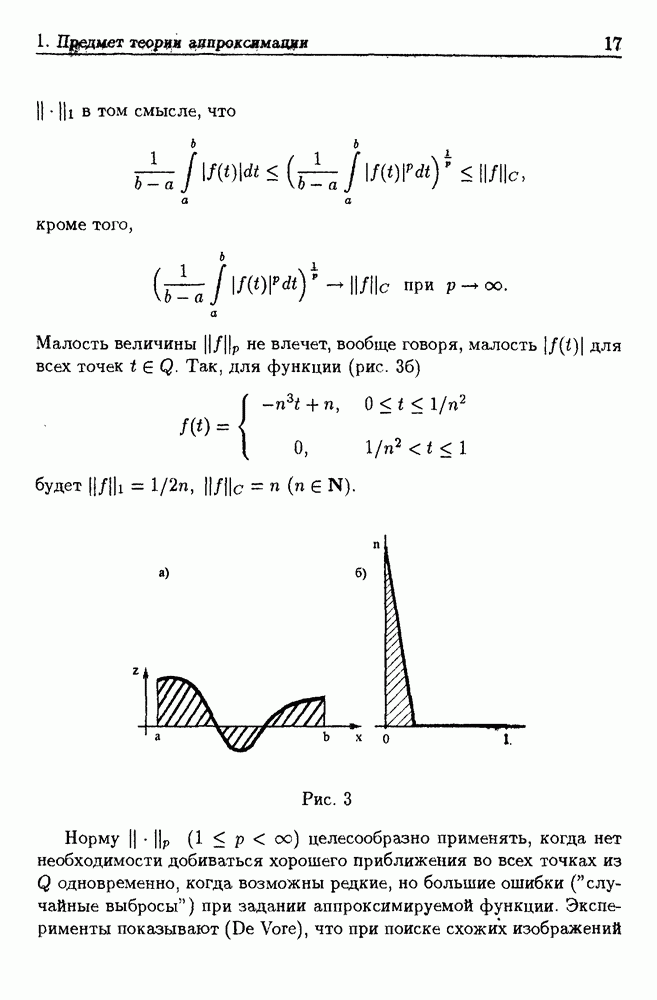
Рассмотрим функцию  где
где  некоторое ограниченное замкнутое множество с мерой. Пусть задана область
некоторое ограниченное замкнутое множество с мерой. Пусть задана область  ("область визирования"),
("область визирования"),  и норма функции
и норма функции  определяется следующим образом:
определяется следующим образом:

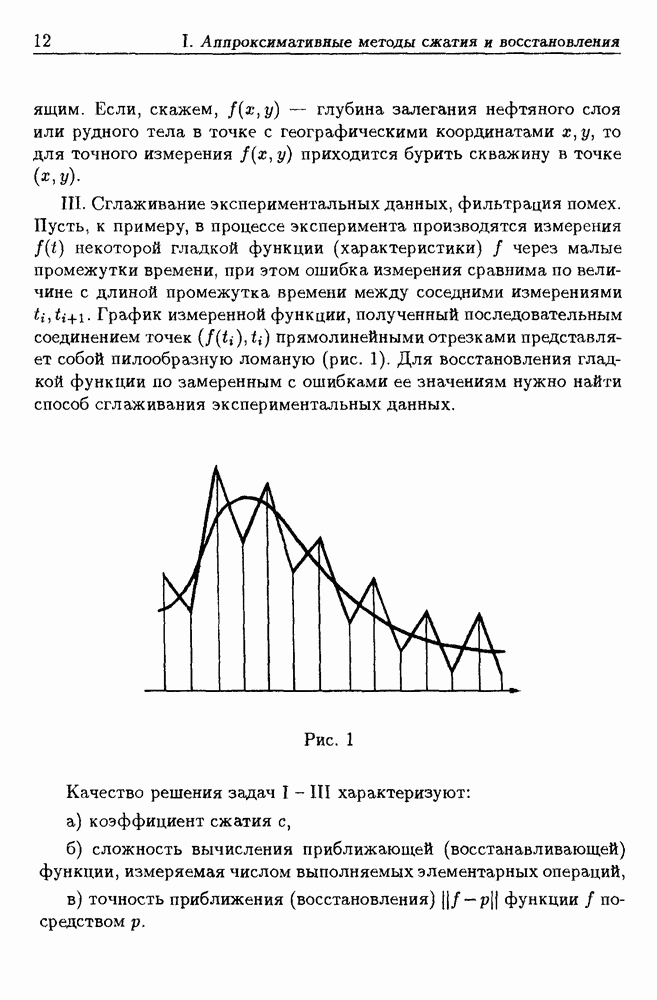
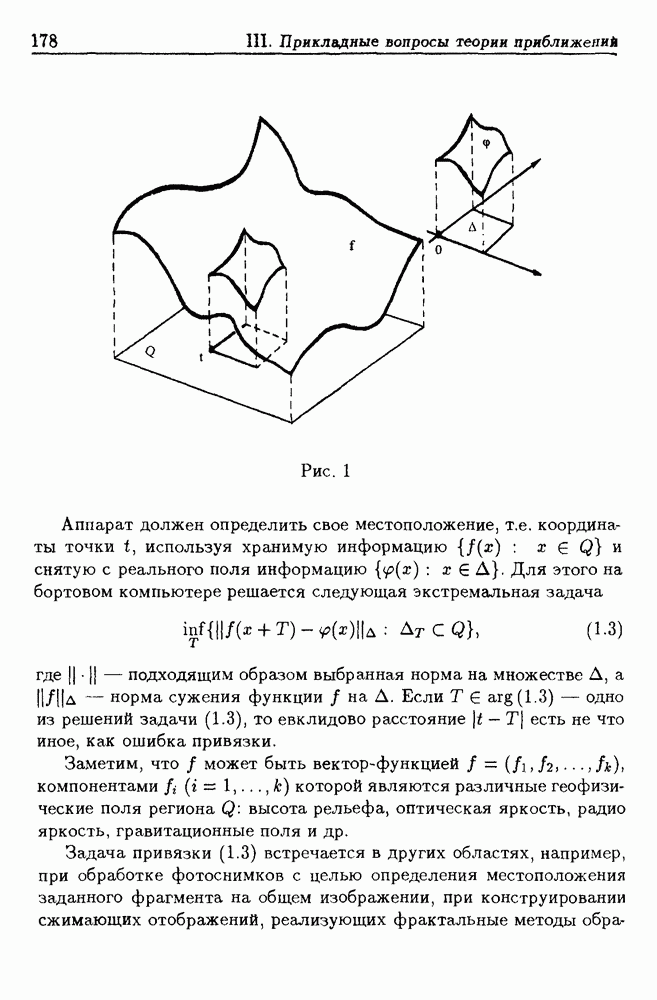
Потребность изучения аппроксимации функций в подобной норме возникает в связи с так называемой задачей навигации по геофизическим полям. Здесь приводится лишь краткая постановка задачи. Задача навигации подробно рассматривается в гл. III, § 1, § 2. Пусть автоматический летательный аппарат движется с постоянным вектором скорости над районом  высота земной поверхности (или иная функция, характеризующая район
высота земной поверхности (или иная функция, характеризующая район  и информация о функции
и информация о функции  хранится в бортовом компьютере в виде аппроксимирующего "полинома"
хранится в бортовом компьютере в виде аппроксимирующего "полинома"  Находясь над некоторой точкой
Находясь над некоторой точкой  координаты которой известны с погрешностью, аппарат измеряет значение
координаты которой известны с погрешностью, аппарат измеряет значение  на малой области
на малой области  т.е. снимает фрагмент
т.е. снимает фрагмент

функции  Задача навигации (привязки) есть задача определения координат точки
Задача навигации (привязки) есть задача определения координат точки  по функции
по функции  ("полиному"
("полиному"  ) и фрагменту
) и фрагменту  Она сводится к следующей задаче:
Она сводится к следующей задаче:

где

 некоторая норма. Если
некоторая норма. Если  тогда евклидово расстояние
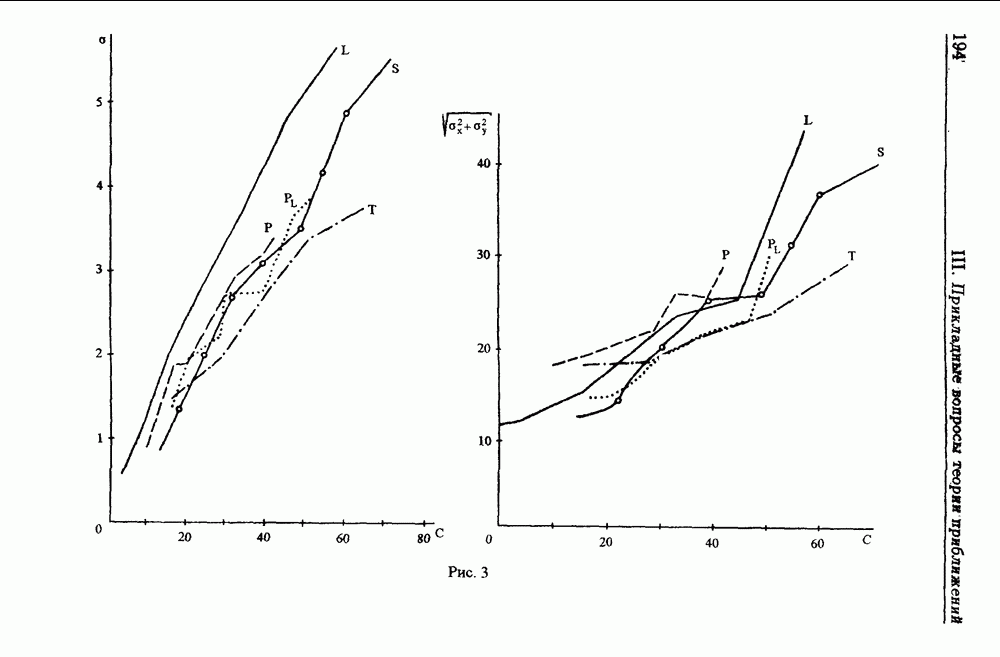
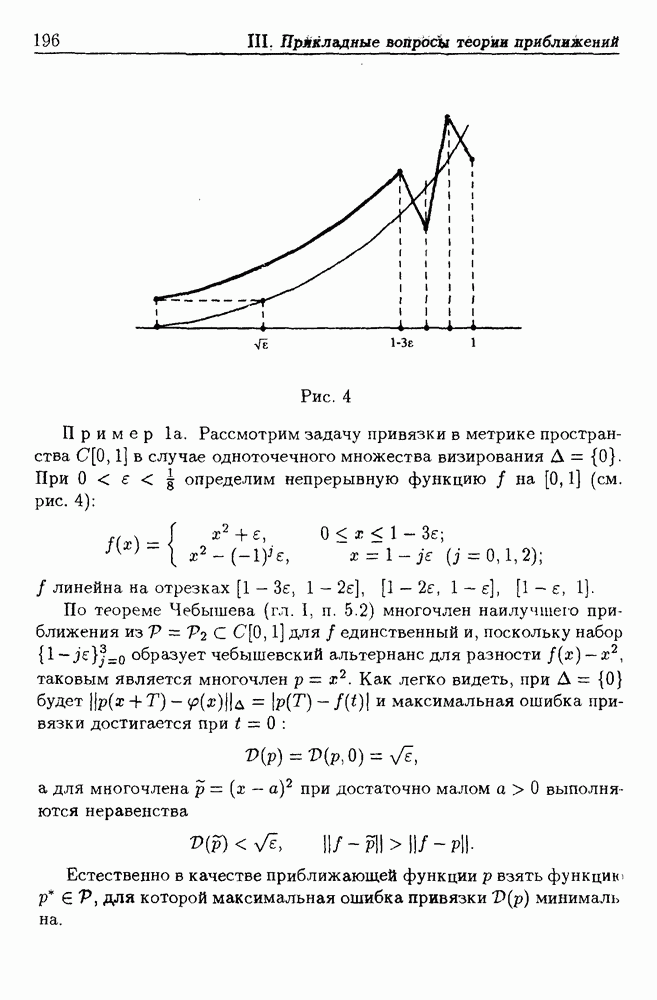
тогда евклидово расстояние  есть ошибка привязки. Ошибка привязки оценивается (см. гл. III, п. 1.2) сверху через величину уклонения полинома
есть ошибка привязки. Ошибка привязки оценивается (см. гл. III, п. 1.2) сверху через величину уклонения полинома  от функции
от функции  в норме (6.1). Этим фактом обосновывается интерес к задаче о наилучшем приближении в норме
в норме (6.1). Этим фактом обосновывается интерес к задаче о наилучшем приближении в норме 
В данном параграфе даются необходимые и достаточные условия на полином наилучшего приближения в случае, когда  есть Ьр-норма.
есть Ьр-норма.
Пусть  есть линейная оболочка
есть линейная оболочка  линейно независимых функций
линейно независимых функций  из
из  Прежде чем перейти к доказательству основных утверждений заметим, что так как
Прежде чем перейти к доказательству основных утверждений заметим, что так как  конечномерное подпространство, то для любой функции
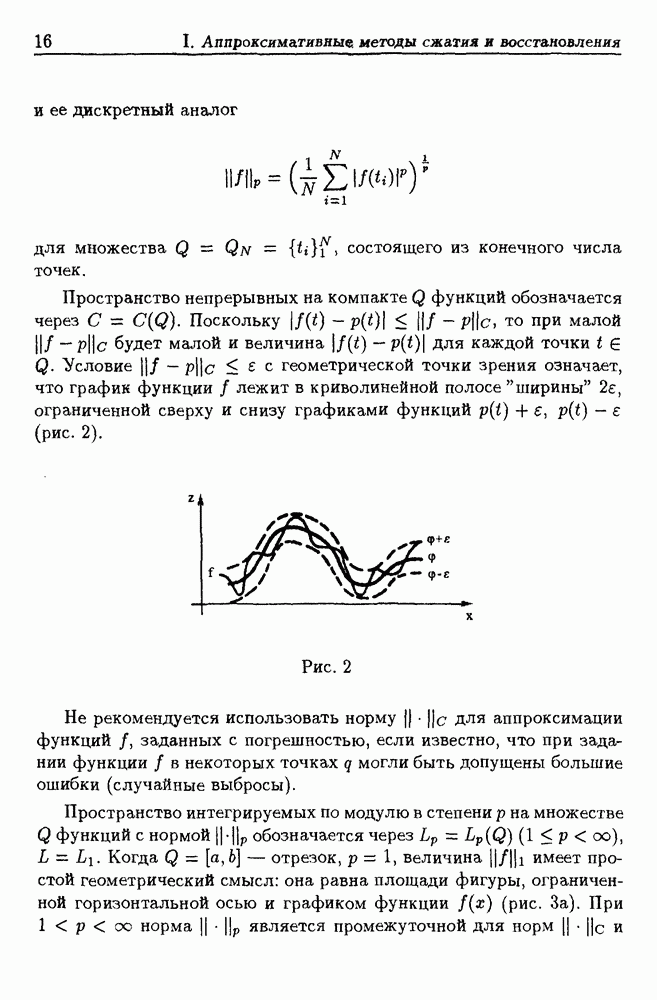
конечномерное подпространство, то для любой функции  существует по крайней мере один полином наилучшего приближения. Легко показать, что норма
существует по крайней мере один полином наилучшего приближения. Легко показать, что норма  при
при  является строго выпуклой как максимум строго выпуклых функций, а значит, (см., напр., гл. I, п. 2.2) полином наилучшего приближения единственный.
является строго выпуклой как максимум строго выпуклых функций, а значит, (см., напр., гл. I, п. 2.2) полином наилучшего приближения единственный.
Обозначим 
В этом параграфе под полиномом наилучшего приближения понимается полином наилучшего приближения относительно нормы 
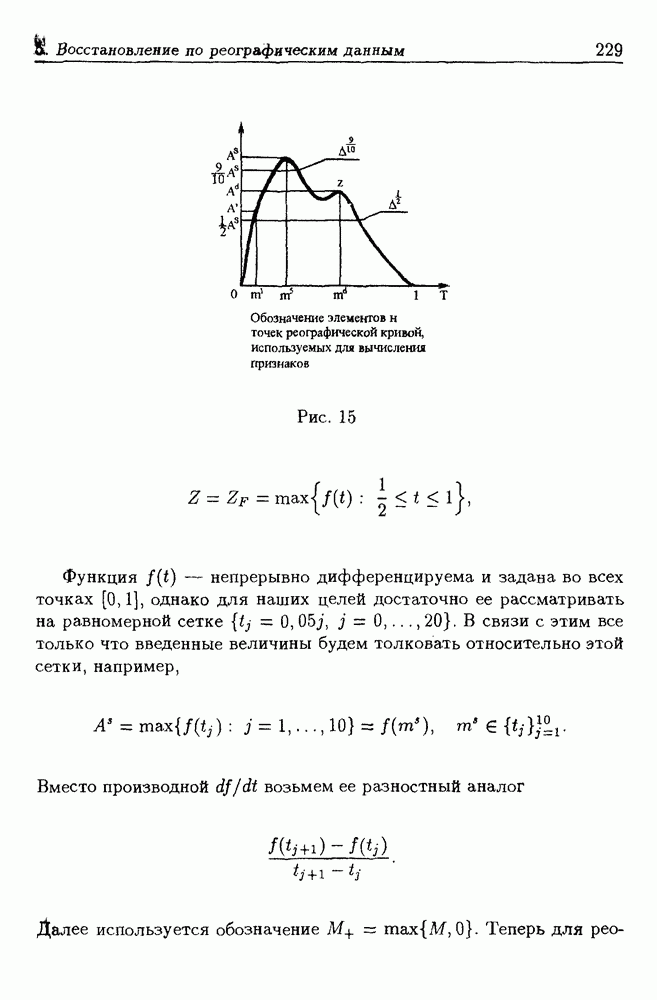
Теорема 1 (П. В. Борисов). Пусть  Полином
Полином

является полиномом наилучшего приближения для  тогда и только тогда, когда существуют точки
тогда и только тогда, когда существуют точки  и положительные числа
и положительные числа
 такие, что выполняются равенства
такие, что выполняются равенства

Доказательство. Полином  является полиномом наилучшего приближения для
является полиномом наилучшего приближения для  тогда и только тогда, когда
тогда и только тогда, когда  минимизирует функционал
минимизирует функционал

где

Заметим, что  а значит, и
а значит, и  выпуклые функционалы. В силу теоремы (Ферма) о минимуме выпуклого функционала (см., напр., [58], гл. 2, § 2, с. 142), для того чтобы
выпуклые функционалы. В силу теоремы (Ферма) о минимуме выпуклого функционала (см., напр., [58], гл. 2, § 2, с. 142), для того чтобы  был полиномом наилучшего приближения для
был полиномом наилучшего приближения для  необходимо и достаточно, чтобы субдифференциал функционала
необходимо и достаточно, чтобы субдифференциал функционала  в точке
в точке  содержал нуль. Субдифференциал
содержал нуль. Субдифференциал  выражается формулой (см., напр., [58], гл. 2, § 3, с. 87)
выражается формулой (см., напр., [58], гл. 2, § 3, с. 87)

где

Учитывая, что

получаем представление (6.2). В силу теоремы Каратеодори (см., напр., гл. I, п. 5.2) можно считать, что  не превосходит
не превосходит  Теорема доказана.
Теорема доказана.
Теперь сформулируем теорему, которая является аналогом теоремы Колмогорова о характеризации полинома наилучшего приближения в С (см. гл. I, п. 5.2)
Теорема 2. Пусть  Для того чтобы полином
Для того чтобы полином  был полиномом наилучшего приближения для
был полиномом наилучшего приближения для  необходимо и достаточно, чтобы не существовало полинома
необходимо и достаточно, чтобы не существовало полинома  такого, что
такого, что

Эта теорема является непосредственным следствием теоремы о минимаксе (см. [25], гл. 6, § 2, с. 240). Используя результаты, полученные Крипке, Ривлином [105] (см. § 4 этой главы), можно сформулировать подобную теорему для случая 
Обозначим через  множество нулей функции
множество нулей функции  будем также полагать, что функция
будем также полагать, что функция  обращается в нуль на множестве
обращается в нуль на множестве 
Теорема 3 (П.В. Борисов). Пусть  Для того чтобы полином
Для того чтобы полином  был полиномом наилучшего приближения для
был полиномом наилучшего приближения для  необходимо и достаточно, чтобы для любого полинома
необходимо и достаточно, чтобы для любого полинома  выполнялось следующее соотношение
выполнялось следующее соотношение

Доказательство. Достаточно доказать следующее равенство для производной по направлению

при  откуда без труда получается утверждение теоремы. Будем пользоваться известным соотношением для
откуда без труда получается утверждение теоремы. Будем пользоваться известным соотношением для  (см. [105],
(см. [105],

При  выпишем оценки для
выпишем оценки для  учитывая, что
учитывая, что 

Так как множество  компактно, то
компактно, то  в предыдущем неравенстве заменили на
в предыдущем неравенстве заменили на  Дословно повторяя доказательство, приведенное в [105], можно показать, что для любого положительного
Дословно повторяя доказательство, приведенное в [105], можно показать, что для любого положительного  существует
существует  такое, что для любого
такое, что для любого  выполняется следующее соотношение
выполняется следующее соотношение

(см. [105], гл. 5, § 2, с. 234 ). В итоге получим следующее неравенство 

Теперь оценим  с другой стороны:
с другой стороны:

Объединяя эти оценки, получим требуемое. Теорема доказана.
Теорема 4. Пусть  Для того чтобы полином
Для того чтобы полином  был полиномом наилучшего приближения для
был полиномом наилучшего приближения для  необходимо и достаточно, чтобы нашлись
необходимо и достаточно, чтобы нашлись  точки
точки  необязательно различные, такие, что не существует полинома
необязательно различные, такие, что не существует полинома  для которого
для которого

Доказательство. Покажем, что условие несовместности системы линейных неравенств (6.3) и необходимые и достаточные условия того, что полином  является наилучшим, эквивалентны. Обозначим
является наилучшим, эквивалентны. Обозначим  Отсутствие
Отсутствие  с условием (6.3) при
с условием (6.3) при  означает, что
означает, что  и это влечет (6.2). Пусть не все
и это влечет (6.2). Пусть не все  совпадают. Записав в новых обозначениях условие того, что не существует полинома
совпадают. Записав в новых обозначениях условие того, что не существует полинома  удовлетворяющего неравенствам
удовлетворяющего неравенствам

для некоторого натурального  получим
получим

Далее будем отождествлять  и набор коэффициентов
и набор коэффициентов  Запишем необходимые и достаточные условия несовместности системы линейных неравенств (6.4) относительно
Запишем необходимые и достаточные условия несовместности системы линейных неравенств (6.4) относительно  сформулированные в теореме Александрова-Фань-Цзи (см., напр., [73], гл, 4, § 1, с. 282), учитывая, что система (6.4) однородная: найдутся положительные числа
сформулированные в теореме Александрова-Фань-Цзи (см., напр., [73], гл, 4, § 1, с. 282), учитывая, что система (6.4) однородная: найдутся положительные числа  такие, что
такие, что

В силу произвольности  будем иметь
будем иметь 

Поскольку все А положительные, то равенства (6.2) теоремы 1 спра ведливы. Таким образом, условие несовместности системы линейных неравенств (6,4) и необходимое и достаточное условие того, что полином  является наилучшим, эквивалентны. Тот факт, что
является наилучшим, эквивалентны. Тот факт, что  не превосходит
не превосходит  , доказывает теорему.
, доказывает теорему.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
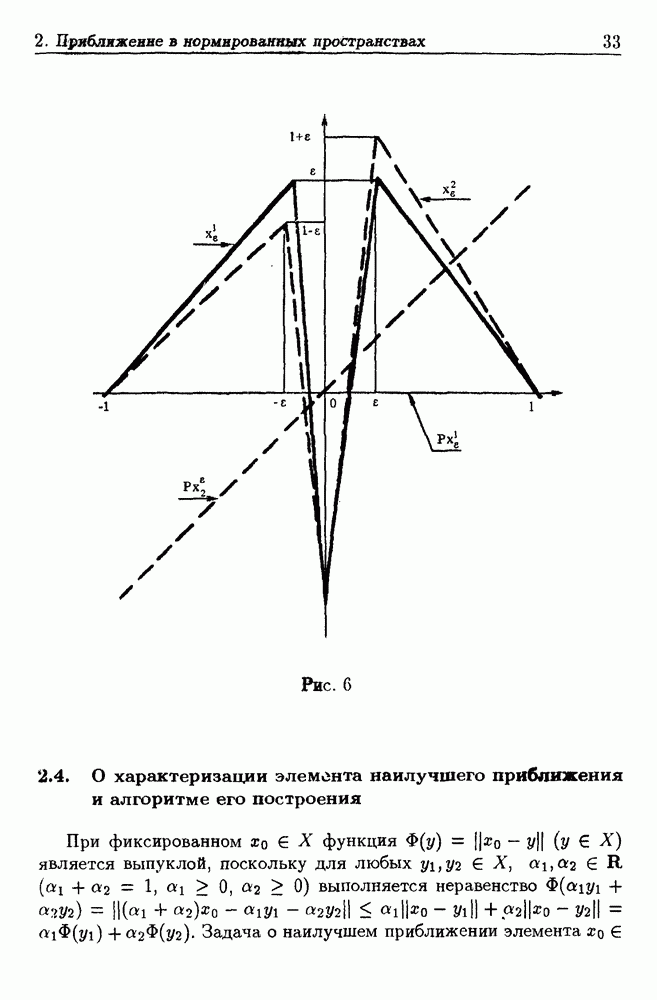
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
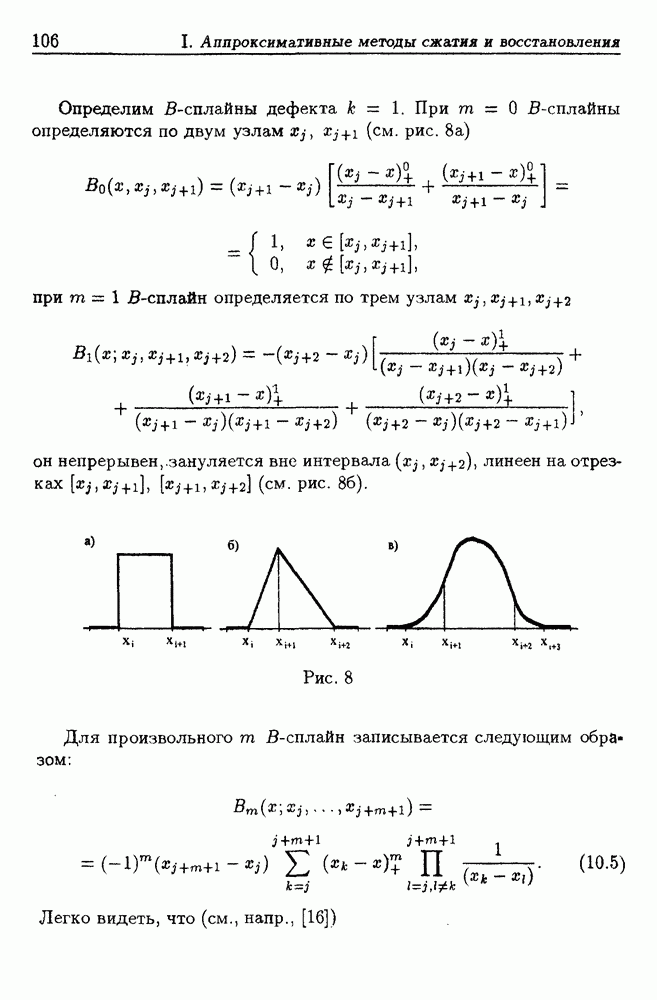
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
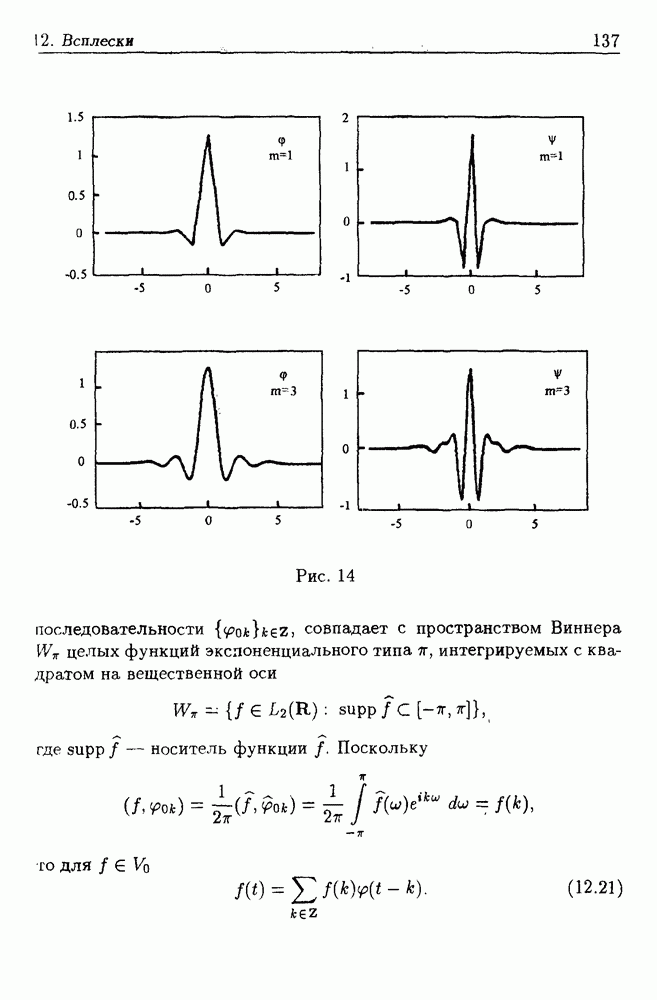
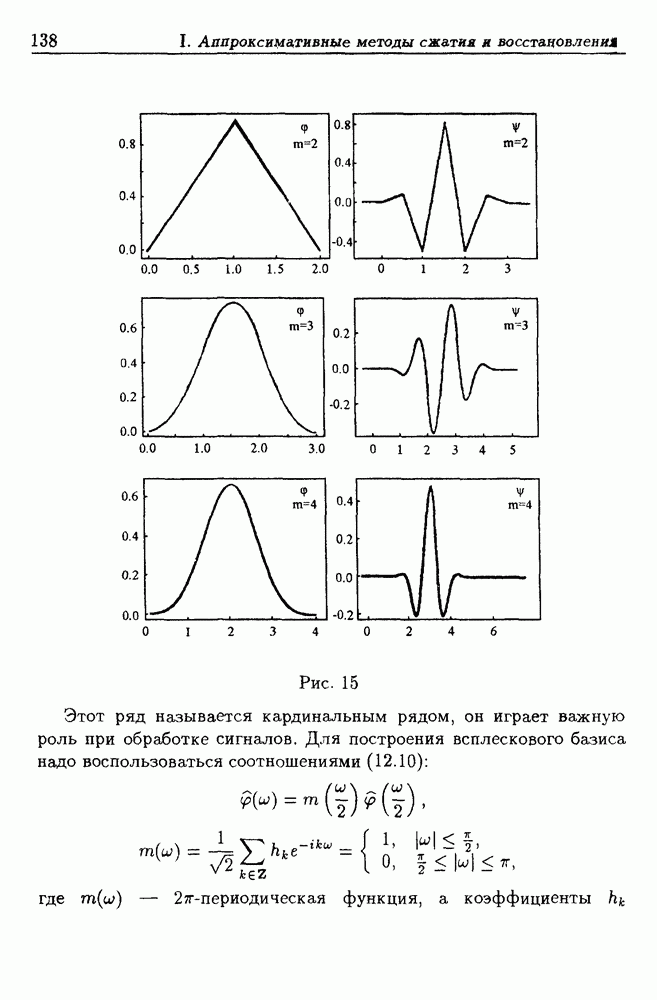
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
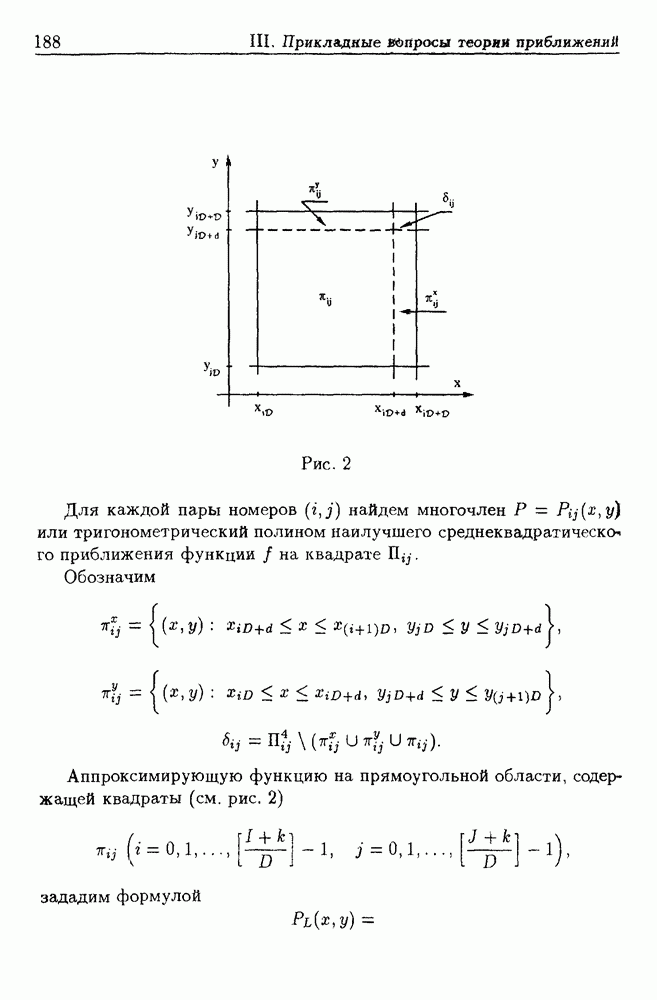
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
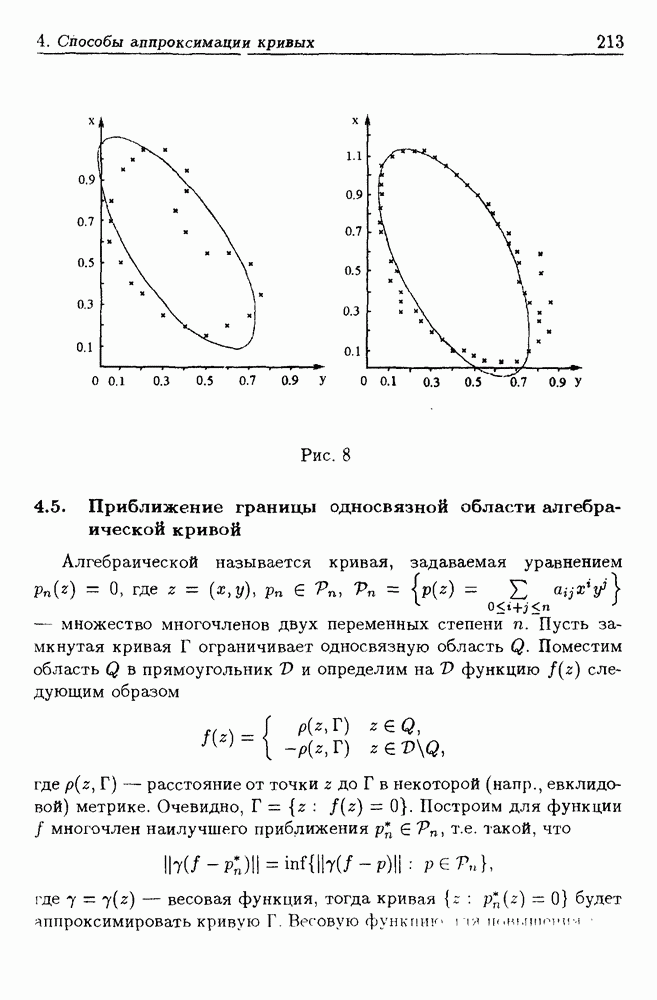
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
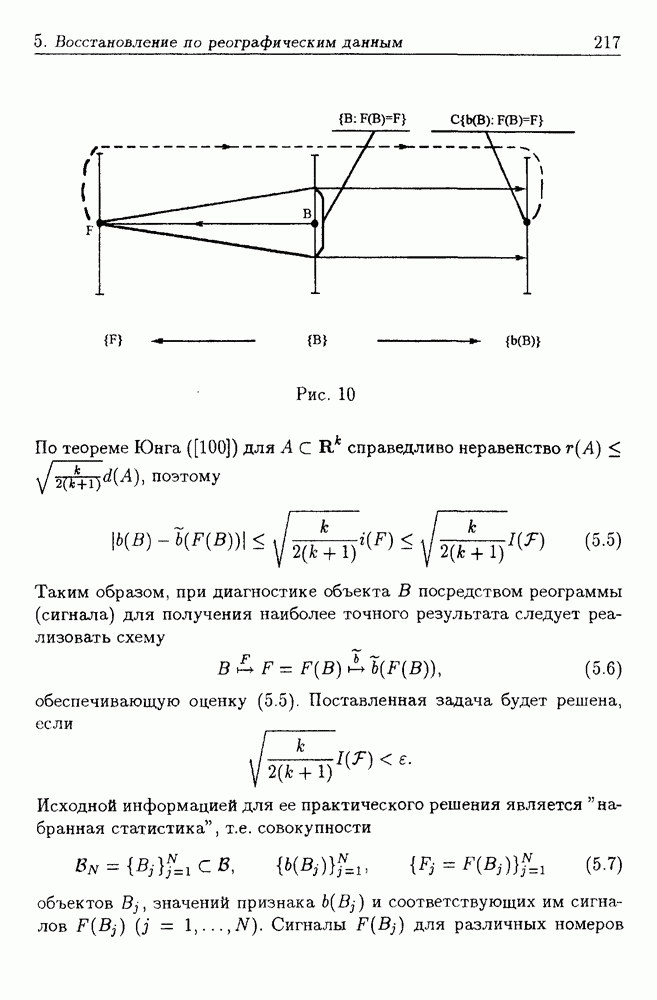
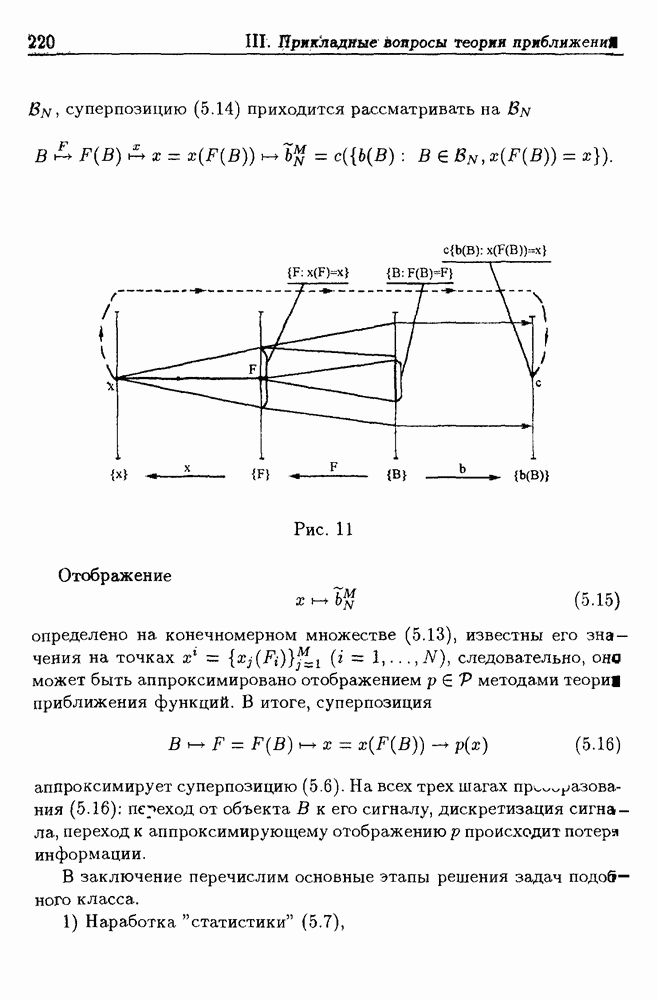
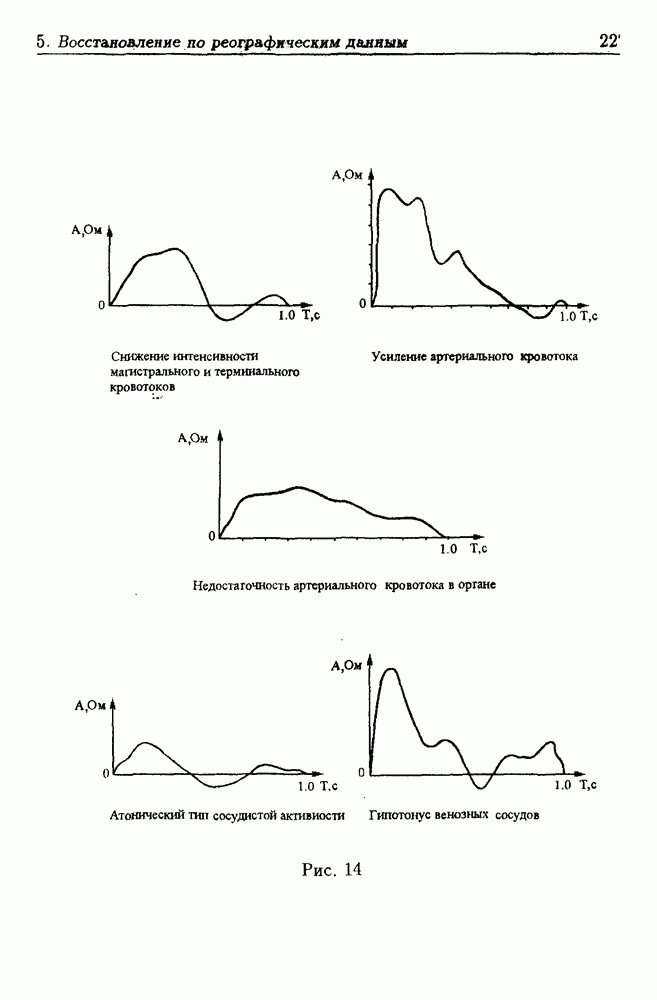
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
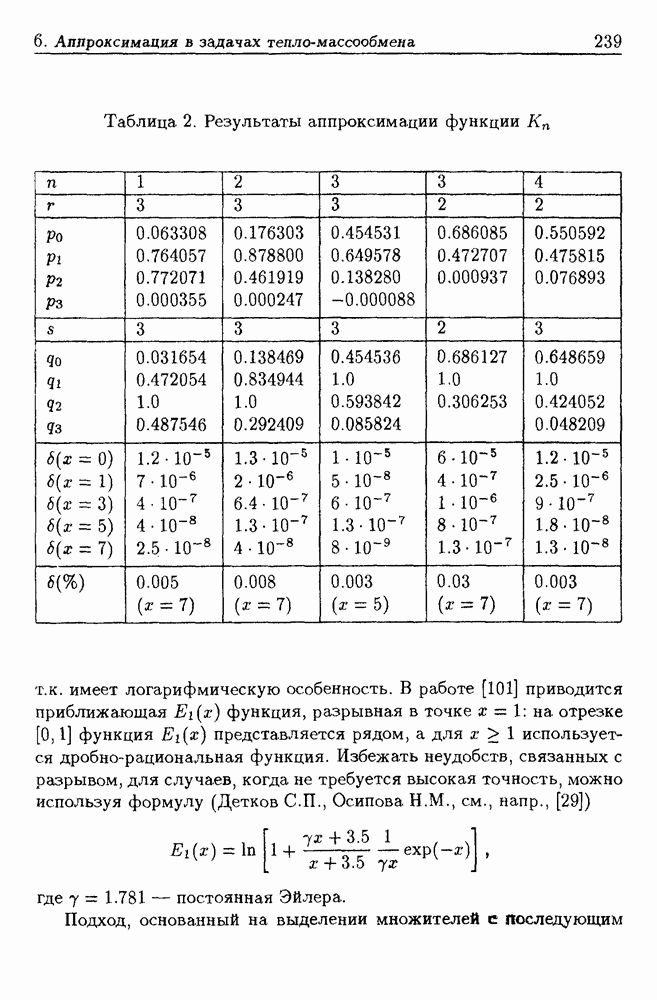
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
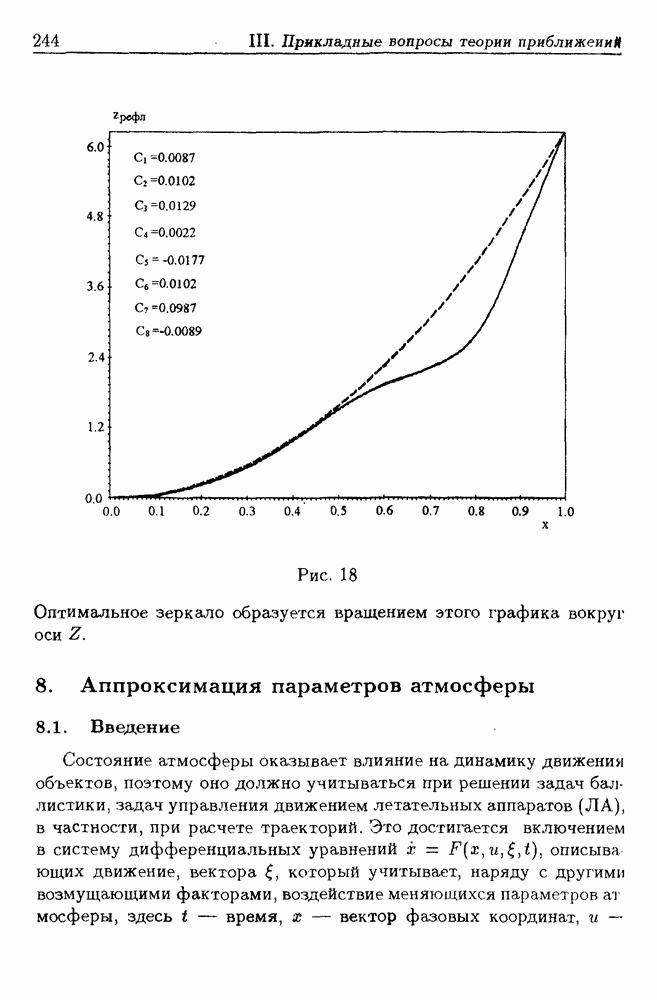
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
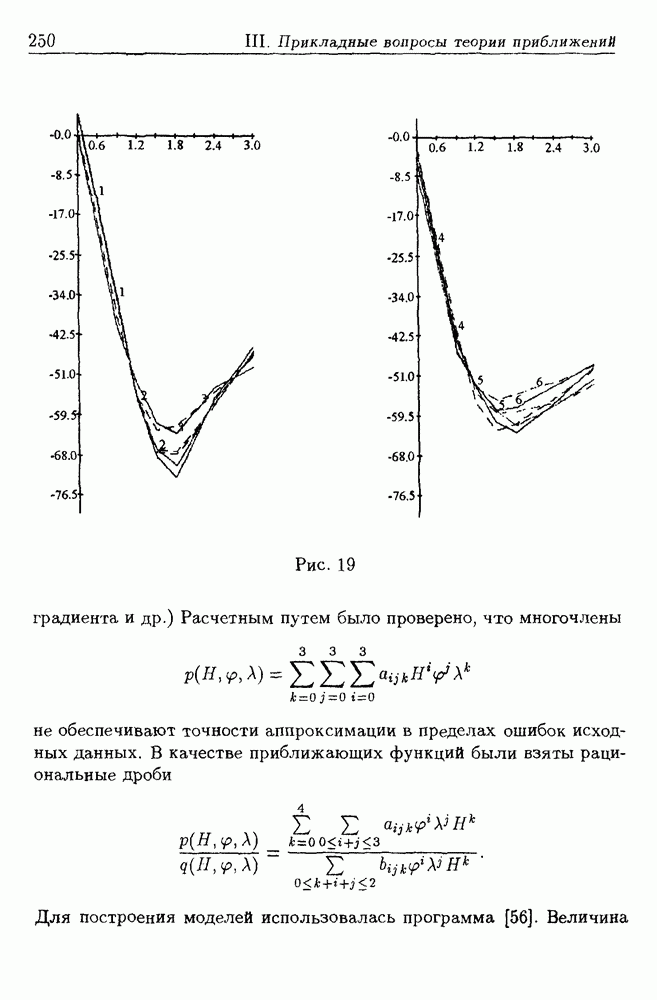
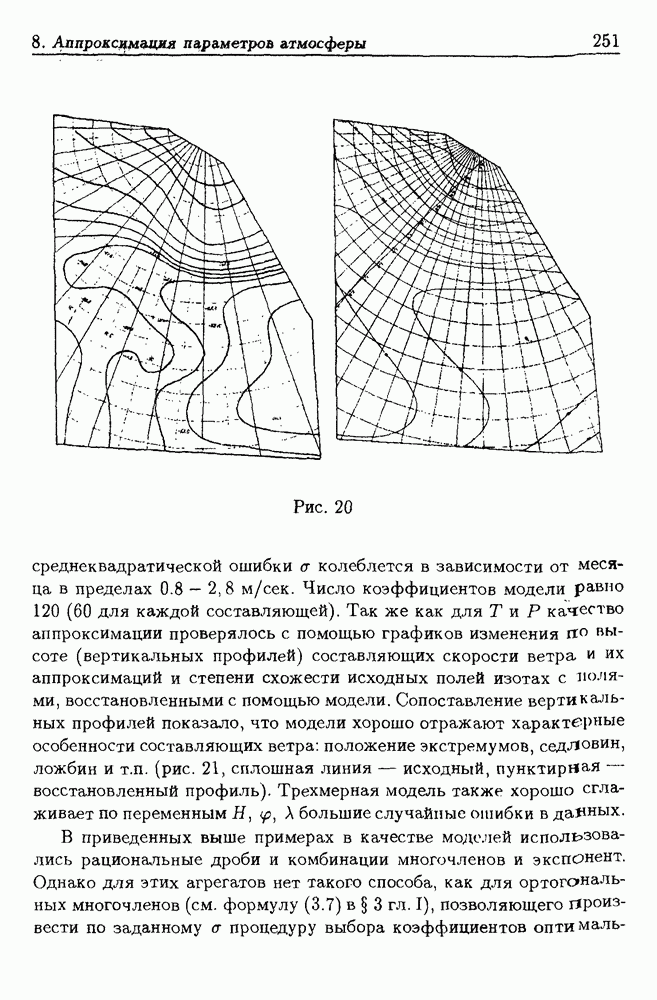
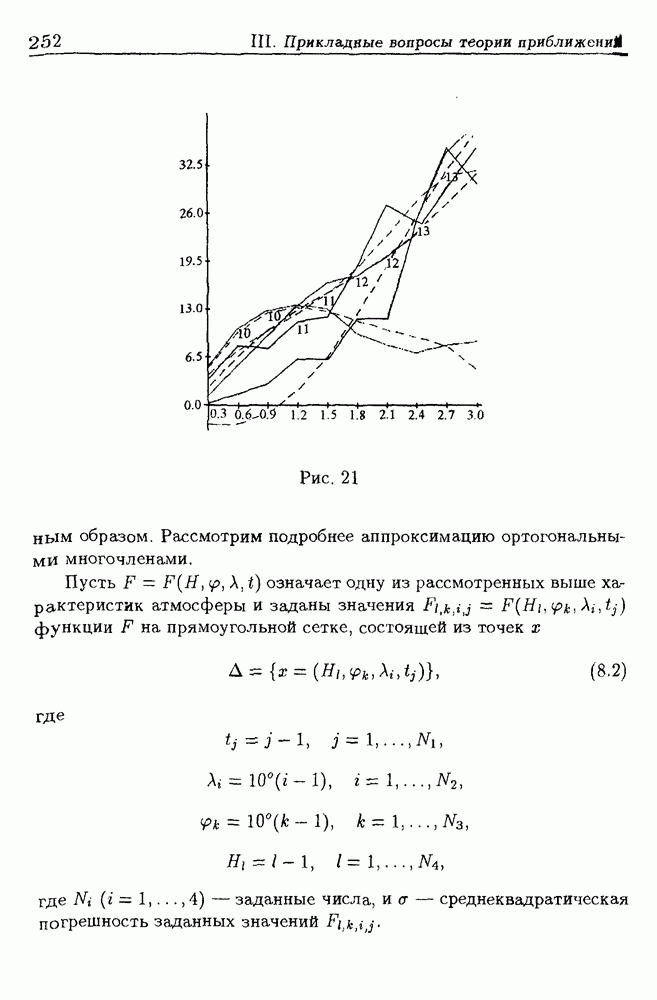
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
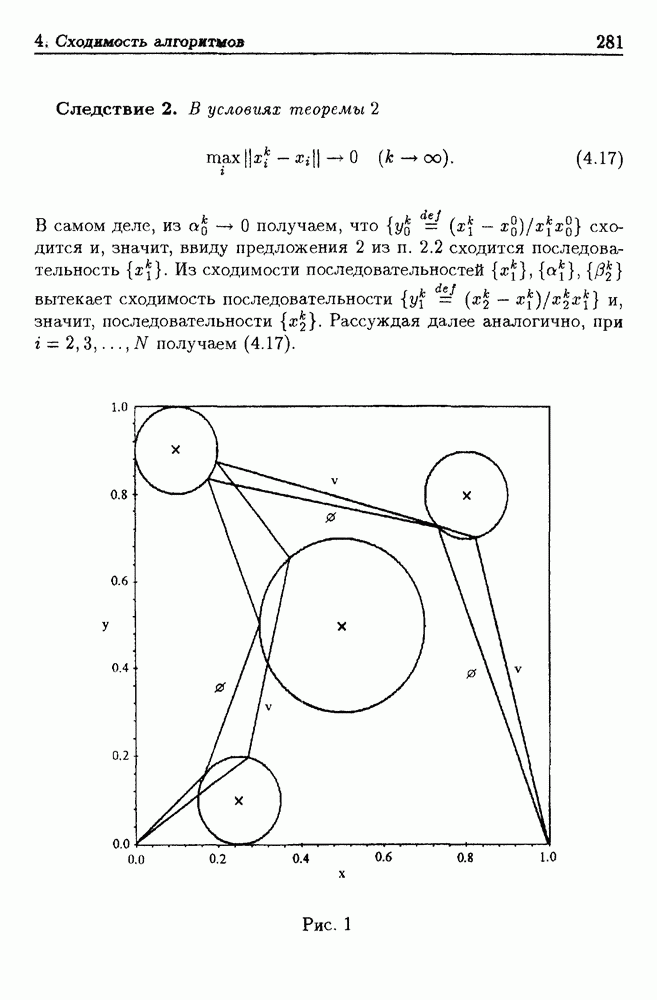
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ