| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
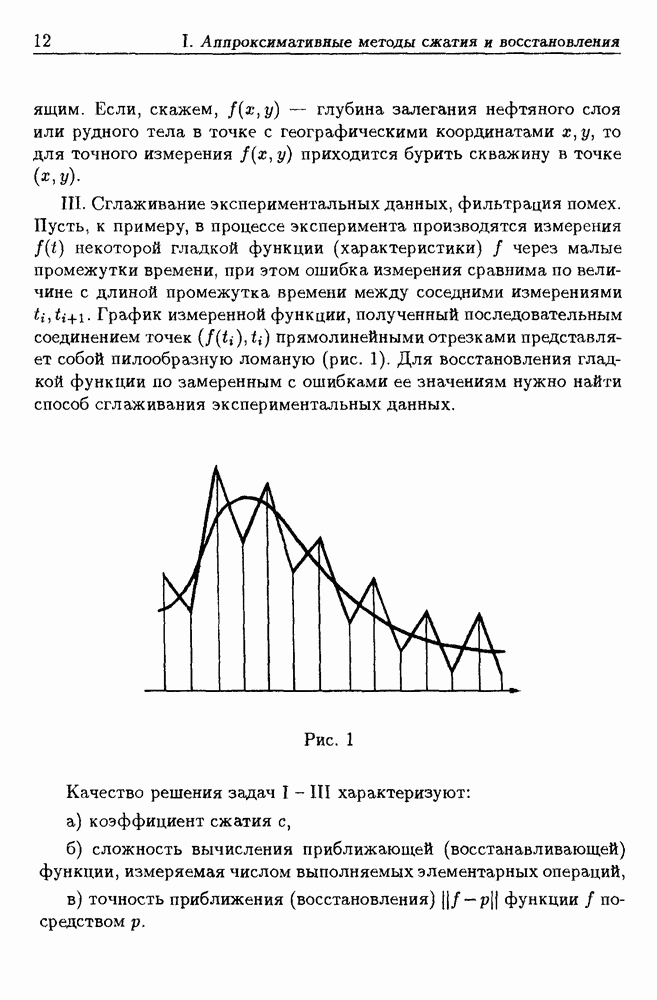
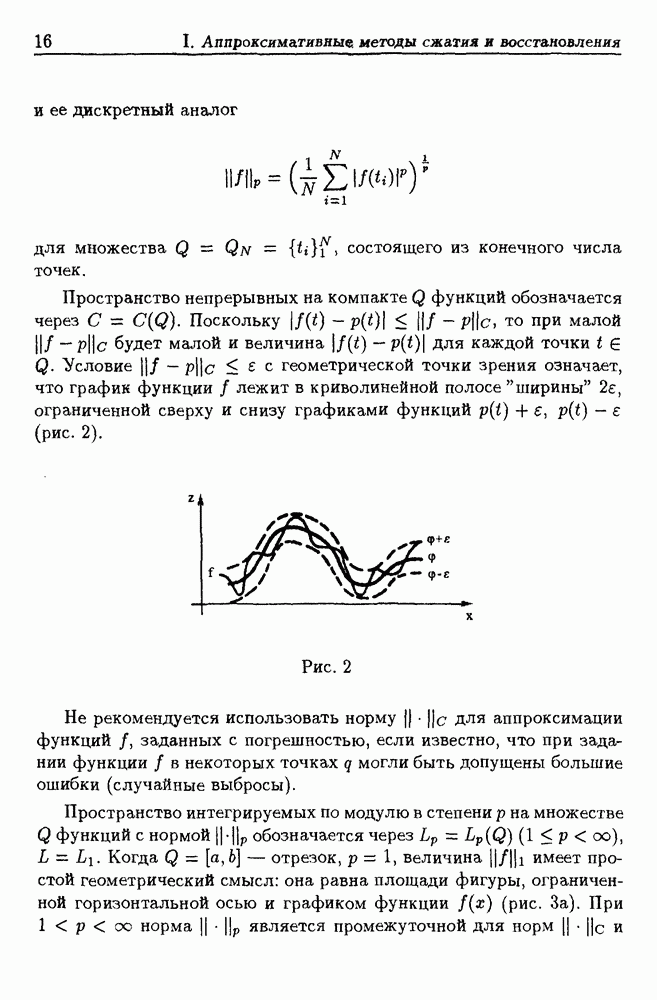
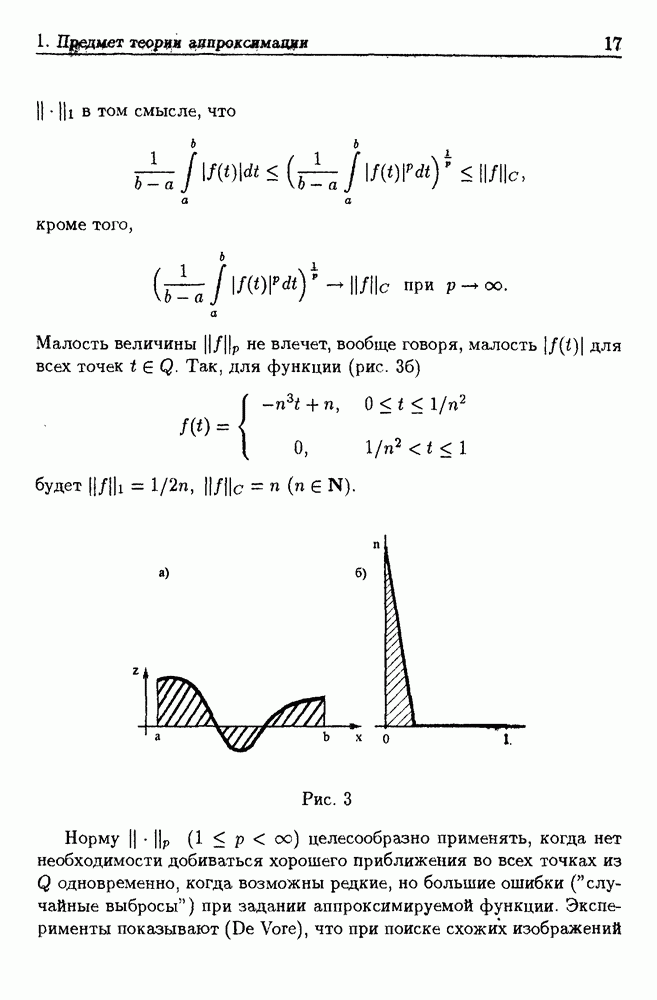
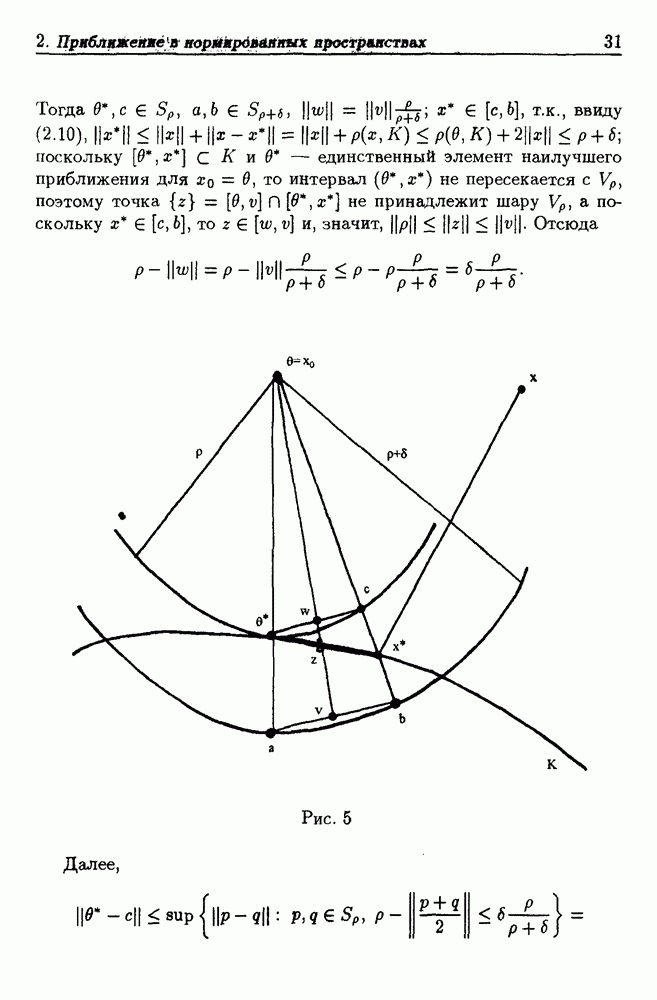
1.5. Полная погрешность решения задачи приближения
Рассмотрим процесс аппроксимации в целом. Предположим, что нам предстоит для функциональной зависимости  построить аппроксимирующую функцию
построить аппроксимирующую функцию  которая задается сравнительно небольшим числом параметров. Допустим, что мы выбрали подходящую норму
которая задается сравнительно небольшим числом параметров. Допустим, что мы выбрали подходящую норму  и класс
и класс  аппроксимирующих функций. Если бы функция
аппроксимирующих функций. Если бы функция  была известна на всем множестве
была известна на всем множестве  то нам следовало бы решать задачу (см. (1.1)) о наилучшем приближении
то нам следовало бы решать задачу (см. (1.1)) о наилучшем приближении

для поиска функции  наилучшего приближения. Однако часто информация о функции
наилучшего приближения. Однако часто информация о функции  задается таблицей значений
задается таблицей значений  замеренных на некоторой сетке
замеренных на некоторой сетке  с погрешностью
с погрешностью  т.е.
т.е.

где  дискретный вариант нормы
дискретный вариант нормы  Поэтому нам вместо
Поэтому нам вместо  приходится аппроксимировать функцию
приходится аппроксимировать функцию  на сетке
на сетке  Будем считать, что существует функция
Будем считать, что существует функция  наилучшего приближения для
наилучшего приближения для 
Для аппроксимации функции  нужен алгоритм построения
нужен алгоритм построения  Для создания алгоритма важно знать характеристические свойства функции наилучшего приближения
Для создания алгоритма важно знать характеристические свойства функции наилучшего приближения  Исходя из определения полинома наилучшего приближения
Исходя из определения полинома наилучшего приближения  надо, чтобы создаваемый алгоритм позволял для заданного малого числа
надо, чтобы создаваемый алгоритм позволял для заданного малого числа  построить функцию
построить функцию  такую, что
такую, что

Программная реализация этого алгоритма и вычисления на  неизбежно выполняемые с погрешностью (округления), приведут нас к функции
неизбежно выполняемые с погрешностью (округления), приведут нас к функции  которая и будет приближенным представлением исходной функции
которая и будет приближенным представлением исходной функции  Оценим величину
Оценим величину  полной погрешности, последовательно вводя обозначения Д» и для краткости заменяя
полной погрешности, последовательно вводя обозначения Д» и для краткости заменяя  на
на 

В этом неравенстве

— погрешность дискретизации,

— погрешность исходных данных,

— величина уклонения функции  от класса V в метрике
от класса V в метрике 

— уклонение функций из класса V наилучшего и почти наилучшего приближения (удовлетворяющих условиям (1.2), (1.4) соответственно),

— погрешность вычислений.
Естественно желание сделать сумму  возможно меньшей, оценить сверху каждую из погрешностей
возможно меньшей, оценить сверху каждую из погрешностей  Погрешность
Погрешность  может быть оценена сверху величиной
может быть оценена сверху величиной

при фиксированном достаточно большом  которая определяется дифференциальными свойствами функций
которая определяется дифференциальными свойствами функций  и уменьшается по мере уплотнения сетки
и уменьшается по мере уплотнения сетки  Погрешность
Погрешность  может быть уменьшена за счет повышения точности измерений функции
может быть уменьшена за счет повышения точности измерений функции  Погрешность
Погрешность  уменьшается за счет удачного выбора класса V, за счет его расширения. Величина
уменьшается за счет удачного выбора класса V, за счет его расширения. Величина

ограничивающая сверху погрешность  зависит от свойств пространства
зависит от свойств пространства  и класса функций V, и, как будет показано далее, тесно связана со свойством непрерывности отображения
и класса функций V, и, как будет показано далее, тесно связана со свойством непрерывности отображения  Для уменьшения
Для уменьшения  нужно уменьшить 8. Погрешность
нужно уменьшить 8. Погрешность  может быть сокращена за счет увеличения точности вычислений.
может быть сокращена за счет увеличения точности вычислений.
При численном решении задачи приближения важно соизмерять погрешности  Так, нецелесообразно выбирать богатый класс V и вести вычисления с высокой точностью, если функция
Так, нецелесообразно выбирать богатый класс V и вести вычисления с высокой точностью, если функция  задана с грубыми ошибками, равно как при плохой точности счета не следует очень точно задавать (измерять) функцию и брать богатый класс функций
задана с грубыми ошибками, равно как при плохой точности счета не следует очень точно задавать (измерять) функцию и брать богатый класс функций 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
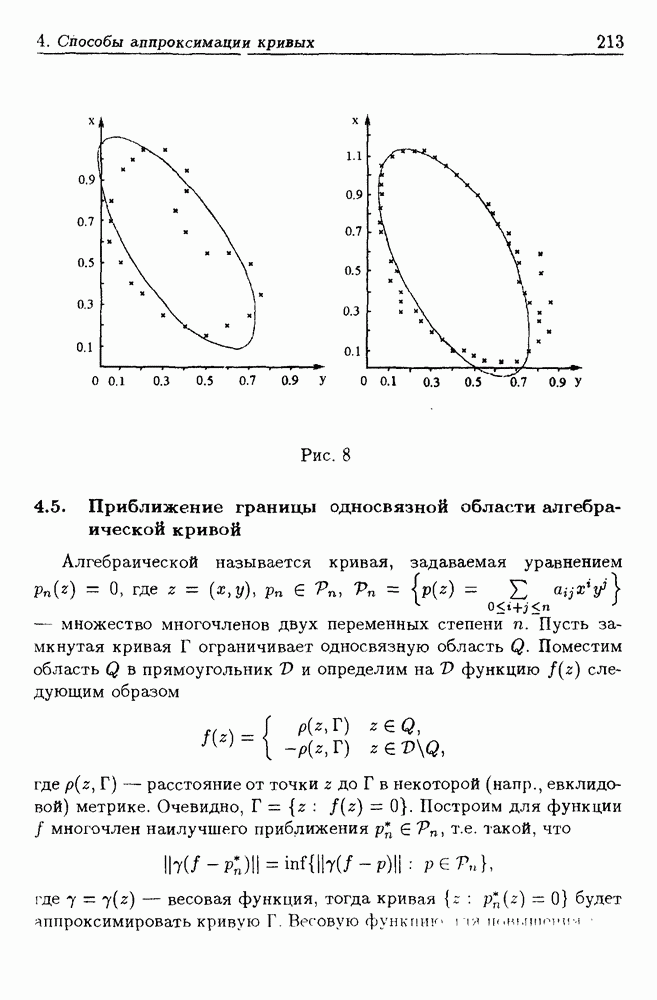
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
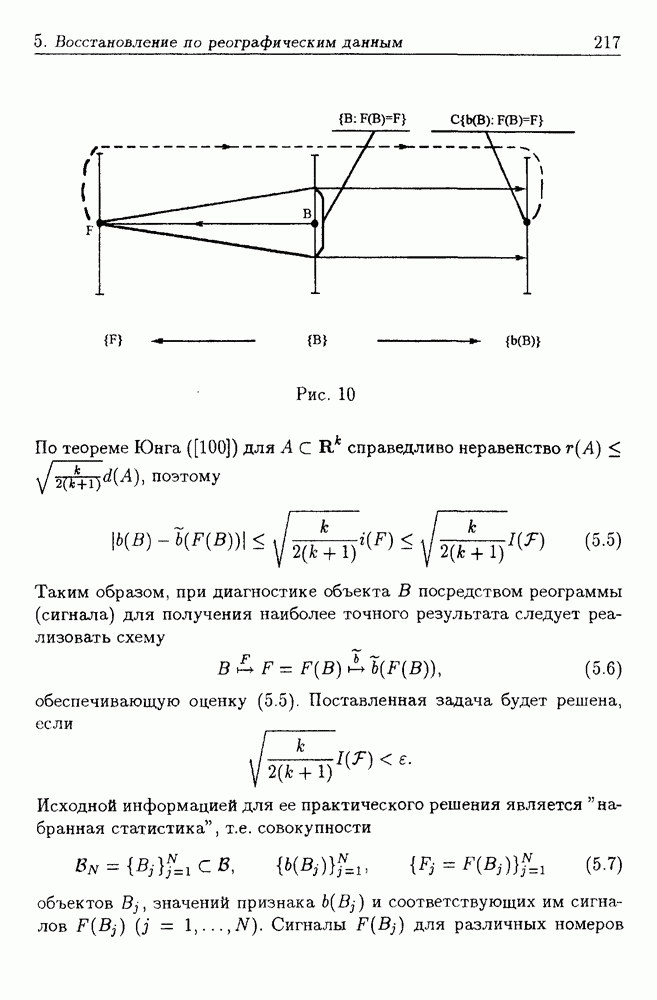
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
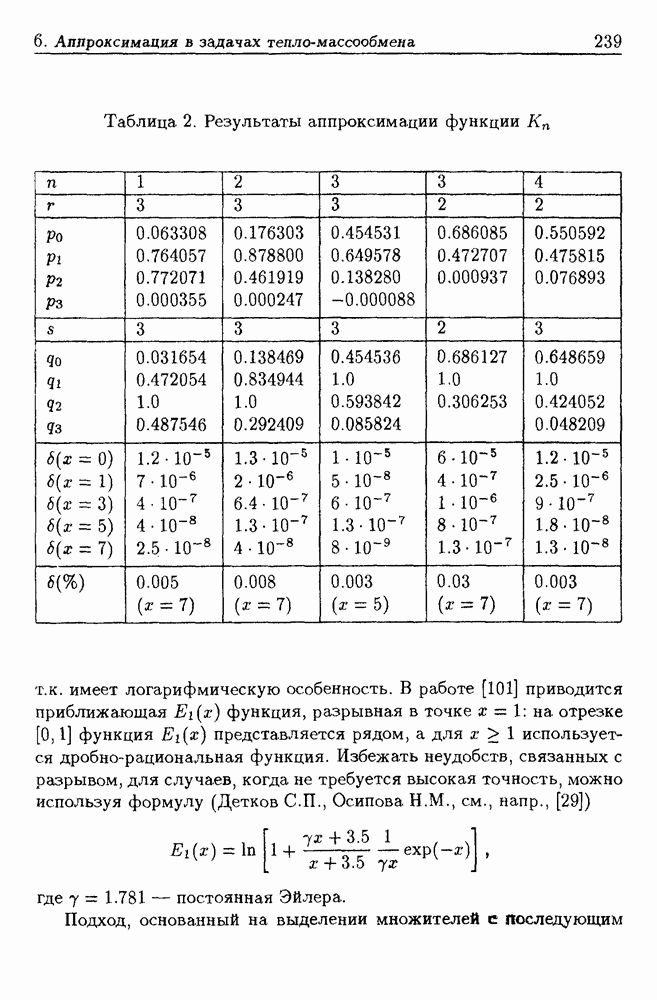
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
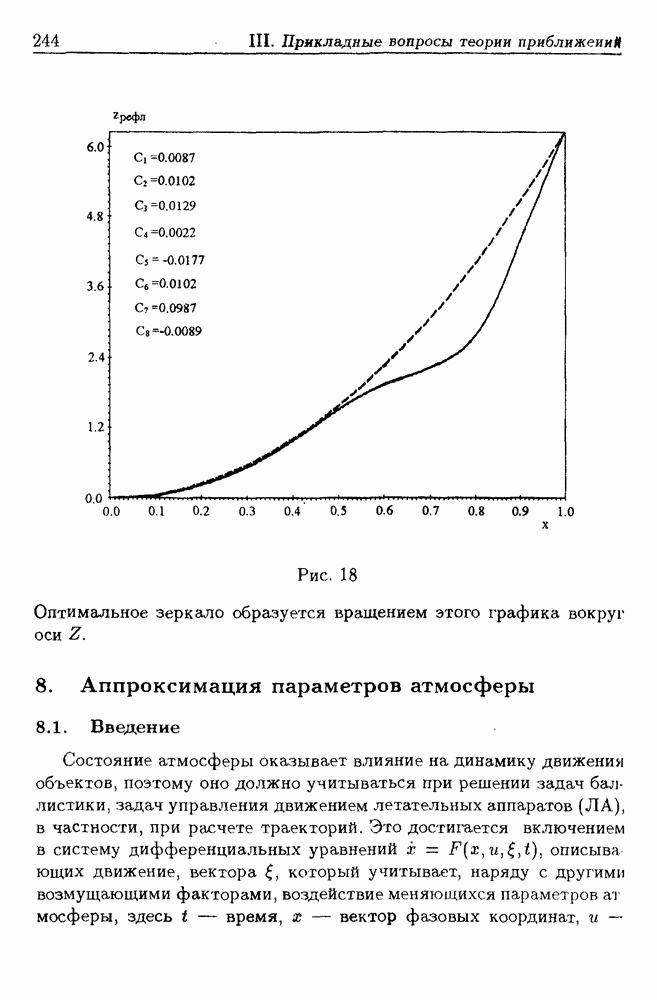
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
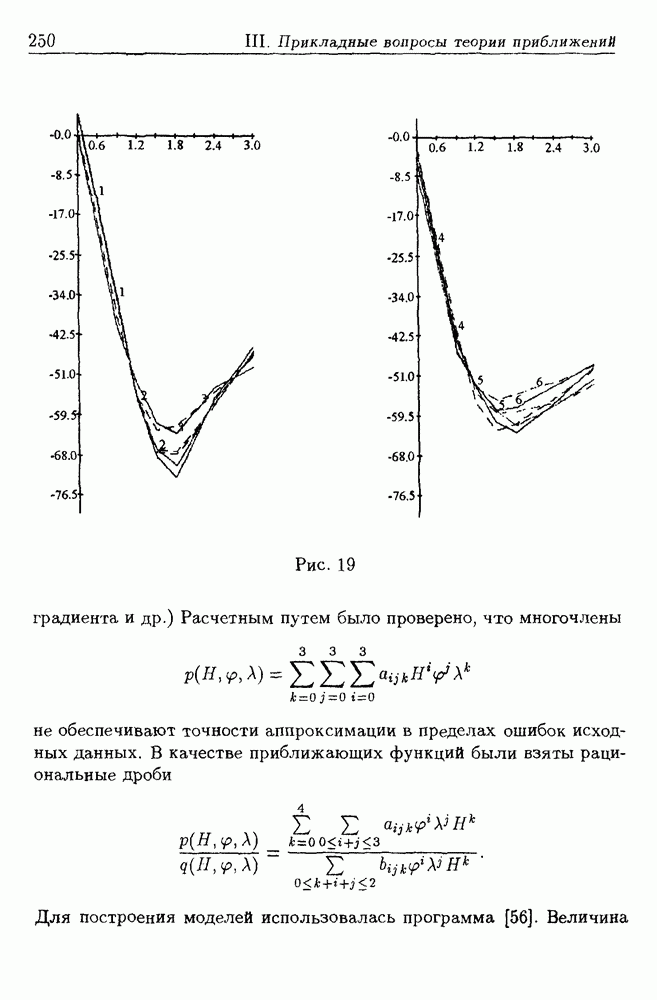
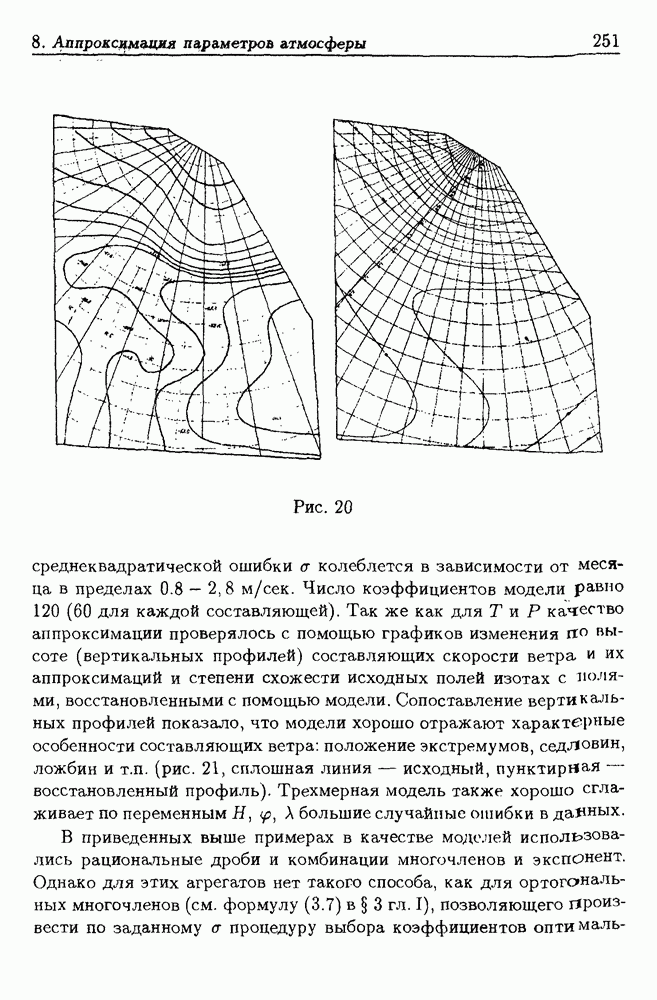
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ