| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. Алгоритмы аппроксимации рациональными дробями
9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
В общем виде задача наилучшего равномерного приближения функций рациональными дробями может быть сведена к задаче минимизации линейной функции при нелинейных ограничениях и может, вообще говоря, решаться или общими методами минимизации, или соответствующими методами нелинейного программирования. Однако алгоритмы специально разработанные для ее решения, использующие специфику задачи, обладают значительно большей эффективностью.
Можно выделить два основных подхода к решению задачи наилучшего равномерного приближения функций рациональными дробями [106]. Первый подход основан на характеристической теореме П.Л. Чебышева и теореме Валле-Пуссена об оценке снизу величины наилучшего приближения. Второй подход основан на сведении исходной нелинейной задачи к последовательности задач линейного программирования. Алгоритмы, реализующие первый подход, предназначены для приближения функций одного независимого переменного. Наиболее эффективными среди алгоритмов этого типа являются аналоги  полиномиального алгоритма Ремеза [118], [57], [82]. Эти алгоритмы отличаются быстродействием, но сходятся не от любого начального приближения. Второй подход связан с именами Чини, Лоеба и Рубинштейна [87], [61]. Среди алгоритмов, реализующих этот подход, исходным и наиболее эффективным является итерационный алгоритм Чини-Лоеба [87] и его аналоги [88], [78], [104] [11], [54], [60]. Эти алгоритмы сходятся при любом начальном приближении.
полиномиального алгоритма Ремеза [118], [57], [82]. Эти алгоритмы отличаются быстродействием, но сходятся не от любого начального приближения. Второй подход связан с именами Чини, Лоеба и Рубинштейна [87], [61]. Среди алгоритмов, реализующих этот подход, исходным и наиболее эффективным является итерационный алгоритм Чини-Лоеба [87] и его аналоги [88], [78], [104] [11], [54], [60]. Эти алгоритмы сходятся при любом начальном приближении.
Описание обобщенного алгоритма Чини-Лоеба.
В этом разделе излагается (см. [54]) алгоритм наилучшего равномерного приближения рациональными дробями функций, заданных на дискретном множестве точек, являющийся обобщением алгоритма Чини-Лоеба.
Пусть  некоторое конечное множество,
некоторое конечное множество,  натуральные числа. На множестве
натуральные числа. На множестве  определена функция
определена функция  Пусть
Пусть  подпространства из
подпространства из  с базисами
с базисами

соответственно.
Определим множество рациональных дробей

Заметим, что требование постоянства знака у знаменателя на множестве точек определения является естественным. Обозначим 
Будем решать задачу наилучшего приближения: найти

и дробь  для которой
для которой 
Общая схема построения сходящихся итерационных алгоритмов типа Чини-Лоэба для численного решения задачи (9.2) имеет следующий вид.
Пусть  множество, обладающее свойством: для любого
множество, обладающее свойством: для любого  такое, что
такое, что  Это условие обеспечивает эквивалентность задачи (9.2) и задачи
Это условие обеспечивает эквивалентность задачи (9.2) и задачи

В качестве начальной берется произвольная дробь  которой
которой  Пусть на
Пусть на  шаге получена дробь
шаге получена дробь  Тогда на
Тогда на  шаге решается минимаксная задача
шаге решается минимаксная задача

где

 фиксированное число. Если
фиксированное число. Если  то в качестве
то в качестве  берется решение задачи (9.3),
берется решение задачи (9.3),  Если
Если  то считаем
то считаем  При практической реализации алгоритма условие
При практической реализации алгоритма условие  означает необходимость останова.
означает необходимость останова.
Опишем некоторый достаточно широкий класс множеств  для которых
для которых  . С точки зрения численной реализации алгоритма наиболее удобным является задание множества
. С точки зрения численной реализации алгоритма наиболее удобным является задание множества  системой линейных неравенств, поскольку в этом случае задача (9.3) легко сводится к задаче линейного программирования. В п. 9.1.3 приведены конкретные примеры таких множеств
системой линейных неравенств, поскольку в этом случае задача (9.3) легко сводится к задаче линейного программирования. В п. 9.1.3 приведены конкретные примеры таких множеств 
Существенной частью алгоритма является решение задачи (9.3). В связи с этим рассмотрим несколько более общую минимаксную задачу:

где

 произвольное (в отличие от
произвольное (в отличие от  ) фиксированное число,
) фиксированное число,  некоторая функция,
некоторая функция,  для любого
для любого 
Введем два определения:
Определение 1. Множество  будем называть допустимым, если множество
будем называть допустимым, если множество

ограничено и замкнуто в равномерной метрике и выполнено следующее
Условие А. Для любой функции  существует такая последовательность дробей
существует такая последовательность дробей  что
что

Определение 2. Множество полиномов  таких, что
таких, что  при любом
при любом  будем называть
будем называть  -границей
-границей  и обозначать через
и обозначать через 
Заметим, что условие А будет выполняться, если в задаче (9.2) существует наилучшая рациональная дробь  такая, что
такая, что  Однако существования наилучшей дроби для функции
Однако существования наилучшей дроби для функции  в алгоритме не требуется.
в алгоритме не требуется.
Рассмотрим зависимость решения задачи (9.5) от величины параметра  когда
когда  или
или 
Лемма 1. Пусть  Тогда
Тогда

3) если  допустимое множество, то существуют такие
допустимое множество, то существуют такие  что
что 
4) если пара  является решением задачи (9.5) и
является решением задачи (9.5) и  то
то 
Похожие утверждения для конкретных множеств  (см. п. 9.1.3) имеются в работах [88], [11].
(см. п. 9.1.3) имеются в работах [88], [11].
Доказательство. Разобьем доказательство леммы на четыре части.
1. Имеем

2. Для любого  имеем
имеем  Отсюда, очевидно,
Отсюда, очевидно,  следовательно,
следовательно, 
3. Согласно условию А, существуют последовательности  для любого
для любого  такие, что
такие, что

Если  то для достаточно больших I имеем
то для достаточно больших I имеем  следовательно, в силу
следовательно, в силу  Пусть
Пусть  Покажем, что последовательность
Покажем, что последовательность  ограничена. Действительно, в силу (9.7) существует
ограничена. Действительно, в силу (9.7) существует  такое, что
такое, что  для любых
для любых  отсюда
отсюда  где
где

и, следовательно,  Так как последовательности
Так как последовательности  принадлежат ограниченным и замкнутым и, следовательно, компактным множествам, то из
принадлежат ограниченным и замкнутым и, следовательно, компактным множествам, то из  можно выделить равномерно сходящиеся подпоследовательности
можно выделить равномерно сходящиеся подпоследовательности

Учитывая (9.7), имеем


откуда 
4. Пусть  являются экстремальными, т.е.
являются экстремальными, т.е.  -Юсли
-Юсли  то для некоторого
то для некоторого  будет
будет  и при этом
и при этом

что противоречит экстремальности 
Следствие 1. Если  допустимое множество,
допустимое множество,  то
то  тогда и только тогда, когда
тогда и только тогда, когда 
Теорема 1. Пусть  допустимое множество. Если
допустимое множество. Если  то задача (9.5) всегда имеет решение и
то задача (9.5) всегда имеет решение и  Если
Если  принадлежит
принадлежит  то пара
то пара  являются решением задачи (9.5) и
являются решением задачи (9.5) и 
Доказательство. Пусть  Если
Если  и хотя бы в одной точке
и хотя бы в одной точке  будет
будет  то
то  если
если  то
то  Отсюда и из утверждения 3) леммы 1 следует, что при иычислении минимума в (9.5) можно ограничиться полиномами
Отсюда и из утверждения 3) леммы 1 следует, что при иычислении минимума в (9.5) можно ограничиться полиномами  такими, что
такими, что  где
где  достаточно большое число, т.е.
достаточно большое число, т.е.

Пусть последовательности  таковы, что
таковы, что  Используя компактность множеств
Используя компактность множеств  выделим сходящиеся подпоследовательности
выделим сходящиеся подпоследовательности  Тогда имеем для любого
Тогда имеем для любого 

Так как неравенство имеет место для всех  то
то  т. е. пара
т. е. пара  является решением задачи (9.9) и, следовательно, задачи 9.5).
является решением задачи (9.9) и, следовательно, задачи 9.5).
Пусть  Покажем, что в этом случае
Покажем, что в этом случае  Предположим, что
Предположим, что  Тогда найдется пара
Тогда найдется пара  такая, что
такая, что  и по свойству 2) леммы 1 будет
и по свойству 2) леммы 1 будет  что противоречит условию
что противоречит условию  Таким образом,
Таким образом,  . С другой стороны, для
. С другой стороны, для  имеем
имеем  Следовательно,
Следовательно, 
Сходимость алгоритма и оценки скорости сходимости
В этом пункте предполагается, что  произвольное допустимое множество, а множество
произвольное допустимое множество, а множество  содержит не менее
содержит не менее  точки.
точки.
Теорема 2. Пусть  допустимое множество,
допустимое множество,  Тогда
Тогда  Равенство
Равенство  выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 
Доказательство. Условия леммы 1 выполняются. Из (9.8) имеем  можно считать, без ограничения общности, что
можно считать, без ограничения общности, что  Тогда
Тогда  для
для  Докажем, что
Докажем, что  Предположим, что
Предположим, что  Тогда
Тогда

а отсюда, очевидно,  что противоречит утверждению 3) леммы 1. Значит,
что противоречит утверждению 3) леммы 1. Значит,  не возрастает и, следовательно, существует
не возрастает и, следовательно, существует 
Предположим, что  . В силу условия А существуют
. В силу условия А существуют

такие, что  Так как
Так как  то в каждой точке имеем
то в каждой точке имеем

Отсюда, применяя (9.6) и учитывая, что  получаем
получаем

где

Если  то из (9.10) при к
то из (9.10) при к  сразу получаем противоречие. Если
сразу получаем противоречие. Если  то при любом
то при любом  из (9.10) и при сходимости разности
из (9.10) и при сходимости разности  к нулю
к нулю  имеем
имеем

для достаточно больших k. Используя это неравенство при  где
где  число точек множества
число точек множества  неравенство (9.11) и очевидное неравенство
неравенство (9.11) и очевидное неравенство  получаем
получаем

откуда следует расходимость последовательности  а это противоречит ограниченности множества
а это противоречит ограниченности множества  Следовательно,
Следовательно, 
Вторая часть теоремы легко доказывается, если использовать следствие 1 и тот факт, что  при любых k.
при любых k.
Далее будем предполагать, что в задаче (9.2) для функции  в множестве
в множестве  существует наилучшая рациональная дробь
существует наилучшая рациональная дробь 
Следствие 2. Пдстпъ  допустимое множество. Если
допустимое множество. Если  наилучшая дробь для функции
наилучшая дробь для функции  то
то

где  некоторая константа, не зависящая от k.
некоторая константа, не зависящая от k.
Оценка (9.12) легко следует из (9.10).
При  и дополнительных предположениях относительно функции
и дополнительных предположениях относительно функции  можно получить квадратичную скорость сходимости алгоритма.
можно получить квадратичную скорость сходимости алгоритма.
Будем предполагать, что пространство, натянутое на

является пространством Хаара размерности  т.е. пространство
т.е. пространство  имеет размерность
имеет размерность  и нет нетривиального элемента из него, имеющего более чем
и нет нетривиального элемента из него, имеющего более чем  нулей в
нулей в  При этих предположениях легко можно доказать теорему о сильной единственности (см. гл. I, п. 7.2) и предшествующие ей леммы 1, 2 ([89], с. 164-166). Приведем формулировку леммы 1:
При этих предположениях легко можно доказать теорему о сильной единственности (см. гл. I, п. 7.2) и предшествующие ей леммы 1, 2 ([89], с. 164-166). Приведем формулировку леммы 1:
Лемма 2 (Чини, [89], с. 164). Пусть  наилучшая дробь в
наилучшая дробь в  для функции
для функции  Если
Если  пространство Хаара, то единственный элементу? из
пространство Хаара, то единственный элементу? из  удовлетворяющий неравенству
удовлетворяющий неравенству  для всех у из множества критических точек
для всех у из множества критических точек  есть нулевой элемент.
есть нулевой элемент.
Определение 3. Наилучшая дробь  из класса
из класса  называется нормальной, если пространство
называется нормальной, если пространство  пространство Хаара (что эквивалентно включению
пространство Хаара (что эквивалентно включению 
Лемма 3. Пусть множество  ограничено и замкнуто, наилучшая дробь
ограничено и замкнуто, наилучшая дробь  для
для  является нормальной,
является нормальной,  Если
Если  равномерно на
равномерно на 
Доказательство. Так как  то в силу теоремы о сильной единственности имеем
то в силу теоремы о сильной единственности имеем  Докажем, что
Докажем, что  Предположим, что
Предположим, что  не сходится к Тогда существуют сходящиеся подпоследовательности
не сходится к Тогда существуют сходящиеся подпоследовательности  (т.е.
(т.е.  наилучшая дробь). Поскольку
наилучшая дробь). Поскольку  замкнуто, то
замкнуто, то  Покажем, что
Покажем, что  Для любого
Для любого  где
где

имеем

где 
Переходя к пределу, получим

откуда в силу леммы 2 будет  при любых
при любых  Так как
Так как  нормальная дробь, то
нормальная дробь, то  причем число
причем число  по предположению. Это противоречит тому, что
по предположению. Это противоречит тому, что  Значит,
Значит,  следовательно,
следовательно,  равномерно на
равномерно на 
Определение 4. Пусть  Будем говорить, что
Будем говорить, что  обладает свойством
обладает свойством  на
на  если для всех
если для всех  таких, что
таких, что  имеет место неравенство
имеет место неравенство

где  не зависит от
не зависит от 
Теорема 3. Пусть в  допустимое множество. Если
допустимое множество. Если  нормальная наилучшая дробь для функции
нормальная наилучшая дробь для функции  обладающая свойством
обладающая свойством  на
на  то
то

где  некоторая константа, не зависящая от k.
некоторая константа, не зависящая от k.
Доказательство. Используем схему доказательства теоремы 3 из [78], несколько изменив оценки для удобства использования на практике. Из свойства  и теоремы о сильной единственности получаем оценку
и теоремы о сильной единственности получаем оценку

где  не зависит от k. Так как
не зависит от k. Так как  , то в каждой точке
, то в каждой точке  выполняется неравенство
выполняется неравенство

Отсюда и из (9.6), учитывая, что  для любой точки
для любой точки  получаем неравенство
получаем неравенство

из которого, в силу того, что  имеем
имеем

Пусть  Из (9,14) следует, что
Из (9,14) следует, что

Действительно, пусть  Тогда
Тогда

откуда

Аналогично доказывается второе неравенство.
Оценим сомножители в правой части неравенства (9.15),

Функция  возрастает при возрастании
возрастает при возрастании  (константа
(константа  следовательно,
следовательно,

Таким образом, для первого сомножителя имеем оценку

Оценим второй сомножитель. Для любой точки 

Тогда

Так как функция  возрастает при возрастании
возрастает при возрастании  то
то

 следовательно, имеем оценку
следовательно, имеем оценку

С помощью этих оценок неравенство (9.15) преобразуем к виду

Используя последнее неравенство и оценку снизу для  из (9.16), получим оценку
из (9.16), получим оценку


где с — константа, не зависящая от  Теорема доказана.
Теорема доказана.
Примеры допустимых множеств
Следующие множества, как легко проверить, допустимы:

Эти множества для алгебраических дробей со степенями, не превосходящими  для числителя и
для числителя и  для знаменателя, и
для знаменателя, и  рассмотрены впервые в
рассмотрены впервые в  [78],
[78],
Для алгебраических дробей множества:

где  некоторые положительные числа,
некоторые положительные числа, 

также допустимы при некоторых условиях на  (обозначение
(обозначение  здесь и далее означает целую часть числа а). Эти множества определяются меньшим числом неравенств, чем множества
здесь и далее означает целую часть числа а). Эти множества определяются меньшим числом неравенств, чем множества  в первых трех случаях — вдвое, в
в первых трех случаях — вдвое, в  случае — в четыре раза меньше минимального числа ограничений на знаменатель в
случае — в четыре раза меньше минимального числа ограничений на знаменатель в  Меньшее число неравенств, входящих в соответствующую задачу линейного программирования, может оказаться существенным при ее решении, ввид ите ационного характера алгоритма.
Меньшее число неравенств, входящих в соответствующую задачу линейного программирования, может оказаться существенным при ее решении, ввид ите ационного характера алгоритма.
Приведем формулировки из [54] теоремы, устанавливающей допустимость множеств  и соответствующие для этих множеств теоремы сходимости.
и соответствующие для этих множеств теоремы сходимости.
Теорема 4. Пусть  произвольное ограниченное множество,
произвольное ограниченное множество,  Множество допустимо, если
Множество допустимо, если  содержит не менее
содержит не менее  различной точки; множество
различной точки; множество  допустимо, если
допустимо, если  содержит хотя бы одну положительную точку; множество допустимо, если
содержит хотя бы одну положительную точку; множество допустимо, если  содержит хотя бы одну отрицательную точку; множество
содержит хотя бы одну отрицательную точку; множество  допустимо в следующих случаях:
допустимо в следующих случаях:  непустое симметричное относительно нуля множество, б)
непустое симметричное относительно нуля множество, б)  содержит симметричное относительно нуля подмножество
содержит симметричное относительно нуля подмножество  состоящее не менее, чем из
состоящее не менее, чем из  точки, в)
точки, в)  таково, что найдется
таково, что найдется  непересекающихся попарно симметричных относительно нуля интервалов, каждый из которых содержит хотя бы одну точку из множества
непересекающихся попарно симметричных относительно нуля интервалов, каждый из которых содержит хотя бы одну точку из множества 
Следствие 3. Если  конечное множество и для множества
конечное множество и для множества  выполняются соответствующие условия теоремы 4, то при
выполняются соответствующие условия теоремы 4, то при  алгоритм сходится.
алгоритм сходится.
Теорема 5. Пусть  конечное множество, содержащее не менее
конечное множество, содержащее не менее  точки,
точки,  допустимые множества,
допустимые множества,  множество алгебраических рациональных дробей. Если наилучшая для функции
множество алгебраических рациональных дробей. Если наилучшая для функции  дробь
дробь  является нормальной, то скорость сходимости алгоритма по крайней мере квадратичная, т.е. верна оценка (9.13).
является нормальной, то скорость сходимости алгоритма по крайней мере квадратичная, т.е. верна оценка (9.13).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
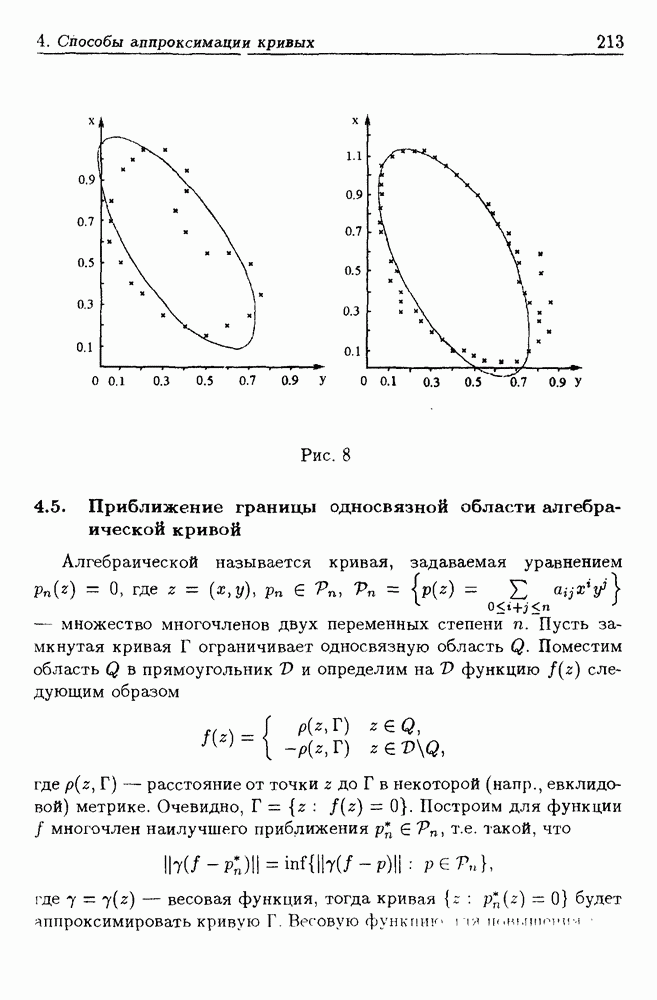
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
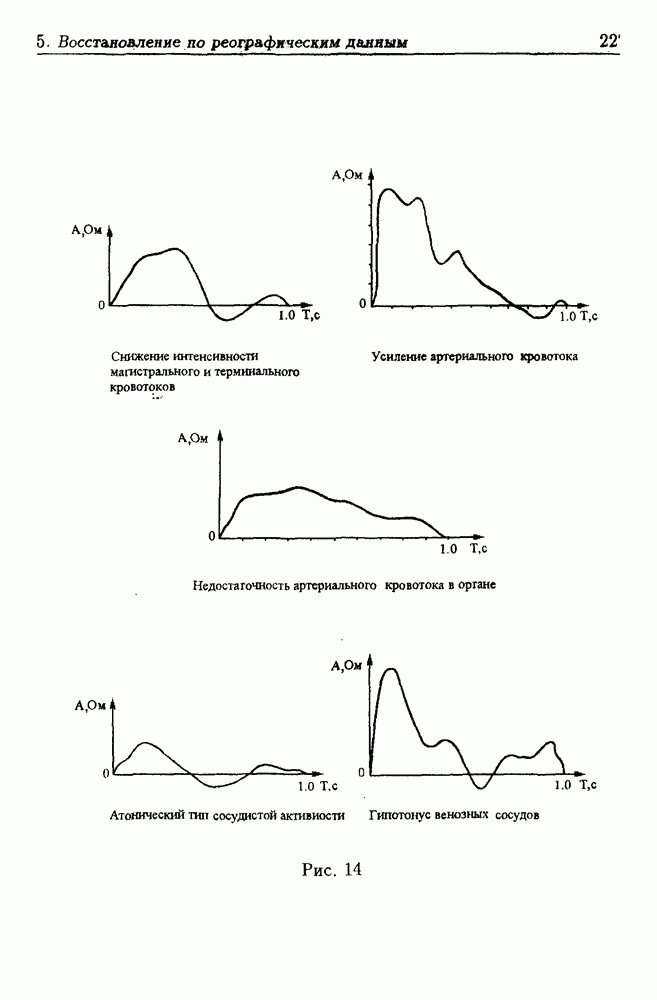
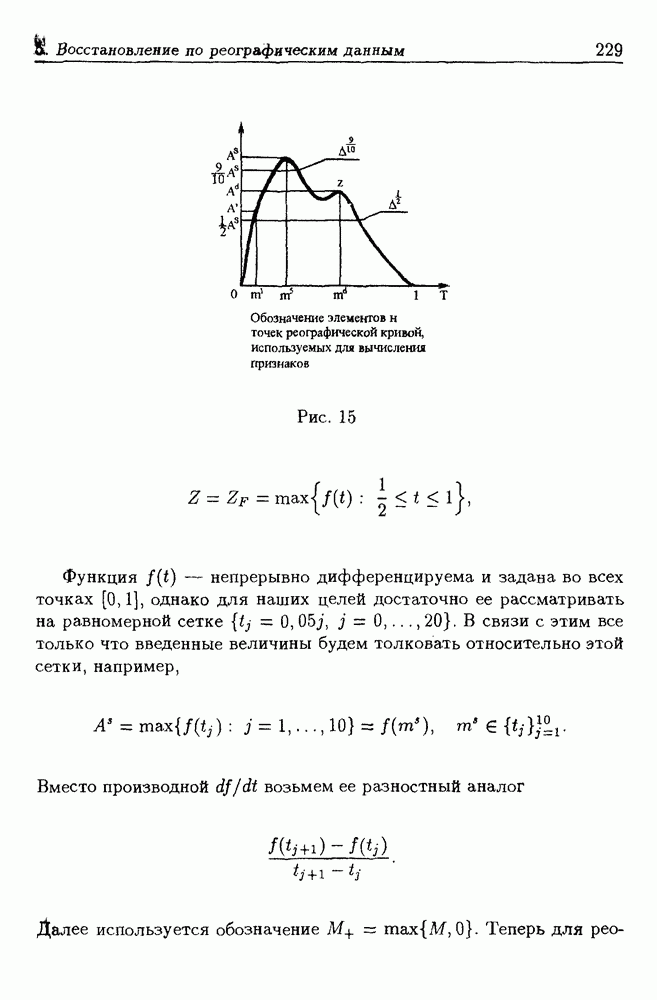
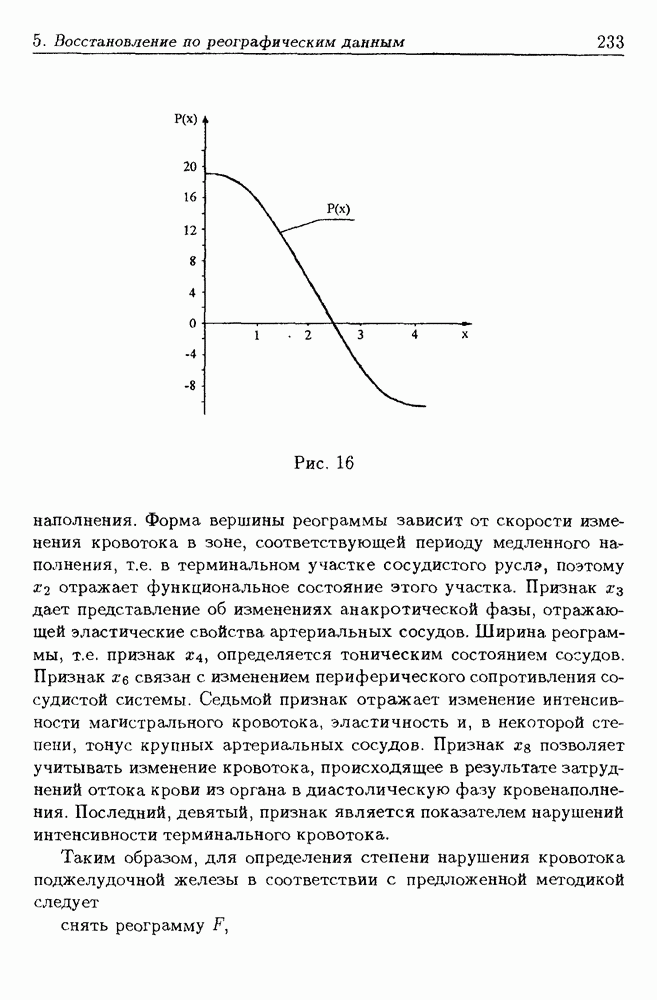
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
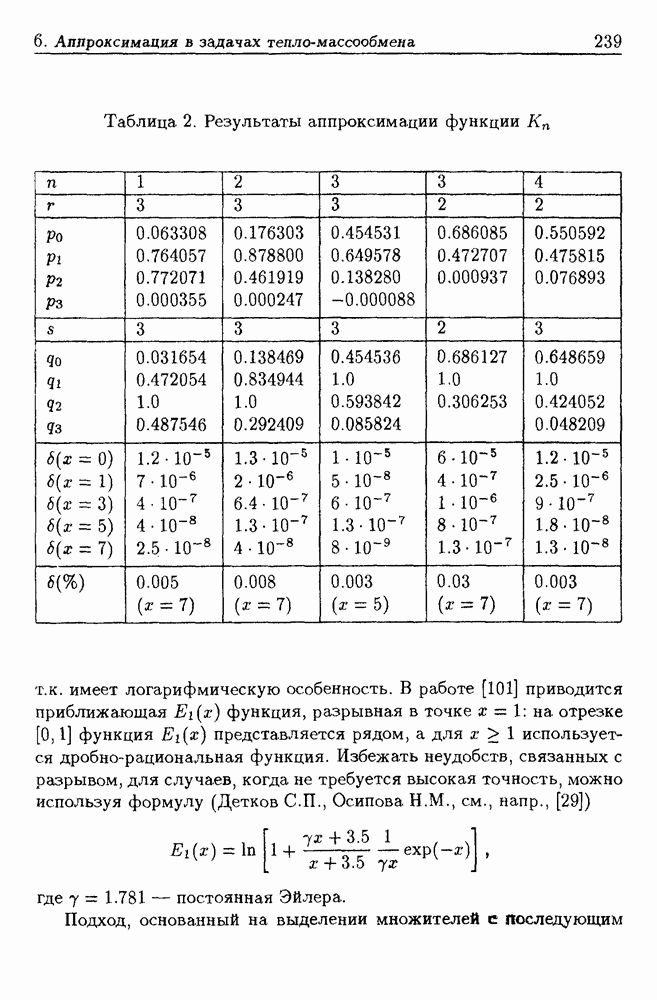
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
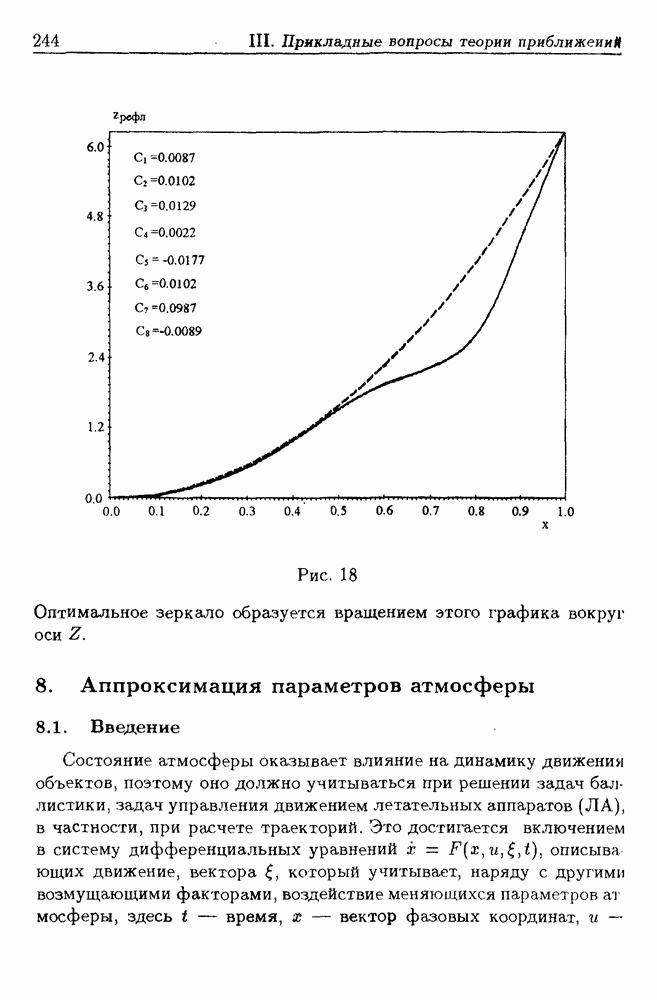
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
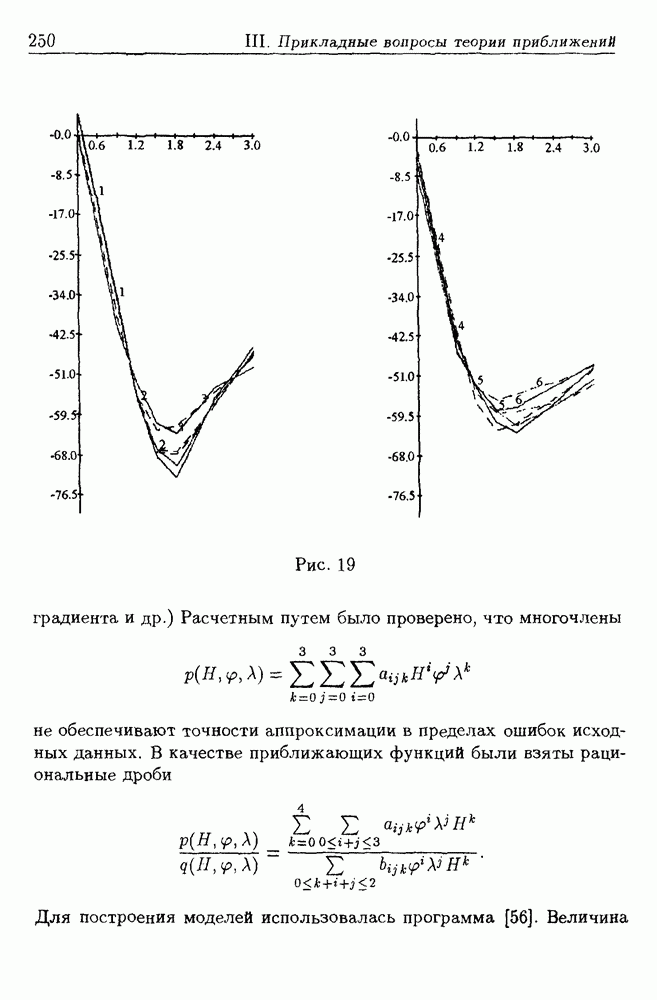
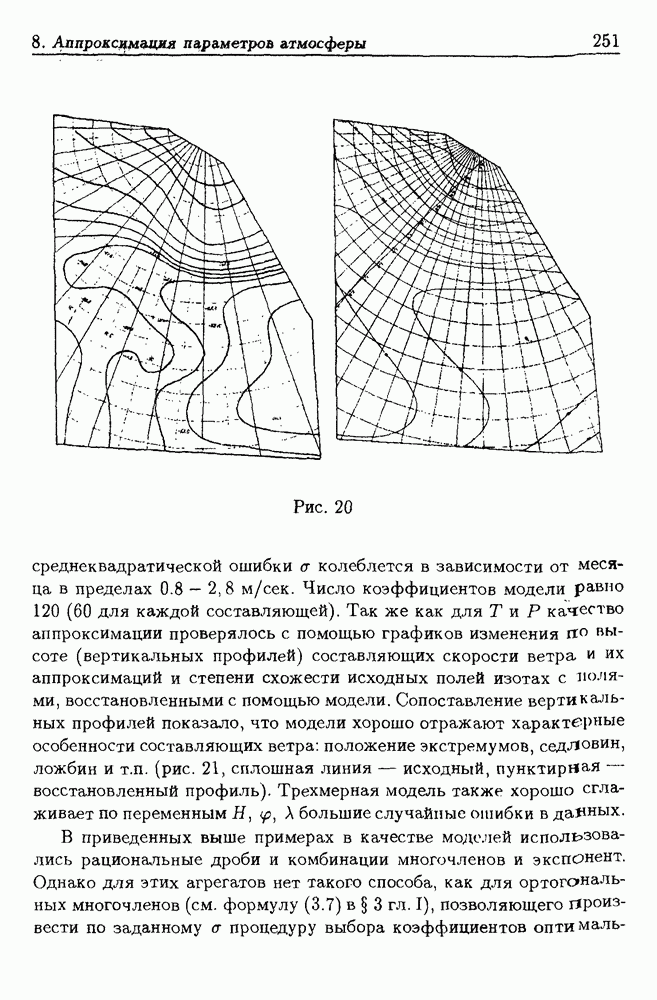
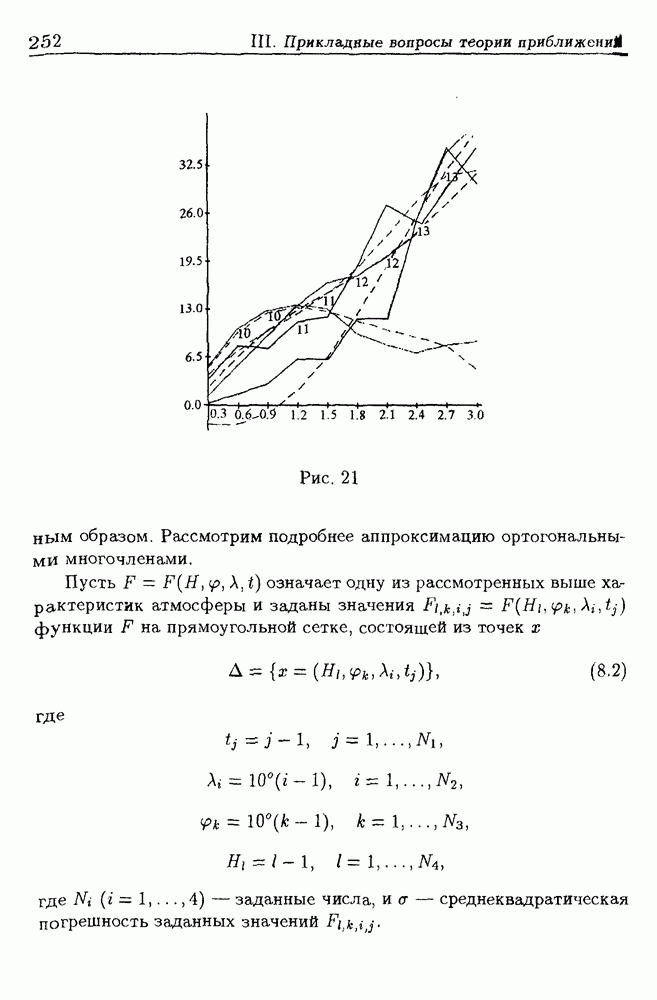
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ