| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
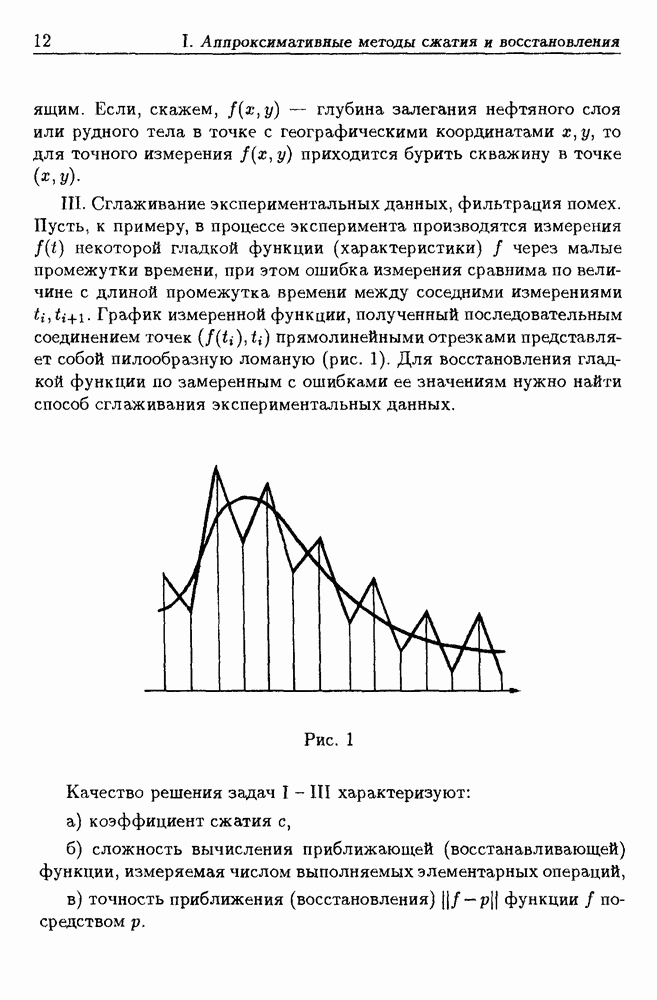
10.4. Сплайны на треугольных сетках
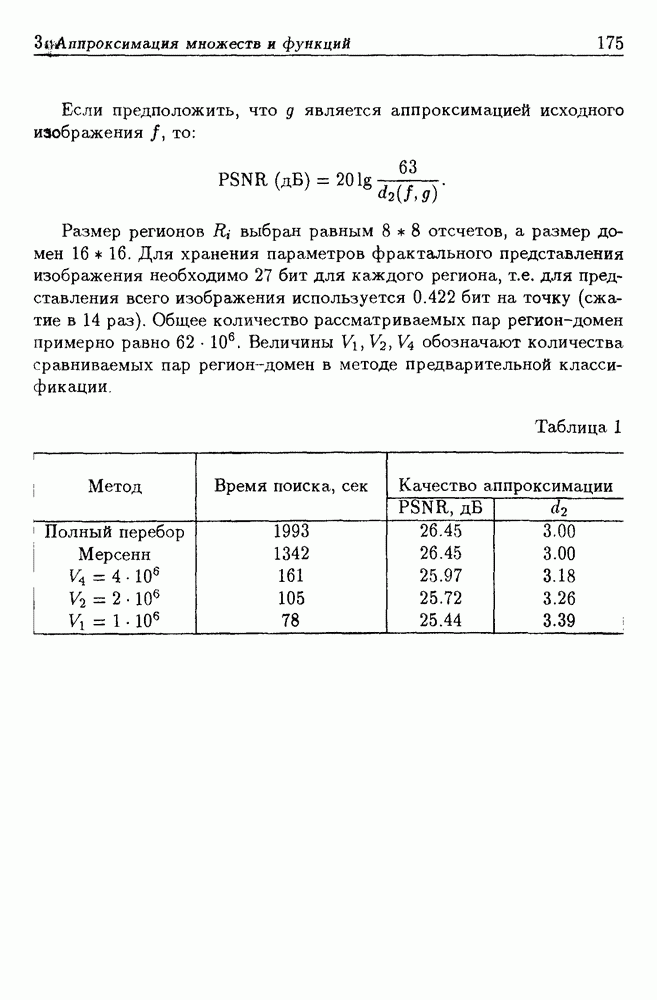
Если сплайны, определенные выше (см. (10.7), (10.8)), задаются набором коэффициентов то для триангулированной (разбитой на треугольники) области сплайны удобно задавать своими значениями в узлах. При построении сплайнов здесь будет использоваться интерполяционный многочлен Лагранжа заданной степени  Приведем формулу Лагранжа, пока не уточняя, как здесь понимается степень многочлена нескольких переменных.
Приведем формулу Лагранжа, пока не уточняя, как здесь понимается степень многочлена нескольких переменных.
Многочлены  степени
степени  называются фундаментальными многочленами интерполяции для сетки узлов
называются фундаментальными многочленами интерполяции для сетки узлов  если
если

Многочлен Лагранжа, интерполирующий значения  в точках
в точках  определяется формулой
определяется формулой

Как линейная комбинация многочленов степени  является многочленом степени
является многочленом степени  Многочлен
Многочлен  удовлетворяет условию интерполяции
удовлетворяет условию интерполяции

поскольку в сумме (10.9) слагаемое  для
для  обращается в нуль и равно
обращается в нуль и равно  при
при  Формула Лагранжа позволяет свести задачу построения многочлена, интерполирующего в точках заданные значения
Формула Лагранжа позволяет свести задачу построения многочлена, интерполирующего в точках заданные значения  к задаче поиска системы фундаментальных многочленов интерполяции
к задаче поиска системы фундаментальных многочленов интерполяции 
Начнем со случая сплайнов от двух переменных. Пусть область  представлена в виде объединения конечного числа треугольников
представлена в виде объединения конечного числа треугольников  так, что пересечением двух разных треугольников могут быть либо пустое множество, либо общая вершина, либо общая сторона (рис. 9а). Такое представление называется триангуляцией. На каждом из треугольников
так, что пересечением двух разных треугольников могут быть либо пустое множество, либо общая вершина, либо общая сторона (рис. 9а). Такое представление называется триангуляцией. На каждом из треугольников  сплайн
сплайн  задается как многочлен степени
задается как многочлен степени  вида
вида

Многочлен (10.10) имеет  коэффициентов, поэтому для его однозначного определения надо задать его значения на сетке, состоящей из такого же количества точек треугольника. Из дальнейшего изложения будет ясно, что сетку узлов на
коэффициентов, поэтому для его однозначного определения надо задать его значения на сетке, состоящей из такого же количества точек треугольника. Из дальнейшего изложения будет ясно, что сетку узлов на  целесообразно образовать как пересечение двух пучков параллельных сторонам треугольника
целесообразно образовать как пересечение двух пучков параллельных сторонам треугольника  прямых (рис. 9б), разбивающих соответствующие противоположные стороны на
прямых (рис. 9б), разбивающих соответствующие противоположные стороны на  равных частей. Число
равных частей. Число 

Рис. 9
 вершины треугольника
вершины треугольника  Точки указанной регулярной сетки удобно записать следующим образом
Точки указанной регулярной сетки удобно записать следующим образом

где  Произвольную же точку
Произвольную же точку  из
из  можно представить в виде:
можно представить в виде:

Координаты точек  называются барицентрическими координатами.
называются барицентрическими координатами.
Рассмотрим подробнее случай малых  Пусть
Пусть  многочлен степени 1
многочлен степени 1

однозначно определяется условиями интерполяции в вершинах  треугольника
треугольника 

и по формуле Лагранжа (10.9)

Фундаментальные полиномы интерполяции могут быть заданы в форме (рис. 10а)

Построив на каждом треугольнике  многочлен (10.10), на области
многочлен (10.10), на области  будем иметь кусочно-линейную функцию
будем иметь кусочно-линейную функцию  (сплайн)
(сплайн)


Рис. 10
интерполирующую значения  в вершинах треугольников
в вершинах треугольников  (рис. 106). Нетрудно видеть, что сплайн
(рис. 106). Нетрудно видеть, что сплайн  является непрерывной функцией на
является непрерывной функцией на 
2. Пусть  многочлен степени 2
многочлен степени 2

однозначно определяется условиями интерполяции в вершинах  треугольника
треугольника  и серединах его сторон
и серединах его сторон

Используя обозначение (10.11), можно записать  По формуле Лагранжа
По формуле Лагранжа

Фундаментальные многочлены интерполяции  (верхний индекс 2 в обозначениях означает, что
(верхний индекс 2 в обозначениях означает, что  многочлены 2-й степени) могут быть выражены через многочлены (10.13) первой степени. Продемонстрируем это на примере номеров
многочлены 2-й степени) могут быть выражены через многочлены (10.13) первой степени. Продемонстрируем это на примере номеров  (рис. 11)
(рис. 11)


Рис. 11
Построив на каждом треугольнике  многочлен (10.14), на всей области
многочлен (10.14), на всей области  получим кусочно-параболическую функцию (параболический сплайн)
получим кусочно-параболическую функцию (параболический сплайн)

интерполирующую заданные значения  в вершинах и серединах сторон треугольников
в вершинах и серединах сторон треугольников  Сплайн
Сплайн  является непрерывной на
является непрерывной на  функцией. Непрерывность сплайна
функцией. Непрерывность сплайна  внутри частичных треугольников очевидна. Напомним, триангуляция области
внутри частичных треугольников очевидна. Напомним, триангуляция области  такова, что пересекающиеся треугольники могут иметь либо общую вершину, либо общую сторону. Другие случаи исключены. Проверим непрерывность сплайна на общей стороне двух треугольников. Пусть
такова, что пересекающиеся треугольники могут иметь либо общую вершину, либо общую сторону. Другие случаи исключены. Проверим непрерывность сплайна на общей стороне двух треугольников. Пусть  смежная сторона для частичных треугольников
смежная сторона для частичных треугольников  соответствующие треугольникам
соответствующие треугольникам  многочлены. Будем рассматривать каждый из многочленов
многочлены. Будем рассматривать каждый из многочленов  как функцию, заданную на отрезке
как функцию, заданную на отрезке 

Другими словами,  есть сужение многочлена
есть сужение многочлена  на отрезок
на отрезок  Ясно, что
Ясно, что  многочлены второй степени. Поскольку они интерполируют в трех точках одни и те же значения
многочлены второй степени. Поскольку они интерполируют в трех точках одни и те же значения 

то они тождественны. Равенство многочленов  на стороне
на стороне  означает непрерывность сплайна
означает непрерывность сплайна  на
на  Непрерывность сплайна
Непрерывность сплайна  на
на  установлена.
установлена.
3) При  многочлен
многочлен  на
на  имеет 10 коэффициентов, регулярная сетка построена посредством разбиения сторон треугольника на три равные части, содержит 10 узлов: из них 9 на сторонах треугольника (точки
имеет 10 коэффициентов, регулярная сетка построена посредством разбиения сторон треугольника на три равные части, содержит 10 узлов: из них 9 на сторонах треугольника (точки  со свойством
со свойством  и одну в центре треугольника —
и одну в центре треугольника —  Фундаментальные многочлены интерполяции строятся из многочленов (10.13). Так, для узлов
Фундаментальные многочлены интерполяции строятся из многочленов (10.13). Так, для узлов  выглядят следующим образом
выглядят следующим образом

Построенная на  кусочно-кубическая функция непрерывна.
кусочно-кубическая функция непрерывна.
Подобная конструкция легко осуществляется для произвольного  результате получается непрерывная сплайн-функция
результате получается непрерывная сплайн-функция  Свойство дифференцируемости этой функции не гарантируется, поскольку в узлах сетки задаются лишь значения сплайна, но не его производных. В случае
Свойство дифференцируемости этой функции не гарантируется, поскольку в узлах сетки задаются лишь значения сплайна, но не его производных. В случае  на
на  можно построить гладкий сплайн. Изложим способ построения такого сплайна. Многочлен пятой степени имеет 21 коэффициент. Зададим в вершинах треугольника значения многочлена и его производных до второго порядка:
можно построить гладкий сплайн. Изложим способ построения такого сплайна. Многочлен пятой степени имеет 21 коэффициент. Зададим в вершинах треугольника значения многочлена и его производных до второго порядка:

и в середине каждой из сторон зададим значения производной  в направлении вектора, ортогонального стороне и направленного, скажем, вовнутрь треугольника. Приведенные интерполяционные условия однозначно определяют многочлен
в направлении вектора, ортогонального стороне и направленного, скажем, вовнутрь треугольника. Приведенные интерполяционные условия однозначно определяют многочлен  Построим такой многочлен
Построим такой многочлен
для каждого треугольника  На стороне, обозначим ее через В, общей для двух соседних треугольников, сплайн
На стороне, обозначим ее через В, общей для двух соседних треугольников, сплайн  непрерывен, поскольку
непрерывен, поскольку  многочлен пятой степени, однозначно задается своим значением
многочлен пятой степени, однозначно задается своим значением  значениями 1-й, 2-й производных на концах стороны В. Производная
значениями 1-й, 2-й производных на концах стороны В. Производная  вдоль нормали к стороне В является многочленом четвертой степени, однозначно определяемым но его значениям на концах отрезка и в его середине и значениям его производной на концах отрезка. Поэтому непрерывна на В.
вдоль нормали к стороне В является многочленом четвертой степени, однозначно определяемым но его значениям на концах отрезка и в его середине и значениям его производной на концах отрезка. Поэтому непрерывна на В.
Схема построения непрерывного сплайна  двух переменных, изложенная выше, может быть реализована и в случае произвольной конечной размерности.
двух переменных, изложенная выше, может быть реализована и в случае произвольной конечной размерности.
Пусть область  представляет собой объединение конечного числа симплексов
представляет собой объединение конечного числа симплексов  при этом для любых
при этом для любых  возможны лишь следующие случаи:
возможны лишь следующие случаи:  пусто, является общей вершиной, общим ребром, общей гранью симплексов
пусто, является общей вершиной, общим ребром, общей гранью симплексов  На каждом из симплексов
На каждом из симплексов  сплайн
сплайн  будет многочленом вида
будет многочленом вида

Этот многочлен содержит  коэффициентов. Для определения коэффициентов построим на
коэффициентов. Для определения коэффициентов построим на  регулярную сетку, узлами которой являются точки пересечения трех пучков параллельных
регулярную сетку, узлами которой являются точки пересечения трех пучков параллельных  граням плоскостей, разделяющих ребра симплекса на
граням плоскостей, разделяющих ребра симплекса на  равных частей (см. рис. 12). Построенная сетка состоит из
равных частей (см. рис. 12). Построенная сетка состоит из  точек.
точек.
Задавая значения многочлена  в узлах сетки, мы однозначно определяем многочлен
в узлах сетки, мы однозначно определяем многочлен  Это проще сделать с помощью интерполяционной формулы Лагранжа (10.9). При
Это проще сделать с помощью интерполяционной формулы Лагранжа (10.9). При  фундаментальными многочленами интерполяции являются многочлены
фундаментальными многочленами интерполяции являются многочлены


Рис. 12
где

Используя  нетрудно построить фундаментальные многочлены интерполяции при
нетрудно построить фундаментальные многочлены интерполяции при  для указанной регулярной сетки.
для указанной регулярной сетки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
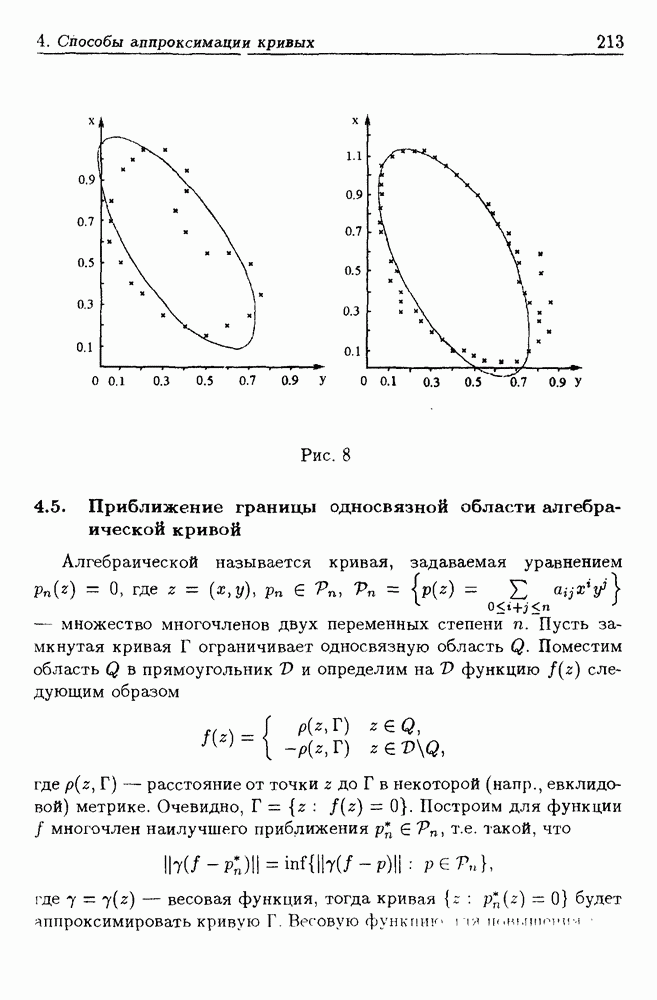
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
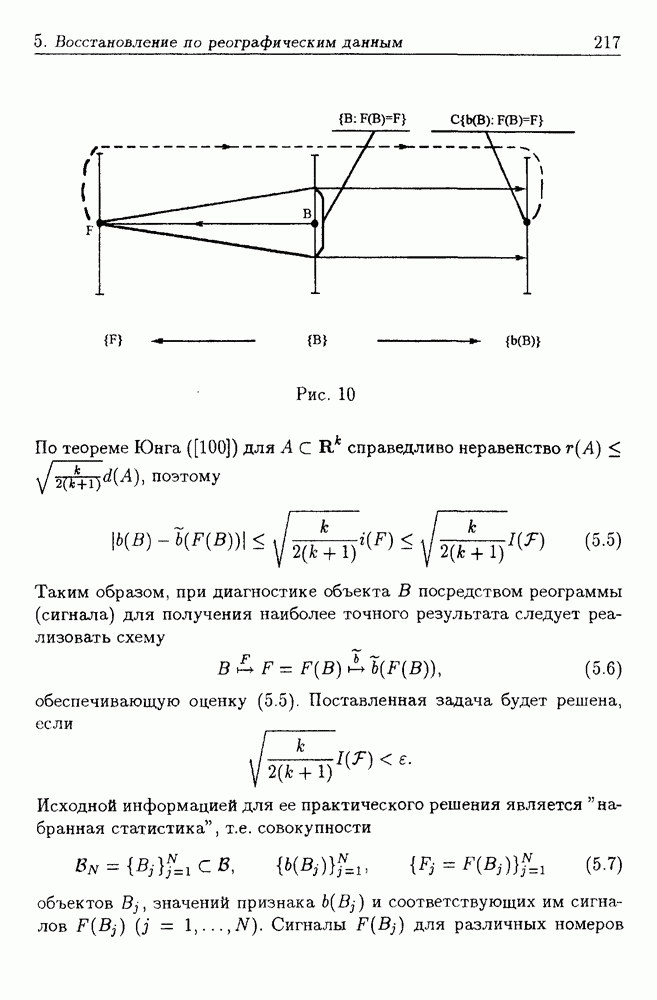
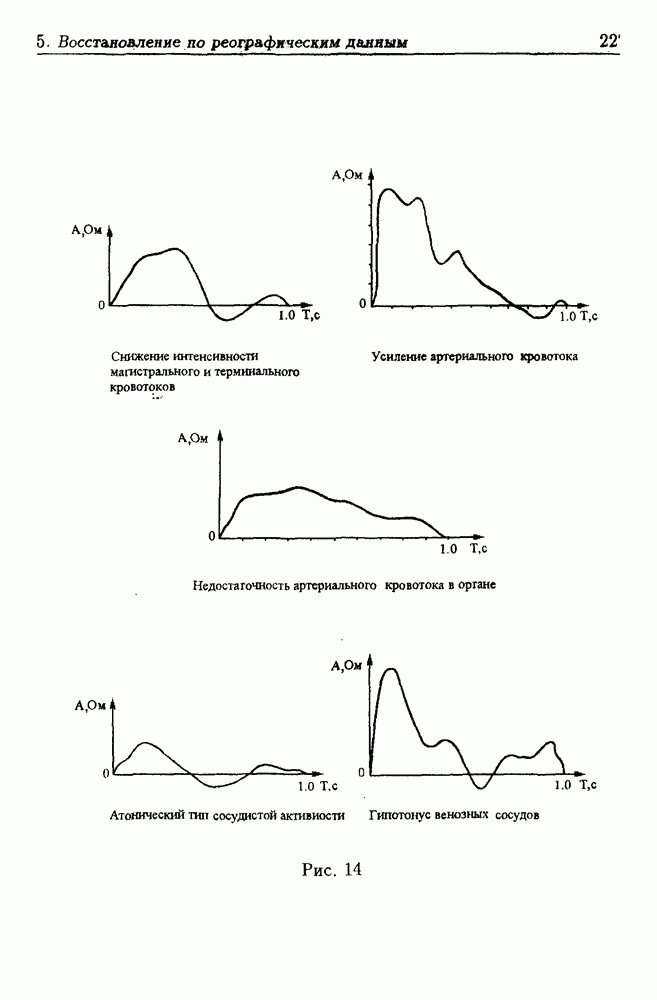
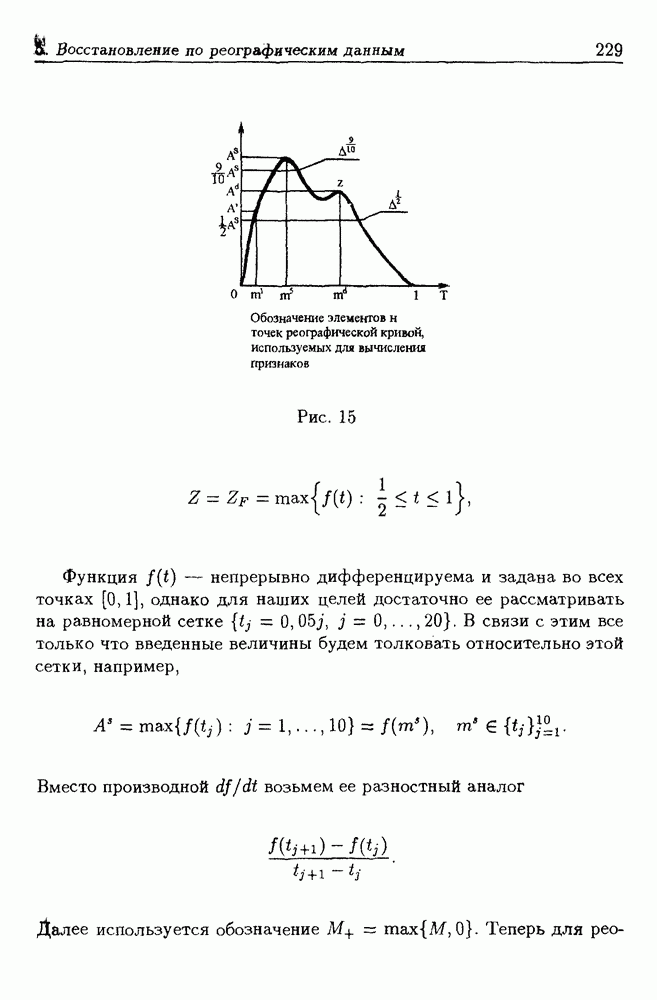
- 5. Восстановление информации по реографическим данным
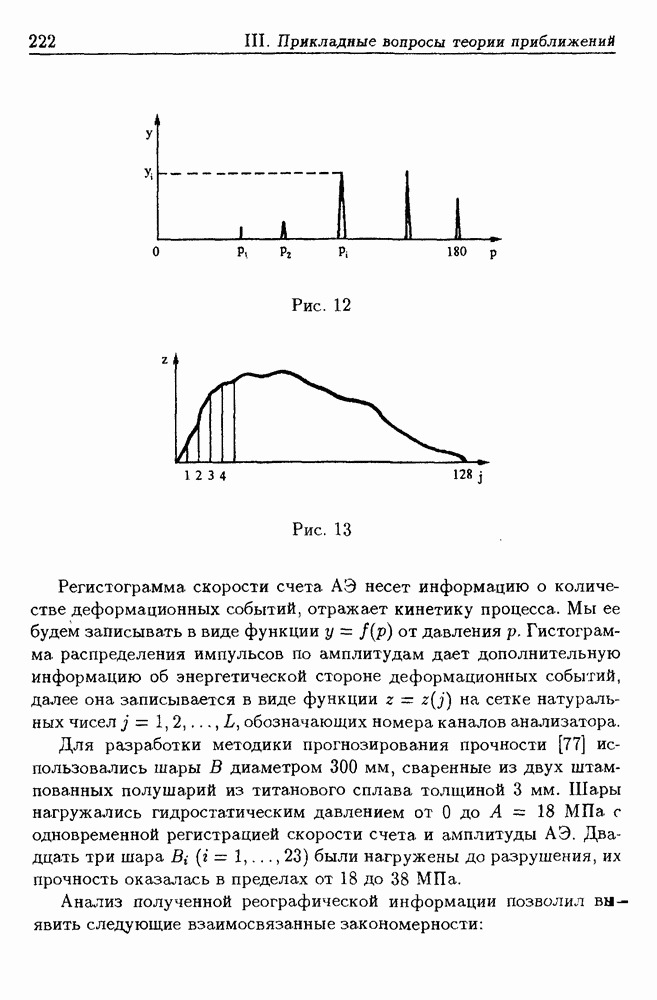
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
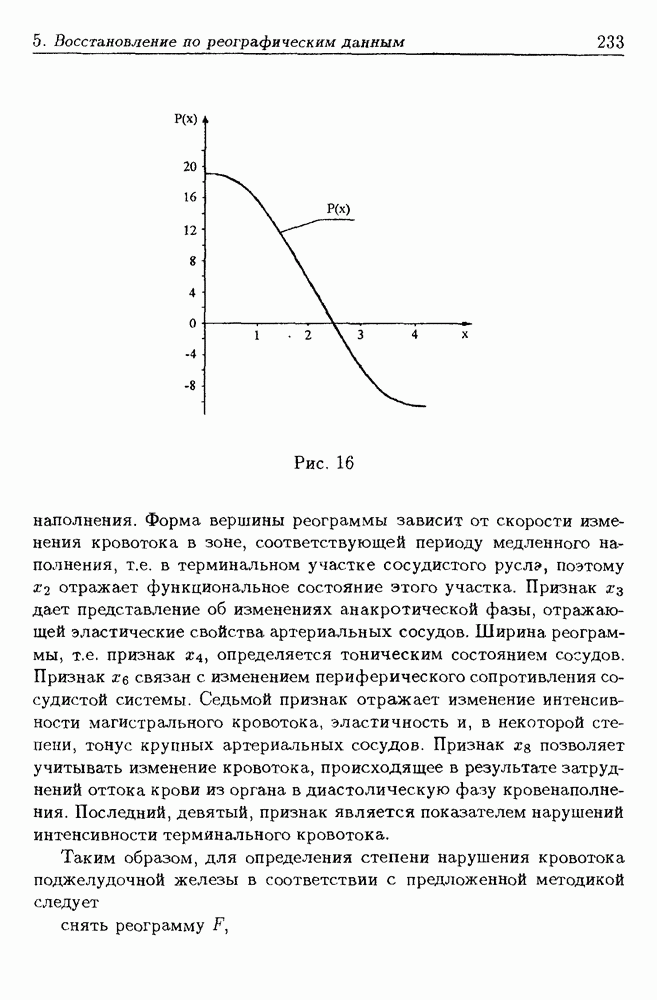
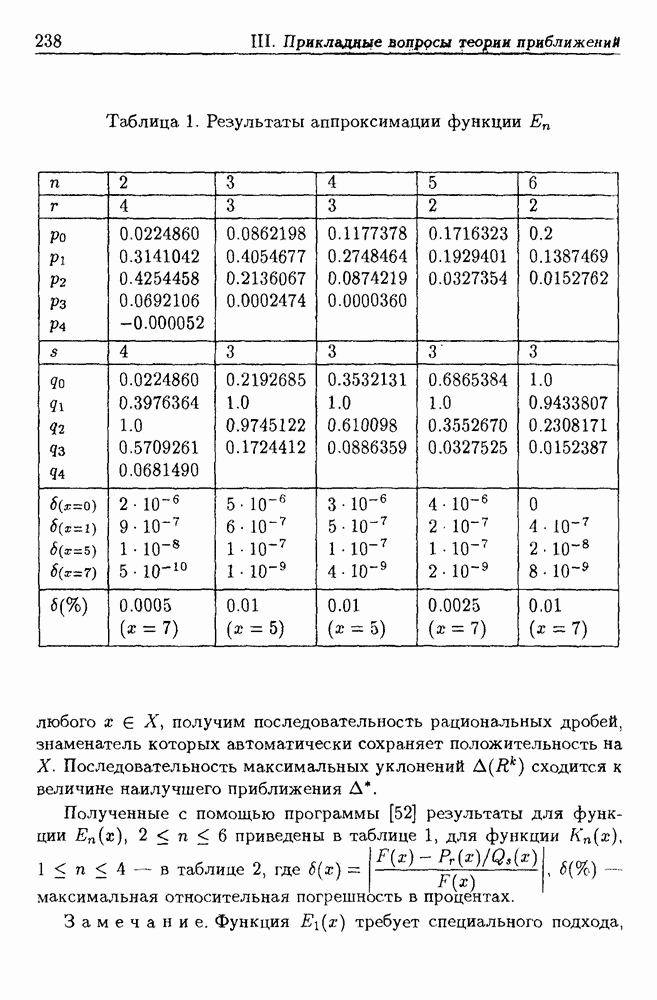
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
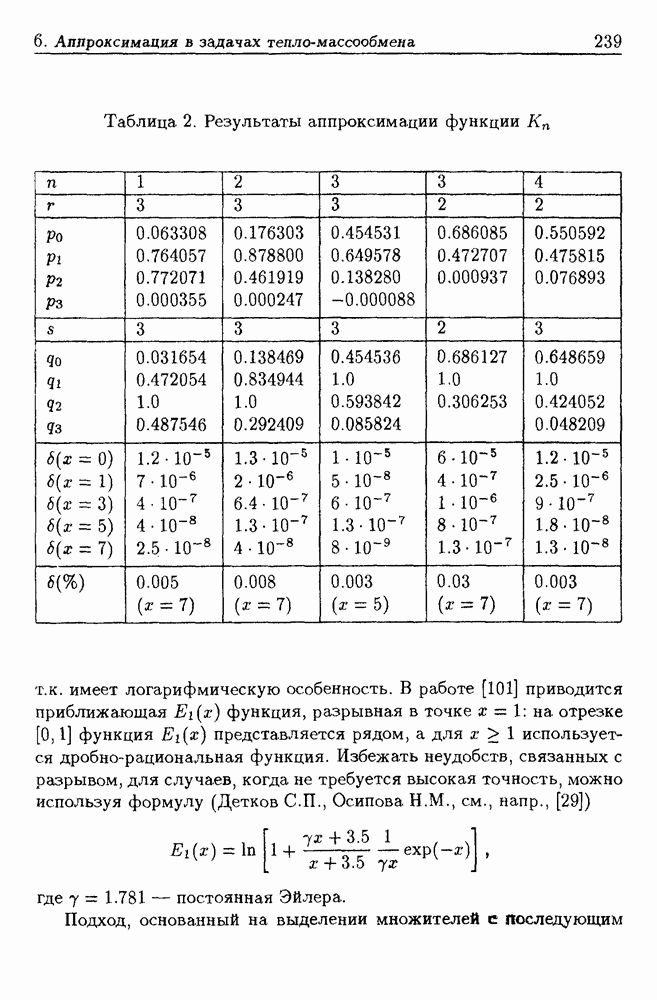
- 6.2. Формулы для функций …
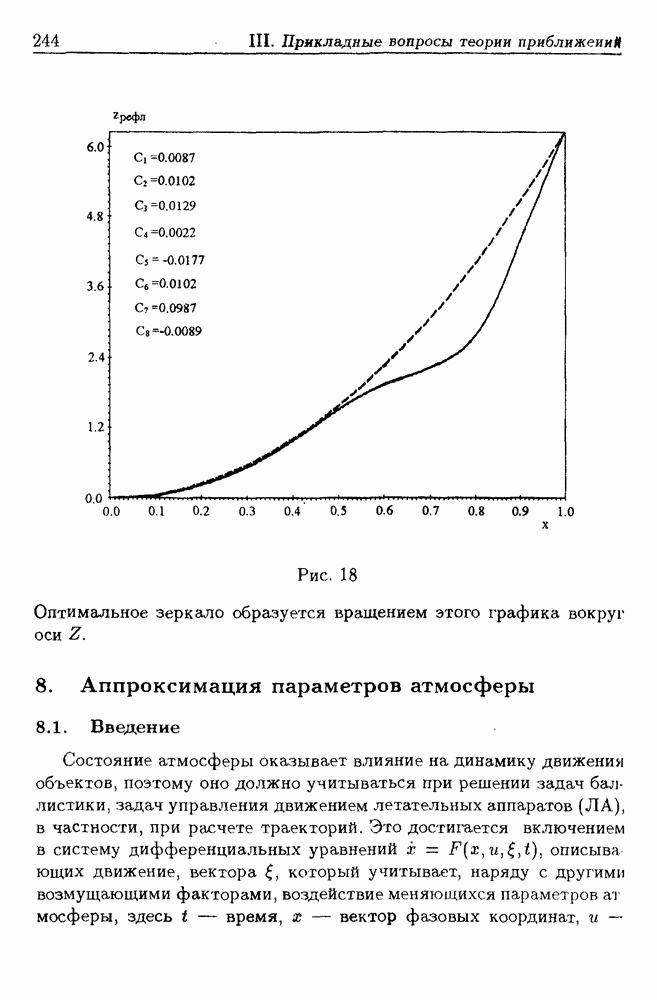
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
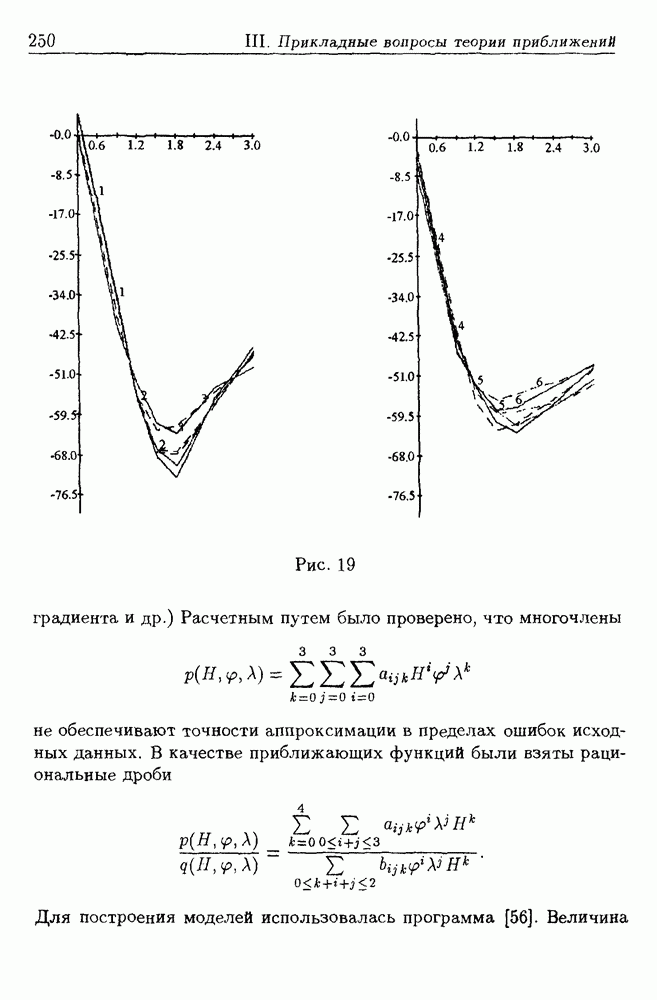
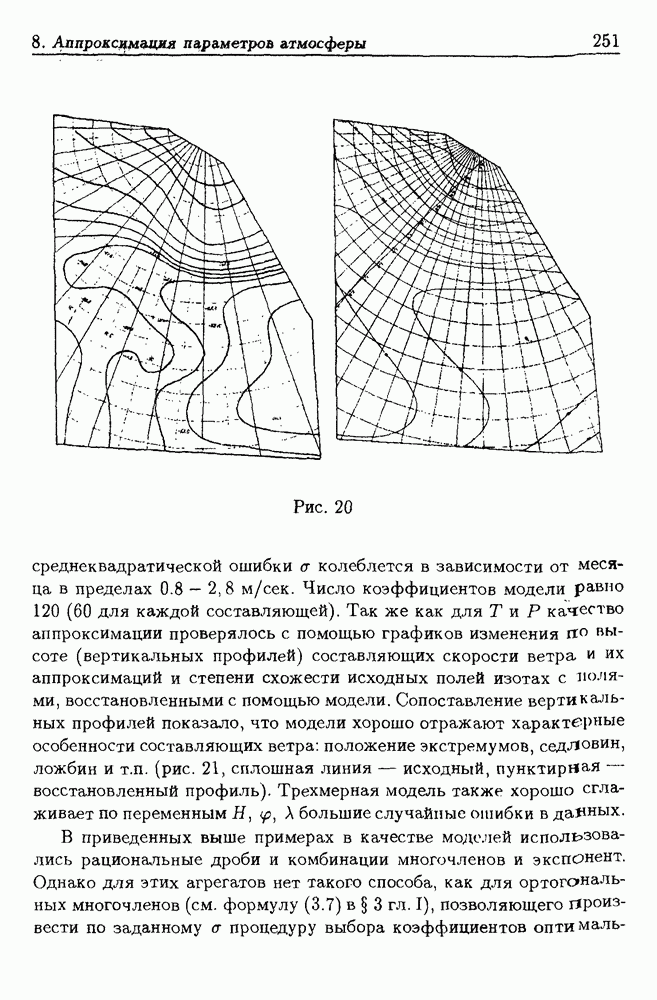
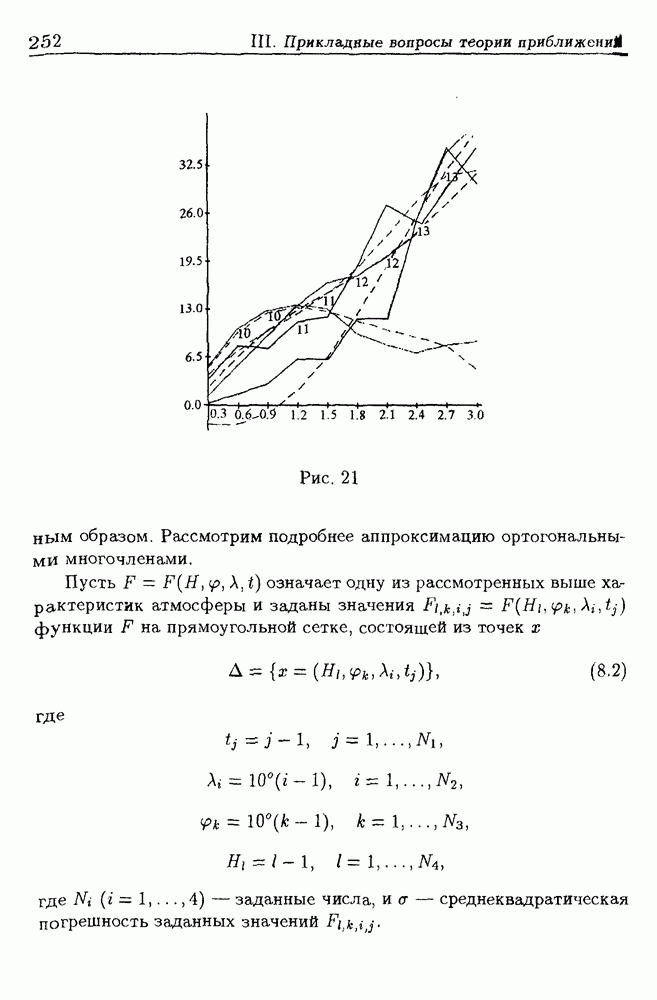
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ