| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
Информация о геофизическом поле  предназначенная для записи на бортовой компьютер, обычно задается в виде таблиц заранее
предназначенная для записи на бортовой компьютер, обычно задается в виде таблиц заранее
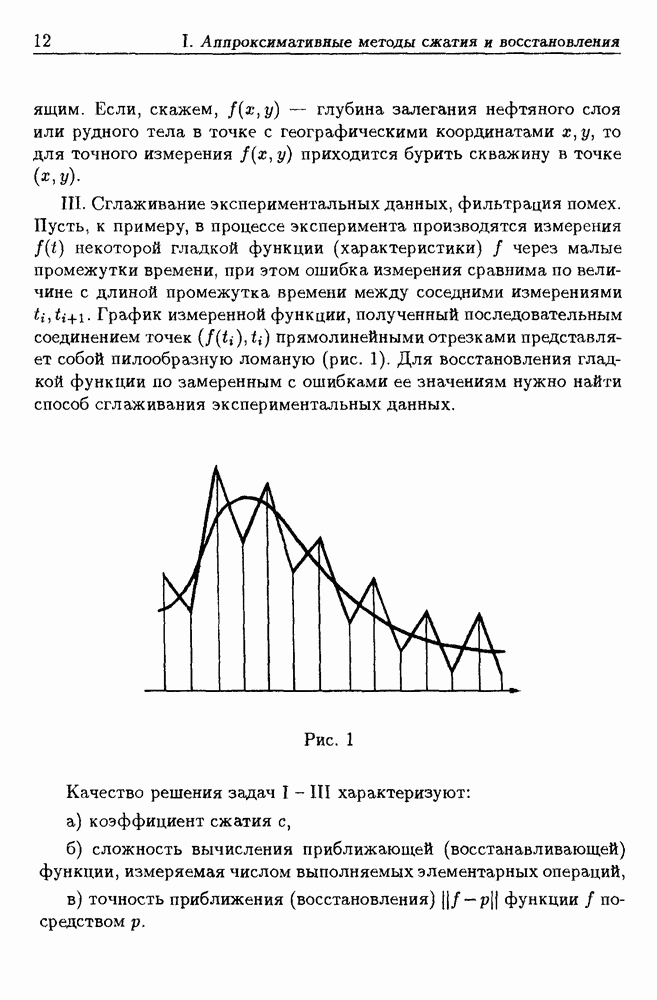
измеренных значений поля в узлах достаточно густой сетки. Хранение таблиц требует больших объемов памяти. Так, информация о высоте земной поверхности предгорий и горных участков с большим числом вершин и впадин содержит сотни тысяч чисел.
Один из возможных способов преодоления этой трудности — приближение поля как функции географических координат посредством функции  являющейся комбинацией элементарных функций. Вместо (1.3) на бортовом компьютере решается следующая задача
являющейся комбинацией элементарных функций. Вместо (1.3) на бортовом компьютере решается следующая задача

Тогда хранению подлежат коэффициенты этой функции  а значения поля в конкретных точках определяются по мере надобности приближенно вычислением
а значения поля в конкретных точках определяются по мере надобности приближенно вычислением  по координатам точек. Такой способ позволяет существенно сократить объем хранимой информации, однако может привести к увеличению, по сравнению с табличным способом, времени вычисления значения поля в точке.
по координатам точек. Такой способ позволяет существенно сократить объем хранимой информации, однако может привести к увеличению, по сравнению с табличным способом, времени вычисления значения поля в точке.
Для использования этого способа предварительно необходимо
1) выбрать класс V функций, предназначенный для приближения геофизического поля,
2) определить метод поиска аппроксимирующей функции  для конкретного геофизического поля.
для конкретного геофизического поля.
Набор возможных классов V перечислен в 1. гл.  Что касается методов поиска аппроксимирующей функции, то с учетом специфики задачи навигации естественно использовать следующие:
Что касается методов поиска аппроксимирующей функции, то с учетом специфики задачи навигации естественно использовать следующие:
а) наилучшее приближение в метрике  поля
поля  классом
классом 
б) наилучшее приближение поля  классом V в норме
классом V в норме 
в) специальные методы, позволяющие минимизировать ошибку привязки.
Выбор метрики пространства  обосновывается тем, что геофизическое поле
обосновывается тем, что геофизическое поле  может быть задано со случайными ошибками и при замере фрагмента
может быть задано со случайными ошибками и при замере фрагмента  могут появиться большие ошибки измерения. Выбор метрики
могут появиться большие ошибки измерения. Выбор метрики  диктуется оценкой (1.7) ошибки привязки через
диктуется оценкой (1.7) ошибки привязки через  Наиболее привлекательны специальные методы минимизации ошибки привязки. В настоящем параграфе на примере поля высот земного рельефа сравниваются следующие методы аппроксимации:
Наиболее привлекательны специальные методы минимизации ошибки привязки. В настоящем параграфе на примере поля высот земного рельефа сравниваются следующие методы аппроксимации:
L) билинейная интерполяция,
Р) кусочно-многочленная аппроксимация (разрывные сплайны) в 
Т) кусочно-тригонометрическая интерполяция,  кусочно-многочленная аппроксимация в
кусочно-многочленная аппроксимация в  с последующей интерполяцией,
с последующей интерполяцией,
S) аппроксимация параболическими В-сплайнами в  Предположим, что непрерывная функция
Предположим, что непрерывная функция  определена в прямоугольной области
определена в прямоугольной области

и известны ее значения и узлах равномерной сетки

С шагом 
Билинейная интерполяция на разреженной сетке. Зададим натуральное число  и построим разреженную сетку
и построим разреженную сетку

с шагом  где
где  целая часть числа а. Эта сетка разбивает область
целая часть числа а. Эта сетка разбивает область  на частичные квадраты со стороной
на частичные квадраты со стороной 

Внутри каждого частичного квадрата  приближающую функцию
приближающую функцию  возьмем в виде интерполяционного многочлена 2-й степени
возьмем в виде интерполяционного многочлена 2-й степени

где


— интерполяционные многочлены 1-й степени по переменной 
Тогда на области  получим непрерывную кусочно-параболическую функцию
получим непрерывную кусочно-параболическую функцию

интерполирующую значения функции  в узлах сетки
в узлах сетки 
Р. Кусочно-многочленная аппроксимация степени  Пусть
Пусть  натуральные числа. На каждом частичном квадрате
натуральные числа. На каждом частичном квадрате

построим многочлен

наилучшего среднеквадратического приближения, т.е. многочлен, реализующий минимум

В итоге, на области  получим кусочно-многочленную функцию, аппроксимирующую исходную функцию
получим кусочно-многочленную функцию, аппроксимирующую исходную функцию  Отметим, что эта функция на прямых
Отметим, что эта функция на прямых  терпит разрыв.
терпит разрыв.
Т. Кусочно-тригонометрическая аппроксимация строится подобно кусочно-многочленной аппроксимации. Задается натуральное число  выделяются частичные квадраты
выделяются частичные квадраты  и на каждом из них определяется тригонометрический полином вида
и на каждом из них определяется тригонометрический полином вида

или

наилучшего среднеквадратического приближения.
Р. Кусочно-многочленная аппроксимация с последующей интерполяцией. Сравнение описанных аппроксимаций показывает, что метод  позволяет строить непрерывную приближающую функцию, но на каждом квадрате
позволяет строить непрерывную приближающую функцию, но на каждом квадрате  использует значение функции
использует значение функции  лишь в вершинах квадрата и не учитывает информацию
лишь в вершинах квадрата и не учитывает информацию  во внутренних узлах, поэтому при больших
во внутренних узлах, поэтому при больших  (начиная с некоторого) не может обеспечить требуемую точность аппроксимации. Методы
(начиная с некоторого) не может обеспечить требуемую точность аппроксимации. Методы  , напротив, дают на каждом квадрате Пнаилучшую полиномиальную аппроксимацию, используя значения функции во всех точках сетки
, напротив, дают на каждом квадрате Пнаилучшую полиномиальную аппроксимацию, используя значения функции во всех точках сетки  попавших в квадрат
попавших в квадрат  но построенная этим методом функция на области
но построенная этим методом функция на области  а точнее, на смежных сторонах частичных квадратов, не является непрерывной. Предлагаемый здесь метод является промежуточным, он в определенной мере объединяет полезные свойства методов
а точнее, на смежных сторонах частичных квадратов, не является непрерывной. Предлагаемый здесь метод является промежуточным, он в определенной мере объединяет полезные свойства методов  .
.
Зададим три натуральных числа  Построим квадраты
Построим квадраты  размером
размером  где
где 

 и внутри каждого
и внутри каждого  выделим квадрат
выделим квадрат  размером
размером 


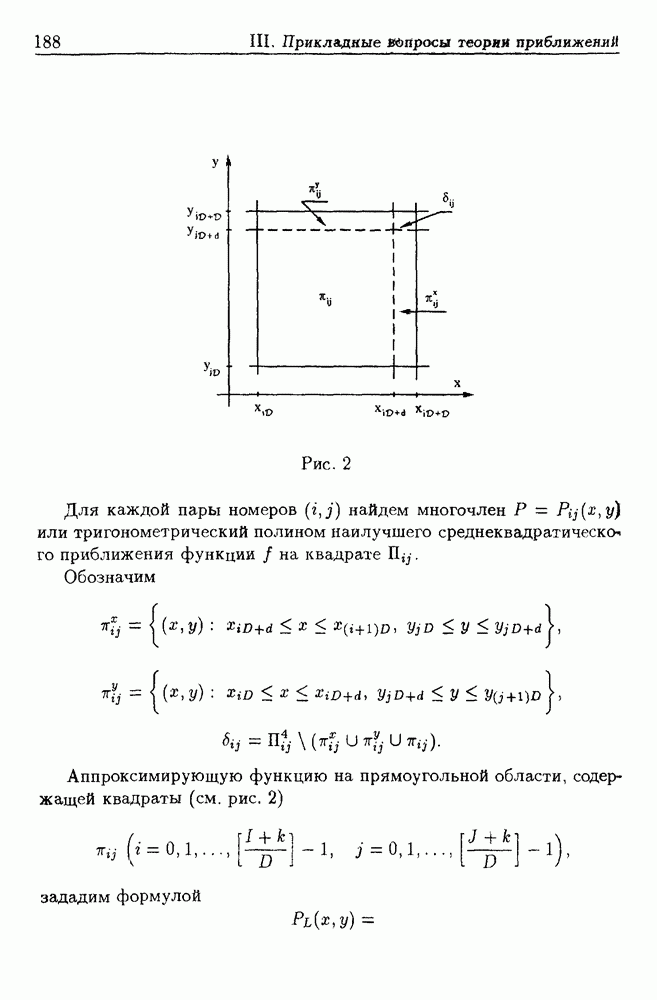
Рис. 2
Для каждой пары номеров  найдем многочлен
найдем многочлен  или тригонометрический полином наилучшего среднеквадратического приближения функции
или тригонометрический полином наилучшего среднеквадратического приближения функции  на квадрате
на квадрате 
Обозначим

Аппроксимирующую функцию на прямоугольной области, содержащей квадраты (см. рис. 2)

зададим формулой


где

Другими словами,  совпадает с
совпадает с  на квадрате
на квадрате  на прямоугольниках
на прямоугольниках  определяется линейной интерполяцией значений двух соседних многочленов
определяется линейной интерполяцией значений двух соседних многочленов  ветственно и билинейной интерполяцией значений четырех соседних многочленов
ветственно и билинейной интерполяцией значений четырех соседних многочленов  в случае, когда точка
в случае, когда точка  принадлежит квадрату
принадлежит квадрату 
Сплайн-аппроксимация. Зададим натуральное число с? и  берем на оси абсцисс сетку узлов сплайна
берем на оси абсцисс сетку узлов сплайна

и на оси ординат сетку

где номера  выбраны из условий
выбраны из условий

В сетку  включены через
включены через  штук узлы исходной сетки
штук узлы исходной сетки  и дополнительно два узла
и дополнительно два узла  слева и два узла
слева и два узла  справа.
справа.
Аналогично устроена сетка  Обозначим
Обозначим

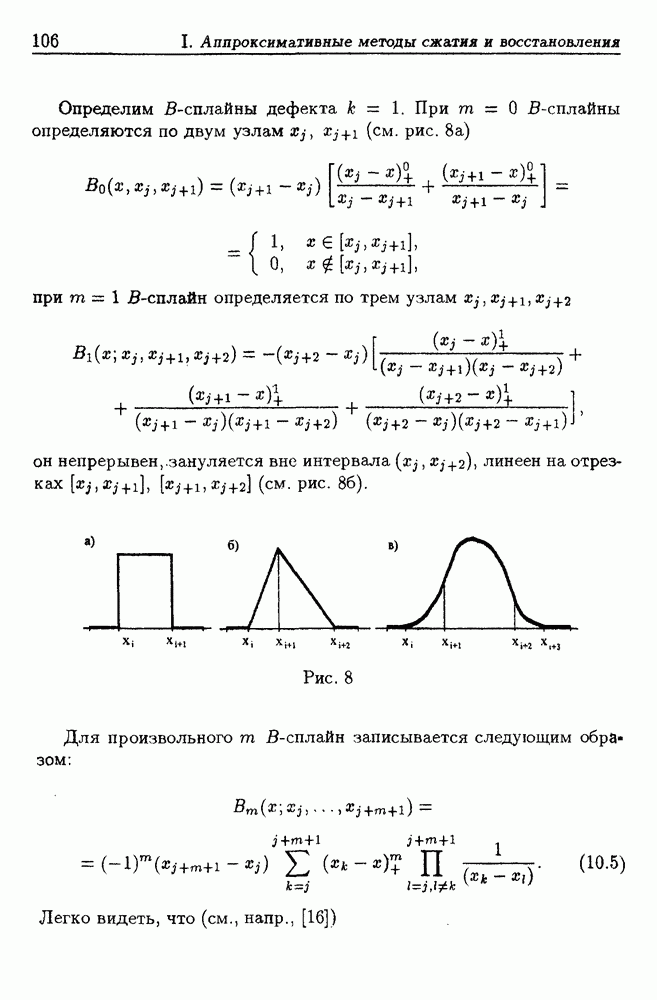
Напомним, что параболическим  -сплайном (см., гл. I, § 10) называется функция
-сплайном (см., гл. I, § 10) называется функция

где

Носителем функции  является отрезок
является отрезок  функция дифференцируема на всей оси, а ее график склеен из трех кусков парабол.
функция дифференцируема на всей оси, а ее график склеен из трех кусков парабол.
В качестве аппроксимирующей функции на области  возьмем сплайн-функцию
возьмем сплайн-функцию

реализующую минимум

Качество метода аппроксимации оценивается (см., гл. I, п. 1) с учетом
сложности вычисления аппроксимирующей функции, степени сжатия информации,
величины уклонения приближаемой и приближающей функции, точности привязки. Сложность вычисления аппроксимирующей функции существенно влияет на скорость решения задачи привязки. Она определяется числом используемых при вычислении функции в точке
операций:  выделение целой части
выделение целой части  числа, вычисление функции
числа, вычисление функции  выбор числа из таблицы. Для каждой из функций L, Р, Т, P, S вычисления начинаются с определения индексов
выбор числа из таблицы. Для каждой из функций L, Р, Т, P, S вычисления начинаются с определения индексов  соответствующего квадрата
соответствующего квадрата  содержащего точку
содержащего точку  и выбора по
и выбора по  из двумерной таблицы значения высоты
из двумерной таблицы значения высоты  либо коэффициентов полинома. Так, для билинейной интерполяции определяются
либо коэффициентов полинома. Так, для билинейной интерполяции определяются

на что расходуется 2 операции взятия целой части числа, 2 операции  и 2 операции
и 2 операции  и выбираются из исходной таблицы значения
и выбираются из исходной таблицы значения  Приведем число операций, необходимых для вычисления самих функций. В приводимой ниже таблице
Приведем число операций, необходимых для вычисления самих функций. В приводимой ниже таблице  - порядок многочленов на 11-,
- порядок многочленов на 11-,

Коэффициенты сжатия информации. Коэффициентом сжатия информации (будем обозначать его через С) называется отношение объемов памяти, необходимой для хранения исходной информации и сжатой информации. Для хранения как численног о значения высоты  в точке, так и значения одного коэффициента приближающей функции требуется одинаковый объем памяти — один байт.
в точке, так и значения одного коэффициента приближающей функции требуется одинаковый объем памяти — один байт.
Область  где
где  содержит
содержит  точек исходной сетки
точек исходной сетки  а прореженная сетка состоит из
а прореженная сетка состоит из
 точек, следовательно,
точек, следовательно,

Прямоугольная область, образованная частичными квадратами  где
где  , содержит
, содержит  точек исходной сетки. Хранению подлежат коэффициенты многочленов: по
точек исходной сетки. Хранению подлежат коэффициенты многочленов: по  коэффициентов
коэффициентов  и
и  В тригонометрическом случае надо хранить также числа
В тригонометрическом случае надо хранить также числа  Учитывая это, получим
Учитывая это, получим

В том случае, когда наряду с коэффициентами полиномов в ЭВМ хранятся значения полиномов в вершинах квадратов  (таких значений
(таких значений  имеем
имеем

Полагая здесь  получаем коэффициент сжатия для
получаем коэффициент сжатия для  -методов.
-методов.
Функция  содержит -
содержит -  коэффициентов, поэтому
коэффициентов, поэтому 

Подчеркнем, что в методе  число элементарных операций одинаково для различных коэффициентов сжатия.
число элементарных операций одинаково для различных коэффициентов сжатия.
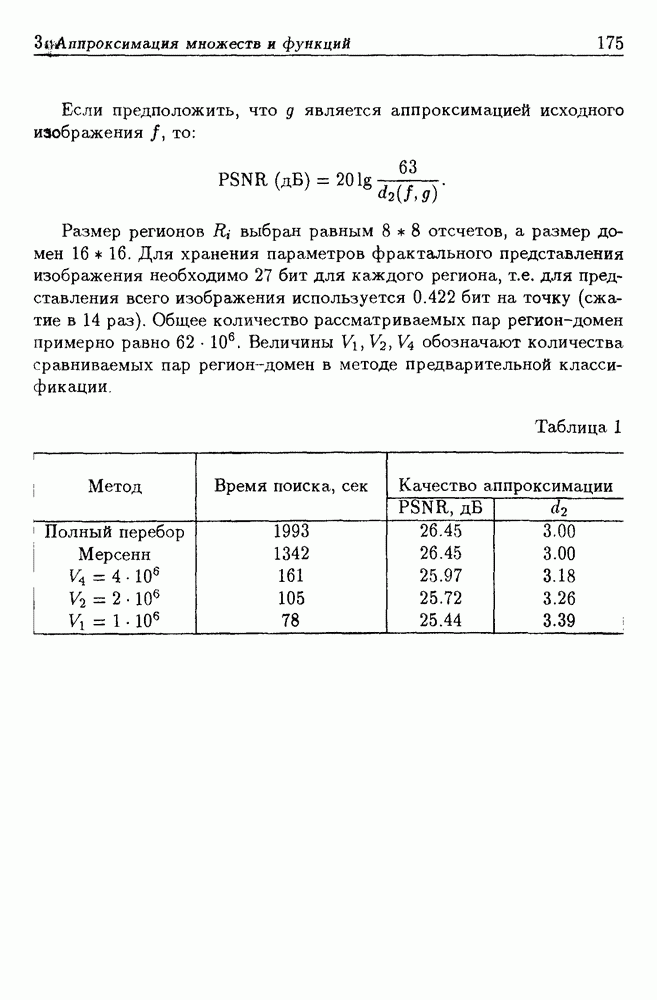
Приведем число элементарных операций для рассматриваемых методов при коэффициенте сжатия, близком к 30 и соответствующие этому коэффициенту сжатия величины среднеквадратических
уклонения а и ошибки привязки  полученные в результате численных расчетов (см. следующий пункт):
полученные в результате численных расчетов (см. следующий пункт):

где  среднеквадратические ошибки привязки координат х, у.
среднеквадратические ошибки привязки координат х, у.
Результаты численных расчетов. Перечисленными методами приближения была проведена аппроксимация двух участков рельефа земной поверхности: 1-й рельеф содержит как гладкие, так и гористые районы, его размеры  рельеф гладкий, его размеры
рельеф гладкий, его размеры  В обоих случаях шаг
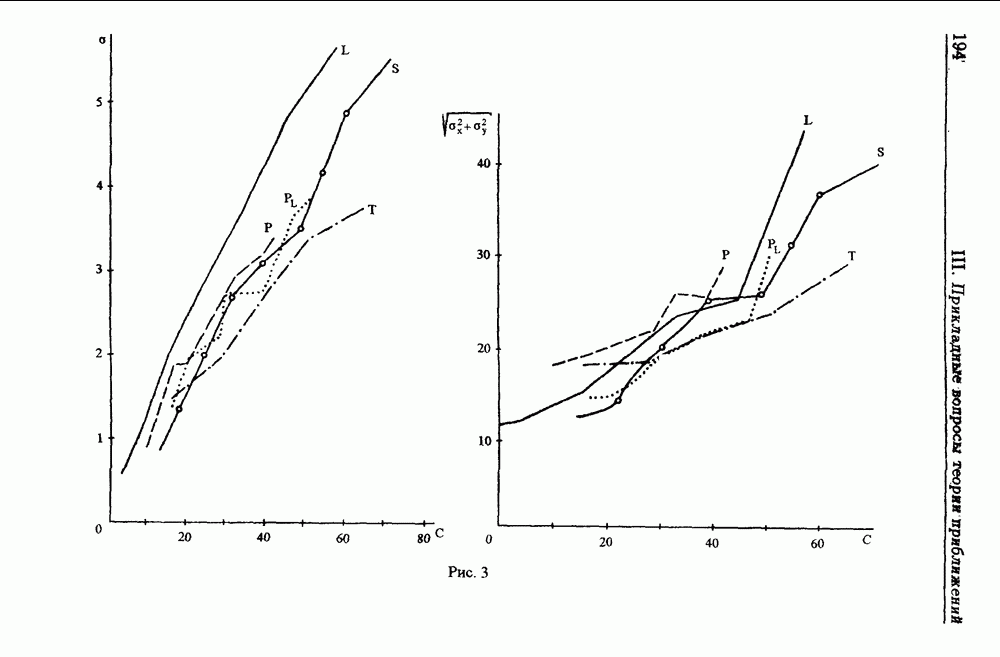
В обоих случаях шаг  Полученные аппроксимирующие функции опробованы в задаче привязки по набору измеренных высот. Результаты расчетов иллюстрируются графиками (рис. 3), на которых С — коэффициент сжатия информации, а — величина среднеквадратического приближения,
Полученные аппроксимирующие функции опробованы в задаче привязки по набору измеренных высот. Результаты расчетов иллюстрируются графиками (рис. 3), на которых С — коэффициент сжатия информации, а — величина среднеквадратического приближения,  среднеквадратические ошибки привязки координат х, у по серии из 100 испытаний при случайных шумовых помехах.
среднеквадратические ошибки привязки координат х, у по серии из 100 испытаний при случайных шумовых помехах.
Необходимо отметить, что правильный выбор метода сжатия информации (аппроксимации) является основой успешного решения задачи навигации. При выборе метода следует учитывать особенности исходной задачи, в частности, возможности ЭВМ (объем памяти, быстродействие) и характер приближаемой функции. Для каждого из предложенных методов, по-видимому, имеется класс поверхностей, на которых он дает лучшую (в сравнении с остальными) аппроксимацию 
Повышение точности аппроксимации достигается ценой усложнения приближающей функции, увеличения времени вычисления одного значения функции и, как показывает расположение графиков  на рис. 3, не всегда улучшает качество решения задачи навигации.
на рис. 3, не всегда улучшает качество решения задачи навигации.

(кликните для просмотра скана)
Здесь наряду с точностью могут играть роль такие свойства приближающей функции, как непрерывность, дифференцируемость.
Качественного решения задачи аппроксимации обычно удается достичь перебором большого числа вариантов разбиения области на частичные подобласти и различных степеней приближающий полиномов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
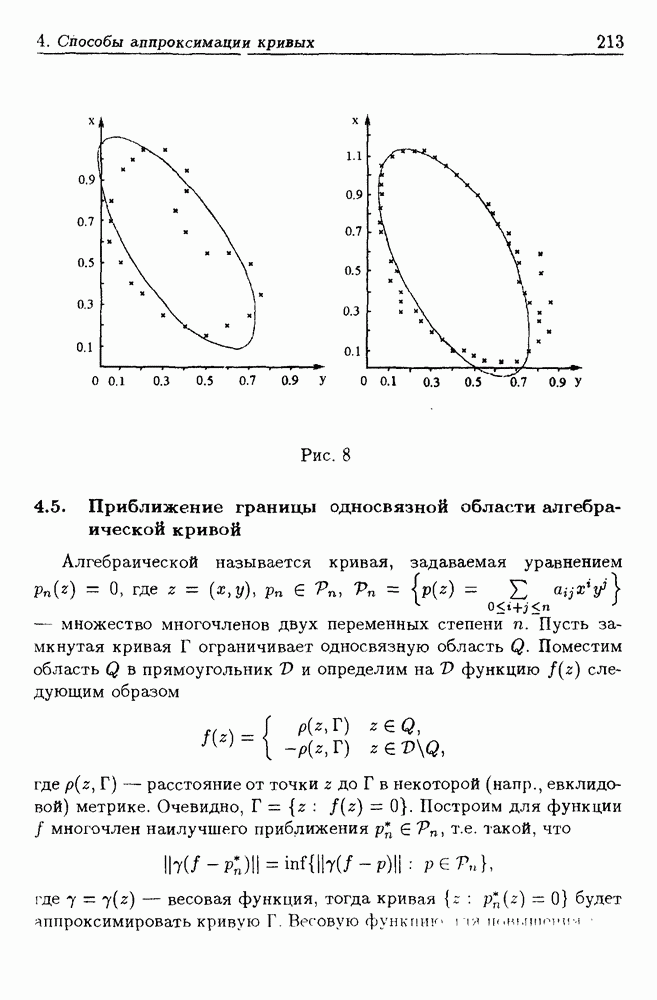
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
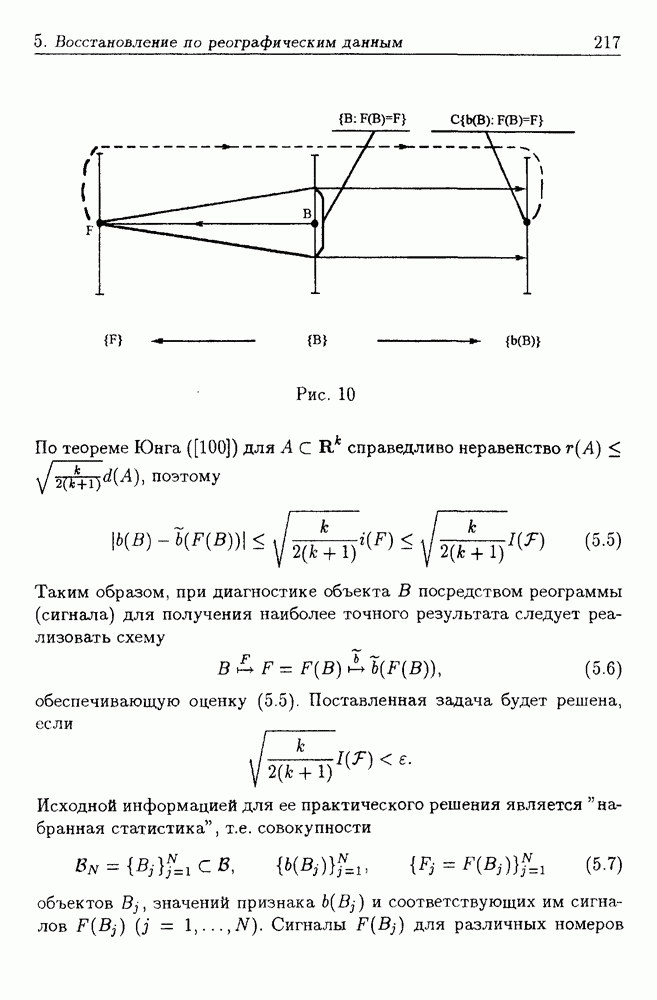
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ