| << Предыдущий параграф |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
КОММЕНТАРИИ
Глава 1.
§ 5. Свойство сильной единственности полиномов наилучшего приближения при аппроксимации непрерывных вещественных функций из  алгебраическими многочленами степени меньше
алгебраическими многочленами степени меньше  было установлено Н.Г. Чеботаревым [72] в 1943 г. К сожалению, этот результат Н.Г. Чеботарева оказался прочно забытым и на него к настоящему моменту есть только одна ссылка в [48]. В 1963 г. свойство сильной единственности было переоткрыто Ньюменом и Шапиро [113] в более общем случае приближения непрерывных вещественных функций из
было установлено Н.Г. Чеботаревым [72] в 1943 г. К сожалению, этот результат Н.Г. Чеботарева оказался прочно забытым и на него к настоящему моменту есть только одна ссылка в [48]. В 1963 г. свойство сильной единственности было переоткрыто Ньюменом и Шапиро [113] в более общем случае приближения непрерывных вещественных функций из  где
где  компакт, конечномерным чебышевским подпространством. Сильная единственность при аппроксимации рациональными дробями
компакт, конечномерным чебышевским подпространством. Сильная единственность при аппроксимации рациональными дробями  в пространстве
в пространстве  доказана Чини [89]. Свойство сильной единственности позволяет обосновывать сходимость алгоритмов ремезовского типа и получать оценки их скорости сходимости.
доказана Чини [89]. Свойство сильной единственности позволяет обосновывать сходимость алгоритмов ремезовского типа и получать оценки их скорости сходимости.
§ 10. Оценки скорости сходимости интерполяционных сплайнов, приведенные в п. 10.5, установлены Ю.Н. Субботиным.
Глава 3.
§ 1., п. 1.2. А.В. Нятиным неравенство (1.9) установлено только в случае 
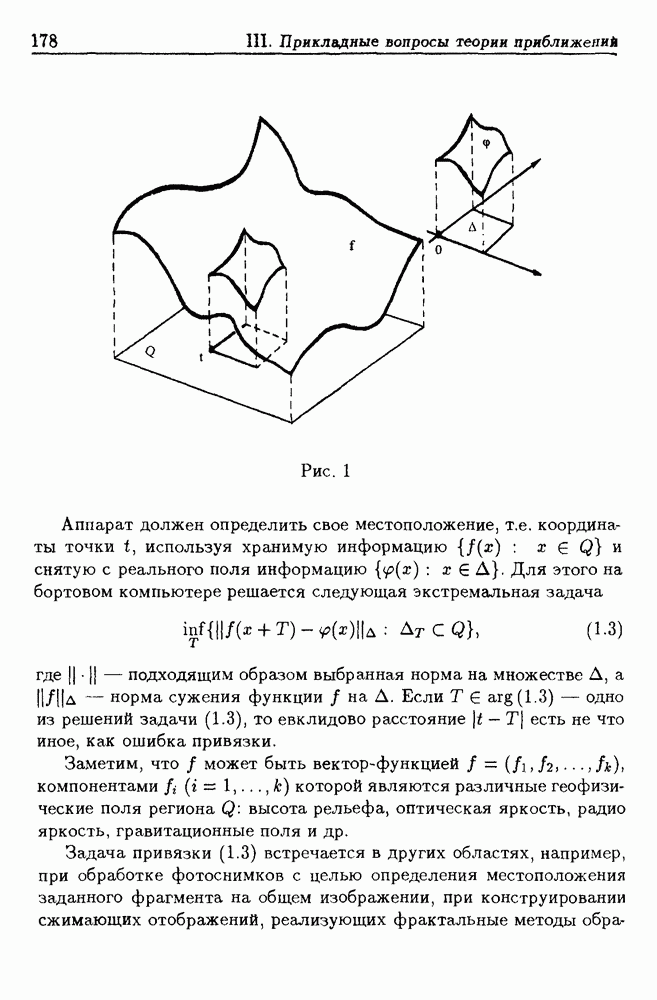
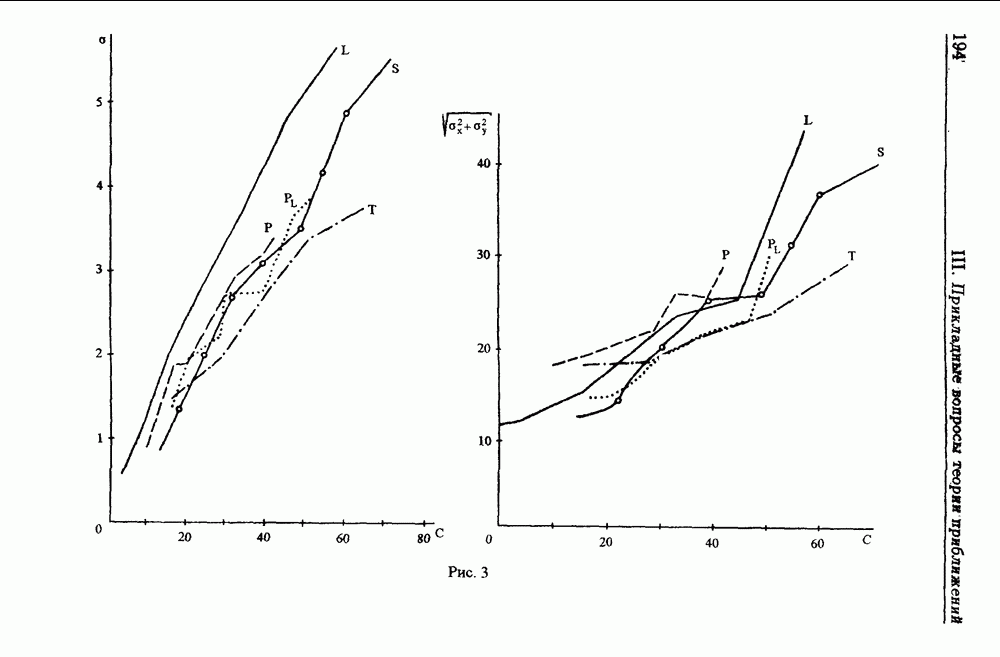
§ 1., п. 1.3. Задача аппроксимации земного рельефа функциями  последующей привязки и сравнения результатов по степени сжатия информации, сложности вычислений, точности аппроксимации и точности навигации решалась авторами совместно с
последующей привязки и сравнения результатов по степени сжатия информации, сложности вычислений, точности аппроксимации и точности навигации решалась авторами совместно с
В.П. Кондратьевым, B.Л. Гасиловым, В.Б. Костоусовым.
§ 3. Задача решалась по инициативе В.Д. Батухтина, Л.А. Майбороды. В работе принимали участие А.Н. Ходаковский, В.И. Бердышев, В.П. Кондратьев, Л.В. Петрах.
§ 5. Работа (см. [23]) по неразрушающему контролю металлических шаров выполнена совместно Институтом математики и механики Уральского отделения АН (В.И. Бердышев, Н.Л. Пацко) и объединением "Машиностроительный заводим. М.И. Калинина (A.M. Шостак, Н.А. Марченков) и была внедрена в производство.
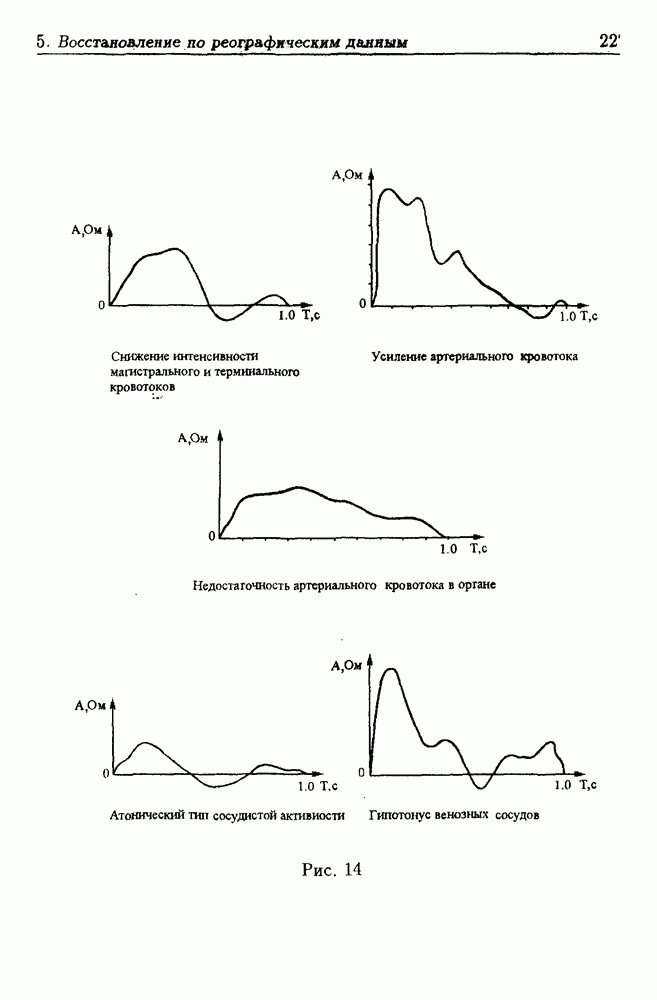
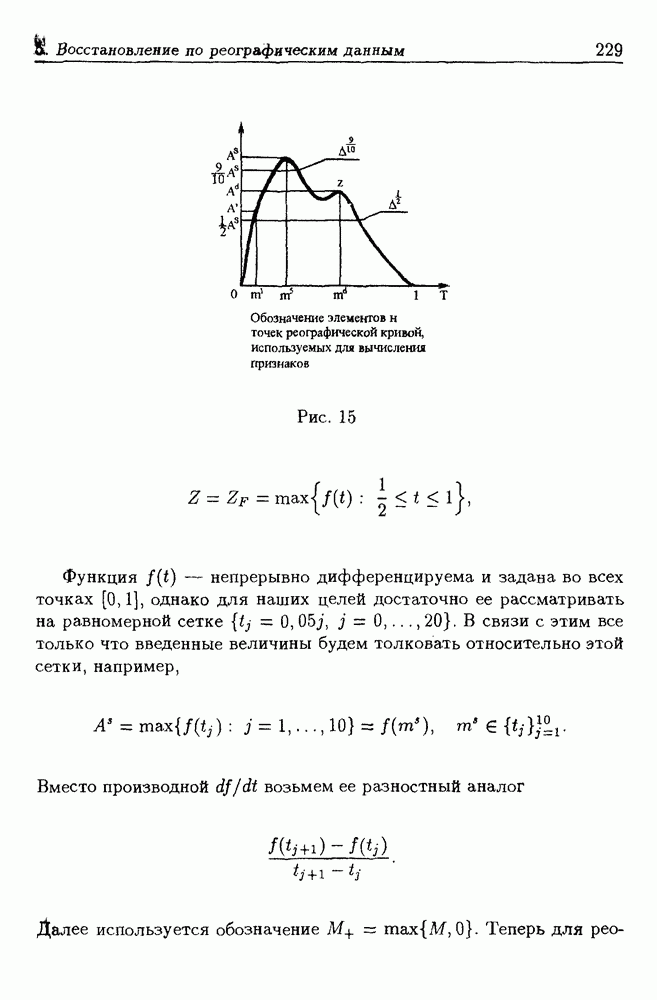
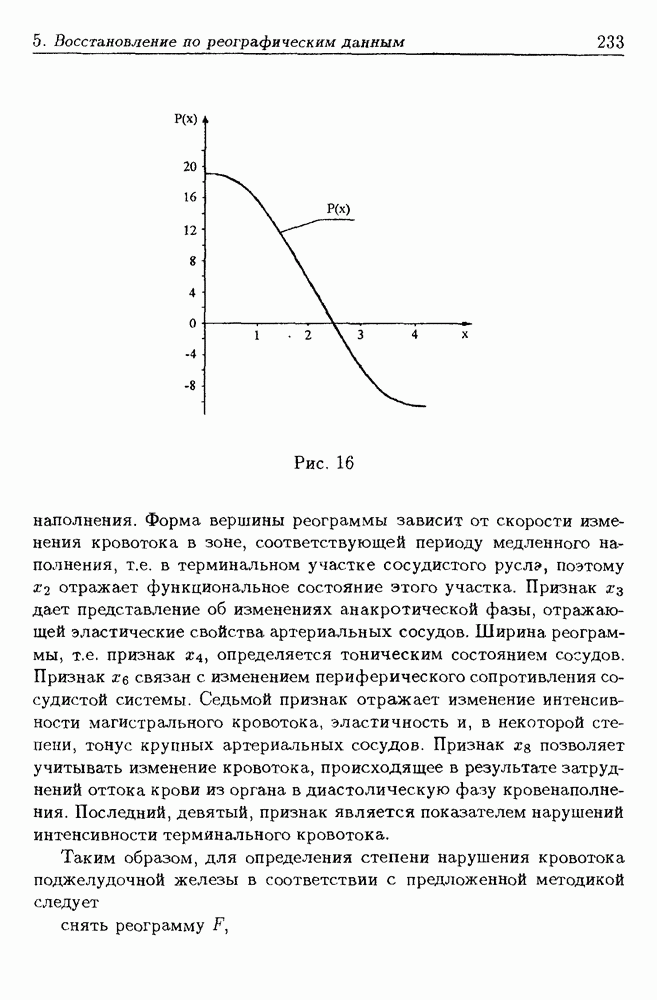
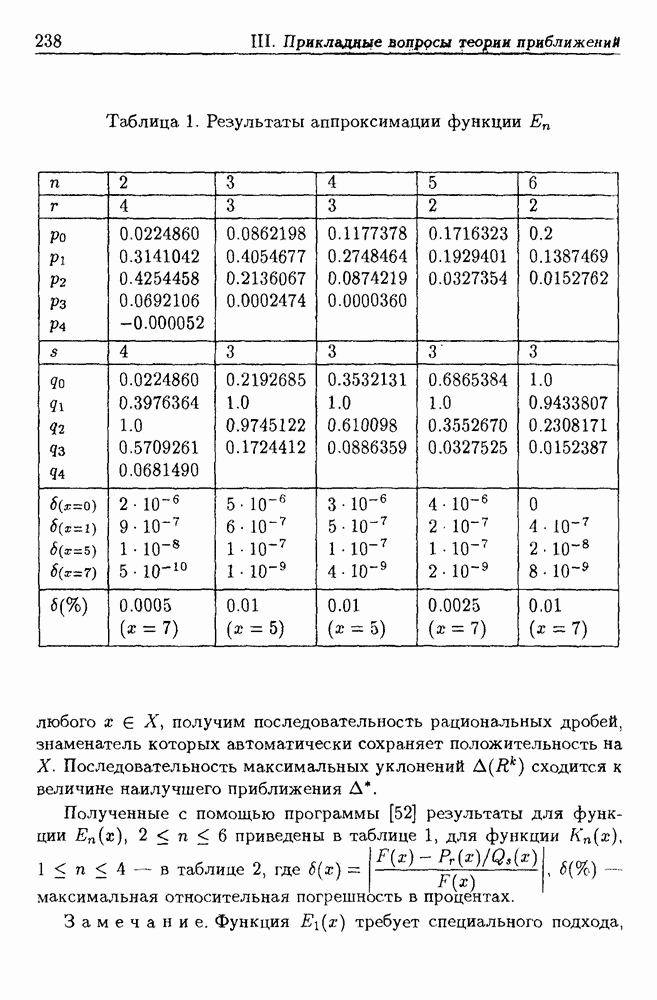
Исследование и развитие реографического способа диагностики поджелудочной железы проводилось [76] по инициативе кафедры  хирургических болезней Свердловского государственного медицинского института (В.А. Козлов, Л.А. Хоменко) совместно с Институтом математики и механики Уральского отделения РАН (В.П. Кондратьев, В.И. Бердышев). Метод реализован на программно-вычислительном комплексе (В.В. Прохоров), внедрен в клинике и запатентован [35].
хирургических болезней Свердловского государственного медицинского института (В.А. Козлов, Л.А. Хоменко) совместно с Институтом математики и механики Уральского отделения РАН (В.П. Кондратьев, В.И. Бердышев). Метод реализован на программно-вычислительном комплексе (В.В. Прохоров), внедрен в клинике и запатентован [35].
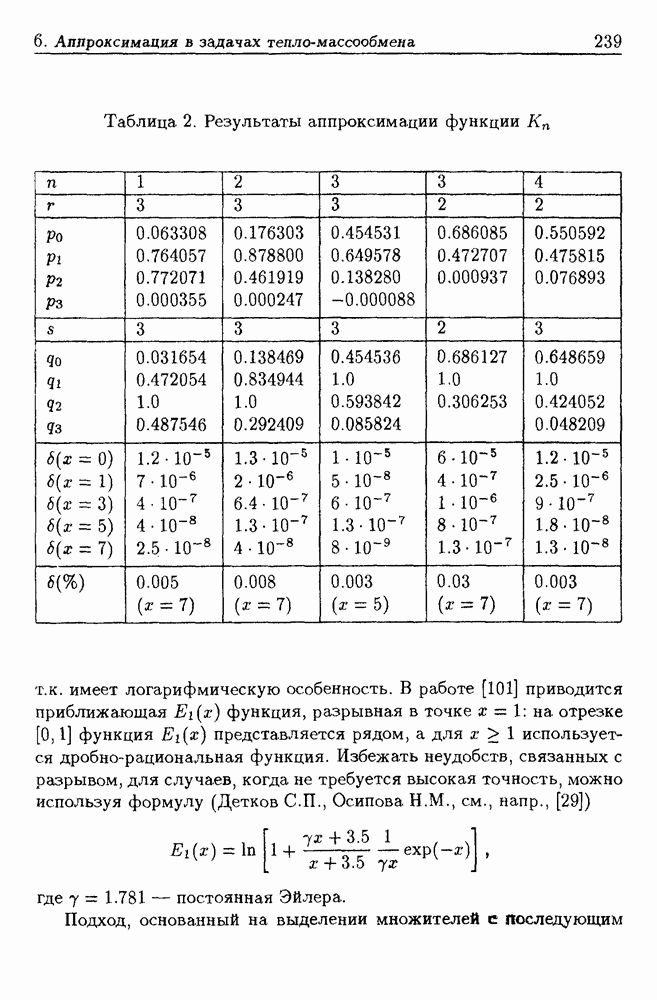
§ 6. Параграф содержит результаты работы, изложенные в совместной статье С.П. Деткова, Н.Н. Пономарева, Л.В. Петрак [29] (аннотация статьи в [28]). Работа выполнялась по инициативе С.Л. Деткова.
§ 7. Приведенные результаты получены в рамках совместной работы УПИ им. С.М. Кирова, ОКБ МЭИ и ИММ УрО РАН. Задача была поставлена Н.И. Черных.
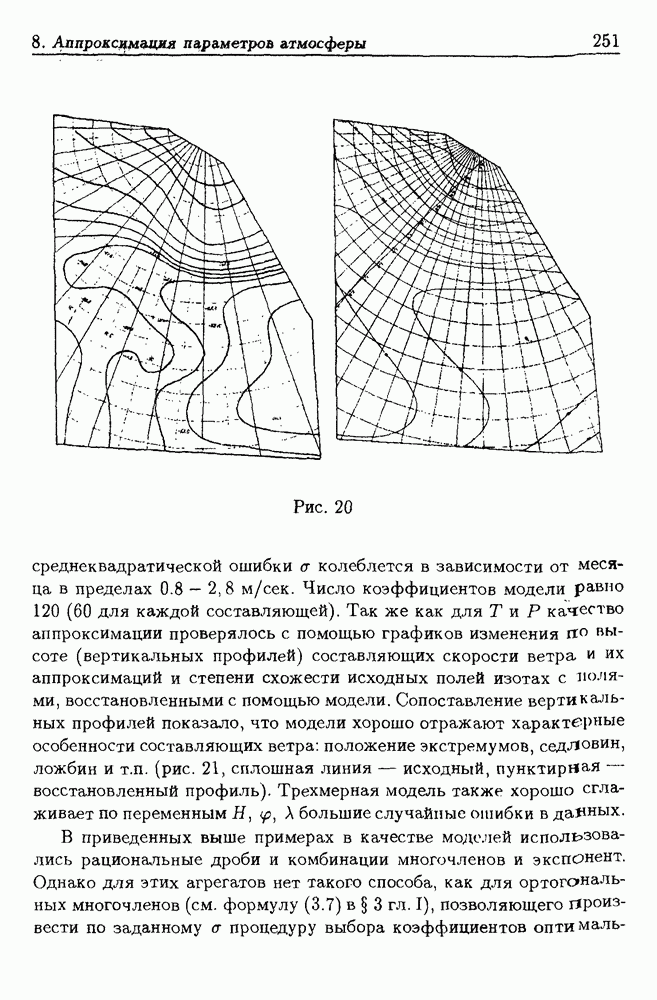
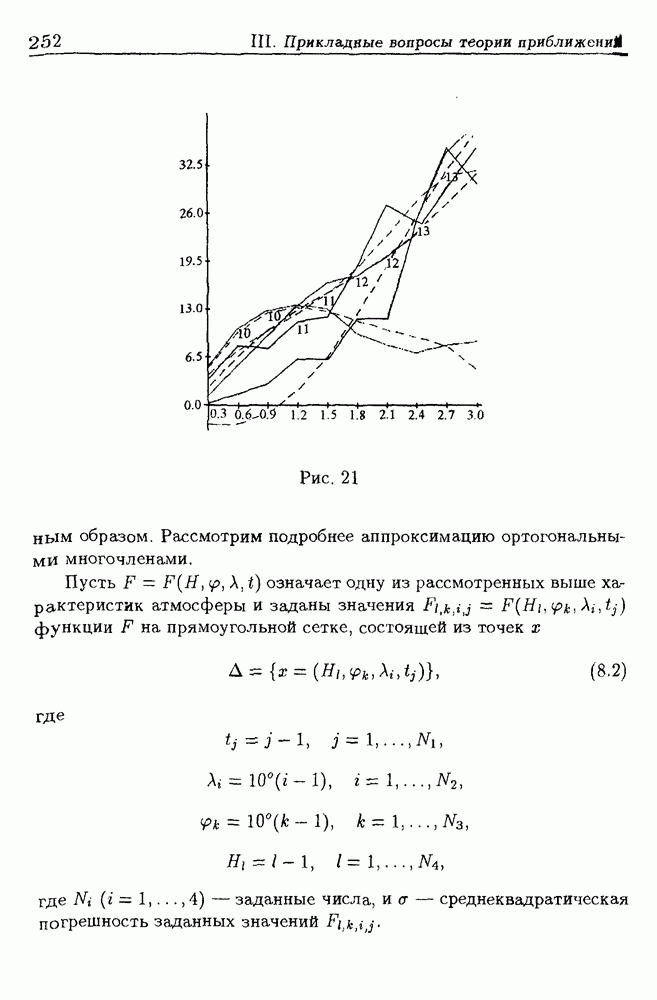
§ 8. Расчеты по аппроксимации параметров атмосферы выполнялись на основе статистических данных, подготовленных сотрудниками Одесского государственного гидро-метеорологического института (Е.П. Школьный, Л.М. Кейбал и др.), и в тесном контакте с ними. Дробно-рациональные модели построены Л.В. Петрак, экспоненциальная — В.П. Кондратьевым. Аппроксимация атмосферы ортогональными многочленами осуществлялась по инициативе В.М. Правдина.
Глава 4.
Приведенные в этом параграфе результаты опубликованы в [84]. В [84] приведены оценки устойчивости наилучших траекторий
относительно погрешностей исходных данных и изучена задача построения гладкой наилучшей траектории с ограниченной кривизной. В.П. Кондратьевым разработан численный алгоритм поиска наилучших траекторий, который также приведен в [15]. Ю.И. Вердышев и А.Г. Ченцов [17] изучали задачу поиска траектории, минимизирующей величину

где  весовые множители, а моменты
весовые множители, а моменты  либо заранее заданы, либо подлежат определению. В [41] исследуются способы выбора наилучшей очередности обхода целей. Дальнейшие результаты см. в [42].
либо заранее заданы, либо подлежат определению. В [41] исследуются способы выбора наилучшей очередности обхода целей. Дальнейшие результаты см. в [42].
ЛИТЕРАТУРА
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
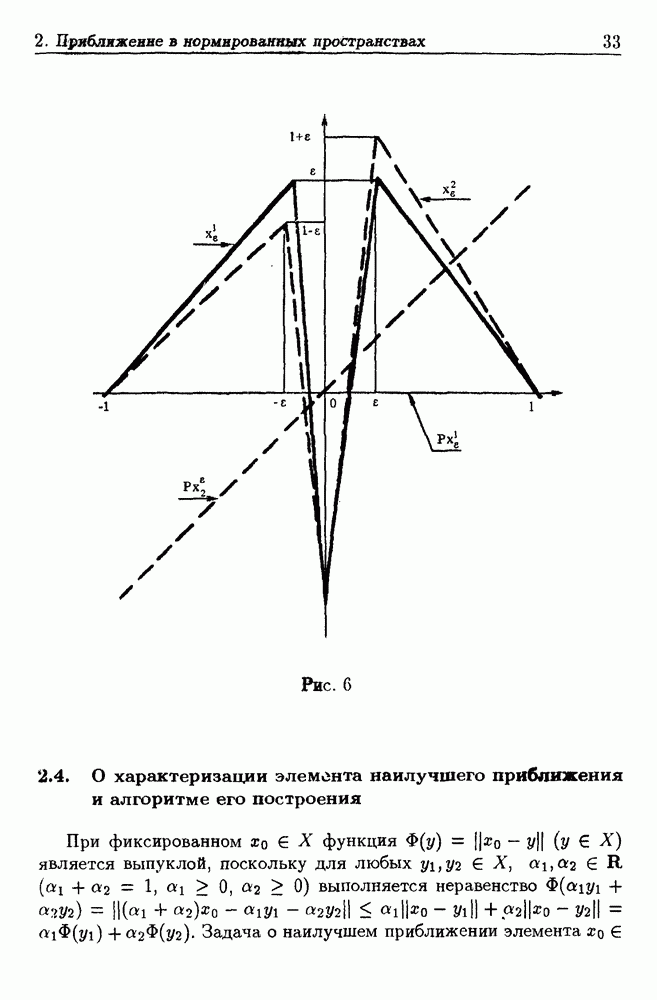
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
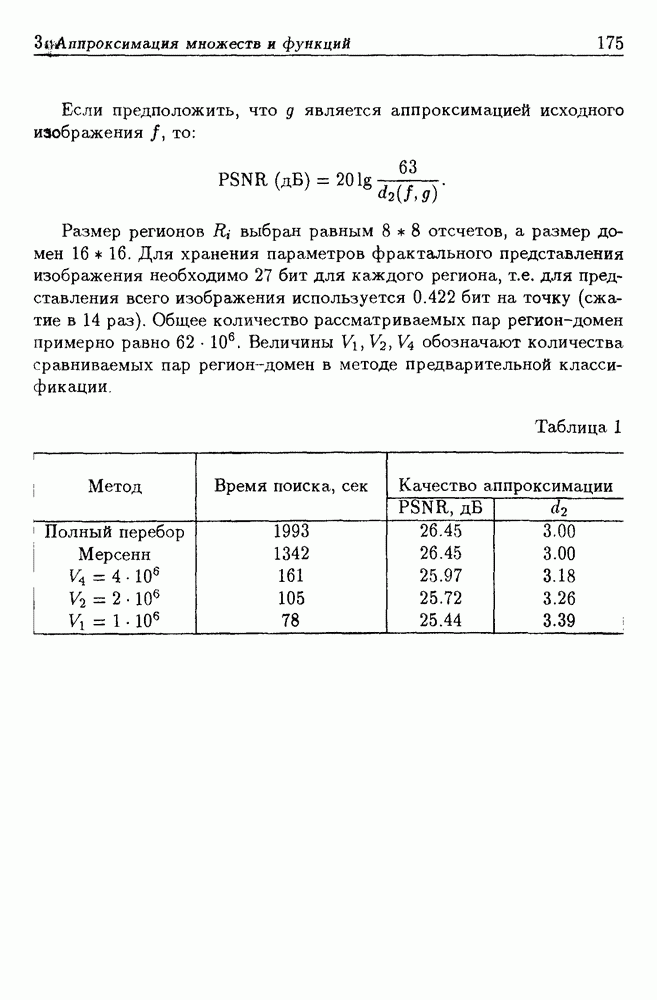
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
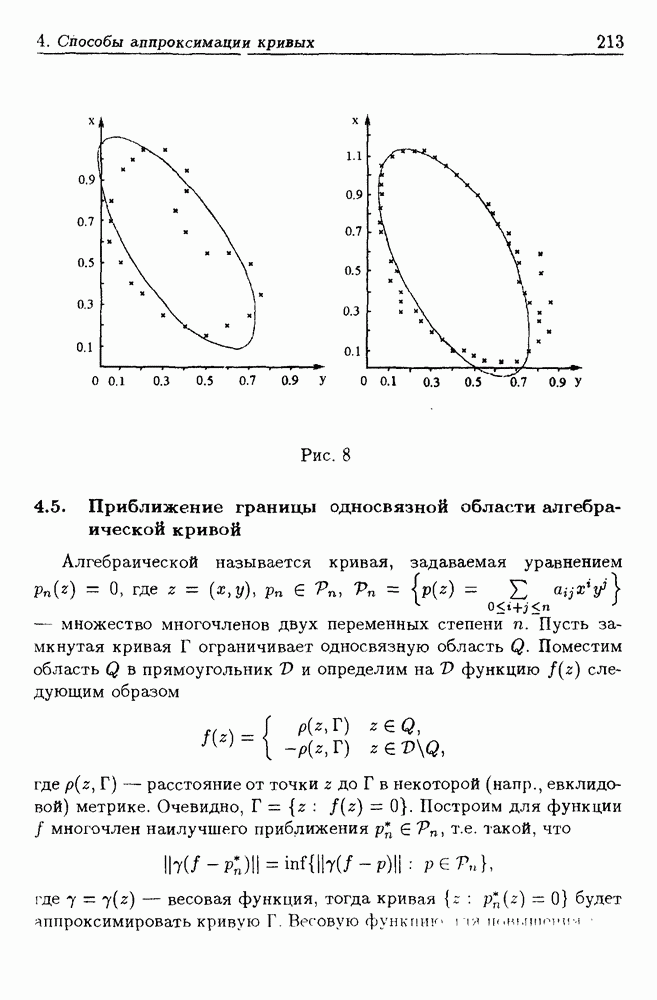
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
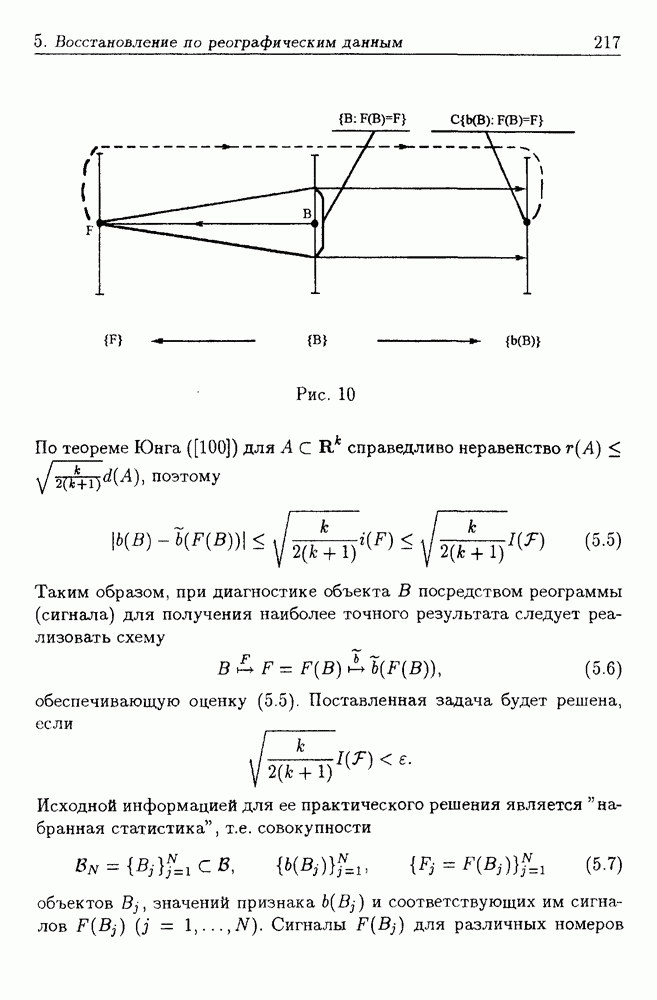
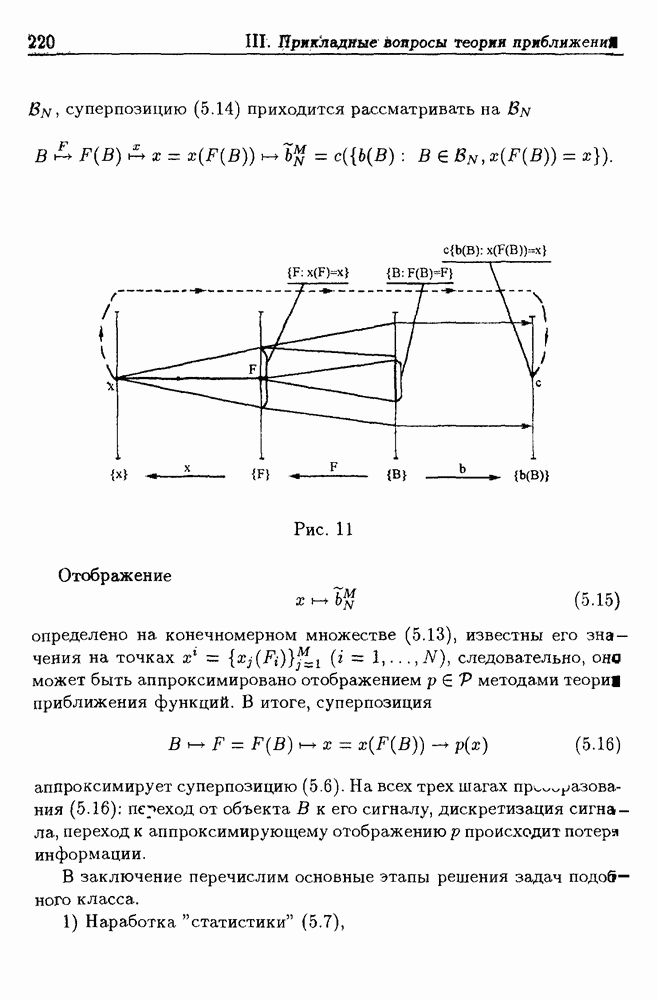
- 5. Восстановление информации по реографическим данным
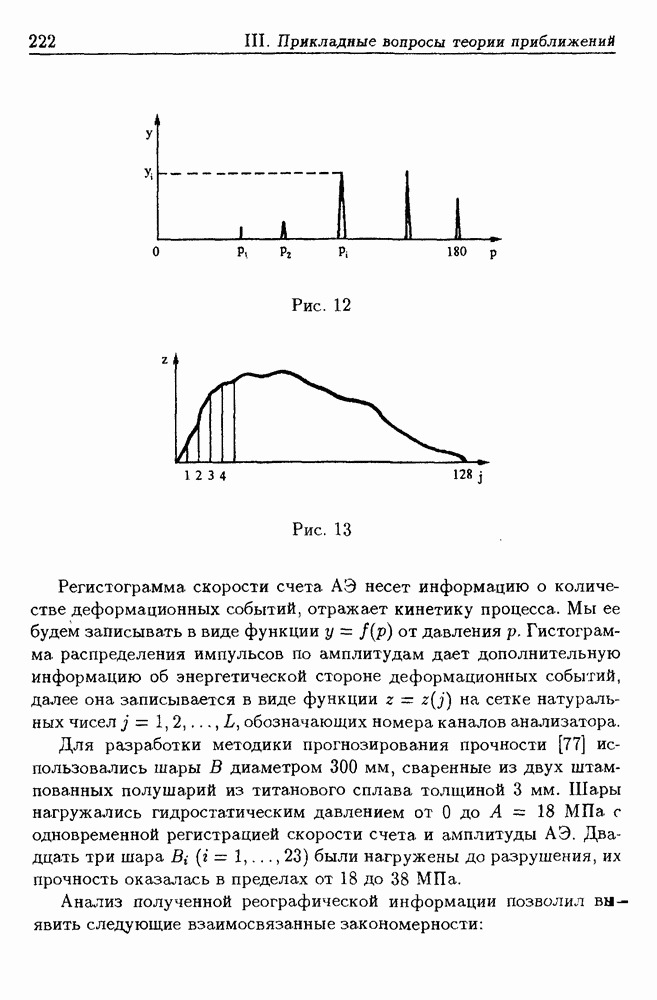
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
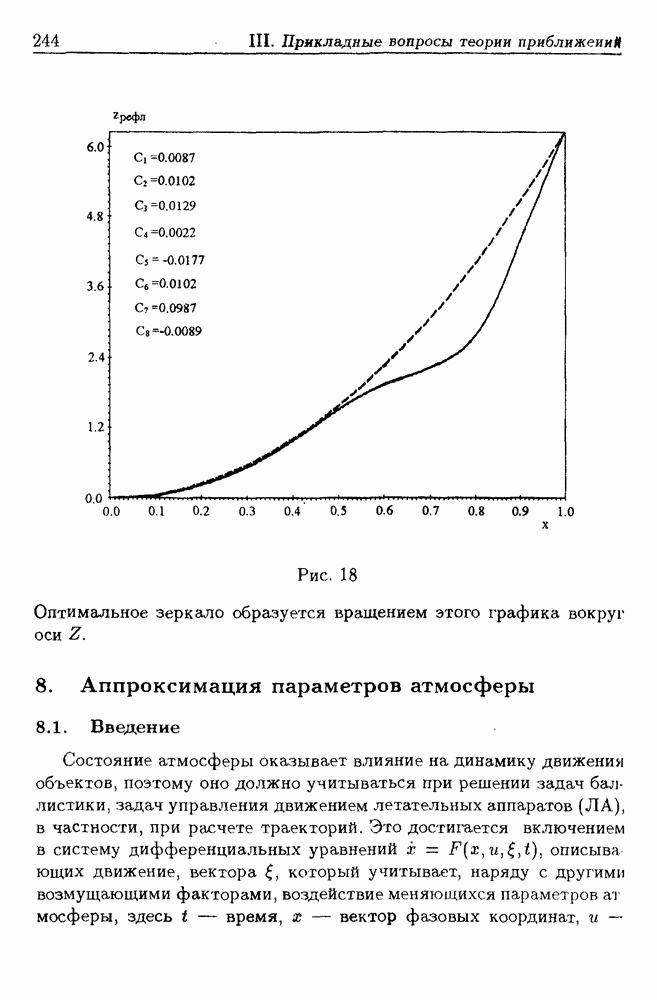
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
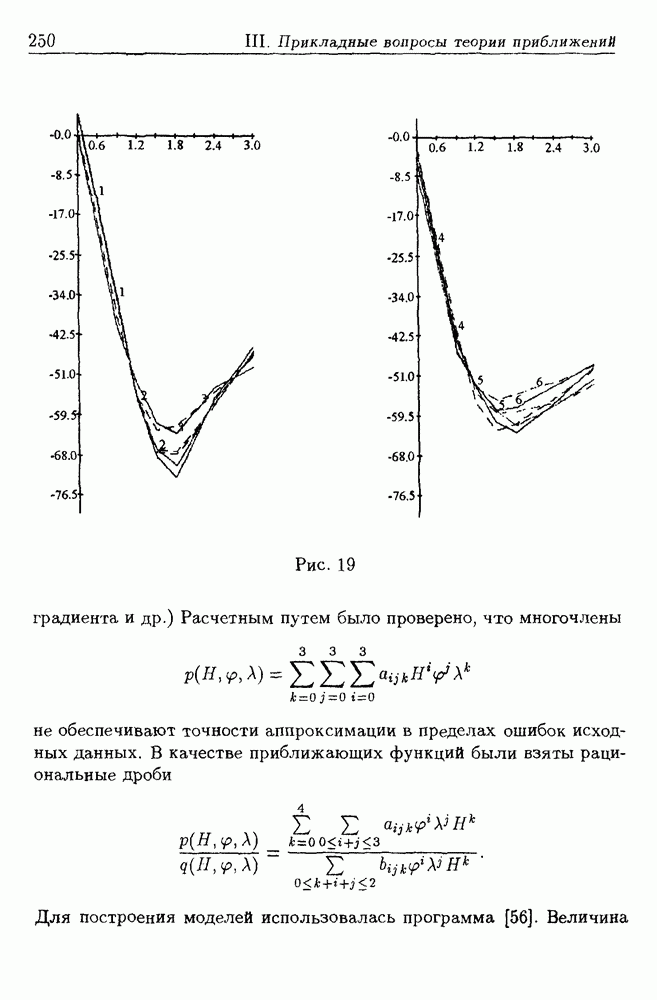
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ