| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Восстановление информации по реографическим данным
5.1. Введение
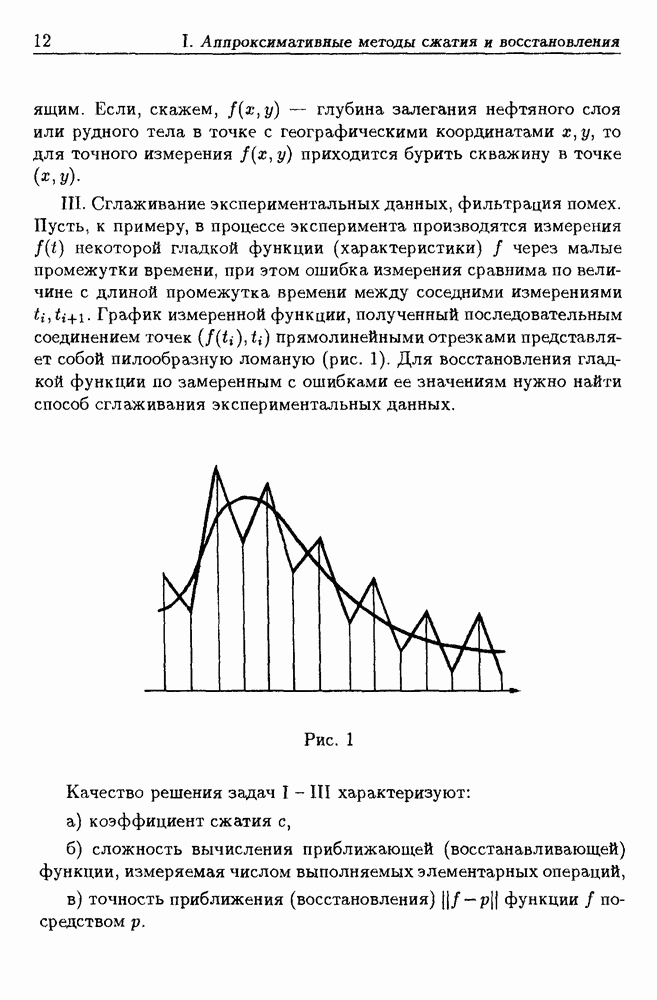
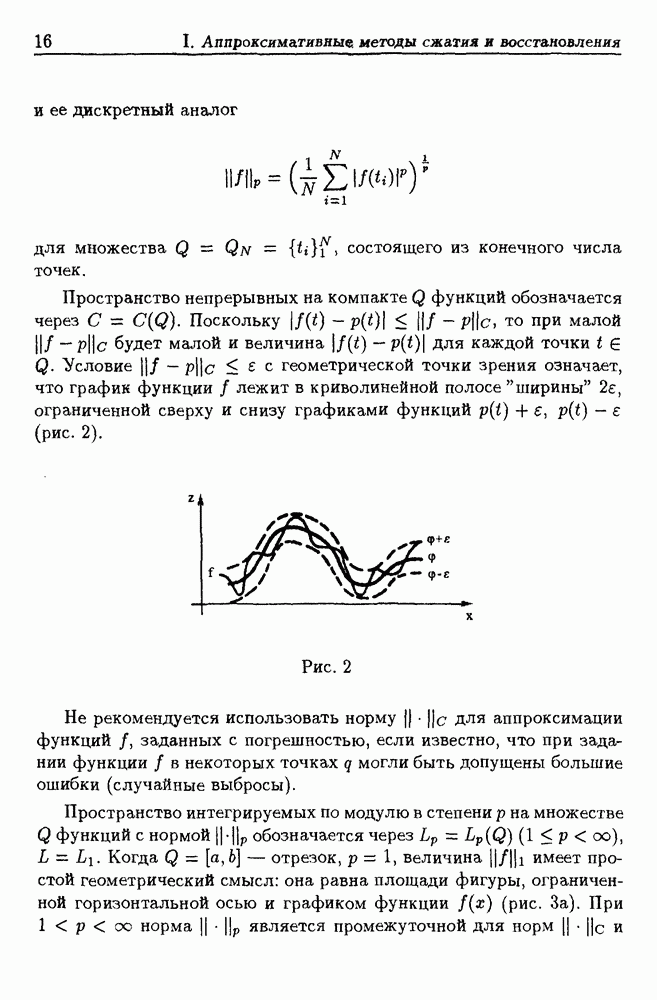
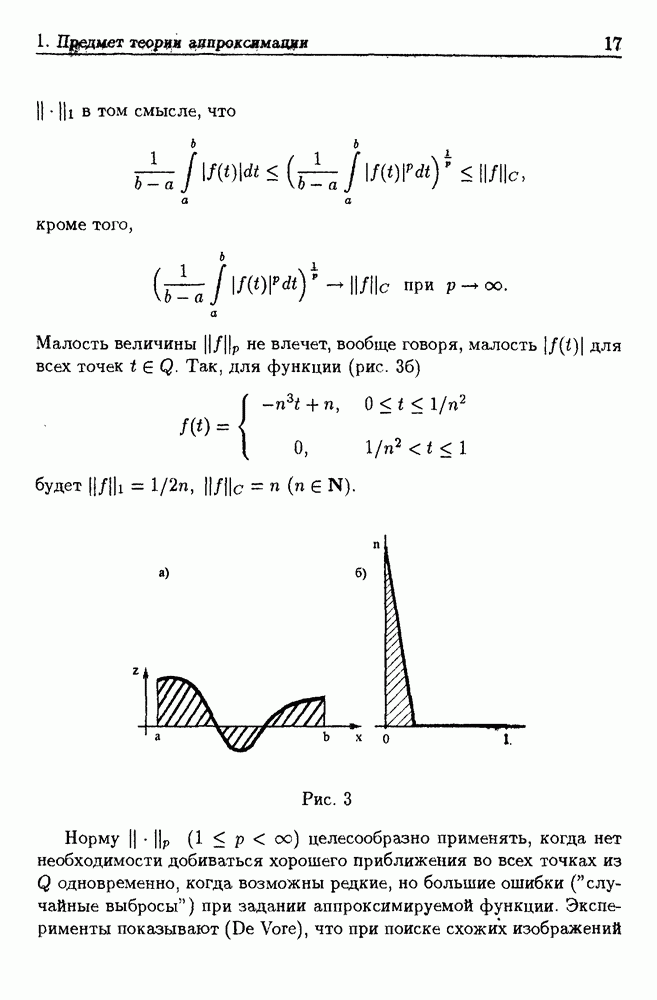
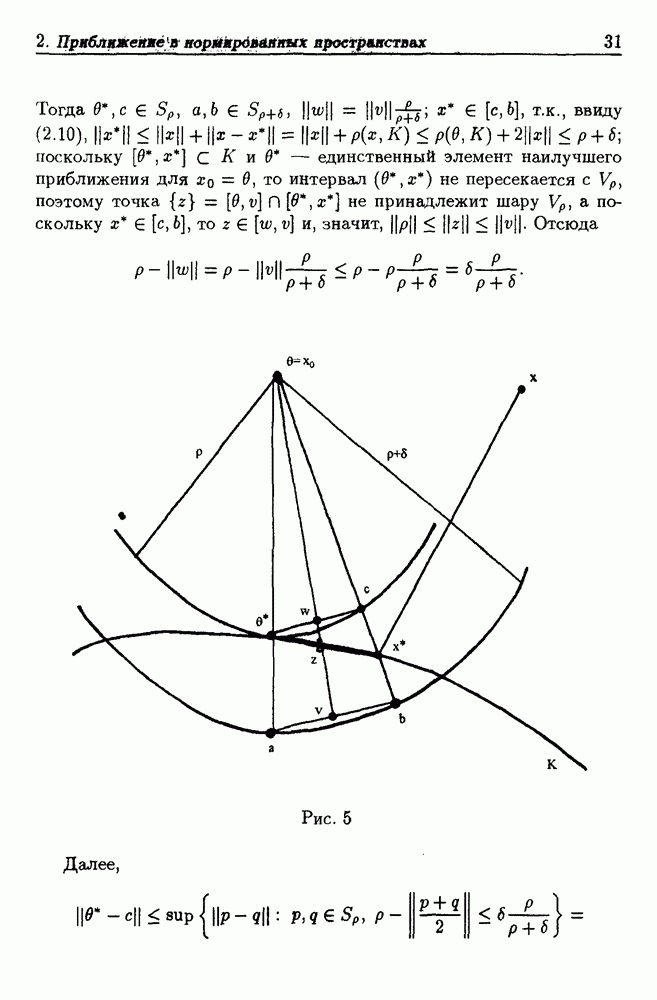
В различных научно-технических областях (машиностроение, геофизика, астрофизика, медицина) встречаются задачи исследования (диагностики) объектов, непосредственное изучение которых по разным причинам затруднено, однако есть возможность использования косвенной информации, содержащейся в сигналах, излучаемых объектом и записанных в виде звуковых регистограмм, электрореограмм и т.д. В благоприятных случаях бывает известно, как состояние объекта отражается на характере сигнала, и, следовательно, по виду сигнала можно судить об объекте. Но зачастую механизм влияния качественного состояния объекта на характер излучаемого сигнала исследователю не известен. В таких случаях приходится использовать опыт работы с изучаемыми объектами или, если возможно, провести серию экспериментов для того, чтобы "набрать статистику" — для большого числа объектов выяснить взаимосвязь

Задачу восстановления информации по реографическим данным можно сформулировать следующим образом. Пусть  множество объектов. Нас интересует значение некоторого качественного признака (скалярного или векторного)
множество объектов. Нас интересует значение некоторого качественного признака (скалярного или векторного)  для
для  Другими словами, нам важно знать отображение
Другими словами, нам важно знать отображение

В результате деятельности объекта В или нашего воздействия на объект возникает сигнал 

на некотором отрезке  где
где  величина сигнала,
величина сигнала,  подходящий параметр (время, напряжение тока и т.д.), определяемый существом задачи. Предполагается, что сигнал
подходящий параметр (время, напряжение тока и т.д.), определяемый существом задачи. Предполагается, что сигнал  может быть замерен в любой точке
может быть замерен в любой точке  или, по крайней мере, в точках густой
или, по крайней мере, в точках густой
сетки  позволяющей уловить особенности поведения сигнала. Пусть
позволяющей уловить особенности поведения сигнала. Пусть

Задача состоит в определении значения  по снятому сигналу
по снятому сигналу  с требуемой точностью
с требуемой точностью  т.е. требуется построить отображение
т.е. требуется построить отображение

такое, что  где через
где через  обозначается некоторая норма, например, евклидова норма в
обозначается некоторая норма, например, евклидова норма в  Эта задача неразрешима, если сигнал недостаточно информативен. Информативность сигнала
Эта задача неразрешима, если сигнал недостаточно информативен. Информативность сигнала  можно измерять величиной
можно измерять величиной

— величиной диаметра множества значений  для объектов В из прообраза
для объектов В из прообраза

сигнала  (т.е. для всех объектов В, порождающих один и тот же сигнал
(т.е. для всех объектов В, порождающих один и тот же сигнал  и можно оценить
и можно оценить  сверху через
сверху через

Сигнал  является представителем всех объектов В из
является представителем всех объектов В из  поэтому вектор
поэтому вектор  должен по возможности представлять множество
должен по возможности представлять множество  (см. схему на рис. 10).
(см. схему на рис. 10).
Проще всего в качестве  взять произвольный элемент из
взять произвольный элемент из  для него, очевидно,
для него, очевидно,

Однако наилучшую оценку позволяет получить элемент  являющийся чебышевским центром с множества
являющийся чебышевским центром с множества  Чебышевский центр
Чебышевский центр  и чебышевский радиус
и чебышевский радиус  множества
множества  определяется следующим образом:
определяется следующим образом:


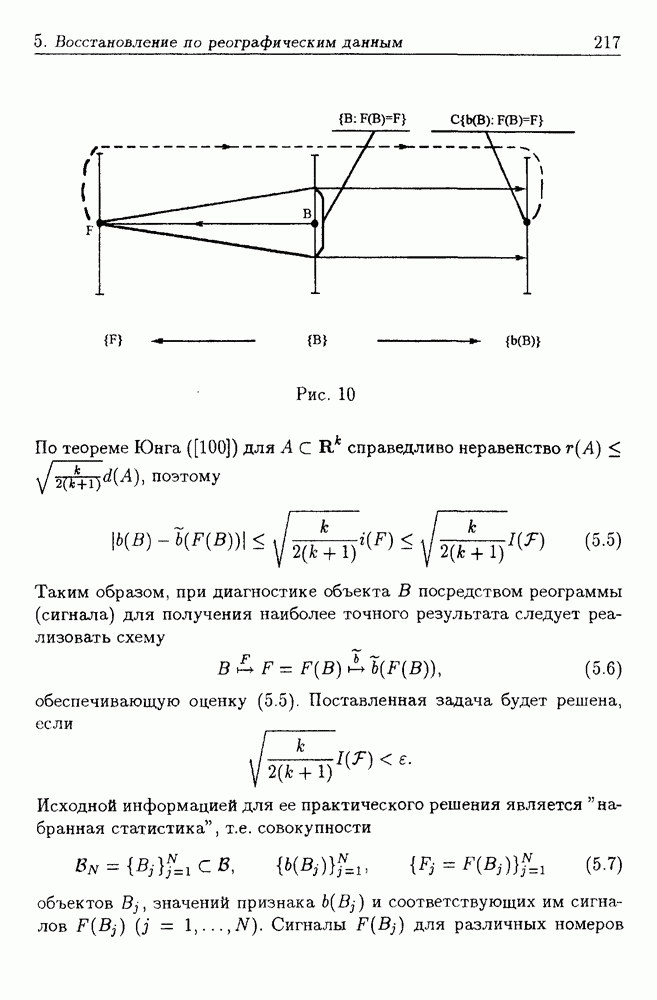
Рис. 10
По теореме Юнга ([100]) для  справедливо неравенство
справедливо неравенство  поэтому
поэтому

Таким образом, при диагностике объекта В посредством реограммы (сигнала) для получения наиболее точного результата следует реализовать схему

обеспечивающую оценку (5.5). Поставленная задача будет решена, если

Исходной информацией для ее практического решения является "набранная статистика", т.е. совокупности

объектов  значений признака
значений признака  и соответствующих им сигналов
и соответствующих им сигналов  Сигналы
Сигналы  для различных номеров
для различных номеров
 могут совпадать. Используя эти данные, зададим отображение
могут совпадать. Используя эти данные, зададим отображение  множества
множества 

где  чебышевский центр множества
чебышевский центр множества  тем самым, на
тем самым, на  определим суперпозицию
определим суперпозицию 

которая В определенном смысле представляет суперпозицию  (5.6).
(5.6).
Наша следующая цель — приблизить отображение (5.9) простым отображением  определенным на всем В. Зададим подходящий класс
определенным на всем В. Зададим подходящий класс  легко вычисляемых отображений из
легко вычисляемых отображений из  в
в

Исходными данными для поиска отображения  являются соотношения (5.8). Сложность данной задачи аппроксимации состоит в том, что областью определения отображений
являются соотношения (5.8). Сложность данной задачи аппроксимации состоит в том, что областью определения отображений  является функциональное множество
является функциональное множество  аффинная размерность которого может быть бесконечной, а методы теории приближения применимы при аппроксимации функций
аффинная размерность которого может быть бесконечной, а методы теории приближения применимы при аппроксимации функций  заданных на множестве
заданных на множестве  из некоторого конечномерного пространства
из некоторого конечномерного пространства  при этом для достижения удовлетворительной точности используются значения
при этом для достижения удовлетворительной точности используются значения  на сетке
на сетке  число точек которой
число точек которой  больше, чем
больше, чем  можно говорить лишь о линейной аппроксимации). Следовательно, для использования стандартных методов аппроксимации надо бесконечномерную область
можно говорить лишь о линейной аппроксимации). Следовательно, для использования стандартных методов аппроксимации надо бесконечномерную область  определения отображения
определения отображения  заменить на конечномерное множество. Проще всего это можно сделать, заменив каждый сигнал
заменить на конечномерное множество. Проще всего это можно сделать, заменив каждый сигнал  на вектор
на вектор  в надежде получить функцию из
в надежде получить функцию из  в
в 

Если сигнал  имеет сложную структуру, то вектор
имеет сложную структуру, то вектор  отражает его особенности лишь при большом
отражает его особенности лишь при большом  . С другой стороны, для хорошей аппроксимации функции (5.2) необходимо знать ее значения в "точках" (см. (5.8))
. С другой стороны, для хорошей аппроксимации функции (5.2) необходимо знать ее значения в "точках" (см. (5.8))

при  т.е. необходимо иметь "богатую статистику". Часто в практических задачах статистика бывает скудной, в таких случаях указанный способ сведения
т.е. необходимо иметь "богатую статистику". Часто в практических задачах статистика бывает скудной, в таких случаях указанный способ сведения  к функции с конечным числом измерений неприменим и приходится искать другие способы замены множества
к функции с конечным числом измерений неприменим и приходится искать другие способы замены множества  на конечномерное множество.
на конечномерное множество.
В излагаемых ниже двух задачах удается подобрать небольшое количество численных характеристик сигнала, по которым можно с удовлетворительной точностью определить значение  Фактически
Фактически  есть набор функционалов над
есть набор функционалов над  более информативных в сравнении с функционалами вида
более информативных в сравнении с функционалами вида  Так сигнал
Так сигнал  дискретизируется
дискретизируется

И мы получаем конечномерное множество

Каждый вектор  из этого множества является представителем множества сигналов
из этого множества является представителем множества сигналов  для которых
для которых  а каждый сигнал
а каждый сигнал  представляет, в свою очередь, множество объектов
представляет, в свою очередь, множество объектов  а множество
а множество  наилучшим образом представляет его чебышевский центр
наилучшим образом представляет его чебышевский центр  Поэтому при диагностике объекта В целесообразно реализовать следующую схему:
Поэтому при диагностике объекта В целесообразно реализовать следующую схему:

(см. пунктирную линию на рис. 11). Поскольку отображения  практически заданы в соответствии с (5.7) не на всем В, а только на
практически заданы в соответствии с (5.7) не на всем В, а только на
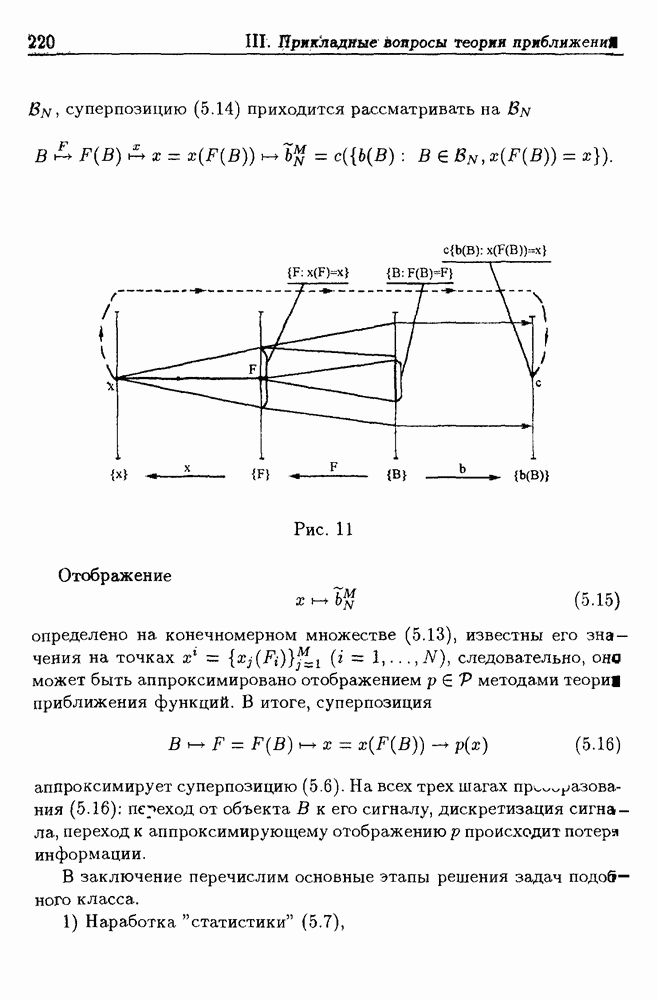
 суперпозицию (5.14) приходится рассматривать на
суперпозицию (5.14) приходится рассматривать на 


Рис. 11
Отображение

определено на конечномерном множестве (5.13), известны его значения на точках  следовательно, оно может быть аппроксимировано отображением
следовательно, оно может быть аппроксимировано отображением  методами теория приближения функций. В итоге, суперпозиция
методами теория приближения функций. В итоге, суперпозиция

аппроксимирует суперпозицию (5.6). На всех трех шагах преобразования (5.16): переход от объекта В к его сигналу, дискретизация сигнала, переход к аппроксимирующему отображению  происходит потеря информации.
происходит потеря информации.
В заключение перечислим основные этапы решения задач подобного класса.
1) Наработка "статистики" (5.7),
2) изучение соответствия объект  сигнал
сигнал  значение признака
значение признака  на основе имеющейся статистики,
на основе имеющейся статистики,
3) формулировка эвристических принципов (такого вида: если определенное свойство реограммы проявляется сильнее, то для большинства соответствующих объектов и значение признака  больше),
больше),
4) реализация замеченных информативных свойств реограмм  в виде численных характеристик
в виде численных характеристик 
5) подбор весовых сомножителей, отражающих степень информативности характеристик 
6) поиск аналитической зависимости признака  от характеристик
от характеристик  с использованием методов теории приближения функций (выбор класса V и аппроксимация),
с использованием методов теории приближения функций (выбор класса V и аппроксимация),
7) автоматизация обработки реограмм, вычисления характеристик  и по ним величины
и по ним величины 
По этому перечню можно убедиться в том, что успех в решении задачи возможен лишь при сотрудничестве математиков и специалистов, имеющих опыт работы с изучаемыми объектами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
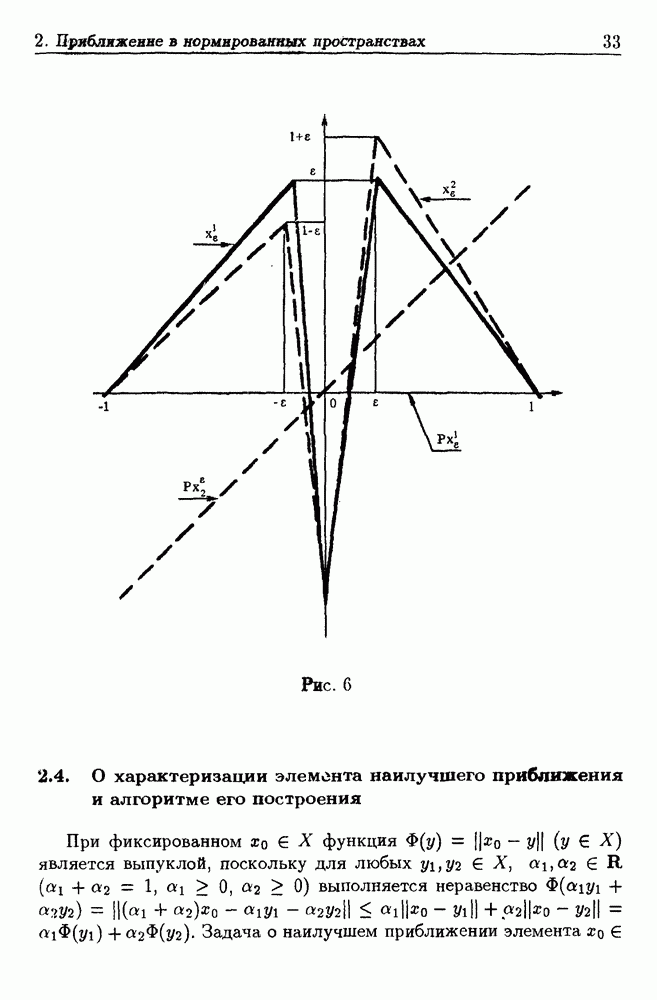
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
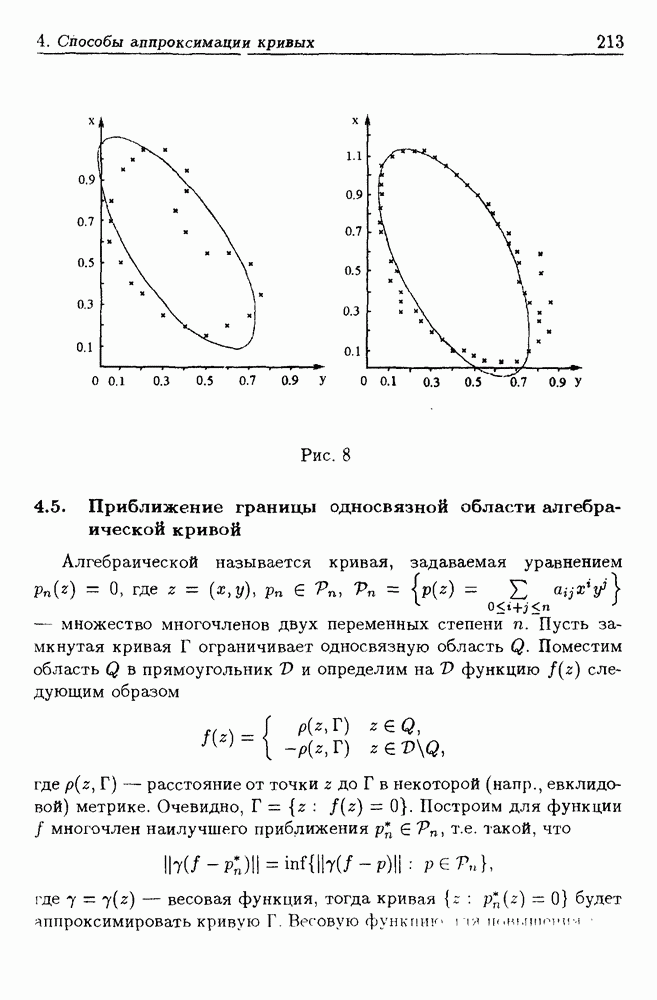
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
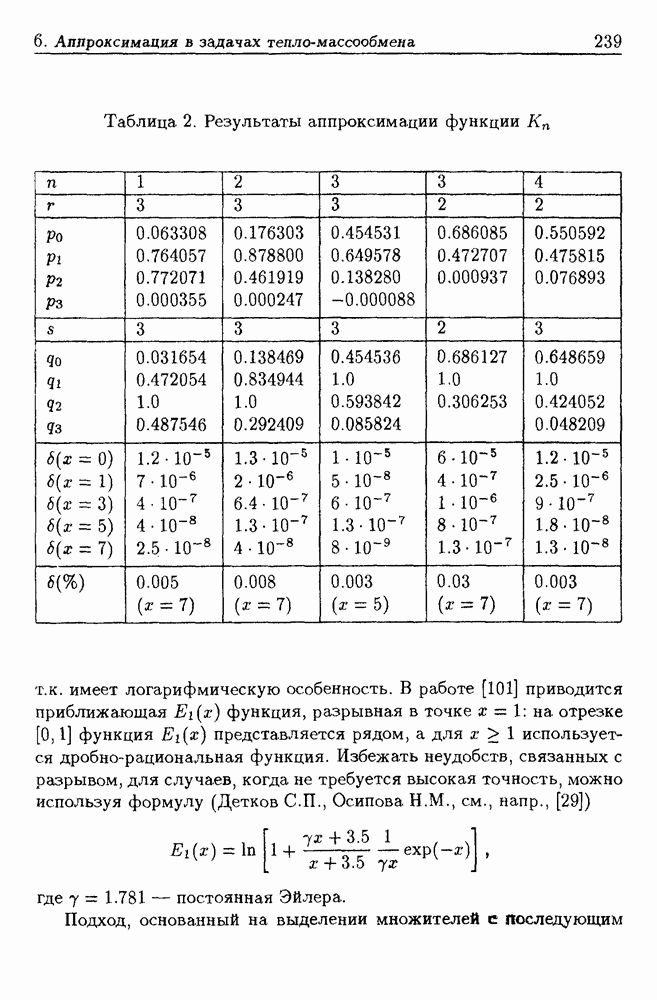
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
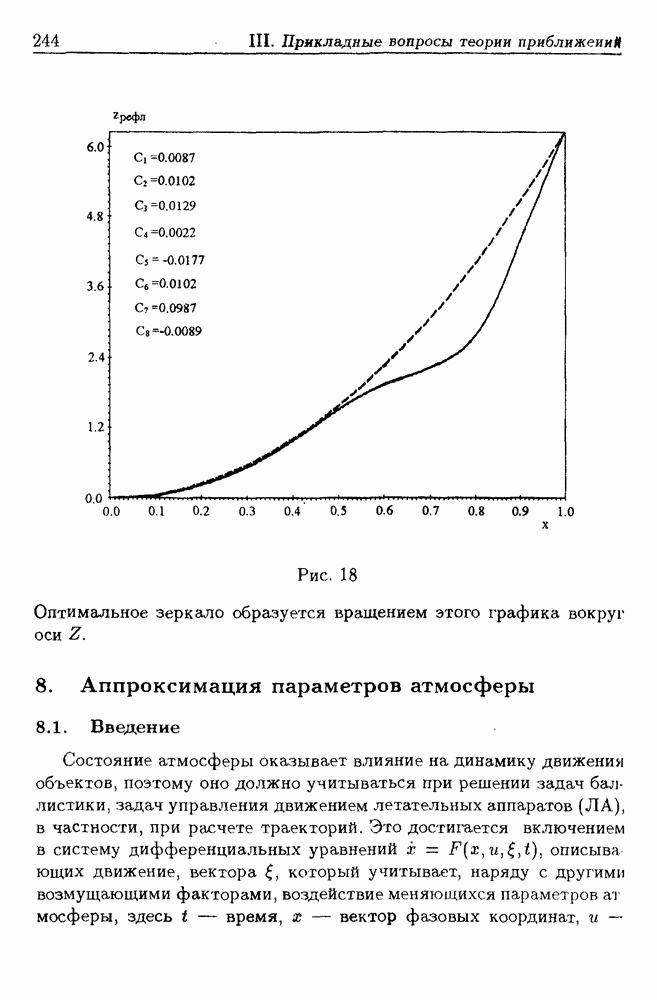
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
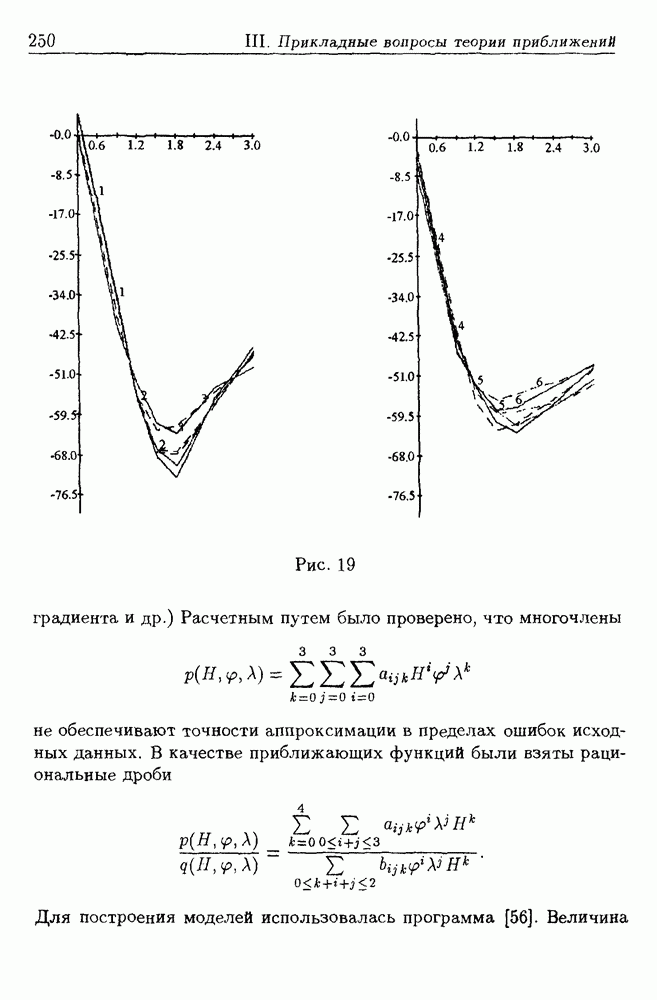
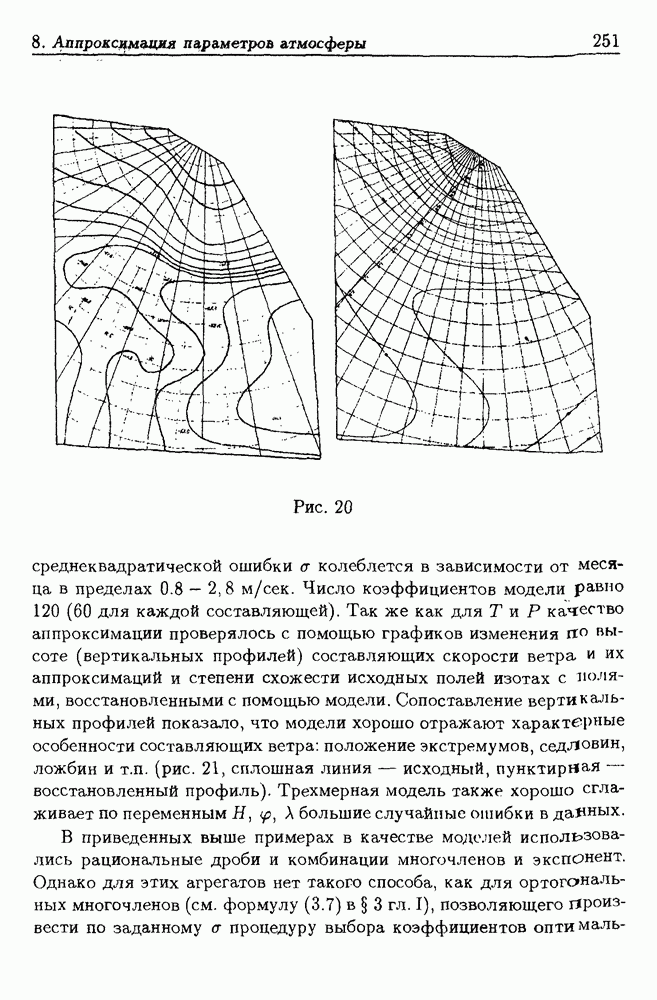
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ