| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. Аппроксимация функций
В п. 3.3 рассматривалось отображение


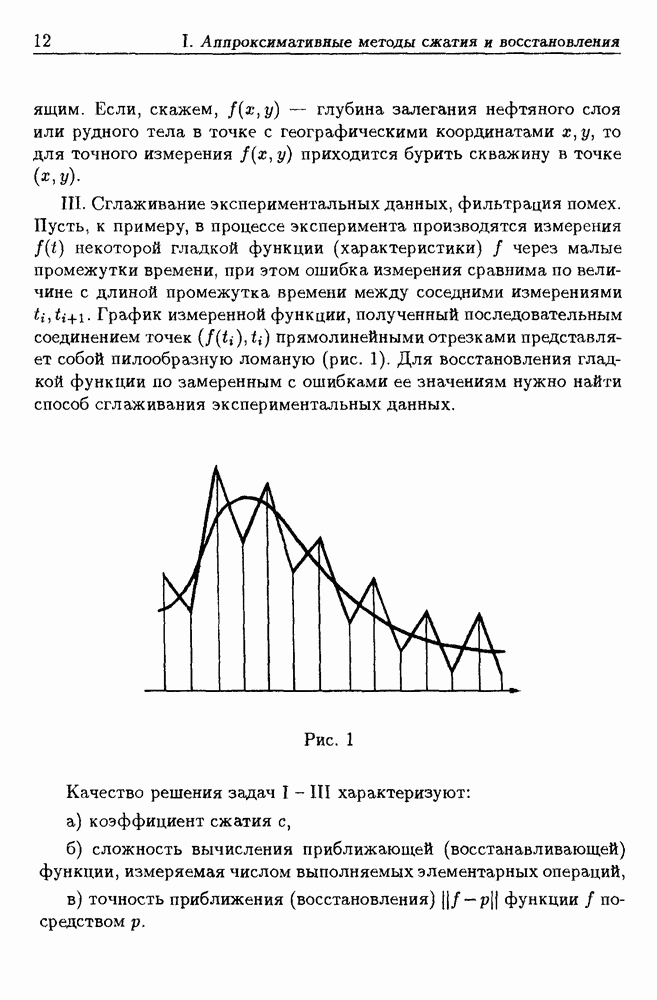
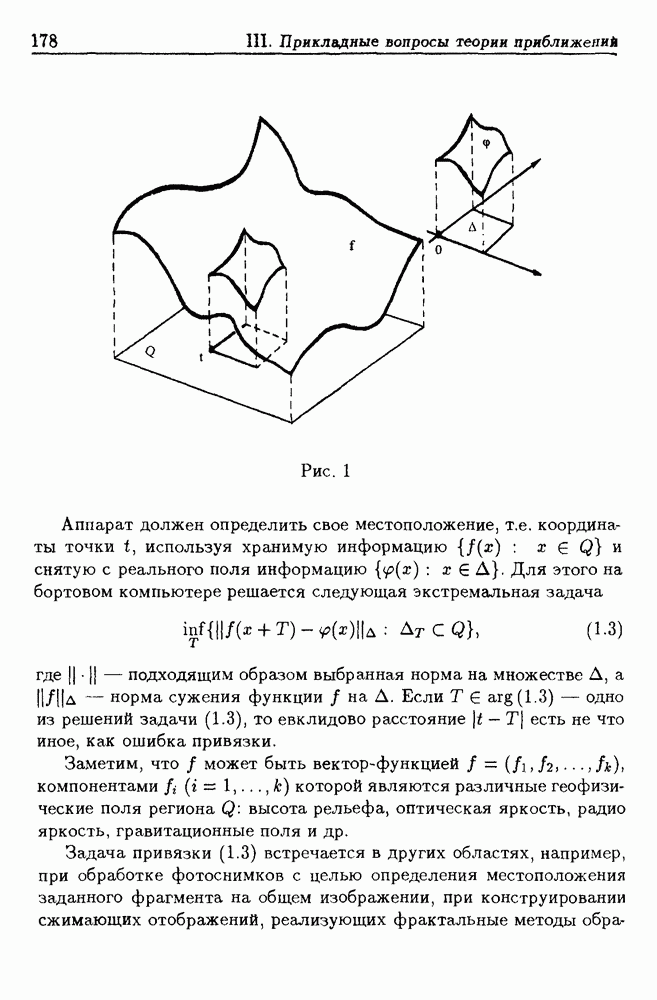
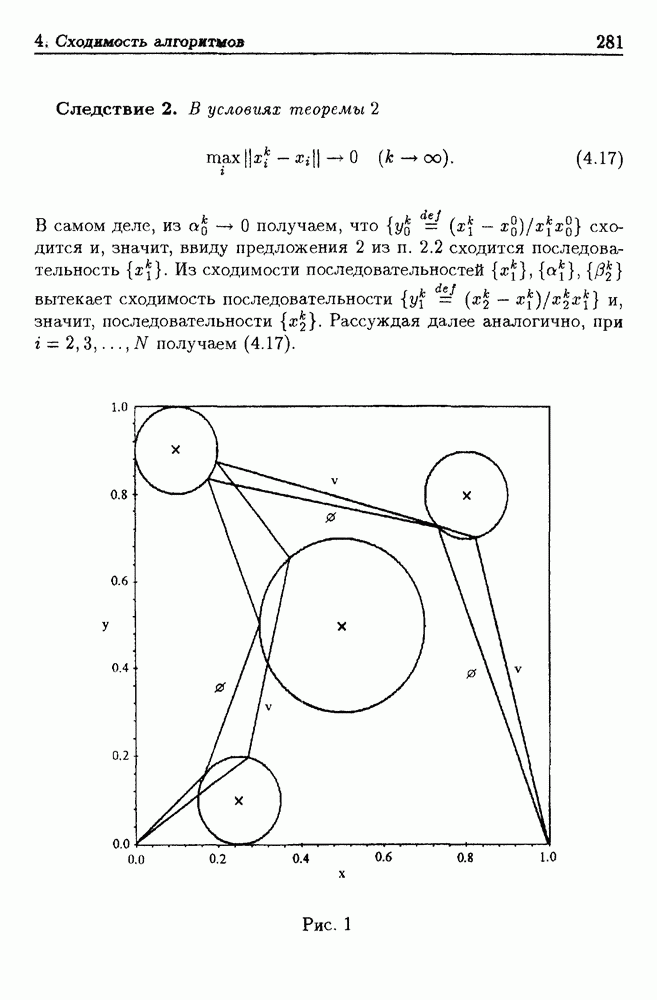
Рис. 1. Множество эпицентров землетрясений, Калифорния, 1932—1994.
пространства  компактных подмножеств из X, задаваемое набором
компактных подмножеств из X, задаваемое набором  сжимающих отображений
сжимающих отображений  Это одно из, несомнённо, богатого многообразия сжимающих отображений
Это одно из, несомнённо, богатого многообразия сжимающих отображений  Более общее отображение в сравнении с названным задается той же формулой (3.14) с набором отображений
Более общее отображение в сравнении с названным задается той же формулой (3.14) с набором отображений 

где  некоторый набор областей (домен) из
некоторый набор областей (домен) из  Такой набор именуется как LIFS или PIFS - Local (Partitioned) Iterated Funtions System. IFS есть частный случай
Такой набор именуется как LIFS или PIFS - Local (Partitioned) Iterated Funtions System. IFS есть частный случай  при
при  Отображения, задаваемые посредством
Отображения, задаваемые посредством  целесообразно применять для обработки множеств, близких по структуре к самоподобным множествам (имеющим большое количество малых частей, подобных всему множеству). Набор
целесообразно применять для обработки множеств, близких по структуре к самоподобным множествам (имеющим большое количество малых частей, подобных всему множеству). Набор  может быть полезен при обработке такого множества
может быть полезен при обработке такого множества  в котором явно выделяется набор составных частей
в котором явно выделяется набор составных частей  каждая из которых имеет много себе подобных подмножеств из
каждая из которых имеет много себе подобных подмножеств из  (не обязательно содержащихся в
(не обязательно содержащихся в  малых размеров. Сказанное в равной степени относится и к задаче компактного хранения функций. Продемонстрируем суть метода,
малых размеров. Сказанное в равной степени относится и к задаче компактного хранения функций. Продемонстрируем суть метода,
опирающегося на  в простейшем случае (см. [98]).
в простейшем случае (см. [98]).
Случай кусочно-аффинных отображений. Пусть  пространство заданных на прямоугольнике
пространство заданных на прямоугольнике  вещественных функций
вещественных функций  для которых
для которых  интегрируема по Лебегу,
интегрируема по Лебегу,

Предположим, что  разбит на регионы
разбит на регионы  (например, прямоугольники)
(например, прямоугольники)

и выделен набор областей  так, что для любого
так, что для любого  указаны номер
указаны номер  и взаимно-однозначное аффинное отображение
и взаимно-однозначное аффинное отображение

Пусть оно задается формулой

здесь верхний индекс означает не степень, а номер региона. Определим отображение  следующим образом:
следующим образом:

где  заданные коэффициенты, а через
заданные коэффициенты, а через  обозначается сужение
обозначается сужение  на множество
на множество  Итак, отображение
Итак, отображение  строится на основе двух преобразований:
строится на основе двух преобразований:
— преобразование по горизонтали (обозначим его через  для определения
для определения  при
при  вычисляется значение функции
вычисляется значение функции  в точке
в точке 
— преобразование по вертикали, действующее на функцию

Это кусочно-аффинные преобразования, они задаются набором коэффициентов

Коэффициенты  в (3.16) могут выбираться как ешение следующей задачи о наилучшем приближении (см. гл. I, § 3,4)
в (3.16) могут выбираться как ешение следующей задачи о наилучшем приближении (см. гл. I, § 3,4)

Для выяснения условия сжимаемости оператора  выпишем оценку при
выпишем оценку при 

где  якобиан преобразований
якобиан преобразований  Следовательно, коэффициент
Следовательно, коэффициент  сжатия отображения
сжатия отображения  удовлетворяет неравенству
удовлетворяет неравенству

и условие сжимаемости отображения  имеет вид
имеет вид

В рассматриваемом случае  задается посредством
задается посредством  коэффициентов (3.16) и величина
коэффициентов (3.16) и величина  (см. (2.8)) оценивается следующим образом:
(см. (2.8)) оценивается следующим образом:

Если  пространство ограниченных на
пространство ограниченных на  функций с нормой
функций с нормой

S - определенное в (3.16) отображение, то для любых  будет
будет

Следовательно, коэффициент сжатия  удовлетворяет неравенству
удовлетворяет неравенству

и, значит,

Заметим, что в случае функции одной переменной отображение (3.16) можно выразить следующим образом:

Возможны обобщения метода по следующим направлениям:
— область  определения функции
определения функции  содержится в
содержится в  или в произвольном метрическом пространстве;
или в произвольном метрическом пространстве;
— разбиение  области
области  на регионы
на регионы  и набор домен
и набор домен  выбирается с учетом особенностей функции
выбирается с учетом особенностей функции  поэтому
поэтому  не обязательно являются прямоугольниками;
не обязательно являются прямоугольниками;
— отображения  являются полиномиальными;
являются полиномиальными;
— задан набор функций  по которому отображение
по которому отображение  определяется так:
определяется так:

— для каждого  задан набор
задан набор  номеров из
номеров из  и коэффициентов
и коэффициентов  и отображение
и отображение  определяется в виде
определяется в виде

Отметим, что если функции  из (3.24) удовлетворяют условию Липшица
из (3.24) удовлетворяют условию Липшица

то, как легко видеть, выполняются неравенства, получающиеся из (3.19)-(3.23) заменой величины  на
на 
Подведем итог. Для реализации предлагаемого метода надо выполнить следующее:
1) разбить область  на конечное число регионов
на конечное число регионов 
2) выбрать набор домен 
3) для каждого региона  подобрать домен
подобрать домен  в случае отображения вида (3.25) подобрать набор домен
в случае отображения вида (3.25) подобрать набор домен 
4) определить отображения 
5) построить отображение  вида (3.24) или (3.25). Этапы 1) - 4) осуществляются так, чтобы
вида (3.24) или (3.25). Этапы 1) - 4) осуществляются так, чтобы
а) отображение  было сжимающим в метрике пространства
было сжимающим в метрике пространства 
б) неподвижная точка  оператора
оператора  была по возможности ближе к обрабатываемой функции
была по возможности ближе к обрабатываемой функции 
Условие сжимаемости проверяется посредством неравенств (3.20), (3.22), а в случае операторов (3.25) для функций, удовлетворяющих условию Липшица, — посредством неравенства

Требование б) напрямую трудно выполнимо. Более доступна задача минимизации по коэффициентам (3.17) отношения (3.21), а в случае отображения (3.24) — минимизация величины

с последующим использованием теоремы 2 из п. 2.3. На практике же, как отмечалось выше (см. (3.18)), с целью удовлетворения требования б) минимизируют величину  Так, в случае отображения
Так, в случае отображения
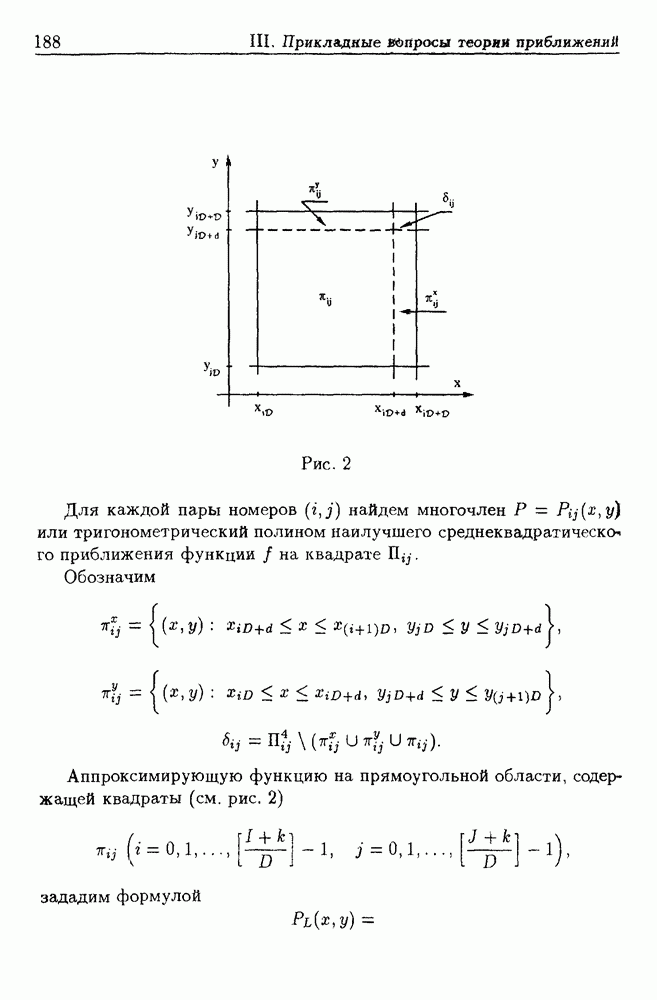
вида (3.16) для каждой пары  находят
находят

затем отыскивают

и полагают в качестве  тот номер
тот номер  на котором дости гается минимум (3.27). Как видим, минимизация величины
на котором дости гается минимум (3.27). Как видим, минимизация величины  связана с большими вычислительными затратами,
связана с большими вычислительными затратами,  для каждого
для каждого  требуется I раз решить задачу (3.26). Известно (см. [47]) несколько способов уменьшения времени поиска.
требуется I раз решить задачу (3.26). Известно (см. [47]) несколько способов уменьшения времени поиска.
Далее излагаются способы, предложенные Я.В. Малыгиным [47].
Ряд способов основан на предварительной классификации "фрагментов"  исходной функции, что позволяет для каждого региона
исходной функции, что позволяет для каждого региона  проводить поиск, т.е. решать задачи (3.26), (3.27) только среди домен, близких в смысле этой классификации к
проводить поиск, т.е. решать задачи (3.26), (3.27) только среди домен, близких в смысле этой классификации к  Удачно подобранный признак классификации позволяет значительно сократить объем требуемых вычислений, лишь незначительно увеличивая погрешность (3.27). Интуитивно понятно стремление проводить поиск
Удачно подобранный признак классификации позволяет значительно сократить объем требуемых вычислений, лишь незначительно увеличивая погрешность (3.27). Интуитивно понятно стремление проводить поиск  для некоторого
для некоторого  скажем, с "гористым" (сильно изломанным) графиком
скажем, с "гористым" (сильно изломанным) графиком  среди таких домен, у которых
среди таких домен, у которых  также является "гористым". При этом в качестве "гористости" графика функции можно принять хаусдорфову размерность
также является "гористым". При этом в качестве "гористости" графика функции можно принять хаусдорфову размерность  (см. § 1): чем больше это число, тем "изломанность" выше.
(см. § 1): чем больше это число, тем "изломанность" выше.
Недостаток такого выбора заключается в том, что  и при решении задачи (3.26) нельзя будет заранее (т.е. до определения
и при решении задачи (3.26) нельзя будет заранее (т.е. до определения  провести классификацию фрагментов
провести классификацию фрагментов  Выходом из этой ситуации может быть использование следующей нормализации фрагментов функции
Выходом из этой ситуации может быть использование следующей нормализации фрагментов функции

где  среднее значение функции
среднее значение функции  на
на  что обеспечивает выполнение равенства
что обеспечивает выполнение равенства

В качестве признака классификации фрагментов выберем такую "нормализованную" размерность  которая также не будет зависеть от параметров
которая также не будет зависеть от параметров  функции
функции 
Таким образом, поиск пар регион-домен будет состоять из двух этапов:
1) нахождение и запоминание "нормализованных" размерностей  для всех рассматриваемых регионов
для всех рассматриваемых регионов  и домен
и домен 
2) для каждого региона  поиск производится лишь среди тех домен, размерности которых
поиск производится лишь среди тех домен, размерности которых  близки к размерности
близки к размерности  этого региона.
этого региона.
Замечание. При реализации данного алгоритма на ЭВМ необходимо имеь в виду, что при представлении функции  в виде двумерного массива (матрицы) отсчетов мы не можем вычислить хаусдорфову размерность. В этом случае имеет смысл воспользоваться одним из следующих способов (см., напр., [116]):
в виде двумерного массива (матрицы) отсчетов мы не можем вычислить хаусдорфову размерность. В этом случае имеет смысл воспользоваться одним из следующих способов (см., напр., [116]):
а) вместо предела при  выбрать просто достаточно малое
выбрать просто достаточно малое  (скажем, наименьшее возможное при данном представлении функции
(скажем, наименьшее возможное при данном представлении функции  в цифровом устройстве) и вычислить
в цифровом устройстве) и вычислить

б) задать два значения  и положить
и положить

В обоих вариантах значение  будет отличаться от истинного
будет отличаться от истинного  но вполне подходит в качестве меры "гористости" графиков функций.
но вполне подходит в качестве меры "гористости" графиков функций.
Другим способом уменьшения времени поиска в случае нормы  может быть модификация механизма вычислений без изменения самой идеи полного перебора.
может быть модификация механизма вычислений без изменения самой идеи полного перебора.
Пусть  квадратные области из
квадратные области из  со сторонами, параллельными координатным осям; линейный размер регионов
со сторонами, параллельными координатным осям; линейный размер регионов  в заранее фиксированное число раз (например в два) меньше линейного размера домен
в заранее фиксированное число раз (например в два) меньше линейного размера домен  Множество домен порождается одним доменом
Множество домен порождается одним доменом  параллельно сдвигаемым на некоторый вектор
параллельно сдвигаемым на некоторый вектор
 Определим преобразование
Определим преобразование  так,
так,  Погрешность между фрагментами функции определяется в виде:
Погрешность между фрагментами функции определяется в виде:

при  будем иметь
будем иметь

Основная вычислительная сложность при нахождении  состоит в многократном вычислении интеграла
состоит в многократном вычислении интеграла  Таких вычислений требуется
Таких вычислений требуется

где  количества рассматриваемых домен и регионов. Известно, что выражения вида
количества рассматриваемых домен и регионов. Известно, что выражения вида

где  отрезок из
отрезок из  можно вычислять, используя преобразование Фурье, которое в одномерном случае выглядит следующим образом:
можно вычислять, используя преобразование Фурье, которое в одномерном случае выглядит следующим образом:

Свертку  можно вычислять, используя соотношение:
можно вычислять, используя соотношение:

При этом требуется, чтобы функции  имели период, равный длине отрезка
имели период, равный длине отрезка 
Вычисление выражений (3.31) и (3.32) с помощью дискретного преобразования Фурье

на ЭВМ вполне возможно, но оказывается неэффективным по следующим причинам:
— вычисления приходится проводить в области комплексных значений, тогда как исходное оцифрованное изображение задано, скажем, массивом целых чисел;
— использование величин типа  и
и  приводит к ошибкам округления и конечный результат получается неточным.
приводит к ошибкам округления и конечный результат получается неточным.
Имеет смысл заменить преобразование Фурье неким другим преобразованием, которое обладает всеми необходимыми свойствами для подобного вычисления сверток и корреляций и оперирует с целыми числами. Таким является, например, преобразование Мерсенна [51], особенностью которого является работа в модулярной арифметике. Одномерное р-точечное преобразование Мерсенна записывается в виде:

Где  простое число. Числа вида
простое число. Числа вида  простое) называются числами Мерсенна. Сравнивая дискретное преобразование Фурье и преобразование Мерсенна, заметим, что
простое) называются числами Мерсенна. Сравнивая дискретное преобразование Фурье и преобразование Мерсенна, заметим, что  т.е. в обоих преобразованиях разложение происходит по базису, составленному из корней
т.е. в обоих преобразованиях разложение происходит по базису, составленному из корней  степени из 1 соответственно.
степени из 1 соответственно.
Обратное преобразование Мерсенна записывается в виде:

где  обратный элемент к
обратный элемент к  т.е.
т.е. 
Нетрудно показать, что  совпадают с точностью до перестановки элементов в наборах, а величина
совпадают с точностью до перестановки элементов в наборах, а величина  где
где  целая часть выражения. Циклическая свертка [51] представляется следующим образом
целая часть выражения. Циклическая свертка [51] представляется следующим образом

а корреляция

при условии, что значения получаемых отсчетов не превосходят величины 
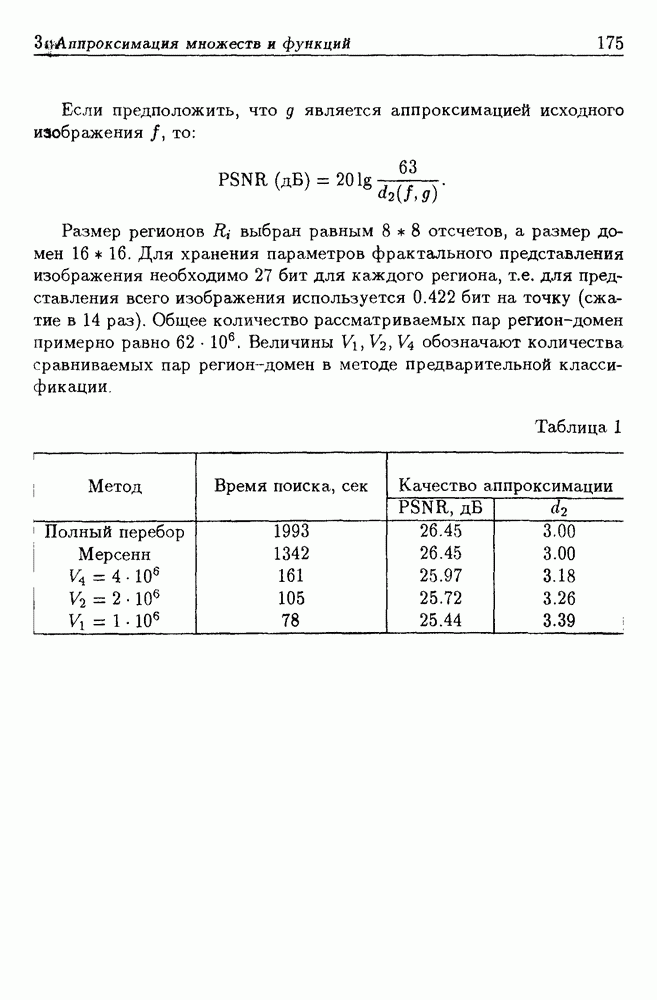
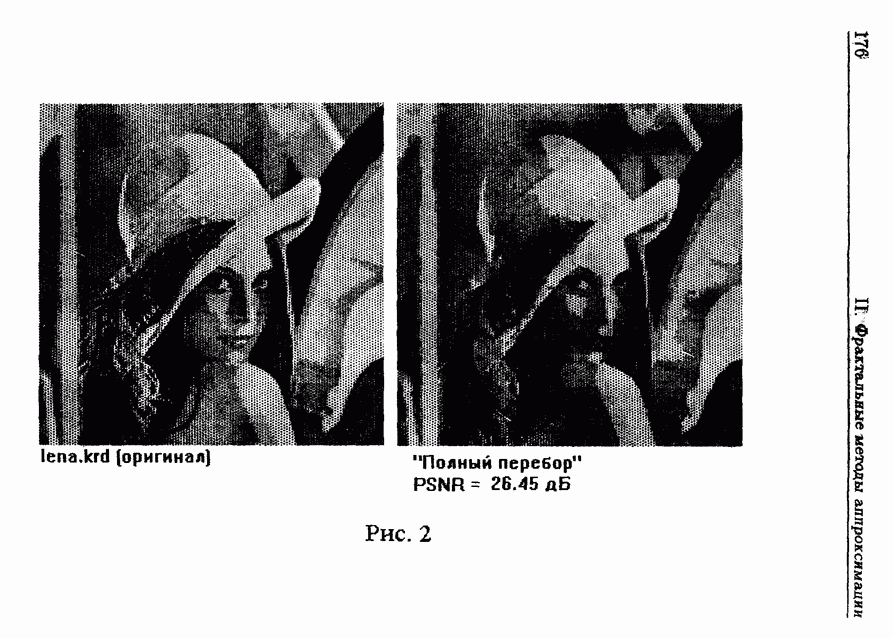
Пример 3 (Я.В. Малыгин). Поиск параметров фрактального сжатия проводился на стандартном монохромном изображении  размером 256 256 графических элементов (пикселей) с глубиной цвета 6 бит на точку (64 оттенка серого). Вычисления осуществлялись на Pentium 150 без программной оптимизации. Результаты расчетов приведены в таблице 1 и на рис. 2. Качество аппроксимации определяется двумя способами: а) расстоянием в 12 между двумя функциями, определяющими изображения, и б) величиной пикового отношения сигнал-шум (PSNR, - peak signal-to-noise ratio) в децибелах. Для двух изображений
размером 256 256 графических элементов (пикселей) с глубиной цвета 6 бит на точку (64 оттенка серого). Вычисления осуществлялись на Pentium 150 без программной оптимизации. Результаты расчетов приведены в таблице 1 и на рис. 2. Качество аппроксимации определяется двумя способами: а) расстоянием в 12 между двумя функциями, определяющими изображения, и б) величиной пикового отношения сигнал-шум (PSNR, - peak signal-to-noise ratio) в децибелах. Для двух изображений  с целочисленными значениями отсчетов
с целочисленными значениями отсчетов  расстояние в 12 определяется в виде:
расстояние в 12 определяется в виде:

Если предположить, что  является аппроксимацией исходного изображения
является аппроксимацией исходного изображения 

Размер регионов  выбран равным 88 отсчетов, а размер домен 16 16. Для хранения параметров фрактального представления изображения необходимо 27 бит для каждого региона, т.е. для представления всего изображения используется 0.422 бит на точку (сжатие в 14 раз). Общее количество рассматриваемых пар регион-домен примерно равно
выбран равным 88 отсчетов, а размер домен 16 16. Для хранения параметров фрактального представления изображения необходимо 27 бит для каждого региона, т.е. для представления всего изображения используется 0.422 бит на точку (сжатие в 14 раз). Общее количество рассматриваемых пар регион-домен примерно равно  Величины
Величины  обозначают количества сравниваемых пар регион-домен в методе предварительной классификации.
обозначают количества сравниваемых пар регион-домен в методе предварительной классификации.
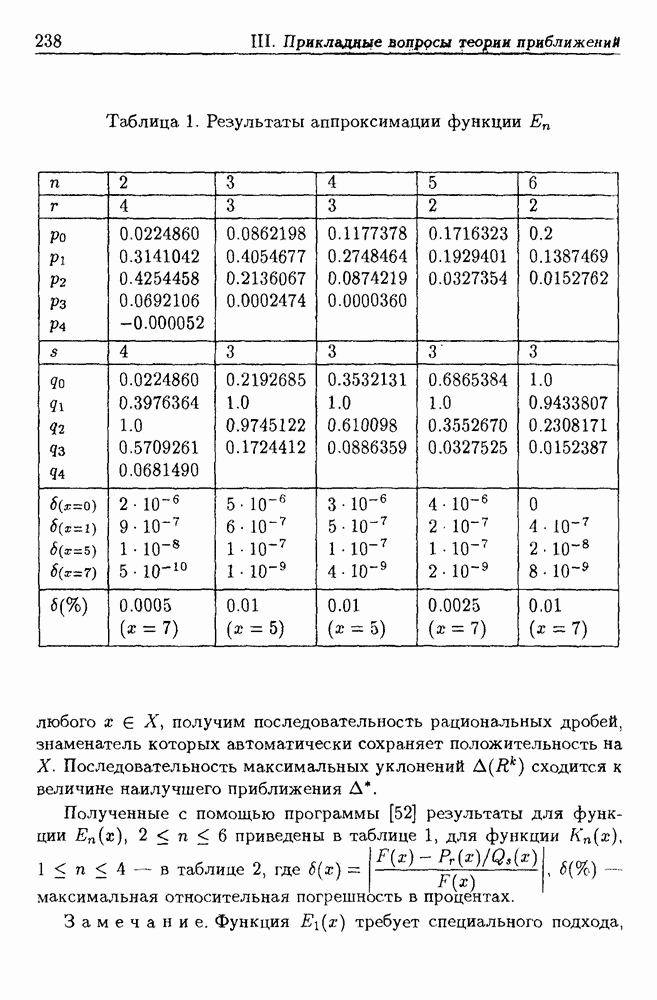
Таблица 1 (см. скан)

(кликните для просмотра скана)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
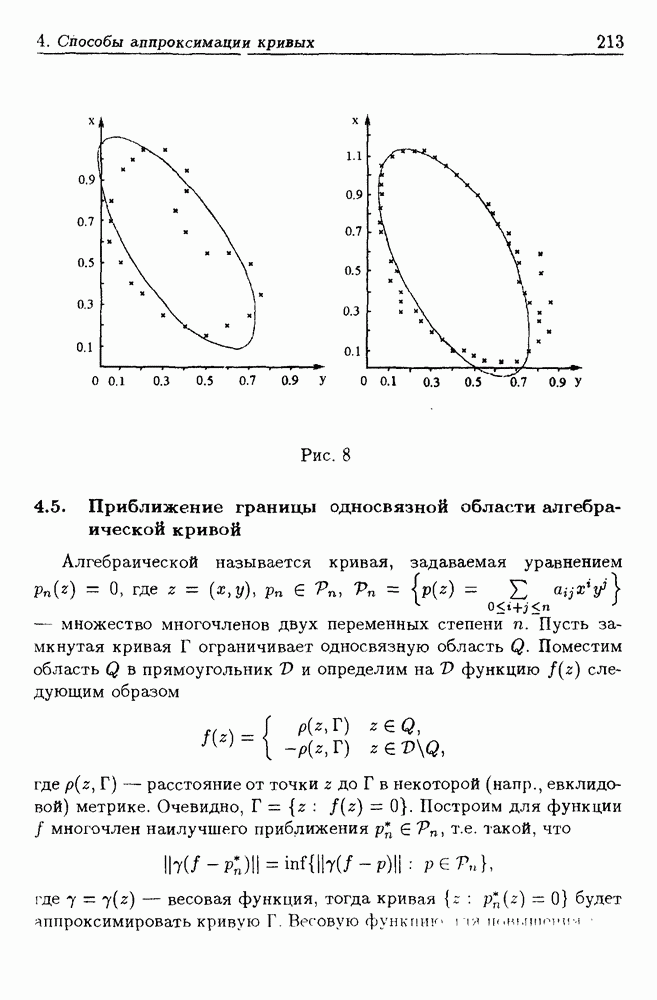
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
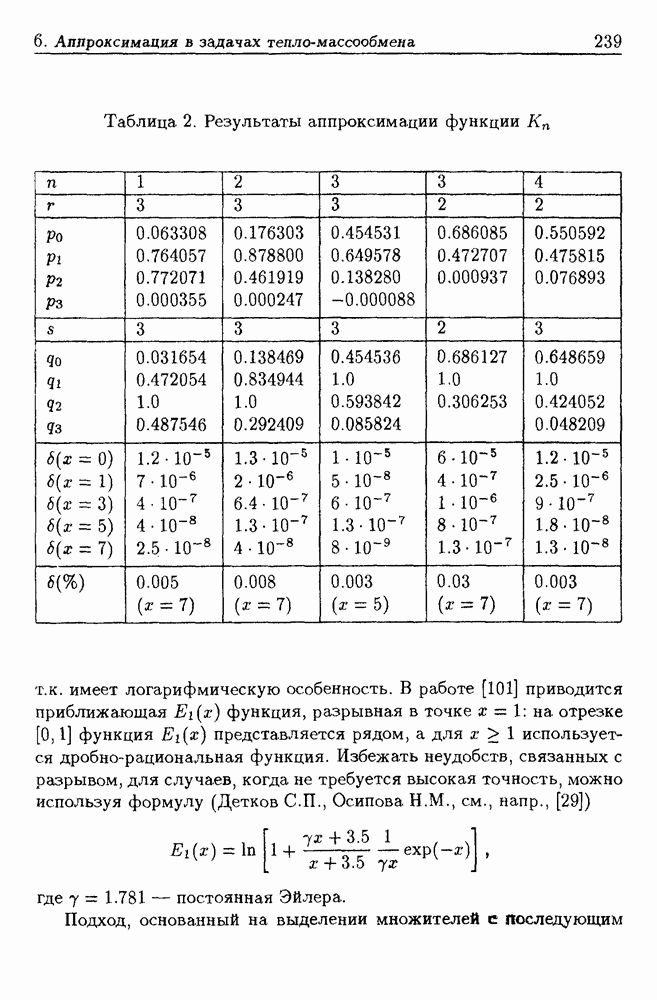
- 6.2. Формулы для функций …
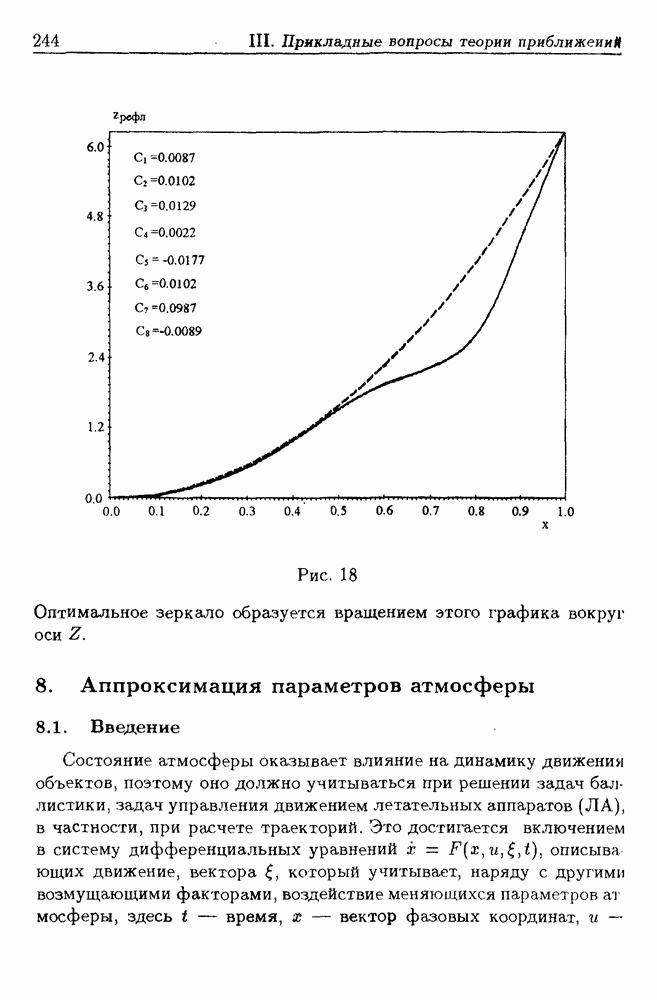
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
- 8. Аппроксимация параметров атмосферы
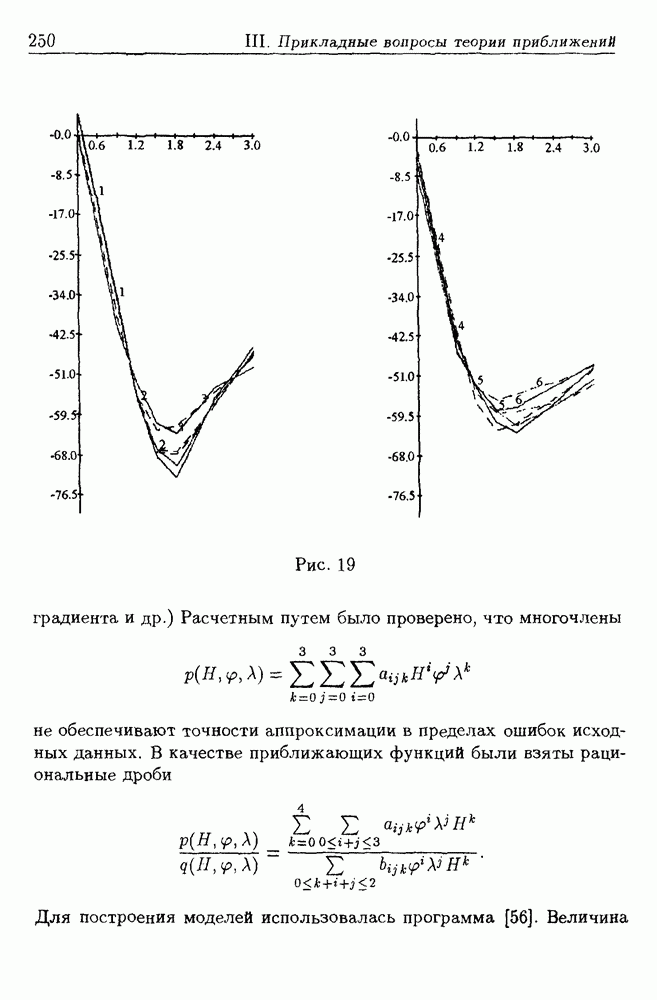
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
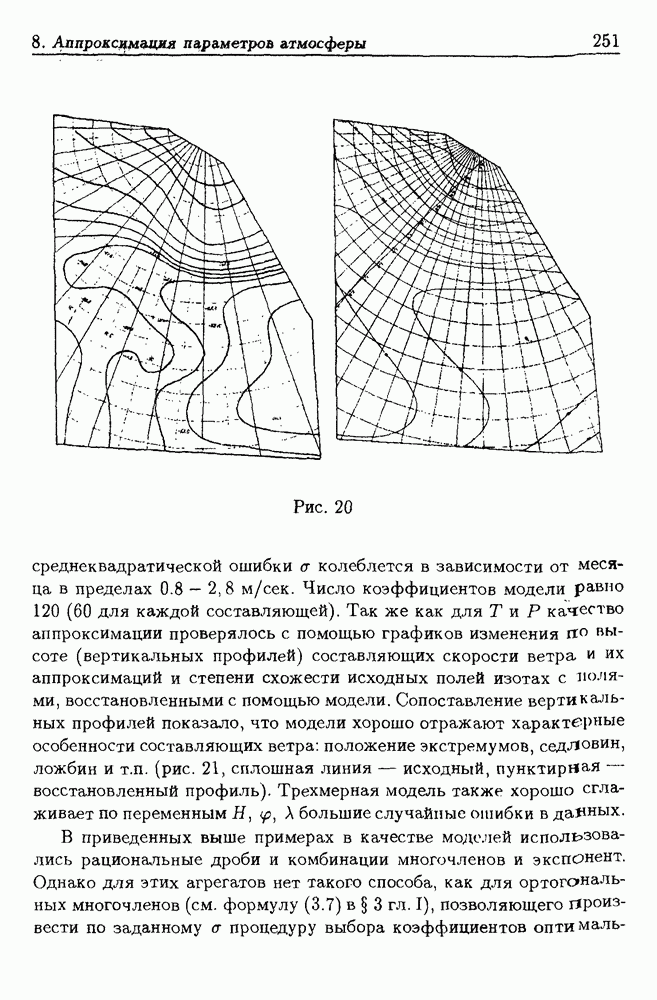
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ