| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
6.1. Введение
Примером эффективного использования рациональных дробей в качестве аппроксимирующих функций являются формулы, дающие аналитическое представление для интегро-экспоненциальных функций  и модифицированных функций Бесселя третьего рода
и модифицированных функций Бесселя третьего рода  Специальные функции
Специальные функции

и

входят в уравнения переноса энергии излучений различной природы, рассматриваемые в задачах нейтронной физики, астрофизики, оптики атмосферы, теплотехники и других разделах науки.
В задачах тепло-массообмена с использованием этих функций вычисляются степени черноты объемов, угловые коэффициенты, коэффициенты облученности и другие безразмерные лучистые потоки.
Приведем примеры использования функций  (см., напр., [26, 27]):
(см., напр., [26, 27]):
— обобщенный угловой коэффициент  для граней бесконечного параллелепипеда с поглощающей средой выражается:
для граней бесконечного параллелепипеда с поглощающей средой выражается:
в случае перпендикулярных граней в виде

где

в случае параллельных граней формулой

где  угловой коэффициент диатермальной среды,
угловой коэффициент диатермальной среды,  и — к
и — к  ширина полос, Я — расстояние между ними, к — коэффициент ослабления;
ширина полос, Я — расстояние между ними, к — коэффициент ослабления;
— локальный угловой коэффициент для поверхности бесконечного полуцилиндра во всех четырех квадрантах описывается формулой

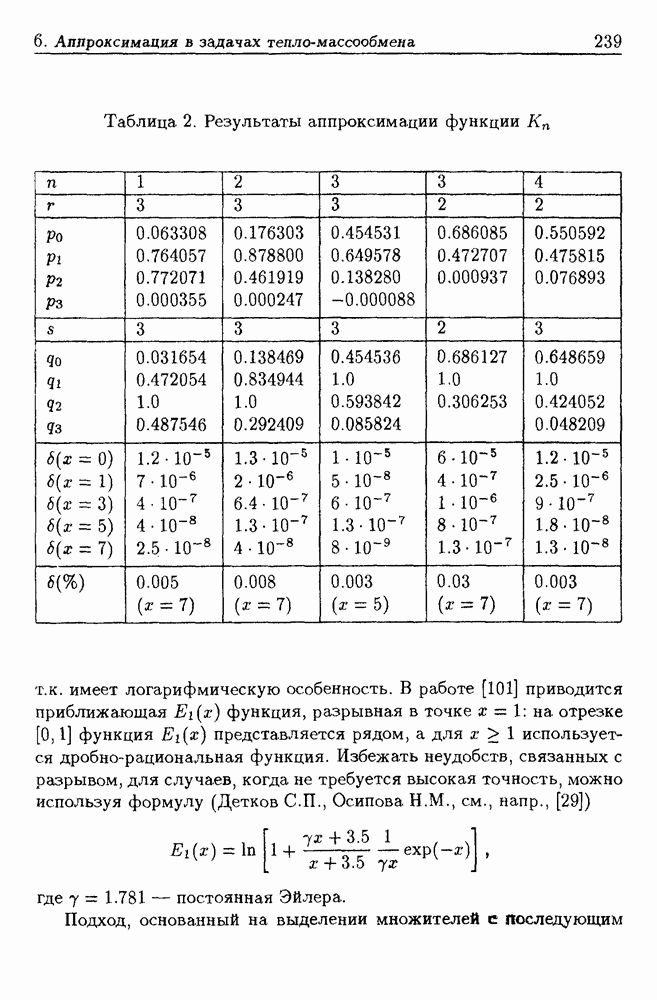
Для вычисления значений  можно использовать соответствующие таблицы, их можно вычислять с помощью рядов и квадратур, что достаточно трудоемко, можно определять их с помощью промежуточных функций
можно использовать соответствующие таблицы, их можно вычислять с помощью рядов и квадратур, что достаточно трудоемко, можно определять их с помощью промежуточных функций  которые, в свою очередь, выражаются через табулированные функции Бесселя второго рода от мнимого аргумента и интегралы от них. В современных справочниках по специальным функциям (см., напр., [62]) в качестве формул для вычисления значений функций
которые, в свою очередь, выражаются через табулированные функции Бесселя второго рода от мнимого аргумента и интегралы от них. В современных справочниках по специальным функциям (см., напр., [62]) в качестве формул для вычисления значений функций  предлагаются ряды: для "малых" х это некоторые степенные ряды, для "больших" — асимптотические ряды, представленные в виде бесконечной непрерывной дроби, причем, в силу того, что разложение в ряд для функций с
предлагаются ряды: для "малых" х это некоторые степенные ряды, для "больших" — асимптотические ряды, представленные в виде бесконечной непрерывной дроби, причем, в силу того, что разложение в ряд для функций с  имеет достаточно громоздкий вид, предлагают получать значения
имеет достаточно громоздкий вид, предлагают получать значения  через рекуррентные соотношения, используя значения функций при
через рекуррентные соотношения, используя значения функций при  Следует отметить, что при использовании современных ЭВМ громоздкость формул во многих случаях не является обременительной, однако неудобства при работе с такими формулами могут сохраняться при использовании персональных
Следует отметить, что при использовании современных ЭВМ громоздкость формул во многих случаях не является обременительной, однако неудобства при работе с такими формулами могут сохраняться при использовании персональных
компьютеров средней мощности, или, возможно, когда предъявляются жесткие требования к времени вычисления значений спецфункции в точке.
При решении конкретных задач, руководствуясь требованиями к точности, естественным является желание упростить вычисления, получив для функций  достаточно легко вычислимые аналитические представления на всем отрезке аргумента, причем такие, чтобы максимальная погрешность не превышала некоторой наперед заданной малой величины. Для получения эффективного представления следует учитывать свойства приближаемых функций, их особенности. Например, если удается описать эти особенности некоторой непрерывной достаточно простой в вычислительном плане функцией
достаточно легко вычислимые аналитические представления на всем отрезке аргумента, причем такие, чтобы максимальная погрешность не превышала некоторой наперед заданной малой величины. Для получения эффективного представления следует учитывать свойства приближаемых функций, их особенности. Например, если удается описать эти особенности некоторой непрерывной достаточно простой в вычислительном плане функцией  которая входит как множитель в приближенное представление исходной функции
которая входит как множитель в приближенное представление исходной функции  тогда задача сводится к аппроксимации более простой (в сравнении с
тогда задача сводится к аппроксимации более простой (в сравнении с  функции
функции 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
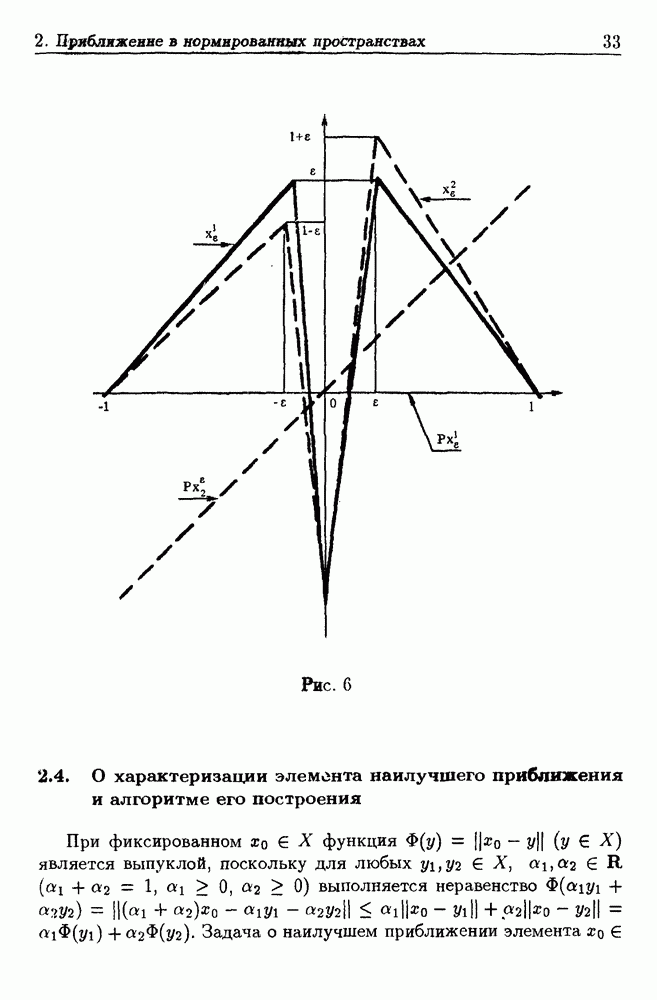
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
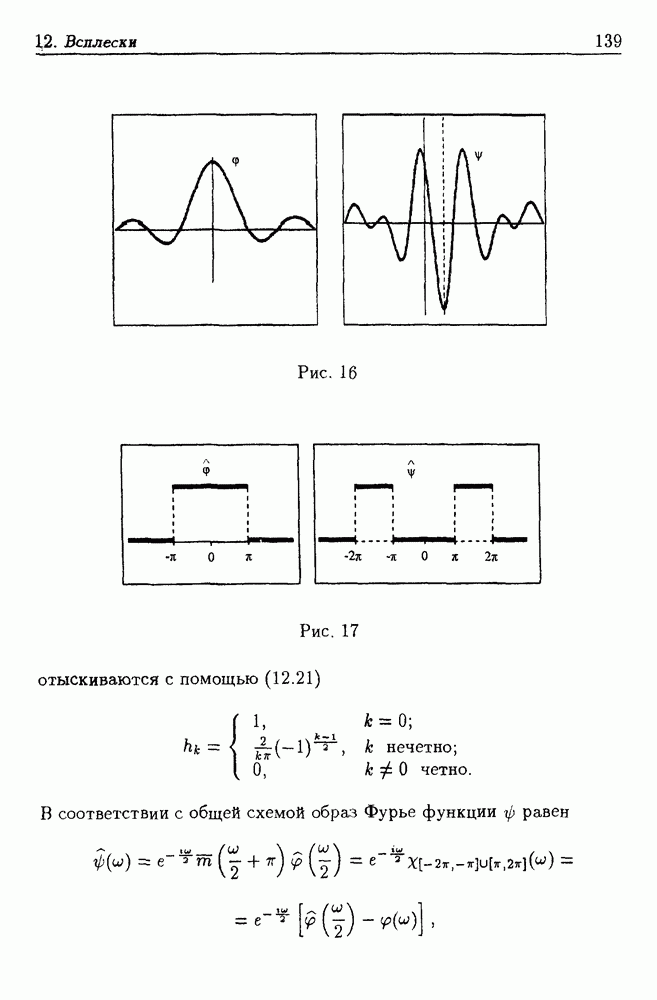
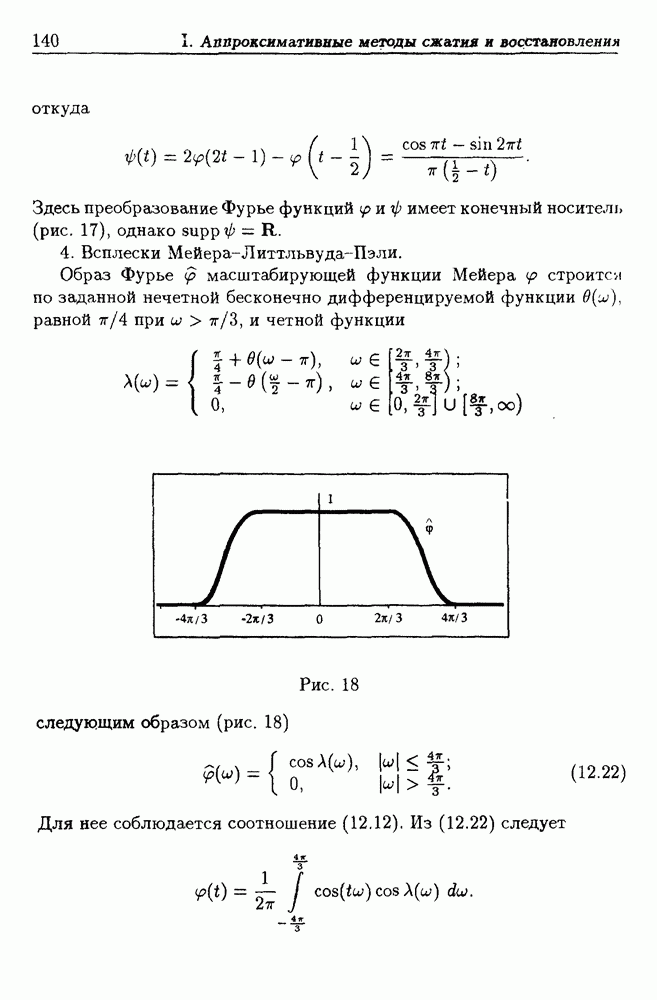
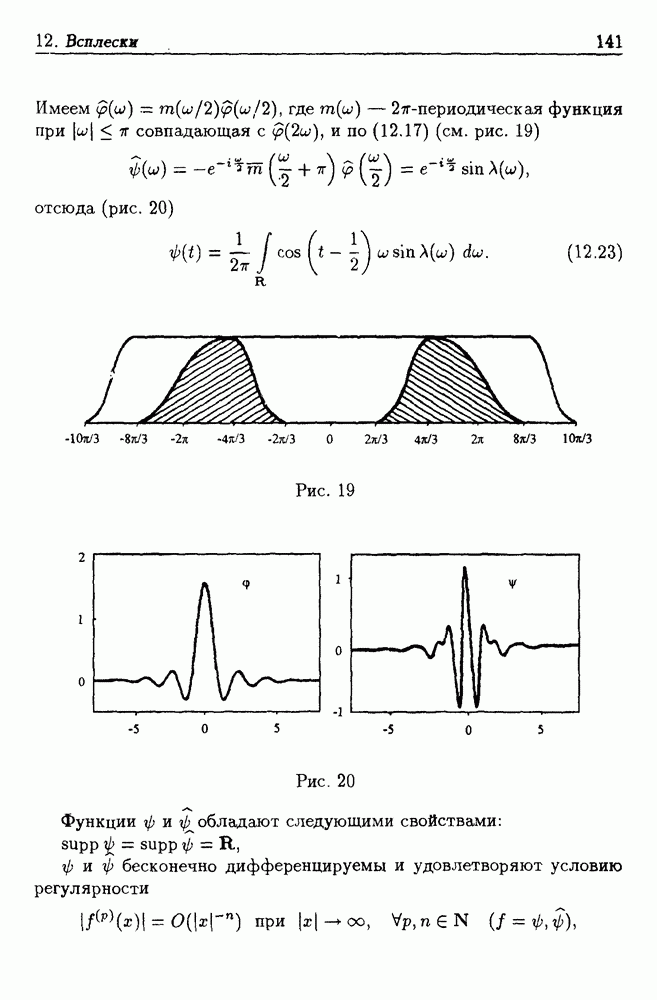
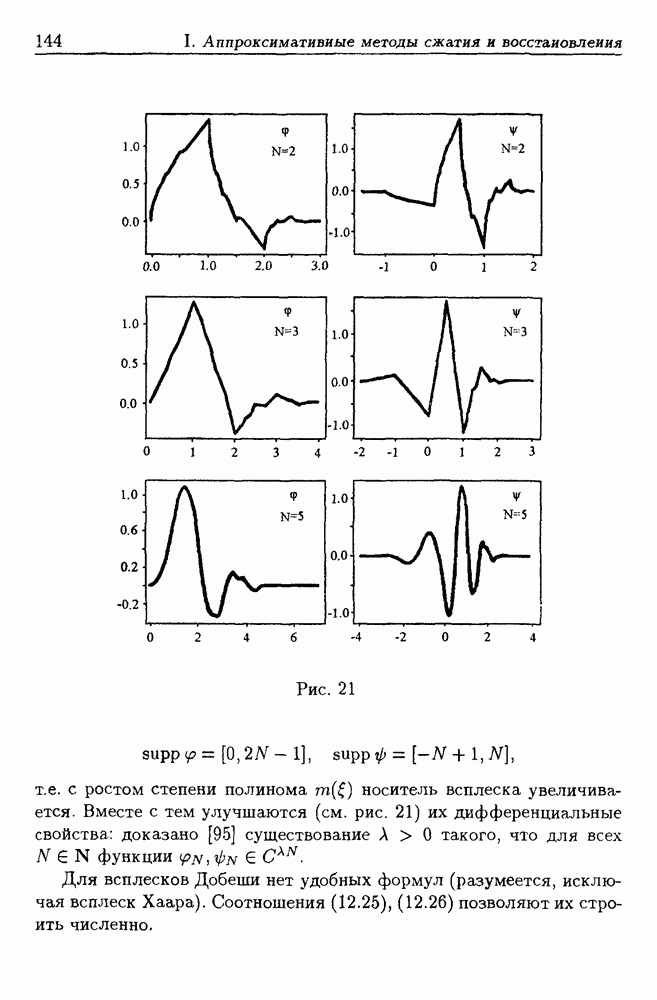
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
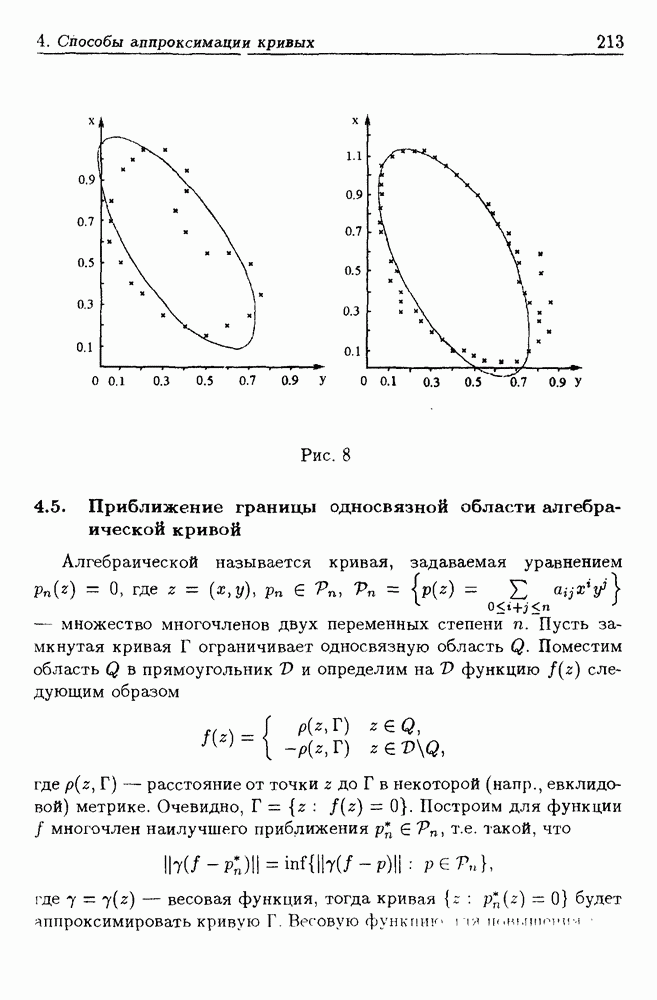
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
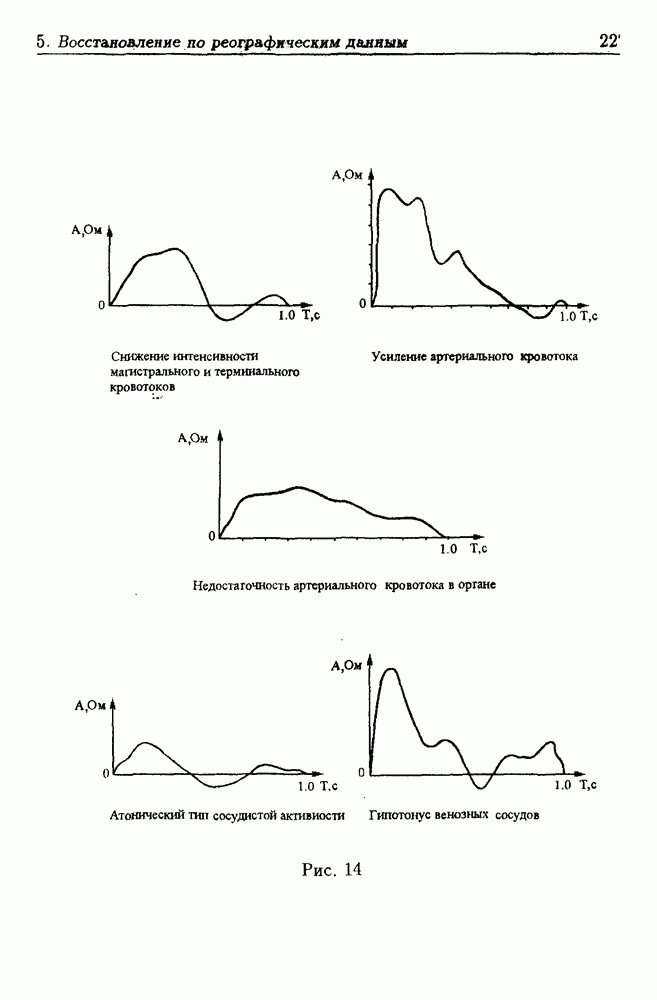
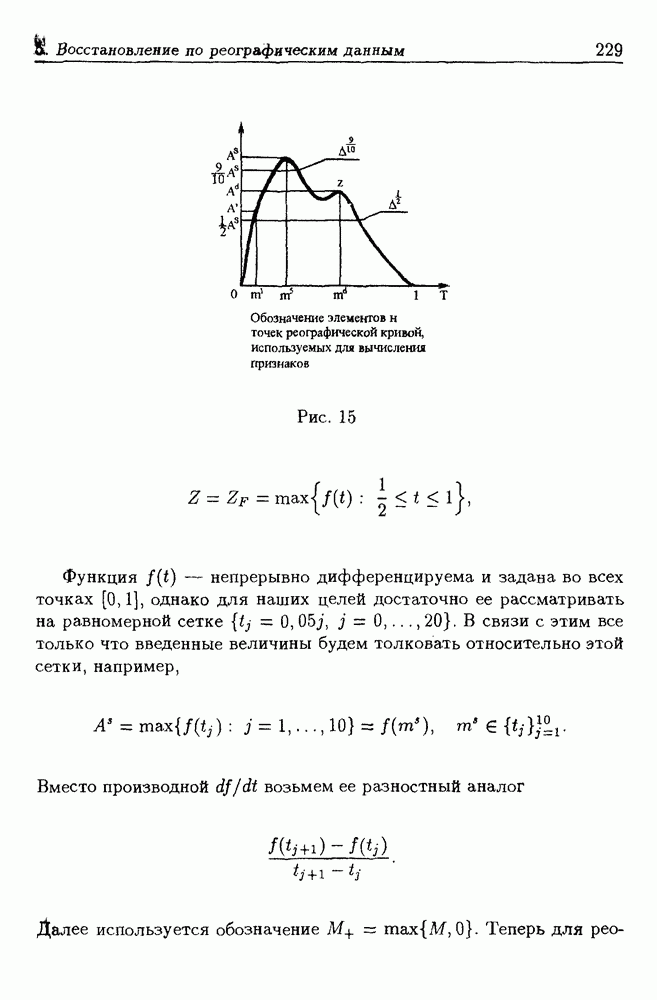
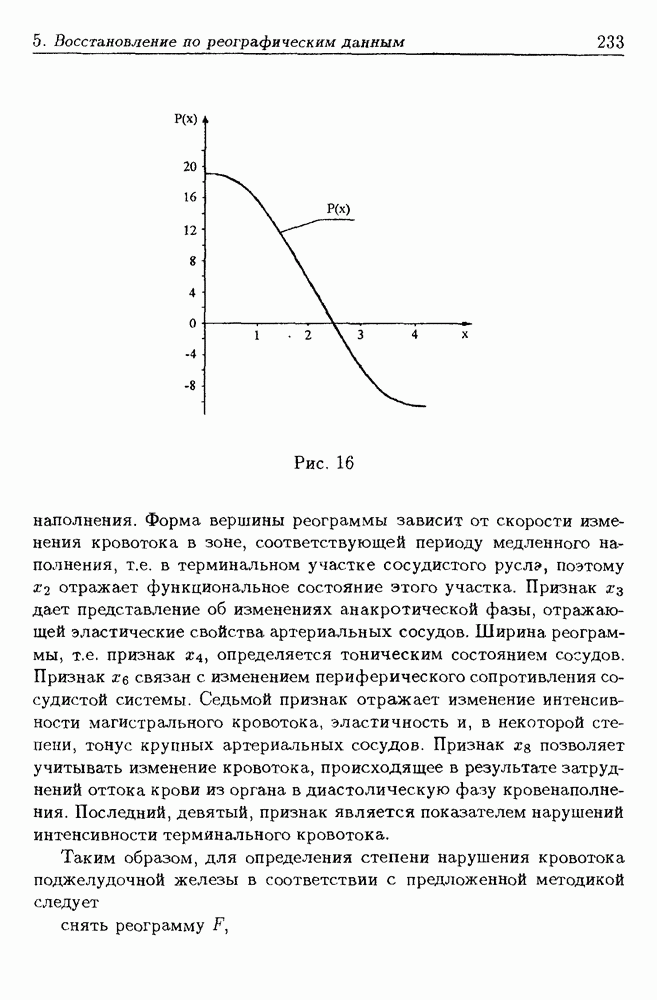
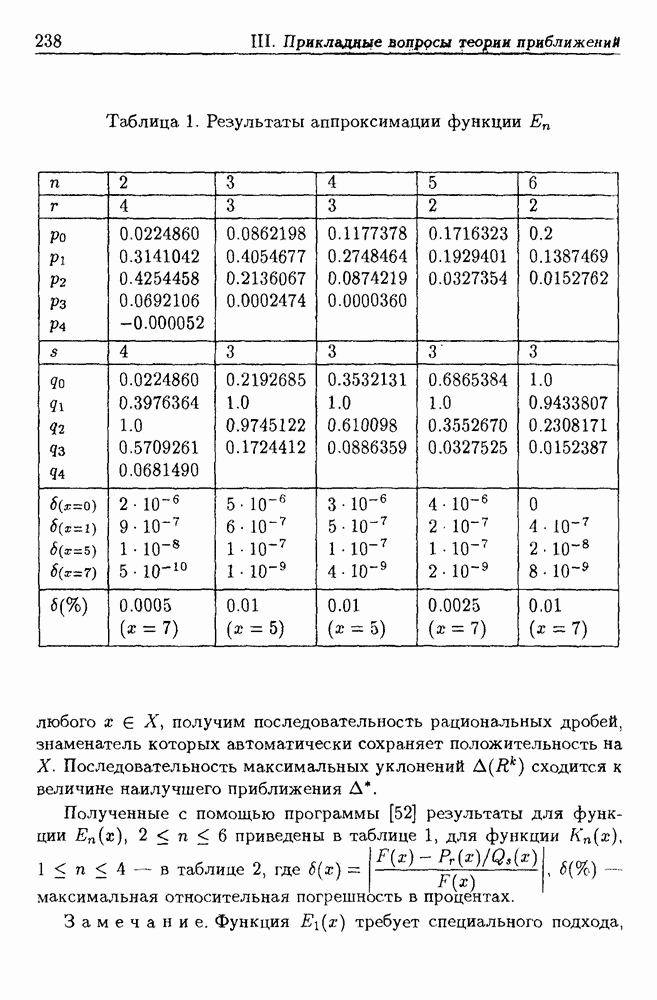
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
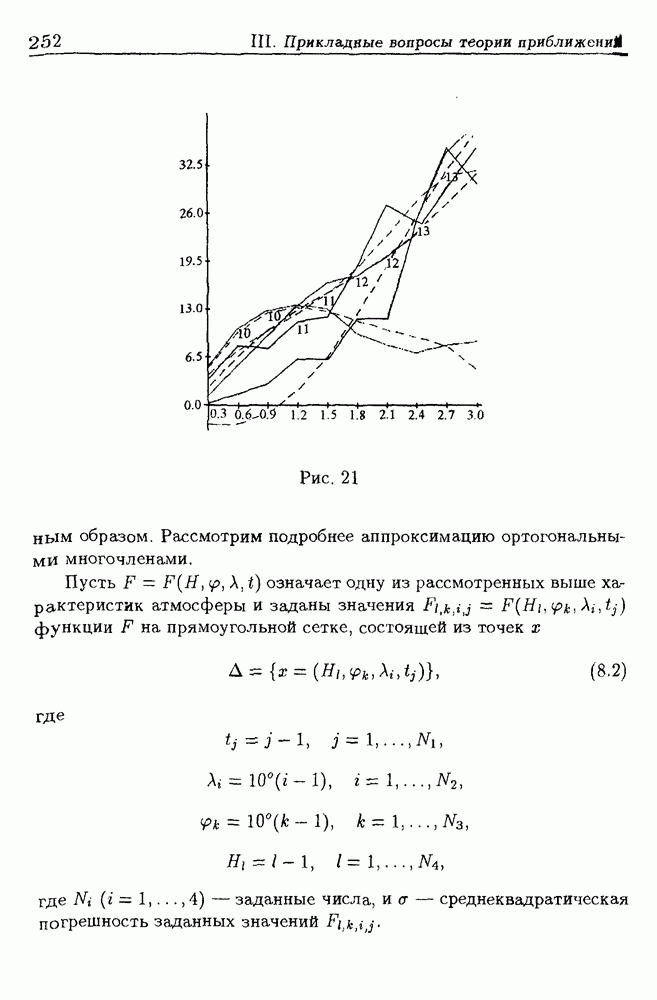
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
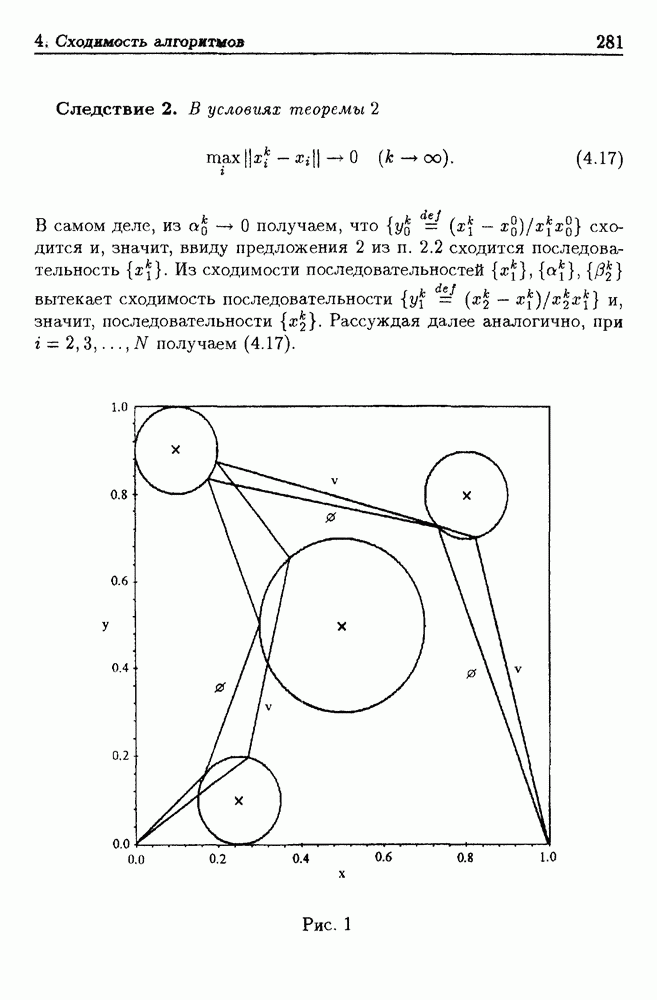
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ