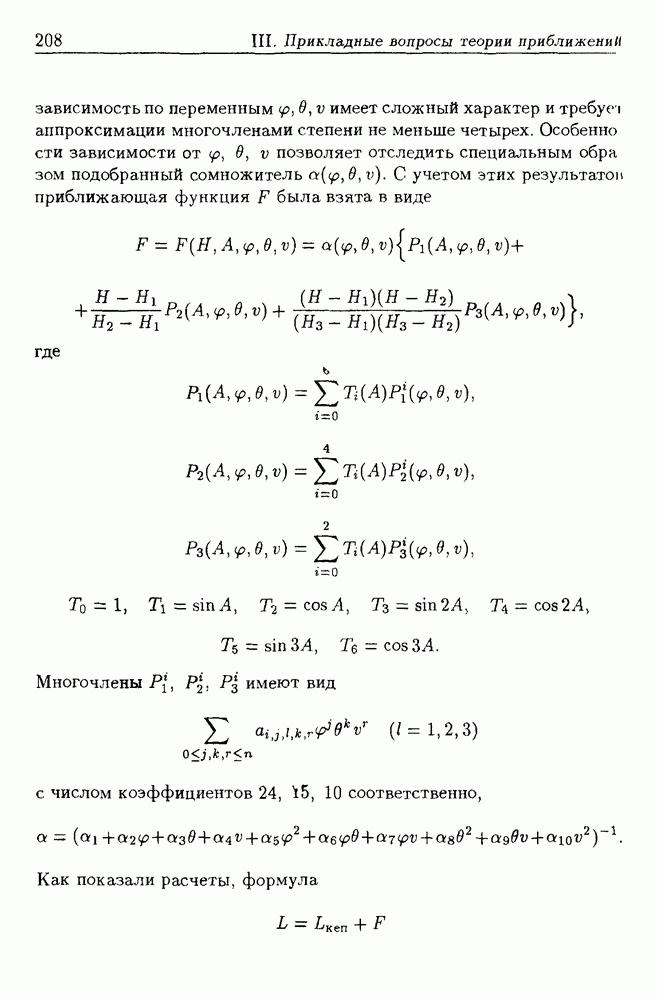| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
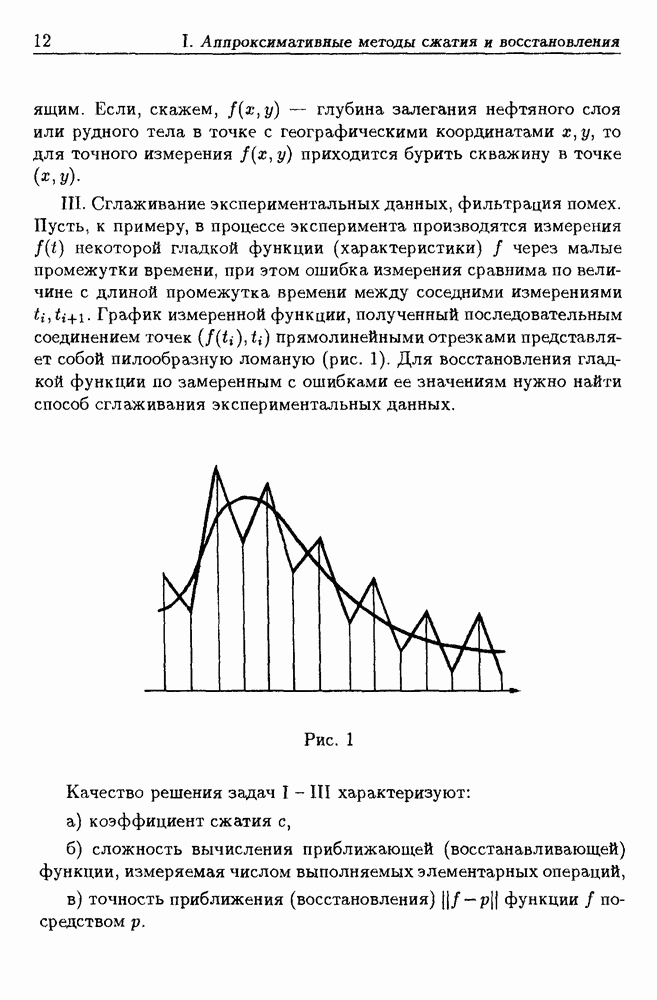
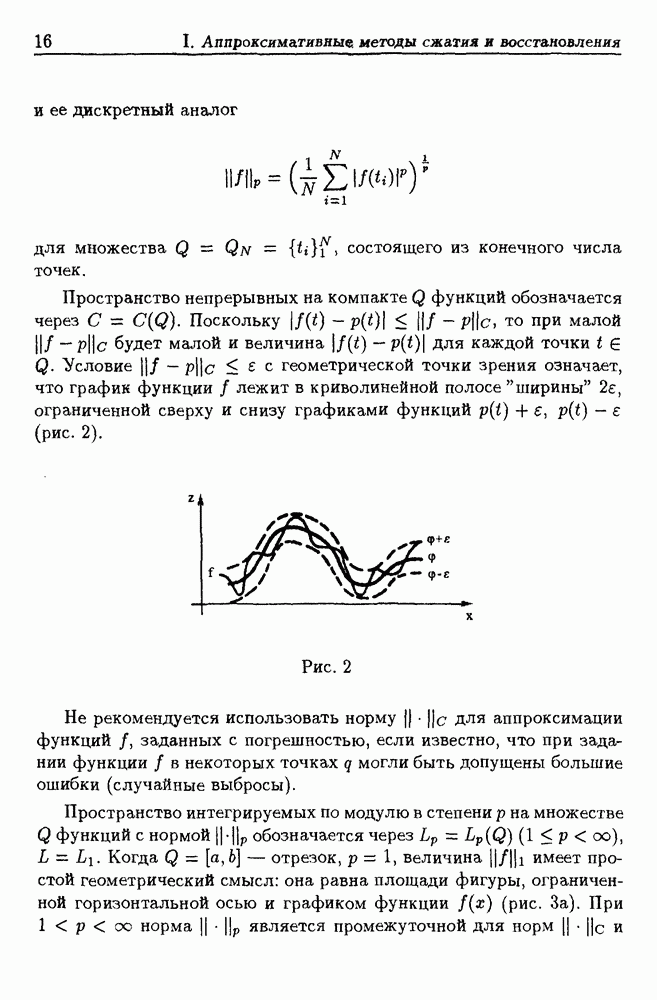
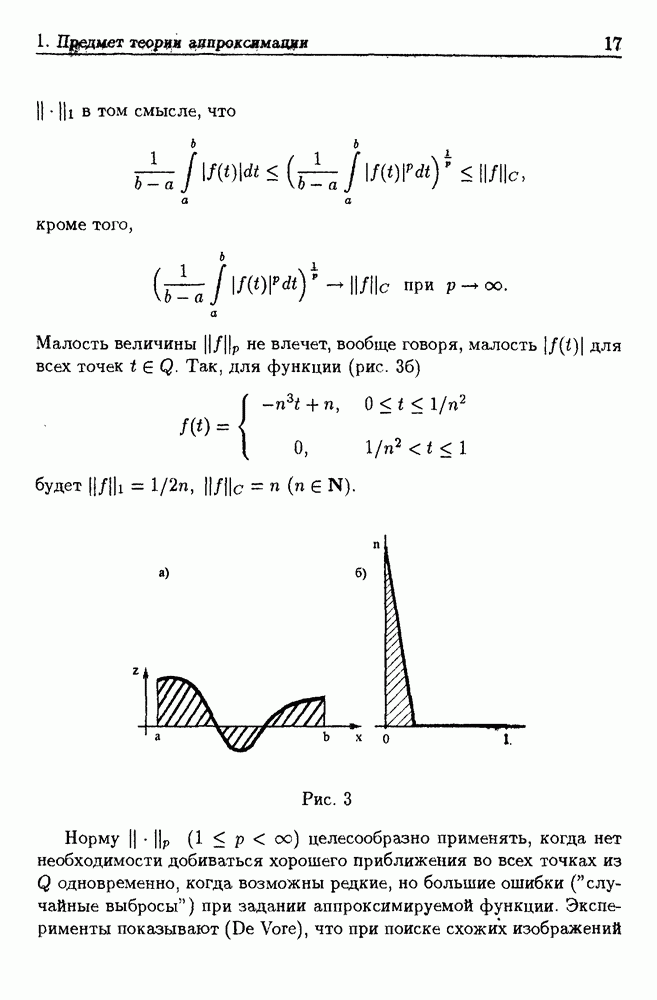
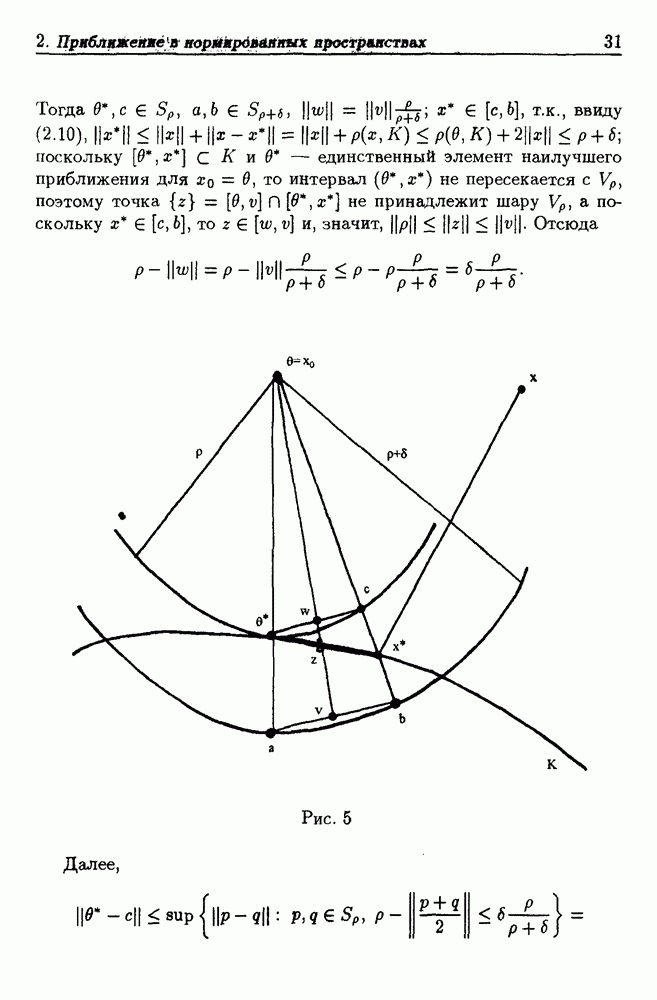
11.2. Приближение экспоненциальными суммами общего вида
Пусть функция  одного переменного задана значениями
одного переменного задана значениями  на равномерной сетке
на равномерной сетке  Обозначим через
Обозначим через  множество всех функций
множество всех функций  являющихся
являющихся
решениями однородных линейных разностных уравнений порядка не выше  с постоянными коэффициентами:
с постоянными коэффициентами:

где

 натуральные,
натуральные,  вещественные числа,
вещественные числа,  причем под полиномом
причем под полиномом  степени —1 следует понимать тождественный нуль. Опишем схему алгоритма. Будем считать, что
степени —1 следует понимать тождественный нуль. Опишем схему алгоритма. Будем считать, что  После замены переменных
После замены переменных  получим новую сетку
получим новую сетку  Пусть
Пусть

— разностное уравнение, которому удовлетворяют заданные значения  Коэффициенты
Коэффициенты  можно определить, решая систему (11.8). Пусть далее
можно определить, решая систему (11.8). Пусть далее  корни характеристического уравнения
корни характеристического уравнения

соответствующего разностному уравнению (11.8). Тогда  можно представить в виде
можно представить в виде

(см. [21], гл. V), где  определяется следующим образом: корень
определяется следующим образом: корень  встречается
встречается  раз в последовательности
раз в последовательности  Величины
Величины  одновременно либо действительные, либо комплексные, причем каждой паре комплексных параметров
одновременно либо действительные, либо комплексные, причем каждой паре комплексных параметров  соответствует пара комплексно-сопряженных параметров
соответствует пара комплексно-сопряженных параметров  Учитывая это и принимая во внимание выполненную замену переменных, преобразуем (11.10) к виду (11.7), т.е.
Учитывая это и принимая во внимание выполненную замену переменных, преобразуем (11.10) к виду (11.7), т.е.

где  вещественные числа,
вещественные числа,  определяется следующим образом:
определяется следующим образом:

Таким образом, для вычисления нелинейно входящих параметров  в (11.7) достаточно знать корни
в (11.7) достаточно знать корни  уравнения (11.9). Коэффициенты в (11.7) можно определить, решая систему линейных уравнений
уравнения (11.9). Коэффициенты в (11.7) можно определить, решая систему линейных уравнений

Изложенная схема рассчитана на случай  На практике число
На практике число  часто бывает неизвестно, кроме того, значения
часто бывает неизвестно, кроме того, значения  могут быть заданы с погрешностью, т.е.
могут быть заданы с погрешностью, т.е.  Описанный алгоритм будем использовать и в этих случаях.
Описанный алгоритм будем использовать и в этих случаях.
Рассмотрим подробнее некоторые части алгоритма. Для определения коэффициентов  в (11.9) рассмотрим переопределенную систему линейных уравнений (11.8). Нетривиальное решение этой системы определяется с точностью до постоянного множителя, следовательно, необходимо какое-либо нормирующее условие, например, одно из следующих трех:
в (11.9) рассмотрим переопределенную систему линейных уравнений (11.8). Нетривиальное решение этой системы определяется с точностью до постоянного множителя, следовательно, необходимо какое-либо нормирующее условие, например, одно из следующих трех:


В указанных выше практических ситуациях система (11.8) вместе с одним из нормирующих условий обычно становится несовместной. Будем решать систему (11-8) с условием (11.14) по методу наименьших квадратов, т.е. находить

где 
Задача (11.15) сводится к решению системы линейных уравнений

где  При этом, если
При этом, если  т.е. для любого
т.е. для любого  существуют
существуют  , такие, что
, такие, что

то такая же линейная зависимость имеет место и в (11.16):

Решение системы (11.16) находим с помощью жордановых исключений [32] с выбором главного элемента по столбцу, исключая каждый раз разрешающую строку из дальнейшего рассмотрения. Для выявления линейной зависимости (11.17) введем параметр  Если при исключении переменной
Если при исключении переменной  элементы
элементы  столбца у оставшихся строк удовлетворяют условию
столбца у оставшихся строк удовлетворяют условию

то переменную  оставляем неисключенной.
оставляем неисключенной.
После окончания процесса исключения вычисляем ранг матрицы  полагая
полагая  где
где  число неисключенных переменных. В случае
число неисключенных переменных. В случае  решаем задачу (11.15) заново с известным теперь значением
решаем задачу (11.15) заново с известным теперь значением  Таким образом, получаем коэффициенты
Таким образом, получаем коэффициенты  и вычисляем каким-либо способом корни
и вычисляем каким-либо способом корни  полинома
полинома  Представим
Представим  в виде (11.11) с неизвестными коэффициентами
в виде (11.11) с неизвестными коэффициентами

Для определения а, решаем систему (11.12) по методу наименьших квадратов

Таким образом, получаем приближенное представление  вида (11.11).
вида (11.11).
Задачу экспоненциальной аппроксимации не всегда удается решить удовлетворительно. Это объясняется, в частности, тем, что малое изменение функции  часто влечет большое изменение коэффициентов
часто влечет большое изменение коэффициентов  наилучшей экспоненциальной суммы. Если
наилучшей экспоненциальной суммы. Если  задана с погрешностью, то результат, следовательно, может сильно отличаться от истинного.
задана с погрешностью, то результат, следовательно, может сильно отличаться от истинного.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
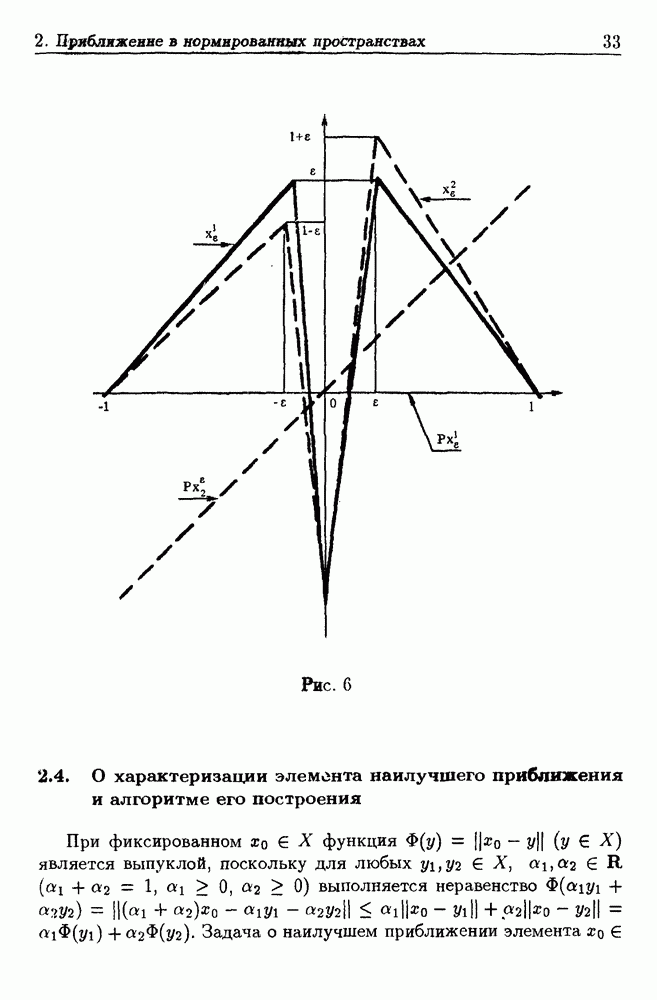
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
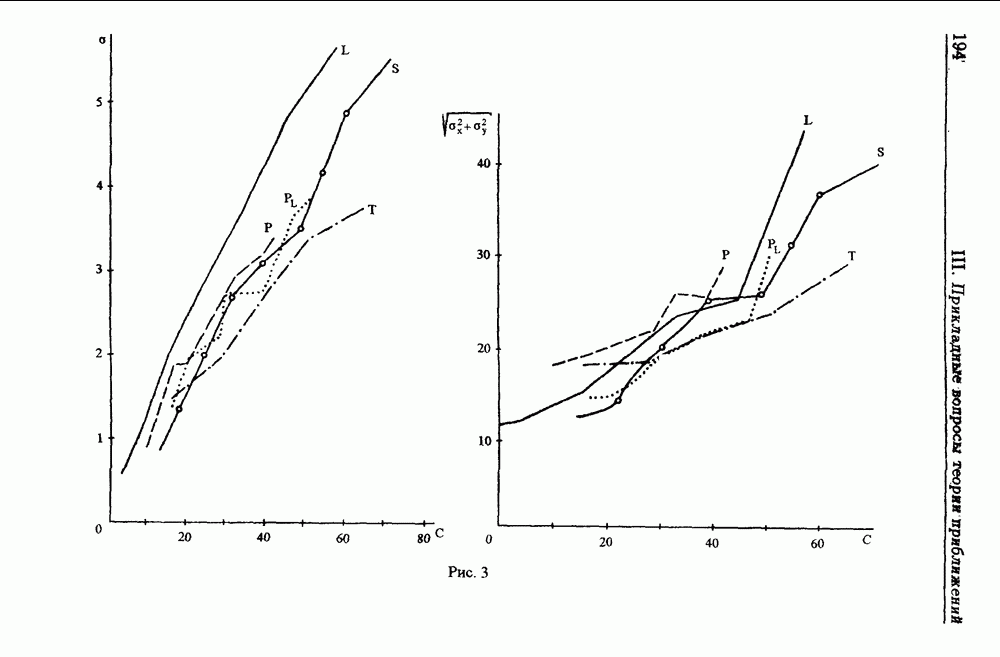
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
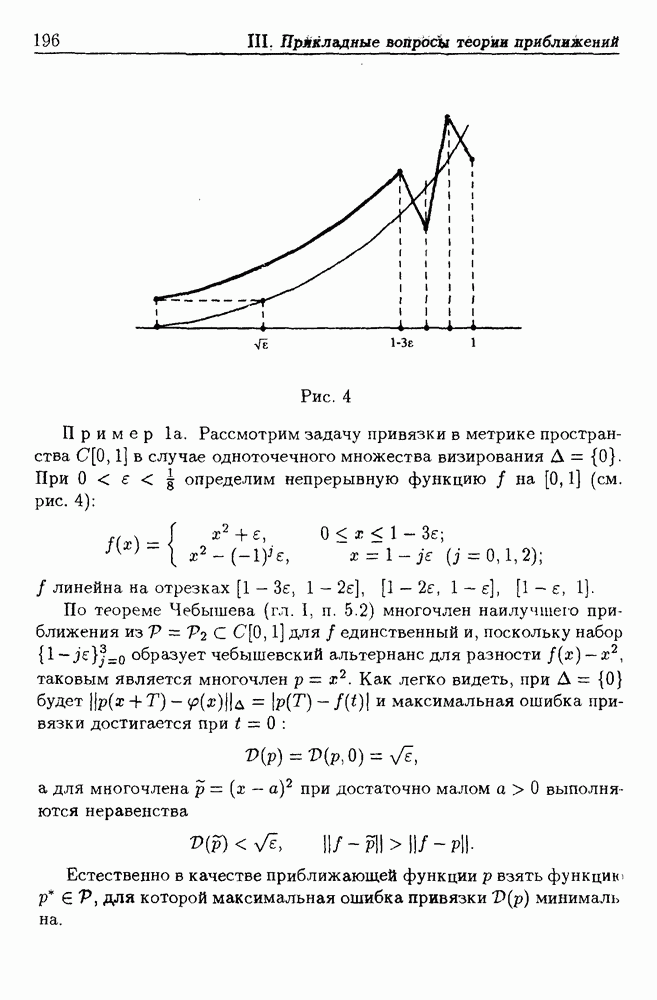
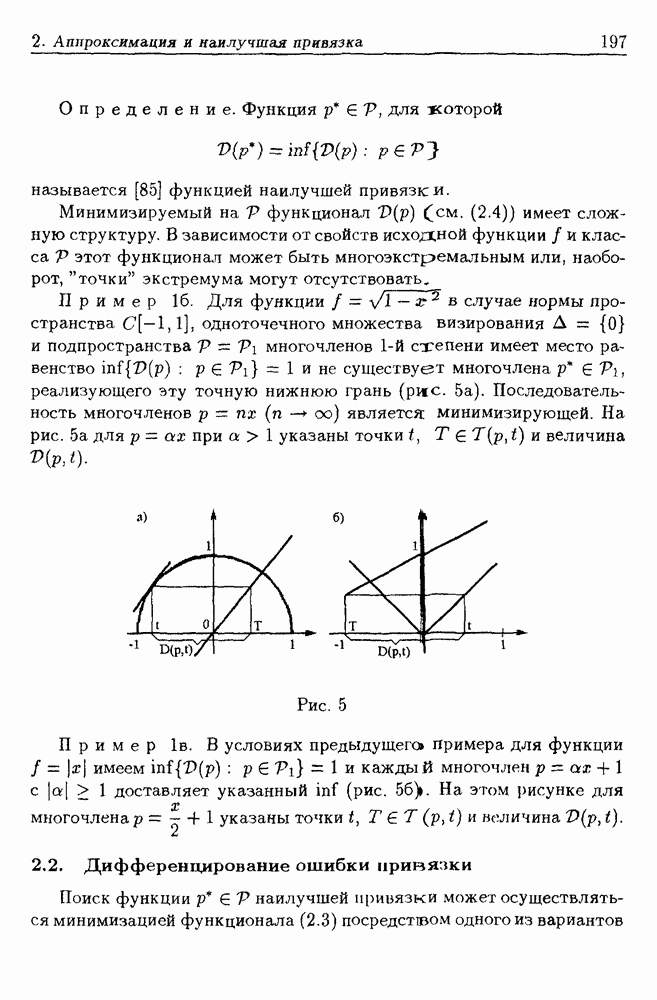
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
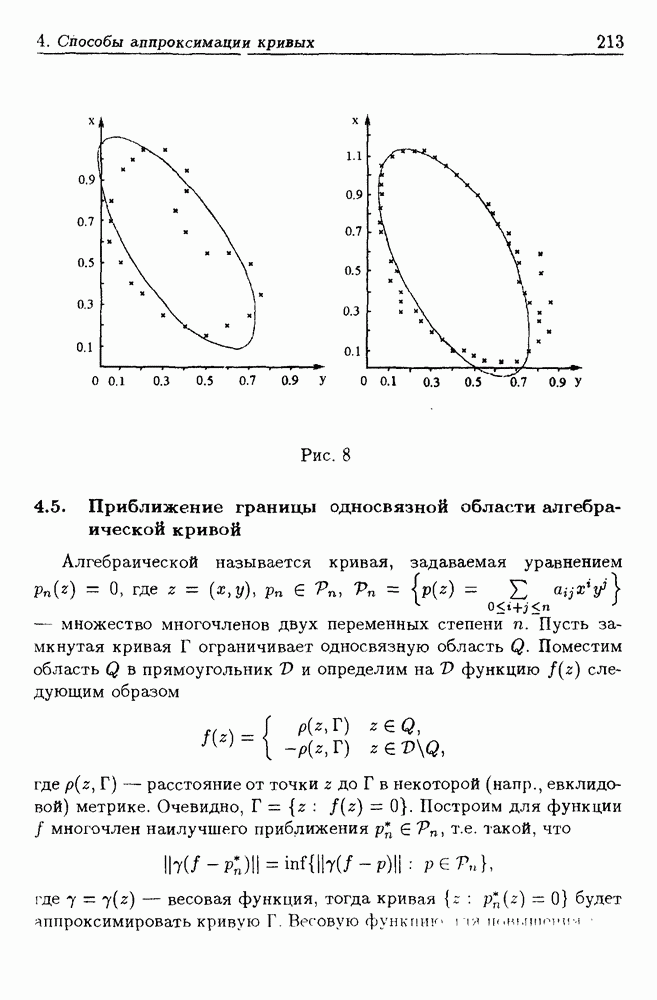
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
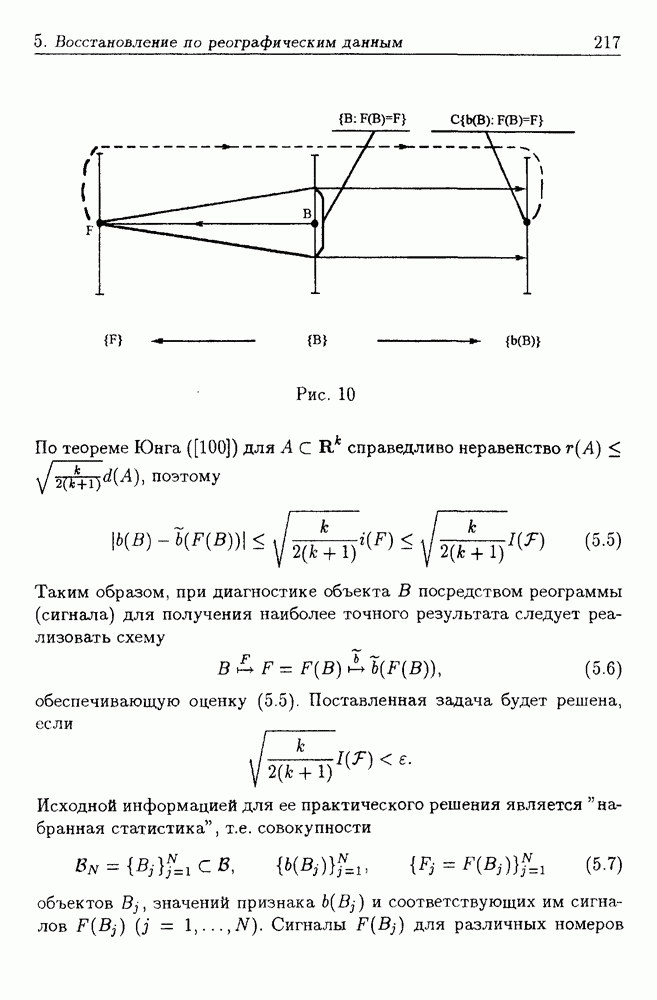
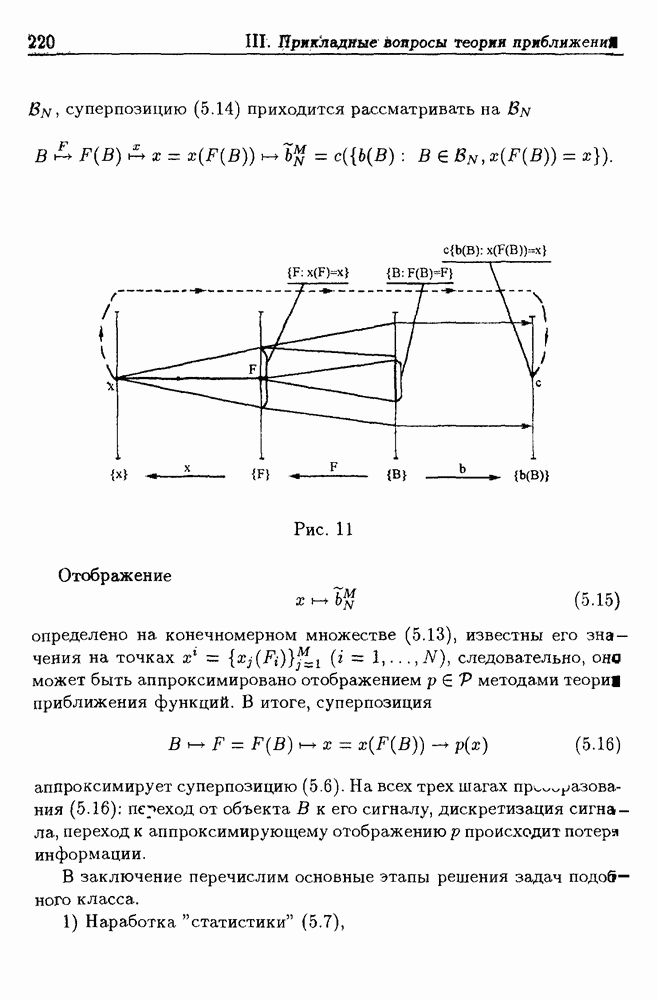
- 5. Восстановление информации по реографическим данным
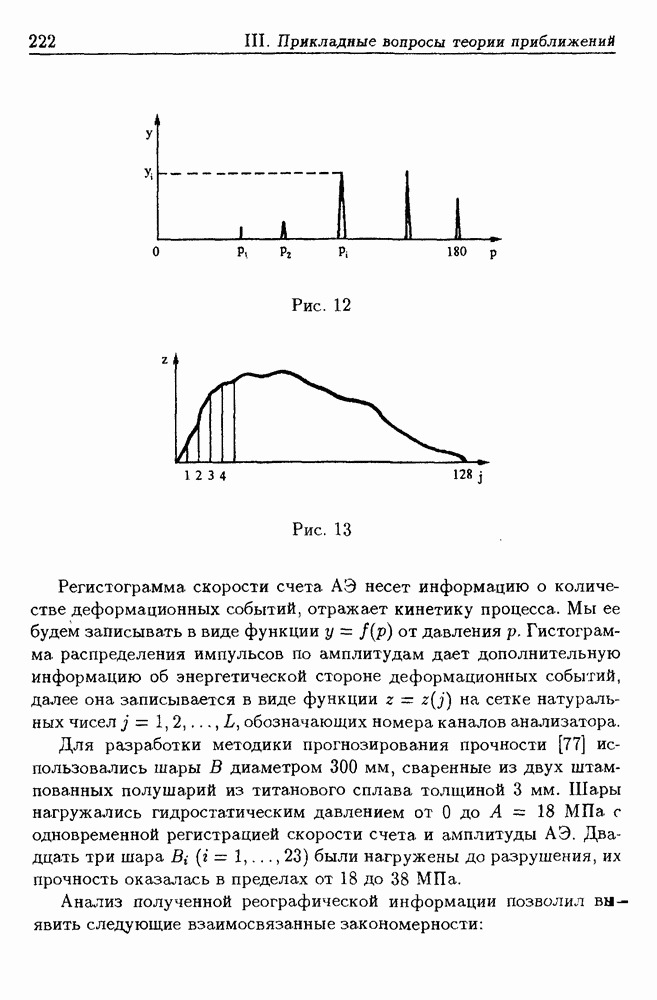
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
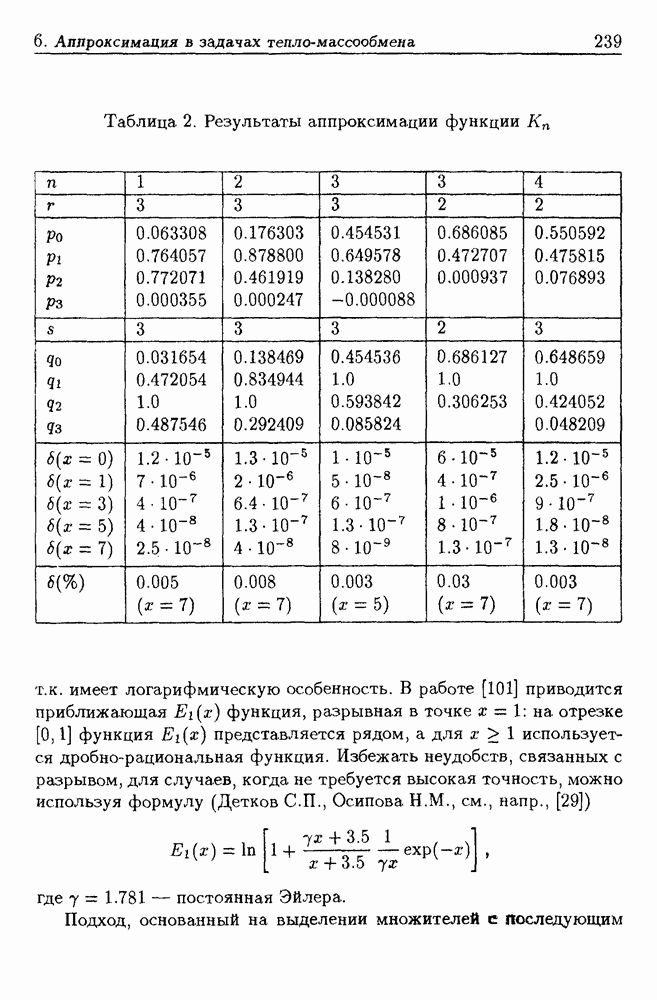
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
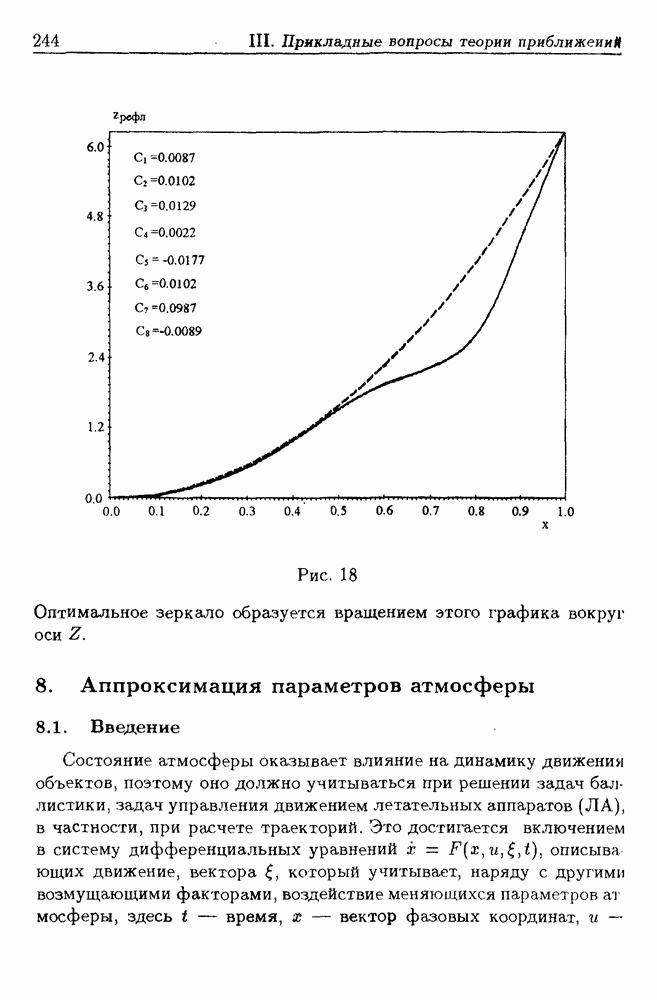
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
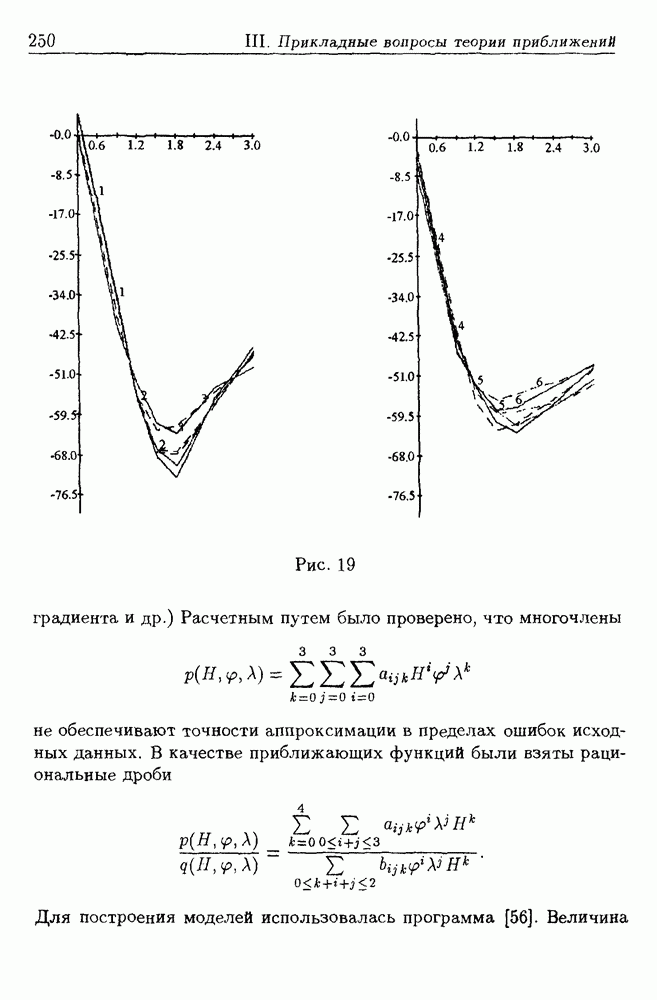
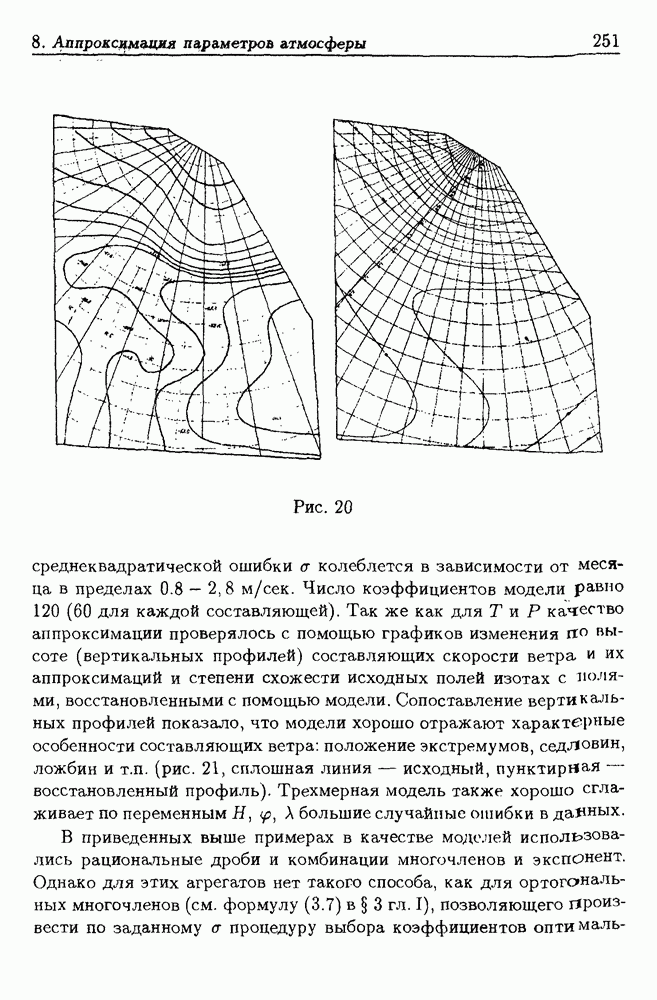
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ