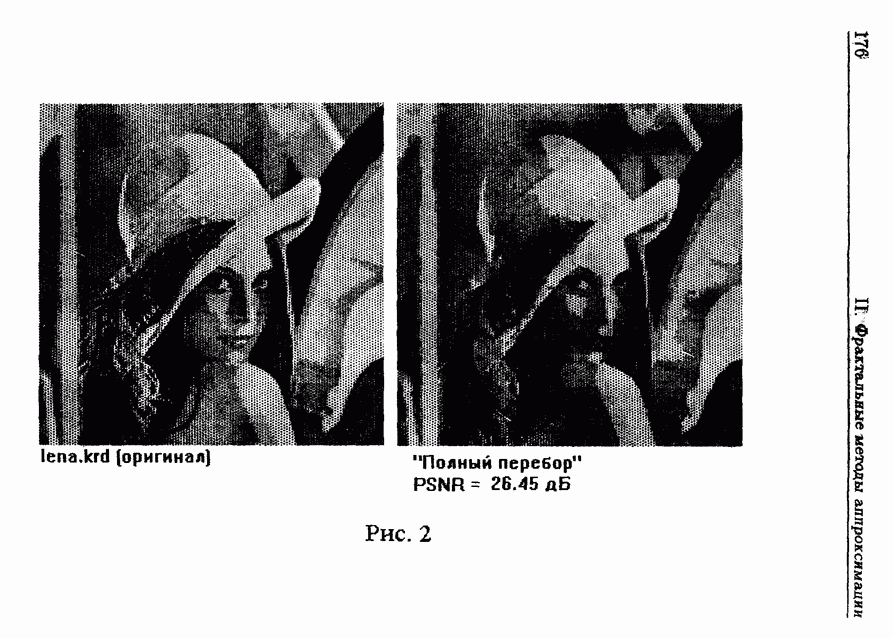
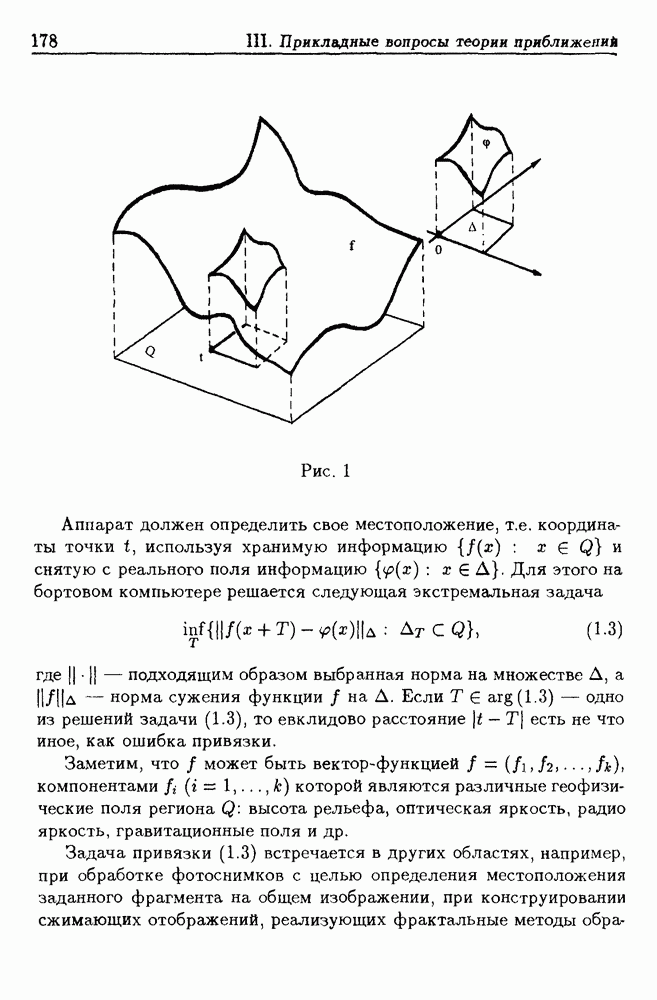
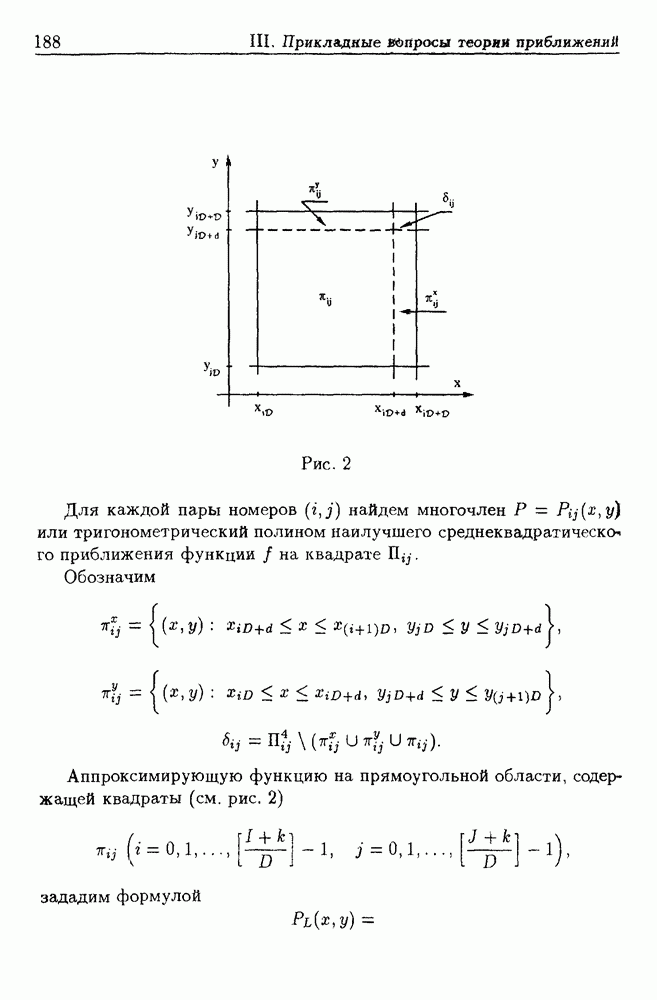
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
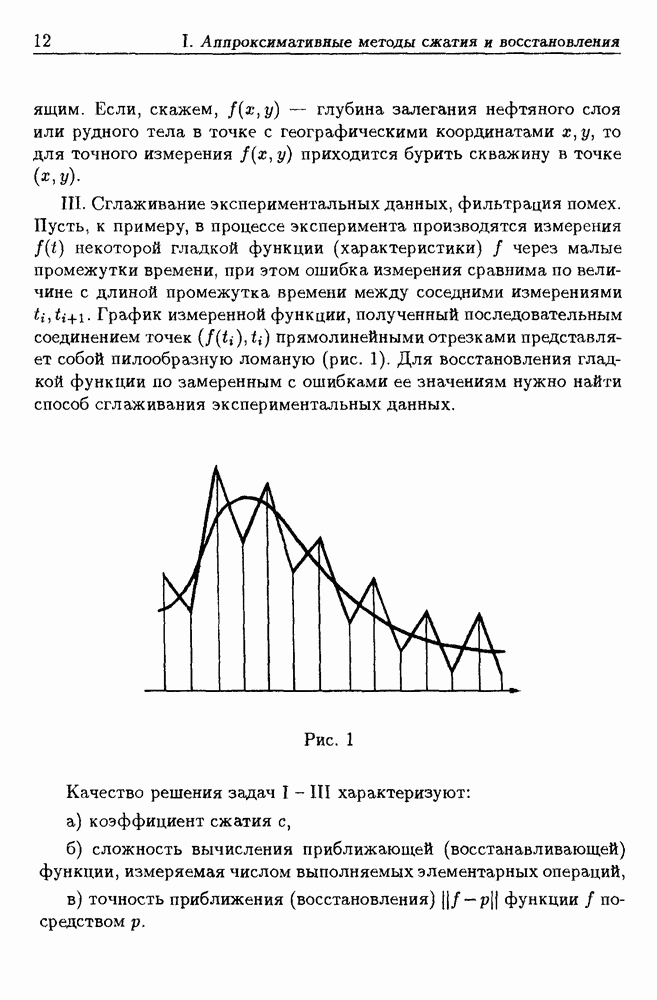
8.4. Примеры региональных моделей атмосферы
Исходной информацией для построения трехмерных моделей температуры и давления являются числовые значения этих параметров для каждого месяца в узлах регулярной сетки

По переменным  взята сетка (из 181 точки), обеспечивающая освещение крупномасштабных особенностей аэроклиматических полей температуры и давления воздуха. Именно эти особенности проявляются в полях среднемесячных значений, другие особенности полей отфильтровываются при осреднении. По переменной
взята сетка (из 181 точки), обеспечивающая освещение крупномасштабных особенностей аэроклиматических полей температуры и давления воздуха. Именно эти особенности проявляются в полях среднемесячных значений, другие особенности полей отфильтровываются при осреднении. По переменной  взята сетка
взята сетка 
Исходя из особенностей функций  и требований точности, для
и требований точности, для  с помощью программы [56] были построены для каждого месяца приближающие функции в виде рациональной дроби
с помощью программы [56] были построены для каждого месяца приближающие функции в виде рациональной дроби

и для  в виде комбинаций многочленов и экспонент
в виде комбинаций многочленов и экспонент

где коэффициенты 11, —3.6, —1.6 найдены с помощью программы [39], а коэффициенты  с использованием программы [38].
с использованием программы [38].
Для построенных рациональных дробей среднеквадратическое уклонение принимает в зависимости от месяца значение от 1.1 до 2.0 градусов, общее число коэффициентов дроби  равно 45 (35 коэффициентов в числителе и 10 коэффициентов в знаменателе).
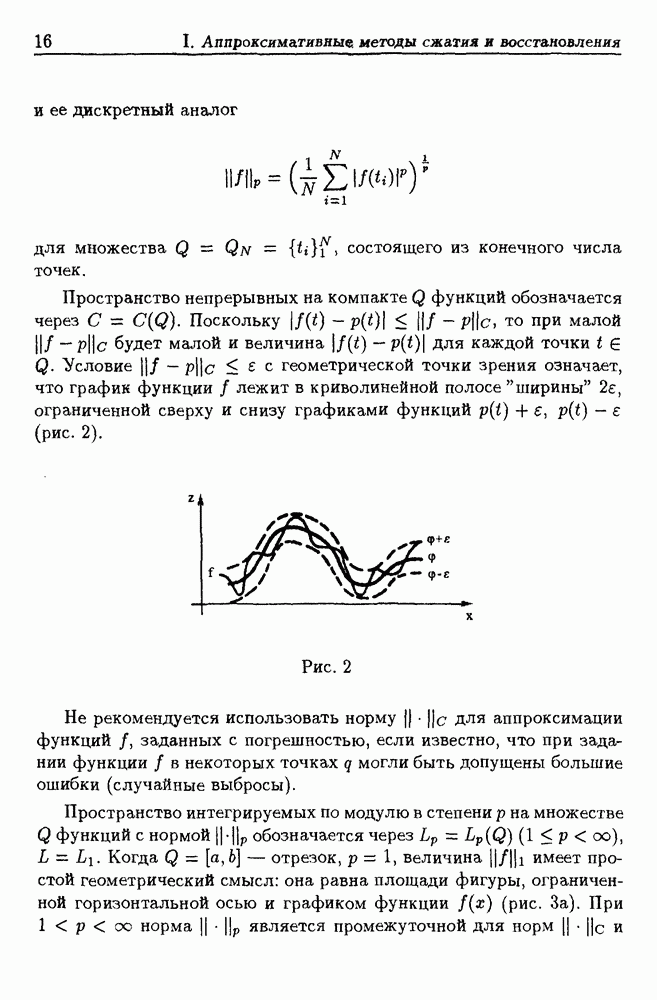
равно 45 (35 коэффициентов в числителе и 10 коэффициентов в знаменателе).
Среднеквадратическое уклонение для экспоненциальных моделей давления в зависимости от месяца меняется в пределах от 1.7 до  число коэффициентов
число коэффициентов  равно 18.
равно 18.
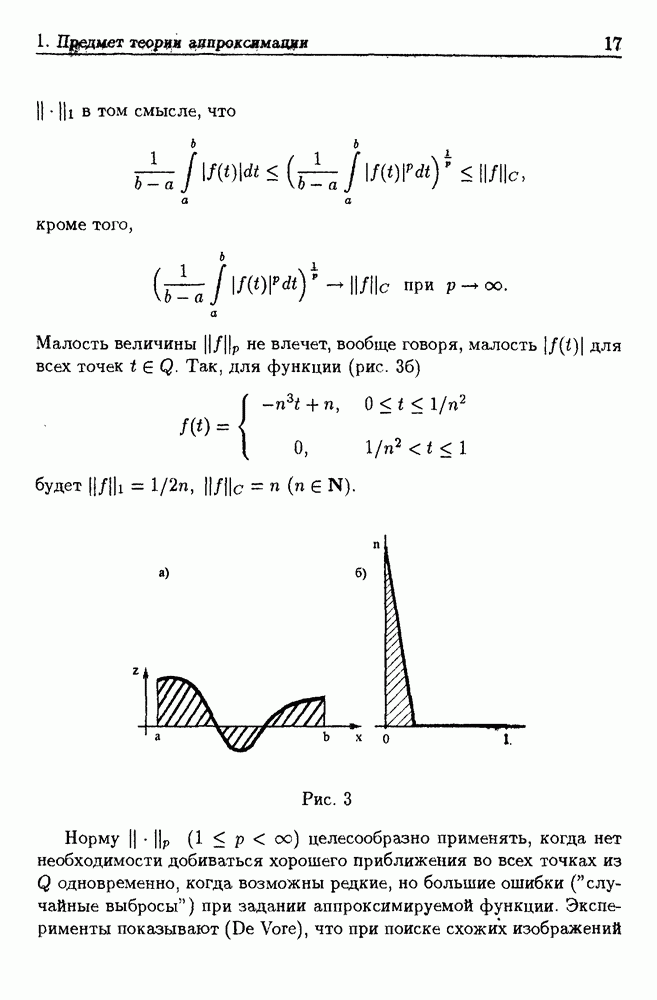
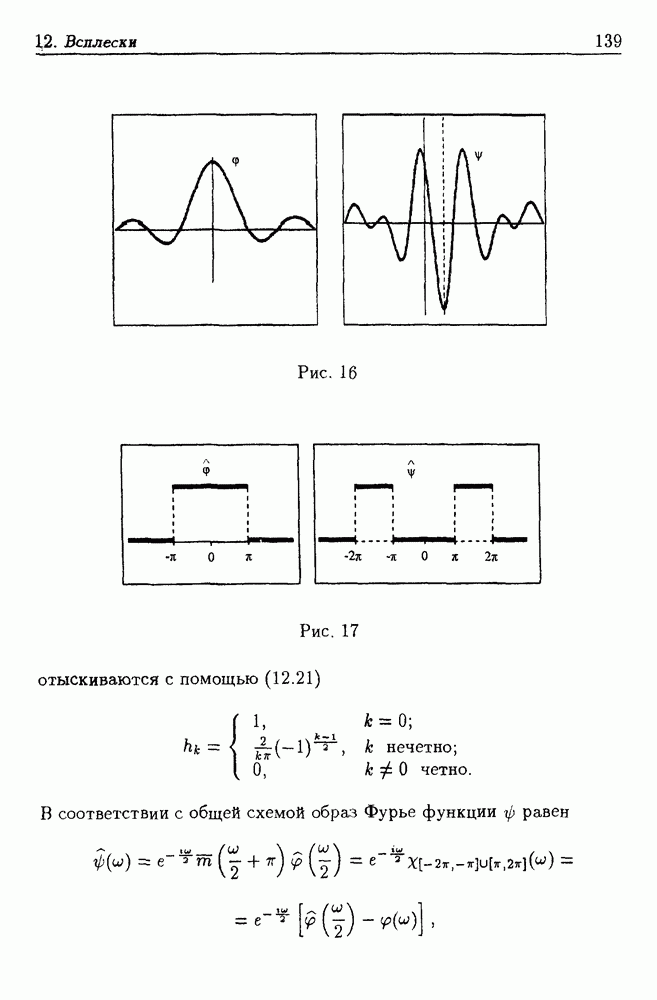
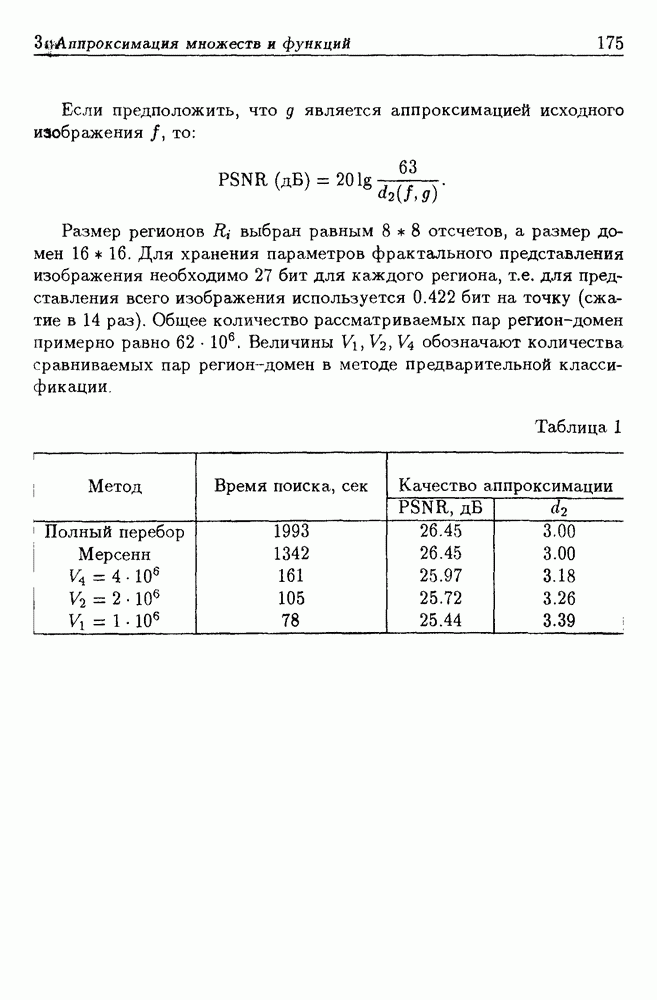
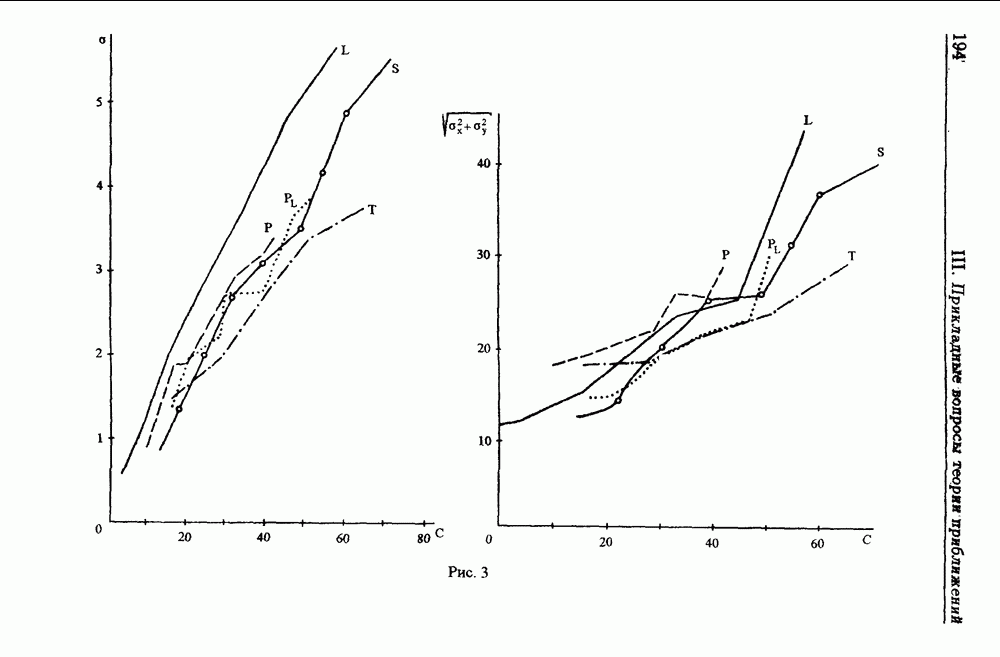
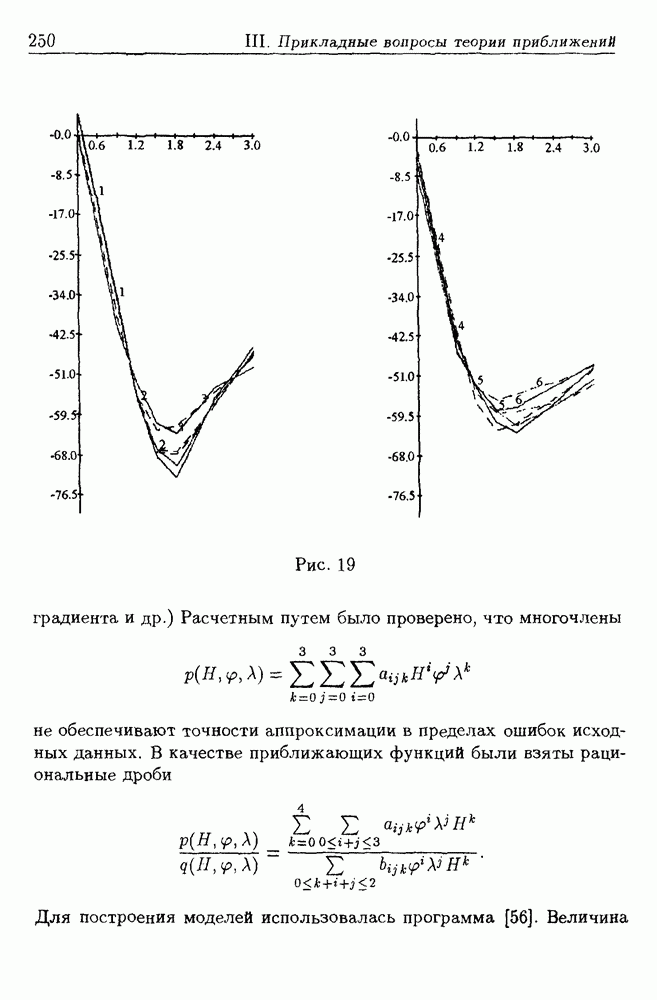
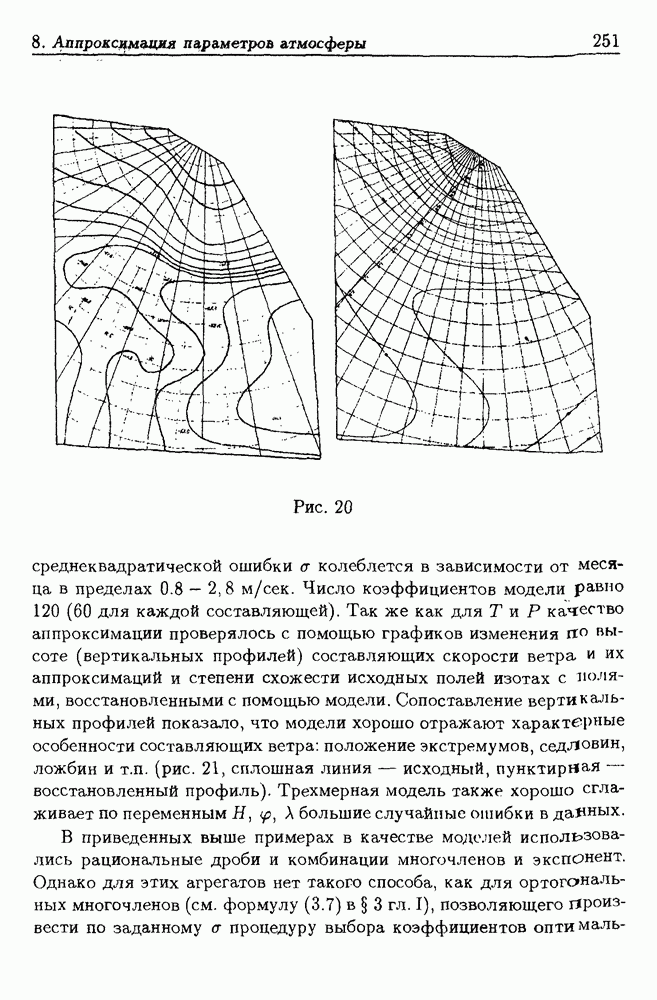
Помимо среднеквадратической ошибки аппроксимации о качестве построенных приближений можно судить по близости исходных и восстановленных вертикальных профилей (рис. 19, сплошная линия — исходный, пунктирная — восстановленный), по степени схожести исходных полей с полями, восстановленными с помощью моделей (рис. 20).
Скорость ветра в рассматриваемом слое является более сложной, с точки зрения приближения, атмосферной характеристикой в сравнении с температурой и давлением. Поэтому в качестве исходной информации для построения трехмерных моделей зональной  и меридиональной
и меридиональной  составляющих скорости ветра взяты числовые значения этих параметров в узлах сетки
составляющих скорости ветра взяты числовые значения этих параметров в узлах сетки

т.е. при каждом фиксированном  и каждой фиксированной высоте
и каждой фиксированной высоте  взята своя сетка узлов по
взята своя сетка узлов по  для
для  Густота сетки
Густота сетки  и число ее узлов
и число ее узлов  определялись особенностями функции
определялись особенностями функции  (количество экстремумов, величина
(количество экстремумов, величина
Рис. 19 (см. скан)
градиента и др.) Расчетным путем было проверено, что многочлены

не обеспечивают точности аппроксимации в пределах ошибок исходных данных. В качестве приближающих функций были взяты рациональные дроби

Для построения моделей использовалась программа [56]. Величина
Рис. 20 (см. скан)
среднеквадратической ошибки а колеблется в зависимости от месяца в пределах  Число коэффициентов модели равно 120 (60 для каждой составляющей). Так же как для
Число коэффициентов модели равно 120 (60 для каждой составляющей). Так же как для  качество аппроксимации проверялось с помощью графиков изменения
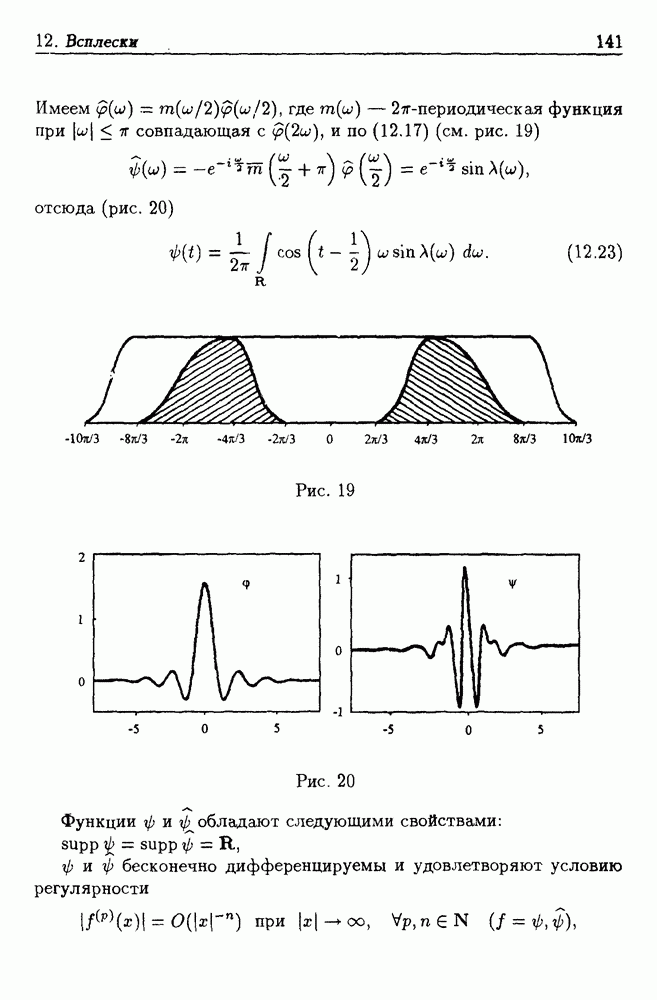
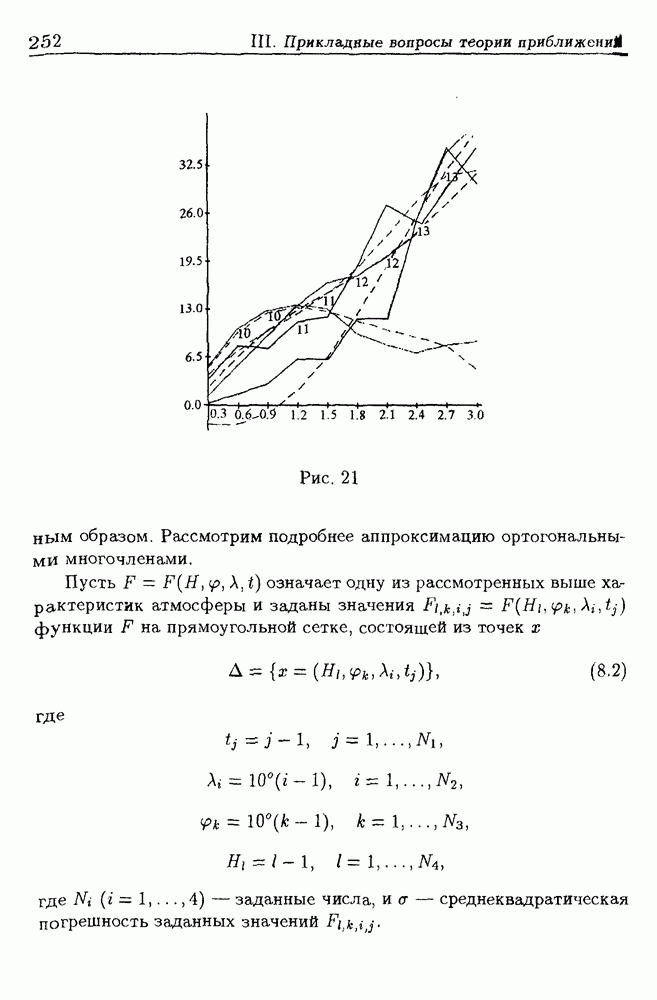
качество аппроксимации проверялось с помощью графиков изменения  высоте (вертикальных профилей) составляющих скорости ветра и их аппроксимаций и степени схожести исходных полей изотах с полями, восстановленными с помощью модели. Сопоставление вертикальных профилей показало, что модели хорошо отражают характерные особенности составляющих ветра: положение экстремумов, седловин, ложбин и т.п. (рис. 21, сплошная линия — исходный, пунктирная восстановленный профиль). Трехмерная модель также хорошо сглаживает по переменным
высоте (вертикальных профилей) составляющих скорости ветра и их аппроксимаций и степени схожести исходных полей изотах с полями, восстановленными с помощью модели. Сопоставление вертикальных профилей показало, что модели хорошо отражают характерные особенности составляющих ветра: положение экстремумов, седловин, ложбин и т.п. (рис. 21, сплошная линия — исходный, пунктирная восстановленный профиль). Трехмерная модель также хорошо сглаживает по переменным  большие случайные ошибки в данных.
большие случайные ошибки в данных.
В приведенных выше примерах в качестве моделей использовались рациональные дроби и комбинации многочленов и экспонент. Однако для этих агрегатов нет такого способа, как для ортогональных многочленов (см. формулу (3.7) в § 3 гл. I), позволяющего произвести по заданному  процедуру выбора коэффициентов
процедуру выбора коэффициентов

Рис. 21
оптимальным образом. Рассмотрим подробнее аппроксимацию ортогональными многочленами.
Пусть  означает одну из рассмотренных выше характеристик атмосферы и заданы значения
означает одну из рассмотренных выше характеристик атмосферы и заданы значения  функции
функции  на прямоугольной сетке, состоящей из точек х
на прямоугольной сетке, состоящей из точек х

где

где  заданные числа, и
заданные числа, и  среднеквадратическая погрешность заданных значений
среднеквадратическая погрешность заданных значений 
Обозначим через  систему ортогональных на целочисленной равномерной сетке
систему ортогональных на целочисленной равномерной сетке  многочленов
многочленов  обозначает степень многочлена) (см., напр., [18]). Для построения аппроксимирующего многочлена используем многочлен вида
обозначает степень многочлена) (см., напр., [18]). Для построения аппроксимирующего многочлена используем многочлен вида

наилучшего среднеквадратического приближения для  где
где 

Требуется подобрать многочлен (8.3) с возможно меньшим числом ненулевых коэффициентов  Для которого ошибка аппроксимации
Для которого ошибка аппроксимации  удовлетворяет неравенству
удовлетворяет неравенству

Коэффициенты многочлена наилучшего приближения являются коэффициентами Фурье (см. гл. I, § 3) по системе и вычисляются по формуле

где


Общее число коэффициентов полинома  равно
равно  Обозначим
Обозначим

Где  квадрат величины среднеквадратического уклонения по равенству Парсеваля равен
квадрат величины среднеквадратического уклонения по равенству Парсеваля равен

Пусть многочлен (8.3) удовлетворяет неравенству стр  Как видно из формулы (8.5), вклад каждого коэффициента
Как видно из формулы (8.5), вклад каждого коэффициента  квадрат
квадрат  определяется величиной
определяется величиной  Чтобы выбрать наименьшее число коэффициентов, позволяющее сохранить заданную точность
Чтобы выбрать наименьшее число коэффициентов, позволяющее сохранить заданную точность  упорядочим последовательность величин
упорядочим последовательность величин  по убыванию. Обозначим полученную последовательность через
по убыванию. Обозначим полученную последовательность через  Найдем минимальный номер при котором выполняется неравенство
Найдем минимальный номер при котором выполняется неравенство

и выбросим из суммы (8.3) слагаемые с коэффициентами  для которых
для которых  Сумма оставшихся слагаемых в (8.3) является искомым аппроксимирующим многочленом.
Сумма оставшихся слагаемых в (8.3) является искомым аппроксимирующим многочленом.
Многочлен вида (8.3) для температуры  заданной своими значениями на сетке (8.2), удовлетворяет неравенству стр
заданной своими значениями на сетке (8.2), удовлетворяет неравенству стр  при
при  с общим числом коэффициентов равным 420. Уменьшение хотя бы одного из номеров
с общим числом коэффициентов равным 420. Уменьшение хотя бы одного из номеров  приводит к нарушению неравенства. Применение изложенной методики позволяет оставить в полиноме только к
приводит к нарушению неравенства. Применение изложенной методики позволяет оставить в полиноме только к  слагаемых с сохранением точности
слагаемых с сохранением точности 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. АППРОКСИМАТИВНЫЕ МЕТОДЫ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ЧИСЛЕННОЙ ИНФОРМАЦИИ
- 1. Предмет теории аппроксимации
- 1.2. Классы приближающих функций
- 1.3. О выборе нормы
- 1.4. Задача о наилучшем приближении
- 1.5. Полная погрешность решения задачи приближения
- 1.6. Проблематика
- 2. Приближение в нормированных пространствах
- 2.1. Существование элемента наилучшего приближения
- 2.2. О единственности элемента наилучшего приближения
- 2.3. Непрерывность метрической проекции
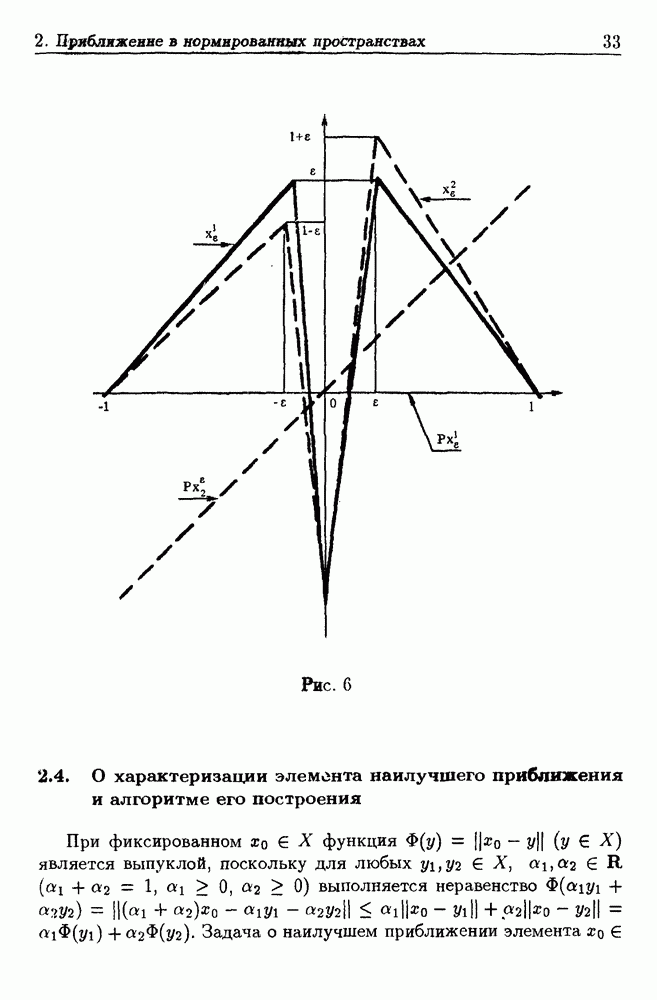
- 2.4. О характеризании элемента наилучшего приближения и алгоритме его построения
- 3. Наилучшее приближение в пространстве со скалярным произведением
- 3.2. Характеризация и устойчивость элемента наилучшего приближения
- 3.3. Построение элемента наилучшего приближения
- 3.4. Оценка погрешности приближения
- 3.5. Классические ортонормированные системы
- 3.6. Кратко о всплесках
- 3.7. О вычислении коэффициентов Фурье
- 3.8. О фильтрации сигналов. Основные понятия
- 4. Характеризация полинома наилучшего приближения в La
- 5. Наилучшее приближение полиномами в пространстве непрерывных функций
- 5.2. Характеризащия полинома наилучшего приближения
- 5.3. Сильная единственность полинома наилучшего приближения
- 6. Аппроксимация полиномами в метрике, связанной с задачей навигации
- 7. Наилучшее приближение рациональными дробями в пространстве C[a, b]
- 7.2. Характеризация наилучшей дроби
- 8. Алгоритмы полиномиальной аппроксимации в равномерной метрике
- 8.2. Сведение задачи аппроксимации к задаче линейного программирования
- 8.3. Алгоритм спуска
- 9. Алгоритмы аппроксимации рациональными дробями
- 9.1. Алгоритмы равномерной дробно-рациональной аппроксимации функций
- 9.2. Алгоритм среднеквадратичного приближения функций рациональными дробями
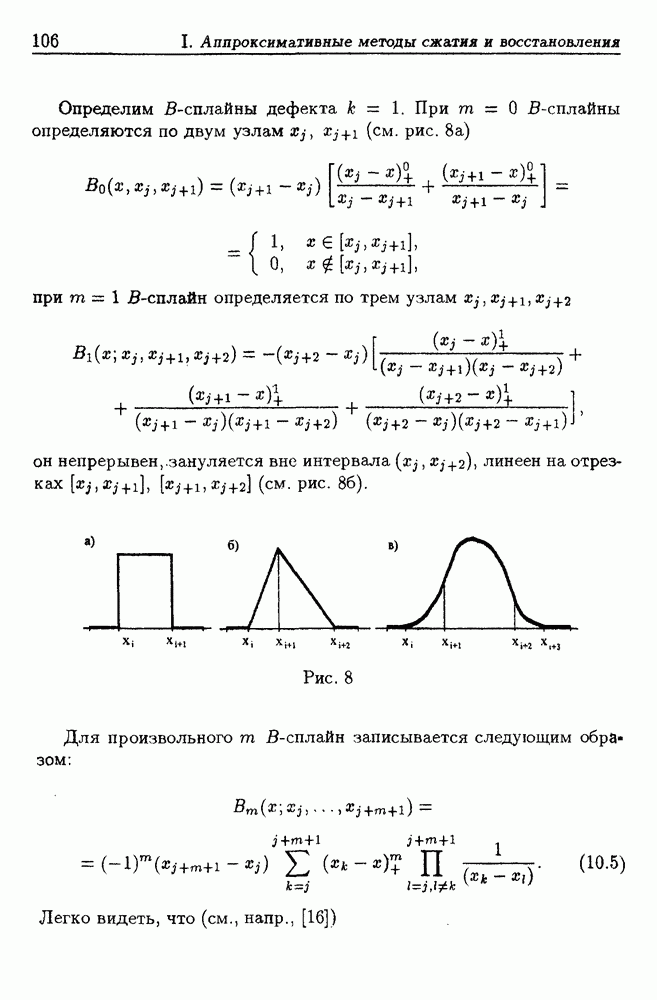
- 10. Полиномиальные сплайны
- 10.2. Сплайны одного переменного
- 10.3. Сплайны нескольких переменных на прямоугольной сетке
- 10.4. Сплайны на треугольных сетках
- 10.5. Интерполирование сплайнами
- 10.6. Сглаживание экспериментальных данных
- 10.7. Метод конечных элементов
- 11. Приближение экспоненциальными суммами
- 11.2. Приближение экспоненциальными суммами общего вида
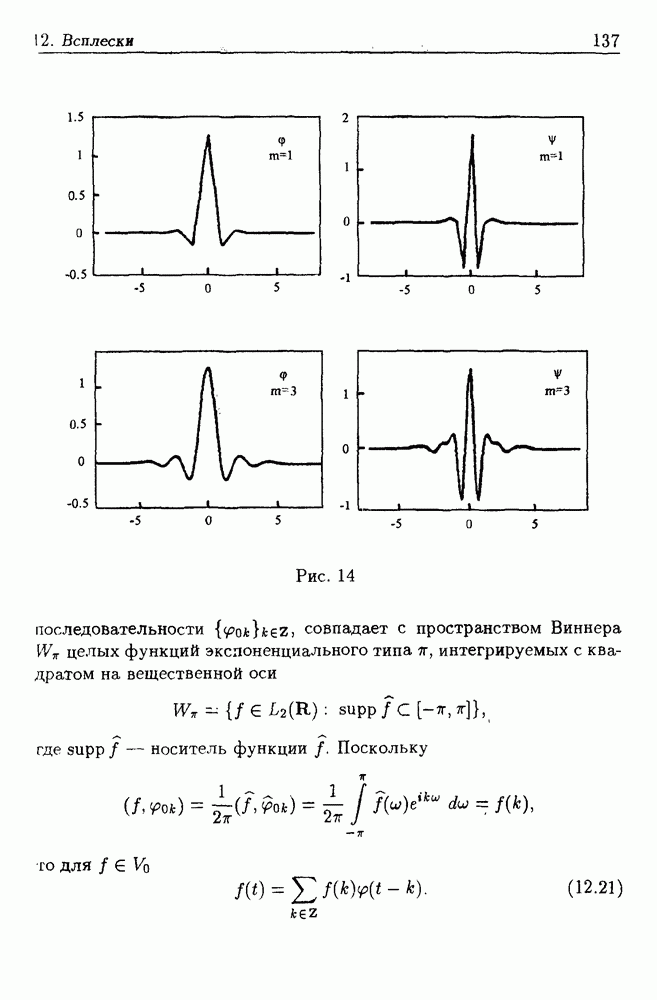
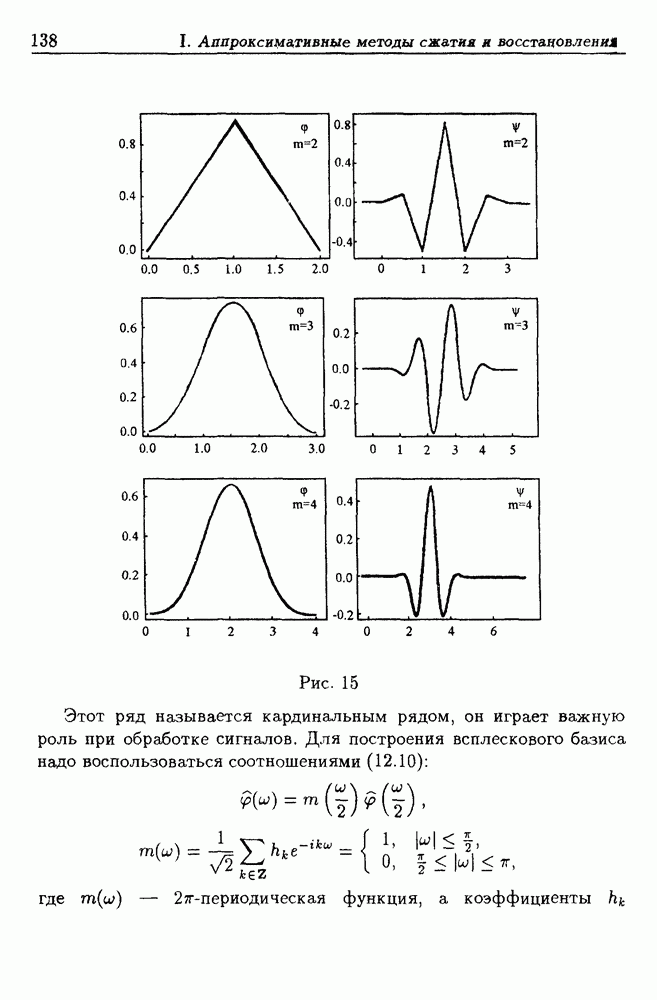
- 12. Всплески
- 12.2. Кратномасштабный анализ в L2(R)
- 12.3. Примеры всплесков
- 12.4. Периодические всплески
- 12.5. Всплески многих переменных
- 12.6. Алгоритм разложения и восстановления всплесков
- Глава II. ФРАКТАЛЬНЫЕ МЕТОДЫ АППРОКСИМАЦИИ МНОЖЕСТВ И ФУНКЦИЙ
- 2. Случай произвольного метрического пространства. Идея метода
- 2.2. Основная задача
- 2.3. Возможные постановки экстремальных задач
- 3. Аппроксимация множеств и функций
- 3.2. Компактные фракталы относительно метрики Хаусдорфа (IFS)
- 3.3. Численный алгоритм аппроксимации множеств
- 3.4. Аппроксимация функций
- Глава III. ПРИКЛАДНЫЕ ВОПРОСЫ ТЕОРИИ ПРИБЛИЖЕНИЙ
- 1. Аппроксимация и задача навигации по геофизическим полям
- 1.2. Характеристика информативности функции
- 1.3. Аппроксимация в задаче навигации. Сравнение различных методов аппроксимации
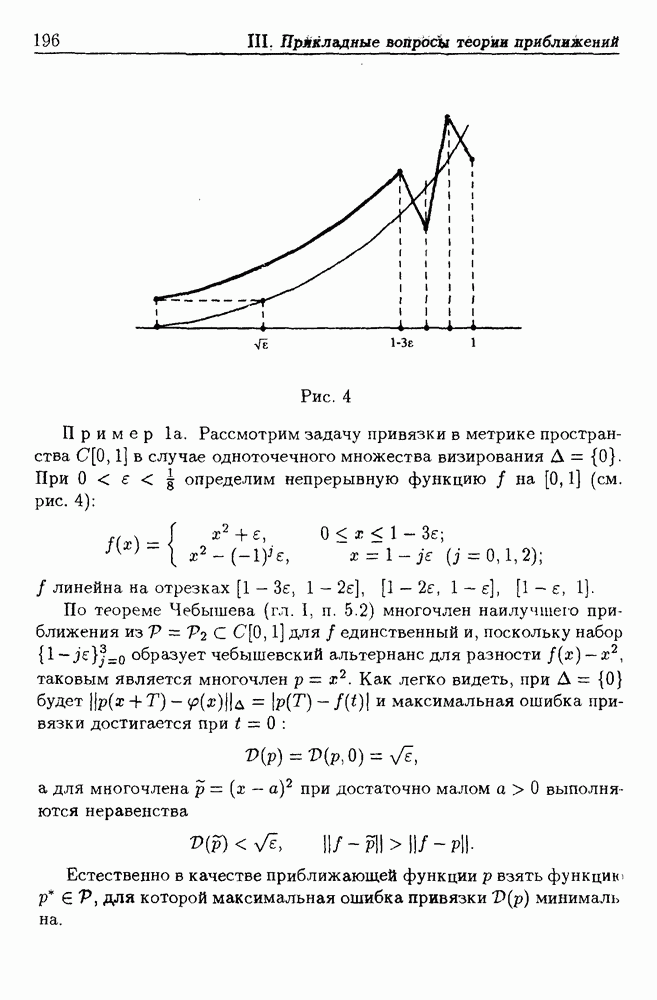
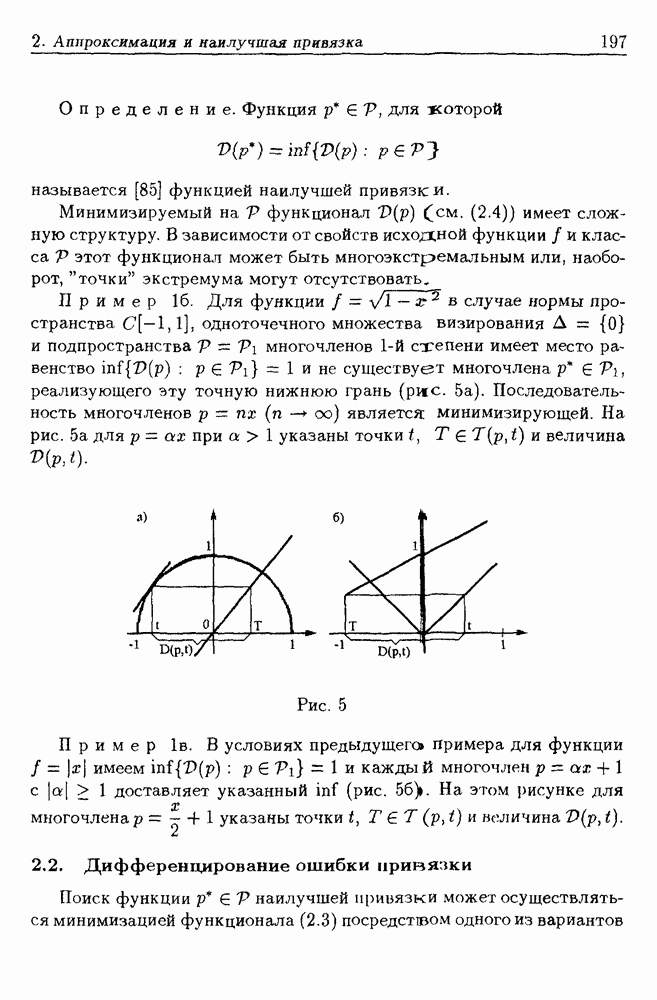
- 2. Аппроксимация, обеспечивающая наилучшую привязку
- 2.2. Дифференцирование ошибки привязки
- 2.3. Алгоритм аппроксимации, наилучшей с точки зрения привязки
- 3. Аппроксимация координат точки падения центра масс
- 3.2. Упрощенная модель движения центра масс
- 3.3. Расчет кеплеровской дальности с учетом вращения Земли
- 3.4. Аппроксимация поправок к кеплеровским координатам точки падения
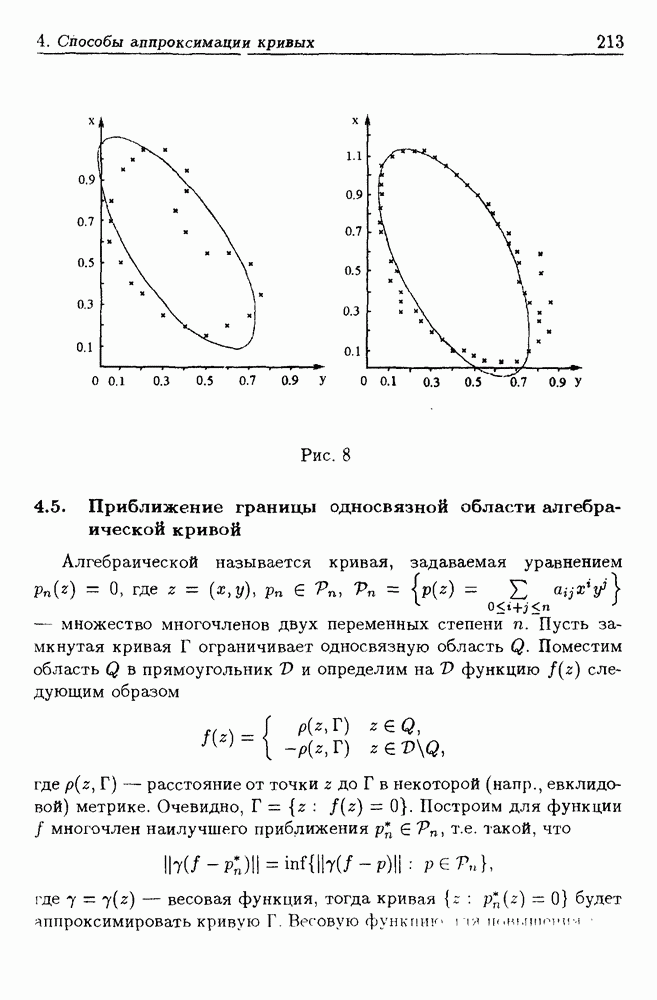
- 4. Простейшие способы аппроксимации плоских кривых, заданных набором точек
- 4.1. Аппроксимация в прямоугольной системе координат
- 4.2. Кривая в полярной системе координат
- 4.3. Параметрическая аппроксимация кривой
- 4.4. Эллипсоидальная аппроксимация границы односвязной области
- 4.5. Приближение границы односвязной области алгебраической кривой
- 4.6. Применение теоретико-множественных операций
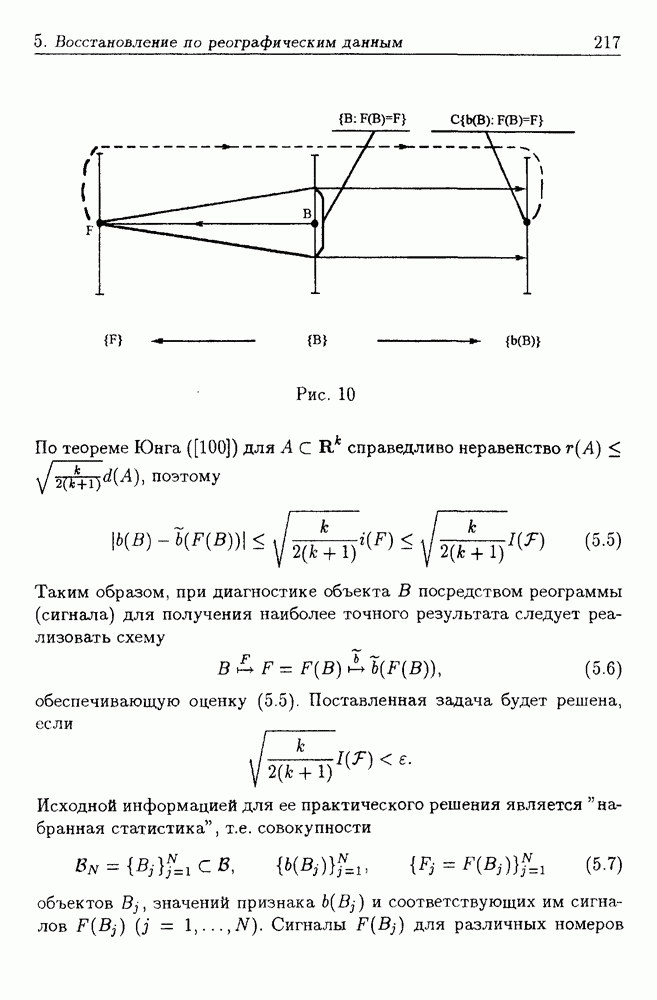
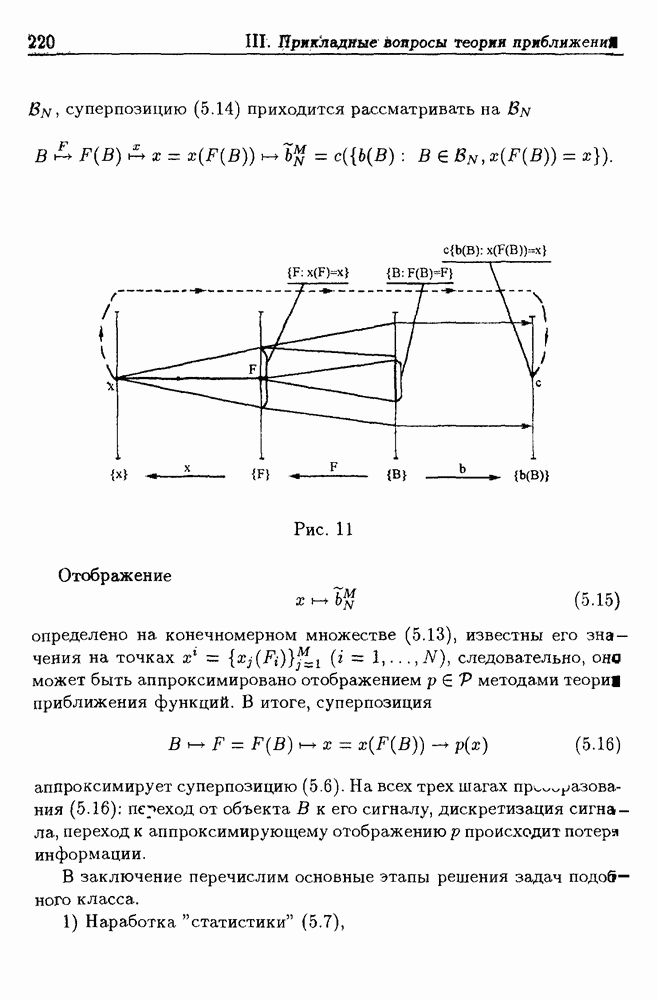
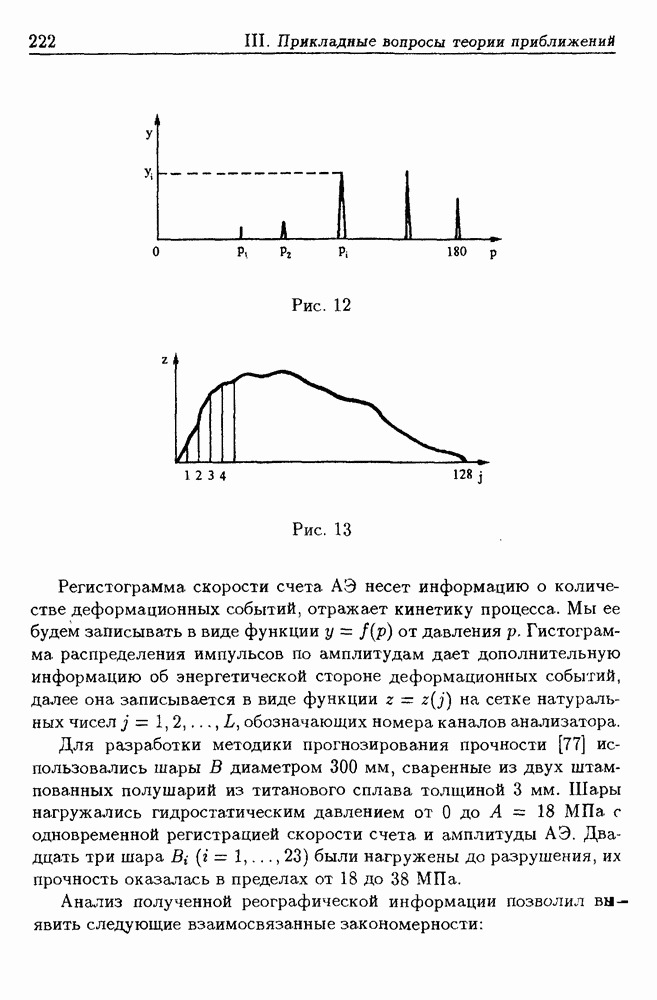
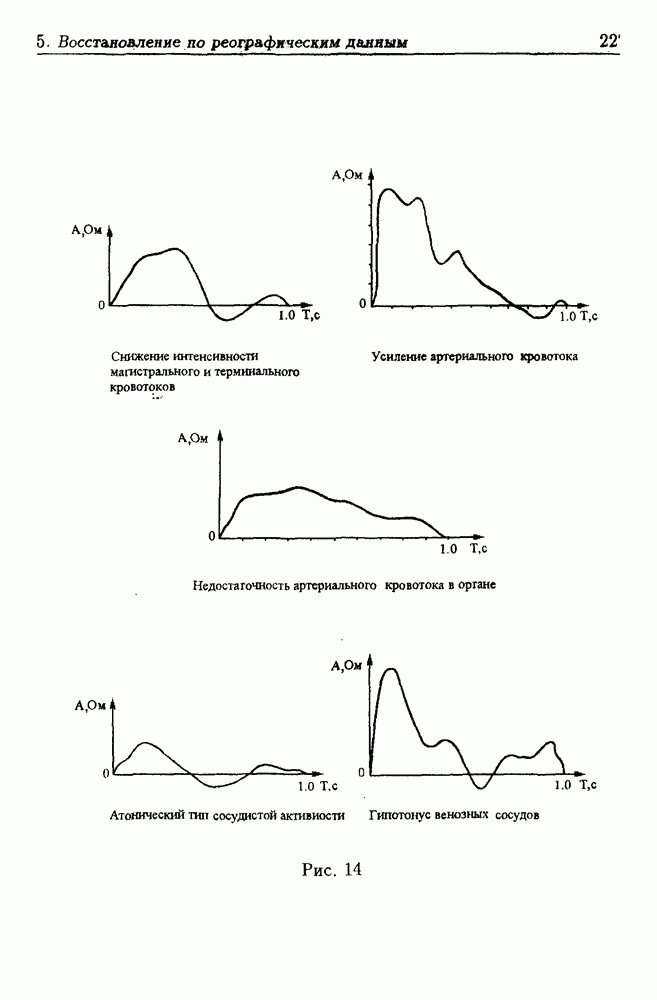
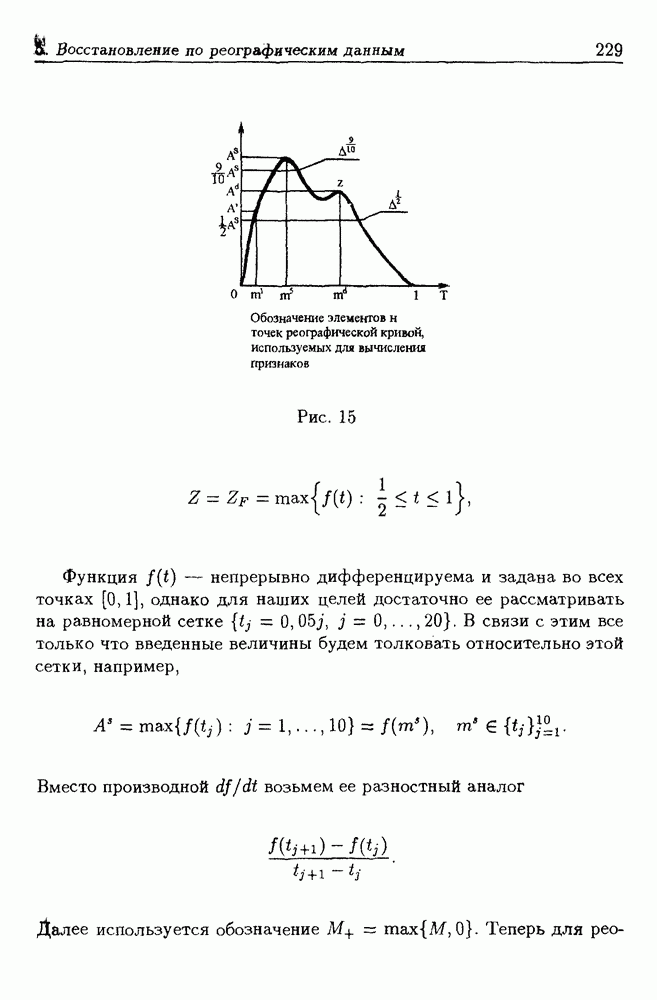
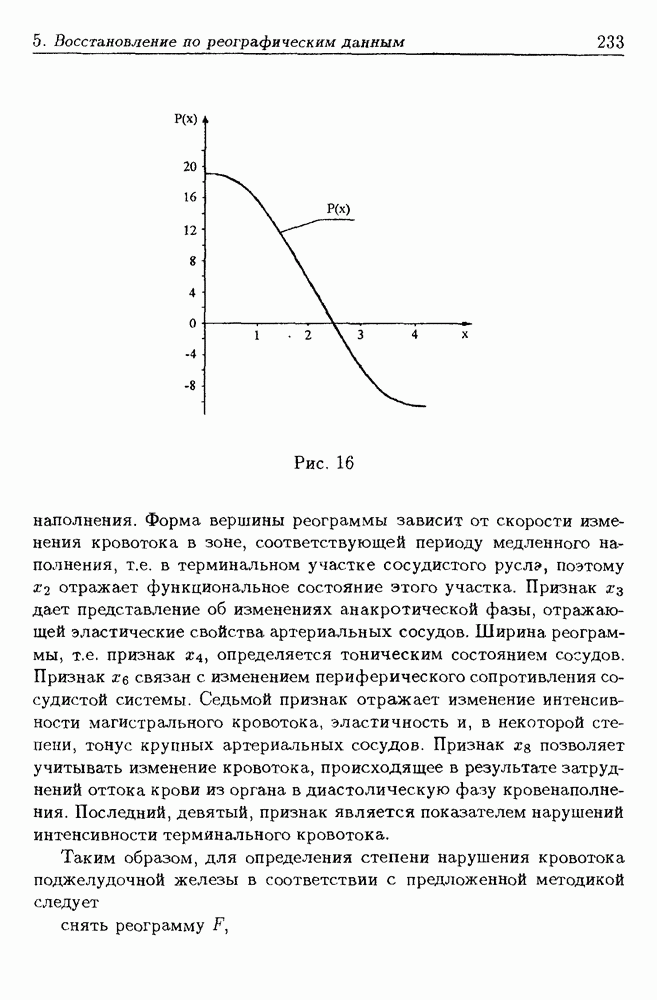
- 5. Восстановление информации по реографическим данным
- 5.2. Алгоритм акустико-эмиссионного прогнозирования прочности изделий
- 5.3. Метод оценки кровенаполнения поджелудочной железы по реограмме
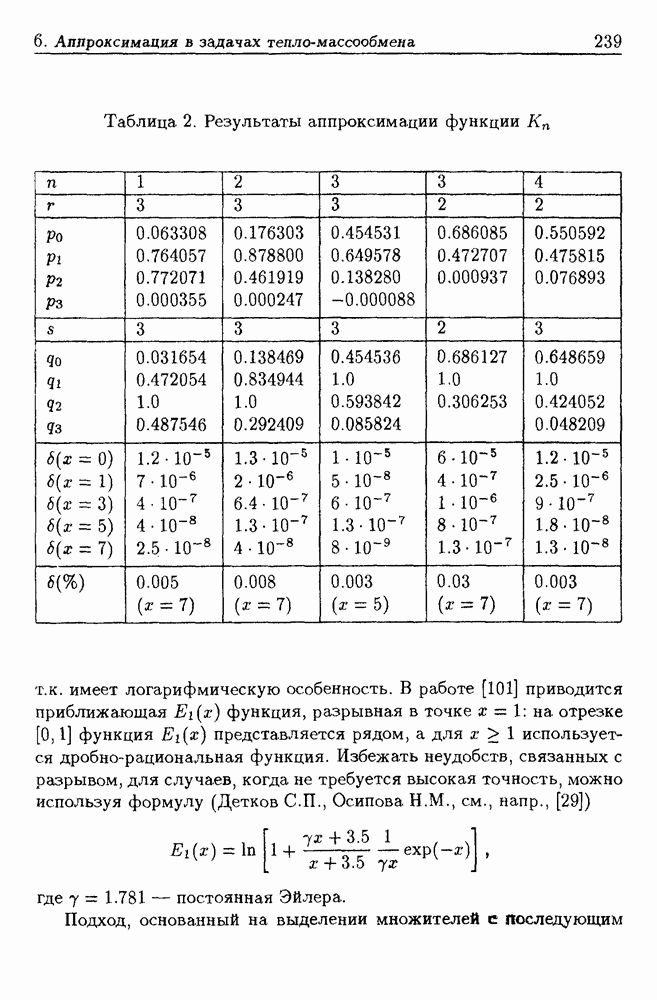
- 6. Дробно-рациональная аппроксимация в задачах тепло-массообмена
- 6.2. Формулы для функций …
- 7. Оптимизация формы зеркала гибридной зеркальной антенны
- 7.2. Оптимизация формы осесимметричного зеркала
- 8. Аппроксимация параметров атмосферы
- 8.2. Методика построения моделей атмосферы
- 8.3. Постановка задачи аппроксимации
- 8.4. Примеры региональных моделей атмосферы
- Глава IV. ПРИБЛИЖЕНИЕ КЛАССОМ ЛИПШИЦА СЕТОЧНЫХ ВЕКТОР-ФУНКЦИЙ И НАИЛУЧШАЯ ТРАЕКТОРИЯ ОБХОДА ЦЕЛЕЙ
- 1. Проектирование на класс Липшица в пространстве абстрактных функций, заданных на сетке
- 1.1. Постановка задачи
- 1.2. Характеризация решения
- 2. Кратчайшая кусочно-линейная траектория
- 2.2. Характеризация кратчайшей траектории
- 3. Алгоритмы построения наилучших траекторий
- 4. Сходимость алгоритмов
- 4.1. Сходимость алгоритма для задачи с фиксированными моментами встречи
- 4.2. Сходимость алгоритма поиска кратчайшей траектории
- 5. Приближение классом Липшица вещественных функций
- КОММЕНТАРИИ