| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Модель Зоммерфельда. Плотность состояний.
Исторически первая и наиболее простая квантовомеханическая модель твердого тела была предложена Зоммерфельдом. Он считал, что потенциальная энергия электрона внутри кристалла везде постоянная, а на поверхности имеется достаточно высокий потенциальный барьер. Электроны, свободно перемещаясь в кристалле, не могут его покинуть, так как их удерживают
силы отталкивания от барьера. Уравнение Шредингера (2.5) для одного электрона при постоянном  можно представить в виде
можно представить в виде

Поскольку величина потенциальной энергии зависит от выбора начала отсчета, то для простоты положим  внутри кристалла и
внутри кристалла и  на его поверхности.
на его поверхности.
Если волновую функцию искать в вице произведения

то (2.5а) распадается на три независимых уравнения и задача сводится к решению уравнения типа

где

Легко убедиться, что уравнению (2.6) удовлетворяют функции  а общее решение равно [2,42]
а общее решение равно [2,42]

Вероятность обнаружить электрон в интервале от х до  пропорциональна
пропорциональна  При
При  электроны не могут покинуть кристалл, и, следовательно, за пределами кристалла
электроны не могут покинуть кристалл, и, следовательно, за пределами кристалла  тождественно равно нулю. Тогда из требования непрерывности решения уравнения Шредингера во всем пространстве следует, что
тождественно равно нулю. Тогда из требования непрерывности решения уравнения Шредингера во всем пространстве следует, что  на границах кристалла
на границах кристалла  также равно нулю. Налагая эти граничные условия на (2.8), получим
также равно нулю. Налагая эти граничные условия на (2.8), получим

Здесь  любое целое положительное число.
любое целое положительное число.
Собственные значения энергии, соответствующие волновым функциям  согласно (2.7) и (2.9), равны
согласно (2.7) и (2.9), равны

 импульс электрона.
импульс электрона.
Таким образом, энергия электрона, запертого в потенциальном ящике, обладает дискретным рядом значений.
Умножая (2.10) на  получим волновую функцию, зависящую от времени
получим волновую функцию, зависящую от времени 

Она описывает стоячую волну с частотой  и узлами в точках
и узлами в точках  где
где  Аналогичные волны устанавливаются на закрепленной с обоих концов струне.
Аналогичные волны устанавливаются на закрепленной с обоих концов струне.
Вместо использованных выше граничных условий  на функции обычно накладывается требование периодичности Борна — Кармана
на функции обычно накладывается требование периодичности Борна — Кармана

где  равно большому числу
равно большому числу  постоянных решетки.
постоянных решетки.
Условия цикличности Борна — Кармана вводятся для того, чтобы избежать рассмотрения граничных условий, в которые в явном виде входят размеры кристалла, поскольку ясно, что при больших значениях  физические процессы в твердом теле не должны зависеть от его геометрии. Если рассматривается трехмерный случай, то число
физические процессы в твердом теле не должны зависеть от его геометрии. Если рассматривается трехмерный случай, то число  должно быть большим во всех трех измерениях.
должно быть большим во всех трех измерениях.
Тогда решение уравнения (2.6) можно брать просто в виде

считая, что  принимает и положительные, и отрицательные значения. Из условия периодичности применительно к (2.14) следует
принимает и положительные, и отрицательные значения. Из условия периодичности применительно к (2.14) следует

а временная функция описывает бегущую волну

Из сравнения (2.15) с (2.9) вытекает, что в бесконечном кристалле уровни расположены в два раза реже, чем в ограниченном. Зато каждому уровню соответствует две волны, бегущие в противоположных направлениях и характеризующиеся равными по величине, но разными по знаку величинами  Из последней формулы следует, что
Из последней формулы следует, что  имеет физический смысл волнового числа электрона. Длина волны,
имеет физический смысл волнового числа электрона. Длина волны,  связана с
связана с  равенством
равенством

Решения, аналогичные (2.16), получаются и для функций, зависящих от  а волновая функция, описывающая трехмерное движение имеет вид
а волновая функция, описывающая трехмерное движение имеет вид

где  единичные векторы, направленные вдоль осей
единичные векторы, направленные вдоль осей  Энергия, соответствующая состоянию
Энергия, соответствующая состоянию  выражается суммой
выражается суммой

Здесь  выступает как квадрат вектора с компонентами
выступает как квадрат вектора с компонентами  так что
так что 
Очевидно, заданному значению энергии  будет соответствовать, как правило, несколько волновых функций, поскольку значение
будет соответствовать, как правило, несколько волновых функций, поскольку значение  может реализовываться при различных комбинациях значений
может реализовываться при различных комбинациях значений  а каждой комбинации этих чисел соответствует своя волновая функция. Так,
а каждой комбинации этих чисел соответствует своя волновая функция. Так,  может относиться к волнам, распространяющимся вдоль оси
может относиться к волнам, распространяющимся вдоль оси  вдоль оси
вдоль оси  или вдоль оси
или вдоль оси  Для больших
Для больших  степень вырождения, естественно, возрастает.
степень вырождения, естественно, возрастает.
Найдем аналитическое выражение для числа состояний, которым соответствует энергия электронов в кристалле от  до
до  или частота от со до
или частота от со до  Поскольку координаты волнового вектора
Поскольку координаты волнового вектора  принимают только дискретный ряд значений, то все
принимают только дискретный ряд значений, то все  -пространство можно представить составленным из кубиков со стороной
-пространство можно представить составленным из кубиков со стороной  и объемом
и объемом  Число кубиков равно числу возможных комбинаций
Число кубиков равно числу возможных комбинаций  Поэтому число состояний со значением волнового вектора от
Поэтому число состояний со значением волнового вектора от  до
до  равно удвоенному отношению объема шарового слоя в
равно удвоенному отношению объема шарового слоя в  -пространстве к объему одного кубика:
-пространстве к объему одного кубика:

где  - объем кристалла. Коэффициент 2 вводится в (2.20) для учета спинового вырождения электронов.
- объем кристалла. Коэффициент 2 вводится в (2.20) для учета спинового вырождения электронов.
Так как, согласно (2.19),

из (2.20) находим  число состояний в расчете на единичный интервал энергии
число состояний в расчете на единичный интервал энергии


Рис. 7. Модель Кронига и Пенни
С увеличением энергии оно растет как корень квадратный из 
Как известно, производная  равна групповой скорости волнового пакета. Поэтому плотность состояний в расчете на единичный интервал частот
равна групповой скорости волнового пакета. Поэтому плотность состояний в расчете на единичный интервал частот  на основании (2.20) и (2.17) можно представить в виде
на основании (2.20) и (2.17) можно представить в виде

где  фазовая скорость бегущей волны (2.16).
фазовая скорость бегущей волны (2.16).
Величина (2.22) равна также плотности состояний электромагнитного поля, поскольку каждому значению волнового вектора поля также соответствуют две волны с разным направлением вектора поляризации [43].
Выражение для плотности состояний (2.21), полученное с помощью простейшей модели вещества, широко используется в теории твердого тела. Оказывается, если заменить в нем  на эффективную массу электрона
на эффективную массу электрона  то (2.21) будет определять плотность состояний в реальном кристалле.
то (2.21) будет определять плотность состояний в реальном кристалле.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
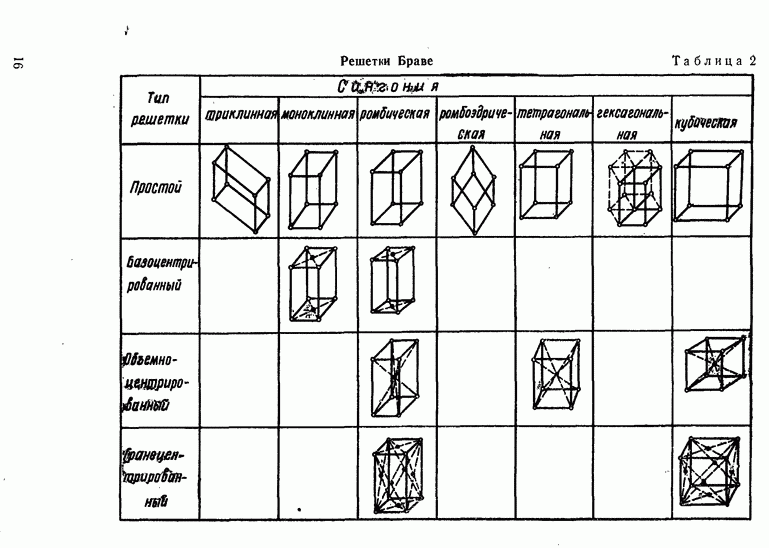
- Классификация кристаллических решеток.
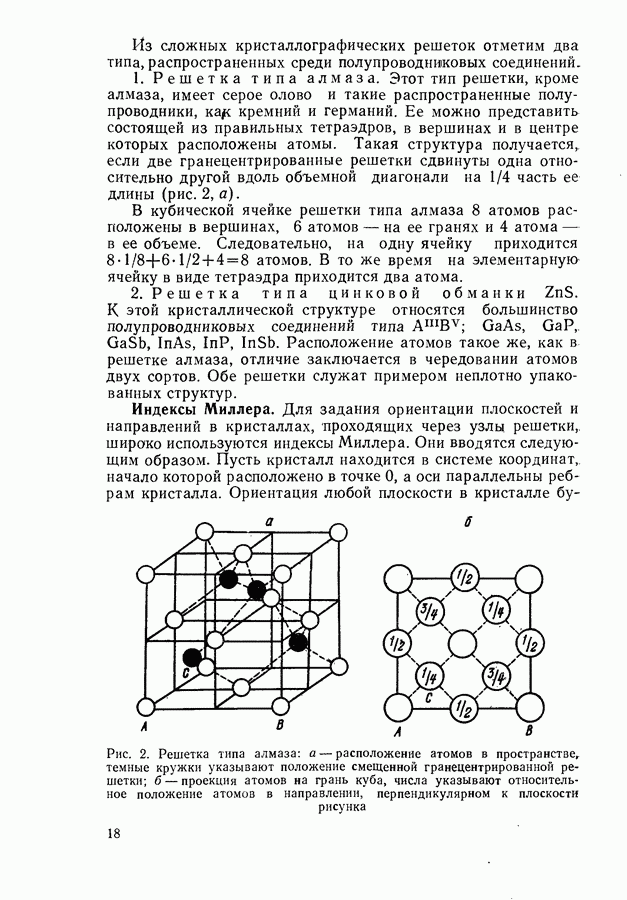
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
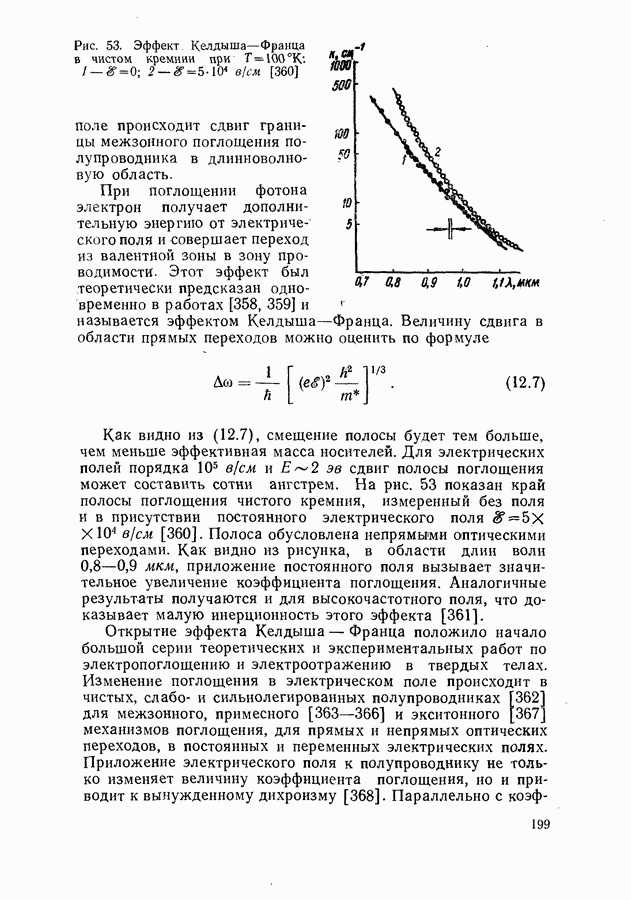
- Эффект Келдыша-Франца.
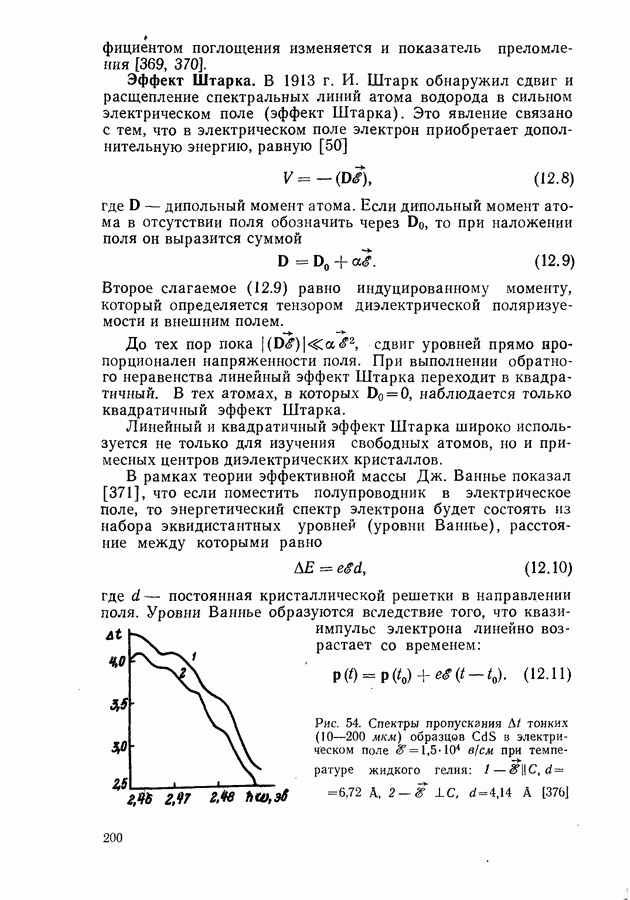
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
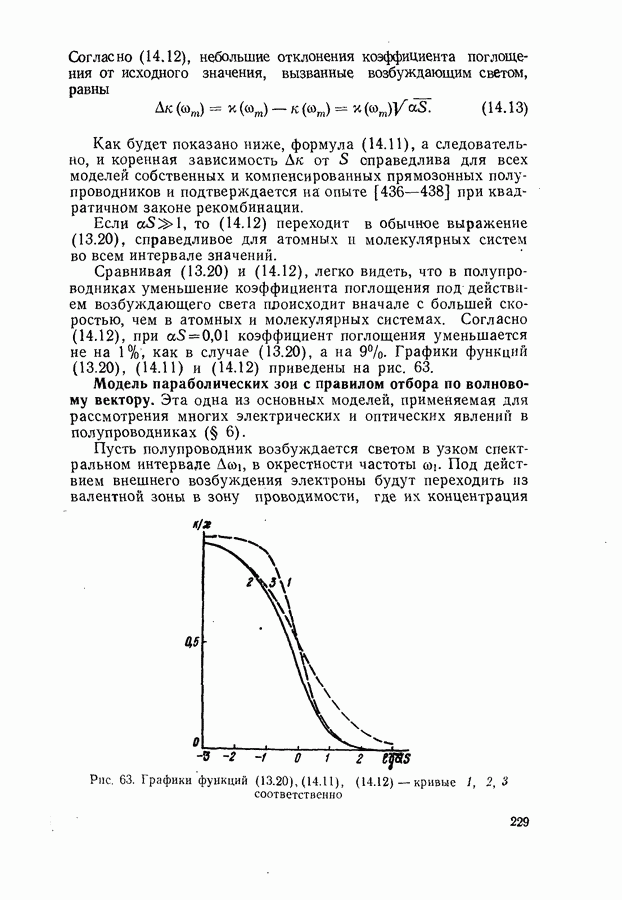
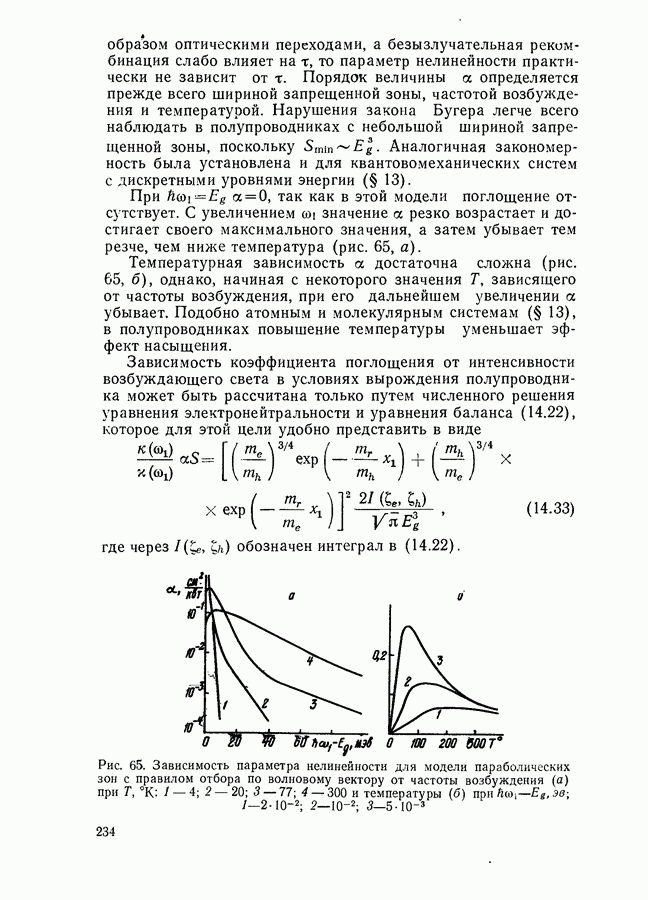
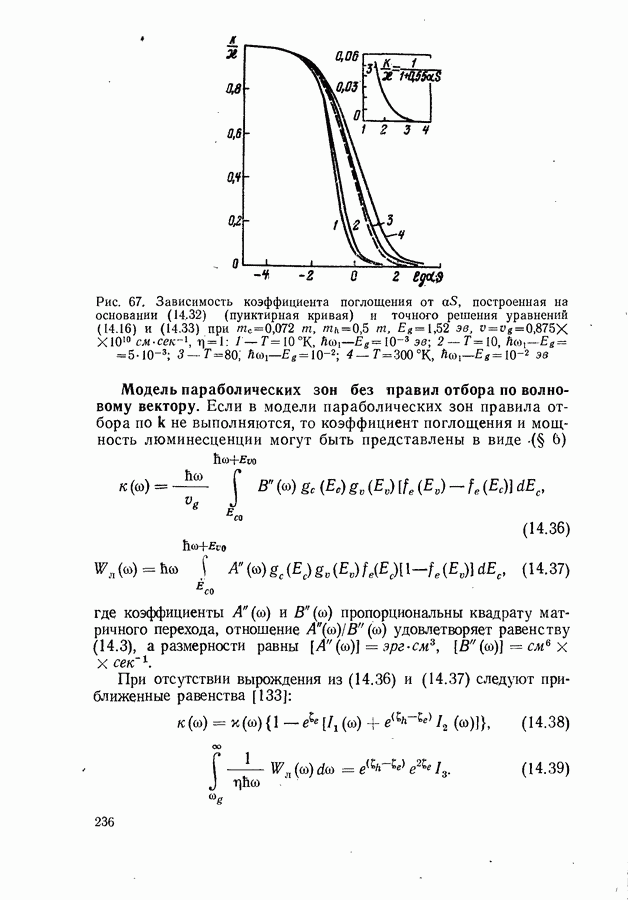
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
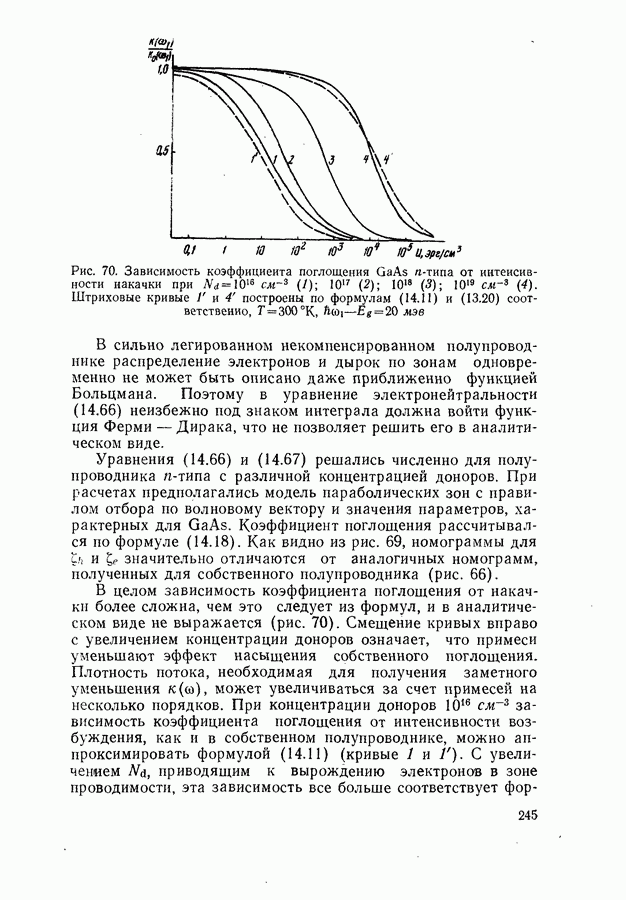
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
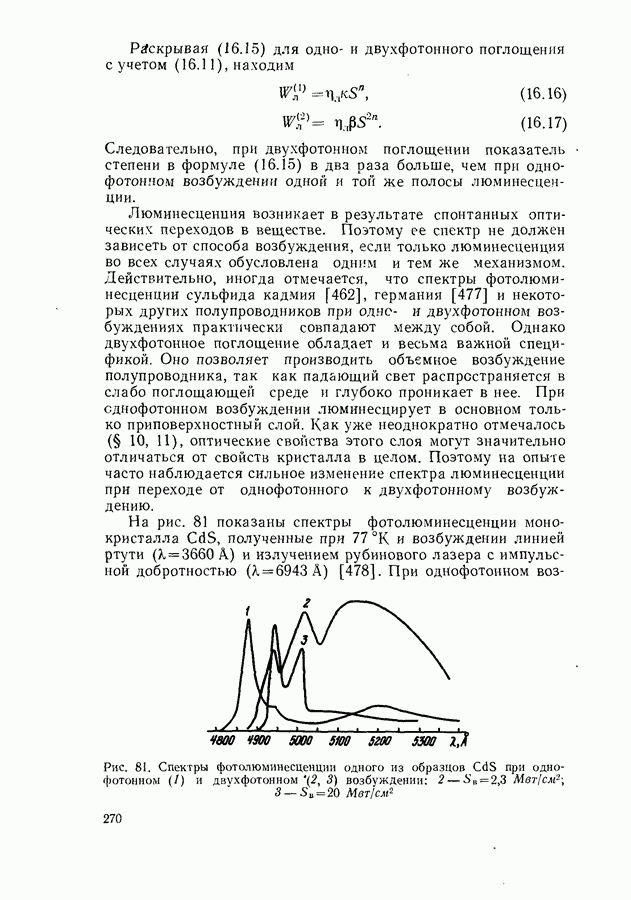
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
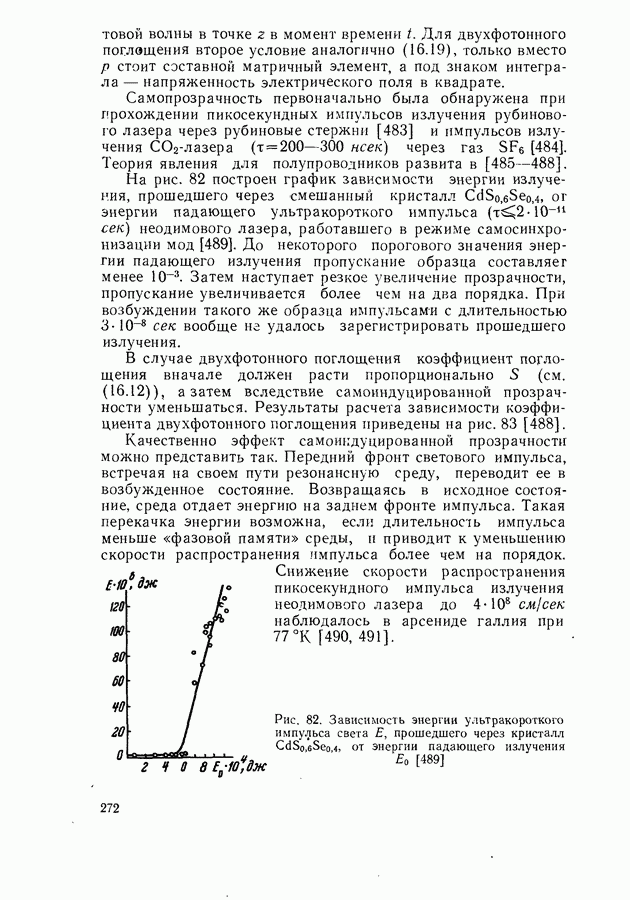
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
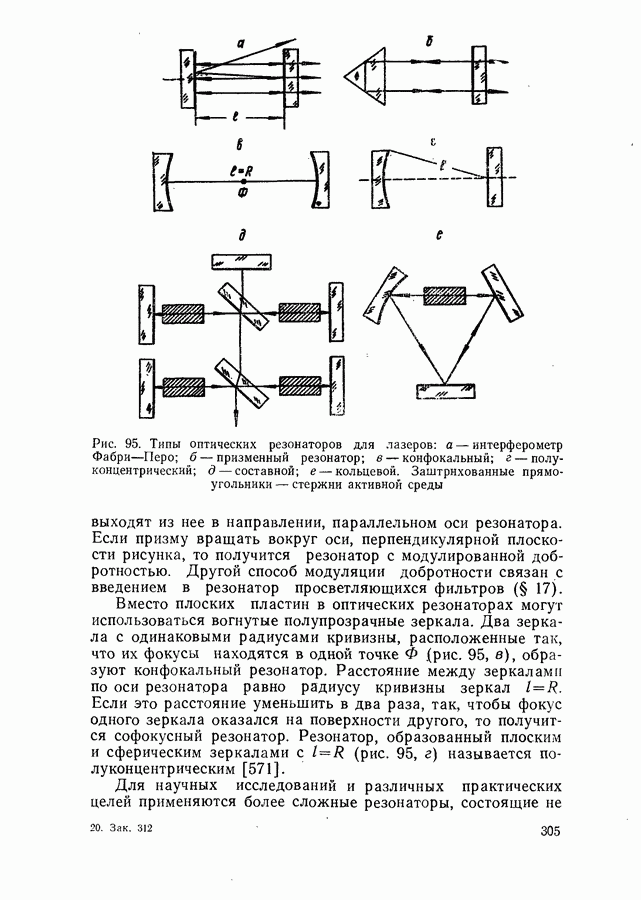
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.