| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Модель параболических зон с правилом отбора по волновому вектору.
Эта одна из основных моделей, применяемая для рассмотрения многих электрических и оптических явлении в полупроводниках (§ 6).
Пусть полупроводник возбуждается светом в узком спектральном интервале  в окрестности частоты
в окрестности частоты  Под действием внешнего возбуждения электроны будут переходить из валентной зоны в зону проводимости, где их концентрация
Под действием внешнего возбуждения электроны будут переходить из валентной зоны в зону проводимости, где их концентрация

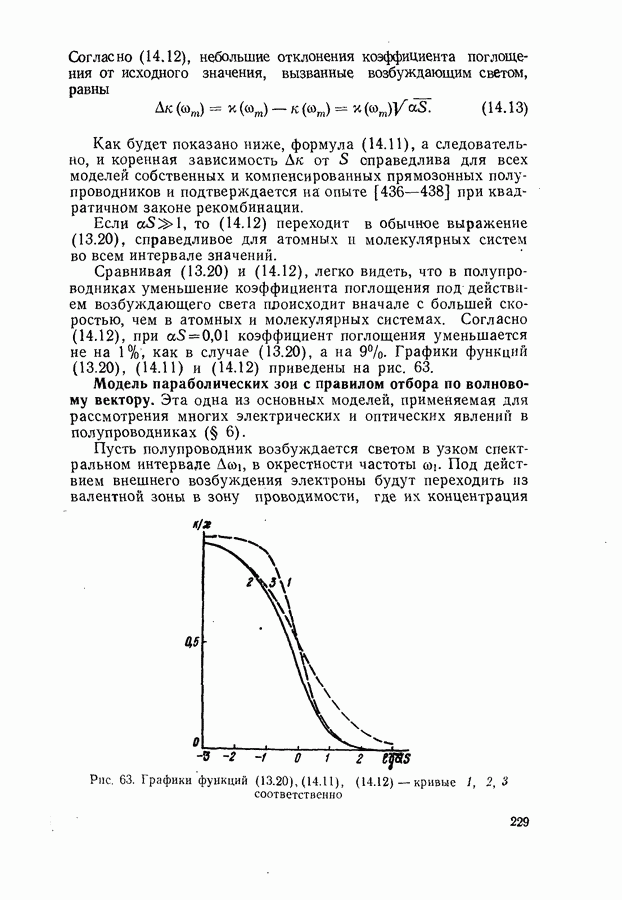
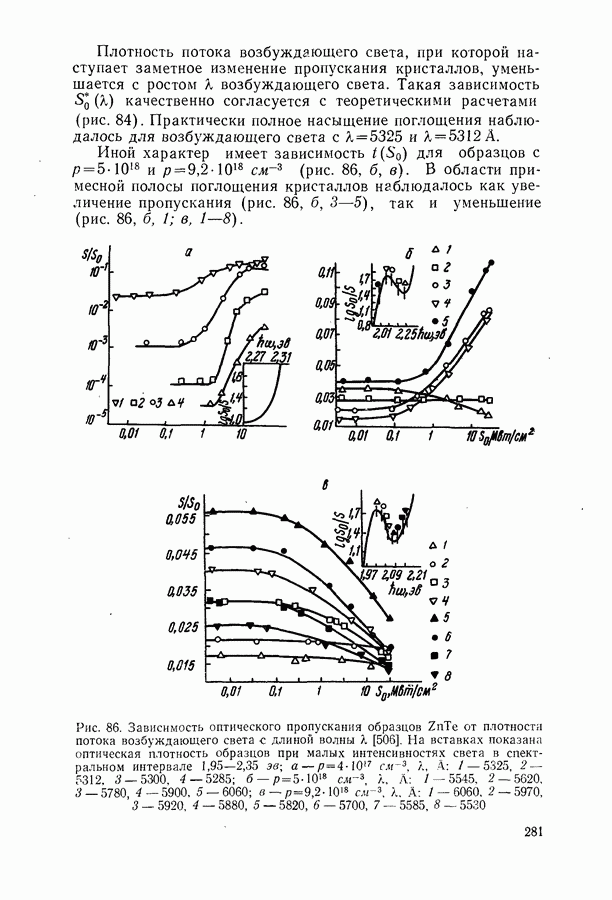
Рис. 63. Графики функций (13.20), (14.11), (14.12) — кривые 1, 2, 3 соответственно

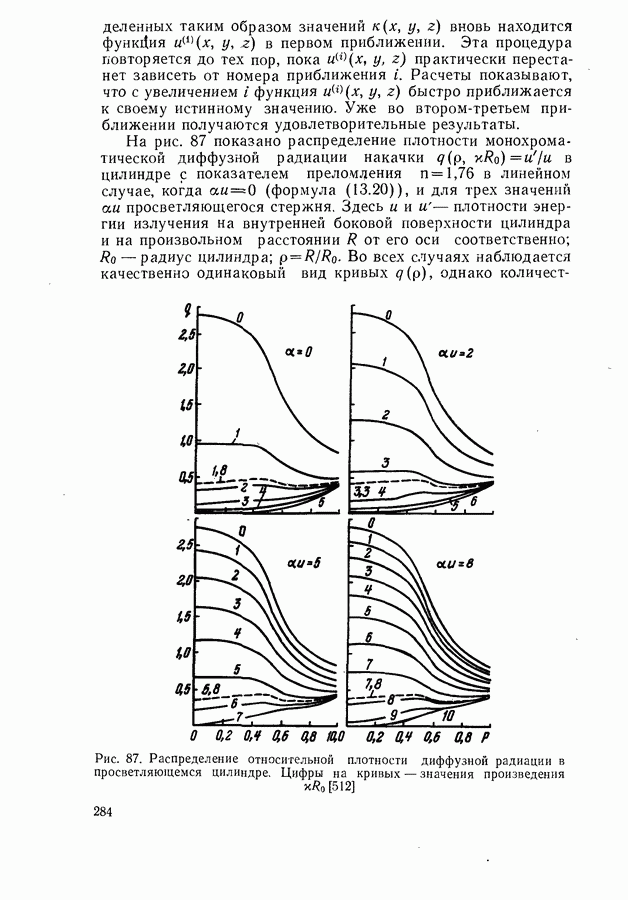
Рис. 64. Модель параболических зон
станет больше, чем при термодинамическом равновесии. Одновременно происходит обратный процесс спонтанной, вынужденной и безызлучательной рекомбинации.
Так как время установления равновесия между носителями в пределах одной зоны порядка  сек, а время рекомбинации, как правило, больше
сек, а время рекомбинации, как правило, больше  сек, то распределение электронов по уровням энергии зоны проводимости
сек, то распределение электронов по уровням энергии зоны проводимости  и валентной зоны
и валентной зоны  будет характеризоваться функцией Ферми-Дирака
будет характеризоваться функцией Ферми-Дирака

и двумя квазиуровнями Ферми  для электронов и дырок соответственно. Здесь введены обозначения:
для электронов и дырок соответственно. Здесь введены обозначения:  приведенная масса;
приведенная масса;  эффективные массы электрона и дырки;
эффективные массы электрона и дырки;  приведенные квазиуровни Ферми (рис. 64).
приведенные квазиуровни Ферми (рис. 64).
При возбуждении межзонных переходов уравнение баланса и уравнение электронейтральности можно представить в виде [242, 433]

где  мощность и квантовый выход люминесценции;
мощность и квантовый выход люминесценции;  интеграл Ферми-Дирака (3.18). Интегрирование в
интеграл Ферми-Дирака (3.18). Интегрирование в  проводится по
проводится по  соответственно.
соответственно.
Величины  связаны между собой законами сохранения энергии и импульса и однозначно определяются частотой испускаемого света:
связаны между собой законами сохранения энергии и импульса и однозначно определяются частотой испускаемого света:

Коэффициент поглощения на произвольной частоте и мощность люминесценции  равны [242]
равны [242]

где

 интегральные коэффициенты Эйнштейна; — матричный элемент дипольного момента;
интегральные коэффициенты Эйнштейна; — матричный элемент дипольного момента;  -магнитная проницаемость в системе
-магнитная проницаемость в системе  [105];
[105];

—приведенная плотность состояний в зонах.
С учетом (14.17) — (14.21) уравнение баланса (14.15) легко представить в виде

При выводе (14.22) сделано предположение, что квантовый выход люминесценции  в пределах полосы люминесценции не зависит от
в пределах полосы люминесценции не зависит от  Величина
Величина  в формуле (14.15) заменена на
в формуле (14.15) заменена на  и для краткости
и для краткости  обозначено через
обозначено через 
Уравнение электронейтральности решается в аналитическом виде только в двух случаях: а)  и б) полупроводник не
и б) полупроводник не
вырожден, так что функции Ферми-Дирака можно заменить экспонентами.
В первом случае из (3.18) и (14.16) находим

Выражение в квадратных скобках (14.18) равно — 1 для всех частот  и равно 1 для
и равно 1 для  где
где  -частота инверсии, в которой коэффициент поглощения обращается в нуль. Приравнивая показатели экспонент, получим
-частота инверсии, в которой коэффициент поглощения обращается в нуль. Приравнивая показатели экспонент, получим

Знаменатель под интегралом в (14.22) равен единице для всех  и обращается в бесконечность, если
и обращается в бесконечность, если  где
где

Поэтому интеграл в (14.22) равен 

Из (14.22) и (14.25) следует

Формулы (14.26) справедливы при  так как при их выводе предполагалось наличие вырожденных электронов и дырок в зонах. Они показывают, по какому закону при температуре абсолютного нуля движутся квазиуровни Ферми в зонах и частота инверсии
так как при их выводе предполагалось наличие вырожденных электронов и дырок в зонах. Они показывают, по какому закону при температуре абсолютного нуля движутся квазиуровни Ферми в зонах и частота инверсии  с ростом плотности потока возбуждающего света. При
с ростом плотности потока возбуждающего света. При  коэффициент поглощения соответственно равен к
коэффициент поглощения соответственно равен к 
Во втором случае, когда возбуждение недостаточно велико, чтобы вызвать вырождение электронов и дырок в зонах, 
 формулы (14.16), (14.18) и (14.22) можно заменить на более простые выражения [433]:
формулы (14.16), (14.18) и (14.22) можно заменить на более простые выражения [433]:

Определяя  из (14.27) и (14.28) и подставляя (14.29), приходим к следующему уравнению для к
из (14.27) и (14.28) и подставляя (14.29), приходим к следующему уравнению для к 

где параметр нелинейности

Решая (14.30), находим [433—435]

что по форме совпадает с (14.11). Однако параметр а имеет здесь другое значение, а формула (14.32) справедлива для модели параболических зон только при отсутствии вырождения.
Параметр нелинейности а однозначно определяет минимальные плотности возбуждающего потока, при которых становится заметным просветление полупроводника. Согласно (14.32), при  Следовательно, коэффициент поглощения уменьшается на 3% от исходного, когда
Следовательно, коэффициент поглощения уменьшается на 3% от исходного, когда 
Как видно из (14.31), параметр нелинейности не зависит от квадрата матричного элемента перехода. Поэтому если время жизни возбужденного состояния определяется главным
образом оптическими переходами, а безызлучательная рекомбинация слабо влияет на  то параметр нелинейности практически не зависит от
то параметр нелинейности практически не зависит от  Порядок величины а определяется прежде всего шириной запрещенной зоны, частотой возбуждения и температурой. Нарушения закона Бугера легче всего наблюдать в полупроводниках с небольшой шириной запрещенной зоны, поскольку
Порядок величины а определяется прежде всего шириной запрещенной зоны, частотой возбуждения и температурой. Нарушения закона Бугера легче всего наблюдать в полупроводниках с небольшой шириной запрещенной зоны, поскольку  Аналогичная закономерность была установлена и для квантовомеханических систем с дискретными уровнями энергии (§ 13).
Аналогичная закономерность была установлена и для квантовомеханических систем с дискретными уровнями энергии (§ 13).
При  так как в этой модели поглощение отсутствует. С увеличением
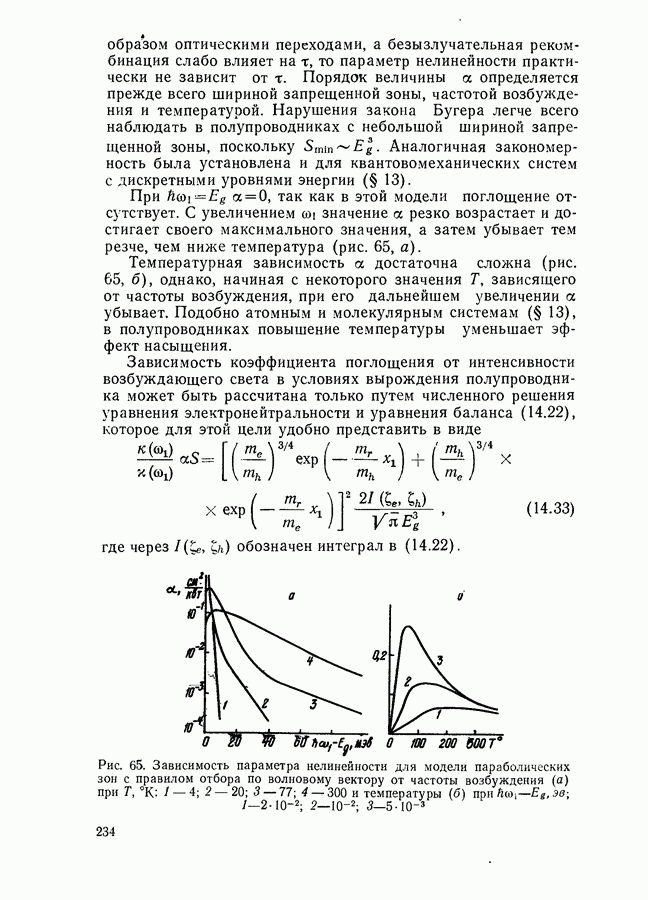
так как в этой модели поглощение отсутствует. С увеличением  значение а резко возрастает и достигает своего максимального значения, а затем убывает тем резче, чем ниже температура (рис. 65, а).
значение а резко возрастает и достигает своего максимального значения, а затем убывает тем резче, чем ниже температура (рис. 65, а).
Температурная зависимость а достаточна сложна (рис. 65, б), однако, начиная с некоторого значения  зависящего от частоты возбуждения, при его дальнейшем увеличении а убывает. Подобно атомным и молекулярным системам (§ 13), в полупроводниках повышение температуры уменьшает эффект насыщения.
зависящего от частоты возбуждения, при его дальнейшем увеличении а убывает. Подобно атомным и молекулярным системам (§ 13), в полупроводниках повышение температуры уменьшает эффект насыщения.
Зависимость коэффициента поглощения от интенсивности возбуждающего света в условиях вырождения полупроводника может быть рассчитана только путем численного решения уравнения электронейтральности и уравнения баланса (14.22), которое для этой цели удобно представить в виде

где через  обозначен интеграл в (14.22).
обозначен интеграл в (14.22).

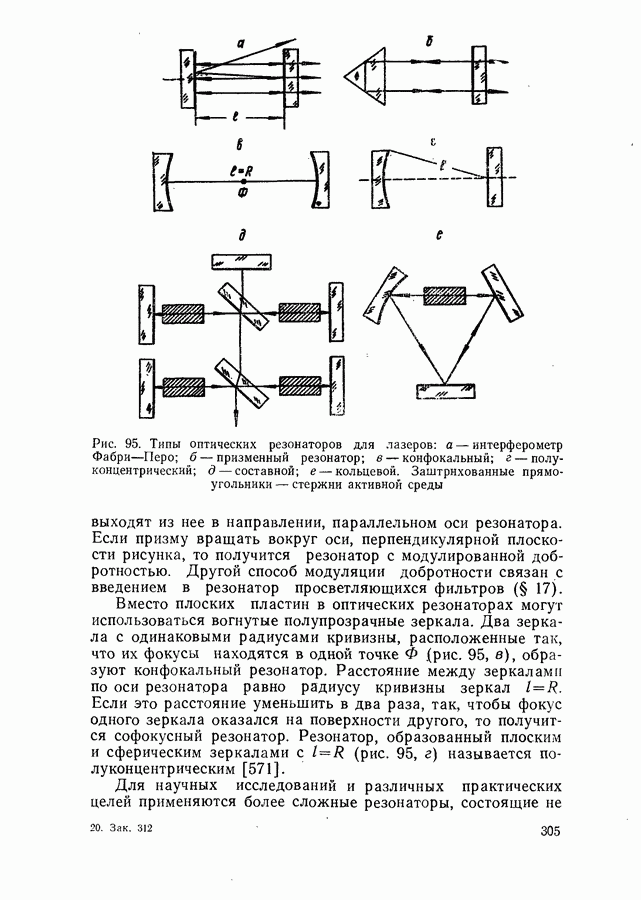
Рис. 65. Зависимость параметра нелинейности для модели параболических зон с правилом отбора по волновому вектору от частоты возбуждения (а) при  и температуры (б) при
и температуры (б) при 

Рис. 66. Номограммы—решения уравнения (14.16). Цифры на кривых — величина отношения 
Графики зависимости  от
от  для собственных и компенсированных полупроводников, построенные на основаниях решения уравнения электронейтральности, показаны на рис. 66 [242]. Для
для собственных и компенсированных полупроводников, построенные на основаниях решения уравнения электронейтральности, показаны на рис. 66 [242]. Для  получается прямая линия
получается прямая линия  Чем больше отношение
Чем больше отношение  тем дальше в область отрицательных значений заходит при
тем дальше в область отрицательных значений заходит при  Линейная зависимость между и
Линейная зависимость между и  при тнфте отсутствует. Поэтому результаты, которые иногда в теории получают, полагая
при тнфте отсутствует. Поэтому результаты, которые иногда в теории получают, полагая  могут качественно отличаться от зависимостей, справедливых для реальных полупроводников, где, как правило,
могут качественно отличаться от зависимостей, справедливых для реальных полупроводников, где, как правило,  .
.
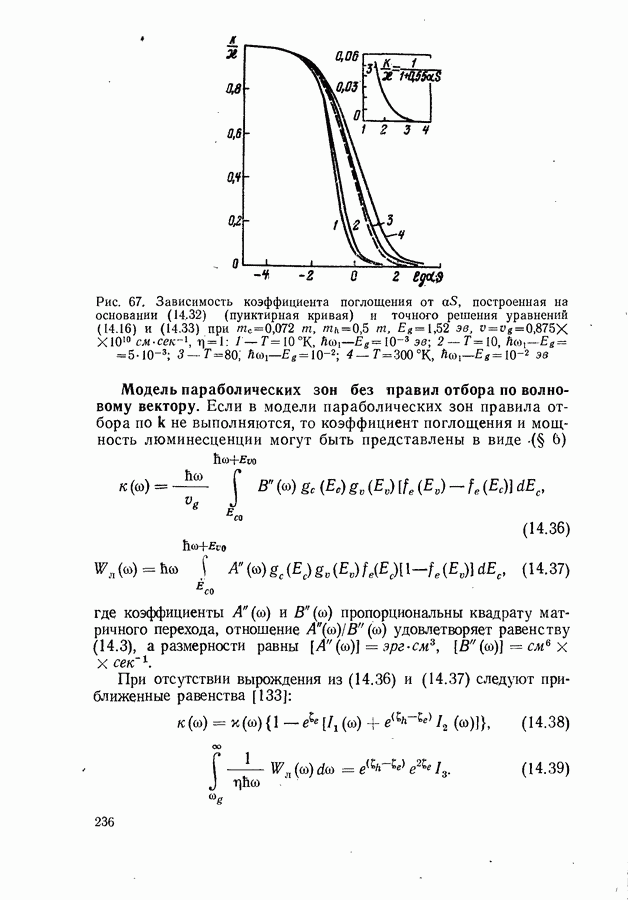
На рис. 67 приведены графики функции  построенные на основании точных решений уравнений (14.16) и (14.33). Там же для сравнения показана зависимость к от
построенные на основании точных решений уравнений (14.16) и (14.33). Там же для сравнения показана зависимость к от  даваемая формулой (14.32) (пунктирная кривая). Характерно, что все сплошные кривые не только сливаются с пунктирной в области малых значений
даваемая формулой (14.32) (пунктирная кривая). Характерно, что все сплошные кривые не только сливаются с пунктирной в области малых значений  но и в целом мало отличаются от нее по форме. Это означает, что переход от невырожденного полупроводника к вырожденному хорошо передается формулой (14.32). В полном соответствии с этой формулой
но и в целом мало отличаются от нее по форме. Это означает, что переход от невырожденного полупроводника к вырожденному хорошо передается формулой (14.32). В полном соответствии с этой формулой  для невырожденного полупроводника и
для невырожденного полупроводника и  в случае вырождения, где
в случае вырождения, где  небольшое изменение
небольшое изменение 
В области больших значений  любую кривую (рис. 67) можно аппроксимировать графиком функции
любую кривую (рис. 67) можно аппроксимировать графиком функции  Значение а может быть как больше, так и меньше а. Например, для кривых 2 и 3 а соответственно равно 8,45 а и 0,55 а.
Значение а может быть как больше, так и меньше а. Например, для кривых 2 и 3 а соответственно равно 8,45 а и 0,55 а.
Указанная зависимость к от  справедлива для всех без исключения веществ, у которых мощность поглощения
справедлива для всех без исключения веществ, у которых мощность поглощения  стремится к конечному пределу при
стремится к конечному пределу при  Действительно, из условия
Действительно, из условия

следует

Такой же вывод для частного случая сделан в работе [439].

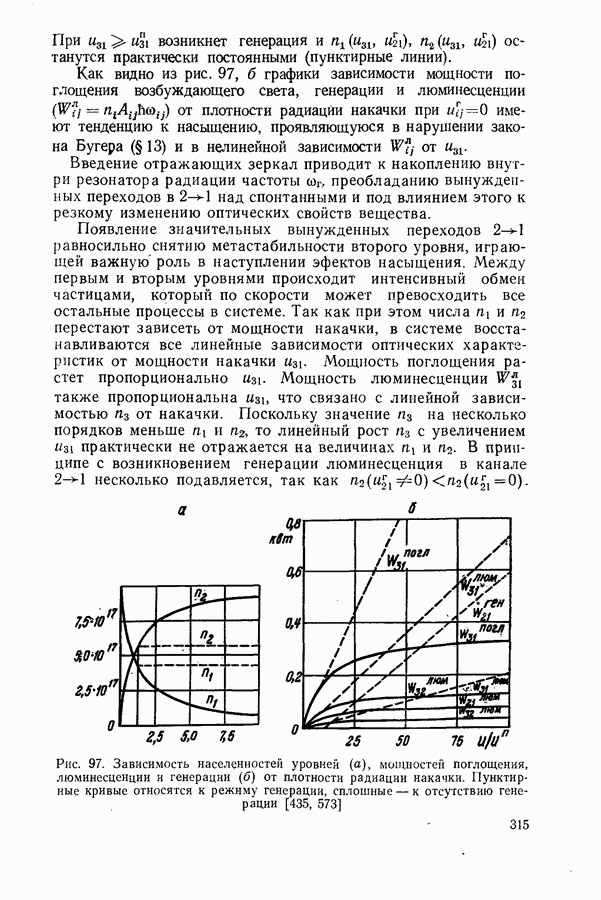
Рис. 67. Зависимость коэффициента поглощения от  построенная на основании (14,32) (пунктирная кривая) и точного решения уравнений (14.16) и (14.33) при
построенная на основании (14,32) (пунктирная кривая) и точного решения уравнений (14.16) и (14.33) при 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
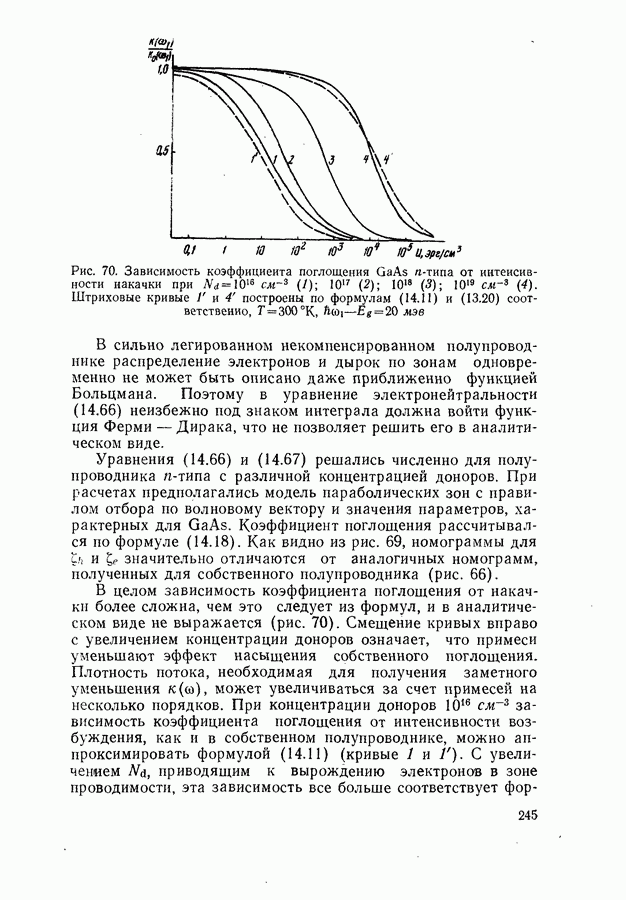
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
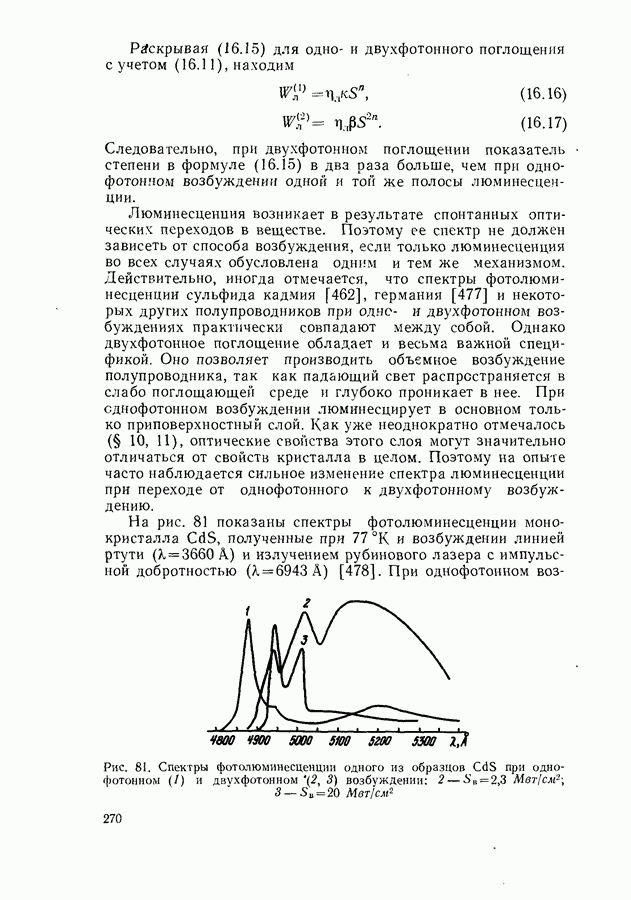
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
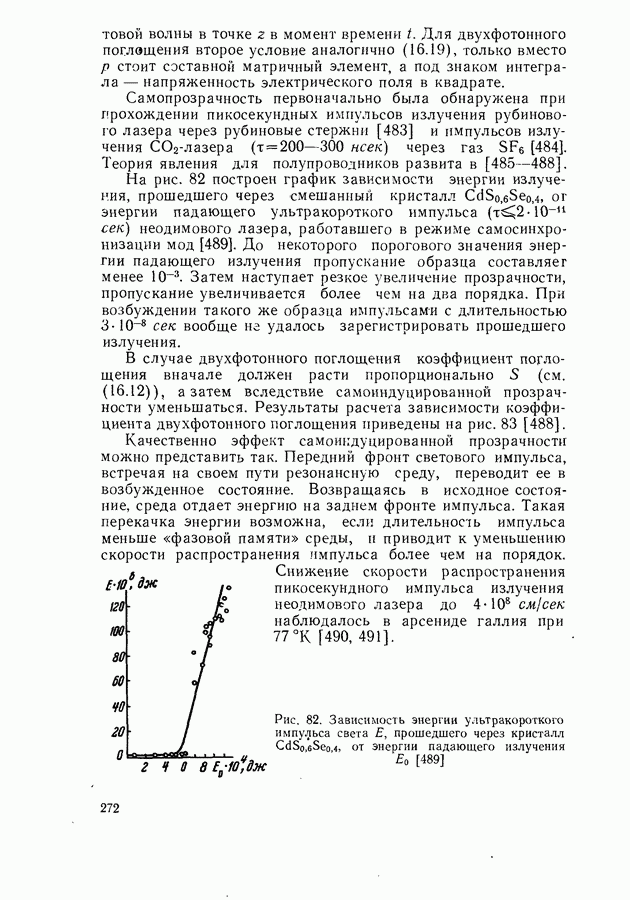
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
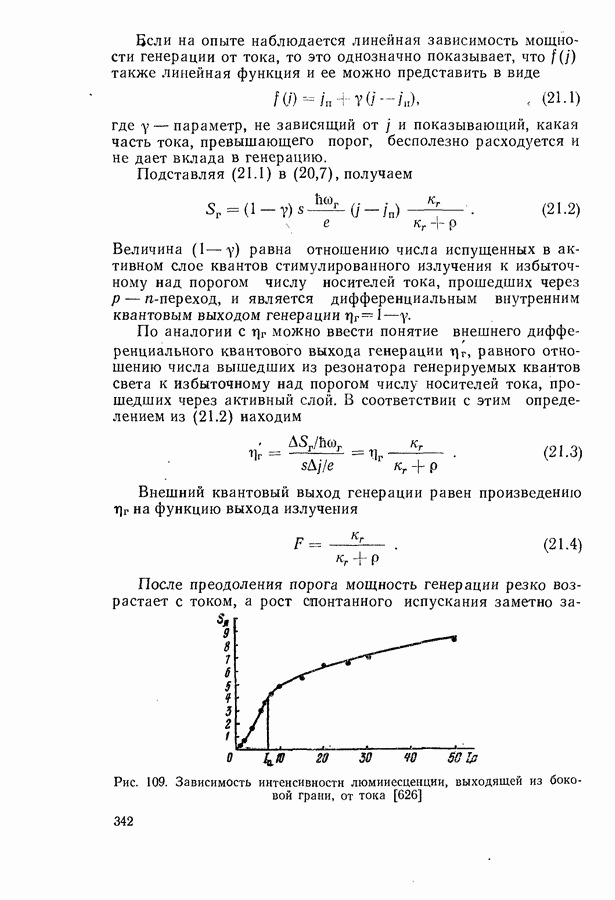
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.