| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
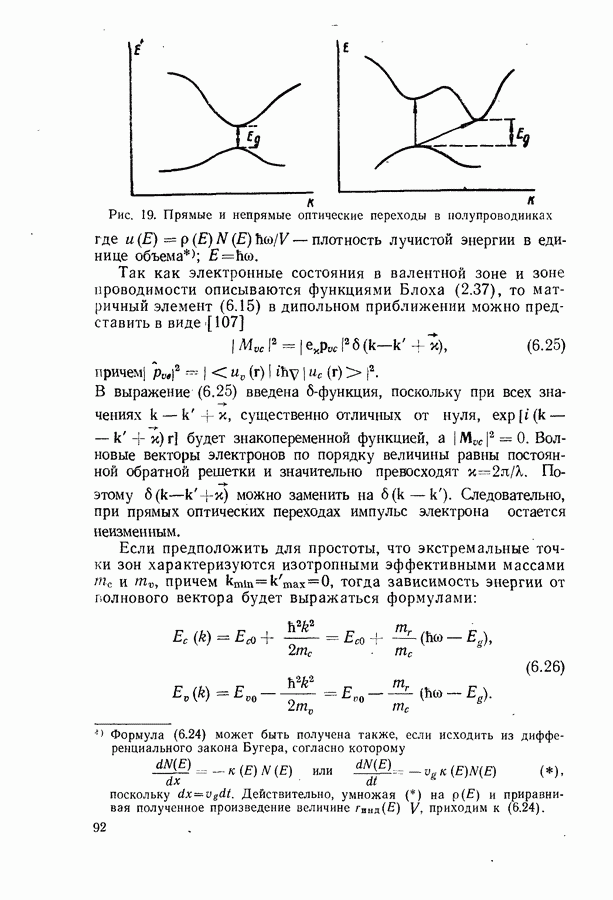
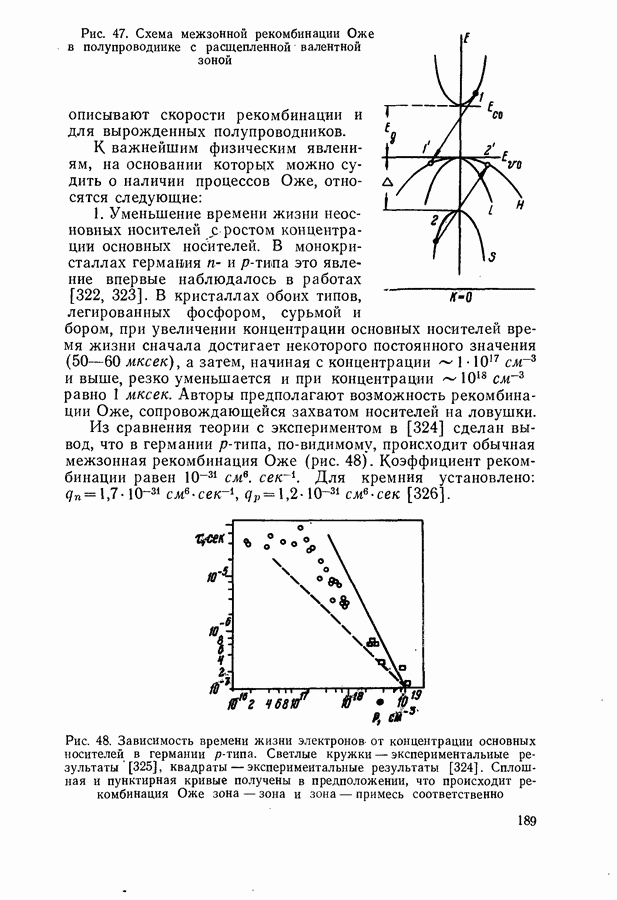
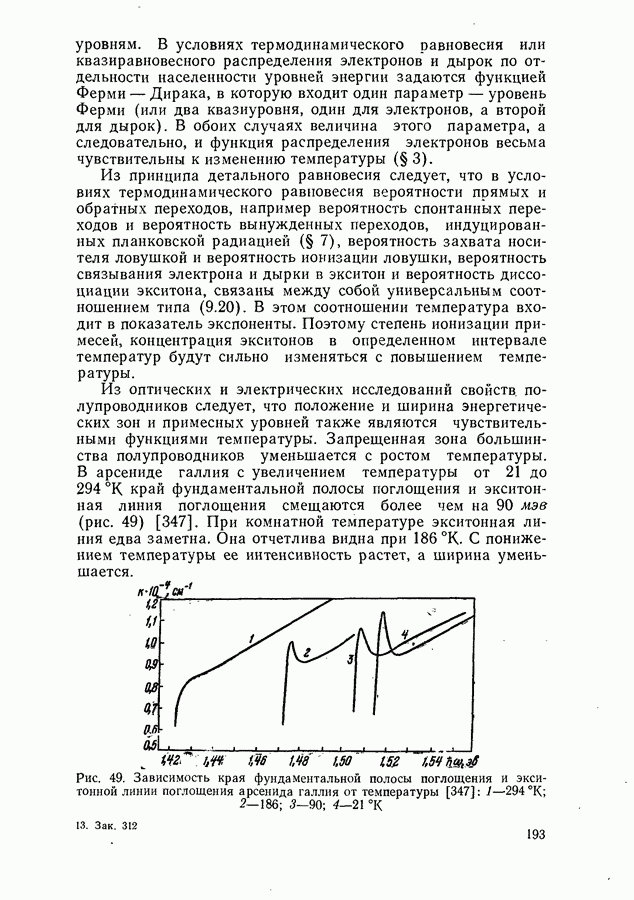
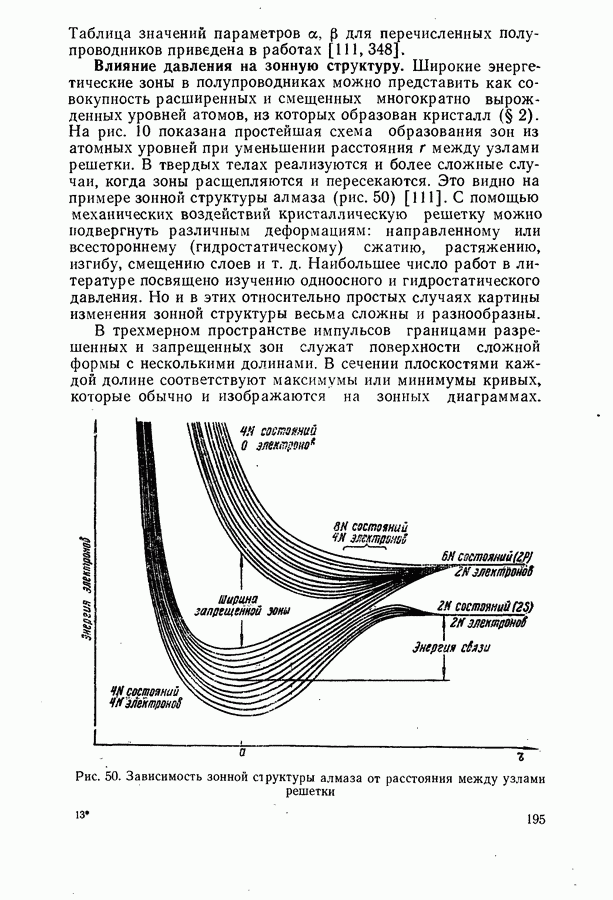
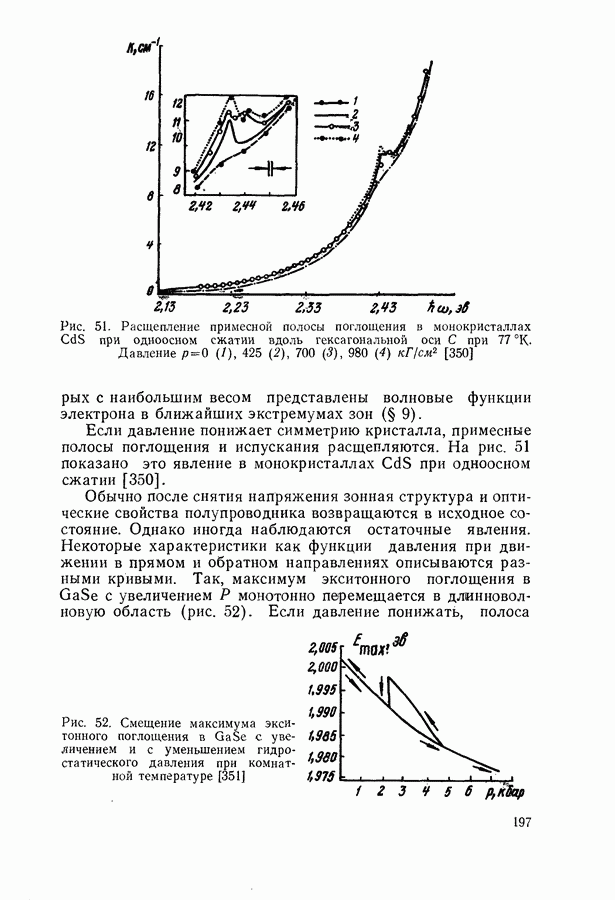
Магнетооптические явления.
Чтобы описать электронные состояния полупроводника, помещенного в магнитное поле, необходимо решить уравнение Шредингера, в котором содержится оператор взаимодействия зарядов с магнитным полем.
Это довольно сложная задача и решается она для каждого кристалла в отдельности. Отметим здесь кратко только наиболее общие закономерности. Более подробное изложение вопроса можно найти в работах [8, 98, 394—398].
Дискретные уровни примесных центров и экситонов в магнитном поле расщепляются и смещаются. Это проявляется на опыте в разнообразных магнетооптических явлениях. Спектральные линии поглощения и испускания расщепляются на  и
и  -компоненты, характеризующиеся линейной и круговой поляризацией (явление Зеемана). Характер расщепления и поляризация линий зависят от природы уровней и направления наблюдения.
-компоненты, характеризующиеся линейной и круговой поляризацией (явление Зеемана). Характер расщепления и поляризация линий зависят от природы уровней и направления наблюдения.
В радиочастотной области обнаруживается селективное поглощение электромагнитных волн, обусловленное
переходами между расщепленными подуровнями одного исходного уровня (электронный парамагнитный резонанс).
Плоскость поляризации линейно поляризованного света, проходящего в кристалле путь  вдоль силовых линий магнитного поля, поворачивается на угол
вдоль силовых линий магнитного поля, поворачивается на угол  (явление Фарадея):
(явление Фарадея):

где  показатели преломления для лучей света с правой и левой круговой поляризацией. В отсутствие магнитного поля
показатели преломления для лучей света с правой и левой круговой поляризацией. В отсутствие магнитного поля  Линейно поляризованный свет, распространяющийся перпендикулярно направлению магнитного поля с электрическим вектором, составляющим угол 45° с направлением магнитного поля, превращается в эллиптически поляризованный свет (эффект Фогта).
Линейно поляризованный свет, распространяющийся перпендикулярно направлению магнитного поля с электрическим вектором, составляющим угол 45° с направлением магнитного поля, превращается в эллиптически поляризованный свет (эффект Фогта).
Согласно классической электродинамике, угол  прямо пропорционален квадрату длины волны падающего света
прямо пропорционален квадрату длины волны падающего света  а сдвиг фаз между двумя циркулярно поляризованными лучами в эффекте Фогта
а сдвиг фаз между двумя циркулярно поляризованными лучами в эффекте Фогта  связан с
связан с  соотношением [8]:
соотношением [8]:

Определение циклотронной частоты  приводится ниже. Под действием магнитного поля в кристаллах вблизи линий поглощения возникают двойное лучепреломление и другие эффекты.
приводится ниже. Под действием магнитного поля в кристаллах вблизи линий поглощения возникают двойное лучепреломление и другие эффекты.
Энергетические зоны полупроводников в магнитном поле также претерпевают значительные изменения. Они расщепляются на подзоны Ландау. Так как этот эффект изменяет порог и мощность генерации (§ 20), остановимся на нем несколько подробнее.
Согласно классической механике, если электрон с эффективной массой  помещен в магнитное поле
помещен в магнитное поле  направленное по оси
направленное по оси  его движение в плоскости
его движение в плоскости  происходит по круговой орбите с угловой частотой [2]
происходит по круговой орбите с угловой частотой [2]

называемой циклотронной частотой. Квантовая механика приводит к таким же результатам, но налагает ограничения на радиусы орбит. Разрешены только такие орбиты, которым соответствует момент количества движения, кратный постоянной Планка  Точный квантовомеханический расчет движения электрона в магнитном поле был выполнен Л. Д. Ландау
Точный квантовомеханический расчет движения электрона в магнитном поле был выполнен Л. Д. Ландау
[399]. Теория Ландау относилась к свободным электронам, однако в дальнейшем было показано, что все ее выводы справедливы для электронов, движущихся в периодическом поле кристаллической решетки. Необходимо только массу электрона заменить эффективной массой.
В присутствии магнитного поля  уравнение Шредингера имеет вид
уравнение Шредингера имеет вид

Это уравнение можно преобразовать к уравнению движения гармонического осциллятора в плоскости  Оно имеет решения для дискретного набора эквидистантных уровней с номером
Оно имеет решения для дискретного набора эквидистантных уровней с номером  (уровни Ландау):
(уровни Ландау):

В то же время для движения в направлении оси  остается справедливым прежний закон дисперсии
остается справедливым прежний закон дисперсии

В направлении магнитного поля электрон, движется как свободная частица с эффективной массой  а в плоскости, перпендикулярной оси
а в плоскости, перпендикулярной оси  совершает гармонические колебания с циклотронной частотой
совершает гармонические колебания с циклотронной частотой 
Плотность состояний в зоне проводимости выражается формулой [400, 401]

Здесь суммирование распространяется на все целые положительные числа, для которых знаменатель в (12.19) выражается действительным числом. Для больших магнитных полей  велико и сумма (12.19) состоит из небольшого числа членов.
велико и сумма (12.19) состоит из небольшого числа членов.  суммирование в (12.19) можно заменить интегрированием, что приводит к обычному выражению для плотности состояний (3.8).
суммирование в (12.19) можно заменить интегрированием, что приводит к обычному выражению для плотности состояний (3.8).

Рис. 58. Функция плотности состояний в зоне проводимости без магнитного поля (пунктирная кривая) н в магнитном поле (сплошная разрывная кривая)
График функции (12.19) приведен на рис. 58. Там же для сравнения показана зависимость плотности состояний от энергии в отсутствие магнитного поля. Как видно из рисунка, исходные уровни энергии как бы сжимаются в узкие подзоны, расстояние между которыми равно 
Первая подзона  смещена относительно дна зоны проводимости вверх на величину
смещена относительно дна зоны проводимости вверх на величину  Потолок валентной зоны смещается вниз на величину
Потолок валентной зоны смещается вниз на величину  , где
, где  — циклотронная частота для дырок.
— циклотронная частота для дырок.
В целом увеличение ширины запрещенной зоны в магнитном поле на основании (12.15) можно представить в виде

где  эффективные массы электрона и дырки.
эффективные массы электрона и дырки.
Если зона проводимости и валентная зона состоят из нескольких вырожденных или отщепленных подзон, то в каждой ветви зоны уровни Ландау образуются в соответствии со значением эффективной массы носителя. Если к тому же эффективные массы анизотропны, то наложение магнитного поля приводит к необычайно сложной зонной структуре [395, 396].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
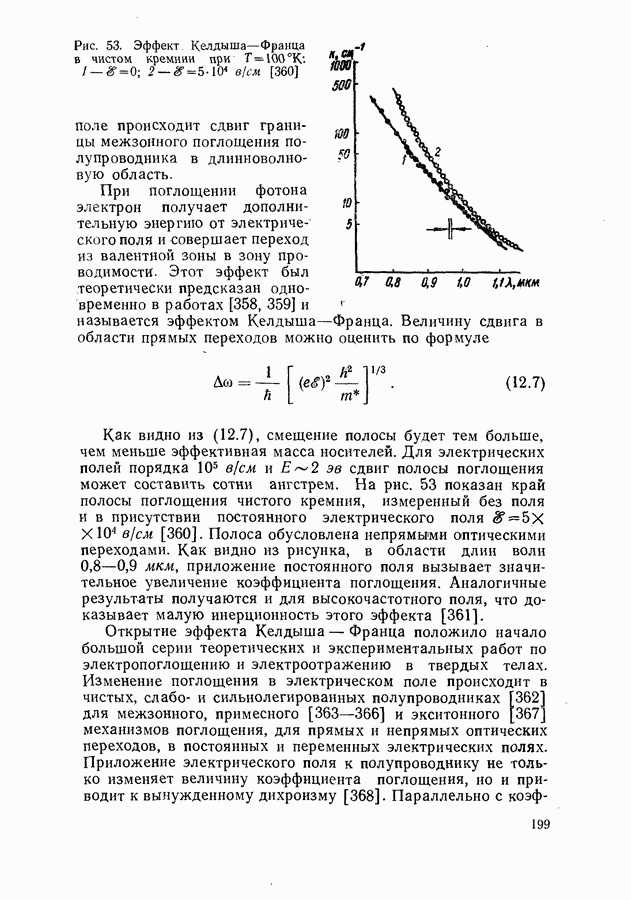
- Эффект Келдыша-Франца.
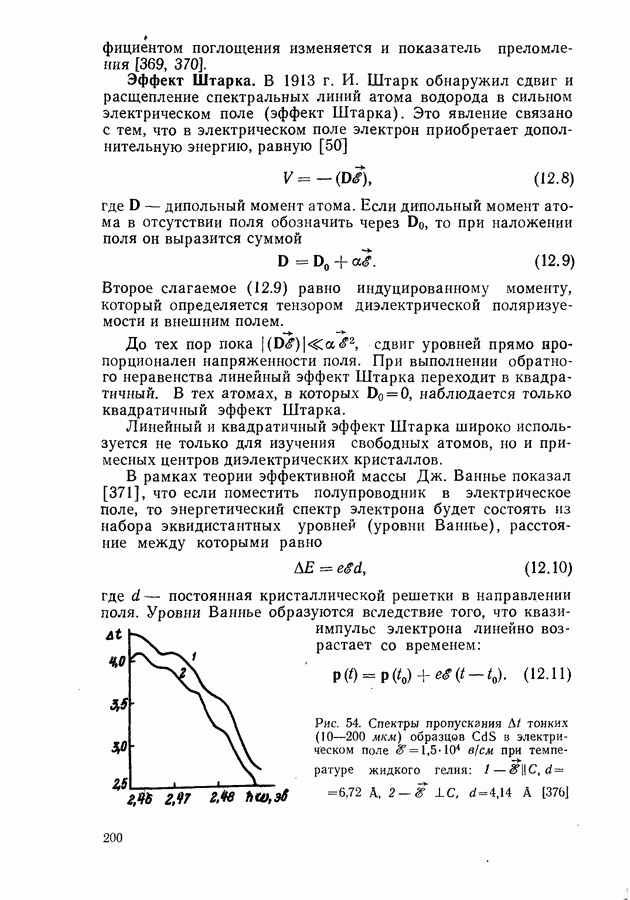
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
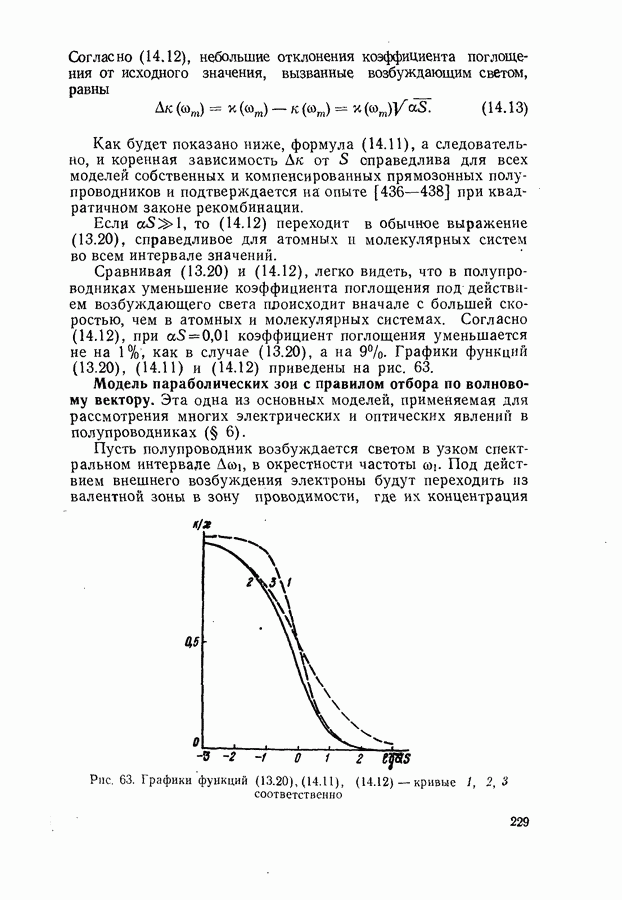
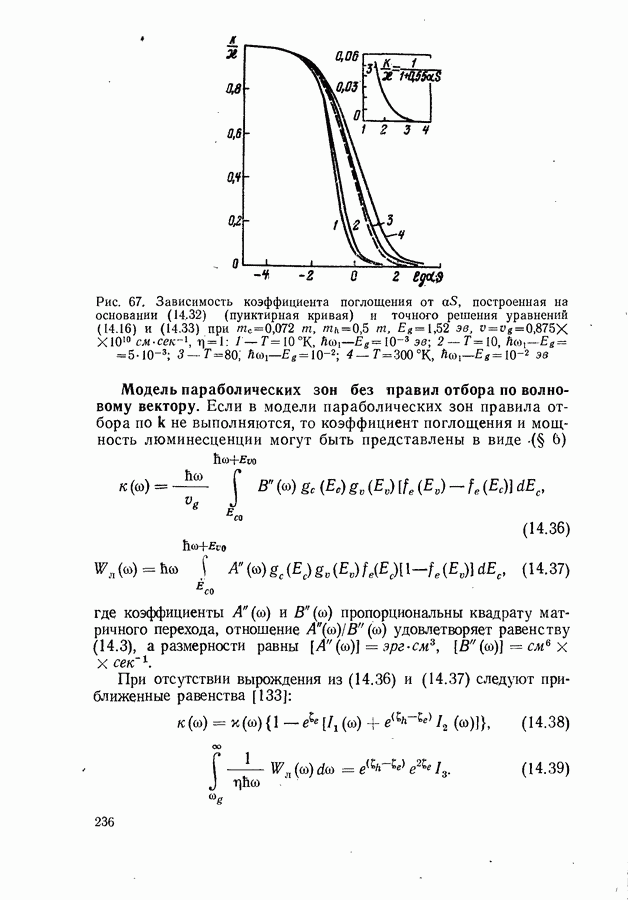
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
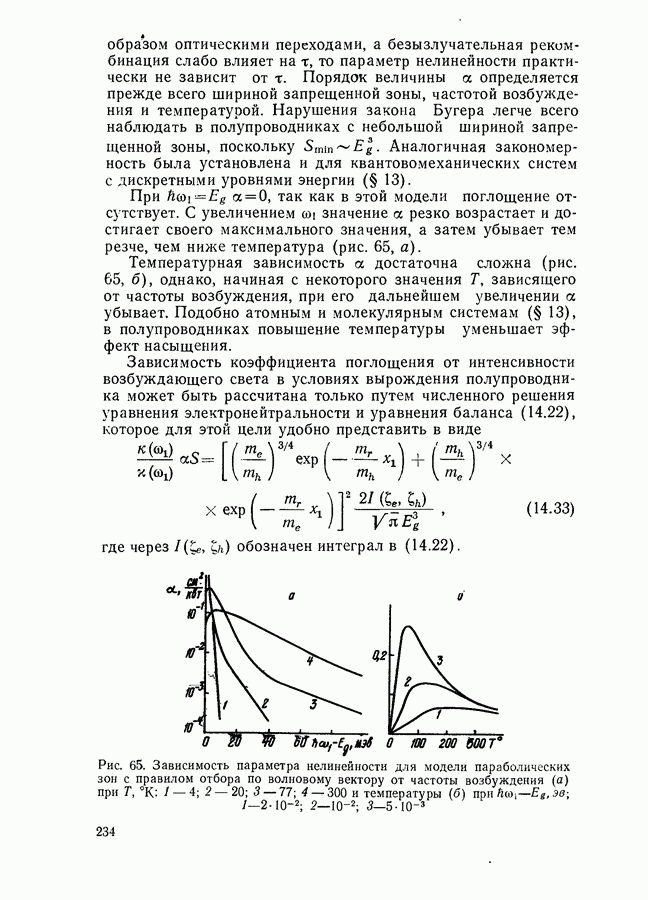
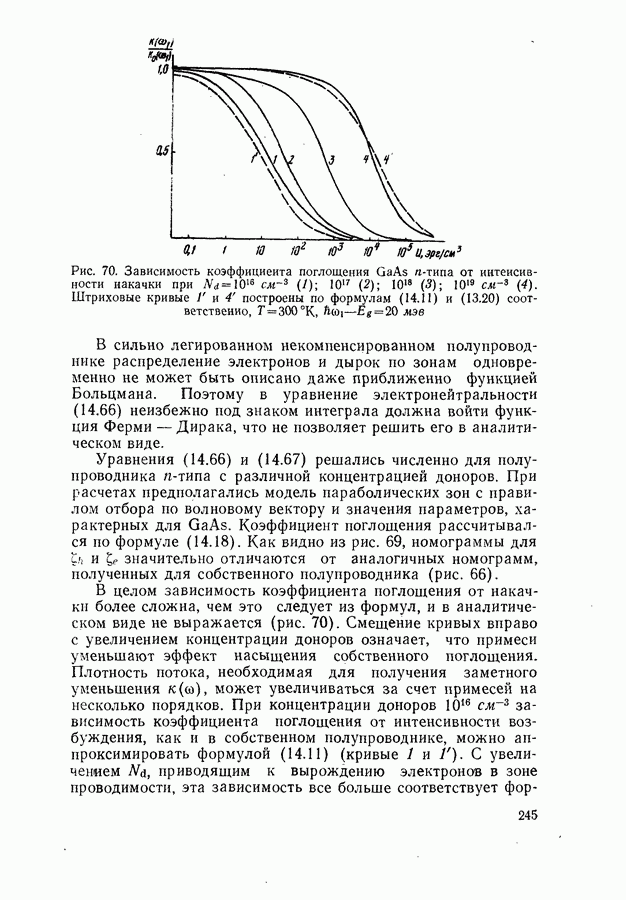
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
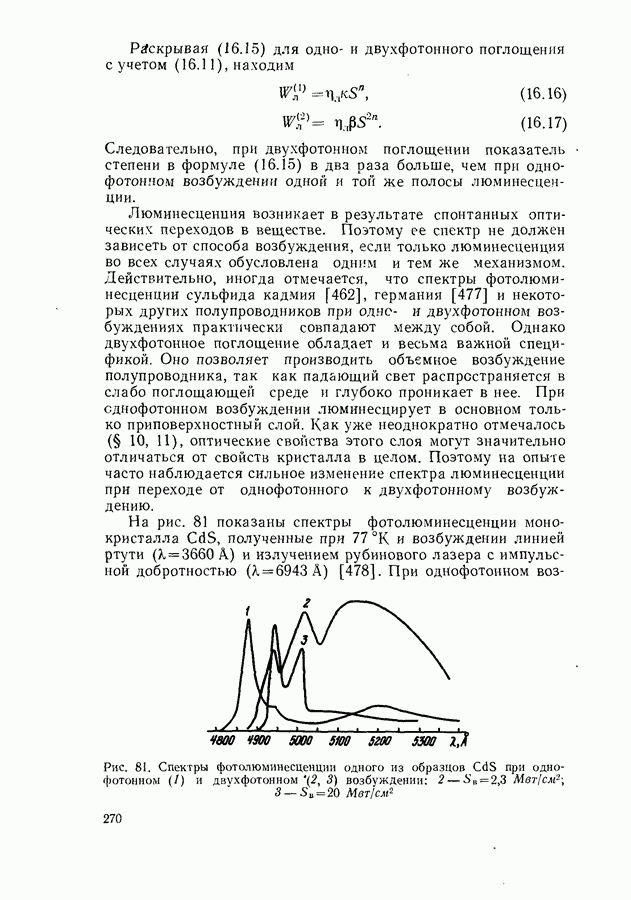
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
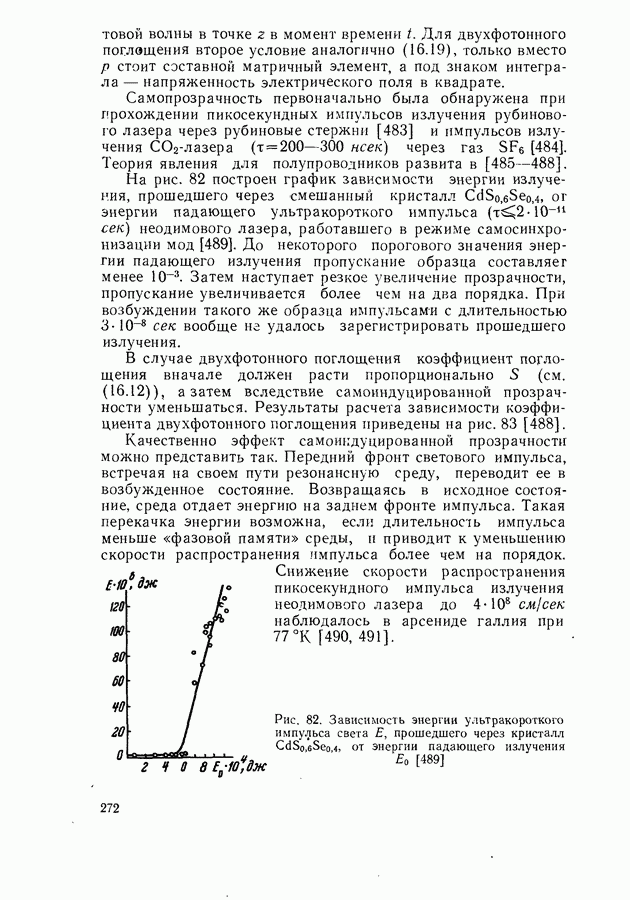
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
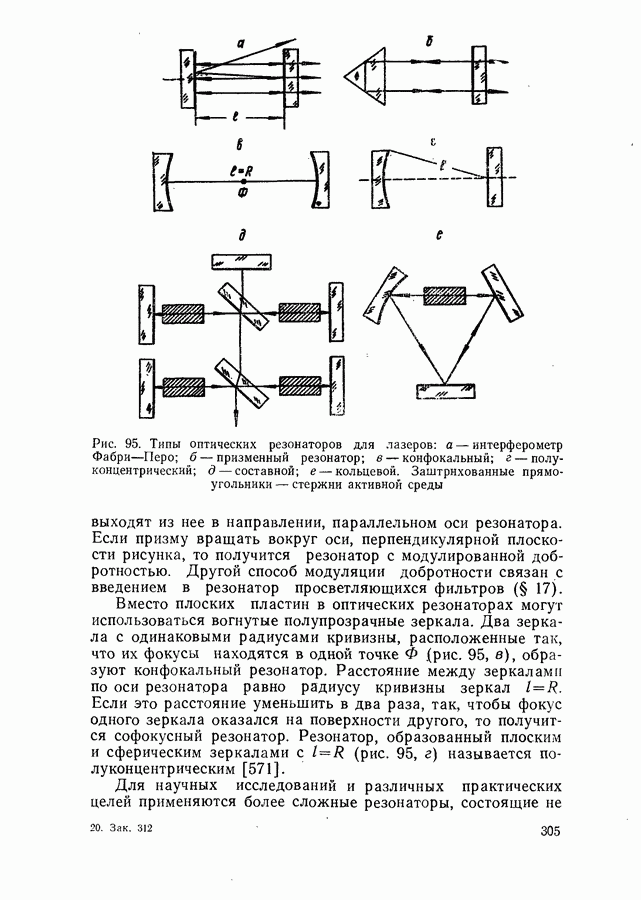
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.