| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
Оптические переходы электронов и дырок в пределах одной зоны (подзоны).
Изменение энергии электрона и дырки в пределах одной разрешенной зоны энергии или одной подзоны (если зона вырождена и состоит из нескольких подзон), как правило, сопровождается изменением импульса носителя заряда. Величина этого изменения значительно больше импульса световых квантов. Поэтому свободные носители в идеальном кристалле, где отсутствует их рассеяние в соответствии с законами сохранения энергии и импульса не могли бы поглощать электромагнитное излучение. Однако в реальном кристалле всегда имеются определенные дефекты, взаимодействие с которыми изменяет импульс электрона. В результате взаимодействия свободных носителей с электромагнитным полем и дефектами кристалла становятся возможными их непрямые оптические переходы в пределах одной зоны, приводящие к поглощению инфракрасного излучения.
Так как возможны различные механизмы рассеяния электронов в кристалле, то в общем случае коэффициент поглощения свободными носителями выражается суммой

Здесь  — коэффициенты поглощения, обусловленного рассеянием электронов на акустических фононах, на оптических фононах и на ионизированных примесных центрах.
— коэффициенты поглощения, обусловленного рассеянием электронов на акустических фононах, на оптических фононах и на ионизированных примесных центрах.
Величина  связана с рассеянием электронов на более сложных дефектах, которые могут образоваться при выращивании кристаллов, в результате внедрения примесей в решетку, при механической обработке поверхности, под воздействием радиации больших энергий и т. д. Сложные дефекты весьма разнообразны, поэтому
связана с рассеянием электронов на более сложных дефектах, которые могут образоваться при выращивании кристаллов, в результате внедрения примесей в решетку, при механической обработке поверхности, под воздействием радиации больших энергий и т. д. Сложные дефекты весьма разнообразны, поэтому  будет отличаться не только количественно, но и качественно для каждого конкретного полупроводника. Необходимость учета
будет отличаться не только количественно, но и качественно для каждого конкретного полупроводника. Необходимость учета  стала очевидной только в последнее время, и вопрос этот практически не изучен.
стала очевидной только в последнее время, и вопрос этот практически не изучен.
В высококачественных собственных полупроводниках концентрации ионизированных примесей и дефектов пренебрежимо малы и основную роль играет рассеяние электронов на колебаниях решетки. Напомним, что во всяком кристалле имеются три ветви акустических колебаний и  ветвей оптических колебаний, где
ветвей оптических колебаний, где  число атомов в элементарной ячейке кристалла. В одноатомных кристаллах, таких, как натрий и рубидий, на элементарную ячейку кристалла приходится один атом, и поэтому оптические колебания отсутствуют. Современная технология позволяет получать эти кристаллы такой высокой степени совершенства, что на них можно изучать в чистом виде рассеяние электронов на акустических фононах. Поэтому величина как изучена наиболее подробно.
число атомов в элементарной ячейке кристалла. В одноатомных кристаллах, таких, как натрий и рубидий, на элементарную ячейку кристалла приходится один атом, и поэтому оптические колебания отсутствуют. Современная технология позволяет получать эти кристаллы такой высокой степени совершенства, что на них можно изучать в чистом виде рассеяние электронов на акустических фононах. Поэтому величина как изучена наиболее подробно.
В полярных полупроводниках типа  имеются и оптические, и акустические ветви колебаний. Однако поскольку оптические колебания обладают большей частотой, чем акустические, то при понижении температуры они «вымораживаются» в первую очередь и основной вклад в поглощение излучения свободными носителями при низких температурах может быть обусловлен их рассеянием на акустических фононах. Слагаемое кжон либо
имеются и оптические, и акустические ветви колебаний. Однако поскольку оптические колебания обладают большей частотой, чем акустические, то при понижении температуры они «вымораживаются» в первую очередь и основной вклад в поглощение излучения свободными носителями при низких температурах может быть обусловлен их рассеянием на акустических фононах. Слагаемое кжон либо  становится определяющим в полупроводниках всех типов при сильном, а иногда и среднем легировании.
становится определяющим в полупроводниках всех типов при сильном, а иногда и среднем легировании.
Первая приближенная квантовомеханическая теория поглощения излучения свободными носителями была развита Фэном [262]. Автор учитывал рассеяние на акустических колебаниях решетки. Поэтому теория была применима к неполярным полупроводникам, таким, как кремний и германий. Применительно к германию она была детализирована и усовершенствована в работах [263—265].
Согласно [263], коэффициент поглощения при рассеянии носителей на акустических фононах равен

Как
где  объем элементарной ячейки решетки кристалла;
объем элементарной ячейки решетки кристалла;  диэлектрическая постоянная;
диэлектрическая постоянная;  приведенная масса атомов в ячейке,
приведенная масса атомов в ячейке,  скорость звука в кристалле;
скорость звука в кристалле;  энергия электронов; С — постоянная. Усреднение в (10.2) проводится по всем энергиям электронов.
энергия электронов; С — постоянная. Усреднение в (10.2) проводится по всем энергиям электронов.
Из (10.2) следует, что при заданной температуре  увеличивается с длиной волны по формуле [266]:
увеличивается с длиной волны по формуле [266]:

Постоянная  не зависит от длины волны возбуждающего света. Такая зависимость как от
не зависит от длины волны возбуждающего света. Такая зависимость как от  справедлива для квантов света, энергия которых значительно больше тепловой энергии электрона. Если же, наоборот,
справедлива для квантов света, энергия которых значительно больше тепловой энергии электрона. Если же, наоборот,

то для любого механизма рассеяния свободных носителей справедлива формула

полученная Друде в классической теории металлов. Здесь  время релаксации электронов по импульсу.
время релаксации электронов по импульсу.
Общая формула для  справедливая для всех частот возбуждающего света, получена в [267] с использованием температурной функции Грина. В качестве частных случаев из нее следуют выражения, полученные ранее для
справедливая для всех частот возбуждающего света, получена в [267] с использованием температурной функции Грина. В качестве частных случаев из нее следуют выражения, полученные ранее для  Она дает также значение
Она дает также значение  для вырожденного распределения электронов.
для вырожденного распределения электронов.
Случай сильного фермиевского вырождения электронов, взаимодействующих с акустическими фононами, рассмотрен в работе [268]. Закон дисперсии для электронов предполагался изотропным и квадратичным. Учет непараболичности зон приводит к более сильной зависимости коэффициента поглощения от длины волны как при рассеянии на акустических фононах, так и при других механизмах рассеяния [269, 270].
Если свободные носители невырождены и рассеиваются на поляризационных оптических колебаниях и электрон-фононное взаимодействие слабое, то коэффициент поглощения выражается формулой [271]

где

 - функция Макдональда 1-го порядка;
- функция Макдональда 1-го порядка;  — энергия продольных оптических фононов,
— энергия продольных оптических фононов,

 статическая диэлектрическая проницаемость кристалла и безынерционная часть диэлектрической проницаемости; а
статическая диэлектрическая проницаемость кристалла и безынерционная часть диэлектрической проницаемости; а  действительная часть диэлектрической проницаемости.
действительная часть диэлектрической проницаемости.
При низких температурах, когда  коэффициент поглощения коп резко возрастает в области частот
коэффициент поглощения коп резко возрастает в области частот  Для частных случаев из (10.5) следуют простые выражения [271]:
Для частных случаев из (10.5) следуют простые выражения [271]:

Если свободные носители вырождены, то частотная зависимость  отличается от зависимости, даваемой формулой (10.5) в области низких частот возбуждения, где
отличается от зависимости, даваемой формулой (10.5) в области низких частот возбуждения, где  При выполнении обратного неравенства вновь получается выражение (10.8). Следовательно, если энергия возбуждающих квантов света значительно больше средней энергии электронов, то коэффициент поглощения свободными носителями при их рассеянии на оптических фононах приближенно равен
При выполнении обратного неравенства вновь получается выражение (10.8). Следовательно, если энергия возбуждающих квантов света значительно больше средней энергии электронов, то коэффициент поглощения свободными носителями при их рассеянии на оптических фононах приближенно равен

Аналогичный результат получен в [272].
В легированных полупроводниках наиболее важную роль играет рассеяние носителей на ионизированных примесях. Для концентрации примесей с зарядом  коэффициент поглощения равен [263]
коэффициент поглощения равен [263]


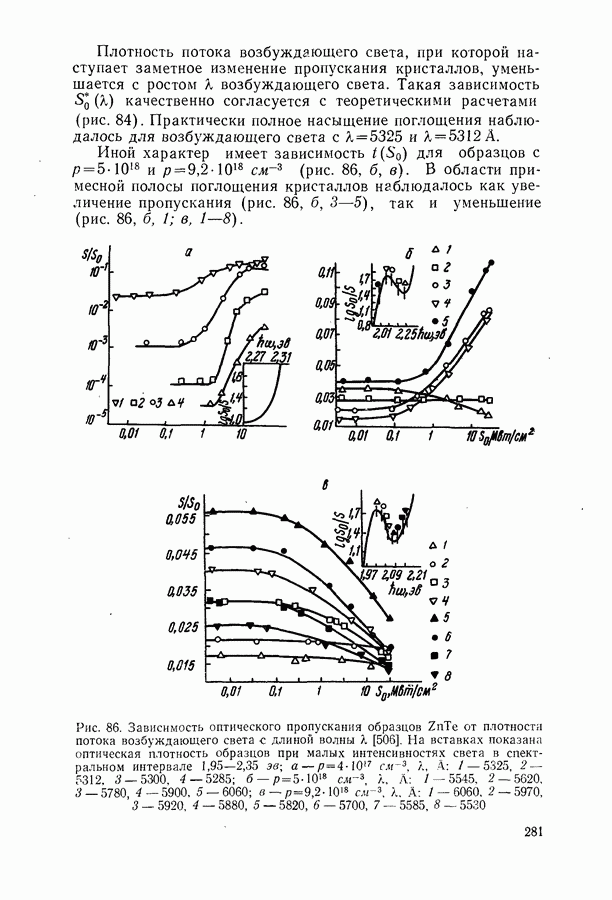
Рис. 38. Спектр поглощения монокристалла 
Различная зависимость коэффициента поглощения свободными носителями от частоты для  используется на опыте для определения механизма рассеяния электронов и дырок в полупроводниках. Этот метод оказался более универсальным, тонким и надежным, чем изучение температурной зависимости подвижности электронов, которое также иногда позволяет установить механизм рассеяния.
используется на опыте для определения механизма рассеяния электронов и дырок в полупроводниках. Этот метод оказался более универсальным, тонким и надежным, чем изучение температурной зависимости подвижности электронов, которое также иногда позволяет установить механизм рассеяния.
Детальное сопоставление теоретических и экспериментальных результатов по поглощению света свободными носителями в полупроводниках типа  проведено в работах [273—278]. В сильнолегированных кристаллах рассеянием носителей на акустических фононах можно пренебречь, так как основной вклад в поглощение инфракрасного света связан с их рассеянием на оптических колебаниях решетки и ионизованных примесях. Например, спектр поглощения
проведено в работах [273—278]. В сильнолегированных кристаллах рассеянием носителей на акустических фононах можно пренебречь, так как основной вклад в поглощение инфракрасного света связан с их рассеянием на оптических колебаниях решетки и ионизованных примесях. Например, спектр поглощения  легированного элементами VI группы:
легированного элементами VI группы:  Те в области
Те в области  можно аппроксимировать формулой [279]:
можно аппроксимировать формулой [279]:

В неполярных полупроводниках, таких, как кремний, германий, теллур, при небольшой концентрации примесей рассеяние свободных носителей происходит в основном на акустических фононах [263—265, 280—281].
В соединениях  как правило, основной вклад в поглощение света свободными носителями обусловлен рассеянием на оптических фононах [282—284]. В качестве примера на рис. 38 приведены спектры поглощения сернистого свинца в области
как правило, основной вклад в поглощение света свободными носителями обусловлен рассеянием на оптических фононах [282—284]. В качестве примера на рис. 38 приведены спектры поглощения сернистого свинца в области  снятые при температурах
снятые при температурах  [282]. Характерно, что образец обладает значительным фоновым поглощением, величина которого не зависит от температуры, а физическая природа не достаточно ясна. Резкий подъем кривых слева соответствует началу поглощения при межзонных переходах. Поглощение свободными носителями характеризуется плавными, но достаточно быстро поднимающимися отрезками кривых правее минимумов.
[282]. Характерно, что образец обладает значительным фоновым поглощением, величина которого не зависит от температуры, а физическая природа не достаточно ясна. Резкий подъем кривых слева соответствует началу поглощения при межзонных переходах. Поглощение свободными носителями характеризуется плавными, но достаточно быстро поднимающимися отрезками кривых правее минимумов.
Б. М. Вул с сотрудниками [285] установили, что в теллуриде кадмия  -типа при концентрации доноров
-типа при концентрации доноров  во всем интервале температур от 80 до
во всем интервале температур от 80 до  поглощение
поглощение
обусловлено взаимодействием с оптическими фононами. В образцах с  заметную роль играет рассеяние на ионизованных примесях. В некоторых образцах с малой подвижностью электронов экспериментальные результаты не укладываются в теоретические представления. В этой работе, по-видимому, впервые высказано предположение о возможности рассеяния электронов на дефектах более сложного типа, чем ионизованные примеси.
заметную роль играет рассеяние на ионизованных примесях. В некоторых образцах с малой подвижностью электронов экспериментальные результаты не укладываются в теоретические представления. В этой работе, по-видимому, впервые высказано предположение о возможности рассеяния электронов на дефектах более сложного типа, чем ионизованные примеси.
М. П. Лисица с сотрудниками [286] при изучении спектра инфракрасного поглощения GaAs также обратил внимание, что уменьшение толщины образцов сопровождается увеличением коэффициента поглощения и ослаблением зависимости  Этот эффект можно объяснить, если предположить, что коэффициент поглощения приповерхностного слоя отличается от коэффициента поглощения в объеме образца. При механической полировке в приповерхностном слое образуются сложные дефекты решетки, которые служат дополнительными центрами рассеяния. Рассеяние на крупных дефектах менее чувствительно к длине волны, чем рассеяние на фононах и точечных примесных центрах. Если выделить в чистом виде зависимость к от
Этот эффект можно объяснить, если предположить, что коэффициент поглощения приповерхностного слоя отличается от коэффициента поглощения в объеме образца. При механической полировке в приповерхностном слое образуются сложные дефекты решетки, которые служат дополнительными центрами рассеяния. Рассеяние на крупных дефектах менее чувствительно к длине волны, чем рассеяние на фононах и точечных примесных центрах. Если выделить в чистом виде зависимость к от  в приповерхностном слое, то она будет выражаться формулой
в приповерхностном слое, то она будет выражаться формулой  в то время как в объеме того же образца
в то время как в объеме того же образца  [286].
[286].
С таких позиций легко объяснить, почему в теллуриде кадмия при замене индия бромом в качестве легирующей примеси зависимость показателя степени, в которую возводится  в формулах типа (10.12), от температуры уменьшается, а от концентрации примеси увеличивается [287]. Бром в силу большей химической активности, чем индий, при внедрении в решетку способствует образованию более дефектной структуры кристалла. С понижением температуры роль колебаний решетки уменьшается, и в легированном полупроводнике рассеяние носителей будет происходить в основном на примесных центрах.
в формулах типа (10.12), от температуры уменьшается, а от концентрации примеси увеличивается [287]. Бром в силу большей химической активности, чем индий, при внедрении в решетку способствует образованию более дефектной структуры кристалла. С понижением температуры роль колебаний решетки уменьшается, и в легированном полупроводнике рассеяние носителей будет происходить в основном на примесных центрах.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
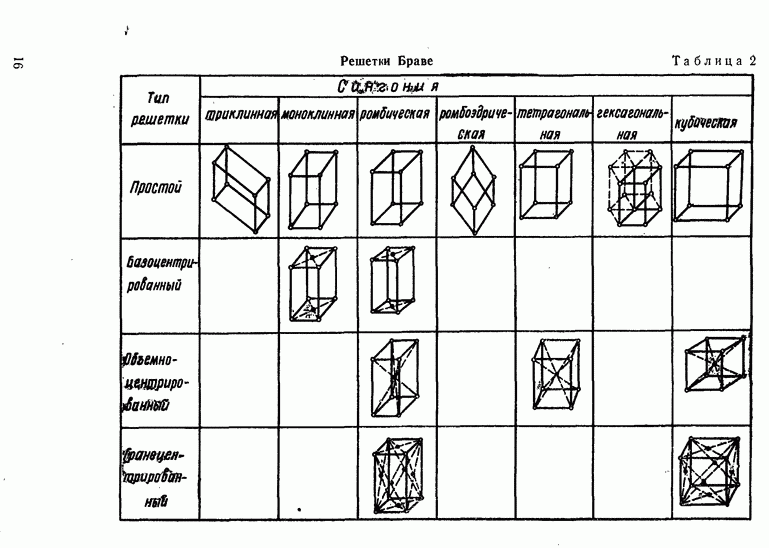
- Классификация кристаллических решеток.
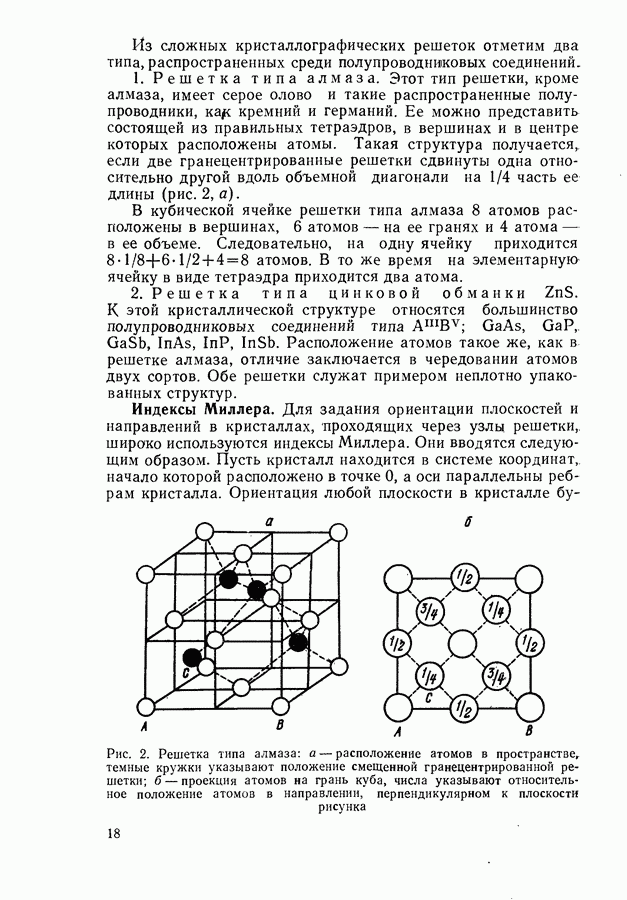
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
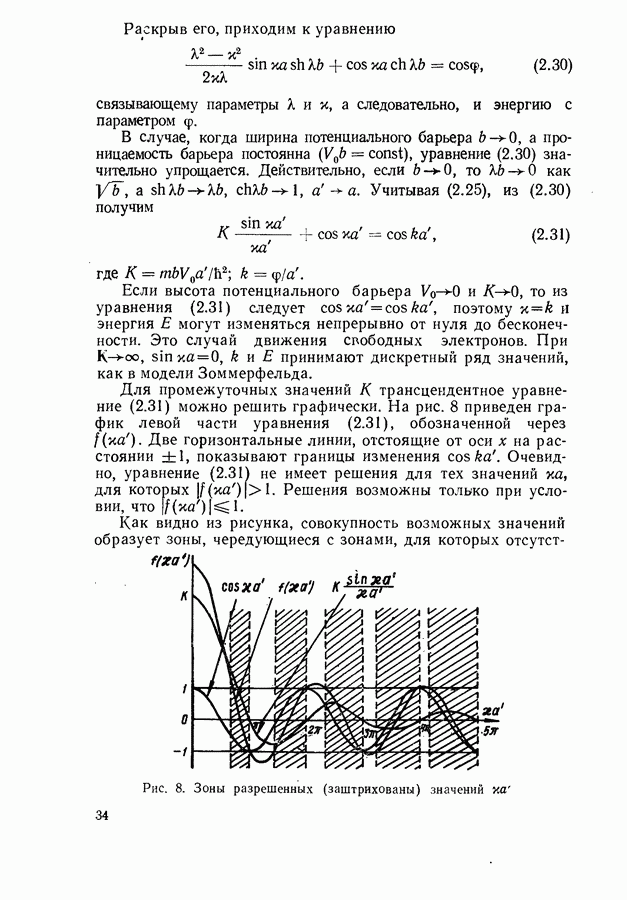
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
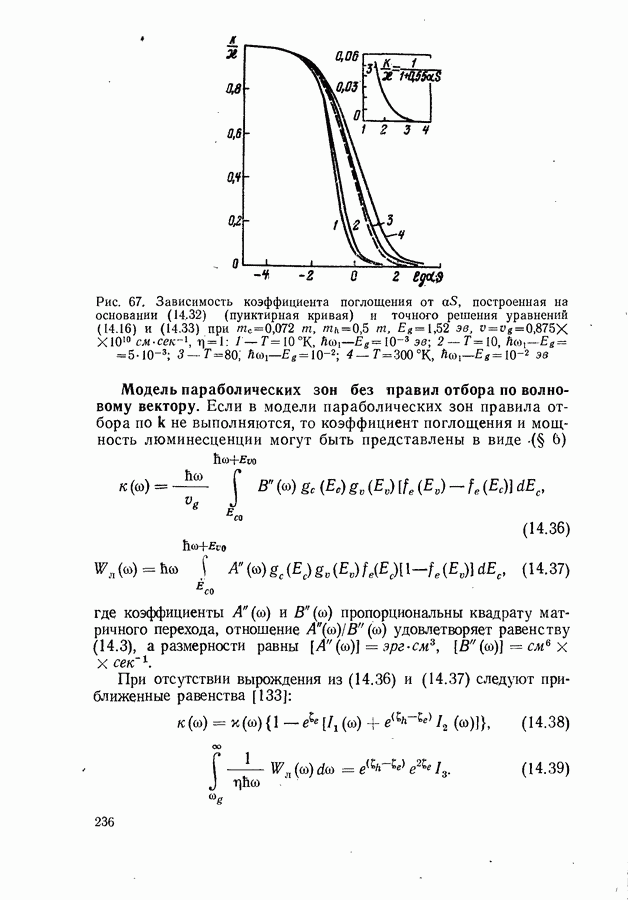
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
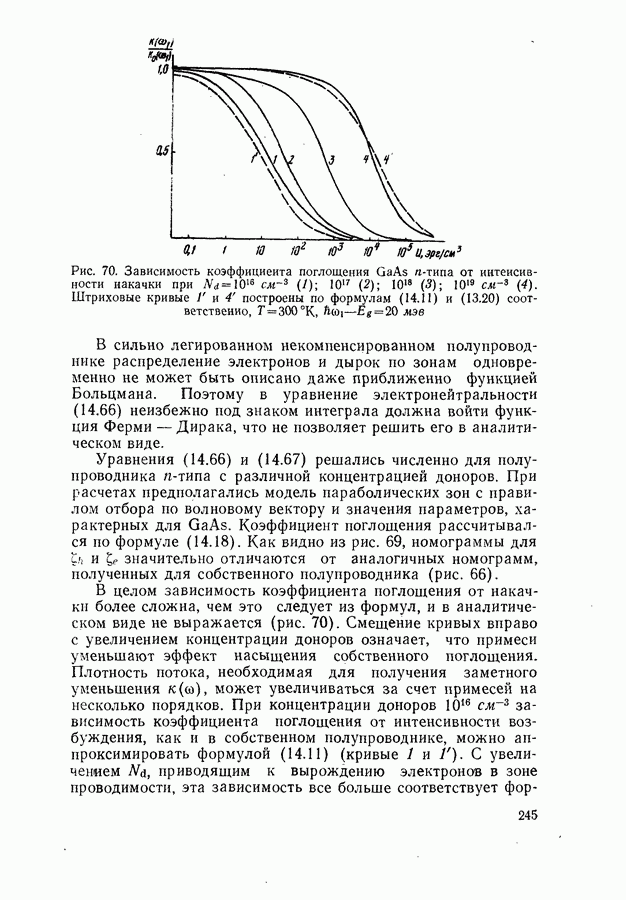
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
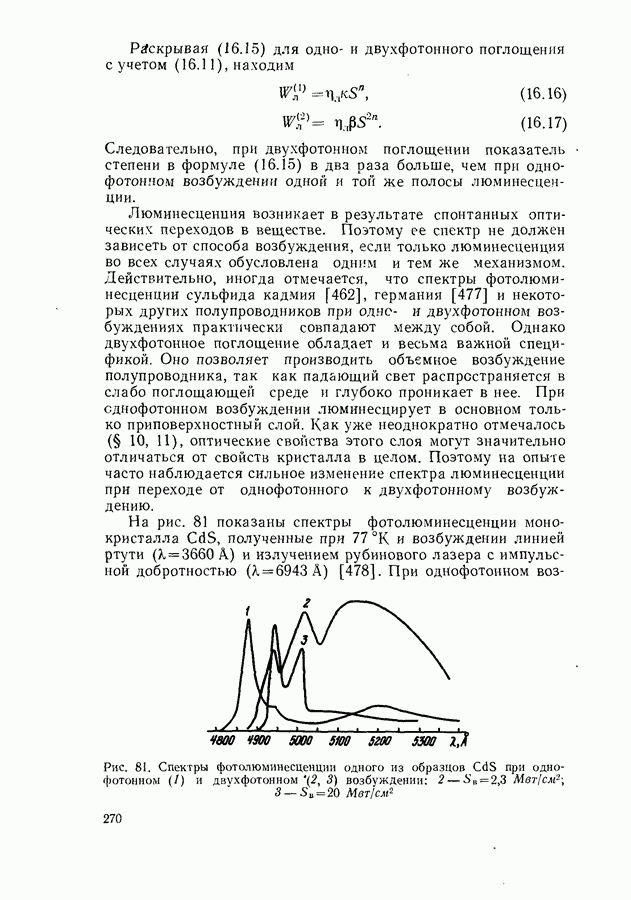
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
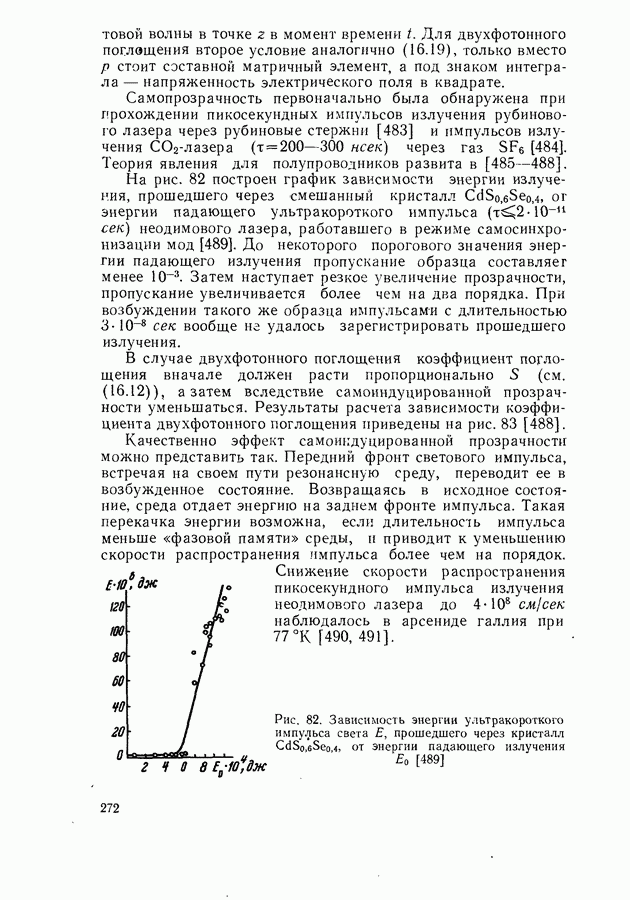
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
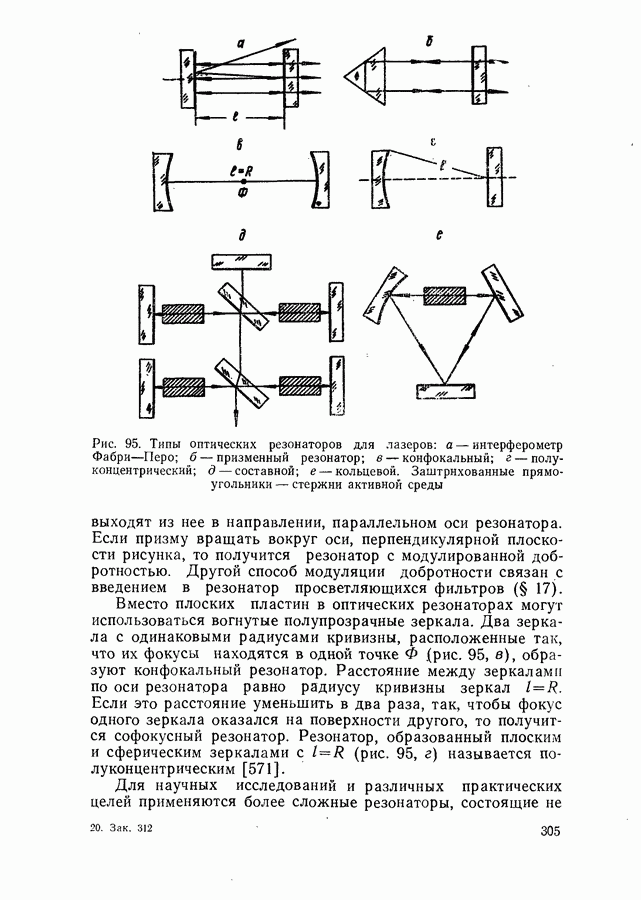
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
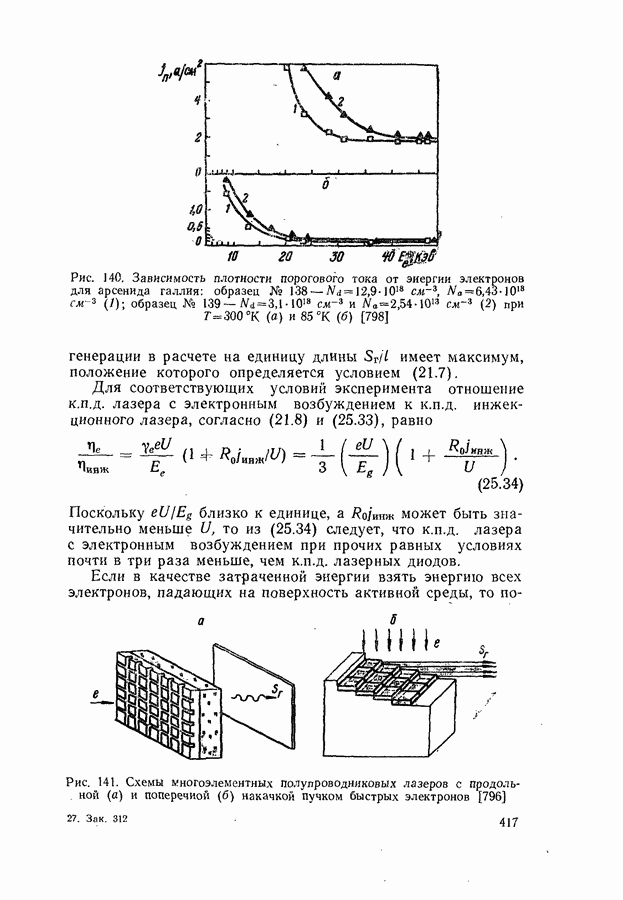
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
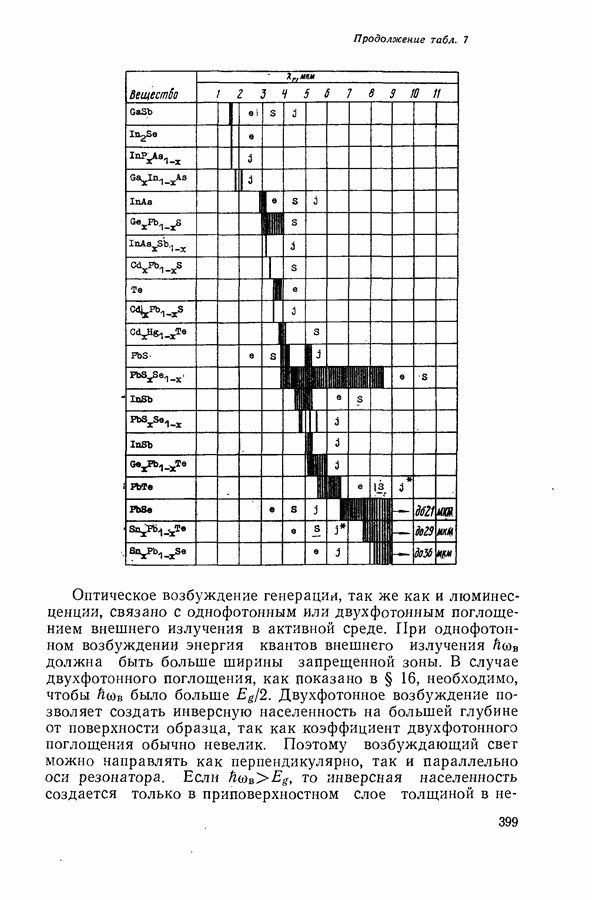
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
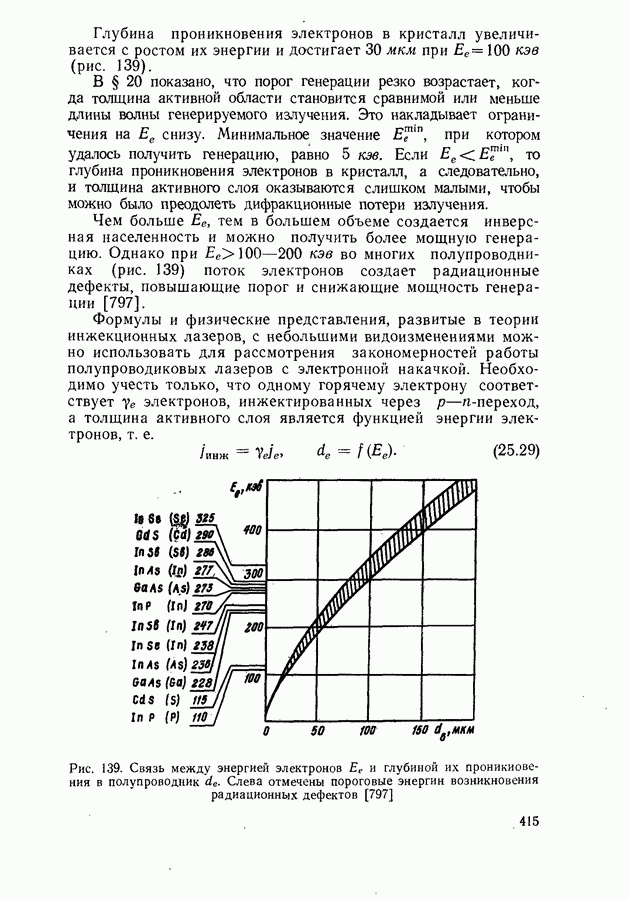
- Возбуждение генерации пучком быстрых электронов.